Thoughts on the Importance of Similitude and Multi-Axial Loads When Assessing the Durability and Damage Tolerance of Adhesively-Bonded Doublers and Repairs
Abstract
:1. Introduction
2. Materials and Methods
3. The Importance of Fatigue Testing under the True Operational Multi-Axial Stress State
3.1. Introduction
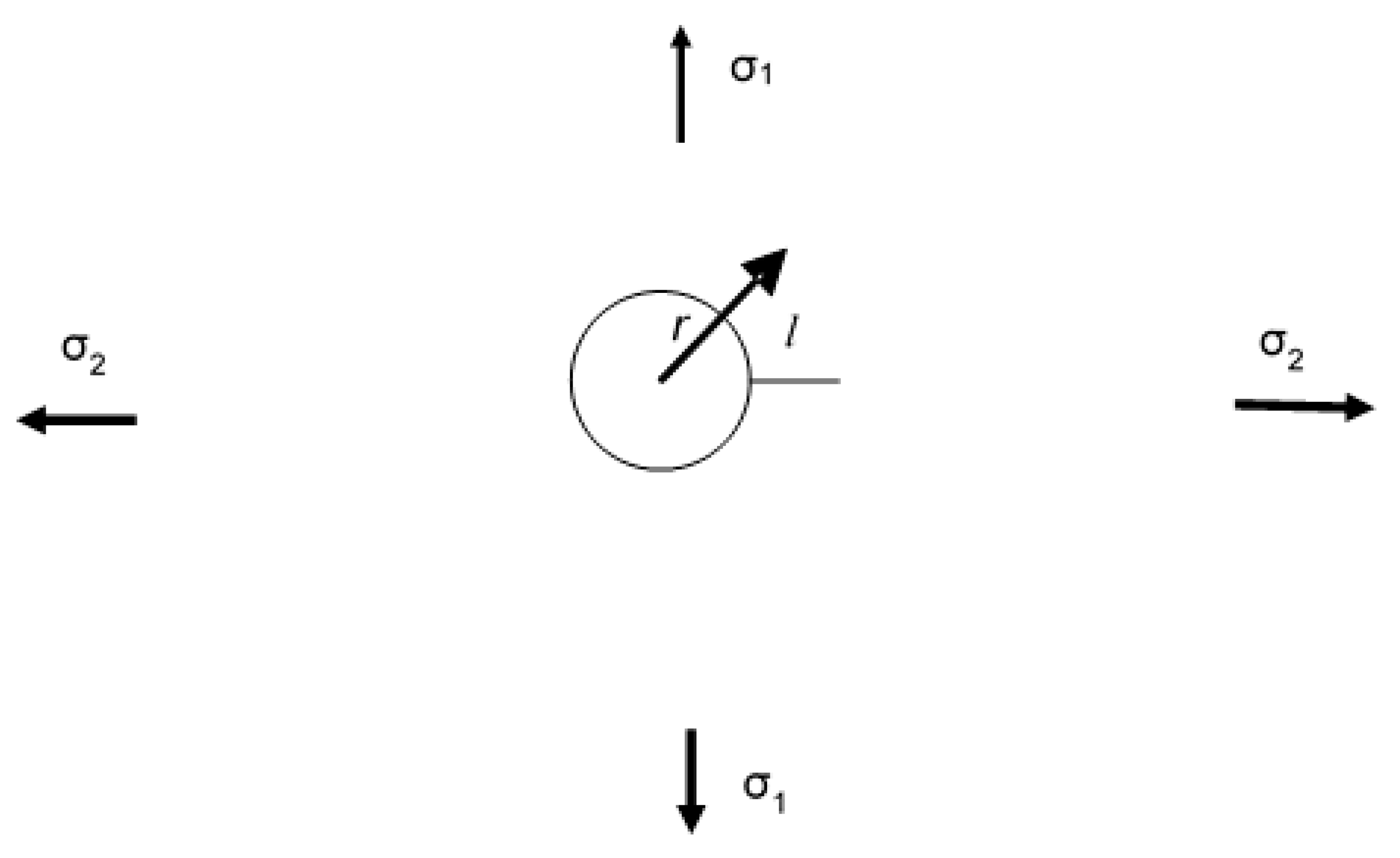
3.2. A Simple Worked Example
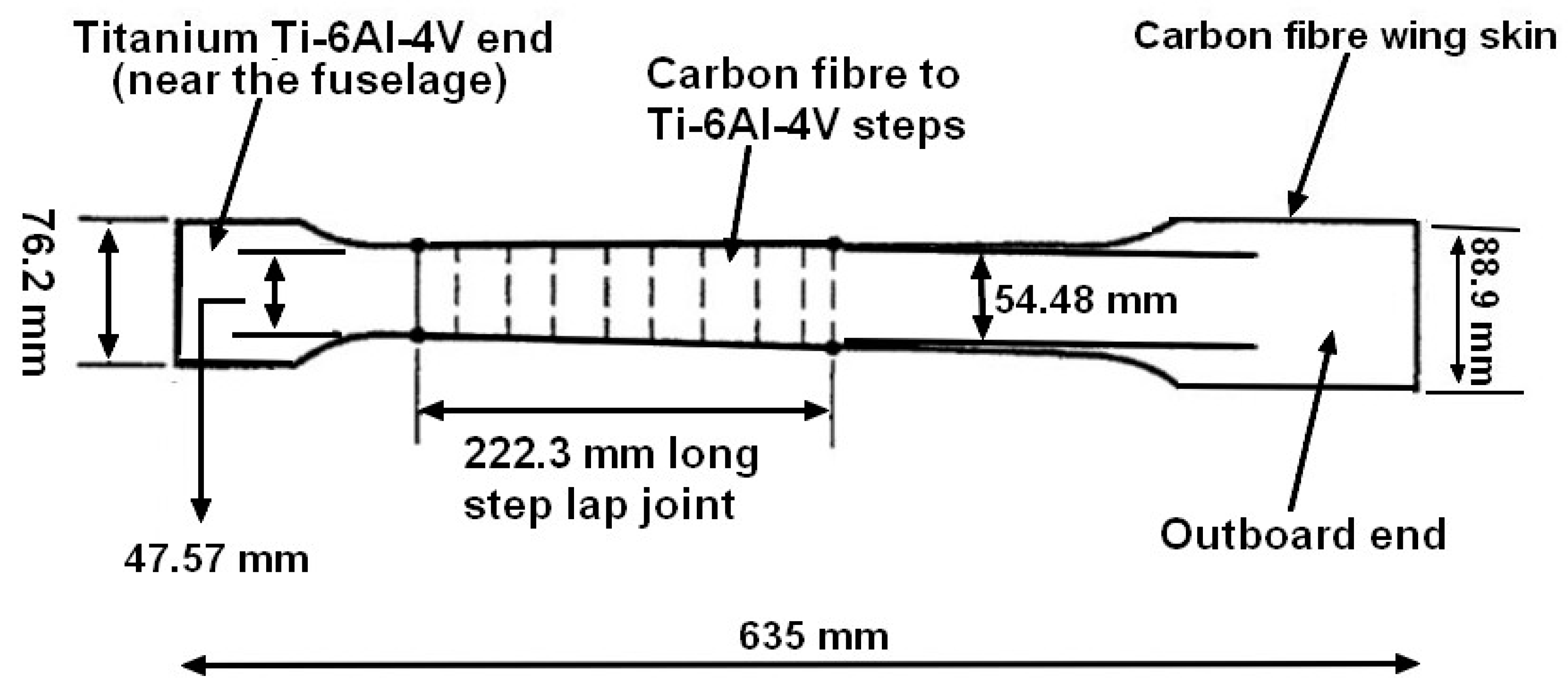
3.3. Adhesively-Bonded Joints
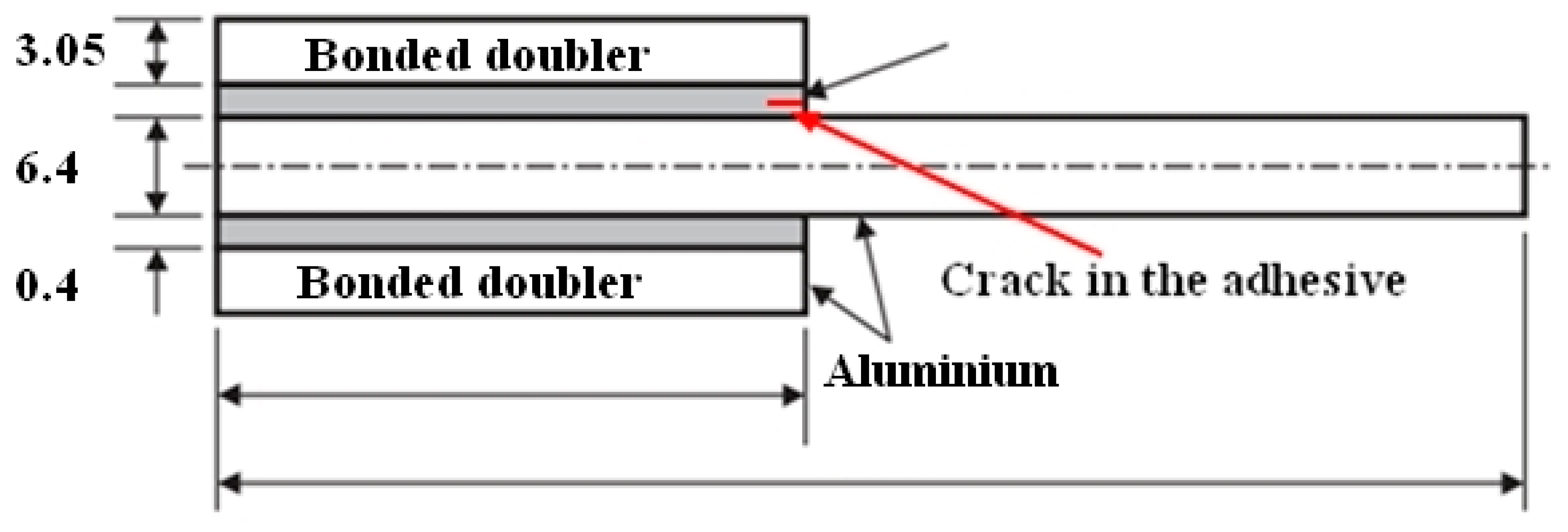
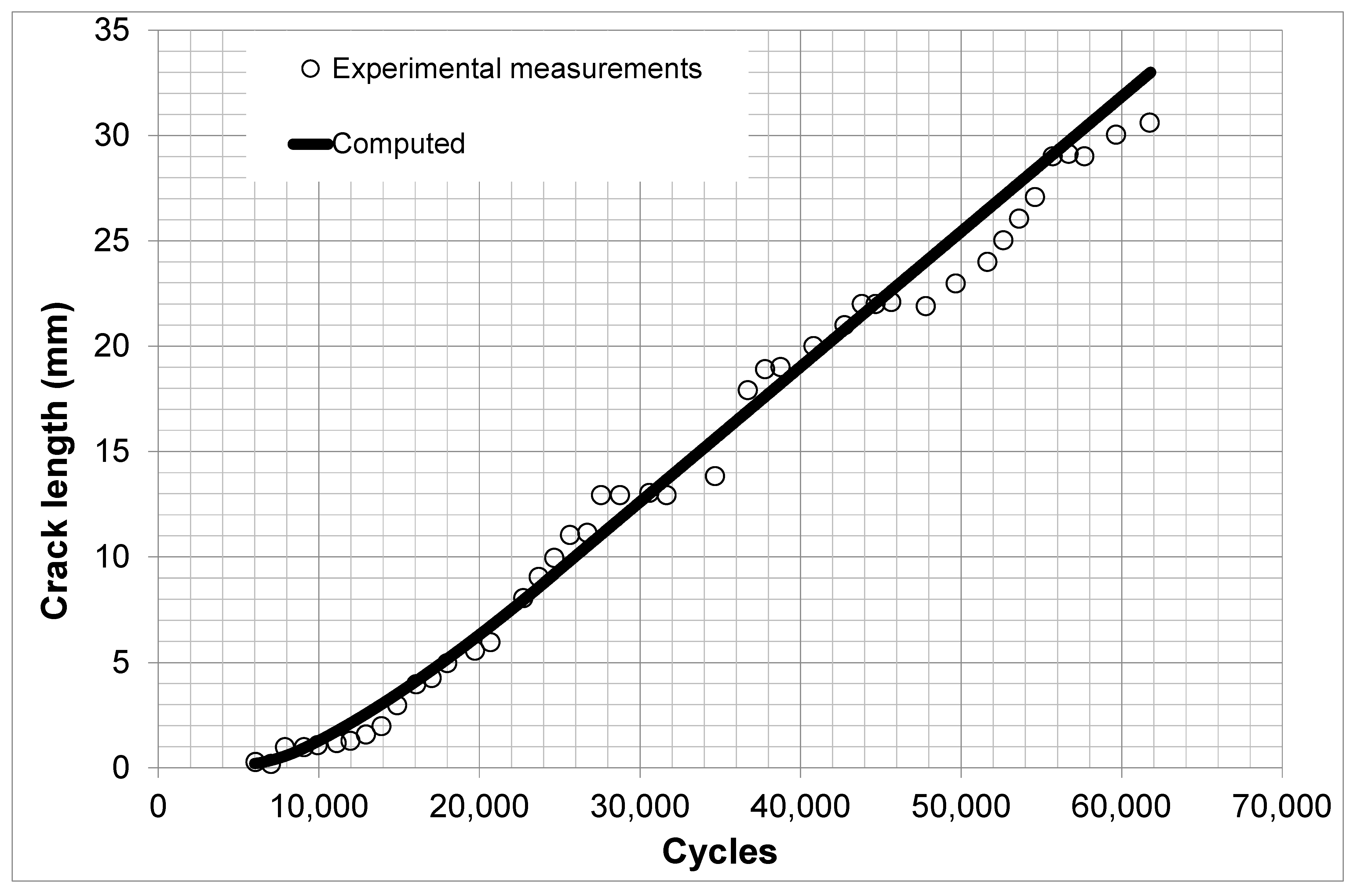
4. Cohesive Crack Growth in Adhesively-Bonded Double Lap Joints under Uniaxial Loads
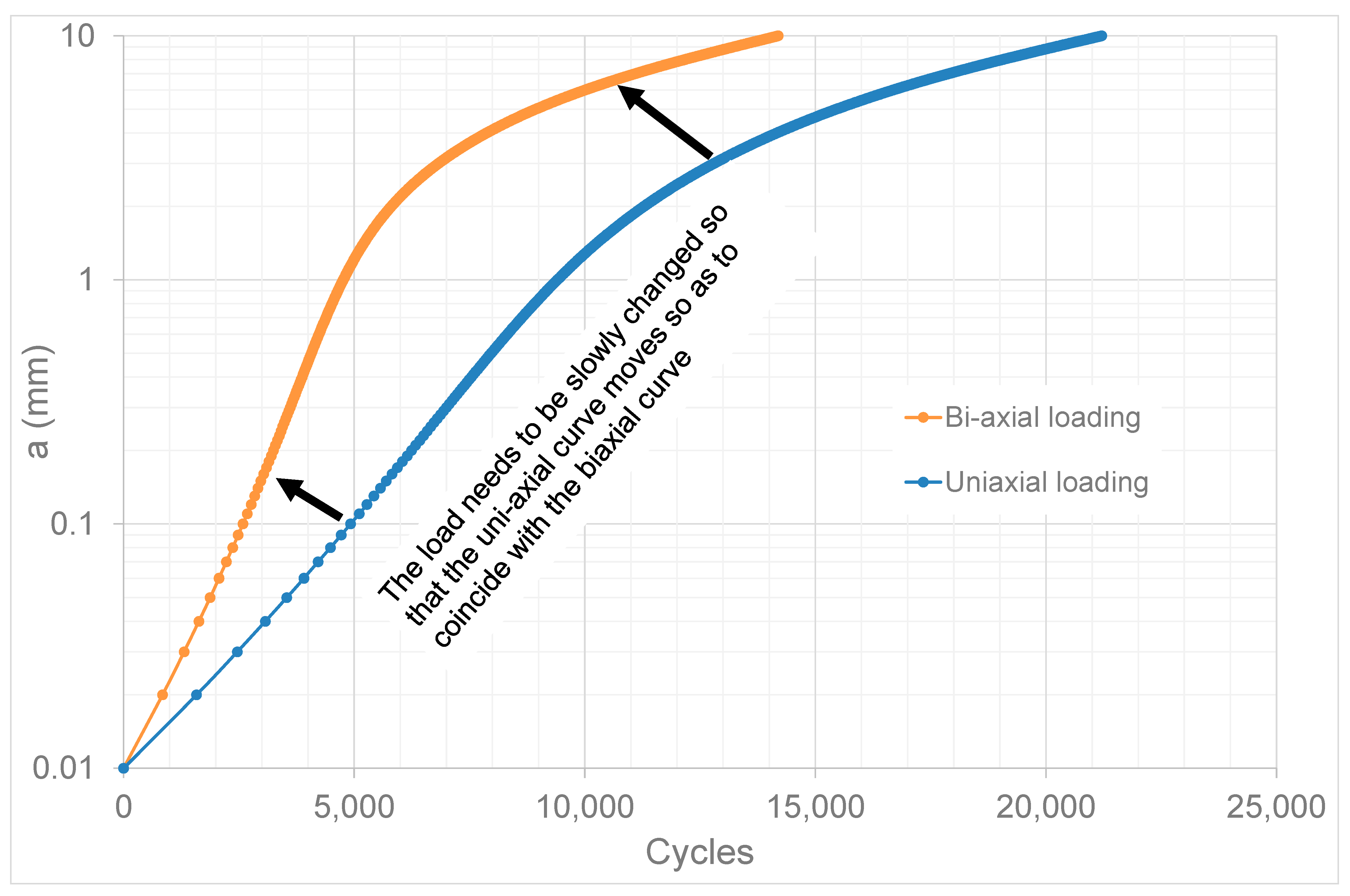
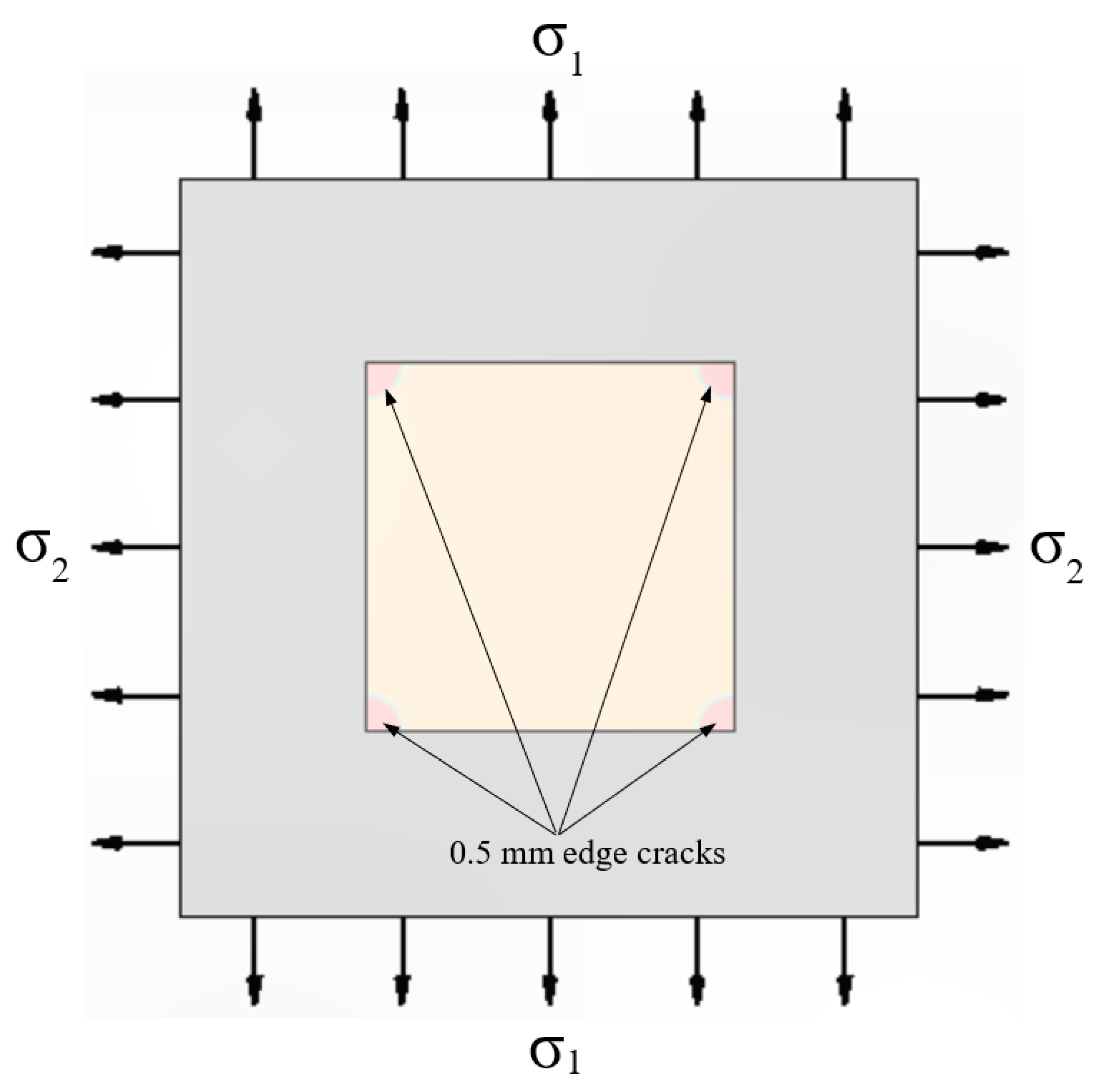
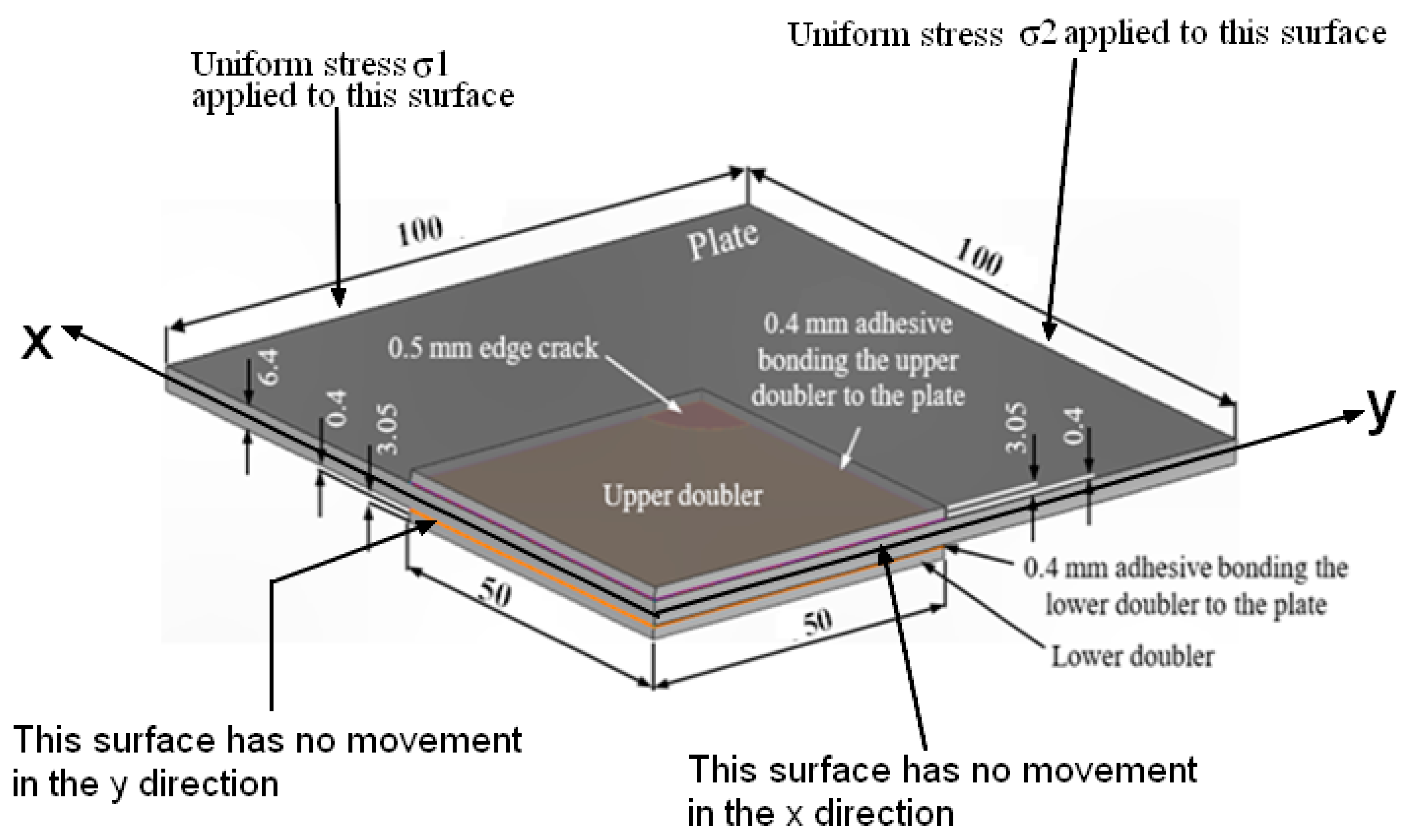
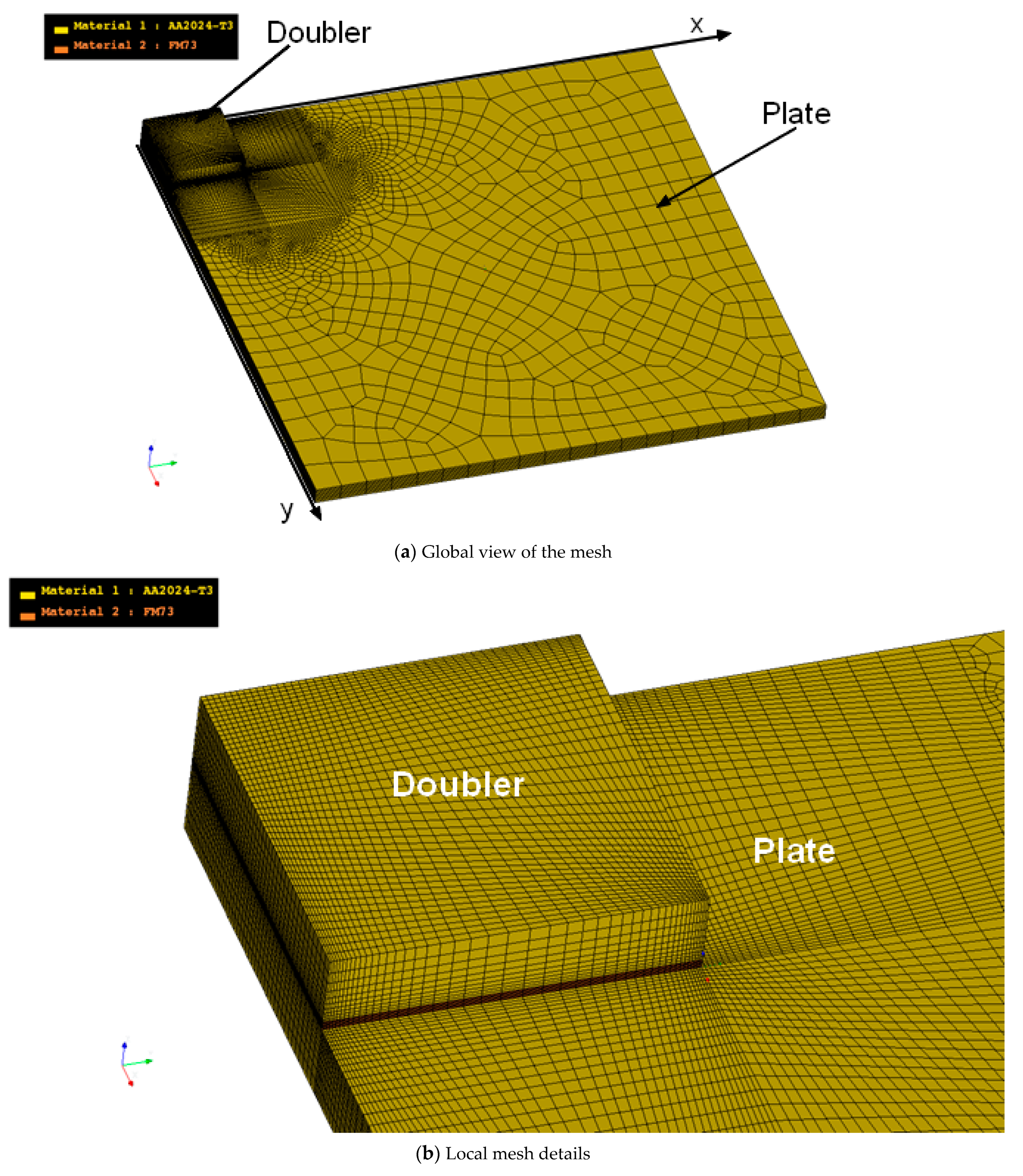
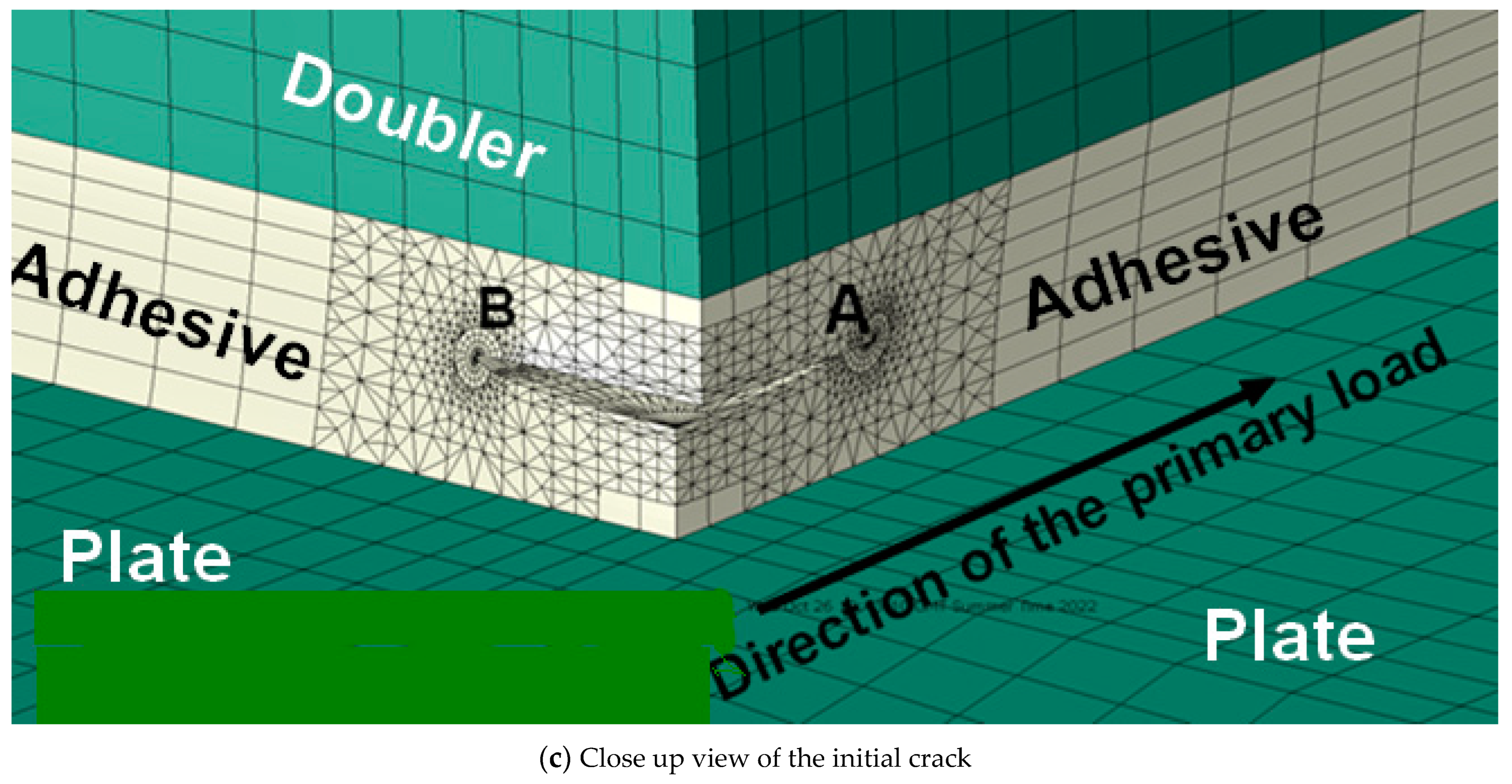
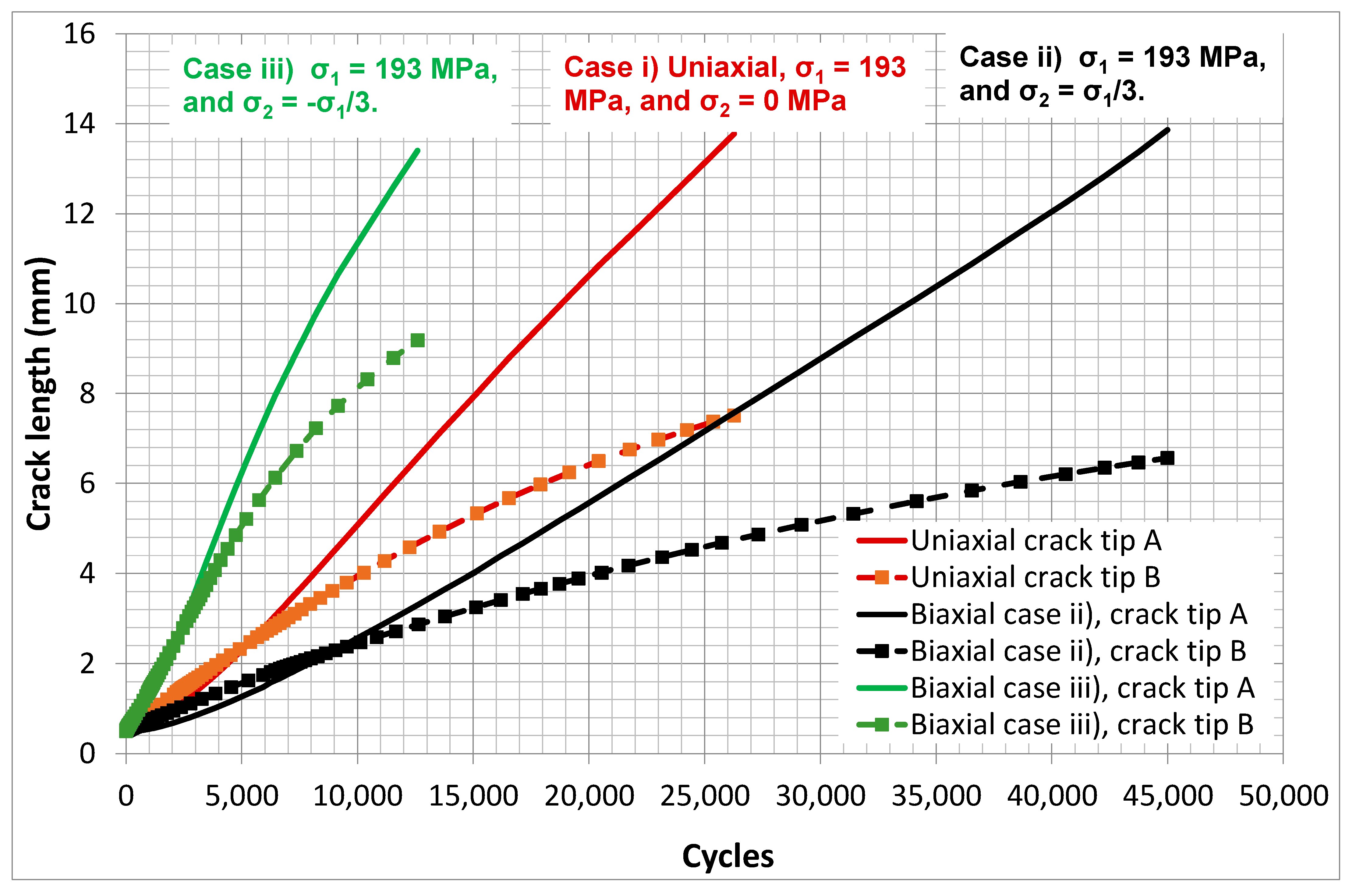
5. Cohesive Crack Growth in Adhesively-Bonded Doublers under Uniaxial and Biaxial Loads
‘How does the growth of sub mm cracks in an adhesive bond subjected to uniaxial loads relate to growth under multi-axial loads?’
- (i)
- Uniaxial constant amplitude fatigue stresses with the peak stresses in the spectrum being σ1 = 193 MPa and σ2 = 0.
- (ii)
- Biaxial constant amplitude fatigue stresses with the peak stresses in the spectrum being σ1 = 193 MPa and σ2 = σ1/3.
- (iii)
- Biaxial constant amplitude fatigue stresses with the peak stresses in the spectrum being σ1 = 193 MPa and σ2 = −σ1/3.
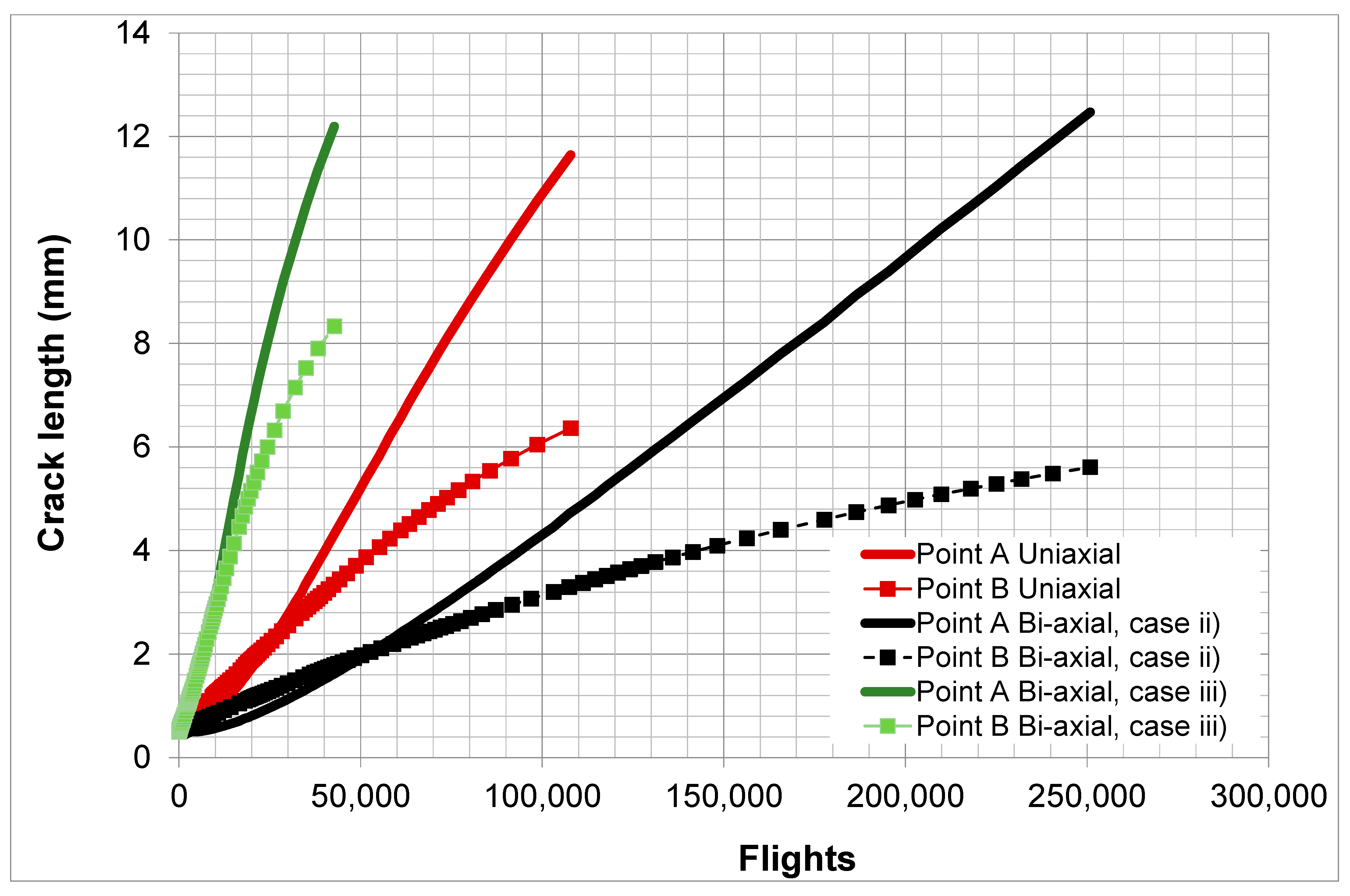
6. Cohesive Crack Growth in Adhesively-Bonded Joints under a Combat Aircraft Flight Load Spectrum
- (i)
- The peak stresses in the spectrum are σ1 = 193 MPa and σ2 = 0.
- (ii)
- The peak stresses in the spectrum are σ1 = 193 MPa and σ2 = σ1/3.
- (iii)
- The peak stresses in the spectrum are σ1 = 193 MPa and σ2 = −σ1/3.
- (i)
- The effect of biaxial loads on crack growth under operational flight loads can be significant.
- (ii)
- When comparing the results shown in Figure 12 and Figure 13, we see that the relative effect of the biaxial stresses on crack growth is similar regardless of whether the fatigue load spectra is a constant amplitude spectrum, as in Figure 12, or a FALSTAFF flight load spectrum, as in Figure 13. By this we mean that case (iii) had faster crack growth than the uniaxial load case, i.e., case (i), and that case (ii) had slower crack growth than the uniaxial load case. This observation reflects the way in which the various stress states interact with the disbond, i.e., with the crack in the adhesive.
7. Conclusions
- (i)
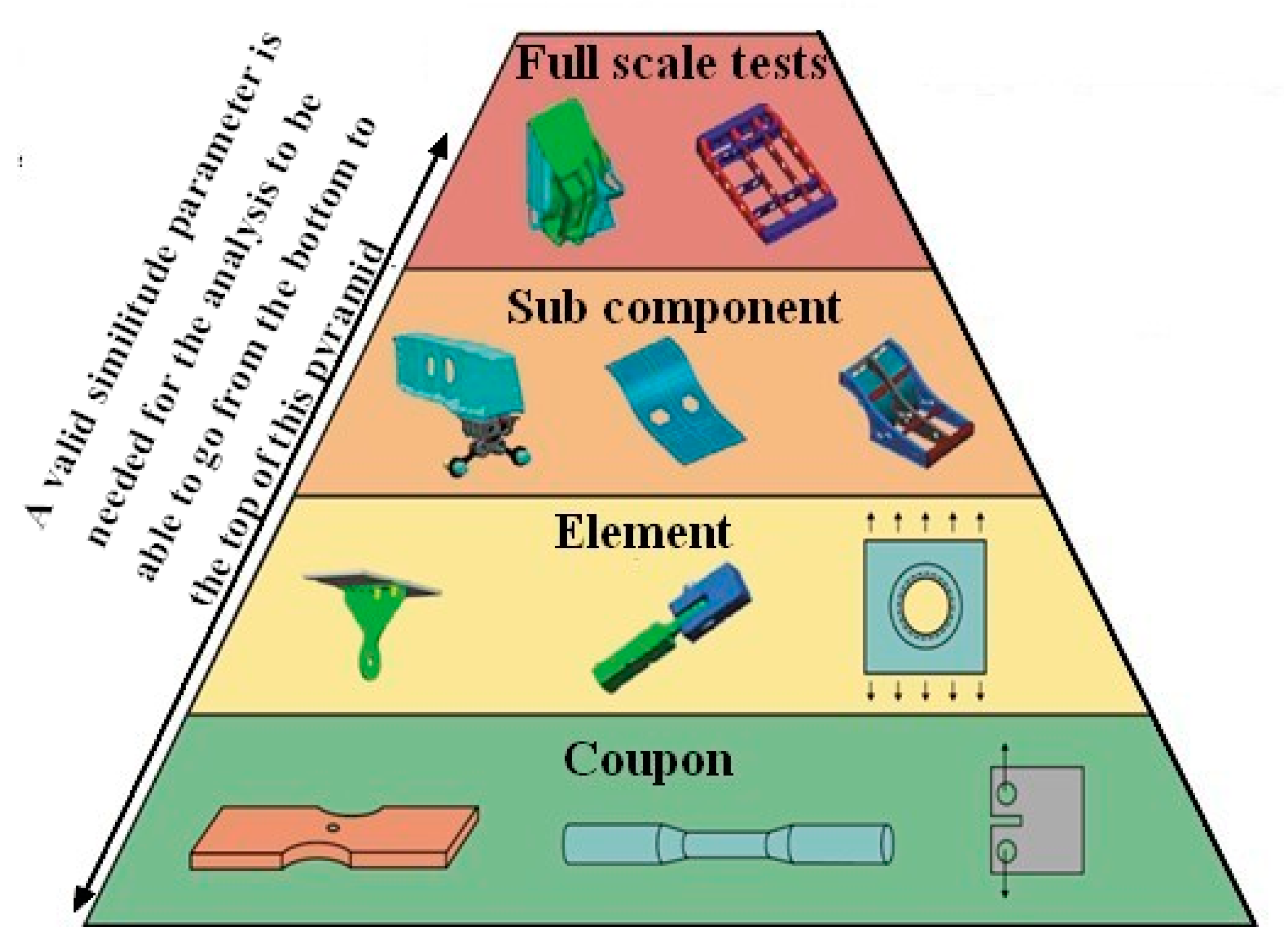
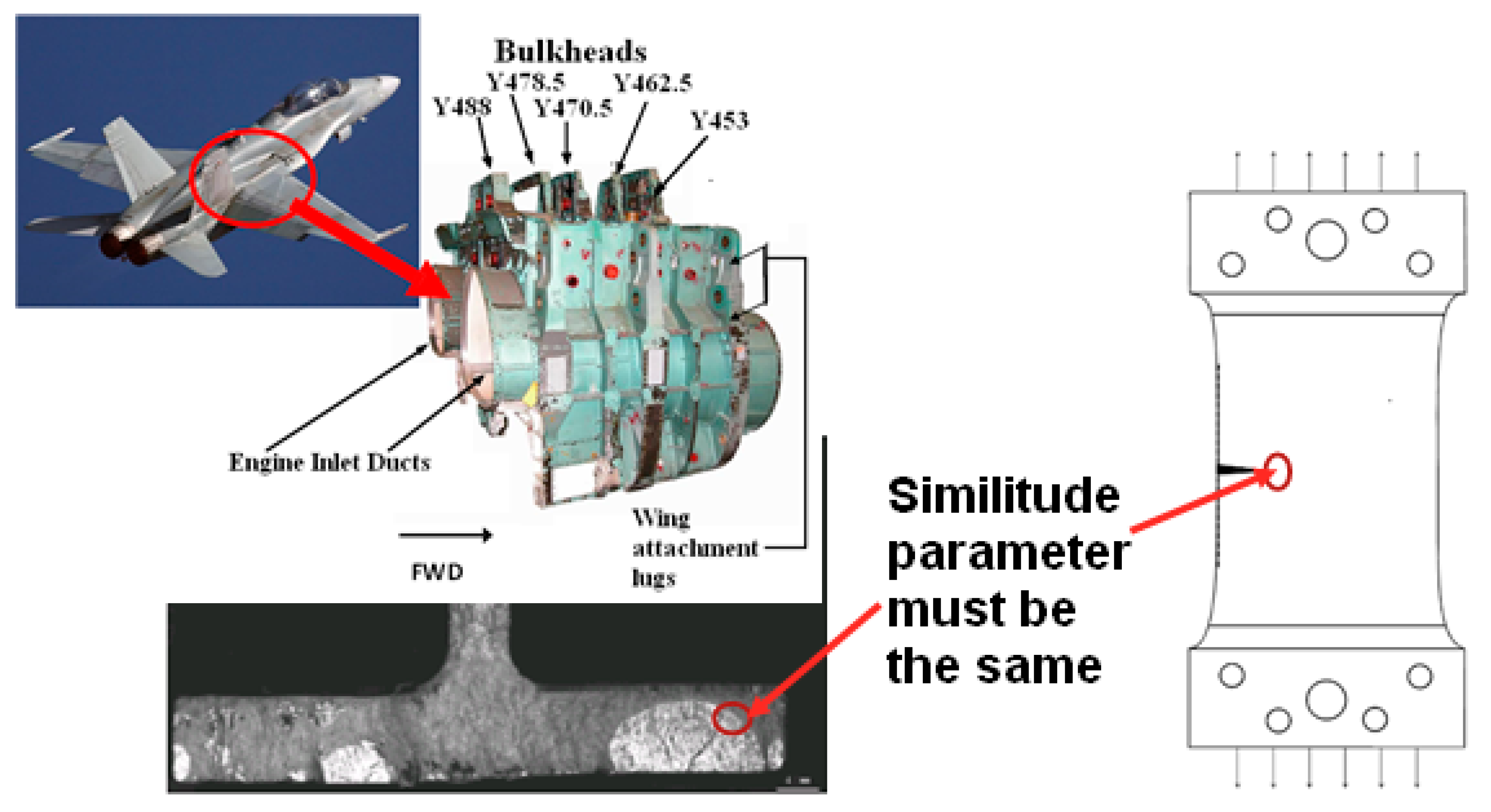
- Firstly, it should be noted that an essential requirement of any such laboratory test program that is performed so as to determine inspection intervals/durability of an adhesively bonded repair/doubler. Regardless of whether uniaxial or biaxial laboratory tests are performed, it is necessary to establish that at each stage in the testing regime the LEFM similitude parameter in the test specimen corresponds to that in the (operational) airframe.
- (ii)
- Secondly, the results of the present study have led to the hypothesis that: For uniaxial coupon tests to yield a crack growth history that is consistent with that seen under a multi-axial stress state representative of an operational aircraft, it may be necessary to adjust the magnitude of the applied loads as the crack grows such that at each crack length the similitude parameter, i.e., Δκ′, in the uniaxial test corresponds to that present under the true multi-axial stress state. The scientific community is challenged to evaluate the potential/validity of this hypothesis.
- (iii)
- Thirdly, a simpler, but possibly less desirable, approach, that is consistent with the building block approach to certification delineated in MIL-STD-1530D and JSSG-2006 and with the approaches outlined in [10,12,15], is to first establish that you can compute both the uniaxial and the multi-axial test crack histories in specimens, albeit with geometries and support conditions that may not be truly representative of the operational structure, using the same input parameters in both cases. (By this it is meant that the crack growth equation used in both studies would be identical, and that there would be no disposable parameters that could be “tweaked” to improve the fit to the experimental data.) Having thus validated the analysis methodology, the engineer would then run the analysis using a finite element model that has the actual geometry, boundary conditions, operational flight loads, etc., and compute the in service performance, i.e., the remaining life, inspection intervals, etc.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
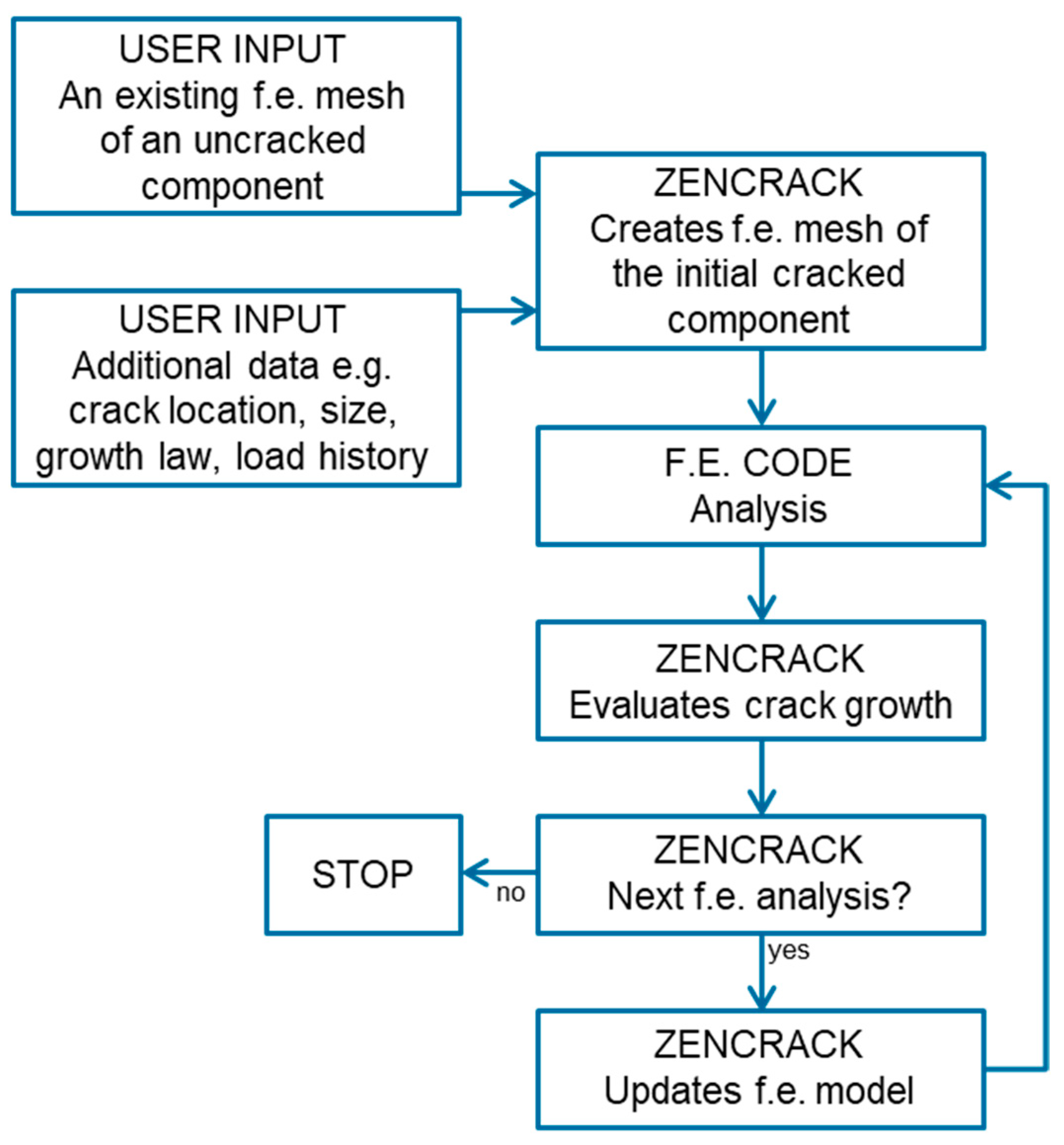
References
- MIL-STD-1530D. Department of Defense Standard Practice; Washington, DC, USA. 2016. Available online: http://everyspec.com/MIL-STD/MIL-STD-1500-1599/MIL-STD-1530D_55392/#:~:text=%2DAUG%2D2016)-,MIL%2DSTD%2D1530D%2C%20DEPARTMENT%20OF%20DEFENSE%20STANDARD%20PRACTICE%3A,while%20managing%20cost%20and%20schedule (accessed on 3 November 2023).
- Griffith, A.A. The phenomena of rupture and flow in solids. Philos. Trans. R. Soc. 1920, A221, 163–198. [Google Scholar]
- Irwin, G.R. Analysis of stresses and strains near the end of a crack traversing a plate. J. Appl. Mech. 1957, 24, 361–364. [Google Scholar] [CrossRef]
- Paris, P.C. A brief history of the crack tip stress intensity factor and its applications. Meccanica 2014, 49, 759–764. [Google Scholar] [CrossRef]
- Department of Defense Joint Service Specification Guide, Aircraft Structures, JSSG-2006. October 1998. Available online: http://everyspec.com/USAF/USAF-General/JSSG-2006_10206/ (accessed on 3 November 2023).
- Gallagher, J.P.; Giessler, F.J.; Berens, A.P.; Wood, H.A. USAF Damage Tolerant Design Handbook: Guidelines For The Analysis and Design of Damage Tolerant Aircraft Structures, Revision B. AFWAL-TR-82-3073. Wright-Patterson Air Force Base, Ohio 4543. May 1984. Available online: https://apps.dtic.mil/sti/citations/ADA153161 (accessed on 3 November 2023).
- Kruse, T.; Körwien, T.; Geistbeck, M.; Schmid Fuertes, T.A. Fatigue behaviour and damage tolerant design of composite bonded joints for aerospace application. In Proceedings of the 20th International Conference on Composite Materials, Copenhagen, Denmark, 19–24 July 2015; Available online: https://www.iccm-central.org/Proceedings/ICCM20proceedings/papers/paper-2219-1.pdf (accessed on 6 November 2023).
- Jones, R.; Kinloch, A.J.; Michopoulos, J.; Iliopoulos, A.P. Crack growth in adhesives: Similitude and the Hartman-Schijve equation. Compos. Struct. 2021, 273, 114260. [Google Scholar] [CrossRef]
- Jones, R.; Peng, D. A Building Block Approach to Sustainment and Durability Assessment: Experiment and Analysis. In Comprehensive Structural Integrity, 2nd ed.; Aliabadi Ferri, M.H., Soboyejo, W., Eds.; Elsevier: Oxford, UK, 2023; Volume 7, pp. 73–101. ISBN 978-0-12-822944-6. [Google Scholar]
- Molent, L.; Jones, R. The F111C wing pivot fitting repair and implications for the design/assessment of bonded joints and composite repairs. In Aircraft Sustainment and Repair; Chapter 10, 511–543; Jones, R., Baker, A.A., Matthews, N., Champagne, V., Jr., Eds.; Butterworth-Heinemann Press: Oxford, UK, 2018; ISBN 9780081005408. [Google Scholar]
- Baker, A.A.; Callinan, R.; Davis, M.; Jones, R.; Williams, J. Repair of Mirage III aircraft using the BFRP crack-patching technique. Theor. Appl. Fract. Mech. 1984, 2, 1–16. [Google Scholar] [CrossRef]
- Roach, D.; Rackow, K. Development and Validation of Bonded Composite Doubler Repairs for Commercial Aircraft. In Aircraft Sustainment and Repair; Sandia Report SAND2007-4088, July 2007; Chapter 11; Jones, R., Matthews, N., Baker, A.A., Champagne, V., Jr., Eds.; Butterworth-Heinemann Press: Oxford, UK, 2018; pp. 545–743. ISBN 9780081005408. [Google Scholar]
- Seneviratne, W.P.; Tomblin, J.S.; Cravens, T.; Kittur, M.; Rahman, A. Durability and Residual Strength Assessment of F/A-18A-D Durability and Residual Strength Assessment of F/A-18A-D WingRoot Stepped-Lap Joint. In Proceedings of the AIAA Centennial of Naval Aviation Forum “100 Years of Achievement and Progress”, Virginia Beach, VA, USA, 21–22 September 2011. [Google Scholar] [CrossRef]
- Mazza, J.; Storage, K.M. Bonded Repair in the United States Air Force and Work to Expand Future Capability. In AGARD STO Meetings Proceedings, STO-MP-AVT-266, Use of Bonded Joints in Military Applications; Paper 4; 2018; pp. 4-1–4-20. ISBN 978-92-837-2172-7. Available online: https://www.sto.nato.int/publications/STO%20Meeting%20Proceedings/STO-MP-AVT-266/MP-AVT-266-04.pdf (accessed on 6 November 2023).
- Baker, A.A.; Wang, J. Adhesively Bonded Repair/Reinforcement of Metallic Airframe Components: Materials, Processes, Design and Proposed Through-Life Management. In Aircraft Sustainment and Repair; Chapter 6; Jones, R., Matthews, N., Baker, A., Champagne, V., Eds.; Butterworth-Heinemann Press: Oxford, UK, 2018; pp. 191–252. ISBN 9780081005408. [Google Scholar]
- Raizenne, D. Case History: CF116 Upper Wing Skin Fatigue Enhancement Boron Doubler. In Advances in the Bonded Composite Repair of Metallic Aircraft Structure; Chapter 36; Baker, A., Rose, L.R.F., Jones, R., Eds.; Elsevier Applied Science Publishers: Amsterdam, The Netherlands, 2002. [Google Scholar]
- Chalkley, P.D.; Wang, C.H.; Baker, A.A. Chapter 5, Fatigue Testing of Generic Bonded Joints. In Advances in the Bonded Composite Repair of Metallic Aircraft Structure; Baker, A.A., Rose, L.F.J., Jones, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2002; Volume 1, pp. 103–125. ISBN 9780080522951. [Google Scholar]
- Mueller, E.M.; Starnes, S.; Strickland, N.; Kenny, P.; Williams, C. The detection, inspection, and failure analysis of a composite wing skin defect on a tactical aircraft. Compos. Struct. 2016, 145, 186–193. [Google Scholar] [CrossRef]
- Potter, J.M.; Gallagher, J.P.; Stalnaker, H.D. The Effect of Spectrum Variations on the Fatigue Behavior of Notched Structures Representing F-4E/S Wing Stations, AFFDL-TM-74-2-FBR. January 1974. Available online: https://apps.dtic.mil/sti/citations/ADA365404 (accessed on 11 June 2023).
- Arrieta, A. C-130 Full Scale Wing Durability Test with an ESL Wing: Coupon Test Program. In Proceedings of the 2015 USAF Aircraft Structural Integrity, San Antonio, TX, USA, 2–3 December 2015. [Google Scholar]
- Huynh, J.; Molent, L.; Barter, S. Experimentally derived crack growth models for different stress concentration factors. Int. J. Fatigue 2008, 30, 1766–1786. [Google Scholar] [CrossRef]
- Polymer Matrix Composites Materials Useage, Design and Analysis. In Composite Materials Handbook; CMH-17-3G; SAE International: Wichita, Kansas, USA, 2012; Volume 3.
- Hart-Smith, L.J. Adhesively Bonded Double Lap Joints. NASA Langley Research Center Report NASA CR-112235. January 1973. Available online: https://ntrs.nasa.gov/api/citations/19740005082/downloads/19740005082.pdf (accessed on 22 August 2023).
- Birchfield, E.B.; Cole, R.T.; Impellizzer, L.F. Reliability of Step-Lap Bonded Joints, Report AFFDL-TR-75-26. 1975. Available online: https://apps.dtic.mil/sti/citations/ADA012009 (accessed on 11 June 2023).
- Lincoln, J.W.; Melliere, R.A. Economic Life Determination for a Military Aircraft. AIAA J. Aircr. 1999, 36, 737–742. [Google Scholar] [CrossRef]
- Manning, S.D.; Garver, W.R.; Henslee, S.P.; Norris, J.W.; Pendley, B.J.; Speaker, S.M.; Smith, V.D.; Yee, B.G.W.; Shinozuka, M.; Yang, Y.N. Durability Methods Development, Volume I—Phase I, AFFDL-TR-79.-3118. 1979. Available online: http://www.dtic.mil/dtic/tr/fulltext/u2/a087301.pdf (accessed on 10 June 2023).
- Jones, R. Fatigue crack growth and damage tolerance. Fatigue Fract. Engng. Mater. Struct. 2014, 37, 463–483. [Google Scholar] [CrossRef]
- Tan, J.L.; Chen, B.K. Prediction of fatigue life in aluminum alloy (AA7050-T7451) structures in the presence of multiple artificial short cracks. Theor. Appl. Fract. Mech. 2015, 78, 1–7. [Google Scholar] [CrossRef]
- Tan, J.L.; Chen, B.K. Coalescence and growth of two coplanar short cracks in AA7050-T7451 aluminium alloys. Eng. Fract. Mech. 2013, 102, 324–333. [Google Scholar] [CrossRef]
- Shamir, M.; Zhang, X.; Syed, A.K. Characterising and representing small crack growth in an additive manufactured titanium alloy. Eng. Fract. Mech. 2021, 253, 107876. [Google Scholar] [CrossRef]
- Sanaei, N.; Fatemi, A. Defects in additive manufactured metals and their effect on fatigue performance: A state-of-the-art review. Prog. Mater. Sci. 2020, 117, 100724. [Google Scholar] [CrossRef]
- Ye, J.; Syed, A.K.; Zhang, X.; Eimer, E.; Williams, S. Fatigue crack growth behaviour in an aluminium alloy Al-Mg-0.3Sc produced by wire based directed energy deposition process. Fatigue Fract. Eng. Mater. Struct. 2023, 46, 3927–3938. Available online: https://onlinelibrary.wiley.com/doi/epdf/10.1111/ffe.14113 (accessed on 3 November 2023). [CrossRef]
- Shamir, M.; Zhang, X.; Syed, A.K.; Sadler, W. Predicting the Effect of Surface Waviness on Fatigue Life of a Wire Arc Additive Manufactured Ti-6Al-4V Alloy. Materials 2023, 16, 5355. [Google Scholar] [CrossRef]
- Dastgerdi, J.N.; Jaberi, O.; Remes, H.; Lehto, P.; Toudeshky, H.H.; Kuva, J. Fatigue damage process of additively manufactured 316 L steel using X-ray computed tomography imaging. Addit. Manuf. 2023, 7, 103559. [Google Scholar] [CrossRef]
- Molent, L. Thoughts on fatigue certification of metal additive manufacturing for aircraft structures. Keynote Lecture. In Proceedings of the EASA-FAA Industry-Regulator AM Event, Cologne, Germany, 8–12 November 2021; Available online: https://www.easa.europa.eu/presentations-2021-easa-faa-industry-regulator-am-event (accessed on 11 June 2023).
- Main, B.; Evans, R.; Walker, K.; Yu, X.; Molent, L. Lessons from a fatigue prediction challenge for an aircraft wing shear tie post. Int. J. Fatigue. 2019, 123, 53–65. [Google Scholar] [CrossRef]
- Markham, M.J.; Fatemi, A. Multiaxial fatigue life predictions of additively manufactured metals using a hybrid of linear elastic fracture mechanics and a critical plane approach. Int. J. Fatigue 2023, 178, 107979. [Google Scholar] [CrossRef]
- Schwalbe, K.H. On the beauty of analytical models for fatigue crack propagation and fracture-A personal historical review. J. ASTM Int. 2010, 7, 3–73. [Google Scholar] [CrossRef]
- Hu, W.; Jones, R.; Kinloch, A.J. Computing the growth of naturally-occurring disbonds in adhesively-bonded patches to metallic structures. Eng. Fract. Mech. 2016, 152, 162–173. [Google Scholar] [CrossRef]
- Clerc, G.; Brunner, A.J.; Niemz, P.; Van De Kuilen, J.W.G. Feasibility study on Hartman-Schijve data analysis for mode II fatigue fracture of adhesively bonded wood joints. Int. J. Fract. 2019, 221, 123–140. [Google Scholar] [CrossRef]
- Rocha, A.V.M.; Akhavan-Safar, A.; Carbas, R.; Marques, E.A.S.; Goyal, R.; El-Zein, M.; da Silva, L.F.M. Paris law relations for an epoxy-based adhesive. J. Mater. Des. Appl. 2020, 234, 291–299. [Google Scholar] [CrossRef]
- Riedl, G.; Pugstaller, R.; Wallner, G.M. Development and implementation of a simultaneous fatigue crack growth test setup for polymeric hybrid laminates. Eng. Fract. Mech. 2022, 267, 108468. [Google Scholar] [CrossRef]
- Kinloch, A.J.; Jones, R.; Michopoulos, J.G. Fatigue crack growth in epoxy polymer nanocomposites. Philos. Trans. R. Soc. 2021, 379, 20200436. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; McGraw Hill Book Company: New York, NY, USA, 1970; ISBN 0-07-Y85805-5. [Google Scholar]
- Molent, L.; Sun, Q.; Green, A.J. Characterisation of equivalent initial flaw sizes in 7050 aluminium alloy. Fatigue Fract. Eng. Mater. Struct. 2006, 29, 916–937. [Google Scholar] [CrossRef]
- Jones, R.; Peng, D.; Pitt, S.; Wallbrink, C. Weight functions, CTOD, and related solutions for cracks at notches. Eng. Fail. Anal. 2004, 11, 79–114. [Google Scholar] [CrossRef]
- Jones, R.; Peng, D.; Michopoulos, J.G.; Kinloch, A.J. Requirements and variability affecting the durability of bonded joints. Materials 2020, 13, 1468. [Google Scholar] [CrossRef]
- Cheuk, P.T.; Tong, L.; Rider, A.N.; Wang, J. Analysis of energy release rate for fatigue cracked metal-to-metal double-lap shear joints. Int. J. Adhes. Adhes. 2005, 25, 181–191. [Google Scholar] [CrossRef]
- Available online: https://www.zentech.co.uk/zencrack_publications.htm (accessed on 11 June 2023).
- Available online: https://www.zentech.co.uk/zencrack.htm (accessed on 3 November 2023).
- Available online: https://www.zentech.co.uk/download/zencrack_brochure.pdf (accessed on 3 November 2023).
- Infante, V.; Silva, J.M. Case studies of computational simulations of fatigue crack propagation using finite elements analysis tools. Eng. Fail. Anal. 2011, 18, 616–624. [Google Scholar] [CrossRef]
- Maligano, A.R.; Citarella, R.; Silbershmidt, V.V. Retardation effects due to overloads in aluminium-alloy aeronautical components. Fatigue Fract. Engng. Mater. Struct. 2017, 40, 1484–1500. [Google Scholar] [CrossRef]
- Pan, J.; Guo, M. Numerical simulation of dynamic fracture toughness tests: Using RKR criterion. SN Appl. Sci. 2019, 1, 1085. [Google Scholar] [CrossRef]
- Malekan, M.; Khosravi, A.; St-Pierre, L. An Abaqus plug-in to simulate fatigue crack growth. Eng. Comput. 2022, 38, 2991–3005. [Google Scholar] [CrossRef]
- Heuler, P.; Klätschke, H. Generation and use of standardized load spectra and load–time histories. Int. J. Fatigue 2005, 27, 974–990. [Google Scholar] [CrossRef]
- Schijve, J. Fatigue damage in aircraft structures, not wanted, but tolerated? Int. J. Fatigue 2009, 31, 998–1011. [Google Scholar] [CrossRef]
- Molent, L.; Aktepe, B. Review of fatigue monitoring of agile military aircraft. Fatigue Fract. Eng. Mater. Struct. 2000, 23, 767–785. [Google Scholar] [CrossRef]
- Bond, I.P.; Farrow, I.R. Fatigue life prediction under complex loading for XAS/914 CFRP incorporating a mechanical fastener. Int. J. Fatigue 2000, 22, 633–644. [Google Scholar] [CrossRef]

| D (m/cycle) | p | A′ (J/m2) | (√(J/m2)) |
|---|---|---|---|
| 1.9 × 10−10 | 2.7 | 2000 | 7.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jones, R.; Chandwani, R.; Timbrell, C.; Kinloch, A.J.; Peng, D. Thoughts on the Importance of Similitude and Multi-Axial Loads When Assessing the Durability and Damage Tolerance of Adhesively-Bonded Doublers and Repairs. Aerospace 2023, 10, 946. https://doi.org/10.3390/aerospace10110946
Jones R, Chandwani R, Timbrell C, Kinloch AJ, Peng D. Thoughts on the Importance of Similitude and Multi-Axial Loads When Assessing the Durability and Damage Tolerance of Adhesively-Bonded Doublers and Repairs. Aerospace. 2023; 10(11):946. https://doi.org/10.3390/aerospace10110946
Chicago/Turabian StyleJones, Rhys, Ramesh Chandwani, Chris Timbrell, Anthony J. Kinloch, and Daren Peng. 2023. "Thoughts on the Importance of Similitude and Multi-Axial Loads When Assessing the Durability and Damage Tolerance of Adhesively-Bonded Doublers and Repairs" Aerospace 10, no. 11: 946. https://doi.org/10.3390/aerospace10110946
APA StyleJones, R., Chandwani, R., Timbrell, C., Kinloch, A. J., & Peng, D. (2023). Thoughts on the Importance of Similitude and Multi-Axial Loads When Assessing the Durability and Damage Tolerance of Adhesively-Bonded Doublers and Repairs. Aerospace, 10(11), 946. https://doi.org/10.3390/aerospace10110946







