A Low-Cost Relative Positioning Method for UAV/UGV Coordinated Heterogeneous System Based on Visual-Lidar Fusion
Abstract
:1. Introduction
- A framework that can automatically complete real-time detection and localization of targets without human intervention, using only CPU is proposed. All components in the system are released as open-source packages. https://github.com/HKPolyU-UAV/GTA (accessed on 20 May 2023);
- Unlike other methods that use a priori target point cloud as a registration reference, this framework combines the advantages of RGB-D and LiDAR to detect and track the desired target without any prior information;
- LiDAR-inertial odometry (LIO) is integrated into the system to provide accurate altitude estimation for vehicle navigation in GPS-denied environments;
- Both indoor and outdoor experiments are designed and carried out to illustrate the proposed ideas and methodologies in this work and validate their performance. These indoor and outdoor experiments also serve to provide experimental ideas to other researchers.
2. Related Works
2.1. Visual-Based Positioning Techniques
2.2. LiDAR-Based Positioning Techniques
2.3. Visual-LiDAR Fusion Approaches
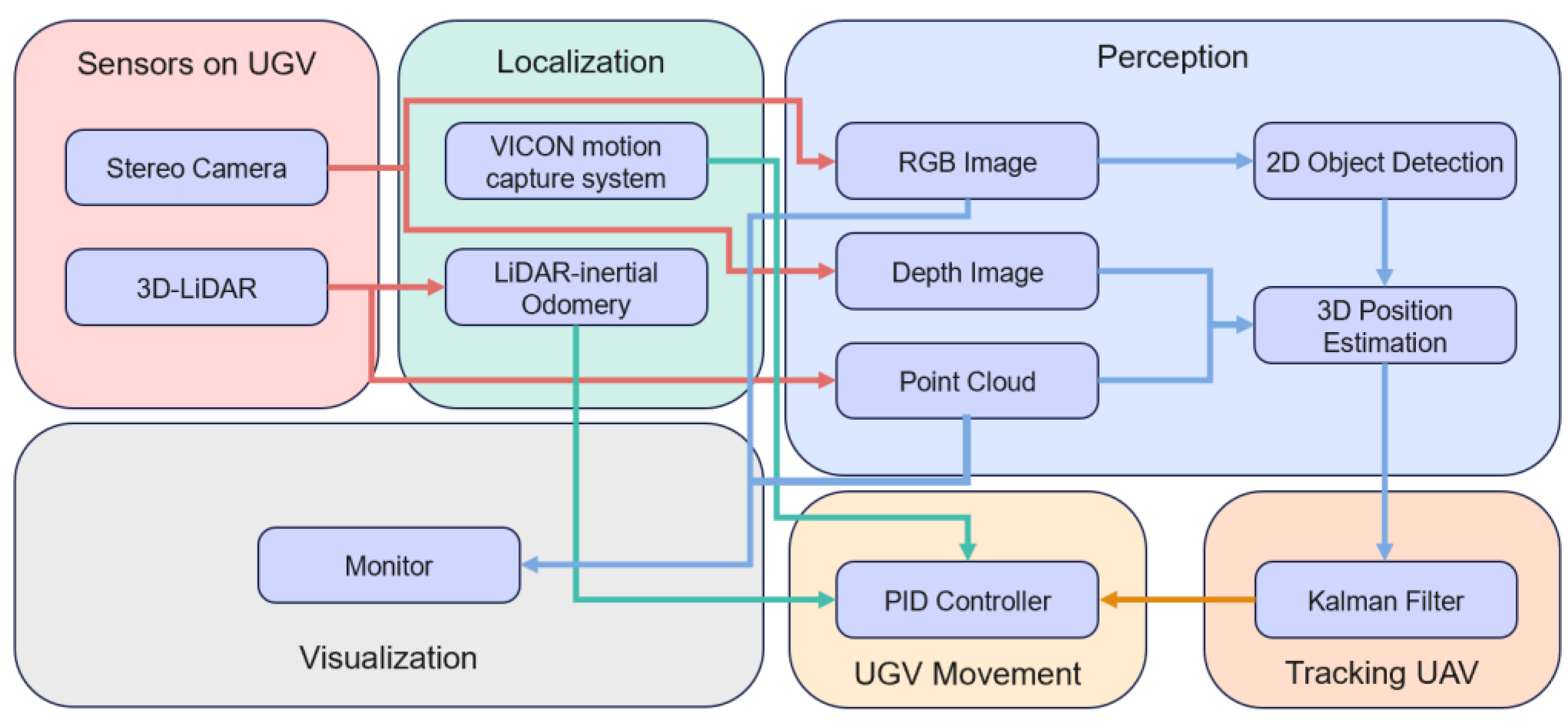
3. System Overview
3.1. Hardware Platform
3.2. Software Architecture
4. Methodology
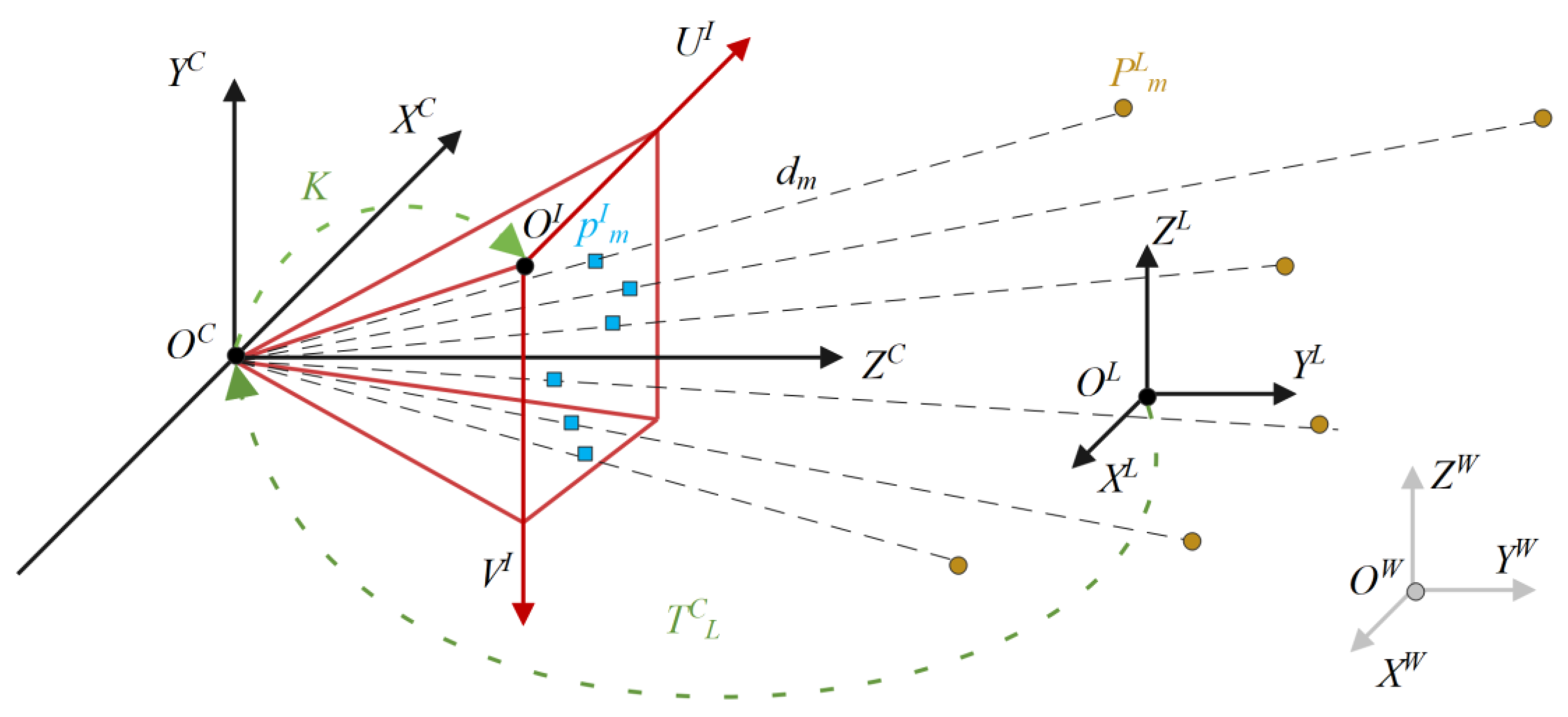
4.1. Extrinsic Calibration between Camera and LiDAR
4.2. Two-Dimensional (2D) Object Detection
4.2.1. Two-Dimensional (2D) Bounding Box Prediction
- , , , and are parameters for the bounding box, with x representing the position of the center (on the image plane), y representing the position of the center, w representing the width, and h representing the height, respectively;
- , , and , and are the predicted values from the network for the bounding box, which is utilized to compute the parameters for the bounding box;
- and are the prior width and height for the bounding box;
- is the sigmoid function applied to constrain the offset range between 0 and 1;
- Figure 7 shows an illustration of the bounding box predicted by YOLOv4-tiny.
4.2.2. Custom Training Dataset Establishment
4.3. Three-Dimensional (3D) Position Estimation
4.3.1. Depth Assignment Based on 2D Bounding Box
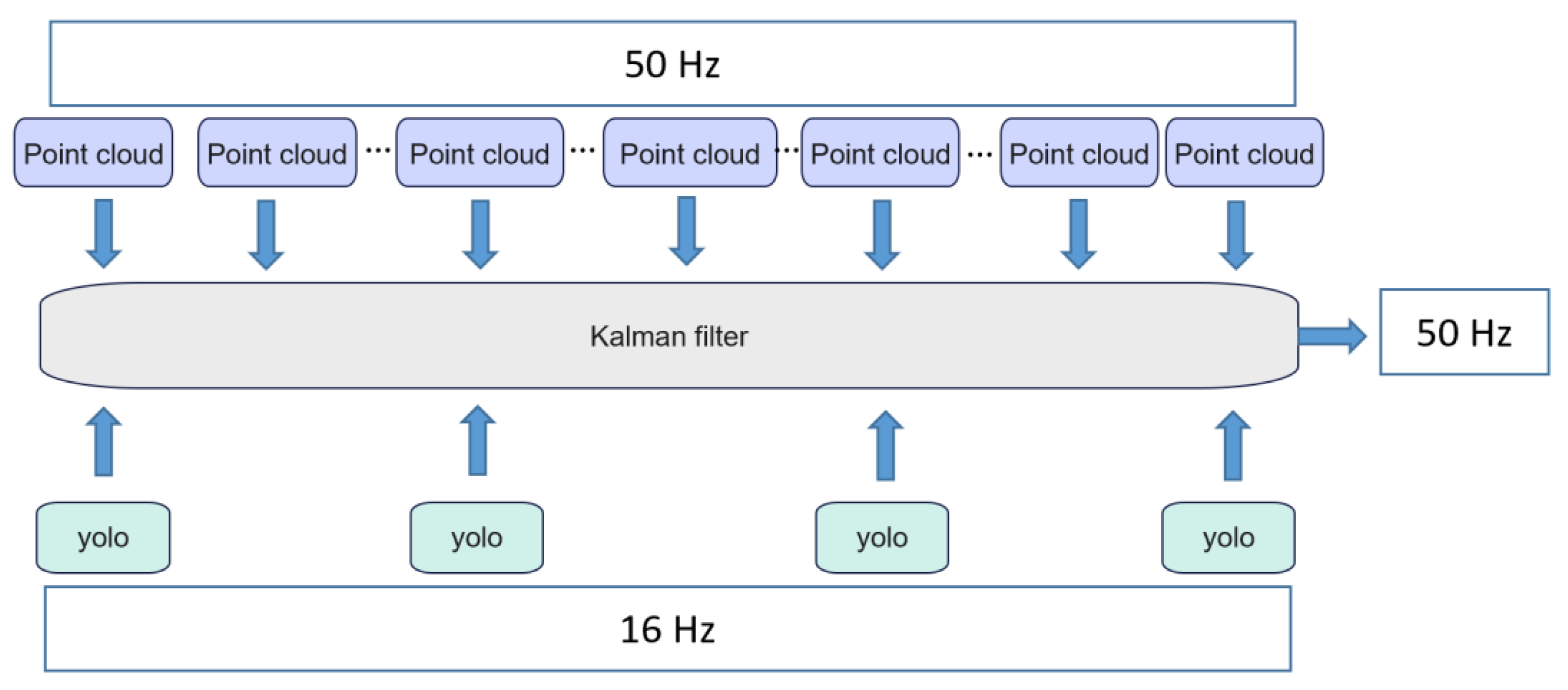
4.3.2. Tracking by Kalman Filter
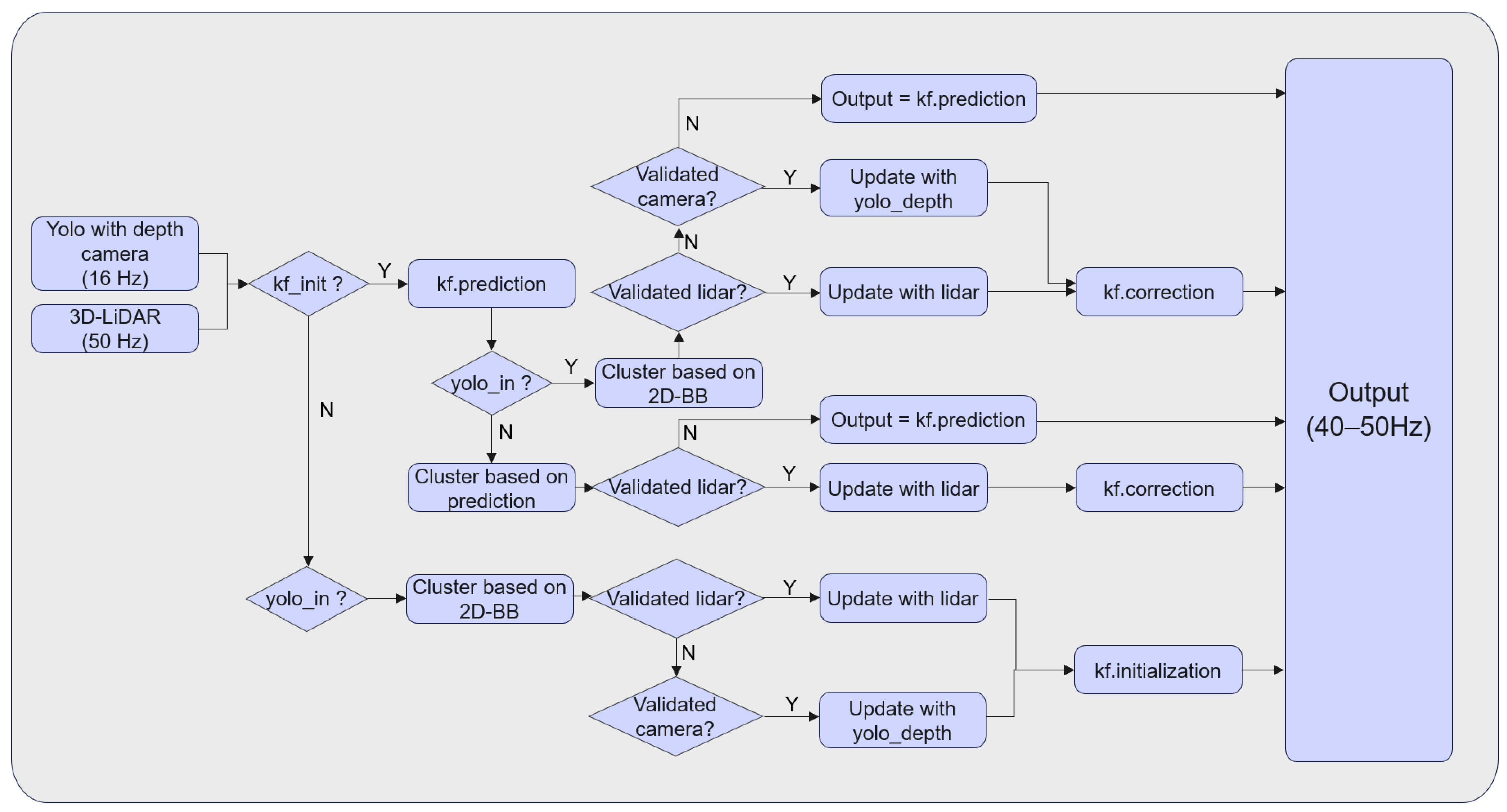
4.4. Overview of 3D Tracking Algorithm
| Algorithm 1. 3D Tracker Based on Learning Model and Filter |
| Notation: RGB image set , depth image set , LiDAR point cloud , object state , measurement , Kalman filter KF Input: RGB image depth image point cloud Output: the actual state of the object at the current moment While true do 2D-Detector.detect(, ) if confidence value > 0.9 then = Detector.output() end if end while While true do if object detected then update by fusing and Detector.output() if KF initiated then KF.predict() if validated measurement then = KF.correct(, KF.predict()) continue else = KF.predict() continue end if else initiate KF continue end if else if KF initiated then KF.predict() point cloud process() if validated measurement then = KF.correct(, KF.predict()) continue else = KF.predict() continue end if else continue end if end while |
5. Results and Discussion
5.1. Training Result for YOLOv4-Tiny Model on Custom Dataset
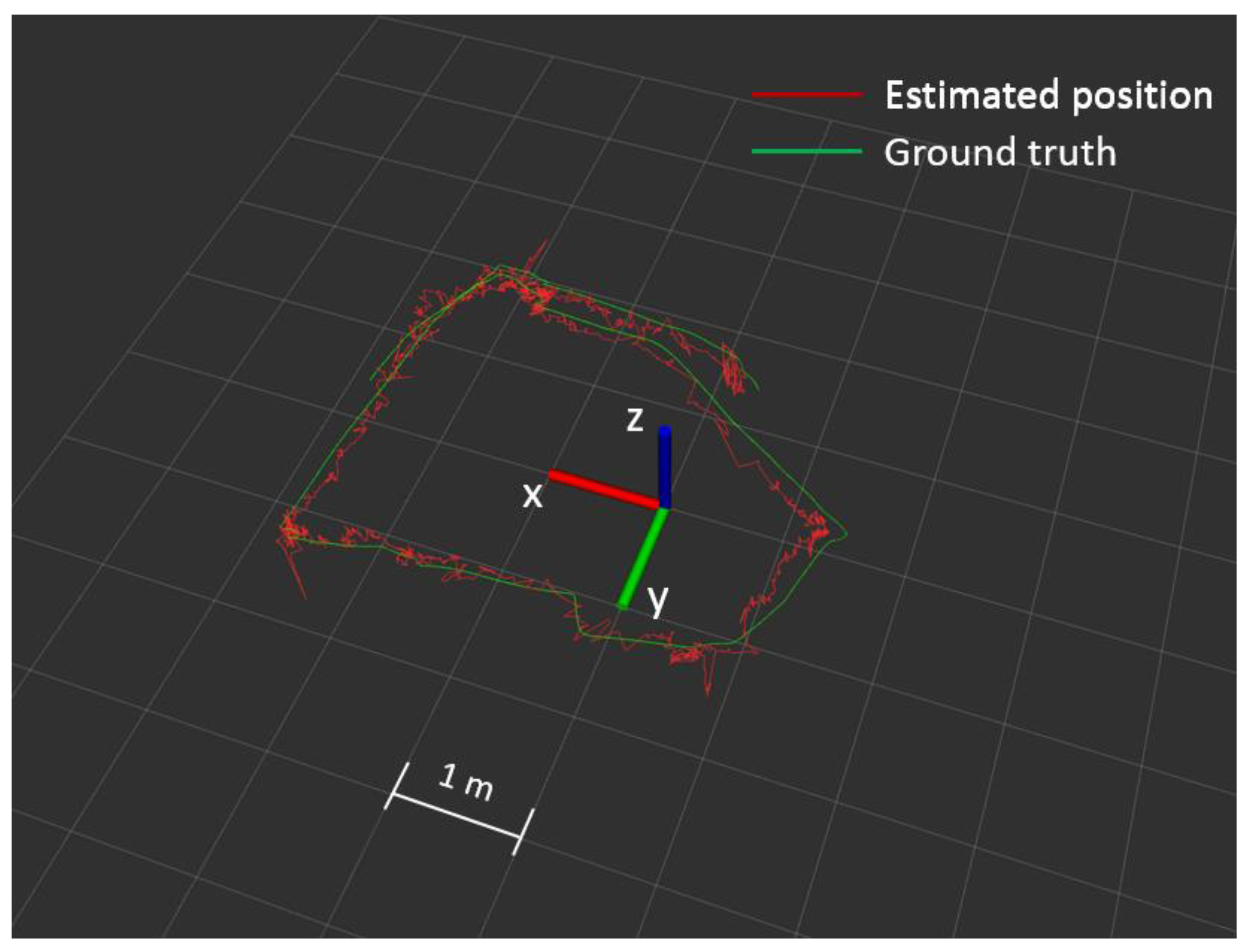
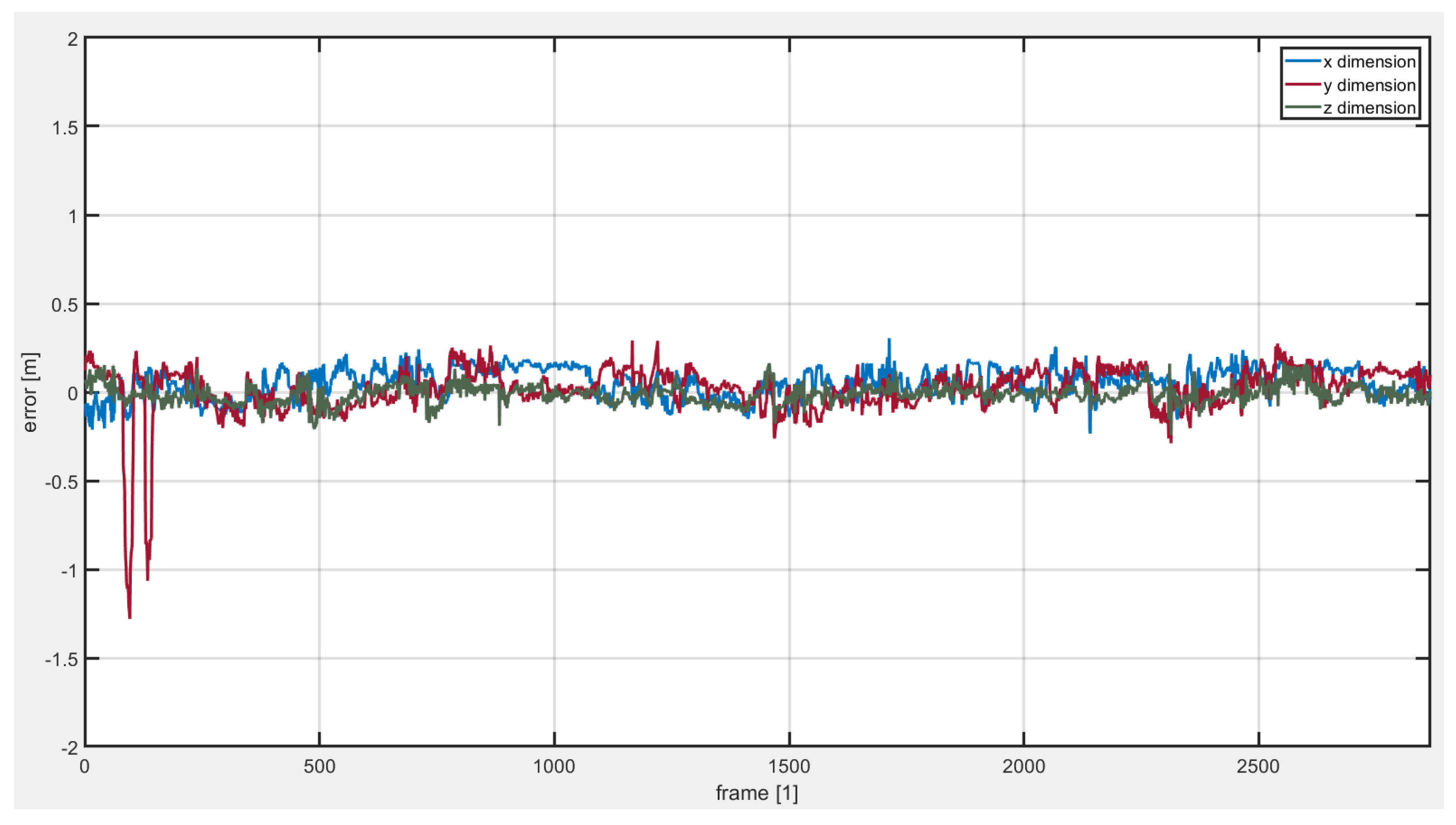
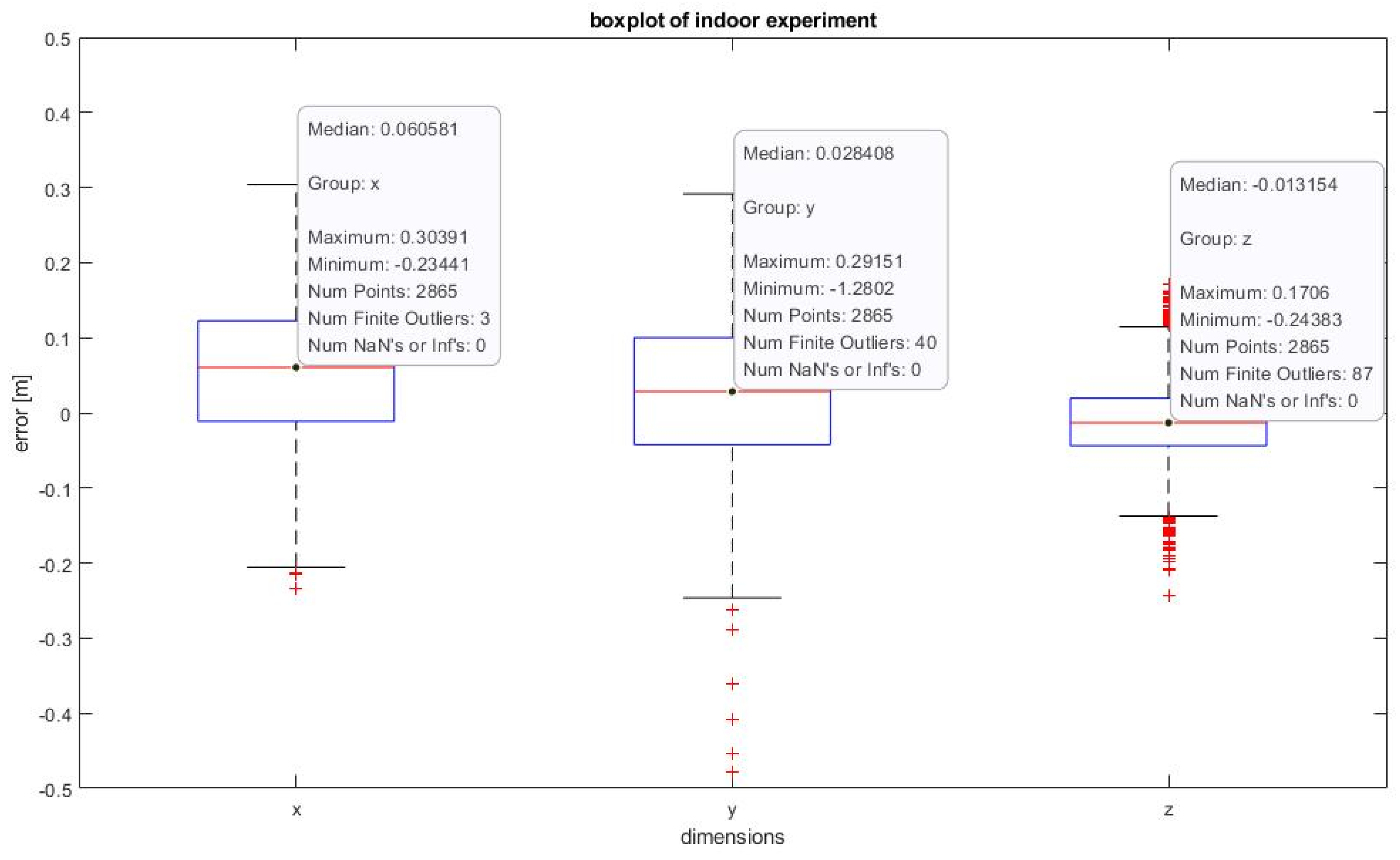
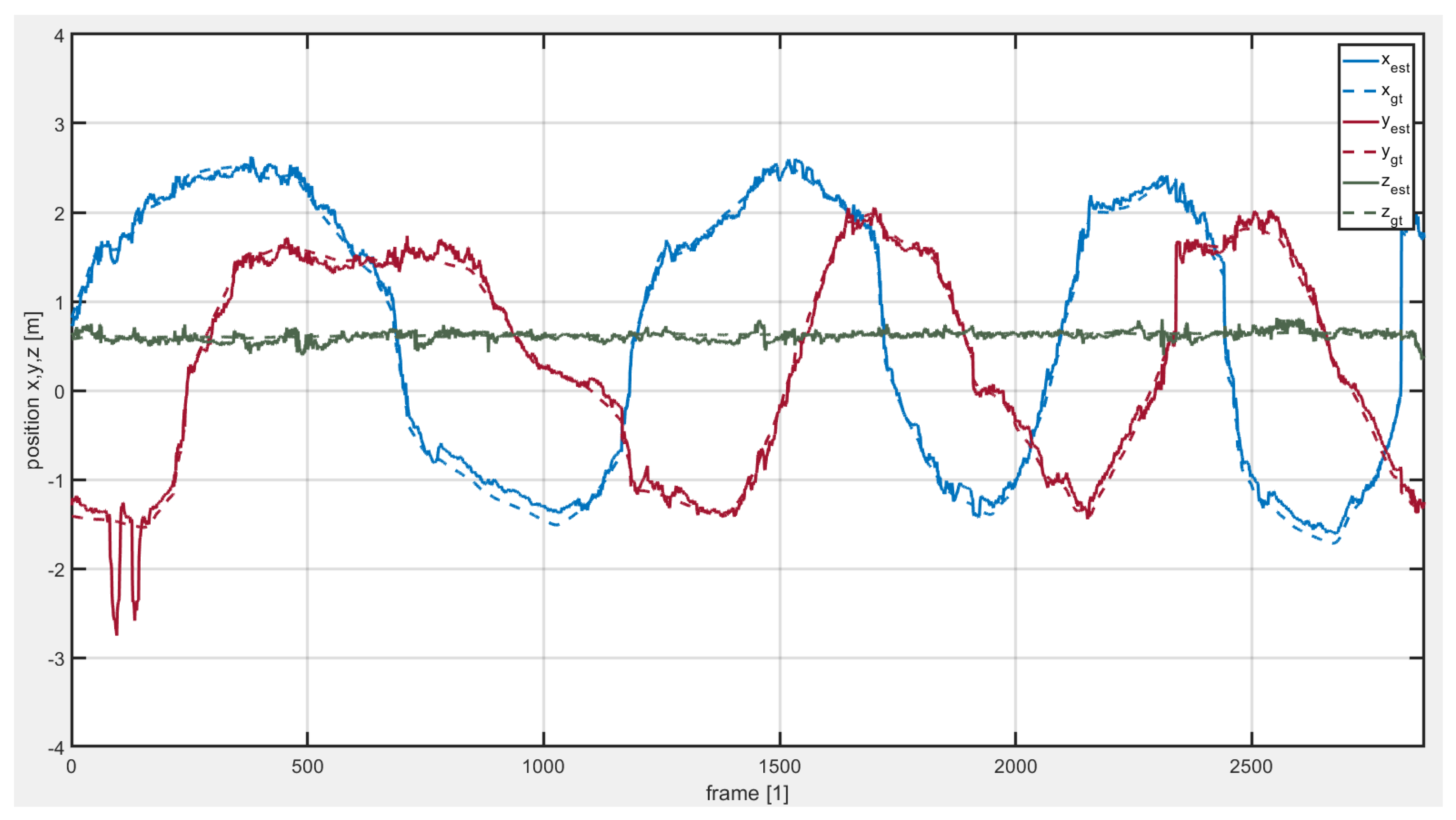
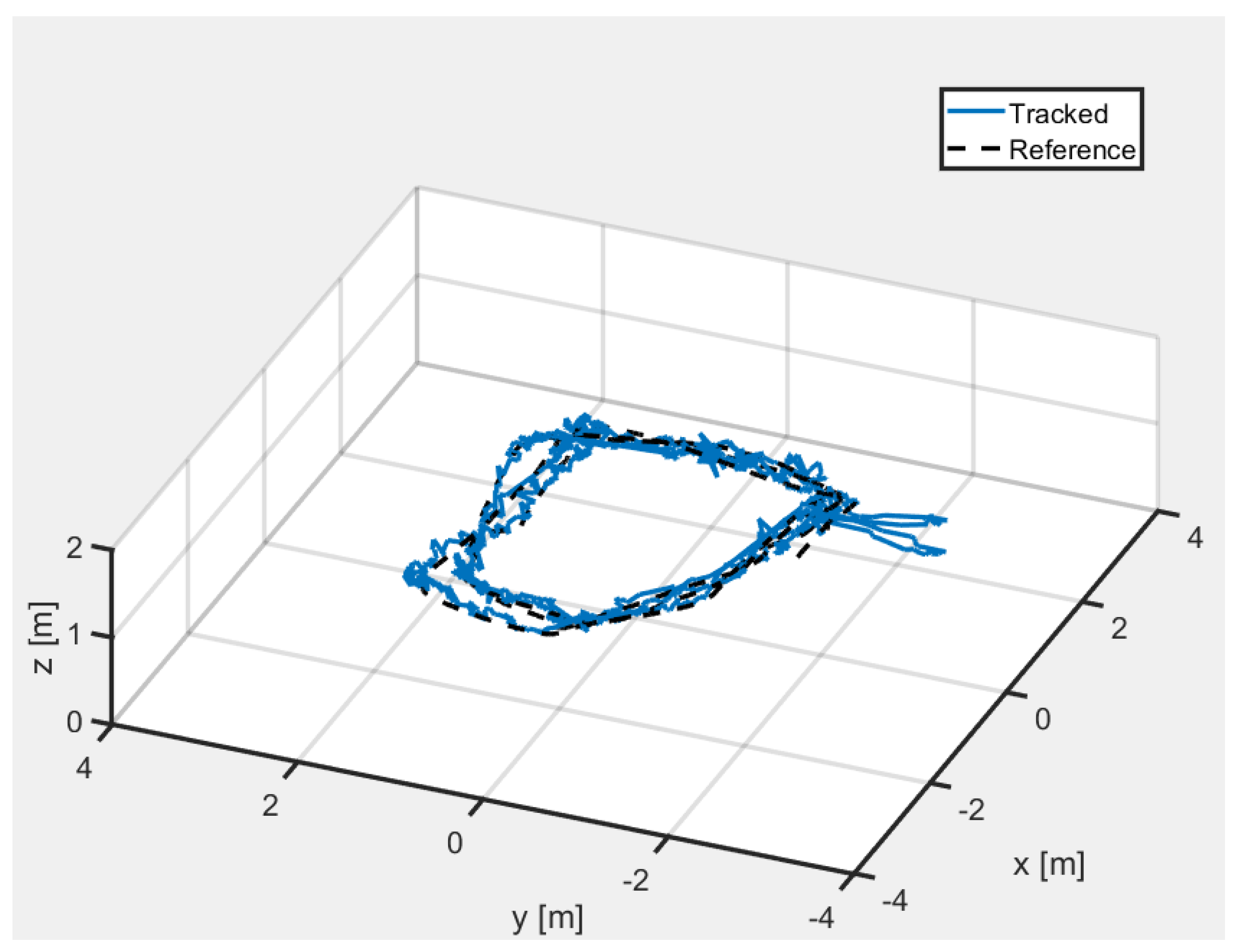
5.2. Indoor Experiment for 3D Position Estimation in VICON Environment
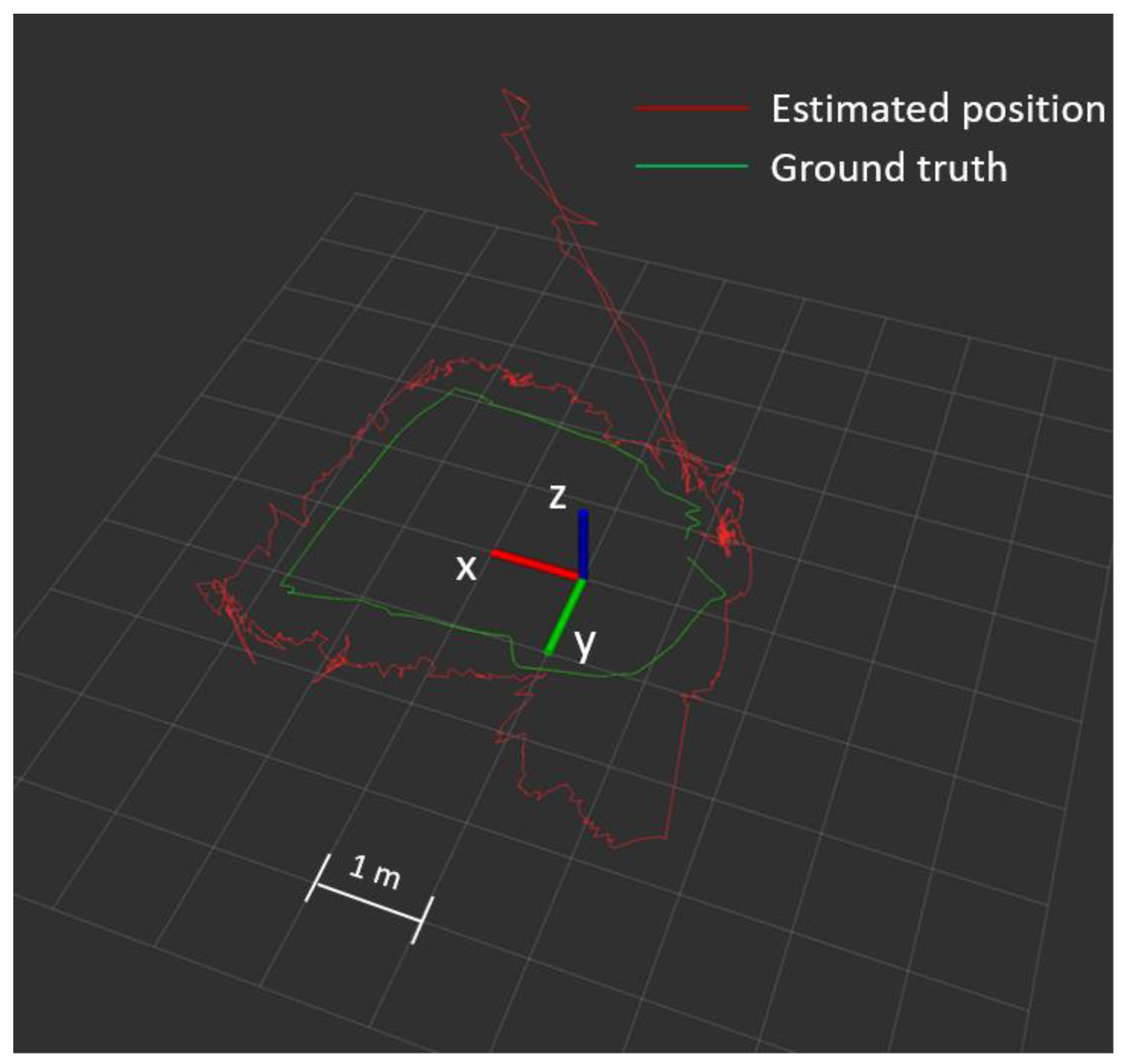
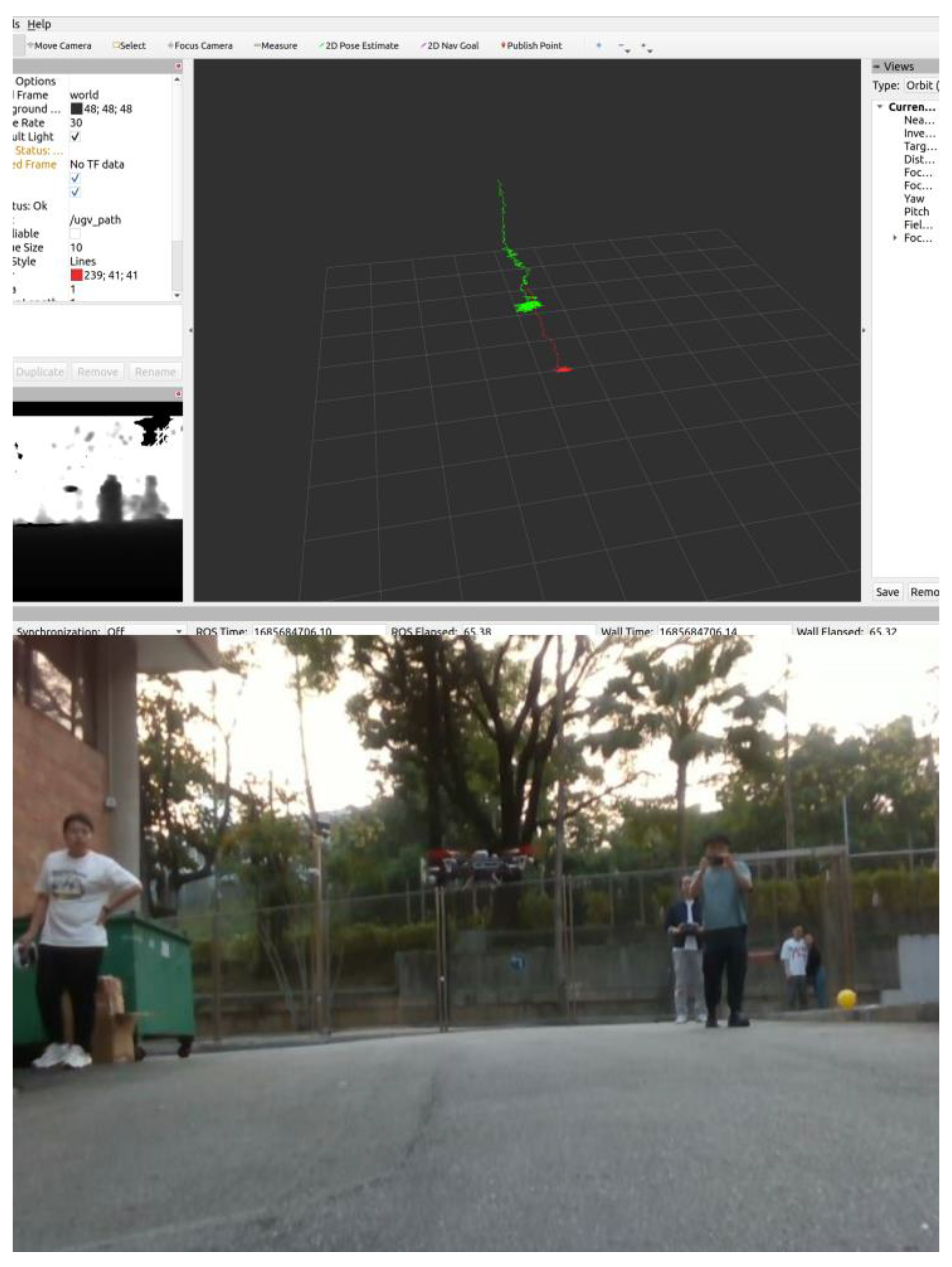
5.3. Filed Test in Outdoor Environment with LiDAR-Inertial Odometry (LIO)
5.4. Limitation Study
6. Conclusions
7. Future Work
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| FPS | Frames Per Second |
| IOU | Intersection over Union |
| ROI | Region of Interest |
| LiDAR | Light Detection and Ranging |
| GNSS | Global Navigation Satellite System |
| GM-APD | Geiger-Mode Avalanche Photodiode |
| DNN | Deep Neural Network |
| RANSAC | Random Sample Consensus |
| CPU | Central Processing Unit |
| mAP | Mean Average Precision |
| ROS | Robot Operating System |
| RMSE | Root Mean Square Error |
| UAV | Unmanned Aerial Vehicles |
| UGV | Unmanned Ground Vehicles |
| LIO | LiDAR Inertial Odometry |
| DOF | Degree of Freedom |
| PTP | Precision Time Protocol |
| GPS | Global Positioning System |
| PPS | Pulse Per Second |
| FOV | Field of View |
| R-CNN | Region-based Convolutional Neural Network |
| 2D-BB | Two-dimensional Bounding Box |
| YOLO | You Only Look Once algorithm. |
References
- Pretto, A.; Aravecchia, S.; Burgard, W.; Chebrolu, N.; Dornhege, C.; Falck, T.; Fleckenstein, F.; Fontenla, A.; Imperoli, M.; Khanna, R.; et al. Building an Aerial–Ground Robotics System for Precision Farming: An Adaptable Solution. IEEE Robot. Autom. Mag. 2021, 28, 29–49. [Google Scholar] [CrossRef]
- Ni, J.; Wang, X.; Tang, M.; Cao, W.; Shi, P.; Yang, S.X. An improved real-time path planning method based on dragonfly algorithm for heterogeneous multi-robot system. IEEE Access 2020, 8, 140558–140568. [Google Scholar] [CrossRef]
- Krizmancic, M.; Arbanas, B.; Petrovic, T.; Petric, F.; Bogdan, S. Cooperative Aerial-Ground Multi-Robot System for Automated Construction Tasks. IEEE Robot. Autom. Lett. 2020, 5, 798–805. [Google Scholar] [CrossRef]
- Magid, E.; Pashkin, A.; Simakov, N.; Abbyasov, B.; Suthakorn, J.; Svinin, M.; Matsuno, F. Artificial Intelligence Based Framework for Robotic Search and Rescue Operations Conducted Jointly by International Teams. In Proceedings of the 14th International Conference on Electromechanics and Robotics “Zavalishin’s Readings” ER (ZR) 2019, Kursk, Russia, 17–20 April 2019; pp. 15–26. [Google Scholar]
- Stampa, M.; Jahn, U.; Fruhner, D.; Streckert, T.; Rohrig, C. Scenario and system concept for a firefighting UAV-UGV team. In Proceedings of the 2022 Sixth IEEE International Conference on Robotic Computing (IRC), Naples, Italy, 5–7 December 2022; pp. 253–256. [Google Scholar]
- Hu, Z.; Bai, Z.; Yang, Y.; Zheng, Z.; Bian, K.; Song, L. UAV Aided Aerial-Ground IoT for Air Quality Sensing in Smart City: Architecture, Technologies, and Implementation. IEEE Netw. 2019, 33, 14–22. [Google Scholar] [CrossRef]
- Hammer, M.; Borgmann, B.; Hebel, M.; Arens, M. UAV detection, tracking, and classification by sensor fusion of a 360 lidar system and an alignable classification sensor. In Proceedings of the Laser Radar Technology and Applications XXIV, Baltimore, MD, USA, 16–17 April 2019; pp. 99–108. [Google Scholar]
- Sier, H.; Yu, X.; Catalano, I.; Queralta, J.P.; Zou, Z.; Westerlund, T. UAV Tracking with Lidar as a Camera Sensor in GNSS-Denied Environments. In Proceedings of the 2023 International Conference on Localization and GNSS (ICL-GNSS), Castellon, Spain, 6–8 June 2023; pp. 1–7. [Google Scholar]
- Dogru, S.; Marques, L. Drone Detection Using Sparse Lidar Measurements. IEEE Robot. Autom. Lett. 2022, 7, 3062–3069. [Google Scholar] [CrossRef]
- Asvadi, A.; Girao, P.; Peixoto, P.; Nunes, U. 3D object tracking using RGB and LIDAR data. In Proceedings of the 2016 IEEE 19th International Conference on Intelligent Transportation Systems (ITSC), Rio de Janeiro, Brazil, 1–4 November 2016; pp. 1255–1260. [Google Scholar]
- Dieterle, T.; Particke, F.; Patino-Studencki, L.; Thielecke, J. Sensor data fusion of LIDAR with stereo RGB-D camera for object tracking. In Proceedings of the 2017 IEEE Sensors, Glasgow, UK, 29 October–1 November 2017; pp. 1–3. [Google Scholar]
- Lo, L.Y.; Yiu, C.H.; Tang, Y.; Yang, A.S.; Li, B.; Wen, C.Y. Dynamic Object Tracking on Autonomous UAV System for Surveillance Applications. Sensors 2021, 21, 7888. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Ye, D.H.; Kolsch, M.; Wachs, J.P.; Bouman, C.A. Fast and Robust UAV to UAV Detection and Tracking from Video. IEEE Trans. Emerg. Top. Comput. 2022, 10, 1519–1531. [Google Scholar] [CrossRef]
- Liu, L.; He, J.; Ren, K.; Xiao, Z.; Hou, Y. A LiDAR–Camera Fusion 3D Object Detection Algorithm. Information 2022, 13, 169. [Google Scholar] [CrossRef]
- An, P.; Liang, J.; Yu, K.; Fang, B.; Ma, J. Deep structural information fusion for 3D object detection on LiDAR–camera system. Comput. Vis. Image Underst. 2022, 214, 103295. [Google Scholar] [CrossRef]
- Faessler, M.; Mueggler, E.; Schwabe, K.; Scaramuzza, D. A monocular pose estimation system based on infrared leds. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 907–913. [Google Scholar]
- Censi, A.; Strubel, J.; Brandli, C.; Delbruck, T.; Scaramuzza, D. Low-latency localization by active LED markers tracking using a dynamic vision sensor. In Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems, Tokyo, Japan, 3–7 November 2013; pp. 891–898. [Google Scholar]
- Hartmann, B.; Link, N.; Trommer, G.F. Indoor 3D position estimation using low-cost inertial sensors and marker-based video-tracking. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 319–326. [Google Scholar]
- Eberli, D.; Scaramuzza, D.; Weiss, S.; Siegwart, R. Vision Based Position Control for MAVs Using One Single Circular Landmark. J. Intell. Robot. Syst. 2010, 61, 495–512. [Google Scholar] [CrossRef]
- Chang, C.-W.; Lo, L.-Y.; Cheung, H.C.; Feng, Y.; Yang, A.-S.; Wen, C.-Y.; Zhou, W. Proactive guidance for accurate UAV landing on a dynamic platform: A visual–inertial approach. Sensors 2022, 22, 404. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Choi, W.; Diaz, J.; Trott, C. The 3D Position Estimation and Tracking of a Surface Vehicle Using a Mono-Camera and Machine Learning. Electronics 2022, 11, 2141. [Google Scholar] [CrossRef]
- Chen, H.; Wen, C.Y.; Gao, F.; Lu, P. Flying in Dynamic Scenes with Multitarget Velocimetry and Perception-Enhanced Planning. IEEE Asme T Mech 2023. [Google Scholar] [CrossRef]
- Quentel, A. A Scanning LiDAR for Long Range Detection and Tracking of UAVs; Normandie Université: Caen, France, 2021. [Google Scholar]
- Qingqing, L.; Xianjia, Y.; Queralta, J.P.; Westerlund, T. Adaptive Lidar Scan Frame Integration: Tracking Known MAVs in 3D Point Clouds. In Proceedings of the 2021 20th International Conference on Advanced Robotics (ICAR), Ljubljana, Slovenia, 6–10 December 2021; pp. 1079–1086. [Google Scholar]
- Qi, H.; Feng, C.; Cao, Z.; Zhao, F.; Xiao, Y. P2b: Point-to-box network for 3d object tracking in point clouds. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 14–19 June 2020; pp. 6329–6338. [Google Scholar]
- Ding, Y.; Qu, Y.; Zhang, Q.; Tong, J.; Yang, X.; Sun, J. Research on UAV Detection Technology of Gm-APD Lidar Based on YOLO Model. In Proceedings of the 2021 IEEE International Conference on Unmanned Systems (ICUS), Beijing, China, 15–17 October 2021; pp. 105–109. [Google Scholar]
- Chen, S.; Feng, Y.; Wen, C.-Y.; Zou, Y.; Chen, W. Stereo Visual Inertial Pose Estimation Based on Feedforward and Feedbacks. IEEE/ASME Trans. Mechatron. 2023, 1–11. [Google Scholar] [CrossRef]
- Gao, X.-S.; Hou, X.-R.; Tang, J.; Cheng, H.-F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Bradski, G. The openCV library. Dr. Dobb’s J. Softw. Tools Prof. Program. 2000, 25, 120–123. [Google Scholar]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 779–788. [Google Scholar]
- Bochkovskiy, A.; Wang, C.-Y.; Liao, H.-Y.M. Yolov4: Optimal speed and accuracy of object detection. arXiv 2020, arXiv:2004.10934. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Tzutalin, D. LabelImg. GitHub Repository. Available online: https://github.com/HumanSignal/labelImg (accessed on 5 October 2015).
- Feng, Y.; Tse, K.; Chen, S.; Wen, C.Y.; Li, B. Learning-Based Autonomous UAV System for Electrical and Mechanical (E&M) Device Inspection. Sensors 2021, 21, 1385. [Google Scholar] [CrossRef]
- Xu, W.; Zhang, F. FAST-LIO: A Fast, Robust LiDAR-Inertial Odometry Package by Tightly-Coupled Iterated Kalman Filter. IEEE Robot. Autom. Lett. 2021, 6, 3317–3324. [Google Scholar] [CrossRef]
- Jiang, B.; Li, B.; Zhou, W.; Lo, L.-Y.; Chen, C.-K.; Wen, C.-Y. Neural network based model predictive control for a quadrotor UAV. Aerospace 2022, 9, 460. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, F.; Hong, X. Low-Cost Retina-Like Robotic Lidars Based on Incommensurable Scanning. IEEE/ASME Trans. Mechatron. 2022, 27, 58–68. [Google Scholar] [CrossRef]







| Method | Backbone | Resolutions | |
|---|---|---|---|
| YOLOv4-Tiny | CSPDarknet-53-tiny | 320 × 320 | 94.17% |
| 416 × 416 | 97.52% | ||
| 512 × 512 | 98.28% | ||
| 608 × 608 | 98.63% |
| Method | Resolutions | FPS (CSPDarknet-53-Tiny) | FPS (NCNN) |
|---|---|---|---|
| YOLOv4-Tiny | 320 × 320 | 22 | 30 |
| 416 × 416 | 20 | 26 | |
| 512 × 512 | 17 | 21 | |
| 608 × 608 | 12 | 17 |
| Method | Backbone | Resolutions | (Without Background Trained) | (With Background Trained) |
|---|---|---|---|---|
| YOLOv4-Tiny | CSPDarknet-53-tiny | 320 × 320 | 92.17% | 96.22% |
| 416 × 416 | 95.52% | 98.67% | ||
| 512 × 512 | 96.28% | 98.55% | ||
| 608 × 608 | 96.63% | 98.89% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Wen, C.-Y. A Low-Cost Relative Positioning Method for UAV/UGV Coordinated Heterogeneous System Based on Visual-Lidar Fusion. Aerospace 2023, 10, 924. https://doi.org/10.3390/aerospace10110924
Luo H, Wen C-Y. A Low-Cost Relative Positioning Method for UAV/UGV Coordinated Heterogeneous System Based on Visual-Lidar Fusion. Aerospace. 2023; 10(11):924. https://doi.org/10.3390/aerospace10110924
Chicago/Turabian StyleLuo, Haojun, and Chih-Yung Wen. 2023. "A Low-Cost Relative Positioning Method for UAV/UGV Coordinated Heterogeneous System Based on Visual-Lidar Fusion" Aerospace 10, no. 11: 924. https://doi.org/10.3390/aerospace10110924
APA StyleLuo, H., & Wen, C.-Y. (2023). A Low-Cost Relative Positioning Method for UAV/UGV Coordinated Heterogeneous System Based on Visual-Lidar Fusion. Aerospace, 10(11), 924. https://doi.org/10.3390/aerospace10110924






