A Model and Methodology for Probability Assessment of Foreign Objects Crossing through an Aircraft Propeller
Abstract
:1. Introduction
- Development of a novel concentric-spherical foreign object substitution model that offers greater versatility and can accommodate various existing configurations of foreign objects;
- Proposal of a numerical simulation algorithm for determining foreign object collisions based on the high-fidelity FEA model of the propeller. This algorithm enables accurate quantification of the probability of foreign object collisions or the traversal of the engine propeller;
- Derivation of analytical models for evaluating the propeller-crossing probability in typical foreign object substitution configurations. These models are combined with the proposed numerical simulation algorithm to validate its usability and accuracy.
2. Methodology
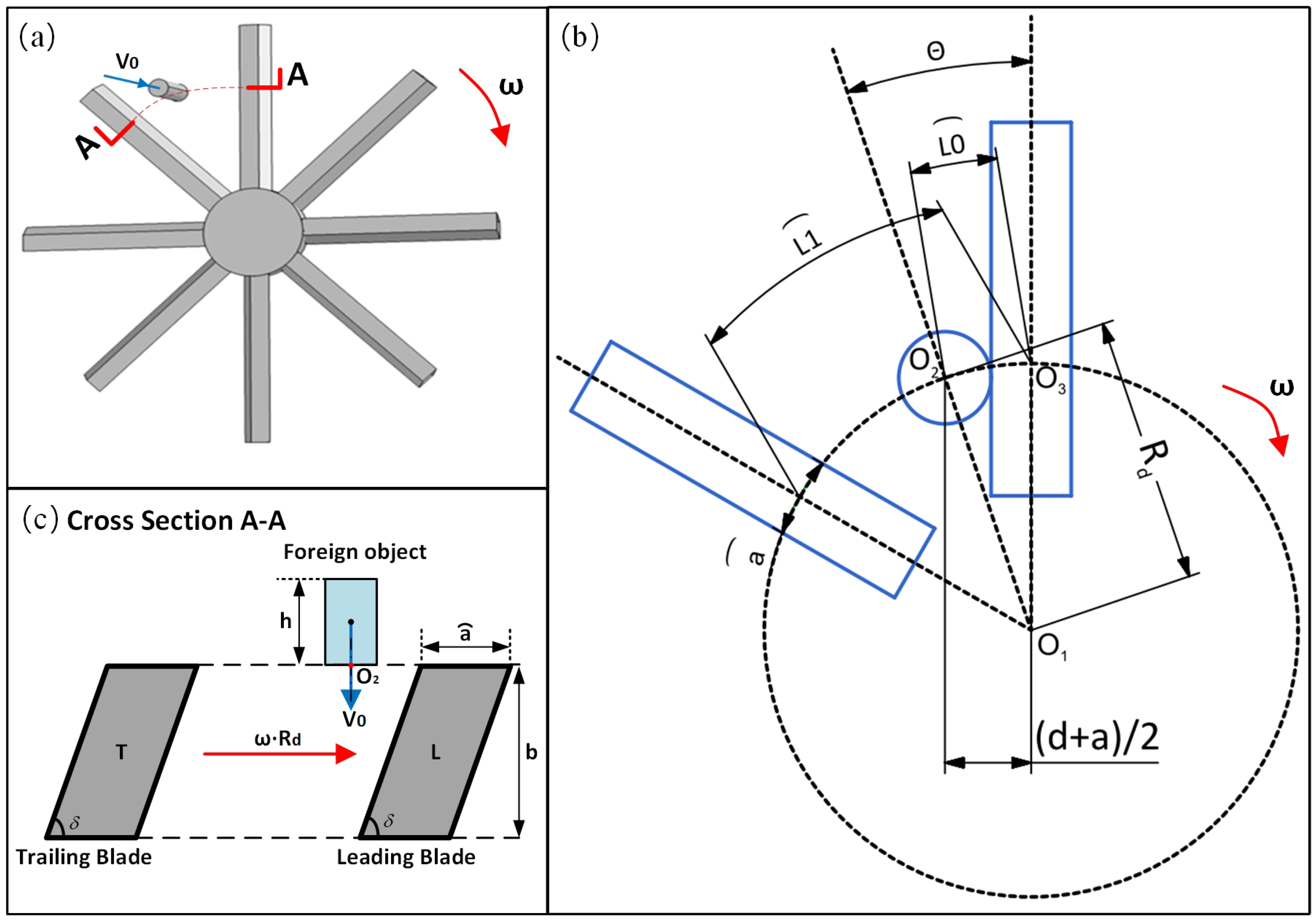
2.1. Model Assumption
2.2. Propeller-Crossing Modeling
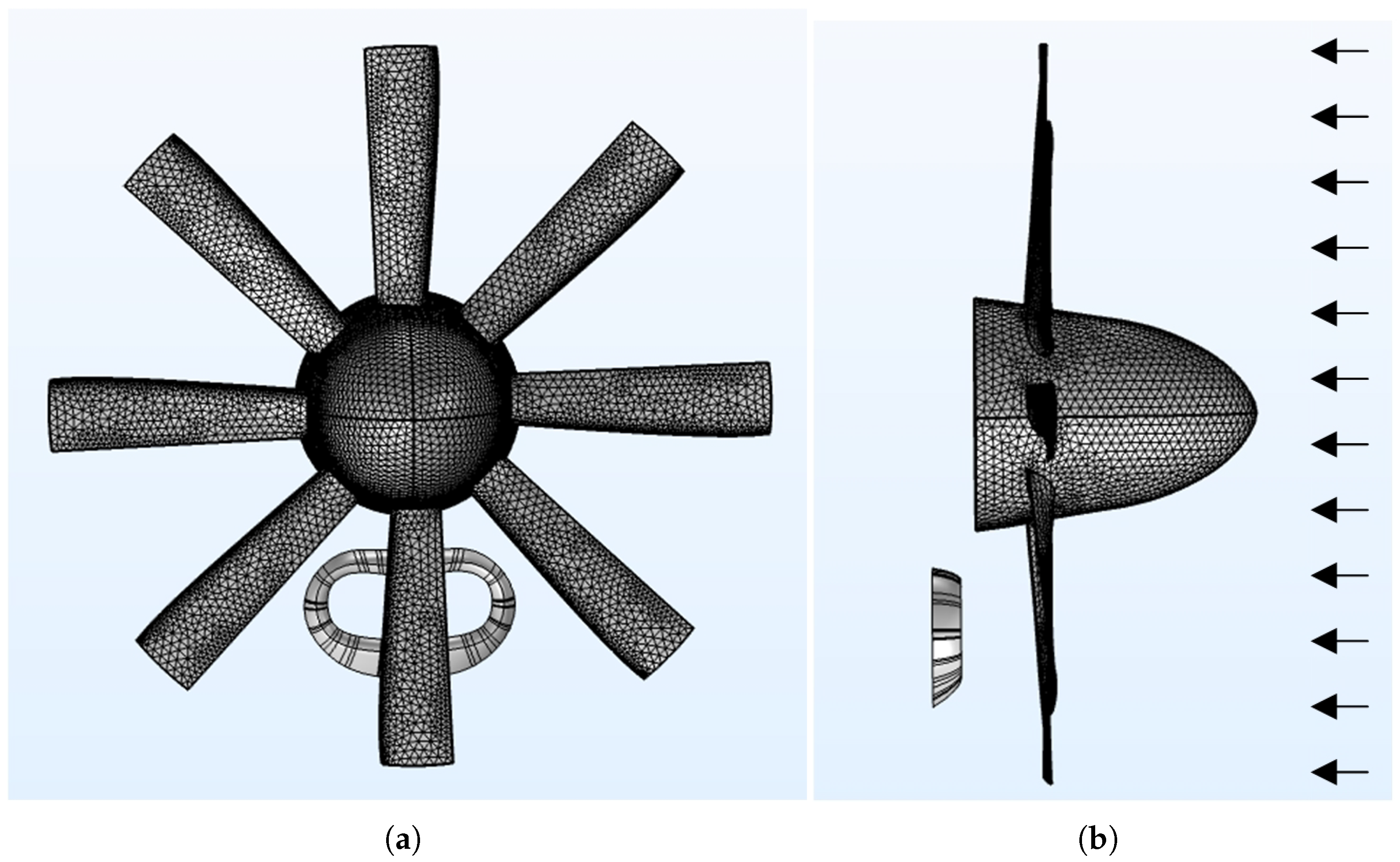
2.2.1. Discretization Model of Turboprop Propeller
2.2.2. Concentric-Spherical Foreign Object Model
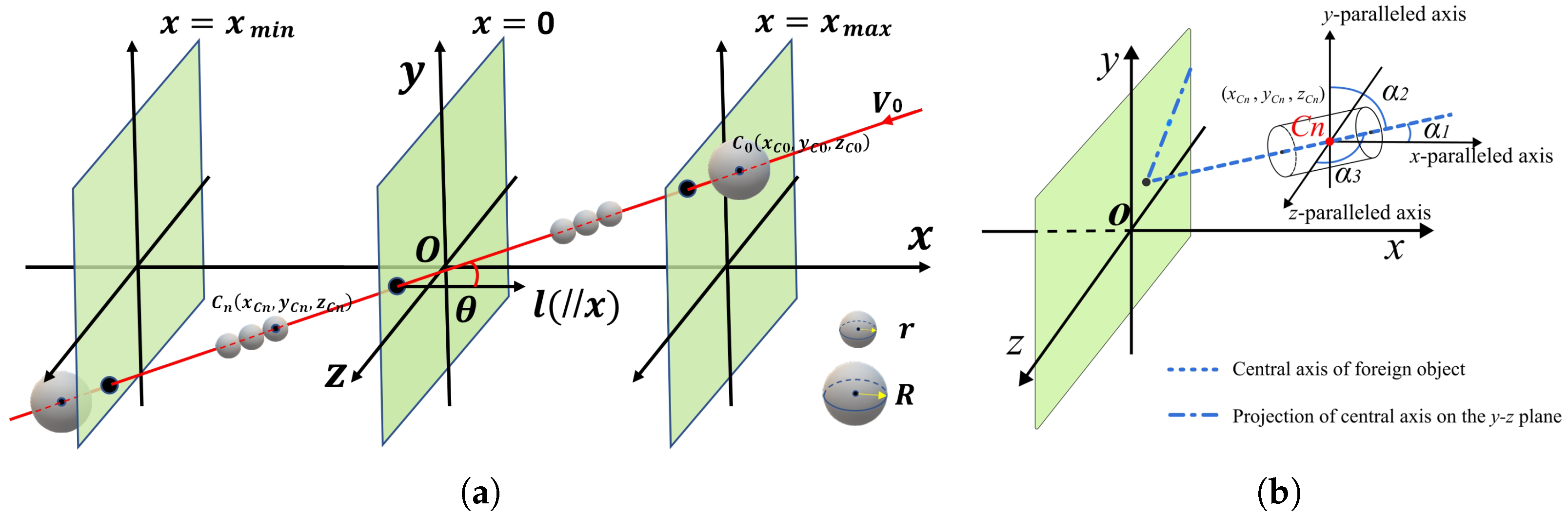
2.2.3. Crossing Process Modeling
2.3. Criteria for Propeller Crossing
2.3.1. Consideration of the Flight Trajectory
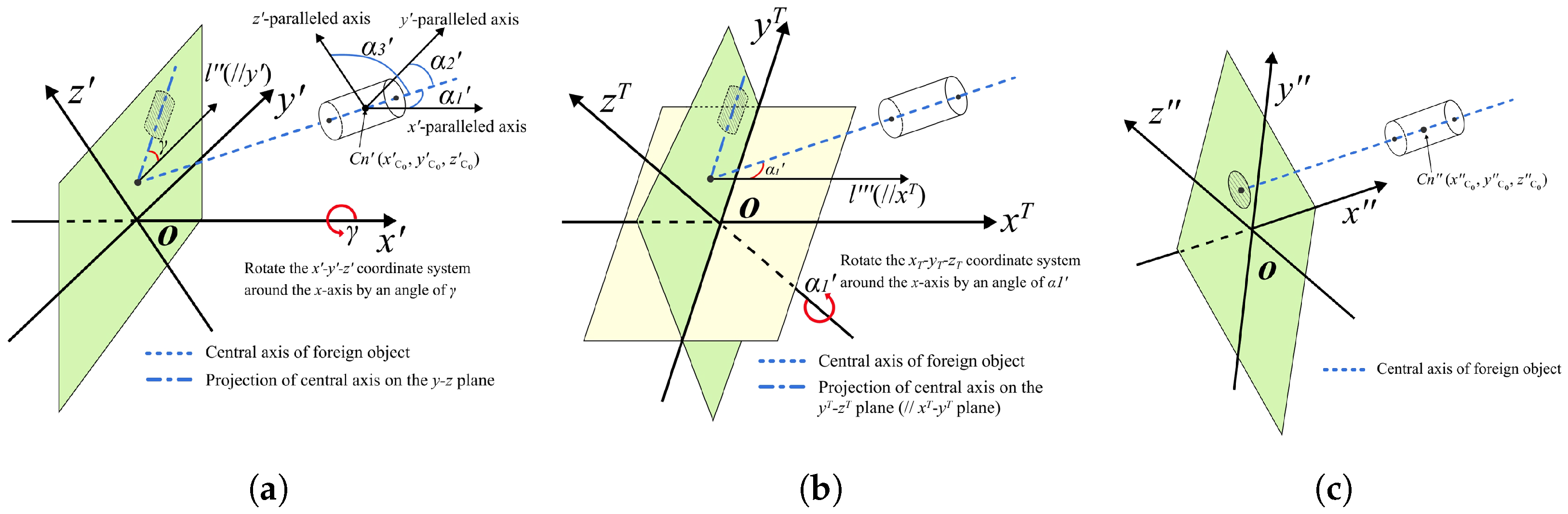
2.3.2. Consideration of the Attitude Angles
2.3.3. Refined Criteria for Typical Foreign Object Configurations
2.4. Algorithm for Propeller-Crossing Probability
| Algorithm 1: Calculating the Probability of Propeller Crossing |
 |
3. Scientific Demonstration
3.1. Geometric Relations in the Crossing Process
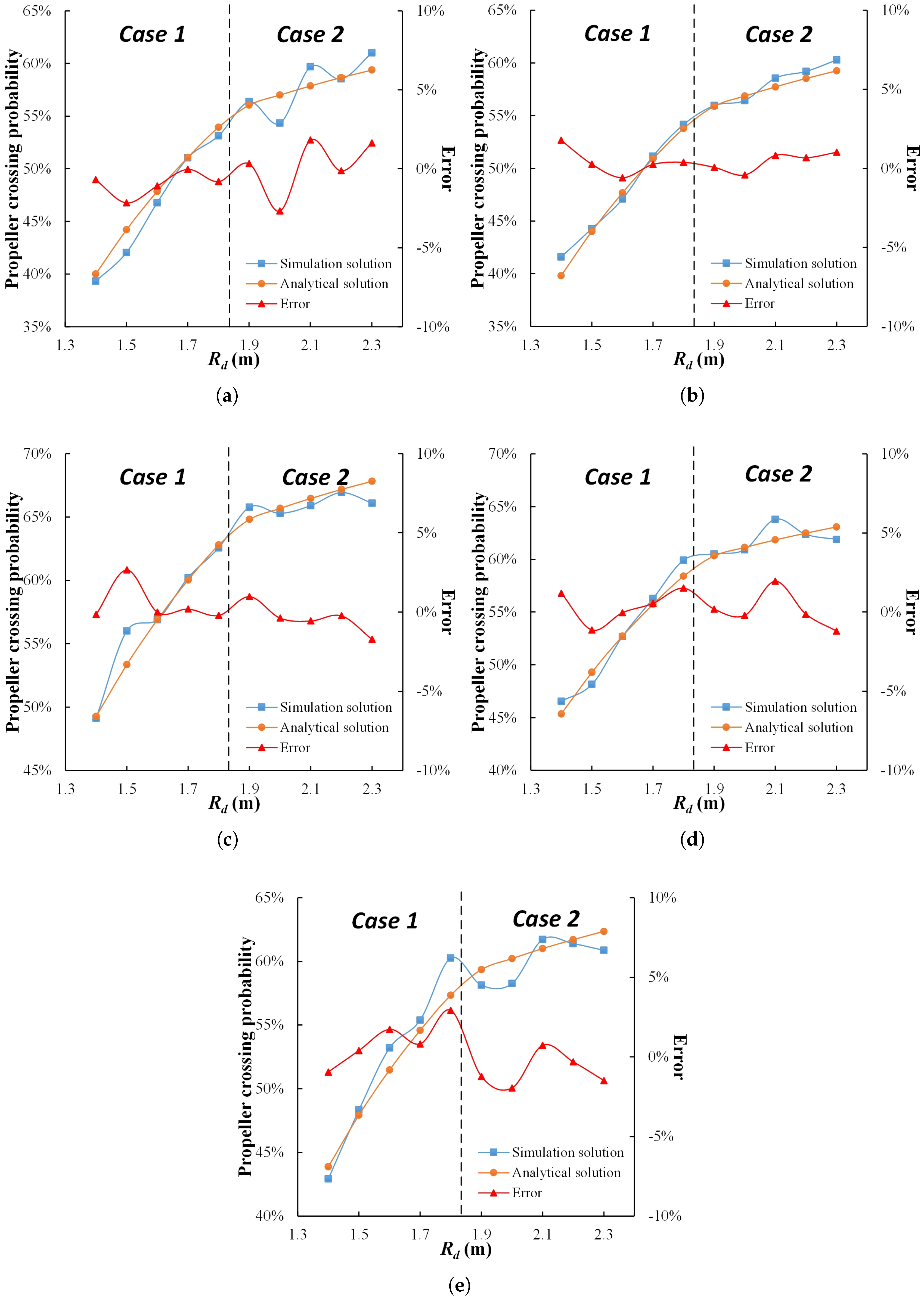
3.2. Model Validation
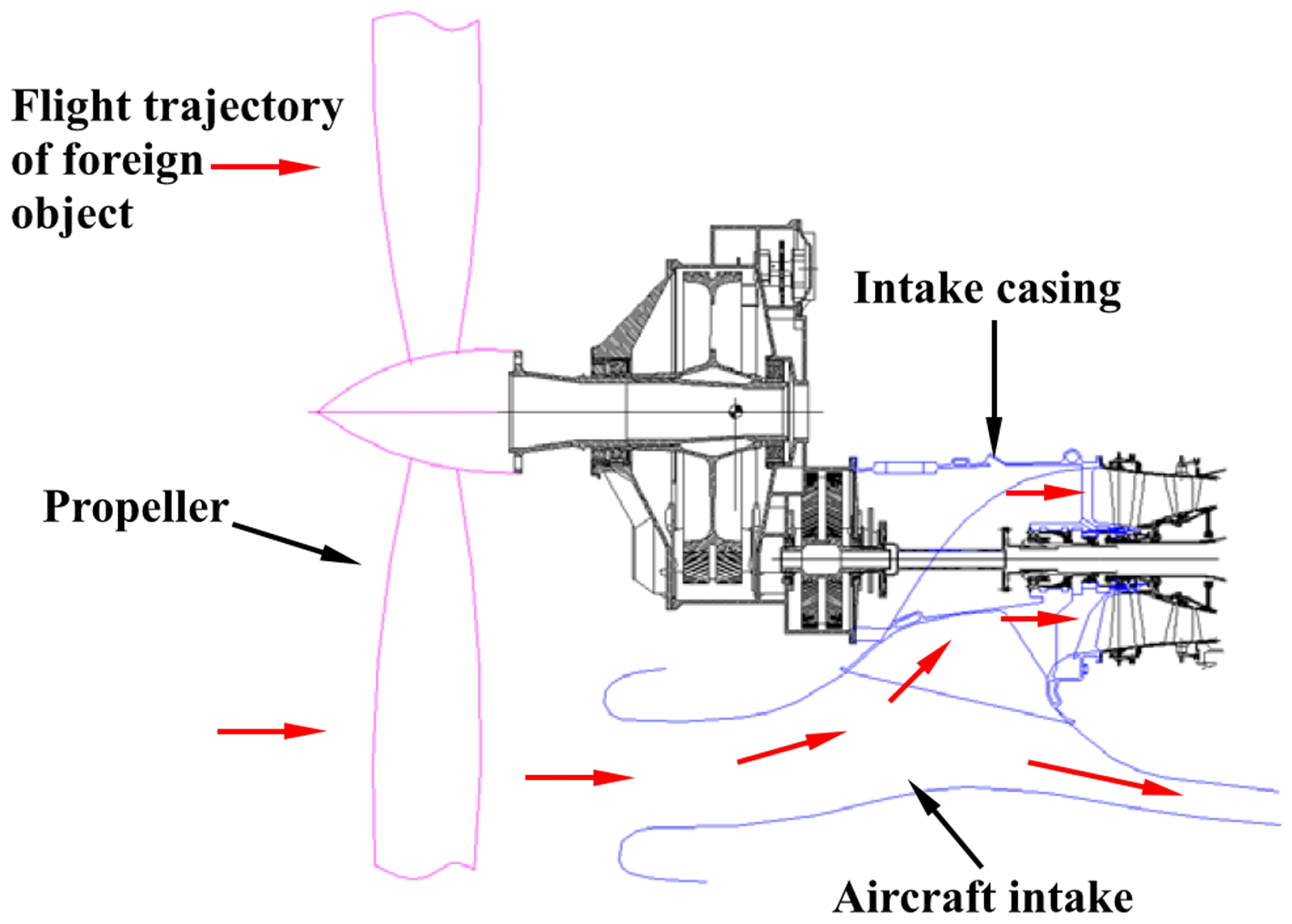
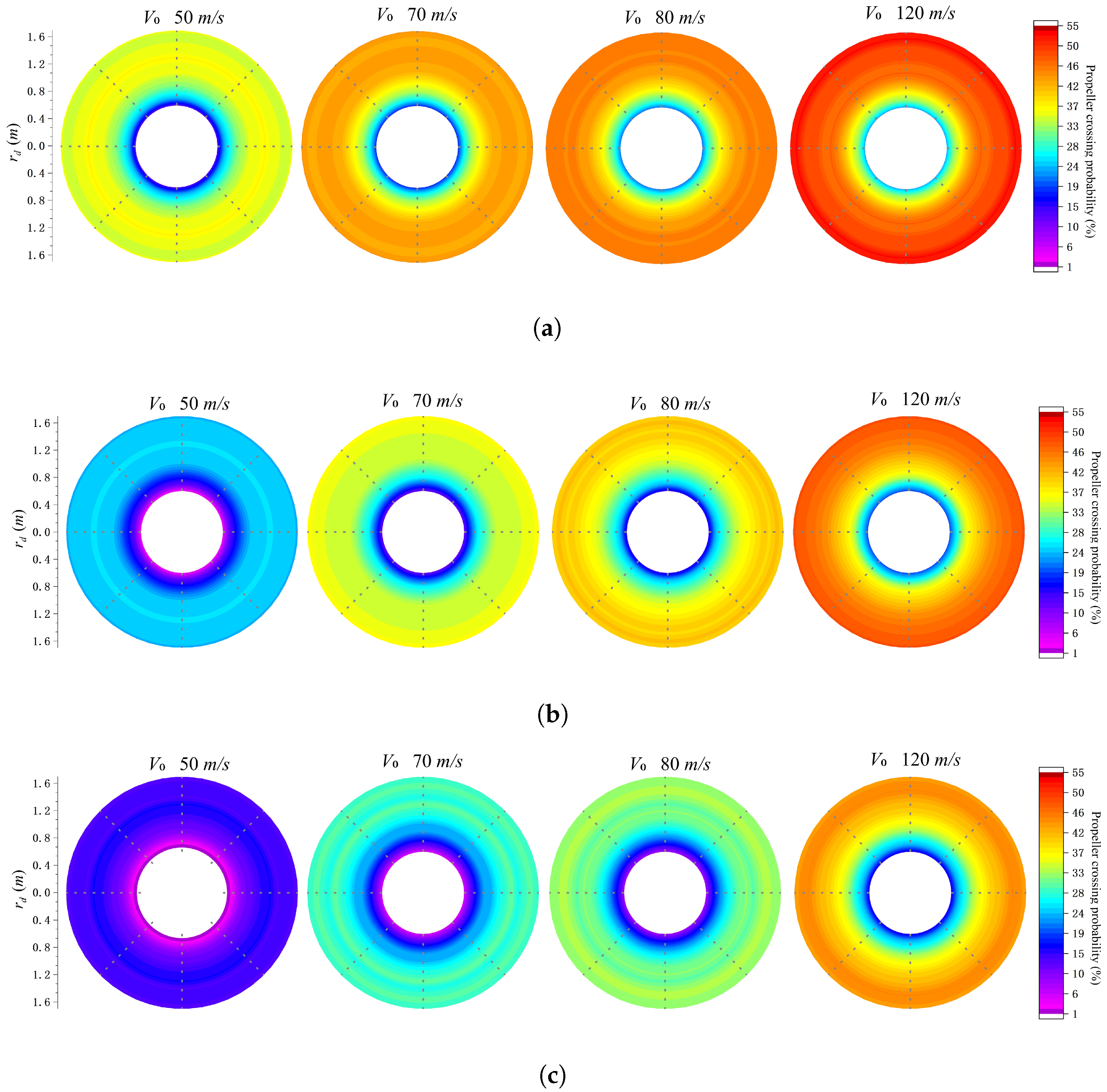
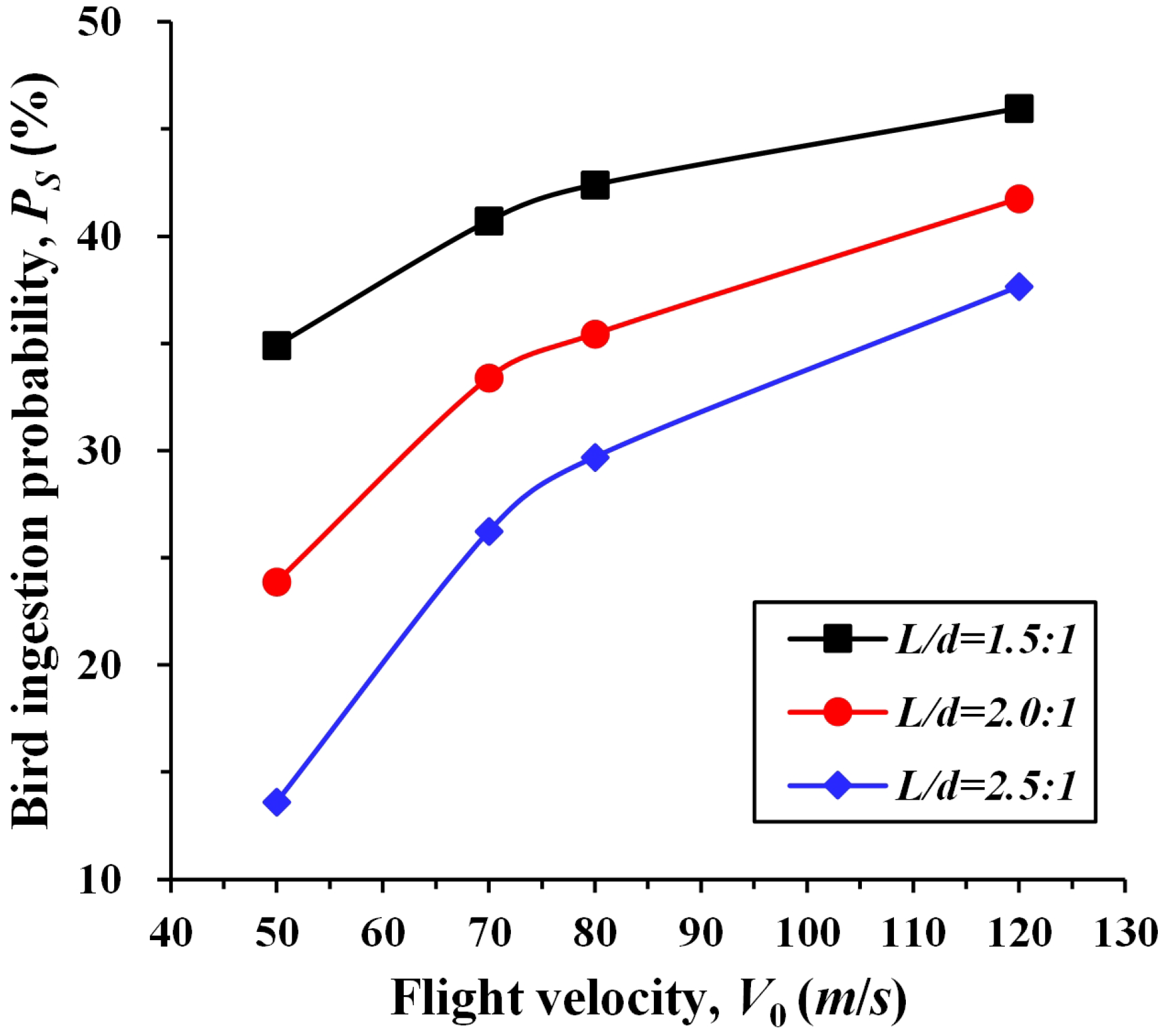
4. Application to bird-ingestion Probability of Turboprop Engine Intake
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Derivation of the Crossing Probability for Analytical Models
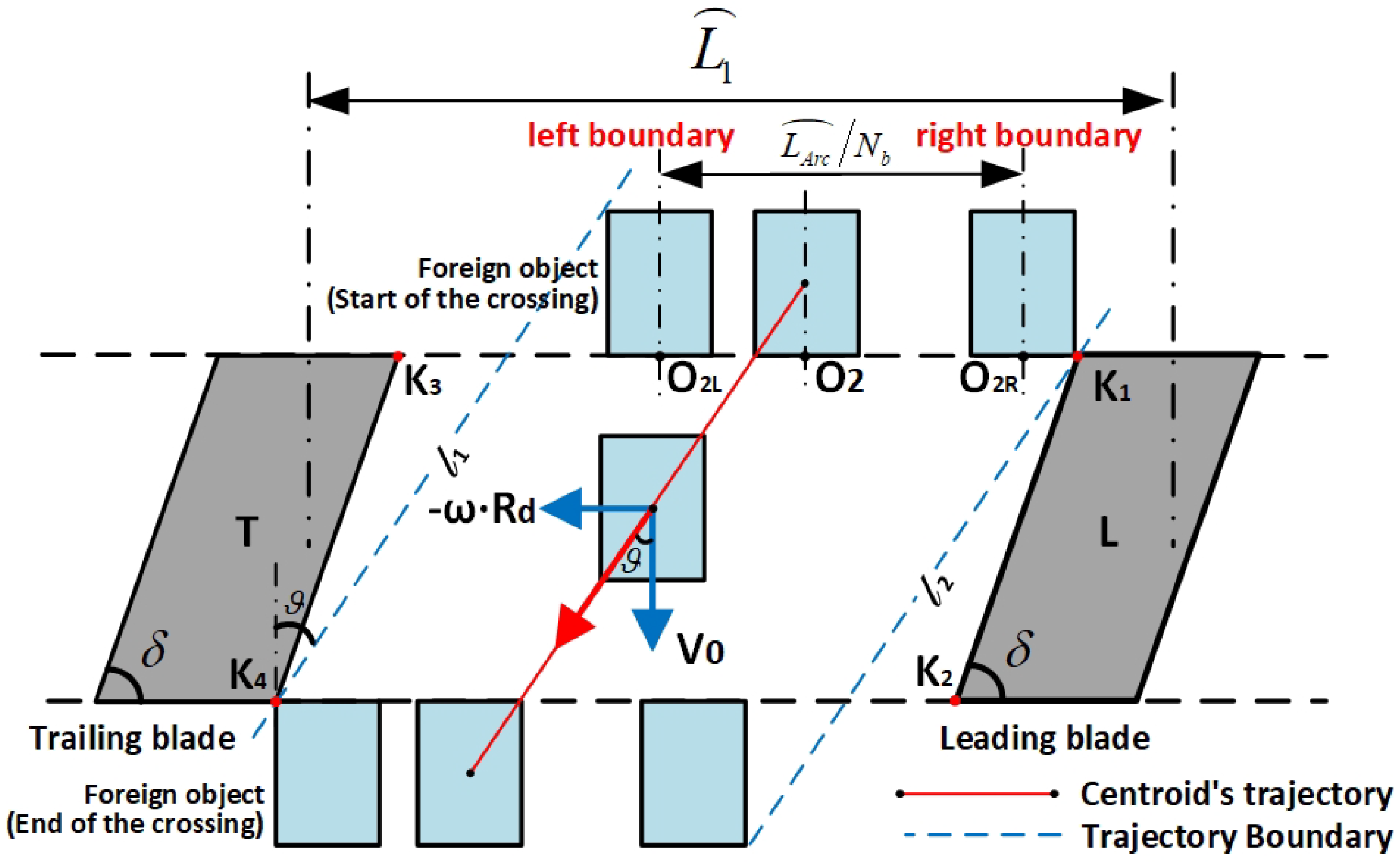
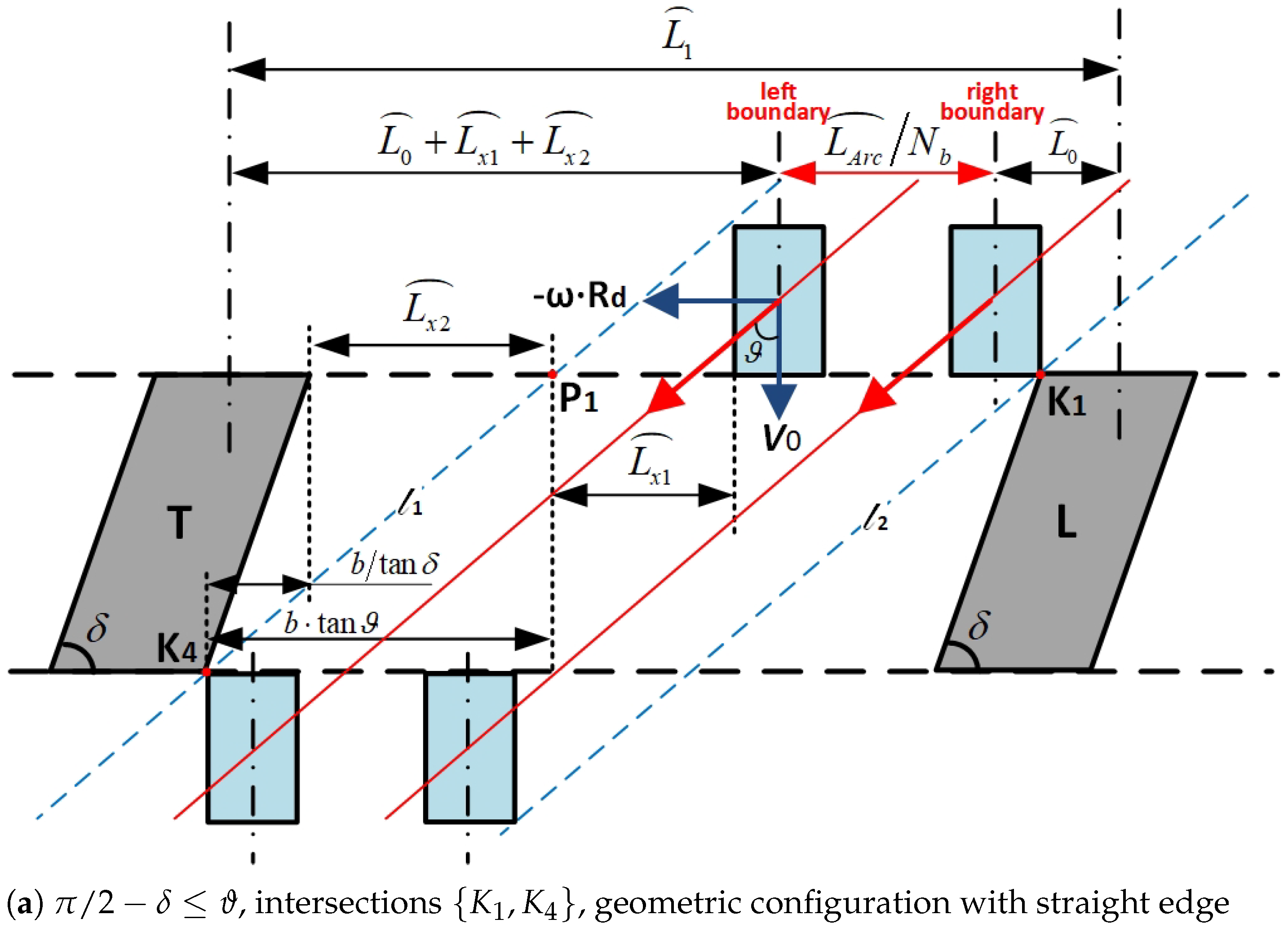
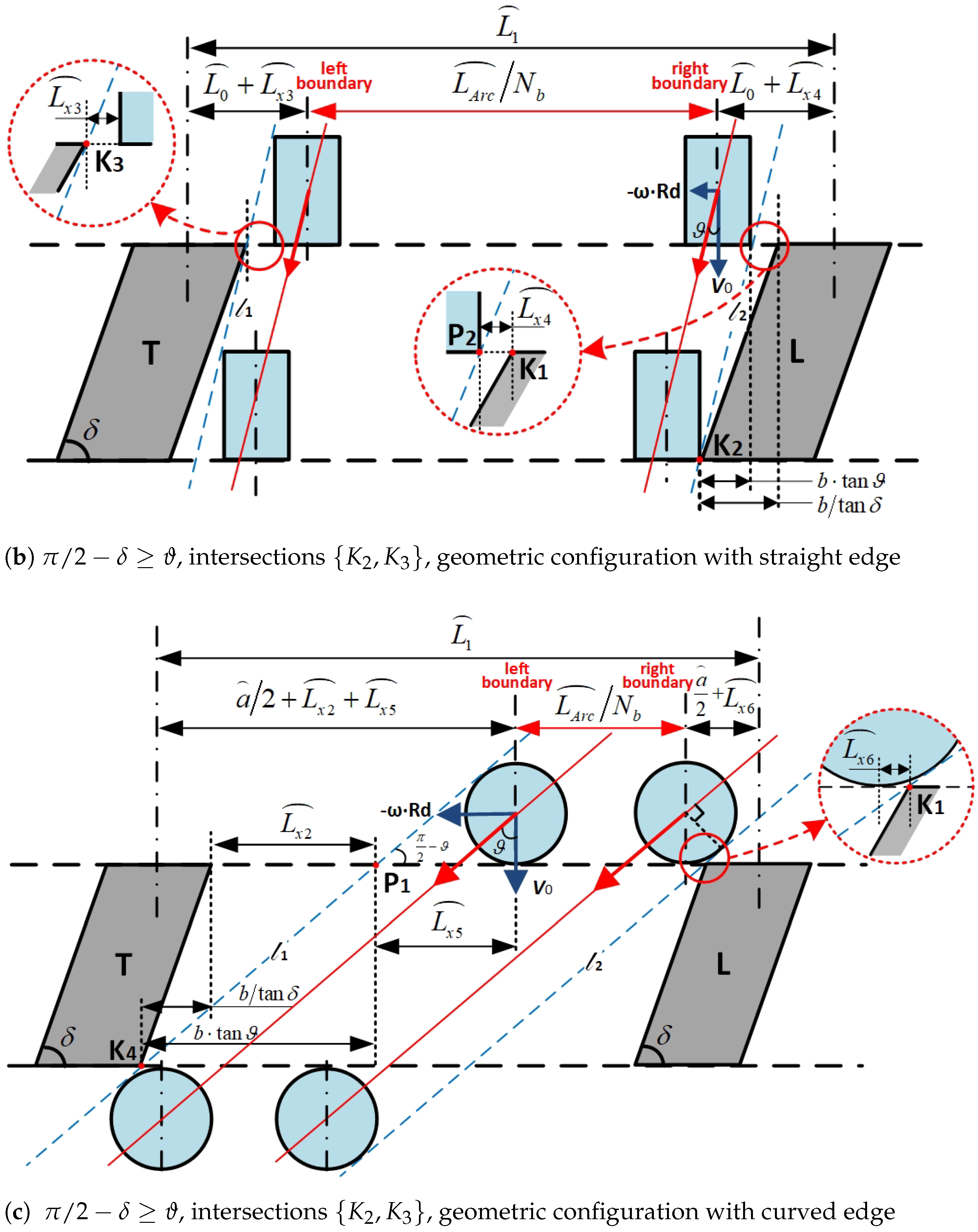
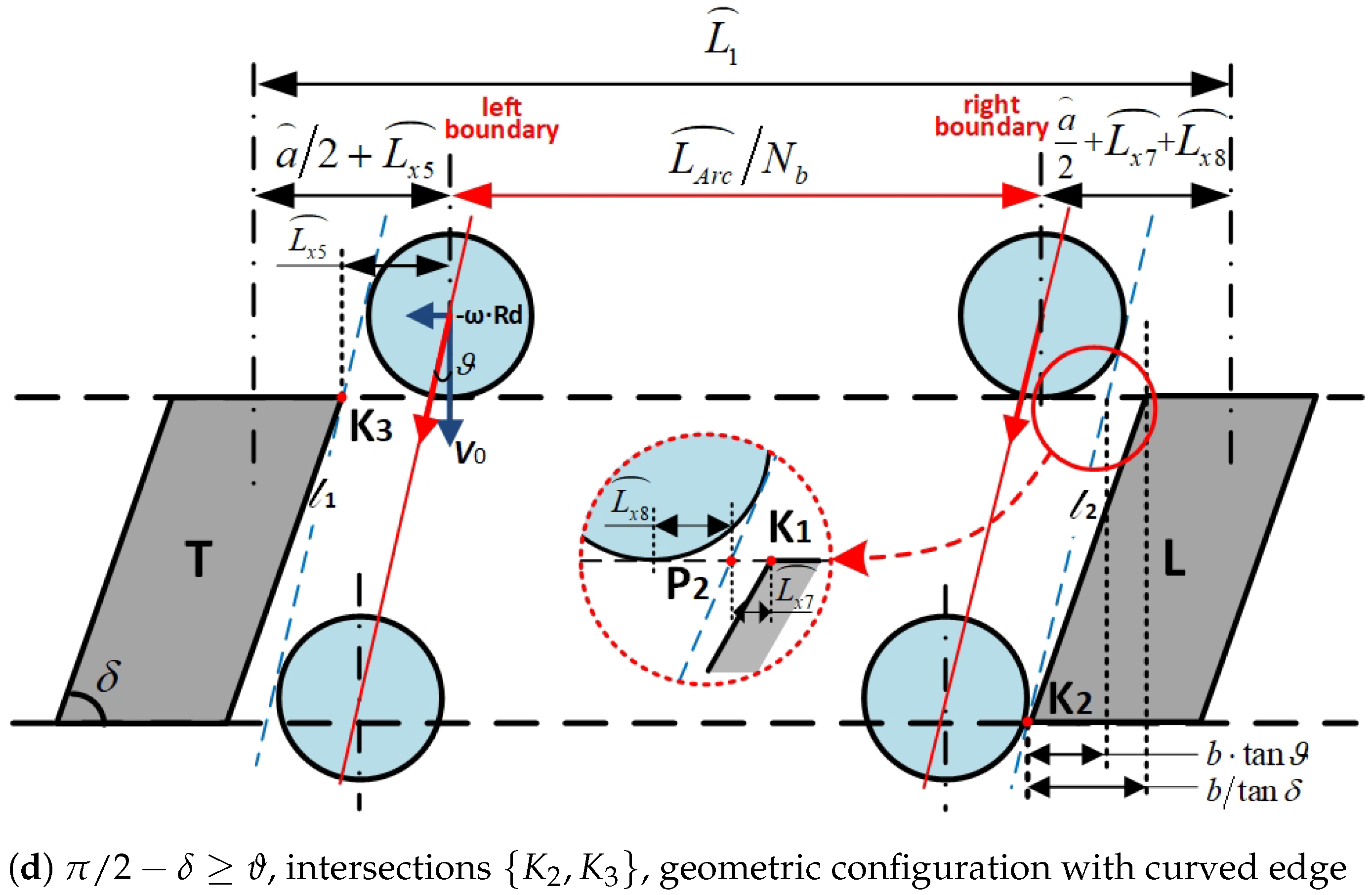
- Scenario 1: Substitute Models With Straight Edges From the Top View
| Expression | Configuration | Straight-Ended Cylinder | Rectangular |
|---|---|---|---|
| Cases and Items | |||
| Common | |||
| Case1 | |||
| Case2 | |||
- Scenario 2: Substitute Models With Curved Edges From the Top View
| Expression | Configuration | Sphere | Hemispherical-Ended Cylinder | Ellipsoid |
|---|---|---|---|---|
| Cases and Items | ||||
| Common | ||||
| Case1 | ||||
| Case2 | ||||
References
- Böhm, H.; Högner, L.; Meyer, M.; Mailach, R.; Hornig, A.; Gude, M. A Methodology for a Coupled Structural–Computational Fluid Dynamics Analysis of Compressor Rotor Blades Subjected to Ice Impact With Uncertain Impactor Parameters. J. Eng. Gas Turbines Power 2023, 145, 031001. [Google Scholar] [CrossRef]
- Yang, Q.; Guo, X.; Dong, W.; Wang, A. Ice Accretion and Aerodynamic Effects on a Turbofan Engine Nacelle under Takeoff Conditions. Aerosp. Sci. Technol. 2022, 126, 107571. [Google Scholar] [CrossRef]
- Dolbeer, R.A.; Begier, M.J.; Miller, P.R.; Weller, J.R.; Anderson, A.L. Wildlife Strikes to Civil Aircraft in the United States, 1990–2019. Technical Report DOT/FAA/TC-21/19; United States Department of Transportation; Federal Aviation Administration; William J. Hughes Technical Center: Atlantic City, NJ, USA, 2021. [Google Scholar]
- Juračka, J.; Chlebek, J.; Hodaň, V. Bird Strike as a Threat to Aviation Safety. Transp. Res. Procedia 2021, 59, 281–291. [Google Scholar] [CrossRef]
- Bojdo, N.; Filippone, A.; Parkes, B.; Clarkson, R. Aircraft Engine Dust Ingestion Following Sand Storms. Aerosp. Sci. Technol. 2020, 106, 106072. [Google Scholar] [CrossRef]
- Liu, H.; Che Man, M.H.; Low, K.H. UAV Airborne Collision to Manned Aircraft Engine: Damage of Fan Blades and Resultant Thrust Loss. Aerosp. Sci. Technol. 2021, 113, 106645. [Google Scholar] [CrossRef]
- Pepi, M.; Squillacioti, R.; Pfledderer, L.; Phelps, A. Solid Particle Erosion Testing of Helicopter Rotor Blade Materials. J. Fail. Anal. Prev. 2012, 12, 96–108. [Google Scholar] [CrossRef]
- Smith, J.G.; Wohl, C.J.; Palacios, J.L.; Connelly, B.D.; Culver, G.F.; Torchia, P.J.; Chauby, M.J.; Denkins, M.H.; Beck, D.M. Impact Ice Adhesion Strength of Stainless Steel 304 as Determined on a Centrifuge Test Stand. Cold Reg. Sci. Technol. 2022, 196, 103492. [Google Scholar] [CrossRef]
- Tan, J.F.; Yon, T.; He, L.; Yu, L.J.; Wang, C. Accelerated Method of Helicopter Brownout with Particle-Particle Collisions. Aerosp. Sci. Technol. 2022, 124, 107511. [Google Scholar] [CrossRef]
- Li, J.; Lou, Y.; Chai, X.; Ma, Z.; Jin, X. Numerical Simulation of Bird Strike on Jet Engine Considering Bird Ingestion Requirements. J. Aircraft 2022, 59, 761–773. [Google Scholar] [CrossRef]
- Guo, J.; Zuo, H.; Zhong, Z.; Jiang, H. Foreign Object Monitoring Method in Aero-Engines Based on Electrostatic Sensor. Aerosp. Sci. Technol. 2022, 123, 107489. [Google Scholar] [CrossRef]
- Cai, J.; Bao, H.; Zuo, H.; Huang, Y. Safety Evaluation of Airworthiness Requirement of Bird-Strike on Aeroplane. Eng. Fail. Anal. 2019, 102, 407–416. [Google Scholar] [CrossRef]
- US Department of Transportation. CFR14 Part 33: Airworthiness Standards: Aircraft Engines; Federal Aviation Administration: Washington, DC, USA, 2015.
- Long, S.; Mu, X.; Liu, Y.; Wang, H.; Zhang, X.; Yao, X. Failure Modeling of Composite Wing Leading Edge under Bird Strike. Compos. Struct. 2021, 255, 113005. [Google Scholar] [CrossRef]
- Luo, G.; Xu, Z.; Shen, H.; Chen, W.; Zhang, H. Experimental Study on the Impact Load of Internally Supported Gelatin Bird Projectiles. Eng. Fail. Anal. 2021, 124, 105336. [Google Scholar] [CrossRef]
- Liu, L.; Shao, H.; Zhu, X.; Zhao, Z.; Zhang, G.; Luo, G.; Chen, W. Bird Impact Response and Damage Mechanism of 3D Orthogonal Woven Composite Aeroengine Blades. Compos. Struct. 2023, 304, 116311. [Google Scholar] [CrossRef]
- Zhou, Y.; Sun, Y.; Cai, W. Bird-Striking Damage of Rotating Laminates Using SPH-CDM Method. Aerosp. Sci. Technol. 2019, 84, 265–272. [Google Scholar] [CrossRef]
- Yupu, G.; Zhenhua, Z.; Wei, C.; Deping, G. Foreign Object Damage to Fan Rotor Blades of Aeroengine Part I: Experimental Study of Bird Impact. Chin. J. Aeronaut. 2007, 20, 408–414. [Google Scholar] [CrossRef]
- Yupu, G.; Zhenhua, Z.; Wei, C.; Deping, G. Foreign Object Damage to Fan Rotor Blades of Aeroengine Part II: Numerical Simulation of Bird Impact. Chin. J. Aeronaut. 2008, 21, 328–334. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, J.; Zhang, X.; Yan, Y.; Jiang, L.; Mohagheghian, I.; Dear, J.P.; Charalambides, M.N. Experimental and Numerical Investigation of High Velocity Soft Impact Loading on Aircraft Materials. Aerosp. Sci. Technol. 2019, 90, 44–58. [Google Scholar] [CrossRef]
- Guida, M.; Marulo, F.; Belkhelfa, F.Z.; Russo, P. A Review of the Bird Impact Process and Validation of the SPH Impact Model for Aircraft Structures. Prog. Aerosp. Sci. 2022, 129, 100787. [Google Scholar] [CrossRef]
- Ruiz-Calavera, L.P.; Cid-Arroyo, S.; Benitez-Montañes, L. Spinner Shed Ice Engine Ingestion Assessment Methodology. In Proceedings of the 29th Congress of the International Council of the Aeronautical Sciences, ICAS Paper. St. Petersburg, Russia, 7–12 September 2014; Volume 66, pp. 1–10. [Google Scholar]
- Metz, I.C.; Ellerbroek, J.; Mühlhausen, T.; Kügler, D.; Hoekstra, J.M. Analysis of Risk-Based Operational Bird Strike Prevention. Aerospace 2021, 8, 32. [Google Scholar] [CrossRef]
- Panpan, J.; Taofeng, H.; Qi, H.; Yiqian, D.; Liming, W. Method for Evaluating Probability of Collision of Flying Birds With Wind Shield Over Oar. CN Patent CN108090257B, 4 May 2021. [Google Scholar]
- Wang, K.; Huang, H.x.; Liu, L.; Zheng, G.j.; Lin, Z.k.; Sun, S.; Tan, H.j. A New Distortion Evaluation Method Based on Geometric Association for Arbitrary Cross-Sectional Shape of Inlet. Aerosp. Sci. Technol. 2022, 128, 107728. [Google Scholar] [CrossRef]
- Xu, K.; Zha, G. System Energy Benefit Using Co-Flow Jet Active Separation Control for a Serpentine Duct. Aerosp. Sci. Technol. 2022, 128, 107746. [Google Scholar] [CrossRef]
- Mi, B.; Zhan, H. Numerical Simulation on Rigid Foreign Object Exclusion in the Turboprop Engine Intake System With a Bypass Duct. IEEE Access 2019, 7, 61920–61933. [Google Scholar] [CrossRef]
- Masden, E.; Cook, A. Avian Collision Risk Models for Wind Energy Impact Assessments. Environ. Impact Assess. Rev. 2016, 56, 43–49. [Google Scholar] [CrossRef]
- Tucker, V.A. A Mathematical Model of Bird Collisions With Wind Turbine Rotors. J. Sol. Energy Eng. 1996, 118, 253–262. [Google Scholar] [CrossRef]
- Johnston, A.; Cook, A.S.C.P.; Wright, L.J.; Humphreys, E.M.; Burton, N.H.K. Modelling Flight Heights of Marine Birds to More Accurately Assess Collision Risk with Offshore Wind Turbines. J. Appl. Ecol. 2014, 51, 31–41. [Google Scholar] [CrossRef]
- Bolker, E.D.; Hatch, J.J.; Zara, C. Modeling How Windfarm Geometry Affects Bird Mortality. arXiv 2014, arXiv:1408.1580. [Google Scholar]
- Podolsky, R. Method of and Article of Manufacture for Determining Probability of Avian Collision. U.S. Patent US7315799B1, 1 January 2008. [Google Scholar]
- Holmstrom, L.A.; Hamer, T.E.; Colclazier, E.M.; Denis, N.; Verschuyl, J.P.; Ruché, D. Assessing Avian-Wind Turbine Collision Risk: An Approach Angle Dependent Model. Wind. Eng. 2011, 35, 289–312. [Google Scholar] [CrossRef]
- Han, C.; Gu, Y.; Sun, X.; Liu, S. Rapid Algorithm for Covariance Ellipsoid Model Based Collision Warning of Space Objects. Aerosp. Sci. Technol. 2021, 117, 106960. [Google Scholar] [CrossRef]
- Meguid, S.A.; Mao, R.H.; Ng, T.Y. FE Analysis of Geometry Effects of an Artificial Bird Striking an Aeroengine Fan Blade. Int. J. Impact Eng. 2008, 35, 487–498. [Google Scholar] [CrossRef]

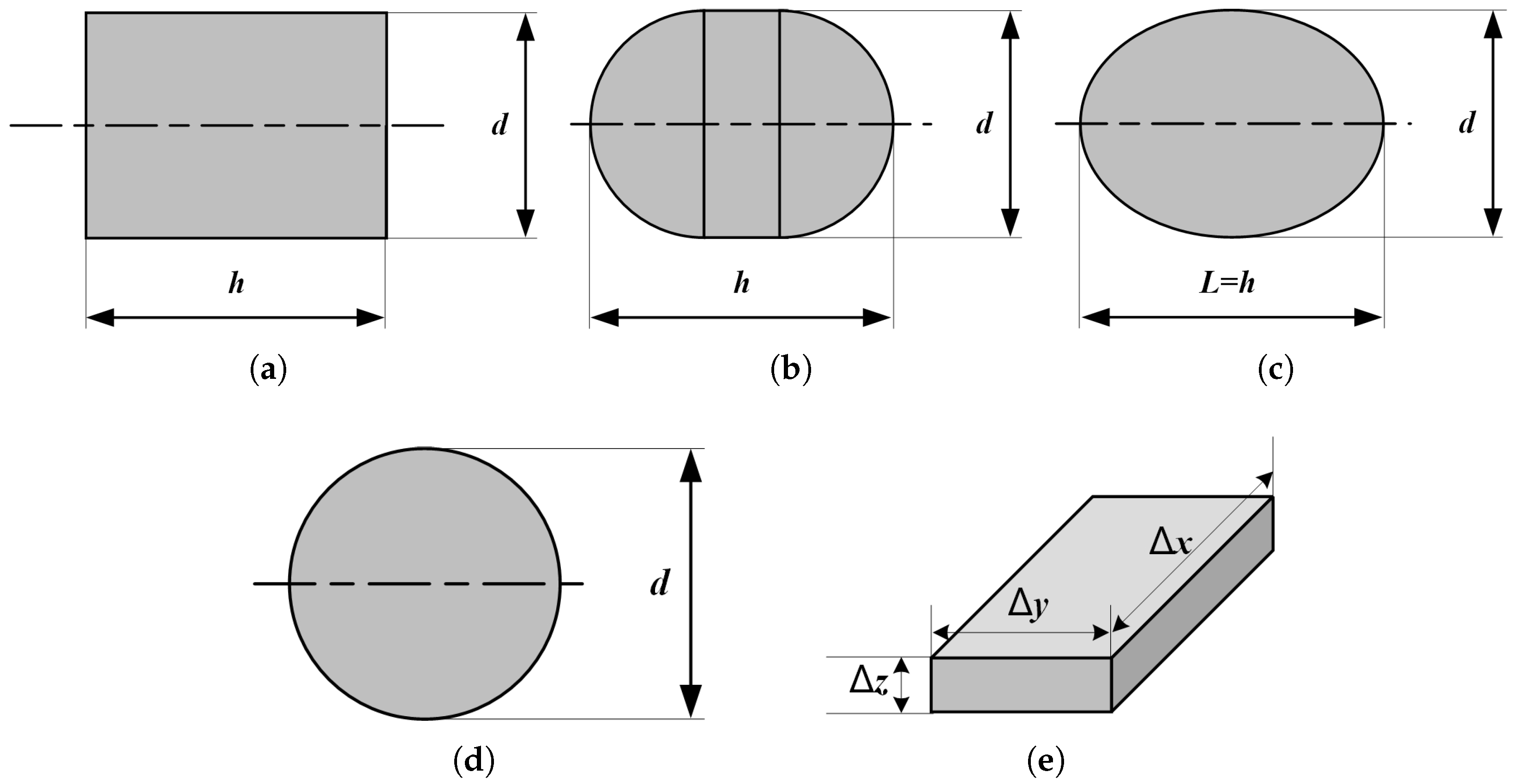


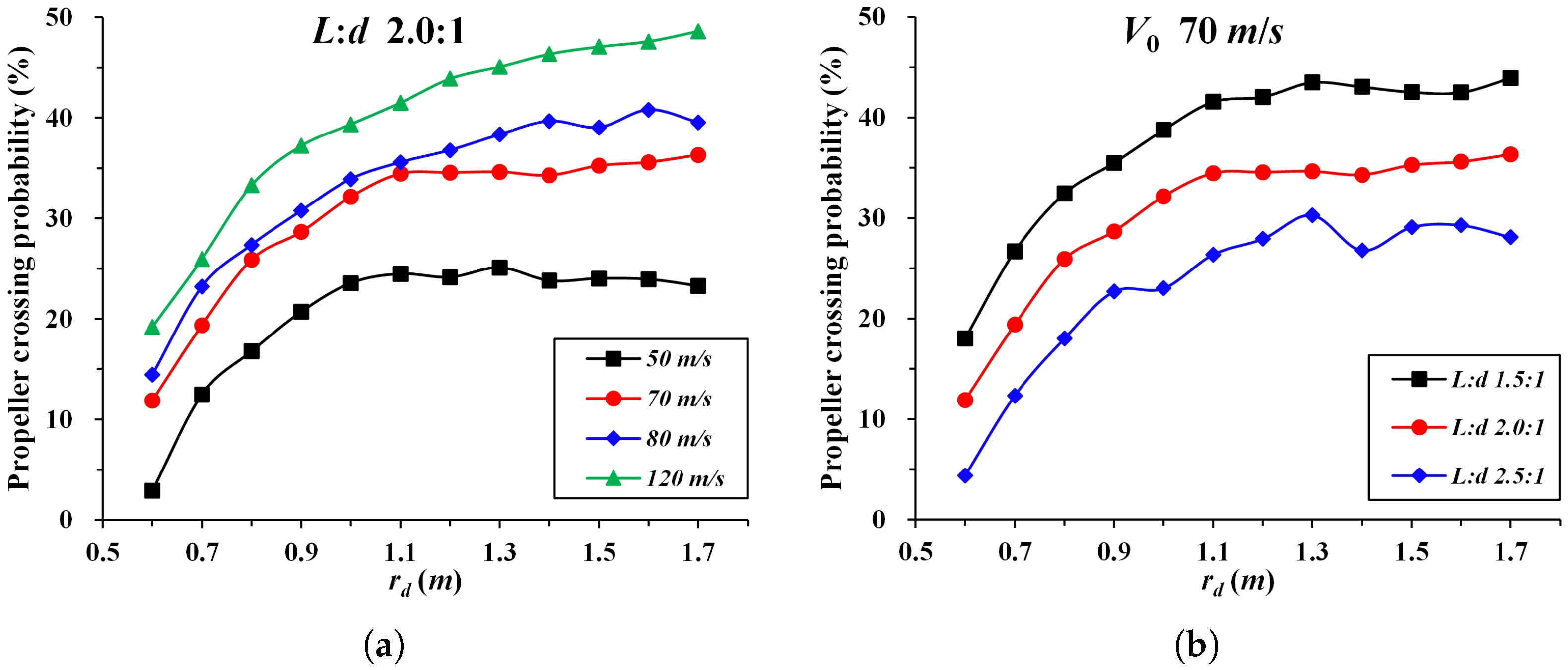
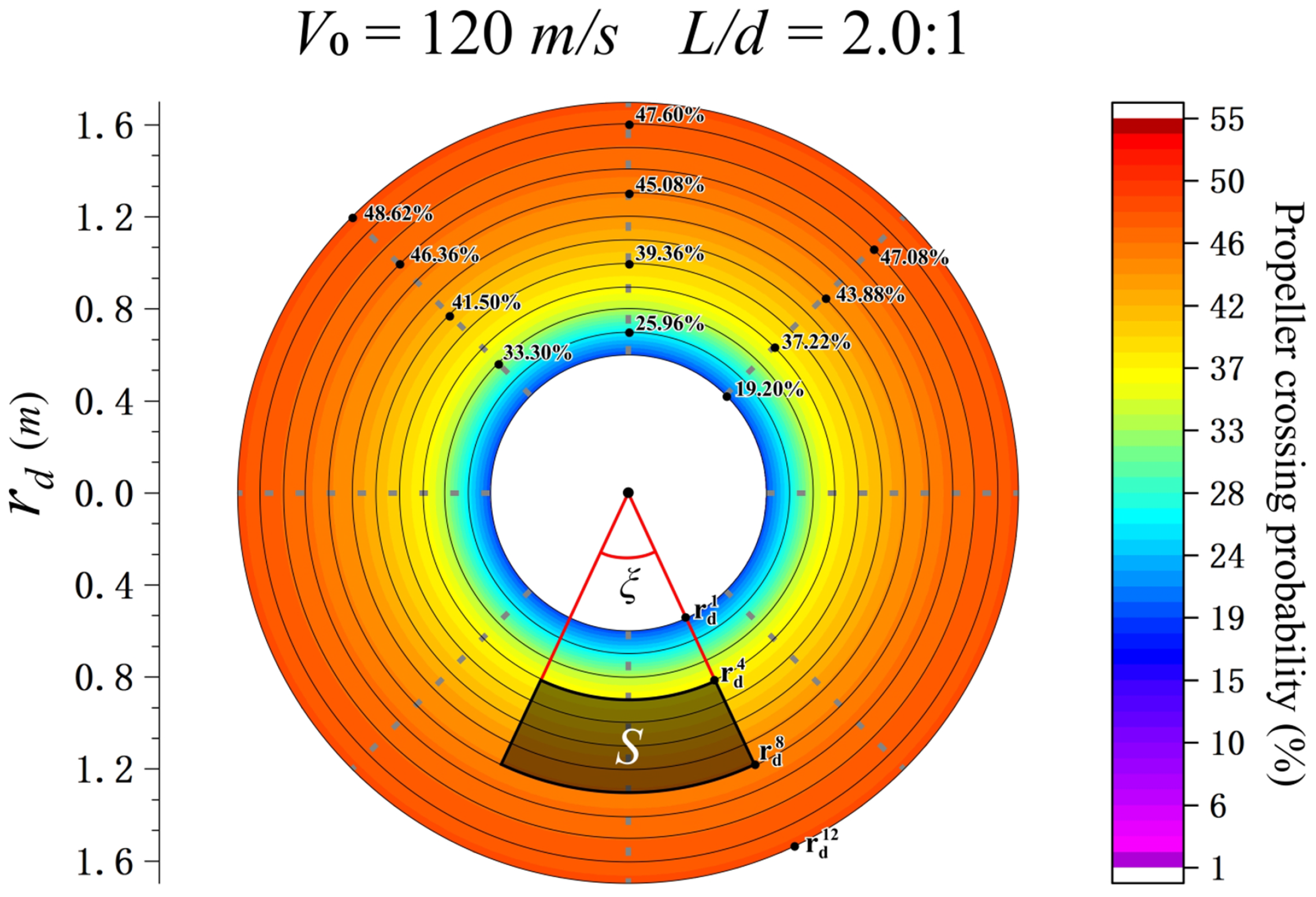
| Typical Foreign Object Configuration | Configuration Parameters | Radius of the Inscribed Sphere (r) | Radius of the Circumscribed Sphere (R) |
|---|---|---|---|
| Straight-ended cylinder | min | ||
| Hemispherical-ended cylinder | ()/2 | ||
| Ellipsoid | min | max | |
| Sphere | d | ||
| Rectangular | min |
| Criterion | Typical Foreign Object Configuration | Configuration Parameters | Description of the Refined Criterion |
|---|---|---|---|
| Straight-ended cylinder | |||
| Ellipsoid | |||
| Rectangular | x, y, z | ||
| Hemispherical-ended cylinder |
| Configuration Type | Shape Parameters (m) |
|---|---|
| Straight-ended cylinder | |
| Rectangular | |
| Sphere | d = 0.085 |
| Hemispherical-ended cylinder | h = 0.083, d = 0.083 |
| Ellipsoid | h = 0.166, d = 0.083 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Chen, K.; Yang, X.; Zhou, Q.; Ye, Z.; Li, Y. A Model and Methodology for Probability Assessment of Foreign Objects Crossing through an Aircraft Propeller. Aerospace 2023, 10, 925. https://doi.org/10.3390/aerospace10110925
Zhu J, Chen K, Yang X, Zhou Q, Ye Z, Li Y. A Model and Methodology for Probability Assessment of Foreign Objects Crossing through an Aircraft Propeller. Aerospace. 2023; 10(11):925. https://doi.org/10.3390/aerospace10110925
Chicago/Turabian StyleZhu, Jiawei, Kenlun Chen, Xuehe Yang, Qijie Zhou, Zhipeng Ye, and Yaqiu Li. 2023. "A Model and Methodology for Probability Assessment of Foreign Objects Crossing through an Aircraft Propeller" Aerospace 10, no. 11: 925. https://doi.org/10.3390/aerospace10110925
APA StyleZhu, J., Chen, K., Yang, X., Zhou, Q., Ye, Z., & Li, Y. (2023). A Model and Methodology for Probability Assessment of Foreign Objects Crossing through an Aircraft Propeller. Aerospace, 10(11), 925. https://doi.org/10.3390/aerospace10110925






