Convex Optimization-Based Techniques for Trajectory Design and Control of Nonlinear Systems with Polytopic Range
Abstract
1. Introduction
1.1. Control Theory
1.2. Optimization and Trajectory Design
1.3. Contributions
- Classical control techniques, which do not account for state and control constraints;
- Lossless convexifications, which do not generate convex problems when nonlinear dynamics are present;
- Sequential convex programming, which requires the solution of many convex programs.
1.4. Outline
2. Problem and Main Result
| Algorithm 1 Resetting Approach. |
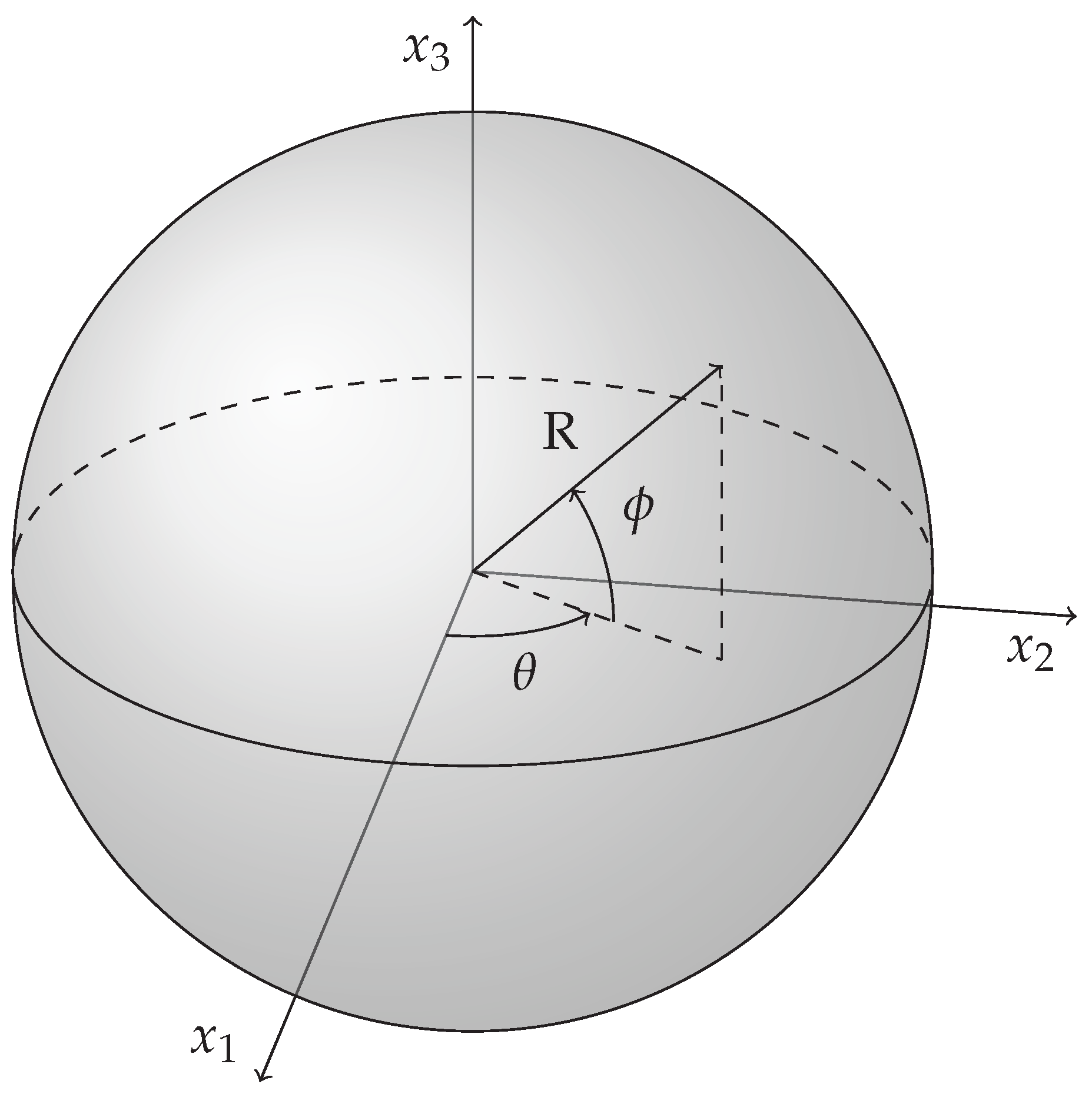
3. Spherically Constrained Relative Motion Trajectory Design
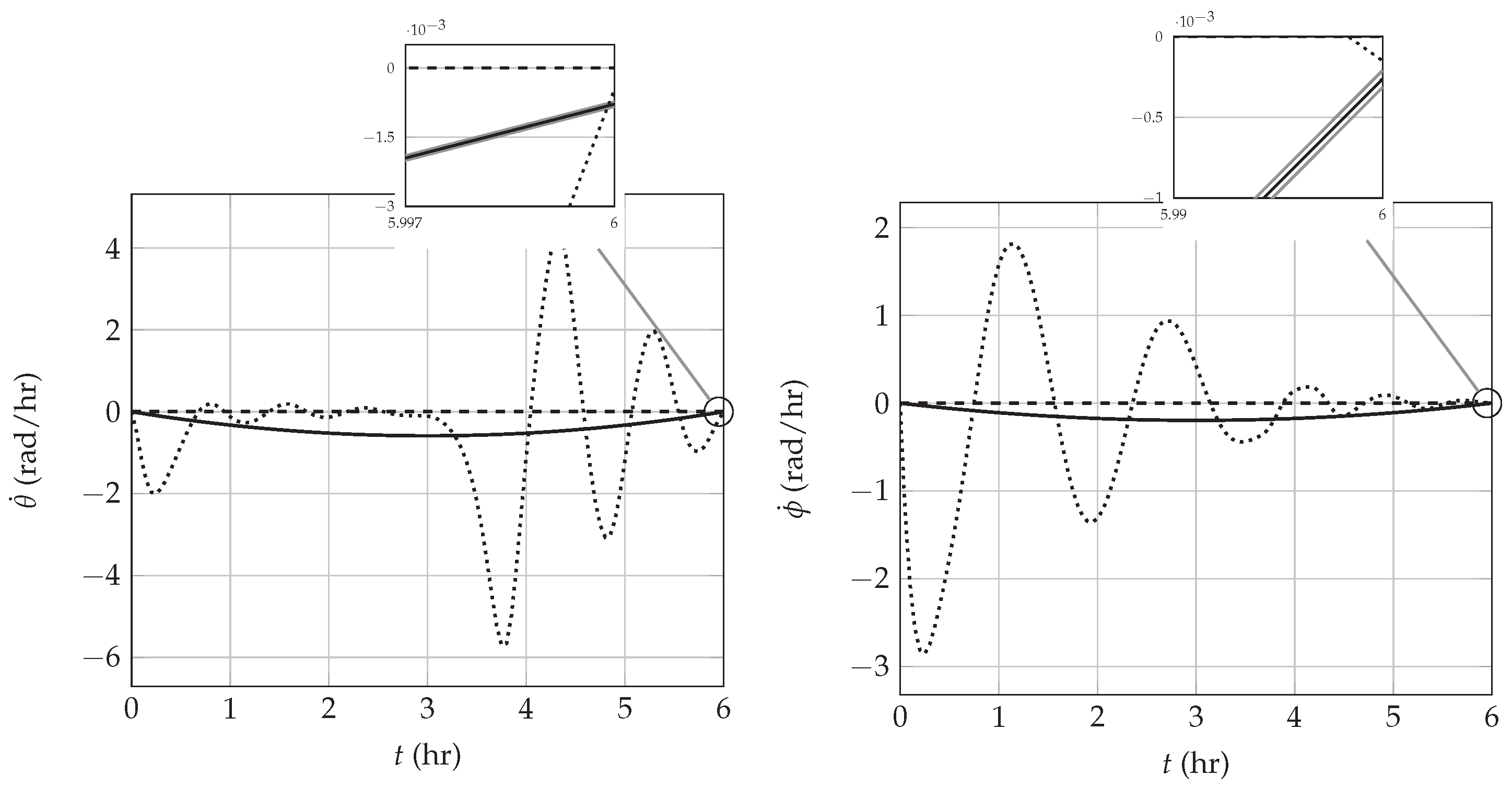
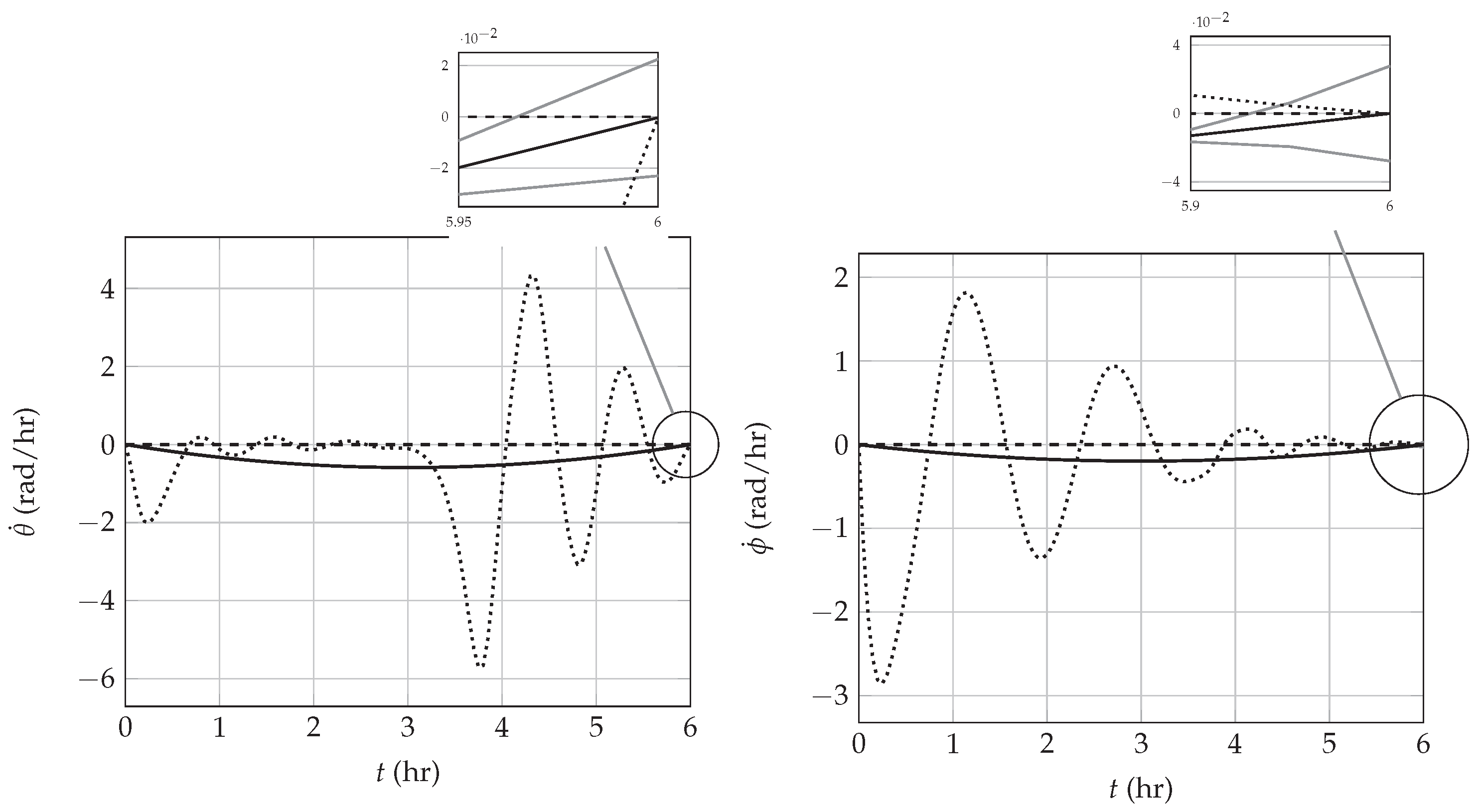
3.1. Constrained Approach
3.2. Resetting Approach
4. Spacecraft Attitude Control
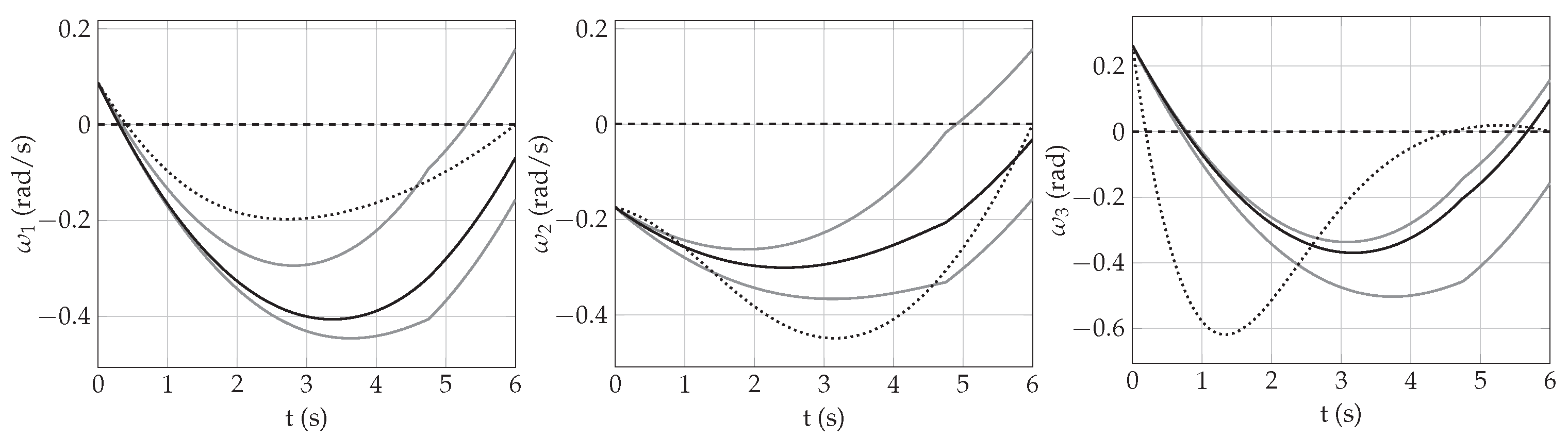
4.1. Constrained Approach
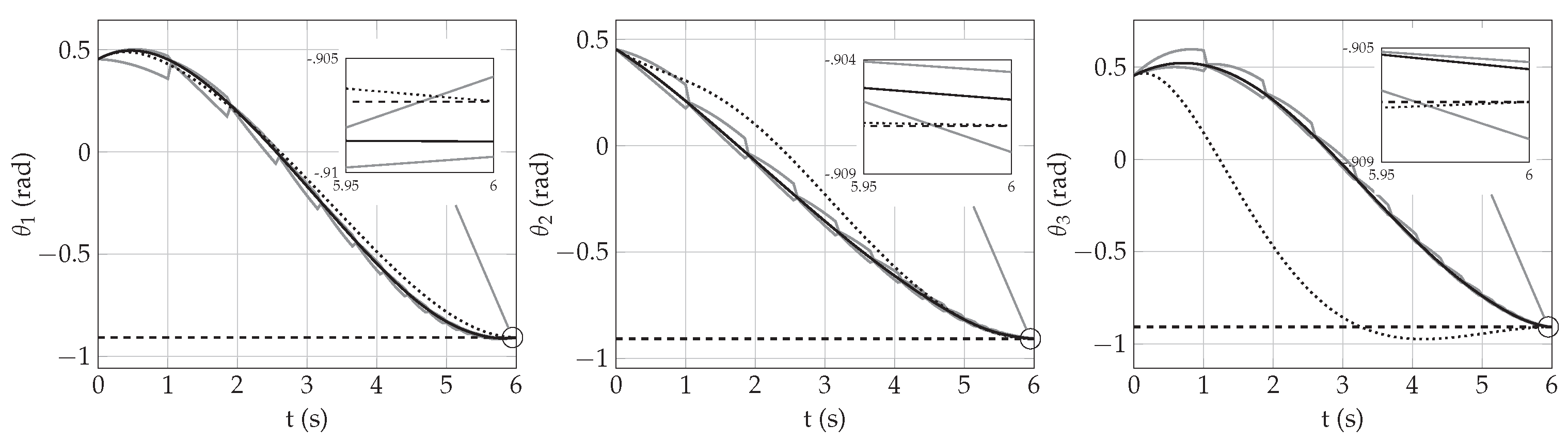
4.2. Resetting Approach
5. Summary and Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Li, W.J.; Cheng, D.Y.; Liu, X.G.; Wang, Y.B.; Shi, W.H.; Tang, Z.X.; Gao, F.; Zeng, F.M.; Chai, H.Y.; Luo, W.B.; et al. On-orbit service (OOS) of spacecraft: A review of engineering developments. Prog. Aerosp. Sci. 2019, 108, 32–120. [Google Scholar] [CrossRef]
- Tsuda, Y.; Yoshikawa, M.; Abe, M.; Minamino, H.; Nakazawa, S. System design of the Hayabusa 2—Asteroid sample return mission to 1999 JU3. Acta Astronaut. 2013, 91, 356–362. [Google Scholar] [CrossRef]
- Gaudet, B.; Linares, R.; Furfaro, R. Terminal adaptive guidance via reinforcement meta-learning: Applications to autonomous asteroid close-proximity operations. Acta Astronaut. 2020, 171, 1–13. [Google Scholar] [CrossRef]
- D’Amico, S.; Benn, M.; Jørgensen, J.L. Pose estimation of an uncooperative spacecraft from actual space imagery. Int. J. Space Sci. Eng. 2014, 2, 171–189. [Google Scholar]
- Stastny, N.B.; Geller, D.K. Autonomous optical navigation at Jupiter: A linear covariance analysis. J. Spacecr. Rocket. 2008, 45, 290–298. [Google Scholar] [CrossRef]
- Bradley, N.; Olikara, Z.; Bhaskaran, S.; Young, B. Cislunar navigation accuracy using optical observations of natural and artificial targets. J. Spacecr. Rocket. 2020, 57, 777–792. [Google Scholar] [CrossRef]
- Curtis, H. Orbital Mechanics for Engineering Students, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2009. [Google Scholar]
- Khalil, H.K. Nonlinear Systems; Pearson: New York, NY, USA, 2001. [Google Scholar]
- Harris, M.W.; Açıkmeşe, B. Maximum divert for planetary landing using convex optimization. J. Optim. Theory Appl. 2014, 162, 975–995. [Google Scholar] [CrossRef]
- Brunton, S.L.; Brunton, B.W.; Proctor, J.L.; Kutz, J.N. Koopman Invariant Subspaces and Finite Linear Representations of Nonlinear Dynamical Systems for Control. PLoS ONE 2016, 11, e0150171. [Google Scholar] [CrossRef]
- Yeung, E.; Kundu, S.; Hodas, N. Learning deep neural network representations for Koopman operators of nonlinear dynamical systems. In Proceedings of the 2019 American Control Conference (ACC), Philadelphia, PA, USA, 10–12 July 2019; pp. 4832–4839. [Google Scholar]
- Brunton, S.L.; Kutz, J.N. Data-Driven science and Engineering: Machine Learning, Dynamical Systems, and Control; Cambridge University Press: Cambridge, UK, 2022. [Google Scholar]
- Lusch, B.; Kutz, J.N.; Brunton, S.L. Deep learning for universal linear embeddings of nonlinear dynamics. Nat. Commun. 2018, 9, 1–10. [Google Scholar] [CrossRef]
- Rugh, W.J.; Shamma, J.S. Research on gain scheduling. Automatica 2000, 36, 1401–1425. [Google Scholar] [CrossRef]
- Sename, O.; Gaspar, P.; Bokor, J. Robust Control and Linear Parameter Varying Approaches: Application to Vehicle Dynamics; Springer: Berlin/Heidelberg, Germany, 2013; Volume 437. [Google Scholar]
- He, T. Smooth Switching LPV Control and Its Applications; Michigan State University: East Lansing, MI, USA, 2019. [Google Scholar]
- Jansson, O.; Harris, M.W. Nonlinear Control Algorithm for Systems with Convex Polytope Bounded Nonlinearities. In Proceedings of the 2022 Intermountain Engineering, Technology and Computing (IETC), Orem, UT, USA, 13–14 May 2022; pp. 1–6. [Google Scholar]
- Malisoff, M.; Sontag, E.D. Universal formulas for feedback stabilization with respect to Minkowski balls. Syst. Control Lett. 2000, 40, 247–260. [Google Scholar] [CrossRef]
- Pylorof, D.; Bakolas, E. Nonlinear control under polytopic input constraints with application to the attitude control problem. In Proceedings of the 2015 American Control Conference (ACC), Chicago, IL, USA, 1–3 July 2015; pp. 4555–4560. [Google Scholar] [CrossRef]
- Ames, A.D.; Coogan, S.; Egerstedt, M.; Notomista, G.; Sreenath, K.; Tabuada, P. Control Barrier Functions: Theory and Applications. In Proceedings of the 2019 18th European Control Conference (ECC), Naples, Italy, 25–28 June 2019; pp. 3420–3431. [Google Scholar] [CrossRef]
- Harris, M.W. Lossless Convexification of Optimal Control Problems; The University of Texas at Austin: Austin, TX, USA, 2014. [Google Scholar]
- Açıkmeşe, B.; Blackmore, L. Lossless convexification for a class of optimal control problems with nonconvex control constraints. Automatica 2011, 47, 341–347. [Google Scholar] [CrossRef]
- Kunhippurayil, S.; Harris, M.W.; Jansson, O. Lossless Convexification of Optimal Control Problems with Annular Control Constraints. Automatica 2021, 133, 109848. [Google Scholar] [CrossRef]
- Harris, M.W.; Açıkmeşe, B. Lossless convexification of non-convex optimal control problems for state constrained linear systems. Automatica 2014, 50, 2304–2311. [Google Scholar] [CrossRef]
- Harris, M.W.; Açıkmeşe, B. Lossless Convexification for a Class of Optimal Control Problems with Linear State Constraints. In Proceedings of the 52nd IEEE Conference on Decision and Control, Florence, Italy, 10–13 December 2013. [Google Scholar]
- Harris, M.W.; Açıkmeşe, B. Lossless Convexification for a Class of Optimal Control Problems with Quadratic State Constraints. In Proceedings of the 2013 American Control Conference, Washington, DC, USA, 17–19 June 2013. [Google Scholar]
- Woodford, N.; Harris, M.W. Geometric Properties of Time Optimal Controls with State Constraints Using Strong Observability. IEEE Trans. Autom. Control 2022, 67, 6881–6887. [Google Scholar] [CrossRef]
- Harris, M.W. Optimal Control on Disconnected Sets using Extreme Point Relaxations and Normality Approximations. IEEE Trans. Autom. Control 2021, 66, 6063–6070. [Google Scholar] [CrossRef]
- Kunhippurayil, S.; Harris, M.W. Strong observability as a sufficient condition for non-singularity and lossless convexification in optimal control with mixed constraints. Control Theory Technol. 2022, 20, 475–487. [Google Scholar] [CrossRef]
- Blackmore, L.; Açıkmeşe, B.; Carson, J.M. Lossless convexification of control constraints for a class of nonlinear optimal control problems. Syst. Control Lett. 2012, 61, 863–871. [Google Scholar] [CrossRef]
- Lu, P.; Liu, X. Autonomous trajectory planning for rendezvous and proximity aperations by conic optimization. J. Guid. Control Dyn. 2013, 36, 375–389. [Google Scholar] [CrossRef]
- Lu, P. Introducing computational guidance and control. J. Guid. Control Dyn. 2017, 40, 193. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P.; Pan, B. Survey of convex optimization for aerospace applications. Astrodynamics 2017, 1, 23–40. [Google Scholar] [CrossRef]
- Liu, X.; Lu, P. Solving nonconvex optimal control problems by convex optimization. J. Guid. Control Dyn. 2014, 37, 750–765. [Google Scholar] [CrossRef]
- Harris, M.W.; Woodford, N.T. Equilibria, Periodicity, and Chaotic Behavior in Spherically Constrained Relative Orbital Motion. Nonlinear Dyn. 2023, 111, 1–17. [Google Scholar] [CrossRef]
- Clohessy, W.; Wiltshire, R. Terminal guidance system for satellite rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar] [CrossRef]
- MATLAB 2021a; The Mathworks, Inc.: Natick, MA, USA, 2021.
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2022. [Google Scholar]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- Shuster, M.D. The kinematic equation for the rotation vector. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 263–267. [Google Scholar] [CrossRef]
- Markley, F.L.; Crassidis, J.L. Fundamentals of Spacecraft Attitude Determination and Control; Springer: New York, NY, USA, 2014; Volume 1286. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jansson, O.; Harris, M.W. Convex Optimization-Based Techniques for Trajectory Design and Control of Nonlinear Systems with Polytopic Range. Aerospace 2023, 10, 71. https://doi.org/10.3390/aerospace10010071
Jansson O, Harris MW. Convex Optimization-Based Techniques for Trajectory Design and Control of Nonlinear Systems with Polytopic Range. Aerospace. 2023; 10(1):71. https://doi.org/10.3390/aerospace10010071
Chicago/Turabian StyleJansson, Olli, and Matthew W. Harris. 2023. "Convex Optimization-Based Techniques for Trajectory Design and Control of Nonlinear Systems with Polytopic Range" Aerospace 10, no. 1: 71. https://doi.org/10.3390/aerospace10010071
APA StyleJansson, O., & Harris, M. W. (2023). Convex Optimization-Based Techniques for Trajectory Design and Control of Nonlinear Systems with Polytopic Range. Aerospace, 10(1), 71. https://doi.org/10.3390/aerospace10010071




