Abstract
This paper presents a solution strategy for deterministic time-optimal pursuit–evasion games with linear state constraints, convex control constraints, and linear dynamics that is consistent with linearized relative orbital motion models such as the Clohessy–Wiltshire equations and relative orbital elements. The strategy first generates polytopic inner approximations of the players’ reachable sets by solving a sequence of convex programs. A bisection method then computes the optimal termination time, which is the least time at which a set containment condition is satisfied. The pursuit–evasion games considered are games with (1) a single pursuer and single evader, (2) multiple pursuers and a single evader, and (3) a single pursuer and multiple evaders. Compared to variational methods, this reachable set strategy leads to a tractable formulation even when there are state and control constraints. The efficacy of the strategy is demonstrated in three numerical simulations for a constellation of satellites in close proximity in low earth orbit.
1. Introduction
This paper studies time-optimal pursuit–evasion games with linear dynamics and convex state and control constraints. Cases with a single pursuer and single evader, multiple pursuers and a single evader, as well as a single pursuer and multiple evaders are considered. The paper takes a geometrical approach in solving these games by modeling them as reachable set problems as first introduced in [1]. By using modern, convex optimization techniques for the reachable set construction of constrained systems, it is now possible to solve constrained, multiplayer games not considered in [1].
Pursuit–evasion games commonly arise in aerospace engineering as well as in economics. The history of differential pursuit–evasion games begins with the seminal work by Isaacs [2]. His work describes several applied problems and their differential pursuit–evasion formulations. An overview of the development of differential pursuit–evasion games is given in [3], which covers seminal work conducted in the 1970s as well as current state-of-the-art work.
Aerial warfare is one of the typical problems that can be modeled as a pursuit–evasion game [4,5]. Multiple assumptions are often made to simplify dynamical complexity. Some common assumptions restrict the motion to be planar, model the aircraft as a point mass, linearize the dynamics, and require an instantaneous control response [6]. Examples of different aerial warfare problems modeled as pursuit–evasion games consist of missile versus aircraft [4,6,7,8], aircraft versus aircraft interception [9,10], and fighter maneuvering [11].
Pursuit–evasion games have also been studied in the context of astrodynamics, particularly collision avoidance and interception [12,13]. Rather than use a nonlinear two-body formulation, linearization and the use of the Clohessy–Wiltshire (CW) equations simplifies the problem so that minimax formulations lead to open-loop and closed-loop control strategies based on kriging [14]. Pursuit–evasion strategies have been used for the tracking of space objects and selection of sensor management strategies [15]. A hybrid global–local technique has been developed for a two-phase (long distance and short distance) game [16]. The two-phase approach has been extended in [17] using reinforcement learning under assumptions of impulse control, incomplete information, and a quadratic objective.
A pursuit–evasion game can be seen as an optimal control problem where the pursuer(s) and evader(s) have different objectives. The addition of multiple agents with opposite objectives generally makes the optimal control problem more difficult to solve than those with an individual pursuer or evader would be. It should be noted that sometimes the single-agent optimal control problems can be complicated to solve as is. A technique utilizing calculus of variations may be used to solve differential games. This technique requires setting an optimal control problem for all the players with the underlying necessary conditions and then finding a solution simultaneously for all the players. Linear–quadratic as well as time-optimal scalar games were solved using this methodology in [18]. A case of one of the players not playing the game optimally based on the variational approach is also included in [18] as part of a short discussion on games with stochastic behavior.
Because of their complexity, it is often difficult to solve differential games using variational theory. This fact is aptly summarized in [17]: “However, for the space [pursuit-evasion] game, it is a challenge to solve the transformed [two-point boundary value problem] due to its high dimensionality and strong nonlinearity.” This is particularly true when there are pointwise constraints on the states and controls. The pointwise constraints introduce switches as trajectories enter and leave the control boundaries, which may violate the smoothness assumptions required for the Newton method. Consequently, direct methods [19,20] and semidirect methods have been introduced to leverage finite-dimensional optimization packages. These methods involve the use of genetic algorithms and neural networks [8,11,21,22].
In contrast to the optimization-based approaches, Mizukami [1] has shown that a two-player time-optimal pursuit–evasion game terminates when the evader’s reachable set is contained in the pursuer’s reachable set, which motivates a geometric approach to solving the game based on reachable set computation. More precisely, the termination point in the state space lies on the boundary of the players’ reachable sets. For problems with linear dynamics and integral-constrained (rather than pointwise-constrained) controls, analytical solutions can be derived for the termination time and optimal trajectories. Motivated by this work, reachable set analyses have been used in dynamic flowfields [23], coordinate control [24], missile/sensor trade studies [25], and other game scenarios [26,27,28].
In the CW setting and with control magnitude constraints, it is possible to approximate reachable sets with a sequence of analytical computations [29]. The presence of state constraints and other types of control constraints complicates the process of computing reachable sets, and in general, numerical methods are utilized to approximate them. Multiple numerical algorithms to calculate a reachable set for control affine systems are provided in [30]. An algorithm for the computation of reachable sets for linear systems with bounded inputs, which approaches the problem by finding inner and outer approximations, is introduced in [31]. Optimal control has also been used to calculate reachable sets [32,33,34,35]. A polytopic approximation of the actual reachable set is computed. In [34], a single semidefinite program (SDP) and multiple sequential second-order cone programs (SOCPs) are solved to find an inner approximation of the reachable set for linear dynamics and convex state and control constraints. An outer approximation is added in [33] as a heuristic to determine the precision of the approximation. Nonconvex control constraints are considered in [35]. The approach from [34] is used as a basis for solving multiplayer games in this paper.
The primary contribution of this work is the construction of reachable set approximations to solve constrained pursuit–evasion games. The inclusion of pointwise, convex constraints on the state and control make the variational approach difficult, while such constraints add minimal complexity to the geometric approach. The inclusion of multiple pursuers and evaders adds complexity to the problem as well, especially if variational techniques were to be used. It is shown that with reachable set methods, constrained pursuit–evasion problems with multiple pursuers and evaders remain tractable. It is assumed that the pursuers and evaders have perfect information about the other players and all players perform optimally. Pursuit–evasion problems with (1) a single pursuer and single evader, (2) multiple pursuers and a single evader, and (3) a single pursuer and multiple evaders are considered.
The remainder of this paper is structured as follows. Section 2 describes a numerical method based in convex optimization for approximating reachable sets. The algorithm is based on the one introduced in [34]. The constrained pursuit–evasion game is introduced in Section 3 and an explanation on how reachable set theory can be used to solve it for a varying number of pursuers and evaders is explained. Section 5 applies the method to aerospace problems whose dynamics and constraints are explained in Section 4. The results are summarized and conclusions are drawn in Section 6.
2. Reachable Sets
An introduction to reachable sets is given in this section. Reachable sets for linear time-varying (LTV) dynamics with second-order cone control constraints and linear state constraints are considered. This system of interest is given as
The state vector is , the control vector is , the output vector is , the system matrix is , the control influence matrix is , and the output matrix is . The quantities and define the linear state constraint . The second-order cone control constraint is . The state and control constraints limit the values that can be taken by the state and control pointwise in time. The initial state vector is at initial time . A feasible control is any control satisfying (1)–(5).
Definition 1.
The reachable set is the set of all points that can be reached from a given initial condition with a feasible control. The first term on the right-hand side of (6) is . Because it is independent of the control, this term is associated with the translation of the reachable set. The second term on the right-hand side is the integral term. This term depends on the control and is associated with the size and shape of the reachable set. In reachable set theory, sets that grow in size are said to be expanding. An illustration of a reachable set in two-dimensional space that is translating and growing in time is shown in Figure 1.
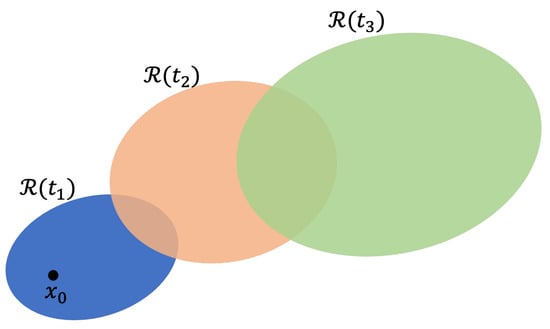
Figure 1.
The initial point is labeled . The reachable set at time is shown as the small blue ellipse. As time increases to , the reachable set translates up and to the right as it grows. The reachable set at is shown as the orange ellipse. As time increases to , the reachable set continues to translate and grow; it is shown as the green ellipse.
Reachable sets do not always expand, and the strategy presented herein has no such requirement. The simplest sufficient condition to ensure the expansion of the reachable set is time invariance [36]. For time-varying systems, a sufficient condition for expansion is properness (see Corollary 17.1 of [37]). Furthermore, because the dynamics of the system are linear and the state and control constraints are convex, the reachable set is convex [36].
2.1. Algorithm for Reachable Set Calculation
An algorithm to calculate an inner polytopic approximation of the reachable set for the system described in (1)–(5) is given next. The algorithm first solves an SDP to compute a largest possible size simplex that fits inside the reachable set. The algorithm then solves a sequence of SOCPs to compute a better inner approximation of the reachable set based on the initial simplex. A more detailed explanation of the algorithm can be found in [34].
Consider the discretized version of the continuous system given in (1)–(5). The discrete-time system is
where N represents the number of time intervals used in discretization. Appendix A explains how discretization is conducted in this paper to obtain the discrete, barred quantities based on their continuous counterparts and discretization time step. Discretization allows for the use of numerical optimization. The reachable set definition given in Definition 1 for the continuous system is analogous to that for the discrete system by replacing t with .
2.1.1. Initial Simplex
The computation of the initial simplex is explained first. Computing the initial simplex requires solving a single SDP. Let be the set containing the vertices of an initial simplex in . Furthermore, define a matrix Q as
The volume of the simplex may then be calculated as
With an expression for the simplex volume, maximizing (13) gives an initial simplex with a maximum volume. This also leads to the vertices of the simplex being on the boundary of the system’s reachable set:
This maximum volume simplex is used as the initial simplex. The volume maximization problem can be written as the following SDP:
The log determinant is denoted as logdet, which acts on square symmetric matrices. The initial simplex requires the calculation of trajectories emanating from the initial point, , to final states. The initial simplex is constructed from the final state vectors which form the vertices of the initial simplex.
2.1.2. Growing Simplices
Following the construction of the initial simplex, improved approximations are achieved by computing additional simplices out of the open faces of the current polytopic approximation. Whereas the computation of the initial simplex required a solution of an SDP, the computation of additional simplices is achieved by solving an SOCP for each additional vertex in the polytopic approximation. This is possible because maximizing the volume of an additional simplex is analogous to maximizing the length of a vector that connects the open face to a point on the boundary of the reachable set and is orthogonal to the face. The point on the boundary of the reachable set is then added as a new vertex to the current polytopic approximation of the reachable set:
The quantity to be maximized is the scaling factor . The point on the open face is such that the minimum distance between it and the reachable set boundary is maximized. The matrix contains the p vertices corresponding to the open face i. The vector identifies the point from the vertices in . A vector normal to the ith open face is given by . A point on the boundary of the reachable set is z. Figure 2 gives a graphical representation of these variables with being represented as a vector from one vertex.
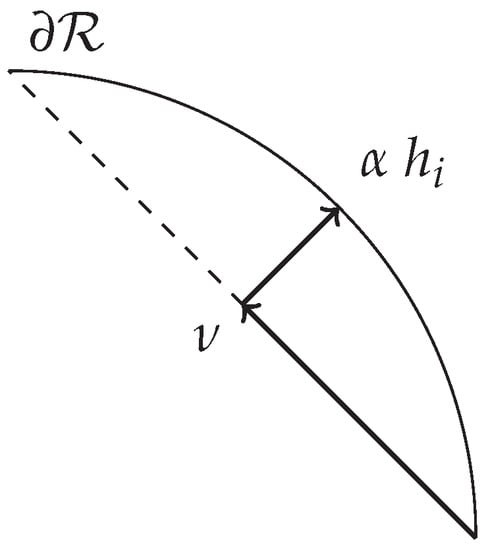
Figure 2.
Illustration of variables used for polytopic approximation in (16).
Overall, the algorithm requires the solution of a single SDP defined in (15) to obtain an initial approximation of the reachable set. A tighter approximation is then reached by solving a sequence of SOCPs given in (16), with each SOCP adding a new vertex to the current polytopic approximation. The first three reachable set approximations are illustrated in Figure 3 along with the actual reachable set. Further explanation and illustration of the approximation process may be found in [34].
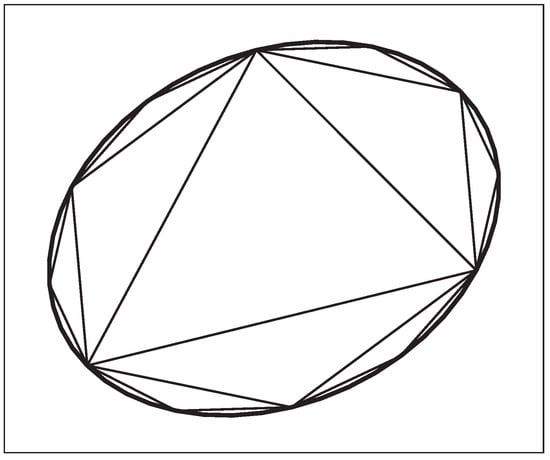
Figure 3.
The initial simplex is the innermost triangle. The next two generations share vertices with the triangle and approximate the reachable set, which appears as the ellipse with a thicker line.
3. Game Theory
This section introduces the pursuit–evasion game of interest. The three pursuit–evasion games considered in this paper are games with (1) a single pursuer and single evader, (2) multiple pursuers and a single evader, and (3) a single pursuer and multiple evaders. The pursuers’ objective is to minimize the capture time of all the evaders. The evaders’ objective is to maximize the time it takes for the pursuers to capture all the evaders. It is assumed that a solution exists, i.e., capture occurs, such that it is a game of degree rather than a game of kind [2].
3.1. Single Pursuer and Single Evader
Consider the simplest case of a single pursuer and single evader. The game may be rewritten as two time-optimal control problems. The pursuer’s problem is:
The evader’s problem is:
The subscript P refers to the pursuer, the subscript E refers to the evader, and is the termination time of the game. It is assumed that both the pursuer and evader have perfect information about the other.
It was shown by Mizukami [1] that such time-optimal games can be recast as reachable-set inclusion problems.
Theorem 1
([1]). If a solution to the game exists, then the game terminates in the least time such that
The question of existence is not explored in this paper. It is assumed that a solution exists, and the theorem is used to find the solution by comparing the players’ reachable sets. The termination time is the first time at which the evader’s reachable set is contained in the pursuer’s reachable set. The game is therefore reduced to a one-dimensional search for . This search is performed in practice by using a bisection, which is a special case of the more generic Algorithm 1 presented in the next subsection, and the method of Section 2.1 for approximating the reachable sets. In the state space, the game terminates at a point on the boundary of both players’ reachable sets, i.e., , where is the capture point.
The simplest situation occurs when is zero (so that the reachable sets do not translate) and the pursuer’s control set is larger than the evader’s (so that it enlarges at a faster rate). Prior to the termination time, the evader’s reachable set is not contained in the pursuer’s. After the termination time, the evader’s reachable set is in the interior of the pursuer’s. At the termination time, the evader’s set is contained in the pursuer’s set, and they share a boundary point. These relationships are demonstrated in Figure 4.
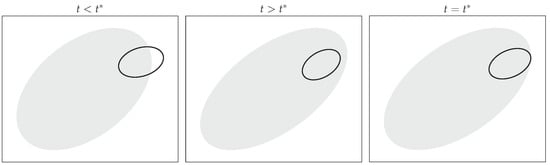
Figure 4.
Pursuer’s (shaded region) and evader’s (solid line) reachable sets before capture (), after capture (), and at capture ().
3.2. Multiple Pursuers and Single Evader
When there are multiple pursuers and a single evader, the game terminates when the evader’s reachable set is contained in the union of the pursuers’ reachable sets [23], i.e.,
where is the number of pursuers. For later use, the bracketed term on the right-hand side is defined to be . If the game has only one pursuer, (20) reduces to (19) as expected. Some of the possible capture scenarios are shown in Figure 5 and Figure 6. In Figure 5, the capture happens at the boundary of the two pursuers’ and evader’s sets. In Figure 6, the capture happens at the boundary of the four pursuers’ sets but is in the interior of the evader’s reachable set. In both cases, however, the capture happens at the first time instance when the evader’s reachable set is contained in the union of the pursuers’ reachable sets.
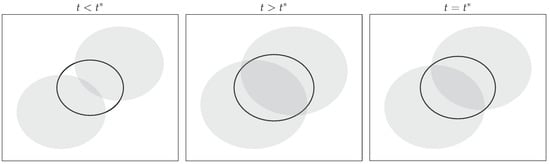
Figure 5.
Pursuers’ (shaded region) and evader’s (solid line) reachable sets before capture, after capture, and at capture.
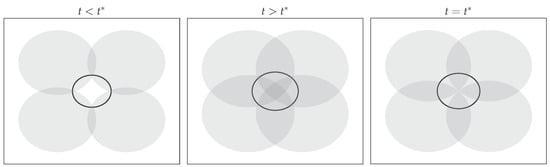
Figure 6.
Pursuers’ (shaded region) and evader’s (solid line) reachable sets before capture, after capture, and at capture.
A line search is conducted to find the capture time. An algorithm that performs this line search is shown in Algorithm 1. The algorithm uses the method from Section 2.1 to generate the inner approximations of the pursuers’ and evader’s reachable sets and checks if (20) is satisfied or not. The algorithm uses a bisection method to find the capture time by checking the set inclusion and tightening the minimum and maximum allowable times.
| Algorithm 1 Line Search for Capture Time in Multiple Pursuer and Single Evader Game |
|
3.3. Single Pursuer and Multiple Evaders
Lastly, a pursuit–evasion game with a single pursuer and multiple evaders is considered. This game is split into multiple single pursuer and single evader games where the pursuer’s reachable set is reset at the capture point when a capture of one of the evaders happens. Figure 7 demonstrates the evolution of the pursuer’s and evaders’ reachable sets where the pursuer’s reachable set is reset after capturing an evader.
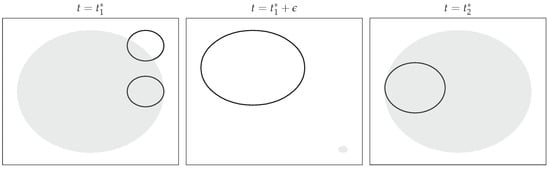
Figure 7.
Pursuer’s (shaded region) and evaders’ (solid line) reachable sets at capture of the first evader, shortly after the capture of the first evader and at capture of the second evader. Notice that shortly after capture of the first evader, the pursuer’s reachable set is reset at the capture point, whereas the second evader’s set continues to grow.
To consider all the possible strategies for the pursuer to capture the evaders, it is in general required to consider possibilities for capturing sequences, where is the number of the evaders. This means that in a case of three evaders, the pursuer could capture the evaders in six different orders: 1,2,3; 1,3,2; 2,1,3; 2,3,1; 3,1,2; or 3,2,1. Figure 8 shows the possible capture order of the pursuer in a three evader game. t with subscripts represents the capture time of the evaders in the order of numeric values in the subscript. is the termination time of the game associated with the shallowest branch, i.e., the branch offering the least time compared to all other branches. In this example, the selected order for capturing the evaders is 2,1,3.
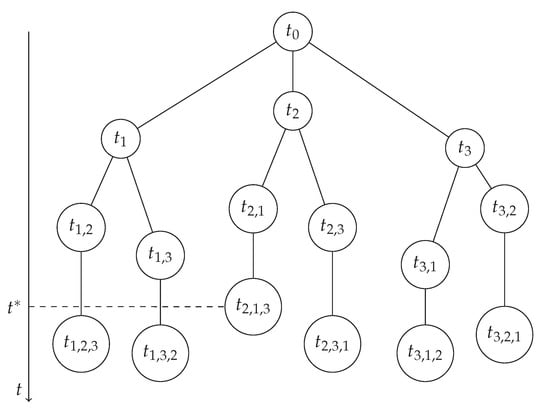
Figure 8.
Tree graph showing the different possibilities (branches) on the order pursuer could capture the evaders. is the termination time for the pursuer to capture all the evaders.
Now consider a case where catching four evaders in the order 1,2,3,4 takes time units. If catching only evaders 4 and 3 in this order takes time units and , then it is not optimal for the pursuer to first capture evader 4 and then evader 3. As a consequence, there is no need to further compute and since it is guaranteed that both are greater than . This logic leads to a pruning strategy that may allow the termination time for the game to be found without enumerating all the capture strategies completely. This pruning strategy is analogous to that in branch and bound, which is used to solve integer optimization problems [38].
An algorithm to find the termination time for the multiple evader and single pursuer game is provided in Algorithm 2. The algorithm begins by finding the termination time of the game by using a greedy approach when choosing the next evader to be captured. The other capturing sequences are then compared to this. If the capture time of an evader is larger than the current estimate for the termination time of the game , that capturing sequence is excluded from further analysis and the branch is pruned. On the other hand, if the game termination time using that sequence is less than the current estimate for the game termination time, the current estimate for the game termination time is updated to that.
| Algorithm 2 Termination Time in Single Pursuer and Multiple Evader Game |
|
4. Dynamics
The dynamics used for the numerical simulations in Section 5 are explained in this section. A planar constellation of satellites near a circular orbit is considered. The dynamics can be modeled linearly with the Clohessy–Wiltshire (CW) equations [39]
where is a state vector with the first two elements corresponding to a satellite’s relative position in a local vertical local horizontal (LVLH) frame and the last two corresponding to a satellite’s relative velocity in the LVLH frame. The external control acceleration is . The matrices and are given by
where is the mean motion of the circular reference orbit and is set to 4 rad/h for the remainder of this paper. This corresponds to a low earth orbit. Other relative motion models such as those based on time-varying relative orbital elements [40,41] are also applicable within the reachable set-based solution strategy. In all the simulations, the output vector y is to be the relative position of the players, which means that the output matrix is , with I being the 2 × 2 identify matrix and 0 being the 2 × 2 zero matrix. The relative position is chosen as the output because capture occurs in position space.
5. Numerical Simulations
Numerical simulations of the three cases introduced in Section 3 are provided in this section. All the agents evolve according to CW dynamics as explained in Section 4. Each agent’s control set is of the form
with being a prescribed upper bound on the control magnitude. This is a second-order cone constraint. Additional constraints consistent with those in Equations (1)–(5) are also present and described in the following subsections.
5.1. Single Pursuer and Single Evader
Consider a single pursuer and single evader pursuit–evasion problem with the players’ dynamics given in (21). The initial states of the pursuer and evader are
The pursuer’s and evader’s states are constrained by a linear inequality as in (3) with
The D matrix is dimensionless. The control of the pursuer is bounded by , and the control of the evader is bounded by .
Figure 9 shows the reachable sets of the pursuer and evader when the capture happens. The trajectories that the pursuer and evader take to reach the capture point are also shown in the figure. The capture happens at h. It is evident from the figure that the capture happens at the boundary of both the pursuer’s and evader’s reachable sets.

Figure 9.
Pursuer’s (shaded) and evader’s (solid) reachable sets at capture time with the trajectories of the pursuer (dashed) and evader (dotted) from their initial position to the capture point (black circle). The black areas at the top and bottom represent keep-out zones generated by the linear constraints.
5.2. Multiple Pursuers and Single Evader
Now consider a pursuit–evasion problem with four pursuers and a single evader. The dynamics of the pursuers and evader are given by the CW Equation (21). The initial states of the players are
The states of all the players are constrained with the same D and b specified in (26) as in the previous simulation. The control input of all the pursuers is constrained by , and the control input of the evader is constrained by .
Figure 10 shows the reachable sets of all the pursuers as well as the evader. The capture happens at the origin. The evader could be captured by either pursuer 1 or pursuer 2, but only pursuer 1’s trajectory from its initial point to the capture point is shown. Interestingly, the capture happens at the evader’s initial location as that is the last point covered by the union of the pursuers’ reachable sets. The capture happens at h.
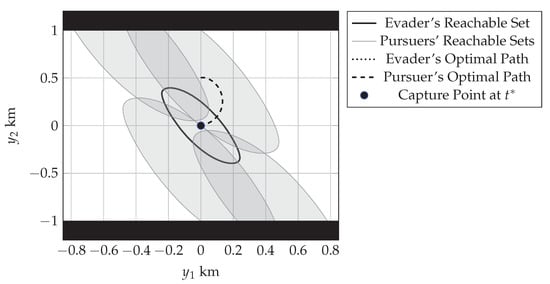
Figure 10.
Pursuers’ (shaded) and evader’s (solid) reachable sets at capture time with the trajectory of the capturing pursuer (dashed) from its initial output to the capture point (black circle). The evader’s trajectory (dotted but invisible to the eye) is stationary at the origin. The black areas at the top and bottom represent keep-out zones generated by the linear constraints.
5.3. Single Pursuer and Multiple Evaders
Lastly, a game with three evaders and a single pursuer is considered. The dynamics of all the agents are again given by the CW equations. The initial states of the pursuer and evaders are
There are no state constraints for the agents but the control inputs are constrained with for the pursuer and for the evaders.
Figure 11 shows the reachable sets of all the agents at the time instance when the first evader is captured. Figure 12 shows the reachable sets of the remaining two evaders as well as the pursuer’s set when the second evader is captured. Figure 13 shows the reachable sets of the pursuer and the third evader at the time of the last capture, which terminates the game. The captures happen at h, h, and h.
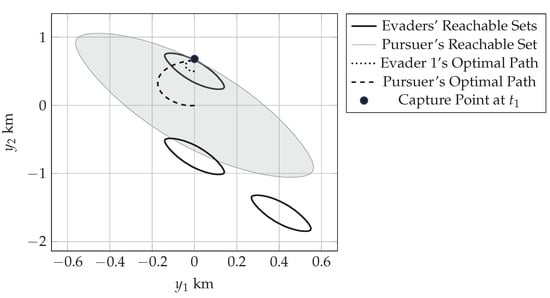
Figure 11.
Pursuer’s (shaded) and evaders’ (solid) reachable sets at the time of the first capture with the trajectories of the pursuer (dashed) and first evader (dotted) from their initial positions to the capture point (black circle). Evader 1’s reachable set is the uppermost. Evader 2’s reachable set is the middle one. Evader 3’s reachable set is the lowermost.
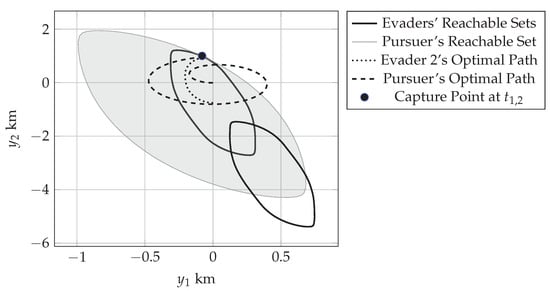
Figure 12.
Pursuer’s (shaded) and evaders’ (solid) reachable sets at the time of the second capture with the trajectories of the pursuer (dashed) and first evader (dotted) from their initial positions to the capture point (black circle). Evader 2’s reachable set is the uppermost. Evader 3’s reachable set is the lowermost.
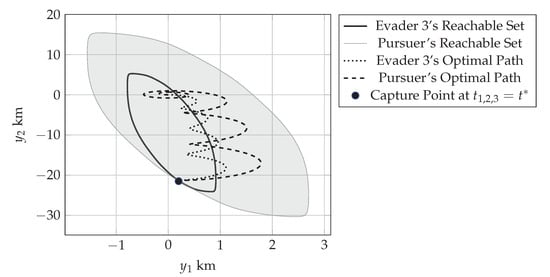
Figure 13.
Pursuer’s (shaded) and evader 3’s (solid) reachable sets at the time of the final capture with the trajectories of the pursuer (dashed) and first evader (dotted) from their initial positions to the capture point (black circle). This final capture terminates the game.
5.4. Computational Performance
The reachable set strategy for solving time-optimal pursuit–evasion games relies upon bisection (see Algorithm 1) and reachable set calculations (see Section 2.1). At each time within a bisection, a reachable set calculation is required for each player in the game. Each reachable set calculation requires the solution of a single SDP (for the initial simplex) and multiple SOCPs (for growing the faces). SDPs are solved by using the software SDPT3 [42], and SOCPs are solved by using the software Gurobi [43]. Problems are parsed using YALMIP [44] in the MATLAB environment [45]. Table 1 shows the average SDP solve time, average SOCP solve time, average number of SOCPs solved, and average time to calculate each reachable set for the three simulations described in Section 5.1, Section 5.2 and Section 5.3. The computations were performed on an HP laptop with a 10th generation Intel i7 1.8 GHz processor.

Table 1.
Reachable set calculation times.
The overall run time of the algorithm is affected primarily by Algorithm 1 parameters , , and because these dictate the number of bisection iterations and hence number of reachable sets that must be calculated. The best way to reduce the total run time is to provide good estimates of the lower and upper bounding times and . Table 2 shows the total run time for the algorithm for the three simulations described in Section 5.1, Section 5.2 and Section 5.3 on instances requiring 5, 10, 25, and 100 bisection iterations (itr).

Table 2.
Total run time for the reachable set algorithm.
To summarize, the reachable set strategy takes minutes (on a personal laptop) to solve constrained time-optimal pursuit–evasion games with two to five players.
6. Conclusions
This paper presented a technique using convex optimization to numerically construct reachable sets and to solve time-optimal pursuit–evasion games when the dynamics are linear and all the constraints are convex. These requirements are consistent with linearized relative orbital motion models such as the Clohessy–Wiltshire equations and relative orbital elements. Games with (1) a single pursuer and single evader, (2) multiple pursuers and a single evader, and (3) a single pursuer and multiple evaders were considered. Traditional formulations, such as those based on variational equations, are not tractable in the presence of practical actuator and state constraints. On the contrary, such constraints add minimal complexity to the reachable set strategy described herein. This is true because construction of the reachable sets has been reduced to a sequence of convex programs. Three numerical simulations were presented to demonstrate the strategy for a constellation of satellites in close proximity in low earth orbit. The computation times for the reachable sets were in subseconds, and the total run times for the algorithm were in minutes.
Author Contributions
Conceptualization, O.J. and M.W.H.; methodology, O.J. and M.W.H.; software, O.J.; validation, O.J. and M.W.H.; formal analysis, O.J. and M.W.H.; investigation, O.J. and M.W.H.; resources, O.J. and M.W.H.; data curation, O.J. and M.W.H.; writing—original draft preparation, O.J.; writing—review and editing, O.J. and M.W.H.; visualization, O.J.; supervision, M.W.H.; project administration, M.W.H.; funding acquisition, M.W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Office of Naval Research, grant number N00014-22-1-2131.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The continuous time system is
Upon defining the state-transition matrix associated with on the interval , it can be shown by direct differentiation that a solution to Equation (A1) on the interval is
For small time steps , evaluation of the integral may be approximated by fixing u at its initial value . Upon defining
a discrete-time approximation of the continuous-time system is
which is the same as Equation (7). Upon fixing all other quantities at the node times, e.g., , the discretization is complete.
References
- Mizukami, K.; Eguchi, K. A geometrical approach to problems of pursuit-evasion games. J. Frankl. Inst. 1977, 303, 371–384. [Google Scholar] [CrossRef]
- Isaacs, R. Differential Games: A Mathematical Theory with Applications to Warfare and Pursuit, Control and Optimization; Dover Publications: Mineola, NY, USA, 1999. [Google Scholar]
- Weintraub, I.E.; Pachter, M.; Garcia, E. An introduction to pursuit-evasion differential games. In Proceedings of the 2020 American Control Conference (ACC), IEEE, Denver, CO, USA, 1–3 July 2020; pp. 1049–1066. [Google Scholar]
- Shinar, J.; Gutman, S. Recent advances in optimal pursuit and evasion. In Proceedings of the 1978 IEEE Conference on Decision and Control Including the 17th Symposium on Adaptive Processes, IEEE, San Diego, CA, USA, 10–12 January 1979; pp. 960–965. [Google Scholar]
- Shinar, J.; Glizer, V.Y.; Turetsky, V. A pursuit-evasion game with hybrid pursuer dynamics. Eur. J. Control 2009, 15, 665–684. [Google Scholar] [CrossRef]
- Shinar, J. Solution techniques for realistic pursuit-evasion games. In Control and Dynamic Systems; Elsevier: Amsterdam, The Netherlands, 1981; Volume 17, pp. 63–124. [Google Scholar]
- Imado, F.; Kuroda, T. A method to solve missile-aircraft pursuit-evasion differential games. IFAC Proc. Vol. 2005, 38, 176–181. [Google Scholar] [CrossRef]
- Carr, R.W.; Cobb, R.G.; Pachter, M.; Pierce, S. Solution of a Pursuit–Evasion game using a near-optimal strategy. J. Guid. Control Dyn. 2018, 41, 841–850. [Google Scholar] [CrossRef]
- Greenwood, N. A differential game in three dimensions: The aerial dogfight scenario. Dyn. Control 1992, 2, 161–200. [Google Scholar] [CrossRef]
- Calise, A.J.; Yu, X.m. An analysis of a four state model for pursuit-evasion games. In Proceedings of the 1985 24th IEEE Conference on Decision and Control, IEEE, Fort Lauderdale, FL, USA, 11–13 December 1985; pp. 1119–1121. [Google Scholar]
- Horie, K.; Conway, B.A. Optimal fighter pursuit-evasion maneuvers found via two-sided optimization. J. Guid. Control Dyn. 2006, 29, 105–112. [Google Scholar] [CrossRef]
- Shen, D.; Pham, K.; Blasch, E.; Chen, H.; Chen, G. Pursuit-evasion orbital game for satellite interception and collision avoidance. In Proceedings of the Sensors and Systems for Space Applications IV, International Society for Optics and Photonics, Orlando, FL, USA, 25–29 April 2011; Volume 8044, p. 80440B. [Google Scholar]
- Blasch, E.P.; Pham, K.; Shen, D. Orbital satellite pursuit-evasion game-theoretical control. In Proceedings of the 2012 11th International Conference on Information Science, Signal Processing and their Applications (ISSPA), IEEE, Montreal, QC, Canada, 2–5 July 2012; pp. 1007–1012. [Google Scholar]
- Stupik, J.; Pontani, M.; Conway, B. Optimal pursuit/evasion spacecraft trajectories in the hill reference frame. In Proceedings of the AIAA/AAS Astrodynamics Specialist Conference, Minneapolis, MN, USA, 13–16 August 2012; p. 4882. [Google Scholar]
- Shen, D.; Jia, B.; Chen, G.; Pham, K.; Blasch, E. Game optimal sensor management strategies for tracking elusive space objects. In Proceedings of the 2017 IEEE Aerospace Conference, IEEE, Big Sky, MT, USA, 4–11 March 2017; pp. 1–8. [Google Scholar]
- Zeng, X.; Yang, L.; Zhu, Y.; Yang, F. Comparison of Two Optimal Guidance Methods for the Long-Distance Orbital Pursuit-Evasion Game. IEEE Trans. Aerosp. Electron. Syst. 2020, 57, 521–539. [Google Scholar] [CrossRef]
- Yang, B.; Liu, P.; Feng, J.; Li, S. Two-Stage Pursuit Strategy for Incomplete-Information Impulsive Space Pursuit-Evasion Mission Using Reinforcement Learning. Aerospace 2021, 8, 299. [Google Scholar] [CrossRef]
- Bryson, A.; Ho, Y. Applied Optimal Control: Optimization, Estimation and Control; CRC Press: Boca Raton, FL, USA, 1975. [Google Scholar]
- Basar, T. Relaxation Techniques and asynchronous algorithms for online computation of non-cooperative equilibria. J. Econ. Dyn. Control 1987, 11, 531–549. [Google Scholar] [CrossRef]
- Uryasev, S.; Rubinstein, R. On relaxation algorithms in computation of noncooperative equilibria. IEEE Trans. Autom. Control 1994, 39, 1263–1267. [Google Scholar] [CrossRef]
- Johnson, P.A. Numerical Solution Methods for dIfferential Game Problems. Master’s Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 2009. [Google Scholar]
- Horie, K.; Conway, B.A. Genetic algorithm preprocessing for numerical solution of differential games problems. J. Guid. Control Dyn. 2004, 27, 1075–1078. [Google Scholar] [CrossRef]
- Sun, W.; Tsiotras, P.; Lolla, T.; Subramani, D.N.; Lermusiaux, P.F. Multiple-pursuer/one-evader pursuit–evasion game in dynamic flowfields. J. Guid. Control Dyn. 2017, 40, 1627–1637. [Google Scholar] [CrossRef]
- Chung, C.F.; Furukawa, T.; Goktogan, A.H. Coordinated control for capturing a highly maneuverable evader using forward reachable sets. In Proceedings of the 2006 IEEE International Conference on Robotics and Automation, ICRA 2006, IEEE, Orlando, FL, USA, 15–19 May 2006; pp. 1336–1341. [Google Scholar]
- Salmon, D.M.; HElNE, W. Reachable sets analysis-an efficient technique for performing missile/sensor tradeoff studies. AIAA J. 1973, 11, 927–931. [Google Scholar] [CrossRef]
- Chung, C.F.; Furukawa, T. A reachability-based strategy for the time-optimal control of autonomous pursuers. Eng. Optim. 2008, 40, 67–93. [Google Scholar] [CrossRef]
- Zanardi, C.; Hervé, J.Y.; Cohen, P. Escape strategy for a mobile robot under pursuit. In Proceedings of the 1995 IEEE International Conference on Systems, Man and Cybernetics. Intelligent Systems for the 21st Century, IEEE, Vancouver, BC, Canada, 22–25 October 1995; Volume 4, pp. 3304–3309. [Google Scholar]
- Jansson, O.; Harris, M.; Geller, D. A Parallelizable Reachable Set Method for Pursuit-Evasion Games Using Interior-Point Methods. In Proceedings of the 2021 IEEE Aerospace Conference (50100), IEEE, Big Sky, MT, USA, 6–13 March 2021; pp. 1–9. [Google Scholar]
- Gong, H.; Gong, S.; Li, J. Pursuit-Evasion Game for Satellites Based on Continuous Thrust Reachable Domain. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4626–4637. [Google Scholar] [CrossRef]
- Colonius, F.; Szolnoki, D. Algorithms for computing reachable sets and control sets. IFAC Proc. Vol. 2001, 34, 723–728. [Google Scholar] [CrossRef]
- Girard, A.; Le Guernic, C.; Maler, O. Efficient computation of reachable sets of linear time-invariant systems with inputs. In Proceedings of the International Workshop on Hybrid Systems: Computation and Control, Santa Barbara, CA, USA, 29–31 March 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 257–271. [Google Scholar]
- Varaiya, P. Reach set computation using optimal control. In Verification of Digital and Hybrid Systems; Springer: Berlin/Heidelberg, Germany, 2000; pp. 323–331. [Google Scholar]
- Dueri, D.; Raković, S.V.; Açıkmeşe, B. Consistently improving approximations for constrained controllability and reachability. In Proceedings of the 2016 European Control Conference (ECC), IEEE, Aalborg, Denmark, 29 June–1 July 2016; pp. 1623–1629. [Google Scholar]
- Dueri, D.; Açıkmeşe, B.; Baldwin, M.; Erwin, R.S. Finite-horizon controllability and reachability for deterministic and stochastic linear control systems with convex constraints. In Proceedings of the 2014 American Control Conference, IEEE, Portland, OR, USA, 4–6 June 2014; pp. 5016–5023. [Google Scholar]
- Yang, R.; Liu, X. Reachable set computation of linear systems with nonconvex constraints via convex optimization. Automatica 2022, 146, 110632. [Google Scholar] [CrossRef]
- Pecsvaradi, T.; Narendra, K.S. Reachable sets for linear dynamical systems. Inf. Control 1971, 19, 319–344. [Google Scholar] [CrossRef]
- Hermes, H.; LaSalle, J.P. Functional Analysis and Time Optimal Control; Academic Press Inc.: New York, NY, USA, 1969. [Google Scholar]
- Guenin, B.; Konemann, J.; Tuncel, L. A Gentle Introduction to Optimization; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Clohessy, W.; Wiltshire, R. Terminal guidance system for satellite rendezvous. J. Aerosp. Sci. 1960, 27, 653–658. [Google Scholar] [CrossRef]
- Bennett, T.; Schaub, H. Continuous-Time Modeling and Control Using Nonsingular Linearized Relative-Orbit Elements. J. Guid. Control Dyn. 2016, 39, 2605–2614. [Google Scholar] [CrossRef]
- Sullivan, J.; Grimberg, S.; D’Amico, S. Comprehensive Survey and Assessment of Spacecraft Relative Motion Dynamics Models. J. Guid. Control Dyn. 2017, 40, 1837–1859. [Google Scholar] [CrossRef]
- Toh, K.C.; Todd, M.J.; Tutuncu, R.H. SDPT3—A Matlab software package for semidefinite programming, Version 1.3. Optim. Methods Softw. 1999, 11, 545–581. [Google Scholar] [CrossRef]
- Gurobi Optimization, LLC. Gurobi Optimizer Reference Manual; Gurobi Optimization, LLC: Houston, TX, USA, 2022. [Google Scholar]
- Löfberg, J. YALMIP: A Toolbox for Modeling and Optimization in MATLAB. In Proceedings of the CACSD Conference, Taipei, Taiwan, 2–4 September 2004. [Google Scholar]
- The Mathworks, Inc. MATLAB 2023; The Mathworks, Inc.: Natick, MA, USA, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).