Numerical Study of Combustion and Emission Characteristics for Hydrogen Mixed Fuel in the Methane-Fueled Gas Turbine Combustor
Abstract
1. Introduction
2. Materials and Methods
2.1. Numerical Model
2.1.1. Governing Equations
2.1.2. Turbulence Model and Combustion Model
2.1.3. NOx Model
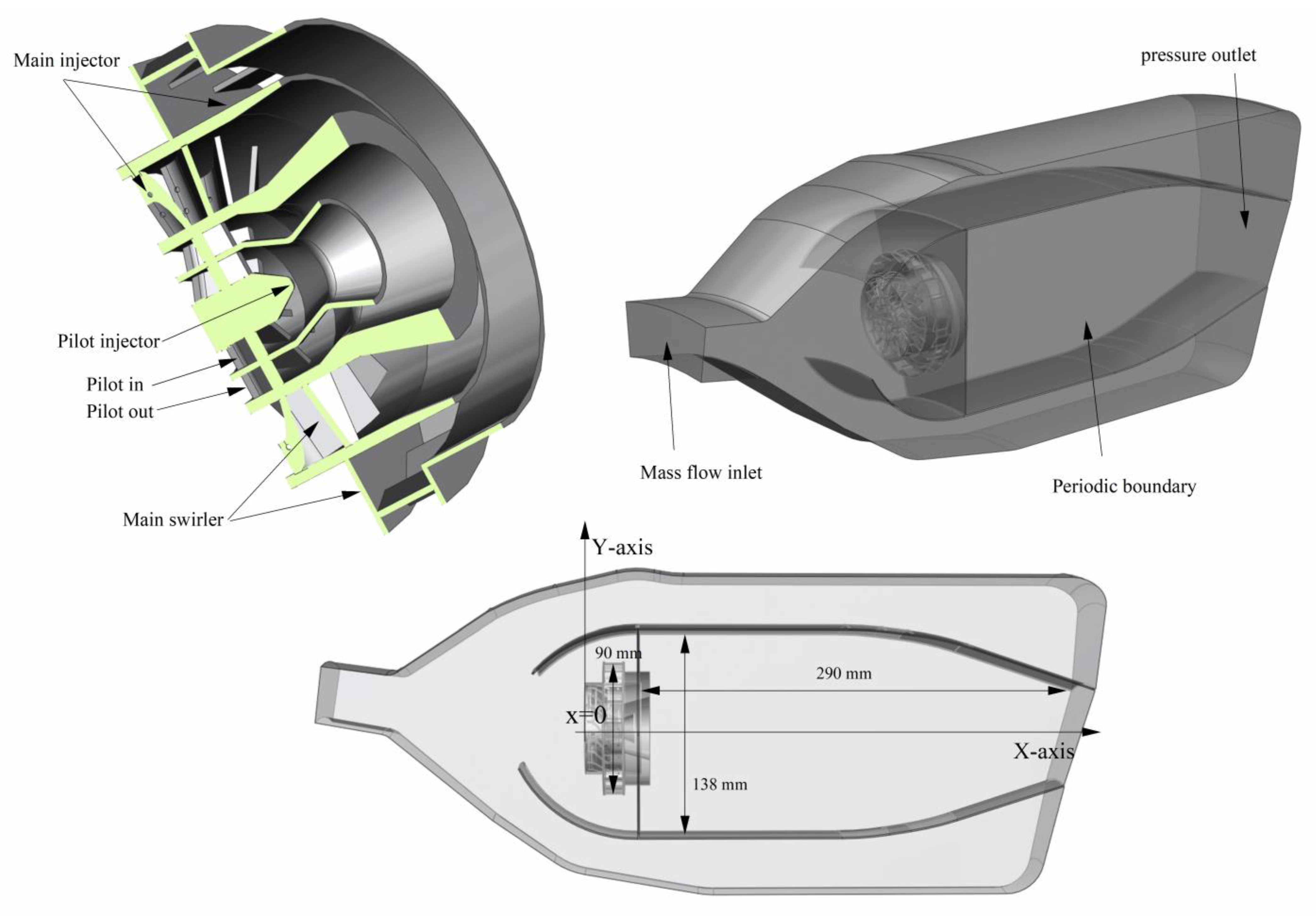
2.2. Numerical Set and Combustor Structure
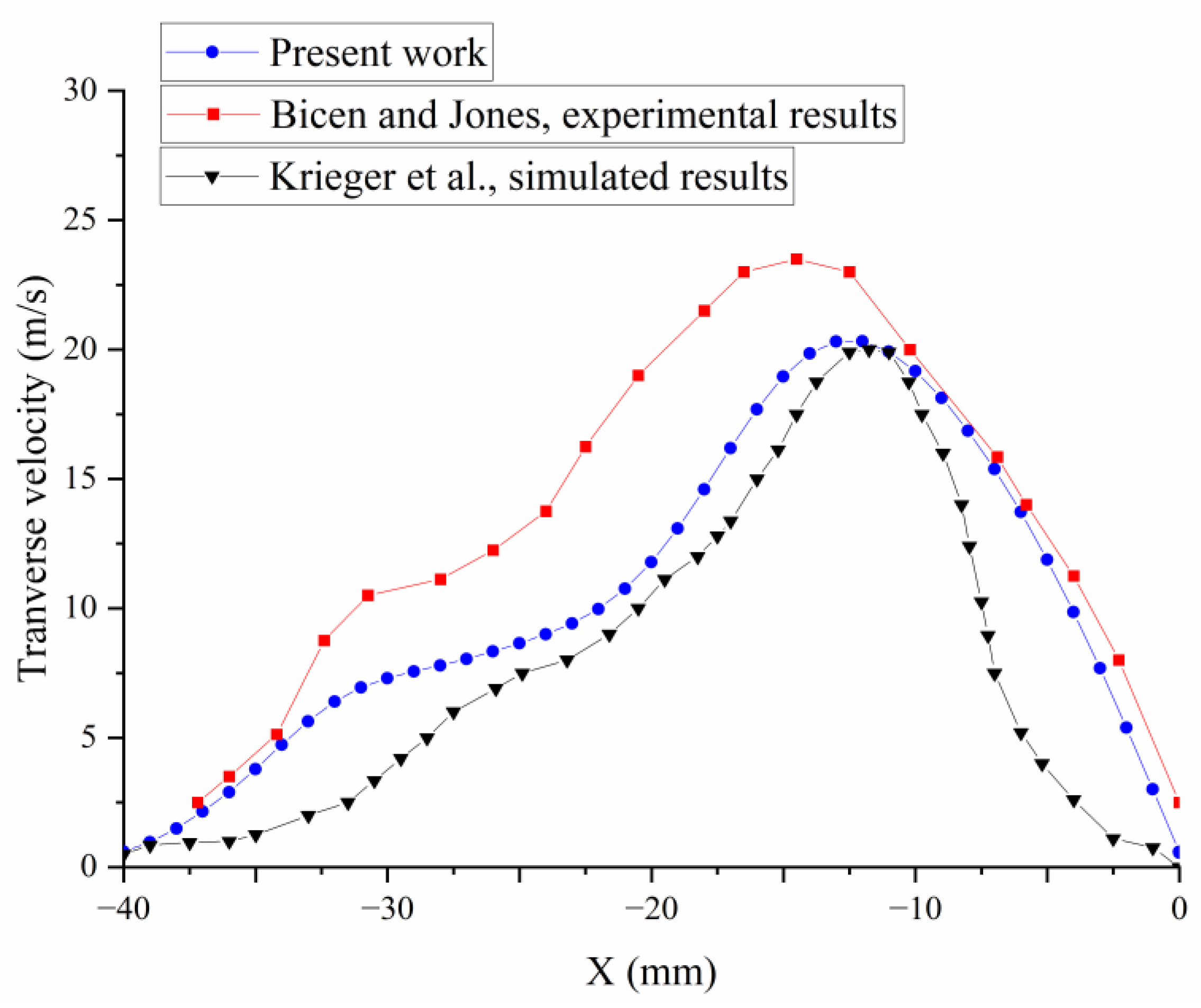
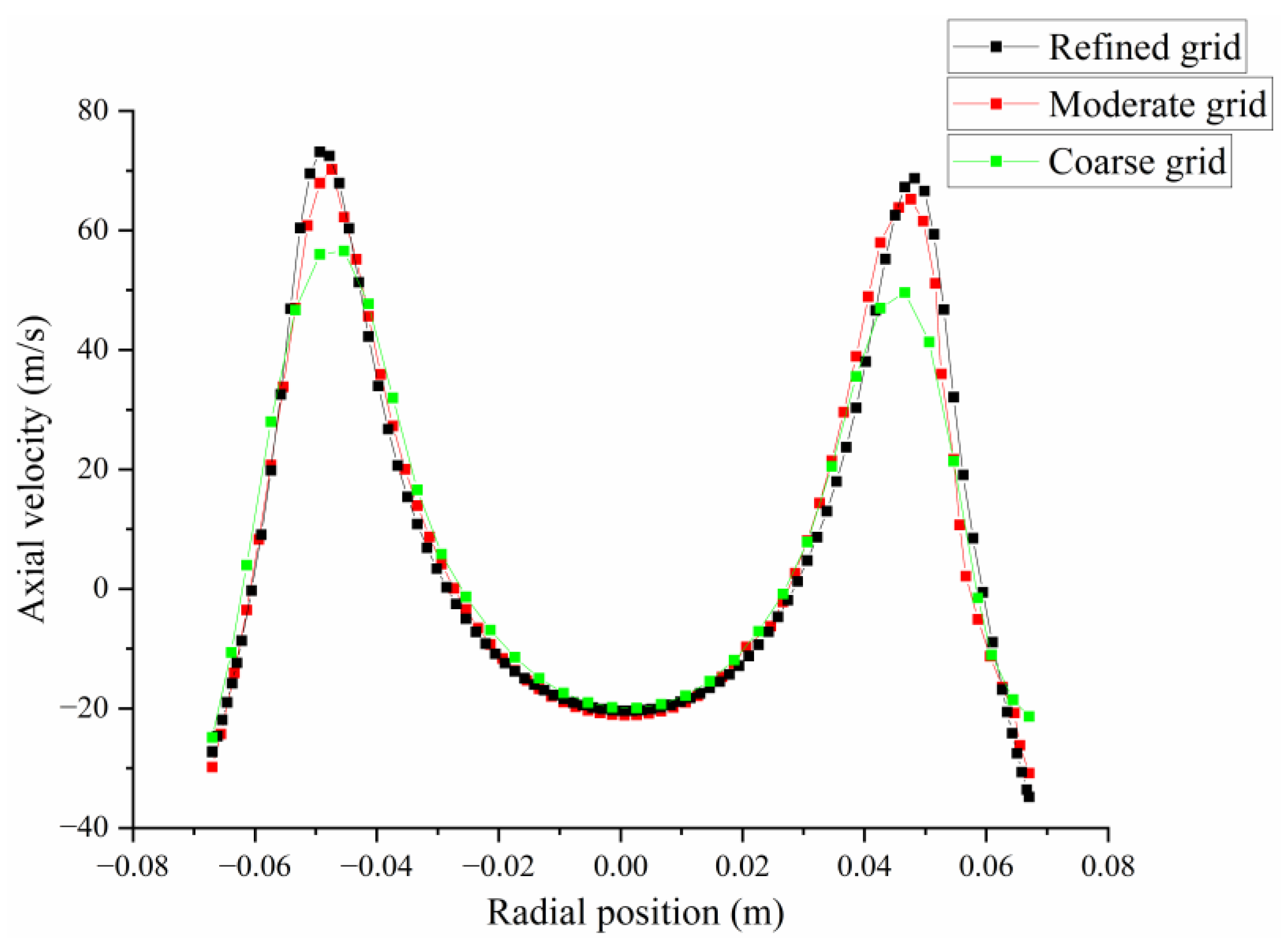
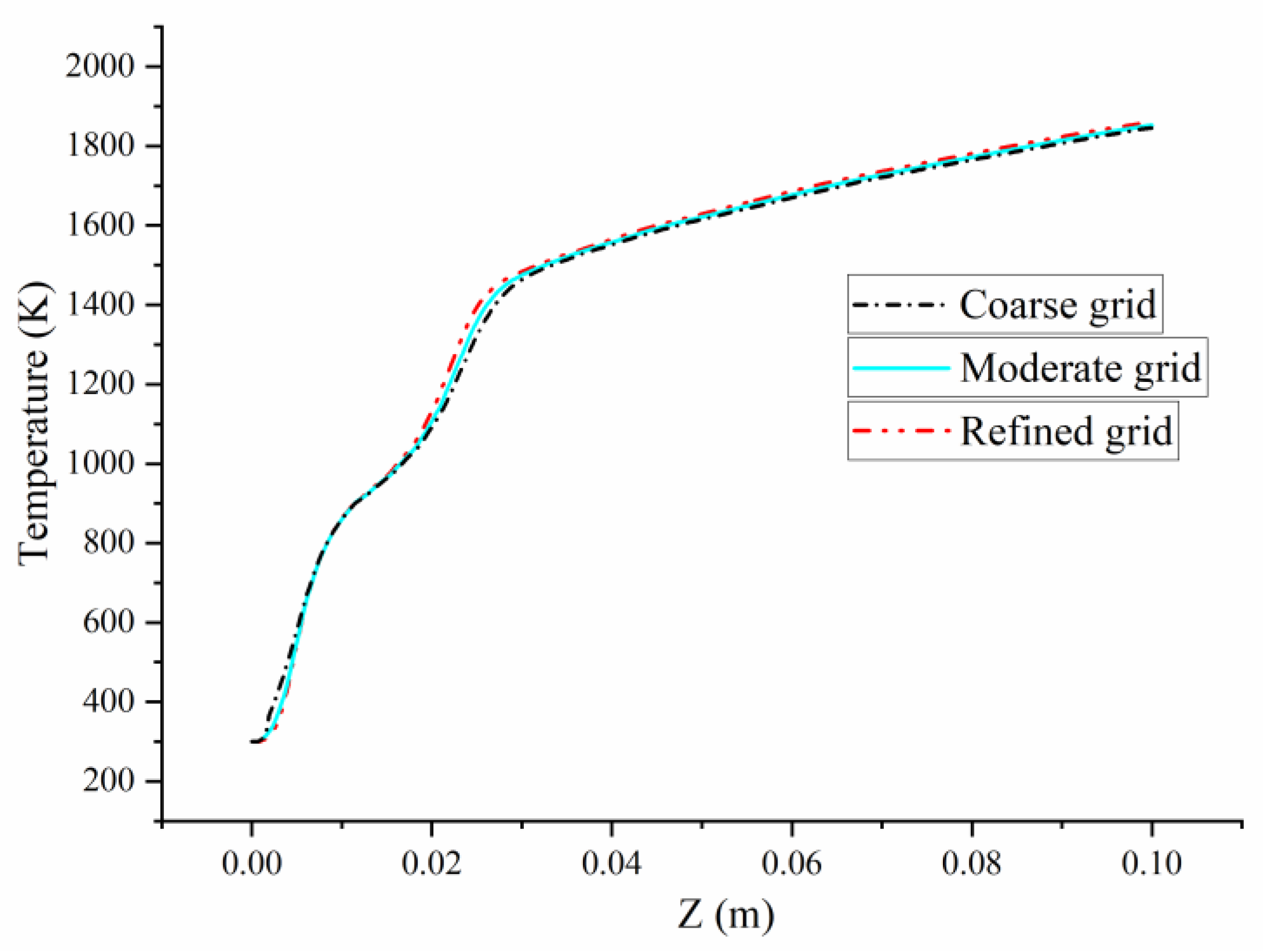
2.3. Numerical Validation
3. Results and Discussion
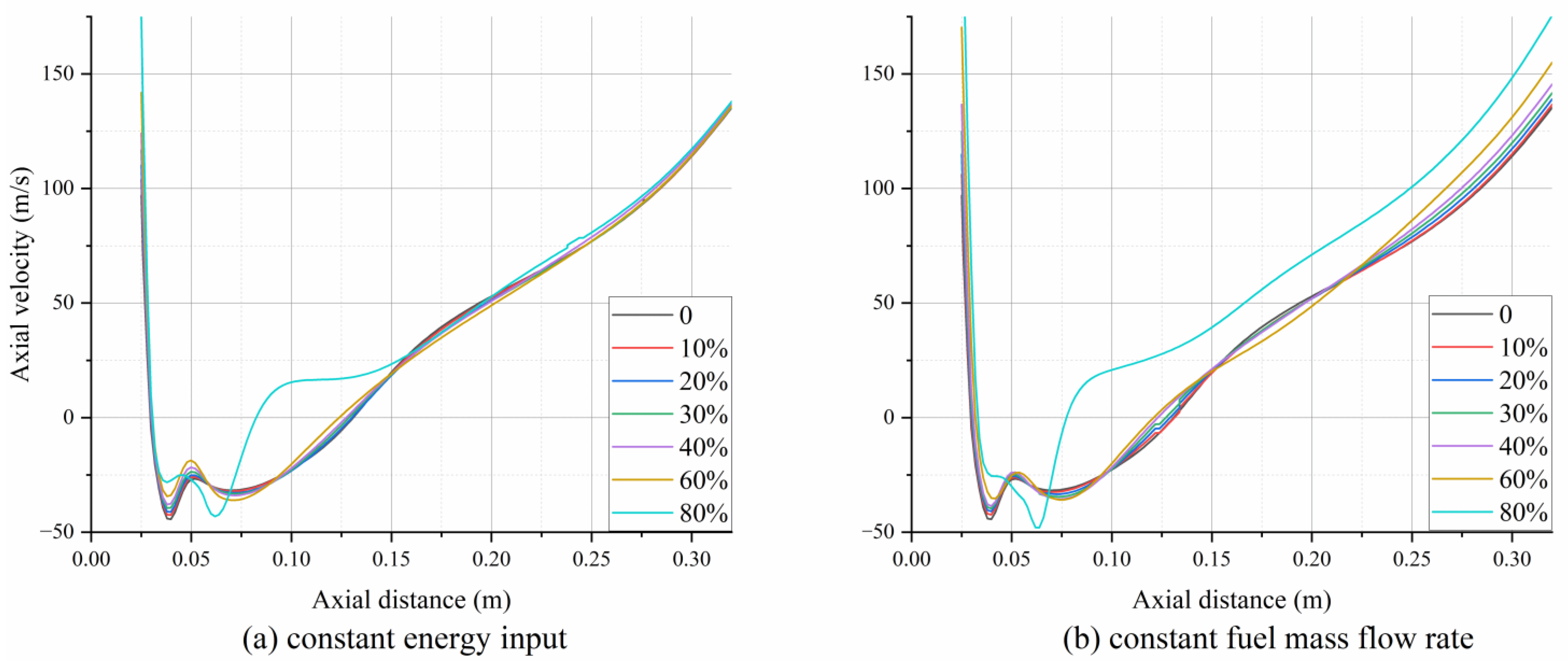
3.1. Velocity Distribution
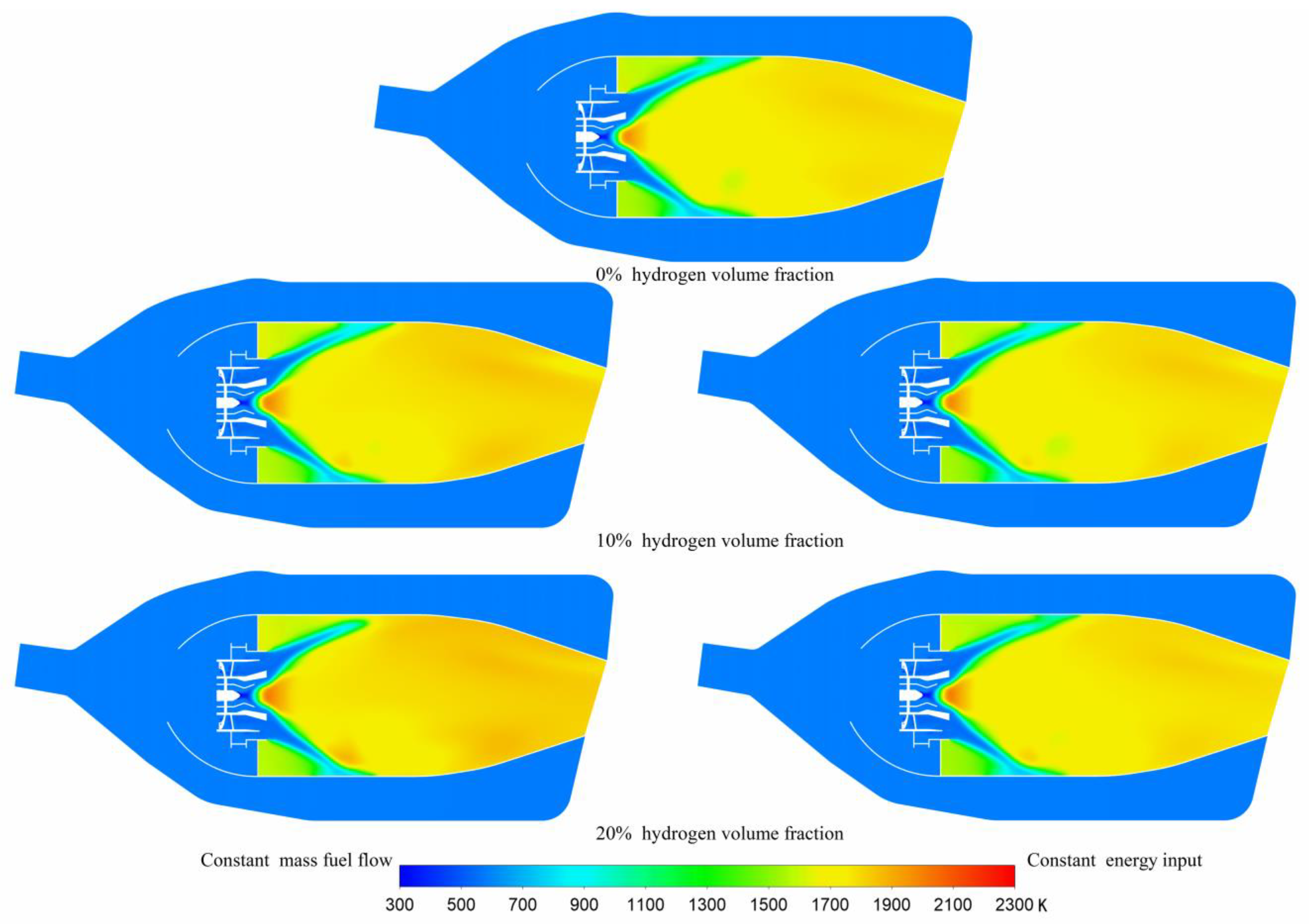
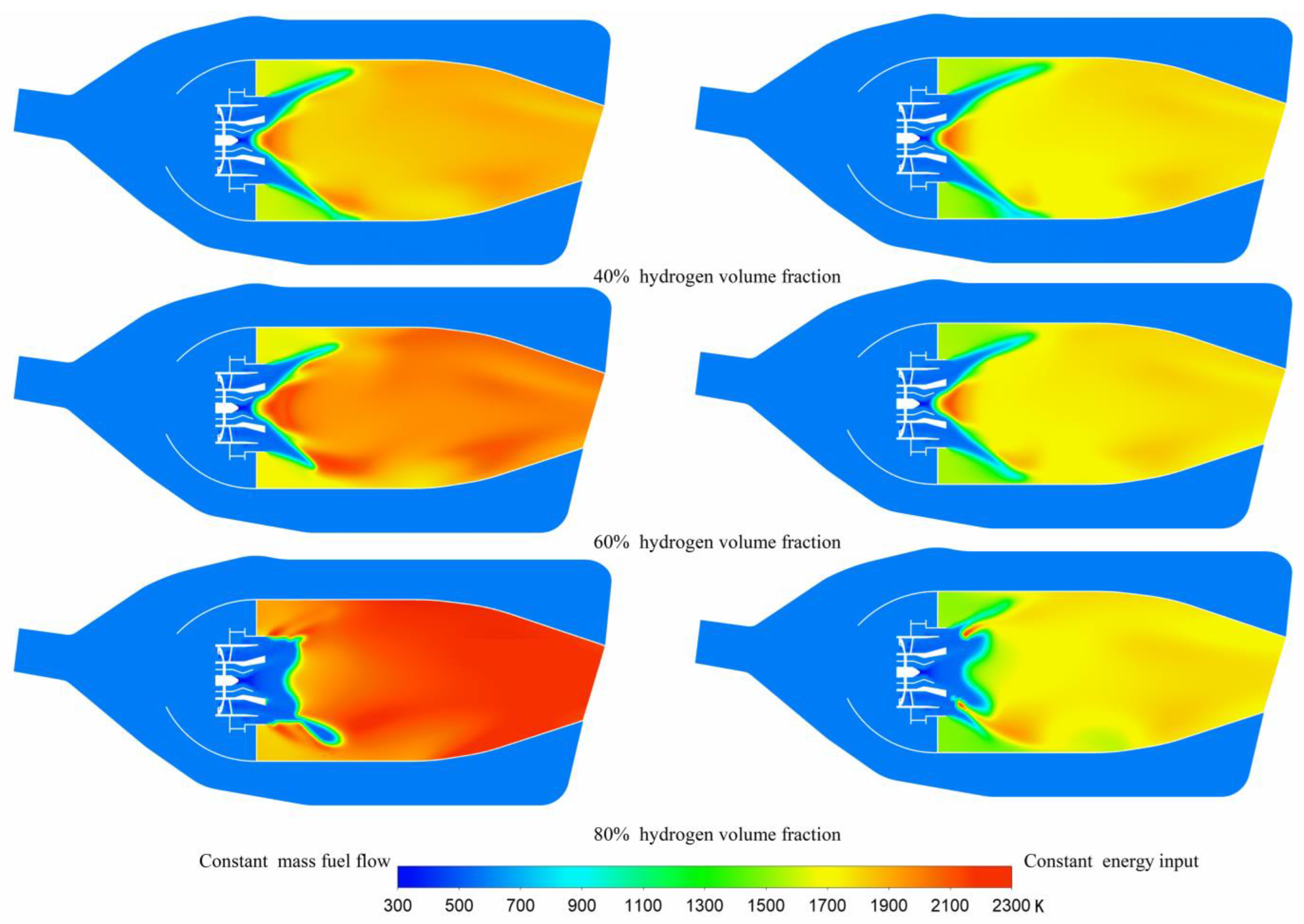
3.2. Temperature Distribution
3.3. Unburned Fuel Emissions
3.4. Combustion Characteristics
3.4.1. Heat Release Rate
3.4.2. Emissions of Combustion
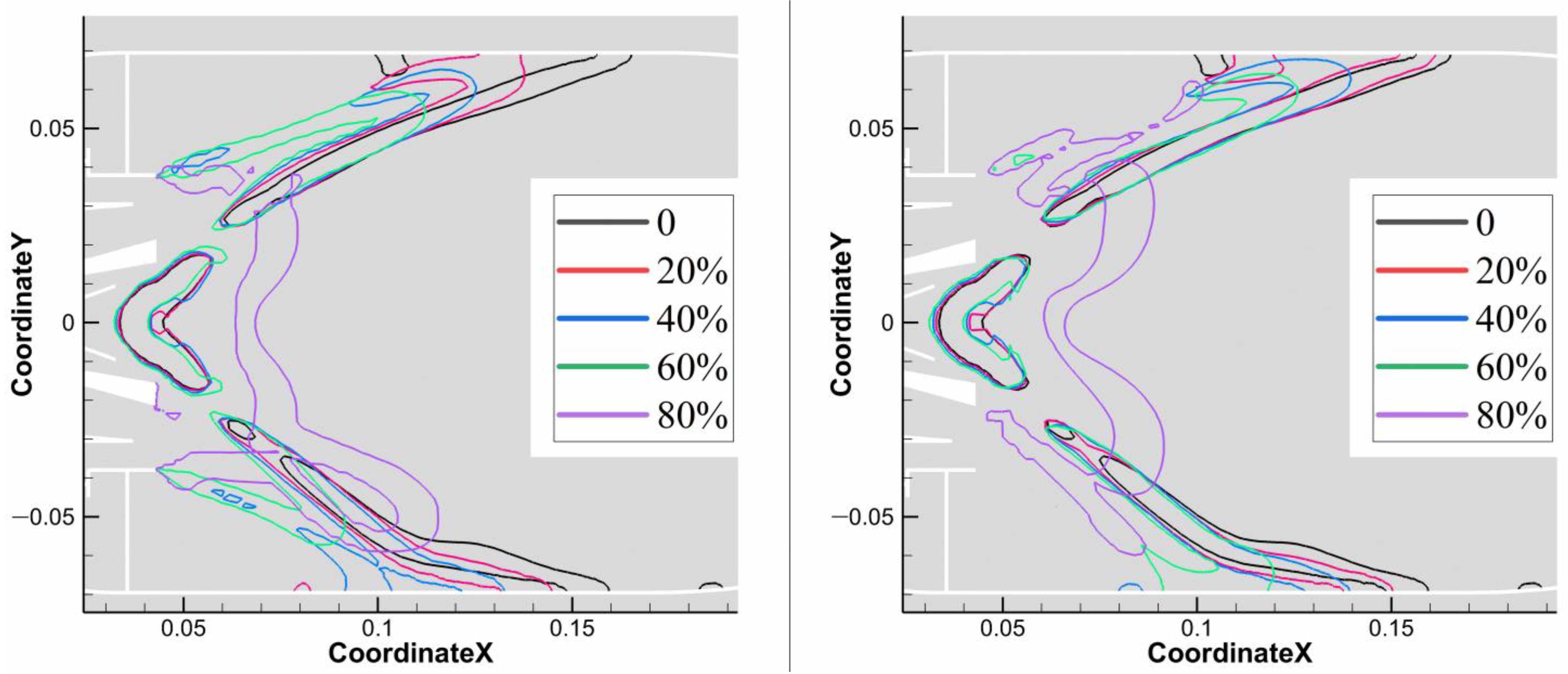
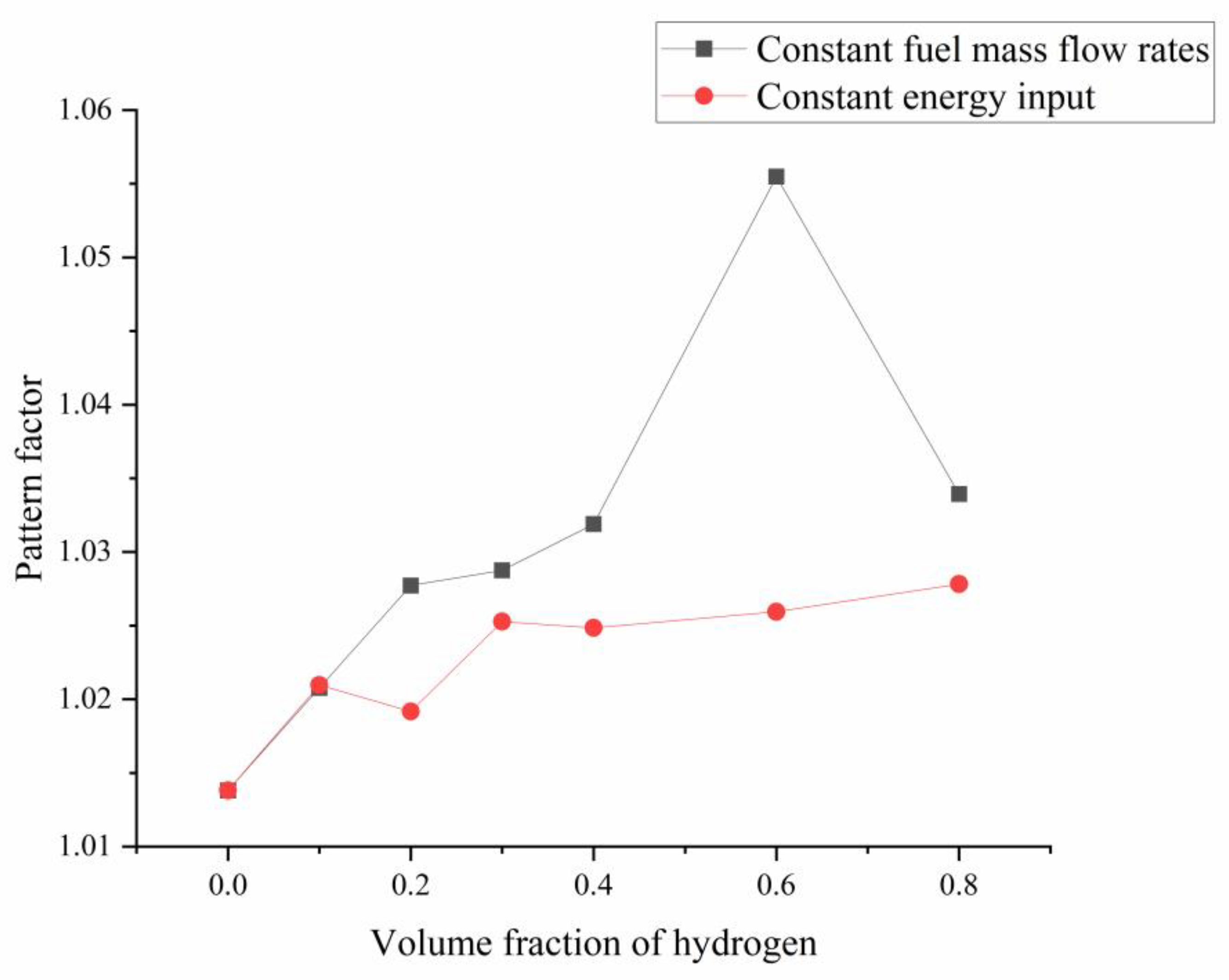
3.4.3. Pattern Factor
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Taamallah, S.; Vogiatzaki, K.; Alzahrani, F.M.; Mokheimer, E.M.A.; Habib, M.A.; Ghoniem, A.F. Fuel flexibility, stability and emissions in premixed hydrogen-rich gas turbine combustion: Technology, fundamentals, and numerical simulations. Appl. Energy 2015, 154, 1020–1047. [Google Scholar] [CrossRef]
- Flaszynski, P.; Piotrowicz, M.; Bacci, T. Clocking and Potential Effects in Combustor–Turbine Stator Interactions. Aerospace 2021, 8, 285. [Google Scholar] [CrossRef]
- Seitz, A.; Nickl, M.; Troeltsch, F.; Ebner, K. Initial Assessment of a Fuel Cell—Gas Turbine Hybrid Propulsion Concept. Aerospace 2022, 9, 68. [Google Scholar] [CrossRef]
- Neilson, C.E. LM2500 gas turbine modifications for biomass fuel operation. Biomass Bioenergy 1998, 15, 269–273. [Google Scholar] [CrossRef]
- Abudu, K.; Igie, U.; Roumeliotis, I.; Szymanski, A.; Di Lorenzo, G. Aeroderivative gas turbine back-up capability with compressed air injection. Appl. Therm. Eng. 2020, 180, 115844. [Google Scholar] [CrossRef]
- Przysowa, R.; Gawron, B.; Białecki, T.; Łęgowik, A.; Merkisz, J.; Jasiński, R. Performance and Emissions of a Microturbine and Turbofan Powered by Alternative Fuels. Aerospace 2021, 8, 25. [Google Scholar] [CrossRef]
- Rochelle, D.; Najafi, H. A review of the effect of biodiesel on gas turbine emissions and performance. Renew. Sustain. Energy Rev. 2019, 105, 129–137. [Google Scholar] [CrossRef]
- Söderholm, P. Fuel flexibility in the West European power sector. Resour. Policy 2000, 26, 157–170. [Google Scholar] [CrossRef]
- Ino, H. Future View of Energy Supply & Role of Gas Turbine in Japan (View of Electric Power Company). Gener. Up Now 2003, 2003–2006. [Google Scholar]
- Neilson, C.E.; Shafer, D.G.; Carpentieri, E. LM2500 Gas Turbine Fuel Nozzle Design and Combustion Test Evaluation and Emission Results with Simulated Gasified Wood Product Fuels. J. Eng. Gas Turbines Power 1998, 121, 600–606. [Google Scholar] [CrossRef]
- Muk, C.H. He Bang-Quan. Spark ignition natural gas engines—A review. Energy Convers. Manag. 2007, 48, 608–618. [Google Scholar]
- Turns, S.R. An Introduction to Combustion: Concepts and Applications, 2nd ed.; McGraw-Hill: Boston, MA, USA, 2000; p. 158. [Google Scholar]
- Wang, J.; Huang, Z.; Tang, C.; Miao, H.; Wang, X. Numerical study of the effect of hydrogen addition on methane-air mixtures combustion. Int. J. Hydrogen Energy 2009, 34, 1084–1096. [Google Scholar] [CrossRef]
- Gondal, I.A. Hydrogen integration in power-to-gas networks. Int. J. Hydrogen Energy 2019, 44, 1803–1815. [Google Scholar] [CrossRef]
- Judd, R.; Pinchbeck, D. Hydrogen admixture to the natural gas grid. Compend. Hydrog. Energy 2016, 165–192. [Google Scholar] [CrossRef]
- Suez, G.D.F. GDF Suez, McPhy in French GRHYD project on methane, hydrogen. Fuel Cells Bull. 2012, 2012, 10. [Google Scholar]
- Emadi, M.; Karkow, D.; Salameh, T.; Gohil, A.; Ratner, A. Flame structure changes resulting from hydrogen-enrichment and pressurization for low-swirl premixed methane-air flames. Int. J. Hydrogen Energy 2012, 37, 10397–10404. [Google Scholar] [CrossRef]
- Schefer, R.W. Reduced turbine emissions using hydrogen enriched fuels. In Proceedings of the 2002 U.S. DOE Hydrogen Program Review, NREL/CP-610-32405, Golden, Colorado, 6–10 May 2002. [Google Scholar]
- Schefer, R.W.; Wicksall, D.M.; Agrawal, A.K. Combustion of hydrogen-enriched methane in a lean premixed swirl stabilized burner. Proc. Combust. Inst. 2002, 29, 843–851. [Google Scholar] [CrossRef]
- Patel, V.; Shah, R. Effect of hydrogen enrichment on combustion characteristics of methane swirling and non-swirling inverse diffusion flame. Int. J. Hydrogen Energy 2019, 44, 28316–28329. [Google Scholar] [CrossRef]
- Lamioni, R.; Bronzoni, C.; Folli, M.; Tognotti, L.; Galletti, C. Feeding H2-admixtures to domestic condensing boilers: Numerical simulations of combustion and pollutant formation in multi-hole burners. Appl. Energy 2022, 309, 118379. [Google Scholar] [CrossRef]
- Lamioni, R.; Lapenna, P.E.; Berger, L.; Kleinheinz, K.; Attili, A.; Pitsch, H.; Creta, F. Pressure-induced Hydrodynamic Instability in Premixed Methane-Air Slot Flames. Combust. Sci. Technol. 2020, 192, 1998–2009. [Google Scholar] [CrossRef]
- Shih, H.Y.; Liu, C.R. A computational study on the combustion of hydrogen/methane blended fuels for a micro gas turbines. Int. J. Hydrogen Energy 2014, 39, 15103–15115. [Google Scholar] [CrossRef]
- Rajpara, P.; Shah, R.; Banerjee, J. Effect of hydrogen addition on combustion and emission characteristics of methane fuelled upward swirl can combustor. Int. J. Hydrogen Energy 2018, 43, 17505–17519. [Google Scholar] [CrossRef]
- Cozzi, F.; Coghe, A. Behavior of hydrogen-enriched non-premixed swirled natural gas flames. Int. J. Hydrogen Energy 2006, 31, 669–677. [Google Scholar] [CrossRef]
- Tsukagoshi, K.; Arimura, H.; Tanaka, K. Development of air cooled combustor for Mitsubishi G class gas turbine. In Proceedings of the ASME Turbo Expo 2010:Power for Land, Sea, and Air, Glasgow, UK, 14–18 June 2010. [Google Scholar]
- Thundil Karuppa Raj, R.; Ganesan, V. Study on the effect of various parameters on flow development behind vane swirlers. Int. J. Therm. Sci. 2008, 47, 1204–1225. [Google Scholar] [CrossRef]
- Lazik, W.; Doerr, T.; Bake, S.; Bank, R.; Rackwitz, L. Development of lean-burn low-NOx combustion technology at Rolls-Royce deutschland. In Proceedings of the ASME Turbo Expo 2008: Power for Land, Sea, and Air, Volume 3: Combustion, Fuels and Emissions, Parts A and B, Berlin, Germany, 9–13 June 2008; pp. 797–807. [Google Scholar] [CrossRef]
- Jiang, Y.; Hajivand, M.; Sadeghi, H.; Gerdroodbary, M.B.; Li, Z. Influence of trapezoidal lobe strut on fuel mixing and combustion in supersonic combustion chamber. Aerosp. Sci. Technol. 2021, 116, 106841. [Google Scholar] [CrossRef]
- Sun, C.; Gerdroodbary, M.B.; Abazari, A.M.; Hosseini, S.; Li, Z. Mixing efficiency of hydrogen multi jet through backward facing steps at supersonic flow. Int. J. Hydrogen Energy 2021, 46, 16075e85. [Google Scholar] [CrossRef]
- Wang, K.; Li, F.; Zhao, K.; Zhou, T. Numerical study on the lobed nozzles for enhancing the mixing and combustion performance of rocket-based combined cycle engine. Energy Reports 2022, 8, 6645–6658. [Google Scholar] [CrossRef]
- Zhang, Y.; Gerdroodbary, M.B.; Hosseini, S.; Abazari, A.M.; Li, Z. Effect of hybrid coaxial air and hydrogen jets on fuel mixing at supersonic crossflow. Int. J. Hydrogen Energy 2021, 46, 16048e62. [Google Scholar] [CrossRef]
- Gerdroodbary, M.B.; Moradi, R.; Babazadeh, H. Computational investigation of multi hydrogen jets at inclined supersonic flow. Int. J. Energy Res. 2021, 45, 1661–1672. [Google Scholar] [CrossRef]
- Shih, T.H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A new k-ϵ eddy viscosity model for high reynolds number turbulent flows. Comput. Fluids 1995, 24, 227–238. [Google Scholar] [CrossRef]
- van Oijen, J.A.; de Goey, L.P.H. Modelling of premixed laminar flames using flamelet-generated manifolds. Combust. Sci. Technol. 2000, 161, 113–137. [Google Scholar] [CrossRef]
- Ren, M.; Wang, S.; Zhao, J.; Zou, C.; Roekaerts, D. Numerical study of a turbulent co-axial non-premixed flame for methanol hydrothermal combustion: Comparison of the EDC and FGM models. J. Supercrit. Fluids 2020, 169, 105132. [Google Scholar] [CrossRef]
- Smith, G.P.; Golden, D.M.; Frenklach, M.; Moriarty, N.W.; Eiteneer, B.; Goldenberg, M.; Bowman, C.T.; Hanson, R.K.; Song, S.; Gardiner, W.C.; et al. Available online: http://www.me.berkeley.edu/gri_mech/ (accessed on 23 November 2022).
- Correa, S.M. A Review of NO x Formation Under Gas-Turbine Combustion Conditions. Combust. Sci. Technol. 1992, 87, 329–362. [Google Scholar]
- Krieger, G.C.; Campos, A.P.V.; Takehara, M.D.B.; Alfaia Da Cunha, F.; Gurgel Veras, C.A. Numerical simulation of oxy-fuel combustion for gas turbine applications. Appl. Therm. Eng. 2015, 78, 471–481. [Google Scholar] [CrossRef]
- Bicen, A.F.; Jones, W.P. Velocity characteristics of isothermal and combusting flows in a model combustor. Combust. Sci. Technol. 1986, 49, 1–15. [Google Scholar] [CrossRef]
- Tamang, S.; Park, H. Numerical investigation of combustion characteristics for hydrogen mixed fuel in a can-type model of the gas turbine combustor. Int. J. Hydrogen Energy 2022, 5, 273. [Google Scholar] [CrossRef]
- Law, C.; Kwon, O. Effects of hydrocarbon substitution on atmospheric hydrogenair flame propagation. Int. J. Hydrogen Energy 2004, 29, 867–879. [Google Scholar] [CrossRef]
- Yin, C.; Zhang, R.; Zhang, C.; Fan, W. Numerical simulation on combustion and exhaust emission of staged combustor. IOP Conf. Ser. Earth Environ. Sci. 2017, 52, 12026. [Google Scholar] [CrossRef]
- Peters, N. Turbulent combustion. Meas. Sci. Technol. 2000, 125. [Google Scholar]
- Cai, X.; Fan, Q.; Bai, X.S.; Wang, J.; Zhang, M.; Huang, Z.; Alden, M.; Li, Z. Turbulent burning velocity and its related statistics of ammoniahydrogenair jet flames at high Karlovitz number: Effect of differential diffusion. Proc. Combust. Inst. 2022, 1–12. [Google Scholar] [CrossRef]


| Hydrogen Volume Fraction (%) | Hydrogen Mass Fraction (%) | Fuel Mass Flow Rate (kg/s) | Air Mass Flow Rate (kg/s) | The Total Heat Energy Input (MW) | |
|---|---|---|---|---|---|
| Case 1 | 0 | 0 | 0.051 | 2.273 | 2.550 |
| Case 2 | 10 | 1.37 | 0.051 | 2.273 | 2.600 |
| Case 3 | 20 | 3.03 | 0.051 | 2.273 | 2.660 |
| Case 4 | 30 | 5.08 | 0.051 | 2.273 | 2.734 |
| Case 5 | 40 | 7.69 | 0.051 | 2.273 | 2.829 |
| Case 6 | 60 | 15.79 | 0.051 | 2.273 | 3.122 |
| Case 7 | 80 | 33.33 | 0.051 | 2.273 | 3.757 |
| Case 8 | 10 | 1.37 | 0.0500 | 2.273 | 2.55 |
| Case 9 | 20 | 3.03 | 0.0489 | 2.273 | 2.55 |
| Case 10 | 30 | 5.08 | 0.0476 | 2.273 | 2.55 |
| Case 11 | 40 | 7.69 | 0.0459 | 2.273 | 2.55 |
| Case 12 | 60 | 15.79 | 0.0417 | 2.273 | 2.55 |
| Case 13 | 80 | 33.33 | 0.0346 | 2.273 | 2.55 |
| Parameter | Value |
|---|---|
| Air inlet total pressure (MPa) | 1 |
| Air inlet static temperature (K) | 600 |
| Fuel inlet static temperature (K) | 300 |
| Wall treatment | adiabatic wall |
| Pressure drop of the combustor | 4.9% |
| Methane Mass Fraction at the Outlet | Hydrogen Mass Fraction at the Outlet | Total Fuel Mass Fraction at the Outlet | Relative Change (%) | Hydrogen Consumption Rate (%) | Methane Consumption Rate (%) | |
|---|---|---|---|---|---|---|
| Case 1 | 7.4592 × 10−5 | 7.747 × 10−7 | 7.5367 × 10−5 | 0 | N/A | 99.75 |
| Case 2 | 6.6058 × 10−5 | 19.261 × 10−7 | 6.7984 × 10−5 | −9.7 | 99.54 | 99.78 |
| Case 3 | 5.3478 × 10−5 | 29.753 × 10−7 | 5.6453 × 10−5 | −25 | 99.68 | 99.82 |
| Case 4 | 4.4744 × 10−5 | 41.254 × 10−7 | 4.8869 × 10−5 | −35.2 | 99.74 | 99.84 |
| Case 5 | 3.5147 × 10−5 | 53.021 × 10−7 | 4.0449 × 10−5 | −46.3 | 99.78 | 99.87 |
| Case 6 | 2.2152 × 10−5 | 93.528 × 10−7 | 3.1477 × 10−5 | −58.2 | 99.83 | 99.93 |
| Case 7 | 4.62 × 10−5 | 5.55 × 10−5 | 1.0178 × 10−4 | +35 | 99.46 | 99.77 |
| Methane Mass Fraction at the Outlet | Hydrogen Mass Fraction at the Outlet | Total Fuel Mass Fraction at the Outlet | Relative Change (%) | Hydrogen Consumption Rate (%) | Methane Consumption Rate (%) | |
|---|---|---|---|---|---|---|
| Case 1 | 7.4592 × 10−5 | 7.747 × 10−7 | 7.5367 × 10−5 | 0 | N/A | 99.75 |
| Case 8 | 6.9732 × 10−5 | 17.513 × 10−7 | 7.1483 × 10−5 | −5.2 | 99.58 | 99.76 |
| Case 9 | 5.8619 × 10−5 | 25.749 × 10−7 | 6.11932 × 10−5 | −18.8 | 99.71 | 99.79 |
| Case 10 | 4.9990 × 10−5 | 34.012 × 10−7 | 5.33907 × 10−5 | −29.2 | 99.76 | 99.82 |
| Case 11 | 4.1124 × 10−5 | 41.106 × 10−7 | 4.52348 × 10−5 | −40.0 | 99.80 | 99.84 |
| Case 12 | 2.4253 × 10−5 | 52.363 × 10−7 | 2.94885 × 10−5 | −60.9 | 99.89 | 99.89 |
| Case 13 | 1.9986 × 10−5 | 1.099 × 10−5 | 3.09822 × 10−5 | −58.9 | 99.89 | 99.86 |
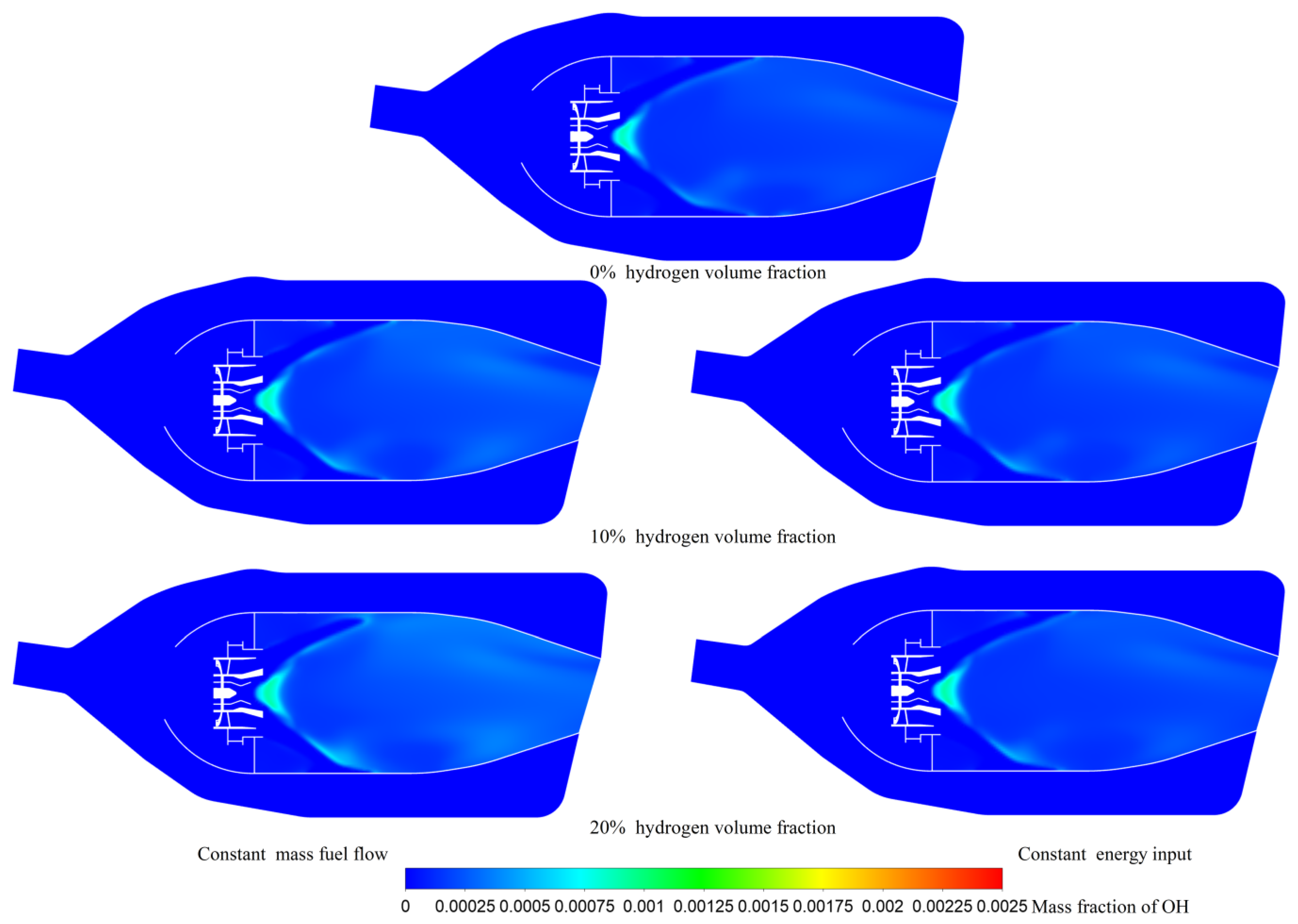
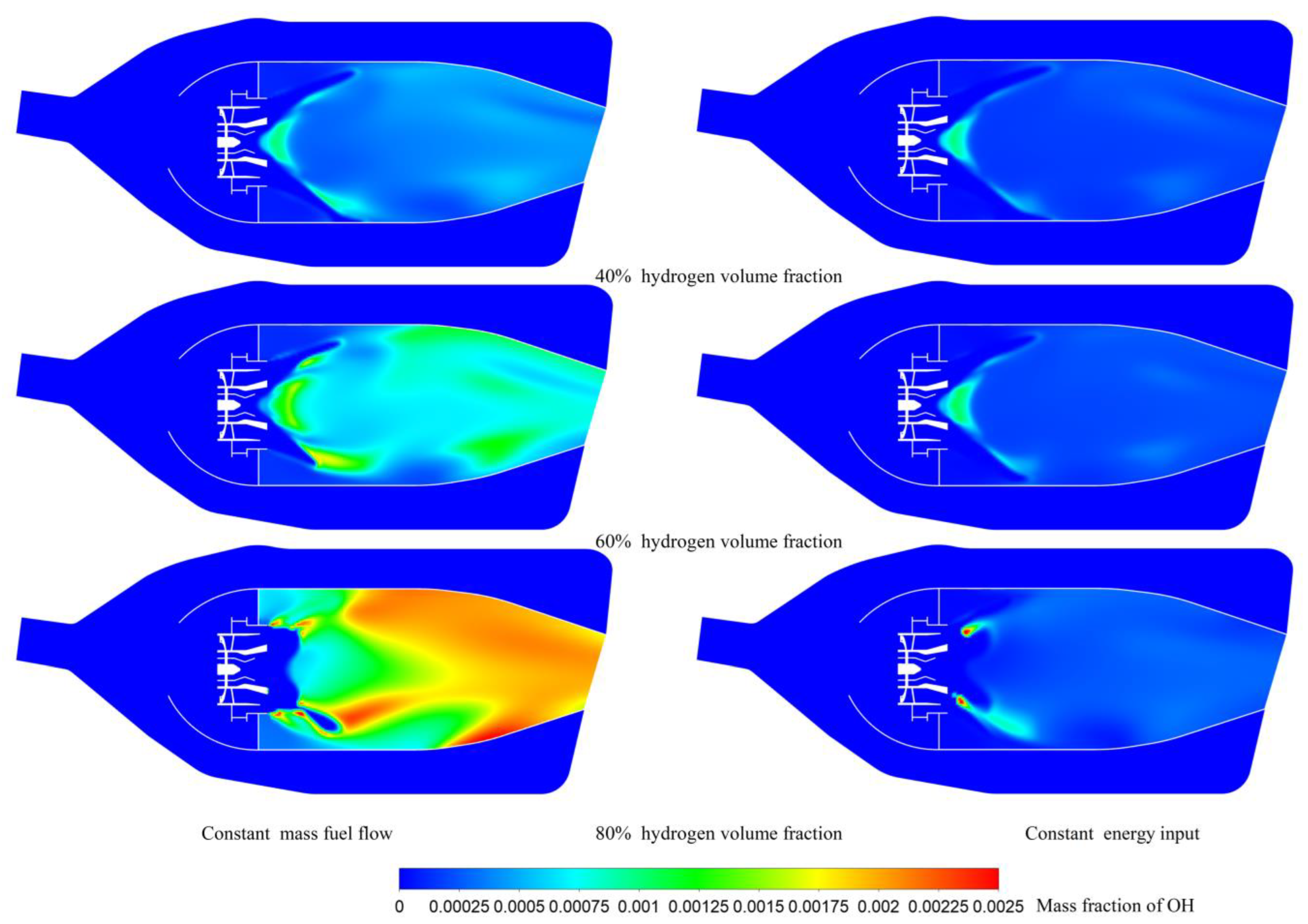
| CH2O Mass Fraction | OH Mass Fraction | C2H2 Mass Fraction | CO Emission (ppm) | NOx Emission (ppm) | |
|---|---|---|---|---|---|
| Case 1 | 47.2 × 10−8 | 2.21 × 10−8 | 45.5 × 10−10 | 33.21 | 0.222 |
| Case 2 | 36.9 × 10−8 | 2.57 × 10−8 | 32.9 × 10−10 | 36.81 | 0.375 |
| Case 3 | 23.0 × 10−8 | 3.03 × 10−8 | 19.0 × 10−10 | 40.45 | 0.577 |
| Case 4 | 14.9 × 10−8 | 3.62 × 10−8 | 11.9 × 10−10 | 47.51 | 1.037 |
| Case 5 | 9.23 × 10−8 | 4.45 × 10−8 | 7.04 × 10−10 | 58.08 | 2.207 |
| Case 6 | 5.11 × 10−8 | 7.47 × 10−8 | 3.55 × 10−10 | 97.87 | 17.5 |
| Case 7 | N/A | N/A | N/A | 400.37 | 109.94 |
| Case 8 | 41.9 × 10−8 | 2.22 × 10−8 | 34.6 × 10−10 | 30.49 | 0.249 |
| Case 9 | 32.5 × 10−8 | 2.23 × 10−8 | 22.6 × 10−10 | 26.27 | 0.250 |
| Case 10 | 26.1 × 10−8 | 2.24 × 10−8 | 15.8 × 10−10 | 23.13 | 0.282 |
| Case 11 | 20.7 × 10−8 | 2.25 × 10−8 | 10.3 × 10−10 | 19.40 | 0.306 |
| Case 12 | 11.5 × 10−8 | 2.41 × 10−8 | 3.51 × 10−10 | 13.31 | 0.398 |
| Case 13 | N/A | N/A | N/A | 9.39 | 1.028 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Li, F.; Zhou, T.; Ao, Y. Numerical Study of Combustion and Emission Characteristics for Hydrogen Mixed Fuel in the Methane-Fueled Gas Turbine Combustor. Aerospace 2023, 10, 72. https://doi.org/10.3390/aerospace10010072
Wang K, Li F, Zhou T, Ao Y. Numerical Study of Combustion and Emission Characteristics for Hydrogen Mixed Fuel in the Methane-Fueled Gas Turbine Combustor. Aerospace. 2023; 10(1):72. https://doi.org/10.3390/aerospace10010072
Chicago/Turabian StyleWang, Kefu, Feng Li, Tao Zhou, and Yiqun Ao. 2023. "Numerical Study of Combustion and Emission Characteristics for Hydrogen Mixed Fuel in the Methane-Fueled Gas Turbine Combustor" Aerospace 10, no. 1: 72. https://doi.org/10.3390/aerospace10010072
APA StyleWang, K., Li, F., Zhou, T., & Ao, Y. (2023). Numerical Study of Combustion and Emission Characteristics for Hydrogen Mixed Fuel in the Methane-Fueled Gas Turbine Combustor. Aerospace, 10(1), 72. https://doi.org/10.3390/aerospace10010072