Exceedance and Return Period of High Temperature in the African Region
Abstract
1. Introduction
2. Data and Methods
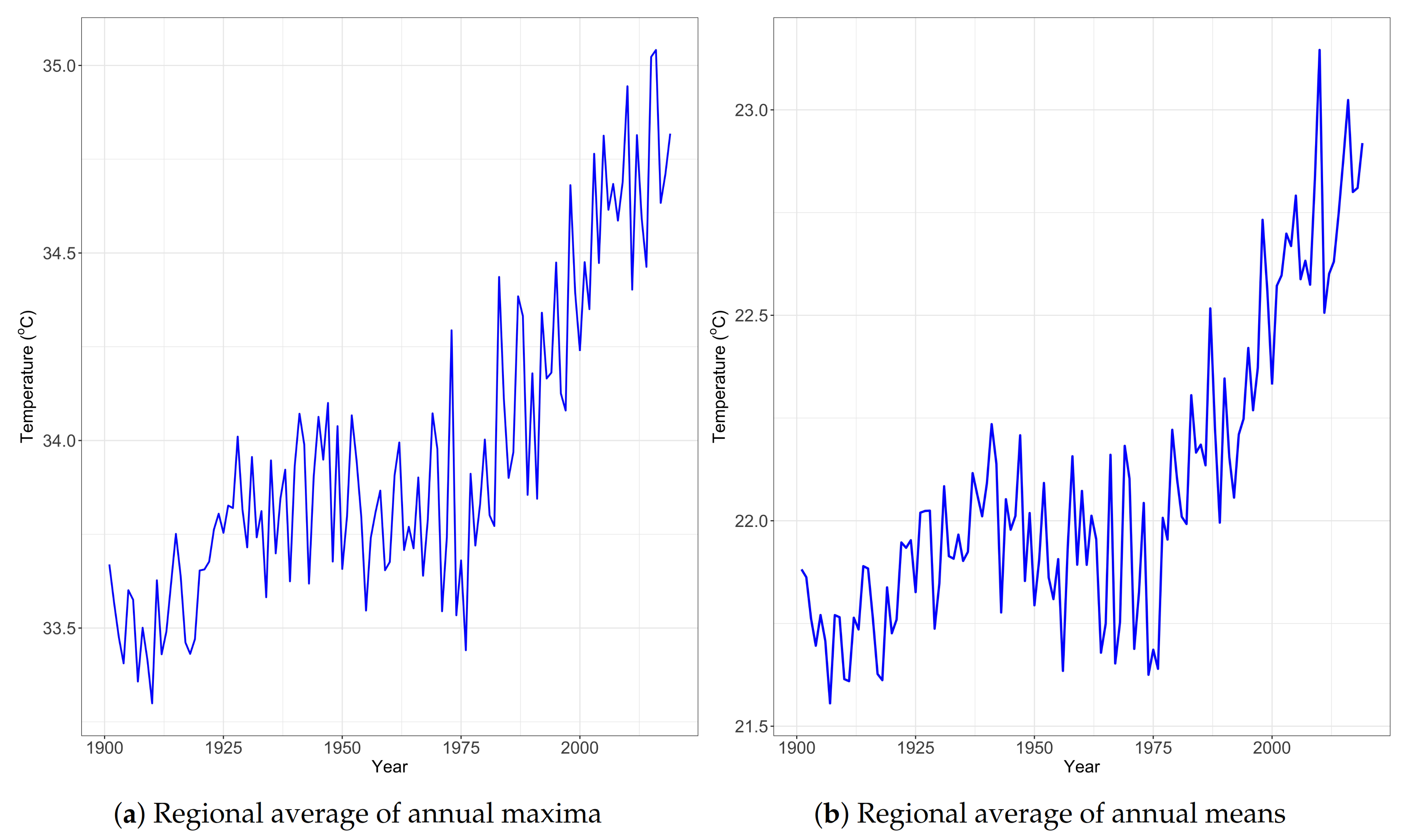
2.1. The Data
2.2. Exceedance Probability
2.3. Return Period
3. Results and Discussions
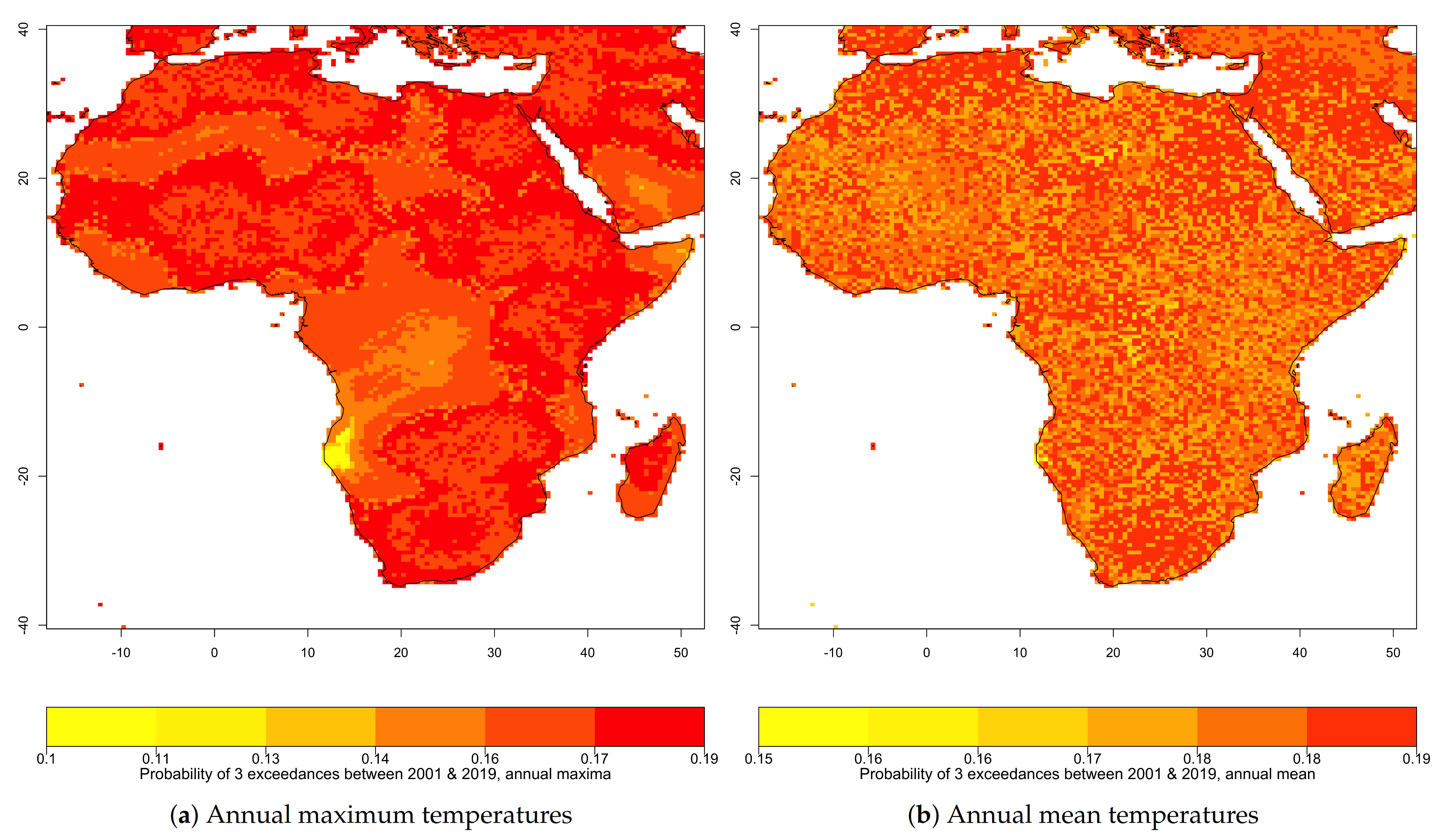
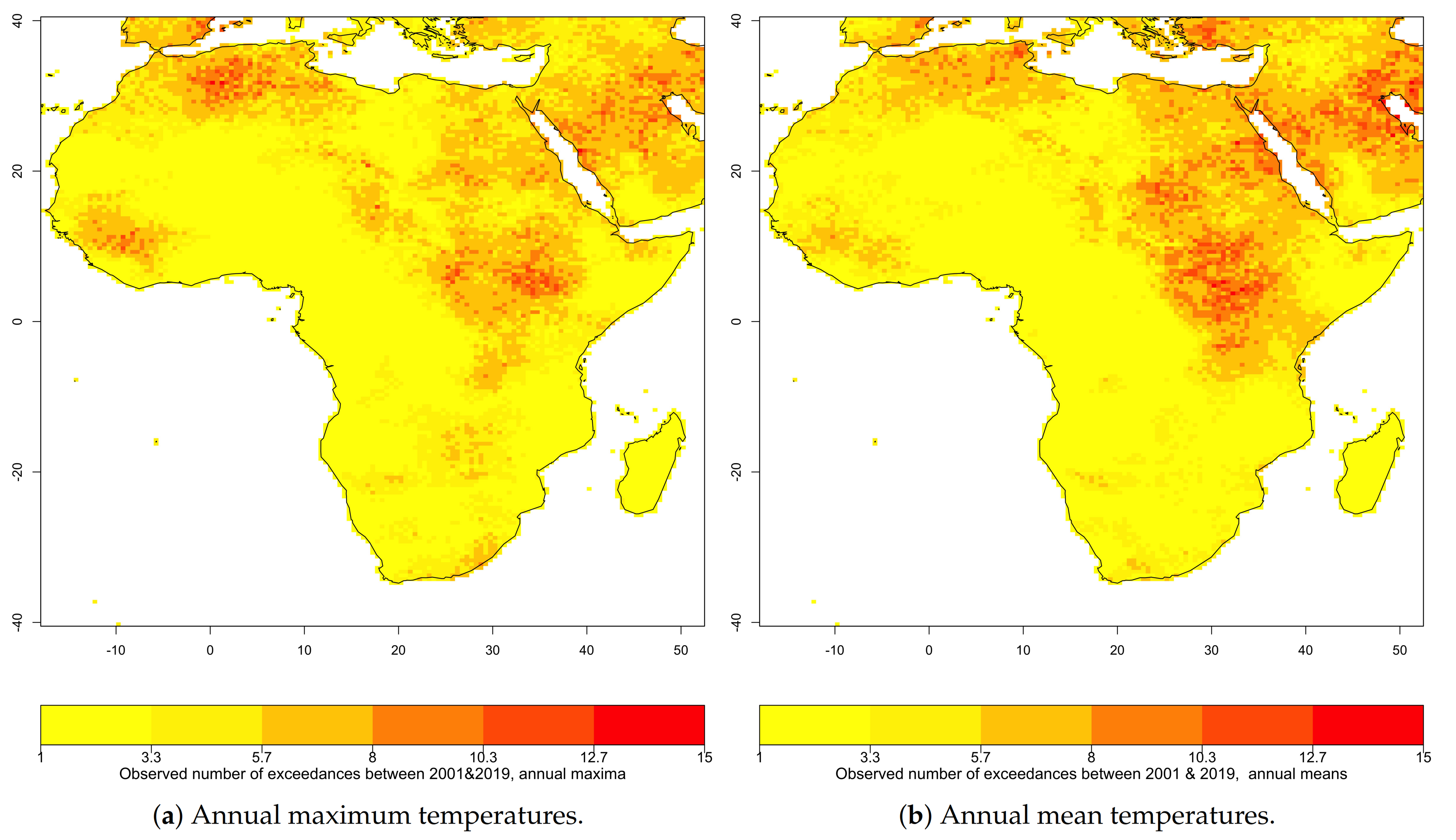
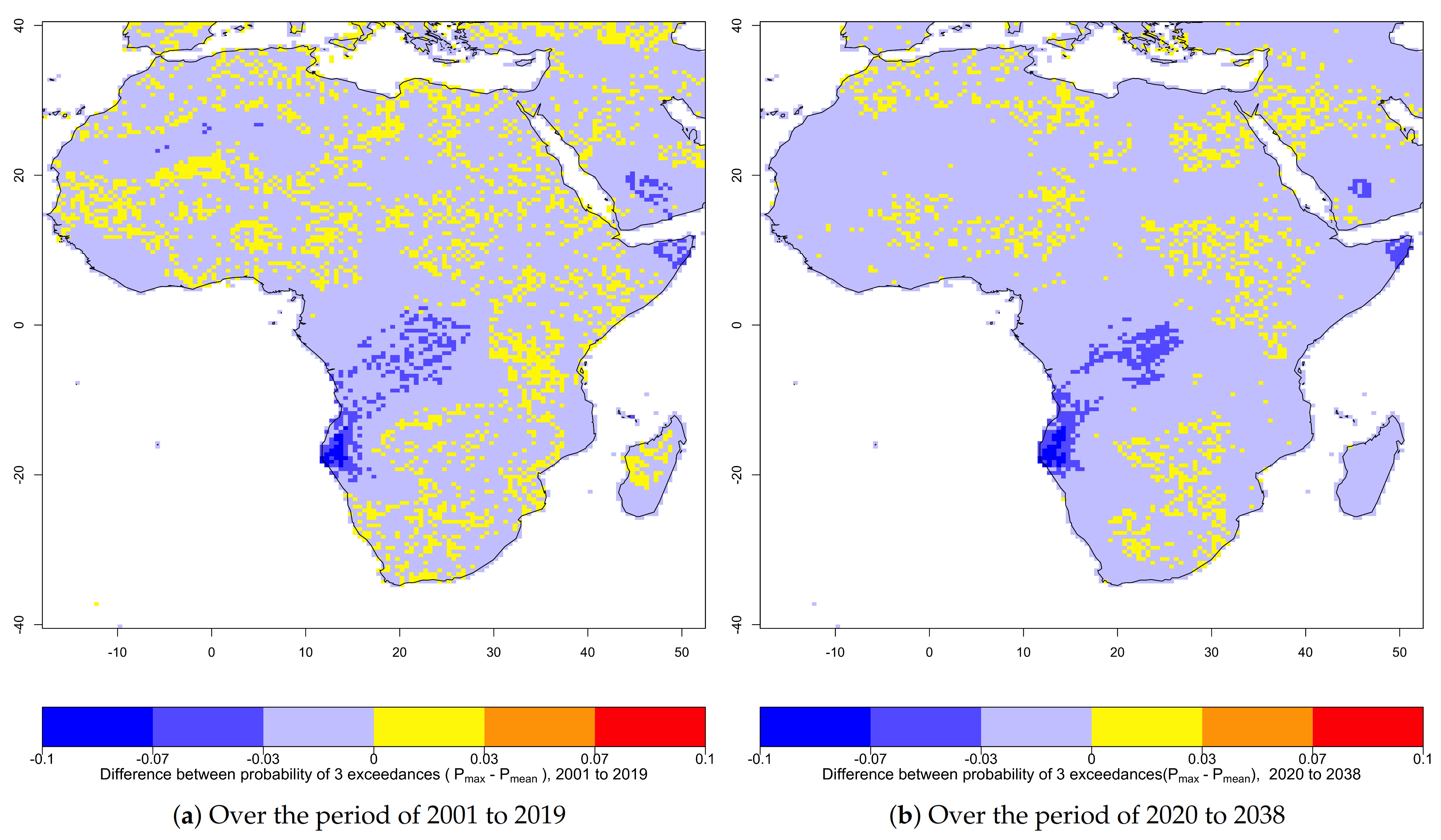
3.1. Exceedance Probability of Threshold Based on 1901–2000 Temperature Distribution
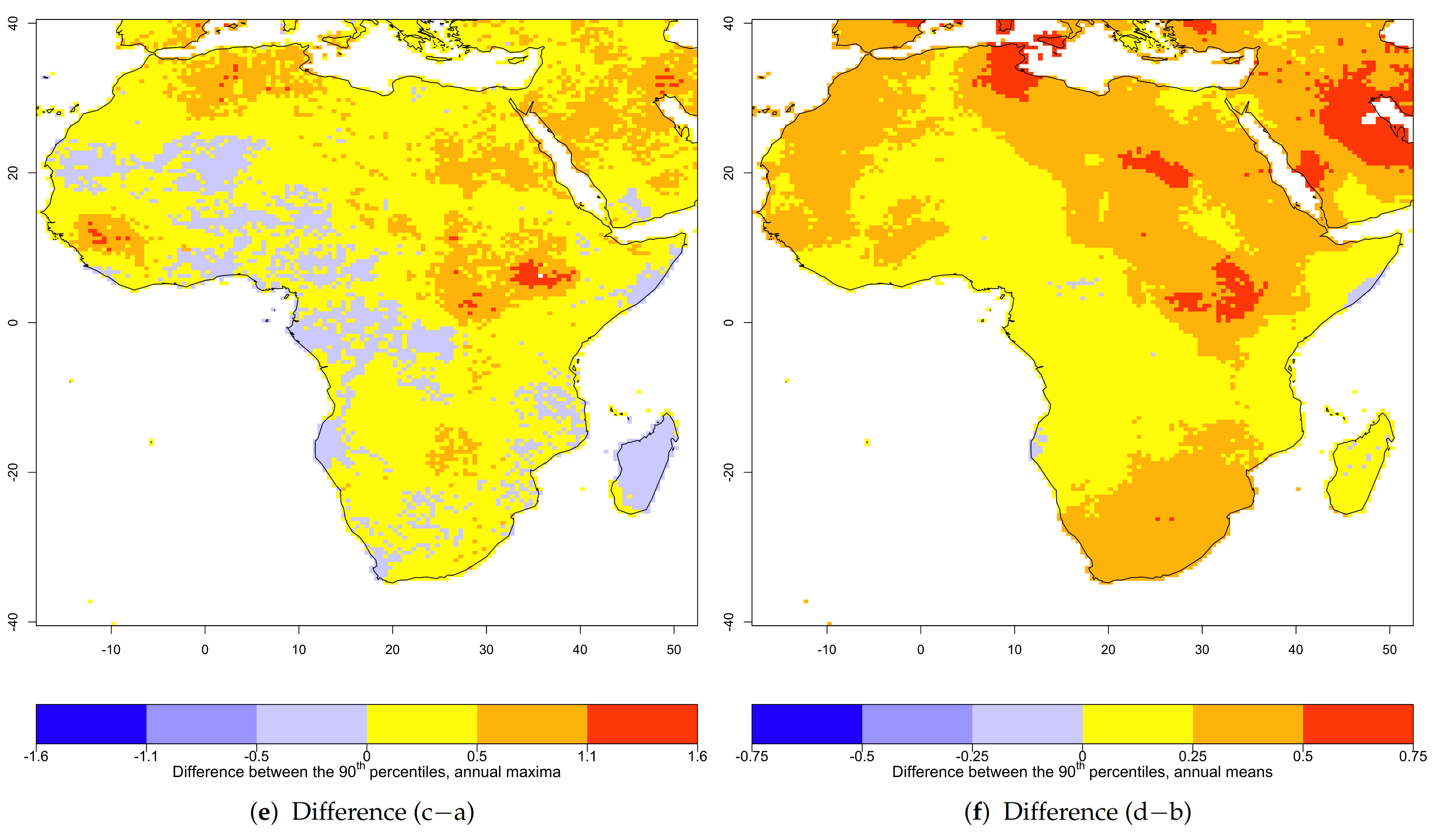
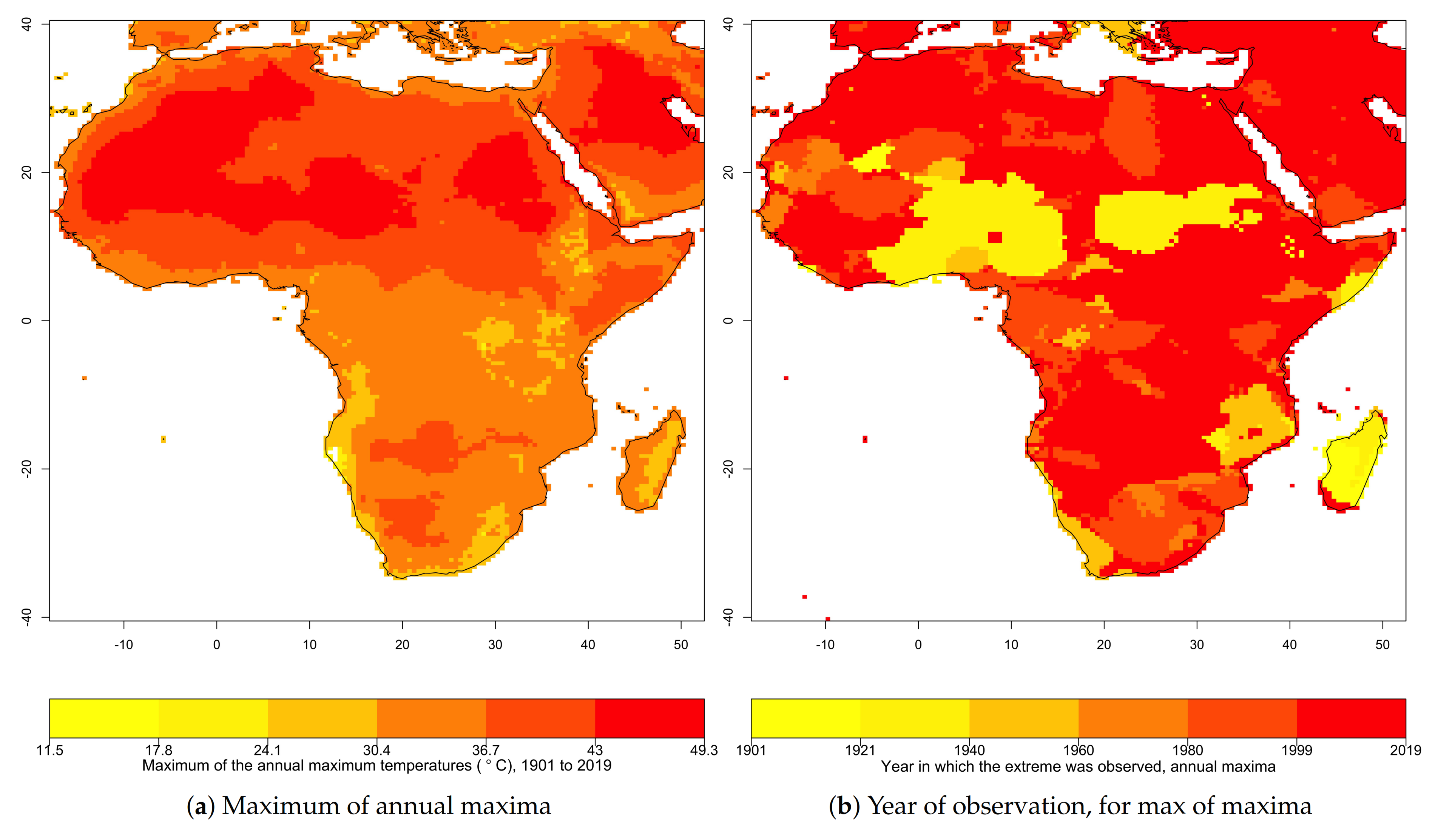
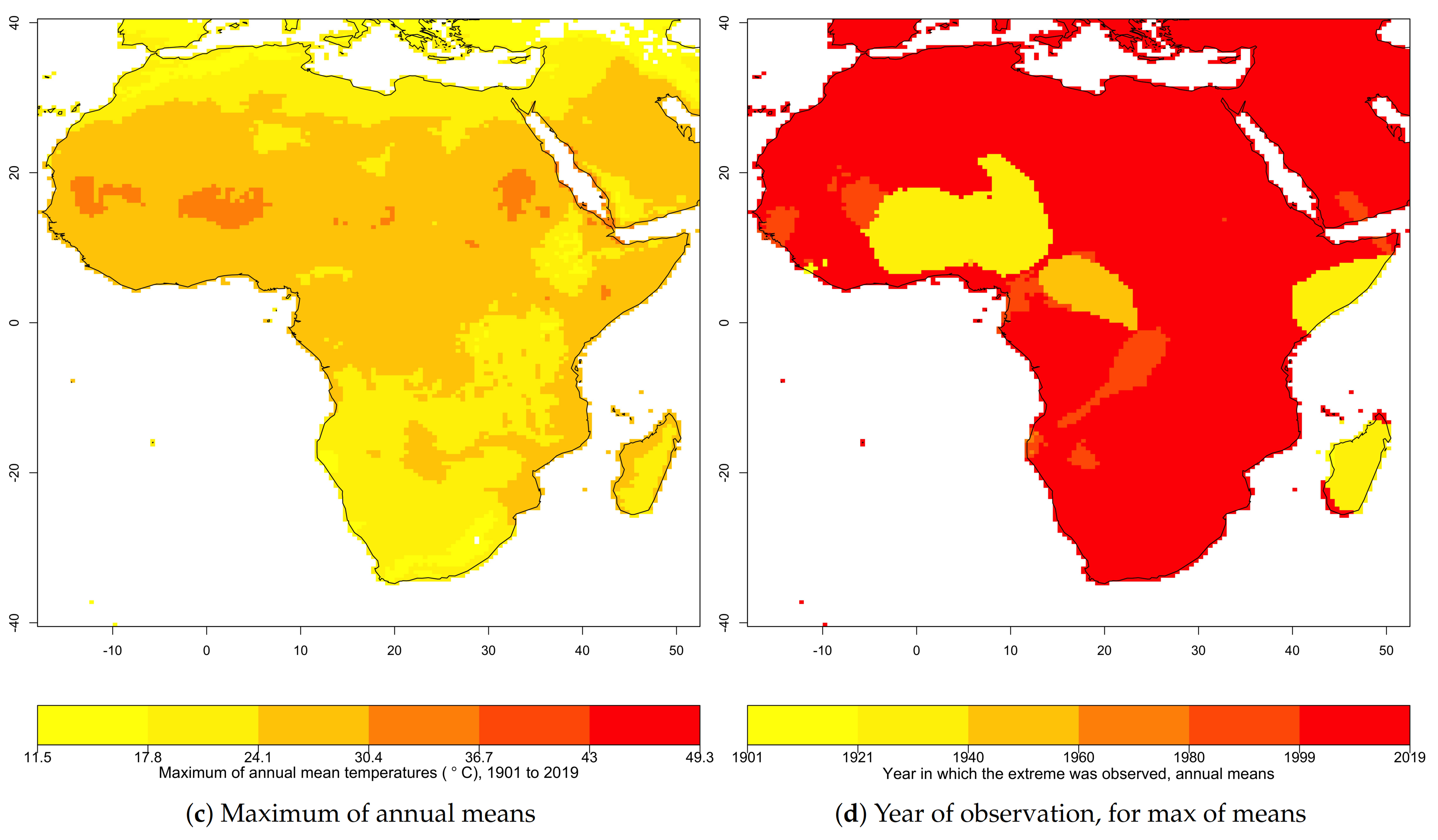
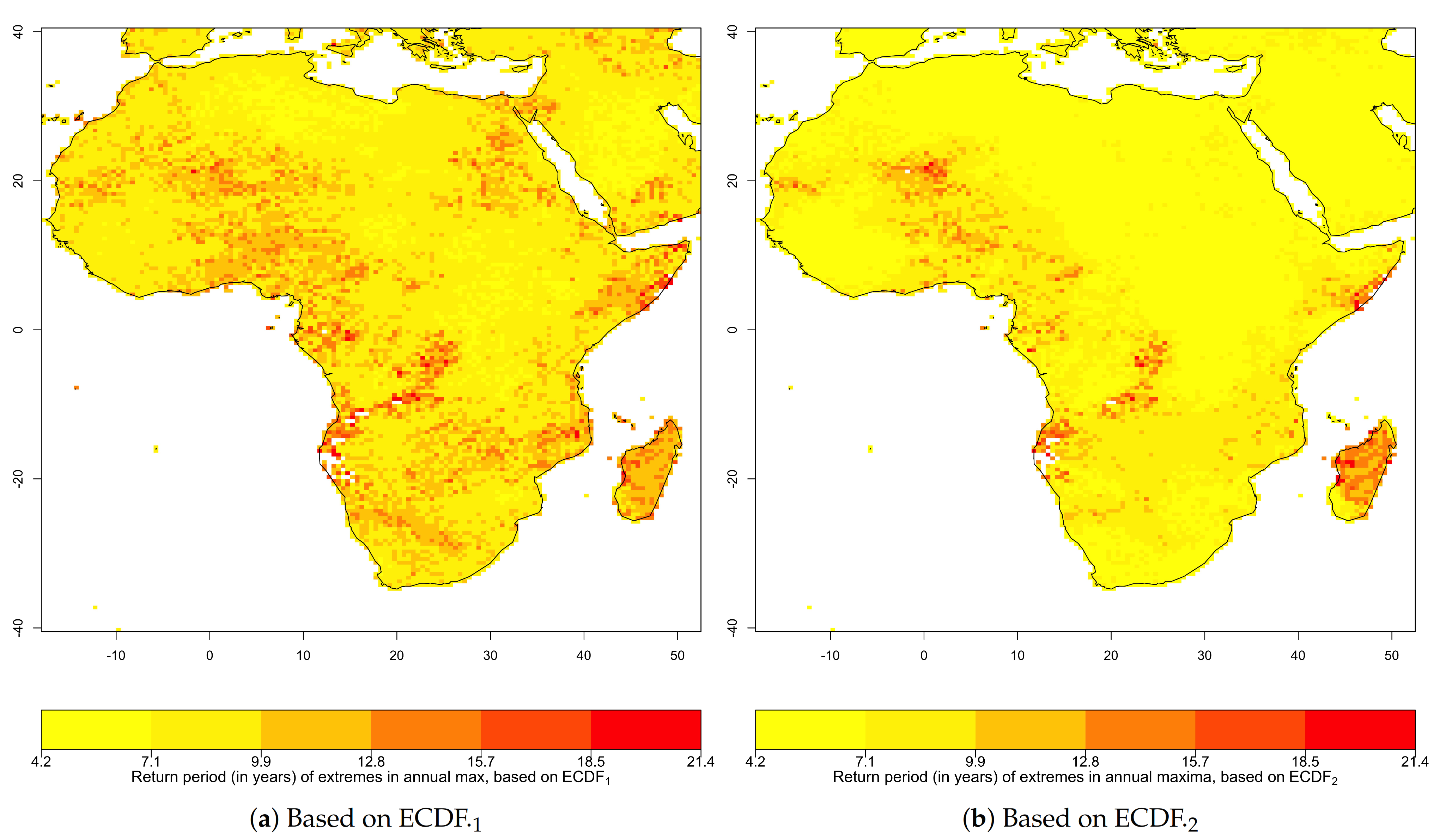
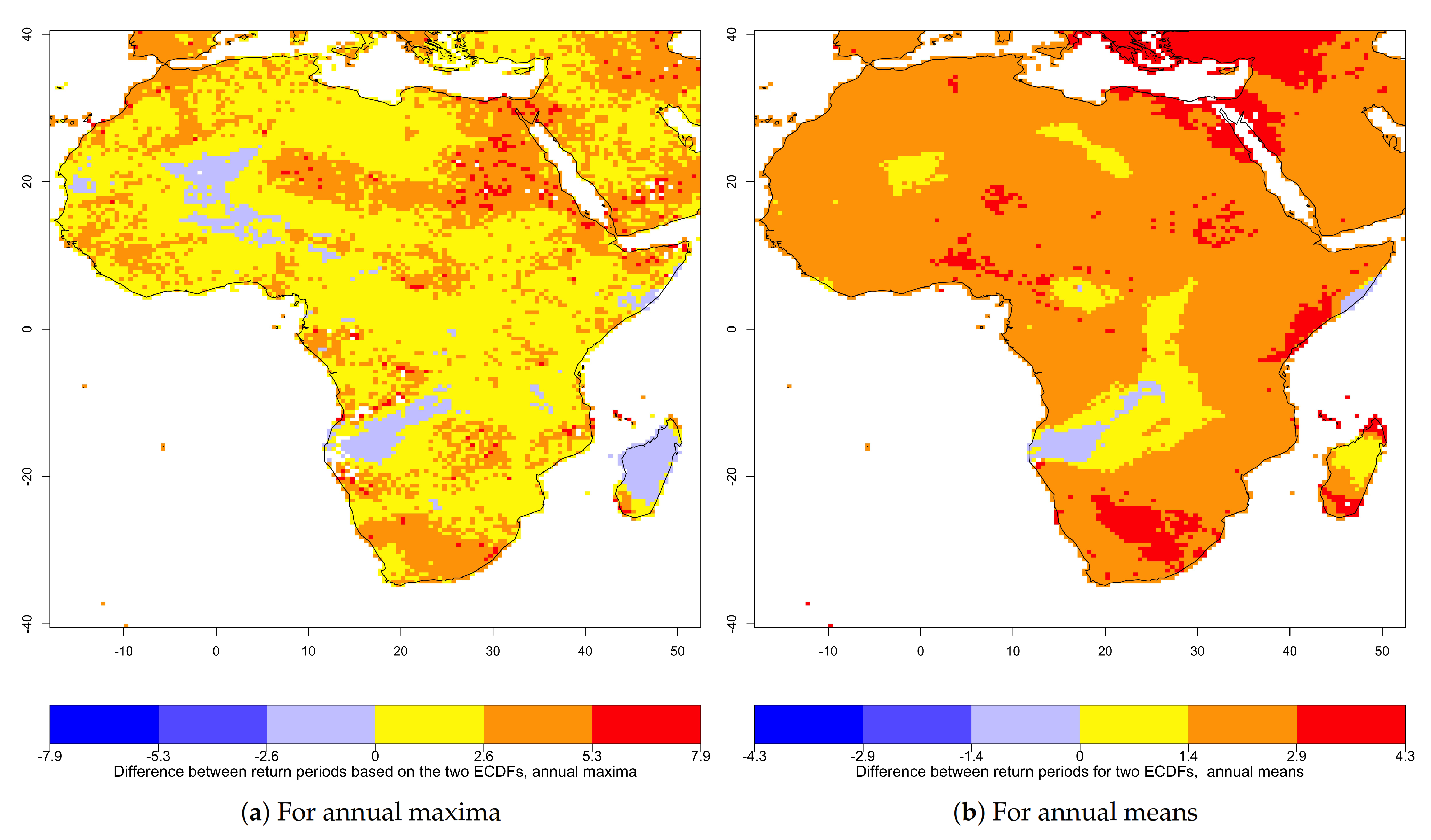
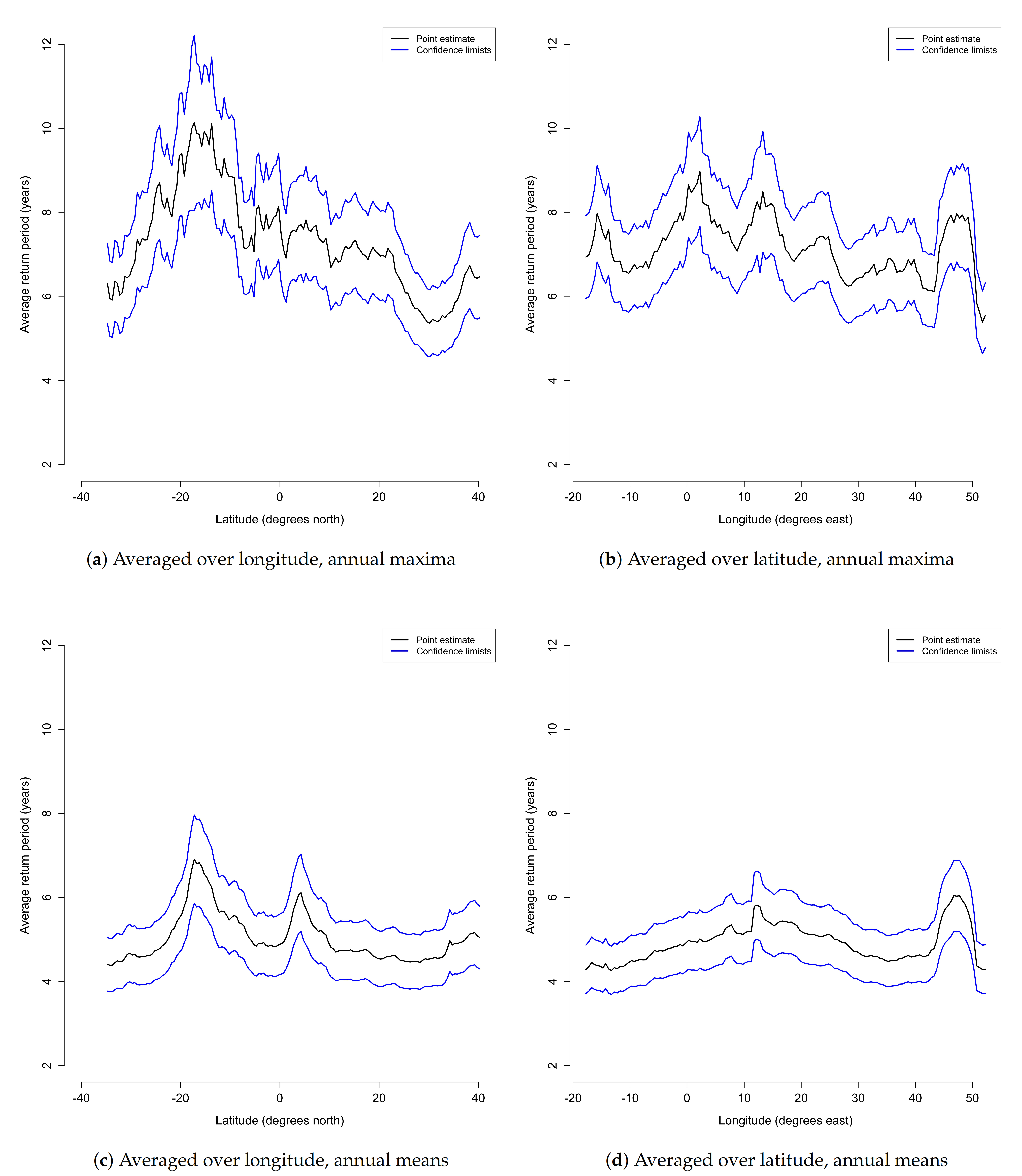
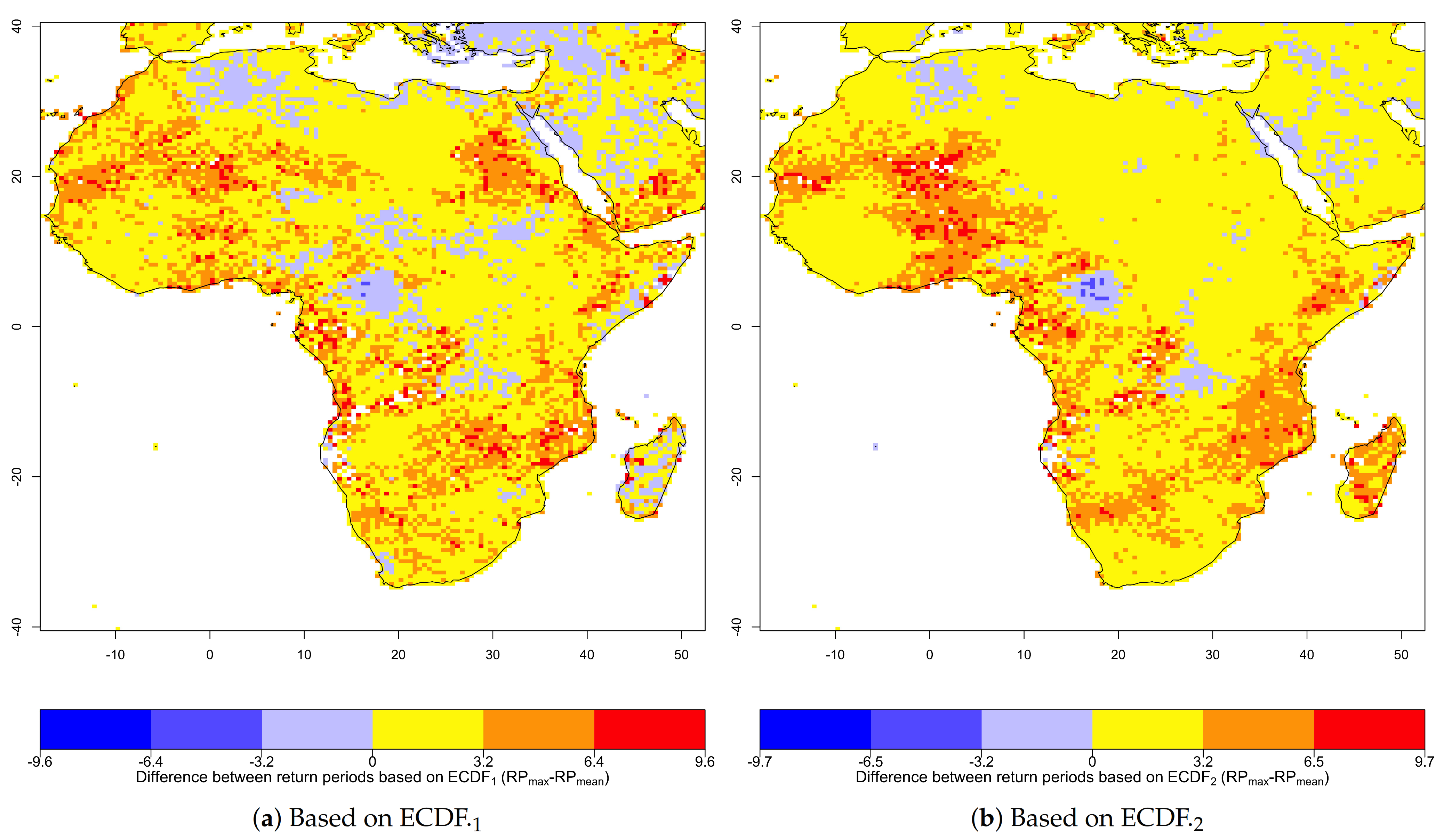
3.2. Return Period of Extremes in Annual Maximum and Annual Mean Temperatures
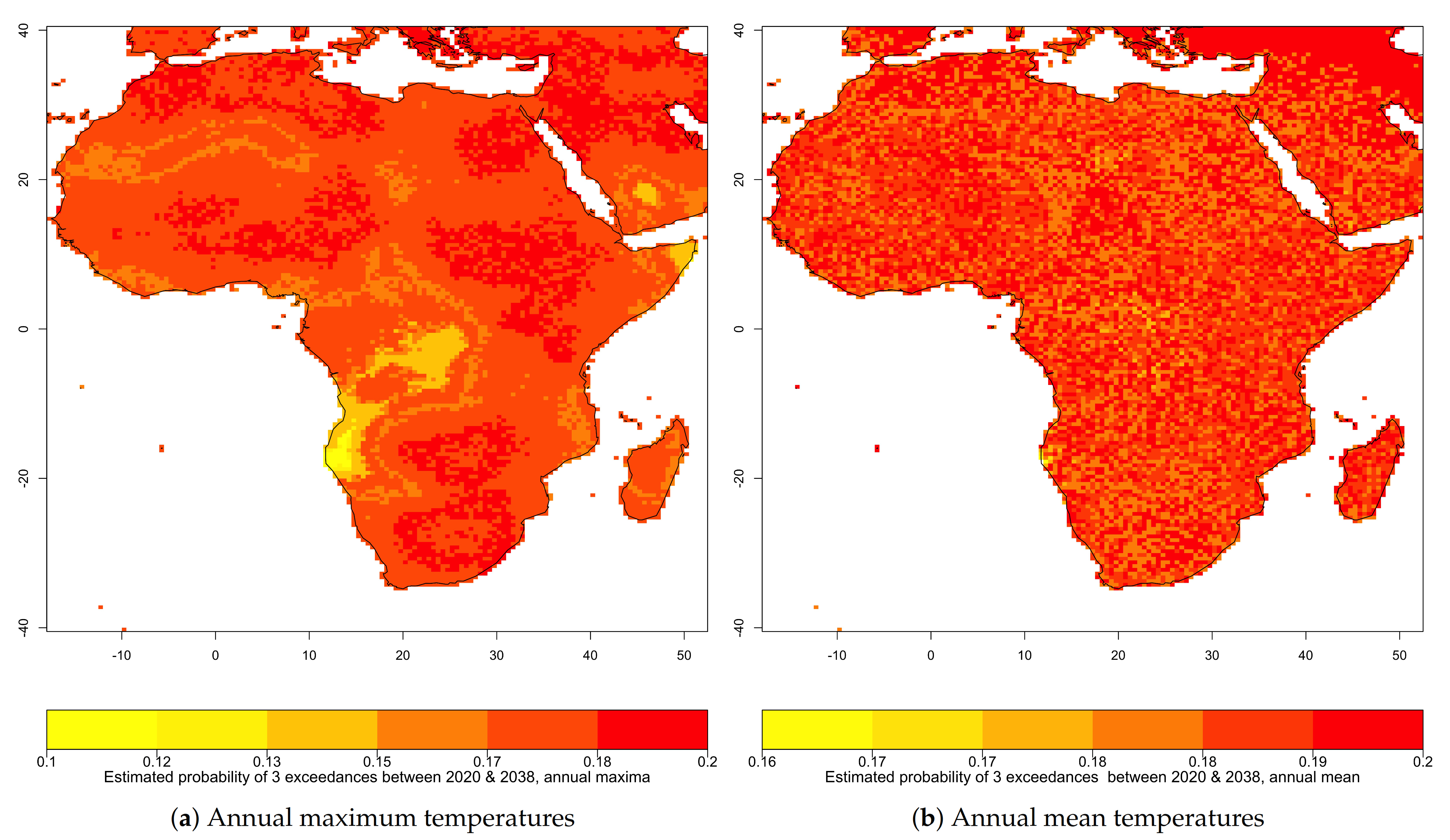
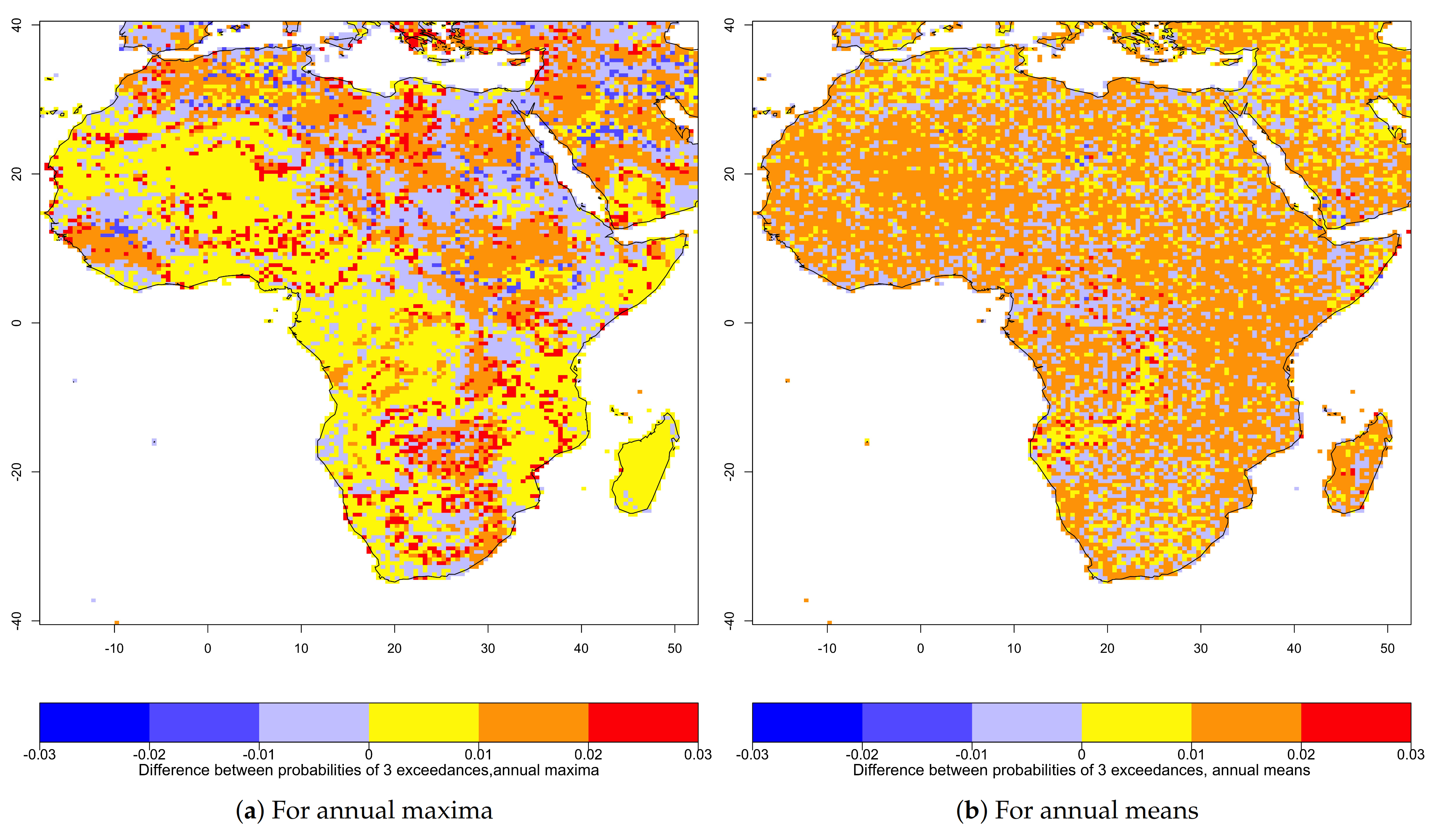
3.3. Exceedance Probability of Threshold Based on 1901–2019 Temperature Distribution
4. Summary
Funding
Data Availability Statement
Conflicts of Interest
References
- Field, C.B.; Barros, V.; Stocker, T.F.; Dahe, Q. Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation: Special Report of the IPCC; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Alexander, L.; Zhang, X.; Peterson, T.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Yan, Z.; Jones, P.; Davies, T.; Moberg, A.; Bergström, H.; Camuffo, D.; Cocheo, C.; Maugeri, M.; Demarée, G.; Verhoeve, T.; et al. Trends of Extreme Temperatures in Europe and China based on Daily Observations. In Improved Understanding of Past Climatic Variability from Early Daily European Instrumental Sources; Springer: New York, NY, USA, 2002; pp. 355–392. [Google Scholar]
- Kaper, H.; Engler, H. Mathematics & Climate; SIAM: Philadelphia, PA, USA, 2013. [Google Scholar]
- Abarbanel, H.; Koonin, S.; Levine, H.; MacDonald, G.; Rothaus, O. Statistics of Extreme Events with Application to Climate; Technical Report; DTIC Document: McLean, VA, USA, 1992. [Google Scholar]
- Kunkel, K.E.; Pielke Jr, R.A.; Changnon, S.A. Temporal fluctuations in weather and climate extremes that cause economic and human health impacts: A review. Bull. Am. Meteorol. Soc. 1999, 80, 1077–1098. [Google Scholar] [CrossRef]
- Yin, H.; Sun, Y.; Wan, H.; Zhang, X.; Lu, C. Detection of anthropogenic influence on the intensity of extreme temperatures in China. Int. J. Climatol. 2017, 37, 1229–1237. [Google Scholar] [CrossRef]
- Donat, M.G.; Sillmann, J.; Wild, S.; Alexander, L.V.; Lippmann, T.; Zwiers, F.W. Consistency of temperature and precipitation extremes across various global gridded in situ and reanalysis datasets. J. Clim. 2014, 27, 5019–5035. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Changnon, S.A.; Pielke, R.A., Jr.; Changnon, D.; Sylves, R.T.; Pulwarty, R. Human factors explain the increased losses from weather and climate extremes. Bull. Am. Meteorol. Soc. 2000, 81, 437–442. [Google Scholar] [CrossRef]
- Mirza, M.M.Q. Climate change and extreme weather events: Can developing countries adapt? Clim. Policy 2003, 3, 233–248. [Google Scholar] [CrossRef]
- Nangombe, S.; Zhou, T.; Zhang, W.; Wu, B.; Hu, S.; Zou, L.; Li, D. Record-breaking climate extremes in Africa under stabilized 1.5° C and 2° C global warming scenarios. Nat. Clim. Chang. 2018, 8, 375. [Google Scholar] [CrossRef]
- Russo, S.; Marchese, A.F.; Sillmann, J.; Immé, G. When will unusual heat waves become normal in a warming Africa? Environ. Res. Lett. 2016, 11, 054016. [Google Scholar] [CrossRef]
- Barros, V.; Field, C.; Dokke, D.; Mastrandrea, M.; Mach, K.; Bilir, T.E.; Chatterjee, M.; Ebi, K.; Estrada, Y.; Genova, R.; et al. Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; Chapter 22. [Google Scholar]
- McCarthy, J.J.; Canziani, O.F.; Leary, N.A.; Dokken, D.J.; White, K.S. Climate Change 2001: Impacts, Adaptation, and Vulnerability: Contribution of Working Group II to the Third Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Russo, S.; Dosio, A.; Graversen, R.G.; Sillmann, J.; Carrao, H.; Dunbar, M.B.; Singleton, A.; Montagna, P.; Barbola, P.; Vogt, J.V. Magnitude of extreme heat waves in present climate and their projection in a warming world. J. Geophys. Res. Atmos. 2014, 119, 12–500. [Google Scholar] [CrossRef]
- New, M.; Hewitson, B.; Stephenson, D.B.; Tsiga, A.; Kruger, A.; Manhique, A.; Gomez, B.; Coelho, C.A.; Masisi, D.N.; Kululanga, E.; et al. Evidence of trends in daily climate extremes over southern and west Africa. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Sillmann, J.; Kharin, V.; Zhang, X.; Zwiers, F.; Bronaugh, D. Climate extremes indices in the CMIP5 multimodel ensemble: Part 1. Model evaluation in the present climate. J. Geophys. Res. Atmos. 2013, 118, 1716–1733. [Google Scholar] [CrossRef]
- Frich, P.; Alexander, L.V.; Della-Marta, P.; Gleason, B.; Haylock, M.; Tank, A.K.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef]
- Kruger, A.; Sekele, S. Trends in extreme temperature indices in South Africa: 1962–2009. Int. J. Climatol. 2013, 33, 661–676. [Google Scholar] [CrossRef]
- Harris, I.; Osborn, T.J.; Jones, P.; Lister, D. Version 4 of the CRU TS monthly high-resolution gridded multivariate climate dataset. Sci. Data 2020, 7, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Dodge, Y. The Oxford Dictionary of Statistical Terms; Oxford University Press: Oxford, UK, 2006. [Google Scholar]
- Kunreuther, H. Risk analysis and risk management in an uncertain world 1. Risk Anal. Int. J. 2002, 22, 655–664. [Google Scholar] [CrossRef]
- Lambert, J.H.; Li, D.; Haimes, Y.Y. Risk of Extreme Flood Losses under Uncertain Physical Conditions. In Engineering Risk in Natural Resources Management; Springer: New York, NY, USA, 1994; pp. 321–329. [Google Scholar]
- Coles, S. An Introduction to Statistical Modeling of Extreme Values; Springer: New York, NY, USA, 2001. [Google Scholar]
- Morris, S.A.; Reich, B.J.; Thibaud, E.; Cooley, D. A space-time skew-t model for threshold exceedances. Biometrics 2017, 73, 749–758. [Google Scholar] [CrossRef] [PubMed]
- Davison, A.C.; Smith, R.L. Models for exceedances over high thresholds. J. R. Stat. Soc. Ser. B 1990, 52, 393–442. [Google Scholar] [CrossRef]
- Draghicescu, D.; Ignaccolo, R. Modeling threshold exceedance probabilities of spatially correlated time series. Electron. J. Stat. 2009, 3, 149–164. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A. Estimating return period of landslide triggering by Monte Carlo simulation. J. Hydrol. 2016, 541, 256–271. [Google Scholar] [CrossRef]
- Nabaei, S.; Sharafati, A.; Yaseen, Z.M.; Shahid, S. Copula based assessment of meteorological drought characteristics: Regional investigation of Iran. Agric. For. Meteorol. 2019, 276, 107611. [Google Scholar] [CrossRef]
- Eslamian, S. Handbook of Engineering Hydrology: Modeling, Climate Change, and Variability; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Casella, G.; Berger, R.L. Statistical Inference, 2nd ed.; Duxbury Pacific Grove: Pacific Grove, CA, USA, 2002. [Google Scholar]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 3rd ed.; Academic Press: Oxford, UK, 2011. [Google Scholar]
- Machado, S.; Paulsen, G.M. Combined effects of drought and high temperature on water relations of wheat and sorghum. Plant Soil 2001, 233, 179–187. [Google Scholar] [CrossRef]
- Pradhan, G.P.; Prasad, P.V.; Fritz, A.K.; Kirkham, M.B.; Gill, B.S. Effects of drought and high temperature stress on synthetic hexaploid wheat. Funct. Plant Biol. 2012, 39, 190–198. [Google Scholar] [CrossRef]
- Barutcular, C.; El Sabagh, A.; Koc, M.; Ratnasekera, D. Relationships between grain yield and physiological traits of durum wheat varieties under drought and high temperature stress in Mediterranean conditions. Fresen. Environ. Bull. 2017, 26, 4282–4291. [Google Scholar]
- Collier, P.; Conway, G.; Venables, T. Climate change and Africa. Oxf. Rev. Econ. Policy 2008, 24, 337–353. [Google Scholar] [CrossRef]
- Collins, J.M. Temperature variability over Africa. J. Clim. 2011, 24, 3649–3666. [Google Scholar] [CrossRef]
- Hu, Q.; Willson, G.D. Effects of temperature anomalies on the Palmer Drought Severity Index in the central United States. Int. J. Climatol. A J. R. Meteorol. Soc. 2000, 20, 1899–1911. [Google Scholar] [CrossRef]
- Engelbrecht, F.; Adegoke, J.; Bopape, M.J.; Naidoo, M.; Garland, R.; Thatcher, M.; McGregor, J.; Katzfey, J.; Werner, M.; Ichoku, C.; et al. Projections of rapidly rising surface temperatures over Africa under low mitigation. Environ. Res. Lett. 2015, 10, 085004. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Turasie, A.A. Exceedance and Return Period of High Temperature in the African Region. Climate 2021, 9, 53. https://doi.org/10.3390/cli9040053
Turasie AA. Exceedance and Return Period of High Temperature in the African Region. Climate. 2021; 9(4):53. https://doi.org/10.3390/cli9040053
Chicago/Turabian StyleTurasie, Alemtsehai A. 2021. "Exceedance and Return Period of High Temperature in the African Region" Climate 9, no. 4: 53. https://doi.org/10.3390/cli9040053
APA StyleTurasie, A. A. (2021). Exceedance and Return Period of High Temperature in the African Region. Climate, 9(4), 53. https://doi.org/10.3390/cli9040053





