Abstract
The core crop region of the Humid Pampa is one of the most productive agricultural lands around the world and depends highly on climate conditions. This study assesses climate variability, climate extremes, and observed and projected climate changes there, using 1911–2019 observations and CMIP5 model simulations. Since 1970, the annual mean temperature has risen by 1 °C and the mean annual minimum and maximum temperatures by 2 and 0.5 °C, respectively. The frequency of warm days and nights increased, and cold days and nights decreased. Heatwaves became longer and more intense, and cold waves decreased with less frost events. Annual precipitation increased by 10% from 1911, mainly in summer, and years with excess precipitation outnumbered those with a deficit. Both intense precipitation events and consecutive dry days grew, suggesting more annual precipitation falling on fewer days. Projections show a warming of 1 °C by 2035, regardless of the scenario. From then on until 2100, mean temperature will increase by 2 and 3–3.5 °C in the RCP4.5 and RCP8.5 scenarios, respectively. Annual precipitation will grow 8 and 16% from current values by 2100 in the RCP4.5 and RCP8.5 scenarios, respectively. No major precipitation changes are projected in the RCP2.6 scenario.
1. Introduction
Global warming brings increased occurrences of extreme weather and climate worldwide [1]. Significant intensification of heavy precipitation can be seen on global and continental scales [2,3]. Consistently, southeastern South America (SSA) tends towards warmer and moister conditions, with a noticeable increase in the magnitude and frequency of extreme temperatures and heavy rainfall (e.g., [4,5]). In particular, central-northeastern Argentina has been experiencing these significant climate changes since the 1960s [6,7]. The continuous increase in frequency and in intensity of heavy rainfall has caused great losses in agro-industrial production, severely damaged water management, and affected the urban centers in the region [8,9]. However, human activities are also impacted by increased occurrence of consecutive dry days, which lead to more seasonal droughts [10,11] as well as by extreme—maximum and minimum—temperature events, which have grown in frequency, intensity, and duration [12].
The Humid Pampa extends over central-northeastern Argentina, and its core crop region is centered in the southern half of the province of Santa Fe (see Figure 1). The core crop region is acknowledged as one of the most productive agricultural lands in the world, thanks to the combination of its climate and the characteristics of soil sediments. Lovino et al. [13] have reported enhanced annual precipitation since the 1960s and a considerable increase in the frequency and magnitude of heavy rainfalls throughout the province of Santa Fe. According to Llano and Vargas [14], the days with extreme precipitation are mostly associated to convective precipitation patterns all over the region. However, the distribution of observed precipitation changes is not uniform throughout the province [13]. Records from weather stations in the north and center indicate that annual precipitation has grown by 15% from 1960. This upward trend seems to have stabilized after 1990; however, the number of consecutive dry days has also grown significantly in recent decades [13]. On the other hand, observations in the core crop region indicate an increase in annual precipitation and in the frequency of heavy rainfall events with upward trends to present days.
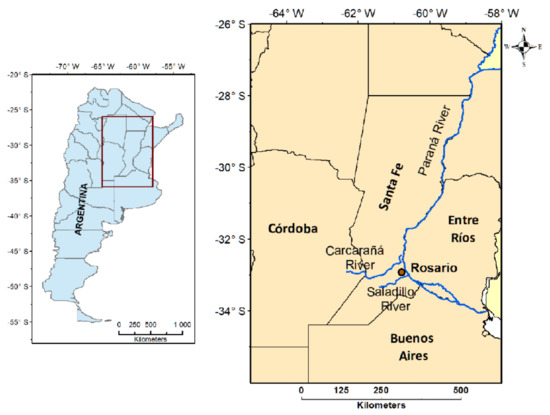
Figure 1.
Central-northeastern region of Argentina delimited by 36° S–26° S latitude and 65° W–58° W longitude and its main rivers.
Extreme precipitation may lead to floods and droughts that have strong negative impacts on human activities and the environment. Floods occurred in the core crop region in 2018–2019. Immediately following the flooding period, a severe drought started in 2019 and lasted during 2020. This drought took place over a large part of SSA and caused extraordinarily low water levels in the Parana River [15,16]. The Rosario Stock Exchange (BCR) estimated a loss of USD 244 million in the agro-export sector of Rosario in the first quarter of 2020 [17,18]. The sector had already faced losses of USD 230 million as a consequence of the 2018–2019 flood [19]. Moreover, low water in the Paraná River also affected the river ecosystem and other essential activities such as fishing and water purification [17].
This study examines climate variability, climate extremes as well as observed and projected climate changes in the core crop region of the Humid Pampa in the 20th and 21st centuries. The resulting information might contribute to estimate the impacts of climate variability and change aiming at reducing disaster risks and implementing appropriate management policies and adaptation actions in the affected sectors. The final goal is to make science-based information available to policy and decision makers in the public and private sectors for the development of policies, actions, and plans aimed at reducing the vulnerability of the region to extreme hydroclimatic events. To fulfill this objective, we analyzed the variability and changes in temperature and precipitation using high-quality meteorological records and future climate projections for the core crop region of the Humid Pampa. The paper is organized as follows; Section 2 describes the methods and the data used. The observed changes in temperature and precipitation from the beginning of the 20th century to present are described in Section 3.1. For the same period, we identified and examined climate extremes using different indices, mainly focused on intense precipitation and extreme temperature events, which are in Section 3.2. Future climate projections in the short-, medium-, and long-term for the 21st century are presented in Section 3.3. The conclusions of the study are in Section 4.
2. Study Region, Data, and Methodology
2.1. The Relevance of the Core Crop Region
The Humid Pampa is an extensive region in central-northeastern Argentina. Its core crop region includes the center and south of Santa Fe province, east of Córdoba province, and north of Buenos Aires province (see Figure 1). The Humid Pampa presents a flat landscape with dominance of Quaternary aeolian sediments. Its prairie-like ecosystem develops in humid to sub-humid temperate to subtropical climates (North Pampa, [20]). The southeast of the Santa Fe province extends over the Pampean loessic belt [21,22], which is the most extensive in the Southern Hemisphere and one of the thickest loess deposits in the world [22]. The characteristics of the Pampean loess and the present climate make soils of the region highly productive and known worldwide for their fertility [21,22].
The Paraná River, which drains the second largest basin (2,600,000 km2) in South America, flows across the Humid Pampa. The city of Rosario is located in the southeast of Santa Fe, on the right margin of the Paraná River, i.e., the core crop region of the Humid Pampa (see Figure 1). Rosario rests over a complex floodplain extending 600 km in the heart of the inland lowlands of the continent [22]. Tributaries to the Paraná River in the area of Rosario are the Carcarañá and the Saladillo Rivers (see Figure 1). Rosario has a privileged location both from the geographic and environmental perspectives. It is the most important city in the core crop region and one of the most important in Argentina, as it is a major industrial, trade, and financial center [23], with 43% of the province population. It is also the main agro-industrial and port hub in the region, and in recent years, it became the largest soybean and by-product export node in the world, with 78% of Argentina’s installed capacity [24]. The port of Rosario is connected to the north with Mercosur countries through the Parana–Paraguay waterway, which is the primary communication corridor with southern Brazil and Paraguay [25].
2.2. Observed Data
Temperature and precipitation were examined using a long-term record of observations from Rosario Aero meteorological station (32.92° S, 60.78° W) of the National Weather Service of Argentina. This station, located in the core crop region of the Humid Pampa, is the only weather station in the region with long, complete, and reliable records of observations. These observations started in the first decades of the 20th century, thus allowing an analysis of long-term variability and historical changes. As a note of caution, the long-term variability as well as the historical and projected trends here reported are localized over the core crop region and do not represent the entire Humid Pampa region.
Daily temperature observations cover the period from 1935 to 2019, daily precipitation from 1936 to 2019, and monthly precipitation from 1911 to 2019. The temperature and precipitation time series meet the quality control requirements established by the World Meteorological Organization [26]. The time series of temperature and precipitation have very few missing data (2.8% for daily temperature, 0.25% for daily precipitation, and 3.1% for monthly precipitation). Data gaps were filled using the normal ratio method [27] and linear regression [28]. We mainly used the normal ratio method, while linear regression was applied when there were good correlations between station time series, or when data were available from only one neighboring station.
2.2.1. Detecting Variability and Changes in Time Series
A singular spectrum analysis (SSA, [29,30]) was applied to study the temporal variability of temperature and precipitation time series, including extreme events. The method determines the spatio-temporal structures of trends and quasi-oscillatory modes in time series (see details in [10]). SSA makes it possible to identify nonlinear long-term trends that describe the changes in temperature, precipitation, and extreme climate indices. Trend significance at the 95% confidence level was tested against a red noise null hypothesis using Monte Carlo method [31] with an ensemble of 1000 independent realizations.
For the long period (1911–2019) of monthly precipitation, we identified the years in which precipitation was above (below) the 90th (10th) percentile in summer (DJF), autumn (MAM), winter (JJA), and spring (SON), for the entire period of analysis. The percentile threshold selected enabled us to obtain a representative sample of excess/deficit events in each season of the year. Precipitation series were detrended applying linear regression. The relationship of these events with ENSO phases was analyzed using the classification by Trenberth [32], based on the Oceanic Niño index (ONI), i.e., the 3-month mean SST anomaly for the Niño 3.4 region [33]. Since ONI starts in 1950, for the previous years, we adopted an ENSO classification presented in Berri et al. [34].
2.2.2. Extreme Climate Indices
The Expert Team on Climate Change Detection and Indices (ETCCDI) defined a set of descriptive indices for temperature and precipitation extremes, which allows analyzing their frequency, intensity, and duration [35]. ETCCDI indices enable a uniform perspective of observed changes in climate extremes. In this study, a subset of ETCCDI indices was computed for Rosario Aero data (see Table 1). Our analysis includes fourteen temperature-based and five precipitation-based indices as the most relevant for extreme events having greatest impact in northeastern Argentina (see [10]), where the study region is located.

Table 1.
Expert Team on Climate Change Detection and Indices (ETCCDI) indices. TXij and TNij are daily maximum and minimum temperature, respectively, on day i in year j. TXin90 or TXin10 (TNin90 or TNin10) are calendar days in the 90th (10th percentile) of daily maximum (minimum) temperature calculated for a 5-day window centered on each calendar day in the base period 1981–2010 (adapted from Donat et al. [36]).
2.3. Simulated Data
2.3.1. Historical Simulations
The fifth phase of the Coupled Models Inter-Comparison Project (CMIP5) used in the Fifth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC) provides historical and future climate simulations. One type of the CMIP5 experiments consisted of long-term historical simulations on the centennial time scale [37]. Long-term historical simulations allow for assessing the model ability to represent historical and present climate together with observed changes. In addition, they provide initial conditions for climate projections under representative concentration pathway scenarios (RCPs, [38], defined in Section 2.3.2 herein). Those long-term historical simulations were carried out for the period 1850–2005—i.e., from the beginning of the industrial revolution era to the near present. Lovino et al. [39] evaluated the ability of 25 CMIP5 models to represent historical and present climate in central-northeastern Argentina during the 1901–2005 period (Figure 1). They selected the best-performing models, which include 9 models for temperature and 7 models for precipitation (see Table A1).
The General Circulation Model (GCM) simulations used by Lovino et al. [39] were corrected using a scaling method [40] to remove systematic errors in the simulated variables by fitting them to observed historical values from the Rosario Aero series. The scaling method (also called “direct approach”) used in this study has been applied successfully in different previous precipitation and temperature studies (e.g., [41,42,43]). The method uses a scaling factor defined as the ratio between observed and simulated mean monthly variables for the period estimated in the historical simulations. Thus, Equation (1) shows that the corrected variable at time t in the future is represented by the value of the predictor in the future , scaled by the relationship between the observed mean variable and the historical simulated mean value .
In summary, the scaling method was used to correct systematic errors of the historical simulations and also adjust the trajectory of future simulated variables to that of historical observations. Bias correction was used to build the area-averaged time series of historical simulations and future projections. We also calculated the spatial distribution of future changes with non-corrected multi-model ensembles, in both historical and future simulations (see Section 2.3.2). Thus, the estimated changes are not affected by the bias correction method.
2.3.2. Future Simulations
Different climate change scenarios were used to estimate future climate trends in precipitation and temperature. Such a modeling exercise required assessing the historical variability and extreme events of these variables. To do so, we used the multi-model ensembles of GCM future projections that best represented historical and current climate in the region. The IPCC representative concentration pathway scenarios (RCPs, [38]) used here were: mitigation (RCP2.6), stabilization (RCP4.5), and high emissions (RCP8.5) were applied to the models listed in Table A1 to simulate monthly temperature and precipitation. No RCP scenario projections were available for three of the models used by Lovino et al. [39], i.e., CESM1-FASTCHEM, MIROCh4, and EC-EARTH. Thus, we used projections from 7 GCMs for temperature and from 5 GCMs for precipitation. Projections for RCP4.5 and RCP8.5 were available from all these models. However, RCP2.6 was available only for 3 models for each variable. Projected time series of temperature and precipitation from each GCM and the average GCM ensemble—called multi-model ensemble—were estimated for the closest grid point to Rosario Aero in the short (2006–2035), medium (2036–2065), and long term (2066–2100). Mean changes were analyzed in each model projection and time period.
Moreover, mean spatial changes were also analyzed for central-northeastern Argentina (Figure 1) using the multi-model ensemble. The spatial distribution of mean expected changes was examined for the three climate change scenarios in the periods 2006–2035, 2036–2065, and 2066–2100. This required re-gridding all the GCMs to a common grid with horizontal resolution 1° longitude–latitude, and time averages were calculated within the region bounded by 36° S–26° S latitude and 65° W–58° W in longitude (Figure 1). Changes were estimated for each GCM, and the ensemble of changes was generated with all the models at every grid point.
3. Results and Discussion
3.1. Variability and Trends
3.1.1. Temperature
Figure 2 shows the annual averages of the mean, maximum, and minimum temperatures at Rosario Aero station in the 1936–2019 period, together with their significant nonlinear long-term trend. A slight increase is observed in the mean temperature (Figure 2a) in the first decades of the 20th century. This warming reached 1 °C from the 1970s to present, from an average value of 17.3 to 18.3 °C. Annual average minimum temperature (Figure 2b) showed a sustained rise throughout the period, although it was more marked in recent decades, reaching a warming of 2 °C (from 10.5 to 12.5 °C). Annual average maximum temperature (Figure 2c) decreased very slightly from the beginning of the analyzed period to the end of the 1970s; but from then on, it progressively increased by about 0.5 °C. Our results suggest that the minimum temperature recorded a fourfold increase compared to maximum temperature. Consistently, minimum temperature increased globally at rates more pronounced than maximum temperature (e.g., [1,36]).
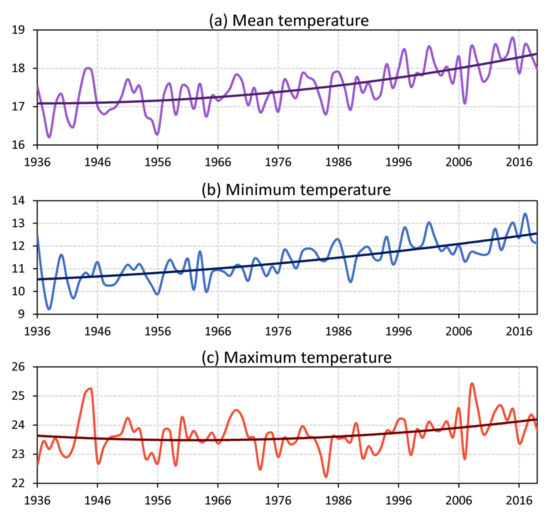
Figure 2.
Time series of (a) mean, (b) maximum, and (c) minimum annual temperature (in °C) at Rosario Aero station in the period 1936–2019. Nonlinear trends detected with the southeastern South America (SSA) method are included in each panel.
The joint analysis of the three temperatures shows that it was minimum temperature that drove the rise in mean temperature, rather than maximum temperature (2 and only 0.5 °C, respectively). Interestingly, Rosario Aero station is located at an airport, in an area that has undergone increasing urbanization over the years. As a consequence, the urban heat island effect could also be causing an increase in minimum temperature, mainly because of limited nighttime cooling.
Seasonal time series of mean, maximum, and minimum temperatures were also analyzed for the same period, along with their resulting nonlinear trends (figures not shown). No significant trends were observed in autumn and winter mean temperatures. On the other hand, we found significant trends in summer and spring, when the largest increase in average temperature—of the order of 2 °C—occurred. In summer, this increase would be explained mainly by an increase of 3 °C in minimum temperature, since the maximum temperature showed almost no variation. In spring, warmer minimum temperature is the major contributor to mean temperature increase, although there is also some contribution from maximum temperature.
The difference between maximum and minimum temperature, that is, the diurnal temperature range (DTR), remains practically unchanged during autumn and winter throughout the analyzed period. Spring and particularly summer DTR has been decreasing over the years. Summer DTR decreased from 15 to 12 °C. This result agrees with the findings by Lovino et al. [10], who reported a DTR decrease in northeastern Argentina during summer.
3.1.2. Precipitation
Figure 3 presents the annual cycle of monthly precipitation as well as the average and maximum values of monthly maximum 1-day precipitation (RX1day) at Rosario Aero station in the 1911–2019 period. The annual cycle of precipitation displays significant intra-annual variability. According to Doyle [44], Rosario has a precipitation regime with a short period of low precipitation in winter and fairly uniform precipitation in the rainiest months. Figure 3 shows that the rainy season runs from October to April, when it rains 78% of the annual average. The main forcing factors during the rainy season include the South American Low-Level Jet (SALLJ) east of the Andes [45,46] and the Mesoscale Convective Systems (MCSs). The SALLJ is a key factor that activates convection and favors precipitation in the subtropical plains of South America [47]. MCSs are frequent and account for a large percentage of total precipitation during the warm rainy season (October–April) over northeastern Argentina [48]. March is the rainiest month, with an RX1day average of 59 mm (Figure 3, light blue dot) and an absolute maximum of 179 mm—the same as the maximum RX1day for December (Figure 3, red dots). Summer months (DJF) exhibit precipitation values close to 110 mm/month and average RX1day of near 43 mm along the study period (Figure 3, light blue dots). Winter months (JJA) registered monthly values of 30 mm and an average RX1day of nearly 19 mm. Low winter precipitation is a common feature throughout the region [13,44]. In this season, the northward displacement of the South Atlantic anticyclone restricts water vapor inflow over the south-central region of the continent, which, added to lower solar radiation, results in the weakening of convective processes and heavy rains [49,50].
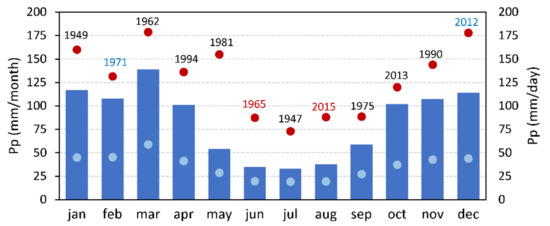
Figure 3.
Annual cycle of mean monthly precipitation at Rosario Aero station in the 1911–2019 period (left axis, blue bars). Light blue dots indicate average maximum daily precipitation; red dots, absolute maximum daily precipitation in the whole series 1936–2019 (right axis). Above each red dot is the year in which maximum daily precipitation occurred and its ENSO-related condition: red (EN), blue (LN), black (Ne).
The connection was examined between years of absolute maximum daily precipitation in the whole series (1936–2019) and the occurrence of ENSO (Figure 3, red dots). Most of the absolute maximum rains occurred in neutral years (Ne), except for two events in La Niña (LN) years during the summers of 1971 and 2012, and two in El Niño (EN) years during the winters of 1965 and 2015. The two years prior to 1950 (1949 and 1947) were neutral according to the classification by Berri et al. [34]. Moreover, although the analysis begins in 1936, it is only 1947 onwards that absolute maximum daily precipitations are recorded, presenting three absolute maxima in the last decade (2012 LN, 2013 Ne, 2015 EN).
Figure 4 presents the inter-annual variability of annual and seasonal precipitation at Rosario Aero in 1911–2019. Average annual precipitation in this period was 1078 mm, with a peak of 1626 mm in 2012 and a minimum record of 544 mm in 1915 (Figure 4a). Annual precipitation showed a significant nonlinear trend that increased substantially from the beginning of the 20th century, with average values of 950 mm until 1960, and up to 1050 mm between 1970 and 2019. Although this increase represents 10% of the annual averages, the positive trend continues to present times. The long-term change in annual precipitation shown in Figure 4a is almost exclusively due to a significant increase of nearly 100 mm during summer (Figure 4b), since autumn and spring (Figure 4c,e, respectively) show no significant trends. Winter exhibits a slight but significant precipitation decrease (Figure 4d).
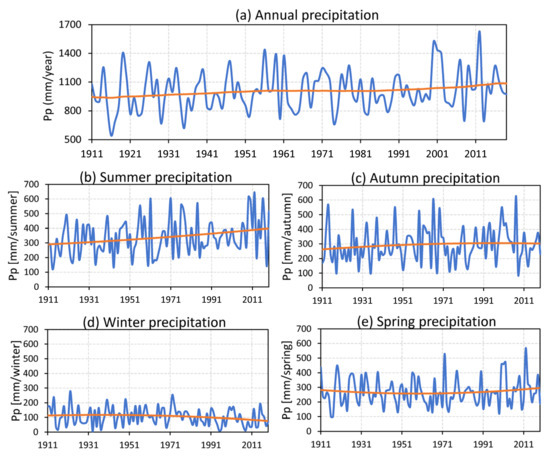
Figure 4.
(a) Annual precipitation (mm/year) and (b–e) seasonal precipitation (mm/season) at Rosario Aero station in the 1911–2019 period. Nonlinear trends detected with the SSA method in orange.
The large inter-annual variability observed in Figure 4, including water deficits and excesses, is characteristic of the central-northeastern region of Argentina and has cycles of 2–6 and 9 years [7]. As shown by Lovino et al. ([10] and references therein), most excesses were related to EN years, while deficits were related to LN years. However, they reported that excess precipitation was observed to be more localized, rather than covering the entire study area. On the contrary, precipitation deficit caused droughts with large spatial extension ([11] and references therein). To assess the connection between precipitation and ENSO at Rosario Aero, the years of excesses and deficits (90th and 10th percentiles, respectively) were identified according to the seasons of the year, for the entire observational period available (1911–2019). The ONI index from 1950 was applied, according to Trenberth [32], to classify years into EN, LN, or Ne. Years of excess/deficit before and after 1950 are presented in Table 2.

Table 2.
Years of precipitation excess/deficit in the period 1911–2019 by season. Years after 1950 are grouped according to EN, LN, Ne.
The analysis of the whole observation period shows that precipitation excess/deficit years were, respectively, 11/3 in summer, 11/0 in autumn, 11/10 in winter, and 11/6 in spring. In other words, except for winter, there were much more years with excess precipitation than with deficit. In particular, no precipitation deficits were observed in the autumns of the 109 years analyzed. Table 2 shows that there were much more excess periods than deficit periods. In addition, the period with water excess has grown in the last two decades with the relationship 7/3 years of excess/deficit. Deficit was more common in winters and springs, although less common than excess, in agreement with Sgroi et al. [11].
Table 2 shows a predominance of years with summer precipitation excess under LN conditions. On the other hand, winter excess occurred under EN conditions, and spring excess was mostly related to Ne years. No remarkable relation was identified between autumn precipitation and large-scale forcing. Contrary to literature findings for the region (e.g., [51,52]), no summer deficits were recorded under LN, but mostly excesses. This result would indicate that mesoscale processes are the drivers of excess precipitation in summer (as noted above). In contrast, winters with excess precipitation occurred during EN conditions, that is, they were modulated by large-scale forcing, in line with what has been found for central-northeastern Argentina [53]. No winter deficit years were observed during EN and LN, and the few deficit years identified were Ne. In the transition seasons, no years were recorded with deficit in autumn; spring deficits occurred in LN and Ne years (Table 2). Note that ENSO-related SST anomalies generally begin in the first half of a calendar year, they peak by the end of that year, and start to vanish in the following year [32]. Therefore, a complete ENSO cycle includes two consecutive years, and its effects are felt at different moments of the event cycle to a variable degree in the regions affected [34].
3.2. Climate Extremes
3.2.1. Frequency of Temperature Extremes
Figure 5a–d presents the changes in occurrence frequency of temperature extremes, i.e., warm days (TX90p, Figure 5a), cold days (TX10p, Figure 5b), warm nights (TN90p, Figure 5c), and cold nights (TN10p, Figure 5d). The frequency of warm days (TX90p, Figure 5a) remained approximately constant during the first decades. Starting in the 1990s, the average frequency of TX90p has grown by approximately 5%, from 10 to 15%, warm days per year in the present. A sustained positive trend in warm night frequency (TN90p, Figure 5c) was observed except at the beginning of the period, since the annual average of warm night frequency increased from 7 to 12% between 1960 and 2019. The frequency of occurrence of cold days (TX10p, Figure 5b) has been decreasing throughout the whole period, while the frequency of occurrence of cold nights showed a noticeable drop (from 18 to 8% annually, see Figure 5d), particularly from the 1960s onwards. Such a remarkable drop could be influenced by the gradual increase in minimum temperatures (Figure 2b).
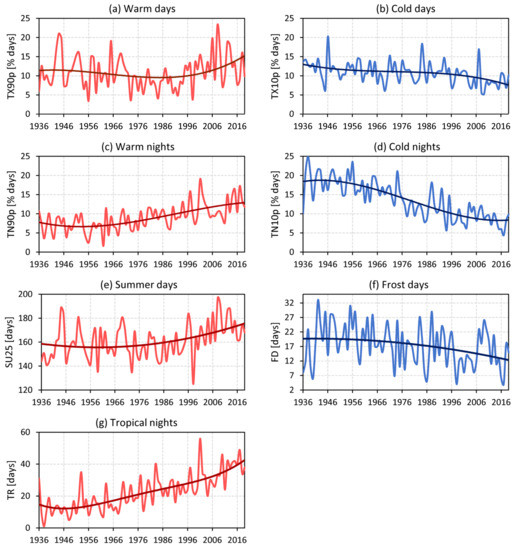
Figure 5.
Frequency of temperature extremes at Rosario Aero station in the period 1936–2019 as characterized by percentile indices: (a) warm days (TX90p), (b) cold days (TX10p), (c) warm nights (TN90p), and (d) cold nights (TN10p); by absolute indices (e) summer days (SU25), (f) frost days (FD), and (g) tropical nights (TR). See Table 1 for index definition. All nonlinear trends detected with the SSA method are significant at the 95% confidence level.
These changes in frequency of temperature extremes are consistent with global trends [35,54]. At regional scales, the changes are also consistent with the results in Rusticucci et al. [55], who analyzed temperature variability in central-eastern Argentina. They reported a decrease in the frequency of cold extremes—TX10 and TN10—and a significant increase in warm extreme occurrence (TX90) in the period 1981–2010. Other authors suggested that temperature-related extremes were influenced by interannual variability (Ref [12] and references therein). Collazo et al. [56] reported interannual cycles in warm-day occurrence with periodicities of 2–4 years and 8 years. They also found that ENSO and the Pacific Decadal Variability (PDO) were key predictors of warm days in Argentina. Moreover, Müller et al. [49] and Collazo et al. [57] suggested that El Niño favored the occurrence of less cold extremes. In particular, the occurrence of El Niño during autumn favored the occurrence of less extreme cold events in the following winter throughout the region, as reported in Collazo et al. [57].
Figure 5e–g shows the number of summer days (SU25, Figure 5e), tropical nights (TR, Figure 5g), and frost days (FD, Figure 5f). The number of summer days (Figure 5e), defined as those in which maximum temperature exceeded 25 °C, showed a slight increase at the beginning of the period that accelerated from the 1970s. SU25 increased by almost 20 days between 1980 and 2019. The number of tropical nights (Figure 5g), in which minimum temperature exceeded 20 °C, showed a systematic increase throughout the study period. This remarkable change implies a growth rate of 25 tropical nights per year from 1950 to 2019, from an average of 16 TR in 1950 to an average of 41 TR in 2019. Consistently, the number of frost days (Figure 5f) has dropped considerably from an average of 18 frost days per year between the 1930s to 1970s, to an average of 12 frost days in 2019. Fernández-Long et al. [58] also observed a decreasing trend in central-northeastern Argentina in a shorter period of analysis. In addition, the drop in the number of frost days is consistent with the drop in the frequency of cold days and nights, as shown in Figure 5b,d.
3.2.2. Intensity and Duration of Temperature Extremes
Figure 6a–d presents the changes in intensity of temperature extremes. Figure 6a,b show the temporal evolution of the highest and lowest annual temperatures in the time series of maximum temperature. Figure 6c,d show the same for minimum temperature. The annual warmest maximum daily temperature (TXx, Figure 6a) showed a decrease from the beginning of the period until the 1980s, when it began a slight increase that continues to the present. From end to end, maximum annual temperature decreased by 2 °C throughout the analyzed period. The coldest maximum daily temperatures (TXn, Figure 6b) showed a minor oscillation with no resulting change throughout the study period. On the other hand, the warmest minimum daily temperature (TNx, Figure 6c) presented a sustained increase of over 2 °C that accelerated in the last decades. Finally, the coldest minimum daily temperature (TNn, Figure 6d) exhibited a slight increase of almost 1 °C. The range of warmest daily temperatures (Figure 6a,c) decreases from 16 °C in 1936 to 12 °C in 2016; but the amplitude of the coldest daily temperatures remains basically unchanged around 14 °C throughout the whole period (Figure 6b,d).
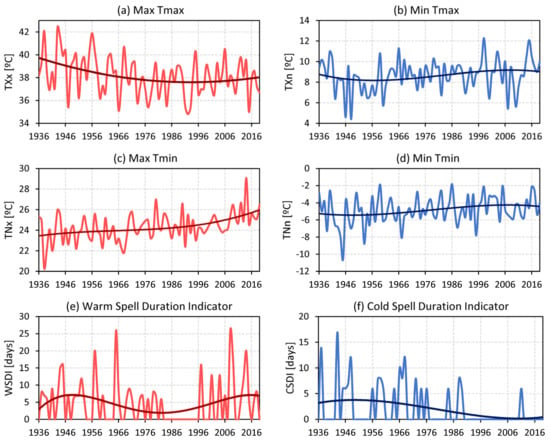
Figure 6.
Intensity and duration of temperature extremes at Rosario Aero station in the 1936–2019 period. Intensity is characterized by absolute indices: (a) warmest maximum daily temperature (TXx), (b) coldest maximum daily temperature (TXn), (c) warmest minimum daily temperature (TNx), and (d) coldest minimum daily temperature (TNn). Duration is represented by (e) warm spell (WSDI) and (f) cold spell (CSDI) indices. See Table 1 for index definition. All nonlinear trends detected with the SSA method are significant at the 95% confidence level.
Changes in duration of extreme temperature values are presented in Figure 6e for warm periods and in Figure 6f for cold periods. The duration of warm spells (Figure 6e, WSDI) showed a tendency to almost double the WSDI in the long term, from an average of 5 days to almost 10 days in duration. Conversely, the duration of cold spells (Figure 6f, CSDI) decreased systematically, and in recent decades, it barely reached 1 to 2 days on average. Alexander et al. [59] also analyzed warm spell duration in Argentina in the period 1951–2003. They found positive and negative trends over different regions in the country, with no significant linear trends of WSDI. More recently, this result was reinforced by two studies, which used global data indices (HadEX2). The first of these studies, by Donat et al. [60] found the same spatial extent and trend inconsistency that Alexander et al. [59] found in the same region. The other study by Lu et al. [61] analyzed the duration of warm and cold spells globally, also using HadEX2 data from 1958–2010, and determined weaker trends for both indices in South America: positive for WSDI and negative for CSDI. Finally, based on observations, Lovino et al. [10] found a significant trend toward longer warm spells and shorter cold spells in the 1963–2013 period in northeastern Argentina.
3.2.3. Intensity and Duration of Precipitation Extremes
Figure 7a–c shows the time series of the indices of precipitation intensity extremes, i.e., the annual maximum 1-day precipitation (Figure 7a, RX1day), the annual maximum 5-consecutive day precipitation (Figure 7b, RX5day), and the simple daily intensity index (SDII), defined as the total annual precipitation divided by the number of rainy days in the year. The RX1day (Figure 7a) remained approximately constant for most part of the period, but in recent decades, it suggested a moderate increase. The RX5day (Figure 7b) showed an increase at the beginning of the study period, it then stabilized until recent decades when it increased again. The SDII (Figure 7c) showed a significant increase during the last three decades, in agreement with the increase observed in annual precipitation in recent decades (Figure 4). This result was also found in the analysis of Table 2, where 7/3 years of excess/deficit corresponded to the last two decades. Similarly, SDII trend values for Rosario Aero station were coincident with the slightly upward trends calculated/projected in southeastern South America [56,59]. In general, the whole of South America is becoming wetter, which is related to the occurrence of heavy rainfall events concentrated in few days [62].
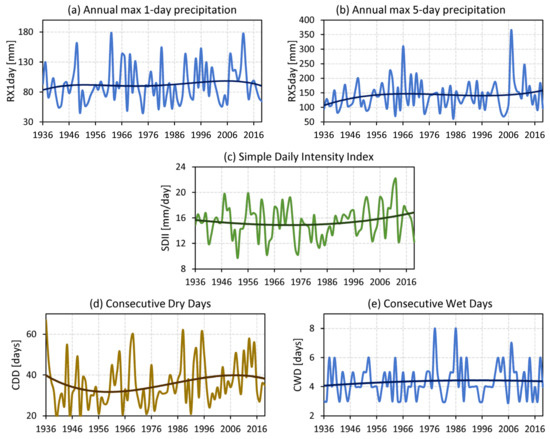
Figure 7.
Intensity and duration of precipitation extremes at Rosario Aero station in the 1936–2019 period. Intensity is characterized by: (a) annual maximum 1-day precipitation (RX1day), (b) annual maximum 5-consecutive-day precipitation (RX5day), and (c) simple daily intensity index (SDII). Duration is represented by (d) consecutive dry days (CDD) and (e) consecutive wet days (CWD). See Table 1 for index definition. All nonlinear trends detected with the SSA method are significant at the 95% confidence level.
Figure 7d,e shows the duration of precipitation extremes characterized by the annual maximum number of consecutive dry days (Figure 7d, CDD) and the annual maximum number of consecutive days with precipitation greater than 1 mm (Figure 7e, CWD). Except for the short decrease during the first two decades, the number of consecutive dry days (Figure 7d) has increased steadily from the 1950s, from 30 to 40 days. In contrast, consecutive wet days (Figure 7e) remained rather constant throughout the whole study period, with a mean value slightly above 4 consecutive days. A recent study considering consecutive days with precipitation greater than 0.1 mm in central-northern Argentina showed that precipitation events of 6 consecutive days were not frequent [63].
3.3. Future Climate Projections
Future climate projections for temperature and precipitation were analyzed using GCM models (Table A1) and their multi-model ensembles, for different time horizons in each of the RCP2.6, RCP4.5, and RCP8.5 scenarios.
3.3.1. Temperature
Figure 8 presents the time series of the multi-model ensembles that provide a graphic view of expected temperature variations in future climate change scenarios. In the RCP2.6 mitigation scenario (Figure 8a), the multi-model ensemble showed that there would be a small Tmean variation, with average values very close to current mean values in 2035, 2065, and 2100 (vertical lines in the figure). The inter-model range (shading in Figure 8a) in future projections is very similar to that of the historical period and relatively small, which makes the projection of the multi-model ensemble more robust.
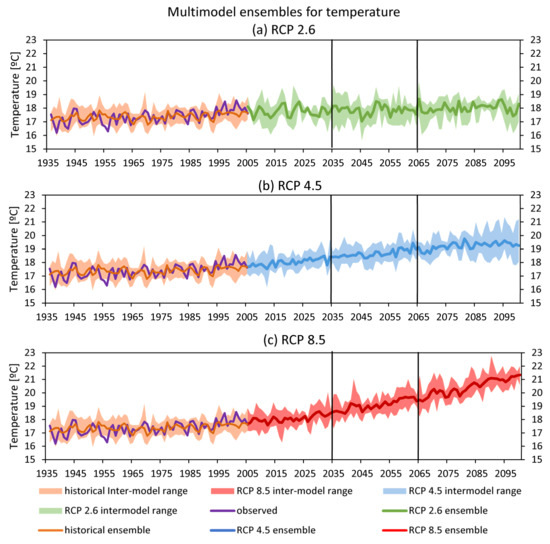
Figure 8.
Simulations of mean annual temperature by multi-model ensembles of the best-performing GCMs. The historical period (1936–2005) and future periods in the short (2006–2035), medium (2036–2065), and long (2066–2100) term are highlighted for scenarios RCP2.6 (a), RCP4.5 (b), and RCP8.5 (c) in Rosario. Historical simulation is contrasted with observed mean annual temperature at Rosario Aero station. Shading represents inter-model ranges.
Figure 8b shows the multi-model ensemble projection for the RCP4.5 scenario. Tmean would increase steadily until 2065, when it would stabilize at around 19 °C. By 2035, Tmean is likely to reach an average value of 18.5 °C, with a small inter-model range until 2070. For the last 30 years of the 21st century, the multi-model ensemble projections presented larger differences. Tmean is likely to reach values above 19 °C in the RCP4.5 stabilization scenario in 2100.
In the scenario of high emissions RCP8.5 (Figure 8c), Tmean would grow steadily, until an average maximum value of 21.5 °C at the end of the 21st century. In the short term, until 2035, an average Tmean close to 18.5 °C would be expected, a similar value to that expected in the stabilization scenario, with an average of 19.5 °C in 2065. The inter-model range is small (Figure 8c), suggesting a coherent projection of the different models, which gives robustness to the results.
Figure A1 presents expected average temperature changes in the short-, medium-, and long-term future periods, according to model projections for different scenarios. In the RCP2.6 scenario (Figure A1a), positive changes of less than 1 °C are expected for the short (to 2035), medium (to 2065), and long term (to 2100). Only one of the analyzed GCMs projected negative changes of less than 0.5 °C. The multi-model ensemble showed changes of 0.4 °C by 2035 and up to 0.6 °C by 2100. In summary, in the mitigation scenario, the expected Tmean increase would be less than 1 °C for the whole 21st century. In the RCP4.5 scenario, all models and their multi-model ensemble showed a consistent increase of 0.6 °C by 2035, of approximately 1.2 °C by 2065, and between 1.5–2 °C by 2100 (Figure A1b). There is high consistency among the average changes projected by each model, projecting robust changes for this scenario in each period. In the RCP8.5 scenario (Figure A1c), all models and their ensemble also showed very consistent positive changes among the different GCMs. For the 2006–2035 period, an increase is expected of about 0.6–1 °C, of 1.7–2 °C for 2036–2065, and of up to 3–3.5 °C for the 2066–2100 period. These results suggest that average annual temperature would increase significantly during the 21st century in the worst-case emission scenario.
Figure 9 shows the spatial distribution of the mean changes in mean annual temperature estimated with the multi-model ensemble in central-northeastern Argentina. The greatest increases were observed in the north of the region in the three scenarios, with decreasing magnitude towards the south. This rise could reach 4 °C by the end of the century in the high greenhouse gas emissions scenario (RCP8.5). In particular, a warming of 0.5–1 °C was projected under the three climate-change scenarios in the core crop region in the 2006–2035 period (first column, Figure 9). Thus, the region would experience a warming between 0.5 and 1 °C by 2035, regardless of the scenario. However, in the following 2036–2065 period, mean temperature would rise 1–1.5 °C in the RCP2.6 and RCP4.5 scenarios, and between 1.5 and 2 °C in the RCP8.5 scenario (second column, Figure 9). By the end of the century—2066–2100—(third column, Figure 9), models projected changes of 1–1.5 °C in the mitigation scenario, 1.5–2 °C in the stabilization scenario, and 3–3.5 °C in the high-emission scenario.
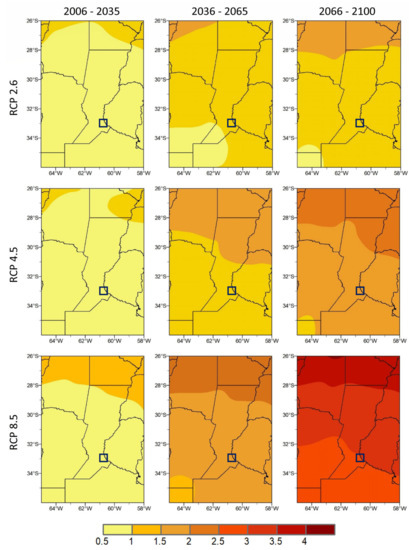
Figure 9.
Spatial distribution of mean future changes in mean annual temperature (in °C) according to the ensemble of the best-performing GCMs for the region, in the periods (columns) 2006–2035, 2035–2065, and 2066–2100, in relation to the simulations of each GCM of the historical base period 1901–2005. By row: RCP2.6 mitigation, RCP4.5 stabilization, and high-emission RCP8.5 scenarios.
3.3.2. Precipitation
Figure 10 presents the multi-model ensemble projections for annual precipitation. Precipitation would remain almost the same in the mitigation scenario (Figure 10a), with no significant differences in the short-, medium-, and long-term periods. The inter-model range is low, which gives greater reliability to the ensemble projection. In the stabilization scenario, precipitation might experience a less significant increase (Figure 10b). The inter-model range for the GCMs studied fluctuates around the average values, especially after 2065. In this scenario, annual precipitation is expected to increase to a mean value of approximately 1100 mm by 2100, while the mean value for the period 1971–2005 is 1020 mm. In the high-emission scenario, an increasing trend of annual precipitation is observed, although not as significant as that for temperature. In this scenario, annual precipitation could reach 1150 mm by 2100. The range of variation among GCMs was considerable, although it did not exceed the variability of the observed historical time series. These results suggest a gradual increase in precipitation along the 21st century in the RCP8.5 scenario.
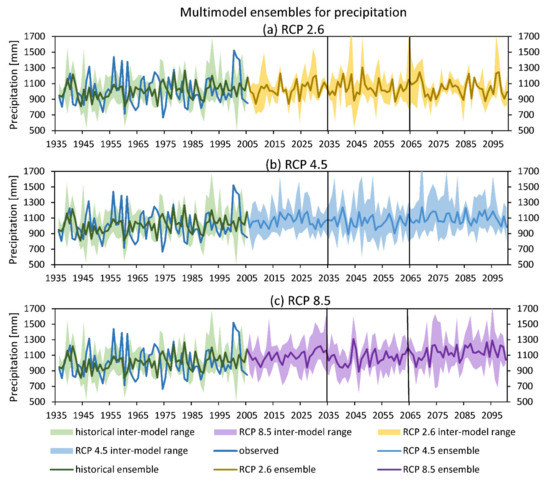
Figure 10.
Simulations of annual precipitation by multi-model ensembles of the best-performing GCMs. The historical period (1936–2005) and future periods in the short (2006–2035), medium (2036–2065), and long (2066–2100) term are highlighted for scenarios RCP2.6 (a), RCP4.5 (b), and RCP8.5 (c) in Rosario. Historical simulation is contrasted with observed mean annual temperature at Rosario Aero station. Shading represents inter-model ranges.
Our results show that none of the models predicted a trend in precipitation as noticeable as in temperature. Changes in precipitation would not be expected to affect annual amounts significantly, although they would likely impact extreme events in southeastern South America, as suggested by Seneviratne et al. [64], Donat et al. [65], and Pfahl et al. [66]. Therefore, the increasing trend observed in intense precipitation events (see Section 3.2.3) would likely continue in the coming decades. In the three emission scenarios, annual precipitation would not undergo significant changes in the study region. In the most unfavorable emission scenarios (RCP4.5 and RCP8.5), there would be slight increases in precipitation, and the variability would remain practically unchanged.
Figure A2 summarizes the annual precipitation changes in future scenarios for the different studied periods. Precipitation changes simulated by the GCMs were not as consistent as those of temperature. In the mitigation scenario (Figure A2a), variations in annual precipitation would be rather small, since expected changes would vary around 20–30 mm in the 2006–2035 period and around 20–60 mm in 2036–2065 and 2066–2100. These variations represent a 2 to 6% increase in annual precipitation, which is not significant given the great interannual variability of precipitation in the region. In the RCP4.5 scenario (Figure A2b), precipitation would increase between 40 and 90 mm from 2006 to 2065. In the period 2066–2100, a greater increase, between 70 and 130 mm, would be expected, which represents 10% of current values. The only GCM model of the group that projects a minimum and slightly negative change is NorESM1-M. The most significant increases would be expected in the high-emission scenario RCP8.5 (Figure A2c). In the 2006–2065 period, the range of variation among models oscillates between 40 and 140 mm (except NorESM1-M). In the 2066–2100 period, GCMs showed consistent increasing projections of 80–160 mm. This increase represents from 8 to 16% of average annual precipitation.
Figure 11 presents the spatial distribution of mean changes in annual precipitation in central-northeastern Argentina. The distribution of mean changes is heterogeneous, a characteristic feature for this variable. Changes were mostly positive, indicating an increase in precipitation. However, under scenario RCP2.6 (first row of Figure 11), some regions in the northwest and the south will undergo negative changes—i.e., precipitation will slightly decrease throughout the century. In the rest of the region, increases will not exceed 50 mm. Under scenarios RCP4.5 and RCP8.5 (second and third rows of Figure 11), projected precipitation increases were greater than those under RCP2.6. Mean changes in precipitation will be greater in the west, center, and south of the region, with peak values of 100 to 150 mm by the end of the century in the high-emission scenario RCP8.5. In particular, in the core crop region around Rosario (Figure 11), projections under the mitigation scenario show a precipitation increase of up to 25 mm in the period 2006–2035 and from 25 to 50 mm for the rest of the 21st century. These values are not significant given the large interannual variability of precipitation (Figure 4a). In the stabilization scenario, precipitation will increase between 25 and 75 mm in the 21st century. The high-emission scenario projects the greatest increase, between 50 to 100 mm, in the first half of the century, and between 100 and 150 by the end of the 21st century. These projections would represent an increase of from 8 to 16% of current values in mean annual precipitation.
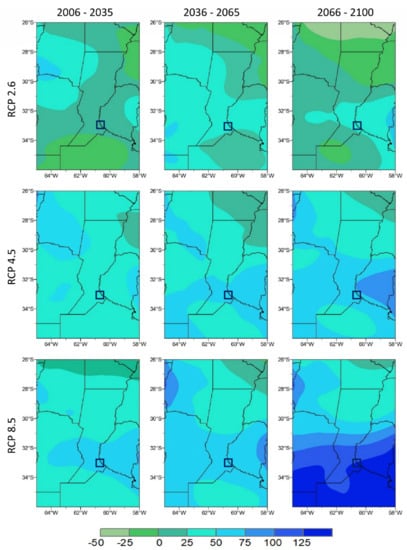
Figure 11.
Spatial distribution of mean future changes in annual precipitation (mm) according to the ensemble of the best-performing GCMs in the region, for the periods (columns) 2006–2035, 2035–2065, and 2066–2100, in relation to the simulations of each GCM of the historical base period 1901–2005. Rows: RCP2.6 mitigation, RCP4.5 stabilization, and high-emission RCP8.5 scenarios.
Several studies have shown that globally averaged precipitation increases with warming [2,3,67,68]. However, at regional scales, the situation may be different, as warming may result in more precipitation in one region and less in another. This lack of connection has been noted in other studies that attempted to evaluate such links in southern South America, where precipitation is projected to increase [2,67,69,70].
These results suggest that changes in precipitation would not be expected to affect annual amounts significantly. However, it would be highly likely that the frequency and intensity of extreme precipitation events would be affected [9,64]. The analysis of historical records showed increasing trends of precipitation intensity (see Figure 7). Should this trend continue in the coming decades as expected, intense precipitation events would continue to be more frequent in the region.
4. Conclusions
The core crop region of the Humid Pampa is one of the richest agricultural lands around the world and the main productive region in Argentina. It concentrates most of the country’s agro-industrial production. The analysis of the climate changes in the 20th and 21st centuries is crucial, because besides its economic importance, the region is densely populated and is home to one of the most important cities in Argentina. This paper assesses climate variability and historical climate extremes from the beginning of the 20th century to the beginning of the 21st century and historical changes in temperature and precipitation. It also includes future simulations of temperature and precipitation under different emission scenarios in the 21st century, for the short, medium, and long term.
The analysis of temperature (1936–2019) revealed a 1 °C rise in annual mean temperature by from 1970 to present. Mean annual values of minimum and maximum temperature have risen by 2 and 0.5 °C, respectively. These changes occurred mainly in spring and summer, while no significant trends were seen in autumn and winter. From the beginning of the 20th century, annual precipitation (1911–2019) rose from an average of 950 mm in 1960 to 1050 mm between 1970 and 2017, which represents a 10% growth in average precipitation. The greatest change (almost 100 mm/season) occurred in summer (wet season), while winter precipitation (dry season) decreased slightly in recent years.
During the 109 years of monthly precipitation observations (1911–2019), 11 excess events were observed in each season of the year. In contrast, years with precipitation deficit showed notable differences depending on the season. There was no precipitation deficit in autumn, but deficits were identified in three summers, six springs, and up to 10 winters. These results reveal that the number of excess periods is much greater than the number of deficit periods. In addition, the number of excess periods has increased faster in the last two decades with a relationship 7/3 years of excess/deficit.
The effects of ENSO on precipitation depend on the season of the year. In summer, there is a predominance of years with excess precipitation in LN years, while winter excesses predominate in EN years. Absolute maximum daily precipitations were recorded in two LN summers in the entire 1936–2019 period. These results suggest a dominance of mesoscale processes in the summers with excess precipitation. Such dominance could be caused by LN inhibiting large-scale precipitation mechanisms ([51,52]). In contrast, large-scale processes predominated in winters with excessive precipitation during EN, as it enhanced precipitation in the center-northeast of the country. In the transition seasons, ENSO seemed to have no influence on excess precipitation, while precipitation deficits during LN events were observed only in two springs and in one summer.
Temperature extremes showed significant trends towards warmer conditions, consistent with observed global trends ([36,59]). The frequency of occurrence of warm days and nights increased considerably and cold days and nights decreased notably, with a significant drop in the number of frost events. Consistently, the duration and intensity of heatwaves increased. The opposite was seen for cold waves. Extremes of precipitation increased in frequency, with events lasting from 1 to 5 consecutive days, while the number of consecutive dry days also increased. These changes led to a concentration of annual precipitation in fewer days, which caused more intense events.
Future climate scenarios were estimated from a subset of GCMs selected in Lovino et al. [39]. Model projections indicated that temperature would continue to rise in central-northeastern Argentina during the 21st century. The growth rate is higher towards the north of the region and decreases towards the south. The warming would not exceed 1 °C in the first period analyzed (2006–2035), regardless of the scenario. From 2035, temperature would be expected to rise, reaching 2 °C at the end of the 21st century under the stabilization scenario. In the high-emission scenario, the rate of increase grows, with temperature changes reaching 3–3.5 °C.
Future average precipitation changes would have heterogeneous spatial distribution throughout central-northeastern Argentina. Future projections of annual precipitation showed gradual changes with a slight to moderate increase depending on the scenario. In the mitigation scenario, total annual precipitation would not undergo major variations during the 21st century. Average precipitation changes under the stabilization and high-emission scenarios would be greater in the west, center, and south of the region, including the area of Rosario. Values could range from 100 to 150 mm by the end of the century in the high-emission scenario. In particular, in the core crop region, annual precipitation is projected to increase during the century in all the cases. The more critical the scenario, the greater increases in projected precipitation.
Our results of observed and projected changes in regional climate and the increase in extreme event occurrence show that new management strategies are needed for natural and human systems in order to prevent life and economic losses, damage to infrastructure, and natural resources. In addition to tending towards sustainability, this information would allow for improving the management of climate risk by adopting preventive measures to face the consequences of climate change and variability in the study region.
Author Contributions
Conceptualization, G.V.M. and M.A.L.; methodology, M.A.L.; validation, L.C.S.; formal analysis, G.V.M., M.A.L., and L.C.S.; writing—original draft preparation, G.V.M.; writing—review and editing, G.V.M., M.A.L., and L.C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of the Environment of the Province of Santa Fe and the Municipality of Rosario, Argentina (Agreement No. 915913) and by the CAI + D 2020 UNL Project (Grant No. 50620190100082LI), which in particular funded the APC.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The CMIP5 multi-model ensemble [37] data presented in this study are openly available in https://esgf-node.llnl.gov/search/cmip5/ (accessed on 26 February 2019). Restrictions apply to the availability of Rosario Aero meteorological station data. Data was obtained from the National Weather Service of Argentina and are available upon request from https://www.smn.gob.ar/ (accessed on 26 February 2019).
Acknowledgments
We are grateful to the anonymous reviewers who helped to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Selection of best-performing CMIP5 models in northeastern Argentina (see text for details). Variables: monthly surface air temperature (T) and precipitation (P).
Table A1.
Selection of best-performing CMIP5 models in northeastern Argentina (see text for details). Variables: monthly surface air temperature (T) and precipitation (P).
| Variable | Model | Institution/Country | Type | Atmospheric Resolution (lon. × lat.) Model Levels (L) |
|---|---|---|---|---|
| T | ACCESS 1.0 | CSIRO-BOM, Australia | AOGCM | 1.875 × 1.250 L38 |
| P | CanESM2 | CCCMA, Canada | ESM | 2.810 × 2.810 L35 |
| T, P | CESM1-BGC | NSF-DOE-NCAR, USA | AOGCM | 1.250 × 0.9424 L26 |
| T, P | CESM1-FASTCHEM | NSF-DOE-NCAR, USA | ChemESM | 1.250 × 0.9424 L26 |
| T | HadGEM2-CC | MOHC, UK | ESM | 1.875 × 1.250 L60 |
| P | INM-CM4 | INM, Russia | AOGCM | 2.000 × 1.500 L21 |
| T | MIROC-ESM-CHEM | MIROC, Japan | ChemESM | 2.810 × 2.810 L80 |
| P | MIROC4h | MIROC, Japan | AOGCM | 0.560 × 0.560 L56 |
| T, P | NorESM1-M | NCC, Norway | ESM | 2.500 × 1.8750 L26 |
| T, P | CCSM4 | NCAR, USA | AOGCM | 1.250 × 0.940 L26 |
| T | CMCC-CM | CMCC, Italy | AOGCM | 0.750 × 0.750 L31 |
| T | EC-EARTH | EC-Earth Consortium | AOGCM | 1.125 × 1.125 L62 |
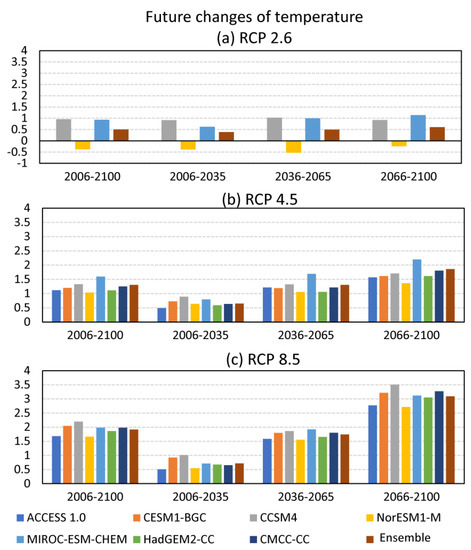
Figure A1.
Average future changes in mean annual temperature (in °C) in Rosario according to the best GCMs in the region and their multi-model ensemble in the periods 2006–2100, 2006–2035, 2036–2065, and 2066–2100 in reference to observations of the historical period 1936–2005 at Rosario AERO station. (a) Mitigation scenario (RCP2.6), (b) stabilization scenario (RCP4.5), and (c) high-emission scenario (RCP8.5).
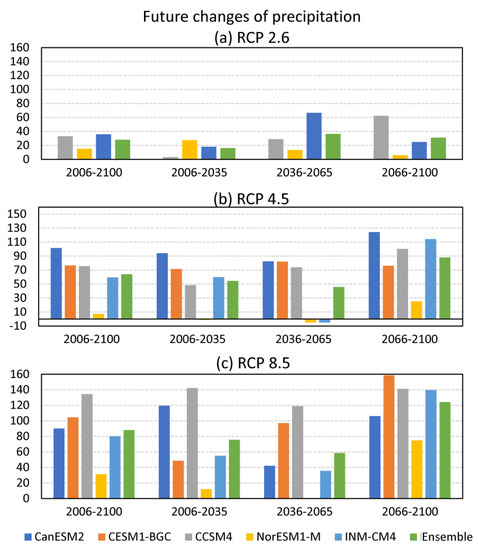
Figure A2.
Average future changes in annual precipitation (in mm) in Rosario according to the best GCMs in the region and their multi-model ensemble in the periods 2006–2100, 2006–2035, 2036–2065, and 2066–2100 in reference to the observations of the historical period 1936–2005 at Rosario AERO station. (a) Mitigation scenario (RCP2.6), (b) stabilization scenario (RCP4.5), and (c) high-emission scenario (RCP8.5).
References
- IPCC. Summary for Policymakers. In Global Warming of 1.5 °C; An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; Masson-Delmotte, V., Zhai, P., Pörtner, H.-O., Roberts, D., Skea, J., Shukla, P.R., Pirani, A., Moufouma-Okia, W., Péan, C., Pidcock, R., et al., Eds.; IPCC: Geneva, Switzerland, 2018. [Google Scholar]
- Westra, S.; Alexander, L.V.; Zwiers, F.W. Global Increasing Trends in Annual Maximum Daily Precipitation. J. Clim. 2013, 26, 3904–3918. [Google Scholar] [CrossRef]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A Global, Continental, and Regional Analysis of Changes in Extreme Precipitation. J. Clim. 2020, 34, 243–258. [Google Scholar] [CrossRef]
- Cavalcanti, I.F.A.; Carril, A.F.; Penalba, O.C.; Grimm, A.M.; Menéndez, C.G.; Sanchez, E.; Chechi, A.; Sörensson, A.; Robledo, F.; Rivera, J.; et al. Precipitation extremes over La Plata Basin—review and new results from observations and climate simulations. J. Hydrol. 2015, 523, 211–230. [Google Scholar] [CrossRef]
- Carril, A.F.; Cavalcanti, I.F.A.; Menéndez, C.G.; Sörensson, A.; López-Franca, N.; Rivera, J.; Robledo, F.; Zaninelli, P.; Ambrizzi, T.; Penalba, O.; et al. Extreme events in the La Plata basin: A retrospective analysis of what we have learned during CLARIS-LPB project. Clim. Res. 2015, 68, 95–116. [Google Scholar] [CrossRef]
- Lovino, M.; García, N.; Baethgen, W. Spatiotemporal analysis of extreme precipitation events in the Northeast region of Argentina (NEA). J. Hydrol. 2014, 2, 140–158. [Google Scholar] [CrossRef]
- Lovino, M.; Müller, O.; Müller, G.; Sgroi, L.; Baethgen, W. Interannual-to-multidecadal hydroclimate variability and its sectoral impacts in northeastern Argentina. Hydrol. Earth Syst. Sci. 2018, 22, 3155–3174. [Google Scholar] [CrossRef]
- Magrin, G.O.; Marengo, J.A.; Boulanger, J.P.; Buckeridge, M.S.; Castellanos, E.; Poveda, G.; Scarano, F.R.; Vicuña, S. Central and South America. In Climate Change 2014: Impacts, Adaptation, and Vulnerability. Part B: Regional Aspects. Contribution of Working Group II to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Barros, V.R., Field, C.B., Dokken, D.J., Mastrandrea, M.D., Mach, K.J., Bilir, T.E., Chatterjee, M., Ebi, K.L., Estrada, Y.O., Genova, R.C., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014; pp. 1499–1566. [Google Scholar]
- Barros, V.; Boninsegna, J.; Camilloni, I.; Chidiak, M.; Magrín, G.; Rusticucci, M. Climate change in Argentina: Trends, projections, impacts and adaptation. Wiley Interdiscip. Rev. Clim. Chang. 2015, 6, 151–169. [Google Scholar] [CrossRef]
- Lovino, M.; Müller, O.; Berbery, E.H.; Müller, G.V. How have daily climate extremes changed in the recent past over northeastern Argentina? Glob. Planet. Chang. 2018, 168, 78–97. [Google Scholar] [CrossRef]
- Sgroi, L.C.; Lovino, M.; Berbery, E.H.; Müller, G.V. Characteristics of droughts in Argentina’s Core Crop Region. Hydrol. Earth Syst. Sci. Discuss. 2020. In review, preprint. [Google Scholar] [CrossRef]
- Rusticucci, M.; Barrucand, M.; Collazo, S. Temperature extremes in the Argentina central region and their monthly relationship with the mean circulation and ENSO phases. Int. J. Climatol. 2017, 37, 3003–3017. [Google Scholar] [CrossRef]
- Lovino, M.; Müller, G.V.; Sgroi, L. How has precipitation changed in the province of Santa Fe? Rev. Investig. Agropecu. RIA, 2020; 46, 226–239. Available online: http://ria.inta.gob.ar/sites/default/files/trabajosenprensa/lovino-castellano-6.pdf (accessed on 29 November 2019). (In Spanish)
- Llano, M.P.; Vargas, W. Spatial and Temporal Variability of Daily Precipitation Concentration in Southeastern South America. Int. J. Climatol. 2020, 41, 1152–1163. [Google Scholar] [CrossRef]
- INA (Instituto Nacional del Agua). Alerta Hidrológico Cuenca del Plata: Informes MENSUALES Emitidos. 2020. Available online: https://www.ina.gov.ar/alerta/index.php?seccion=2&year=2020 (accessed on 10 July 2020). (In Spanish)
- Reuters. Argentina’s Ebbing Parana River Costs Grains Sector $244 Million: Exchange. Available online: https://www.reuters.com/article/us-argentina-grains-parana/argentinas-ebbing-parana-river-costs-grains-sector-244-million-exchange-idUSKCN2263B0 (accessed on 1 August 2020).
- BCR (Bolsa de Comercio de Rosario). Río Paraná: La Bajante Más Severa en los Últimos 50 Años Representa un Costo de US$ 244 Millones Para el Complejo Agroexportador. Available online: https://bcr.com.ar/es/sobre-bcr/medios/noticias/rio-parana-la-bajante-mas-severa-en-los-ultimos-50-anos-representa-un (accessed on 30 June 2020). (In Spanish).
- NASA Earth Observatory. The Parched Paraná River. Available online: https://earthobservatory.nasa.gov/images/147031/the-parched-parana-river (accessed on 1 August 2020).
- BCR (Bolsa de Comercio de Rosario). La Bolsa de Rosario Estima en 230 Millones de Dólares las Pérdidas de Ingresos por Las Inundaciones. Available online: https://www.diarioelinforme.com.ar/2019/01/28/la-bolsa-de-rosario-estima-en-230-millones-de-dolares-las-perdidas-de-ingresos-por-las-inundaciones (accessed on 1 April 2020). (In Spanish).
- Iriondo, M.H. Climatic changes in the South American plains: Records of a continent-scale oscillation. Quat. Int. 1999, 57, 93–112. [Google Scholar] [CrossRef]
- Iriondo, M.H.; Kröhling, D.M. Los Sedimentos Eólicos del Noreste de la Llanura Pampeana (Cuaternario Superior). In Abstracts XIII Congreso Geológico Argentino (AGA); Ramos, V., Ed.; Asociación Geológica Argentina: Buenos Aires, Argentina, 1996; Volume 4, pp. 27–48. [Google Scholar]
- Iriondo, M.H.; Kröhling, D.M. Non-classical types of loess. Sediment. Geol. 2007, 202, 352–368. [Google Scholar] [CrossRef]
- PAR (Plan Ambiental Rosario). Municipalidad de Rosario. 2016. Available online: https://www.rosario.gob.ar/ArchivosWeb/libro%20PAR_10%2002.pdf (accessed on 18 May 2020). (In Spanish)
- PER (Plan Estratégico Rosario 2030). Municipalidad de Rosario. 2019. Available online: https://www.rosario.gob.ar/web/rosario-2030 (accessed on 18 May 2020). (In Spanish)
- PERM (Plan Estratégico Rosario Metropolitana). Municipalidad de Rosario. 2018. Available online: https://www.rosario.gob.ar/web/sites/default/files/perm.pdf (accessed on 18 May 2020). (In Spanish)
- World Meteorological Organization (WMO). Manual for Estimation of Probable Maximum Precipitation. In Publication No.1045; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Young, K. A Three-Way Model for Interpolating for Monthly Precipitation Values. Mon. Weather Rev. 1992, 120, 2561–2569. [Google Scholar] [CrossRef]
- Eischeid, J.; Pasteris, P.; Diaz, H.; Plantico, M.; Lott, N. Creating a serially complete, national daily time series of temperature and precipitation for the western United States. J. Appl. Meteorol. 2000, 39, 1580–1591. [Google Scholar] [CrossRef]
- Ghil, M.; Allen, M.; Dettinger, M.; Ide, K.; Kondrashov, D.; Mann, M.; Robertson, A.; Saunders, A.; Tian, Y.; Varadi, F.; et al. Advanced spectral methods for climatic time series. Rev. Geophys. 2002, 40, 3-1–3-41. [Google Scholar] [CrossRef]
- Wilks, D.S. Statistical Methods in the Atmospheric Sciences, 2nd ed.; Academic Press: Cambridge, MA, USA, 2006; p. 627. [Google Scholar]
- Allen, M.R.; Smith, L.A. Monte Carlo SSA: Detecting irregular oscillations in the presence of colored noise. J. Clim. 1996, 9, 3373–3404. [Google Scholar] [CrossRef]
- Trenberth, K. The Definition of El Niño. Bull. Am. Meteorol. Soc. 1997, 78, 2771–2777. [Google Scholar] [CrossRef]
- NOAA/NWS/CPC; Oceanic Niño Index (ONI). NOAA National Weather Service, Center for Climate Prediction. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 21 April 2020).
- Berri, G.J.; Bianchi, E.; Müller, G.V. El Niño and La Niña influence on mean river flows of southern South America in the 20th century. Hydrol. Sci. J. 2019, 64, 900–909. [Google Scholar] [CrossRef]
- Klein Tank, A.M.G.; Zwiers, F.W.; Zhang, X. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation, WMO-TD; No. 1500/WCDMP-No. 72; World Meteorological Organization: Geneva, Switzerland, 2009; p. 52. [Google Scholar]
- Donat, M.; Alexander, L.; Yang, H.; Durre, I.; Vose, R.; Caesar, J. Global land-based datasets for monitoring climatic extremes. Bull. Am. Meteorol. Soc. 2013, 94, 997–1006. [Google Scholar] [CrossRef]
- Taylor, K.; Stouffer, R.; Meehl, G. An Overview of CMIP5 and the Experiment Design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Moss, R.; Edmonds, J.; Hibbard, K.; Manning, M.; Rose, S.; van Vuuren, D.; Carter, T.; Emori, S.; Kainuma, M.; Kram, T.; et al. The next generation of scenarios for climate change research and assessment. Nature 2010, 463, 747–756. [Google Scholar] [CrossRef] [PubMed]
- Lovino, M.; Müller, O.; Berbery, E.H.; Müller, G.V. Evaluation of CMIP5 retrospective simulations of temperature and precipitation in northeastern Argentina. Int. J. Climatol. 2018, 38, e1158–e1175. [Google Scholar] [CrossRef]
- Maraun, D.; Wetterhall, F.; Ireson, A.; Chandler, R.; Kendon, E.; Widmann, M.; Brienen, S.; Rust, H.; Sauter, T.; Themel, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Widmann, M.; Bretherton, C.S.; Salathé, E.P. Statistical precipitation downscaling over the northwestern United States using numerically simulated precipitation as a predictor. J. Clim. 2003, 16, 799–816. [Google Scholar] [CrossRef]
- Engen-Skaugen, T. Refinement of dynamically downscaled precipitation and temperature scenarios. J. Clim. 2007, 84, 365–382. [Google Scholar] [CrossRef]
- Casanueva, A.; Frías, M.D.; Herrera, S.; San-Martín, D.; Zaninovic, K.; Gutiérrez, J.M. Statistical downscaling of climate impact indices: Testing the direct approach. J. Clim. 2014, 127, 547–560. [Google Scholar] [CrossRef]
- Doyle, M.E. Observed and simulated changes in precipitation seasonality in Argentina. Int. J. Climatol. 2019, 40, 1716–1737. [Google Scholar] [CrossRef]
- Virji, H. A preliminary study of Summer time tropospheric circulation patterns over South America estimated from cloud winds. Mon. Weather Rev. 1981, 109, 599–610. [Google Scholar] [CrossRef]
- Berbery, E.H.; Collini, E.A. Springtime precipitation and water vapor flux over southeastern South America. Mon. Weather Rev. 2000, 128, 1328–1346. [Google Scholar] [CrossRef]
- Nogués-Paegle, J.; Mechoso, C.; Fu, R.; Berbery, E.H.; Winston, C.; Chen, T.C.; Cook, K.; Diaz, A.; Enfield, D.; Ferreira, R.; et al. Progress in Pan American CLIVAR research: Understanding the south American monsoon. Meteor Forschung 2002, 27, 3–32. [Google Scholar]
- Laing, A.G.; Fritch, J.M. The large-scale environments of the global populations of mesoscale convective complexes. Mon. Weather Rev. 2000, 128, 2756–2776. [Google Scholar] [CrossRef]
- Müller, G.; Nuñez, M.; Seluchi, M. Relationship between ENSO cycles and frost events within the Pampa Húmeda region. Int. J. Climatol. 2000, 20, 1619–1637. [Google Scholar] [CrossRef]
- Vera, C.; Vigliarolo, P.K.; Berbery, E.H. Cold season synoptic scale waves over subtropical South America. Mon. Weather Rev. 2002, 130, 684–699. [Google Scholar] [CrossRef]
- Berri, G.J.; Bertossa, G. The influence of the tropical and subtropical Atlantic and Pacific Oceans on precipitation variability over Southern Central South America on seasonal time scales. Int. J. Climatol. 2004, 24, 415–435. [Google Scholar] [CrossRef]
- Penalba, O.; Rivera, J. Precipitation response to El Niño/La Niña events in Southern South America-emphasis in regional drought occurrences. Adv. Geosci. 2016, 42, 1–14. [Google Scholar] [CrossRef]
- Barros, V.; Silvestri, G. The relation between sea surface temperature at the subtropical South-Central Pacific and precipitation in southeastern South America. J. Clim. 2002, 15, 251–267. [Google Scholar] [CrossRef]
- Dunn, R.J.H.; Alexander, L.V.; Donat, M.G. Development of an updated global land in situ- based data set of temperature and precipitation extremes: HadEX3. J. Geophys. Res. Atmos. 2020, 125, e2019JD032263. [Google Scholar] [CrossRef]
- Rusticucci, M. Observed and simulated variability of extreme temperature events over South America. Atmos. Res. 2017, 106, 1–17. [Google Scholar] [CrossRef]
- Collazo, S.; Barrucand, M.; Rusticucci, M. Summer seasonal predictability of warm days in Argentina: Statistical model approach. Theor. Appl. Climatol. 2019, 138, 1853–1876. [Google Scholar] [CrossRef]
- Collazo, S.; Barrucand, M.; Rusticucci, M. Variability and predictability of winter cold nights in Argentina. Weather Clim. Extrem. 2019, 26, 100236. [Google Scholar] [CrossRef]
- Fernández-Long, M.; Müller, G.; Beltrán-Przekurat, A.; Scarpati, O. Long-term and recent changes in temperature-based agroclimatic indices in Argentina. Int. J. Climatol. 2013, 33, 1673–1686. [Google Scholar] [CrossRef]
- Alexander, L.; Zhang, X.; Peterson, T.; Caesar, J.; Gleason, B.; Klein Tank, A.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Donat, M.; Alexander, L.; Yang, H.; Durre, I.; Vose, R.; Dunn, R.; Willett, K.; Aguilar, E.; Brunet, M.; Caesar, J.; et al. Updated analyses of temperature and precipitation extreme indices since the beginning of the twentieth century: The HadEX2 dataset. J. Geophys. Res. Atmos. 2013, 118, 2098–2118. [Google Scholar] [CrossRef]
- Lu, C.; Sun, Y.; Zhang, X. Multimodel detection and attribution of changes in warm and cold spell durations. Environ. Res. Lett. 2018, 13, 074013. [Google Scholar] [CrossRef]
- Skansi, M.; Brunet, M.; Sigró, J.; Aguilar, E.; Arevalo Groening, J.; Bentancur, O.; Castellón Geier, Y.; Correa Amaya, R.; Jácome, H.; Malheiros Ramos, A.; et al. Warming and wetting signals emerging from analysis of changes in climate extreme indices over South America. Glob. Planet. Chang. 2013, 100, 295–307. [Google Scholar] [CrossRef]
- Scardilli, A.; Llano, M.; Vargas, W. Temporal analysis of precipitation and rain spells in Argentinian centenary reference stations. Theor. Appl. Climatol. 2015, 127, 339–360. [Google Scholar] [CrossRef]
- Seneviratne, S.I.; Nicholls, N.; Easterling, D.; Goodess, C.M.; Kanae, S.; Kossin, J.; Luo, Y.; Marengo, J.; McInnes, K.; Rahimi, M.; et al. Changes in climate extremes and their impacts on the natural physical environment. In Managing the Risks of Extreme Events and Disasters to Advance Climate Change Adaptation; IPCC: Geneva, Switzerland, 2012. [Google Scholar]
- Donat, M.; Lowry, A.; Alexander, L.; O’Gorman, P.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 6, 508–513. [Google Scholar] [CrossRef]
- Pfahl, S.; O’Gorman, P.; Fischer, E. Understanding the regional pattern of projected future changes in extreme precipitation. Nat. Clim. Chang. 2017, 7, 423–427. [Google Scholar] [CrossRef]
- Llopart, M.; Simões Reboita, M.; Porfírio da Rocha, R. Assessment of multi-model climate projections of water resources over South America CORDEX domain. Clim. Dyn. 2019, 54, 99–116. [Google Scholar] [CrossRef]
- Menéndez, C.; Zaninelli, P.; Carril, A.; Sánchez, E. Hydrological Cycle, Temperature, and Land Surface−Atmosphere Interaction in the La Plata Basin during Summer: Response to Climate Change. Clim. Res. 2016, 68, 231–241. [Google Scholar] [CrossRef]
- Paik, S.; Min, S.K.; Zhang, X.; Donat, M.G.; King, A.D.; Sun, Q. Determining the anthropogenic greenhouse gas contribution to the observed intensification of extreme precipitation. Geophys. Res. Lett. 2020, 47, e2019GL086875. [Google Scholar] [CrossRef]
- Thaler, V.M. A Multivariate Assessment of Climate Change Projections over South America Using CMIP5. Master’s Thesis, Portland State University, Portland, OR, USA, 17 June 2020. Paper 5550. Available online: https://archives.pdx.edu/ds/psu/33659 (accessed on 18 November 2020).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).