Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index
Abstract
1. Introduction
2. Methodology
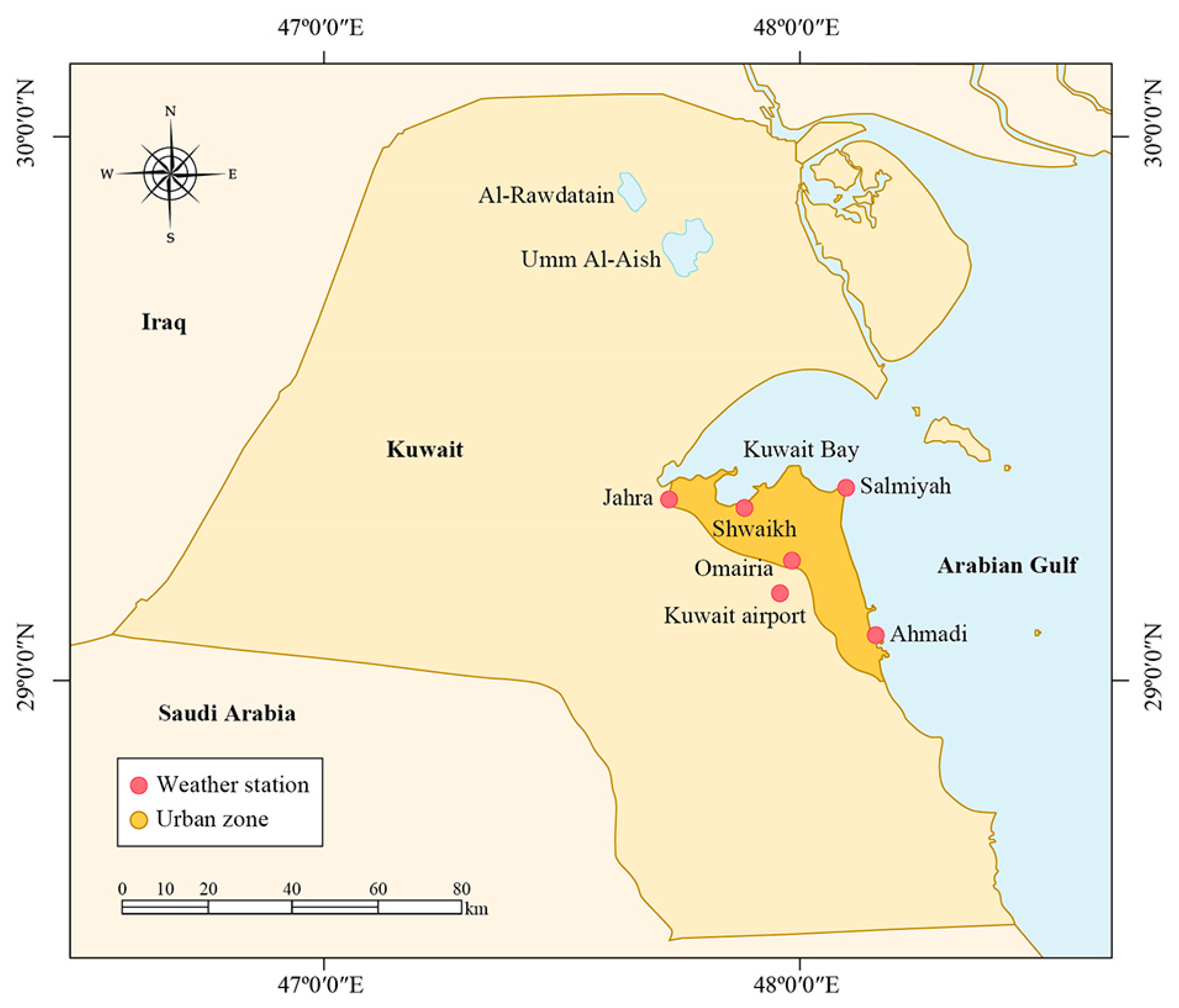
2.1. Study Area
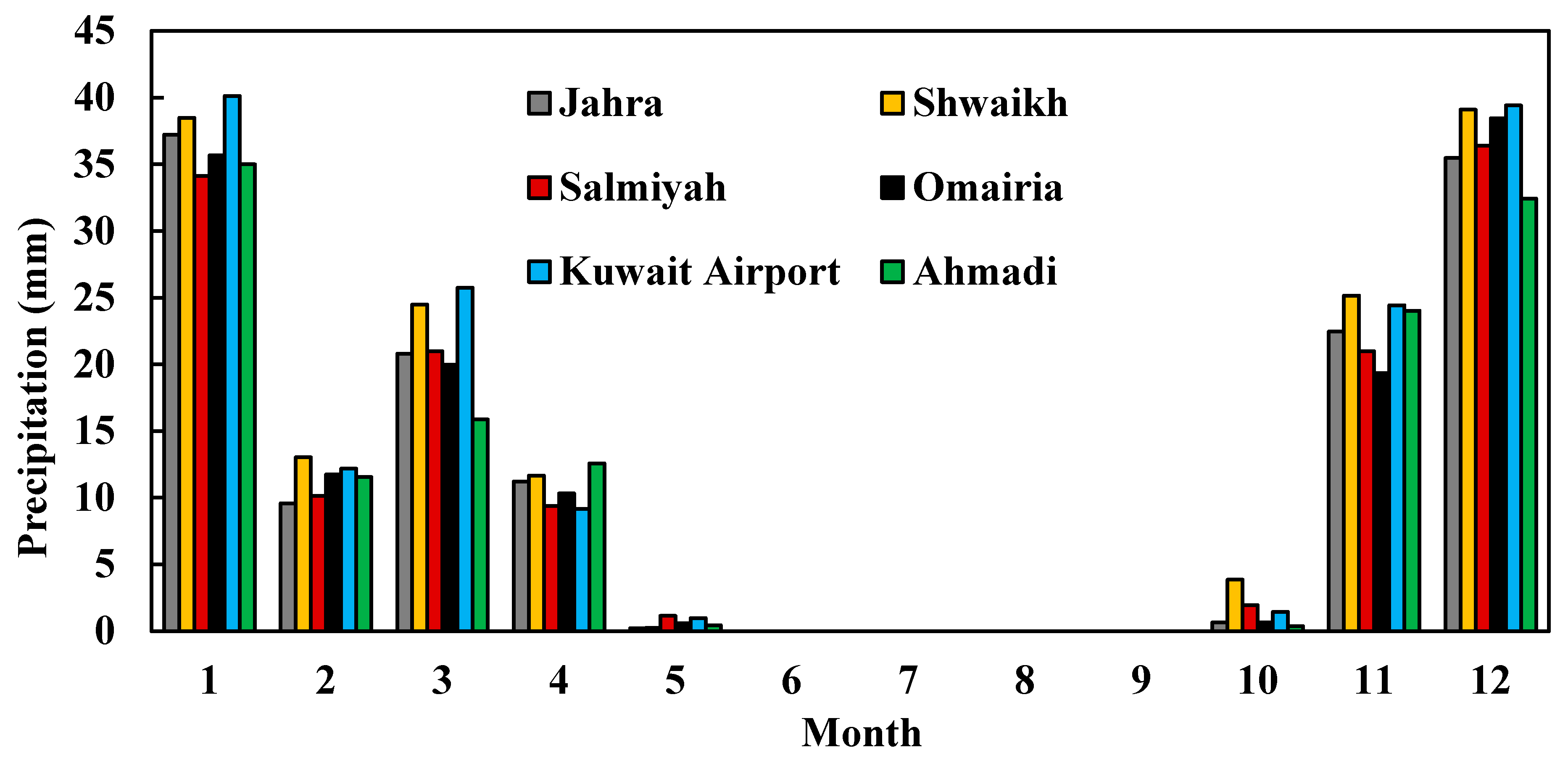
2.1.1. Climatology and Water Supply
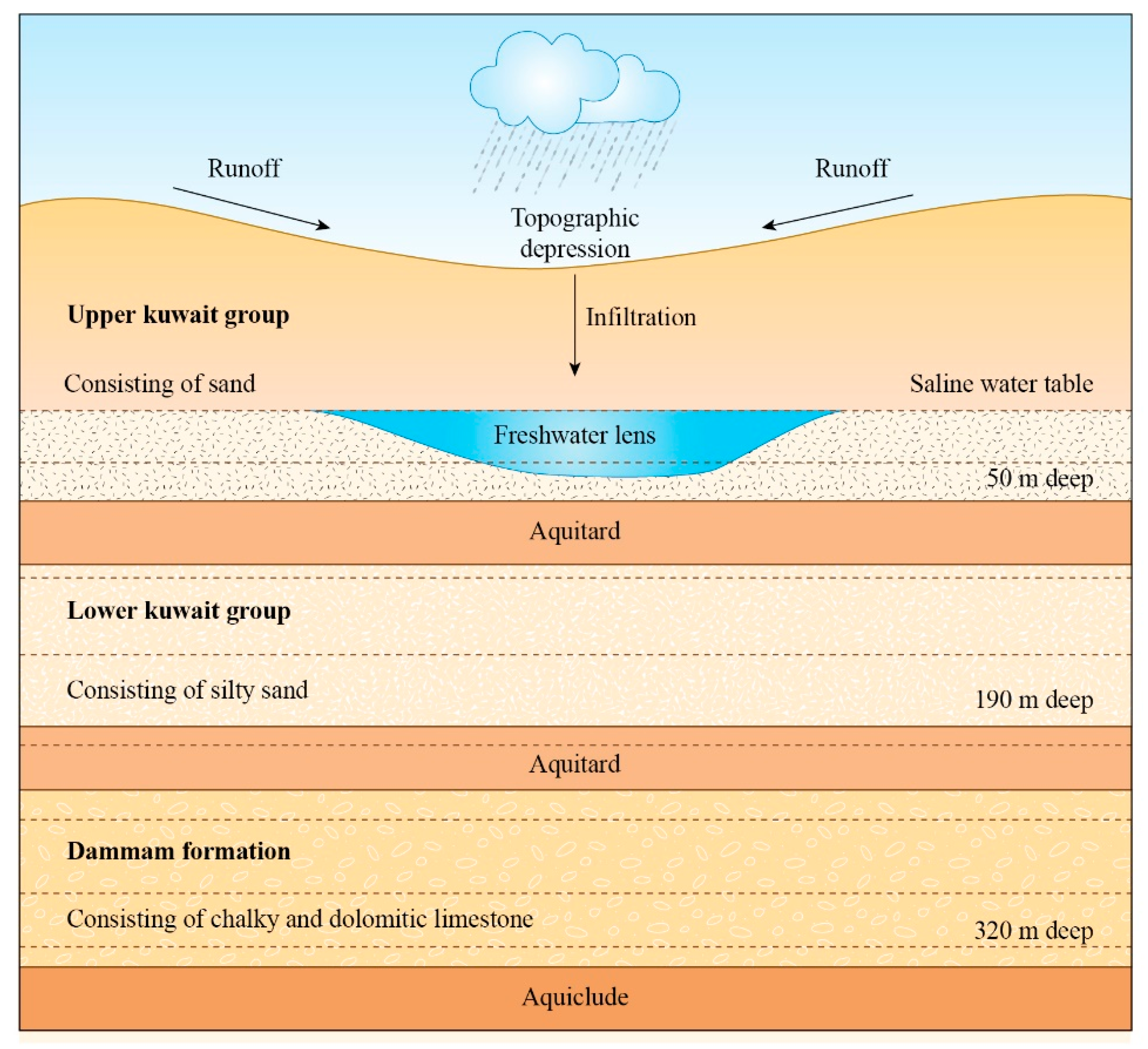
2.1.2. Groundwater Resources
2.1.3. Available Data
2.2. Model Development
3. Results and Discussion
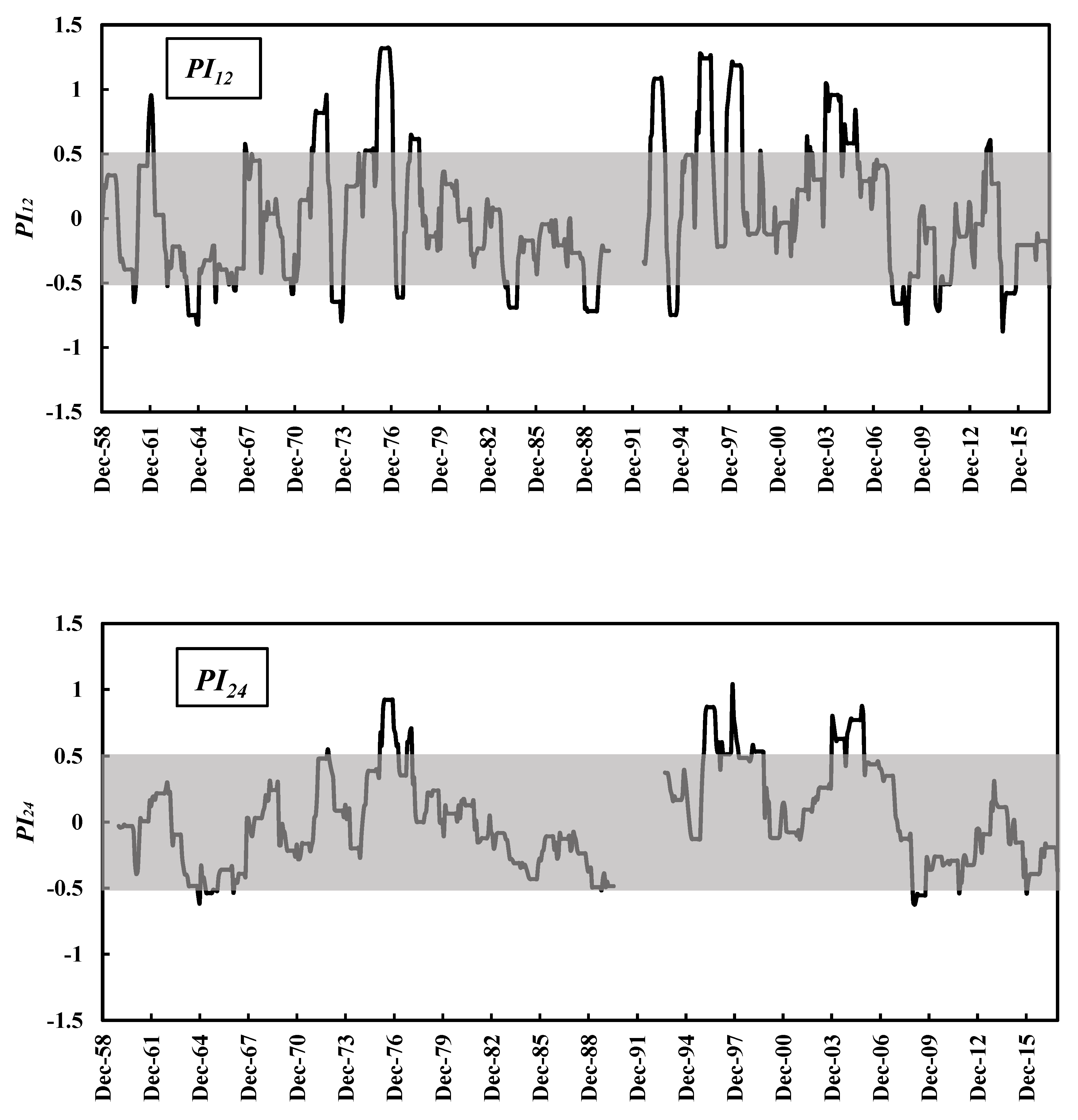
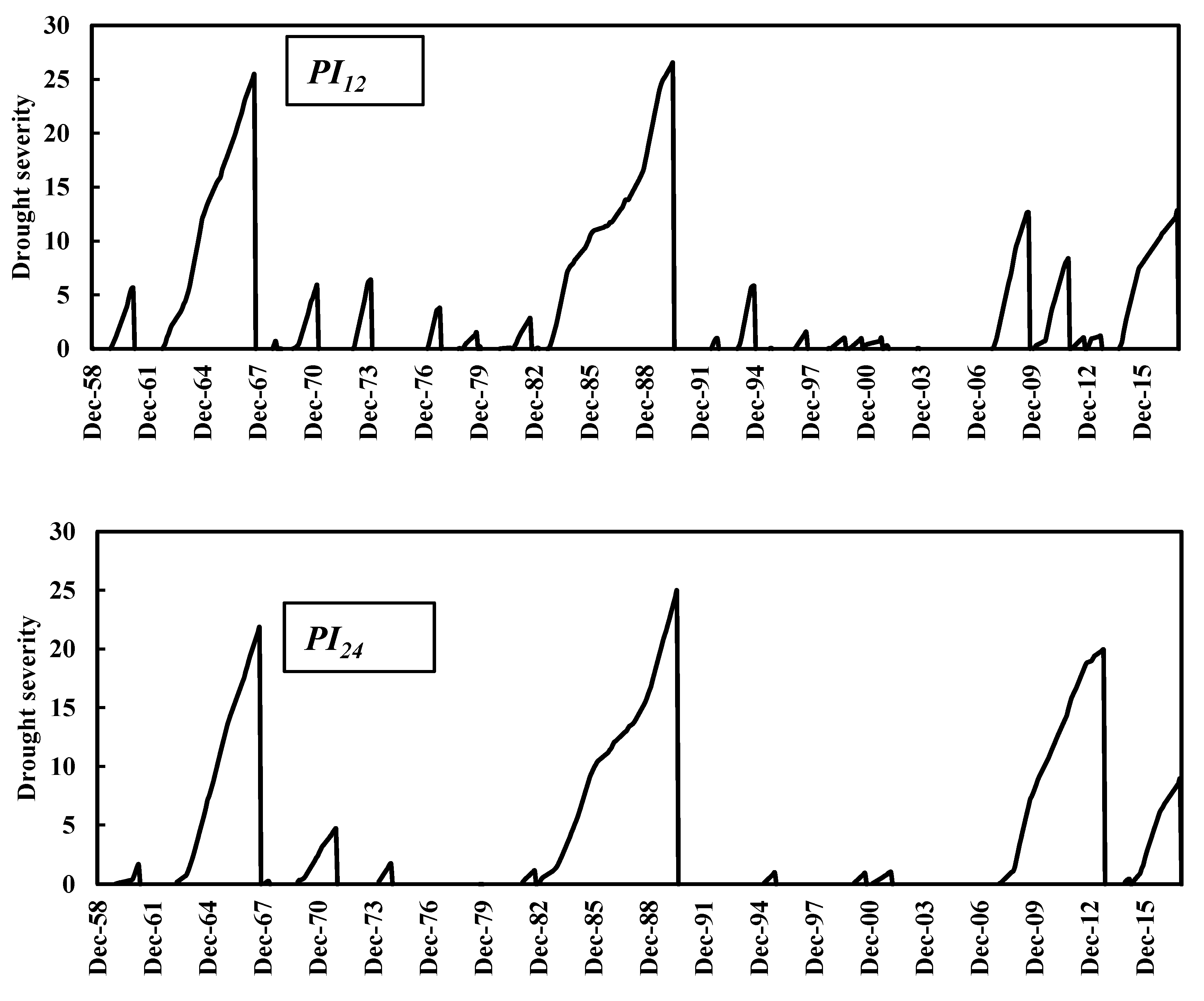
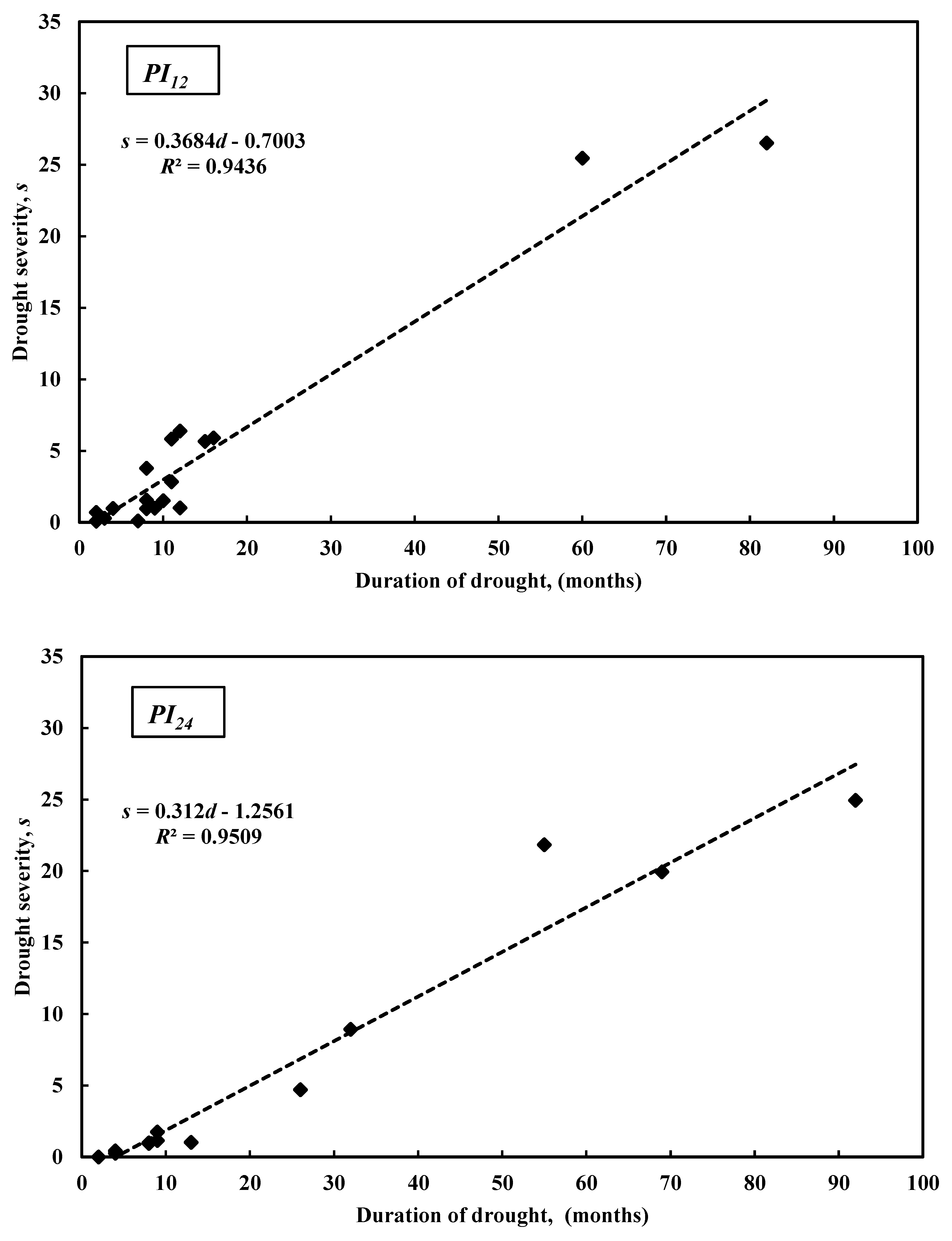
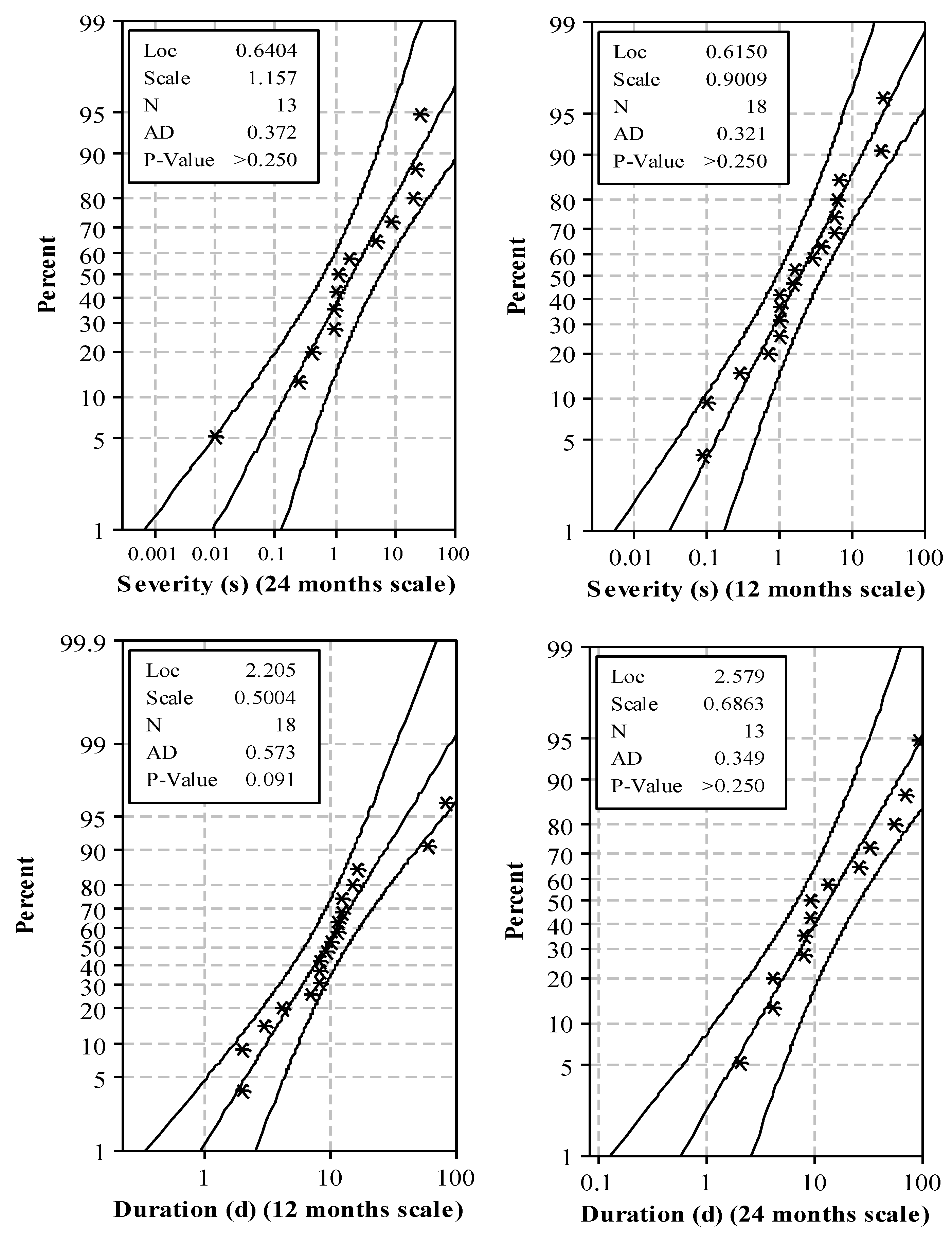
3.1. PI Implementation Results
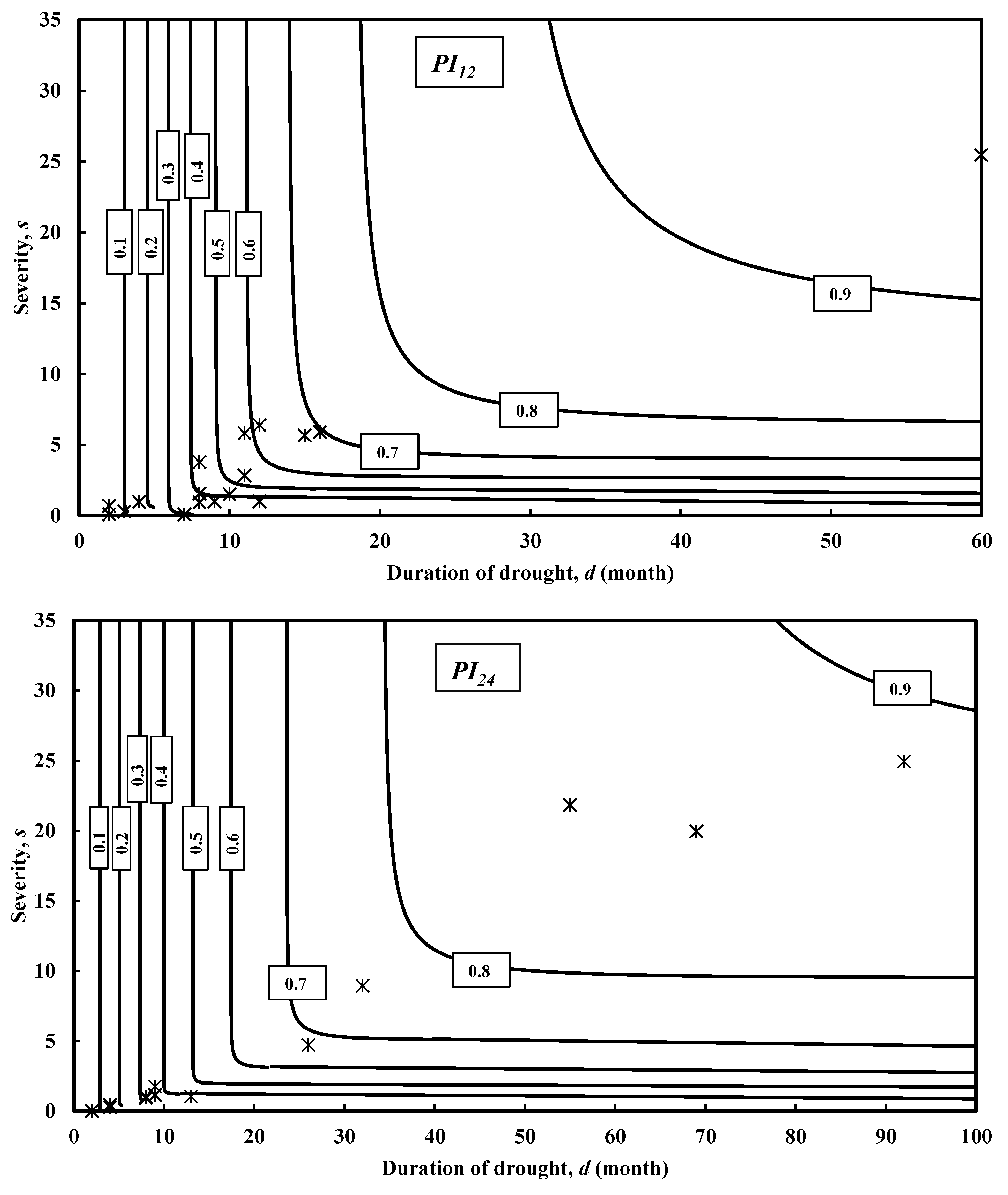
3.2. Suitability of PI as a Meteorological Drought Index for Hydrological Droughts Assessment
3.2.1. Case Study of Groundwater Aquifers in the State of Kuwait
3.2.2. Limitations of PI for Hydrological Droughts Assessment
3.2.3. Non-Normality of Precipitation Time Series in Arid Climates
4. Conclusions
Funding
Conflicts of Interest
References
- Lettenmaier, D.P.; McCabe, G.; Stakhiv, E.Z. Global climate change: Effect on hydrologic cycle. In Water Resources Handbook; McGraw-Hill: New York, NY, USA, 1996; pp. 21–29. [Google Scholar]
- Aswathanarayana, U. Water Resources Management and the Environment; CRC Press: Boca Raton, FL, USA, 2001; ISBN 1439834288. [Google Scholar]
- Riebsame, W.E.; Changnon, S.A., Jr.; Karl, T.R. Drought and Natural Resources Management in the United States: Impacts and Implications of the 1987–89 Drought; Westview Press Inc.: Boulder, CO, USA, 1991; ISBN 081338026X. [Google Scholar]
- Guo, Y.; Huang, S.; Huang, Q.; Wang, H.; Wang, L.; Fang, W. Copulas-based bivariate socioeconomic drought dynamic risk assessment in a changing environment. J. Hydrol. 2019. [Google Scholar] [CrossRef]
- Mosley, L.M. Drought impacts on the water quality of freshwater systems; review and integration. Earth Sci. Rev. 2015, 140, 203–214. [Google Scholar] [CrossRef]
- Mishra, A.K.; Singh, V.P. A review of drought concepts. J. Hydrol. 2010, 391, 202–216. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Tsakiris, G.; Loukas, A.; Pangalou, D.; Vangelis, H.; Tigkas, D.; Rossi, G.; Cancelliere, A. Drought characterization. Drought Management Guidelines Technical Annex. In Options Méditérr; CIHEAM: Zaragoza, Spain, 2007; pp. 85–102. [Google Scholar]
- Lawson, M.P.; Reiss, A.; Phillips, R.; Livingston, K. Nebraska Droughts A Study of Their Past Chronological and Spatial Extent with Implications for the Future. 1971. Available online: https://digitalcommons.unl.edu/geographyfacpub/31/ (accessed on 10 January 2020).
- Karl, T.R.; Quayle, R.G. The 1980 summer heat wave and drought in historical perspective. Mon. Weather Rev. 1981, 109, 2055–2073. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; Reserch Paper No. 45; US Weather Bureau: Silver Spring, MD, USA, 1965.
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drought frequency and duration to time scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, January 1993; Volume 17, pp. 179–183. [Google Scholar]
- Svoboda, M.; Hayes, M.; Wood, D. Standardized Precipitation Index User Guide; World Meteorological Organization: Geneva, Switzerland, 2012. [Google Scholar]
- Thom, H.C.S. A note on the gamma distribution. Mon. Weather Rev. 1958, 86, 117–122. [Google Scholar] [CrossRef]
- Goodarzi, M.; Abedi-Koupai, J.; Heidarpour, M.; Safavi, H.R. Development of a new drought index for groundwater and its application in sustainable groundwater extraction. J. Water Resour. Plan. Manag. 2016, 142, 4016032. [Google Scholar] [CrossRef]
- Bloomfield, J.P.; Marchant, B.P. Analysis of groundwater drought building on the standardised precipitation index approach. Hydrol. Earth Syst. Sci. 2013, 17, 4769–4787. [Google Scholar] [CrossRef]
- Shukla, S.; Wood, A.W. Use of a standardized runoff index for characterizing hydrologic drought. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- López-Moreno, J.I.; Vicente-Serrano, S.M.; Beguería, S.; García-Ruiz, J.M.; Portela, M.M.; Almeida, A.B. Dam effects on droughts magnitude and duration in a transboundary basin: The Lower River Tagus, Spain and Portugal. Water Resour. Res. 2009, 45. [Google Scholar] [CrossRef]
- Sheffield, J.; Goteti, G.; Wen, F.; Wood, E.F. A simulated soil moisture based drought analysis for the United States. J. Geophys. Res. Atmos. 2004, 109. [Google Scholar] [CrossRef]
- Mukhopadhyay, A.; Al-Sulaimi, J.; Barrat, J.M. Numerical Modeling of Ground-Water Resource Management Options in Kuwait. Groundwater 1994, 32, 917–928. [Google Scholar] [CrossRef]
- Kwarteng, A.Y.; Viswanathan, M.N.; Al-Senafy, M.N.; Rashid, T. Formation of fresh ground-water lenses in northern Kuwait. J. Arid Environ. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Almedeij, J. Modeling rainfall variability over urban areas: A case study for Kuwait. Sci. World J. 2012, 2012. [Google Scholar] [CrossRef]
- Sienz, F.; Bothe, O.; Fraedrich, K. Monitoring and quantifying future climate projections of dryness and wetness extremes: SPI bias. Hydrol. Earth Syst. Sci. 2012, 16, 2143–2157. [Google Scholar] [CrossRef]
- Stagge, J.H.; Tallaksen, L.M.; Gudmundsson, L.; Van Loon, A.F.; Stahl, K. Candidate distributions for climatological drought indices (SPI and SPEI). Int. J. Climatol. 2015, 35, 4027–4040. [Google Scholar] [CrossRef]
- Thom, H.C.S. Some Methods of Climatological Analysis; Note 81; WMO Tech: Geneva, Switzerland, 1966. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions: With Formulas, Graphs, and Mathematical Tables; Courier Corporation: North Chelmsford, MA, USA, 1965; Volume 55, ISBN 0486612724. [Google Scholar]
- Chen, L.; Singh, V.P.; Guo, S.; Zhou, J.; Zhang, J. Copula-based method for multisite monthly and daily streamflow simulation. J. Hydrol. 2015, 528, 369–384. [Google Scholar] [CrossRef]
- Chang, J.; Li, Y.; Wang, Y.; Yuan, M. Copula-based drought risk assessment combined with an integrated index in the Wei River Basin, China. J. Hydrol. 2016, 540, 824–834. [Google Scholar] [CrossRef]
- Shiau, J.T. Fitting drought duration and severity with two-dimensional copulas. Water Resour. Manag. 2006, 20, 795–815. [Google Scholar] [CrossRef]
- Shiau, J.; Feng, S.; Nadarajah, S. Assessment of hydrological droughts for the Yellow River, China, using copulas. Hydrol. Process. 2007, 21, 2157–2163. [Google Scholar] [CrossRef]
- Laux, P.; Wagner, S.; Wagner, A.; Jacobeit, J.; Bárdossy, A.; Kunstmann, H. Modelling daily precipitation features in the Volta Basin of West Africa. Int. J. Climatol. 2009, 29, 937–954. [Google Scholar] [CrossRef]
- Shiau, J.-T.; Modarres, R. Copula-based drought severity-duration-frequency analysis in Iran. Meteorol. Appl. 2009, 16, 481–489. [Google Scholar] [CrossRef]
- Li, B.; Rodell, M. Evaluation of a model-based groundwater drought indicator in the conterminous US. J. Hydrol. 2015, 526, 78–88. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; López-Moreno, J.I.; Beguería, S.; Lorenzo-Lacruz, J.; Azorin-Molina, C.; Morán-Tejeda, E. Accurate computation of a streamflow drought index. J. Hydrol. Eng. 2011, 17, 318–332. [Google Scholar] [CrossRef]
- Al-Senafy, M.; Fadlelmawla, A.; Bhandary, H.; Al-Khalid, A.; Rashid, T.; Al-Fahad, K.; Al-Salman, B. Assessment of Usable Groundwater Reserve in Northern Kuwait. Int. J. Sci. Eng. Res. 2013, 4, 2427–2436. [Google Scholar]
- Al-Dousari, A.; Milewski, A.; Din, S.U.; Ahmed, M. Remote sensing inputs to SWAT model for groundwater recharge estimates in Kuwait. Adv. Nat. Appl. Sci. 2010, 4, 71–77. [Google Scholar]
- Al-Otaibi, M.M. Artificial Groundwater Recharge in Kuwait: Planning and Management. 1997. Available online: https://theses.ncl.ac.uk/jspui/handle/10443/3581 (accessed on 10 January 2020).
- Alrashidi, M.S.; Bailey, R.T. Estimating Groundwater Recharge for a Freshwater Lens in an Arid Region: Formative and Stability Assessment. Hydrol. Process. 2019. [Google Scholar] [CrossRef]
- Wu, H.; Svoboda, M.D.; Hayes, M.J.; Wilhite, D.A.; Wen, F. Appropriate application of the standardized precipitation index in arid locations and dry seasons. Int. J. Climatol. 2007, 27, 65–79. [Google Scholar] [CrossRef]

| KIA Station | N (years) | Mean | Standard Deviation | Maximum |
| 55 | 115.7 | 52.2 | 242.4 | |
| Minimum | Q1 | Median | Q3 | |
| 19.9 | 79.4 | 110.5 | 140.5 |
| Station | Period | N (Months) | Mean | Std dev. | Q1 | Median | Q3 | Maximum |
|---|---|---|---|---|---|---|---|---|
| KIA | May 2011- May 2018 | 85 | 7.51 | 13.66 | 0 | 0.45 | 7.46 | 63.21 |
| Saberya | 85 | 7.44 | 12.69 | 0 | 1.89 | 8.25 | 57.12 |
| Class | SPI value | PI value |
|---|---|---|
| Extremely wet | >2.0 | >1.0 |
| Very wet | 1.5 to 2.0 | 0.75 to 1.0 |
| Moderately wet | 1.0 to 1.5 | 0.5 to 0.75 |
| Normal | 1.0 to -1.0 | 0.5 to -0.5 |
| Moderate drought | −1.0 to −1.5 | −0.5 to −0.75 |
| Severe drought | −1.5 to −2.0 | −0.75 to −1.0 |
| Extreme drought | <−2.0 | −1.0 |
| Statistical Measure | 12-Month Scale | 24-Month Scale |
|---|---|---|
| Kendall’s tau (τ) | 0.740 | 0.902 |
| Spearman correlation | 0.886 | 0.974 |
| Pearson correlation | 0.971 | 0.975 |
| θ | 5.692 | 18.408 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alsumaiei, A.A. Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index. Climate 2020, 8, 19. https://doi.org/10.3390/cli8020019
Alsumaiei AA. Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index. Climate. 2020; 8(2):19. https://doi.org/10.3390/cli8020019
Chicago/Turabian StyleAlsumaiei, Abdullah A. 2020. "Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index" Climate 8, no. 2: 19. https://doi.org/10.3390/cli8020019
APA StyleAlsumaiei, A. A. (2020). Monitoring Hydrometeorological Droughts Using a Simplified Precipitation Index. Climate, 8(2), 19. https://doi.org/10.3390/cli8020019





