Projected Changes in the Frequency of Peak Flows along the Athabasca River: Sensitivity of Results to Statistical Methods of Analysis
Abstract
1. Introduction
2. Materials and Methods
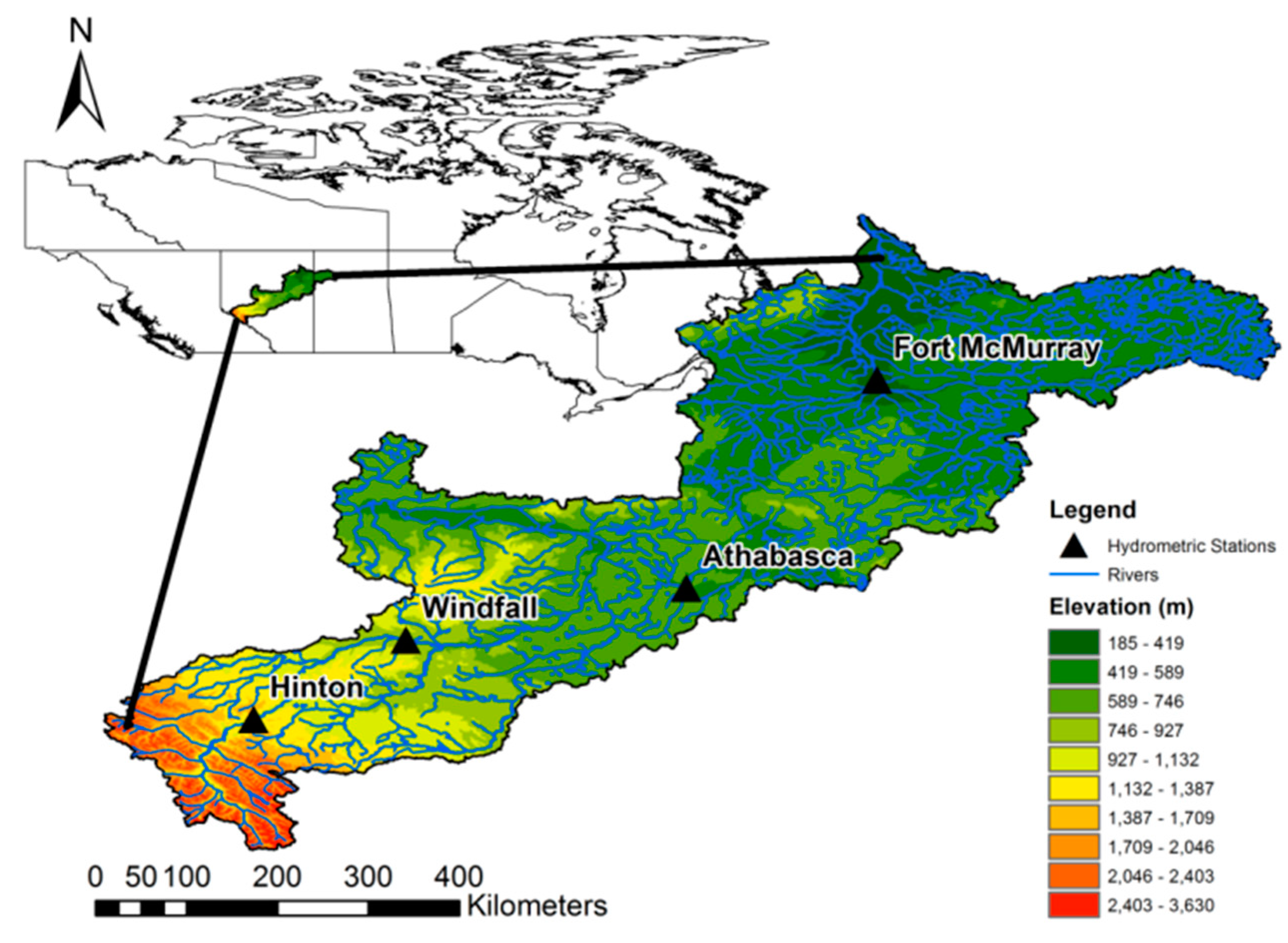
2.1. Study Area
2.2. Climate Scenarios and Hydrologic Projections
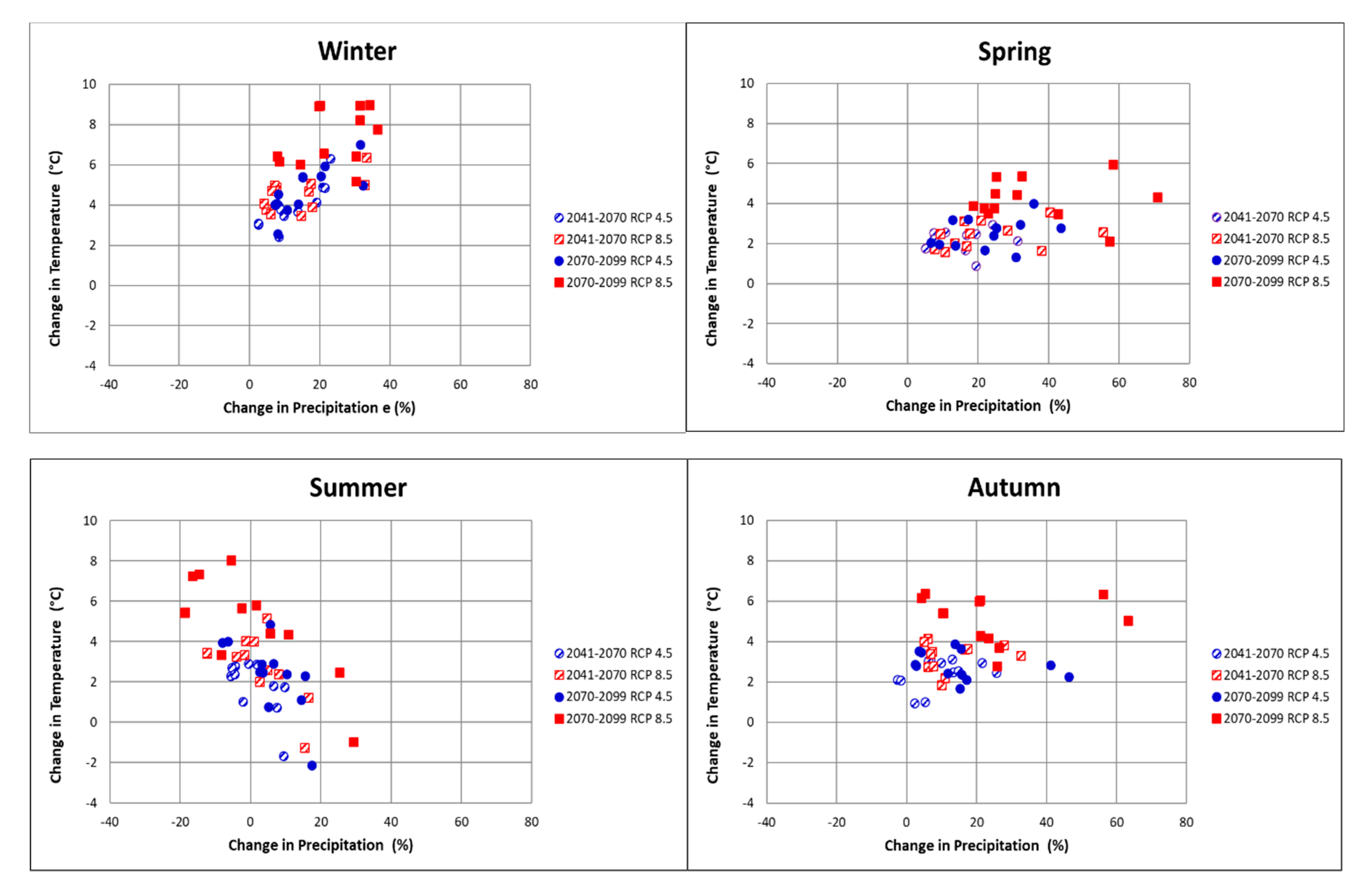
2.2.1. Climate Model Projection
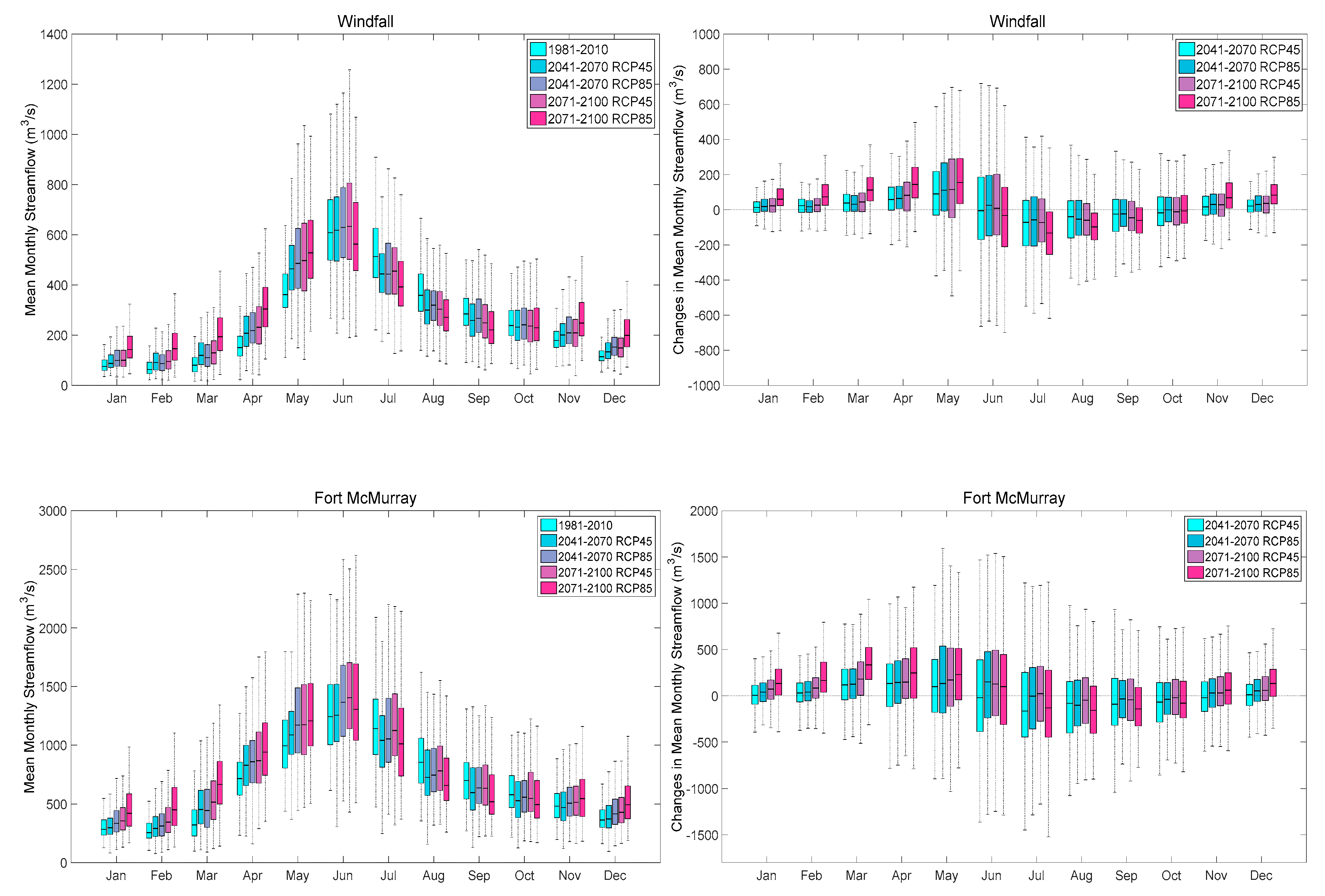
2.2.2. Hydrologic Modelling and River Flow Scenario Simulation
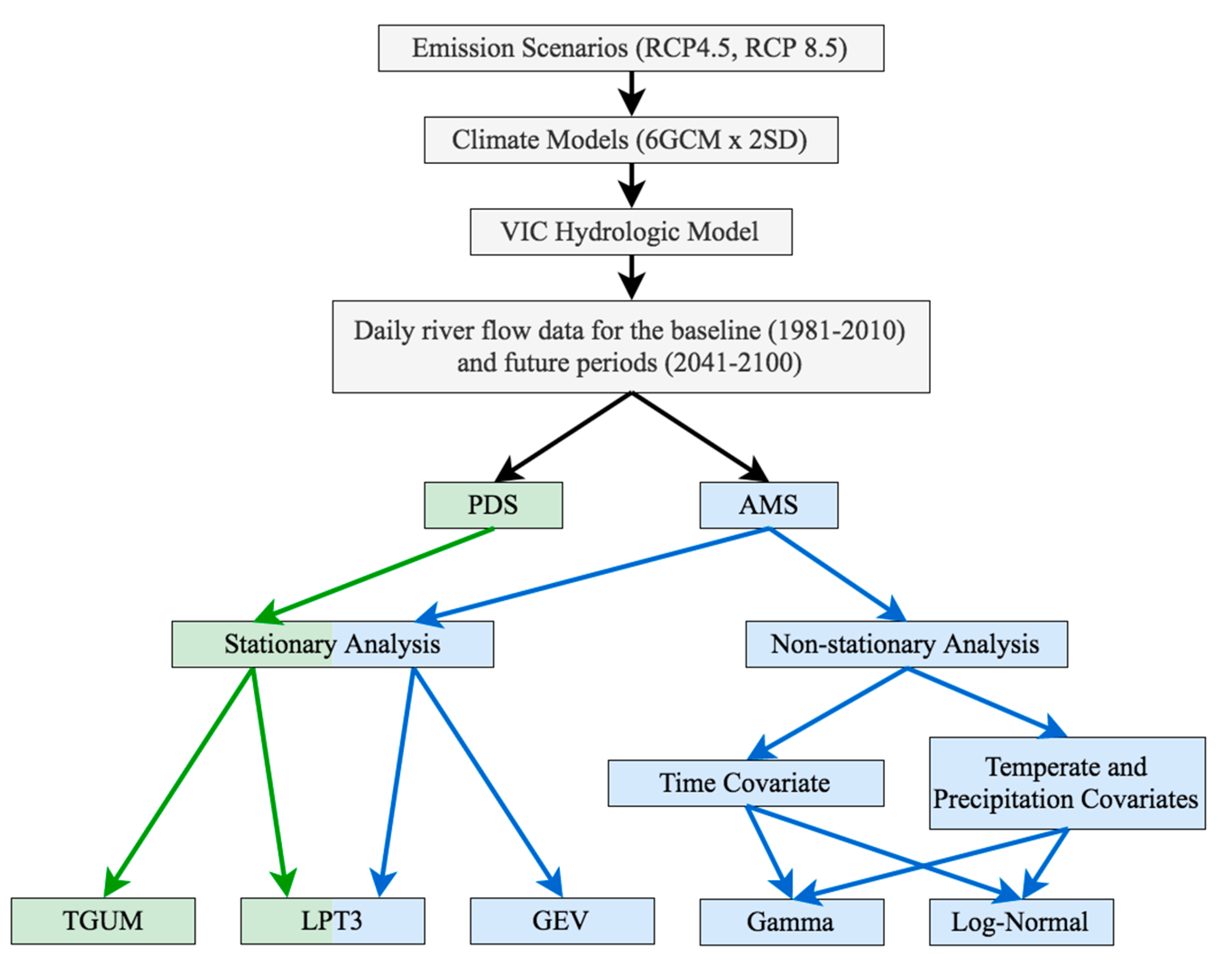
2.3. Methods of Peak Flow Analysis
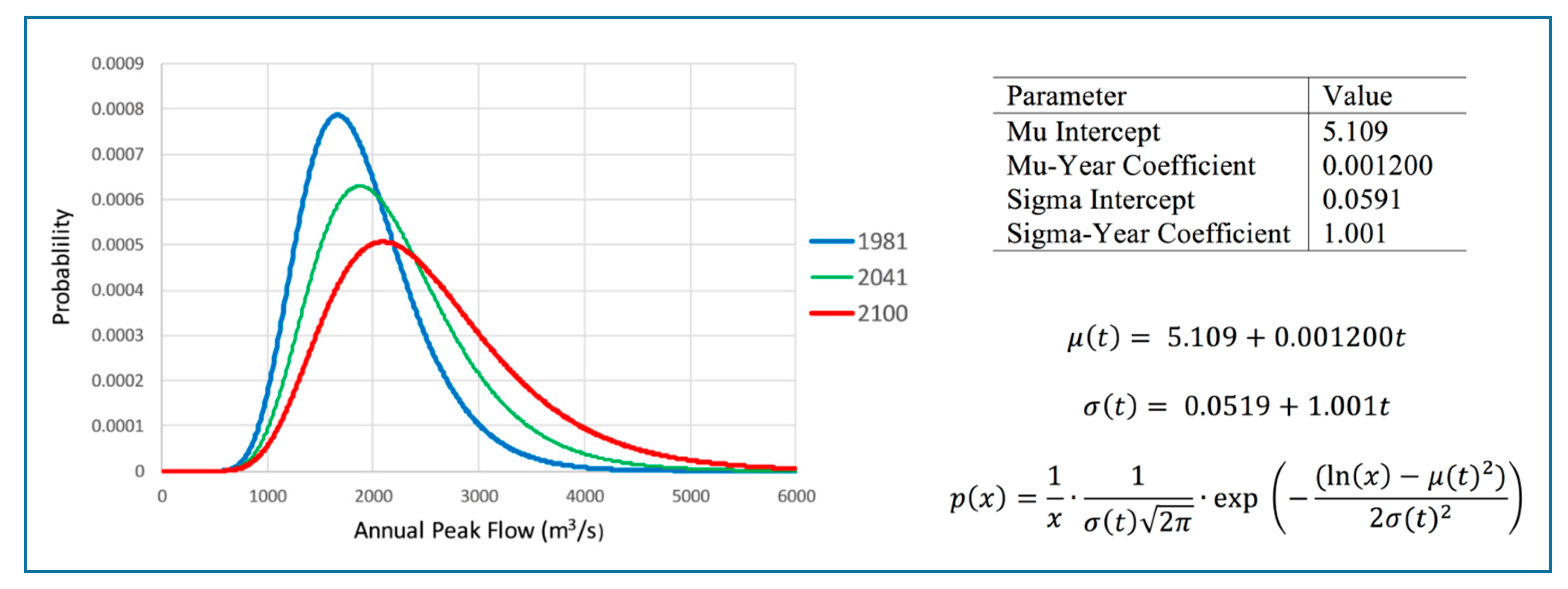
2.3.1. Stationary and Non-Stationary Analysis
2.3.2. Uncertainty in Peak Flow Projections
3. Results
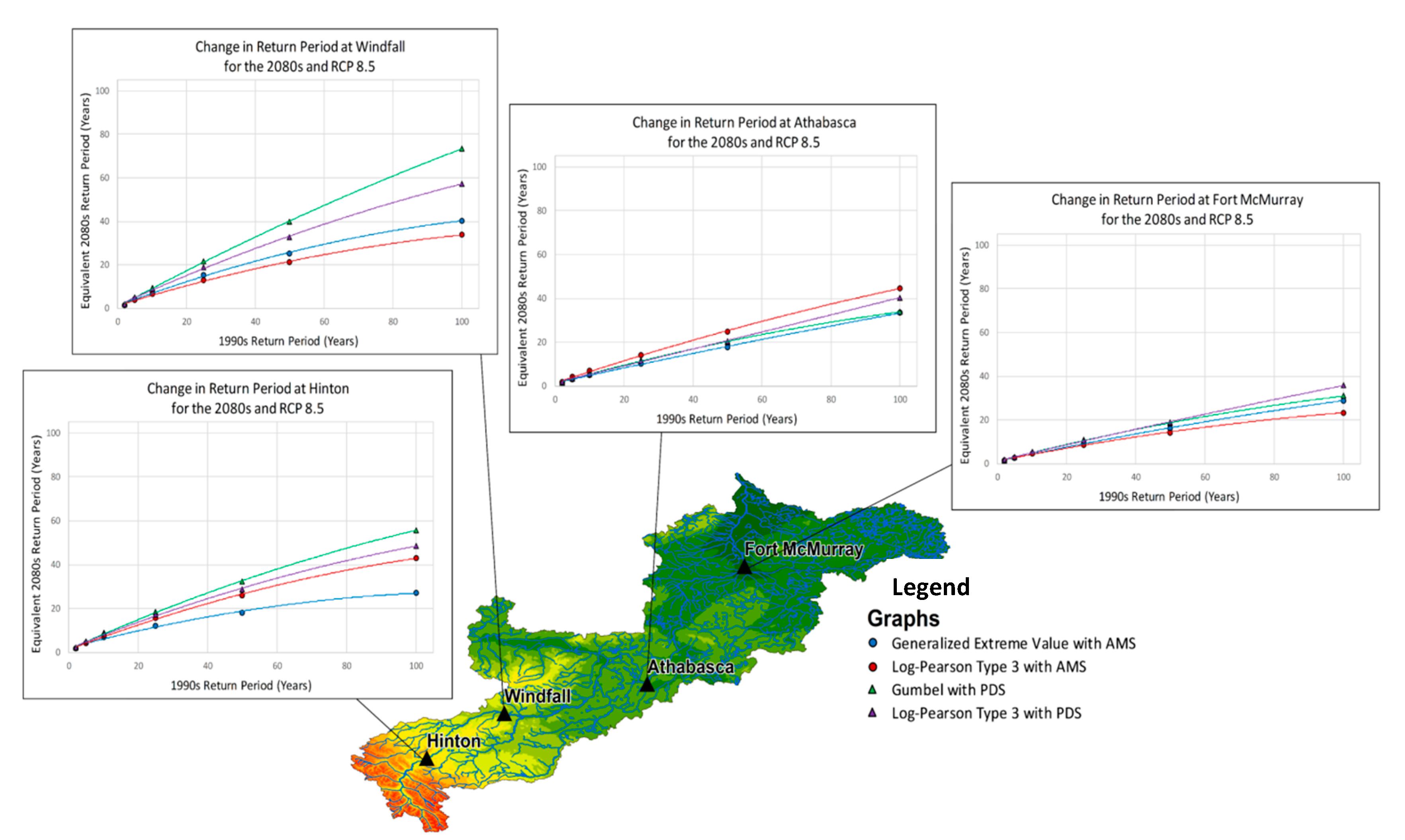
3.1. Stationary Analysis
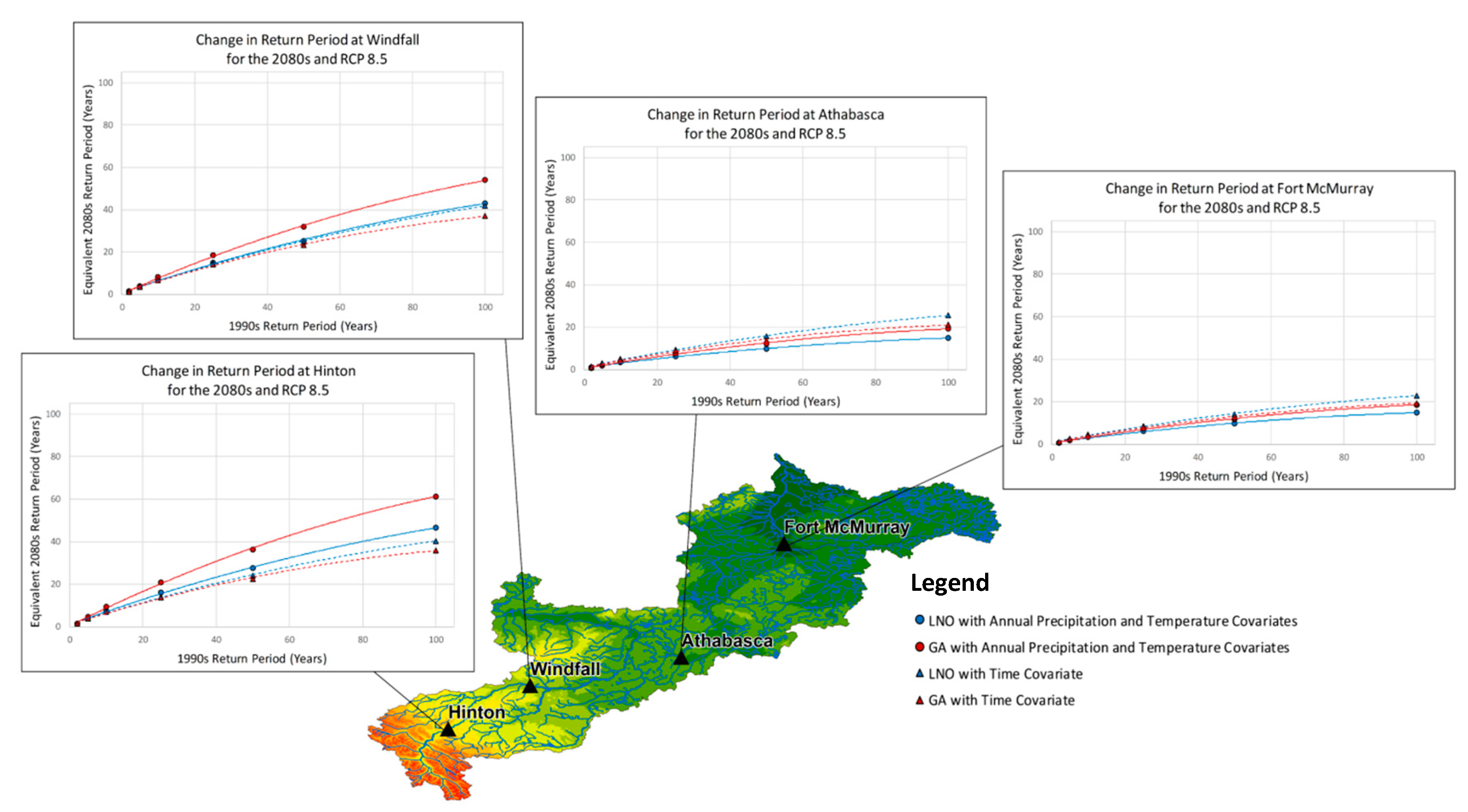
3.2. Non-Stationary Analysis
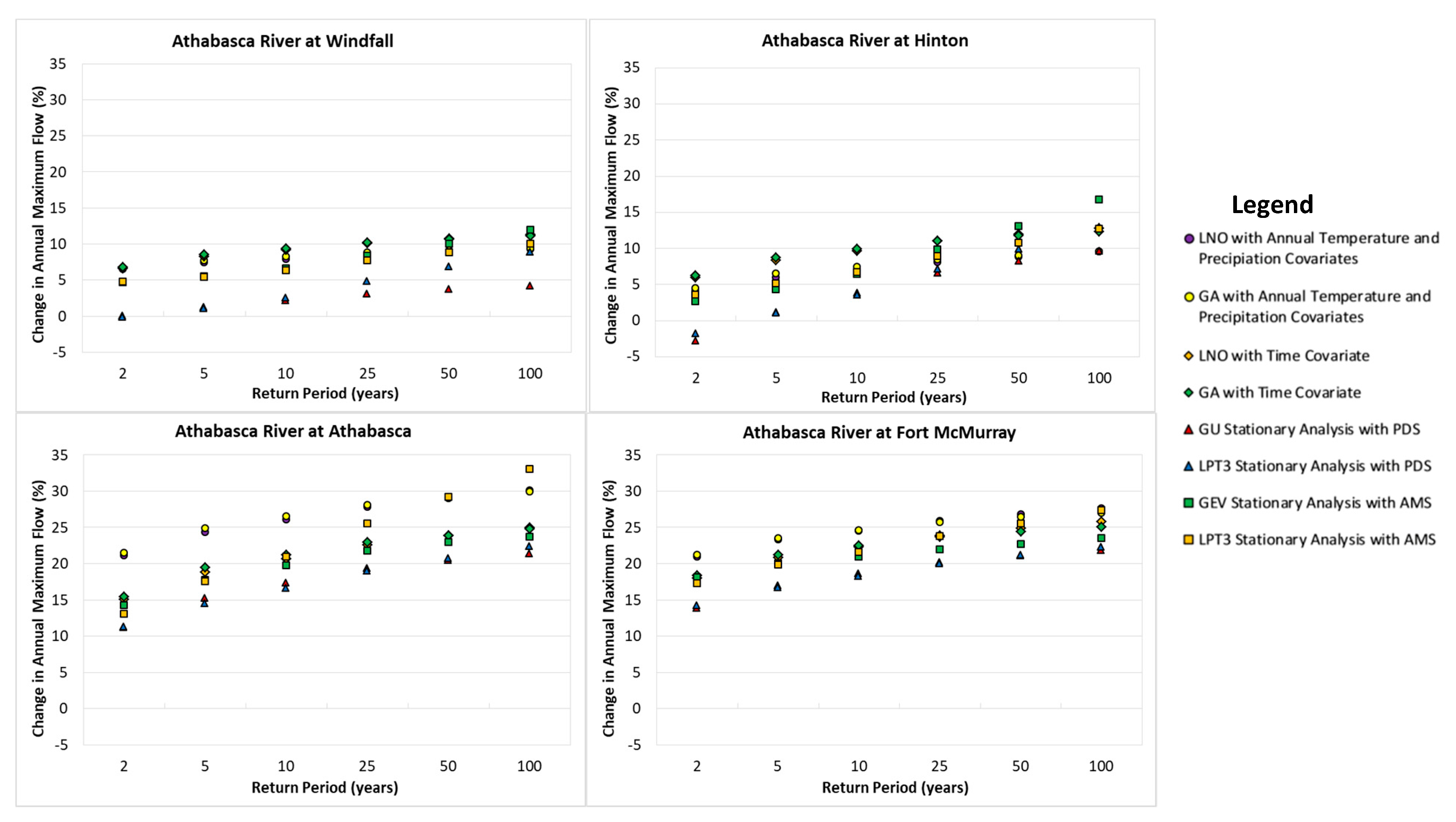
3.3. Changes in Peak Flows
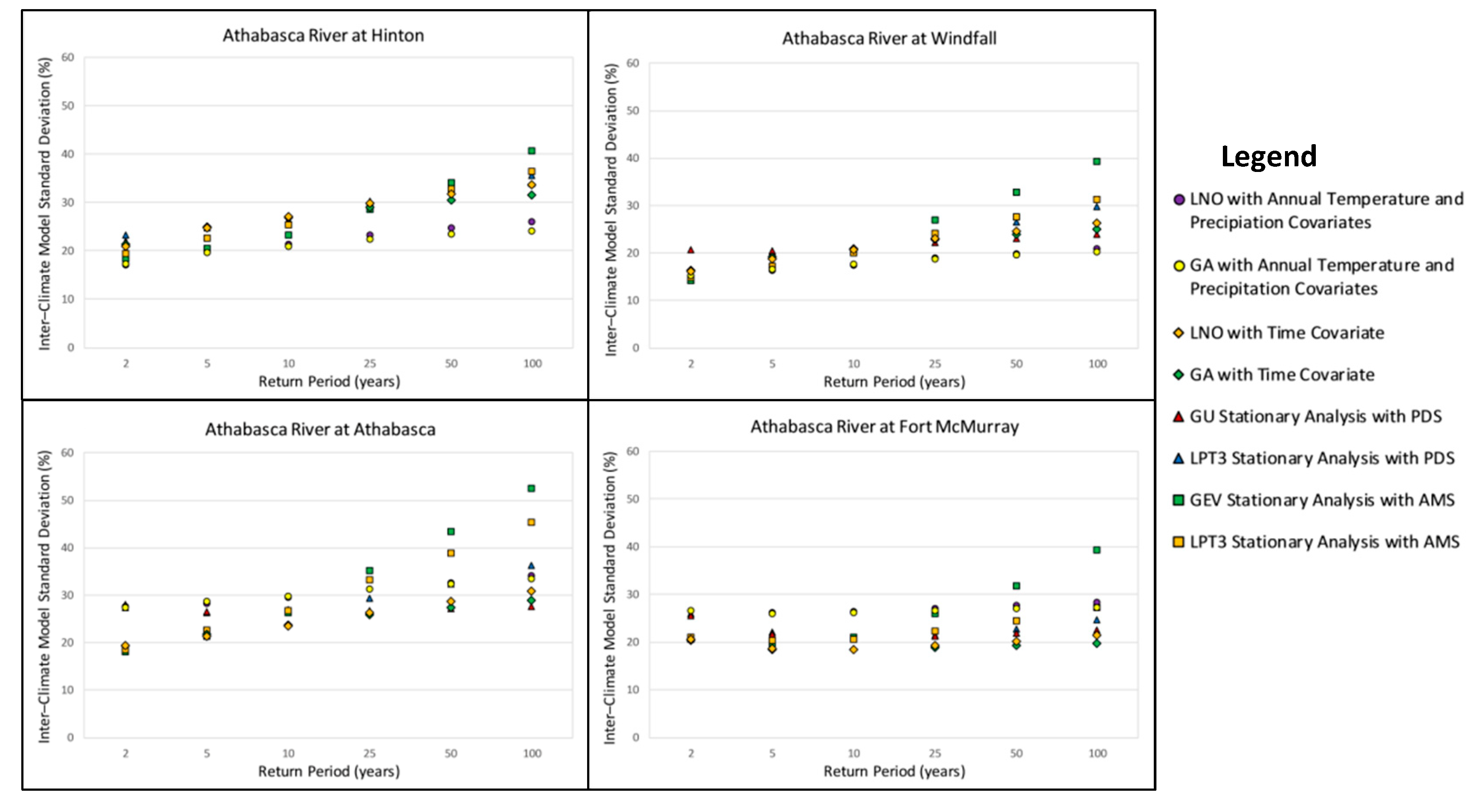
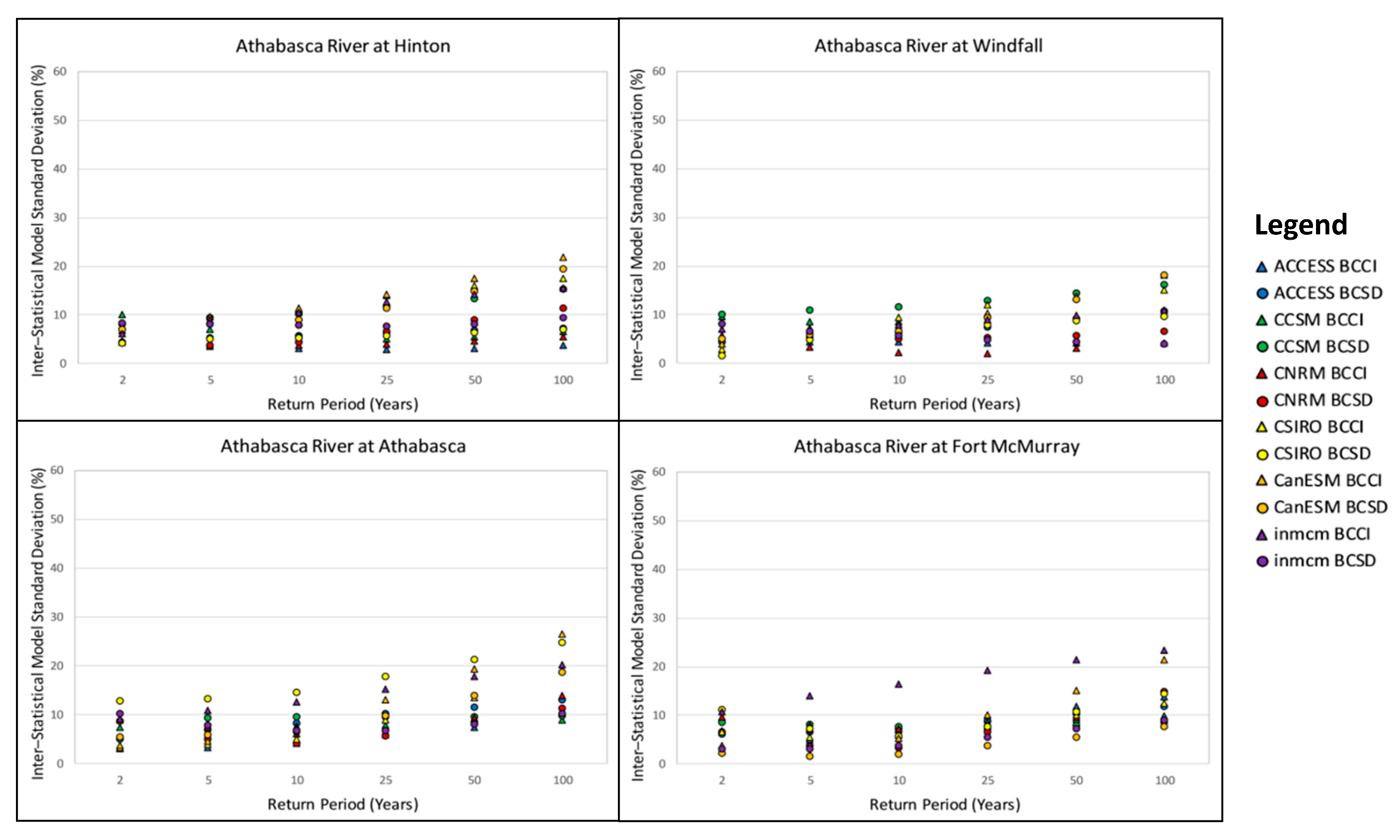
3.4. Inter-Model Variability
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cunderlik, J.M.; Ouarda, T.B.M.J. Trends in the timing and magnitude of floods in Canada. J. Hydrol. 2009, 375, 471–480. [Google Scholar] [CrossRef]
- Park, D.; Markus, M. Analysis of a changing hydrologic flood regime using the Variable Infiltration Capacity model. J. Hydrol. 2014, 515, 267–280. [Google Scholar] [CrossRef]
- Buttle, J.M.; Allen, D.M.; Caissie, D.; Davison, B.; Hayashi, M.; Peters, D.L.; Pomeroy, J.W.; Simonovic, S.; St-Hilaire, A.; Whitfield, P.H. Flood processes in Canada: regional and special aspects. Can. Water Resour. J. 2016, 41, 7–30. [Google Scholar] [CrossRef]
- Beltaos, S.; Prowse, T. River-ice hydrology in a shrinking cryosphere. Hydrol. Process. 2009, 23, 122–144. [Google Scholar] [CrossRef]
- Prowse, T.D.; Beltaos, S. Climatic control of river-ice hydrology: a review. Hydrol. Process. 2002, 16, 805–822. [Google Scholar] [CrossRef]
- Burn, D.H.; Sharif, M.; Zhang, K. Detection of trends in hydrological extremes for Canadian watersheds. Hydrol. Process. 2010, 24, 1781–1790. [Google Scholar] [CrossRef]
- Ganguli, P.; Coulibaly, P. Does nonstationarity in rainfall require nonstationary intensity–duration–frequency curves? Hydrol. Earth Syst. Sci. 2017, 21, 6461–6483. [Google Scholar] [CrossRef]
- Burn, D.H. Climatic influences on streamflow timing in the headwaters of the Mackenzie River Basin. J. Hydrol. 2008, 352, 225–238. [Google Scholar] [CrossRef]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC press: New York, NY, USA, 2000. [Google Scholar]
- Cooley, D. Return periods and return levels under climate change. In Extremes in a Changing Climate; AghaKouchak, A., Easterling, D., Hsu, K., Sorooshian, S., Eds.; Springer: Dordrecht, The Netherlands, 2013; Volume 65, pp. 97–114. [Google Scholar]
- Tramblay, Y.; Neppel, L.; Carreau, J.; Najib, K. Non-stationary frequency analysis of heavy rainfall events in southern France. Hydrol. Sci. J. 2013, 58, 280–294. [Google Scholar] [CrossRef]
- Khaliq, M.N.; Ouarda, T.B.M.J.; Ondo, J.C.; Gachon, P.; Bob´ee, B. Frequency analysis of a sequence of dependent and/or non-stationary hydro-meteorological observations: A review. J. Hydrol. 2006, 329, 534–552. [Google Scholar] [CrossRef]
- Cunderlik, J.M.; Burn, D.H. Non-stationary pooled flood frequency analysis. J. Hydrol. 2003, 276, 210–223. [Google Scholar] [CrossRef]
- Tan, X.; Gan, T.Y. Nonstationary analysis of annual maximum streamflow of Canada. J. Clim. 2015, 28, 1788–1805. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; El-Adlouni, S. Bayesian nonstationary frequency analysis of hydrological variables 1. JAWRA 2011, 47, 496–505. [Google Scholar]
- López, J.; Francés, F. Non-stationary flood frequency analysis in continental Spanish rivers, using climate and reservoir indices as external covariates. Hydrol. Earth Syst. Sci. 2013, 17, 3189–3203. [Google Scholar] [CrossRef]
- Li, J.; Tan, S. Nonstationary flood frequency analysis for annual flood peak series, adopting climate indices and check dam index as covariates. Water Resour. Manag. 2015, 29, 5533–5550. [Google Scholar] [CrossRef]
- Seidou, O.; Ramsay, A.; Nistor, I. Climate change impacts on extreme floods I: combining imperfect deterministic simulations and non-stationary frequency analysis. Nat. Hazards 2012, 61, 647–659. [Google Scholar] [CrossRef]
- Zhang, T.; Wang, Y.; Wang, B.; Tan, S.; Feng, P. Nonstationary flood frequency analysis using univariate and bivariate time-varying models based on GAMLSS. Water 2018, 10, 819. [Google Scholar] [CrossRef]
- Dong, N.D.; Agilan, V.; Jayakumar, K.V. Bivariate Flood Frequency Analysis of Nonstationary Flood Characteristics. J. Hydrol. Eng. 2019, 24, 04019007. [Google Scholar] [CrossRef]
- Shrestha, R.R.; Cannon, A.J.; Schnorbus, M.A.; Zwiers, F.W. Projecting future nonstationary extreme streamflow for the Fraser River, Canada. Clim. Chang. 2017, 145, 289–303. [Google Scholar] [CrossRef]
- Bonsal, B.R.; Cuell, C. Hydro-climatic variability and extremes over the Athabasca River basin: Historical trends and projected future occurrence. Can. Water Resour. J. 2017, 42, 315–335. [Google Scholar] [CrossRef]
- Dibike, Y.; Prowse, T.; Bonsal, B.; O’Neil, H. Implications of future climate on water availability in the western Canadian river basins. Int. J. Clim. 2017, 37, 3247–3263. [Google Scholar] [CrossRef]
- Dibike, Y.; Eum, H.I.; Prowse, T. Modelling the Athabasca watershed snow response to a changing climate. J. Hydrol. Reg. Stud. 2018, 15, 134–148. [Google Scholar] [CrossRef]
- Eum, H.I.; Dibike, Y.; Prowse, T. Climate-induced alteration of hydrologic indicators in the Athabasca River Basin, Alberta, Canada. J. Hydrol. 2017, 544, 327–342. [Google Scholar] [CrossRef]
- Rogers, M.E. Surface Oil Sands Water Management Summary Report; Cumulative Environmental Management Association (CEMA): Fort McMurray, AB, Canada, 2010. [Google Scholar]
- Prowse, T.D.; Beltaos, S.; Gardner, J.T.; Gibson, J.J.; Granger, R.J.; Leconte, R.; Peters, D.L.; Pietroniro, A.; Romolo, L.A.; Toth, B. Climate change, flow regulation and land-use effects on the hydrology of the Peace-Athabasca-Slave system; Findings from the Northern Rivers Ecosystem Initiative. Environ. Monit. Assess. 2006, 113, 167–197. [Google Scholar] [CrossRef] [PubMed]
- Stocker, T.; Qin, D. (Eds.) Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: New York, NY, USA, 2014. [Google Scholar]
- Liang, X. A Two-Layer Variable Infiltration Capacity Land Surface Representation for General Circulation Models. Ph.D. Dissertation, NASA, Washington, DC, USA, 1994. [Google Scholar]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Cannon, A.J. Selecting GCM scenarios that span the range of changes in a multimodel ensemble: application to CMIP5 climate extremes indices. J. Clim. 2015, 28, 1260–1267. [Google Scholar] [CrossRef]
- Murdock, T.Q.; Cannon, A.J.; Sobie, S.R. Statistical Downscaling of Future Climate Projections; Pacific Climate Impacts Consortium (PCIC): Victoria, BC, Canada, 2013. [Google Scholar]
- Maurer, E.P.; Hidalgo, H.G. Utility of daily vs. monthly large-scale climate data: an intercomparison of two statistical downscaling methods. Hydrol. Earth Syst. Sci. 2008, 12, 551–563. [Google Scholar] [CrossRef]
- Hunter, R.D.; Meentemeyer, R.K. Climatologically aided mapping of daily precipitation and temperature. J. Appl. Meteorol. 2005, 44, 1501–1510. [Google Scholar] [CrossRef]
- Voldoire, A.; Sanchez-Gomez, E.; Mélia, D.S.; Decharme, B.; Cassou, C.; Sénési, S.; Valcke, S.; Beau, I.; Alias, A.; Chevallier, M.; et al. The CNRM-CM5.1 global climate model: description and basic evaluation. Clim. Dyn. 2013, 40, 2091–2121. [Google Scholar] [CrossRef]
- Arora, V.K.; Scinocca, J.F.; Boer, G.J.; Christian, J.R.; Denman, K.L.; Flato, G.M.; Kharin, V.V.; Lee, W.S.; Merryfield, W.J. Carbon emission limits required to satisfy future representative concentration pathway of greenhouse gases. Geophys. Res. Lett. 2011, 38, L05805. [Google Scholar] [CrossRef]
- Marsland, S.J.; Bi, D.; Uotila, P.; Fiedler, R.; Griffies, S.M.; Lorbacher, K.; O’Farrell, S.; Sullivan, A.; Uhe, P.; Zhou, X.; et al. Evaluation of ACCESS climate model ocean diagnostics in CMIP5 simulations. Austral. Meteorol. Oceanogr. J. 2013, 63, 101–119. [Google Scholar] [CrossRef]
- Volodin, E.M.; Dianskii, N.A.; Gusev, A.V. Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izv. Atmos. Ocean. Phys. 2010, 46, 414–431. [Google Scholar] [CrossRef]
- Jeffrey, S.J.; Rotstayn, L.D.; Collier, M.A.; Dravitzki, S.M.; Hamalainen, C.; Moeseneder, C.; Wong, K.K.; Syktus, J.I. Australia’s CMIP5 submission using the CSIRO Mk3.6 model. Austral. Meteorol. Oceanogr. J. 2013, 63, 1–13. [Google Scholar] [CrossRef]
- Gent, P.R.; Danabasoglu, G.; Donner, L.J.; Holland, M.M.; Hunke, E.C.; Jayne, S.R.; Lawrence, D.M.; Neale, R.B.; Rasch, P.J.; Vertenstein, M.; et al. The community climate system model version 4. J. Clim. 2011, 24, 4973–4991. [Google Scholar] [CrossRef]
- Werner, A.T.; Schnorbus, M.A.; Shrestha, R.R.; Eckstrand, H.D. Spatial and temporal change in the hydro-climatology of the Canadian portion of the Columbia River basin under multiple emissions scenarios. Atmos. Ocean. 2013, 51, 357–379. [Google Scholar] [CrossRef]
- Elsner, M.M.; Cuo, L.; Voisin, N.; Deems, J.S.; Hamlet, A.F.; Vano, J.A.; Mickelson, K.E.; Lee, S.Y.; Lettenmaier, D.P. Implications of 21st century climate change for the hydrology of Washington State. Clim. Chang. 2010, 102, 225–260. [Google Scholar] [CrossRef]
- Wenger, S.J.; Luce, C.H.; Hamlet, A.F.; Isaak, D.J.; Neville, H.M. Macroscale hydrologic modeling of ecologically relevant flow metrics. Water Resour. Res. 2010, 46, W09513. [Google Scholar] [CrossRef]
- Västilä, K.; Kummu, M.; Sangmanee, C.; Chinvanno, S. Modelling climate change impacts on the flood pulse in the Lower Mekong floodplains. J. Water Clim. Chang. 2010, 1, 67–86. [Google Scholar] [CrossRef]
- Hamlet, A.F.; Lettenmaier, D.P. Effects of 20th century warming and climate variability on flood risk in the western US. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef]
- Eum, H.I.; Dibike, Y.; Prowse, T. Comparative evaluation of the effects of climate and land-cover changes on hydrologic responses of the Muskeg River, Alberta, Canada. J. Hydrol. Reg. Stud. 2016, 8, 198–221. [Google Scholar] [CrossRef]
- Eum, H.I.; Yonas, D.; Prowse, T. Uncertainty in modelling the hydrologic responses of a large watershed: a case study of the Athabasca River Basin, Canada. Hydrol. Process. 2014, 28, 4272–4293. [Google Scholar] [CrossRef]
- Chow, V.T.; Maidment, D.R.; Mays, L.W. Applied Hydrology; Editions McGraw-Hill: New York, NY, USA, 1988; 572p. [Google Scholar]
- Lang, M.; Ouarda, T.B.M.J.; Bobée, B. Towards operational guidelines for over-threshold modeling. J. Hydrol. 1999, 225, 103–117. [Google Scholar] [CrossRef]
- DHI. Extreme Value Analysis (EVA) Technical Reference and Documentation. 2017. Available online: manuals.mikepoweredbydhi.help/2017/General/EVA_SciDoc.pdf (accessed on 12 June 2019).
- Salvadori, G.; De Michele, C. Multivariate extreme value methods. In Extreme in a Changing Climate; Springer: Dordrecht, The Netherlands, 2013; pp. 115–162. [Google Scholar]
- Rigby, R.A.; Stasinopoulos, D.M. Generalized additive models for location, scale and shape. J. R. Stat. Soc. Ser. C (Appl. Stat.) 2005, 54, 507–554. [Google Scholar] [CrossRef]
- Stasinopoulos, M.D.; Rigby, R.A.; Heller, G.Z.; Voudouris, V.; De Bastiani, F. Flexible Regression and Smoothing: Using GAMLSS in R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2017. [Google Scholar]

| GCM Abbreviation | Institution | Resolution (Lon. × Lat.) | Primary Reference |
|---|---|---|---|
| CNRM-CM5.1 | Centre National de Recherches Meteorologiques and Cerfacs | 1.4 × 1.4 | Voldoire et al. [35] |
| CanESM2 | Canadian Centre for Climate Modelling and Analysis | 2.8 × 2.8 | Arora et al. [36] |
| ACCESS1 | Centre for Australian Weather and Climate Research | 1.875 × 1.25 | Marsland et al. [37] |
| INM-CM4 | Institute of Numerical Mathematics | 2.00 × 1.50 | Volodin et al. [38] |
| CSIRO-Mk3.6.0 | Commonwealth Scientific and Industrial Re search Organisation | 1.875 × 1.86 | Jeffrey et al. [39] |
| CCSM4 | National Center for Atmospheric Research (NCAR) | 1.25 × 0.94 | Gent et al. [40] |
| Station | Hinton | Windfall | Athabasca | Ft.McMurray |
|---|---|---|---|---|
| Calibration | 0.90 | 0.81 | 0.78 | 0.79 |
| Validation | 0.78 | 0.80 | 0.75 | 0.74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dibike, Y.; Eum, H.-I.; Coulibaly, P.; Hartmann, J. Projected Changes in the Frequency of Peak Flows along the Athabasca River: Sensitivity of Results to Statistical Methods of Analysis. Climate 2019, 7, 88. https://doi.org/10.3390/cli7070088
Dibike Y, Eum H-I, Coulibaly P, Hartmann J. Projected Changes in the Frequency of Peak Flows along the Athabasca River: Sensitivity of Results to Statistical Methods of Analysis. Climate. 2019; 7(7):88. https://doi.org/10.3390/cli7070088
Chicago/Turabian StyleDibike, Yonas, Hyung-Il Eum, Paulin Coulibaly, and Joshua Hartmann. 2019. "Projected Changes in the Frequency of Peak Flows along the Athabasca River: Sensitivity of Results to Statistical Methods of Analysis" Climate 7, no. 7: 88. https://doi.org/10.3390/cli7070088
APA StyleDibike, Y., Eum, H.-I., Coulibaly, P., & Hartmann, J. (2019). Projected Changes in the Frequency of Peak Flows along the Athabasca River: Sensitivity of Results to Statistical Methods of Analysis. Climate, 7(7), 88. https://doi.org/10.3390/cli7070088







