Application of the GEV Distribution in Flood Frequency Analysis in Romania: An In-Depth Analysis

Abstract

This manuscript investigates the applicability and behavior of the Generalized Extreme Value (GEV) distribution in flood frequency analysis, comparing it with the Pearson III and Wakeby distributions. Traditional approaches often rely on a limited set of statistical distributions and estimation techniques, which may not adequately capture the behavior of extreme events. The study focuses on four hydrometric stations in Romania, analyzing maximum discharges associated with rare and very rare events. The research employs seven parameter estimation methods: the method of ordinary moments (MOM), the maximum likelihood estimation (MLE), the L-moments, the LH-moments, the probability-weighted moments (PWMs), the least squares method (LSM), and the weighted least squares method (WLSM). Results indicate that the GEV distribution, particularly when using L-moments, consistently provides more reliable predictions for extreme events, reducing biases compared to MOM. Compared to the Wakeby distribution for an extreme event (T = 10,000 years), the GEV distribution produced smaller deviations than the Pearson III distribution, namely +7.7% (for the Danube River, Giurgiu station), +4.9% (for the Danube River, Drobeta station), and +35.3% (for the Ialomita River). In the case of the Siret River, the Pearson III distribution generated values closer to those obtained by the Wakeby distribution, being 36.7% lower than those produced by the GEV distribution. These results support the use of L-moments in national hydrological guidelines for critical infrastructure design and highlight the need for further investigation into non-stationary models and regionalization techniques.

1. Introduction

Flood frequency analysis plays a critical role in hydrological design, infrastructure safety, and risk assessment, particularly in the context of increasing hydroclimatic variability [1].

Romania has historically faced significant challenges related to flood events, which have had severe socio-economic and environmental impacts [2,3]. The Danube River, forming the southern border of the country, is prone to extreme flood events due to a combination of upstream contributions from Central Europe and snowmelt-induced high flows during spring. Notable floods occurred in 2006 and 2010, affecting large portions of southern Romania, including urban areas such as Giurgiu and Drobeta-Turnu Severin [4]. The Siret River, one of the largest tributaries of the Danube, is characterized by rapid runoff from the Carpathian region and has generated destructive flash floods, particularly in northeastern Romania (e.g., in 2005 and 2008) [5]. The Ialomita River, although smaller in size, also presents a high flood risk due to its torrential regime and the presence of densely populated and agricultural areas along its lower course. These events underscore the need for robust flood frequency modeling to support infrastructure planning and disaster risk reduction strategies.

In Romania, traditional flood frequency analysis methods—typically based on the Pearson III distribution and the method of moments—employ a limited range of statistical tools which may not adequately represent the behavior of extreme hydrological events [6]. This limitation highlights the need for a more detailed assessment of the applicability and performance of the GEV distribution.

The GEV distribution is widely used to analyze and model extremes in datasets from various fields [7,8,9]. Its flexibility and adaptability make it a valuable resource in hydrology, climate science, and other fields dealing with extreme value analysis.

In hydrology, the GEV distribution is used in frequency analysis to forecast the probability and magnitude of extreme hydrological events, providing vital information for hydrological infrastructure design, water resource management, and flood risk assessment [10,11]. Frequency analysis represents a direct method for determining this information, relying exclusively on the use of statistical distributions, particularly the statistical indicators of the analyzed data [6].

Characterized by three parameters (shape, scale, and location), the GEV distribution is flexible and capable of modeling different hydrological data sets with varied statistical characteristics, being a heavy-tailed distribution with no upper bound.

Alongside the Pearson III, Log-Pearson, Generalized Pareto, Weibull, and Generalized Logistic distributions, the GEV distribution is one of the most widely used three-parameter statistical distributions in frequency analyses of extreme events (maximum and minimum) in hydrological and meteorological processes. It is used to evaluate the probability of occurrence of extraordinary events of varying magnitudes (at site and regional levels), such as maximum discharges [7,8,9,10,11], maximum precipitation [12,13,14,15], the design of Intensity–Duration–Frequency (IDF) curves [16,17,18,19], and the analysis of extreme temperatures [20,21,22].

Regarding parameter estimation methods, the GEV distribution has been used in frequency analyses primarily with the method of ordinary moments (MOM) [23,24,25,26,27], the method of linear moments (L-moments) [24,26,28,29], the method of maximum likelihood (ML) [26,30,31], the method of least squares (MLS) [26,32], the probability weighted moments method [26,33,34], and the Bayesian method [35,36,37]. Of all these estimation methods, the most common are the MOM and L-moments methods, commonly used both for in situ analyses, but especially in analyses regarding the regionalization of extreme events. These methods facilitate the derivation of statistical indicators, such as mean, coefficient of variation, skewness (in the case of MOM), or L-skewness and L-kutozis (in the case of L-moments), which are essential for the regionalization of extreme hydrological events.

In the case of the L-moments method, it is currently one of the most popular and widely used methods in regional frequency analyses of extreme events [26,38,39,40,41]. The widespread applicability of this method is due to its advantages and superiority over other methods, the most important of which include the following: (1) parameter estimation based on statistical indicators that can be determined both in situ and regionally; (2) the stability and robustness of this method to the influence of variability in the lengths of available observed data, as well as the presence of outliers [26,38,39]; (3) the existence of rigorous numerical and graphical criteria for selecting the best distribution [26,40,41]; (4) the availability of an accessible approach for constructing the confidence interval [24,26,38,39,42].

Of course, there are other methods, such as the MOM or Bayesian approaches, but these present certain difficulties in application. The Bayesian method is less used due to its higher mathematical and computational complexity, requiring specialized programming/software. It also introduces additional uncertainties in the choice of the prior distribution of parameter variability, requiring additional data such as precipitation, temperature, etc.

Regarding the MOM, its applicability in the regionalization of extreme events is increasingly limited (especially in Eastern Europe) due to the disadvantages related to the corrections required for higher-order statistical indicators (skewness and kurtosis), which lead to significant uncertainties and errors [6,24,43].

In general, the results of extreme event frequency analysis are characterized by two important categories of uncertainty, namely, the uncertainty in selecting the best distribution and the uncertainty in choosing the most suitable parameter estimation method.

The interpretation of results involves two components: the objective component and the subjective component. These two modes of interpreting results are heavily influenced by the parameter estimation method used for the analyzed distributions, the existence or absence of rigorous criteria for selecting the best model, and the availability of data lengths. For example, in cases with short data lengths and applications requiring the forecasting of values beyond the range of recorded probabilities (such as flood frequency analysis or maximum precipitation analysis), most estimation methods (like maximum likelihood, least squares, Bayesian methods, and mixed moments methods) render statistical tests and performance criteria less relevant. In such situations, the dominant selection criteria are subjective, such as graphical model selection based on the researcher’s experience and available historical information, which can lead to unreliable parameter estimates and misleading conclusions.

Regarding the uncertainties, the analysis presents the uncertainties in selecting the best model and the uncertainties regarding the behavior of the GEV distribution as a “parent” distribution. In many cases the “parent” distributions have already been established. The rigor in choosing these “parent” models is indeed an important issue but will not be explored in depth in the present manuscript. For example, in the U.S., the parent distribution is the Log-Pearson distribution, both for maximum flows and for maximum precipitation [8,9,38,39]. In Canada, the parent distribution for maximum flows is the two-parameter log-normal distribution [9], while for maximum precipitation the reference distribution is the Gumbel distribution [9]. In Finland and Spain, the recommended distribution is the Gumbel distribution [8]. The generalized Pareto distribution is recommended in Belgium [8]. In the U.K., the parent distribution is the three-parameter Log-Logistic distribution (generalized Logistic) [8]. In Italy, the recommended distribution is the Two-Component Extreme Values (TCEVs) distribution [8,44]. Regarding the GEV distribution, it is the parent distribution in Austria, and is recommended in Germany, Italy, Spain, and Slovakia [8].

In Romania, the Pearson Type III distribution is commonly adopted as the parent distribution for modeling hydrological extremes [24,45,46,47]. However, this choice is often not supported by rigorous and comprehensive statistical validation. In many cases, it is applied using the method of ordinary moments, with skewness values imposed based on assumptions regarding the genesis of maximum flows. Subsequently, quantiles for various annual exceedance probabilities are estimated through standard tables and linear interpolation. Such practices may introduce notable uncertainties in the estimation process.

Another important aspect is the examination of the GEV distribution’s behavior with respect to the variability in the lengths of available data. This includes highlighting theoretical biases for representative samples typically encountered in such analyses. The biases are identified for statistical indicators, estimated parameters, and predicted quantile values, under the assumption that the analyzed samples come from a GEV population. These theoretical biases of the distribution are highlighted for the following: (1) the entire range of definition of statistical indicators; (2) the full range of annual exceedance probabilities, particularly in the domain of rare and very rare events (low and very low annual exceedance probabilities, events considered “impossible” in terms of occurrence).

Such theoretical analyses regarding the influence of data lengths were made by Hosking [40] for the GEV distribution, who highlighted the theoretical biases of the distribution over a relatively narrow range of the theoretical values matrix (coefficient of L-variation–L-skewness), using the L-moments method; Singh [48], who identified biases in the two-parameter Log-Logistic distribution using MOM and L-moments for various data lengths; Jokiel Rokita et al. [49], who identified biases in the three-parameter Weibull distribution for the maximum likelihood method and other methods; Anghel [24], who highlighted the theoretical biases of the Gumbel distribution. In [10], Mertins and Stedinger analyzed the biases of the Gumbel distribution for restricted ranges of the shape parameter (between −0.25 and 0.30) and not for specific theoretical values of the higher statistical indicators specific to the L-moments method. In other materials, only the biases reported exclusively for the analyzed data (at-site wind analysis) were highlighted [50].

Thus, the manuscript aims to improve and expand Hosking’s analysis [40] by highlighting these theoretical biases across the entire range of definition for the two statistical indicators related to the L-moments method. Additionally, it seeks to introduce a new element by identifying theoretical biases for the method of ordinary moments over a broader range of statistical indicators (coefficient of variation and skewness), so that these reflect the most common cases encountered in the field of flood frequency analysis.

Since the L-moment method is recognized as the most robust and stable method for parameter estimation, it requires the use of a distribution with at least four parameters to correctly calibrate all four linear moments specific to this method. Thus, the Wakeby distribution was chosen as the reference distribution as it is one of the most stable and robust distributions with a large number of parameters [18,24,26,40,41].

As novel elements of the manuscript, we highlight the most important ones:

−

The particularization and highlighting of the behavior of the probability density function (PDF), cumulative distribution function (CDF), and quantile function (x(p)), with a statistical and hydrological approach from Romania (as well as other regions in southeastern Europe, and some regions in China), regarding the choice of data skewness in the genesis function of maximum flows [51,52], as well as the representation of these curves based on theoretically relevant values of these statistical indicators.

−

The presentation of new improved approximate relationships for estimating the parameters of the GEV distribution using MOM, L-moments, and LH-moments.

−

The presentation of variation curves for the shape parameter as a function of skewness and L-skewness, providing important information for selecting initial values for accurately determining the parameters that require solving a system of three nonlinear equations.

−

The presentation of exact and approximate relationships for the frequency factors in the inverse function component, an approach that eliminates the need to solve nonlinear equations, within acceptable relative error limits.

−

The presentation of the influence of available data lengths on the behavior of the GEV distribution, highlighting theoretical biases across the entire matrix defining higher-order statistical indicators. This matrix theoretically covers any statistical and hydrological situation in FFA, thus providing essential information for considering the uncertainties associated with forecasted values. Representative samples from a statistical and hydrological perspective are selected (n = 20, 35, 55, 90).

−

A detailed analysis regarding the determination of the empirical probability of historical data in the case of the PWMs method and LSM. A significant number of empirical probabilities are comparatively analyzed, highlighting the behavior of the GEV quantile tail in relation to these choices, which generally represent a “subjective choice” into statistical analysis.

This is the first time such a holistic analysis regarding the methods for estimating the parameters of the GEV distribution and the applicability of this distribution is being carried out in Romania, especially considering the specific characteristics of maximum discharge frequency analysis in Romania (i.e., determining skewness based on the genesis of maximum discharges).

Since the most effective way to illustrate the behavior of a statistical distribution is through cases where the estimation of values for extremely rare events is necessary, the behavior of the GEV distribution is demonstrated using four case studies with varied morphometric, hydrological, and statistical characteristics, such as the number of years of analysis, the catchment area, the average altitude, the variability of peak flows, etc. These studies conduct an at-site flood frequency analysis, predicting values for extreme events considered “impossible” [53] in terms of occurrence probability (T = 10,000 years), but which are crucial for designing Class 1 critical structures like dams [54].

2. Methods

2.1. Probability Density Function, Cumulative Distribution Function, and Quantile Function

2.1.1. GEV Distribution

If a random variable X follows a GEV distribution, the probability density function $f(x)$ with parameters, $\alpha \in ℝ$, $\beta >0$, and $\gamma \in ℝ$ is defined by the following:

$$f\left(x|\alpha ,\beta ,\gamma \right)={\left(1-{\displaystyle \frac{\alpha }{\beta }}\cdot \left(x-\gamma \right)\right)}^{{\displaystyle \frac{1}{\alpha }}-1}\cdot {\displaystyle \frac{1}{\beta }}\cdot \exp \left(-{\left(1-{\displaystyle \frac{\alpha }{\beta }}\cdot \left(x-\gamma \right)\right)}^{{\displaystyle \frac{1}{\alpha }}}\right)$$

(1)

where $x<\left(\gamma +{\displaystyle \frac{\beta }{\alpha }}\right)$ for $\alpha >0$, or $x>\left(\gamma +{\displaystyle \frac{\beta }{\alpha }}\right)$ for $\alpha <0$.

The complementary cumulative distribution function, $F\left(x\right)$, is as follows:

$$F\left(x|\alpha ,\beta ,\gamma \right)=1-\exp \left(-{\left(1-{\displaystyle \frac{\alpha }{\beta }}\cdot \left(x-\gamma \right)\right)}^{{\displaystyle \frac{1}{\alpha }}}\right)$$

(2)

And the Quantile function is as follows:

$$x\left(p|\alpha ,\beta ,\gamma \right)=\gamma +{\displaystyle \frac{\beta }{\alpha }}\cdot \left(1-{\left(-\ln \left(1-p\right)\right)}^{\alpha }\right)$$

(3)

Figure 1 demonstrates the flexibility of the distribution for MOM and L-moments by showing the different shapes the GEV distribution can assume for various values of the coefficient of variation and skewness. For simplicity, the arithmetic mean, which acts as the scaling factor, has been fixed at 1.

In Figure 1c,d, both the cumulative distribution function (CDF) and the quantile function are presented because they always overlap.

Table S3 in Supplementary Files presents the values for the shape, scale, and location parameters associated with the curves depicted in Figure 1. The scale and location parameters have been adjusted relative to the arithmetic mean (expected value).

2.1.2. Pearson III Distribution

The probability density function, the complementary cumulative distribution function, and the quantile function for Pearson III (PE3) are as follows:

$$F\left(x|\alpha ,\beta ,\gamma \right)={\displaystyle \frac{{\left(x-\gamma \right)}^{\alpha -1}}{{\beta }^{\alpha }\cdot \Gamma \left(\alpha \right)}}\cdot \exp \left(-{\displaystyle \frac{x-\gamma }{\beta }}\right)$$

(4)

$$F\left(x|\alpha ,\beta ,\gamma \right)=1-{\displaystyle \frac{1}{\beta \cdot \Gamma \left(\alpha \right)}}\cdot {{\displaystyle \underset{\gamma }{\overset{x}{\int }}\left(\frac{x-\gamma }{\beta }\right)}}^{\alpha -1}\cdot \exp \left(-{\displaystyle \frac{x-\gamma }{\beta }}\right)dx={\displaystyle \frac{\Gamma \left(\alpha ,\frac{x-\gamma }{\beta }\right)}{\Gamma \left(\alpha \right)}}$$

(5)

where $\alpha ,\beta ,\gamma$ are the shape, the scale, and the position parameters; $x$ can take any values of the range $\gamma <x<\infty$ if $\beta >0$ or $-\infty <x<\gamma$ if $\beta <0$ and $\alpha >0$; $\Gamma \left(\alpha ,{\displaystyle \frac{x-\gamma }{\beta }}\right)$ returns the value of the incomplete gamma function of ${\displaystyle \frac{x-\gamma }{\beta }}$ with parameter $\alpha$; and $\Gamma \left(\alpha \right)$ returns the value of the Euler gamma function of $\alpha$.

The Pearson III quantile functions are as follows:

$$x\left(p|\alpha ,\beta ,\gamma \right)=F^{-1}\left(x\right)=\gamma +\beta \cdot {\Gamma }^{-1}\left(1-p,\alpha \right)=\gamma +\beta \cdot Gamma.INV\left(1-p,\alpha \right)$$

(6)

where $p$ is the probability of exceedance. If $\beta <0$ (negative skewness) then the first argument of the inverse of the distribution function Gamma becomes $Gamma.INV\left(p,\alpha \right)$, where $Gamma.INV\left(\dots \dots \right)$ returns the inverse cumulative probability distribution for the Gamma distribution.

2.1.3. Wakeby Distribution

The Wakeby distribution does not have a defined shape in terms of the density function and the complementary cumulative distribution function, as can be seen in the following:

$$x\left(p|\alpha ,\beta ,\gamma ,\xi ,\delta \right)=\xi +{\displaystyle \frac{\alpha }{\beta }}\cdot \left(1-p^{\beta }\right)-{\displaystyle \frac{\gamma }{\delta }}\cdot \left(1-p^{-\delta }\right)$$

(7)

where $\xi$ represents the position parameter; $\alpha$ and $\gamma$ represent the scale parameters; and $\beta$ and $\delta$ represent the shape parameters.

2.2. Aspects Regarding Parameters and Their Estimation

This section focuses on estimating the parameters of the GEV distribution. The equations necessary for estimating the parameters of the Pearson III and Wakeby distributions are presented in the Supplementary Files.

Regarding GEV distribution, for MOM, L-moments, and LH-moments this manuscript introduces improvements regarding the approximate relationships for estimating the shape parameter. These improvements consist of presenting more accessible relationships by using functions with fewer terms or a different type of function, while ensuring that the resulting errors remain within reasonable limits.

Given that parameter estimation, especially the estimation of the shape parameter, requires solving nonlinear equation systems, it is important to present the range in which the shape parameter values fall. These values can serve as initial values for methods requiring iterative processes.

Figure S1 in the Supplementary Files shows the two shape parameter variation curves for MOM and L-moments. In the case of MOM, the parameter depends on skewness, while for L-moments it depends on L-skewness.

Considering that the inverse function (quantile function) of statistical distributions can also be expressed in terms of the frequency factor [24,38,39,42], the mathematical expression and the approximate estimation relationships for this factor will be presented for both methods. These elements are important as they significantly simplify the calculation and application of the GEV distribution.

For the most commonly used non-exceedance probabilities the values obtained are characterized by very small errors (<1%), making it unnecessary to estimate the distribution parameters.

All predicted values are presented relative to those obtained using the five-parameter Wakeby distribution, which is selected as the reference (model) distribution. This choice is justified by the distribution’s flexibility (its five parameters allow for an accurate fitting of all four L-moments, a key advantage within the L-moment framework).

2.2.1. Method of Ordinary Moments (MOM)

The exact relationships for parameter estimation using MOM are as follows [26,55,56,57]:

$$\mu =\gamma +{\displaystyle \frac{\beta }{\alpha }}\cdot \left(1-\Gamma \left(\alpha +1\right)\right)$$

(8)

$${\sigma }^2={\displaystyle \frac{{\beta }^2}{{\alpha }^2}}\cdot \left(\Gamma \left(2\cdot \alpha +1\right)-\Gamma {\left(\alpha +1\right)}^2\right)$$

(9)

$$C_s=sign\left(\alpha \right)\cdot {\displaystyle \frac{3\cdot \Gamma \left(2\cdot \alpha +1\right)\cdot \Gamma \left(\alpha +1\right)-\Gamma \left(3\cdot \alpha +1\right)-2\cdot \Gamma {\left(\alpha +1\right)}^3}{\sqrt{{\left(\Gamma \left(2\cdot \alpha +1\right)-\Gamma {\left(\alpha +1\right)}^2\right)}^3}}}$$

(10)

In the case of skewness, the shape parameter must satisfy the conditions $\alpha \ne 0,\alpha >-{\displaystyle \frac{1}{3}}$. The Supplementary Files present the relationships and methodology for obtaining raw and centered moments.

By analyzing Equation 10, it can be easily observed that skewness depends solely on the shape parameter and vice versa. Thus, the shape parameter can be obtained using an approximate relationship ($0.01<C_s<6$) as follows:

$$\alpha ={\displaystyle \frac{0.279530254-0.244456673\cdot C_s}{1+0.332978277\cdot C_s+0.075850709\cdot C_s^2-0.00487301\cdot C_s^3}}$$

(11)

The errors of the relationship across the entire domain of skewness are highlighted in Figure S2 in the Supplementary Files.

With the shape parameter estimated, the scale and location parameters are determined using relationships (12) and (13), which are as follows:

$$\beta ={\displaystyle \frac{\alpha }{\left|\alpha \right|}}\cdot {\displaystyle \frac{\sigma \cdot \alpha }{\sqrt{\Gamma \left(1+2\cdot \alpha \right)-\Gamma {\left(1+\alpha \right)}^2}}}$$

(12)

$$\gamma =\mu -{\displaystyle \frac{\alpha }{\left|\alpha \right|}}\cdot {\displaystyle \frac{\sigma \cdot \left[1-\Gamma \left(1+\alpha \right)\right]}{\sqrt{\Gamma \left(1+2\cdot \alpha \right)-\Gamma {\left(1+\alpha \right)}^2}}}$$

(13)

The expression of the inverse function, whose parameters are estimated using MOM, is as follows:

$$x\left(p|\alpha ,\beta ,\gamma \right)=\mu +\sigma \cdot K\left(p|\alpha ,\beta ,\gamma \right)$$

(14)

where the frequency factor, $K_p\left(p|\alpha ,\beta ,\gamma \right)$, has the following exact expression:

$$K_p\left(p|\alpha ,\beta ,\gamma \right)=sign\left(\alpha \right)\cdot {\displaystyle \frac{\left(\Gamma \left(1+\alpha \right)-{\left(-\ln \left(1-p\right)\right)}^{\alpha }\right)}{{\left(\Gamma \left(1+2\cdot \alpha \right)-\Gamma \left(1+\alpha \right)\right)}^{0.5}}}$$

(15)

It can be observed that the frequency factor depends only on the shape parameter. Considering that the shape parameter can be estimated based on skewness, the frequency factor can be approximately estimated using the following polynomial relationship:

$$K_p\left(p|\alpha ,\beta ,\gamma \right)=a+b\cdot C_s+c\cdot C_s^2+d\cdot C_s^3+e\cdot C_s^4+f\cdot C_s^5$$

(16)

The coefficients of the polynomial approximation, for the usual probabilities of exceedance, are presented in Table S1 in the Supplementary Files.

Regarding the skewness ($C_s$)–kurtosis ($C_k$) relationship, the equation for the interdependence of these statistical indicators is as follows:

$$\begin{array}{l}{C}_k(C_s)=2.695079+0.185786\cdot C_s+1.73401\cdot C_s^2+0.110735\cdot C_s^3+0.037691\cdot C_s^4+0.0036\cdot C_s^5+\\ 0.00219\cdot C_s^6+0.000663\cdot C_s^7+0.000056\cdot C_s^8\end{array}$$

(17)

2.2.2. Method of Linear Moments (L-Moments)

Similarly to the method of ordinary moments, in the case of the L-moments method the exact determination of the shape parameter requires solving a system with a nonlinear equation. The three conditions necessary for the exact estimation of the three parameters are as follows:

$$L_1=\gamma +{\displaystyle \frac{\beta }{\alpha }}\cdot \left(1-\Gamma \left(1+\alpha \right)\right)$$

(18)

$$L_2=\Gamma \left(\alpha \right)\cdot \left(1-2^{-\alpha }\right)\cdot \beta$$

(19)

$$L_3=\Gamma \left(\alpha \right)\cdot \left(1-2^{-\alpha }\right)\cdot \beta \cdot \left({\displaystyle \frac{\left(1-3^{-\alpha }\right)\cdot 2}{1-2^{-\alpha }}}-3\right)$$

(20)

The first four linear moments of the GEV distribution are obtained by integrating the inverse function and are presented in the Supplementary Files.

It can be observed that L-skewness (${\tau }_3={\displaystyle \raisebox{1ex}{$L_3$}\!\left/ \!\raisebox{-1ex}{$L_2$}\right.}$) is defined solely by the shape parameter, and vice versa. Thus, for a given, $0<{\tau }_3<1$, the approximate relationship for estimating the shape parameter is as follows:

$$\alpha ={\displaystyle \frac{0.283788705-1.364389119\cdot {\tau }_3-1.777059609\cdot {\tau }_3^2-0.128881381\cdot {\tau }_3^3}{1+1.522804754\cdot {\tau }_3+0.463666303\cdot {\tau }_3^2}}$$

(21)

The graph of the estimation errors of the parameter is presented in Figure S3 in the Supplementary Files.

The expressions for the relationships to obtain the scale and location parameter values are as follows [26,54]:

$$\beta ={\displaystyle \frac{L_2}{\Gamma \left(\alpha \right)\cdot \left(1-2^{-\alpha }\right)}}$$

(22)

$$\gamma =L_1+{\displaystyle \frac{\beta }{\alpha }}\cdot \left[\Gamma \left(1+\alpha \right)-1\right]$$

(23)

The expression of the inverse function, whose parameters are estimated using L-moments, is as follows:

$$x\left(p|\alpha ,\beta ,\gamma \right)=L_1+L_2\cdot K_p\left(p|\alpha ,\beta ,\gamma \right)$$

(24)

where

$$K_p\left(p|\alpha ,\beta ,\gamma \right)={\displaystyle \frac{1}{1-2^{-\alpha }}}\cdot \left(1-{\displaystyle \frac{{\left(-\ln \left(1-p\right)\right)}^{\alpha }}{\Gamma \left(1+\alpha \right)}}\right)$$

(25)

It can be observed that the frequency factor depends only on the shape parameter. Considering that the shape parameter can be estimated based on L-skewness, the frequency factor can be estimated approximately using the following rational relationship:

$$K_p\left(p|\alpha ,\beta ,\gamma \right)={\displaystyle \frac{a+b\cdot {\tau }_3+c\cdot {\tau }_3^2}{1+d\cdot {\tau }_3+e\cdot {\tau }_3^2+f\cdot {\tau }_3^3+g\cdot {\tau }_3^4}}$$

(26)

The coefficients of the rational function for usual exceedance probabilities are presented in the Supplementary Files, Table S2.

Another important element regarding the GEV distribution and its applicability is the relationship between variation and interdependence, ${\tau }_4\left({\tau }_3\right)$. This represents an important aspect in choosing the best distribution (in general, frequency analysis requires the use of multiple distributions) based on these two higher-order statistical indicators. Considering that the distribution, like many three-parameter statistical distributions, manages to calibrate L-skewness, the selection criterion is L-kurtosis so that its value specific to the GEV distribution is as close as possible to the characteristic value of the analyzed data series. For the GEV distribution, the relationship has the following expression:

$${\tau }_4\left({\tau }_3\right)=0.1072214+0.1143838\cdot {\tau }_3+0.8341466\cdot {\tau }_3^2-0.0632425\cdot {\tau }_3^3+0.0074607\cdot {\tau }_3^4$$

(27)

2.2.3. Method of High-Order Linear Moments (LH-Moments)

In the case of the LH-moments method (first-order), the exact determination of the shape parameter requires solving a system with a nonlinear equation.

The three conditions necessary for the exact estimation of the three parameters are as follows:

$$L_{H1}=\gamma +{\displaystyle \frac{\beta }{\alpha }}\cdot \left(1-\Gamma \left(1+\alpha \right)\cdot 2^{-\alpha }\right)$$

(28)

$$L_{H2}=-{\displaystyle \frac{\beta }{2}}\cdot \left(\Gamma \left(\alpha \right)\cdot 3^{1-\alpha }-3\cdot \Gamma \left(\alpha \right)\cdot 2^{-\alpha }\right)$$

(29)

$$L_{H3}={\displaystyle \frac{4\cdot L_{H2}\cdot \left(5\cdot 4^{-\alpha }+3\cdot 2^{-\alpha }-8\cdot 3^{-\alpha }\right)}{3^{2-\alpha }-9\cdot 2^{-\alpha }}}$$

(30)

The approximate relationship for estimating the shape parameter is as follows:

$$\alpha =0.4823-2.1494\cdot {\tau }_{3H}+0.7269\cdot {\tau }_{3H}^2-0.2103\cdot {\tau }_{3H}^3$$

(31)

Thus, with the shape parameter approximately determined, the location and scale parameters are obtained from relationships (27) and (28).

2.2.4. The Maximum Likelihood Estimation Method (MLE)

The MLE method is a statistical technique used to estimate the parameters of a probability distribution so that the distribution is as compatible as possible with the observed data. It starts with the likelihood function L, which expresses the probability that the observed data were generated by a distribution with a certain set of parameters.

The likelihood function is as follows:

$$L={\displaystyle \prod _{i=1}^{n}f\left(x_i,\alpha ,\beta ,\gamma \right)}$$

(32)

In practice, the log-likelihood ln (L) is maximized because the product can become very small for large data sets, and the logarithm transforms the product into a sum. This is expressed as follows:

$$\ln \left(L\right)=\ln \left({\displaystyle \prod _{i=1}^{n}f\left(x_i,\alpha ,\beta ,\gamma \right)}\right)={\displaystyle \sum _{i=1}^n\ln \left(f\left(x_i,\alpha ,\beta ,\gamma \right)\right)}$$

(33)

For the GEV distribution, the relationship is as follows:

$$\ln \left(L\right)=-n\cdot \ln \left(\beta \right)+{\displaystyle \sum _{i=1}^n\left[\left(\frac{1}{\alpha }-1\right)\cdot \ln \left(1-\alpha \cdot \left(\frac{X_i-\gamma }{\beta }\right)\right)-{\left(1-\alpha \cdot \left(\frac{X_i-\gamma }{\beta }\right)\right)}^{1/\alpha }\right]}$$

(34)

The parameter estimation is performed by maximizing the log-likelihood function. For each parameter, the partial derivative of the log-likelihood must be zero. The explicit equations can be found in [26,57].

2.2.5. The Probability-Weighted Moments (PWMs)

The PWMs method was first described in by Greenwood [58]. It is a method that has the advantage of using the empirical probability (Hazen, Weibull, Blom, [42,51]) in a differentiated manner, depending on the hydrological characteristics of the analyzed data set. For the recorded data set, the weighted moments result from the following general formula:

$$W_k={\displaystyle \frac{1}{n}}\cdot {{\displaystyle \sum _{i=1}^n{x}_i\cdot \left(1-P_{e_i}\right)}}^k$$

(35)

where $P_{e_i}$ represents the chosen empirical probability and $k=0, 1, 2, 3, 4$ represents the degree of weighting.

The weighted moments for the theoretical distribution are expressed using the quantile function, with the following general expression:

$$W_k={\displaystyle \underset{0}{\overset{1}{\int }}x\left(p\right)\cdot p^k\cdot dp}$$

(36)

where for $k=0$ we have the expected value.

In the case of the GEV distribution, the equations for parameter estimation are as follows:

$$W_1=\gamma +{\displaystyle \frac{\beta }{\alpha }}\cdot \left(1-\Gamma \left(1+\alpha \right)\right)$$

(37)

$$W_2={\displaystyle \frac{\gamma }{2}}+\beta \cdot \left({\displaystyle \frac{1}{2\cdot \alpha }}+\Gamma \left(\alpha \right)\cdot \left(2^{-\alpha -1}-1\right)\right)$$

(38)

$$W_3={\displaystyle \frac{\gamma }{3}}+\beta \cdot \left({\displaystyle \frac{1}{3\cdot \alpha }}+\Gamma \left(\alpha \right)\cdot \left(-3^{-\alpha -1}+2^{-\alpha }-1\right)\right)$$

(39)

The method for obtaining them is presented in the Supplementary Files.

2.2.6. The Least Squares Method (LSM)

The least squares method is less commonly used because the estimation of parameters is not robust; however, it can be used for an initial estimate of the parameters, which are then used as starting values for methods that apply the gradient method or for determining the empirical probability used in the weighted moments method.

The least squares method minimizes the sum of the squared errors. By minimization, the equations are as follows:

$${\displaystyle \sum _{i=1}^n\left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\alpha }}=0$$

(40)

$${\displaystyle \sum _{i=1}^n\left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\beta }}=0$$

(41)

$${\displaystyle \sum _{i=1}^n\left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\gamma }}=0$$

(42)

where $F\left(x_i,\alpha ,\beta ,\gamma \right)$ is the cumulative function of the theoretical distribution.

2.2.7. The Weighted Least Squares Method (WLSM)

It represents an alternative method to LSM, with the advantage of assigning greater weight to extreme values [59]. The general minimization equations are as follows:

$${\displaystyle \sum _{i=1}^n\frac{{\left(n+1\right)}^2\cdot \left(n+2\right)}{i\cdot \left(n-i+1\right)}\cdot \left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\alpha }}=0$$

(43)

$${\displaystyle \sum _{i=1}^n\frac{{\left(n+1\right)}^2\cdot \left(n+2\right)}{i\cdot \left(n-i+1\right)}\cdot \left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\beta }}=0$$

(44)

$${\displaystyle \sum _{i=1}^n\frac{{\left(n+1\right)}^2\cdot \left(n+2\right)}{i\cdot \left(n-i+1\right)}\cdot \left(F\left(x_i,\alpha ,\beta ,\gamma \right)-P_{e_i}\right)}\cdot {\displaystyle \frac{\partial F\left(x_i,\alpha ,\beta ,\gamma \right)}{\gamma }}=0$$

(45)

where the meanings of the terms have been presented in previous sections.

The structure of the analysis presented in the manuscript follows these steps:

• Data collection and preparation by checking data quality, verifying data stationarity, and the presence of extreme values (Section 3, Table 1).
• Calculation of the following basic statistical characteristics: expected value, standard deviation, coefficient of variation, skewness, kurtosis, the first four linear moments, L-variation coefficient, L-skewness, and L-kurtosis (Section 3, Table 2 and Table 3).
• Estimation of the parameters of the analyzed distributions (GEV, Pearson III, and Wakeby) using the 7 parameter estimation methods (MOM, L-moments, LH-moments, PWMs, LSM, PLSM, and MLE).
• Calculation and graphical representation of quantile functions. Calculation of maximum discharges corresponding to rare and very rare events of interest in hydrology, with return periods up to T = 10,000 years. Presentation of data in tables and graphs.
• Selection of the best distribution, using standard performance indicators (RAE and RME), but especially the selection criterion specific to the L-moments method.
• Highlighting uncertainties of the distributions based on the parameter estimation method, particularly depending on the empirical probability used (PWN, LSM, and WLSM), and uncertainties in the behavior of distributions based on the variability of the available data lengths. Presentation of these uncertainties in tables and graphs.
• Recommendations regarding the applicability of the GEV distribution in Romania, as well as recommendations for adopting a robust and rigorous estimation method (L-moments).

3. Case Studies

The case studies involve conducting in situ frequency analyses of annual maximum discharges, with the aim of determining extreme maximum values corresponding to annual exceedance probabilities of interest in technical hydrology.

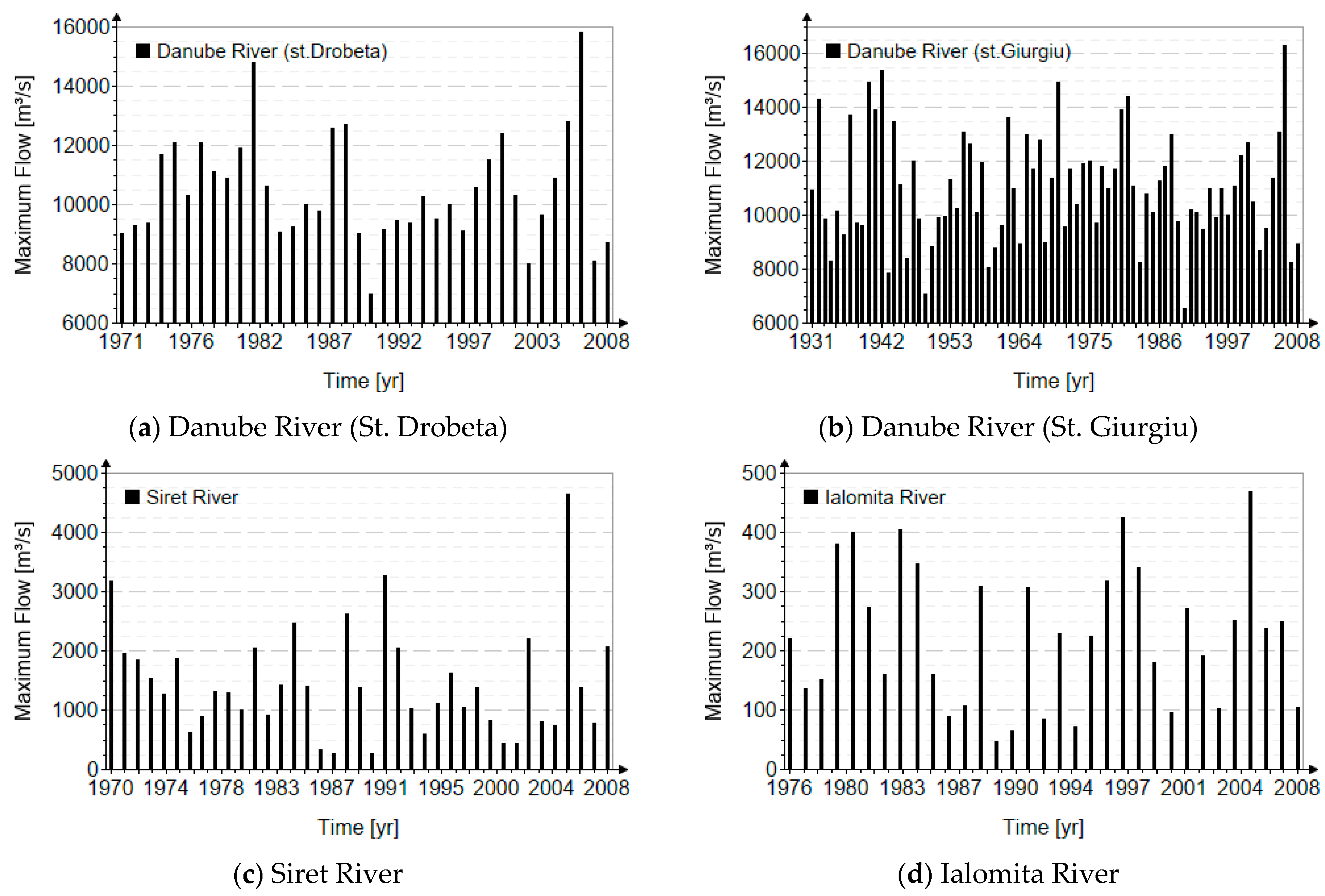
Figure 2 shows the four analyzed locations. Two of them are associated with the Danube River, one location on the Siret River, and one on the Ialomita River, all situated in Romania.

The Danube River is the second longest river in Europe (after the Volga), with a total length of approximately 2860 km. It originates in the Black Forest Mountains (Germany) and flows into the Black Sea through the Danube Delta, crossing the territories of Romania and Ukraine. In Romania, the Danube travels approximately 1075 km and forms the border with Serbia, Bulgaria, Moldova, and Ukraine. Between Baziaș and Drobeta-Turnu Severin, the river passes through a spectacular gorge with rocky cliffs and deep waters. Here, the Iron Gates I and II dams are located. Between Drobeta-Turnu Severin and Călărași, the river flows through a lower area with wide floodplains and meanders. The delta section starts at Brăila and includes the actual delta area, where the river splits into three main branches: Chilia, Sulina, and Sfântu Gheorghe. The waters of the Danube are influenced by the melting of snow from the Alps and Carpathians, as well as by precipitation. The most important rivers that flow into the Danube are the Cerna, Jiu, Olt, Argeș, Ialomita, and Siret.

The Siret River originates in the Obcina Feredeului Mountains (Eastern Carpathians, Ukraine), with a length of approximately 706 km, of which 559 km are in Romanian territory. It has a catchment area of approximately 47,610 km², making it the largest catchment area among the Danube’s tributaries on Romanian territory, flowing into the Danube near Galați. The Siret has a nival–pluvial hydrological regime, meaning it is fed both by snowmelt and precipitation, with a variable discharge that increases in spring (March-April) due to snowmelt and secondary increases in autumn due to heavy rainfall. It is a river with a high flood risk, having numerous flash floods, especially in years with abundant rainfall. Along its course, dams and reservoirs have been constructed to mitigate floods and produce hydroelectric power. The Siret River basin area is influenced by a temperate continental climate, with significant variations between the mountain regions and the plains. The temperatures are 4–6 °C in the mountainous area and 9–11 °C in the plains. Precipitation is more abundant in spring and autumn, and summer drought episodes can occur, particularly in the southern part of the basin. The average annual precipitation ranges from 800–1200 mm/year in the mountainous area to 450–600 mm/year in the hilly and plain areas.

The Ialomita River originates in the Bucegi Mountains (Southern Carpathians) at an altitude of approximately 2300 m, below the Omu Peak. With a drainage basin of 10,350 km² and a length of about 417 km, it is one of the most important rivers in southern Romania. The regime is nival–pluvial, primarily fed by the melting of snow from the Bucegi Mountains and precipitation from the subcarpathian and plain areas. Maximum discharges occur in spring (March–April) due to snowmelt and rainfall, while minimum discharges occur in summer, when severe droughts can be recorded. The river poses a high flood risk, especially in the plain areas. The average annual temperature ranges from 0–5 °C in the mountain area to 10–11 °C in the plain area.

Figure 3 shows the chronological series of data analyzed at each hydrometric station.

In Figure 4, box plot graphs of the analyzed data are presented, showing the distribution and variability of the data.

To verify stationarity, the t-test was used [54], and the analyzed data were found to be stationary. No outliers were identified in the analyzed series after applying the Grubbs [38,39,60] test (Table 1).

Table 1. The results of the stationarity and outliers check.

Series	t-Test		Grubbs
	Results	Critical Value (10%)	Rezults (Upper)	Max (Q)
Danube/Drobeta	−0.242	1.992	18,544	16,300
Danube/Giurgiu	1.157	2.028	16,146	15,800
Siret/Lungoci	0.277	2.026	7040	4650
Ialomita/Tandarei	−0.087	2.04	943	468

Table 1. The results of the stationarity and outliers check.

Series	t-Test		Grubbs
	Results	Critical Value (10%)	Rezults (Upper)	Max (Q)
Danube/Drobeta	−0.242	1.992	18,544	16,300
Danube/Giurgiu	1.157	2.028	16,146	15,800
Siret/Lungoci	0.277	2.026	7040	4650
Ialomita/Tandarei	−0.087	2.04	943	468

Considering that the method of ordinary moments and the method of linear moments are two methods that exclusively use characteristic moments and higher-order statistical indicators, their corresponding values for the analyzed sites are highlighted in Table 2 and Table 3.

Table 2. The statistical indicators of the observed data: MOM.

River	Station	Record Length	$\mathit{\mu }$	$\mathit{\sigma }$	${\mathit{C}}_{\mathit{v}}$	${\mathit{C}}_{\mathit{s}}$	${\mathit{C}}_{\mathit{k}}$
			[m3/s]	[m3/s]	[−]	[−]	[−]
Danube	Drobeta	38	10,480.4	1816.6	0.173	0.881	6.167
Danube	Giurgiu	78	10,972.7	2016.5	0.184	0.379	4.853
Siret	Lungoci	39	1442.5	915.1	0.634	1.413	7.872
Ialomita	Tandarei	33	224.1	118.1	0.527	0.327	4.074

Where $\mu$ represents the arithmetic mean; $\sigma$ represents the root mean square deviation; $C_v$ represents the coefficient of variation; $C_s$ and $C_k$ represents skewness and kurtosis, respectively.

Table 2. The statistical indicators of the observed data: MOM.

River	Station	Record Length	$\mathit{\mu }$	$\mathit{\sigma }$	${\mathit{C}}_{\mathit{v}}$	${\mathit{C}}_{\mathit{s}}$	${\mathit{C}}_{\mathit{k}}$
			[m3/s]	[m3/s]	[−]	[−]	[−]
Danube	Drobeta	38	10,480.4	1816.6	0.173	0.881	6.167
Danube	Giurgiu	78	10,972.7	2016.5	0.184	0.379	4.853
Siret	Lungoci	39	1442.5	915.1	0.634	1.413	7.872
Ialomita	Tandarei	33	224.1	118.1	0.527	0.327	4.074

Where $\mu$ represents the arithmetic mean; $\sigma$ represents the root mean square deviation; $C_v$ represents the coefficient of variation; $C_s$ and $C_k$ represents skewness and kurtosis, respectively.

Table 3. The statistical indicators of the observed data: L-moments method.

River/Station	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$	${\mathit{L}}_4$	${\mathit{\tau }}_2={\mathit{L}}_2/{\mathit{L}}_1$	${\mathit{\tau }}_3={\mathit{L}}_3/{\mathit{L}}_2$	${\mathit{\tau }}_4={\mathit{L}}_4/{\mathit{L}}_2$
	[m3/s]	[m3/s]	[m3/s]	[m3/s]	[−]	[−]	[−]
Danube/Drobeta	10,480.4	999.9	172	159.1	0.095	0.172	0.159
Danube/Giurgiu	10,972.7	1142.3	100.1	138.5	0.104	0.088	0.121
Siret/Lungoci	1442.5	489.5	111.5	90.6	0.339	0.228	0.185
Ialomita/Tandarei	224.1	68.6	6.1	1.7	0.306	0.089	0.025

Where $L_1$, $L_2$, $L_3$, and $L_4$ represent the first four linear moments; ${\tau }_2$ represents the L-variation coefficient; ${\tau }_3$ and ${\tau }_4$ represent L-skewness and L-kurtosis, respectively.

Table 3. The statistical indicators of the observed data: L-moments method.

River/Station	${\mathit{L}}_1$	${\mathit{L}}_2$	${\mathit{L}}_3$	${\mathit{L}}_4$	${\mathit{\tau }}_2={\mathit{L}}_2/{\mathit{L}}_1$	${\mathit{\tau }}_3={\mathit{L}}_3/{\mathit{L}}_2$	${\mathit{\tau }}_4={\mathit{L}}_4/{\mathit{L}}_2$
	[m3/s]	[m3/s]	[m3/s]	[m3/s]	[−]	[−]	[−]
Danube/Drobeta	10,480.4	999.9	172	159.1	0.095	0.172	0.159
Danube/Giurgiu	10,972.7	1142.3	100.1	138.5	0.104	0.088	0.121
Siret/Lungoci	1442.5	489.5	111.5	90.6	0.339	0.228	0.185
Ialomita/Tandarei	224.1	68.6	6.1	1.7	0.306	0.089	0.025

Where $L_1$, $L_2$, $L_3$, and $L_4$ represent the first four linear moments; ${\tau }_2$ represents the L-variation coefficient; ${\tau }_3$ and ${\tau }_4$ represent L-skewness and L-kurtosis, respectively.

4. Results

The analysis of maximum discharges included a holistic approach, using seven parameter estimation methods to verify the applicability of the GEV distribution in determining maximum discharges for rare and very rare events relevant to case studies for the hydrological regime in Romania.

The forecasted quantile values for annual exceedance probabilities of interest in FFA and technical hydrology are presented in

Table 4. Quantile results for Danube (st. Giurgiu).

Method	Qp%, Danube River (st. Giurgiu)
	0.01	0.1	0.5	1	2	3	5	10	40
	GEV
MOM	18,927	17,809	16,725	16,158	15,519	15,106	14,539	13,670	11,352
L-moments	19,902	18,441	17,119	16,455	15,725	15,262	14,638	13,702	11,308
PWMs	19,648	18,258	16,988	16,347	15,638	15,189	14,580	13,665	11,310
LSM	22,217	19,877	18,001	17,123	16,199	15,634	14,893	13,824	11,282
LH-moments	19,817	18,391	17,091	16,436	15,713	15,255	14,635	13,704	11,311
MLE	18,667	17,611	16,576	16,032	15,415	15,016	14,466	13,620	11,347
WLSM	20,560	18,845	17,359	16,632	15,844	15,351	14,693	13,721	11,298
	PEARSON III
MOM	20,096	18,271	16,859	16,200	15,500	15,066	14,487	13,623	11,365
L-moments	20,989	18,865	17,253	16,511	15,730	15,250	14,615	13,680	11,313
	WAKEBY
L-moments	18,372	17,649	16,796	16,297	15,694	15,285	14,701	13,767	11,276

,

Table 5. Quantile results for Danube (st. Drobeta).

Method	Qp%, Danube River (st. Drobeta)
	0.01	0.1	0.5	1	2	3	5	10	40
	GEV
MOM	17,532	16,565	15,617	15,119	14,554	14,188	13,684	12,909	10,829
L-moments	23,095	19,694	17,329	16,312	15,293	14,696	13,938	12,894	10,613
PWMs	21,857	18,985	16,909	15,995	15,068	14,517	13,813	12,830	10,633
LSM	23,165	19,826	17,475	16,456	15,432	14,828	14,061	12,999	10,662
LH-moments	23,573	19,919	17,432	16,376	15,326	14,714	13,942	12,885	10,605
MLE	20,078	18,042	16,422	15,668	14,875	14,392	13,759	12,849	10,694
WLSM	22,628	19,427	17,175	16,200	15,220	14,642	13,908	12,893	10,659
	PEARSON III
MOM	18,615	17,000	15,748	15,163	14,540	14,153	13,636	12,865	10,840
L-moments	21,586	18,903	16,947	16,074	15,176	14,636	13,936	12,939	10,627
	WAKEBY
L-moments	22,023	19,386	17,319	16,367	15,375	14,776	14,001	12,911	10,587

,

Table 6. Quantile results for Siret (st. Lungoci).

Method	Qp%, Siret River (st. Lungoci)
	0.01	0.1	0.5	1	2	3	5	10	40
	GEV
MOM	8069	6180	4911	4376	3847	3540	3153	2626	1497
L-moments	10,193	7157	5371	4676	4019	3651	3203	2617	1455
PWMs	9305	6717	5136	4506	3904	3563	3144	2590	1466
LSM	8573	6377	4972	4397	3838	3517	3119	2584	1471
LH-moments	10,598	7321	5438	4714	4037	3660	3203	2611	1451
MLE	10,946	7449	5481	4734	4040	3656	3194	2597	1443
WLSM	9658	6893	5231	4575	3950	3599	3168	2602	1463
	PEARSON III
MOM	7454	5937	4846	4363	3871	3578	3200	2668	1480
L-moments	7706	6097	4945	4438	3922	3616	3223	2673	1463
	WAKEBY
L-moments	7916	6329	5128	4586	4028	3695	3266	2670	1427

and

Table 7. Quantile results for Ialomita (st. Tandarei).

Method	Qp%, Ialomita River (st. Tandarei)
	0.01	0.1	0.5	1	2	3	5	10	40
	GEV
MOM	979	787	649	589	527	491	444	379	234
L-moments	765	676	595	555	510	482	444	388	244
PWMs	730	650	577	539	498	472	436	383	244
LSM	774	690	612	572	528	499	460	402	248
LH-moments	599	568	531	509	482	463	436	391	252
MLE	705	630	560	525	486	461	427	375	242
WLSM	793	695	608	566	519	490	451	392	245
	PEARSON III
MOM	942	768	642	585	527	492	447	382	233
L-moments	829	700	602	558	510	481	443	387	244
	WAKEBY
L-moments	495	492	483	476	464	453	436	400	251

.

Figure 5 illustrates the fitted distributions for the four rivers analyzed in the study. To determine the plotting positions, the Hazen empirical probability formula was applied, as referenced in [24].

The horizontal axis is presented on a logarithmic scale, specifically a decimal logarithmic scale, which allows for a more effective visualization of the wide range of values typically encountered in extreme event analysis. This scaling helps highlight the behavior of the distributions in the tail regions, which are crucial for predicting rare and extreme events.

The various distributions are compared to assess their accuracy and suitability for modeling the river flow data, enabling a deeper understanding of their performance in capturing the characteristics of the observed data.

5. Discussions

In all four case studies, the GEV distribution was compared to the Pearson III distribution (considered the “parent” distribution in Romania, using MOM) and the Wakeby distribution (with five parameters, used as a robust reference model due to its ability to calibrate all four L-moments).

The main objectives of the presented analysis are as follows:

(1)

To verify the applicability of the GEV distribution in Romania by determining the maximum discharges associated with rare and very rare events required in technical hydrology, assuming apriori that the data come from a GEV distribution.

(2)

To compare the maximum values predicted by the GEV distribution with those predicted by the Pearson III distribution, which is considered the “parent” distribution in Romania.

(3)

To compare the values predicted by GEV and PE3 with those predicted by the Wakeby distribution, which has five parameters estimated using the L-moments method, chosen as the reference distribution and method.

(4)

To highlight the behavior of the GEV distribution, particularly the uncertainties characterizing the predicted values due to the variability in the lengths of available data series.

The results are compared with the distribution considered the “parent” distribution in Romania, namely the Pearson III distribution, with its three parameters (location, scale, and shape) estimated using the method of ordinary moments, which is the parameter estimation method used in Romania. The results are also compared with the Wakeby distribution, which has five parameters estimated using the method of linear moments [41,58,61]. The justification for choosing this distribution as the reference distribution is explained in the previous sections, with the most important reasons being the high number of parameters which manage to properly calibrate all four linear moments specific to the L-moments method. As a result, the uncertainties regarding the values estimated using this method and distribution are characterized by reduced uncertainties, with the predicted values having a high degree of confidence.

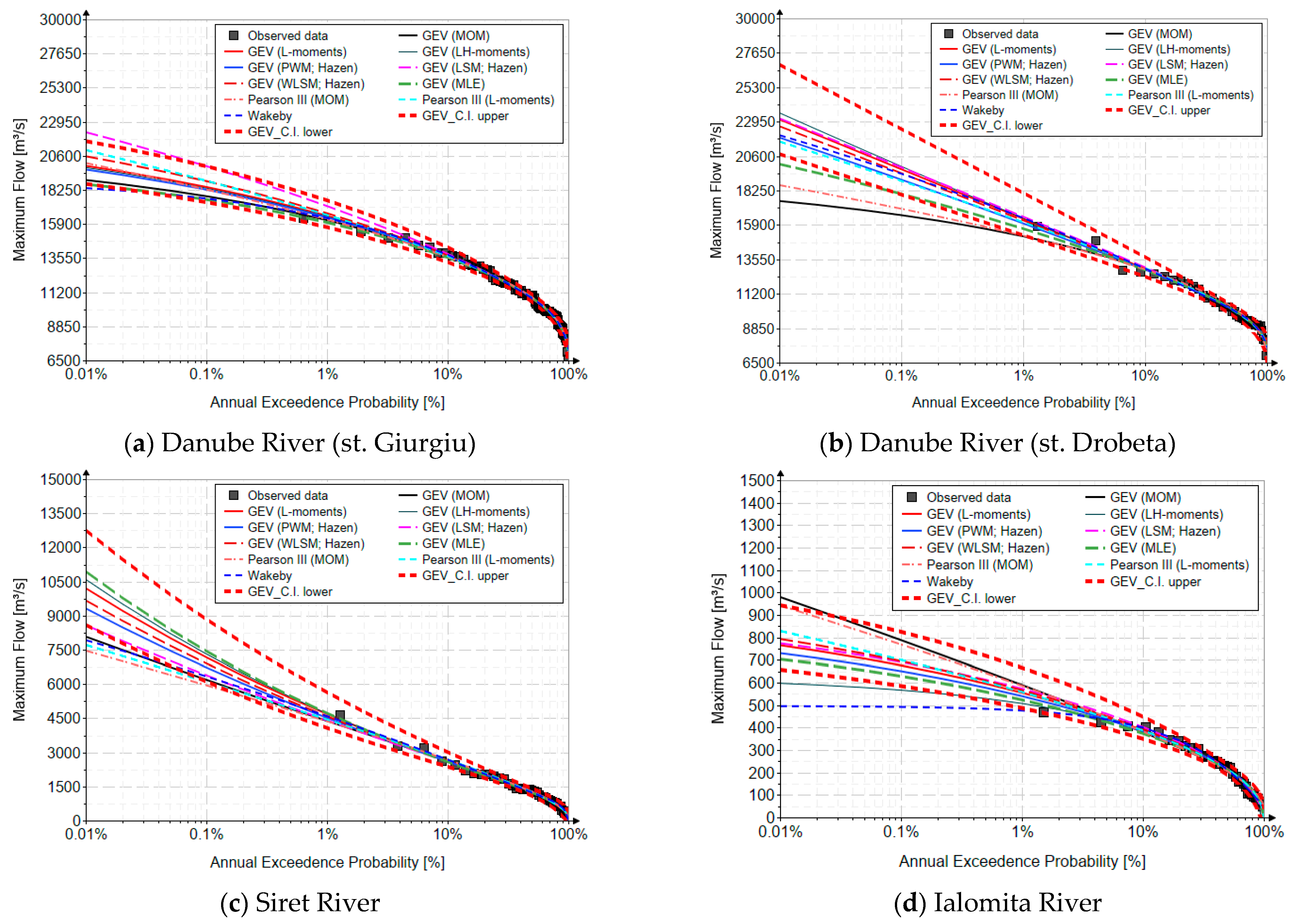
Analyzing the obtained results, the GEV distribution showed consistent differences in the predicted maximum discharges compared to the Pearson III and Wakeby distributions.

In the domain of very rare events (probabilities of exceedance p < 1%), the GEV distribution’s tail behavior was noticeably influenced by the estimation method. The L-moments method resulted in a smoother, more reliable extrapolation for extreme quantiles, reducing bias compared to MOM.

For the Danube River, Giurgiu station (for T = 10,000 years), the Wakeby distribution predicted a maximum discharge of 18,372 m³/s. The GEV distribution predicted a maximum discharge ranging from 18,667 m³/s (MLE) to 22,217 m³/s (LSM). Compared to Pearson III (20,096 m³/s), GEV (L-moments) produced a lower value of 19,902 m³/s. By comparing the results to the Wakeby distribution (selected based on the considerations mentioned earlier), the GEV distribution generated higher percentage values, specifically +3% (MOM), +8.3% (L-moments), +7% (PWMs), +20.9% (LSM), +7.9% (LH-moments), +1.6% (MLE), and +11.9% (WLSM). Likewise, the Pearson III distribution produced higher percentage values, ranging from +9.4% (MOM) to +14.2% (L-moments).

In the case of the Danube River, Drobeta station, the Wakeby distribution predicted a maximum discharge of 22,023 m³/s. The GEV distribution predicted a maximum discharge ranging from 17,532 m³/s (MOM) to 23,573 m³/s (LH-moments). Compared to Pearson III (21,586 m³/s), GEV (L-moments) produced a higher value of 23,095 m³/s. By comparing the results to the Wakeby distribution, GEV generated percentage values of −20.4% (MOM), +4.9% (L-moments), −0.8% (PWMs), +5.2% (LSM), +7.0% (LH-moments), −8.8% (MLE), and +2.7% (WLSM). The Pearson III distribution produced lower percentage values, ranging from −2.0% (L-moments) to −15.4% (MOM).

Regarding the Siret River, the Wakeby distribution predicted a maximum discharge of 7916 m³/s. The GEV distribution predicted a maximum discharge ranging from 8069 m³/s (MOM) to 10,946 m³/s (MLE). Compared to Pearson III (7706 m³/s), GEV (L-moments) produced a higher value of 10,193 m³/s. By comparing the results to the Wakeby distribution, GEV generated percentage values of +1.9% (MOM), +28.8% (L-moments), +17.5% (PWMs), +8.3% (LSM), +33.9% (LH-moments), +38.2% (MLE), and +22.0% (WLSM). The Pearson III distribution produced lower percentage values, ranging from −2.7% (L-moments) to −5.8% (MOM).

For the Ialomita River, the Wakeby distribution predicted a maximum discharge of 495 m³/s. The GEV distribution predicted a maximum discharge ranging from 705 m³/s (MLE) to 979 m³/s (MOM). Compared to Pearson III (829 m³/s), GEV (L-moments) produced a lower value of 765 m³/s. By comparing the results to the Wakeby distribution, GEV generated higher percentage values, specifically +97.7% (MOM), +54.5% (L-moments), +47.5% (PWMs), +56.4% (LSM), +21% (LH-moments), +42.4% (MLE), and +60.2% (WLSM). The Pearson III distribution produced higher percentage values, ranging from +67.5% (L-moments) to +90.3% (MOM).

This variability in the predicted values is mainly due to the inability of the three-parameter distributions to calibrate the L-kurtosis [34]. The statistical indicators L-skewness and L-kurtosis play a crucial role in influencing the predicted maximum discharges. L-kurtosis reflects the variability and extremity of maximum discharge values—higher L-kurtosis values indicate a greater tendency toward extreme events, leading to higher predicted quantiles [34]. In the Danube River (Drobeta station), with an L-kurtosis of 0.159, the predicted values with GEV (L-moments) were relatively stable, aligning closely with Pearson III but slightly lower than Wakeby. At the Siret River (Lungoci station), where L-kurtosis was 0.185—signaling more extreme variability—the GEV distribution produced significantly higher quantiles than Pearson III, although they were still lower than Wakeby. The Ialomita River (Tandarei station) exhibited a relatively low L-kurtosis (0.025) which corresponded to less variable maximum discharges, resulting in lower quantile predictions across all distributions.

The criteria for choosing the best distribution are in compliance with the conditions imposed by the L-moments method (also chosen in these cases as a reference) but also in the use of some performance indicators that are based on highlighting the relative errors between recorded and forecasted values.

For the analyzed case studies, the RME (relative mean error) and RAE (relative absolute error) performance indicators are used [60,62]. In terms of performance indicators RME and RAE, their results are presented in

Table 8. RME and RAE score values for Danube River (st. Giurgiu).

Distribution	RME
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0016	0.0017	0.0017	0.0023	0.0017	0.0017	0.0019
Pearson III	0.0017	0.0018	-	-	-	-	-
Wakeby	-	0.0022	-	-	-	-	-
	RAE
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0121	0.0121	0.0119	0.0132	0.0122	0.0122	0.0122
Pearson III	0.0127	0.0125	-	-	-	-	-
Wakeby	-	0.0134	-	-	-	-	-

,

Table 9. RME and RAE score values for Danube River (st. Drobeta).

Distribution	RME
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.005	0.0039	0.0039	0.0039	0.004	0.0039	0.004
Pearson III	0.0051	0.0043	-	-	-	-	-
Wakeby	-	0.0043	-	-	-	-	-
	RAE
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0249	0.0171	0.0174	0.0179	0.0171	0.0189	0.0174
Pearson III	0.0257	0.0177	-	-	-	-	-
Wakeby	-	0.0191	-	-	-	-	-

,

Table 10. RME and RAE score values for Siret River (st. Lungoci).

Distribution	RME
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0254	0.0173	0.0172	0.0198	0.0161	0.0157	0.0171
Pearson III	0.0131	0.0121	-	-	-	-	-
Wakeby	-	0.0317	-	-	-	-	-
	RAE
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0671	0.0571	0.0591	0.058	0.0584	0.0601	0.0582
Pearson III	0.0582	0.0615	-	-	-	-	-
Wakeby	-	0.0876	-	-	-	-	-

and

Table 11. RME and RAE score values for Ialomita River (st. Tandarei).

Distribution	RME
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.0231	0.0364	0.034	0.0517	0.082	0.0312	0.0361
Pearson III	0.0203	0.0361	-	-	-	-	-
Wakeby	-	0.0105	-	-	-	-	-
	RAE
	MOM	L-mom	PWM	LSM	LH-mom	MLE	WLSM
GEV	0.1039	0.1074	0.1061	0.1262	0.1737	0.1064	0.1067
Pearson III	0.0918	0.1073	-	-	-	-	-
Wakeby	-	0.0429	-	-	-	-	-

.

However, it should be noted that these performance indicators generally highlight only the calibration within the range of observed values. Outside of this range (for selecting the best distribution for very rare events, T = 10,000 years) these indicators lose their relevance. For this reason, the L-moments method and distributions with at least four parameters are preferred, as it is an extremely stable and robust method and using distributions with a high number of parameters ensures that all calibration conditions associated with the method are met.

For distributions with two or three parameters, the selection of the best model is made by comparing the values of the statistical indicators L-skewness and L-kurtosis of the analyzed data with those characteristics of the statistical distributions, the latter being defined by specific interdependence relationships between these two statistical indicators [24].

For the Danube River (Giurgiu station), the best result for the GEV distribution was obtained using the MOM method (RME = 0.0016) and the PWMs method (RAE = 0.0119). Analyzing exclusively the scores for L-moments, the GEV distribution provided the best result (RME = 0.0017, RAE = 0.0121).

In the case of the Danube River (Drobeta station), the RME scores were very close, around 0.0039. Regarding RAE, the best result with GEV was achieved using the L-mom and LH-mom methods (RAE = 0.0171). For L-moments, the GEV distribution provided the best result (RME = 0.0039, RAE = 0.0171).

For the Siret River (Lungoci station), the best result for the GEV distribution was obtained using the MLE method (RME = 0.0157) and the L-moments method (RAE = 0.0571). L-moments with GEV distribution gave the best result for RAE (0.0571), while the Pearson III distribution had the best RME score (0.0121).

For the Ialomita River (Tandarei station), the best result for the GEV distribution was obtained using the MOM method (RME = 0.0231 and RAE = 0.1039). Analyzing exclusively the scores for L-moments, the Wakeby distribution provided the best result for RME (0.0105), while the Pearson III distribution had the best RAE score (0.1073).

It is essential that when applying the L-moments method model selection be guided by criteria specifically tailored to this approach. In particular, emphasis should be placed on the accurate calibration of higher-order statistical indicators, namely L-skewness and L-kurtosis, which play a crucial role in characterizing the shape and tail behavior of the distribution. This process should involve both the use of theoretical interdependence relationships between L-moments and a preliminary visual (graphical) assessment, which helps identify candidate distributions that align with the empirical L-moment ratios. Such a dual approach ensures that the selected model not only fits the central tendency of the data but also reliably captures the behavior of extreme values, which is of primary interest in hydrological frequency analysis.

The Influence of Available Data Lengths on Forecasted Values.

In hydrological/hydrotechnical practice there is an apparent but inevitable contradiction between the stringent requirements imposed by national technical standards and international regulations, on the one hand, and the limited reality of available hydrological data, on the other.

Despite the fact that in the vast majority of cases long observation series are not available, especially those with over 100 years of records, standards still require the frequency analysis and estimation of extreme quantiles of annual maximum flows, even for very large return periods, such as T = 1,000, 5,000, or even 10,000 years. This requirement has a solid justification as hydrotechnical works of strategic importance—such as dams, dikes, water intakes, or flood defense works—must be designed to ensure a high degree of safety throughout the lifespan of the construction, considering even events with very low probability but potentially devastating impact.

However, the hydrometric reality in many countries—including Romania—is that the networks of hydrometric stations are relatively sparse or have been reduced in recent decades; the operating period of many stations is under 30–40 years and unmonitored sites or sites with discontinuous data series are common in mountainous areas or in small basins.

In these conditions, performing flood frequency analyses becomes an extremely difficult task and highly vulnerable to uncertainties. However, these analyses cannot be abandoned, and the solution lies in methodological rigor.

It is important to emphasize that estimating extreme flows does not mean exact prediction, but rather a probabilistic assessment of an extreme risk. This assessment, even if not perfect, is preferable to the complete disregard of the hazard. In this context, it is important to offer the confidence intervals associated with the estimates to perform a sensitivity analysis of the results to the length of the series and the choice of model, and an evaluation of residual risk and possible adaptation or protection measures.

The limited availability of sufficiently large data series, ensuring that the obtained values closely approximate those of the population, necessitates highlighting the theoretical biases associated with small- and medium-length data samples. Generally, these are the most common cases in frequency analysis. As previously mentioned, in general this analysis represents a secondary stage following the selection of the most suitable distribution and parameter estimation method. Thus, this section starts from the general assumption that the sample data would originate from a GEV distribution with parameters estimated using the method of moments (MOM) and L-moments.

Biases are presented both in the estimation of parameters and in the estimation of event magnitudes with large return periods. This also illustrates how parameter biases propagate into the biases of the inverse function.

In the sampling process Hazen’s empirical probability was used as the values obtained with this method were the closest to the theoretical curve (n = 1000 values).

Probabilities corresponding to recorded values, representing samples rather than populations—as small or medium data lengths are generally available—should not be directly associated with the relative frequency (i/n) but rather with an empirical probability where the minimum value exceeds the range of relative frequencies of the observed data. Thus, Hazen’s empirical probability generated the smallest errors compared to theoretical values with other empirical probabilities. Similar results were observed for the Gumbel distribution [24]. The subjective choice of the empirical probability is most clearly highlighted in the case of the PWMs and LSM parameter estimation methods, which generate significant biases, especially in the case of the rarest events (T = 10,000 years).

Figure 6 graphically presents these differences (based on the case study of the Danube River, St. Giurgiu) following the analysis of six empirical probabilities, Hazen, Weibull, Tukey, Cunnane, Beard, and Chegodayev, whose expressions can be found in [26,42,51]. Significant differences can be observed, considering that for this station the length of the records is relatively relevant (n = 78 values). In the case of shorter data lengths, these deviations increase significantly, with generated values being characterized by substantial uncertainties. For this reason these two methods are less commonly used. They can have relevant applicability when the probability range of the forecasted values is closer to that of the recorded data.

To cover as extensive a range as possible regarding statistical indicators and available data lengths, sample sizes of 25, 50, and 80 values are chosen to highlight the theoretical biases in estimating statistical indicators, parameter estimation, and quantile estimation.

To reflect real data applications, scenarios were selected with coefficients of variation ranging between 0.1 and 2 and skewness values between 0.1 and 6 for the MOM. For the L-moments analysis, coefficients of L-variation between 0.01 and 1 and L-skewness values between 0.01 and 1 were used. In the case of L-moments, a detailed analysis is presented with a smaller increment of statistical indicators, specifically samples of 20, 35, 55, and 90 values.

In general, in frequency analysis of extreme events in hydrology—especially for maximum flow rates, precipitation, volumes, and levels—the range of interest corresponds to low exceedance probabilities p < 1% [24,38,39]. This is also the range where the behavior of distributions varies, and real data extrapolation processes are strongly influenced by the particularities of statistical distributions and parameter estimation methods. Therefore, the results are presented for values characteristic of this range (left-hand, upper part of the graph).

Tables S4 and S5 of the Supplementary Files show the results obtained with the GEV distribution. It can be seen that the influence of data variability is much more pronounced due to the heavy-tail nature of this distribution.

For the rarest event of interest in hydrology (T = 10,000 years), the bi-axes of the GEV distribution, across the entire domain of the parameters obtained using L-moments, are presented in Table S6 of the Supplementary Files. These values provide crucial insights into the behavior of the GEV distribution when applied to extreme events, particularly those with a very low probability of occurrence. The bi-axes represent the theoretical coefficient of L-variation and L-skewness, which both play a key role in accurately estimating the extreme values of the hydrological data. By using the L-moments method to estimate these statistical indicators, the calibration process ensures that the model remains robust and stable, allowing for more reliable predictions of rare hydrological events.

Table S6 in the Supplementary Files allows for a detailed comparison of these values, providing a deeper understanding of the GEV distribution’s performance in capturing extreme events, which is essential for the design and safety of critical infrastructure like dams and flood control systems.

It can be easily observed that the biases for extreme quantiles (predicted with GEV) varied significantly with data length, with the most notable discrepancies occurring for shorter records, especially for MOM.

These systematic theoretical biases are essential for understanding the uncertainty associated with extreme estimates using the GEV distribution with parameters estimated by MOM and L-moments.

The biases in the tables indicate the systematic deviation (i.e., the average difference between the estimated value and the actual value of the parameter). Negative values indicate a systematic underestimation of the quantiles (i.e., extreme values are smaller than the actual ones). Positive values indicate an overestimation. As n increases the biases tend to approach 0, indicating that the estimates become more precise as more data is available. If the biases are large, the estimates of maximum discharge for a very large T (e.g., 10,000 years) may be significantly wrong—which can have serious implications in the design of hydraulic structures (dams and levees). For small n values (e.g., 20) the deviations are very large, and extremes can be underestimated or overestimated by tens of percent. For large n values (e.g., 90) the estimates become more reliable, and the biases decrease.

These biases (specific percentage values for each distribution) cannot be “avoided,” regardless of how well the method selection was made. Thus, in addition to the uncertainty associated with the process of selecting the best model (distribution and estimation method), it is essential to present these systematic theoretical biases (generally adapted to the statistical indicators of the analyzed series, the distribution model, and the length of the available data series).

In the particular case of the four analyzed case studies and considering the values of the statistical indicator characteristics of the analyzed data series and the lengths of the available data, the biases associated with the values predicted using the GEV distribution (with the L-moments method), solely as a function of this variability in the availability of historical data, are presented in

Table 12. Theoretical biases (%) in L-moment-based GEV estimates due to sample size for the four case studies.

River	Statistical Indicators				Parameters			Quantile
	${\mathit{L}}_1$	${\mathit{\tau }}_2$	${\mathit{\tau }}_3$	${\mathit{\tau }}_4$	$\mathit{\alpha }$	$\mathit{\beta }$	$\mathit{\gamma }$	${\mathit{Q}}_{0.01\mathit{\%}}$
Danube (st. Giurgiu), n = 78	0.02	−0.85	−1.11	−3.12	−1.2	0.71	−0.1	0.6
Danube (st. Drobeta), n = 38	0.11	−1.15	−0.02	−3.71	1.4	1.02	−0.2	0.53
Siret (st. Lungoci), n = 39	0.61	−0.99	1.07	−1.79	−4.3	0.76	−0.94	−1.12
Ialomita (st. Tandarei), n = 33	0.13	−1.97	−2.12	−6.4	−2.5	1.58	−0.81	1.94

. The biases (%, referenced to the theoretical curve values corresponding to a set of 1000 data) are shown both for the estimation of statistical indicators, the three parameters, and for the quantile with an annual exceedance probability of 0.01%.

It can be observed that for similar lengths of the available data series (n = 33, n = 38, and n = 39), the relative differences are still significant, mainly due to the torrentiality and variability of the data, expressed through higher values of the statistical indicators ${\tau }_2$, ${\tau }_3$, and ${\tau }_4$. Nevertheless, the biases in forecasting such a rare event (which in many cases is considered “impossible” in terms of occurrence probability) are extremely small, ranging between 0.53% and 1.94%, once again highlighting the advantages of the L-moments method in flood frequency analysis.

This analysis will help researchers assess how “reliable” the extreme quantiles calculated with GEV are and adjust maximum discharge frequency analyses based on the sample size and chosen method.

6. Conclusions and Recommendations

The results suggest that the GEV distribution can indeed serve as a viable alternative to the Pearson III distribution, particularly when using the L-moments method for parameter estimation.

The GEV distribution is more adaptable for modeling extreme events, especially for return periods of T = 10,000 years, where it consistently outperforms Pearson III in terms of capturing tail behavior.

Regarding higher-parameter distributions like Wakeby (four or five parameters), whilst these models provide more flexibility and stability they also involve solving complex nonlinear systems which can introduce computational challenges [63].

An important advantage of the GEV distribution is that its parameters can be approximated with small errors, simplifying the estimation process compared to the intricate procedures required by higher-parameter models.

The influence of data length is crucial: for short data series GEV with L-moments shows more stability than MOM and yields more realistic extreme quantiles compared to Pearson III. Therefore, the GEV distribution can be a reliable option in flood frequency analysis, especially when longer data series are unavailable or when the complexity of higher-parameter models poses practical challenges.

These results have direct applications in hydrological infrastructure planning, particularly for dam design and flood mitigation strategies. Accurate flood frequency analysis informs the sizing of spillways, the design of retention basins, and the setting of flood protection levels. Misestimating extreme quantiles can result in either overdesign (leading to unnecessary costs) or underdesign (posing safety risks).

The study highlights the stability of the L-moments method for estimating extreme events, suggesting that hydrological designs should prioritize distributions and estimation methods that are less sensitive to data length variability. This is especially important in regions with limited historical data.

The comparison between GEV and Pearson III distributions reveals that using the latter, which is currently the “parent” distribution in Romania, may underestimate rare event magnitudes. Therefore, updating national guidelines to incorporate the GEV distribution—especially for critical infrastructure—is recommended.

In conclusion, the GEV distribution, particularly with L-moments estimation, is a valuable tool for flood frequency analysis. However, for maximum reliability in predicting extreme events, combining the GEV distribution with a higher-parameter reference model like Wakeby is recommended. The results will help researchers gain an understanding of the intrinsic behavior of the GEV distribution in frequency analyses, as well as its correct and robust applicability.

Given the influence of climate change on extreme events, future studies will investigate non-stationary models in which distribution parameters vary over time [64,65,66].

An extension of the analysis to other river basins will be carried out to validate the findings and develop more generalized recommendations. A future direction will also consist of combining statistical distributions with machine learning algorithms to better capture the complex relationships between extreme events and their climatic drivers.