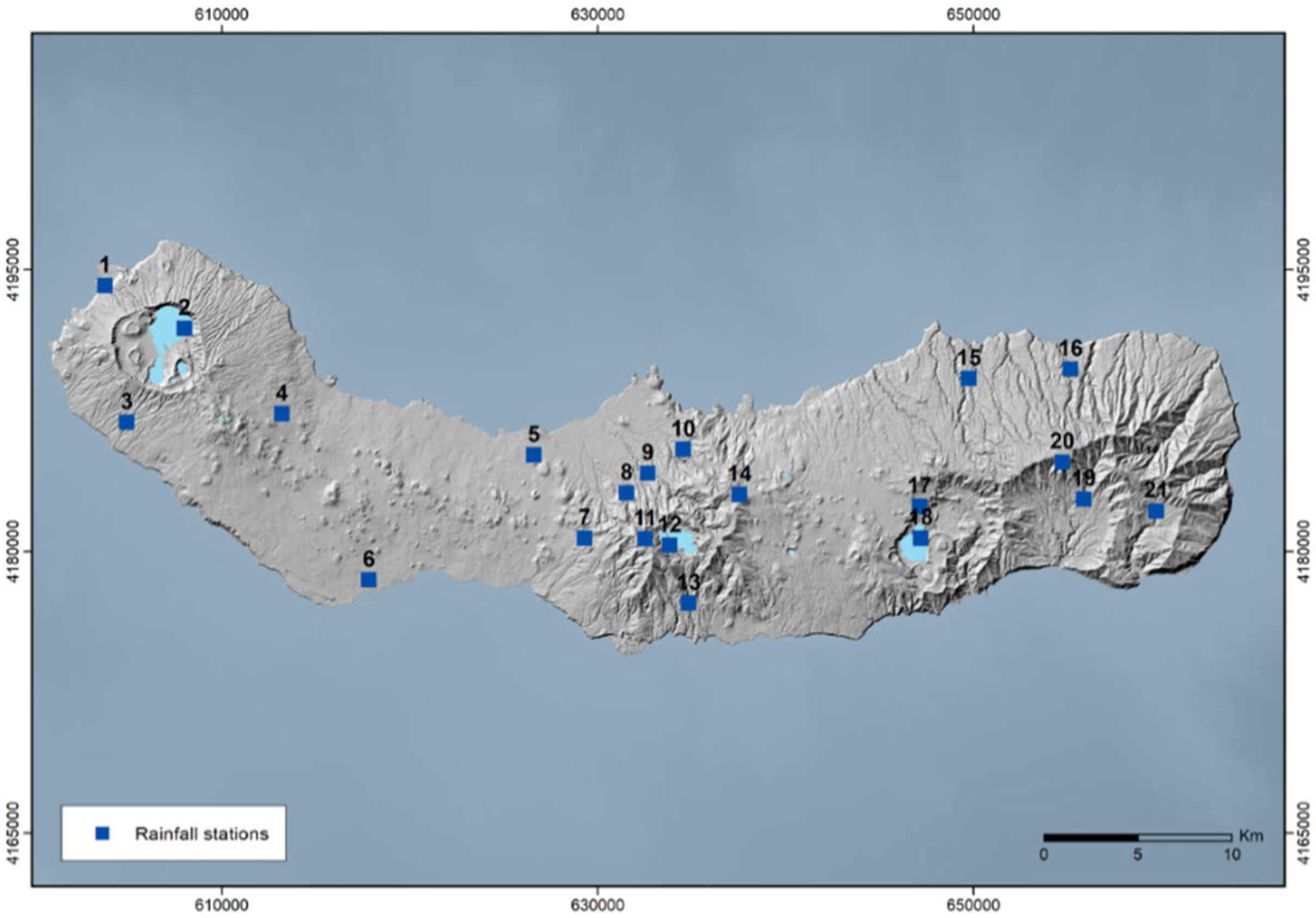
4.2. Clustering of Rainfall Stations and Statistical Analysis
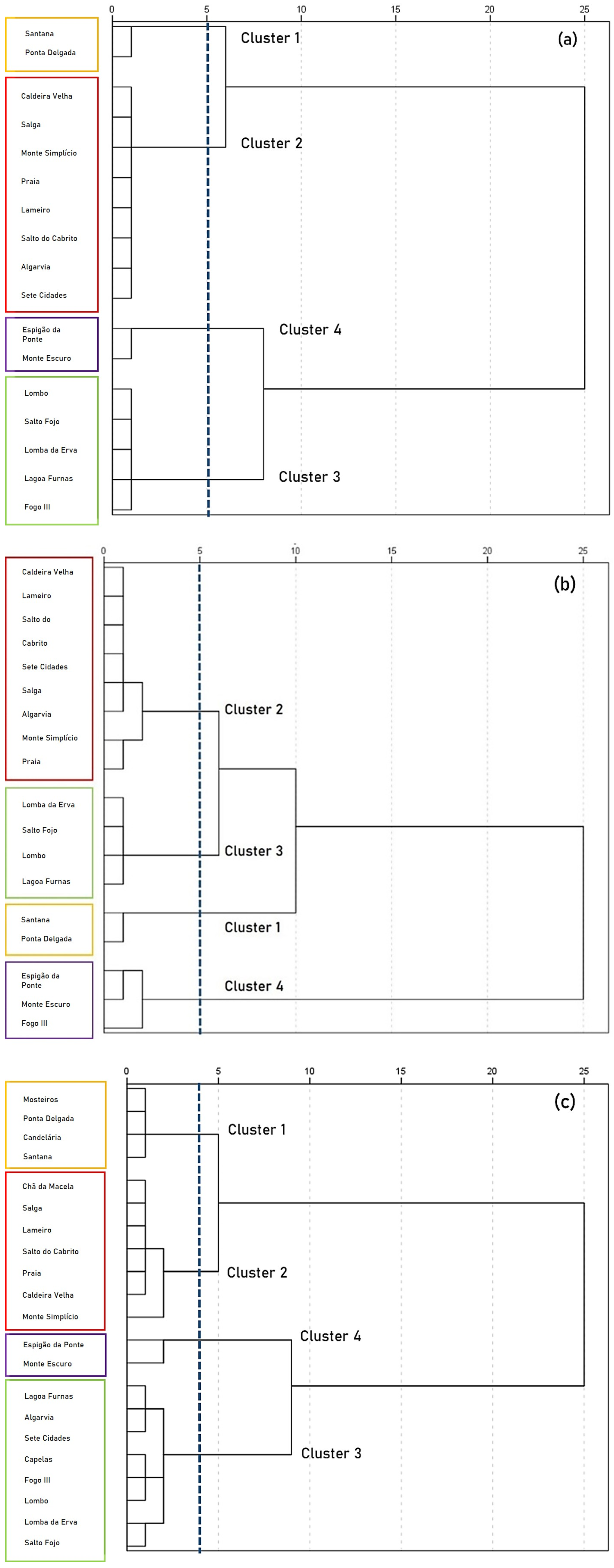
Hierarchical clustering analysis based on Ward’s method identified four main groups of rainfall stations with similar rainfall characteristics (
Figure 5). The clustering structure was validated using the Silhouette Coefficient, calculated for k = 2 to k = 8, confirming that four clusters provide the most appropriate classification (
Figure 6). The average silhouette values were consistently higher for k = 4 across the full dataset (0.55), the oldest sub-dataset (0.55), and the latest sub-dataset (0.48), indicating a good balance between cluster compactness and separation.
For the full dataset (
Figure 5a), Cluster 1 comprises the stations of Santana and Ponta Delgada. Cluster 2 includes eight stations: Caldeira Velha, Salga, Monte Simplício, Praia, Lameiro, Salto do Cabrito, Algarvia, and Sete Cidades. Cluster 3 consists of five stations: Lombo, Salto do Fojo, Lomba da Erva, Lagoa das Furnas, and Fogo III. Lastly, Cluster 4 includes the stations of Monte Escuro and Espigão da Ponte.
In the oldest sub-dataset (
Figure 5b), Clusters 1 and 2 remained unchanged, indicating temporal stability in the rainfall patterns of these stations. However, Clusters 3 and 4 underwent reconfiguration. Cluster 3 includes four stations (Lomba da Erva, Salto do Fojo, Lombo, and Lagoa das Furnas), while Cluster 4 includes three stations (Espigão da Ponte, Monte Escuro, and Fogo III). This shift reflects subtle changes in rainfall behaviour, particularly the migration of Fogo III from Cluster 3 to Cluster 4.
The latest sub-dataset (
Figure 5c) exhibits a more pronounced reorganisation of the clusters. Cluster 1 expands to include four stations: Mosteiros, Ponta Delgada, Candelária, and Santana. Cluster 2 includes seven stations: Chã da Macela, Salga, Lameiro, Salto do Cabrito, Praia, Caldeira Velha, and Monte Simplício. Cluster 3 consists of eight stations: Lagoa das Furnas, Algarvia, Sete Cidades, Capelas, Fogo III, Lombo, Lomba da Erva, and Salto do Fojo. Cluster 4 maintains the same composition as in the full dataset, with the stations of Espigão da Ponte and Monte Escuro.
Out of the 21 stations analysed, 15 remained in the same cluster throughout the periods considered. Overall, Clusters 1 and 4 show a high degree of temporal stability, reflecting persistent rainfall regimes. In contrast, Clusters 2 and 3 exhibit greater variability, with changes in the number and composition of stations over time. Notably, after 2010, Algarvia and Sete Cidades migrated from Cluster 2 to Cluster 3, suggesting increased rainfall in these areas. The transitional behaviour of the Fogo III station, which shifted between Clusters 3 and 4, highlights the sensitivity of stations that are located in more exposed areas to slight variations in atmospheric circulation patterns.
The mean values of the variables used in the analysis (MAP, P10, P50, and P90) for each cluster are summarised in
Table 3. The results highlight the variability in rainfall amounts across different clusters during each considered period. Significant variability in MAP is observed across the clusters. For the full dataset, Cluster 1 exhibits an average MAP of 1059.8 mm, whereas Cluster 4 shows a significantly higher average of 2925.5 mm. Clusters 2 and 3 record average MAP values of 1704.8 mm and 2229.6 mm, respectively. For the oldest sub-dataset, the pattern remains consistent: Cluster 1 maintains a lower average MAP of 1124.2 mm, while Cluster 2 is at 1800.9 mm, Cluster 3 at 2301.0 mm, and Cluster 4 at 2954.4 mm The latest sub-dataset reveals a reduction in overall MAP values and a decrease in the contrast between Clusters 1 and 2, with average MAP vales of 835.8 mm and 1292.6 mm, respectively. Meanwhile, Clusters 3 and 4 also show lower averages compared with previous periods, at 1762.0 mm and 2335.3 mm, respectively. This reduction may indicate a recent shift in rainfall distribution patterns, with a tendency towards drier conditions, especially in the lower-altitude clusters.
The analysis of P10, P50, and P90 values reveals the seasonal fluctuation of rainfall, with higher values typically being recorded in winter, progressively decreasing through spring, and reaching their lowest level in summer. This seasonal trend corroborates the expected annual rainfall cycle. The P10 values are relatively uniform across all seasons and clusters, suggesting a uniformity in the lower limits of rainfall distribution. In contrast, P50 values, representing the median rainfall, show similar trends between clusters in winter and autumn; however, these values diverge significantly in summer, indicating more pronounced differences in median rainfall amounts within each cluster during the drier season. The P90 values, reflecting the upper limits of the rainfall distribution, exhibit significant variability between clusters, particularly in winter and autumn, highlighting the differences in extreme rainfall events across the clusters. During summer, however, differences in P90 values between clusters become less significant, which is consistent with the lower occurrence of extreme rainfall in the drier season.
The coefficient of variation (CV) values of the variables used in the analysis (MAP, P10, P50, and P90) within each cluster are summarised in
Table 4, providing insights into intra-cluster homogeneity. For the full dataset, the rainfall stations in each cluster show high similarity, with CV values generally being less than 15%. Clusters 1 and 3 present lower CV values, indicating greater similarity between the stations within these clusters. In Cluster 2, the P10 variable shows higher CV values in autumn, winter, and summer (18.5%, 18.0%, and 19.3%, respectively). In Cluster 4, the greatest heterogeneity within the cluster is observed in the P10 variable for winter and summer (20.9% and 17.3%, respectively).
For the oldest sub-dataset, the CV values remain generally low across clusters, indicating homogeneity among the rainfall stations that make up each cluster. Notably, in Cluster 1, the P90 in summer shows the highest CV value (17.5%), while in Cluster 2, the P10 in spring is the most different among the rainfall stations in the cluster (20.4%). In Cluster 3, the CV values are lower for all variables, reinforcing its homogeneity. Cluster 4 presents its highest CV values in P10 during spring and summer (15.4% and 18.3%, respectively).
In contrast, the latest sub-dataset shows generally higher CV values, frequently exceeding 15%, which reflects increased heterogeneity within clusters. In Cluster 1, the highest value is observed in the P90 variable for summer (27.3%). Cluster 2 exhibits the most variability in P10 during spring (35.8%). Cluster 3 shows the highest CV in P10 during winter (36.3%), and Cluster 4 exhibits the greatest variation in P50 during winter (37.0%). This rise in CV values corresponds to the inclusion of new rainfall stations into the clusters, whose differing characteristics contribute to increased heterogeneity within each group.
4.3. Spatial Distribution of Rainfall Station Clusters
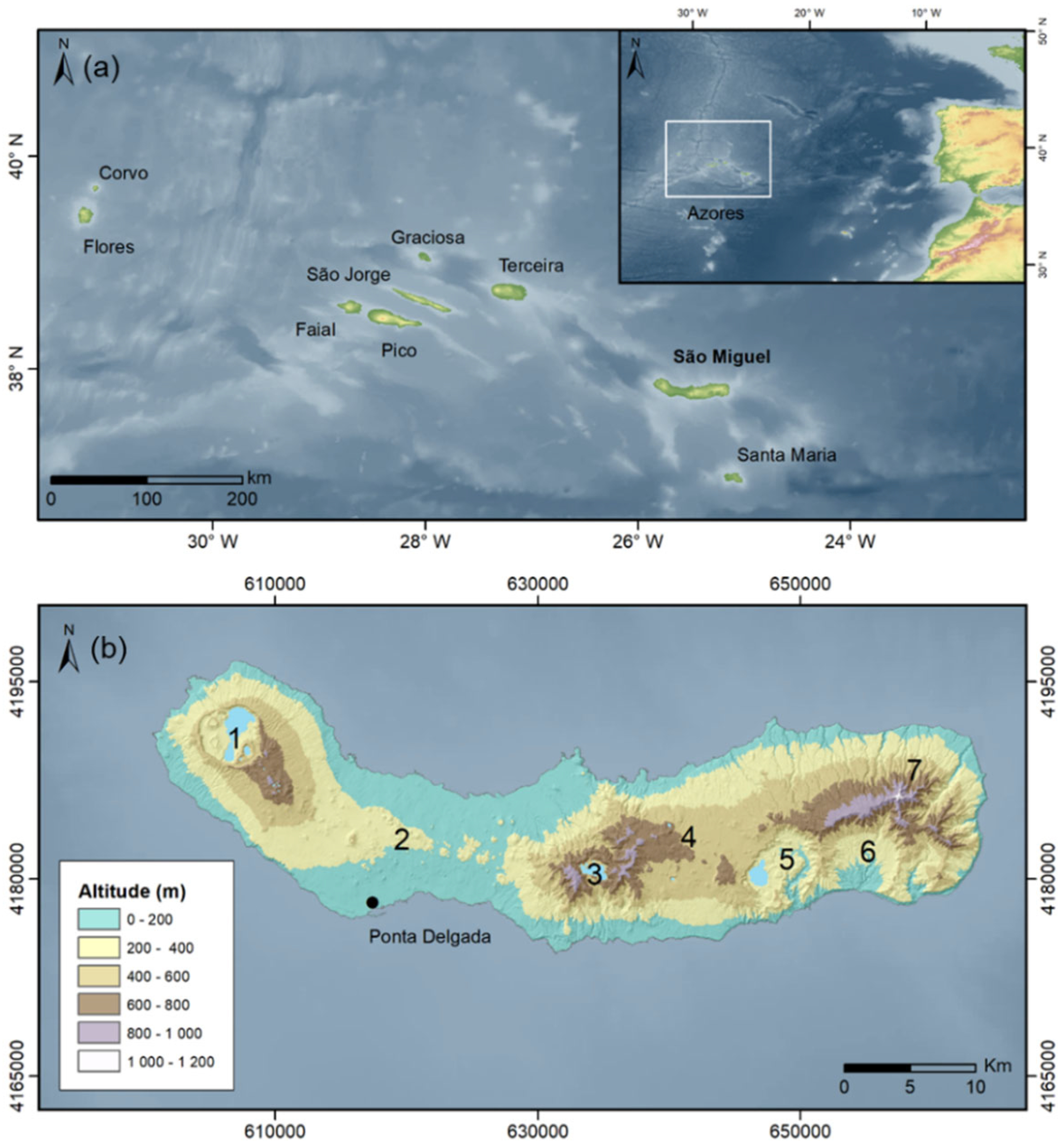
The spatial distribution of the rainfall station clusters provides valuable insights into the relationship between altitude and rainfall patterns across São Miguel Island.
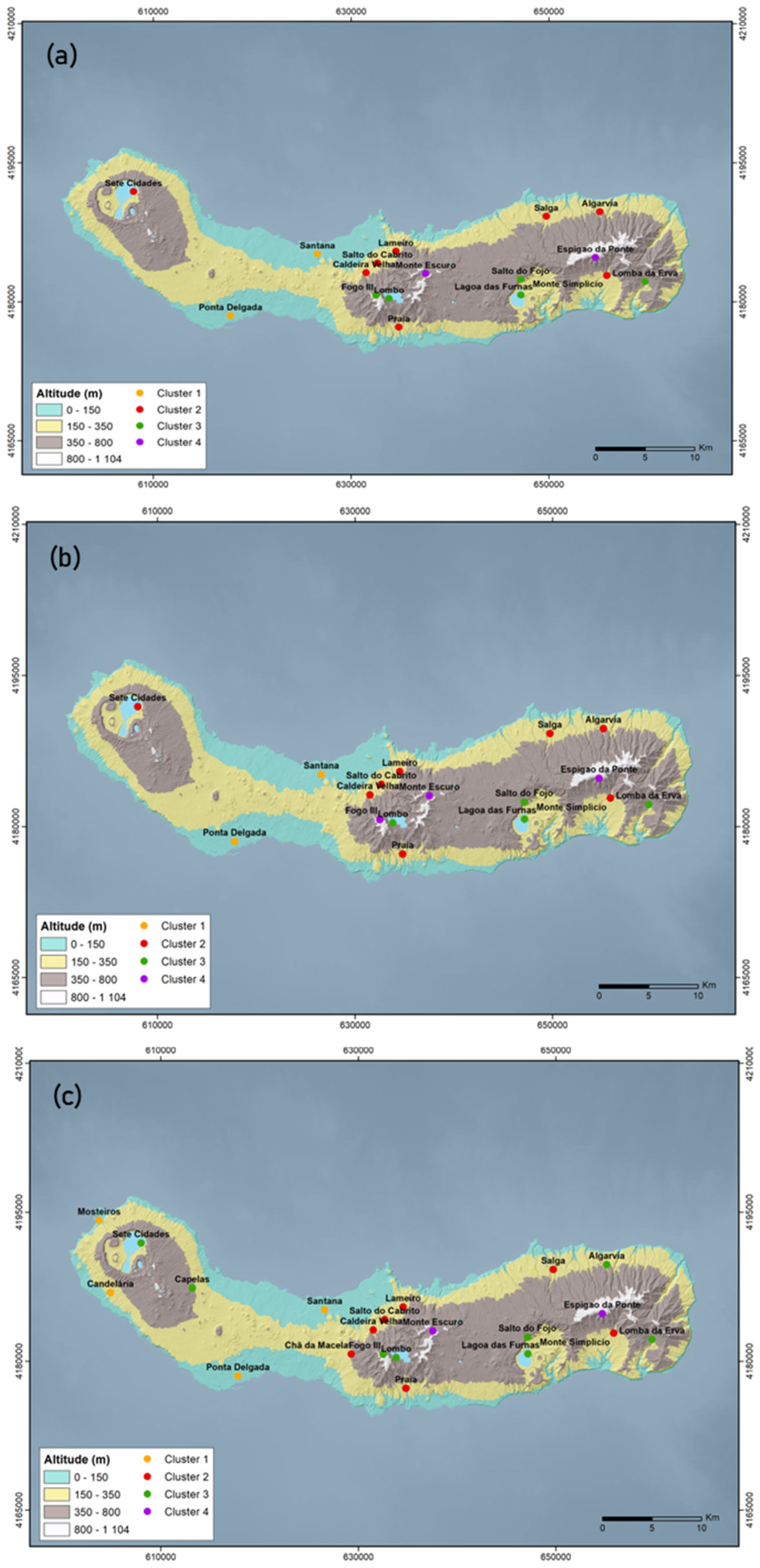
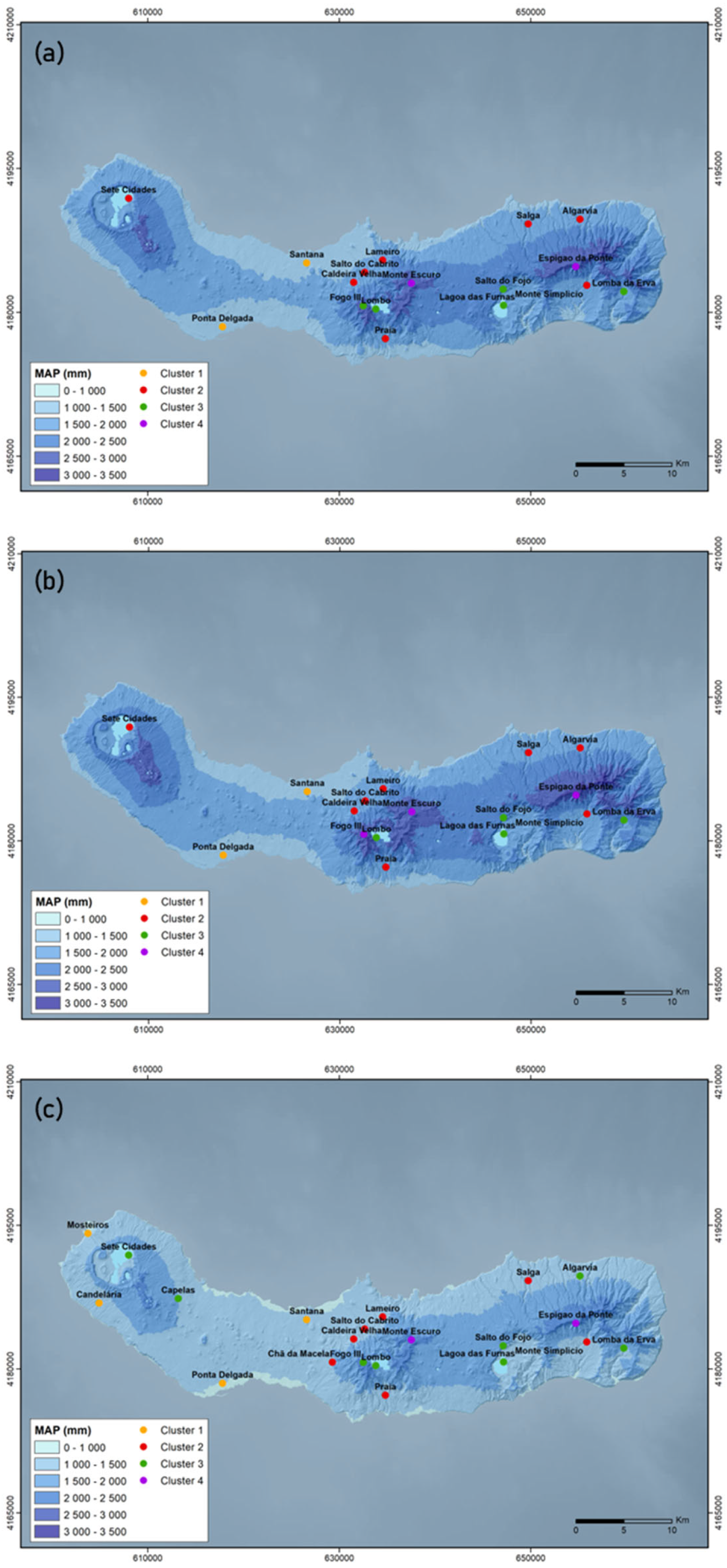
Figure 7 illustrates the spatial distribution of stations within each cluster for the full dataset, the oldest sub-dataset, and the latest sub-dataset, respectively, over the hypsometric map of São Miguel Island.
The analysis of the full dataset (
Figure 7a) indicates that the geographical positioning of stations within Cluster 1 is confined to lower altitudinal zones, specifically below 150 m. Stations belonging to Cluster 2 are located at intermediate altitudes, ranging from 150 to 350 m. Stations within Cluster 3 are found at higher altitudes, between 350 and 800 m, with the notable exceptions of Lagoa das Furnas station, located inside the Furnas Volcano caldera, and Fogo III station, situated near the rim of the Fogo Volcano caldera. Despite their altitudes of 280 and 893 m, respectively, they are included in Cluster 3. Stations grouped into Cluster 4 are found at the highest altitudes on the island, exceeding 800 m. These results suggest that factors beyond altitude are influencing rainfall patterns.
For both the oldest and latest sub-datasets (
Figure 7b,c), Cluster 1 consistently comprises stations located at the lowest altitudes, specifically between 0 and 150 m. Notably, the Candelária station, which is slightly higher at 201 m, is also included in this cluster in the latest sub-dataset (
Figure 7c). Rainfall stations belonging to Cluster 2 are located within the intermediate altitude range of 150 to 350 m, whereas rainfall stations in Cluster 3 are generally found at higher altitudes, between 350 and 800 m, except Lagoa das Furnas station. Despite its altitude of 280 m, it consistently remains within Cluster 3, as observed for the full dataset. The analysis of the latest sub-dataset shows that the Sete Cidades and Algarvia stations, located at altitudes of 260 m and 340 m, respectively, are included in Cluster 3 (
Figure 7c), despite their altitudes aligning more closely with Cluster 2, underscoring the complex relationship between altitude, geographical factors, and rainfall distribution. Stations belonging to Cluster 4 are located at the highest altitudes on the island (above 800 m), with the latest sub-dataset including Fogo III station in Cluster 3, despite its altitude of 893 m (
Figure 7c). This classification emphasises the complex interplay of topography and climate affecting rainfall distribution, suggesting that altitude is a significant, but not exclusive, determinant of rainfall distribution across São Miguel Island.
4.4. Rainfall Trends
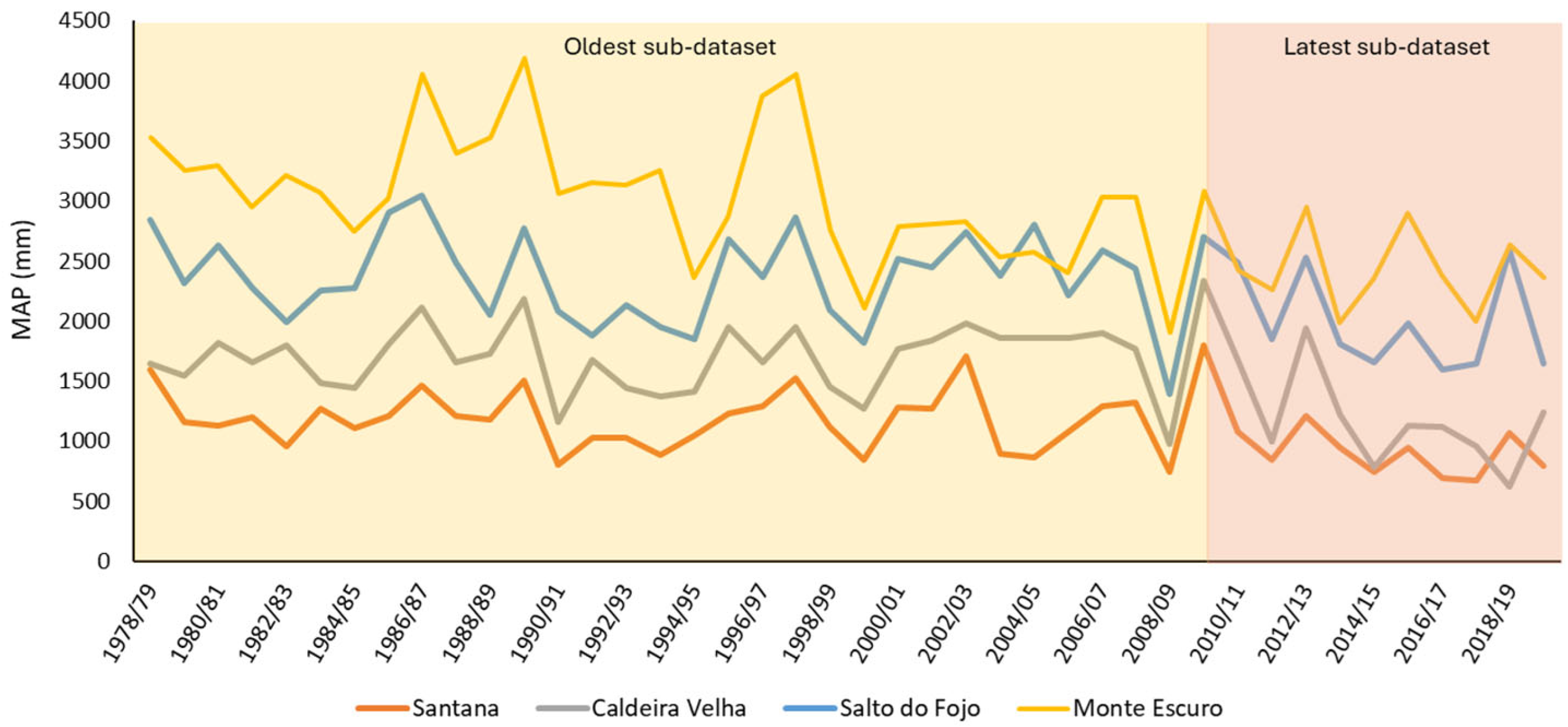
Figure 8 shows the evolution of the Mean Annual Rainfall (MAP) at four representative stations with the most pronounced decreasing rainfall trends—Santana (Cluster 1), Caldeira Velha (Cluster 2), Salto do Fojo (Cluster 3), and Monte Escuro (Cluster 4)—over the climatological years of 1978/79 and 2019/20. During the period corresponding to the oldest sub-dataset (1978/79 to 2009/10), all stations exhibit high interannual variability, reflecting the markedly unstable nature of the regional rainfall regime. However, in the most recent sub-dataset (2010/11 to 2019/20), a general reduction in MAP becomes evident.
Monte Escuro registers the highest annual totals yet shows a declining trend in the most recent decade, particularly with a reduced frequency of years with rainfall exceeding 3000 mm. At Salto do Fojo, the downward trend is more gradual but still evident, with several consecutive years over the last decade in which the rainfall is below the long-term average. At Caldeira Velha, a downward trend in rainfall has also been observed since 2009/10, with several consecutive years recording less than 1200 mm. Santana, while generally exhibiting a more stable pattern, also reveals subtle signs of decreasing rainfall, with an increasing number of recent years registering totals below 1000 mm.
The rate of change in the rainfall variable values between the oldest and latest sub-datasets is summarised in
Table 5, which reveals a pronounced decrease in rainfall values, ranging from 20% to 30%. Nonetheless, differences are observed across variables and clusters. The MAP value exhibits a reduction of approximately 25% across the two sub-datasets. This reduction is most marked in Cluster 2, where it reaches −28.2%. The decrease in rainfall values during autumn is more pronounced in years with lower rainfall levels (P10), particularly in Clusters 1 and 2. In winter, there is a sharp decrease in rainfall in the driest years, ranging from −30% to −55%. In spring, the decrease in rainfall values is more pronounced in years with higher rainfall levels (P90) in all clusters, where the decreases are around −30%. The rates of change in summer are also high, particularly in years with lower levels of rainfall (P10), but yield a diminished impact, due to the season’s typically lower rainfall compared with other periods of the year.
The Mann–Kendall test, paired with Sen’s slope estimator, was used to identify rainfall trends at the 17 stations with data covering the period from 1978/79 to 2019/20. The outcomes, summarised in
Table 6, reveal declining trends in rainfall on both the annual and seasonal scales, with autumn exhibiting the most significant decreases. Although visual inspection of the time series and slope estimates indicates decreasing rainfall at many stations, only 5 of the 17 stations showed statistically significant downward annual trends (α ≤ 0.05), highlighting the spatial heterogeneity of rainfall changes across the island.
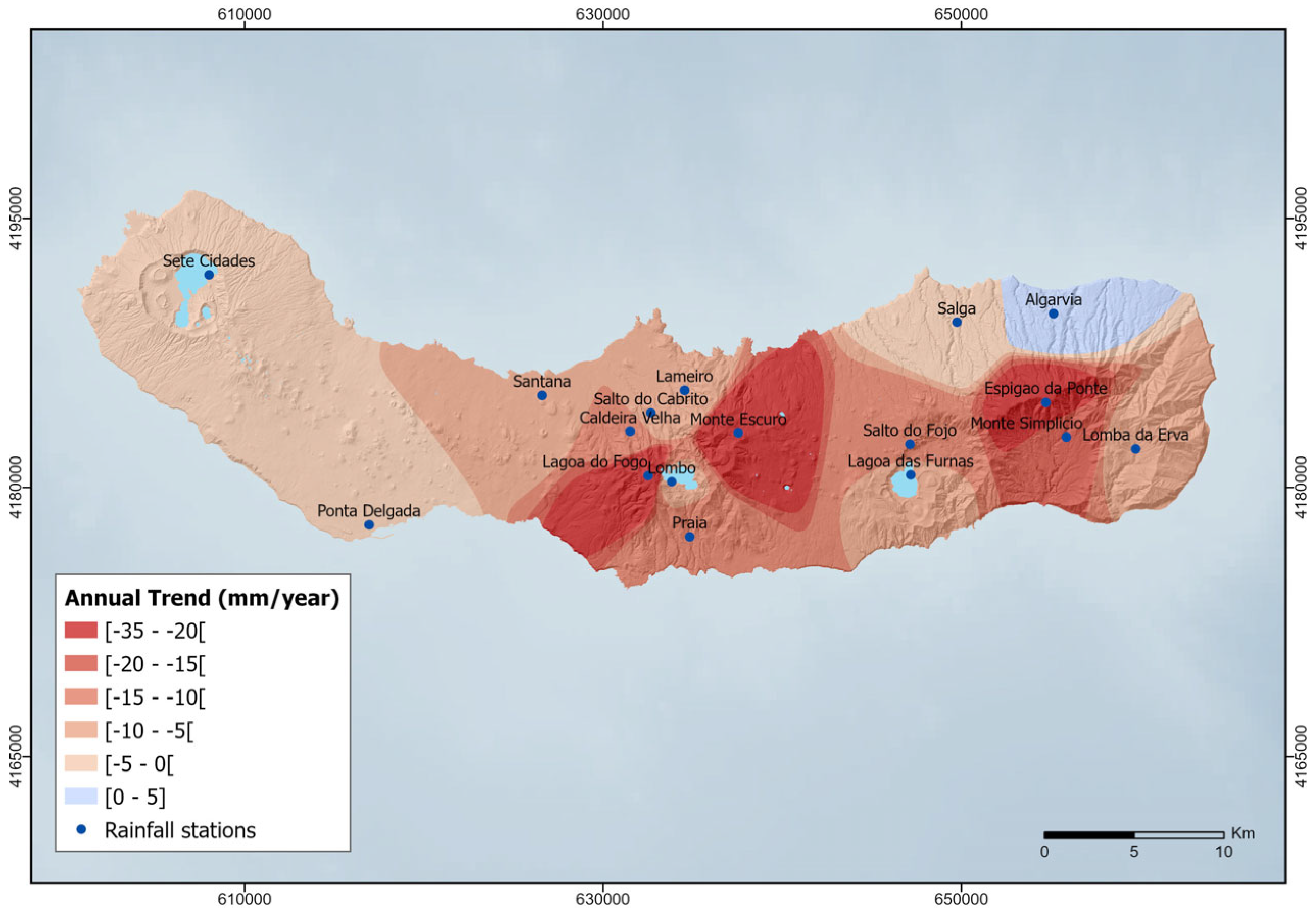
Figure 9 shows the spatial distribution of the annual rainfall trends obtained from the M-K test.
When analysing the rainfall data by clusters, distinct patterns and trends emerge across different regions, underscored by significant changes in rainfall measurements. In Cluster 1, autumn registered the most significant decreases, specifically in Santana (−3.71 mm/year **) and Ponta Delgada (−3.43 mm/year **), pointing to a trend towards drier autumns and an overall reduction in annual rainfall, with Santana being particularly affected. Cluster 2 is characterised by significant reductions, with Monte Simplício showing a notable annual decrease (−19.18 mm/year *). Caldeira Velha exhibits significant decreases in autumn (−6.91 mm/year **), a trend that is also observed at Sete Cidades (−4.19 mm/year *), Lameiro (−4.06 mm/year *), and Salto do Cabrito (−3.96 mm/year *). Moreover, Monte Simplício reveals significant decreases in winter (−7.77 mm/year *) and spring (−5.37 mm/year **), indicating localised environmental changes affecting rainfall patterns. Cluster 3 is highlighted by the severe annual rainfall reduction at Fogo III (−31.57 mm/year ***), along with a considerable decrease at Salto do Fojo (−13.04 mm/year *). This cluster shows the most pronounced rainfall decline across all seasons, especially at Fogo III, with significant reductions in autumn (−12.08 mm/year ***), winter (−10.01 mm/year **), spring (−5.87 mm/year *), and summer (−6.14 mm/year ***). In Cluster 4, Monte Escuro and Espigão da Ponte both show significant annual decreases in rainfall (−25.55 mm/year *** and −21.34 mm/year **, respectively). Monte Escuro also experiences substantial reductions in autumn, spring, and summer (−9.11 mm/year **, −7.10 mm/year *, and −3.57 mm/year *, respectively), while Espigão da Ponte experiences a notable decrease in summer (−4.05 mm/year *). These stations exhibit significant negative variations during summer when compared with other clusters, indicating pronounced seasonal influences on rainfall patterns.
4.5. NAO–Rainfall Relationship
Across the 17 rainfall stations, the Spearman rank correlations reveal a broadly consistent negative association between the Hurrell PC-based NAO index and rainfall, particularly for annual totals and for the autumn season (
Table 7).
During autumn, correlations remain predominantly negative and statistically significant at several stations, such as Lomba da Erva (ρ = −0.46, p < 0.01), Monte Simplício (ρ = −0.43, p < 0.01), Salto Fojo (ρ = −0.44, p < 0.01), and Espigão da Ponte (ρ = −0.41, p = 0.01).
By contrast, winter correlations are generally weaker and mostly non-significant (−0.1 to −0.2), while spring and summer correlations are low and spatially inconsistent.
At the annual scale, most stations exhibit negative coefficients, several of which are statistically significant at the 95% confidence level, notably at Salto do Cabrito (ρ = −0.46, p < 0.01), Ponta Delgada (ρ = −0.38, p = 0.01), Sete Cidades (ρ = −0.33, p = 0.03), Monte Simplício (ρ = −0.33, p = 0.04), Lagoa das Furnas (ρ = −0.35, p = 0.02), and Lomba da Erva (ρ = −0.33, p = 0.04).
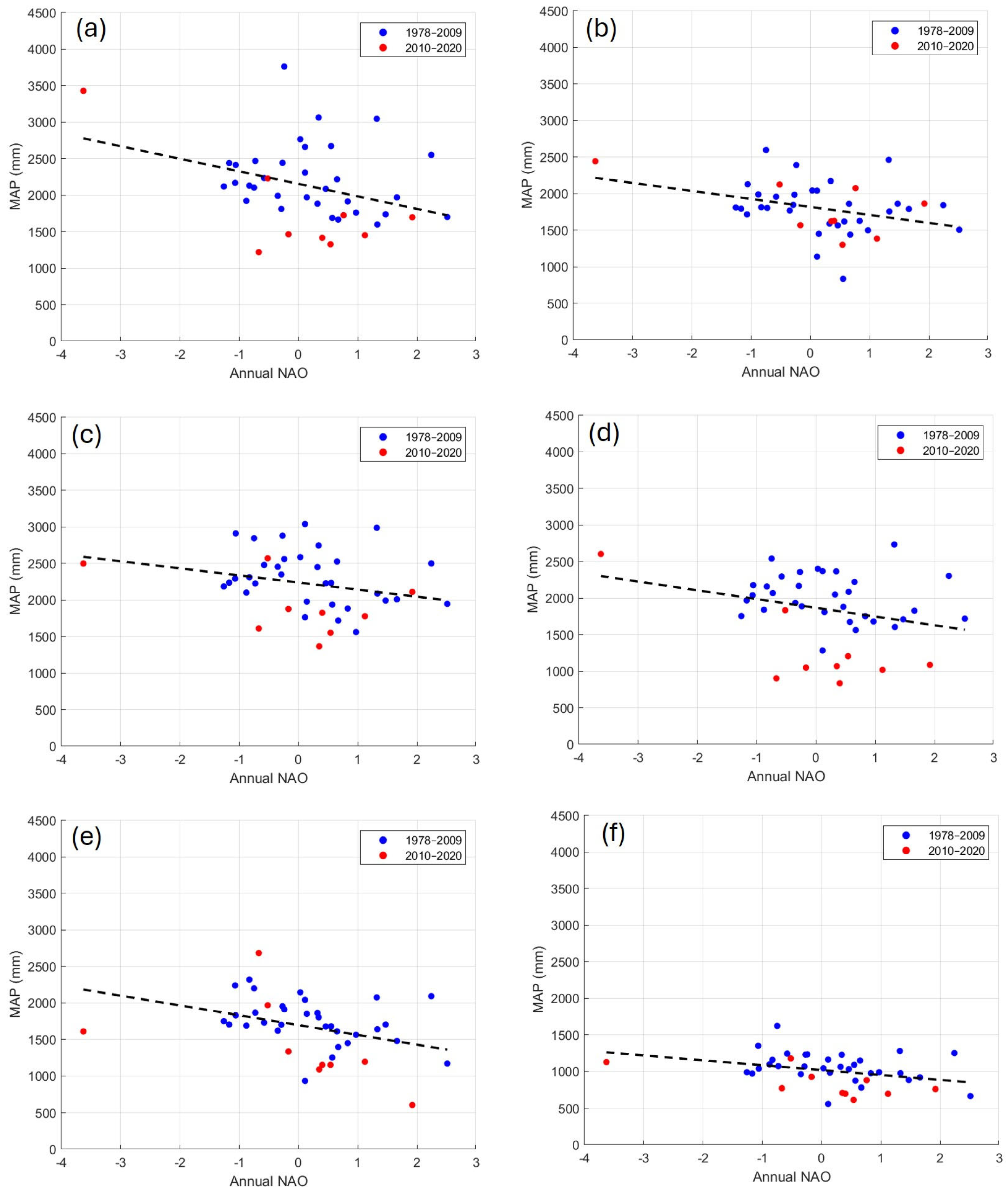
These six stations are illustrated in
Figure 10, which presents scatter plots of annual rainfall versus the NAO index, with data points from the latest sub-dataset (2010–2020) highlighted in red. In general, years with higher NAO values correspond to lower annual rainfall totals. The MAP values in the latest sub-dataset are consistently lower than would be expected.
4.6. Altitude-Rainfall Relationship
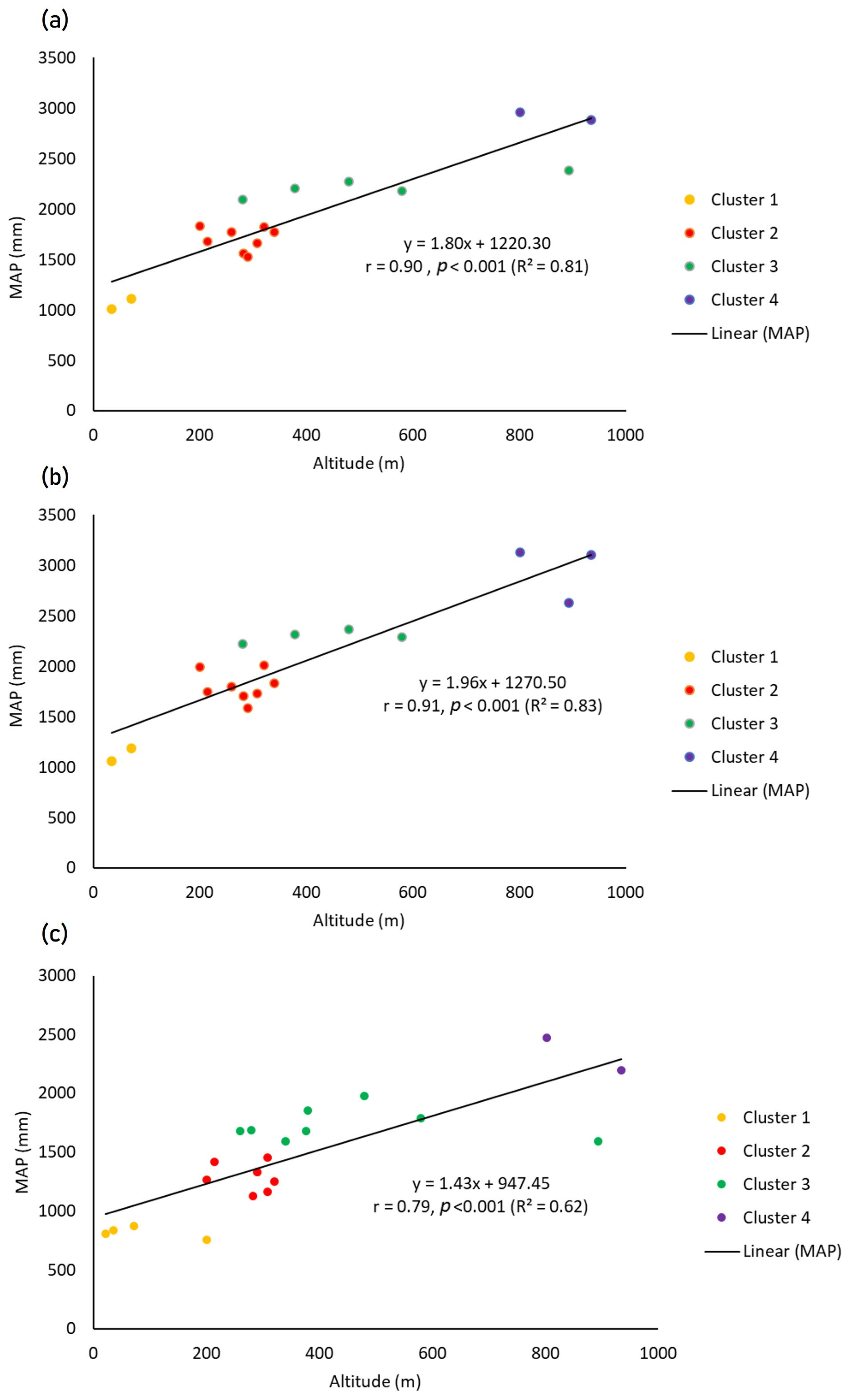
Analysing rainfall’s correlations with altitude provides an insightful examination of the interplay between rainfall metrics and altitude across different climatological periods. As expected, the linear regression analysis, presented in
Figure 11 and
Figure 12, indicates a strong correlation between the various rainfall variables and altitude, highlighting the influence of altitude on rainfall distribution.
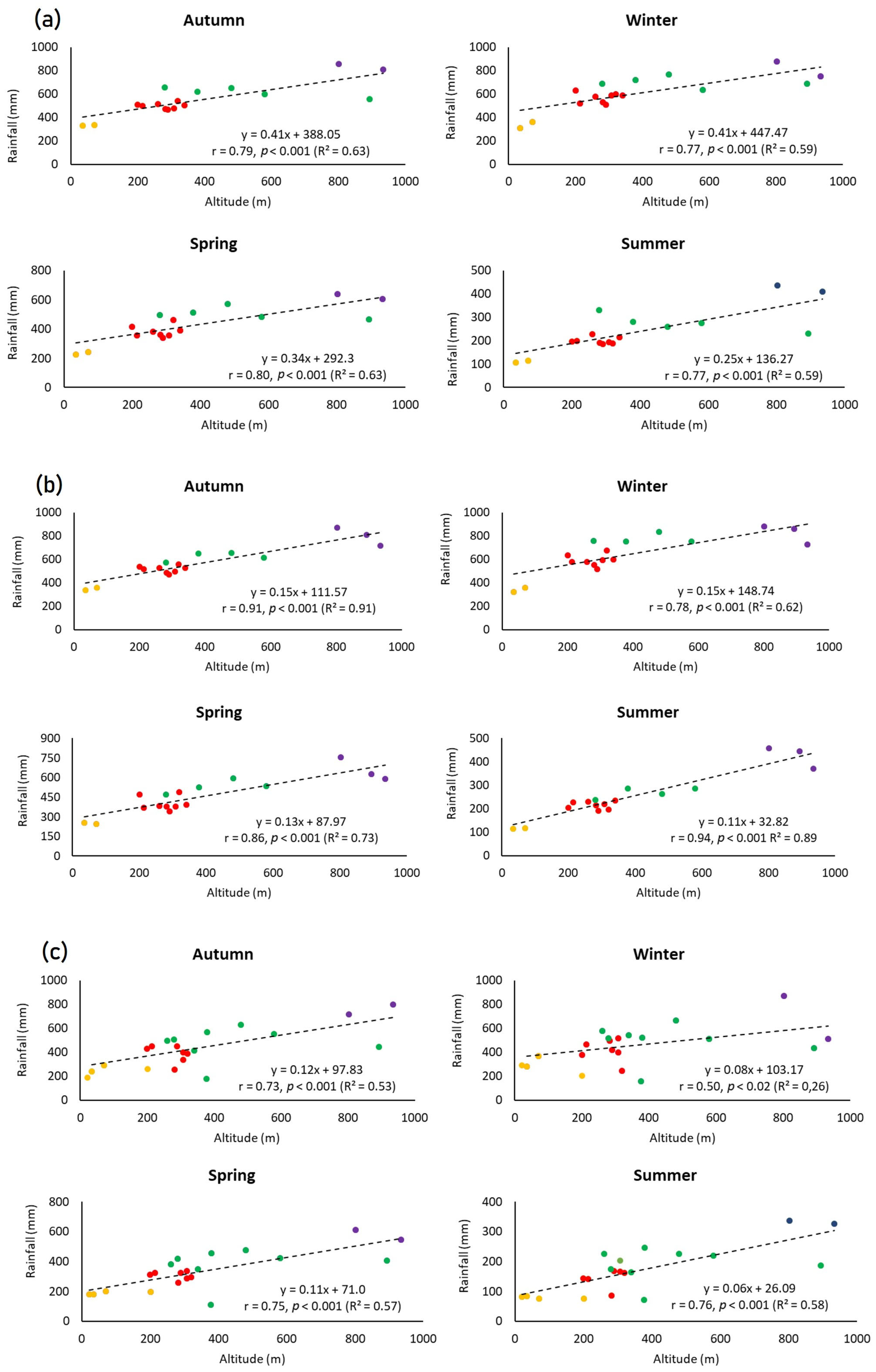
Based on the analysis of the P50 variable (
Figure 11), a positive correlation with altitude is observed across all datasets, with stronger relationships occurring in autumn and summer. Winter and spring show a weaker, though still significant, correlation. For the P10 and P90 variables, the results indicate the same behaviour. This observation suggests the presence of additional physiographic factors, such as the existence of central volcanoes, dismantled calderas, and lakes; geological formations’ alignment; ventilation corridors; vegetation; and the orientation of slopes and sea cliffs, which contribute to the variability of the variables beyond that caused by altitude, which can all play significant roles in determining the intensity and distribution of high-magnitude rainfall events.
For the full dataset, the correlation coefficient between MAP and altitude is 0.81, indicating a strong positive relationship. The linear regression model suggests that MAP increases by approximately 180 mm for every 100 m of elevation gain (
Figure 12a). The spatial distribution of MAP illustrates the altitude influence, with rainfall accumulation ranging from 1120 mm at sea level to 3209 mm at the highest altitude on the island (
Figure 13a), reflecting a clear altitudinal gradient in rainfall.
In the oldest sub-dataset, the correlation coefficient increases slightly to 0.83, suggesting an even stronger altitude influence, with a 196 mm increase in MAP per 100 m elevation gain (
Figure 12b) and rainfall ranging from 1270 mm at sea level to 3444 mm at the highest points on the island (
Figure 13b).
In the latest sub-dataset, the correlation coefficient is 0.62, indicating a slightly weaker but still significant relationship between MAP and altitude. Notably, the rate of increase in rainfall with elevation gain decreases, with MAP rising 144 mm per 100 m altitude gain (
Figure 12c). Rainfall values range from 947 mm at sea level to 2537 mm at the highest altitudes (
Figure 13c), reflecting an overall reduction in rainfall at higher elevations.