It Is Normal: The Probability Distribution of Temperature Extremes
Abstract
1. Introduction
2. Methods
2.1. Temperature Data
2.1.1. Reanalysis
2.1.2. Station Observations
2.2. Temperature Probabilistic Forecasts
2.2.1. The Generalized Extreme Value Distribution
2.2.2. The Normal Distribution
2.2.3. Trend or Stationarity
2.3. Forecast Performance Metric
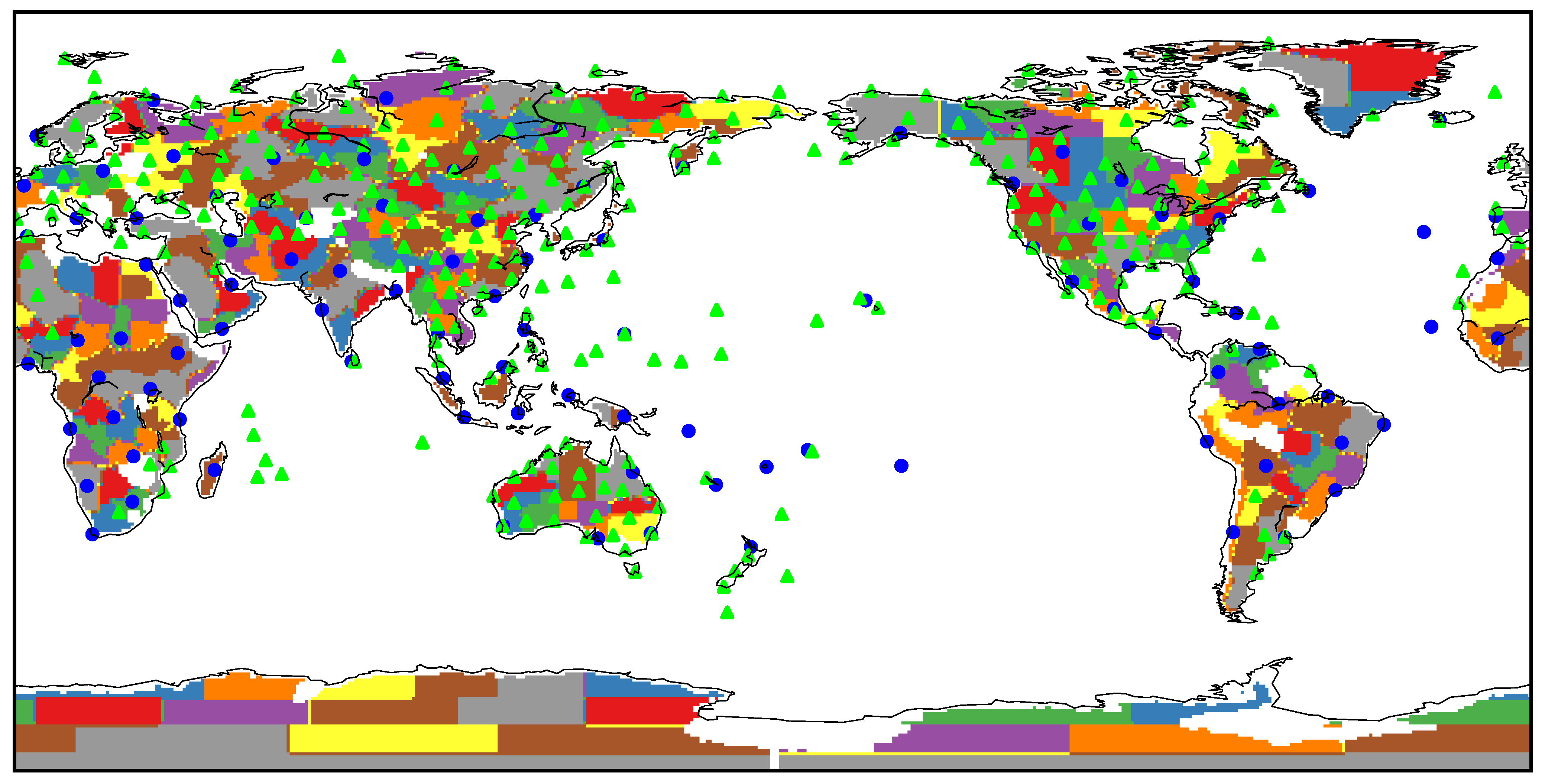
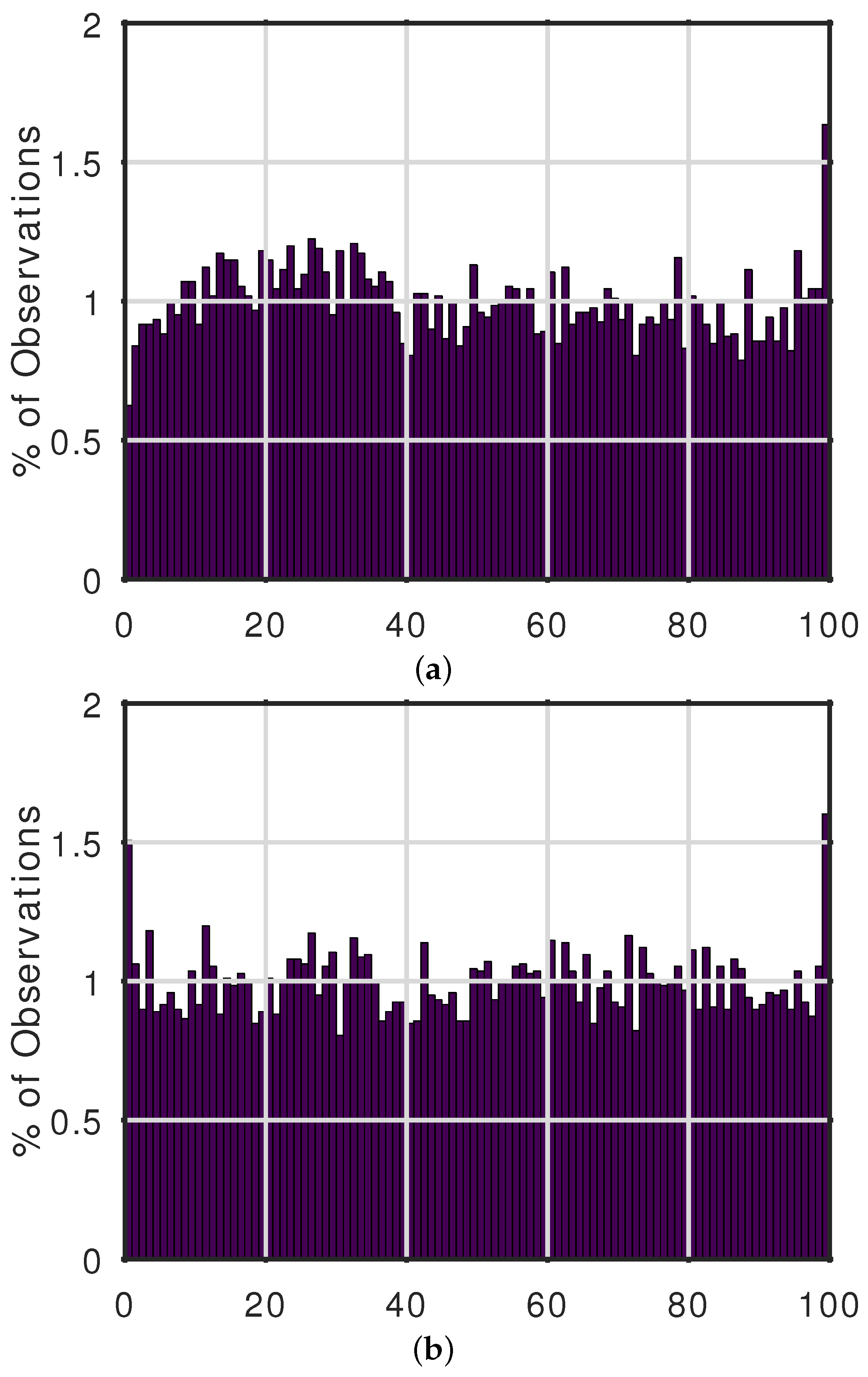
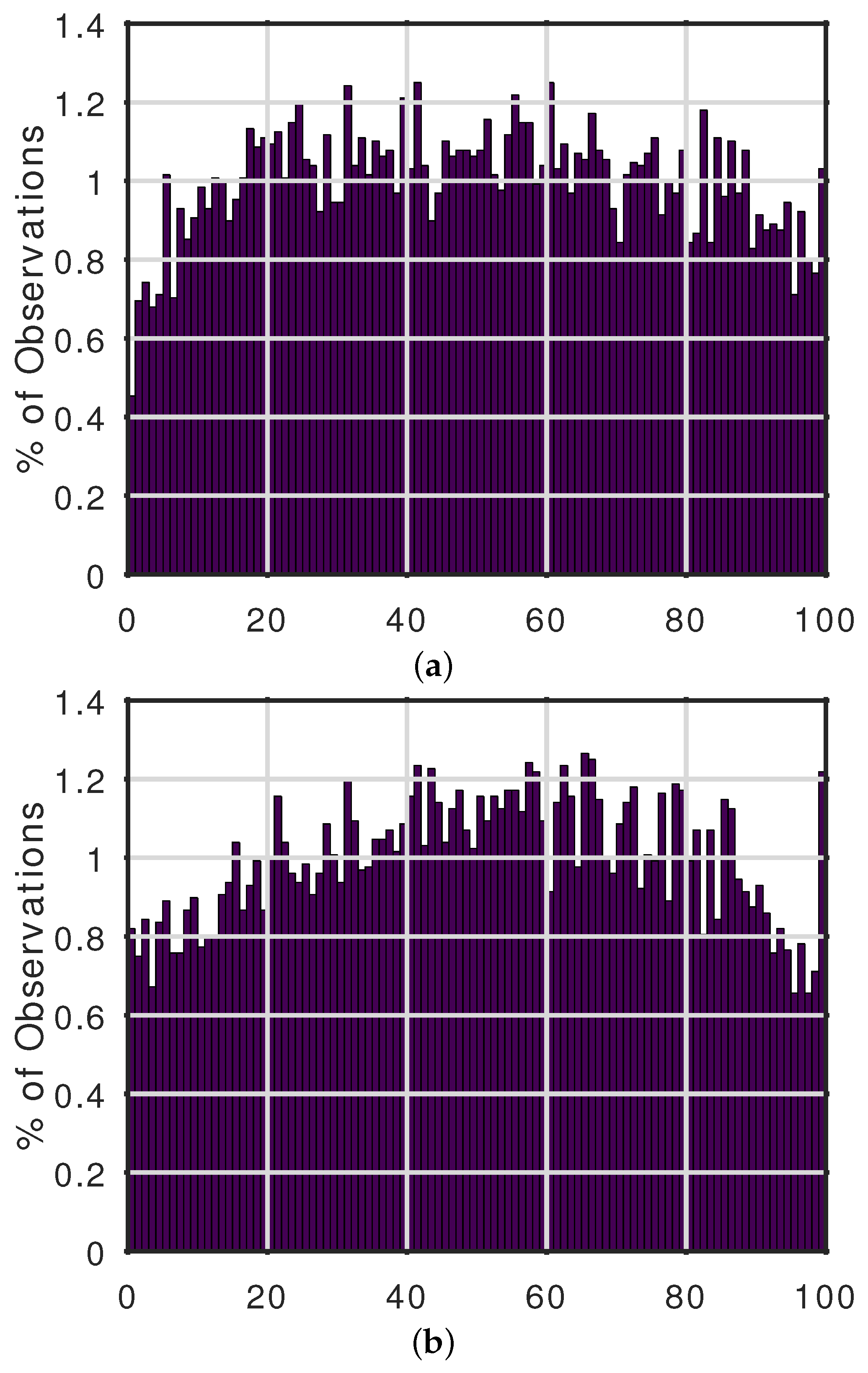
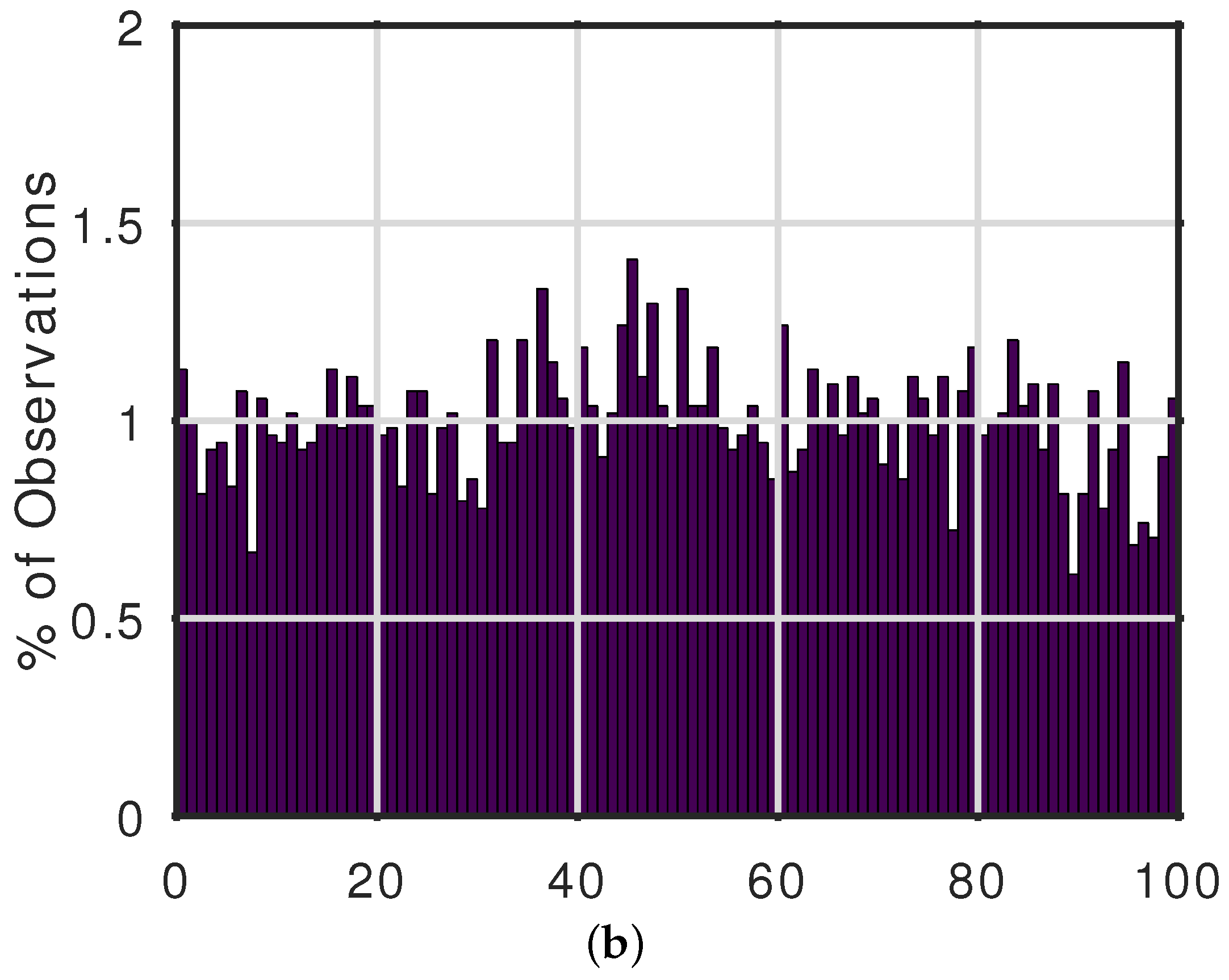
3. Results
4. Discussion
4.1. Why Are Extreme Temperatures So Normal?
4.2. Extensions and Future Research Directions
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nerantzaki, S.D.; Papalexiou, S.M.; Rajulapati, C.R.; Clark, M.P. Nonstationarity in high and low-temperature extremes: Insights from a global observational data set by merging extreme-value methods. Earth’s Future 2023, 11, e2023EF003506. [Google Scholar] [CrossRef]
- Stillman, J.H. Heat waves, the new normal: Summertime temperature extremes will impact animals, ecosystems, and human communities. Physiology 2019, 34, 86–100. [Google Scholar] [CrossRef] [PubMed]
- Thompson, V.; Mitchell, D.; Hegerl, G.C.; Collins, M.; Leach, N.J.; Slingo, J.M. The most at-risk regions in the world for high-impact heatwaves. Nat. Commun. 2023, 14, 2152. [Google Scholar] [CrossRef] [PubMed]
- Matthews, T.K.R.; Wilby, R.L.; Murphy, C. Communicating the deadly consequences of global warming for human heat stress. Proc. Natl. Acad. Sci. USA 2017, 114, 3861–3866. [Google Scholar] [CrossRef]
- Oldenborgh, G.J.V.; Wehner, M.F.; Vautard, R.; Otto, F.E.L.; Seneviratne, S.I.; Stott, P.A.; Hegerl, G.C.; Philip, S.Y.; Kew, S.F. Attributing and projecting heatwaves is hard: We can do better. Earth’s Future 2022, 10, e2021EF002271. [Google Scholar] [CrossRef]
- de Haan, L.; Ferreira, A. Extreme Value Theory; Springer: New York, NY, USA, 2006. [Google Scholar] [CrossRef]
- Klein Tank, A.M.; Zwiers, F.W.; Zhang, X. Guidelines on Analysis of Extremes in a Changing Climate in Support of Informed Decisions for Adaptation; Technical Report; World Meteorological Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Jenkinson, A.F. The frequency distribution of the annual maximum (or minimum) values of meteorological elements. Q. J. R. Meteorol. Soc. 1955, 81, 158–171. [Google Scholar] [CrossRef]
- Hall, P.; Tajvidi, N. Nonparametric analysis of temporal trend when fitting parametric models to extreme value data. Stat. Sci. 2000, 15, 153–167. [Google Scholar] [CrossRef]
- Slater, R.; Freychet, N.; Hegerl, G. Substantial changes in the probability of future annual temperature extremes. Atmos. Sci. Lett. 2021, 22, e1061. [Google Scholar] [CrossRef]
- Castillo-Mateo, J.; Asín, J.; Cebrián, A.C.; Mateo-Lázaro, J.; Abaurrea, J. Bayesian variable selection in generalized extreme value regression: Modeling annual maximum temperature. Mathematics 2023, 11, 759. [Google Scholar] [CrossRef]
- Rai, S.; Hoffman, A.; Lahiri, S.; Nychka, D.W.; Sain, S.R.; Bandyopadhyay, S. Fast parameter estimation of generalized extreme value distribution using neural networks. Environmetrics 2024, 35, e2845. [Google Scholar] [CrossRef]
- Cannon, A.J. A flexible nonlinear modelling framework for nonstationary generalized extreme value analysis in hydroclimatology. Hydrol. Process. 2009, 24, 673–685. [Google Scholar] [CrossRef]
- Otto, F.E.L.; Massey, N.; van Oldenborgh, G.J.; Jones, R.G.; Allen, M.R. Reconciling two approaches to attribution of the 2010 Russian heat wave. Geophys. Res. Lett. 2012, 39, L04702. [Google Scholar] [CrossRef]
- Fischer, E.M.; Knutti, R. Anthropogenic contribution to global occurrence of heavy-precipitation and high-temperature extremes. Nat. Clim. Change 2015, 5, 560–564. [Google Scholar] [CrossRef]
- Zhang, L.; Yu, X.; Zhou, T.; Zhang, W.; Hu, S.; Clark, R. Understanding and attribution of extreme heat and drought events in 2022: Current situation and future challenges. Adv. Atmos. Sci. 2023, 40, 1941–1951. [Google Scholar] [CrossRef]
- Tejedor, E.; Benito, G.; Serrano-Notivoli, R.; González-Rouco, F.; Esper, J.; Büntgen, U. Recent heatwaves as a prelude to climate extremes in the western Mediterranean region. NPJ Clim. Atmos. Sci. 2024, 7, 218. [Google Scholar] [CrossRef]
- Philip, S.; Kew, S.; van Oldenborgh, G.J.; Otto, F.; Vautard, R.; van der Wiel, K.; King, A.; Lott, F.; Arrighi, J.; Singh, R.; et al. A protocol for probabilistic extreme event attribution analyses. Adv. Stat. Climatol. Meteorol. Oceanogr. 2020, 6, 177–203. [Google Scholar] [CrossRef]
- van Oldenborgh, G.J.; van der Wiel, K.; Kew, S.; Philip, S.; Otto, F.; Vautard, R.; King, A.; Lott, F.; Arrighi, J.; Singh, R.; et al. Pathways and pitfalls in extreme event attribution. Clim. Change 2021, 166, 13. [Google Scholar] [CrossRef]
- Philip, S.Y.; Kew, S.F.; van Oldenborgh, G.J.; Anslow, F.S.; Seneviratne, S.I.; Vautard, R.; Coumou, D.; Ebi, K.L.; Arrighi, J.; Singh, R.; et al. Rapid attribution analysis of the extraordinary heat wave on the Pacific coast of the US and Canada in June 2021. Earth Syst. Dyn. 2022, 13, 1689–1713. [Google Scholar] [CrossRef]
- Bercos-Hickey, E.; O’Brien, T.A.; Wehner, M.F.; Zhang, L.; Patricola, C.M.; Huang, H.; Risser, M.D. Anthropogenic contributions to the 2021 Pacific Northwest heatwave. Geophys. Res. Lett. 2022, 49, e2022GL099396. [Google Scholar] [CrossRef]
- Zeder, J.; Sippel, S.; Pasche, O.C.; Engelke, S.; Fischer, E.M. The effect of a short observational record on the statistics of temperature extremes. Geophys. Res. Lett. 2023, 50, e2023GL104090. [Google Scholar] [CrossRef]
- Bruhn, J.A.; Fry, W.E.; Fick, G.W. Simulation of daily weather data using theoretical probability distributions. J. Appl. Meteorol. 1980, 19, 1029–1036. [Google Scholar] [CrossRef]
- Harmel, R.D.; Richardson, C.W.; Hanson, C.L.; Johnson, G.L. Evaluating the adequacy of simulating maximum and minimum daily air temperature with the normal distribution. J. Appl. Meteorol. 2002, 41, 744–753. [Google Scholar] [CrossRef]
- Corobov, R.; Overcenco, A. To normality of air temperature distribution with an emphasis on extremes. In Academician Eugene Fiodorov–100 Years: Collection of Scientific Articles; Eco-TIRAS: Bendery, Moldova, 2010; pp. 36–42. [Google Scholar]
- Krakauer, N.Y.; Devineni, N. Up-to-date probabilistic temperature climatologies. Environ. Res. Lett. 2015, 10, 024014. [Google Scholar] [CrossRef]
- Singh, T.; Saha, U.; Prasad, V.; Gupta, M.D. Assessment of newly-developed high resolution reanalyses (IMDAA, NGFS and ERA5) against rainfall observations for Indian region. Atmos. Res. 2021, 259, 105679. [Google Scholar] [CrossRef]
- Mistry, M.N.; Schneider, R.; Masselot, P.; Royé, D.; Armstrong, B.; Kyselý, J.; Orru, H.; Sera, F.; Tong, S.; Lavigne, É.; et al. Comparison of weather station and climate reanalysis data for modelling temperature-related mortality. Sci. Rep. 2022, 12, 5178. [Google Scholar] [CrossRef]
- Hersbach, H.; de Rosnay, P.; Bell, B.; Schepers, D.; Simmons, A.; Soci, C.; Abdalla, S.; Alonso-Balmaseda, M.; Balsamo, G.; Bechtold, P.; et al. Operational Global Reanalysis: Progress, Future Directions and Synergies with NWP; Technical Report 27; ECMWF: Reading, UK, 2018. [Google Scholar] [CrossRef]
- ERA5 Reanalysis (0.25 Degree Latitude-Longitude Grid). 2024. Available online: https://rda.ucar.edu/datasets/d633000/ (accessed on 1 June 2024). [CrossRef]
- Kennedy-Asser, A.T.; Andrews, O.; Mitchell, D.M.; Warren, R.F. Evaluating heat extremes in the UK Climate Projections (UKCP18). Environ. Res. Lett. 2020, 16, 014039. [Google Scholar] [CrossRef]
- Rogers, C.D.W.; Ting, M.; Li, C.; Kornhuber, K.; Coffel, E.D.; Horton, R.M.; Raymond, C.; Singh, D. Recent increases in exposure to extreme humid-heat events disproportionately affect populated regions. Geophys. Res. Lett. 2021, 48, e2021GL094183. [Google Scholar] [CrossRef]
- Speizer, S.; Raymond, C.; Ivanovich, C.; Horton, R.M. Concentrated and intensifying humid heat extremes in the IPCC AR6 regions. Geophys. Res. Lett. 2022, 49, e2021GL097261. [Google Scholar] [CrossRef]
- Kong, Q.; Huber, M. Regimes of soil moisture-wet bulb temperature coupling with relevance to moist heat stress. J. Clim. 2023, 36, 7925–7942. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Amplification of extreme hot temperatures over recent decades. Climate 2023, 11, 42. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Extending the blended generalized extreme value distribution. Discov. Civ. Eng. 2024, 1, 97. [Google Scholar] [CrossRef]
- Doxsey-Whitfield, E.; MacManus, K.; Adamo, S.B.; Pistolesi, L.; Squires, J.; Borkovska, O.; Baptista, S.R. Taking advantage of the improved availability of census data: A first look at the Gridded Population of the World, Version 4. Pap. Appl. Geogr. 2015, 1, 226–234. [Google Scholar] [CrossRef]
- Center For International Earth Science Information Network-CIESIN-Columbia University. Gridded Population of the World, Version 4 (GPWv4): Population count, Revision 11, 2018. Available online: https://earthdata.nasa.gov/data/catalog/sedac-ciesin-sedac-gpwv4-popcount-r11-4.11 (accessed on 1 June 2024).
- Cattiaux, J.; Ribes, A.; Thompson, V. Searching for the most extreme temperature events in recent history. Bull. Am. Meteorol. Soc. 2024, 105, E239–E256. [Google Scholar] [CrossRef]
- Stone, D.A. A hierarchical collection of political/economic regions for analysis of climate extremes. Clim. Change 2019, 155, 639–656. [Google Scholar] [CrossRef]
- Durre, I.; Menne, M.J.; Gleason, B.E.; Houston, T.G.; Vose, R.S. Comprehensive automated quality assurance of daily surface observations. J. Appl. Meteorol. Climatol. 2010, 49, 1615–1633. [Google Scholar] [CrossRef]
- Menne, M.; Durre, I.; Vose, R.; Gleason, B.; Houston, T. An overview of the Global Historical Climatology Network-Daily database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Jaffrés, J.B. GHCN-Daily: A treasure trove of climate data awaiting discovery. Comput. Geosci. 2019, 122, 35–44. [Google Scholar] [CrossRef]
- Kotz, S.; Nadarajah, S. Extreme Value Distributions: Theory and Applications; Imperial College Press: London, UK, 2000. [Google Scholar]
- Beirlant, J.; Goegebeur, Y.; Teugels, J.; Segers, J. Statistics of Extremes: Theory and Applications; Wiley: Hoboken, NJ, USA, 2004. [Google Scholar] [CrossRef]
- Rohde, R.; Muller, R.; Jacobsen, R.; Perlmutter, S.; Rosenfeld, A.; Wurtele, J.; Curry, J.; Wickham, C.; Mosher, S. Berkeley Earth temperature averaging process. Geoinf. Geostat. Overv. 2013, 1, 1000103. [Google Scholar] [CrossRef]
- Rohde, R.; Muller, R.A.; Jacobsen, R.; Muller, E.; Perlmutter, S.; Rosenfeld, A.; Wurtele, J.; Groom, D.; Wickham, C. A new estimate of the average Earth surface land temperature spanning 1753 to 2011. Geoinf. Geostat. Overv. 2013, 1, 1000101. [Google Scholar] [CrossRef]
- Martins, E.S.; Stedinger, J.R. Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour. Res. 2000, 36, 737. [Google Scholar] [CrossRef]
- Ailliot, P.; Thompson, C.; Thomson, P. Mixed methods for fitting the GEV distribution. Water Resour. Res. 2011, 47, W05551. [Google Scholar] [CrossRef]
- Smith, R.l. Maximum likelihood estimation in a class of nonregular cases. Biometrika 1985, 72, 67–90. [Google Scholar] [CrossRef]
- Castillo, E.; Hadi, A.S. Parameter and quantile estimation for the generalized extreme-value distribution. Environmetrics 1994, 5, 417–432. [Google Scholar] [CrossRef]
- Coles, S.G.; Dixon, M.J. Likelihood-based inference for extreme value models. Extremes 1999, 2, 5–23. [Google Scholar] [CrossRef]
- Lee, Y.; Shin, Y.; Park, J.S. A data-adaptive maximum penalized likelihood estimation for the generalized extreme value distribution. Commun. Stat. Appl. Methods 2017, 24, 493–505. [Google Scholar] [CrossRef]
- Gelman, A.; Hill, J. Data Analysis Using Regression and Multilevel/Hierarchical Models; Cambridge University Press: Cambridge, UK, 2006; ISBN 052168689X. [Google Scholar]
- Yoon, S.; Cho, W.; Heo, J.H.; Kim, C.E. A full Bayesian approach to generalized maximum likelihood estimation of generalized extreme value distribution. Stoch. Environ. Res. Risk Assess. 2010, 24, 761–770. [Google Scholar] [CrossRef]
- Tokdar, S.T.; Kass, R.E. Importance sampling: A review. WIREs Comput. Stat. 2009, 2, 54–60. [Google Scholar] [CrossRef]
- Koch, K.R. Introduction to Bayesian Statistics, 2nd ed.; updated and enlarged edition ed.; Springer: Berlin/Heidelberg, Germany, 2007; p. 250. [Google Scholar]
- Krakauer, N.Y.; Grossberg, M.D.; Gladkova, I.; Aizenman, H. Information content of seasonal forecasts in a changing climate. Adv. Meteorol. 2013, 2013, 480210. [Google Scholar] [CrossRef]
- Aizenman, H.; Grossberg, M.D.; Krakauer, N.Y.; Gladkova, I. Ensemble forecasts: Probabilistic seasonal forecasts based on a model ensemble. Climate 2016, 4, 19. [Google Scholar] [CrossRef]
- Benedetti, R. Scoring rules for forecast verification. Mon. Weather Rev. 2010, 138, 203–211. [Google Scholar] [CrossRef]
- Tödter, J. New Aspects of Information Theory in Probabilistic Forecast Verification. Master’s Thesis, Goethe University, Frankfurt am Main, Germany, 2011. [Google Scholar]
- Prates, F.; Buizza, R. PRET, the Probability of RETurn: A new probabilistic product based on generalized extreme-value theory. Q. J. R. Meteorol. Soc. 2011, 137, 521–537. [Google Scholar] [CrossRef]
- Dong, Q. Calibration and quantitative forecast of extreme daily precipitation using the extreme forecast index (EFI). J. Geosci. Environ. Prot. 2018, 6, 143–164. [Google Scholar] [CrossRef]
- Efron, B.; Gong, G. A leisurely look at the bootstrap, the jackknife, and cross-validation. Am. Stat. 1983, 37, 36–48. [Google Scholar] [CrossRef]
- Embrechts, P.; Resnick, S.I.; Samorodnitsky, G. Extreme value theory as a risk management tool. N. Am. Actuar. J. 1999, 3, 30–41. [Google Scholar] [CrossRef]
- Chen, W.; Zhao, X.; Zhou, M.; Chen, H.; Ji, Q.; Cheng, W. Statistical inference and application of asymmetrical generalized Pareto distribution based on peaks-over-threshold modela. Symmetry 2024, 16, 365. [Google Scholar] [CrossRef]
- Cherkassky, V.; Mulier, F. Learning from Data: Concepts, Theory, and Methods; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- van den Dool, H.; Becker, E.; Chen, L.C.; Zhang, Q. The probability anomaly correlation and calibration of probabilistic forecasts. Weather Forecast 2017, 32, 199–206. [Google Scholar] [CrossRef]
- Singh, A.; Sahoo, R.K.; Nair, A.; Mohanty, U.C.; Rai, R.K. Assessing the performance of bias correction approaches for correcting monthly precipitation over India through coupled models. Meteorol. Appl. 2017, 24, 326–337. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V. The shifting probability distribution of global daytime and night-time temperatures. Geophys. Res. Lett. 2012, 39, L14707. [Google Scholar] [CrossRef]
- Ruff, T.W.; Neelin, J.D. Long tails in regional surface temperature probability distributions with implications for extremes under global warming. Geophys. Res. Lett. 2012, 39, L04704. [Google Scholar] [CrossRef]
- Nadarajah, S. A generalized normal distribution. J. Appl. Stat. 2005, 32, 685–694. [Google Scholar] [CrossRef]
- Azzalini, A. The skew-normal distribution and related multivariate families. Scand. J. Stat. 2005, 32, 159–188. [Google Scholar] [CrossRef]
- McKinnon, K.A.; Rhines, A.; Tingley, M.P.; Huybers, P. The changing shape of Northern Hemisphere summer temperature distributions. J. Geophys. Res. Atmos. 2016, 121, 8849–8868. [Google Scholar] [CrossRef]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.J.; Shepherd, T.G. Changes in Northern Hemisphere temperature variability shaped by regional warming patterns. Nat. Geosci. 2020, 13, 414–421. [Google Scholar] [CrossRef]
- Mishra, V.; Ganguly, A.R.; Nijssen, B.; Lettenmaier, D.P. Changes in observed climate extremes in global urban areas. Environ. Res. Lett. 2015, 10, 024005. [Google Scholar] [CrossRef]
- Belkhiri, L.; Kim, T.J. Individual influence of climate variability indices on annual maximum precipitation across the global scale. Water Resour. Manag. 2021, 35, 2987–3003. [Google Scholar] [CrossRef]
- Wu, X.; Wang, L.; Yao, R.; Luo, M.; Li, X. Identifying the dominant driving factors of heat waves in the North China Plain. Atmos. Res. 2021, 252, 105458. [Google Scholar] [CrossRef]
- Zhong, P.; Huser, R.; Opitz, T. Modeling nonstationary temperature maxima based on extremal dependence changing with event magnitude. Ann. Appl. Stat. 2022, 16, 272–299. [Google Scholar] [CrossRef]
- Magarey, R.D.; Borchert, D.M.; Schlegel, J.W. Global plant hardiness zones for phytosanitary risk analysis. Sci. Agric. 2008, 65, 54–59. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Estimating climate trends: Application to United States plant hardiness zones. Adv. Meteorol. 2012, 2012, 404876. [Google Scholar] [CrossRef]
- Krakauer, N.Y. Shifting hardiness zones: Trends in annual minimum temperature. Climate 2018, 6, 15. [Google Scholar] [CrossRef]
- Suh, J.N.; Kang, Y.I.; Choi, Y.J.; Seo, K.H.; Kim, Y.H. Plant hardiness zone map in Korea and an analysis of the distribution of evergreen trees in Zone 7b. J. People Plants Environ. 2021, 24, 519–527. [Google Scholar] [CrossRef]
- Matthews, T. Humid heat and climate change. Prog. Phys. Geogr. Earth Environ. 2018, 42, 391–405. [Google Scholar] [CrossRef]
- Wang, P.; Yang, Y.; Jianping, T.; Leung, L.R.; Liao, H. Intensified humid heat events under global warming. Geophys. Res. Lett. 2020, 48, e2020GL091462. [Google Scholar] [CrossRef]
- Willett, K.M. HadlSDH.extremes part II: Exploring humid heat extremes using wet bulb temperature indices. Adv. Atmos. Sci. 2023, 40, 1968–1985. [Google Scholar] [CrossRef]

| NLL | (%) | (%) | |||||
|---|---|---|---|---|---|---|---|
| Station data | |||||||
| GEVD | 2.041 | 0.0076 | 0.007 | 4.73 | 8680.10 | 183 (1.57) | 47 (0.40) |
| Normal | 2.022 | 0.0197 | 0.003 | 0.28 | 30.01 | 191 (1.64) | 29 (0.25) |
| GEVD-Stat | 2.057 | 0.0704 | 0.025 | 1.59 | 683.20 | 243 (2.08) | 70 (0.60) |
| Normal-Stat | 2.044 | 0.0572 | 0.025 | 0.93 | 233.55 | 264 (2.26) | 54 (0.46) |
| ERA5 grid | |||||||
| GEVD | 1.615 | 0.0204 | −0.002 | 2.247 | 3978.32 | 62 (1.15) | 11 (0.20) |
| Normal | 1.595 | 0.0340 | −0.003 | 0.033 | −0.45 | 66 (1.22) | 9 (0.17) |
| GEVD-Stat | 1.757 | 0.1808 | 0.054 | 63.62 | 1,122,590.46 | 140 (2.60) | 30 (0.56) |
| Normal-Stat | 1.739 | 0.1589 | 0.055 | 1.09 | 34.87 | 181 (3.35) | 29 (0.54) |
| ERA5 region | |||||||
| GEVD | 1.465 | 0.0293 | −0.0006 | 0.38 | 89.02 | 160 (1.25) | 42 (0.33) |
| Normal | 1.430 | 0.0263 | −0.002 | 0.014 | 0.12 | 132 (1.03) | 16 (0.12) |
| GEVD-Stat | 1.702 | 0.2444 | 0.073 | 110.54 | 8,683,674.37 | 392 (3.06) | 126 (0.98) |
| Normal-Stat | 1.675 | 0.2420 | 0.073 | 1.13 | 20.23 | 396 (3.09) | 61 (0.48) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krakauer, N.Y. It Is Normal: The Probability Distribution of Temperature Extremes. Climate 2024, 12, 204. https://doi.org/10.3390/cli12120204
Krakauer NY. It Is Normal: The Probability Distribution of Temperature Extremes. Climate. 2024; 12(12):204. https://doi.org/10.3390/cli12120204
Chicago/Turabian StyleKrakauer, Nir Y. 2024. "It Is Normal: The Probability Distribution of Temperature Extremes" Climate 12, no. 12: 204. https://doi.org/10.3390/cli12120204
APA StyleKrakauer, N. Y. (2024). It Is Normal: The Probability Distribution of Temperature Extremes. Climate, 12(12), 204. https://doi.org/10.3390/cli12120204






