Methodology for Obtaining ETo Data for Climate Change Studies: Quality Analysis and Calibration of the Hargreaves–Samani Equation
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Meteorological Data
2.2. Data Quality Analysis
2.3. Evapotranspiration Equations
2.4. Approaches for Hargreaves–Samani Calibration and Validation
2.4.1. Annual Calibration of the Hargreaves–Samani Equation for the Entire Year
2.4.2. Independent Calibrations for Annual and Monthly Clusters of Meteorological Data
2.5. Goodness-of-Fit and Evaluation Criteria for Hargreaves–Samani Calibration and Validation
3. Results and Discussion
3.1. Data Quality Results
3.2. Calibration of the Hargreaves–Samani Equation
3.2.1. Annual Calibration
3.2.2. Calibration of the Hargreaves–Samani Equation by Clusters of Years and Months
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- The number k of clusters was set, and the center Ck was determined.
- For each monthly or annual data, the Euclidean distances (d) from the centers were calculated:
- where d is the Euclidean distances from the centers; T is the weighting factor; x1 − x2 are data points or vectors representing monthly or annual input data, and Ck is the center of the cluster.
- All monthly or annual input data was assigned to the nearest center based on distance d;
- New centers were recalculated as follows, and the process was repeated until convergence.
- The process from 2 to 4 was repeated until convergence.
| Indicators | Equation | |
|---|---|---|
| Regression coefficient | (A3) | |
| Coefficient of determination | (A4) | |
| Root mean square error | (A5) | |
| Root mean square error normalized. | (A6) | |
| Percent bias | (A7) | |
| Efficiency | (A8) |
| Weather Station | Variable | Shapiro–Wilk Normality Test | Mann–Kendall Test | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Year | Month | Year | Month | ||||||
| Statistics | p-Value | Statistics | p-Value | Statistics | p-Value | Statistics | p-Value | ||
| DV | Tmax | 0.92496 | 0.1235 | 0.90771 | 0.1994 | 0.2 | 0.22997 | 0.212 | 0.37269 |
| Tmin | 0.91286 | 0.07227 | 0.90859 | 0.2046 | 0.274 | 0.09799 | 0.333 | 0.14986 | |
| RHmax | 0.95318 | 0.4179 | 0.88265 | 0.09477 | 0.0632 | 0.72118 | −0.152 | 0.53713 | |
| RHmin | 0.94245 | 0.2666 | 0.93314 | 0.4146 | −0.253 | 0.12729 | −0.121 | 0.63122 | |
| u2 | 0.87161 | 0.01254 * | 0.91965 | 0.283 | −0.4 | 0.01496 * | −0.273 | 0.24372 | |
| RS | 0.92463 | 0.1217 | 0.98225 | 0.9911 | 0.295 | 0.07435 | −0.0303 | 0.94533 | |
| MR | Tmax | 0.91255 | 0.1482 | 0.91477 | 0.2455 | 0.162 | 0.42848 | 0.242 | 0.30367 |
| Tmin | 96612 | 0.797 | 0.90634 | 0.1914 | −0.333 | 0.09246 | 0.333 | 0.14986 | |
| RHmax | 0.91751 | 0.1765 | 0.87927 | 0.08578 | 0.0476 | 0.84309 | −0.152 | 0.53713 | |
| RHmin | 0.97625 | 0.9374 | 0.93001 | 0.3802 | 0.333 | 0.09246 | −0.182 | 0.45067 | |
| u2 | 0.93438 | 0.3169 | 0.96313 | 0.8274 | 0.295 | 0.13765 | −0.333 | 0.14986 | |
| RS | 0.84487 | 0.0147 * | 0.96313 | 0.8274 | 0.181 | 0.37305 | −0.0303 | 0.94533 | |
| MT | Tmax | 0.94985 | 0.4873 | 0.91558 | 0.2514 | −0.15 | 0.44404 | 0.242 | 0.30367 |
| Tmin | 0.91588 | 0.1448 | 0.90718 | 0.1963 | 0.15 | 0.44404 | 0.333 | 0.14986 | |
| RHmax | 0.85999 | 0.9809 | 0.92343 | 0.3157 | 0.167 | 0.39231 | −0.152 | 0.53713 | |
| RHmin | 0.98262 | 0.9809 | 0.93963 | 0.4933 | 0.433 | 0.02167 * | −0.152 | 0.53713 | |
| u2 | 0.84487 | 0.0147 * | 0.96485 | 0.8502 | 0.5 | 0.07956 | −0.0909 | 0.7317 | |
| RS | 0.84854 | 0.01297 * | 0.91458 | 0.2441 | −0.717 | 0.01754 * | −0.0303 | 0.94533 | |
| VA | Tmax | 0.94415 | 0.3707 | 0.90709 | 0.1958 | 0.382 | 0.03566 | 0.242 | 0.30367 |
| Tmin | 0.954 | 0.5227 | 0.89777 | 0.1484 | 0.353 | 0.05286 | 0.333 | 0.14986 | |
| RHmax | 0.93691 | 0.2833 | 0.91468 | 0.2449 | 0.0294 | 0.90165 | −0.212 | 0.37269 | |
| RHmin | 0.97357 | 0.8773 | 0.93296 | 0.4126 | 0.0588 | 0.77308 | −0.152 | 0.53713 | |
| u2 | 0.98642 | 0.9936 | 0.90735 | 0.1973 | −0.397 | 0.02902 * | 0.152 | 0.53713 | |
| RS | 0.96041 | 0.6393 | 0.9255 | 0.3349 | −0.0735 | 0.71084 | −0.0303 | 0.94533 | |
| Divor | Maranhão | Montargil | Viana de Alentejo | ||||
|---|---|---|---|---|---|---|---|
| Year | Cluster | Year | Cluster | Year | Cluster | Year | Cluster |
| 2003 | 1 | 2006 | 1 | 2007 | 1 | 2008 | 1 |
| 2004 | 1 | 2007 | 1 | 2008 | 1 | 2010 | 1 |
| 2006 | 1 | 2010 | 1 | 2010 | 1 | 2011 | 1 |
| 2007 | 1 | 2011 | 1 | 2012 | 1 | 2012 | 1 |
| 2008 | 1 | 2012 | 1 | 2013 | 1 | 2013 | 1 |
| 2009 | 1 | 2013 | 1 | 2014 | 1 | 2014 | 1 |
| 2010 | 1 | 2014 | 1 | 2016 | 1 | 2016 | 1 |
| 2011 | 1 | 2016 | 1 | 2018 | 1 | 2018 | 1 |
| 2012 | 1 | 2018 | 1 | 2019 | 1 | 2020 | 1 |
| 2013 | 1 | 2019 | 1 | 2020 | 1 | 2007 | 2 |
| 2014 | 1 | 2020 | 1 | 2005 | 2 | 2009 | 2 |
| 2016 | 1 | 2005 | 2 | 2006 | 2 | 2015 | 2 |
| 2018 | 1 | 2009 | 2 | 2009 | 2 | 2017 | 2 |
| 2019 | 1 | 2015 | 2 | 2011 | 2 | 2019 | 2 |
| 2020 | 1 | 2017 | 2 | 2015 | 2 | 2021 | 2 |
| 2005 | 2 | 2017 | 2 | 2022 | 2 | ||
| 2015 | 2 | 2023 | 2 | ||||
| 2017 | 2 | ||||||
| 2021 | 2 | ||||||
| 2022 | 2 | ||||||
References
- Barberis, D.; Chiadmi, I.; Humblot, P.; Jayet, P.A.; Lungarska, A.; Ollier, M. Climate Change and Irrigation Water: Should the North/South Hierarchy of Impacts on Agricultural Systems Be Reconsidered? Environ. Model. Assess. 2021, 26, 13–36. [Google Scholar] [CrossRef]
- Fader, M.; Shi, S.; Bondeau, A.; Cramer, W. Mediterranean Irrigation under Climate Change: More Efficient Irrigation Needed to Compensate For increases in irrigation water requirements. Hydrol. Earth Syst. Sci. 2016, 20, 953–973. [Google Scholar] [CrossRef]
- Fischer, G.; Tubiello, F.N.; van Velthuizen, H.; Wiberg, D.A. Climate Change Impacts on Irrigation Water Requirements: Effects of Mitigation, 1990–2080. Technol. Forecast. Soc. Chang. 2007, 74, 1083–1107. [Google Scholar] [CrossRef]
- Wang, X.; Mueller, C.; Elliot, J.; Mueller, N.D.; Ciais, P.; Jaegermeyr, J.; Gerber, J.; Dumas, P.; Wang, C.; Yang, H.; et al. Global Irrigation Contribution to Wheat and Maize Yield. Nat. Commun. 2021, 12, 1235. [Google Scholar] [CrossRef] [PubMed]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration. In Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage: Rome, Italy, 1998; p. 56. [Google Scholar]
- Paredes, P.; Pereira, L.S.; Almorox, J.; Darouich, H. Reference Grass Evapotranspiration with Reduced Data Sets: Parameterization of the FAO Penman-Monteith Temperature Approach and the Hargeaves-Samani Equation Using Local Climatic Variables. Agric. Water Manag. 2020, 240, 106210. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.E. Evapotranspiration Information Reporting: II. Recommended Documentation. Agric. Water Manag. 2011, 98, 921–929. [Google Scholar] [CrossRef]
- Goyal, P.; Kumar, S.; Sharda, R. A Review of the Artificial Intelligence (AI) Based Techniques for Estimating Reference Evapotranspiration: Current Trends and Future Perspectives. Comput. Electron. Agric. 2023, 209, 107836. [Google Scholar] [CrossRef]
- Alves, I.; Cameira, M.D.R. Evapotranspiration Estimation Performance of Root Zone Water Quality Model: Evaluation and Improvement. Agric. Water Manag. 2002, 57, 61–73. [Google Scholar] [CrossRef]
- Cameira, M.d.R.; Pereira, L.S. Innovation Issues in Water, Agriculture and Food. Water 2019, 11, 1230. [Google Scholar] [CrossRef]
- Karimi, P.; Bastiaanssen, W.G.M.; Sood, A.; Hoogeveen, J.; Peiser, L.; Bastidas-Obando, E.; Dost, R.J. Spatial Evapotranspiration, Rainfall and Land Use Data in Water Accounting–Part 2: Reliability of Water Acounting Results for Policy Decisions in the Awash Basin. Hydrol. Earth Syst. Sci. 2015, 19, 533–550. [Google Scholar] [CrossRef]
- Pereira, L.S.; Allen, R.G.; Smith, M.; Raes, D. Crop Evapotranspiration Estimation with FAO56: Past and Future. Agric. Water Manag. 2015, 147, 4–20. [Google Scholar] [CrossRef]
- Zhang, K.; Kimball, J.S.; Running, S.W. A Review of Remote Sensing Based Actual Evapotranspiration Estimation. Wiley Interdiscip. Rev. Water 2016, 3, 834–853. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Estimating Potential Evapotranspiration. J. Irrig. Drain. Eng. 1982, 108, 225–230. [Google Scholar] [CrossRef]
- Xiang, K.; Li, Y.; Horton, R.; Feng, H. Similarity and Difference of Potential Evapotranspiration and Reference Crop Evapotranspiration—A Review. Agric. Water Manag. 2020, 232, 106043. [Google Scholar] [CrossRef]
- Lin, E.; Qiu, R.; Chen, M.; Xie, H.; Khurshid, B.; Ma, X.; Quzhen, S.; Zheng, S.; Cui, Y.; Luo, Y. Assessing Forecasting Performance of Daily Reference Evapotranspiration: A Comparative Analysis of Updated Temperature Penman-Monteith and Penman-Monteith Forecast Models. J. Hydrol. 2023, 626, 130317. [Google Scholar] [CrossRef]
- Kim, H.J.; Chandrasekara, S.; Kwon, H.H.; Lima, C.; Kim, T. woong A Novel Multi-Scale Parameter Estimation Approach to the Hargreaves-Samani Equation for Estimation of Penman-Monteith Reference Evapotranspiration. Agric. Water Manag. 2023, 275, 108038. [Google Scholar] [CrossRef]
- Moratiel, R.; Bravo, R.; Saa, A.; Tarquis, A.M.; Almorox, J. Estimation of Evapotranspiration by the Food and Agricultural Organization of the United Nations (FAO) Penman-Monteith Temperature (PMT) and Hargreaves-Samani (HS) Models under Temporal and Spatial Criteria—A Case Study in Duero Basin (Spain). Nat. Hazards Earth Syst. Sci. 2020, 20, 859–875. [Google Scholar] [CrossRef]
- Paredes, P.; Fontes, J.C.; Azevedo, E.B.; Pereira, L.S. Daily Reference Crop Evapotranspiration in the Humid Environments of Azores Islands Using Reduced Data Sets: Accuracy of FAO-PM Temperature and Hargreaves-Samani Methods. Theor. Appl. Climatol. 2018, 134, 595–611. [Google Scholar] [CrossRef]
- Paredes, P.; Trigo, I.; de Bruin, H.; Simões, N.; Pereira, L.S. Daily Grass Reference Evapotranspiration with Meteosat Second Generation Shortwave Radiation and Reference ET Products. Agric. Water Manag. 2021, 248, 106543. [Google Scholar] [CrossRef]
- Paredes, P.; Fontes, J.C.; Azevedo, E.B.; Pereira, L.S. Daily Reference Crop Evapotranspiration with Reduced Data Sets in the Humid Environments of Azores Islands Using Estimates of Actual Vapor Pressure, Solar Radiation, and Wind Speed. Theor. Appl. Climatol. 2018, 134, 1115–1133. [Google Scholar] [CrossRef]
- Todorovic, M.; Karic, B.; Pereira, L.S. Reference Evapotranspiration Estimate with Limited Weather Data across a Range of Mediterranean Climates. J. Hydrol. 2013, 481, 166–176. [Google Scholar] [CrossRef]
- Almorox, J.; Quej, V.H.; Martí, P. Global Performance Ranking of Temperature-Based Approaches for Evapotranspiration Estimation Considering Köppen Climate Classes. J. Hydrol. 2015, 528, 514–522. [Google Scholar] [CrossRef]
- Lai, C.; Chen, X.; Zhong, R.; Wang, Z. Implication of Climate Variable Selections on the Uncertainty of Reference Crop Evapotranspiration Projections Propagated from Climate Variables Projections under Climate Change. Agric. Water Manag. 2022, 259, 107273. [Google Scholar] [CrossRef]
- Ukhurebor, K.E.; Azi, S.O.; Aigbe, U.O.; Onyancha, R.B.; Emegha, J.O. Analyzing the Uncertainties between Reanalysis Meteorological Data and Ground Measured Meteorological Data. Measurement 2020, 165, 108110. [Google Scholar] [CrossRef]
- Ippolito, M.; De Caro, D.; Cannarozzo, M.; Provenzano, G.; Ciraolo, G. Evaluation of Daily Crop Reference Evapotranspiration and Sensitivity Analysis of FAO Penman-Monteith Equation Using ERA5-Land Reanalysis Database in Sicily, Italy. Agric. Water Manag. 2024, 295, 108732. [Google Scholar] [CrossRef]
- Gualtieri, G. Analysing the Uncertainties of Reanalysis Data Used for Wind Resource Assessment: A Critical Review. Renew. Sustain. Energy Rev. 2022, 167, 112741. [Google Scholar] [CrossRef]
- Paredes, P. Accuracy of Daily PM-ETo Estimations with ERA-Interim Reanalysis Products. Eur. Water 2017, 59, 239–246. [Google Scholar]
- Raziei, T.; Parehkar, A. Performance Evaluation of NCEP/NCAR Reanalysis Blended with Observation-Based Datasets for Estimating Reference Evapotranspiration across Iran. Theor. Appl. Climatol. 2021, 144, 885–903. [Google Scholar] [CrossRef]
- Davidson, M.R.; Millstein, D. Limitations of Reanalysis Data for Wind Power Applications. Wind Energy 2022, 25, 1646–1653. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Samani, Z.A. Reference Crop Evapotranspiration from Temperature. Appl. Eng. Agric. 1985, 1, 96–99. [Google Scholar] [CrossRef]
- Raziei, T.; Pereira, L.S. Estimation of ETo with Hargreaves-Samani and FAO-PM Temperature Methods for a Wide Range of Climates in Iran. Agric. Water Manag. 2013, 121, 1–18. [Google Scholar] [CrossRef]
- Alam, M.M.; Akter, M.Y.; Islam, A.R.M.T.; Mallick, J.; Kabir, Z.; Chu, R.; Arabameri, A.; Pal, S.C.; Masud, M.A.A.; Costache, R.; et al. A Review of Recent Advances and Future Prospects in Calculation of Reference Evapotranspiration in Bangladesh Using Soft Computing Models. J. Environ. Manag. 2024, 351, 119714. [Google Scholar] [CrossRef]
- Cakir, R.; Raimonet, M.; Sauvage, S.; Paredes-Arquiola, J.; Grusson, Y.; Roset, L.; Meaurio, M.; Navarro, E.; Sevilla-Callejo, M.; Luis Lechuga-Crespo, J.; et al. Hydrological Alteration Index as an Indicator of the Calibration Complexity of Water Quantity and Quality Modeling in the Context of Global Change. Water 2020, 12, 115. [Google Scholar] [CrossRef]
- Ferro, C.A.T.; Jupp, T.E.; Lambert, F.H.; Huntingford, C.; Cox, P.M. Model Complexity versus Ensemble Size: Allocating Resources for Climate Prediction. Phil. Trans. R. Soc. A 2012, 370, 1087–1099. [Google Scholar] [CrossRef] [PubMed]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. Reference Evapotranspiration Projections in Southern Spain (until 2100) Using Temperature-Based Machine Learning Models. Comput. Electron. Agric. 2023, 214, 108327. [Google Scholar] [CrossRef]
- Kim, H.J.; Cho, K.; Kim, Y.; Park, H.; Lee, J.W.; Kim, S.J.; Chae, Y. Spatial Assessment of Water-Use Vulnerability under Future Climate and Socioeconomic Scenarios within a River Basin. J. Water Resour. Plan. Manag. 2020, 146, 05020011. [Google Scholar] [CrossRef]
- Dinh, T.L.A.; Aires, F. Revisiting the Bias Correction of Climate Models for Impact Studies. Clim. Chang. 2023, 176, 140. [Google Scholar] [CrossRef]
- Maraun, D. Bias Correcting Climate Change Simulations—A Critical Review. Curr. Clim. Chang. Rep. 2016, 2, 211–220. [Google Scholar] [CrossRef]
- Teutschbein, C.; Seibert, J. Bias Correction of Regional Climate Model Simulations for Hydrological Climate-Change Impact Studies: Review and Evaluation of Different Methods. J. Hydrol. 2012, 456–457, 12–29. [Google Scholar] [CrossRef]
- Teutschbein, C.; Jonsson, E.; Todorović, A.; Tootoonchi, F.; Stenfors, E.; Grabs, T. Future Drought Propagation through the Water-Energy-Food-Ecosystem Nexus—A Nordic Perspective. J. Hydrol. 2023, 617, 128963. [Google Scholar] [CrossRef]
- Hargreaves, G.H.; Allen, R.G. History and Evaluation of Hargreaves Evapotranspiration Equation. J. Irrig. Drain. Eng. 2003, 129, 53–63. [Google Scholar] [CrossRef]
- Gavilán, P.; Lorite, I.J.; Tornero, S.; Berengena, J. Regional Calibration of Hargreaves Equation for Estimating Reference et in a Semiarid Environment. Agric. Water Manag. 2006, 81, 257–281. [Google Scholar] [CrossRef]
- Shahidian, S.; Serralheiro, R.P.; Serrano, J.; Teixeira, J.L. Parametric Calibration of the Hargreaves-Samani Equation for Use at New Locations. Hydrol. Process. 2013, 27, 605–616. [Google Scholar] [CrossRef]
- Vanderlinden, K.; Giráldez, J.V.; Van Meirvenne, M. Assessing Reference Evapotranspiration by the Hargreaves Method in Southern Spain. J. Irrig. Drain. Eng. 2004, 130, 184–191. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Qin, S.; Guo, H.; Yang, D.; Lam, H.M. How Can Drip Irrigation Save Water and Reduce Evapotranspiration Compared to Border Irrigation in Arid Regions in Northwest China. Agric. Water Manag. 2020, 239, 106256. [Google Scholar] [CrossRef]
- Yang, Y.; Chen, R.; Han, C.; Liu, Z. Evaluation of 18 Models for Calculating Potential Evapotranspiration in Different Climatic Zones of China. Agric. Water Manag. 2021, 244, 106545. [Google Scholar] [CrossRef]
- Martínez-Cob, A.; Tejero-Juste, M. A Wind-Based Qualitative Calibration of the Hargreaves ETo Estimation Equation in Semiarid Regions. Agric. Water Manag. 2004, 64, 251–264. [Google Scholar] [CrossRef]
- Jensen, D.T.; Hargreaves, G.H.; Temesgen, B.; Allen, R.G. Computation of ETo under Nonideal Conditions. J. Irrig. Drain. Eng. 1997, 123, 394–400. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; Vanschoren, J.; García-Marín, A.P. AgroML: An Open-Source Repository to Forecast Reference Evapotranspiration in Different Geo-Climatic Conditions Using Machine Learning and Transformer-Based Models. Agronomy 2022, 12, 656. [Google Scholar] [CrossRef]
- Berti, A.; Tardivo, G.; Chiaudani, A.; Rech, F.; Borin, M. Assessing Reference Evapotranspiration by the Hargreaves Method in North-Eastern Italy. Agric. Water Manag. 2014, 140, 20–25. [Google Scholar] [CrossRef]
- Droogers, P.; Allen, R.G. Estimating Reference Evapotranspiration Under Inaccurate Data Conditions. Irrig. Drain. Syst. 2002, 16, 33–45. [Google Scholar] [CrossRef]
- Trajkovic, S.; Kolakovic, S. Evaluation of Reference Evapotranspiration Equations under Humid Conditions. Water Resour. Manag. 2009, 23, 3057–3067. [Google Scholar] [CrossRef]
- Feng, Y.; Jia, Y.; Cui, N.; Zhao, L.; Li, C.; Gong, D. Calibration of Hargreaves Model for Reference Evapotranspiration Estimation in Sichuan Basin of Southwest China. Agric. Water Manag. 2017, 181, 1–9. [Google Scholar] [CrossRef]
- Giuseppe, M.; Alfonso, S. Regionalization of the Hargreaves Coefficient for the Assessment of Distributed Reference Evapotranspiration in Southern Italy. J. Irrig. Drain. Eng. 2013, 139, 349–362. [Google Scholar] [CrossRef]
- Rodrigues, G.C.; Braga, R.P. Estimation of Reference Evapotranspiration during the Irrigation Season Using Nine Temperature-Based Methods in a Hot-Summer Mediterranean Climate. Agriculture 2021, 11, 124. [Google Scholar] [CrossRef]
- Amani, S.; Shafizadeh-Moghadam, H. A Review of Machine Learning Models and Influential Factors for Estimating Evapotranspiration Using Remote Sensing and Ground-Based Data. Agric. Water Manag. 2023, 284, 108324. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez, J.; García-Marín, A.P. A Regional Machine Learning Method to Outperform Temperature-Based Reference Evapotranspiration Estimations in Southern Spain. Agric. Water Manag. 2022, 274, 107955. [Google Scholar] [CrossRef]
- Bellido-Jiménez, J.A.; Estévez Gualda, J.; García-Marín, A.P. Assessing New Intra-Daily Temperature-Based Machine Learning Models to Outperform Solar Radiation Predictions in Different Conditions. Appl. Energy 2021, 298, 117211. [Google Scholar] [CrossRef]
- Feng, Y.; Peng, Y.; Cui, N.; Gong, D.; Zhang, K. Modeling Reference Evapotranspiration Using Extreme Learning Machine and Generalized Regression Neural Network Only with Temperature Data. Comput. Electron. Agric. 2017, 136, 71–78. [Google Scholar] [CrossRef]
- Kang, Y.; Chen, P.; Cheng, X.; Zhang, S.; Song, S. Novel Hybrid Machine Learning Framework with Decomposition–Transformation and Identification of Key Modes for Estimating Reference Evapotranspiration. Agric. Water Manag. 2022, 273, 107882. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Kwon, H.H.; Kim, Y.T. A Local-Regional Scaling-Invariant Bayesian GEV Model for Estimating Rainfall IDF Curves in a Future Climate. J. Hydrol. 2018, 566, 73–88. [Google Scholar] [CrossRef]
- Mandal, N.; Chanda, K. Performance of Machine Learning Algorithms for Multi-Step Ahead Prediction of Reference Evapotranspiration across Various Agro-Climatic Zones and Cropping Seasons. J. Hydrol. 2023, 620, 129418. [Google Scholar] [CrossRef]
- Su, Y.; Li, Y.; Liu, Y.; Huang, G.; Jia, Q.; Li, Y. An Integrated Multi-GCMs Bayesian-Neural-Network Hydrological Analysis Method for Quantifying Climate Change Impact on Runoff of the Amu Darya River Basin. Int. J. Climatol. 2021, 41, 3411–3424. [Google Scholar] [CrossRef]
- Mohammed, S.; Elbeltagi, A.; Bashir, B.; Alsafadi, K.; Alsilibe, F.; Alsalman, A.; Zeraatpisheh, M.; Széles, A.; Harsányi, E. A Comparative Analysis of Data Mining Techniques for Agricultural and Hydrological Drought Prediction in the Eastern Mediterranean. Comput. Electron. Agric. 2022, 197, 106925. [Google Scholar] [CrossRef]
- Althoff, D.; Santos, R.A.D.; Bazame, H.C.; Cunha, F.F.D.; Filgueiras, R. Improvement of Hargreaves–Samani Reference Evapotranspiration Estimates with Local Calibration. Water 2019, 11, 2272. [Google Scholar] [CrossRef]
- Di Nunno, F.; De Matteo, M.; Izzo, G.; Granata, F. A Combined Clustering and Trends Analysis Approach for Characterizing Reference Evapotranspiration in Veneto. Sustainability 2023, 15, 11091. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Spatio-Temporal Analysis of Drought in Southern Italy: A Combined Clustering-Forecasting Approach Based on SPEI Index and Artificial Intelligence Algorithms. Stoch. Environ. Res. Risk Assess. 2023, 37, 2349–2375. [Google Scholar] [CrossRef]
- Ikotun, A.M.; Ezugwu, A.E.; Abualigah, L.; Abuhaija, B.; Heming, J. K-Means Clustering Algorithms: A Comprehensive Review, Variants Analysis, and Advances in the Era of Big Data. Inf. Sci. 2023, 622, 178–210. [Google Scholar] [CrossRef]
- Di Nunno, F.; Granata, F. Future Trends of Reference Evapotranspiration in Sicily Based on CORDEX Data and Machine Learning Algorithms. Agric. Water Manag. 2023, 280, 108232. [Google Scholar] [CrossRef]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World Map of the Köppen-Geiger Climate Classification Updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Allen, R.G. Assessing Integrity of Weather Data for Reference Evapotranspiration Estimation. J. Irrig. Drain Eng. 1996, 122, 97–106. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paulo, A.A.; Matias, P.G.; Espırito Santo, M.F.; Pires, V.C. Tratamento da qualidade das séries de dados climáticos quanto a homogeneidade, aleatoriedade e tendência e completagem de séries de dados. In Gestão do Risco em Secas; Pereira, L.S., Mexia, J.T., Pires, C.A.L., Eds.; Métodos, Tecnologias e Desafios, Ediçoes Colibri and Centro de Engenharia e Biossistemas: Lisboa, Portugal, 2010; pp. 119–139. ISBN 9789896890667. [Google Scholar]
- Hirsch, R.M.; Slack, J.R. A Nonparametric Trend Test for Seasonal Data with Serial Dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef]
- Gocic, M.; Trajkovic, S. Analysis of Changes in Meteorological Variables Using Mann-Kendall and Sen’s Slope Estimator Statistical Tests in Serbia. Global Planet. Chang. 2013, 100, 172–182. [Google Scholar] [CrossRef]
- Ademe, D.; Zaitchik, B.F.; Tesfaye, K.; Simane, B.; Alemayehu, G.; Adgo, E. Climate Trends and Variability at Adaptation Scale: Patterns and Perceptions in an Agricultural Region of the Ethiopian Highlands. Weather Clim. Extrem. 2020, 29, 100263. [Google Scholar] [CrossRef]
- Van Giersbergen, N.P.A. On the Effect of Deterministic Terms on the Bias in Stable AR Models. Econ. Lett. 2005, 89, 75–82. [Google Scholar] [CrossRef]
- Jato-Espino, D.; Charlesworth, S.M.; Perales-Momparler, S.; Andrés-Doménech, I. Prediction of Evapotranspiration in a Mediterranean Region Using Basic Meteorological Variables. J. Hydrol. Eng. 2017, 22, 04016064. [Google Scholar] [CrossRef]
- Masanta, S.K.; Srinivas, V.V. Regionalization of Evapotranspiration in India Using Fuzzy Dynamic Clustering Approach. Part 2: Applications of Regions. Int. J. Climatol. 2021, 41, 1371–1395. [Google Scholar] [CrossRef]
- Wu, L.; Peng, Y.; Fan, J.; Wang, Y.; Huang, G. A Novel Kernel Extreme Learning Machine Model Coupled with K-Means Clustering and Firefly Algorithm for Estimating Monthly Reference Evapotranspiration in Parallel Computation. Agric. Water Manag. 2021, 245, 106624. [Google Scholar] [CrossRef]
- Di Nunno, F.; Diodato, N.; Bellocchi, G.; Tricarico, C.; De Marinis, G.; Granata, F. Evapotranspiration Analysis in Central Italy: A Combined Trend and Clustering Approach. Climate 2024, 12, 64. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River Flow Forecasting through Conceptual Models Part I—A Discussion of Principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- WMO. World Meteorological Organization. Global Atmosphere Watch (GAW) Implementation Plan: 2016-Weather Climate Water. 2017 GAW Report No. IBSN: 978-92-63-11156-2. Available online: https://library.wmo.int/idurl/4/55442 (accessed on 27 June 2024).
- Ren, X.; Qu, Z.; Martins, D.S.; Paredes, P.; Pereira, L. Daily reference evapotranspiration for hyper-arid to moist sub-humid climates in Inner Mongolia, China: I. Assessing temperature methods and spatial variability. Water Resour. Manag. 2016, 30, 3769–3791. [Google Scholar] [CrossRef]
- Zhu, X.; Luo, T.; Luo, Y.; Yang, Y.; Guo, L.; Luo, H.; Fang, C.; Cui, Y. Calibration and Validation of the Hargreaves-Samani Model for Reference Evapotranspiration Estimation in China. Irrig. Drain. 2019, 68, 822–836. [Google Scholar] [CrossRef]
- Zanetti, S.S.; Dohler, R.E.; Cecílio, R.A.; Pezzopane, J.E.M.; Xavier, A.C. Proposal for the Use of Daily Thermal Amplitude for the Calibration of the Hargreaves-Samani Equation. J. Hydrol. 2019, 571, 193–201. [Google Scholar] [CrossRef]
- Aguilar, C.; Polo, M.J. Generating Reference Evapotranspiration Surfaces from the Hargreaves Equation at Watershed Scale. Hydrol. Earth Syst. Sci. 2011, 15, 2495–2508. [Google Scholar] [CrossRef]
- Teixeira, J.; Shahidian, S.; Rolim, J. Regional Analysis and calibration for the South of Portugal of a simple evapotranspiration model for use in an autonomous lanscape irrigation controller. WSEAS Trans. Environ. Dev. 2008, 8, 676–686. [Google Scholar]
- Irmak, S.; Allen, R.G.; Whitty, E. Daily grass and alfalfa-reference evapotranspiration estimates and alfalfa-to-grass evapotranspiration ratios in Florida. J. Irrig. Drain Eng. 2003, 129, 360–370. [Google Scholar] [CrossRef]
- Yoder, R.E.; Odhiambo, L.O.; Wright, W.C. Evaluation of methods for estimating daily reference crop evapotranspiration at a site in the humid southeast United States. Appl. Eng. Agric. 2005, 21, 197–202. Available online: https://digitalcommons.unl.edu/biosysengfacpub/450 (accessed on 25 July 2024).

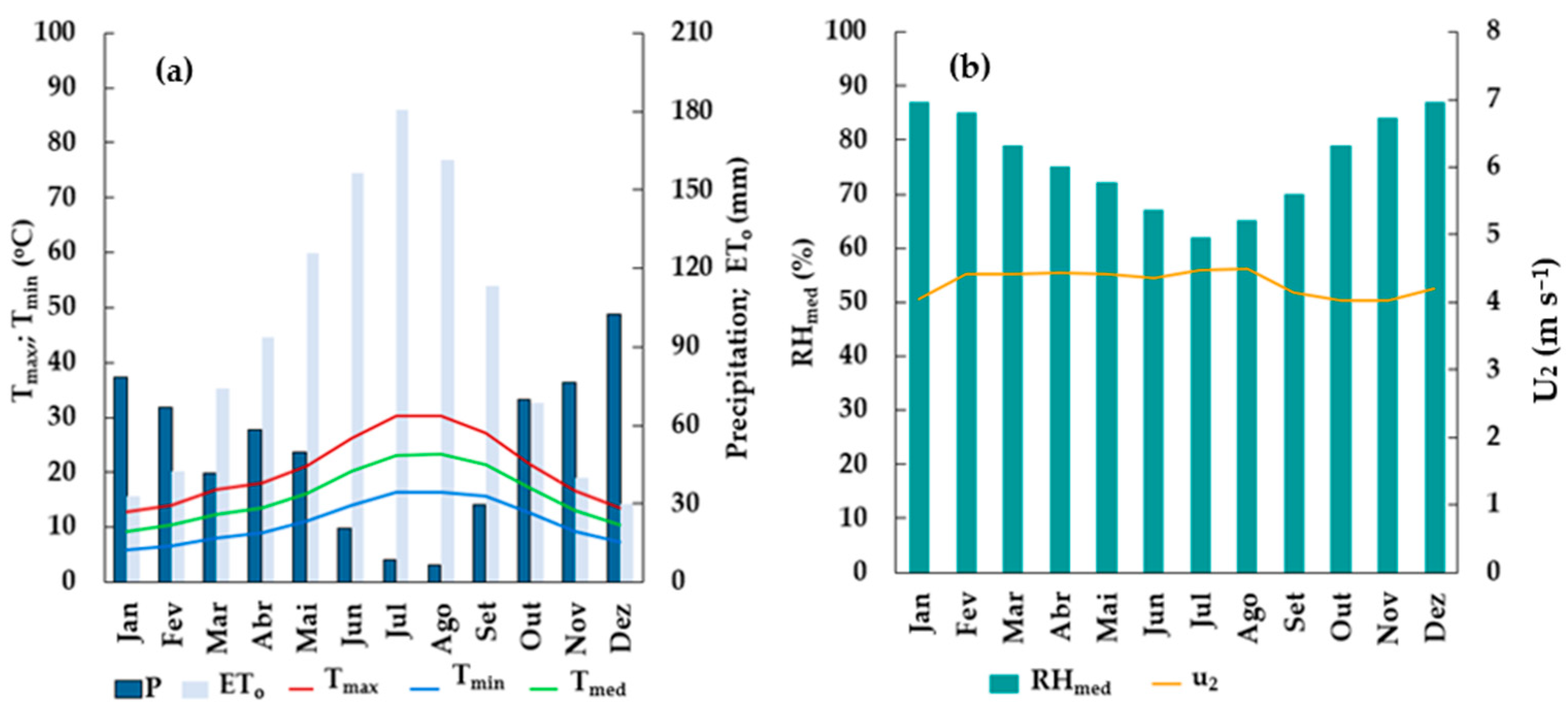









| Weather Station | Code | Latitude (N) | Longitude (W) | Elevation (m) | Measured Period | Source |
|---|---|---|---|---|---|---|
| Évora | EV | 38.54 | 7.89 | 247.5 | Jan/1996–Mai/2023 | IPMA |
| Divor | DV | 38.74 | 7.94 | 246.0 | Sep/2001–Ago/2023 | COTR |
| Maranhão | MR | 39.00 | 8.00 | 94.0 | Jan/2005–Apr/2021 | WUASV |
| Montargil | M | 39.05 | 8.17 | 92.0 | Jan/2005–Apr/2021 | WUASV |
| Viana do Alentejo | VA | 38.36 | 8.12 | 138.0 | Jan/2007–April/2023 | COTR |
| Weather Station | N | Initial kRS | Mean and SD (mm d−1) | b1 | R2 | RMSE | NRMSE | PBIAS | EF | |
|---|---|---|---|---|---|---|---|---|---|---|
| (°C−0.5) | ETo–HS | ETo–PM | (mm d−1) | (%) | (%) | |||||
| DV | 7690 | 0.17 | 3.45 (±2.1) | 3.77 (±2.2) | 1.06 | 0.89 | 0.82 | 22.99 | −9.00 | 0.86 |
| MR | 5987 | 3.44 (±2.1) | 3.74 (±2.2) | 1.07 | 0.96 | 0.59 | 16.23 | 8.80 | 0.93 | |
| MT | 5621 | 3.55 (± 2.2) | 3.72 (±2.2) | 1.03 | 0.95 | 0.56 | 14.90 | 4.91 | 0.94 | |
| VA | 6445 | 3.55 (±2.2) | 3.62 (±2.1) | 1.00 | 0.93 | 0.62 | 16.94 | −1.96 | 0.93 | |
| Weather Station | Process | N | Adjusted kRS | Mean and SD (mm d−1) | b1 | R2 | RMSE | NRMSE | PBIAS | EF | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C−0.5) | ETo–HS | ETo–PM | (mm d−1) | (%) | (%) | ||||||
| DV | Calibration | 5108 | 0.159 | 3.55 (±2.2) | 3.54 (±2.1) | 0.97 | 0.97 | 0.71 | 19.82 | 0.09 | 0.90 |
| Validation | 2582 | 3.51 (±2.2) | 3.56 (±2.1) | 0.99 | 0.97 | 0.73 | 20.59 | −1.51 | 0.90 | ||
| MR | Calibration | 4383 | 0.157 | 3.54 (±2.1) | 3.52 (±2.1) | 0.99 | 0.99 | 0.47 | 13.30 | 0.47 | 0.95 |
| Validation | 1604 | 3.37 (±2.0) | 3.39 (±2.0) | 0.99 | 0.99 | 0.47 | 13.80 | 0.65 | 0.95 | ||
| MT | Calibration | 4526 | 0.163 | 3.62 (±2.2) | 3.62 (±2.2) | 0.99 | 0.99 | 0.46 | 12.79 | 0.03 | 0.96 |
| Validation | 1095 | 3.45 (±2.1) | 3.48 (±2.0) | 1.01 | 0.99 | 0.45 | 13.32 | 1.00 | 0.96 | ||
| VA | Calibration | 4500 | 0.165 | 3.52 (±2.8) | 3.53 (±2.1) | 0.98 | 0.98 | 0.59 | 16.80 | −0.30 | 0.93 |
| Validation | 1945 | 3.51 (±2.2) | 3.50 (±2.0) | 0.97 | 0.98 | 0.59 | 16.80 | 0.51 | 0.92 | ||
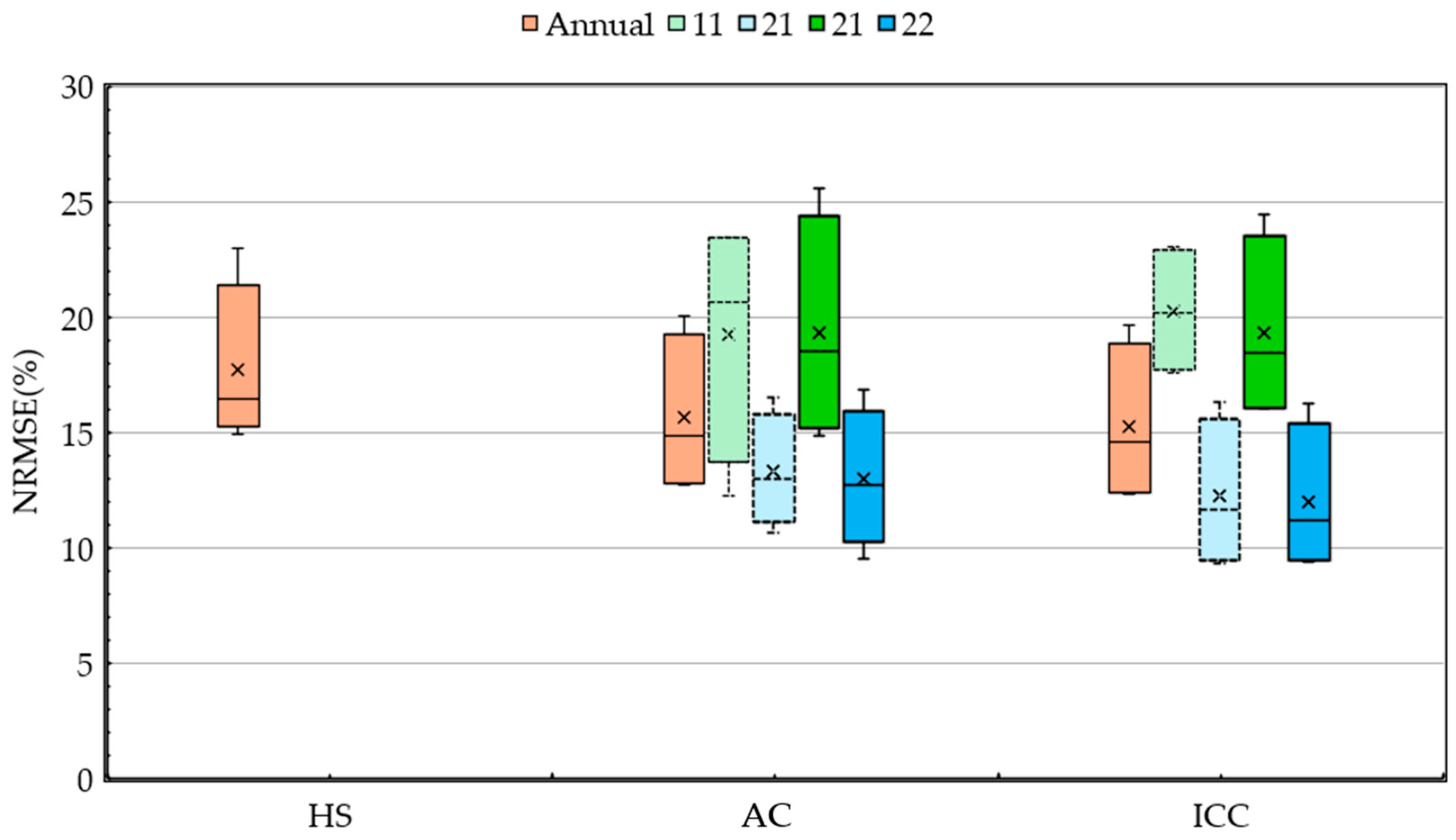
| Cluster | N | kRS | Mean and SD (mm d−1) | b1 | R2 | RMSE | NRMSE | PBIAS | EF | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (°C−0.5) | ETo–HS | ETo–PM | (mm d−1) | (%) | (%) | |||||||
| DV | 11 | Cal. | 2122 | 0.151 | 1.95 (±1.0) | 1.94 (±0.9) | 0.96 | 0.96 | 0.45 | 23.25 | 0.57 | 0.81 |
| Val. | 1058 | 2.05 (±1.1) | 2.03 (±1.1) | 0.96 | 0.96 | 0.46 | 22.61 | 0.89 | 0.84 | |||
| 12 | Cal. | 1526 | 0.162 | 5.66 (±1.4) | 5.6 (±1.4) | 0.97 | 0.97 | 0.91 | 16.11 | 1.10 | 0.58 | |
| Val. | 795 | 5.42 (±1.5) | 5.42 (±1.3) | 0.97 | 0.97 | 0.90 | 16.68 | −0.01 | 0.64 | |||
| 21 | Cal. | 636 | 0.156 | 2.16 (±1.2) | 2.13 (±1.1) | 0.96 | 0.96 | 0.50 | 23.07 | 1.24 | 0.82 | |
| Val. | 423 | 1.85 (±1.0) | 2.01 (±0.9) | 1.02 | 0.94 | 0.53 | 27.46 | −3.06 | 0.78 | |||
| 22 | Cal. | 459 | 0.165 | 5.92 (±1.5) | 5.84 (±1.5) | 0.97 | 0.97 | 0.93 | 15.81 | 1.27 | 0.59 | |
| Val. | 306 | 5.45 (±1.6) | 5.95 (±1.5) | 1.07 | 0.97 | 0.99 | 16.96 | −1.79 | 0.64 | |||
| MR | 11 | Cal. | 2031 | 0.152 | 1.97 (±1.0) | 1.98 (±1.0) | 1.00 | 0.98 | 0.35 | 17.7 | 0.59 | 0.89 |
| Val. | 424 | 1.91 (±0.9) | 2.04 (±1.1) | 0.96 | 0.98 | 0.32 | 16.9 | 1.64 | 0.90 | |||
| 12 | Cal. | 1400 | 0.156 | 5.39 (±1.3) | 5.40 (±1.3) | 0.99 | 0.99 | 0.54 | 9.9 | 0.52 | 0.83 | |
| Val. | 306 | 5.44 (±1.3) | 5.27 (±1.5) | 1.03 | 0.99 | 0.50 | 9.2 | 1.43 | 0.85 | |||
| 21 | Cal. | 636 | 0.155 | 2.18 (±1.1) | 2.16 (±1.2) | 0.98 | 0.98 | 0.34 | 15.4 | 0.13 | 0.92 | |
| Val. | 212 | 2.05 (±1.1) | 2.03 (±1.0) | 0.99 | 0.98 | 0.32 | 15.7 | 0.52 | 0.92 | |||
| 22 | Cal. | 459 | 0.161 | 5.70 (±1.3) | 5.89 (±1.3) | 0.99 | 0.99 | 0.55 | 9.6 | 0.12 | 0.81 | |
| Val. | 153 | 5.84 (±1.3) | 5.82 (±1.4) | 0.99 | 0.99 | 0.57 | 9.8 | 0.38 | 0.81 | |||
| MT | 11 | Cal. | 1819 | 0.161 | 2.03 (±1.1) | 2.04 (±1.0) | 0.98 | 0.98 | 0.35 | 17.28 | −0.21 | 0.89 |
| Val. | 424 | 2.11 (±1.1) | 2.05 (±1.0) | 0.98 | 0.97 | 0.38 | 18.46 | 2.86 | 0.89 | |||
| 12 | Cal. | 1247 | 0.164 | 5.73 (±1.4) | 5.72 (±1.4) | 0.99 | 0.99 | 0.52 | 9.22 | 0.19 | 0.87 | |
| Val. | 306 | 5.36 (±1.3) | 5.46 (±1.2) | 1.01 | 0.99 | 0.52 | 9.84 | −1.97 | 0.84 | |||
| 21 | Cal. | 848 | 0.168 | 2.28 (±1.2) | 2.28 (±1.2 | 0.98 | 0.98 | 0.36 | 15.91 | −0.02 | 0.92 | |
| Val. | 424 | 2.21 (±1.3) | 2.25 (±1.2) | 1.03 | 0.98 | 0.37 | 16.87 | 1.93 | 0.92 | |||
| 22 | Cal. | 612 | 0.169 | 6.08 (±1.4) | 6.05 (±1.3) | 0.99 | 0.99 | 0.56 | 9.29 | 0.47 | 0.83 | |
| Val. | 306 | 5.92 (±1.1) | 5.91 (±1.3) | 1.04 | 0.99 | 0.58 | 9.94 | −0.25 | 0.70 | |||
| VA | 11 | Cal. | 1395 | 0.159 | 1.92 (±1.0) | 1.92 (±0.9) | 0.96 | 0.96 | 0.42 | 21.9 | −0.10 | 0.83 |
| Val. | 424 | 2.07 (±1.1) | 1.93 (±1.0) | 0.89 | 0.96 | 0.51 | 24.7 | 4.87 | 0.79 | |||
| 12 | Cal. | 918 | 0.163 | 5.56 (±1.5) | 5.55 (±1.4) | 0.98 | 0.98 | 0.75 | 13.5 | 0.32 | 0.75 | |
| Val. | 306 | 5.35 (±1.5) | 5.36 (±1.3) | 0.98 | 0.98 | 0.72 | 13.5 | −0.06 | 0.77 | |||
| 21 | Cal. | 1269 | 0.168 | 2.18 (±1.5) | 2.19 (±1.0) | 0.96 | 0.96 | 0.47 | 21.5 | −0.36 | 0.84 | |
| Val. | 423 | 2.20 (±1.3) | 2.25 (±1.0) | 0.99 | 0.98 | 0.40 | 18.1 | 2.02 | 0.91 | |||
| 22 | Cal. | 918 | 0.169 | 5.57 (±1.5) | 5.75 (±1.3) | 0.98 | 0.98 | 0.74 | 12.8 | 0.37 | 0.74 | |
| Val. | 306 | 5.96 (±1.5) | 6.09 (±1.3) | 1.01 | 0.99 | 0.76 | 12.7 | 2.26 | 0.73 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, A.; Cameira, M.d.R.; Rolim, J. Methodology for Obtaining ETo Data for Climate Change Studies: Quality Analysis and Calibration of the Hargreaves–Samani Equation. Climate 2024, 12, 205. https://doi.org/10.3390/cli12120205
Ferreira A, Cameira MdR, Rolim J. Methodology for Obtaining ETo Data for Climate Change Studies: Quality Analysis and Calibration of the Hargreaves–Samani Equation. Climate. 2024; 12(12):205. https://doi.org/10.3390/cli12120205
Chicago/Turabian StyleFerreira, Antónia, Maria do Rosário Cameira, and João Rolim. 2024. "Methodology for Obtaining ETo Data for Climate Change Studies: Quality Analysis and Calibration of the Hargreaves–Samani Equation" Climate 12, no. 12: 205. https://doi.org/10.3390/cli12120205
APA StyleFerreira, A., Cameira, M. d. R., & Rolim, J. (2024). Methodology for Obtaining ETo Data for Climate Change Studies: Quality Analysis and Calibration of the Hargreaves–Samani Equation. Climate, 12(12), 205. https://doi.org/10.3390/cli12120205









