Abstract
Rainfall irregularity in Mediterranean regions is a characterizing feature of their climate. The aim of this manuscript is to analyze, in a climate change context, the evolution of this irregularity in Barcelona. A very long monthly database (1786–2023) enables detailed analysis of rainfall evolution, with its irregularity quantified using the concept of disparity, the trends of which are assessed using moving windows and a modified Mann–Kendall test. The relationship between disparity and the Western Mediterranean Oscillation index (WeMOi) is also explored. Additionally, the study compares rainfall amounts to the 1961–1990 reference period and evaluates autumn’s contribution to annual totals. A significant and increasing disparity trend over the years is detected for the autumn months. While correlations between disparity and WeMOi are limited, the WeMOi and monthly precipitation are significantly correlated for two autumn months, October and November, and for December, aligning with previous studies. This suggests the potential influence of the WeMOi fluctuations on future rainfall during these three months. Recent evidence of the increasing autumn irregularity is seen in the consecutive low-rainfall years of 2021, 2022 and 2023, which stand out as the driest since 1835, with the last two autumns ranking among the 5% driest.
1. Introduction
The Mediterranean region displays a diverse climate, exhibiting semi-arid conditions, particularly along its southern coastline [1]. This climate features mild, humid winters paired with dry, warm to hot summers. Acting as a major evaporation source, the Mediterranean Sea plays a crucial role in the regional hydrological cycle [2]. Intense storms are known to form over the Mediterranean [3] which can result in heavy rainfall, leading to flash flooding and other severe weather impacts. Additionally, the region is characterized by strong interactions and feedback between land and atmosphere [4], which can lead to extended periods of drought and severe heatwaves.
In recent decades, the Mediterranean has undergone substantial climate variability, particularly marked by intense heatwaves and drought conditions [5]. Climate models project a reduction in precipitation across all seasons [6], along with a northward and eastward expansion of the Mediterranean climate, where affected areas are expected to become more arid, experiencing increased summer drying [7,8]. Additionally, recent projections suggest that the characteristics of Mediterranean cyclones [9,10] could shift due to ongoing climate changes [11]. There is a strong consensus that hydrological droughts have intensified across the region and are projected to continue increasing throughout the 21st century under most scenarios [12,13]. Rising summer temperatures are expected to increase both the frequency and intensity of these extreme events.
In Europe, substantial evidence indicates that the frequency and intensity of extreme precipitation events have likely increased since the 1950s [14,15,16]. However, there is a lack of consensus regarding trends in the Mediterranean region, which exhibit significant inconsistency across different areas [17,18,19,20,21].
Within the Mediterranean region, the rainfall regime in Catalonia, the Spanish region where Barcelona is located in the northeast of the Iberian Peninsula (Figure 1), is characterized by remarkable irregularities [22,23], evident even at monthly and annual scales [24,25,26]. A study utilizing the precipitation concentration index (CI), related to rainfall irregularity, reveals that the highest European values of CI are found in the western Mediterranean basin, particularly along the Spanish and French coasts [27]. Furthermore, drought episodes can be frequent and severe in Spain [28,29,30,31], where dry spells can exceed three months. This aligns with the ongoing challenges within the Mediterranean climate framework, emphasizing the critical need for adaptive strategies. The primary characteristics of Mediterranean climate variability have been documented in other studies [1,32]. Recent analyses have also explored the relationship between seasonal temperatures and precipitation in Spain [33].
Figure 1.
Map showing the locations and main geographical features mentioned in the text.
The methods employed for quantifying rainfall irregularity often rely on fractal structures at several scales. In the monofractal approach [34,35,36], the scaling fractal parameter relating rainfall intensity distributions at different time scales has been established as an indicator closely linked to the rainfall pattern characteristics in the studied area, demonstrating its efficacy in measuring rainfall irregularity [37,38,39]. The disparity concept [24,26,40] has also been beneficial in the quantification of rainfall irregularity and to stablish relationships with some specific geographical factors. A potential dependence on the elevation above sea level or the distance to the coastline of the raingauge emplacements has also been considered [41]. A detailed analysis of these disparities, bearing in mind the complex fractal structure of the monthly rainfall regime [42,43], could represent some improvements on the monthly amounts forecasted, applying strategies based on, for instance, the ARIMA algorithm [44] to obtain, among other questions, the expected length of a dry spell.
The aim of this article is to enhance the understanding of the precipitation pattern and its irregularity in Barcelona by analyzing various aspects of monthly precipitation records spanning more than two centuries (1789–2023). In addition to common elements such as descriptive statistics and trends identification, the series have been examined in order to detect rainfall discrepancies in comparison with the 1961–1990 reference period. Furthermore, the possible impact of the monthly Western Mediterranean Oscillation index, WeMOi, has been also explored. The WeMOi [26,45], is a dynamic atmospheric parameter that is well correlated with rainfall irregularity in the Spanish Mediterranean coast. The WeMOi identifies atmospheric circulation patterns that correlate with either a deficit or surplus of rainfall, impacting the Eastern Iberian Peninsula [46,47]. Therefore, one of the objectives of this manuscript is to identify possible correlations between the rainfall disparity of Barcelona and the WeMOi, at monthly scale. Finally, considering that historically, the highest monthly amounts in Barcelona were recorded in autumn, the most relevant autumn amounts’ characteristics and their contribution to annual amounts have been analyzed.
The different sections are structured as follows: The extensive monthly rainfall database exceeding two hundred years (1786–2023) is presented in Section 2, along with the definition of the WeMOi. It also introduces the concept of disparity and provides specific definitions of other methods used throughout the article. The results are described in Section 3, with five subsections that include the main characteristics of the rainfall series, comparisons with the reference period 1961–1990, the disparity of monthly amounts computed for periods of 31 years, the correlations between those disparities and the average WeMOi and the autumn calendar months’ characteristics. The analysis of results is discussed in Section 4. Finally, the most relevant conclusions are summarized in Section 5.
2. Materials and Methods
The present research was based on two very long series including monthly rainfall records of Barcelona and the Western Mediterranean Oscillation indices, WeMOi. The first series was published as a very long rainfall record at monthly scale (years 1786–2014) [48]. From 1786 to 1913, the rainfall data were obtained from several weather stations in Barcelona, accurately analyzed and adapted by [48] to ensure continuity with the monthly series of the Fabra Observatory, which has records from 1914 to the present. This observatory is located on the boundary of Barcelona, at an altitude of 415 m above sea level, on the Collserola mountain, surrounded by forested hills. Its UTM coordinates are as follows: Zone 31T, Easting: 426811, Northing: 4585564 (or in DMS: latitude 41.4184° N; longitude 2.1239° E).
The quality control and homogenization of this series was extensively explained in [48]. This pluviometric series also facilitated the detection of relationships between changes in the rainfall regime in Barcelona and potential effects attributed to CO2 emissions, as well as an analysis of the multifractal structure of the rainfall data extending to 2019 [43]. For the present research, the dataset has been updated to 2023, using data from the still-operational Fabra Observatory [49]. Consequently, a complete monthly rainfall series of 238 years, from 1786 to 2023, has been used in this manuscript.
The second series corresponds to the Western Mediterranean Oscillation index (WeMOi), defined as the difference between the normalized monthly barometric series at San Fernando (southwest of Spain, Figure 1) (36°17′ N, 06°07′ W) and at Padova (north of Italy) (45°24′ N, 11°52′ E) (Figure 1). This index is highly correlated with daily precipitation along the coastal areas of the eastern Iberian Peninsula, even at the monthly scale. This is in contrast to the poor correlation of the North Atlantic Oscillation index (NAOi), with this side of Spain [45,50]. This atmospheric circulation index shows a strong relationship with Mediterranean climate patterns. During its positive phases, an Azores anticyclone dominates the southwest quadrant of the Iberian Peninsula, while low pressures occur in the Ligurian Sea. Conversely, negative phases are often associated with anticyclones in Central Europe (north of the Italian Peninsula) and low-pressure systems in the southwest Iberian Peninsula. In addition to these distinct patterns, there are neutral phases, often characterized by northeast and southwest advections or low-pressure gradients over the Western Mediterranean area. A detailed analysis of the complex structure of the WeMOi series, in terms of complexity and predictability, based on fractal and multifractal theory, can be found in [51]. The available period of the WeMOi series (1821–2020, with a 1.1% of missing data) has been kindly provided by the Climate Change and Landscape Ecology group [52].
2.1. Database Characteristics
The Gamma distribution at annual scale was notably recommended by the World Meteorological Organization as the most appropriate for climatological rainfall research [53]. Some examples were those corresponding to rainfall intensity and changes on average and extreme daily rainfall due to global warming [54,55] and rainfall distribution at monthly scale [56] and at annual scale [57]. The parameter values of the Gamma distribution [58], and , were deduced by means of the average, µ, and the standard deviation, σ, of the annual amounts previously divided by the minimum annual amount of the annual database (Equations (1a) and (1b)):
The cumulative distribution function, CDF, was numerically computed in agreement with the mathematical formulation of Equation (2):
For annual amounts, a moving window of 31 years, MW31, was applied, with the aim of detecting possible periodicities, oscillations or trends. These moving windows were computed with a one-year shift and were represented with respect to the centered year of the window. The selection of the 31 years for the moving window size was a good choice due the similarity with the reference periods of 30 years used for climatological studies. These moving windows were also applied for the monthly and annual disparity.
Using moving windows for rainfall analysis helps smooth out short-term fluctuations and provides a clearer view of the underlying trends and patterns in the data, making it a valuable technique in environmental science and resource management. This method has been extensively used in climatological research, although it has a known limitation regarding the potential influence of individual extreme events. Nevertheless, it is effective for capturing broader, persistent shifts in the dataset. A recent study [59] applied this technique to the seasonal precipitation changes of the Spanish mainland. Nonetheless, the resultant moving average series exhibited autocorrelation due to the overlap in windows, which causes dependency among adjacent data points. The presence of positive autocorrelation increases the likelihood of detecting spurious trends [60], a consideration that will be addressed in detail later in Section 2.4.
The evolution of the coefficient of variation (CV) over time was also calculated, by dividing the standard deviation of the annual rainfall values within each 31-year moving window by the mean of the same values.
2.2. Rainfall Discrepancies with Respect to Years 1961–1990
The comparison of monthly (or annual) rainfall from 1786 to 2023 with the reference period 1961–1990 could reveal outstanding rainfall irregularities. This interval is recommended by the World Meteorological Organization, WMO [61] and also proposed by the Meteorological Service of Catalonia, SMC [62] to detect climatic changes.
These comparisons are easily established by computing the positive or negative relative deviations of rainfall amounts with respect to the average values of reference obtained for the mentioned 30 years. The monthly discrepancies in terms of percentages, , are computed as Equation (3):
where are the average amounts deduced from the years of reference (1961–1990) for every one of the 12 calendar months and the j-calendar months’ values along the 238 recorded years. The extreme negative discrepancy at monthly scale (−100%) represents null monthly amounts, and null discrepancies at annual scale correspond to annual amounts coinciding with the 1961–1990 annual average.
2.3. Monthly and Annual Rainfall Disparity
The concept of disparity [24,26,40,41] quantifies the irregularity degree of a rainfall regime. The disparity, D, of a positive series {, i = 1, 2, …, n} of consecutive monthly rainfall amounts can be determined by the Equation (4).
being the disparity index [26], which would be equal to 0 for an absolute regularity {= , i = 1, 2, …, n}. Conversely, the higher the disparity, every data point could be different in comparison with previous and successive . In spite of the mathematical formulation of the disparity being based on positive time series, two problems generated some uncertainty about these computations. Firstly, there was a possibility that some monthly data was missing. Fortunately, this issue was not detected after reviewing the monthly pluviometry from 1786 to 2023. Second was the existence of monthly zero rainfall amounts, a not-negligible question in Mediterranean domains, where heavy drought episodes (long dry spells) are detected. Several rules can be considered to prevent this computational problem in Equation (4). If is one of the zero monthly rainfall data, quotients and can be removed when computing Equation (4) being substituted by . Alternatively, can be substituted, for instance, by 1.0 mm, 0.01 times the monthly mean of the analyzed series, or adding 1.0 mm to every monthly amount, with the aim of smoothing the computational problem of a null monthly amount [63]. In the present case, bearing in mind the absolute completeness of the rainfall series, the computational problems caused by a small number of real null monthly amounts () were solved by adding 1.0 mm to the non-rainfall months. As for the annual amounts, the disparity was computed for moving windows of 31 years, MW31, with a one-year shift.
2.4. Trends and Correlations
In addition to applying the moving windows technique to annual amounts and disparity to analyze possible oscillations, time trends were also studied through linear regression. The significance was assessed using the Mann–Kendall test [53], and the different percentages of the confidence level were analyzed. However, when dealing with autocorrelated series, as is often the case with moving window averages, the original Mann–Kendall test cannot be applied, because it assumes that the data are independent and randomly ordered [60]. Therefore, this study utilized the modified Mann–Kendall test for autocorrelated data, as proposed by [60], to assess the significance of detected trends in the time series processed using the moving windows technique.
For the relationships between disparity and WeMOi, the Pearson correlation coefficient was computed. The significance in this case was calculated by determining the p-value. A Student’s t-distribution was used to calculate this value. This formula depends on the sample size and the value of the correlation coefficient (Equation (5)).
Once the p-value is obtained, for n − 2 degrees of freedom, it is compared to a pre-defined significance threshold, commonly equal to 0.05 (95% confidence level). If the p-value is less than the significance threshold, the correlation is considered statistically significant, suggesting a possible linear relationship between the two variables in the population from which the sample was drawn. If the p-value is greater than the significance threshold, the correlation is not considered statistically significant, indicating that the observed relationship could be due to chance and may not reflect a true association in the population.
As with trend detection, calculating the Pearson correlation between autocorrelated time series derived from moving windows can lead to overestimated relationships. In this scenario, an effective approach is to fit an ARIMA model to each series, compute the residuals and then determine the Pearson correlation for these residuals [44,64,65]. This method was applied to identify monthly and annual relationships between two autocorrelated variables obtained through the moving windows approach, specifically the disparity D and the WeMOi moving windows averages.
3. Results
3.1. Main Characteristics of the Annual and Monthly Series
Time trends corresponding to the monthly and annual amounts presented in [43] have been actualized in the present work for the years 1786–2023 (Table 1). According to the Mann–Kendall test, only September has a confidence level of 97% significance. The September trend is negative, with a value of −0.082 mm/year. In addition, February and August show positive trends but with slightly lower level of 94% and 92%, respectively. Although it is not the objective of this manuscript, a comparison of the annual and monthly trends presented here with those reported in the previous study [43] for the period 1786–2019 reveals minor discrepancies, as expected, due to the addition of only four years. However, it should be noted that the confidence level of the trend observed in September, the only month with a significant negative trend, increases from 90% to 97%. Examining the temporal evolution of this month, a period from 1840 to 1900 can be distinguished, during which higher amounts are observed compared to subsequent periods.

Table 1.
Trends (mm/year), Mann–Kendall test and percentage of linear trends confidence for monthly and annual amounts. The most relevant values are written in bold types.
The evolution of the meteorological autumn months (September, October and November) is depicted in Figure 2, and the annual amounts in Figure 3a, including linear trends and either a fifth- or a seventh-degree polynomial fit along the recorded years. A clear period of very low annual amounts is detected prior to 1850, with seven years recording less than 300 mm and a minimum of 215.6 mm in 1817. Even though a positive trend is obtained for the whole series, with a confidence level of 86%, some periods have negative trends. For instance, a decrease in annual amounts should be considered from 1980 to the present, with consecutive very low annual amounts for the years 2021, 2022 and 2023 (327.6, 307.7 and 309.5 mm, respectively), the driest since 1835. From 1980 to 2023, a negative trend of −3.19 mm/year has been detected, characterized by a Mann–Kendall test with a confidence level of 89%.
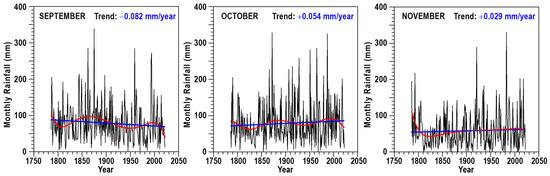
Figure 2.
Evolution of monthly rainfall amounts for September, October and November from 1786 to 2023. Linear trends (blue) and fifth-degree polynomial fits (red) are included.
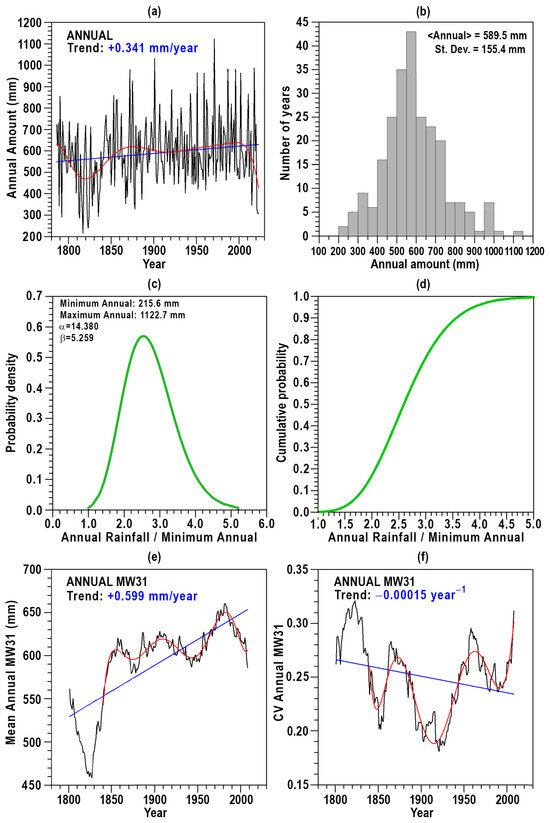
Figure 3.
(a) Evolution of annual rainfall amounts from 1786 to 2023 and (b) histogram of annual rainfall. For the ratio of annual rainfall to the minimum annual rainfall recorded: (c) probability density fitted to the Gamma distribution and (d) cumulative probability fitted to the Gamma cumulative distribution function. Evolution of: (e) annual average rainfall and (f) coefficients of variation (CV), using 31-year moving windows (MW31) with 1-year shifts. Linear trends (blue) and seventh-degree polynomial fits (red) are included in selected panels.
Figure 3b describes the histogram corresponding to the annual scale, with remarkably wide intervals of annual data ranging from 215.6 to 1122.7 mm, an average of 589.5 mm and a standard deviation of 155.4 mm, with only a few years varying from 900 to 1150 mm. The annual rainfall amounts between 500 and 600 are the most frequent, with 33% (78 of 238 years).
The ratio between the annual amount values and the minimum annual amount recorded (215.6 mm) has been fitted to a Gamma distribution [58], with parameters = 14.380 and = 5.259. Figure 3c,d depict the probability density function and the cumulative distribution function of the fitted Gamma distribution for this ratio.
Figure 3e,f describe the evolution of the mean and coefficient of variation for annual moving windows of length 31 years and shift of 1 year. The oscillations since 1786 up to 2023 are evident, and a 7th degree polynomial has been represented with red color from 1840, avoiding the first pronounced minimum. With respect to the evolution of the average amounts, an increasing trend of 0.6 mm/year is obtained. A pronounced minimum is detected between the centered years of 1820 to 1830, equivalent to the 31-year periods of 1805–1835 to 1815–1845, and three maxima close to central moving window years 1860, 1900 and 1980. Nevertheless, after the last maximum close to 1980, a notable reduction of mean values is observed up to 2008 (the center of the last moving window). The maximum coefficients of variation (Figure 3f) are detected close to years 1830, 1870 and 1960, and a third maximum could be expected some years after 2008. When a minimum is detected in the average MW31 amounts, a maximum is depicted for the CV.
Table 2 summarizes the basic characteristics of the complete rainfall regime, noting that the extreme minimum annual amount recorded is 215.6 mm, and the minimum amounts for calendar months are all close to or equal to zero. Conversely, the recorded extreme maximum annual amount, corresponding to 1971, exceeded 1100 mm. In agreement with these extreme examples, signs of notable irregularity (disparity) have to be expected. The maximum amounts at monthly scale recorded in September, October, November and December are notable, also characterized by the highest standard deviations. Additionally, the annual standard deviation of 155.4 mm is substantial. September and October are characterized by the highest average amounts, and the most relevant skewness of monthly amounts are detected for winter months (January, February and December). Two examples with low annual values are those corresponding to years 1817 (215.6 mm) and 2022 (307.7 mm), when the corresponding amounts of September, October and November were, respectively, 32.2, 69.4 and 9.9 mm (year 1817) and 13.1, 11.3 and 7.6 mm (year 2022). Conversely, year 1971 is characterized by the highest amount of 1122.7 mm, with notable contributions of September, October and November (121.3 mm, 141.1 mm and 119.1 mm, respectively) and an unusually high amount of 365.8 mm for December, all of them representing a notable contribution to the annual amount.

Table 2.
Basic characteristics of rainfall amounts (in mm) at annual and monthly scales (minimum, maximum, average, standard deviation and skewness). The most relevant values are written in bold type.
3.2. Rainfall Discrepancies with Respect to Years 1961–1990
A different point of view of the irregularity of the series is the comparison between the rainfall amounts, with the average values corresponding to the reference period 1961–1990. Figure 4 and Figure 5a depict the evolution of these discrepancies (relative deviations) of monthly and annual amounts.
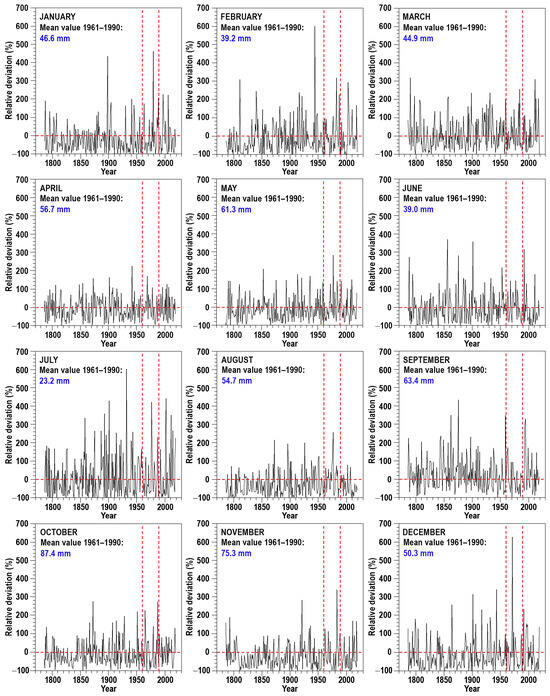
Figure 4.
Relative deviations (%) of monthly rainfall amounts compared to the average for each month during 1961–1990. Red vertical dashed lines mark this reference period.
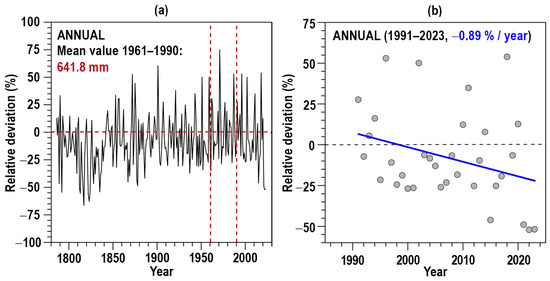
Figure 5.
(a) Relative deviations (%) of annual rainfall amounts compared to the 1961–1990 average (reference period marked by red vertical dashed lines). (b) Detailed view for 1991–2023, showing a non-significant negative trend of −0.89% per year (blue trend line).
In agreement with the definition of the mentioned rainfall discrepancies, explained in Section 2, the extreme negative percentage at monthly scale, −100%, of Figure 4 represents null monthly amounts. The highest positive percentages are obtained in July, February and December, with a percentage of 600%. Conversely, the lowest discrepancies correspond to April, May, August, October and November.
From the point of view of the tendency of the annual rainfall amounts, the negative discrepancies for the interval 1991–2023 are notably dominant (Figure 5b). Additionally, a negative trend of −0.89%/year has been found for this interval, although it is not statistically significant.
3.3. Disparity of Monthly Amounts
The disparity, D, for the twelve calendar months has been computed for a set of moving windows, including every step of 31 years, with a shift of one year for every step, and the most relevant details are summarized in Table 3 and Table 4. The disparity values (Table 3) are dispersed; January, February, July, August, November and December exhibit high maximum and average values of D, with the highest average rainfall disparity observed in January and July. Conversely, April, May, June, August, September and October display lower minimum values, and the lowest average disparity is observed in April and September. In short, consistent disparities among calendar months belonging to the same season are not always detected. From the viewpoint of the annual scale, the corresponding disparity is notably smaller, as expected.

Table 3.
Main characteristics of the disparity D (maximum and minimum values, average and standard deviation) computed for every calendar month and at annual scale using moving windows of 31 years length.

Table 4.
Trends, modified Mann–Kendall test for autocorrelated data (mM-K test, [60]) and confidence level (%) for the evolution of the disparity D for moving windows of 31 years length. In bold, significant trends at 99% confidence level.
To detect trends in the MW31 disparity series at monthly and annual scale, a modified Mann–Kendall test for autocorrelated data has been used [60]. In agreement with Table 4, the evolution of D along the years has shown statistically significant increasing trends for the autumn months September, October and November, with a confidence level exceeding 99%. It is relevant to note that the maximum positive trend of 3.6 × 10−3 year−1 is for November. For January and February, the increasing trends found are only significant at a confidence level of 91% and 85%, respectively, and from March to August, together with December and at annual scale, the percentages of confidence level are notably lower. Therefore, an increasing disparity of the monthly rainfalls is particularly evident throughout the autumn season, for which the highest amounts could be more probable, and part of the winter. Bearing in mind that some of these calendar months (especially those of the autumn season) could contribute to compensating previous monthly droughts, their increasing disparities represent an additional difficulty to forecast their monthly amounts and, consequently, the end of continuity of severe drought episodes.
The evolution of the disparity at both monthly and annual scales is described in Figure 6 and Figure 7. Clear oscillations in the disparity are observed along the moving windows, with the exception of March and September, which are characterized by small fluctuations. The most pronounced oscillations are seen in July and August, with periodicities exceeding 100 years, while relatively clear periodicities between 40 and 75 years are detected for the other months. For the annual scale, D also shows signs of oscillations with periodicities between 50 and 90 years, demonstrating a clear correlation with annual rainfall amounts, which exhibit similar periodic oscillations (see Figure 3e).
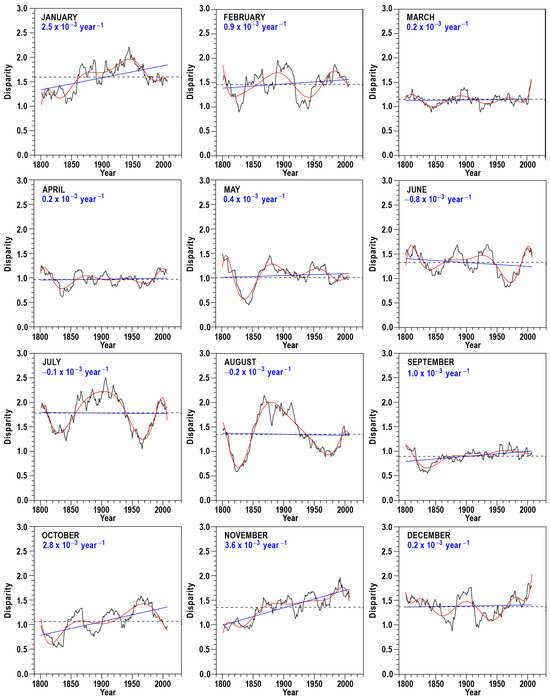
Figure 6.
Evolution of the disparity for every calendar month (1786–2023) using moving windows, with corresponding linear (blue) and polynomial (red) fits. The dashed line represents the mean disparity value.
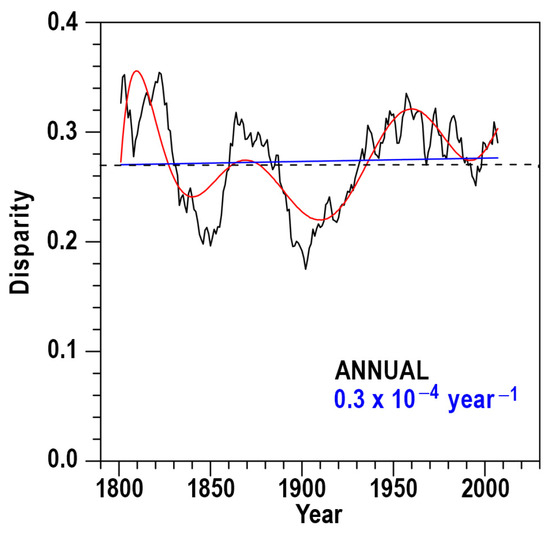
Figure 7.
Evolution of annual disparity (1786–2023) using moving windows, with corresponding linear (blue) and polynomial (red) fits. The dashed line represents the mean disparity value.
3.4. Disparity and WeMO Relationships with Moving Windows
After revising the results of the disparity at monthly and annual scale, it has to be accepted that every one of the calendar months and the annual series depict different evolutions of D along the two-hundred years records. This fact probably increases the difficulty of monthly amounts forecasting, generating more difficulties and uncertainties on the length of a dry spell, a very important factor in the Western Mediterranean, as well as in many areas of the whole southern Europe, where drought episodes are quite usual [29,30]. The forecasting results of monthly amounts could be improved by means of the Western Mediterranean Oscillation index [26,45,46,47] and the disparity, with a process quite similar to those applied by means of the ARIMA algorithm to only consecutive series of monthly amounts [31,42].
The monthly WeMOi series are represented in Figure 8. The relationships between the disparities and the WeMOi (Figure 9) have been investigated after averaging the latter variable with the same 31-year moving windows as those applied to the disparity. To avoid overestimated relationships between these two autocorrelated variables, we have determined the Pearson correlation for the residuals obtained after fitting an ARIMA model to each series [44,64]. The results show that no significant correlations were found at the 95% confidence level. Only three months, January, February and July, have shown a significant linear relationship between the averaged disparities and WeMOi, at a confidence level above 90%. At the annual scale (Figure 10), the dependence of annual disparities on WeMO annual values shows a non-significant negative tendency, with the maximum disparity values corresponding to an average WeMO around 0.4 hPa.
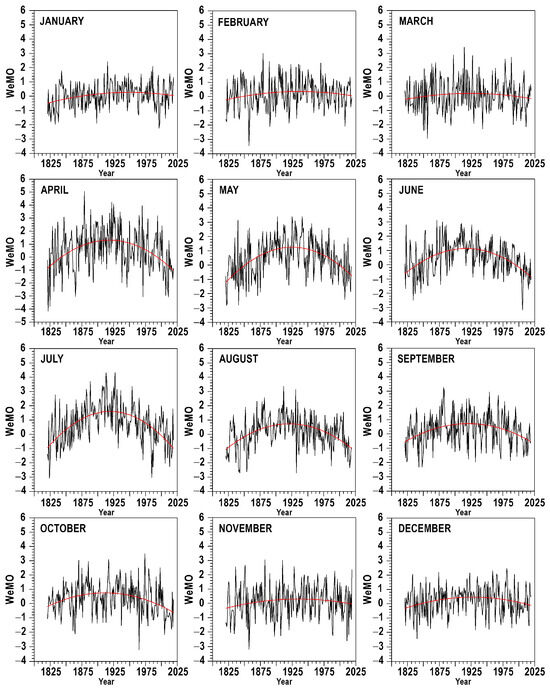
Figure 8.
Evolution of the WeMO (hPa) for each calendar month (1821–2020). The red line represents a second-order polynomial fit. The WeMO dataset has been kindly provided for the Climate Change and Landscape Ecology Research Group of the University of Barcelona and is available at [52].
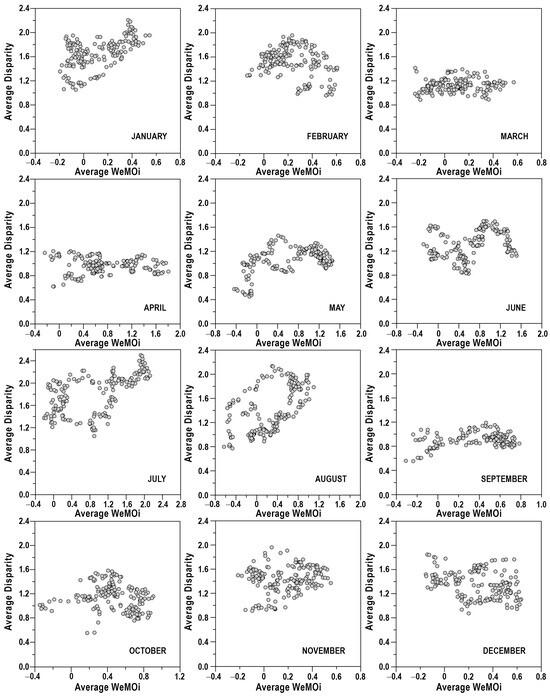
Figure 9.
Relationship between the mean monthly disparity and the mean monthly WeMOi (hPa).
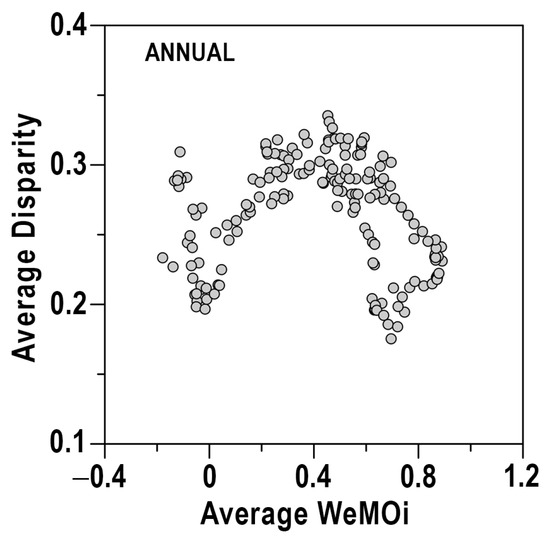
Figure 10.
Relationship between the mean annual disparity and the mean annual WeMOi (hPa).
3.5. Autumn Calendar Months Characteristics
Areas of NE Spain close to the Mediterranean coast are typically characterized by a high contribution of the autumn period to the corresponding annual amount. Nevertheless, this contribution could notably change year by year. The specific case of Barcelona series is described in Figure 11a–d. The autumn amounts (Figure 11a), including September, October and November in this research, have a global average contribution to the annual amount of 36.3%. Sometimes these contributions exceed 60% of the corresponding annual amounts; nevertheless, contributions of 20–30% are also evident. These discrepancies on the contribution to annual amounts have to be attributed to the disparity of every one of these three months, being also relevant the small, but negative tendency, of −0.023% per year, Mann–Kendall significant at the 98% confidence level. The complex contribution of these three months to the annual amounts is also described in Figure 11b, indicating that the possible percentage range of autumn contributions is wider for low annual amounts than for higher ones. For instance, for relatively dry years with annual rainfall between 200 and 400 mm, autumn contribution percentages range from 10% to 67%, whereas for rainy years, with a total annual rainfall above 900 mm, the autumn contribution percentages vary within a narrower band, between 27% and 53%. Another point of view of the relevance of these three months on the contribution to the annual amounts is described in the histogram of Figure 11c. Close to 140 autumn amounts, almost for the 60% of years, generate 30–50% of their corresponding total annual amount. Finally, Figure 11d describes the contribution of September, the autumn month with the highest negative trend, highlighting three relevant factors. First, the oscillations of the September amounts throughout the years are notable. Second, for a not negligible number of years, the September amount contribution is very relevant (>30%). Third, the negative trend of the cumulated three months (Figure 11a) and that corresponding to September are very similar. It is important to note that, although the overall annual trend is positive, the considerable contribution of the autumn season to the annual totals tends to decrease.
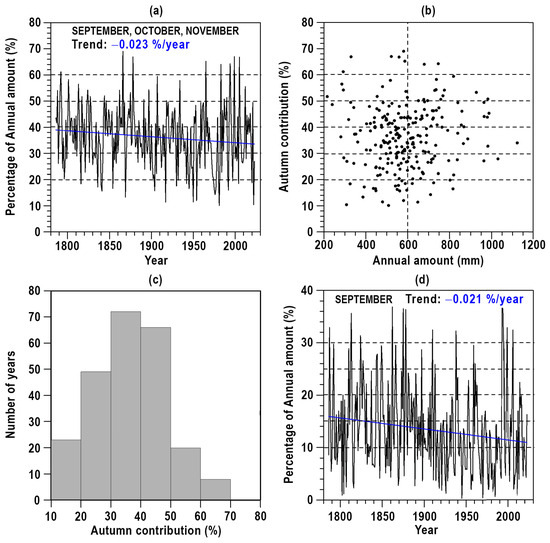
Figure 11.
(a) Percentage of the total amounts recorded along September, October and November. (b) Relationship between annual amounts and autumn amounts corresponding to the mentioned percentages. (c) Histogram of the percentage of years with the percentage of autumn amounts contributing to annual amounts. (d) In detail, percentage of the total amounts recorded along September. Trend lines in blue.
Another relevant factor to bring into the analysis could be the distribution of the autumn monthly amounts depending on WeMOi values. The highest monthly amounts are usually obtained by negative or small positive values of WeMOi. As anticipated from known results [45], a clear linear relationship between monthly amounts and WeMOi has not been observed for all months. Both September and October are the two months with the highest mean contribution to the annual amount, each at 13.3%. However, while a negative slope of −3.6 mm hPa−1 between monthly amounts and WeMOi, with a non-significant correlation, has been observed for September, the negative slope for October is statistically significant. Pearson correlations with significant coefficients of −0.28 and −0.32 and similar negative slopes (−15.0 and −13.8 mm hPa−1) were detected for the autumn months October and November. In addition, a similar and significant negative slope (−14.5 mm hPa−1, with a correlation of −0.32) has also been found for the month of December (see Figure 12). For these three months, October, November and December, future amounts could be affected by the evolution of the WeMOi.
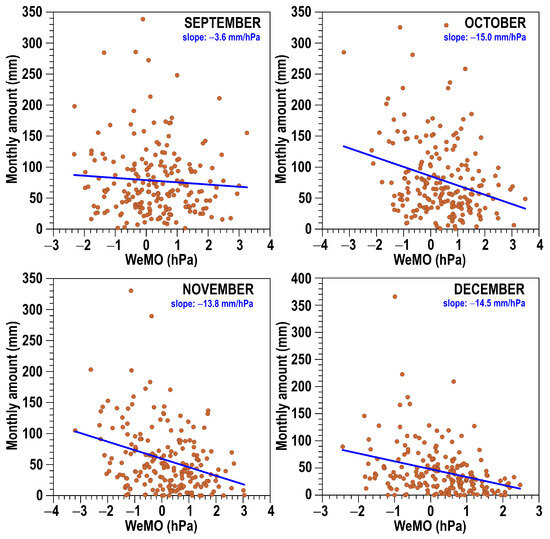
Figure 12.
WeMO values (hPa) associated with the rainfall amounts for September, October, November and December. Linear fits are shown in blue.
An illustrative example of the contributions of September, October and November in recent years is summarized in Table 5. Years with lower-than-average annual rainfall (<589.5 mm) over the 238-year record are listed, beginning in 2000. Of the fifteen years shown, the lowest annual amounts occur in the consecutive years 2021, 2022 and 2023. The ratios of the autumn contributions to the annual totals are notably small in 2004 and 2022, with ratios of only 18.5% and 10.4%, respectively. In eight of the fifteen cases, the ratio is lower than the average percentage of 36.3%

Table 5.
Fifteen years between 2000 and 2023 with annual rainfall amounts below the average of 589.5 mm from the complete database. This table includes the corresponding contributions of September, October and November (in mm) and the percentage of the cumulative three-month total, referred to as the Ratio, relative to the annual amount. Values in bold indicate ratios lower than 36.3%, which is the average Ratio for the entire series.
It is remarkable that the three recent years of the series, 2021, 2022 and 2023, have been the driest years since 1835. In particular, the autumn of 2022 is the driest autumn of the entire series and ranks second in terms of its contribution to the annual total. Furthermore, the autumn of 2023 is among the driest 5% of the entire series. The autumns of the years 2022 and 2023 rank among the 10% that contributed the least to their respective annual total amounts.
4. Discussion
The analysis of monthly and annual precipitation series in Barcelona has provided updated information (up to 2023) on their main characteristics. The results obtained are consistent with those found for these series in other studies [43,48]. In particular, the annual amounts exhibit a good fit to the Gamma statistical distribution, potentially supporting the validation of the two unified segments of rainfall data (years 1786–1913 and 1914–2013 [48]), employed to obtain the overall dataset. The update from 2019 to 2023 has allowed the inclusion of the low rainfall values recorded in the past three years in the analysis, the driest since 1835.
Although the overall annual trend of the entire period is positive, the study of the evolution of the annual moving windows of length 31 years and shift of 1 year has shown a non-monotonic evolution, with clear oscillations since 1786 and up to 2023 (Figure 3e). A very pronounced minimum has been detected between the centered years of 1820 to 1830, equivalent to the 31-year periods of 1805–1835 to 1815–1845, corresponding to the extremely dry years of the first quarter of the 19th century. Extensive documentary sources and literature attest to a period of significant distress that affected Catalonia, including Barcelona, among other areas of the Iberian Peninsula, during those years. Drought and poor harvesting led to a known subsistence crisis in 1817 [66,67]. The beginning of the 19th century was exceptionally cold and dry, especially during the years 1815–1818 [68,69,70]. There was a period of low solar activity known as the Dalton Minimum (1790–1830), which falls at the end of what is known as the Little Ice Age (spanning from the early fourteenth century to the mid-nineteenth century). This period of low solar activity coincided with a time of significant volcanic activity, which also contributed to the overall decrease in temperatures. In April 1815, one of the most powerful volcanic eruptions of the last millennium occurred, that of the Tambora volcano (Indonesia), which resulted in what is known as the “year without a summer” of 1816, with unusually low temperatures [71]. It has recently been attributed that the widening of the Hadley cell acted as the primary cause of the notable decrease in precipitation across southern Europe during this period [72]. This widening was primarily influenced by the elevated volcanic activity, which surpassed the significance of solar forcing. If this coincidence of extreme climatic events does not occur, it is not expected that the observed oscillations will lead us, in the evolution of the annual moving windows, to minima as pronounced as those corresponding to the early 19th century (Figure 3e). However, in 62.5% of the years in the period 2000–2023, annual amounts below the average have been registered (Table 5), and the last three years of the series—2021, 2022 and 2023—have been the driest since 1835 (Figure 3a). In the absence of extreme climatic events like those previously cited, the latest observations suggest that the ongoing dry conditions may be related to anthropogenic influences.
Since the end of the 20th century and extending into a significant portion of the 21st century, the annual rainfall levels in Barcelona have shown a trend characterized by both a decrease in their overall values and a substantial increase in the coefficient of variation. Notice the resemblance between the coefficient of variation (CV) over time (Figure 3f) and the disparity D (Figure 7), confirming that these two statistics are similarly effective in evaluating the rainfall irregularity of a place [47]. In other words, a growing disparity has been detected in consecutive annual rainfall amounts, also exhibiting a tendency towards decreased overall amounts. This behavior has been reported in other studies, some of them using other ways to measure the increasing irregularity of the rainfall pattern in the area [20,23,73].
An alternative perspective on the irregularity of the series is to compare the rainfall amounts with the average values from the reference period 1961–1990, as proposed by the World Meteorological Organization for historical comparison and climate change monitoring for long-term climate change assessments [61]. The discrepancies with respect to the reference period 1961–1990 during the period 1991–2023 are predominantly negative (23 out of 33 years). A linear fit of these discrepancies has revealed a negative trend of −0.89% per year, indicating a probable continuing reduction in annual rainfall amounts in the near future in the area [74,75].
At the monthly scale, the maximum amounts recorded in September, October, November and December for the studied sample were notable (Table 2). However, equally noteworthy were their highest standard deviations, particularly during the autumn months. Regarding the evolution of disparity at the monthly scale, there is a notable increase during the autumn season, during which the highest amounts could be more expected. Bearing in mind that some of these autumn months could contribute to compensating for previous monthly droughts and mitigate the effects on agriculture, human health and water supplies, their increasing disparities raise questions about their potential contribution to ending the continuity of severe drought episodes that are quite usual in many areas of Southern Europe [76,77]. Thus, the found disparity trends suggest a more irregular pattern of rainfall at both the monthly and annual scales in the forthcoming years, potentially leading to increased frequency or severity of droughts.
Monthly rainfall forecasting could be enhanced by incorporating disparity, utilizing a methodology akin to that employed by the ARIMA algorithm for analyzing consecutive series of monthly amounts [31,42]. Even so, the dispersed disparity values and trends observed according to the calendar month, as well as throughout the over-200-year time series, suggest that it would be appropriate to introduce a variable that carries information about atmospheric dynamics into the analysis: the WeMOi [45,46,47].
Due to the presence of autocorrelation in the average series obtained after using moving windows, the correlation between the averaged disparity and WeMOi has been assessed by examining the residuals of each series after fitting an ARIMA model to them [44,64]. This refined correlation study has not revealed significant correlations between disparity and WeMOi for spring and autumn. However, for winter, significant correlations between the residuals were observed for January and February, and only July exhibited a significant correlation during the summer period. These inconclusive results suggest that more variables need to be introduced into the analysis to capture the possible indirect relationship between disparity and WeMOi. For instance, significant linear relationships between disparity (and also CV) and the correlation of WeMOi with precipitation at several weather stations in Catalonia were found for both seasonal and annual scales [47].
In light of the present results, one can infer that low annual rainfall amounts have been quite common during the first two decades of the 21st century. Moreover, the contribution of autumn months has not been sufficient to compensate for drought episodes, likely due to the negative trend observed in autumnal rainfall. Notably, the last three years of the series, 2021, 2022 and 2023, have been the driest since 1835. In particular, the autumn of 2022 stands out as the driest in the entire series, ranking second in terms of its contribution to the annual total. Similarly, the autumn of 2023 is among the driest 5% of the series. These exceptionally dry conditions have prompted authorities to implement stringent water usage restrictions to manage the crisis [78].
Given that autumn is a season when rainfall can compensate for previous dry months, changes in atmospheric circulation that result in reduced autumn precipitation should not be discarded. Basically, a relatively copious rainfall regime on the northeastern Spanish coast is more associated with Mediterranean cyclogenesis and mesoscale convective systems, rather than with Atlantic fronts crossing the Iberian Peninsula from west to east. Therefore, the observed negative trends in autumn rainfall could be linked to changes in the frequency of these types of disturbances affecting the area. Figure 13 illustrates the synoptic maps at sea level and 500 hPa [79], corresponding to six rainy episodes in autumn 2018, one of the rainiest autumns in the series, with a total rainfall of 448.1 mm and a contribution of 45% to the annual total (988.0 mm). In the first five cases shown, cold air at high altitudes over Barcelona and low surface pressure can be observed, with the center of a deep low-pressure system located in the northern latitudes extending its influence over Spain. The daily rainfall amounts recorded during these events range from 21.8 mm to 56 mm. The maps for 9 October and 9 November depict an isolated depression at 500 hPa over northeastern Spain. In contrast, the situation on 15 November, which produced the highest daily precipitation of 139.9 mm, has different characteristics. Although surface pressure is not low (1020 hPa), the isolated depression at 500 hPa is situated southwest of the Iberian Peninsula, with maritime easterly advections providing the necessary humidity towards the coast of Barcelona. This pattern results in heavy precipitation along the Mediterranean coast of Spain.
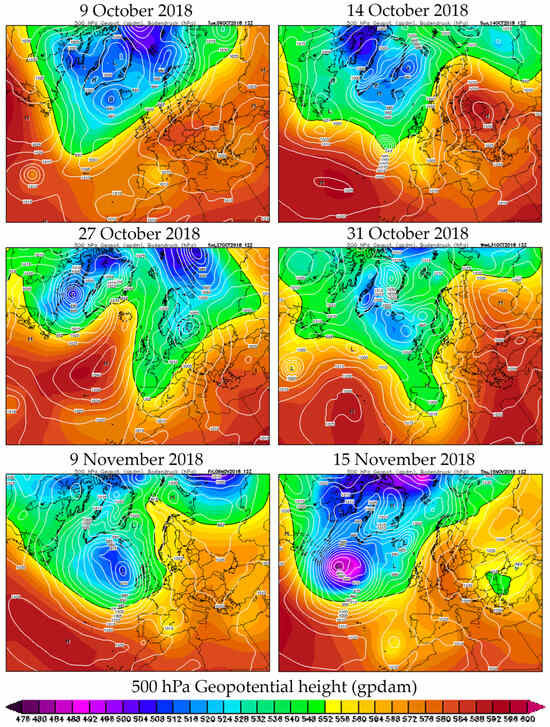
Figure 13.
Synoptic maps at sea level and 500 hPa [79] corresponding to six rainy episodes in autumn 2018, one of the rainiest autumns in the series, with a total rainfall of 448.1 mm and a contribution of 45% to the annual total (988.0 mm).
Conversely, Figure 14 represents one of the driest autumns in 2022, with only 32 mm of rainfall and an annual total of just 307.7 mm. The panel for 2 October shows a stable situation, characterized by a high-pressure system centered over Spain. In the panels for 14 and 18 October and 2 and 14 November, despite the high-pressure center being displaced relative to the Iberian Peninsula, its influence reaches the northeastern Spanish coast with pressures above 1020 hPa. At 500 hPa, cold air does not reach our latitudes or is located to the west or east of the Iberian Peninsula.
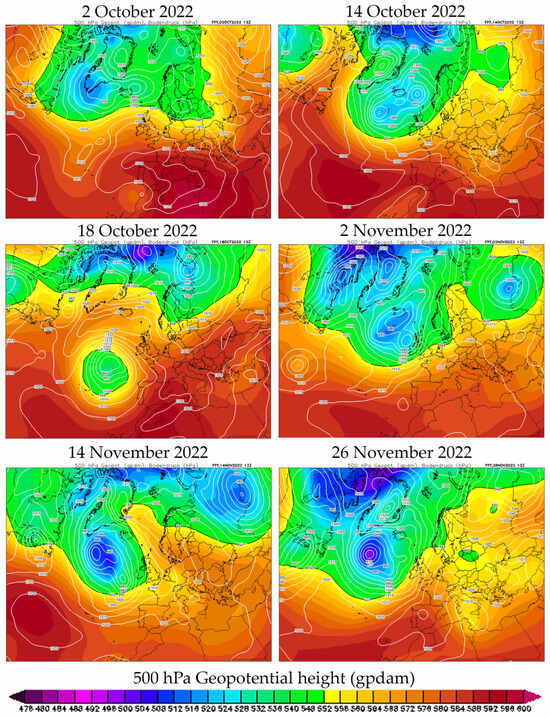
Figure 14.
Synoptic maps at sea level and 500 hPa [79] corresponding to autumn 2022, one of the driest autumns in the series, with only 32 mm of rainfall and a contribution of only 10% to the annual total (of just 307.7 mm).
5. Conclusions
The importance of having a long and complete series is crucial for understanding the rainfall behavior of a region. In previous studies with shorter series, monotonic trends, either positive or negative, were obtained, depending on the period considered. In this work, it has been shown that alternating periods of positive and negative trends have occurred in the past, and that drier episodes than those observed in recent years were detected in the early 19th century. The good fit of the annual precipitation data in Barcelona to the Gamma statistical distribution supports the validation of the combined dataset derived from historic records spanning two distinct periods reconstructed by [48]. This validation enhances confidence in the reliability and consistency of the dataset, further enriching the understanding of long-term rainfall trends and variability in the area.
The study of annual moving windows of 31-year length and 1-year shift has revealed clear oscillations from 1786 to 2023, including a pronounced minimum between 1820 and 1830, coinciding with extremely dry years in the early 19th century. This drought period has been attributed to the coincidence of astronomic and geologic causes implied in changes in the atmospheric circulation, which caused a notable decrease in precipitation across southern Europe. It is unlikely that the extreme minimum observed in the annual moving windows of the early 19th century will recur without a convergence of similar climatic causes. However, in 62.5% of the years in the period 2000–2023, annual amounts below the average have been recorded, with the last three years of the series, 2021, 2022 and 2023, being the driest in the last 190 years. In fact, the cumulative rainfall over those three years has been the lowest of any three consecutive years in the past 200 years. Given the notable average contribution of the autumn months to the annual totals, which stands at 36.3%, this exceptionally low total rainfall can be linked to the extremely dry autumns of 2022 and 2023, both of which rank among the driest 5% of the entire series.
By incorporating rainfall values from recent years, the rainiest month in the area, September, is confirmed as having a significant negative trend, with its confidence level reinforced up to 97%. The contribution of this month to the annual total decreases by 0.21% every 10 years, a trend very similar to that of autumn (−0.023% per year).
At the monthly scale, the disparity trends suggest a more irregular rainfall pattern for autumn months, when high monthly rainfall amounts are typically expected. As autumn months usually play a crucial role in compensating for previous dry months, the increasing disparities raise uncertainty about the frequency and severity of droughts in the area.
The monthly amounts corresponding to October, November and December have shown a linear relationship with the WeMOi, with significant correlations and similar negative slopes ranging between −15.0 and −13.8 mm hPa−1. This fact suggests that the future rainfall amounts during these months could be influenced by the WeMOi fluctuations.
Future research should focus on enhancing our understanding of rainfall behaviors and their effects on the Barcelona metropolitan area and neighboring regions. One objective is to improve the forecasting of monthly rainfall data by incorporating WeMOi values into suitable forecasting algorithms, particularly during autumn months when WeMOi has a significant influence. Another aim is to apply similar strategies to rainfall data from other rain gauges throughout Catalonia, which could provide insights into the impact of the region’s complex topography and varying distances from the Mediterranean Sea and the Pyrenees. Finally, analyzing changes in atmospheric circulation and the frequency with which disturbances, such as Mediterranean cyclogenesis and mesoscale convective systems, affect the region will be essential in explaining the observed rainfall variability.
Author Contributions
Conceptualization, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Methodology, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Software, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Validation, X.L., C.S., M.d.C.C.-C., R.R.-S. and M.P.; Formal analysis, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Investigation, X.L. and M.d.C.C.-C.; Resources, X.L. and M.P.; Data Curation, X.L. and M.P.; Writing—Original Draft Preparation, X.L. and M.d.C.C.-C.; Writing—Review & Editing, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Figures and Visualization, X.L., C.S., M.d.C.C.-C. and R.R.-S.; Supervision, X.L. and M.d.C.C.-C. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Rainfall data used to support the findings of this study were supplied by Servei Meteorològic de Catalunya (Generalitat de Catalunya), available at Accés a la sèrie de precipitació acumulada mensual de Barcelona (des de 1786). WeMOi series were kindly provided by the Climate Change and Landscape Ecology research group and are available at WeMOi 1821–2020.
Acknowledgments
The authors thank the Servei Meteorològic of Catalunya (SMC) and the Climate Change and Landscape Ecology research group for providing the rainfall and climate data used in this work. The authors also thank the anonymous referees for their constructive comments and suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Lionello, P.; Abrantes, F.; Congedi, L.; Dulac, F.; Gacic, M.; Gomis, D.; Goodess, C.; Hoff, H.; Kutie, L.H.; Luterbacher, J.; et al. Introduction: Mediterranean climate: Background information. In The Climate of the Mediterranean Region. From the Past to the Future; Lionello, P., Ed.; Elsevier Oxford: Amsterdam, The Netherlands, 2012; pp. 35–90. ISBN 9780124160422. [Google Scholar] [CrossRef]
- Lionello, P.; Trigo, I.F.; Gil, V.; Liberato, M.L.R.; Nissen, K.; Pinto, J.G.; Raible, C.; Reale, M.; Tanzarella, A.; Trigo, R.M.; et al. Objective Climatology of Cyclones in the Mediterranean Region: A consensus view among methods with different system identification and tracking criteria. Tellus A 2016, 68, 29391. [Google Scholar] [CrossRef]
- Campins, J.; Jansà, A.; Genovés, A.; Picornell, M.A. Climatology of Mediterranean cyclones using the ERA-40 dataset. Int. J. Climatol. 2011, 31, 1596–1614. [Google Scholar] [CrossRef]
- Seneviratne, S.; Lüthi, D.; Litschi, M.; Schär, C. Land–atmosphere coupling and climate change in Europe. Nature 2006, 443, 205–209. [Google Scholar] [CrossRef] [PubMed]
- Hoegh-Guldberg, O.; Jacob, D.; Taylor, M.; Bindi, M.; Brown, S.; Camilloni, I.; Diedhiou, A.; Djalante, R.; Ebi, K.L.; Engelbrecht, F.; et al. Impacts of 1.5 °C global warming on natural and human systems. In Global Warming of 1.5 °C: An IPCC Special Report on the Impacts of Global Warming of 1.5 °C Above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty; IPCC: Geneva, Switzerland, 2018; Available online: https://www.ipcc.ch/sr15/chapter/chapter-3/ (accessed on 16 October 2024).
- Coppola, E.; Nogherotto, R.; Ciarlò, J.M.; Giorgi, F.; van Meijgaard, E.; Kadygrov, N.; Iles, C.; Corre, L.; Sandstad, M.; Somot, S.; et al. Assessment of the European climate projections as simulated by the large EURO-CORDEX regional and global climate model ensemble. J. Geophys. Res. Atmos. 2021, 126, e2019JD032356. [Google Scholar] [CrossRef]
- Barredo, J.I.; Mauri, A.; Caudullo, G.; Dosio, A. Assessing Shifts of Mediterranean and Arid Climates Under RCP4.5 and RCP8.5 Climate Projections in Europe. Pure Appl. Geophys. 2018, 175, 3955–3971. [Google Scholar] [CrossRef]
- Spinoni, J.; Vogt, J.V.; Naumann, G.; Barbosa, P.; Dosio, A. Will drought events become more frequent and severe in Europe? Int. J. Climatol. 2018, 38, 1718–1736. [Google Scholar] [CrossRef]
- Kotsias, G.; Lolis, C.; Hatzianastassiou, N.; Bakas, N.; Lionello, P.; Bartzokas, A. Objective climatology and classification of the Mediterranean cyclones based on the ERA5 data set and the use of the results for the definition of seasons. Theor. Appl. Climatol. 2023, 152, 581–597. [Google Scholar] [CrossRef]
- Flaounas, E.; Aragão, L.; Bernini, L.; Dafis, S.; Doiteau, B.; Flocas, H.; Gray, S.L.; Karwat, A.; Kouroutzoglou, J.; Lionello, P.; et al. A composite approach to produce reference datasets for extratropical cyclone tracks: Application to Mediterranean cyclones. Weather. Clim. Dyn. 2023, 4, 639–661. [Google Scholar] [CrossRef]
- Reale, M.; Cabos Narváez, W.D.; Cavicchia, L.; Conte, D.; Coppola, E.; Flaounas, E.; Giorgi, F.; Gualdi, S.; Hochman, A.; Li, L.; et al. Future projections of Mediterranean cyclone characteristics using the Med-CORDEX ensemble of coupled regional climate system models. Clim. Dyn. 2022, 58, 2501–2524. [Google Scholar] [CrossRef]
- Forzieri, G.; Feyen, L.; Russo, S.; Vousdoukas, M.; Alfieri, L.; Outten, S.; Migliavacca, M.; Bianchi, A.; Rojas, R.; Cid, A. Multi-hazard assessment in Europe under climate change. Clim. Change 2016, 137, 105–119. [Google Scholar] [CrossRef]
- Petrova, I.Y.; Miralles, D.G.; Brient, F.; Donat, M.G.; Min, S.-K.; Kim, Y.-H.; Bador, M. Observation-constrained projections reveal longer-than-expected dry spells. Nature 2024, 633, 594–600. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Zhang, X.; Zwiers, F.; Westra, S.; Alexander, L.V. A Global, Continental, and Regional Analysis of Changes in Extreme Precipitation. J. Clim. 2021, 34, 243–258. [Google Scholar] [CrossRef]
- Cioffi, F.; Lall, U.; Rus, E.; Krishnamurthy, C.K.B. Space-time structure of extreme precipitation in Europe over the last century. Int. J. Climatol. 2015, 35, 1749–1760. [Google Scholar] [CrossRef]
- van den Besselaar, E.J.M.; Klein Tank, A.M.G.; Buishand, T.A. Trends in European precipitation extremes over 1951–2010. Int. J. Climatol. 2013, 33, 2682–2689. [Google Scholar] [CrossRef]
- Reale, M.; Lionello, P. Synoptic climatology of winter intense precipitation events along the Mediterranean coasts. Nat. Hazards Earth Sys. Sci. 2013, 13, 1707–1722. [Google Scholar] [CrossRef]
- Sunyer, M.A.; Hundecha, Y.; Lawrence, D.; Madsen, H.; Willems, P.; Martinkova, M.; Vormoor, K.; Bürger, G.; Hanel, M.; Kriaučiūnienė, J.; et al. Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe. Hydrol. Earth Syst. Sci. 2015, 19, 1827–1847. [Google Scholar] [CrossRef]
- Pedron, I.T.; Silva Dias, M.A.F.; de Paula Dias, S.; Carvalho, L.M.; Freitas, E.D. Trends and variability in extremes of precipitation in Curitiba–Southern Brazil. Int. J. Climatol. 2017, 37, 1250–1264. [Google Scholar] [CrossRef]
- Serrano-Notivoli, R.; Beguería, S.; Saz, M.; de Luis, M. Recent trends reveal decreasing intensity of daily precipitation in Spain. Int. J. Climatol. 2018, 38, 4211–4224. [Google Scholar] [CrossRef]
- Ribes, A.; Thao, S.; Vautard, R.; Dubuisson, B.; Somot, S.; Colin, J.; Planton, S.; Soubeyroux, J.M. Observed increase in extreme daily rainfall in the French Mediterranean. Clim. Dyn. 2019, 52, 1095–1114. [Google Scholar] [CrossRef]
- Lana, X.; Martínez, M.D.; Serra, C.; Burgueño, A. Spatial and temporal variability of the daily rainfall regime in Catalonia (Northeastern Spain), 1950–2000. Int. J. Climatol. 2004, 24, 613–641. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Navarro, X. A single scaling parameter as a first approximation to describe the rainfall pattern of a place: Application on Catalonia. Acta Geophys. 2018, 66, 415–424. [Google Scholar] [CrossRef]
- Lana, X.; Burgueño, A. Some statistical characteristics of monthly and annual pluviometric irregularity for the Spanish Mediterranean coast. Theor. Appl. Climatol. 2000, 65, 79–98. [Google Scholar] [CrossRef]
- Llabrés-Brustenga, A.; Rius, A.; Rodríguez-Solà, R.; Casas-Castillo, M.C. Influence of regional and seasonal rainfall patterns on the ratio between fixed and unrestricted measured intervals of rainfall amounts. Theor. Appl. Climatol. 2020, 140, 389–399. [Google Scholar] [CrossRef]
- Martín-Vide, J.; Lopez-Bustins, J.A.; Lemus, M.; Moreno-García, M.C.; Balagué, X.; González-Hidalgo, J.C.; Beguería, S.; Peña-Angulo, D.; Trullenque, V. The consecutive disparity of precipitation in conterminous Spain. Theor. Appl. Climatol. 2022, 147, 1151–1161. [Google Scholar] [CrossRef]
- Cortesi, N.; González-Hidalgo, J.C.; Brunetti, M.; Martín-Vide, J. Daily precipitation concentration across Europe (1971–2010). Nat. Hazards Earth Sys. 2012, 12, 2799–2810. [Google Scholar] [CrossRef]
- Martín-Vide, J.; Gómez, L. Regionalization of Peninsular Spain based on the length of dry spells. Theor. Appl. Climatol. 1999, 19, 537–555. [Google Scholar] [CrossRef]
- Serra, C.; Burgueño, A.; Martínez, M.D.; Lana, X. Trends of dry spells across Catalonia (NE Spain) for the second half of the 20th century. Theor. Appl. Climatol. 2006, 85, 165–183. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; McVicar, T.R.; Tomas-Burguera, M.; Peña-Gallardo, M.; Noguera, I.; López-Moreno, J.I.; Peña, D.; El Kenawy, A. Global characterization of hydrological and meteorological droughts under future climate change: The importance of timescales, vegetation-CO2 feedbacks and changes to distribution functions. Int. J. Climatol. 2020, 40, 2557–2567. [Google Scholar] [CrossRef]
- Lana, X.; Rodríguez-Solà, R.; Martínez, M.D.; Casas-Castillo, M.C.; Serra, C.; Kirchner, R. Autoregressive process of monthly rainfall amounts in Catalonia (NE Spain) and improvements on predictability of length and intensity of drought episodes. Int. J. Climatol. 2021, 41, 3178–3194. [Google Scholar] [CrossRef]
- Lionello, P.; Abrantes, F.; Gacic, M.; Planton, S.; Trigo, R.; Ulbrich, U. The climate of the Mediterranean region: Research progress and climatic change impacts. Reg. Environ. Change 2014, 14, 1679–1684. [Google Scholar] [CrossRef]
- Rodrigo, F.S. Spatio-temporal variability of the relationship between seasonal temperatures and precipitation in Spain, 1951–2019. Theor. Appl. Climatol. 2023, 153, 1371–1391. [Google Scholar] [CrossRef]
- Menabde, M.; Seed, A.; Pegram, G. A simple scaling model for extreme rainfall. Water Resour. Res. 1999, 35, 335–339. [Google Scholar] [CrossRef]
- Yu, P.S.; Yang, T.H.; Lin, C.S. Regional rainfall intensity formulas based on scaling property rainfall. J. Hydrol. 2004, 29, 108–123. [Google Scholar] [CrossRef]
- Bara, M.; Gaál, L.; Kohnová, S.; Szolgay, J.; Hlavčová, K. On the use of the simple scaling of heavy rainfall in a regional estimation of IDF curves in Slovakia. J. Hydrol. Hydromech. 2010, 58, 49–63. [Google Scholar] [CrossRef]
- Innocenti, S.; Mailhot, A.; Frigon, A. Simple scaling of extreme precipitation in North America. Hydrol. Earth Syst. Sci. 2017, 21, 5823–5846. [Google Scholar] [CrossRef]
- Rodríguez-Solà, R.; Casas-Castillo, M.C.; Navarro, X.; Redaño, À. A study of the scaling properties of rainfall in Spain and its appropriateness to generate intensity-duration-frequency curves from daily records. Int. J. Climatol. 2017, 37, 770–780. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Rodríguez-Solà, R.; Llabrés-Brustenga, A.; García-Marín, A.P.; Estévez, J.; Navarro, X. A simple scaling analysis of rainfall in Andalusia (Spain) under different precipitation regimes. Water 2022, 14, 1303. [Google Scholar] [CrossRef]
- Martín-Vide, J. Propiedades y aplicaciones de un índice de disparidad en pluviometría. In Proceedings of the X Congreso Nacional de Geografía, Asociación de Geógrafos Españoles, Zaragoza, Spain, 28 September–3 October 1987; pp. 267–276. [Google Scholar]
- Lana, X.; Rodríguez-Solà, R.; Casas-Castillo, M.C.; Serra, C.; Kirchner, R.; Martínez, M.D. Rainfall disparity at monthly scale on Catalonia (NE Spain): Dependence on geographic coordinates, altitude and distance to the Mediterranean coast. Theor. Appl. Climatol. 2023, 153, 1293–1306. [Google Scholar] [CrossRef]
- Lana, X.; Rodríguez-Solà, R.; Martínez, M.D.; Casas-Castillo, M.C.; Serra, C.; Kirchner, R. Multifractal structure of the monthly rainfall regime in Catalonia (NE Spain): Evaluation of the non-linear structural complexity of the monthly rainfall. Chaos 2020, 30, 073117. [Google Scholar] [CrossRef]
- Lana, X.; Casas-Castillo, M.C.; Rodríguez-Solà, R.; Prohom, M.; Serra, C.; Martínez, M.D.; Kirchner, R. Time trends, irregularity, multifractal structure and effects of CO2 emissions on the monthly rainfall regime at Barcelona city, NE Spain, years 1786–2019. Int. J. Climatol. 2023, 43, 499–518. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Martin-Vide, J.; López-Bustins, J.A. The Western Mediterranean Oscillation and rainfall in the Iberian Peninsula. Int. J. Climatol. 2006, 26, 1455–1475. [Google Scholar] [CrossRef]
- Martín-Vide, J.; Sánchez-Lorenzo, A.; López-Bustins, J.A.; Cordobilla, M.J.; García-Manuel, A.; Raso, J.M. Torrential rainfall in northeast of the Iberian Peninsula: Synoptic patterns and WeMO influence. Adv. Sci. Res. 2008, 2, 99–105. [Google Scholar] [CrossRef]
- López-Bustins, J.A.; Lemus-Cánovas, M. The influence of the Western Mediterranean Oscillation upon the spatio-temporal variability of precipitation over Catalonia (northeastern of the Iberian Peninsula). Atmos. Res. 2020, 236, 104819. [Google Scholar] [CrossRef]
- Prohom, M.; Barriendos, M.; Sánchez-Lorenzo, A. Reconstruction and homogenization of the longest instrumental precipitation series in the Iberian Peninsula (Barcelona, 1786–2014). Int. J. Climatol. 2015, 36, 3072–3087. [Google Scholar] [CrossRef]
- Servei Meteorològic de Catalunya (Generalitat de Catalunya). Climatologia, Dades i Productes Climàtics. Sèrie de Precipitació de Barcelona (des de 1786). Available online: https://www.meteo.cat/wpweb/climatologia/dades-i-productes-climatics/serie-climatica-de-barcelona-des-de-1780/ (accessed on 30 September 2024).
- Lemus-Cánovas, M.; López-Bustins, J. Variabilidad espaciotemporal de la precipitación en el sur de Cataluña y su relación con la oscilación del mediterráneo occidental (WEMO). In Proceedings of the X Congreso Internacional Asociación Española de Climatología: Clima, Sociedad, Riesgos y Ordenación del Territorio, Alicante, Spain, 5–8 October 2016. [Google Scholar] [CrossRef]
- Lana, X.; Burgueño, A.; Martínez, M.D.; Serra, C. Complexity and predictability of the monthly western Mediterranean oscillation index. Int. J. Climatol. 2016, 36, 435–2450. [Google Scholar] [CrossRef]
- Mediterranean Oscillation Indices (MOI) with Saharan Oscillation Index (SaOI) and Western Mediterranean Oscillation (WeMOI), Climatic Research Unit, University of East Anglia. Available online: https://crudata.uea.ac.uk/cru/data/moi/ (accessed on 30 September 2024).
- Sneyers, R. On the Statistical Analysis of Series of Observations; Technical Note No. 143, WMO No. 415; World Meteorological Organization: Geneva, Switzerland, 1990; 192p. [Google Scholar]
- Watterson, I.G.; Dix, M.R. Simulated changes due to global warming in daily precipitation means and extremes and their interpretation using the gamma distribution. J. Geophys. Res. 2023, 108, 4379. [Google Scholar] [CrossRef]
- Martínez-Villalobos, C.; Neelin, J.D. Why do precipitation intensities tend to follow Gamma distributions? J. Atmos. Sci. 2019, 76, 3611–3631. [Google Scholar] [CrossRef]
- Husak, G.J.; Michaelsen, J.; Funk, C. Use of the gamma distribution to represent monthly rainfall in Africa for drought monitoring applications. Int. J. Climatol. 2007, 27, 935–944. [Google Scholar] [CrossRef]
- Michaelides, S.C.; Tymvios, F.S.; Michaelidou, T. Spatial and temporal characteristics of the annual rainfall frequency distribution in Cyprus. Atmos. Res. 2009, 94, 606–615. [Google Scholar] [CrossRef]
- Wilks, D.S. Parametric Probability Distributions. In Statistical Methods in the Atmospheric Sciences, 2nd ed.; Dmowska, R., Hartmann, D., Thomas Rossby, H., Eds.; Elsevier: London, UK, 2006; Chapter 4; pp. 95–97. Available online: https://sunandclimate.files.wordpress.com/2009/05/statistical-methods-in-the-atmospheric-sciences-0127519661.pdf (accessed on 30 September 2024).
- González-Hidalgo, J.C.; Trullenque-Blanco, V.; Beguería, S.; Peña-Angulo, D. Seasonal precipitation changes in the western Mediterranean Basin: The case of the Spanish mainland, 1916–2015. Int. J. Climatol. 2024, 44, 1800–1815. [Google Scholar] [CrossRef]
- Hamed, K.H.; Rao, A.R. A modified Mann-Kendall trend test for autocorrelated data. J. Hydrol. 1998, 204, 182–196. [Google Scholar] [CrossRef]
- World Meteorological Organization Climatological Normals. Climatological Standard Normals. Available online: https://community.wmo.int/en/activity-areas/climate-services/climate-products-and-initiatives/wmo-climatological-normals (accessed on 29 September 2024).
- Servei Meteorològic de Catalunya (Generalitat de Catalunya). Climatologia. Evolució Observada del Clima. Evolució Observada de la Precipitació. Available online: https://www.meteo.cat/wpweb/climatologia/evolucio-observada-del-clima/evolucio-observada-de-la-precipitacio/ (accessed on 30 September 2024).
- Fernández-Martínez, M.; Vicca, S.; Janssens, I.A.; Carnicer, J.; Martín-Vide, J.; Peñuelas, J. The consecutive disparity index, D: A measure of temporal variability and ecological studies. Ecosphere 2018, 9, 02527. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Phinney, B.; Cavadias, G. The influence of autocorrelation on the ability to detect trend in hydrological series. Hydrol. Process. 2002, 16, 1807–1829. [Google Scholar] [CrossRef]
- Din, M.A. ARIMA by Box Jenkins Methodology for Estimation and Forecasting Models in Higher Education. No: EMS2015-1846. In Proceedings of the 18th Annual International Conference on Education, Athens, Greece, 16–19 May 2016. [Google Scholar] [CrossRef]
- Barriendos, M.; Prohom, M.; Sánchez-Lorenzo, A. Extreme drought conditions over NE Iberia in early 19th century (1812–1825) and its possible relationship to major volcanic eruptions. In Proceedings of the European Geosciences Union General Assembly, Vienna, Austria, 3–7 May 2010; Volume 12, p. 4926. Available online: http://salva-sinobas.uvigo.es/index.php/download_file/-/view/54 (accessed on 16 October 2024).
- Moruno, C. La sequera de 1817 a Catalunya. Abast i conseqüències socials en un context de postguerra. Estud. Hist. Agràr. 2021, 32, 97–113. [Google Scholar] [CrossRef]
- Martin-Vide, J.; Barriendos, M. The use of rogation ceremony records in climatic reconstruction: A case study from Catalonia (Spain). Clim. Change 1995, 30, 201–221. [Google Scholar] [CrossRef]
- Trigo, R.M.; Vaquero, J.M.; Alcoforado, M.J.; Barriendos, M.; Taborda, J.; García-Herrera, R.; Luterbacher, J. Iberia in 1816, the year without a summer. Int. J. Climatol. 2009, 29, 99–115. [Google Scholar] [CrossRef]
- Domínguez-Castro, F.; Ribera, P.; García-Herrera, R.; Vaquero, J.M.; Barriendos, M.; Cuadrat, J.M.; Moreno, J.M. Assessing extreme droughts in Spain during 1750–1850 from rogation ceremonies. Clim. Past 2012, 8, 705–722. [Google Scholar] [CrossRef]
- Harrington, C.R. (Ed.) The Year Without a Summer? World Climate in 1816; Canadian Museum of Nature: Ottawa, ON, Canada, 1992; ISBN 0660130637. [Google Scholar] [CrossRef]
- Anet, J.G.; Muthers, S.; Rozanov, E.V.; Raible, C.C.; Stenke, A.; Shapiro, A.I.; Brönnimann, S.; Arfeuille, F.; Brugnara, Y.; Beer, J.; et al. Impact of solar versus volcanic activity variations on tropospheric temperatures and precipitation during the Dalton Minimum. Clim. Past 2014, 10, 921–938. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; López-Ballesteros, A.; Jimeno-Sáez, P.; Pérez-Sánchez, J. Recent precipitation trends in Peninsular Spain and implications for water infrastructure design. J. Hydrol. Reg. Stud. 2023, 45, 101308. [Google Scholar] [CrossRef]
- Casas-Castillo, M.C.; Rodríguez-Solà, R.; Lana, X.; Serra, C.; Martínez, M.D.; Biere, R.; Arellano, B.; Roca, J. Consecuencias hidrológicas del cambio climático en entornos urbanos. In Proceedings of the XIII International Conference on Virtual City and Territory: Challenges and Paradigms of the Contemporary City, Barcelona, Spain, 2–4 October 2019; p. 8291, E-ISSN 2604-6512. [Google Scholar] [CrossRef]
- Forero-Ortiz, E.; Martínez-Gomariz, E.; Monjo, R. Climate change implications for water availability: A case study of Barcelona City. Sustainability 2020, 12, 1779. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Domínguez-Castro, F.; Reig, F.; Beguería, S.; Tomas-Burguera, M.; Latorre, B.; Peña-Angulo, D.; Noguera, I.; Rabanaque, I.; Luna, Y.; et al. A near real-time drought monitoring system for Spain using automatic weather station network. Atmos. Res. 2022, 271, 106095. [Google Scholar] [CrossRef]
- Toreti, A.; Bavera, D.; Acosta Navarro, J.; Arias-Muñoz, C.; Avanzi, F.; Marinho Ferreira Barbosa, P.; De Jager, A.; Di Ciollo, C.; Ferraris, L.; Fioravanti, G.; et al. Drought in Europe March 2023; Publications Office of the European Union: Luxembourg, 2023; JRC133025; ISBN 978-92-68-01068-6. [Google Scholar] [CrossRef]
- Barcelona City Council (2023, March 1). Drought Alert Protocol Activated in Barcelona. Available online: https://www.barcelona.cat/infobarcelona/en/tema/environment-and-sustainability/drought-alert-protocol-activated-in-barcelona-2-2_1260262.html (accessed on 16 October 2024).
- Wetterzentrale: NCEP Climate Forecast System Reanalysis (CFSRv1). Available online: https://www.wetterzentrale.de/en/reanalysis.php?model=cfsr (accessed on 8 October 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).