Next Article in Journal
Two Centuries of Monthly Rainfall in Barcelona (NE Spain): Disparity Trends, Correlation of Autumnal Rainfall with the WeMO Index and Its Contribution to Annual Amounts
Previous Article in Journal
Determinants of Adapting to the Consequences of Climate Change in the Peruvian Highlands: The Role of General and Behavior-Specific Evaluations, Experiences, and Expectations
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Climate
Volume 12
Issue 10
10.3390/cli12100165
climate-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Reconstructing and Hindcasting Sea Ice Conditions in Hudson Bay Using a Thermal Variability Framework

by
William A. Gough
Department of Physical and Environmental Sciences, University of Toronto Scarborough, Toronto, ON M1C 1A4, Canada
Climate 2024, 12(10), 165; https://doi.org/10.3390/cli12100165
Submission received: 23 September 2024 / Revised: 11 October 2024 / Accepted: 17 October 2024 / Published: 19 October 2024
Browse Figures
Versions Notes

Abstract

:
The Hudson Bay seasonal sea ice record has been well known since the advent of satellite reconnaissance, with a continuous record since 1971. To extend the record to earlier decades, a thermal variability framework is used with the surface temperature climatological records from four climate stations along the Hudson Bay shoreline: Churchill, Manitoba; Kuujjurapik, Quebec; Inukjuak, Quebec; and Coral Harbour, Nunavut. The day-to-day surface temperature variation for the minimum temperature of the day was found to be well correlated to the known seasonal sea ice distribution in the Bay. The sea ice/thermal variability relationship was able to reproduce the existing sea ice record (the average breakup and freeze-up dates for the Bay) largely within the error limits of the sea ice data (1 week), as well as filling in some gaps in the existing sea ice record. The breakup dates, freeze-up dates, and ice-free season lengths were generated for the period of 1922 to 1970, with varying degrees of confidence, adding close to 50 years to the sea ice record. Key periods in the spring and fall were found to be critical, signaling the time when the changes in the sea conditions are first notable in the temperature variability record, often well in advance of the 5/10th ice coverage used for the sea ice record derived from ice charts. These key periods in advance of the breakup and freeze-up could be potentially used, in season, as a predictor for navigation. The results are suggestive of a fundamental change in the nature of the breakup (faster) and freeze-up (longer) in recent years.

1. Introduction

Seasonal sea ice in Hudson Bay (Figure 1), due to optimal climatological conditions, form a complete cryogenic annual cycle [1]. Winters are sufficiently cold for the creation of a sustained ice platform, covering the entire Bay for several months, and summers are warm enough to remove all the ice, producing an ice-free season of two or more months [1,2,3,4,5,6,7,8]. Sea ice exists at the interface of the atmosphere and ocean and is a function of the physical properties of both. Solar radiation, the energetic driver of the atmosphere, varies by latitude, maximized at the equator and minimized at the poles, and modified by seasonality due to the Earth’s tilt. This insolation is partially absorbed and reflected by atmospheric constituents. Sea ice is also highly reflective (high albedo). This radiative surface energy balance acts to preserve an ice platform, once established. At other times of the year when there is open water, more energy is absorbed due to the lower albedo of the water surface, resulting in a seasonal thermal flywheel that delays the production of new sea ice. This has been observed in the Hudson Bay sea ice data, with the ice-free season being delayed by several months from the timing of maximum seasonal insolation [1,4,5,7,8].
Atmospheric dynamics play a seasonally varying role in sea ice formation, maintenance, and dissolution and are particularly notable for sea ice breakup. During the breakup, the prevailing wind aids in the advection of the melting sea ice, moving the ice away from its source region, potentially by many hundreds of kilometers. Winds contribute to the development of year-round open water polynyas [9]. Ocean dynamics as well work to contribute to the circulation of sea water and sea ice. The Hudson Bay circulation is cyclonic [1]. Relatively warm, salty North Atlantic waters enter from Hudson Strait at depth in the north part of the Bay. The main circulation is to the south and west along the western coast of Hudson Bay, turning along the south coast, moving north along the east coast of the Bay, and then exiting along the southern part of Hudson Strait [1,4,10,11]. This flow, particularly during breakup, facilitates the signature lingering distribution of sea ice in southwestern Hudson Bay [1,4,5,6,7,8,12,13,14,15,16].
These seasonal sea conditions, spatially and temporally, have been well documented using ice charts derived from satellite reconnaissance from 1971 to the present day [5,6,7,8,12,13,16,17,18,19,20]. This body of work documents a consistent pattern of sea ice seasonality that exhibits some interannual variability as well as some net temporal changes (earlier breakup and later freeze-up) due to regional climate change.
McGovern and Gough (2015) [21] made an initial attempt to extend the climate record to the decades before the satellite data were available, during a period when climate data were available from surface observing stations around the Bay. Specifically, they examined surface temperature at Churchill, MB, on the west coast of the Bay and Inukjuak, QC, on the east coast and produced the first reconstruction of the ice-free season in Hudson Bay to the 1940s (using the existing coincident climate records for the two stations). They exploited the relative difference between these two stations when the ice is present and when it is not. Gough and He (2015) [22] examined subtle changes in the diurnal variations in temperature by examining the difference in the calculation of daily temperature using hourly data and using diurnal extremes (averaging the minimum and maximum temperature of the day). While a link to the sea ice was not fully identified, the difference was found to be clearly linked to the onset of the fog season in the spring which is related to the sea ice distribution. However, a formal reconstruction of the sea ice record was not attempted.
In this work, more sophisticated measures of temperature variability are employed to detect changes in the sea ice conditions. We use a day-to-day thermal variability framework to detect the onset of the ice-free season (breakup) and the onset of the Hudson Bay ice platform (freeze-up) and, using these two measures, the ice-free season length.
A day-to-day thermal variability framework (DTD) developed by [23], based on [24], has been found to provide a useful suite of metrics for detecting thermal variations that reflect the local environments where data are collected. These include urban, rural, peri-urban, marine, island, airport, and mountain environments [25,26]. The absolute difference between a day’s surface mean temperature and the previous day’s surface mean temperature (DTD) was introduced as the basic measure of thermal variability [23]. Day-to-day thermal metrics have been applied to the examination of climate variation [25,26,27,28,29], including the detection of fog and cloud cover [22,30]. It has been considered in other disciplines, such as health [31,32,33,34,35], economics [36,37], agriculture [38], and transportation safety [39].
One of the day-to-day metrics is ΔDTD which was also introduced by [40]. This is the difference between the DTD calculated from the maximum temperature of the day (DTDTmax) and that from the minimum temperature (DTDTmin) of the day. This metric has shown utility in detecting the difference between urban and rural environments [40,41,42]. At the surface, insolation is partitioned into sensible heat, subsurface heat, and latent heat (the evaporation of surface water). For urban landscapes, the partitioning into latent heat is muted. Thus, the urban response is usually a detectable increase in temperature (sensible heat) for a given radiative input. Rural environments and marine (coastal) environments, with the same radiative input as an urban setting, partitions more energy into latent heat, thus evaporating surface water and providing the potential for fog and clouds. This tends to mitigate the day-to-day variability. The day-to-day variability of the minimum temperature of the day (DTDTmin) was found to be a clear indicator of coastalization. This measure has been used to detect the marine influence in a number of locations, including the Adriatic Sea of Croatia [43], the South China coast [42], two Canadian coasts [44], and islands in large Canadian lakes [26]. For the two Canadian studies, due to sea and lake ice in winter, which tends to suppress the marine effect, an adjusted ADTDTmin was used that excluded the winter months of December, January, and February [26,44] in the calculation. Gough and Li (2024) [26] examined thirty-one locations in the Canadian Prairies. Included among the thirty-one were two climate stations from Churchill, Manitoba (Churchill A, Churchill Marine). For these two stations, a marine climate was only detected when the excluded months were extended to match the months when sea ice dominates Hudson Bay. This is illustrated in the annual cycle of the DTDTmin for Churchill A, shown in Figure 2. For the ice-free season, late spring to fall, the DTDTmin metric is substantially lower than in the ice-covered months. This observation was the seed for the research objective explored in this work. Since the DTDTmin responds to the presence of sea ice, can this measure be used to detect the breakup and freeze-up of sea ice in Hudson Bay using coastal climate stations that have lengthy temperature time series?

2. Materials and Methods

2.1. Surface Air Temperature Data

Four climate stations (Churchill, Kuujjurapik, Inukjuak, and Coral Harbour) with substantial climate records along the shore of Hudson Bay were identified (Table 1, Figure 3). All the locations have data from the period of 1944 to 2010 and some stations extend to the early 1920s. For Churchill, the pre-1944 period is covered by an additional station, Churchill Marine (Figure 3). Two stations are used for Inukjuak (Inukjuak UA and Inukjuak A), with Inukjuak UA covering the early record from 1922 and Inukjuak A covering the latter part of the record after 1996. The data were extracted from the climate data archive at Environment and Climate Change Canada (https://climate.weather.gc.ca/historical_data/search_historic_data_e.html) during the 23 August 2024.

2.2. Sea Ice Data

The sea ice data were accessed from a dataset generated in previous work [5,7,8]. In those works, the Bay was analyzed on a 36-point grid (Figure 4) and breakup and freeze-up time series starting from 1971 were generated. These extended to 2003 for [5], to 2012 for [7], and 2018 for [8]. They used sea ice charts produced for navigation purposes with a threshold of the 5/10 sea ice coverage as the threshold for both the breakup and freeze-up. For this work, the 36-grid data were averaged to produce a single breakup and freeze-up date per year. Since the sea ice charts are available weekly, 1 week (7 days) is the error associated with the data.

2.3. Day-to-Day Temperature Analysis

The DTD metric used arises from a day-to-day temperature variability framework. The formulation for the DTD temperature variability metrics, DTD, are taken from [23]:
DTD = Σi (Ti − Ti−1)/(N − 1)
where i is the daily counter over the time period of interest, and a total of N − 1 pairs of values are used. In this work, only the minimum temperature of the day is used consistently with the marine climate found in [26,44]. In the latter three Canadian studies, the winter months were excluded.

2.4. Correlation Analysis

The Hudson Bay averaged sea ice data (average of 36 grid points in Figure 4) for each of the breakup and freeze-up dates time series were sorted into the ten lowest and ten highest values within the years 1971 to 2010 (40 years). Using the corresponding springtime DTDTmin values (Figure 2), an optimal range of dates of the DTDTmin was sought that generated the strongest correlation with the sea ice breakup data for each of the four locations, and similar was conducted in the fall for the freeze-up. From this, a linear relationship between the DTDTmin and sea ice breakup (and separately for the freeze-up) was generated for all the locations. Using these equations, the remaining years then acted as a test for the applicability of the formula, by comparing an equation-generated sea ice date with the value obtained from the sea ice charts. An aggregate of the four locations was also examined and compared to the sea ice record. Using the linear regression equations, a hindcast first for the years 1944 to 1970, a time period well represented by all four locations, and second for 1922 to 1943, with less ubiquitous data, was conducted using the temperature data. Within the original sea ice dataset, there were a few years with missing data (largely related to the lack of the availability of the sea ice charts). For those years, we used the results as an imputation method to fill the gaps. The end result is a complete dataset running from 1922 to 2010, an eighty-nine-year record.

3. Results

3.1. Correlation Analysis

For each of the four locations, the Bay’s averaged breakup and freeze-up values were correlated to the DTDTmin time series by identifying a range of dates for the DTDTmin in the spring and in the fall that had the highest correlation with the corresponding sea ice record for twenty years of the forty-year period (1971–2010). The years were binned by the sea ice breakup and freeze-up dates and the twenty years consisted of ten low values and ten high values of the respective sea ice time series. The results of this analysis are reported in Table 2, which records the Pearson r correlation and the p value (statistical significance), an equation derived from the linear regression and the standard deviation of the difference between the equation-generated breakup and freeze-up dates and the sea ice record from observations. The correlations (Pearson r) ranged from 0.48 to 0.61 for the breakup and −0.53 to −0.79 for the freeze-up. The DTDTmin is higher for ice-covered conditions and lower for ice-free conditions. Thus, for the breakup, the lower the DTDTmin, the more likely an early breakup, hence a positive r value, and vice versa for the freeze-up yielding a negative r correlation. All the correlations were statistically significant (p < 0.05), with the strongest correlations at Coral Harbour and the weakest at Kuujjurapik. The uncertainty, as measured by the standard deviation, in reproducing the sea ice record ranges from 6.23 days to 10.38 days. This is consistent with the uncertainty associated with the sea ice observations that use maps that are generated once a week. The uncertainty was generally lower for the freeze-up than the breakup. This is a reflection of the nature of the freeze-up versus the breakup. The freeze-up is more thermally driven, starting in the north and spreading south in a relatively short period of time whereas the breakup is a combination of thermal and dynamical (advection) forcing [8], which takes longer from its onset to reach the 5/10th sea ice threshold.
The equations derived in this exercise (and reported in Table 3) were then applied to all of the years in the 1971–2010 period. This fuller record is reported in Table 3. While the correlations decrease for some of the locations, the difference between the observations and equation-generated values in general decreases to a range of 6.35 to 8.20 days. A substantial decrease in this difference is realized by aggregating the data for the four locations using a simple average of the dates generated and then correlating these with the observations. This leads to higher correlations than the individual stations and a decrease in the difference to below 7 days (the observational uncertainty), with 6.85 days for the breakup and 5.06 days for the freeze-up.

3.2. Imputation

Another possible use of this analysis is to fill in the gaps of the 1971–2010 sea ice record. For the breakup, the year 2002 was missing (due to a lack of relevant sea ice charts), and for the freeze-up, the years 1971, 1973, 1997, 1998, 1999, and 2001 were missing. These values were generated using an aggregate of all four locations as described in the previous section, and these are listed in Table 4.

3.3. Reconstruction Pre-1971

The results of the previous section provide considerable confidence in applying these equations to an earlier time frame. This is performed for the period of 1941 to 1970, a period of time in which all four stations were reporting temperature observations. The breakup and freeze-up dates were generated for the four locations and then aggregated. These are shown in Figure 5 and Figure 6 as blue dots, along with the 1971–2010 reconstruction of the sea ice data (in orange). Additionally, in red, the sea ice dates are generated for the years 1922 to 1944. There is less confidence in these numbers due to the lack of data recordings or missing temperature data among the stations. Thus, some of these data points rely only on the temperature record from one location, leading to a lower confidence. The green dots are the imputed values from the temperature record to replace the missing data in the sea ice record (described in the previous section). In addition to the breakup and freeze-up, Figure 7 shows the ice-free season. This is calculated by taking the difference between the freeze-up and breakup dates. Since both have uncertainty, the uncertainty for the ice-free season compounds these uncertainties, and this is seen in the greater variability in the results, both for the observations and equation-generated dates (Figure 7).
One notable result is the sea ice behaviour in 1991. In Figure 5, both the observation (orange) and reconstructed value indicate a late breakup. This is consistent with the short-term global cooling as a result of the Mount Pinatubo eruption in 1991 [45,46]. A recent reassessment suggests that the impact of the eruption caused a cooling around the globe for 13 months after the summer of the 1991 eruption [47]. This is consistent with the notable impact on the breakup dates for 1992 (Figure 6) but not the freeze-up dates (Figure 6) in the fall of 1992. There is a notably shorter ice-free season (Figure 7) as a result of the late breakup.

3.4. Early Warning?

The timing for the DTDTmin values and the timing of the sea ice record that produced the highest correlation were not coincident. For the breakup, the DTDTmin timing was from days 105–157 across all four stations, whereas the recorded breakup dates ranged from day 164 to 206. Figure 2 provides an explanation for these time periods. On this figure, the marine climate DTDTmin threshold of 2.35 as developed in [44] is plotted for illustration purposes. Also in the figure are the two periods used for the Churchill correlations in grey. As is clearly evident, the two identified periods reflect the timing when the DTDTmin transitions through the 2.35 DTDTmin threshold, marking the beginning and end of the marine influence on the Churchill climate. The generated values for onset of the marine climate are approximately two months in advance of the recorded breakup dates. This is the result of using the 5/10th sea ice coverage threshold for the ice breakup (navigation definition). The DTDTmin metric detects the onset of the marine influence breakup at an earlier time, reflective of higher sea ice coverage. This metric then has the potential of providing an indication of the breakup two months in advance of the 5/10th breakup and would be a useful aid for navigation in the Bay [14,15,48,49,50,51,52]. Similarly for the freeze-up, the DTDTmin range is from day 261 to 330, whereas the sea ice record ranges from day 315 to 346, thus providing a possibility for forecasting the freeze-up by up to almost two months. We explore this in the next section.

3.5. “Forecast” 2011–2018

The relationships reported in Table 3 were based on data drawn from the period of 1971 to 2010, a period of relatively good data quality for all four stations. This enabled the reconstruction of a sea ice record back to 1922. The relationships can also be used to estimate sea ice conditions after 2010. The sea ice record taken from [8] extends to 2018. In this section, we use the relationships developed to estimate the sea ice conditions for the years 2011–2018 and compare them to the values from [8] derived from the sea ice charts and using the 5/10th threshold. Data from three of the stations were used: Coral Harbour, Churchill, and Inukjuak. The Kuujjurapik dataset had too many missing data to be used. The results are presented in Figure 8 and Figure 9. While the differences are small between the two breakup lines (Figure 8), on average 8 days, which is consistent with the uncertainty of the sea ice chart analysis, all the reconstructed (DTD) values are higher, thus suggesting the 5/10th breakup was later than it actually was. This suggests that the timing from onset of the marine conditions to achieving the 5/10th ice coverage is shorter than it was in the 1971–2010 period used to create the predictive equations in Table 3. While there is not as large a difference for the freeze-up (Figure 9), the freeze-up appears to take longer than it did during the 1971–2010 period. This is a very interesting result, suggesting that the increase in the ice-free season (using the 5/10th threshold for the sea ice coverage) is a result of two mechanisms, the earlier onset and later end of the marine conditions, and a faster breakup and slower freeze-up.

4. Discussion

In this work, we have successfully used a day-to-day thermal variability framework [23] to produce a metric, the DTDTmin, that enables the identification of the presence of sea ice in Hudson Bay. The DTDmin was found in previous work to be adept at identifying marine and island climates [26,42,43,44]. This metric was used successfully to reproduce the sea ice record for Hudson Bay for the period of 1971–2010. It was then used to hindcast the sea ice conditions from 1922 to 1970. Four shoreline climate stations were used: Churchill, MB; Kuujjurapik, QC; Inukjuak, QC; and Coral Harbour (Figure 2), well-spaced locations that represented the western, southern, eastern, and northern aspects of the Bay. An aggregate of these four (equally weighted) produced results that departed the least from the sea ice record derived from the ice charts. The departure from the sea ice record was within the one-week accuracy of the sea ice charts. The period of 1944 to 1970 used data from all four locations and is thus associated with a high confidence. The data for 1922 to 1943 were spottier and should be treated with less confidence.
The timing of the temperature data used in the correlation analysis was in advance of the actual breakup and freeze-up dates. This indicates, unsurprisingly, that the ice breakup and freeze-up are detectable before the 5/10th ice coverage threshold is met. This earlier thermal period (up to two months in advance of the 5/10th threshold) suggests that an in-season thermally based forecast of the eventual breakup and freeze-up is possible and should be explored.
The success of this first attempt at sea ice reconstruction using thermal variability metrics bodes well for its application in other seasonal sea ice basins such as Hudson Strait and Foxe Basin, located to the northeast and north of Hudson Bay, respectively. It may also be applicable in recreating ice conditions in the North American Great Lakes, in particular, using island climate stations.
In this work, the existing sea ice record was aggregated over the entire basin. The sea ice data (Figure 4) were calculated on a 36-point grid and thus there may be the possibility of using local climate stations in isolation so the granularity of the sea ice distribution can be determined by thermal methods.
The “forecast” results for the period of 2011–2018 suggest that the nature of the breakup (faster during 2011–2018) and freeze-up (longer during 2011–2018) may be fundamentally changing, as has been observed in Igloolik for the freeze-up period [30].

5. Conclusions

The Hudson Bay seasonal sea ice record is extended beyond the record using satellite data (from 1971 onwards) to earlier decades using a thermal variability framework. The surface temperature climatological records are from four climate stations along the Hudson Bay coast: Churchill, MB; Kuujjarapik, QC; Inukjuak, QC; and Coral Harbour, NU. The day-to-day surface temperature variation for the minimum temperature of the day was found to be well correlated to the 1971–2010 seasonal sea ice record derived from the ice charts. Critical periods in the spring and fall were found to be well correlated to the observed basin averaged sea ice data, but the two were not coincident. This is an indication that the time when the changes in the sea conditions is first detectable in the temperature variability record is often well in advance of the 5/10th spatial ice coverage used for the observed sea ice record. These key periods, leading to the breakup and freeze-up, could be used as in-season predictors of ice conditions for navigation and possibly other purposes.
The thermal variability, DTDTmin, was able to successfully reproduce the existing sea ice record (the average breakup and freeze-up dates for the Bay) within the error limits of the sea ice data (1 week), as well as filling in some gaps in the existing sea ice record. The breakup dates, freeze-up dates, and ice-free season lengths were generated for the period of 1922 to 1970, with variable confidence, adding approximately 50 years to the sea ice record of Hudson Bay. The extended record will allow a time series analysis of the sea ice conditions in Hudson Bay for a longer time period, suitable for low-frequency oscillation analysis and the evolution of more recent climate changes experienced in the region [53,54,55].
The results for more recent years (2011–2018) indicate that there may be a fundamental shift in how the breakup (faster) and freeze-up (longer) are taking place as a result of a changing climate, and the two may be linked [56].

Author Contributions

Conceptualization, W.A.G.; methodology, W.A.G.; formal analysis, W.A.G.; investigation, W.A.G.; resources, W.A.G.; data curation, W.A.G.; writing—original draft preparation, W.A.G.; writing—review and editing, W.A.G.; supervision, W.A.G.; project administration, W.A.G.; funding acquisition, W.A.G. All authors have read and agreed to the published version of the manuscript.

Funding

This research was funded by NSERC RGPIN-2018-06801.

Data Availability Statement

Temperature data were accessed from the national archive (Environment and Climate Change Canada), https://climate.weather.gc.ca/historical_data/search_historic_data_e.html (accessed on 23 August 2024); sea ice data were obtained from the Canadian Ice Service, https://iceweb1.cis.ec.gc.ca/Archive/page1.xhtml?lang=en (accessed on 1 June 2019).

Conflicts of Interest

The author declares no conflict of interest.

References

  1. Danielson, J.E.W. Hudson Bay Ice Conditions. ARCTIC 1971, 24, 90–107. [Google Scholar] [CrossRef]
  2. Catchpole, A.; Halpin, J. Measuring summer sea ice severity in eastern Hudson Bay 1751–1870. Can. Geogr. Can. 1987, 31, 233–244. [Google Scholar] [CrossRef]
  3. Etkin, D.A. Break-up in Hudson Bay: Its sensitivity to air temperatures and implications for climate warming. Climatological Bulletin 1991, 25, 21–34. [Google Scholar]
  4. Wang, J.; Mysak, L.A.; Ingram, R.G. Interannual variability of sea-ice cover in Hudson Bay, Baffin Bay and the Labrador Sea. Atmosphere-Ocean 1994, 32, 421–447. [Google Scholar] [CrossRef]
  5. Gagnon, A.S.; Gough, W.A. Trends in the Dates of Ice Freeze-up and Breakup over Hudson Bay, Canada. Arctic 2005, 58, 370–382. [Google Scholar] [CrossRef]
  6. Hochheim, K.P.; Barber, D.G. An Update on the Ice Climatology of the Hudson Bay System. Arctic Antarct. Alp. Res. 2014, 46, 66–83. [Google Scholar] [CrossRef]
  7. Kowal, S.; Gough, W.A.; Butler, K. Temporal evolution of Hudson Bay Sea Ice (1971–2011). Theor. Appl. Clim. 2017, 127, 753–760. [Google Scholar] [CrossRef]
  8. Kowal, S.; Gough, W.A.; Butler, K. Spatial clustering of seasonal sea ice of Hudson Bay, Canada, 1971–2018. Arctic Antarct. Alp. Res. 2024, 56. [Google Scholar] [CrossRef]
  9. Bruneau, J.; Babb, D.; Chan, W.; Kirillov, S.; Ehn, J.; Hanesiak, J.; Barber, D.G. The ice factory of Hudson Bay: Spatiotemporal variability of the Kivalliq Polynya. Elementa 2021, 9, 00168. [Google Scholar]
  10. Crane, R.G. Seasonal variations of sea ice extent in the Davis Strait–Labrador Sea area and relationship with synoptic-scale atmospheric circulation. Arctic 1978, 31, 434–447. [Google Scholar] [CrossRef]
  11. Ridenour, N.A.; Straneo, F.; Holte, J.; Gratton, Y.; Myers, P.G.; Barber, D.G. Hudson Strait Inflow: Structure and Variability. J. Geophys. Res. Oceans 2021, 126. [Google Scholar] [CrossRef]
  12. Hochheim, K.P.; Barber, D.G. Atmospheric forcing of sea ice in Hudson Bay during the fall period, 1980–2005. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef]
  13. Hochheim, K.; Lukovich, J.; Barber, D. Atmospheric forcing of sea ice in Hudson Bay during the spring period, 1980–2005. J. Mar. Syst. 2011, 88, 476–487. [Google Scholar] [CrossRef]
  14. Andrews, J.; Babb, D.; Barber, D.G. Climate change and sea ice: Shipping accessibility on the marine transportation corridor through Hudson Bay and Hudson Strait (1980–2014). Elementa Sci. Anthr. 2017, 5. [Google Scholar] [CrossRef]
  15. Andrews, J.; Babb, D.; Barber, D.G. Climate change and sea ice: Shipping in Hudson Bay, Hudson Strait, and Foxe Basin (1980–2016). Elementa Sci. Anthr. 2018, 6. [Google Scholar] [CrossRef]
  16. Gupta, K.; Mukhopadhyay, A.; Barber, D.G.; Ehn, J.K. Landfast sea ice in Hudson Bay and James Bay. Elementa Sci. Anthr. 2022, 10. [Google Scholar] [CrossRef]
  17. Galbraith, P.S.; Larouche, P. Reprint of “Sea-surface temperature in Hudson Bay and Hudson Strait in relation to air temperature and ice cover breakup, 1985–2009”. J. Mar. Syst. 2011, 88, 463–475. [Google Scholar] [CrossRef]
  18. Joly, S.; Senneville, S.; Caya, D.; Saucier, F.J. Sensitivity of Hudson Bay Sea ice and ocean climate to atmospheric temperature forcing. Clim. Dyn. 2010, 36, 1835–1849. [Google Scholar] [CrossRef]
  19. Kirillov, S.; Babb, D.; Dmitrenko, I.; Landy, J.; Lukovich, J.; Ehn, J.; Sydor, K.; Barber, D.; Stroeve, J. Atmospheric Forcing Drives the Winter Sea Ice Thickness Asymmetry of Hudson Bay. J. Geophys. Res. Oceans 2020, 125. [Google Scholar] [CrossRef]
  20. Lukovich, J.V.; Jafarikhasragh, S.; Myers, P.G.; Ridenour, N.A.; de la Guardia, L.C.; Hu, X.; Grivault, N.; Marson, J.; Pennelly, C.; Stroeve, J.C.; et al. Simulated impacts of relative climate change and river discharge regulation on sea ice and oceanographic conditions in the Hudson Bay Complex. Elementa Sci. Anthr. 2021, 9. [Google Scholar] [CrossRef]
  21. McGovern, P.G.; Gough, W.A. East-West Asymmetry in Coastal Temperatures of Hudson Bay as a Proxy for Sea Ice. ARCTIC 2015, 68, 445. [Google Scholar] [CrossRef]
  22. Gough, W.A.; He, D. Diurnal temperature asymmetries and fog at Churchill, Manitoba. Theor. Appl. Clim. 2014, 121, 113–119. [Google Scholar] [CrossRef]
  23. Gough, W.A. Theoretical considerations of day-to-day temperature variability applied to Toronto and Calgary, Canada data. Theor. Appl. Clim. 2008, 94, 97–105. [Google Scholar] [CrossRef]
  24. Karl, T.R.; Knight, R.W.; Plummer, N. Trends in high-frequency climate variability in the twentieth century. Nature 1995, 377, 217–220. [Google Scholar] [CrossRef]
  25. Gough, W.A.; Leung, A.C.W. Do Airports Have Their Own Climate? Meteorology 2022, 1, 171–182. [Google Scholar] [CrossRef]
  26. Gough, W.A.; Li, Z. Climate Classification in the Canadian Prairie Provinces Using Day-to-Day Thermal Variability Metrics. Atmosphere 2024, 15, 1111. [Google Scholar] [CrossRef]
  27. Przybylak, R.; Vizi, Z. Air temperature changes in the Canadian Arctic from the early instrumental period to modern times. Int. J. Clim. 2005, 25, 1507–1522. [Google Scholar] [CrossRef]
  28. Wu, F.T.; Fu, C.; Qian, Y.; Gao, Y.; Wang, S.-Y. High frequency daily temperature variability in China and its relationship to large scale circulation. Int. J. Clim. 2017, 37, 570–582. [Google Scholar] [CrossRef]
  29. Przybylak, R.; Singh, G.; Wyszyński, P.; Araźny, A.; Chmist, K. Air temperature changes in SW Greenland in the second half of the 18th century. Clim. Past 2024, 20, 1451–1470. [Google Scholar] [CrossRef]
  30. Laidler, G.J.; Ford, J.D.; Gough, W.A.; Ikummaq, T.; Gagnon, A.S.; Kowal, S.; Qrunnut, K.; Irngaut, C. Travelling and hunting in a changing Arctic: Assessing Inuit vulnerability to sea ice change in Igloolik, Nunavut. Clim. Chang. 2008, 94, 363–397. [Google Scholar] [CrossRef]
  31. Guo, Y.; Barnett, A.G.; Yu, W.; Pan, X.; Ye, X.; Huang, C.; Tong, S. A Large Change in Temperature between Neighbouring Days Increases the Risk of Mortality. PLoS ONE 2011, 6, e16511. [Google Scholar] [CrossRef] [PubMed]
  32. Liu, Q.; Tan, Z.-M.; Sun, J.; Hou, Y.; Fu, C.; Wu, Z. Changing rapid weather variability increases influenza epidemic risk in a warming climate. Environ. Res. Lett. 2020, 15, 044004. [Google Scholar] [CrossRef]
  33. Hovdahl, I. The deadly effect of day-to-day temperature variation in the United States. Environ. Res. Lett. 2022, 17, 104031. [Google Scholar] [CrossRef]
  34. Savić, S.; Arsenović, D.; Lužanin, Z.; Milošević, D.; Dunjić, J.; Šećerov, I.; Kojić, M.; Radić, I.; Harhaji, S.; Arsić, M. Hospital admission tendencies caused by day-to-day temperature changes during summer: A case study for the city of Novi Sad (Serbia). Int. J. Biometeorol. 2023, 67, 695–704. [Google Scholar] [CrossRef]
  35. Blondeel, A.; Hermans, F.; Breuls, S.; Wuyts, M.; De Maeyer, N.; Verniest, T.; Derom, E.; Van Calster, B.; Janssens, W.; Troosters, T.; et al. The association of weather conditions with day-to-day variability in physical activity in patients with COPD. ERJ Open Res. 2023, 9. [Google Scholar] [CrossRef]
  36. Kinsenmeier, M. Temperature variability and long-run economic development. J. Environ. Econ. Manag. 2023, 121, 102840. [Google Scholar] [CrossRef]
  37. Kotz, M.; Wenz, L.; Stechemesser, A.; Kalkuhl, M.; Levermann, A. Day-to-day temperature variability reduces economic growth. Nat. Clim. Chang. 2021, 11, 319–325. [Google Scholar] [CrossRef]
  38. Garner, A.J.; Duran, D.P.; Schubert, W.H.; Klemp, J.B.; Heideman, K.F.; Brasseur, O.; Cassano, J.J.; Parish, T.R.; King, J.C.; Pagowski, M.; et al. Late-Winter and Springtime Temperature Variations throughout New Jersey in a Warming Climate. J. Appl. Meteorol. Clim. 2024, 63, 197–207. [Google Scholar] [CrossRef]
  39. Pińskwar, I.; Choryński, A.; Graczyk, D. Good weather for a ride (or not?): How weather conditions impact road accidents—A case study from Wielkopolska (Poland). Int. J. Biometeorol. 2023, 68, 317–331. [Google Scholar] [CrossRef]
  40. Tam, B.Y.; Gough, W.A.; Mohsin, T. The impact of urbanization on day-to-day temperature variation. Urban Clim. 2015, 12, 1–10. [Google Scholar] [CrossRef]
  41. Bonacci, O.; Roje-Bonacci, T.; Vrsalovic, A. The day-to-day temperature variability method as a tool for urban heat island analysis: A case of Zagreb-Gric Observatory (1887–2018). Urban Clim. 2022, 45, 101281. [Google Scholar] [CrossRef]
  42. Tong, X.; Wang, P.; Wu, S.; Luo, M. Urbanization effects on high-frequency temperature variability over South China. Urban Clim. 2022, 42, 101092. [Google Scholar] [CrossRef]
  43. Bonacci, O.; Bonacci, D.; Roje-Bonacci, T. Different air temperature changes in continental and Mediterranean regions: A case study from two Croatian stations. Theor. Appl. Climatol. 2021, 145, 1333–1346. [Google Scholar] [CrossRef]
  44. Gough, W.A. Thermal Metrics to Identify Canadian Coastal Environments. Coasts 2022, 2, 93–101. [Google Scholar] [CrossRef]
  45. Minnis, P.; Harrison, E.F.; Stowe, L.L.; Gibson, G.G.; Denn, F.M.; Doelling, D.R.; Smith, W.L. Radiative Climate Forcing by the Mount Pinatubo Eruption. Science 1993, 259, 1411–1415. [Google Scholar] [CrossRef]
  46. McCormick, M.P.; Thomason, L.W.; Trepte, C.R. Atmospheric effects of the Mt Pinatubo eruption. Nature 1995, 373, 399–404. [Google Scholar] [CrossRef]
  47. Boretti, A. Reassessing the cooling that followed the 1991 volcanic eruption of Mt. Pinatubo. J. Atmospheric Solar-Terrestrial Phys. 2024, 256. [Google Scholar] [CrossRef]
  48. Tivy, A.; Howell, S.E.L.; Alt, B.; McCourt, S.; Chagnon, R.; Crocker, G.; Carrieres, T.; Yackel, J.J. Trends and variability in summer sea ice cover in the Canadian Arctic based on the Canadian Ice Service Digital Archive, 1960–2008 and 1968–2008. J. Geophys. Res. 2011, 116. [Google Scholar] [CrossRef]
  49. Pizzolato, L.; Howell, S.E.L.; Derksen, C.; Dawson, J.; Copland, L. Changing sea ice conditions and marine transportation activity in Canadian Arctic waters between 1990 and 2012. Clim. Chang. 2014, 123, 161–173. [Google Scholar] [CrossRef]
  50. Pizzolato, L.; Howell, S.E.L.; Dawson, J.; Laliberté, F.; Copland, L. The influence of declining sea ice on shipping activity in the Canadian Arctic. Geophys. Res. Lett. 2016, 43, 12146–12154. [Google Scholar] [CrossRef]
  51. Babb, D.G.; Kirillov, S.; Galley, R.J.; Straneo, F.; Ehn, J.K.; Howell, S.E.L.; Brady, M.; Ridenour, N.A.; Barber, D.G. Sea Ice Dynamics in Hudson Strait and Its Impact on Winter Shipping Operations. J. Geophys. Res. Oceans 2021, 126. [Google Scholar] [CrossRef]
  52. Copland, L.; Dawson, J.; Tivy, A.; Delaney, F.; Cook, A. Changes in shipping navigability in the Canadian Arctic between 1972 and 2016. FACETS 2021, 6, 1069–1087. [Google Scholar] [CrossRef]
  53. Cao, Y.; Liang, S. Recent advances in driving mechanisms of the Arctic amplification: A review. Chin. Sci. Bull. 2018, 63, 2757–2771. [Google Scholar] [CrossRef]
  54. Nielsen-Englyst, P.; Høyer, J.L.; Kolbe, W.M.; Dybkjær, G.; Lavergne, T.; Tonboe, R.T.; Skarpalezos, S.; Karagali, I. A combined sea and sea-ice surface temperature climate dataset of the Arctic, 1982–2021. Remote. Sens. Environ. 2022, 284. [Google Scholar] [CrossRef]
  55. Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun. Earth Environ. 2022, 3, 1–10. [Google Scholar] [CrossRef]
  56. Stroeve, J.C.; Crawford, A.D.; Stammerjohn, S. Using timing of ice retreat to predict timing of fall freeze-up in the Arctic. Geophys. Res. Lett. 2016, 43, 6332–6340. [Google Scholar] [CrossRef]
Climate 12 00165 g001
Figure 1. Study area for Hudson Bay including relevant climate stations: Churchill, MB; Kuujjurapik, QC; Inukjuak, QC; and Coral Harbour, NU. Scale 1:13,000,000.
Figure 1. Study area for Hudson Bay including relevant climate stations: Churchill, MB; Kuujjurapik, QC; Inukjuak, QC; and Coral Harbour, NU. Scale 1:13,000,000.
Climate 12 00165 g001
Climate 12 00165 g002
Figure 2. The annual cycle of the DTDTmin (°C) for Churchill, MB, averaged over the period of 1971 to 2010. The orange line represents the 2.35 (°C) DTDTmin threshold for marine climates determined in [44]. The grey bars are the critical areas of change that are used in Section 3.1 (Table 2).
Figure 2. The annual cycle of the DTDTmin (°C) for Churchill, MB, averaged over the period of 1971 to 2010. The orange line represents the 2.35 (°C) DTDTmin threshold for marine climates determined in [44]. The grey bars are the critical areas of change that are used in Section 3.1 (Table 2).
Climate 12 00165 g002
Climate 12 00165 g003
Figure 3. Location of the two Churchill climate stations. Scale 1:50,000.
Figure 3. Location of the two Churchill climate stations. Scale 1:50,000.
Climate 12 00165 g003
Climate 12 00165 g004
Figure 4. Grid of sea ice locations used in [5,7,8]. Scale 1:20,000,000.
Figure 4. Grid of sea ice locations used in [5,7,8]. Scale 1:20,000,000.
Climate 12 00165 g004
Climate 12 00165 g005
Figure 5. Breakup dates. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are imputed values from the temperature analysis for the missing years in the sea ice record.
Figure 5. Breakup dates. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are imputed values from the temperature analysis for the missing years in the sea ice record.
Climate 12 00165 g005
Climate 12 00165 g006
Figure 6. Freeze-up dates. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are imputed values from the temperature analysis for the missing years in the sea ice record.
Figure 6. Freeze-up dates. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are imputed values from the temperature analysis for the missing years in the sea ice record.
Climate 12 00165 g006
Climate 12 00165 g007
Figure 7. Ice-free season length. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are derived from imputed values of the breakup and freeze-up dates from the temperature analysis for the missing years in the sea ice record.
Figure 7. Ice-free season length. Blue and red represent the reconstructed record, and orange represents the sea ice record for Hudson Bay. The reconstructed record (blue) uses the aggregated temperature analysis from Churchill, Kuujjurarpik, Inukjuak, and Coral Harbour. The reconstructed record (red), due to data availability, did not use all four stations. Green dots are derived from imputed values of the breakup and freeze-up dates from the temperature analysis for the missing years in the sea ice record.
Climate 12 00165 g007
Climate 12 00165 g008
Figure 8. The breakup for 2011 to 2018 in Hudson Bay. The orange line (Obs) is the average sea ice breakup for Hudson Bay based on the sea ice charts [8]. The blue line is calculated based on the DTDTmin.
Figure 8. The breakup for 2011 to 2018 in Hudson Bay. The orange line (Obs) is the average sea ice breakup for Hudson Bay based on the sea ice charts [8]. The blue line is calculated based on the DTDTmin.
Climate 12 00165 g008
Climate 12 00165 g009
Figure 9. The freeze-up for 2011 to 2018 in Hudson Bay. The orange line (Obs) is the average sea ice breakup for Hudson Bay based on the sea ice charts [8]. The blue line is calculated based on the DTDTmin.
Figure 9. The freeze-up for 2011 to 2018 in Hudson Bay. The orange line (Obs) is the average sea ice breakup for Hudson Bay based on the sea ice charts [8]. The blue line is calculated based on the DTDTmin.
Climate 12 00165 g009
Table 1. List of climate stations used in this work, including latitude, longitude, elevation, and available data.
Table 1. List of climate stations used in this work, including latitude, longitude, elevation, and available data.
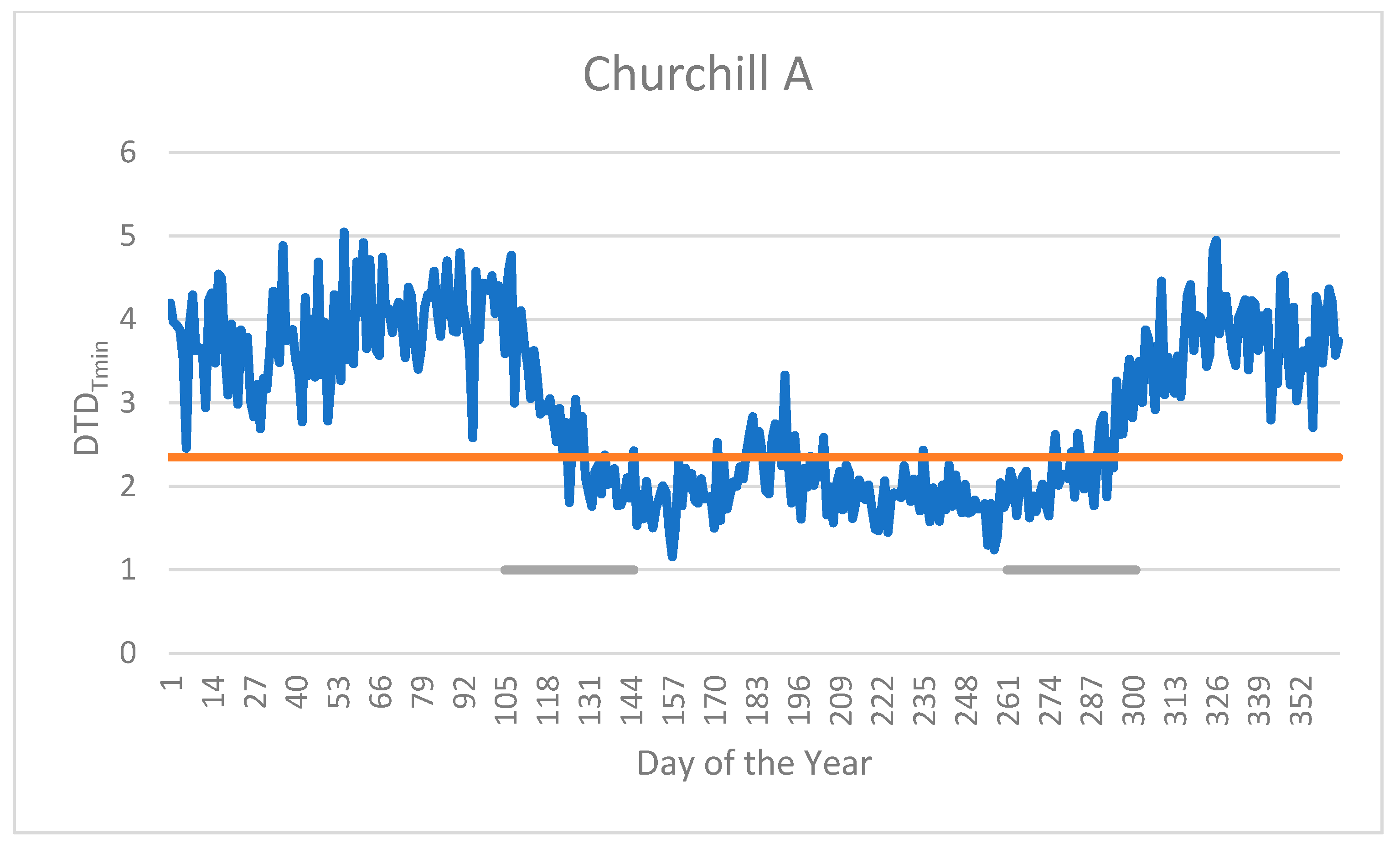
StationLatitudeLongitudeElevation (m)Period
Churchill A58.74° N94.07° W29.301944–2010
Churchill Marine58.78° N94.18° W13.401932–1951
Kuujjurapik A55.28° N77.75° W12.201926–2010
Inukjuak UA58.47° N78.08° W24.401922–1996
Inukjuak A58.47° N78.08° W26.201995–2010
Coral Harbour A64.19° N83.36° W62.201934–2010
Table 2. The results of the correlation analysis, including the Pearson r (Pearson correlation) calculated from the sea ice record and the DTDTmin for the twenty years within the period of 1971–2010, statistical significance (p-value), temperature data range (days of the year; Start date, End date), and regression equation (Equation), where y is the date of the year and x is the DTDTmin measurement averaged over the period between the Start date and End date. In the last column, the standard deviation of the difference between the equation-generated value and the observations from the sea ice charts is recorded. The years selected for the correlation analysis correspond to the ten highest and ten lowest years for the breakup and freeze-up sea ice record.
Table 2. The results of the correlation analysis, including the Pearson r (Pearson correlation) calculated from the sea ice record and the DTDTmin for the twenty years within the period of 1971–2010, statistical significance (p-value), temperature data range (days of the year; Start date, End date), and regression equation (Equation), where y is the date of the year and x is the DTDTmin measurement averaged over the period between the Start date and End date. In the last column, the standard deviation of the difference between the equation-generated value and the observations from the sea ice charts is recorded. The years selected for the correlation analysis correspond to the ten highest and ten lowest years for the breakup and freeze-up sea ice record.
Pearson Correlationp-ValueStart DateEnd DateEquationDifference (Standard Deviation)
Churchill
Breakup0.53170.019105145y = 9.8256 × x + 159.158.15
Freeze-up−0.766<0.0001261301y = −18.773 × x + 373.846.56
Inukjuak
Breakup0.54850.018111157y = 16.219 × x + 149.7310.04
Freeze-up−0.74450.0003271301y = −18.483 × x + 367.076.86
Kuujjurapik
Breakup0.47510.04106146y = 10.017 × x + 156.1510.38
Freeze-up−0.52950.02290330y = −15.935 × x + 368.888.66
Coral Harbour
Breakup0.60710.005123155y = 10.078 × x + 161.689.77
Freeze-up−0.7925<0.0001261297y = −14.75 × x + 369.386.23
Table 3. Correlation analysis for the same locations as Table 2 including all the years in the 1971–2010 period. The final entry (Aggregate) is the average of the generated sea ice dates for all four locations.
Table 3. Correlation analysis for the same locations as Table 2 including all the years in the 1971–2010 period. The final entry (Aggregate) is the average of the generated sea ice dates for all four locations.
Pearsonp-ValueDifference (Standard Deviation)
Churchill
Breakup 0.49000.0038.02
Freeze-up−0.60820.00036.86
Inukjuak
Breakup0.40110.028.20
Freeze-up−0.65810.00016.35
Kuujjurapik
Breakup0.48730.0028.31
Freeze-up−0.40260.028.07
Coral Harbour
Breakup 0.49000.0038.20
Freeze-up−0.60820.00037.99
Aggregate
Breakup 0.6212<0.00016.82
Freeze-up−0.8002<0.00015.06
Table 4. Imputation for missing sea ice data.
Table 4. Imputation for missing sea ice data.
Time SeriesYearImputed Value
Breakup2002186.8
Freeze-up1971335.5
Freeze-up1973337.6
Freeze-up1997330.6
Freeze-up1998335.4
Freeze-up1999331.0
Freeze-up2001332.2
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Gough, W.A. Reconstructing and Hindcasting Sea Ice Conditions in Hudson Bay Using a Thermal Variability Framework. Climate 2024, 12, 165. https://doi.org/10.3390/cli12100165

AMA Style

Gough WA. Reconstructing and Hindcasting Sea Ice Conditions in Hudson Bay Using a Thermal Variability Framework. Climate. 2024; 12(10):165. https://doi.org/10.3390/cli12100165

Chicago/Turabian Style

Gough, William A. 2024. "Reconstructing and Hindcasting Sea Ice Conditions in Hudson Bay Using a Thermal Variability Framework" Climate 12, no. 10: 165. https://doi.org/10.3390/cli12100165

APA Style

Gough, W. A. (2024). Reconstructing and Hindcasting Sea Ice Conditions in Hudson Bay Using a Thermal Variability Framework. Climate, 12(10), 165. https://doi.org/10.3390/cli12100165

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop