Climatology of Synoptic Non-Gaussian Meteorological Anomalies in the Northern Hemisphere during 1979–2018
Abstract
1. Introduction
2. Materials and Methods
- 1.
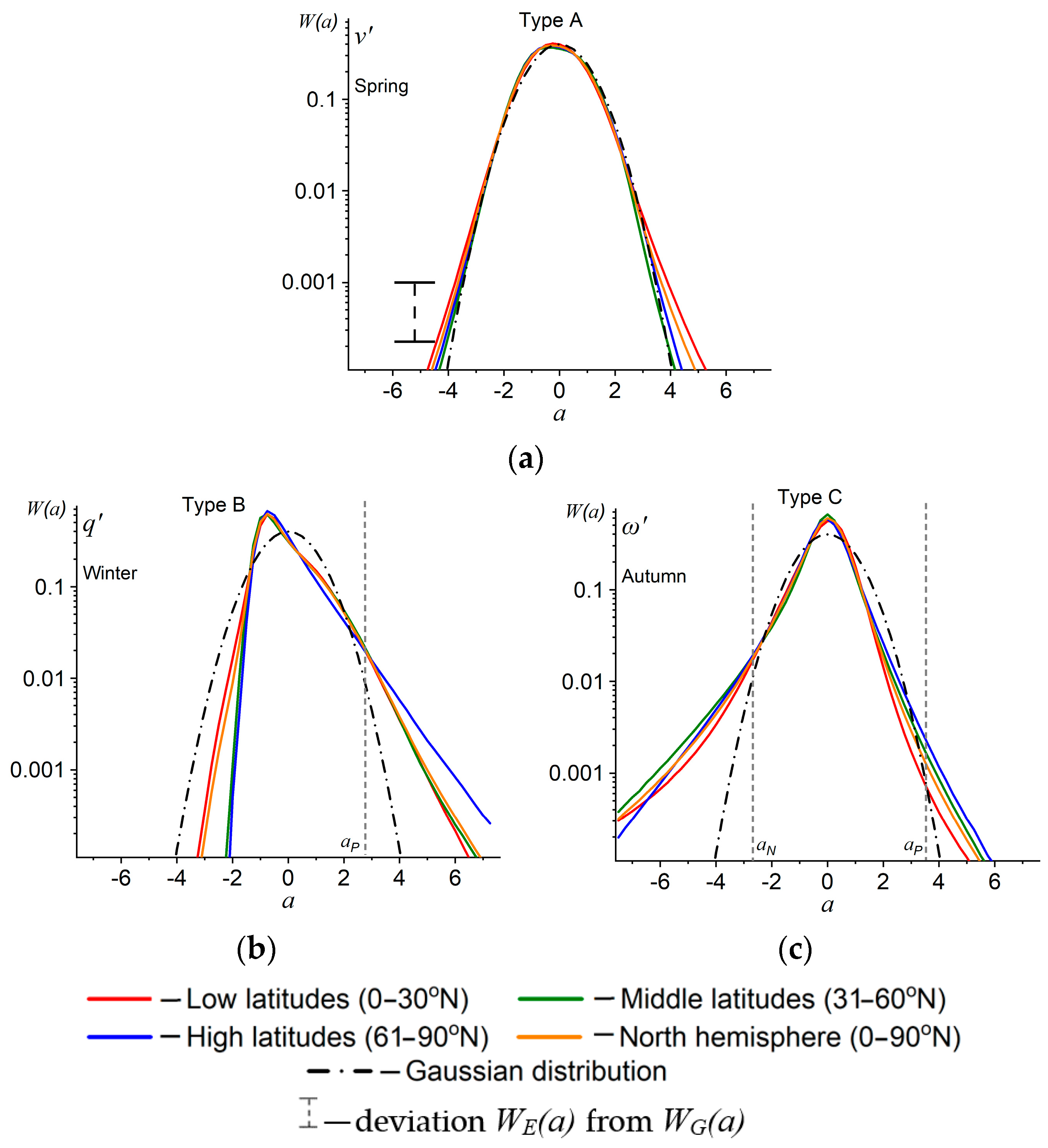
- Type A, when WE(a) values are close to normal distribution:
- 2.
- Type B, when the exceedance of empirical distribution values occurs in the negative or positive parts of the range, and the skewness coefficient value in distributions of this type will be significant:
- 3.
- Type C, when the WE(a) values exceed WG(a) simultaneously in the negative and positive parts of the range, and the kurtosis coefficient value in distributions of this type will be significant:
3. Results
3.1. Types of Probability Distribution Densities
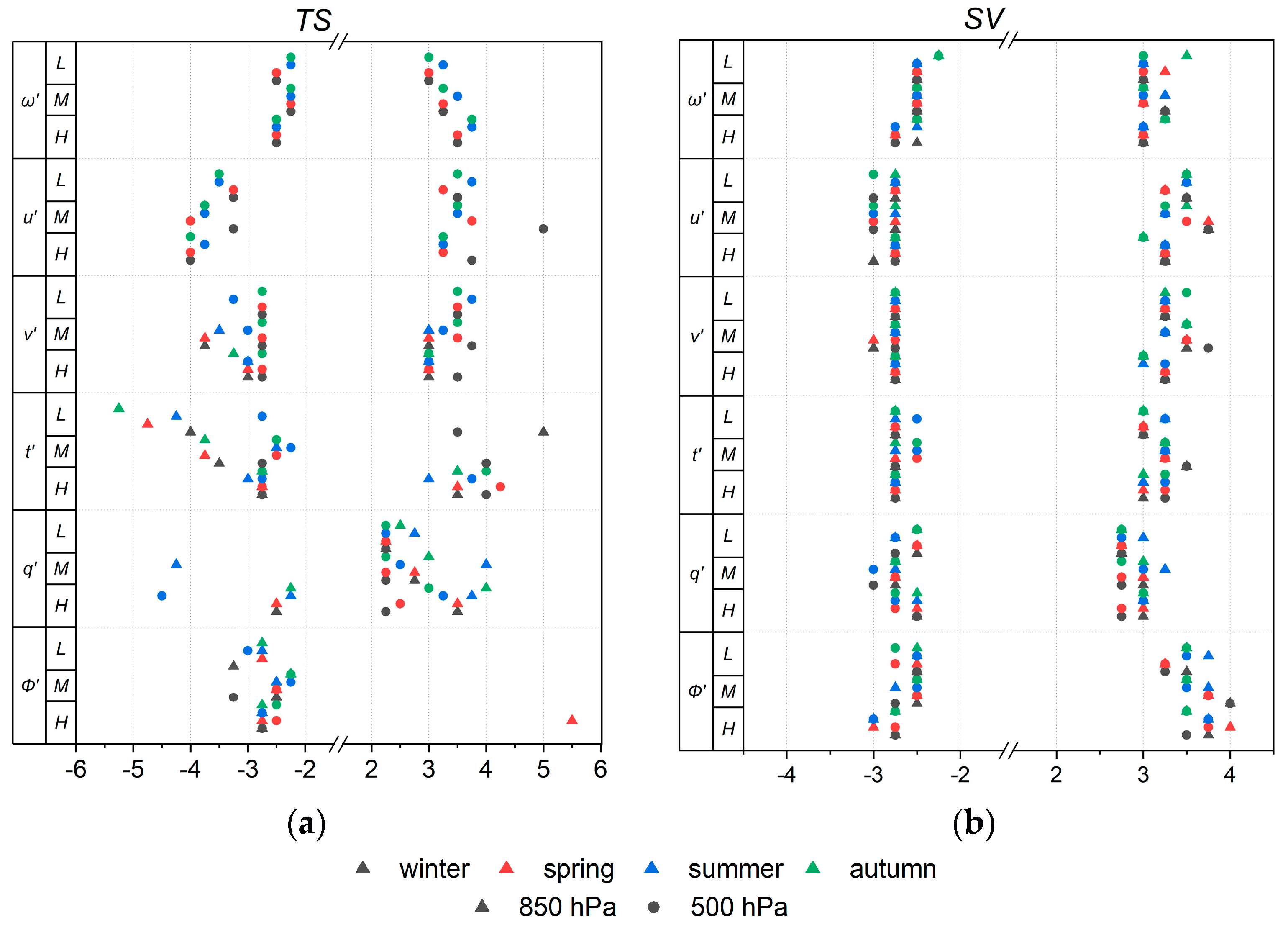
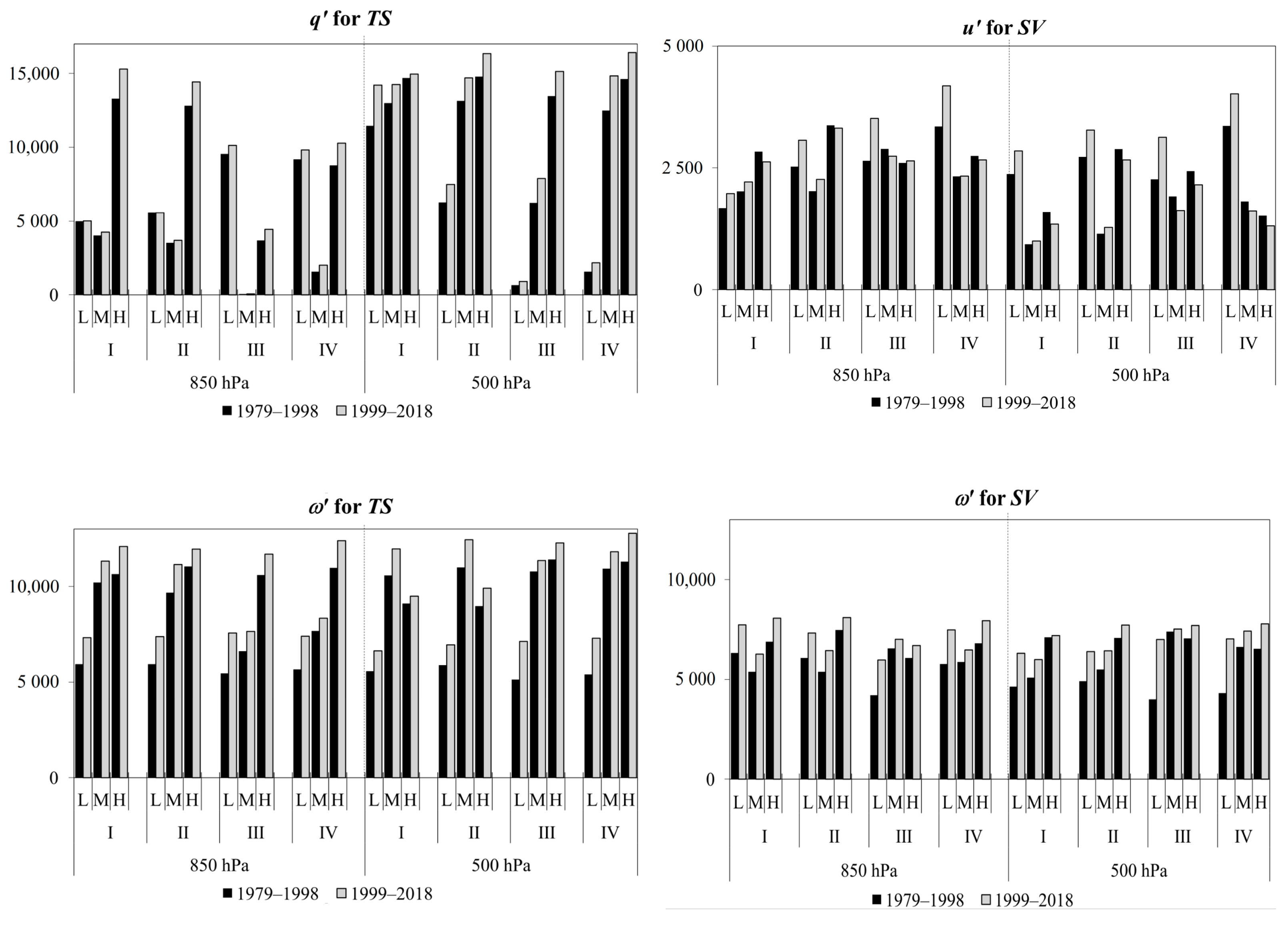
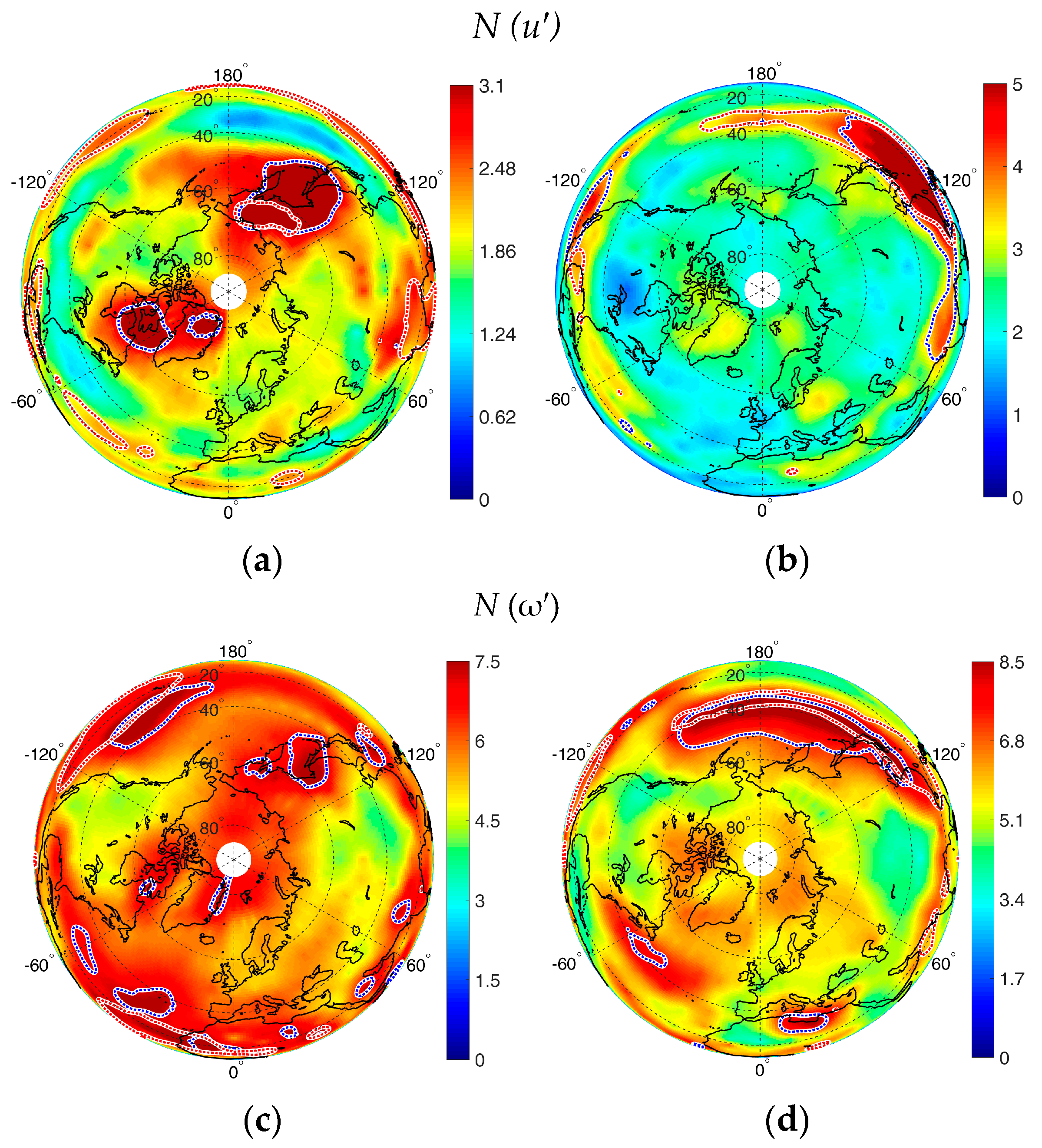
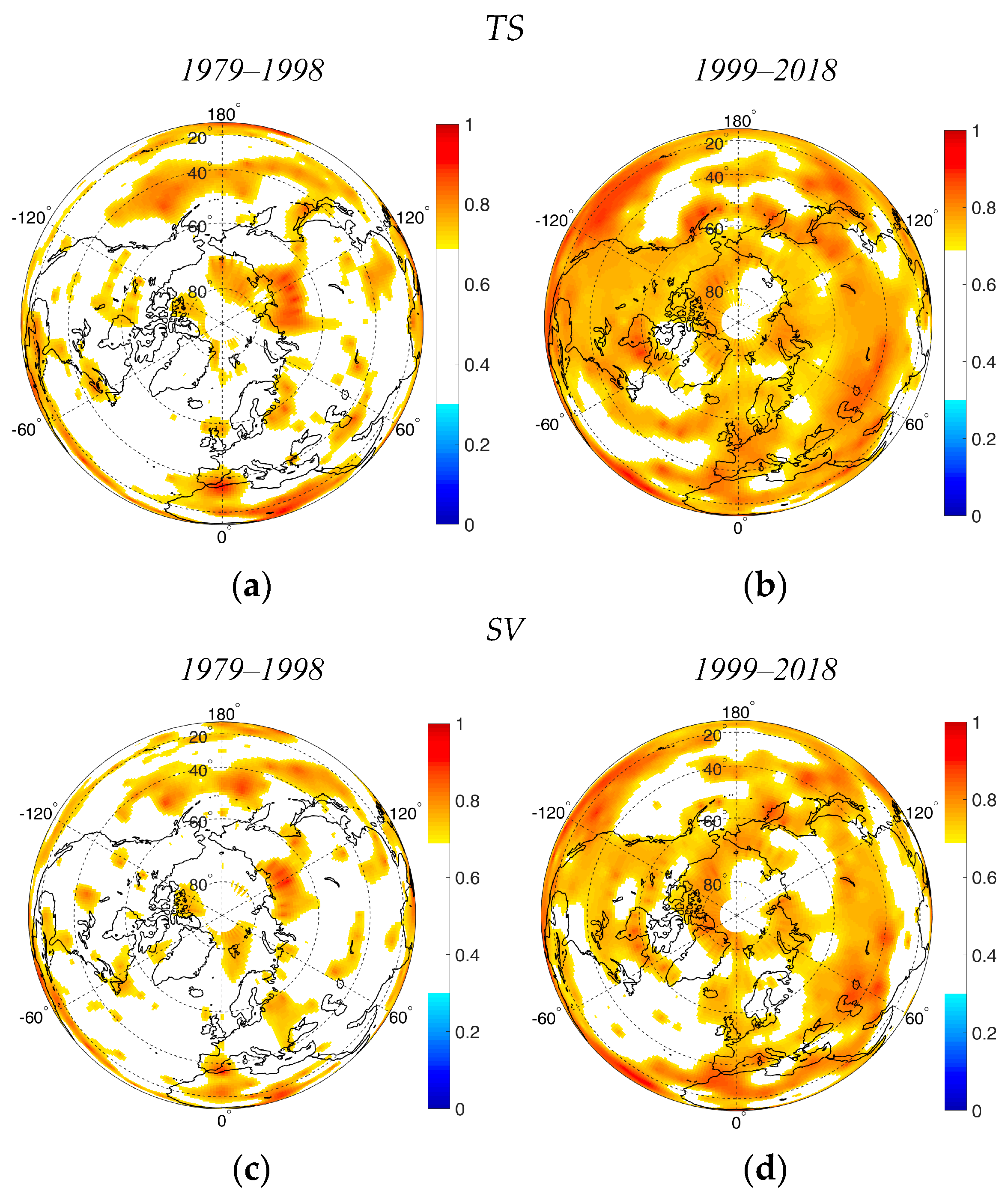
3.2. Spatiotemporal Variability in the Anomalies of Climatic Parameters in the Northern Hemisphere
3.3. Persistence Estimates of Climatic Parameter Anomalies
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Probability distribution function | |
| TS | Initial time series |
| SV | Time series of synoptic variability |
| t′ | Air temperature anomaly |
| q′ | Specific air humidity anomaly |
| u′ | Zonal wind speed component anomaly |
| v′ | Meridional wind speed component anomaly |
| ω′ | Vertical wind speed component anomaly |
| Φ′ | Geopotential anomaly |
| Number of negative anomalies | |
| Number of positive anomalies | |
| N | Number of anomalies , , or + ) |
| aN | The area of negative anomalies |
| aP | The area of positive anomalies |
| Gaussian distribution | |
| Non-Gaussian (empirical) distribution | |
| H | Hurst parameter |
| L | Low latitudes |
| M | Middle latitudes |
| H | High latitudes |
References
- IPCC. 2021: Climate Change 2021: The Physical Science Basis Contribution of Working Group I to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Masson-Delmotte, V., Zhai, P., Pirani, A., Connors, S.L., Péan, C., Berger, S., Caud, N., Chen, Y., Goldfarb, L., Gomis, M.I., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2021; 2391p. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Ruedy, R. Perception of climate change. Proc. Natl. Acad. Sci. USA 2012, 109, E2415–E2423. [Google Scholar] [CrossRef] [PubMed]
- Castillo, F.; Wehner, M.; Stone, D.A. Extreme Events and Climate Change: A Multidisciplinary Approach; John Wiley & Sons: Hoboken, NJ, USA, 2021; p. 226. [Google Scholar]
- Goyal, M.K.; Gupta, A.K.; Gupta, A. Hydro-Meteorological Extremes and Disasters; Springer Nature: Singapore, 2022; p. 328. [Google Scholar]
- Kirtman, B.; Power, S.B.; Adedoyin, A.J.; Boer, G.J.; Bojariu, R.; Camilloni, I.; Doblas-Reyes, F.J.; Fiore, A.M.; Kimoto, M.; Meehl, G.A.; et al. Near-term climate change: Projections and predictability. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK, 2013; pp. 953–1028. [Google Scholar]
- Bardin, M.Y.; Platova, T.V. Long-period variations in extreme temperature statistics in Russia as linked to the changes in large-scale atmospheric circulation and global warming. Russ. Meteorol. Hydrol. 2019, 44, 791–801. [Google Scholar] [CrossRef]
- Kharyutkina, E.V.; Loginov, S.V.; Moraru, E.I.; Pustovalov, K.N.; Martynova, Y.V. Dynamics of extreme climatic characteristics and trends of dangerous meteorological phenomena over the Territory of Western Siberia. Atmos. Ocean. Opt. 2022, 35, 394–401. [Google Scholar] [CrossRef]
- Shumakov, I.A. Third Roshydromet Assessment Report on Climate Change and Its Consequences in Russian Federation; Roshydromet, Naukoemkie Tekhnologii: Saint Petersburg, Russia, 2022; 124p. [Google Scholar]
- Quan, H.; Zhang, B.; Bourguet, S.; Linz, M.; Chen, G. How Do Different Processes Shape Temperature Probability Distributions? A Percentile-Averaged Temperature Tendency Decomposition. J. Clim. 2023, 36, 5179–5196. [Google Scholar] [CrossRef]
- Schneider, T.; Bischoff, T.; Płotka, H. Physics of changes in synoptic midlatitude temperature variability. J. Clim. 2015, 28, 2312–2331. [Google Scholar] [CrossRef]
- Kononova, N.K. Types of the global atmospheric circulation: Monitoring and retrospective assessment results of 1899–2017 Fundament. Prikl. Klimatol. 2018, 3, 108–123. [Google Scholar] [CrossRef]
- Garfinkel, C.I.; Harnik, N. The non-Gaussian and spatial asymmetry of temperature extremes relative to the storm track: The role of horizontal advection. J. Clim. 2017, 30, 445–464. [Google Scholar] [CrossRef]
- Hassanzadeh, P.; Kuang, Z. Blocking variability: Arctic Amplification versus Arctic Oscillation. Geophys. Res. Lett. 2015, 42, 8586–8595. [Google Scholar] [CrossRef]
- Semenov, V.A.; Mokhov, I.I.; Latif, M. Influence of the ocean surface temperature and sea ice concentration on regional climate changes in Eurasia in recent decades. Izv. Atmos. Ocean. 2012, 48, 355–372. [Google Scholar] [CrossRef]
- Semenov, V.A. Link between anomalously cold winters in Russia and sea-ice decline in the Barents Sea. Izv. Atmos. Ocean. Phys. 2016, 52, 225–233. [Google Scholar] [CrossRef]
- Loikith, P.C.; Lintner, B.R.; Kim, J.; Lee, H.; Neelin, J.D.; Waliser, D.E. Classifying reanalysis surface temperature probability density functions (PDFs) over North America with cluster analysis. Geophys. Res. Lett. 2013, 40, 3710–3714. [Google Scholar] [CrossRef]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.J.; Shepherd, T.G. A Dynamical Perspective on atmospheric temperature variability and its response to climate change. J. Clim. 2019, 32, 1707–1724. [Google Scholar] [CrossRef]
- Perron, M.; Sura, P. Climatology of Non-Gaussian Atmospheric Statistics. J. Clim. 2013, 26, 1063–1083. [Google Scholar] [CrossRef]
- Easterling, D.R.; Meehl, G.A.; Parmesan, C.; Changnon, S.A.; Karl, T.R.; Mearns, L.O. Climate extremes: Observations, modeling, and impacts. Science 2000, 289, 2068–2074. [Google Scholar] [CrossRef] [PubMed]
- Brönnimann, S.; Luterbacher, J.; Ewen, T.; Diaz, H.F.; Stolarski, R.S.; Neu, U. Climate Variability and Extremes during the Past 100 Years, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2008; 364p. [Google Scholar]
- Houghton, J. Global Warming: The Complete Briefing, 4th ed.; Cambridge University Press: Cambridge, UK, 2009; 438p. [Google Scholar]
- Ruff, T.W.; Neelin, J.D. Long tails in regional surface temperature probability distributions with implications for extremes under global warming. Geophys. Res. Lett. 2012, 39, L04704. [Google Scholar] [CrossRef]
- Loikith, P.C.; Neelin, J.D. Short-tailed temperature distributions over North America and implications for future changes in extremes. Geophys. Res. Lett. 2015, 42, 8577–8585. [Google Scholar] [CrossRef]
- Loikith, P.C.; Broccoli, A.J. Characteristics of Observed Atmospheric Circulation Patterns Associated with Temperature Extremes over North America. J. Clim. 2012, 25, 7266–7281. [Google Scholar] [CrossRef]
- Sardeshmukh, P.D.; Compo, G.P.; Penland, C. Need for caution in interpreting extreme weather statistics. J. Clim. 2016, 28, 9166–9187. [Google Scholar] [CrossRef]
- Blackmon, M.L.; Wallace, J.M.; Lau, N.-C.; Mullen, S.L. An observational study of the Northern Hemi-sphere wintertime circulation. J. Atmos. Sci. 1977, 34, 1040–1053. [Google Scholar] [CrossRef]
- Petoukhov, V.; Eliseev, A.V.; Klein, R.; Oesterle, H. On statistics of the free-troposphere synoptic component: An evaluation of skewnesses and mixed third-order moments contribution to the synoptic-scale dynamics and fluxes of heat and humidity. Tellus 2008, 60 Pt A, 11–31. [Google Scholar] [CrossRef]
- Loginov, S.V.; Eliseev, A.V.; Mokhov, I.I. Impact of non-Gaussian statistics of atmospheric variables on extreme intramonth anomalies. Izv. Atmos. Ocean. Phys. 2017, 53, 269–278. [Google Scholar] [CrossRef]
- Linz, M.; Chen, G.; Hu, Z. Large-scale atmospheric control on non-Gaussian tails of midlatitude temperature distributions. Geophys. Res. Lett. 2018, 45, 9141–9149. [Google Scholar] [CrossRef]
- Loikith, P.C.; Neelin, J.D.; Meyerson, J.; Hunter, J.S. Short warm-side temperature distribution tails drive hotspots of warm temperature extreme increases under near-future warming. J. Clim. 2018, 31, 9469–9487. [Google Scholar] [CrossRef]
- Moraru, E.I.; Loginov, S.V.; Kharyutkina, E.V. Features of the spatiotemporal variability of the advective heat transfer in the troposphere over the Pacific and Atlantic oceans in the Northern Hemisphere for 1979–2018. Izv. Atmos. Ocean. Phys. 2021, 57, 693–700. [Google Scholar] [CrossRef]
- Mokhov, I.I.; Chernokulsky, A.V.; Osipov, A.M. Atmospheric centers of action in the Northern and Southern hemispheres: Features and variability. Russ. Meteorol. Hydrol. 2020, 45, 749–761. [Google Scholar] [CrossRef]
- Loginov, S.V.; Kharyutkina, E.V. Application of fractal and wavelet analysis to the assessment of climate changes in West Siberia over winter season. Izv. Vuzov Fizika 2016, 59, 139–143. [Google Scholar] [CrossRef]
- Ippolitov, I.I.; Kabanov, M.V.; Loginov, S.V. Spatiotemporal scales of warming observed in Siberia. Dokl. Earth Sci. 2007, 413, 248–251. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, S.P. Hilbert-Huang Transform and Its Application; World Scientific: Singapore, 2005; 311p. [Google Scholar]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Feder, E. Fractals; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2013; 284p. [Google Scholar]
- Weron, R. Estimating long-range dependence: Finite sample properties and confidence intervals. Phys. A Stat. Mech. Appl. 2002, 312, 285–299. [Google Scholar] [CrossRef]
- Lyubushin, A.A. Low-Frequency Seismic Noise Properties in the Japanese Islands. Entropy 2013, 23, 474. [Google Scholar] [CrossRef]
- Ventura, V.; Paciorek, C.J.; Risbey, J.S. Controlling the proportion of falsely rejected hypotheses when conducting multiple tests with climatological data. J. Clim. 2004, 17, 4343–4356. [Google Scholar] [CrossRef]
- Osipov, A.M.; Gushchina, D.Y. El-Nino 2015–2016: Evolyuciya, mekhanizmy, soputstvuyushchie udalennye anomalii. Fund. Prikl. Klim. 2018, 3, 54–81. [Google Scholar]
- Franceschetti, G.; Riccio, D. Scattering, Natural Surfaces, and Fractals; Elsevier: Amsterdam, The Netherlands, 2007; 304p. [Google Scholar] [CrossRef]
- Stefanova, L.; Sura, P.; Griffin, M. Quantifying the non-Gaussianity of wintertime daily maximum and minimum temperatures in the Southeast. J. Clim. 2016, 26, 838–850. [Google Scholar] [CrossRef][Green Version]
- Eichler, T.P.; Gaggini, N.; Pan, Z. Impacts of global warming on Northern Hemisphere winter storm tracks in the CMIP5 model suite. Geophys. Res. Lett. 2013, 118, 3919–3932. [Google Scholar] [CrossRef]
- Tamarin, T.; Kaspi, Y. The poleward shift of storm tracks under global warming: A Lagrangian perspective. Geophys. Res. Lett. 2017, 20, 10666–10674. [Google Scholar] [CrossRef]
- Martynova, Y.V.; Vargin, P.N.; Volodin, E.M. Variation of Northern Hemispheric wintertime storm tracks under future climate change in INM-CM5 simulations. Izv. Atmos. Ocean. 2022, 58, 208–218. [Google Scholar] [CrossRef]
- Wang, J.; Kim, H.-M.; Chang, E. Interannual Modulation of Northern Hemisphere Winter Storm Tracks by the QBO. Geophys. Res. Lett. 2018, 45, 2786–2794. [Google Scholar] [CrossRef]
- Afargan-Gerstman, H.; Domeisen, D. Pacific Modulation of the North Atlantic Storm Track Response to Sudden Stratospheric Warming Events. Geophys. Res. Lett. 2020, 47, e2019GL085007. [Google Scholar] [CrossRef]
- Mitas, C.M.; Clement, A. Recent behavior of the Hadley cell and tropical thermodynamics in climate models and reanalyses. Geophys. Res. Lett. 2006, 33, L01810. [Google Scholar] [CrossRef]
- Fu, Q.; Johanson, C.M.; Wallace, J.M.; Reichler, T. Enhanced mid-latitude tropospheric warming in satellite measurements. Science 2006, 312, 1179. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.; Vecchi, G.A.; Reichler, T. Expansion of the Hadley cell under global warming. Geophys. Res. Lett. 2007, 34, L06805. [Google Scholar] [CrossRef]
- Mbengue, C.; Schneider, T. Storm-track shifts under climate change: Toward a mechanistic understanding using baroclinic mean available potential energy. J. Atmos. Sci. 2017, 74, 93–110. [Google Scholar] [CrossRef]
- Dima, I.M.; Wallace, J.M. On the seasonatity of the Hadley cell. J. Atmos. Sci. 2003, 60, 1522–1527. [Google Scholar] [CrossRef]
- Loginov, S.V.; Moraru, E.I.; Kharyutkina, S.V. Relationship of tropospheric circulation cells with the variability of meridional heat flows over Siberia. Opt. Atmos. Okeana 2016, 29, 640–646. [Google Scholar] [CrossRef]
- Doos, K.; Nilsson, J. Analysis of the meridional energy transport by atmospheric overturning circulations. J. Atmos. Sci. 2011, 68, 1806–1819. [Google Scholar] [CrossRef]
- Thorncroft, C.D.; Hoskins, B.J.; McIntyre, M.E. Two Paradigms of Baroclinic-Wave Life-Cycle Behaviour. Q. J. R. Meteorol. Soc. 1993, 119, 17–55. [Google Scholar] [CrossRef]
- Hoskins, B.J.; McIntyre, M.E.; Robertson, A.W. On the Use and Significance of Isentropic Potential Vorticity Maps. Q. J. R. Meteorol. Soc. 2007, 111, 877–946. [Google Scholar] [CrossRef]
- Iwao, K.; Takahashi, M.A. Precipitation seesaw mode between Northeast Asia and Siberia in summer caused by Rossby Waves over the Eurasian continent. J. Clim. 2008, 21, 2401–2419. [Google Scholar] [CrossRef]
- Schubert, S.D.; Wang, H.; Koster, R.D.; Suarez, M.J.; Groisman, P.Y. Northern Eurasian heat waves and droughts. J. Clim. 2014, 27, 3169–3207. [Google Scholar] [CrossRef]
- Chernokulsky, A.V.; Bulygina, O.N.; Mokhov, I.I. Recent variations of cloudiness over Russia from surface daytime observations. Environ. Res. Lett. 2011, 6, 035202. [Google Scholar] [CrossRef]



| Height | TS, % | SV, % | ||||
|---|---|---|---|---|---|---|
| Type A | Type B | Type C | Type A | Type B | Type C | |
| 850 hPa | 26 | 53 | 21 | 3 | 34 | 63 |
| Anomalies | t′, u′, v′ | q′, Φ′ | ω′, v′ | v′, Φ′ | Φ′, u′ | ω′, q′, t′ |
| 500 hPa | 19 | 48 | 33 | 6 | 37 | 57 |
| Anomalies | u′, Φ′ | q′, Φ′, t′ | ω′, v′ | v′, u′ | Φ′, u′ | ω′, q′ |
| Season | Winter | Summer | ||||||
|---|---|---|---|---|---|---|---|---|
| Anomaly Sign | N− | N+ | N− | N+ | ||||
| Period | I | II | I | II | I | II | I | II |
| q′ | ||||||||
| TS | 0 | 0 | 14.7 | 13.6 | 2.9 | 4.3 | 0.3 | 1.7 |
| SV | 11.1 | 18.2 | 15.7 | 25.6 | 10.2 | 13.6 | 11.1 | 11.6 |
| t′ | ||||||||
| TS | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| SV | 0 | 0.1 | 0.3 | 0 | 0.1 | 0 | 0 | 1.4 |
| u′ | ||||||||
| TS | 0.3 | 2.9 | 1.5 | 2.5 | 0.9 | 3.1 | 0.5 | 1.3 |
| SV | 0 | 0.5 | 0 | 0.6 | 1.6 | 8 | 0 | 3.6 |
| v′ | ||||||||
| TS | 0.4 | 1.0 | 4.8 | 13.9 | 0.6 | 1.7 | 13.1 | 19.6 |
| SV | 0 | 0.2 | 0 | 0.2 | 0.4 | 2.1 | 0.5 | 4.3 |
| ω′ | ||||||||
| TS | 27.6 | 46.0 | 18.1 | 54.0 | 23.9 | 63.2 | 16.6 | 69.0 |
| SV | 25.3 | 40.7 | 33.1 | 47.8 | 20.8 | 49.5 | 19.2 | 50.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Loginov, S.; Moraru, E.; Kharyutkina, E.; Sudakow, I. Climatology of Synoptic Non-Gaussian Meteorological Anomalies in the Northern Hemisphere during 1979–2018. Climate 2024, 12, 8. https://doi.org/10.3390/cli12010008
Loginov S, Moraru E, Kharyutkina E, Sudakow I. Climatology of Synoptic Non-Gaussian Meteorological Anomalies in the Northern Hemisphere during 1979–2018. Climate. 2024; 12(1):8. https://doi.org/10.3390/cli12010008
Chicago/Turabian StyleLoginov, Sergey, Evgeniia Moraru, Elena Kharyutkina, and Ivan Sudakow. 2024. "Climatology of Synoptic Non-Gaussian Meteorological Anomalies in the Northern Hemisphere during 1979–2018" Climate 12, no. 1: 8. https://doi.org/10.3390/cli12010008
APA StyleLoginov, S., Moraru, E., Kharyutkina, E., & Sudakow, I. (2024). Climatology of Synoptic Non-Gaussian Meteorological Anomalies in the Northern Hemisphere during 1979–2018. Climate, 12(1), 8. https://doi.org/10.3390/cli12010008






