Impact of Accelerated Climate Change on Maximum Temperature Differences between Western and Coastal Sydney
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Sources and Pre-Processing
2.2. Permutation Testing
2.3. Wavelet Analysis
2.4. Machine Learning for Attribution
2.4.1. Linear Regression (LR)
2.4.2. Support Vector Regression (SVR)
2.4.3. Random Forests (RF)
2.4.4. Forward and Backward Selection
2.4.5. Expanding Window Cross Validation
2.5. Australian Climate Drivers
2.5.1. Global Temperature (GlobalT)
2.5.2. Global and Tasman Sea Surface Temperature Anomalies (GlobalSSTA and TSSTA)
2.5.3. The Dipole Mode Index (DMI)
2.5.4. The Southern Annular Mode (SAM)
2.5.5. Southern Oscillation Index (SOI)
3. Results
3.1. Exploratory Data Analysis
3.1.1. Percentile Plots
3.1.2. Box Plots
3.2. Permutation Testing
3.3. Daily Data
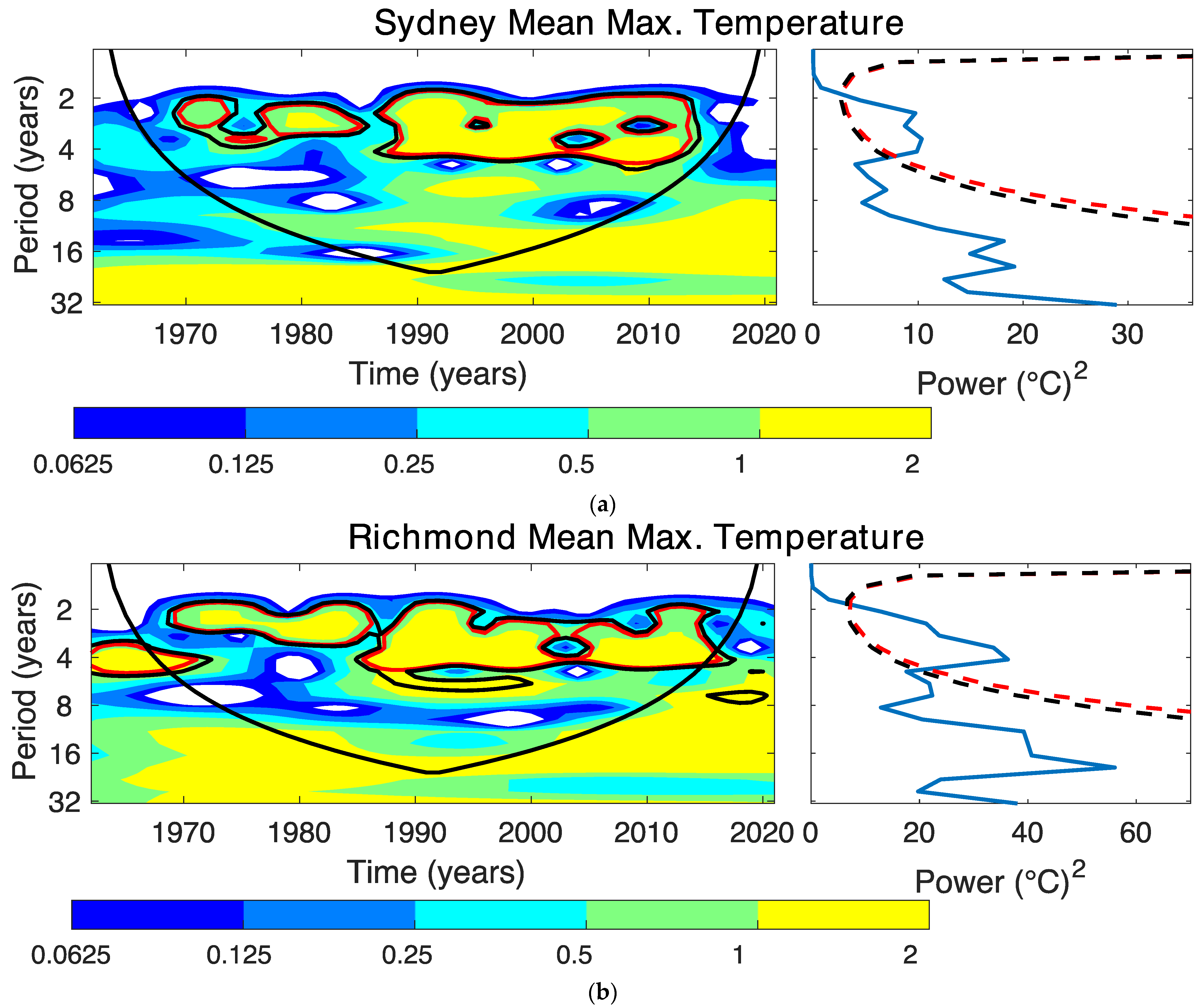
3.4. Wavelet Analysis
3.5. Machine Learning Attribution Results
4. Discussion
Analysis of Maximum Temperatures
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Melville-Rea, H. Western Sydney Will Swelter through 46 Days Per Year over 35 °C by 2090, Unless Emissions Drop Significantly. Available online: https://theconversation.com/westernsydney-will-swelter-through-46-days-per-year-over-35-c-by-2090-unless-emissions-drop-significantly-177056 (accessed on 9 October 2022).
- HeatWatch: Extreme Heat in Western Sydney. Available online: https://australiainstitute.org.au/report/HeatWatch-extreme-heat-in-western-sydney-2022/ (accessed on 9 October 2022).
- Out of Season: Expanding Summers and Shrinking Winters in Subtropical and Temperate Australia. Available online: https://australiainstitute.org.au/wp-content/uploads/2020/12/P834-Out-of-Season-WEB.pdf (accessed on 18 February 2023).
- Royal Commission into National Natural Disaster Arrangements: Report. Available online: https://apo.org.au/node/309191 (accessed on 9 October 2022).
- Policymakers on Notice to Address Human-Induced Climate Change, ‘Half-Measures’ No Longer an Option. Available online: https://www.themandarin.com.au/182988-policymakers-on-notice-human-induced-climate-change/ (accessed on 14 February 2023).
- HeatWatch: Extreme Heat in Western Sydney. Available online: https://australiainstitute.org.au/wp-content/uploads/2020/12/Western-Sydney-HeatWatch-WEB.pdf (accessed on 9 October 2022).
- Untouchable Playgrounds: Urban Heat and the Future of Western Sydney. Available online: https://www.climatecouncil.org.au/urban-heat-island-effect-western-sydney/ (accessed on 9 October 2022).
- About Greater Western Sydney. Available online: https://www.westernsydney.edu.au/rcegws/rcegws/About/about_greater_western_sydney (accessed on 6 November 2022).
- ‘Homes Aren’t Safe’: Western Sydney Prepares Evacuation Shelters for Hot Summers. Available online: https://www.smh.com.au/national/nsw/homes-aren-t-safe-western-sydney-preparesevacuation-shelters-for-hot-summers-20220505-p5aioj.html (accessed on 9 October 2022).
- Hartigan, J.; MacNamara, S.; Leslie, L.M. Application of Machine Learning to Attribution and Prediction of Seasonal Precipitation and Temperature Trends in Canberra, Australia. Climate 2020, 8, 76. [Google Scholar] [CrossRef]
- Hartigan, J.; MacNamara, S.; Leslie, L.M. Comparing precipitation and temperature trends between inland and coastal locations. ANZIAM J. 2019, 60, C109–C126. [Google Scholar] [CrossRef]
- Climate Change Datasets. Available online: http://www.bom.gov.au/climate/data/index.shtml (accessed on 9 October 2022).
- Climate Data Quality Control. Available online: http://www.bom.gov.au/climate/data-services/about-data-observations.shtml#tabs=Quality-control (accessed on 18 February 2023).
- IPCC. Climate Change 2022: Impacts, Adaptation, and Vulnerability. Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change; Pörtner, H.-O., Roberts, D.C., Tignor, M., Poloczanska, E.S., Mintenbeck, K., Alegría, A., Craig, M., Langsdorf, S., Löschke, S., Möller, V., Okem, A., Rama, B., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2022; p. 3056. [Google Scholar] [CrossRef]
- Canny, J. Combinatorics and Discrete Probability: Stats: Permutation Tests and Bootstrapping [Lecture Notes]; EECS: Berkeley, CA, USA, 2008; p. 154+196. Available online: https://inst.eecs.berkeley.edu/~cs174/sp08/lecs/index.html (accessed on 14 October 2022).
- Wilcox, R.R. Introduction to Robust Estimation and Hypothesis Testing, 5th ed.; Elsevier, Inc.: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. The 2015–2017 Cape Town Drought: Attribution and Prediction Using Machine Learning. Procedia Comput. Sci. 2018, 140, 248–257. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. Machine Learning for Attribution of Heat and Drought in Southwestern Australia. Procedia Comput. Sci. 2020, 168, 3–10. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M. Attribution and Prediction of Maximum Temperature Extremes in SE Australia. Procedia Comput. Sci. 2014, 36, 612–617. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Kuhn, M.; Johnson, K. Applied Predictive Modeling; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Richman, M.B.; Leslie, L.M.; Ramsay, H.A.; Klotzbach, P.J. Reducing Tropical Cyclone Prediction Errors Using Machine Learning Approaches. Procedia Comput. Sci. 2017, 114, 314–323. [Google Scholar] [CrossRef]
- Cutler, A.; Cutler, D.R.; Stevens, J.R. Random Forests. In Ensemble Machine Learning; Zhang, C., Ma, Y., Eds.; Springer: New York, NY, USA, 2012; pp. 157–175. [Google Scholar] [CrossRef]
- Maldonado, S.; Weber, R. A wrapper method for feature selection using Support Vector Machines. Inf. Sci. 2009, 179, 2208–2217. [Google Scholar] [CrossRef]
- Brownlee, J. Long Short-Term Memory Networks with Python Develop Sequence Prediction Models with Deep Learning; Machine Learning Mastery EBook: San Juan, PR, USA, 2017. [Google Scholar]
- Hartigan, J.; MacNamara, S.; Leslie, L.M.; Speer, M. Attribution and Prediction of Precipitation and Temperature Trends within the Sydney Catchment Using Machine Learning. Climate 2020, 8, 120. [Google Scholar] [CrossRef]
- Foster, G.; Rahmstorf, S. Global temperature evolution 1979–2010. Environ. Res. Lett. 2011, 6, 044022. [Google Scholar] [CrossRef]
- Farmer, G.T.; Cook, J. (Eds.) Earth’s Surface Temperature. In Climate Change Science: A Modern Synthesis: Volume 1—The Physical Climate; Springer: Dordrecht, The Netherlands, 2013; pp. 135–157. [Google Scholar] [CrossRef]
- Hansen, J.; Ruedy, R.; Sato, M.; Lo, K. Global Surface Temperature Change. Rev. Geophys. 2010, 48, RG4004. [Google Scholar] [CrossRef]
- Rantanen, M.; Karpechko, A.Y.; Lipponen, A.; Nordling, K.; Hyvärinen, O.; Ruosteenoja, K.; Vihma, T.; Laaksonen, A. The Arctic has warmed nearly four times faster than the globe since 1979. Commun Earth Env. 2022, 3, 168. [Google Scholar] [CrossRef]
- Ham, Y.-G. El Niño events will intensify under global warming. Nature 2018, 564, 192–193. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Borlace, S.; Lengaigne, M.; van Rensch, P.; Collins, M.; Vecchi, G.; Timmermann, A.; Santoso, A.; McPhaden, M.J.; Wu, L.; et al. Increasing frequency of extreme El Niño events due to greenhouse warming. Nat. Clim. Change 2014, 4, 111–116. [Google Scholar] [CrossRef]
- Nasa Earth Observations. Sea Surface Temperature Anomaly (1 Month—AQUA/AMSR-E, 2002-11): Nasa Earth Observations. Available online: https://neo.gsfc.nasa.gov/view.php?dtasetId=AMSRE_SSTAn_M (accessed on 9 October 2022).
- About the Sea Surface Temperature Timeseries Graphs. Available online: http://www.bom.gov.au/climate/change/about/sst_timeseries.shtm (accessed on 9 October 2022).
- Hobday, A.J.; Pecl, G.T. Identification of global marine hotspots: Sentinels for change and vanguards for adaptation action. Rev. Fish Biol. Fish. 2014, 24, 415–425. [Google Scholar] [CrossRef]
- Oliver, E.C.J.; Benthuysen, J.A.; Bindoff, N.L.; Hobday, A.J.; Holbrook, N.J.; Mundy, C.N.; Perkins-Kirkpatrick, S.E. The unprecedented 2015/16 Tasman Sea marine heatwave. Nat. Commun. 2017, 8, 16101. [Google Scholar] [CrossRef] [PubMed]
- Ridgway, K.R. Long-term trend and decadal variability of the southward penetration of the East Australian Current: East Australian Current Trend. Geophys. Res. Lett. 2007, 34, L13613. [Google Scholar] [CrossRef]
- About ENSO Outlooks. Available online: http://www.bom.gov.au/climate/ahead/about-ENSO-outlooks.shtml (accessed on 9 October 2022).
- Southern Oscillation Index (SOI): National Oceanic. Available online: https://www.ncei.noaa.gov/access/monitoring/enso/soi (accessed on 10 August 2022).
- State of The Climate 2018. Available online: https://www.csiro.au/en/research/environmental-impacts/climate-change/State-of-the-Climate/Previous/State-of-the-Climate-2018 (accessed on 9 October 2022).
- ENSO Forecast. Available online: http://www.bom.gov.au/climate/enso/outlook/#tabs=ENSO-Forecast (accessed on 9 October 2022).
- Rayner, N.A. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J. Geophys. Res. 2003, 108, 4407. [Google Scholar] [CrossRef]
- McPhaden, M.J.; Santoso, A.; Cai, W. (Eds.) El Niño Southern Oscillation in a Changing Climate, 1st ed.; Wiley: Hoboken, NJ, USA, 2020. [Google Scholar] [CrossRef]
- Gao, Z.; Hu, Z.-Z.; Zheng, F.; Li, X.; Li, S.; Zhang, B. Single-year and double-year El Niños. Clim. Dyn. 2022, 1–9. [Google Scholar] [CrossRef]
- Weisheimer, A.; Balmaseda, M.A.; Stockdale, T.N.; Mayer, M.; Sharmila, S.; Hendon, H.; Alves, O. Variability of ENSO Forecast Skill in 2-Year Global Reforecasts over the 20th Century. Geophys. Res. Lett. 2022, 49, e2022GL097885. [Google Scholar] [CrossRef]
- Why Are There So Many ENSO Indexes, Instead of Just One? Available online: https://climate.gov/author/anthony-barnston (accessed on 18 February 2023).
- Dipole Mode Index (DMI). Available online: http://psl.noaa.gov/gcos_wgsp/Timeseries/DMI/index.html (accessed on 5 March 2022).
- Climate Driver Update. Available online: http://www.bom.gov.au/climate/enso/#tabs=Overview (accessed on 9 October 2022).
- Saji, N.H.; Yamagata, T. Possible impacts of Indian Ocean Dipole mode events on global climate. Clim. Res. 2003, 25, 151–169. [Google Scholar] [CrossRef]
- Australian Rainfall during El Niño and La Niña Events. Available online: http://www.bom.gov.au/climate/history/enso/ (accessed on 10 August 2022).
- Polonsky, A.-T.; Anton, T.I. The IOD–ENSO Interaction: The Role of the Indian Ocean Current’s System. Atmosphere 2021, 12, 1662. [Google Scholar] [CrossRef]
- Fogt, R.L.; Marshall, G.J. The Southern Annular Mode: Variability, trends, and climate impacts across the Southern Hemisphere. WIREs Clim. Change 2020, 11, e652. [Google Scholar] [CrossRef]
- Marshall, G.J. Trends in the Southern Annular Mode from Observations and Reanalyses. J. Clim. 2003, 16, 4134–4143. [Google Scholar] [CrossRef]
- Hendon, H.H.; Thompson, D.W.J.; Wheeler, M.C. Australian Rainfall and Surface Temperature Variations Associated with the Southern Hemisphere Annular Mode. J. Clim. 2007, 20, 2452–2467. [Google Scholar] [CrossRef]
- Bureau of Meteorology. (2019, December 6). Southern Annular Mode. Available online: http://www.bom.gov.au/watl/about-weather-and-climate/australian-climateinfluences.shtml?bookmark=sam (accessed on 9 October 2022).
- Ropelewski, C.F.; Jones, P.D. An Extension of the Tahiti–Darwin Southern Oscillation Index. Mon. Weather. Rev. 1987, 115, 2161–2165. [Google Scholar] [CrossRef]
- The three phases of the El Niño–Southern Oscillation (ENSO). Available online: http://www.bom.gov.au/climate/enso/history/ln-2010-12/three-phases-of-ENSO.shtml (accessed on 18 February 2023).
- Holton, J.R.; Hakim, G.J. Chapter 11—Tropical Dynamics. In An Introduction to Dynamic Meteorology, 5th ed.; Holton, J.R., Hakim, G.J., Eds.; Academic Press: Cambridge, MA, USA, 2013; pp. 377–411. [Google Scholar] [CrossRef]
- Lebassi-Habtezion, B.; González, J.; Bornstein, R. Modeled large-scale warming impacts on summer California coastal-cooling trends. J. Geophys. Res. 2011, 116, D20114. [Google Scholar] [CrossRef]
- Zhoua, Y.; Guana, H.; Huanga, C.; Lingli Fana, L.; Saeedeh Ghariba, S.; Batelaana, O.; Simmons, C. Sea breeze cooling capacity and its influencing factors in a coastal city. Build. Environ. 2019, 166, 106408. [Google Scholar] [CrossRef]



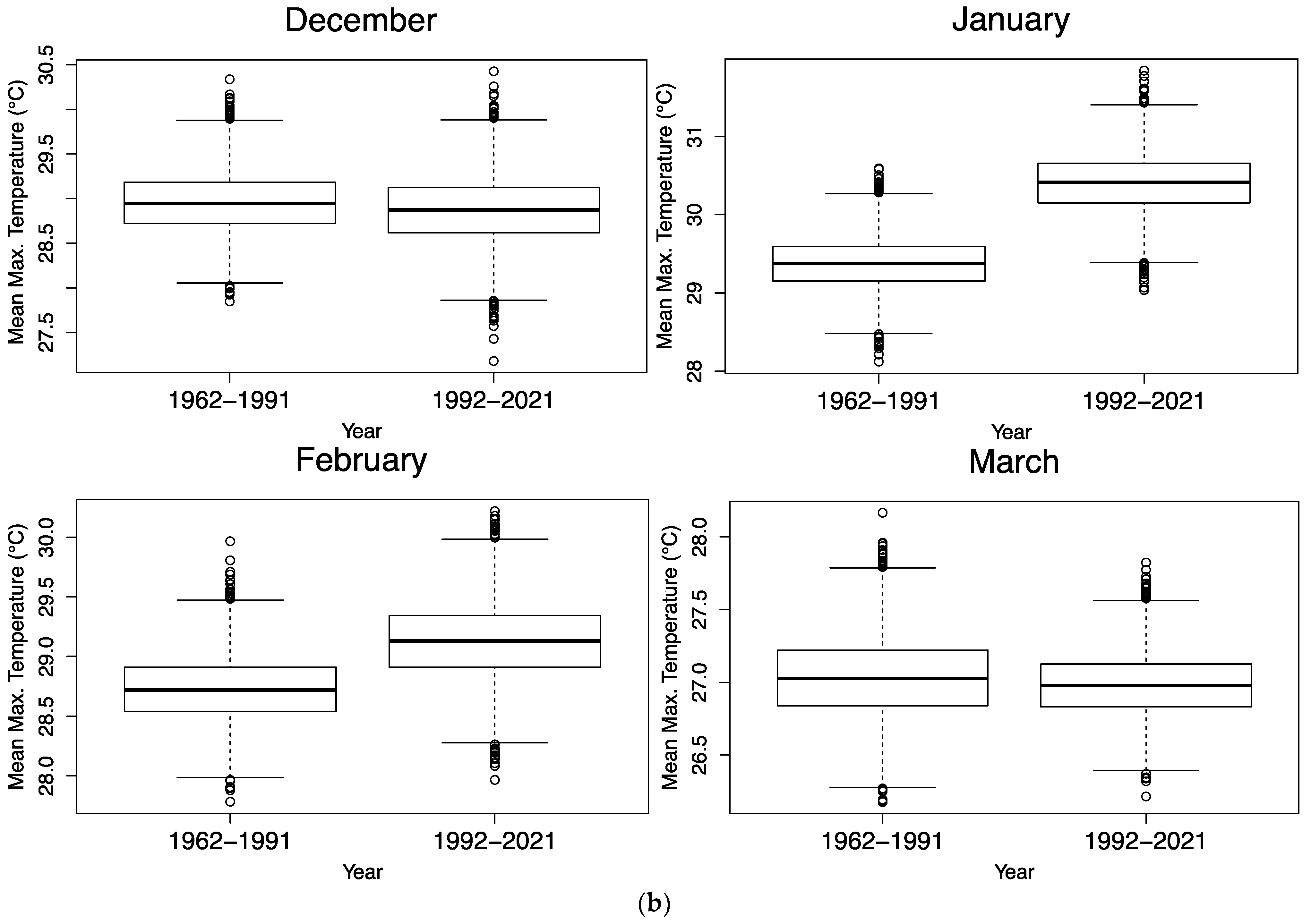


| Mean | Median | Variance | 25th Percentile | 90th Percentile | ||
|---|---|---|---|---|---|---|
| Sydney | December | 0.5674 | 0.2254 | 0.6450 | 0.8470 | 0.7654 |
| January | 0.0066 | 0.0024 | 0.4996 | 0.0340 | 0.0316 | |
| February | 0.0490 | 0.0138 | 0.1322 | 0.3262 | 0.0300 | |
| March | 0.0250 | 0.0112 | 0.2646 | 0.1962 | 0.0406 | |
| Richmond | December | 0.8598 | 0.5884 | 0.5222 | 0.6534 | 0.9114 |
| January | 0.0492 | 0.2642 | 0.6308 | 0.1414 | 0.0222 | |
| February | 0.3456 | 0.1578 | 0.3524 | 0.3748 | 0.6270 | |
| March | 0.8912 | 0.8142 | 0.2938 | 0.7790 | 0.6814 |
| Mean | Median | Variance | 25th Percentile | 90th Percentile | |
|---|---|---|---|---|---|
| Sydney | 0.0026 | 0.0054 | 0.0466 | 0.1686 | 0.0008 |
| Richmond | 0.2272 | 0.0870 | 0.1040 | 1.0000 | 0.1732 |
| 90th Percentile | 95th Percentile | ||
|---|---|---|---|
| SYDNEY | Mean | 0.9498 | 0.3476 |
| Median | 0.6086 | 0.2070 | |
| RICHMOND | Mean | 0.0728 | 0.2036 |
| Median | 0.2120 | 0.7924 |
| Period | Days Above 90th Percentile | Days Above 95th Percentile | |
|---|---|---|---|
| SYDNEY | 1962–1991 | 358 | 181 |
| 1992–2021 | 354 | 139 | |
| RICHMOND | 1962–1991 | 375 | 188 |
| 1992–2021 | 495 | 252 |
| ATTRIBUTES | LR F | SVM RBF F | SVM Poly F | RF F | LR B | SVM RBF B | SVM Poly B | RF B | Mean | Std Dev |
|---|---|---|---|---|---|---|---|---|---|---|
| DMI | 92 | 46 | 69 | 41 | 74 | 21 | 38 | 77 | 57.37 | 24.32 |
| GlobalSSTA | 10 | 59 | 77 | 51 | 38 | 21 | 44 | 77 | 47.12 | 24.17 |
| GlobalT | 51 | 54 | 77 | 33 | 36 | 26 | 49 | 62 | 48.40 | 16.59 |
| Niño3.4 | 21 | 64 | 67 | 49 | 51 | 31 | 56 | 74 | 51.60 | 18.26 |
| SAM | 8 | 44 | 72 | 49 | 21 | 15 | 46 | 90 | 42.95 | 28.21 |
| SOI | 46 | 49 | 64 | 51 | 13 | 28 | 51 | 85 | 48.40 | 21.56 |
| TSSSTA | 31 | 64 | 72 | 54 | 77 | 15 | 62 | 97 | 58.97 | 25.97 |
| DMI * GlobalSSTA | 33 | 49 | 49 | 31 | 51 | 23 | 33 | 74 | 42.95 | 16.26 |
| DMI * GlobalT | 36 | 38 | 46 | 38 | 77 | 18 | 36 | 64 | 44.23 | 18.38 |
| DMI * Niño3.4 | 38 | 46 | 69 | 49 | 18 | 21 | 49 | 85 | 46.79 | 22.47 |
| DMI * SAM | 0 | 33 | 69 | 46 | 18 | 10 | 46 | 82 | 38.14 | 28.50 |
| DMI * SOI | 18 | 54 | 67 | 46 | 36 | 62 | 51 | 87 | 52.56 | 20.70 |
| DMI * TSSST | 3 | 54 | 62 | 49 | 44 | 33 | 44 | 87 | 46.79 | 24.08 |
| GlobalSSTA * GlobalT | 21 | 36 | 59 | 44 | 33 | 33 | 49 | 79 | 44.23 | 18.32 |
| GlobalSSTA * Niño3.4 | 33 | 44 | 59 | 38 | 33 | 41 | 64 | 79 | 49.04 | 16.70 |
| GlobalSSTA * SAM | 13 | 38 | 44 | 46 | 15 | 33 | 44 | 85 | 39.74 | 22.18 |
| GlobalSSTA * SOI | 26 | 44 | 64 | 41 | 23 | 44 | 69 | 82 | 49.04 | 20.94 |
| GlobalSSTA * TSSSTA | 13 | 59 | 62 | 64 | 46 | 28 | 38 | 95 | 50.64 | 25.15 |
| GlobalT * Niño3.4 | 51 | 38 | 51 | 41 | 26 | 54 | 56 | 64 | 47.76 | 12.10 |
| GlobalT * SAM | 41 | 38 | 54 | 36 | 56 | 62 | 56 | 85 | 53.53 | 15.77 |
| GlobalT * SOI | 49 | 41 | 41 | 36 | 8 | 41 | 41 | 77 | 41.67 | 18.83 |
| GlobalT * TSSSTA | 64 | 67 | 49 | 59 | 5 | 59 | 59 | 92 | 56.73 | 24.38 |
| Niño3.4 * SAM | 18 | 38 | 41 | 46 | 15 | 15 | 62 | 82 | 39.74 | 23.82 |
| Niño3.4 * SOI | 31 | 62 | 72 | 51 | 10 | 54 | 72 | 87 | 54.81 | 24.63 |
| Niño3.4 * TSSSTA | 13 | 49 | 56 | 49 | 21 | 21 | 64 | 87 | 44.87 | 25.46 |
| SAM * SOI | 46 | 44 | 56 | 51 | 44 | 41 | 64 | 90 | 54.49 | 16.20 |
| SAM * TSSSTA | 87 | 41 | 67 | 54 | 3 | 15 | 67 | 82 | 51.92 | 30.42 |
| SOI * TSSSTA | 8 | 54 | 64 | 59 | 8 | 33 | 64 | 82 | 46.47 | 27.46 |
| Mean | 32.14 | 48.08 | 60.62 | 46.52 | 32.14 | 32.05 | 52.66 | 81.78 | ||
| Std Dev | 23.28 | 9.48 | 10.54 | 7.98 | 21.65 | 15.23 | 10.84 | 8.67 |
| ATTRIBUTES | LR F | SVM RBF F | SVM Poly F | RF F | LR B | SVM RBF B | SVM Poly B | RF B | Mean | Std Dev |
|---|---|---|---|---|---|---|---|---|---|---|
| DMI | 100 | 62 | 64 | 36 | 62 | 46 | 54 | 79 | 62.82 | 19.81 |
| GlobalSSTA | 21 | 49 | 67 | 44 | 26 | 28 | 38 | 77 | 43.59 | 19.96 |
| GlobalT | 41 | 41 | 51 | 41 | 31 | 18 | 41 | 74 | 42.31 | 16.22 |
| Niño3.4 | 79 | 62 | 69 | 46 | 46 | 31 | 56 | 82 | 58.97 | 17.71 |
| SAM | 23 | 56 | 67 | 44 | 23 | 8 | 49 | 79 | 43.59 | 24.33 |
| SOI | 21 | 56 | 64 | 31 | 31 | 28 | 46 | 72 | 43.59 | 18.84 |
| TSSSTA | 38 | 64 | 67 | 46 | 46 | 26 | 36 | 85 | 50.96 | 19.36 |
| DMI * GlobalSSTA | 62 | 72 | 62 | 41 | 44 | 23 | 59 | 56 | 52.24 | 15.44 |
| DMI * GlobalT | 59 | 59 | 51 | 44 | 59 | 23 | 36 | 77 | 50.96 | 16.59 |
| DMI * Niño3.4 | 13 | 62 | 72 | 36 | 18 | 28 | 46 | 92 | 45.83 | 27.67 |
| DMI * SAM | 18 | 62 | 64 | 44 | 21 | 5 | 44 | 87 | 42.95 | 27.54 |
| DMI * SOI | 13 | 59 | 54 | 36 | 33 | 64 | 49 | 82 | 48.72 | 21.28 |
| DMI * TSSST | 8 | 62 | 64 | 59 | 26 | 23 | 49 | 90 | 47.44 | 26.86 |
| GlobalSSTA * GlobalT | 21 | 51 | 41 | 49 | 41 | 31 | 56 | 79 | 46.15 | 17.71 |
| GlobalSSTA * Niño3.4 | 44 | 44 | 59 | 38 | 38 | 26 | 54 | 85 | 48.40 | 17.79 |
| GlobalSSTA * SAM | 3 | 46 | 64 | 41 | 41 | 28 | 59 | 85 | 45.83 | 24.61 |
| GlobalSSTA * SOI | 21 | 46 | 51 | 46 | 31 | 38 | 64 | 82 | 47.44 | 19.19 |
| GlobalSSTA * TSSSTA | 28 | 56 | 59 | 44 | 44 | 51 | 49 | 87 | 52.24 | 17.00 |
| GlobalT * Niño3.4 | 23 | 38 | 56 | 36 | 23 | 44 | 54 | 72 | 43.27 | 16.87 |
| GlobalT * SAM | 49 | 41 | 51 | 49 | 59 | 36 | 69 | 77 | 53.85 | 13.84 |
| GlobalT * SOI | 15 | 46 | 49 | 41 | 13 | 26 | 51 | 77 | 39.74 | 21.23 |
| GlobalT * TSSSTA | 46 | 38 | 59 | 44 | 10 | 31 | 46 | 85 | 44.87 | 21.45 |
| Niño3.4 * SAM | 28 | 44 | 62 | 41 | 38 | 18 | 44 | 82 | 44.55 | 19.72 |
| Niño3.4 * SOI | 36 | 62 | 56 | 54 | 15 | 38 | 72 | 92 | 53.21 | 23.61 |
| Niño3.4 * TSSSTA | 5 | 44 | 69 | 44 | 21 | 15 | 64 | 87 | 43.59 | 28.75 |
| SAM * SOI | 62 | 44 | 64 | 41 | 51 | 26 | 54 | 79 | 52.56 | 16.39 |
| SAM * TSSSTA | 15 | 72 | 62 | 54 | 0 | 46 | 56 | 79 | 48.08 | 27.30 |
| SOI * TSSSTA | 10 | 56 | 64 | 38 | 10 | 36 | 67 | 90 | 46.47 | 28.00 |
| Mean | 32.14 | 53.30 | 60.07 | 43.04 | 32.14 | 30.04 | 52.20 | 81.14 | ||
| Std Dev | 23.54 | 9.83 | 7.27 | 6.10 | 16.03 | 12.75 | 9.57 | 7.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bubathi, V.; Leslie, L.; Speer, M.; Hartigan, J.; Wang, J.; Gupta, A. Impact of Accelerated Climate Change on Maximum Temperature Differences between Western and Coastal Sydney. Climate 2023, 11, 76. https://doi.org/10.3390/cli11040076
Bubathi V, Leslie L, Speer M, Hartigan J, Wang J, Gupta A. Impact of Accelerated Climate Change on Maximum Temperature Differences between Western and Coastal Sydney. Climate. 2023; 11(4):76. https://doi.org/10.3390/cli11040076
Chicago/Turabian StyleBubathi, Varsha, Lance Leslie, Milton Speer, Joshua Hartigan, Joanna Wang, and Anjali Gupta. 2023. "Impact of Accelerated Climate Change on Maximum Temperature Differences between Western and Coastal Sydney" Climate 11, no. 4: 76. https://doi.org/10.3390/cli11040076
APA StyleBubathi, V., Leslie, L., Speer, M., Hartigan, J., Wang, J., & Gupta, A. (2023). Impact of Accelerated Climate Change on Maximum Temperature Differences between Western and Coastal Sydney. Climate, 11(4), 76. https://doi.org/10.3390/cli11040076







