Abstract
The complex dynamics of solar activity appear to be characterized by a number of oscillations ranging from monthly to multimillennial timescales, the most well-known of which being the 11-year Schwabe sunspot cycle. Solar oscillations are important because they also characterize the oscillations observed in Earth’s climate and can thus be used to explain and forecast climate changes. Thus, it is important to investigate the physical origin of solar oscillations. There appear to be two possibilities: either the oscillations in solar activity are exclusively controlled by internal solar dynamo mechanisms, or the solar dynamo is partially synchronized to planetary frequencies by planetary forcings. The latter concept has recently gained support from a growing amount of evidence. In this work, we provide an overview of the many empirical facts that would support a planetary hypothesis of the variability of solar activity and emphasize their importance for climate research. We show that the frequencies produced by the complex interactions of all of the planets are coherent with the major solar activity and climate cycles, from monthly to multimillennial timescales, including the well-known Schwabe 11-year solar cycle. We provide some persuasive theoretical and empirical support for the planetary hypothesis of solar and climate variability.
1. Introduction
Throughout its 4.7-billion-year history, the Earth has seen significant climate changes. For example, throughout the Phanerozoic period, that is, the last 600,000 years, the global surface temperature oscillated between ice ages, with temperatures up to 5 °C below 20th-century temperatures, and hot eras, with temperatures up to 14 °C above current temperatures. Natural climate changes have occurred at all timescales. So far, comprehending the natural forcings that drive climate changes remains a contentious issue due to a lack of physical understanding of the various involved phenomena. Yet, most of this variability appears to be tied to a wide number of astronomical and solar factors, many of which exhibit various sorts of cyclical behavior. The lack of accurate representation of such forcings in climate models, particularly those responsible for the decadal to millennial oscillations, has a significant impact on climate science and projections for the future decades and centuries and, therefore, this issue must be thoroughly examined.
Figure 1 shows a composite of temperature records from the Phanerozoic up to 2015 AD with a schematic spectrum of its climate variance at several timescales [1]. The figure divides the main known periodicities into three main timescales: (a) the galactic periodicities, such as those at about 150 [2,3] and 32 millions years [4], which appear to be due to the solar system’s trajectory around the Galaxy, where it moves through its spiral arms and its vertical oscillation with respect to the galactic plane, respectively; (b) the Milankovitch cycles associated with the astronomical orbital forcings that are related to variations in the eccentricity of the Earth’s orbit (100,000 and 400,000 years), of the Earth’s axial tilt (41,000 years), and of the axial precession (21,000–26,000 years) [5]; and (c) the cycles ranging from decadal to multimillennial scales, which are likely related to solar activity variability cycles such as the 2100–2500-year Bray–Hallstatt cycle, the 1000-year Eddy cycle, the 170–240-year Jose and Suess–de Vries cycles, the secular Gleissberg cycles, and others [6,7]. The interannual timescale oscillations (e.g., the El Niño–Southern Oscillations) are typically associate with the so-called internal variability of the climate system, but they too may have a solar or astronomical origin because there are very similar interannual solar and orbital oscillations as well [8,9,10,11]. Moreover, climate data also present long decadal and multidecadal soli-lunar tidal cycles [12]. Climate change is once again associated to the intensity of cosmic ray fluxes on billion-year timeframes [13].
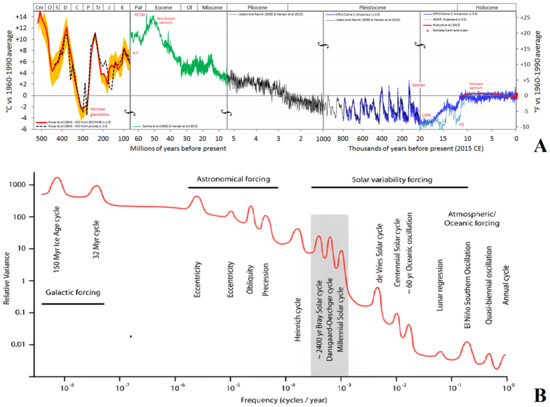
Figure 1.
(A) Composite of global average surface air temperature records over the 540 million years of the Phanerozoic up to 2015 AD (adapted from http://gergs.net/all_palaeotemps/ accessed on 24 March 2023, using data from Refs. [14,15,16,17,18,19,20,21]). (B) Schematic spectrum of the climate variance at multiple timescales (adapted from Vinós [1]).
It is worth noting that the link between atmospheric CO2 content and global temperature has been fairly poor throughout the last 600 million years [2,22,23]. CO2 concentration, for example, has also lagged for centuries behind temperatures during deglaciation and glaciation periods, as occurred during the last 420,000 years, as shown in the Vostok ice core record [24]; although, if the data are processed in some way and some specific places are analyzed, the two variables appears much more tightly coupled [20,25]. Hence, carbon dioxide cannot have typically been the primary driver of climate changes for nearly all of Earth’s history, but rather, it worked as one of the climate (positive) feedback mechanisms in response to solar, astronomical, orbital, and other natural forcings, although it was likely less important than water vapor and clouds. In fact, the atmospheric CO2 concentration significantly depends on the surface temperature of the oceans and on the status of the biosphere, although it might also be suddenly altered by volcanic activity.
This review complements another recent review from the same authors [26] by focusing on the impact on climate change produced by solar activity variability cycles. These cycles account for most of the decadal to multimillennial climatic variability across the Holocene. We show that these variations appear to be linked to orbital planetary oscillations, thus making the solar activity and climate changes theoretically predictable.
2. Overview of the Planetary Hypothesis of the Origin of Solar Activity Cycles
The hypothesis of the planetary origin of the 11-year sunspot cycle was first put forward when Wolf [27] suggested that “the fluctuations of spot-frequency rely on the influences of Venus, Earth, Jupiter, and Saturn”. A small number of scientists supported the planetary hypothesis of solar activity oscillations during the 20th century [28,29,30], but, during the last 15 years, this interest has grown significantly, leading to an increasing number of publications [31]. Recently, Scafetta and Bianchini [26] offered an extended review that was largely based on Scafetta’s prior work. The planetary origin of solar activity oscillations is not restricted to the 11-year solar cycle but includes all major solar oscillations on timescales ranging from monthly to multimillennial. Although the physical mechanisms explaining how the Sun may be modulating climate change are still debated (e.g., there are proposals of additional solar-related forcings [2,3] as well as of complex dynamical responses of the climate system to insolation variability [32,33]), the fact that the Earth’s temperature and the solar records display common oscillations throughout the Holocene has substantial implications for climate science [7,34,35,36,37,38,39,40,41,42,43,44,45]. Indeed, numerous criteria show that solar variability is driven by planetary beats that also affect a variety of terrestrial variables, including 14C and 10Be production, Earth’s rotation, ocean circulation, paleoclimate, geomagnetism, and so on [46].
At the moment, there are just two main hypotheses regarding the origin of solar oscillations. One idea is that solar activity changes are controlled solely by the solar dynamo mechanisms (let us call it the “reductionist” hypothesis). The second possibility is that the solar dynamo itself is partially synchronized by external harmonic planetary forcings, such as tides or other possible mechanisms (let us call it the “holistic” hypothesis). The debate is still ongoing since the physics of solar activity changes is still poorly understood. However, we think that the arguments for a planetary synchronized solar dynamo concept should be better investigated because they could be the key to understand both solar activity and climate oscillations.
In recent years, there has been increasing interest in the concept that planets can influence solar activity [31,47]. We believe that this approach could yield the development of methodologies useful for long-time-range solar activity forecasts, similarly to how ocean tides are currently predicted using harmonic constituent models. This research should also have an impact on space weather and climate change forecasting [12,37,48]. We also address several frequent critiques of the planetary hypothesis of solar and climatic variability.
One of the primary objectives of this research is to find repeating patterns and harmonics in solar activity records that could be linked to planetary harmonics. The frequency and phase of planetary harmonics is compared with solar activity records. However, the amplitude of the secular solar activity changes cannot be determined by the planetary harmonics. Actually, the scientific literature is still hotly debating the precise amplitude of the secular solar activity changes.
Numerous total solar irradiance (TSI) proxy models have been proposed [38,42,49,50,51,52,53,54,55,56], which greatly differ from each other regarding the amplitude of the solar activity secular changes. For example, the TSI rise from the Maunder Minimum to the minimum of solar cycle 24 (2008–2019) varies from 0.75 W/m to 6.3 W/m according to the proposed TSI proxy model. Some models show a very limited range of secular variability [38,50,51,52,56], while other models show a much larger secular variability [42,49,54,55]. Yeo et al. [57] claimed that the dimmest state of the Sun cannot be below 2 W/m. However, Schmutz [58] objected that a too low TSI secular variability would poorly explain the good correlations found between paleoclimatic and solar records during the Holocene.
The fact that all TSI proxy models indicate simultaneous, albeit not identical, multidecadal periods of low and high solar activity is a key aspect. Secular/bisecular large oscillations, for example, have been observed. The grand minima of these solar activity cycles throughout the last millennium are named Oort, Wolf, Spörer, Maunder, and Dalton. There are other millennial oscillations known as Eddy cycles, as well as multimillennial oscillations, such as the Bray–Hallstatt cycles, which last roughly 2100–2500 years [37,38,53,59,60]. Similar oscillations are also found in climate records [38,39,41,42,60,61,62]. The origin of solar activity oscillations is unknown, but the phenomenon could be due to complex patterns generated by the interference of several oscillations, which could be possibly linked to planetary harmonics. If this is so, a planetary model of solar activity changes could be empirically adopted to hindcast and forecast them.
There are also shorter multidecadal oscillations, such as quasi-45-, 60-, and 80–100-year solar activity oscillations [34,35]. Some of them might already be confirmed using the TSI satellite data, available since 1978. However, even here there are uncertainties.
In fact, TSI satellite measurements started in 1978, and their composites are rather controversial [63,64,65,66,67]. A major issue that has not been solved yet is whether from 1980 to 2000 TSI increased, as the ACRIM TSI satellite composite indicates [63], or slightly decreased, as the PMOD composite suggests [64]; see Figure 2. This debate has been detailed in Scafetta and Willson [68] and Scafetta et al. [65]. These works showed evidences supporting the TSI increase from 1980 to 2000 and its slight decrease afterward. Actually, they critiqued a number of TSI proxy models that suggest a low secular TSI variability [56,69,70].
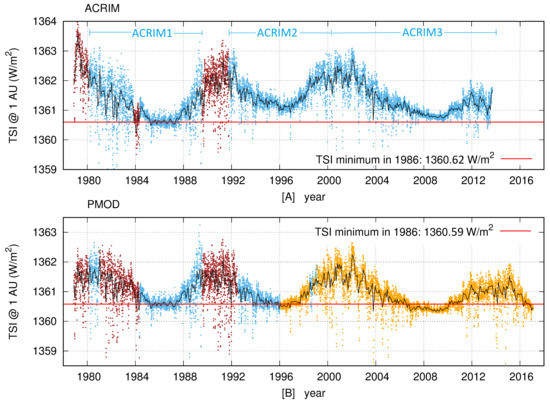
Figure 2.
(A) ACRIM TSI satellite composite [63,68]. (B) PMOD TSI satellite composite [64]. ACRIM 1, 2, and 3 (cyan); Nimbus7/ERB (brown); and TIM-SORCE (orange).
If solar activity changes are partially controlled by planetary harmonics, for example, through tides, a planetary model could help in solving the TSI satellite composite controversy between ACRIM and PMOD. Solving this controversy is rather important for both solar and climate change studies. In fact, the current global climate models (GCMs) adopt a solar forcing derived from TSI proxy models with low secular variability, which match the PMOD TSI satellite composite decreasing trend from 1980–2020 [71]. If, on the other hand, TSI grew from 1980 to 2000, as suggested by the ACRIM TSI satellite composite, the solar contribution to climate change should properly evaluated [72,73].
3. Empirical Evidences for the Planetary Origin of Solar and Climate Variability Cycles
Several academics have recently investigated the idea that the planets of the solar system might have an impact on solar activity since, especially over the last 15 years, more and more scientific data have been discovered to support this hypothesis. Many of these findings were examined by Scafetta and Bianchini [26]. Let us now overview the most supporting evidences.
Section 3.1 demonstrates that realistic tidal models predict a tidal cycle of 10–12 years, which corresponds to the observed Schwabe 11-year sunspot cycle. Section 3.2 provides additional data in support of a planetary synchronized solar dynamo hypothesis.
3.1. The Venus–Earth–Jupiter–Saturn Model for the Schwabe 11-Year Solar-Activity Cycle
Since the second half of the 19th century, it has been clear that complex combinations of several planets should have been examined in order to find a potential connection between solar activity and planetary motion. Admittedly, all the planets should influence the Sun concurrently. However, according to Wolf [27], the quartet Venus, Earth, Jupiter, and Saturn had to be the basis of any minimal model that could account for the 11-year solar cycle. In fact, single-planet models are ineffective. For example, due to its eccentric orbit, Jupiter would produce a tidal oscillation of 11.86 years, but this period is too long to suit the 11-year sunspot cycle, albeit fortuitous correlations may appear during certain time intervals.
Wolf’s hypothesis was based on the observation that the planetary order of the relative tidal significance is Jupiter, Venus, Earth, Mercury, Saturn, Mars, Uranus, and Neptune [74]. Mercury, on the other hand, appeared to move too quickly, whereas Mars, Uranus, and Neptune seemed to be less important because their tides are much weaker than those of the other planets. Wolf’s suggestion of the planets Venus, Earth, Jupiter, and Saturn as a potentially working quartet made sense. Some authors even focused on an even more constrained planetary collection that only consists of Venus, Earth, and Jupiter, which are the first three planets with the largest tidal influence, but, as we argue below, this triplet appears to be too reductive.
In any case, rudimentary versions of the Venus–Earth–Jupiter triple syzygies tidal alignment model had already been proposed over a century ago [28,29,75]. More recently, various complex variants of the same model were developed [74,76,77,78,79,80,81,82,83]. The general conjecture on which these models are based is that the smaller the difference in days between the conjunctions/oppositions of Jupiter and Venus with Earth and the Sun, the greater the action they exerted on the Sun. The planetary functions created by these models appear to be tightly associated with the 11-year sunspot cycle from 1700 to the present; see Figure 3.
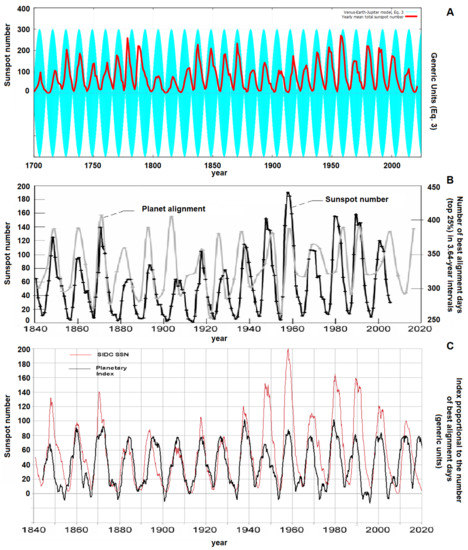
Figure 3.
(A) The Venus–Earth–Jupiter model, Equation (3), plotted against the average annual number of sunspots from 1700 to 2021. (B) Hung [76]’s model. (C) Tattersall [82]’s model. From Scafetta [84].
Scafetta [74] demonstrated that the principal recurrent period of the Venus, Earth, and Jupiter triple-syzygies tidal alignment model is given by the invariant inequality
where days, days, and days are the sidereal orbital periods of Venus, Earth, and Jupiter, respectively. Equation (1) can be also rewritten as
which has significant mathematical properties, because can be interpreted as the complex beat function between the third harmonic of the Venus–Earth synodic cycle ( year, year) and the second harmonic of the Earth–Jupiter synodic cycle ( year).
The factor 1/2 in Equation (1) transforms synodic cycles into tidal cycles. Therefore, Equation (2) can also be interpreted as the spring beat period between the Venus–Earth synodic period () and the beat between the spring tide between Venus and Earth ( year) and the spring tide between Earth and Jupiter ( year). Table 1 reports the spring periods of all planet pairs.

Table 1.
Spring tidal periods, , of pairs of the planets in (up) days and (down) years. The most relevant ones are in bold.
Equation (1) is also an important example of orbital invariant inequality, which is the orbital resonance characterized by the property of being invariant with respect to any rotating system. This property should be physically necessary for synchronizing the solar dynamo, which is generated by the differential rotation of the Sun [7].
The tidal beats of Equation (1) can be simulated by the function
where and are epochs of one Venus–Earth conjunction and one Earth–Jupiter conjunction, respectively. The cosine function is used to predict the spring tidal maxima during the conjunction epochs for each spring tide. As a result, Equation (3) is entirely based on astronomical data.
Figure 3A compares Equation (3) with the annual sunspots number from 1700 to 2021. The graphic demonstrates that there is good timing between the sunspot cycle and the 11.07-year Venus–Earth–Jupiter alignment beats. In essence, it seems that more sunspots form when the three planets are more often closely aligned, which is when their tides can more forcefully twist the tachocline and affect the solar dynamo. Figure 3B,C demonstrates that different approaches of the Venus, Earth, and Jupiter triple-syzygies model are as effective at predicting both the timing and the frequency of the sunspot cycles across centuries [76,82].
We notice that without the 1/2 factor in Equation (1), the major period of the Venus, Earth, and Jupiter triple-syzygies alignments would be 22.14 years, which corresponds to the 22-year Hale solar magnetic cycle [83].
A realistic, although simplistic, tidal function can be written as
where is the planet’s average distance from the Sun, is its mass, days is the solar rotation period, and is the orbital period of the planet P. Moreover, and are the aphelion distance and one of its occurrence epochs, respectively, whereas is the angular distance of the planet P from Jupiter on 1 January 2000 at 00:00. The planetary data are reported in Table 2.

Table 2.
The planetary orbital data. From https://nssdc.gsfc.nasa.gov/planetary/factsheet/ accessed on 24 March 2023.
Scafetta [74] pointed out that what physically matters is the power dissipated by the tides inside the Sun, i.e., their work done in a time unit, which is proportional to the following function
Equation (5) is proportional to the tidal power dissipated inside the Sun. Scafetta [74] hypothesized that the fraction of the dissipated power in the solar core would trigger an increase and a modulation of its luminosity production. Actually, Equation (4) approximates the full luminosity-tidal equation proposed by Scafetta [74], which was given as
which is similar to Equations (4) and (5) but uses the actual ephemeris coordinates of all eight planets from Mercury to Neptune. Moreover, the tidal function is integrated from the solar core to the surface, and an amplification factor is introduced to take into account the H-burning rate increase due to the tidal gravitational power dissipated in the solar core, as suggested by Scafetta [74]. The original paper explains the various parameters and functions of Equation (6), which are , the distance of a planet from the Sun; , the mass of the planet P; , the angles denoting the location of the planet P relative to the angular position on the Sun; , the effective tidal dissipation factor; , the radius of the Sun; , the integration time interval, which is set to 1 day; , the function for converting gravitational power into TSI at 1 AU from the Sun; , the solar density function; , the normalized distance from the Sun’s center; and G, the universal gravitational constant.
Figure 4A depicts the function (Equation (5)) with only Jupiter and Saturn as inputs. A quasi-11.86-year oscillation is observed, which is tied to Jupiter’s orbital period, because its distance from the Sun varies between the aphelion and the perihelion. Yet, the year neap–spring tidal cycle between Jupiter and Saturn also influences such oscillations. As a result, at the decadal timeframe, the tidal signal is clearly defined by two cycles with durations of 9.93 and 11.86 years, with an average length of close to 11 years. The figure also shows a clear beat with a period of about 60 years, whose maxima occurred in 1940–1950 and 2000–2010, which correspond to the maxima of a quasi- 60-year oscillation observed in global surface temperature and other climatic records [37,85]. Figure 4B uses Wolf [27]’s planetary quartet to illustrate the function using Venus, Earth, Jupiter, and Saturn. The synthetic data clearly show the same 10–12-year oscillation. Once again, Figure 4C demonstrates that the patterns of quick tidal changes recur every 11 years. Figure 4D shows the hypothetical brightness signal produced by all planetary tides estimated by Scafetta [74] using Equation (6).
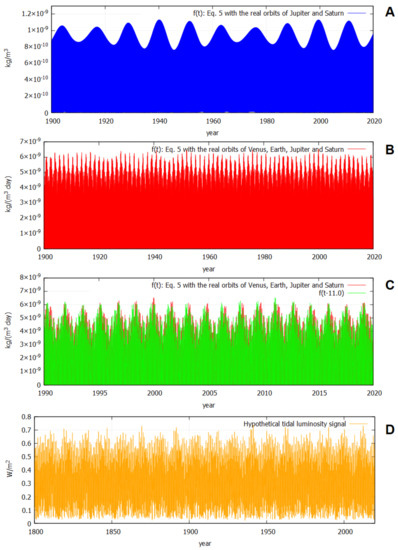
Figure 5 compares the power spectra of the tidal function shown in Figure 4B using Venus, Earth, Jupiter, and Saturn and of the tidally induced luminosity function (Equation (6)), using all the planets derived by Scafetta [74] and depicted in Figure 4D.
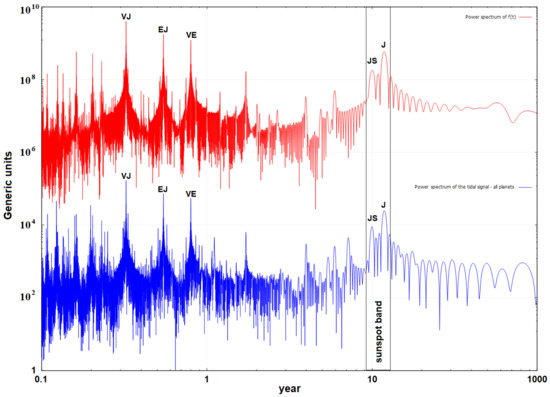
The two power spectra share a number of harmonics, particularly the planets’ neap–spring tides. The power spectrum clearly increases between 9 and 13 years because of the clustering of the 9.93-year neap–spring tidal cycle between Jupiter and Saturn and the 11.86-year tidal oscillation associated with the elliptic orbit of Jupiter. The neap–spring Jupiter–Saturn tidal oscillation is approximately three times smaller than Jupiter’s orbital tidal cycle, which allows the two tidal cycles to produce complex beats. The measured Schwabe cycle spectral band fits the two tidal cycles well. As a result, using the real orbits of Jupiter and Saturn is critical for appropriately connecting the planetary tidal power spectrum to the 11-year sunspot cycle. The result clearly refutes the assertion by Okal and Anderson [86] and Nataf [87] that there is no proof for a periodicity close to 11 years in the tidal functions [84].
Scafetta [37,74] showed that the 11-year sunspot cycle is actually composed of three closely spaced frequencies. In fact, the presence of the two tidal frequencies with periods at about 10 and 12 years implies that the Schwabe cycle could be characterized by a primary spectral peak close to 11 years (which could be generated by the primary synchronization of the solar dynamo), surrounded by two minor spectral peaks at about 9.93 and 11.86 years, which correspond to and . This prediction is confirmed in Figure 6A, which shows several power spectra of different sunspot number records and suggests that the solar dynamo could be actually controlled by the neap–spring tide between Jupiter and Saturn and the tidal oscillation associated with Jupiter’s eccentric orbit, because the two frequencies appear at the left and the right side of the main 11-year spectral peak. The same result was obtained also by other authors, such as by Tan and Cheng [88].
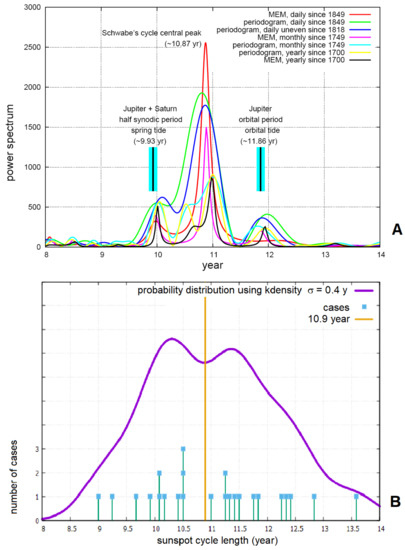
Figure 6.
(A) Sunspot record power spectra. Adapted from Scafetta [89]. (B) Bimodal distribution of the solar cycle lengths. Updated from Scafetta [37].
Scafetta [74] corroborated this conclusion by also showing that the distribution of the solar cycle lengths is bimodal instead of being a simple Gaussian centered at 11 years. In fact, of the 23 solar cycles that were examined between February 1755 and December 2008, 11 of them had a period between 9.0 and 10.5 years, with an average of years (which optimally corresponds to the period of the Jupiter–Saturn neap–spring tide), and 12 of them had a period between 11.25 and 13.6 years, with an average of years. No sunspot cycle length was recorded with a period larger than 10.5 years or smaller than 11.25 years. To date, solar cycle #24 from December 2008 to December 2019 is the only “Schwabe 11-year solar cycle” to have lasted exactly 11 years. This cycle should be included in the second list of the longer cycles, because the mean between and is about 10.9 years. Thus, including this last cycle, the average of the 13 solar cycle lengths larger than 10.9 years is years, which agrees well with the tidal period associated with the orbit of Jupiter. This result supports the hypothesis that two physical attractors operating at the periodicities of the Jupiter–Saturn neap–spring tide ( years) and of the Jupiter tide ( years) could be responsible for the apparent dynamics of the sunspot cycle. Figure 6B shows the likely bimodality of the distribution of the solar cycle lengths, because two peaks appear on the left and right side of the 10.9-year period. The depicted distribution function was obtained using a smooth k-density function with a bandwidth of years, estimated by averaging the default bandwidth (, with being the standard deviation of N samples) for the two sets under the hypothesis that the distribution is bimodal. Table 3 reports the main characteristics of the 24 solar cycles from 1755 to 2019.

Table 3.
Sunspot cycle data.
Scafetta [37] provided even additional confirmation of this finding by showing that a three-frequency model based on the two tidal harmonics produced by Jupiter and Saturn hindcast a number of traits found in long solar data throughout the Holocene; see Section 3.2.
Using Wolf [27]’s planetary set, the five strongest tidal spectral peaks are , , , , and , as shown in Figure 5. The periodicities and fit the Schwabe 11-year sunspot cycle perfectly. Let us now discuss the key physical property associated with the Venus–Earth–Jupiter triple-syzygies tidal alignment paradigm, which is based on the other three spring tidal harmonics: , , and .
The high-frequency, which is connected with the spring tides between Venus and Jupiter ( 0.3244 year), Venus and Earth ( 0.7993 year), and Earth and Jupiter ( 0.5460 year), shows periodic patterns. The main patterns can be identified by looking for combinations of integers , and , such that
and such that recurrence times are as close as possible to each other The three best combinations are years, years, and years. The best centered combination between and is . By averaging the latter combination of the three fast spring tides among Venus, Earth, and Jupiter, and the two tidal harmonics of Jupiter and Saturn, we obtain
We also found that the recurrent pattern years optimally fulfills the more general condition , when the integers are varied between 1 and 50. Interestingly, a quasi 10.4-year cycle is found in quite a number of climatic records [12,85] and even in meteorite fall records [90]. The beat between the 10.4-year recurrent tidal period and the spring tide between Jupiter and Saturn ( years) produces a fast beat periodicity of years. If this cycle beats with the Jupiter orbital period, a new periodicity is produce at year, which is very close to the central spectral peak of the the sunspot number record shown in Figure 6.
In conclusion, the five most important tides produced by Venus, Earth, Jupiter, and Saturn (, , , , and ) fit the whole spectral band of the Schwabe 11-year sunspot cycle. The above considerations show that the Schwabe 11-year solar cycle is caused by the combined influence of Venus, Earth, Jupiter, and Saturn on the Sun, as initially proposed by Wolf [27] in the 19th century.
3.2. Empirical Evidences for Planetary Control of Solar Variability across Several Timescales
The spectral compatibility of the tidal planetary models with an 11-year solar cycle is just the first piece of evidence supporting the planetary synchronized solar dynamo theory. There is a substantial body of data showing that the primary planetary frequencies do indeed characterize changes in solar activity at all timescales, from the monthly to the multimillennial ones.
The main planetary harmonics that could have a possible physical relevance are the orbital periods, spring tidal periods, synodic conjunction periods, and their combinations, which were labeled orbital invariant inequalities [7]. Here, we give a brief summary of what we consider to be the most important empirical findings supporting the planetary theory of solar activity changes.
3.2.1. Monthly to Annual Timescales
Bigg [91] discovered a minor but constant periodicity in the relative daily sunspot number records at the sidereal period of the planet Mercury, modified by Venus, Earth, and Jupiter. This author came to the conclusion that extrasolar factors could have an impact on the creation of sunspots.
The planetary tidal signal, as seen in Figure 5, is made of a number of quick oscillations that are mostly related to the spring tidal periods between pairs of planets (see Table 1). The most important ones are , , and , which, as we saw in Section 2, could be connected to the Schwabe 11-year solar cycle. Therefore, the question is whether the solar records show any evidence of these rapid tidal oscillations and/or of their corresponding synodic planetary oscillations, which have periods twice as long. Scafetta and Willson [92,93] presented a study in which numerous daily total solar irradiance (TSI) satellite records were compared with the spring and synodic periods of the planets from the monthly to yearly timescales. Figure 7 summarizes the key findings.
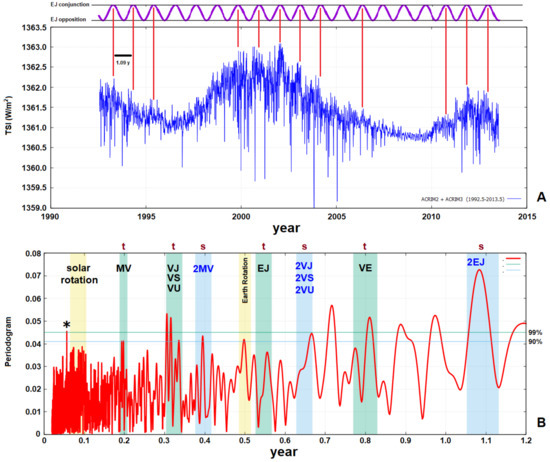
Figure 7.
(A) ACRIM TSI composite data from 1992.5 to 2013.5. The top shows the angular separation cycle between Earth and Jupiter. The red lines indicate planetary conjunctions (period of 1.09 years) when solar brightening occurs. (B) Periodogram of (A). The colored vertical boxes in (B) illustrate the primary anticipated planetary frequencies: the black pairs (t) represent the spring tidal periods, while the blue pairs (s) represent the synodic periods, which are twice as long as the tidal ones. See Table 1 [92,93]. The period labeled “∗” appears related to Mercury and the solar rotation.
Figure 7A shows the ACRIM TSI satellite composite for the years 1992.5 through 2013.5, which collects the data from ACRIM II and ACRIM III high-precision measurements. Here, the TSI record is preferred to other solar observables (such as the number of sunspots), because it is the most accurate and complete indicator of changes in solar activity. The ACRIM TSI composite was chosen above other TSI datasets due to its duration, for the perception of being more sensitive to minute TSI changes, and for being more accurate than other proposed satellite records [65,93]. Similar results were also obtained by using the PMOD/VIRGO TSI composite and SORCE/TIM TSI satellite record [92,93].
Figure 7B shows the periodogram of this TSI record. The colored vertical boxes in Figure 7B illustrate the predicted primary planetary frequencies; the black labels indicate the neap–spring tidal periods, while the blue labels indicate the planetary synodic periods. See Table 1 and References [92,93].
The figure shows that the TSI periodogram includes all of the primary spring and synodic planetary harmonics from monthly to the annual timescales. The prominent spectral peaks between 0.30 and 0.33 years refer to Venus’s spring tidal cycles with Jupiter, Saturn, Uranus, and Neptune; see Table 1. Other TSI spectral peaks are seen in the frequency range of 0.065–0.105 years, which corresponds to the differential solar rotation: close to Mercury and Venus’s spring tidal periods ( years), Earth and Jupiter ( years), and Venus and Earth ( years), as well as near the synodic cycles between Mercury and Venus ( years) and Earth and Jupiter ( years). A 0.5-year oscillation is also observed; this harmonic is most likely caused by the Earth’s orbit crossing the solar equatorial plane twice a year, as the solar luminosity depends on the Sun’s latitude. In fact, sunspots almost never appear below 5 or above 40, both in north and south latitudes.
Figure 7B also shows a significant TSI spectral peak with a period days. This period may be related to Mercury and to the solar rotation. In fact, assuming an average solar rotation of days (at about 45 latitude, [94]), its synodic cycle with Mercury ( days) would be days. Thus, the relative tide would have a period of about 20 days.
The 1.09-year oscillation is outstanding in the TSI record, particularly from 1998 to 2004, during the maximum of solar cycle 23. More specifically, it was discovered that TSI rises during the conjunction of Earth and Jupiter, that is, when the two planets are at their closest angular separation relative to the Sun (Figure 7A, top), as if the solar side facing Jupiter were slightly brighter so that the Earth can receive more light when it crosses the line connecting the Sun and Jupiter [92]. In fact, it has been discovered that stars with hot Jupiter-like planets exhibit a comparable hot spot brightening, albeit more intense. These brightenings are most likely caused by a direct magnetic contact between the planet and the stellar surface [95,96]. The finding is further supported by the existence of a near 13-month periodicity in the flux of cosmic rays, probably related to the Earth–Jupiter synodic cycle [97]. This result underlines the importance of looking into how the solar system’s space weather and interplanetary fluxes of particles are structured in relation to the relative positions of the planets.
3.2.2. Multidecadal to Millennial Timescales
A large number of scientific data indicate that the Sun’s activity is also characterized by a variety of unique oscillations that occur across timeframes ranging from decades to millennia. These periods seem to fall into distinct ranges. The most frequently documented solar oscillations cover the periods of 40–45 years, 55–65 years, 80–105 years (Gleissberg cycle), 115–150 years, 170–240 years (Jose and Suess–de Vries cycles), 800–1200 years (Eddy cycle), and 2000–2500 years (Bray–Hallstatt cycle) [35,59]. These oscillations fall into the major clusters created by the body of the planetary periods, as described by Scafetta and Bianchini [26] and their cited references. Let us now review the key findings.
(1) Scafetta [37] developed a multiscale harmonic solar and climatic model based on the Jupiter–Saturn neap–spring tidal oscillation, Jupiter’s orbital tidal oscillation, and a solar dynamo cycle that was hypothesized to have a period of 10.87 years (see Figure 6). Four primary beats with periods of years, years, years, and years result from the combination of the three cycles. The model successfully predicts all the major secular solar activity maxima and minima over the last millennium, including the Oort, Wolf, Spörer, Maunder, and Dalton grand solar minima (Figure 8A), which are approximately given by the quasi-115–130-year oscillation predicted by the model and are observed in all solar activity proxy records, including the 14C and 10Be radionucleotide [38,53]. The same model also predicts a quasi-1000-year oscillation, which has been well observed in detailed temperature reconstructions of the Northern Hemisphere over the last 2000 years (Figure 8B). Finally, Figure 8C compares the same solar harmonic model against a global surface temperature record from 1850 to 2010 [37], where a similar 60-year modulation plus a secular upward trend is observed. Figure 8C, which was published in 2012 by Scafetta [37], predicted an incoming grand solar minimum from 2015 to 2045, induced by the interference of the 115–130-year oscillation and the 60-year oscillation produced by the planetary model following the Maunder, the Dalton, the 1900–1920, and the 1970s grand solar minima. An alternative planetary model based on the Venus, Earth, and Jupiter tides did the same [98,99]. Courtillot et al. [100], still using planetary resonances, predicted the same modern solar minimum. Scafetta [37] also predicted a new solar maximum between 2050 and 2070, which would also coincide with the millennial solar cycle maximum. Indeed, Scafetta [37] predicted the incoming grand solar minimum from 2015 to 2045, also from the similitude of solar cycles 1–6 with the solar cycles 20–24. Scafetta [7] and Scafetta and Bianchini [26] observed that planetary resonances are not distributed randomly but rather cluster around specific frequency ranges. This could explain why different models based on planetary resonances can produce comparable findings.
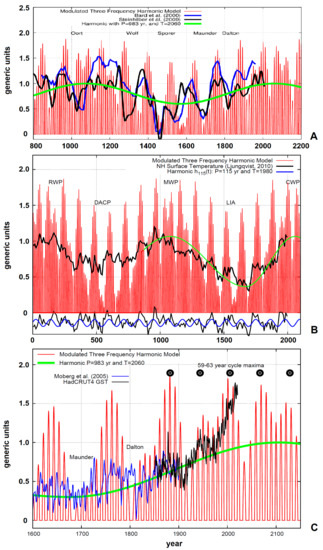
Figure 8.
(A) A comparison of the Jupiter–Saturn planetary three-frequency model (red) with two solar activity reconstructions based on cosmogenic isotopes of and cosmogenic isotopes [52,53]. (B) The identical model (red) overlaid over a reconstruction of the Northern Hemisphere’s proxy temperature [101]. (C) The same planetary–solar model (red) is displayed against the HadCRUT4 global surface temperature record (black) [102], which was combined in 1850–1900 with Moberg et al. [103] proxy model (blue). The green curves illustrate the skewness of the quasi-millennial oscillation, which approximates the millennial temperature oscillation from 1700 to 2013 [37,48]. The black dots represent the maxima of a quasi-60-year oscillation produced by the model and also observed in the climate records.
(2) During the course of the last 10,000 years (the Holocene), the quasi-millennial three-frequency beat cycle properly predicts the observed solar and climate millennial cycles [37,48]. Figure 9A shows a comparison between the TSI proxy model by Steinhilber et al. [52] (red) and the millennial oscillation indicated by the three-frequency planetary–solar model (blue) [37,48]. Figure 9B shows a quasi-millennial oscillation in the summer temperatures of the European Alps throughout the Holocene [104]. The millennial oscillation predicted by the planetary model appears to be well synchronized for 12,000 years with the temperature record. An exception is observed in the 5500–5000 BC time interval, which, however, could be due to a poor coverage of data, since the two peaks are clearly seen in the GISP2 ice core air temperature record of the Greenland Ice Sheet [105], as shown Figure 9C. Another discrepancy is seen in 1500–1000 BC in the phase shift between the GISP2 temperature peak and that of the model, which, however, is better reproduced by the alpine record. These discrepancies could be explained by chaotic climatic dynamics and by possible dating and measurement uncertainties.
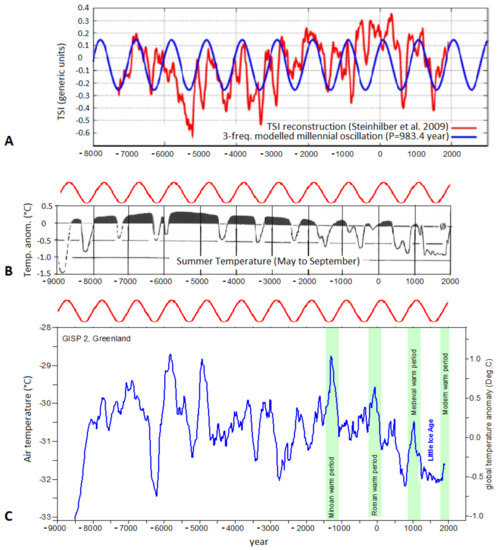
Figure 9.
(A) Steinhilber et al. [52]’s solar proxy model (red). (B) The quasi-millennial oscillation in the summer temperatures in the European Alps throughout the Holocene found by Kutschera et al. [104]. (C) Alley [105]’s reconstruction of the air temperature at the summit of the Greenland Ice Sheet from GISP2 ice core data. The millennial oscillation revealed by the three-frequency planetary–solar model is shown in blue in (A) and in red in (B,C) [37,48].
(3) Scafetta [48] demonstrated that the same planetary–solar three-frequency model also generates two sets of oscillations with periods of 57, 61, and 65 years and 103, 115, 130, and 150 years. The latter four periods, which control grand solar minima and maxima, were also identified in records of solar activity from 340,000 to 320,000 years ago. Thus, Scafetta [48] demonstrated that Cauquoin et al. [106] were wrong when they asserted that there was no evidence for a planetary modulation of solar activity around 330,000 years ago. The finding refuted the main claim by Smythe and Eddy [107] that planetary tidal models were unable to account for phenomena, such as the Maunder sunspot grand minimum, and also refutes critiques such as that all solar records from the secular to millennial range, with the exception of the Schwabe cycle, could be some kind of random fluctuation [108,109].
(4) Scafetta et al. [6] and Scafetta [7] specified that variations in solar activity on timescales ranging from multidecades to millennia are spectrally coherent with the orbital invariant inequalities generated by Jupiter, Saturn, Uranus, and Neptune. The orbital invariant inequalities are the beats among the planetary synodic cycles. In the differentially rotating Sun, these periodicities were shown to have mathematical features that could favor the setting of synchronized dynamics. The invariant inequality clusters have periods of 42–47, 55–65, 80–105 (the Gleissberg cycle), 160–185 (the Jose cycles), 200–240 (the Suess–de Vries cycles), 770–1160 (the Eddy cycle), and the Bray–Hallstatt cycle of 2000–2500 years [6,59]. The latter is accurately predicted by the invariant inequality produced by the beats between the synodic cycles of Saturn with Jupiter and Uranus and Neptune—the period being 2318 years. Figure 10 depicts the outcome. Figure 10A compares a solar () and a climate () record from 9500 and 6000 years ago (adapted from (Figure 5 in [34])). Figure 10B compares the orbital invariant inequalities of the solar system (red bars) determined by Scafetta [7], with the cross-spectral analysis peaks between the two records shown in Figure 10A. Finally, Figure 10C directly compares the invariant inequality oscillation (blue), whose phase is calculated by astronomical data only [7,110], with the (‰) record ([111], IntCal04.14c, black and red). In both cases, a perfect match between theoretical and experimental oscillations exists. These same cycles also emerge in the solar inertial motion [110,112,113,114]. The Bray–Hallstatt cycle of 2000–2500 years is observed in several solar [59,115,116] and climate records [6,117,118] as well. For example, the Greek Dark Ages (between 1000–550 B.C.) and the Little Ice Age (between about 1350–1850 A.D.) are well-established and historically confirmed colder periods of the Holocene, characterized by numerous historical climatic crises which occurred during the solar activity lows related to the Bray–Hallstatt cycle [116], as Figure 10C shows.
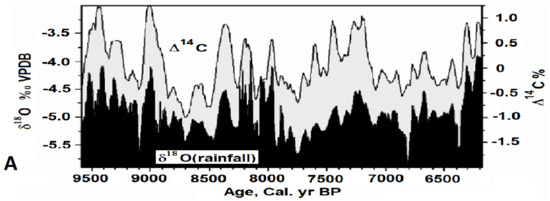
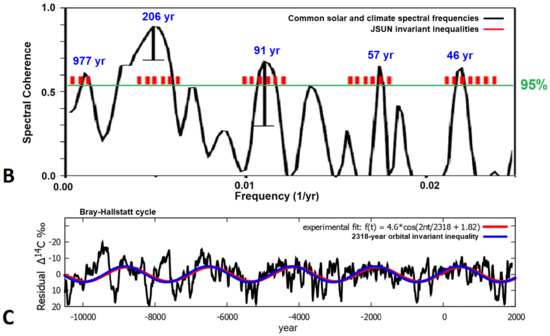
Figure 10.
(A,B) Comparison between the cross-spectral analysis peaks between solar () and climate () records from 9500 and 6000 years BP (adapted from Figure 5 in [34]) versus the orbital invariant inequalities of the solar system (red bars) calculated in Scafetta [7]. (C) The Bray–Hallstatt 2318-year orbital invariant inequality oscillation (blue) versus the residual of the (‰) ([111], IntCal04.14c) record (black and red) [6,7].
3.2.3. Miscellaneous Evidences
There are additional empirical evidences that support the planetary hypothesis of solar activity variations.
For example, Hung [76] discovered that at least 25 of the 38 biggest solar flares began when one or more of the planets—Mercury, Venus, Earth, or Jupiter—were either immediately above or just on the opposite side of the Sun. Bertolucci et al. [119] discovered a statistically significant increase in solar flares and EUV emission from 1976 to 2015 and 1999 to 2015, when one or more planets had heliocentric longitudes mostly between 230 and 300. They also found a link between total atmospheric electron content (TEC) and the orbital positions of the inner three planets from 1995 to 2012. Petrakou [120] discovered connections between solar flares and planetary harmonics as well.
Planetary harmonics were also discovered in aurora [121,122] and climate records [12,48]. Sharp [123] showed that several angular momentum perturbations on the Sun—mostly induced by Uranus and Neptune—coincide with the maxima observed in and solar proxy records during the Holocene. Similarly, McCracken et al. [115] suggested that solar activity is modulated by planetary harmonics, because the incoming cosmic ray flux intensity was found to be low when Uranus and Neptune were in superior conjunction and higher when they were in inferior conjunction. Moreover, excellent agreement was found by Abreu et al. [124] between the long-term cycles in solar activity proxies and the periodicities in the planetary torque acting on a hypothesized nonspherical tachocline at the base of the Sun’s convective zone. In particular, they found that some periodicities remained phase-locked for more than 9400 years. An alternative model of the Venus–Earth–Jupiter tidal torque was proposed by Wilson [83]. The Chandler wobble also exhibits harmonics of the Jovian planets [125].
In this overview, it is not possible to examine all of the empirical results suggesting that planetary motion affects solar activity. We acknowledge, however, that not all published results are equally credible: some may be dubious, and others may appear to be nothing more than coincidences and numerology. However, it should be acknowledged that there already is a substantial body of evidence in the scientific literature that strongly supports the planetary synchronized solar dynamo hypothesis. This mass of evidence must be seriously taken into consideration.
3.3. Evidences for Interannual and Multidecadal Planetary Periods in Global Surface Temperature Records
In the previous subsections, we have seen that planetary cycles characterize the variability observed in both solar and climate records (Figure 8, Figure 9 and Figure 10). Additional evidence for a signature of multiple planetary cycles from the interannual to the multidecadal scales in the global surface temperature records from 1850 to 2020 has been discussed in several studies [11,12,48,110,126].
Figure 11A,B compare the time–frequency analyses between the HadCRUT3 global surface record [127] and the speed of the Sun relative to the center of mass of the solar system. As first observed by Scafetta [48], and later confirmed by sophisticated spectral coherence investigations [110,126], the observed changes in global surface temperatures mirror multiple astronomical cycles at the decadal and multidecadal scales. The Sun’s speed has major spectral peaks at periods of 5.93, 6.62, 7.42, 9.93, 11.86, 13.8, 20, and 60 years. The majority of them are connected to Jupiter and Saturn’s orbits. The temperature record has major spectral peaks at periods of about 5.93, 6.62, 7.42, 9.1, 10.4, 13.8, 20, and 60 years. Therefore, the majority of the climate oscillations appear to match the astronomical cycles, with the exception of the 9.1- and 10.4-year cycles. Scafetta [12,128] argued that the 9.1-year global surface temperature cycle is related to the lunar apsidal line rotation period of 8.85 years, the Saros eclipse cycle’s first harmonic of 9.0 years, and the soli-lunar nodal cycle’s first harmonic of 9.3 years [9,30,128,129]. The 10.4-year temperature cycle falls within the sunspot cycle frequency band and should represent the temperature signature of the 11-year solar cycle, because it is consistent with the variability of the solar cycle observed from 1900 (when it was longer) to 2000 (when it was shorter).
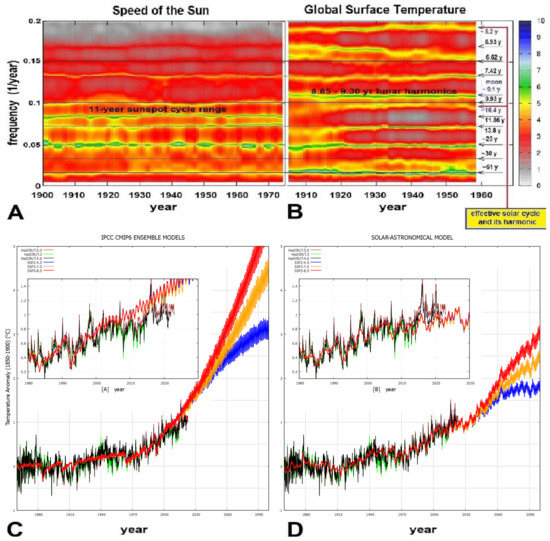
Figure 11.
(A) Time–frequency analysis ( years) of the Sun’s speed relative to the solar system’s barycenter. (B) Time–frequency analysis ( years) of the HadCRUT3 temperature record, detrended of its quadratic trend. [48]. (C) Ensemble CMIP6 GCM mean simulations versus the HadCRUT global surface temperatures for various emission scenarios [102,127,130]. (D) The same record compared against the solar astronomical harmonic climate model by Scafetta et al. [131], as updated in Scafetta [11].
The aforementioned periodicities were essential in order to build a semiempirical global surface temperature model based on astronomical oscillations [12,85]. The same model was later upgraded with the addition of some interannual cycles by Scafetta [11]. To validate the model predictions made after 2014, the calibration was only based on the HadCRT4 data [102] from 1850 to that year. It was discovered that the model was accurate in predicting the two strong El Niño events that took place in 2015–2016 and 2020.
The model assumed two components: an astronomically based oscillating component superimposed on an anthropogenic plus volcano component. The astronomical component is based on a number of interannual periodicities, the 9.1-year solar–lunar cycle, and the astronomical–solar cycles at 10.5, 20, and 60, as well as the two longer cycles at 115 years and at about 1000 year. The millennial cycle was assumed to be asymmetric (because of additional multisecular and multimillennial cycles) with maxima in 1080 and 2060 and a minimum in 1700 (the Maunder Minimum). The millennial cycle was deduced from the Jupiter–Saturn model that is shown in Figure 8.
The equation of the harmonic model is
which uses 13 harmonics whose frequency, amplitude, and phase of the adopted oscillations including the fast interannual ones, reported in Table 4.

Table 4.
Parameters of the harmonic component of the astronomical climate model used for Equation (9).
The anthropogenic plus volcano component was estimated by dividing the mean of the ensemble of CMIP6 global climate model simulations of global surface temperature (GCMs). Scafetta [85]’s model made use of the CMIP5 GCMs. This halving was suggested by the fact that the adopted natural oscillations already accounted for at least 50% of the warming observed from 1970 to 2000, whereas the models used a set of radiative forcings that hindcasted that the observed warming was primarily anthropogenic during the same period [85,128]. According this estimate, natural variability has contributed to the global warming since 1900 substantially more than what climate models and some research suggest [132,133,134].
In fact, the specific solar forcing adopted by those models used the the low secular variability TSI record by Matthes et al. [71]. However, there exist different alternative reconstructions of the solar forcing that suggest a much larger secular variability [42,54,65], and those based on the ACRIM total solar irradiance satellite composite [42,65] show a significant solar luminosity increase between 1970 and 2000. We notice that an increase in solar activity from 1970 to 2000 is also predicted by the planetary–solar model shown in Figure 8. Table 3 also shows that solar cycle 22 (from September 1986 to August 1996) was very short, 9.92 years, and short cycles are usually linked to higher solar activity [135].
Figure 11C plots the ensemble average simulations of the CMIP6 global circulation models (GCMs) [136], utilizing historical forcings (1850–2014) that are extended from 2015 to 2100, according to three distinct shared socioeconomic pathway (SSP) scenarios compared with the HadCRUT3, HadCRUT4 and HadCRUT5 global surface temperature records [102,127,130]. The adopted emission scenarios are SSP2-4.5 (intermediate GHG emissions), SSP3-7.0 (high GHG emissions), and SSP5-8.5 (very high GHG emissions). Using the same SSP scenarios, Figure 11D compares the three temperature records to the proposed semiempirical astronomical harmonic model. The comparison of panels C and D shows that the semiempirical harmonic model performs better than the global climate models in hindcasting temperature changes from 1850 to 2020. The proposed model also forecasts mild warming for the ensuing decades [11,85].
4. Addressing the Critiques
The last 15 years have witnessed an increase in the number of publications advocating the planetary hypothesis of solar activity and climate changes. This is a classic example of science progressing from empirical relationship towards hypotheses and predictions and, hopefully, to a full theory in the future. It is clear that we are not there yet and, as a consequence, only a minority of scholars are today endorsing the planetary control hypothesis of solar and climate changes. Many critiques still exist. Some are physically founded and others empirically founded, while still others are blatantly unscientific. Let us go over them quickly.
4.1. How should the Sun’s Wobbling Be Understood?
Several authors found evidence supporting the planetary hypothesis for the origin of the solar activity oscillations by comparing solar activity records with the inertial motion of the Sun around the barycenter of the solar system [6,12,112,114,137,138,139]. The Sun’s wobbling mechanism is sometimes criticized as having no effect on solar activity, because the center of the Sun is in free-fall movement with no significant forces stressing the star.
This critique ignores the fact that the Sun’s wobbling function can be used as a proxy for conveniently evaluating most of the oscillations of the gravitational field within the solar system due to the orbiting planets. It is the observed frequencies that must be compared with the solar activity oscillations. This approach works because all the dynamical functions of the planetary orbits share a common set of frequencies related to the orbital periods, planetary conjunction cycles, and their various beats. For this reason, the Sun’s wobbling can be used for partially testing the planetary hypothesis of solar activity variability from the spectral point of view, because it should share at least a set of frequencies with those of the actual physical mechanisms responsible for the observed oscillations.
The critique also ignores that the Sun is observed wobbling from any point outside the solar system. Similarly, the fluxes of anything coming from far away toward the Sun—such as cosmic rays, interstellar dusts, etc.—would fluctuate with the same frequencies of the solar wobbling. Thus, any forcings associated with these fluxes would also fluctuate in the same way.
Charvátová [112] first noted that solar wobbling presents alternating complicated ordered and disordered dynamics that are correlated with, for example, the Bray–Hallstat solar and climate oscillations. Scafetta et al. [6] noted that such ordered and disordered dynamics, being related to changes in the gravitational and magnetic properties of the heliosphere, could modulate the particle fluxes from outside and within the solar system. These could then affect both the solar activity and/or the Earth’s climate.
Suggestions of probable physical mechanisms associated with the wobbling, which might affect the dynamo mechanism, the large scale structure of the heliosphere and the climate system, have been discussed in Scafetta et al. [6] and in Scafetta and Bianchini [26].
Cionco and Compagnucci [137] discussed solar acceleration radial impulses in the Sun–barycenter direction and angular momentum inversion characterizing the last prolonged solar minima and Cionco and Soon [138] proposed both a precise calculation and a physical model for exchange between two rotating flux–mass elements that conserve angular momentum, also predicting future solar activity and grand solar minimum events.
One incorrect interpretation of the Sun’s wobbling is to assume that the focus of the Earth’s orbit is placed in the barycenter of the solar system, and that as a result, the sunlight that the Earth receives is heavily modulated by the solar wobbling (see for example Zharkova et al. [140]). This is incorrect, because the Earth’s orbit is not Keplerian around the solar system’s barycenter, which is not the gravitational attraction center of the solar system and, in particular, of the Earth. As a matter of fact, the Earth does not clearly see the solar wobbling, because it wobbles nearly simultaneously together with the Sun.
4.2. The “Homeopathic” Tiny-Tidal Problem
It is currently believed that a solar dynamo operating in the convective solar zone is responsible for fluctuations in solar activity [141]. A common critique against the possibility that the planetary motions could somehow have synchronized the solar dynamo activity and the climate on Earth is that the amplitude of the planetary tidal acceleration on the Sun (and/or the Earth) is very small [142,143]. This is a fact that has been known since the 19th century, which is still presented as if it were a conclusive argument against the planetary hypothesis. Moreover, Charbonneau [144] noted that the planetary tidal forcings could only have what he labeled a “homeopathic” effect on the solar tachocline and came to the conclusion that they should not be able to synchronize the solar dynamo. However, he also rightly stressed that the issue was not insurmountable, because it could be solved under the condition of discovering a solar mechanism that greatly amplifies the impact of the tidal forces.
Scafetta et al. [131] answered Jager and Versteegh [142] and Callebaut et al. [143] by arguing that such a kind of reasoning is only based on a classical Newtonian understanding of the tidal phenomenon. In reality, the most obvious objection to such a critique could be that more mechanisms instead of just a basic Newtonian one could be simultaneously at play. Therefore, the critique could not serve as a persuasive refutation of the planetary hypothesis of solar variability.
In fact, the ability of the Sun to generate large amounts of energy through H-burning could make possible a significant amplification of the tidal harmonic perturbations [74,145]. Under specific circumstances, these periodic perturbations might become strong enough to synchronize the solar dynamo—which is an oscillator in and of itself—to external planetary frequencies [26]. Thus, in order to examine and evaluate the planetary hypothesis of solar activity variation, it should be required to look into this option.
Scafetta [74] specifically addressed the tiny-tidal problem and proposed that the Sun may act as a nuclear fusion amplifier of the planetary tidal forcing, as previously proposed by Wolff and Patrone [145]. More specifically, Scafetta [74] calculated that any tidal gravitational power dissipated in the solar core might be up to four million times enhanced by a modulation of the H-burning rate. Using this amplification factor, the cumulative impact of all planetary tides on the Sun was estimated to increase total solar irradiance (TSI) by about 0.3–0.8 W/m. The frequencies of tidally induced oscillations could be preserved even if a signal is produced by a tidally induced variation of the H-burning rate, which would changes the local temperature of the plasma, as first proposed by Scafetta [74]. In fact, in the radiative central region of the Sun, tidal forces produce g- and p-mode oscillations [146,147,148] that can quickly propagate with the speed of sound (a few hundred kilometers per second) up to the tachocline layer, which is the base of the solar dynamo. As a result, the perturbations caused by the arriving g-waves may be strong enough to synchronize the solar dynamo with the planetary tidal frequencies. As a matter of fact, the original 4 million amplification factor of the dissipated tidal energy in the solar core predicted by the tidal-to-luminosity model of Scafetta [74] could produce more energetic g-waves that are capable to synchronize the solar dynamo to the frequencies of the planetary tides [26,74].
Scafetta [74] did not assert that the physical issue has been fully resolved. In any case, as detailed in Scafetta and Bianchini [26], the scientific literature also suggests several alternative physical mechanisms via which the planets may be modulating solar activity. These include torques, electromagnetic forcings, and the modulation of solar wind and interplanetary particle fluxes that may also directly influence the Earth’s climate by modulating the albedo by affecting cloud formation [6,90,96,119,124,149]. Consequently, it should at least be acknowledged that efforts are being made to solve the “homeopathic” tiny-tidal problem and/or to develop alternative solutions to explain the apparent spectral coherence between solar activity and climate change oscillations and the frequency set emerging from the complex interactions of all the planets. In general, the current magneto-hydrodynamic dynamo models are still unsatisfactory because, although the models predict a periodicity in solar activity changes, they can only roughly mimic the Schwabe 11-year cycle by choosing ad hoc values for their free parameters [150,151]. The timing of the maxima and minima of the 11-year solar cycle is also neither hindcasted nor predicted, but results from the initial conditions imposed on the model equations, which are also free parameters. Similarly, all the other known solar oscillations, from the monthly to the Bray–Hallstatt timescales, cannot be obtained by the solar dynamo models that are now available.
Figure 3, Figure 7, Figure 8 and Figure 10 demonstrate that harmonic models based on planetary ephemeris and fundamental astronomical data appear to be capable of accurately predicting the period and timing of all the major observed solar oscillations. In this way, the first challenge posed by Callebaut et al. [143]—that planetary influences should be able to reproduce at least the most basic periodicities emerging in solar records—is met. Theses results appear to give the planetary theory an empirical advantage over the reductionist theory that assumes that solar activity changes are due to internal solar mechanisms alone. Here, we support the idea that the planetary hypothesis aims not just to substitute but to complement the solar dynamo models, as also commented by Charbonneau [31]. In fact, the existence of a solar dynamo that can naturally oscillate could be a required condition for solar activity to be synchronized by weak external periodic forcings, as the synchronization of pendulums discovered by Huygens in the 17th century demonstrates [152].
However, it is possible to argue that at least part of the observed solar and/or climatic oscillations could be more directly linked to space weather being modified by the oscillations of the magnetic and gravitational fields of the planets [6,7,90]. Space weather variations are connected to particle flux variations interacting with the physical and chemical properties of the terrestrial atmosphere. For example, they could modulate the cloud formation and, therefore, the Earth’s albedo. Finally, the planets induce small oscillations in the orbital motion of the Earth [9,10,125,153,154]. These sub-Milankovic orbital oscillations cause only slight changes in the incoming solar radiation, which may nonetheless affect the climate.
4.3. Rebuttals of the Claims That Planetary Harmonics Are Incompatible with Solar Activity Cycles
In Section 2, we showed that planetary harmonics are compatible with solar activity cycles. Here, the main arguments against the planetary theory of solar activity changes are succinctly discussed.
(1) Okal and Anderson [86] evaluated the power spectrum of a planetary tidal function made up of Mercury, Venus, Earth, and Jupiter and compared it with that of the sunspot number record. These authors concluded that the sunspot cycle had a periodicity of 11 years, while the tidal function only displayed the 11.86-year cycle associated with Jupiter’s orbit. The difference between the two periods was significant. In essence, this critique confirms that Jupiter alone cannot fully account for the Schwabe 11-year sunspot cycle. The problem, however, could be solved in two ways (see Section 3.1):
(a) by the Venus–Earth–Jupiter triple-syzygies tidal alignment models (some of them having been already proposed a century ago [28,29,74,75,76,82,83]) and (b) by the tidal model function produced by Jupiter and Saturn, which includes the tidal oscillation related to the neap–spring tide of Jupiter and Saturn (9.93 years) and the orbital related tide of Jupiter (11.86 year), as discussed above [37,74,84].
(2) Smythe and Eddy [107] analyzed the planetary conjunctions during the Maunder minimum (1645–1715) and concluded that “the failure of planetary conjunction patterns to reflect the drastic drop in sunspots during the Maunder Minimum casts doubt on the tidal theory of solar activity”. This critique was rebutted by Scafetta [37], who showed that grand solar minima, such as Oort, Wolf, Spörer, Maunder, and Dalton, likely derive from the interference among the neap–spring tide of Jupiter and Saturn (9.93 years), the orbital tide of Jupiter (11.86 years), and a period close to 11 years that represents the mean solar dynamo cycle; see Section 3.2.2.
(3) Callebaut et al. [143] noted that the solar activity records show multiple periodicities: the Schwabe 11-year sunspot cycle, the Hale 22-year magnetic cycle, the 88-year Gleissberg cycle, the De Vries (Suess) period of 203–208 years, and the Hallstatt cycle of about 2300 years, and we can add also the Eddy quasi-1000-year cycle. They claimed that it “should be remarked …that virtually none of the papers on planetary influences on solar variability succeeded in identifying these …periodicities in the planetary attractions”. However, Callebaut et al. [155] later retracted their claim in response to the rebuttal by Scafetta et al. [131] and admitted that “it is well-known that there are some periodicities that are common to solar activity and planetary motions”. See the various planetary modelings discussed in Section 2 and Scafetta et al. [6] and Scafetta [7].
(4) Cauquoin et al. [106] investigated the spectral properties of high-resolution records of 10Be in the EPICA Dome C (EDC) ice core from Antarctica during the Marine Interglacial Stage 9.3 (MIS 9.3), 325–336 k years ago and concluded that there are “No evidence for planetary influence on solar activity 330,000 years ago”. However, their power spectra showed four significant spectral peaks at about 103, 115, 130, and 150 years. Scafetta [48] showed that these frequencies emerge from the three-frequency model based on the tides of Jupiter and Saturn beating with the quasi-11-year solar dynamo cycle [37], once some nonlinear coupling between planetary and solar harmonics is assumed. In fact, these frequencies are those that generate Grand Solar Minima such as the Maunder and Dalton ones.
(5) Nataf [87] “built synthetic tidal forcings to illustrate the lack of evidence for a” quasi 11 “years periodicity” and concluded that “the astrological quest for a link between solar cycles and planetary tides remains as unfounded as ever”. He also stated that it was “therefore surprising that this idea has received a renewed attention”. Nataf actually made an even more serious error than that made by Okal and Anderson [86], because he ignored the role of Saturn and, in addition, assumed the orbits to be circular. In fact, his hypothesis that the orbits are circular is evidently erroneous. Nataf [87]’s critique was already rebutted by numerous works Scafetta [37,74], Hung [76], Tattersall [82], Wilson [83]; see Section 3.1 and also the formal recent rebuttal by Scafetta [84]. In his reply, Nataf [156] erroneously claimed that Saturn could be neglected because its tidal oscillation is 20 times smaller than that of Jupiter. However, Scafetta [84] was talking about the oscillation related to the neap–spring tide of Jupiter and Saturn (9.93 years), whose amplitude is only three times smaller than that related to Jupiter’s orbital movement (11.86 year), as shown by the power spectra in Figure 5.
4.4. A Brief Response to Some Unscientific Critiques
Investigating open issues is the way for science to develop. Suitable physical mechanisms are identified only after empirical proofs. In fact, science moves from merely observing a phenomenon and finding empirical correlations among the observables to a physical understanding of it. However, even when only empirical data are available, this process must go on through trial and error until a suitable model is found, which might take a long time. For example, in antiquity, it was well known that ocean tides track the motion of the Moon [157]. In the early 17th century, Kepler formulated the three laws of planetary motion without using any physical mechanism. Only in 1687, Newton [158] postulated his universal gravitational law as a potential physical process for both the tides and Kepler’s laws.
The history of science provides numerous examples where a “tiny-tide”-like objection was used to reject hypotheses based on empirical data, which were later fully confirmed. For example, in 1863, Lord Kelvin (William Thomson) rejected the link between sunspot activity and geomagnetic activity, such as auroras, as mere coincidences [159], because he reasoned that a solar magnetic field could not alter the Earth’s magnetosphere, since the Sun and the Earth are too far away. In his 1892 presidential address to the Royal Society, Lord Kelvin reiterated the same prejudice, despite some scientists having already made discoveries suggesting that the Sun was expelling matter that might have transported the solar magnetic field over long distances. Today, the existence of solar wind is confirmed. Similarly, according to modern skeptics of the planetary synchronized solar dynamo hypothesis, the planets are considered to be too far away to have any impact on the Sun.
Another case is when, shortly before World War I, the German scientist Alfred Wegener [160] put forth a theory of continental drift based on a large number of topographical, sedimentary, and fossil patterns across continents. Wegener’s theory, however, received unreasonable criticism by the majority of conservative scientists, who were hostile to any novel geophysical theory for the simple reason that he could not propose a fully convincing scientific justification for the migration of the continents. At that time, from a geophysical point of view, it was frequently objected that the solar and lunar tidal torques on the Earth’s crust were too weak to move the continents. Once again, a large body of clear empirical facts was ignored or exotically interpreted, and the most obvious interpretation of the evidences was rejected only because its full physical explanation was still missing. As we know today, Wegener’s work is fully acknowledged. Similarly, the many evidences supporting the planetary hypothesis of solar activity variations are ignored only because the underlying physical processes are still controversial.
Finally, we wish to comment on the tendency of dismissing as “astrology” the possibility that the solar dynamo itself might be partially synchronized by planetary harmonic forcings. We point out that the modern understanding of how the Sun, Moon, and planets can influence processes occurring on Earth developed through a rigorous examination of many ancient astrological claims regarding the origin of the seasons, ocean tides, weather events, climate changes, seismic activity, etc. This investigation was mostly conducted in the 16th and 17th centuries by professional astrologers, such as Kepler, who had the patience and skills to distinguish between the facts and the superstitions that tainted earlier astrological works, including the Tetrabiblos by Ptolemy [157], who already tried to build up a scientific astrology in opposition to a mythological view of natural phenomena. Kepler himself was convinced that celestial configurations of the Sun, Moon, and planets had a real physical impact on people by modifying the Earth’s climate and weather [161]. In any case, ancient astrologers did discover correlations between astronomical configurations and events, such as the rise and fall of civilizations, probably associated with cyclical climate changes [162]. For example, important references were made about the 60-year and quasi-millennial cycles, which were associated with the Trigon of Great Conjunctions of Jupiter and Saturn and its millennial rotation through the constellations, know as the Great Inequality between Jupiter and Saturn [162,163]. It is also known that traditional Chinese and Indian calendars adopted a sexagesimal system associated with the cycle of Brihaspati, that is, Jupiter, probably because a quasi-60-year cycle has been observed in the monsoon rainfall cycles since antiquity [164,165,166]. As a matter of fact, the quasi-60- and 1000-year cycles, together with other planetary cycles, are observed both in climate and solar records, as shown here in Figure 8 and Figure 10 [35,37,38,48,52,60,85,89,166]. Now, if it were demonstrated that the planets can somehow synchronize solar activity changes and, directly or indirectly, the space weather conditions around the Earth, a number of ancient astrologers’ claims might find a physical interpretation and answer. For this reason, it would be wise to approach these topics with an open mind, as Kepler himself did.
5. Conclusions
Figure 1 depicts how the Earth’s climate has substantially changed over time. The most well-known climatic periodicities are associated with galactic cycles [2,3,4], various astronomical orbital forcings associated with Milankovitch cycles [5], and numerous solar activity variability cycles, ranging from decadal to multimillennial timescales. Since there are interannual solar, orbital, and soli-lunar tidal oscillations, the interannual timescale oscillations (e.g., the El Niño–Southern Oscillations) may also have a solar or astronomical origin [9,10,11]. Herein, we examined the solar activity variability cycles, their possible planetary origin, and their implications for climate variations, which range from decadal to multimillennial timescales during the Holocene.
The scientific evidences presented in Section 2 suggest that the Sun is subject to planetary influence from monthly to millennial timescales. The most frequently documented solar cycles are those with periods of 0.3–0.33, 1.05–1.15, 10–12 (Schwabe cycle), 20–24 (Hale cycle), 40–45, 55–65, 80–105 (Gleissberg cycle), 115–150, 170–190 (Jose cycle), 200–240 (Suess–de Vries cycles), 800–1200 (Eddy cycle), and 2000–2500 (Bray–Hallstatt cycle) years. Many of these oscillation are also found in climate records and could be used to forecast an important component of the natural climate variability [48,85]. On the contrary, the idea that changes in solar activity might be only governed by internal dynamo mechanisms appears to still fall short of fully explaining why all of these solar cycles coincide with the most significant planetary periods derived from the planets’ orbits, spring tides, synodic cycles, and invariant inequalities.
We acknowledge that the exact physical mechanisms underlying a planetary synchronization of solar activity are still being investigated and are somehow still mysterious, but the empirical evidences are quite compelling and cannot be easily discounted. Gravitational tides may be able to explain some of the observed behavior, especially if internal solar mechanisms dramatically increase their impact on the solar luminosity production rate, as suggested by Wolff and Patrone [145], Scafetta [74] and Scafetta and Bianchini [26]. Additional mechanisms may be at work. For example, certain planetary orbital configurations and conjunctions, even those that include tidally weak planets such as Uranus and Neptune, may be able to modify the interplanetary space weather conditions. For example, they could modulate the large scale structure of the heliospheric electromagnetic field and the particle fluxes coming from interstellar space (such as cosmic rays or even dark matter), or solar wind and the fluxes of interplanetary dust [6,7]. In addition, even small variations in the orbital motion of the Earth and lunar tides could induce some other oscillations in the climate system. Even if the precise nature of the physical processes that could account for the findings is not yet fully understood, it might be in the future. Thus, we call for additional investigation into these issues given the empirical data now accessible and the fact that the specific physical mechanisms underlying the solar cycles are still unknown.
Figure 12 proposes a schematic representation of the planetary model of solar activity oscillations and climate changes, together with various possible involved mechanisms. A planetary hypothesis of solar activity could actually shed light on the physical mechanisms that may have gone unnoticed or underestimated in the past, and we advise searching for planetary-induced synchronization mechanisms of the solar dynamo or of the space weather inside the heliosphere. A planetary model of solar activity cycles would be extremely valuable for predicting changes in solar activity as well as climate oscillations on several timescales.
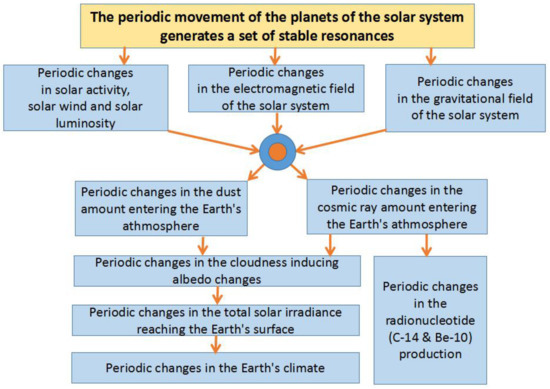
Figure 12.
Schematic representation of the planetary model of solar activity changes and climate oscillations.
Author Contributions
N.S. wrote a first draft of the paper. N.S. and A.B. have discussed in more details all the topics and prepared the final manuscript together. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All websites were assessed on 24 March 2023. Orbital data of the planets: https://nssdc.gsfc.nasa.gov/planetary/factsheet/; Sunspot number record: https://www.sidc.be/silso/datafiles ACRIM TSI satellite composite: ftp://ftp.ngdc.noaa.gov/STP/SOLAR_DATA/SOLAR_IRRADIANCE/ACRIM3/ 9400-year solar activity reconstruction [52]: https://www.ncei.noaa.gov/access/paleo-search/study/8744 9400-year solar activity reconstruction [38]: https://www.ncei.noaa.gov/access/paleo-search/study/12894 The (‰) record ([111], IntCal04.14c): https://www.radiocarbon.org/IntCal04.htm.
Acknowledgments
We would like to thank the referees for encouraging comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Vinós, J. Nature Unbound III—Holocene Climate Variability (Part B). Posted on 28 May 2017. Available online: https://judithcurry.com/2017/05/28/nature-unbound-iii-holocene-climate-variability-part-b/ (accessed on 24 March 2023).
- Shaviv, N.J.; Veizer, J. Celestial driver of Phanerozoic climate? GSA Today 2003, 13, 4. [Google Scholar] [CrossRef]
- Svensmark, H. Cosmoclimatology: A new theory emerges. Astron. Geophys. 2007, 48, 1.18–1.24. [Google Scholar] [CrossRef]
- Rampino, M.R.; Caldeira, K. A 32-million year cycle detected in sea-level fluctuations over the last 545 Myr. Geosci. Front. 2020, 11, 2061–2065. [Google Scholar] [CrossRef]
- Laskar, J.; Robutel, P.; Joutel, F.; Gastineau, M.; Correia, A.C.M.; Levrard, B. A long-term numerical solution for the insolation quantities of the Earth. Astron. Astrophys. 2004, 428, 261–285. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A.; Ortolani, S. On the astronomical origin of the Hallstatt oscillation found in radiocarbon and climate records throughout the Holocene. Earth-Sci. Rev. 2016, 162, 24–43. [Google Scholar] [CrossRef]
- Scafetta, N. Solar Oscillations and the Orbital Invariant Inequalities of the Solar System. Sol. Phys. 2020, 295, 33. [Google Scholar] [CrossRef]
- Cionco, R.G.; Soon, W.W.H. Short-term orbital forcing: A quasi-review and a reappraisal of realistic boundary conditions for climate modeling. Earth-Sci. Rev. 2017, 166, 206–222. [Google Scholar] [CrossRef]
- Cionco, R.G.; Kudryavtsev, S.M.; Soon, W.W.H. Possible Origin of Some Periodicities Detected in Solar-Terrestrial Studies: Earth’s Orbital Movements. Earth Space Sci. 2021, 8, e2021EA001805. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. Multiscale Analysis of the Instantaneous Eccentricity Oscillations of the Planets of the Solar System from 13,000 BC to 17,000 AD. Astron. Lett. 2019, 45, 778–790. [Google Scholar] [CrossRef]
- Scafetta, N. Reconstruction of the Interannual to Millennial Scale Patterns of the Global Surface Temperature. Atmosphere 2021, 12, 147. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical evidence for a celestial origin of the climate oscillations and its implications. J. Atmos. Sol.-Terr. Phys. 2010, 72, 951–970. [Google Scholar] [CrossRef]
- Svensmark, H. Supernova rates and burial of organic matter. Geophys. Res. Lett. 2021, 48, e2021GL096376. [Google Scholar] [CrossRef]
- Hansen, J.; Sato, M.; Russell, G.; Kharecha, P. Climate sensitivity, sea level and atmospheric carbon dioxide. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 2013, 371, 20120294. [Google Scholar] [CrossRef] [PubMed]
- Jouzel, J.; Masson-Delmotte, V.; Cattani, O.; Dreyfus, G.; Falourd, S.; Hoffmann, G.; Minster, B.; Nouet, J.; Barnola, J.M.; Chappellaz, J.; et al. Orbital and Millennial Antarctic Climate Variability over the Past 800,000 Years. Science 2007, 317, 793–796. [Google Scholar] [CrossRef] [PubMed]
- Lisiecki, L.E.; Raymo, M.E. A Pliocene-Pleistocene stack of 57 globally distributed benthic δ18O records. Paleoceanography 2005, 20, PA1003. [Google Scholar] [CrossRef]
- Marcott, S.A.; Shakun, J.D.; Clark, P.U.; Mix, A.C. A Reconstruction of Regional and Global Temperature for the Past 11,300 Years. Science 2013, 339, 1198–1201. [Google Scholar] [CrossRef]
- North Greenland Ice Core Project members: High-resolution record of Northern Hemisphere climate extending into the last interglacial period. Nature 2004, 431, 147–151. [CrossRef]
- Rohde, R.A.; Hausfather, Z. The Berkeley Earth Land/Ocean Temperature Record. Earth Syst. Sci. Data 2020, 12, 3469–3479. [Google Scholar] [CrossRef]
- Royer, D.L.; Berner, R.A.; Montañez, I.P.; Tabor, N.J.; Beerling, D.J. CO2 as a primary driver of Phanerozoic climate. GSA Today 2004, 14, 4. [Google Scholar] [CrossRef]
- Zachos, J.C.; Dickens, G.R.; Zeebe, R.E. An early Cenozoic perspective on greenhouse warming and carbon-cycle dynamics. Nature 2008, 451, 279–283. [Google Scholar] [CrossRef]
- Berner, R.A. GEOCARB III: A revised model of atmospheric CO2 over Phanerozoic time. Am. J. Sci. 2001, 301, 182–204. [Google Scholar] [CrossRef]
- Davis, W. The Relationship between Atmospheric Carbon Dioxide Concentration and Global Temperature for the Last 425 Million Years. Climate 2017, 5, 76. [Google Scholar] [CrossRef]
- Petit, J.R.; Jouzel, J.; Raynaud, D.; Barkov, N.I.; Barnola, J.M.; Basile, I.; Bender, M.; Chappellaz, J.; Davis, M.; Delaygue, G.; et al. Climate and atmospheric history of the past 420,000 years from the Vostok ice core, Antarctica. Nature 1999, 399, 429–436. [Google Scholar] [CrossRef]
- Shakun, J.D.; Clark, P.U.; He, F.; Marcott, S.A.; Mix, A.C.; Liu, Z.; Otto-Bliesner, B.; Schmittner, A.; Bard, E. Global warming preceded by increasing carbon dioxide concentrations during the last deglaciation. Nature 2012, 484, 49–54. [Google Scholar] [CrossRef]
- Scafetta, N.; Bianchini, A. The Planetary Theory of Solar Activity Variability: A Review. Front. Astron. Space Sci. 2022, 9. [Google Scholar] [CrossRef]
- Wolf, R. Extract of a Letter from Prof. R. Wolf, of Zurich, to Mr. Carrington, dated Jan. 12, 1859. Mon. Not. R. Astron. Soc. 1859, 19, 85–86. [Google Scholar] [CrossRef]
- Malburet, J. Sur la période des maxima d’activité solaire. Comptes Rendus Geosci. 2019, 351, 351–354. [Google Scholar] [CrossRef]
- Malburet, J. Sur la cause de la périodicité des tâches solaires. L’Astronomie 1925, 39, 503–515. [Google Scholar]
- Wood, K.D. Physical Sciences: Sunspots and Planets. Nature 1972, 240, 91–93. [Google Scholar] [CrossRef]
- Charbonneau, P. The planetary hypothesis revived. Nature 2013, 493, 613–614. [Google Scholar] [CrossRef]
- Fedorov, V.M.; Frolov, D.M.; Herrera, V.M.N.V.; Soon, W.H.; Cionco, R.G. Role of the Radiation Factor in Global Climatic Events of the Late Holocene. Izv. Atmos. Ocean. Phys. 2021, 57, 1239–1253. [Google Scholar] [CrossRef]
- Soon, W.; Legates, D.R. Solar irradiance modulation of Equator-to-Pole (Arctic) temperature gradients: Empirical evidence for climate variation on multi-decadal timescales. J. Atmos. Sol.-Terr. Phys. 2013, 93, 45–56. [Google Scholar] [CrossRef]
- Neff, U.; Burns, S.J.; Mangini, A.; Mudelsee, M.; Fleitmann, D.; Matter, A. Strong coherence between solar variability and the monsoon in Oman between 9 and 6kyr ago. Nature 2001, 411, 290–293. [Google Scholar] [CrossRef] [PubMed]
- Ogurtsov, M.G.; Nagovitsyn, Y.A.; Kocharov, G.E.; Jungner, H. Long-Period Cycles of the Sun’s Activity Recorded in Direct Solar Data and Proxies. Sol. Phys. 2002, 211, 371–394. [Google Scholar] [CrossRef]
- Scafetta, N.; Grigolini, P.; Imholt, T.; Roberts, J.; West, B.J. Solar turbulence in earth’s global and regional temperature anomalies. Phys. Rev. E 2004, 69, 26303. [Google Scholar] [CrossRef] [PubMed]
- Scafetta, N. Multi-scale harmonic model for solar and climate cyclical variation throughout the Holocene based on Jupiter–Saturn tidal frequencies plus the 11-year solar dynamo cycle. J. Atmos. Sol.-Terr. Phys. 2012, 80, 296–311. [Google Scholar] [CrossRef]
- Steinhilber, F.; Abreu, J.A.; Beer, J.; Brunner, I.; Christl, M.; Fischer, H.; Heikkilä, U.; Kubik, P.W.; Mann, M.; McCracken, K.G.; et al. 9400 years of cosmic radiation and solar activity from ice cores and tree rings. Proc. Natl. Acad. Sci. USA 2012, 109, 5967–5971. [Google Scholar] [CrossRef]
- Kerr, R.A. A Variable Sun Paces Millennial Climate. Science 2001, 294, 1431–1433. [Google Scholar] [CrossRef] [PubMed]
- Kirkby, J. Cosmic Rays and Climate. Surv. Geophys. 2007, 28, 333–375. [Google Scholar] [CrossRef]
- Easterbrook, D.J. Solar Magnetic Cause of Climate Changes and Origin of the Ice Ages; Amazon Distribution: Bellingham, WA, USA, 2019. [Google Scholar]
- Hoyt, D.V.; Schatten, K.H. A discussion of plausible solar irradiance variations, 1700–1992. J. Geophys. Res. Space Phys. 1993, 98, 18895–18906. [Google Scholar] [CrossRef]
- Hoyt, D.V.; Schatten, K.H. The Role of the Sun in Climate Change; Oxford University Press,: Oxford, UK, 1997. [Google Scholar]
- Roy, I. Solar cyclic variability can modulate winter Arctic climate. Sci. Rep. 2018, 8, 4864. [Google Scholar] [CrossRef] [PubMed]
- Dobrica, V.; Pirloaga, R.; Stefan, C.; Demetrescu, C. Inferring geoeffective solar variability signature in stratospheric and tropospheric Northern Hemisphere temperatures. J. Atmos. Sol.-Terr. Phys. 2018, 180, 137–147. [Google Scholar] [CrossRef]
- Mörner, N.A. Planetary beat and solar-terrestrial responses. Pattern Recognit. Phys. 2013, 1, 107–116. [Google Scholar] [CrossRef]
- Baidolda, F. Search for Planetary Influences on Solar Activity; Université Paris, Sciences et Lettres: Paris, France, 2017. [Google Scholar]
- Scafetta, N. Discussion on the spectral coherence between planetary, solar and climate oscillations: A reply to some critiques. Astrophys. Space Sci. 2014, 354, 275–299. [Google Scholar] [CrossRef]
- Lean, J.; Beer, J.; Bradley, R. Reconstruction of solar irradiance since 1610: Implications for climate change. Geophys. Res. Lett. 1995, 22, 3195–3198. [Google Scholar] [CrossRef]
- Wang, Y.M.; Lean, J.L.; Sheeley, N.R., Jr. Modeling the Sun’s Magnetic Field and Irradiance since 1713. Astrophys. J. 2005, 625, 522–538. [Google Scholar] [CrossRef]
- Vieira, L.E.A.; Solanki, S.K.; Krivova, N.A.; Usoskin, I. Evolution of the solar irradiance during the Holocene. Astron. Astrophys. 2011, 531, A6. [Google Scholar] [CrossRef]
- Steinhilber, F.; Beer, J.; Fröhlich, C. Total solar irradiance during the Holocene. Geophys. Res. Lett. 2009, 36, 40142. [Google Scholar] [CrossRef]
- Bard, E.; Raisbeck, G.; Yiou, F.; Jouzel, J. Solar irradiance during the last 1200 years based on cosmogenic nuclides. Tellus B Chem. Phys. Meteorol. 2000, 52, 985. [Google Scholar] [CrossRef]
- Egorova, T.; Schmutz, W.; Rozanov, E.; Shapiro, A.I.; Usoskin, I.; Beer, J.; Tagirov, R.V.; Peter, T. Revised historical solar irradiance forcing. Astron. Astrophys. 2018, 615, A85. [Google Scholar] [CrossRef]
- Shapiro, A.I.; Schmutz, W.; Rozanov, E.; Schoell, M.; Haberreiter, M.; Shapiro, A.V.; Nyeki, S. A new approach to the long-term reconstruction of the solar irradiance leads to large historical solar forcing. Astron. Astrophys. 2011, 529, A67. [Google Scholar] [CrossRef]
- Coddington, O.; Lean, J.L.; Pilewskie, P.; Snow, M.; Lindholm, D. A Solar Irradiance Climate Data Record. Bull. Am. Meteorol. Soc. 2016, 97, 1265–1282. [Google Scholar] [CrossRef]
- Yeo, K.L.; Solanki, S.K.; Krivova, N.A.; Rempel, M.; Anusha, L.S.; Shapiro, A.I.; Tagirov, R.V.; Witzke, V. The Dimmest State of the Sun. Geophys. Res. Lett. 2020, 47, e2020GL090243. [Google Scholar] [CrossRef]
- Schmutz, W.K. Changes in the Total Solar Irradiance and climatic effects. J. Space Weather. Space Clim. 2021, 11, 40. [Google Scholar] [CrossRef]
- McCracken, K.G.; Beer, J.; Steinhilber, F.; Abreu, J. A Phenomenological Study of the Cosmic Ray Variations over the Past 9400 Years, and Their Implications Regarding Solar Activity and the Solar Dynamo. Sol. Phys. 2013, 286, 609–627. [Google Scholar] [CrossRef]
- Eddy, J.A. Climate and the changing sun. Clim. Chang. 1977, 1, 173–190. [Google Scholar] [CrossRef]
- Eichler, A.; Olivier, S.; Henderson, K.; Laube, A.; Beer, J.; Papina, T.; Gäggeler, H.W.; Schwikowski, M. Temperature response in the Altai region lags solar forcing. Geophys. Res. Lett. 2009, 36, 35930. [Google Scholar] [CrossRef]
- Vahrenholt, F.; Lüning, S. The Neglected Sun—Why the Sun Precludes Climate Catastrophe; Stacey International: London, UK, 2013. [Google Scholar]
- Willson, R.C.; Mordvinov, A.V. Secular total solar irradiance trend during solar cycles 21–23. Geophys. Res. Lett. 2003, 30, 1199. [Google Scholar] [CrossRef]
- Fröhlich, C. Total Solar Irradiance Observations. Surv. Geophys. 2012, 33, 453–473. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.; Lee, J.; Wu, D. Modeling Quiet Solar Luminosity Variability from TSI Satellite Measurements and Proxy Models during 1980–2018. Remote Sens. 2019, 11, 2569. [Google Scholar] [CrossRef]
- Montillet, J.P.; Finsterle, W.; Kermarrec, G.; Sikonja, R.; Haberreiter, M.; Schmutz, W.; de Wit, T.D. Data Fusion of Total Solar Irradiance Composite Time Series Using 41 Years of Satellite Measurements. J. Geophys. Res. Atmos. 2022, 127, e2021JD036146. [Google Scholar] [CrossRef]
- De Wit, T.D.; Kopp, G.; Fröhlich, C.; Schöll, M. Methodology to create a new total solar irradiance record: Making a composite out of multiple data records. Geophys. Res. Lett. 2017, 44, 1196–1203. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. ACRIM total solar irradiance satellite composite validation versus TSI proxy models. Astrophys. Space Sci. 2014, 350, 421–442. [Google Scholar] [CrossRef]
- Krivova, N.A.; Solanki, S.K.; Wenzler, T. ACRIM-gap and total solar irradiance revisited: Is there a secular trend between 1986 and 1996? Geophys. Res. Lett. 2009, 36, 40707. [Google Scholar] [CrossRef]
- Yeo, K.L.; Krivova, N.A.; Solanki, S.K.; Glassmeier, K.H. Reconstruction of total and spectral solar irradiance from 1974 to 2013 based on KPVT, SoHO/MDI, and SDO/HMI observations. Astron. Astrophys. 2014, 570, A85. [Google Scholar] [CrossRef]
- Matthes, K.; Funke, B.; Andersson, M.E.; Barnard, L.; Beer, J.; Charbonneau, P.; Clilverd, M.A.; de Wit, T.D.; Haberreiter, M.; Hendry, A.; et al. Solar forcing for CMIP6 (v3.2). Geosci. Model Dev. 2017, 10, 2247–2302. [Google Scholar] [CrossRef]
- Scafetta, N. Empirical analysis of the solar contribution to global mean air surface temperature change. J. Atmos. Sol.-Terr. Phys. 2009, 71, 1916–1923. [Google Scholar] [CrossRef]
- Connolly, R.; Soon, W.; Connolly, M.; Baliunas, S.; Berglund, J.; Butler, C.J.; Cionco, R.G.; Elias, A.G.; Fedorov, V.M.; Harde, H.; et al. How much has the Sun influenced Northern Hemisphere temperature trends? An ongoing debate. Res. Astron. Astrophys. 2021, 21, 131. [Google Scholar] [CrossRef]
- Scafetta, N. Does the Sun work as a nuclear fusion amplifier of planetary tidal forcing? A proposal for a physical mechanism based on the mass-luminosity relation. J. Atmos. Sol.-Terr. Phys. 2012, 81–82, 27–40. [Google Scholar] [CrossRef]
- Bendandi, R. Un Principio Fondamentale Dell’Universo; Osservatorio Bendandi: Faenza, Italy, 1931. [Google Scholar]
- Hung, C.C. Apparent Relations Between Solar Activity and Solar Tides Caused by the Planets. NASA Rep. 2007, TM-2007-214817, 1–34. [Google Scholar]
- Okhlopkov, V.P. The gravitational influence of Venus, the Earth, and Jupiter on the 11-year cycle of solar activity. Mosc. Univ. Phys. Bull. 2016, 71, 440–446. [Google Scholar] [CrossRef]
- Okhlopkov, V.P. 11-Year Index of Linear Configurations of Venus, Earth, and Jupiter and Solar Activity. Geomagn. Aeron. 2020, 60, 381–390. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. Synchronized Helicity Oscillations: A Link Between Planetary Tides and the Solar Cycle? Sol. Phys. 2016, 291, 2197–2212. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weber, N.; Weier, T. On the Synchronizability of Tayler–Spruit and Babcock–Leighton Type Dynamos. Sol. Phys. 2018, 293, 12. [Google Scholar] [CrossRef]
- Stefani, F.; Giesecke, A.; Weier, T. A Model of a Tidally Synchronized Solar Dynamo. Sol. Phys. 2019, 294, 60. [Google Scholar] [CrossRef]
- Tattersall, R. The Hum: Log-normal distribution and planetary–solar resonance. Pattern Recognit. Phys. 2013, 1, 185–198. [Google Scholar] [CrossRef]
- Wilson, I.R.G. The Venus–Earth–Jupiter spin–orbit coupling model. Pattern Recognit. Phys. 2013, 1, 147–158. [Google Scholar] [CrossRef]
- Scafetta, N. Comment on “Tidally Synchronized Solar Dynamo: A Rebuttal” by Nataf (Solar Phys. 297, 107, 2022). Sol. Phys. 2023, 298, 24. [Google Scholar] [CrossRef]
- Scafetta, N. Discussion on climate oscillations: CMIP5 general circulation models versus a semi-empirical harmonic model based on astronomical cycles. Earth-Sci. Rev. 2013, 126, 321–357. [Google Scholar] [CrossRef]
- Okal, E.; Anderson, D.L. On the planetary theory of sunspots. Nature 1975, 253, 511–513. [Google Scholar] [CrossRef]
- Nataf, H.C. Tidally Synchronized Solar Dynamo: A Rebuttal. Sol. Phys. 2022, 297, 107. [Google Scholar] [CrossRef]
- Tan, B.; Cheng, Z. The mid-term and long-term solar quasi-periodic cycles and the possible relationship with planetary motions. Astrophys. Space Sci. 2012, 343, 511–521. [Google Scholar] [CrossRef]
- Scafetta, N. The complex planetary synchronization structure of the solar system. Pattern Recognit. Phys. 2014, 2, 1–19. [Google Scholar] [CrossRef]
- Scafetta, N.; Milani, F.; Bianchini, A. A 60-Year Cycle in the Meteorite Fall Frequency Suggests a Possible Interplanetary Dust Forcing of the Earth’s Climate Driven by Planetary Oscillations. Geophys. Res. Lett. 2020, 47, e2020GL089954. [Google Scholar] [CrossRef]
- Bigg, E.K. Influence of the planet Mercury on sunspots. Astron. J. 1967, 72, 463. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. Empirical evidences for a planetary modulation of total solar irradiance and the TSI signature of the 1.09-year Earth-Jupiter conjunction cycle. Astrophys. Space Sci. 2013, 348, 25–39. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. Multiscale comparative spectral analysis of satellite total solar irradiance measurements from 2003 to 2013 reveals a planetary modulation of solar activity and its nonlinear dependence on the 11 yr solar cycle. Pattern Recognit. Phys. 2013, 1, 123–133. [Google Scholar] [CrossRef]
- Snodgrass, H.B.; Ulrich, R.K. Rotation of Doppler features in the solar photosphere. Astrophys. J. 1990, 351, 309. [Google Scholar] [CrossRef]
- Shkolnik, E.; Walker, G.A.H.; Bohlender, D.A. Evidence for Planet-induced Chromospheric Activity on HD 179949. Astrophys. J. 2003, 597, 1092–1096. [Google Scholar] [CrossRef]
- Shkolnik, E.; Walker, G.A.H.; Bohlender, D.A.; Gu, P.G.; Kurster, M. Hot Jupiters and Hot Spots: The Short- and Long-Term Chromospheric Activity on Stars with Giant Planets. Astrophys. J. 2005, 622, 1075–1090. [Google Scholar] [CrossRef]
- Pizzella, G. Emission of cosmic rays from Jupiter: Magnetospheres as possible sources of cosmic rays. Eur. Phys. J. C 2018, 78, 1–7. [Google Scholar] [CrossRef]
- Salvador, R.J. A mathematical model of the sunspot cycle for the past 1000 yr. Pattern Recognit. Phys. 2013, 1, 117–122. [Google Scholar] [CrossRef]
- Mörner, N.A. The Approaching New Grand Solar Minimum and Little Ice Age Climate Conditions. Nat. Sci. 2015, 7, 510–518. [Google Scholar] [CrossRef]
- Courtillot, V.; Lopes, F.; Mouël, J.L.L. On the Prediction of Solar Cycles. Sol. Phys. 2021, 296, 1–23. [Google Scholar] [CrossRef]
- Ljungqvist, F.C. A new reconstruction of temperature variability in the extra-tropical northern hemisphere during the last two millennia. Geogr. Ann. Ser. A Phys. Geogr. 2010, 92, 339–351. [Google Scholar] [CrossRef]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Jones, P.D. Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J. Geophys. Res. Atmos. 2012, 117, 17187. [Google Scholar] [CrossRef]
- Moberg, A.; Sonechkin, D.M.; Holmgren, K.; Datsenko, N.M.; Karlén, W. Highly variable Northern Hemisphere temperatures reconstructed from low- and high-resolution proxy data. Nature 2005, 433, 613–617. [Google Scholar] [CrossRef]
- Kutschera, W.; Patzelt, G.; Steier, P.; Wild, E.M. The Tyrolean Iceman and His Glacial Environment During the Holocene. Radiocarbon 2017, 59, 395–405. [Google Scholar] [CrossRef]
- Alley, R.B. GISP2—Temperature Reconstruction and Accumulation Data. In IGBP PAGES/World Data Center for Paleoclimatology Data Contribution Series 2004-013; NOAA National Centers for Environmental Information: Asheville, NC, USA, 2004. [Google Scholar] [CrossRef]
- Cauquoin, A.; Raisbeck, G.M.; Jouzel, J.; Bard, E. No evidence for planetary influence on solar activity 330,000 years ago. Astron. Astrophys. 2014, 561, A132. [Google Scholar] [CrossRef]
- Smythe, C.M.; Eddy, J.A. Planetary tides during the Maunder Sunspot Minimum. Nature 1977, 266, 434–435. [Google Scholar] [CrossRef]
- Poluianov, S.; Usoskin, I. Critical Analysis of a Hypothesis of the Planetary Tidal Influence on Solar Activity. Sol. Phys. 2014, 289, 2333–2342. [Google Scholar] [CrossRef]
- Abreu, J.A.; Albert, C.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Response to: “Critical Analysis of a Hypothesis of the Planetary Tidal Influence on Solar Activity” by S. Poluianov and I. Usoskin. Sol. Phys. 2014, 289, 2343–2344. [Google Scholar] [CrossRef]
- Scafetta, N. High resolution coherence analysis between planetary and climate oscillations. Adv. Space Res. 2016, 57, 2121–2135. [Google Scholar] [CrossRef]
- Reimer, P.J.; Baillie, M.; Bard, E.; Bayliss, A.; Beck, J.W.; Bertrand, C.J.H.; Blackwell, P.G.; Buck, C.E.; Burr, G.S.; Cutler, K.B.; et al. Intcal04 Terrestrial Radiocarbon Age Calibration, 0–26 Cal Kyr BP. Radiocarbon 2004, 46, 1029–1058. [Google Scholar] [CrossRef]
- Charvátová, I. Can origin of the 2400-year cycle of solar activity be caused by solar inertial motion? Ann. Geophys. 2000, 18, 399–405. [Google Scholar] [CrossRef]
- Cionco, R.G.; Pavlov, D.A. Solar barycentric dynamics from a new solar-planetary ephemeris. Astron. Astrophys. 2018, 615, A153. [Google Scholar] [CrossRef]
- Fairbridge, R.W.; Shirley, J.H. Prolonged minima and the 179-yr cycle of the solar inertial motion. Sol. Phys. 1987, 110, 191–210. [Google Scholar] [CrossRef]
- McCracken, K.G.; Beer, J.; Steinhilber, F. Evidence for Planetary Forcing of the Cosmic Ray Intensity and Solar Activity Throughout the Past 9400 Years. Sol. Phys. 2014, 289, 3207–3229. [Google Scholar] [CrossRef]
- Usoskin, I.G.; Gallet, Y.; Lopes, F.; Kovaltsov, G.A.; Hulot, G. Solar activity during the Holocene: The Hallstatt cycle and its consequence for grand minima and maxima. Astron. Astrophys. 2016, 587, A150. [Google Scholar] [CrossRef]
- Bray, J.R. Glaciation and Solar Activity since the Fifth Century BC and the Solar Cycle. Nature 1968, 220, 672–674. [Google Scholar] [CrossRef]
- Vasiliev, S.S.; Dergachev, V.A. The 2400-year cycle in atmospheric radiocarbon concentration: Bispectrum of 14C data over the last 8000 years. Ann. Geophys. 2002, 20, 115–120. [Google Scholar] [CrossRef]
- Bertolucci, S.; Zioutas, K.; Hofmann, S.; Maroudas, M. The Sun and its Planets as detectors for invisible matter. Phys. Dark Univ. 2017, 17, 13–21. [Google Scholar] [CrossRef]
- Petrakou, E. Planetary statistics and forecasting for solar flares. Adv. Space Res. 2021, 68, 2963–2973. [Google Scholar] [CrossRef]
- Scafetta, N. A shared frequency set between the historical mid-latitude aurora records and the global surface temperature. J. Atmos. Sol.-Terr. Phys. 2012, 74, 145–163. [Google Scholar] [CrossRef]
- Scafetta, N.; Willson, R.C. Planetary harmonics in the historical Hungarian aurora record (1523–1960). Planet. Space Sci. 2013, 78, 38–44. [Google Scholar] [CrossRef]
- Sharp, G.J. Are Uranus and Neptune Responsible for Solar Grand Minima and Solar Cycle Modulation? Int. J. Astron. Astrophys. 2013, 3, 260–273. [Google Scholar] [CrossRef]
- Abreu, J.A.; Beer, J.; Ferriz-Mas, A.; McCracken, K.G.; Steinhilber, F. Is there a planetary influence on solar activity? Astron. Astrophys. 2012, 548, A88. [Google Scholar] [CrossRef]
- Lopes, F.; Mouël, J.L.; Courtillot, V.; Gibert, D. On the shoulders of Laplace. Phys. Earth Planet. Inter. 2021, 316, 106693. [Google Scholar] [CrossRef]
- Scafetta, N. Reply on Comment on “High resolution coherence analysis between planetary and climate oscillations” by S. Holm. Adv. Space Res. 2018, 62, 334–342. [Google Scholar] [CrossRef]
- Brohan, P.; Kennedy, J.J.; Harris, I.; Tett, S.F.B.; Jones, P.D. Uncertainty estimates in regional and global observed temperature changes: A new data set from 1850. J. Geophys. Res. 2006, 111, 6548. [Google Scholar] [CrossRef]
- Scafetta, N. Testing an astronomically based decadal-scale empirical harmonic climate model versus the IPCC (2007) general circulation climate models. J. Atmos. Sol.-Terr. Phys. 2012, 80, 124–137. [Google Scholar] [CrossRef]
- Keeling, C.D.; Whorf, T.P. The 1800-year oceanic tidal cycle: A possible cause of rapid climate change. Proc. Natl. Acad. Sci. USA 2000, 97, 3814–3819. [Google Scholar] [CrossRef] [PubMed]
- Morice, C.P.; Kennedy, J.J.; Rayner, N.A.; Winn, J.P.; Hogan, E.; Killick, R.E.; Dunn, R.J.H.; Osborn, T.J.; Jones, P.D.; Simpson, I.R. An Updated Assessment of Near-Surface Temperature Change From 1850: The HadCRUT5 Data Set. J. Geophys. Res. Atmos. 2021, 126, e2019JD032361. [Google Scholar] [CrossRef]
- Scafetta, N.; Humlum, O.; Solheim, J.E.; Stordahl, K. Comment on “The influence of planetary attractions on the solar tachocline” by Callebaut, de Jager and Duhau. J. Atmos. Sol.-Terr. Phys. 2013, 102, 368–371. [Google Scholar] [CrossRef]
- Stocker, T.F.; Qin, D.; Plattner, G.-K.; Tignor, M.; Allen, S.K.; Boschung, J.; Nauels, A.; Xia, Y.; Bex, V.; Midgley, P.M. (Eds.) Climate Change 2013 The Physical Science Basis: Assessment Working Group I Contribution to the IPCC Fifth Assessment Report; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Masson-Delmotte, V.; Zhai, P.; Pirani, A.; Connors, S.L.; Péan, C.; Berger, S.; Caud, N.; Chen, Y.; Goldfarb, L.; Gomis, M.I.; et al. (Eds.) Climate Change 2021 The Physical Science Basis: Assessment Working Group I Contribution to the IPCC Sixth Assessment Report; Cambridge University Press: Cambridge, UK, 2021. [Google Scholar]
- Jager, C.D.; Nieuwenhuizen, A.; Duhau, S. The relation between the average northern hemisphere ground temperature and solar equatorial and polar magnetic activity. Phys. Astron. Int. J. 2018, 2, 175–185. [Google Scholar] [CrossRef]
- Richards, M.T.; Rogers, M.L.; Richards, D.S.P. Long-term Variability in the Length of the Solar Cycle. Publ. Astron. Soc. Pac. 2009, 121, 797–809. [Google Scholar] [CrossRef]
- Eyring, V.; Bony, S.; Meehl, G.A.; Senior, C.A.; Stevens, B.; Stouffer, R.J.; Taylor, K.E. Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization. Geosci. Model Dev. 2016, 9, 1937–1958. [Google Scholar] [CrossRef]
- Cionco, R.G.; Compagnucci, R.H. Dynamical characterization of the last prolonged solar minima. Adv. Space Res. 2012, 50, 1434–1444. [Google Scholar] [CrossRef]
- Cionco, R.G.; Soon, W. A phenomenological study of the timing of solar activity minima of the last millennium through a physical modeling of the Sun-Planets Interaction. New Astron. 2015, 34, 164–171. [Google Scholar] [CrossRef]
- Yndestad, H.; Solheim, J.E. The influence of solar system oscillation on the variability of the total solar irradiance. New Astron. 2017, 51, 135–152. [Google Scholar] [CrossRef]
- Zharkova, V.V.; Shepherd, S.J.; Zharkov, S.I.; Popova, E. RETRACTED ARTICLE: Oscillations of the baseline of solar magnetic field and solar irradiance on a millennial timescale. Sci. Rep. 2019, 9, 9197. [Google Scholar] [CrossRef] [PubMed]
- Charbonneau, P. Dynamo models of the solar cycle. Living Rev. Sol. Phys. 2020, 17, 1–104. [Google Scholar] [CrossRef]
- Jager, C.D.; Versteegh, G.J.M. Do Planetary Motions Drive Solar Variability? Sol. Phys. 2005, 229, 175–179. [Google Scholar] [CrossRef]
- Callebaut, D.K.; de Jager, C.; Duhau, S. The influence of planetary attractions on the solar tachocline. J. Atmos. -Sol.-Terr. Phys. 2012, 80, 73–78. [Google Scholar] [CrossRef]
- Charbonneau, P. External Forcing of the Solar Dynamo. Front. Astron. Space Sci. 2022, 9, 48. [Google Scholar] [CrossRef]
- Wolff, C.L.; Patrone, P.N. A New Way that Planets Can Affect the Sun. Sol. Phys. 2010, 266, 227–246. [Google Scholar] [CrossRef]
- Hartlep, T.; Mansour, N. Acoustic Wave Propagation in the Sun; Annual Research Briefs; Center for Turbulence Research: Stanford, CA, USA, 2005; pp. 357–365. Available online: https://web.stanford.edu/group/ctr/ResBriefs05/hartlep.pdf (accessed on 24 March 2023).
- Ahuir, J.; Mathis, S.; Amard, L. Dynamical tide in stellar radiative zones. General formalism and evolution for low-mass stars. Astron. Astrophys. 2021, 651, A3. [Google Scholar] [CrossRef]
- Barker, A.J.; Ogilvie, G.I. On internal wave breaking and tidal dissipation near the centre of a solar-type star. Mon. Not. R. Astron. Soc. 2010, 404, 1849–1868. [Google Scholar] [CrossRef]
- Stefani, F.; Stepanov, R.; Weier, T. Shaken and Stirred: When Bond Meets Suess–de Vries and Gnevyshev–Ohl. Sol. Phys. 2021, 296, 88. [Google Scholar] [CrossRef]
- Chatterjee, P.; Nandy, D.; Choudhuri, A.R. Full-sphere simulations of a circulation-dominated solar dynamo: Exploring the parity issue. Astron. Astrophys. 2004, 427, 1019–1030. [Google Scholar] [CrossRef]
- Jiang, J.; Chatterjee, P.; Choudhuri, A.R. Solar activity forecast with a dynamo model. Mon. Not. R. Astron. Soc. 2007, 381, 1527–1542. [Google Scholar] [CrossRef]
- Pikovsky, A. Synchronization—A Universal Concept in Nonlinear Sciences; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Lopes, F.; Courtillot, V.; Gibert, D.; Mouël, J.L.L. On Two Formulations of Polar Motion and Identification of Its Sources. Geosciences 2022, 12, 398. [Google Scholar] [CrossRef]
- Lopes, F.; Courtillot, V.; Gibert, D.; Mouël, J.L.L. Extending the Range of Milankovic Cycles and Resulting Global Temperature Variations to Shorter Periods (1–100 Year Range). Geosciences 2022, 12, 448. [Google Scholar] [CrossRef]
- Callebaut, D.; de Jager, C.; Duhau, S. Reply to “The influence of planetary attractions on the solar tachocline” by N. Scafetta, O. Humlum, J.E. Solheim, K. Stordahl. J. Atmos. Sol.-Terr. Phys. 2013, 102, 372. [Google Scholar] [CrossRef]
- Nataf, H.C. Response to Comment on “Tidally Synchronized Solar Dynamo: A Rebuttal”. Sol. Phys. 2023, 298, 33. [Google Scholar] [CrossRef]
- Ptolemy. Tetrabiblos, or Quadripartite (2nd Century); Astrology Classics: Bondi, Australia, 2002. [Google Scholar]
- Newton, I. The Principia—Mathematical Principles of Natural Philosophy (1687); Univ. of California Press: Oakland, CA, USA, 1999. [Google Scholar]
- Moldwin, M.B. An Introduction to Space Weather; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Wegener, A. The Origin of Continents And Oceans (1915); Dover Publications: Mineola, NY, USA, 1966. [Google Scholar]
- Brackenridge, J.; Rossi, M. Johannes Kepler’s on the More Certain Fundamentals of Astrology Prague 1601. Proc. Am. Philos. Soc. 1979, 123, 85–116. [Google Scholar]
- Yamamoto, K.; Burnett, C. Abu Ma’sar on Historical Astrology: The Book of Religions and Dynasties (on the Great Conjunctions); Brill: Leiden, The Netherlands, 2000. [Google Scholar]
- Kepler, J. De Stella Nova in Pede Serpentarii; Typis Pauli Sessii: Pragae, Czech Republic, 1606. [Google Scholar]
- Agnihotri, R.; Dutta, K. Centennial scale variations in monsoonal rainfall (Indian, east equatorial and Chinese monsoons): Manifestations of solar variability. Curr. Sci. 2003, 240, 459–463. [Google Scholar]
- Iyengar, R.N. Monsoon rainfall cycles as depicted in ancient Sanskrit texts. Curr. Sci. 2009, 97, 444–447. [Google Scholar]
- Gupta, S.M. Indian monsoon cycles through the last twelve million years. Earth Sci. India 2010, 3, 248–280. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).