Abstract
With increased interest in climate forecasts and projections, it is important to understand more about their sources and levels of skill. A starting point here is to describe the nature of the skill associated with forecasts and projections. Climate forecasts and projections typically both include time varying forcing of the climate, but only forecasts have initial conditions set close to the observed climate state. Climate forecasts therefore derive skill from both initial conditions and from forcing. The character of the initial condition skill and forcing skill is different. Skill from initial conditions results in a narrowing of expectations relative to a climatological distribution and points toward a more favoured part of the distribution. Forcing skill could result from a shift in the preferred parts of the climatological distribution in response to forcing, or it could result from a shift in the entire distribution, or both. Assessments of forcing skill require time averages of the target variable that are long enough so that the contributions from internal variations are small compared to the forced response. The assessment of skill of climate forecasts and projections is inherently partial because of the small number of repeated trials possible on typical climate time scales but is nonetheless the only direct measure of their performance.
1. Introduction
The process of adapting to climate variability and change requires us to formulate conceptions of what the future climate will look like [1]. Information about the future climate is generated by running climate models forward in time. The term ‘climate’ covers a vast range of timescales and typically means anything beyond the weather time scale of a couple of weeks [2]. Climate forecasts are typically conducted on subseasonal to seasonal (S2S) [3,4] and seasonal to decadal (S2D) [5,6] timescales. Climate projections usually relate to timescales beyond a decade. Climate forecasts provide information to help adapt to variability and extremes in climate, and projections are used to adapt to a changing climate [7].
Climate forecasts and projections also differ from more familiar weather forecasts in the spatial and temporal scales over which they are assessed. While weather forecasts are often verified over hours or days at individual weather stations [8], the potential predictability of the climate system is thought to reside in large features that span continental and ocean scales that evolve over months or years [9]. As such, climate forecasts and projections should be assessed over long enough periods or large enough spatial scales to capture the relevant scale features.
Since decisions to adapt to climate are partly based on climate forecasts and projections, we want to be able to evaluate forecasts and projections to see how reliable they are [10,11,12]. A comprehensive ‘evaluation’ of climate model forecasts and projections would be based on a range of different criteria [13]. This might include the theoretical underpinnings of results [14,15], the dynamical consistency and coherency of results [14,16,17,18,19], the ability to simulate relevant processes [20,21,22], and the empirical comparison of forecast results with observed outcomes [23,24,25]. In this work we consider issues around only the latter criterion of comparing forecast model outcomes with observed outcomes.
The process of comparing modelled and observed outcomes of a forecast target variable is often called ‘verification’, and there is a rich literature on this in weather and climate forecasting [26]. We are applying the concept of verification to both forecasts and projections here and using it to clarify differences between the two. Of course, a projection of the future climate cannot be ‘verified’ until the time pertaining to the projection is observed. However, projections can be run in a ‘hindcast’ mode, where the projection is initiated from a point in the past to apply to a period for which we do already have observations. Thus, this hindcast mode for projections is assumed here when referring to the verification of projections.
The terms ‘climate forecast’ and ‘climate projection’ are often used interchangably. This can create confusion, since they are not the same thing [27]. The experiments used to generate forecasts and projections are configured differently, and the goals are different [28]. We elaborate on these differences and the consequences for verification in the text that follows.
Any exercise to compare the forecast of a model with observed outcomes requires some measure of the success or otherwise of the model in predicting the outcome. The term for such a measure is the ‘skill’ of a forecast [29]. Skill is central to any discussion of verification. In the section that follows we introduce basic skill concepts and then apply these to forecasts and projections.
Climate ‘forecasts’ and ‘projections’ address different attributes of climate. Climate forecasts are ‘initialised’ to a starting point in time where some desired features of the climate system in the model are set as close as possible to the observed values of these features. For example, in a forecast of the El Niño Southern Oscillation (ENSO), the sea surface temperature (SST) and tropical subsurface ocean state are set close to observations to start the forecast [30,31,32]. The forecast then tracks the time evolution of the ENSO from this starting point and attempts to resolve any transitions of the ENSO from its current state (El Niño/neutral/La Niña) to another state. When the forecast is no longer capable of resolving what state the ENSO is in, it is then said to have lost skill.
For a climate projection, the flow state of the ocean and atmosphere in the model are not initialised to take values close to the real system at the start. The ocean and atmosphere can start in any flow configuration in a projection, and so there is no point trying to track the evolution of individual flow features such as the ENSO from one point in time to the next to compare with the observed evolution. Since many projection experiments are interested in climate change through time, the model is given specified values of the climate forcings (from greenhouse gases and aerosols) that match the historical forcings through time, together with some estimate of the evolution of those forcings in the future [33]. Those forcings can change the climate of the model, including changes in the statistics of processes such as the ENSO [34]. Thus, in a projection, one would generally assess changes in the statistical properties of features like the ENSO rather than worry about what state it was in at any particular point in time.
2. Skill
The skill of a weather or climate forecast is an estimate of how well the forecast performs relative to some well-defined reference forecast (baseline) over repeated forecast trials [35]. For example, one might define a baseline as a ‘chance’ forecast, which would be the success rate for forecasts based on a random guess [36]. For weather forecasts, the baseline is often the ‘persistence’ forecast, which is a forecast that simply persists the initial conditions unchanging, forward in time [37]. In weather terms, ‘persistence’ means that tomorrow will be just like today, and so on for successive days. For climate forecasts, the reference forecast is often ‘climatology’, which is effectively the set of all observed outcomes of the target variable in the past (or a sample of these outcomes over some well-defined period). Together, these outcomes make up an expectation of what the climate of a region will be like. The idea of a ‘climatological’ reference is that users are typically aware of the range of variations of climate in their location, and so we want to improve on that in a forecast by providing a narrowing of expectation down to some subset of all possible outcomes.
Skill is assessed over repeated forecast comparisons between the forecast and the reference forecast [38]. As such, ‘skill’ is a property of a forecast system, which is required to produce repeated forecasts. It is not strictly meaningful to refer to a single forecast as ‘skillful’, though each single forecast contributes to the skill of a forecast system. Many forecast comparisons are needed to get reliable statistical estimates of skill [26]. This is often a problem for climate forecasts because relatively few actual forecasts have been made to test. Even for the more common seasonal climate forecasts, sample size is an issue in estimating skill [5,39,40].
The use of hindcasts to estimate skill is generally applicable for S2S and S2D climate forecasts, where the climate applying in the hindcast period over recent decades is ostensibly not too different from the climate that applies for current forecasts. However, in the case of climate projections, we may be projecting many decades into the future, where greenhouse gas forcing has changed the underlying climatology [41] and some climate feedbacks and processes [42]. The extent to which the skill assessed in ‘projecting’ past decades is relevant to periods well into the future is an open question [13]. Such ‘hindcast’ projections may not be sufficient indicators of future projection skill, but they do provide one of the few forms of verification for climate projections. Alternatively, climate projections have been carried out for some decades now, and this provides a small sample on which to compare actual projections with observations [24,43,44,45].
Skill assessments provide formal comparison of forecasts and projections with observed outcomes. These comparisons are not always straightforward because there are different sources of skill, with different manifestations, and which play out differently in forecasts and projections. We describe here the role of skill from initial conditions and from forcing of the climate.
2.1. Initial Condition Skill
Skill that derives from the initial conditions applies only to forecasts, since projections are not initialised. If a model is well initialised to the currently observed state of the climate, it would start out with high skill. In practice, there is uncertainty in the estimation of the current state of the climate, and a model cannot be systematically initialised in all its free dimensions (over many variables and grid points). Further, the initial conditions are perturbed so that many different runs are made from a set of starting points that are all close to the observed state. The set of runs comprise an ‘ensemble’, which helps characterise the error growth in the forecasts and which allows the forecast outcome to be expressed in probabilistic terms [30]. For all these reasons, the initial skill is high, but not perfect.
We can visualise the forecast process schematically in Figure 1. The forecast starts at some initial time with a set of ensemble members all sitting close to the currently observed value of the forecast target variable. The initialised members sit inside the red ellipse in the left of the figure. Since the initial condition is from observations, the red ellipse in turn sits inside the much broader space representing the climatology (from observations) of all past outcomes for the target variable (represented by the grey space here). The forecast model generates its own climatology, which is defined by all past outcomes of the target variable in past forecasts. The forecast climatology changes as a function of the lead time of the forecasts. When the forecast commences (denoted lead 0), the model climatology is close to the observed climatology because the model is initialised to observations. Thus, the model climatology at lead 0 on the left is represented by the solid green line, which is almost the same as the observational climatology (for a well-initialised system).
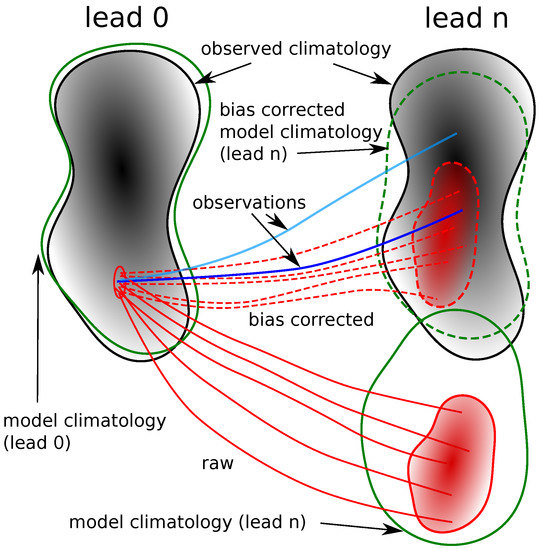
Figure 1.
Schematic of a forecast ensemble with biases. The shaded grey area represents the climatological space of the target variable as defined by past observations, with darker shading indicating regions that are occupied more frequently. The area inside the green line on the left represents the climatological space of the target variable at lead 0 defined by many past forecasts in the forecast model. The current forecast is initiated in the red ellipse around the point in climatological space where the target variable is observed to start. The forecast ensemble members follow the solid red lines and land in a region of climatological space (red shading inside solid red line) at a given lead time. The forecast climatology of the model at this lead time is defined by many past forecasts at this lead time and is given by the space inside the solid green line on the right. The bias-corrected forecast ensemble members are represented by the dashed red lines and land inside the space enclosed by dashed red lines. The dashed green lines represent the climatology of the bias-corrected forecasts at lead n. The dark/light blue lines represent the observed outcome for a case where this lies inside/outside the bias-corrected forecast ensemble.
The solid red lines in Figure 1 represent a handful of forecast ensemble members (in practice, there may be hundreds). These members typically spread as lead time increases. At the lead time at which the forecast is assessed (lead n), the members span a broader space of the climatology (than when they started) given by the red shaded area enclosed by the solid red line on the right. This red area, in turn, sits within the climatology of the forecast model for this given lead time, represented by the solid green line. This forecast climatology at lead is not the same as the observed climatology. The differences in these climatologies are related to a combination of model errors and experimental set up [46]. The difference between the model and observed climatology is referred to as ‘model bias’. If the bias is large enough, a ‘bias correction’ is usually performed to map the forecast ensemble back into the climatological space of observations [40,47]. This bias-corrected forecast is represented here by the dashed red lines that transform the ensemble members into the space spanned by the dashed red line around the red shaded region. The forecast climatology at this lead time is now transformed by the bias correction and is represented by the dashed green line. This bias-corrected model climatology will, in general, not be identical to the observed climatology (grey shading) because the bias correction process is imperfect.
In this example the dashed red shaded forecast ensemble area is still much smaller than the larger observational climatological space (grey shading), and so this forecast is less spread than climatology. If the (bias corrected) forecast ensemble contains the observed outcome as a plausible member within it, then it is termed a ‘good ensemble’ [30]. Repeated good ensembles like this one would contribute to the skill of the forecast system [35]. The ‘good ensemble’ case is represented by the dark blue observation line falling within the ensemble, and this forecast would have skill relative to a climatological forecast. On the other hand, if the observed outcome is not a plausible member of the ensemble (as shown by the light blue line that is well outside the ensemble), this is termed a ‘bad ensemble’ [30], and the forecast contributes to low skill.
In most cases considered here, we assume that the forecasting system well represents the climatology of the real climate system, either directly (using the raw forecast values) or after some appropriate bias correction. In our example schematic (Figure 1), that means that either the raw model climatology at some given lead (solid green line) or the bias-corrected climatology (dashed green line) is nearly identical to the observed climatology (black line). In practice, neither the raw nor bias-corrected climatology will be identical to the observed climatology, and some bias remains in the forecast ensembles [40]. These biases can have important influences on the evolution of the resulting forecasts by influencing the trajectories of all ensemble members after initiation [41,48]. Treating this topic is beyond the scope of this work, but should be kept in mind by the reader.
Ignoring the biases for now, we can redepict the forecast ensemble through time as in Figure 2. At some sufficiently short lead time, the skillful forecast successfully encapsulates the part of climatological space visited by the observations (middle panel). As the forecast continues with lead time, the ensemble members spread up to a point where they reach a maximum spread (right panel). Though the ensemble members still encapsulate the observations, they ‘predict’ such a wide range of outcomes that they are no more skillful than a climatological forecast. The forecast spread in the right panel ‘saturates’ when the errors in the forecast (the difference between the forecast and observations) have ceased growing. At that point, the forecast has lost all skill from the initial conditions. If the model’s forecast climatology is well representative of the real-world climatology, then there may still be some utility in a saturated forecast, even if no skill is present. We will return to this point in Section 4.1.
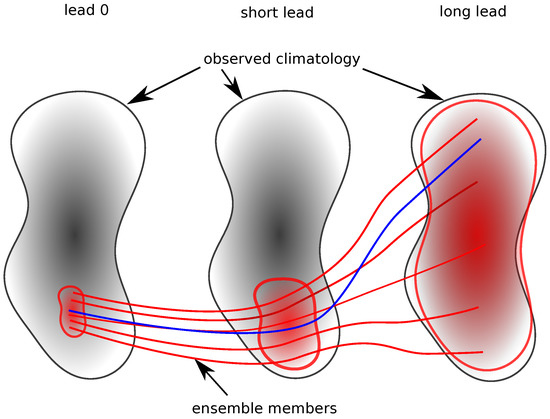
Figure 2.
Schematic of a forecast ensemble without biases. At lead 0, the forecast members (red) are initialised close to observations (blue). At short lead times (middle panel), the forecast ensemble members have spread somewhat (within the space enclosed by the red line), but still span only a part of the whole climatological space of observations (spanned by the black line). At sufficiently long lead times, the forecast has lost skill and the ensemble members now effectively span the whole climatological space of observations (red and black lines nearly colocated).
2.2. Forcing Skill
The forcing applied to a climate model is another source of skill. For climate projections, the forcing is one of the primary interests, and the goal is to examine the response to the forcing. Climate forecasts also usually contain estimates of climate forcing because it also plays a role, particularly on S2D timescales. For forecasts, initial condition skill tends to be more important in the first year or two (depending on the target variable) and then declines, whereas forcing skill is evident on longer time scales.
The effect of forcing in a climate forecast is not strictly the same as it is in a climate projection. The response of the climate system to forcing depends on the ‘state’ of the system. For example, some climate feedbacks to forcing depend on temperature [42], and so the Earth might respond to forcing at different rates depending on whether it is in a cool or warm phase of ocean cycles, such as the Pacific Decadal Oscillation [49,50]. Thus, a climate forecast might generate a more accurate response to forcing over a given interval (than a climate projection) because it started off in the right place to better reproduce the actual state-dependent response to the forcing. Thus, in a climate forecast, there is a component of initial condition skill that relates to the forcing [51], and one cannot neatly separate out skill from initial conditions and from forcing. This initialised component of forcing skill is likely modest compared to the skill from forcing that is unrelated to whether the model is initialised or not [51]. In the examples and discussion that follow, we assume very simple forcing profiles. As such, we ignore any extra skill from forcing related to initialising. Our focus is on the skill from forcing that is common in initialised (forecast) and uninitialised (projection) experiments.
Forcing can impact model climate in a range of different ways. We outline two different responses to forcing here. One response is by changing the shape of the distribution. It is likely that any applied forcing will have some impact on the shape of the distribution of a climate variable. We will illustrate this behaviour by considering a special case of this, where the change in shape is due to the shift in relative preference for a particular region in climatological space. A second response to forcing is a shift in the climatological distribution of a variable to regions (values) not previously visited. We discuss changes in shape and shifts in distribution separately (to illustrate the concepts), but in practice, both processes operate together, and forcing is likely to change the shape of, and shift, a distribution.
2.2.1. Changing Shape
One possible response to forcing is a shift in the preference for different natural modes of variability. If the climate system has preferred modes [52] or regimes [53], one response to forcing can be a shift in the preference (amount of time spent) in each of these modes [54]. This will result in a change in the distribution of the climatology without necessarily shifting the boundaries of the climatological space per se.
This situation is shown schematically in Figure 3. The climate of the projection variable is given by the broad grey space on the left. Within this space, there is one weakly preferred region in lighter grey and a strongly preferred region in darker grey. The strongly preferred region will typically contain more projection members at any given point in time as they are attracted to this space. A possible response to the applied forcing is a switch such that the weakly preferred region is now strongly preferred, and vice versa. That corresponds to the majority of projection members now sitting in the lower grey space on the right in Figure 3, which is now darker to signify the shift in preference to it. Any projection or forecast that successfully captured this change in preference would maintain skill relative to the original climatology.
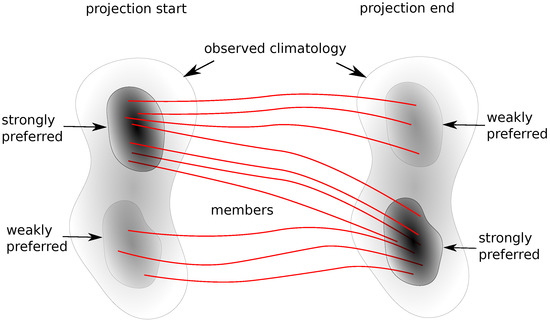
Figure 3.
Internal response to forcing. The projection starts on the left with most of the projection members resident in a strongly preferred region of the climatology represented by the upper darker grey space. In response to forcing, the weakly preferred lower grey space (on the left) becomes the strongly preferred region, attracting more members, as shown by its darker shading on the right.
2.2.2. Climatology Shift
The second response to forcing shown here is through a shift in the climatological distribution to occupy parts of phase space not previously occupied. The most common example of this is when temperature is the target variable, and forcing induces warming that shifts the climatological distribution to warmer temperatures. Some of the temperatures in the new climatology are warmer than any experienced in the original climatology. This case is represented schematically in Figure 4. The climatological space of the target variable is represented by the grey region on the left. If the model was insensitive to the forcing, then this region would be unchanged after forcing, as shown by the faint grey region on the right. In the example here, all projection members respond to the forcing by shifting the entire distribution upwards, as represented by the red region. The shifted distribution is no narrower than the observed climatology, but it has occupied new parts of climate space that differentiate it from the original observed climatology. If the observed climate were to shift into this new space in response to forcing, then a model that captures this shift would have accuracy (lie closer to the observed outcome) relative to a reference forecast based on the original climatology. If repeated tests of this kind were performed, the forecast system would have skill relative to (the original) climatology, generated by the forcing.
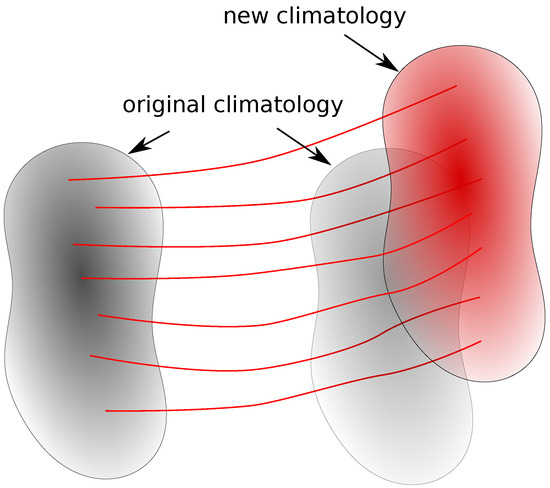
Figure 4.
Climatology shifts in response to forcing. The climatological space of the target variable is represented by the grey region on the left. This region shifts in response to forcing to yield the red region on the right.
The amount of skill reflected in a shift in climatology depends on the size of the shift. That shift, in turn, depends on the climate response time [55] and on the period used to define the reference climatology [56]. In climate forecast systems, the reference climatology typically spans the past three decades [57]. That period is, on average, much cooler than the present decade for most regions because of the considerable warming of the planet in recent decades [58,59,60,61,62]. Forecasts initialised in the present decade will start warmer (than past climatology) because the observed climate is warmer (than past climatology) and will therefore invariably have ‘skill’ relative to that past climatology in forecasting temperature.
With this view of types and sources of skill in place, we next move to an examination of climate forecasts and projections to show further where this skill can and cannot be realised. We develop and apply a simple model for this purpose and carry out a range of idealised forecast and projection experiments.
3. Forecast and Projection Experiments
We performed a series of idealised experiments with and without initial conditions and with and without climate forcing in order to draw out the implications for forecast and projection skill. The four experiments corresponded in simple terms to the projection runs or forecasts shown in Table 1.

Table 1.
Simple model experiments.
Our experiments use a simple statistical climate model, since it suffices to make the main points about skill. Our simple climate model is an idealised representation of the global mean surface temperature (gmst) time series [58]. We want a simple model that captures some of the persistence characteristics of this series. We chose to use an autoregressive AR(2) model of the form
where y represent annual values of gmst, , , is normally distributed random noise, and t is time. The simple model is intended to perform illustrative experiments only. The details of the model time series are in no way intended as realistic and do not mirror actual variations in gmst.
Experiments with initial conditions were set up as follows. We ran an ensemble of realisations of the model with perturbed initial conditions at the two times prior to initiating the forecast, and . The spread in initial conditions was generated by sampling from a normal distribution with standard deviation taken from the standard deviation of ‘total uncertainty’ specified with the Cowtan and Way data. In real climate forecasts, there is a data assimmilation process to bring a whole sequence of model climate steps near to the observed state for each member [63]. For climate projection runs with no initial conditions, we generated a set of random start values for the projection members, drawn from a normal distribution with the standard deviation corresponding to that of the climatological distribution of y. Each ensemble size was set to 100 members to generate the statistics of the ensemble distribution, but only 30 members are shown on the plots in each case for ease of viewing.
Each experiment ran for 20 years. That is longer than the usual climate forecast timescale of a season to a decade, but shorter than the usual projection timescale of many decades. This compromise allows for inspection of initial condition skill, where it is present, over the first decade, and a clear role for skill from forcing over the second decade.
The observed or ‘truth’ value for the forecast and projection experiments was taken to be one of the ensemble members. This means that the ‘observations’ here have the same statistical characteristics as the model, but with a different time evolution. For the ‘observations’, a long control run was performed for 1000 years to generate well sampled statistics. The ‘observations’ and the model shared this same climatology by construction here. We constructed it this way to keep our examples simple. In practice, the construction of ‘climatologies’ representing observations and the forecast system is complicated by the non-stationarity of the climate [64,65]. This is an important issue (which is not addressed here) because the assessed skill of forecasts depends on the ways in which the reference climatologies are constructed [23,40,66].
In the following, when we use the term ‘observations’, we always mean the ensemble member from the model selected to represent the ‘truth’ for the purposes of the experiment. We do not use actual observations in these experiments, and so the dates and magnitudes cannot be related to actual observed temperature time series. Since we are not using actual observations here, the skill measures we calculate are idealised and relate only to the model experiment. The role of our idealised skill is to assess the relative change in skill over the course of the experiment (with lead time) and how it differs between experiments with differing initial condition and forcing configurations.
The forcing experiments were generated by simply adding a linear forcing term, , to all model runs. The magnitude of was set to 0.02 C/year, which is roughly the linear rate of warming that applied during the period from 1970 to the early 2000s [62,67,68].
The toy model forecasts were scored using two different measures, the mean square error () of the forecast and the mean squared skill score (). The measures the difference between the forecast ensemble mean and the ‘observation’. For a set of instances, i, of m matched forecasts, , and observations, , . We use the here to show the degree to which forecasts have exhausted their initial condition skill, which occurs when the errors are no longer growing with lead time. The can be applied to a reference forecast such as the ‘climatology’ of observations, , as . The is then defined from these terms as . For , a perfect forecast scores 1, and a climatological forecast scores 0, so scores greater than 0 are better than climatology and scores less than 0 are worse than climatology. The is used here to show where the forecasts and projections sit relative to a climatological forecast.
The and skill score were calculated over a set of forecasts. Such sets of forecasts are often called ‘hindcasts’ when carried out over past years with a forecast system [69]. For this purpose, we generated a set of 150 forecasts with the toy model, stepping through a sequence of 150 years and initiating a new forecast each year. In the set of experiments that follow, with and without initial conditions and with and without applying forcing, we show one illustrative forecast (for the purpose of visualising the forecast data in each case), together with the skill scores from the hindcast set. The sample of 150 forecasts in the hindcast set is large enough to provide rough estimates of skill, but there is still noticeable sampling uncertainty in the scores. This is manifest as small non-monotonic variations in skill from one lead time to the next and is also evident in skill assessments of real forecast systems, which are invariabily undersampled [40]. The results for the four experiments are shown in Figure 5. We discuss each experiment in the subsections below.
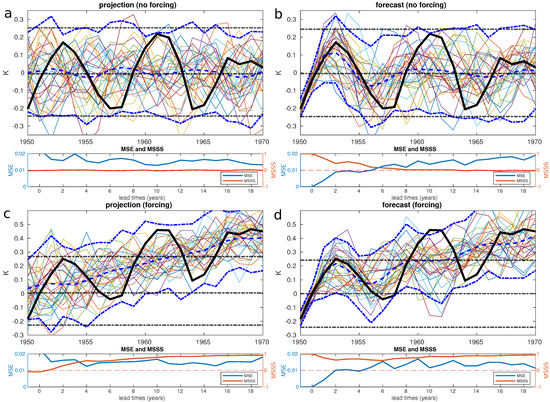
Figure 5.
Experiments without and with initial conditions and forcing. The four cases correspond to experiments with (a) no initial conditions and no forcing, (b) initial conditions and no forcing, (c) no initial conditions and forcing, and (d) both initial conditions and forcing. In part (a), top panel, the colored lines show a set of 30 idealised climate projections, nominally starting in 1950. The solid black line is the member taken to represent the ‘observations’. The horizontal dashed black lines represent the 2.5, 50, and 97.5 percentile values of the climatological distribution of ‘observations’ calculated from the long control run of the model. The dashed blue lines are the values of the 2.5 percentile, ensemble mean, and 97.5 percentile from the distribution of 100 projection members, calculated each year to show their variation in time. In part (a), the bottom panel shows the MSE and MSSS skill scores from this experiment as a function of lead time. The skill scores are calculated over the 150 forecasts in each experiment. In part (b), the colored lines are a set of 30 forecast members without forcing. The solid and dashed lines are defined as in part a. In part (c), top panel, the colored lines are a set of 30 projection members with forcing. The observations are represented by the black line, which has the same linear forcing term as the projection members. In part (d), top panel, the colored lines are 30 forecast members with forcing. The same linear forcing has been applied to the forecast members and the observed member (black line).
3.1. No Initial Conditions, No Forcing
With no initial conditions, we have a projection, not a forecast. Since there is no forcing either in this case, this experiment is more like what is often called a ‘control’ run. If we start a projection at a particular point in time, the members of the projection ensemble will be spread out in a distribution similar to the model’s climatological distribution for the projection variable. We depict what this might look like for an arbitrary projection ensemble in Figure 5a.
The projections in Figure 5a nominally start from 1950 as labelled, though the year has no real meaning here. Remember that the ‘observations’ as shown by the solid black line are not actual observations, but simply a member from the ensemble chosen to represent observations. The simple projection experiment (without forcing) makes the point that the projection ensemble has no additional skill relative to climatology. The 2.5 and 97.5 percentile bounds on the 100 member projection ensemble (in blue) approximately match the ‘observed’ 2.5 and 97.5 percentile bounds (in black) for the entire duration of the experiment (subject to sampling uncertainty). This result is also apparent from the MSSS (bottom panel), which is near 0 at all lead times, indicating skill comparable to climatology. The projection thus has no skill in forecast terms, since it simply ‘forecasts’ the climatological distribution at each point in time.
The MSE score in the bottom panel is roughly constant with lead time. In particular, the error is high, not low, for short lead times, indicating that the model error has already saturated. This is as expected in evaluating a projection in forecast terms.
3.2. Initial Conditions, No Forcing
With initial conditions specified, our experiment now represents a forecast and is shown in Figure 5b. This case with no forcing is more akin to a weather forecast than a climate forecast. The 100 forecast members are all initialised close to the ‘observations’ at the first two times and then spread as the forecast is let go.
For the forecast ensemble in Figure 5b, it is apparent that there is an initial period of skill, followed by a period where skill has been lost. The initial skill is apparent in the narrowing of the forecast ensemble envelope (dashed blue lines) relative to the climatological envelope (dashed black lines) and illustrates the skill response depicted in Figure 1. For the first half decade here the forecast ensemble has less spread than climatology, and the ensemble contains the observed value (black line). Futhermore, the ensemble mean is non-zero and tends to shadow the observed line during this period. Thus, we have a ‘good ensemble’ that is not yet saturated, yielding some initial period of skill.
In the second half of the forecast period the forecast ensemble mean is near constant and the ensemble envelope (dashed blue) nearly matches the climatological envelope (dashed black). We saw in the projection example above that these characteristics indicate that the ensemble has saturated and lost skill relative to climatology. These same characteristics are born out in the hindcast skill scores in the bottom panel of Figure 5b. The score is better than climatology for the first 5-year lead, reflecting the initial condition skill. The model error () grows during the first 5-year lead while initial condition skill is present. After lead 5, the model error stabilises with the lead, indicating saturation of the forecast ensemble and skill dropping to the level of climatology (indicated by the near 0).
3.3. No Initial Conditions, Forcing
We now have the more usual case for climate projections where forcing is applied, but of course, no initial conditions are given, as in ‘historical’ climate runs. This experiment is shown in Figure 5c. As expected, the projection ensemble mean (dashed blue line) responds to the forcing and increases smoothly. What it does not do, and could not do, because it is not initialised, is follow the year-to-year variations of the observations (black line). Even in the first year or two, the projection ensemble mean is not expected to track the observations.
On the longer timescale here (two decades), both the observations and the projection ensemble respond to the forcing. Towards the end of the projection period shown in Figure 5c, the climate has warmed sufficiently that the projection ensemble envelope (dashed blue lines) has shifted almost entirely outside the original observations’ climatalogical envelope (dashed black lines). The observations also lie inside the projection envelope then, and have shifted outside the original observations’ climatology. The projections thus have forcing skill due to a climatology shift as depicted schematically in Figure 4. The projection ensemble would be a better guide to climate a decade or two ahead here than expectations based around the original observations’ climatology.
While we say that this projection has forcing skill, a large number of these projections need to be made in hindcast mode and scored against observed outcomes in order to make a determination that the system is skillful. The hindcast results (bottom panel of Figure 5c) do bear that out in this case. The is 0 at a short lead, indicating no more skill than climatology, but then grows steadily with lead time, indicating forcing skill that is much better than climatology.
3.4. Initial Conditions, Forcing
Climate forecasts usually include changes in forcing and can benefit from both initial condition skill and forcing skill. This case is shown in Figure 5d. The initial condition skill is evident here in that the forecast ensemble envelope (dashed blue lines) is narrower than the observational climatology envelope (dashed black lines) in the first few years and in that the forecast ensemble mean (dashed blue) tracks the interannual variations in the observations (black line) quite well for the first half decade.
By the second decade in Figure 5d the forecast ensemble mean is no longer tracking the interannual variations in the observations and the forecast has lost skill from initial conditions. However, like the previous projection example, the forecast ensemble captures the shift in climatology due to the forcing and thus has forcing skill. The hindcast results (bottom panel) show this behaviour. The skill () starts out high and is due to the initial conditions. The skill from the initial conditions diminishes with lead time over the first few leads as the model errors () grow. The skill then slowly rises again with lead time (after lead 5), even as the growth of error saturates ( roughly constant with lead). This is because the forecast is gaining ‘skill’ from the forcing.
It is clear here that the skill conferred by forcing and initial conditions is different in nature. The initial condition skill derives from a narrowing of expected distribution of the target variable (relative to climatology), and the ability to say something about where in the distribution the target variable is more likely to be found. On the other hand, forcing skill leading to a climatological shift tells us how the overall climatology of the target variable is changing, but does not tell us whether one part of the distribution is more favoured or not.
4. Mixing Forecasts and Projections
There are some occasions where it might be convenient to use a set of forecasts as if they were projections, or conversely, to use projections as if they were forecasts. Forecasts can be treated as projections once they have lost initial condition skill. Projections can be treated as forecasts when forcing skill dominates initial condition skill. We discuss these cases in more detail here.
4.1. Forecasts as Projections
Climate forecasts can have both initial condition skill and forcing skill. Once the skill from initial conditions has been exhausted in a forecast, the forecast functions effectively like a projection. Like a projection, the forecast can then reap forcing skill. Such skill is potentially important in any S2D forecast because the change in forcing has an impact on these timescales [68,70,71].
However, suppose there was no change in forcing over the forecast period, as in our example in Section 3.2. What use is such a forecast ensemble when initial condition skill has been lost? The forecast ensemble now effectively just represents climatology, assuming the model climatology is representative of the observed climatology. In our simple example, the model and observed climatology are statistically identical, so this is indeed the case. On the face of it, representing the observed climatology is not offering much. In practice, however, this can be very useful information because the observed climatology of the target variable may not be well known. In particular, we are often interested in cases where the target variable takes on extreme values in its distribution, such as when a severe drought [72], flooding rain [73,74,75] or prolonged heatwave [76] occurs. These extremes sit in the tail of the distribution. For many climate datasets, we will have, at best, a century of instrumental observations. When we consider outcomes like extreme multiyear droughts, there will be very few extreme events in the hundred-year sequence, so the tails of the distribution will be poorly sampled [74].
S2D forecast groups have recognized that the collection of large ensembles of hindcasts and forecasts provides a sample of the population of the target variable that is many orders of magnitude larger than the observed population of the target variable [73]. If the model population has similar statistical characteristics to the observed population, then the model ensemble presents an opportunity to provide much better resolution of the extreme outcomes in the tails of the distribution.
The concept underlying this approach using the model large ensemble is represented schematically in Figure 6. A previously ‘unseen’ [73] event ‘X’ occurs that sits outside the sampled observations’ climatology. Perhaps such events would be observed in a longer sample of observations. However, lacking such observations, we do not know where this event might sit in a better-sampled distribution (represented hypothetically by the unknown region labelled ‘unsampled observations’). With few or no other events of this magnitude, there is little empirical basis to estimate the likelihood of such an event. One way around this is via extreme value theory [77], where one makes assumptions about the shape of the (unobserved) long tail of the observational distribution. The alternate approach considered here uses the large ensemble hindcast data to generate a much larger sample in the model world, represented by the outer shaded red region in Figure 6. The extreme event ‘X’ now lies inside this much broader climatological sample. If the model is deemed to be a sufficiently good representation of the statistics of the observed climate, then the model large ensemble climatology can be used to estimate the likelihood of event ‘X’ occurring, since there are many events of equivalent (or greater) magnitude to ‘X’ in the large ensemble.
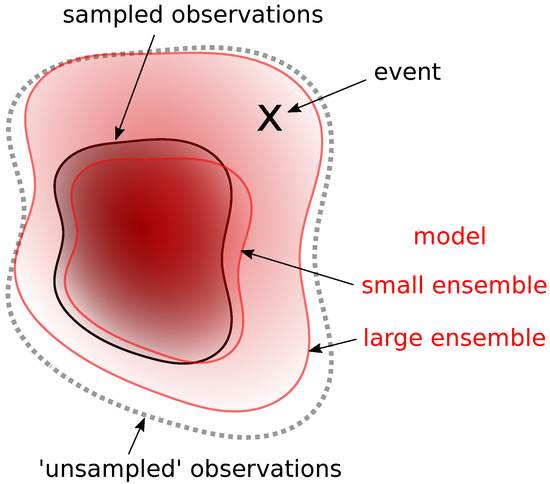
Figure 6.
Observed and large ensemble climatologies. The observed climatology is represented by the shaded gray area labeled ‘sampled observations’. With a hypothetical longer sample of observations, the observed climatology could be broader and is represented here as ‘unsampled observations’. The model climatology from a small/large hindcast ensemble is represented by the small/large shaded red regions. A single extreme event ’X’ occurs, which is outside the sampled observation space but inside the large ensemble space.
Of course, in practice, our model would not have the same statistics underlying its climatology as observations, and we could not be certain that any change in the model tail were not simply a property of the model alone. In order to have some confidence in the model climatology, some tests need to be performed to assess how well the model climatology matches the observed climatology [72,73,78]. Systematic approaches to assess model climatologies are being undertaken as part of the project to share multimodel ensembles from initialised climate model runs [79].
If the model climatology is representative of the observed, then the very large sample generated from the model forecasts can provide a better indication of the likelihoods of very extreme events. Further, the circulation data to explore the mechanisms underlying these events is also available from the model forecasts, which presents an opportunity to better understand the events [73]. In this example, the model forecasts have exhausted their initial condition skill and are not useful for narrowing the expectation from a climatological distribution. However, they help elucidate that distribution more fully.
4.2. Projections as Forecasts
We noted earlier that projections are not initialised and can therefore have no skill from initial conditions. For most climate variables of interest, the short-term variation in values of the variable is driven by internal climate processes, and the response to forcing is felt more slowly over time. These internal variations can be tracked by initialising, as in forecasts. Without initialising, the internal variations in observations are generally not in sequence with equivalent variations in the models. In a projection ensemble, these internal variations will tend to ‘average-out’ in the ensemble mean at any given point in time. This is so because none of the individual projection members are initialised and will each have effectively random sequences of natural variability. For the observations, we only have one realisation, and so there is no ‘averaging-out’ of natural variations. At any given point in time, the observations will have some excursion away from the mean climate state due to internal variability. Therefore, for observations, we need to average over time (rather than members) to arrive at a target variable that can be meaningfully compared with the projections [80].
The time average for comparing observations with projections needs to be long enough so that the contributions from internal variations are small compared to the forced response (but not so long that even the forced response is obscured). Issues can arise in cases where this period is not sufficiently long. For example, the warming trends in climate projections have been compared with the observed trend to assess whether projections are warming at about the right rate [81]. The issues at play in making this judgement can be illustrated in Figure 5c with the toy model data. The projection ensemble here is a ‘good ensemble’ in that it encompasses the observations over the entire time series. While the ensemble mean of the projections (dashed blue line) increases fairly smoothly, the observations (and individual ensemble members) fluctuate between the warm and cold extremes of the projection ensemble envelope. The longer-term trend in observations over the entire period is close to the ensemble mean trend, but the observed trend over shorter periods of a decade or so can be zero, or even negative, for the right choice of start and end years. An assessment of projection trends and observed trend over a single period of a decade or so [81] is thus not an adequate test of model skill because the time average of the observations is not long enough [62,68] and because skill cannot be meaningfully assessed with a single trial. Many such comparisons would need to be performed to make a fair judgement about the projection forcing skill.
Methods have been developed to subsample model projections to more closely mimic forecasts [28,82,83,84]. In a large ensemble of projections, some of the projection members may be more or less in sequence with natural observed variations by chance alone. Such members have about the same initial state as observations, and thus might perform as if they were forecasts. To illustrate the subsampling method, we subsampled the projection members in the projection experiment in Figure 5c, retaining only those members that started close to the observed member and which had the same trend sign as the observed member at that initial time. The subsampled projections are shown in Figure 7. In this case, the ensemble mean of the projection subsample (dashed blue line) now tracks the observations member for half a decade and looks much more like the ensemble mean in the experiment with both forcing and initial conditions (Figure 5d).
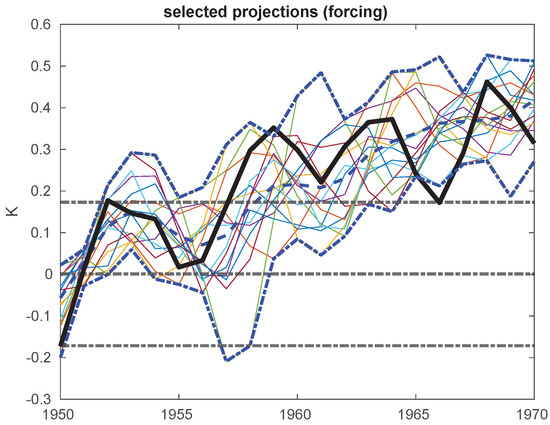
Figure 7.
As in Figure 5c, but where only a selected subset of projection members have been included in the projection ensemble. The selected subset are within K of the observation member at the second time step and have the same sign of change from the first to second time step.
5. Conclusions
The evaluation of climate forecasts and projections relates to a broad set of attributes about the quality of a set of model outputs. Verification is only one component of evaluation, but it is the component where model outcomes are compared with real world outcomes. The verification process is formalised through skill measures. The concept of skill is simple enough in as much as it requires comparison of a model forecast with a reference forecast. In practice, the assessment of skill is difficult because that assessment requires large numbers of comparable cases to develop stable skill estimates.
For the case of climate projections many decades ahead, there is no direct comparison with observed outcomes, and the concept of skill is not directly applicable. In this case, hindcasts over past decades can be performed to assess the skill of the system over past climate. Such assessment will be partial because the climate state may be different in the past and because the number of hindcast experiments is still likely to be very limited. Nonetheless, this is the only way to provide some empirical skill assessment pertinent to longer term climate projections.
For shorter-term climate projections over a decade or two, there have been past projections made that can now be compared with observations. However, skill assessment for short term projections is problematic when the target climate variable is influenced by natural variations as well as climate forcing on the time scale assessed. This is the case, for example, with surface temperature projections.
When natural variability is not small relative to the role of forcing, then it is important to initialise the model runs: that is, provide a forecast, not a projection. Climate forecasts are both initialised and provide an estimate of time varying forcing. When skill from initial conditions is exhausted, climate forecasts may still provide skill from forcing.
The skill conferred by initial conditions and forcing is manifested differently. Initial condition skill is usually associated with a narrowing of the expected distribution relative to a forecast baseline such as the climatological distribution. Forcing skill could be expressed through a shift in the overall climatological distribution without narrowing of the distribution per se. There may also be cases where forcing leads to a shift in residence between different preferred climate modes. In this case, forcing is associated with a change in shape of the distribution and could provide information about which part of the distribution is more favoured. In practice, both shifts and changes in the shape of the distribution will occur in response to forcing.
With ongoing warming and changes in the climate, the background climate that sets the experience of variability and extremes is changing. It will be important to update our views of these new climate normals with climate forecasts and projections, and in turn, to provide skill assessments of these outlooks. Without good faith efforts at verification, the accuracy of climate forecasts and projections remains partly, and perhaps substantially, open-ended. With verification, there are still limited trials on climate timescales and limited numbers of forecasts, that mean any resulting skill assessment is also partial. While partial skill assessments may provide only weak ‘truthing’ of a climate product, that is still better than no ‘truthing’. The concept of skill is subtle and there are pitfalls in interpretation [5,26,40,66,69]. Users of climate forecasts and projections may be better placed to interpret skill in climate products and apply them when they have an appreciation of the limitations and sources of skill as outlined here. However, this assessment was substantially simplified and ignored some of the key challenges in skill assessment [85,86,87,88], which need to be addressed and communicated in future work.
Author Contributions
All authors contributed jointly and equally to the conceptualisation, methodology, review, and editing of the paper. The analysis and writing were primarily carried out by J.S.R. All authors have read and agreed to the published version of the manuscript.
Funding
Funding for a workshop on Climate Information for Adaptation was from the U.K. Economic and Social Research Council (ES/R009708/1) Centre for Climate Change, Economics and Policy (CCCEP), and the University of Leeds.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The gmst data used in this work is available at https://www-users.york.ac.uk/~kdc3/papers/, accessed on 20 May 2021.
Acknowledgments
We are grateful for the support of the Multiyear Climate Project at CSIRO. The participants at a Workshop on Climate Information for Adaptation contributed valuable feedback on this work.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| gmst | global mean surface temperature |
| S2S | subseasonal to seasonal |
| S2D | seasonal to decadal |
| ENSO | El Niño Southern Oscillation |
| MSE | mean square error |
| MSSS | mean squared skill score |
References
- Fiedler, T.; Pitman, A.; Mackenzie, K.; Wood, N.; Jakob, C.; Perkins-Kirkpatrick, S. Business risk and the emergence of climate analytics. Nat. Clim. Chang. 2021, 11, 87–94. [Google Scholar] [CrossRef]
- Lorenz, E. The predictability of a flow which possesses many scales of motion. Tellus 1969, 21, 289–307. [Google Scholar] [CrossRef]
- Kirtman, B.; Min, D.; Infanti, J.; Kinter, J.K.; Paolino, D.; Zhang, Q.; Dool, H.V.D.; Saha, S.; Mendez, M.; Becker, E.; et al. The North American multimodel ensemble: Phase-1 seasonal-to-interannual prediction; phase-2 toward developing intraseasonal prediction. Bull. Am. Met. Soc. 2014, 95, 585–601. [Google Scholar] [CrossRef]
- Pegion, K.; Kirtman, B.P.; Becker, E.; Collins, D.C.; LaJoie, E.; Burgman, R.; Bell, R.; DelSole, T.; Min, D.; Zhu, Y.; et al. The Subseasonal Experiment (SubX): A Multimodel Subseasonal Prediction Experiment. Bull. Am. Met. Soc. 2019, 100, 2043–2060. [Google Scholar] [CrossRef]
- Goddard, L.; Kumar, A.; Solomon, A.; Smith, D.; Boer, G.; Gonzalez, P.; Kharin, V.; Merryfield, W.; Deser, C.; Mason, S.; et al. A verification framework for interannual-to-decadal predictions experiments. Clim. Dyn. 2013, 40, 245–272. [Google Scholar] [CrossRef] [Green Version]
- Meehl, G.A.; Richter, J.H.; Teng, H.; Capotondi, A.; Cobb, K.; Doblas-Reyes, F.; Donat, M.G.; Engl, M.H.; Fyfe, J.C.; Han, W.; et al. Initialized Earth system prediction from subseasonal to decadal timescales. Nat. Rev. Earth Environ. 2021, 2, 340–357. [Google Scholar] [CrossRef]
- Dessai, S.; Lu, X.; Risbey, J. On the role of climate scenarios for adaptation planning. Glob. Environ. Chang. 2005, 15, 87–97. [Google Scholar] [CrossRef]
- Simmons, A.; Hollingsworth, A. Some aspects of the improvement in skill of numerical weather prediction. Q. J. R. Meteor. Soc. 2002, 128, 647–677. [Google Scholar] [CrossRef]
- Shukla, J. Predictability in the midst of chaos: A scientific basis for climate forecasting. Science 1998, 282, 728–731. [Google Scholar] [CrossRef]
- Dessai, S.; Hulme, M. Does climate adaptation policy need probabilities? Clim. Policy 2004, 4, 107–128. [Google Scholar] [CrossRef]
- Dessai, S.; Hulme, M. Assessing the robustness of adaptation decisions to climate change uncertainties: A case study on water resources management in the East of England. Glob. Environ. Chang. 2007, 17, 59–72. [Google Scholar] [CrossRef]
- Weisheimer, A.; Palmer, T. On the reliability of seasonal climate forecasts. J. R. Soc. Interface 2003, 11, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Baldissera Pacchetti, M.; Dessai, S.; Bradley, S.; Stainforth, D. Assessing the quality of regional climate information. Bull. Am. Met. Soc. 2021, 102, 476–491. [Google Scholar] [CrossRef]
- Held, I. Large-scale dynamics and global warming. Bull. Am. Met. Soc. 1993, 74, 228–241. [Google Scholar] [CrossRef] [Green Version]
- Held, I.; Soden, B. Robust responses of the hydrological cycle to global warming. J. Clim. 2006, 19, 5686–5699. [Google Scholar] [CrossRef]
- Risbey, J.S.; Lamb, P.J.; Miller, R.L.; Morgan, M.C.; Roe, G.H. Exploring the Structure of Regional Climate Scenarios by Combining Synoptic and Dynamic Guidance and GCM output. J. Clim. 2002, 15, 1036–1050. [Google Scholar] [CrossRef] [Green Version]
- Schneider, T.; O’Gorman, P.; Levine, X. Water vapor and the dynamics of climate changes. Rev. Geophys. 2010, 48, RG3001. [Google Scholar] [CrossRef] [Green Version]
- Seager, R.; Naik, N.; Vecchi, G. Thermodynamic and dynamic mechanisms for large-scale changes in the hydrological cycle in response to global warming. J. Clim. 2010, 23, 4561–4668. [Google Scholar] [CrossRef] [Green Version]
- Tamarin-Brodsky, T.; Hodges, K.; Hoskins, B.; Shepherd, T. A Dynamical Perspective on Atmospheric Temperature Variability and its Response to Climate Change. J. Clim. 2019, 32, 1707–1724. [Google Scholar] [CrossRef] [Green Version]
- Risbey, J.S.; Stone, P.H. A Case Study of the Adequacy of GCM Simulations for Input to Regional Climate Change Assessments. J. Clim. 1996, 9, 1441–1467. [Google Scholar] [CrossRef]
- Risbey, J.; O’Kane, T. Sources of knowledge and ignorance in climate research. Clim. Chang. 2011, 108, 755–773. [Google Scholar] [CrossRef]
- Shepherd, T. Atmospheric circulation as a source of uncertainty in climate change projections. Nat. Geosci. 2014, 7, 703–708. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.; L’Heureux, M.; Li, S.; DeWitt, D. Skill of real-time seasonal ENSO model predictions during 2002–2011: Is our capability increasing? Bull. Am. Met. Soc. 2012, 93, 631–651. [Google Scholar] [CrossRef]
- Grose, M.; Risbey, J.; Whetton, P. Tracking regional temperature projections from the early 1990s in light of variations in regional warming, including ‘warming holes’. Clim. Chang. 2017, 140, 307–322. [Google Scholar] [CrossRef]
- Barnston, A.G.; Tippett, M.; Ranganathan, M.; L’Heureux, M. Deterministic skill of ENSO predictions from the North American Multimodel Ensemble. Clim. Dynam. 2019, 53, 7215–7234. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jolliffe, I.; Stephenson, D. Forecast Verification: A Practioner’s Guide in Atmospheric Science; Wiley: Exeter, UK, 2012; 292p. [Google Scholar]
- Bray, D.; von Storch, H. Prediction or projection: The nomenclature of climate science. Sci. Commun. 2009, 30, 534–543. [Google Scholar] [CrossRef] [Green Version]
- Risbey, J.; Lewandowsky, S.; Langlais, C.; Monselesan, D.; O’Kane, T.; Oreskes, N. Well-estimated global surface warming in climate projections selected for ENSO phase. Nat. Clim. Chang. 2014, 4, 835–840. [Google Scholar] [CrossRef]
- Murphy, A. Skill scores based on the mean square error and their relationships to the correlation coefficient. Mon. Weather Rev. 1988, 116, 2417–2424. [Google Scholar] [CrossRef]
- Kalnay, E. Atmospheric Modeling, Data Assimilation and Predictability; Cambridge Univ. Press: Cambridge, UK, 2002; 364p. [Google Scholar]
- Peña, M.; Kalnay, E. Separating fast and slow modes in coupled chaotic systems. Nonlinear Proc. Geoph. 2004, 11, 319–327. [Google Scholar] [CrossRef]
- O’Kane, T.; Squire, D.; Sandery, P.; Kitsios, V.; Matear, R.; Moore, T.; Risbey, J.; Watterson, I. Enhanced ENSO prediction via augmentation of multi-model ensembles with initial thermocline perturbations. J. Clim. 2020, 33, 2281–2293. [Google Scholar] [CrossRef]
- Forster, P.; Andrews, T.; Good, P.; Gregory, J.; Jackson, L.; Zelinka, M. Evaluating adjusted forcing and model spread for historical and future scenarios in the CMIP5 generation of climate models. J. Geophys. Res. 2013, 118, 1139–1150. [Google Scholar] [CrossRef] [Green Version]
- Power, S.; Haylock, M.; Colman, R.; Wang, X. The predictability of interdecadal changes in ENSO activity and ENSO teleconnections. J. Clim. 2006, 19, 4755–4771. [Google Scholar] [CrossRef] [Green Version]
- Murphy, A.H. What Is a Good Forecast? An Essay on the Nature of Goodness in Weather Forecasting. Weather Forecast. 1993, 8, 281–293. [Google Scholar] [CrossRef] [Green Version]
- Gerrity, J. A note on Gandin and Murphy’s equitable skill score. Mon. Weather Rev. 1992, 120, 2709–2712. [Google Scholar] [CrossRef]
- Mittermaier, M. The Potential Impact of Using Persistence as a Reference Forecast on Perceived Forecast Skill. Weather Forecast. 2008, 23, 1022–1031. [Google Scholar] [CrossRef]
- DelSole, T.; Tippett, M.K. Forecast comparison based on random walks. Mon. Weather Rev. 2016, 144, 615–626. [Google Scholar] [CrossRef]
- Barnston, A.; Li, S.; Mason, S.; DeWitt, D.; Goddard, L.; Gong, X. Verification of the first 11 years of IRI’s seasonal climate forecasts. J. Appl. Meteorol. Climatol. 2010, 49, 493–520. [Google Scholar] [CrossRef]
- Risbey, J.; Squire, D.; Black, A.; DelSole, T.; Lepore, C.; Matear, R.; Monselesan, D.; Moore, T.; Richardson, D.; Schepen, A.; et al. Standard assessments of climate forecast skill can be misleading. Nat. Commun. 2021, 12, 4346. [Google Scholar] [CrossRef]
- Kharin, V.; Boer, G.; Merryfield, W.; Scinocca, J.; Lee, W. Statistical adjustment of decadal predictions in a changing climate. Geophys. Res. Lett. 2012, 39, L19705. [Google Scholar] [CrossRef]
- Hansen, J.; Takahashi, T. Climate processes and climate sensitivity. AGU Geophys. Monogr. 1984, 29, 1–32. [Google Scholar]
- Rahmstorf, S.; Cazenave, A.; Church, J.; Hansen, J.; Keeling, R.; Parker, D.; Somerville, R. Recent climate observations compared to projections. Science 2007, 316, 709. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dessai, S.; Hulme, M. How do UK climate scenarios compare with recent observations? Atmos. Sci. Let. 2008, 9, 189–195. [Google Scholar] [CrossRef]
- Hausfather, Z.; Drake, H.; Abbott, T.; Schmidt, G. Evaluating the performance of past climate model projections. Geophys. Res. Lett. 2020, 47, e2019GL085378. [Google Scholar] [CrossRef]
- Stockdale, T. Coupled ocean-atmosphere forecasts in the presence of climate drift. Mon. Weather Rev. 1997, 125, 809–818. [Google Scholar] [CrossRef]
- Manzanas, R.; Gutierrez, J.; Bhend, J.; Hemri, S.; Doblas-Reyes, F.; Torralba, V.; Penabad, E. Bias adjustment and ensemble recalibration methods for seasonal forecasting: A comprehensive intercomparison using the C3S dataset. Clim. Dynam. 2019, 53, 1287–1305. [Google Scholar] [CrossRef]
- Choudhury, D.; Sen Gupta, A.; Sharma, A.; Mehrotra, R.; Sivakumar, B. An Assessment of Drift Correction Alternatives for CMIP5 Decadal Predictions. J. Geophys. Res. 2017, 122, 10282–10296. [Google Scholar] [CrossRef]
- Mantua, N.; Hare, S. The Pacific Decadal Oscillation. J. Oceanogr. 2002, 58, 35–44. [Google Scholar] [CrossRef]
- Risbey, J.; Lewandowsky, S.; Hunter, J.; Monselesan, D. Betting strategies on fluctuations in the transient response of greenhouse warming. Phil. Trans. R. Soc. A 2015, 373, 14–27. [Google Scholar] [CrossRef]
- Sospedra-Alfonso, R.; Boer, G. Assessing the Impact of Initialization on Decadal Prediction Skill. Geophys. Res. Lett. 2020, 47, e2019GL086361. [Google Scholar] [CrossRef] [Green Version]
- Lorenz, E. Climatic determinism. Meteor. Monogr. 1968, 8, 1–3. [Google Scholar]
- Charney, J.G.; DeVore, J.G. Multiple Flow Equilibria in the Atmosphere and Blocking. J. Atmos. Sci. 1979, 36, 1205–1216. [Google Scholar] [CrossRef] [Green Version]
- Corti, S.; Molteni, F.; Palmer, T. Signature of recent climate change in frequencies of natural atmospheric circulation regimes. Nature 1999, 398, 799–802. [Google Scholar] [CrossRef]
- Hansen, J.; Russell, G.; Lacis, A.; Fung, I.; Rind, D.; Stone, P. Climate response times: Dependence on climate sensitivity and ocean mixing. Science 1985, 229, 857–859. [Google Scholar] [CrossRef] [PubMed]
- Hulme, M.; Dessai, S.; Lorenzoni, I.; Nelson, D. Unstable climates: Exploring the statistical and social constructions of ‘normal’ climate. Geoforum 2009, 40, 197–206. [Google Scholar] [CrossRef]
- Arguez, A.; Vose, R. The definition of the standard WMO climate normal: The key to deriving alternative climate normals. Bull. Am. Met. Soc. 2011, 92, 699–704. [Google Scholar] [CrossRef]
- Cowtan, K.; Way, R. Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q. J. R. Meteor. Soc. 2014, 140, 1935–1944. [Google Scholar] [CrossRef] [Green Version]
- Cowtan, K.; Hausfather, Z.; Hawkins, E.; Jacobs, P.; Mann, M.; Miller, S.; Steinman, B.; Stolpe, M.; Way, R. Robust comparison of climate models with observations using blended land air and ocean sea surface temperatures. Geophys. Res. Lett. 2015, 42, 6526–6534. [Google Scholar] [CrossRef] [Green Version]
- Lewandowsky, S.; Risbey, J.; Oreskes, N. On the definition and identifiability of the alleged “hiatus” in global warming. Sci. Rep. 2015, 5, 16784. [Google Scholar] [CrossRef]
- Lewandowsky, S.; Risbey, J.; Oreskes, N. The ‘pause’ in global warming: Turning a routine fluctuation into a problem for science. Bull. Am. Met. Soc. 2016, 97, 723–733. [Google Scholar] [CrossRef] [Green Version]
- Risbey, J.; Lewandowsky, S.; Cowtan, K.; Oreskes, N.; Rahmstorf, S.; Jokimäki, A.; Foster, G. A fluctuation in surface temperature in historical context: Reassessment and retrospective on the evidence. Environ. Res. Lett. 2018, 13, 123008. [Google Scholar] [CrossRef]
- Toth, Z.; Kalnay, E. Ensemble forecasting at NCEP and the breeding method. Mon. Weather Rev. 1997, 125, 3297–3319. [Google Scholar] [CrossRef]
- Franzke, C.; Crommelin, D.; Fischer, A.; Majda, A. A hidden Markov model perspective on regimes and metastability in atmospheric flows. J. Clim. 2008, 21, 1740–1757. [Google Scholar] [CrossRef]
- Monselesan, D.; O’Kane, T.; Risbey, J.; Church, J. Internal climate memory in observations and models. Geophys. Res. Lett. 2015, 42, 1232–1242. [Google Scholar] [CrossRef]
- Tippett, M.; Ranganathan, M.; L’Heureux, M.; Barnston, A.; DelSole, T. Assessing probabilistic predictions of ENSO phase and intensity from the North American Multimodel Ensemble. Clim. Dynam. 2019, 53, 7497–7518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Risbey, J.; Grose, M.; Monselesan, D.; O’Kane, T.; Lewandowsky, S. Transient response of the global mean warming rate and its spatial variation. Weather Clim. Extrem. 2017, 18, 55–64. [Google Scholar] [CrossRef]
- Lewandowsky, S.; Cowtan, K.; Risbey, J.; Mann, M.; Steinman, B.; Oreskes, N.; Rahmstorf, S. The ‘pause’ in global warming in historical context: Comparing models to observations. Environ. Res. Lett. 2018, 13, 123007. [Google Scholar] [CrossRef]
- Kumar, A.; Hu, Z.; Jha, B.; Peng, P. Estimating ENSO predictability based on multi-model hindcasts. Clim. Dynam. 2017, 48, 39–51. [Google Scholar] [CrossRef]
- Schmidt, G.; Shindell, D.; Tsigaridis, K. Reconciling warming trends. Nat. Geosci. 2014, 7, 158–160. [Google Scholar] [CrossRef]
- Marotzke, J.; Forster, P. Forcing, feedback, and internal variability in global temperature trends. Nature 2015, 517, 565–570. [Google Scholar] [CrossRef] [Green Version]
- Squire, D.; Richardson, D.; Risbey, J.; Black, A.; Kitsios, V.; Matear, R.; Monselesan, D.; Moore, T.; Tozer, C. Likelihood of unprecedented drought and fire weather during Australia’s 2019 megafires. NPJ Clim. Atmos. Sci. 2021, 4, 64. [Google Scholar] [CrossRef]
- Thompson, V.; Dunstone, N.; Scaife, A.; Smith, D.; Slingo, J.; Brown, S.; Belcher, S. High risk of unprecedented UK rainfall in the current climate. Nat. Commun. 2017, 8, 107–113. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tozer, C.; Risbey, J.; Grose, M.; Monselesan, D.; Squire, D.; Black, A.; Richardson, D.; Sparrow, S.; Li, S.; Wallom, D. A one-day extreme rainfall event in Tasmania: Process evaluation and long tail attribution. Bull. Am. Met. Soc. 2020, 101, s123–s128. [Google Scholar] [CrossRef] [Green Version]
- Kelder, T.; Müller, M.; Slater, L.; Marjoribanks, T.; Wilby, R.; Prudhomme, C.; Bohlinger, P.; Ferranti, L.; Nipen, T. Using UNSEEN trends to detect decadal changes in 100-year precipitation extremes. NPJ Clim. Atmos. Sci. 2020, 3, 47. [Google Scholar] [CrossRef]
- Kay, G.; Dunstone, N.; Smith, D.; Dunbar, T.; Eade, R.; Scaife, A. Current likelihood and dynamics of hot summers in the UK. Environ. Res. Lett. 2020, 15, 094099. [Google Scholar] [CrossRef]
- Katz, R. Extreme value theory for precipitation: Sensitivity analysis for climate change. Adv. Water Res. 1999, 23, 133–139. [Google Scholar] [CrossRef]
- Kelder, T.; Wanders, N.; van der Wiel, K.; Marjoribanks, T.; Slater, L.; Wilby, R.; Prudhomme, C. Interpreting extreme climate impacts from large ensemble simulations; are they unseen or unrealistic? Environ. Res. Lett. 2022, 17, 044052. [Google Scholar] [CrossRef]
- Deser, C.; Lehner, F.; Rodgers, K.; Ault, T.; Delworth, T.; DiNezio, P.; Fiore, A.; Frankignoul, C.; Fyfe, J.; Horton, D.; et al. Insights from Earth system model initial-condition large ensembles and future prospects. Nat. Clim. Chang. 2020, 10, 277–286. [Google Scholar] [CrossRef]
- Baldissera Pacchetti, M. A role for spatiotemporal scales in modeling. Stud. Hist. Phil. Sci. 2018, 67, 14–21. [Google Scholar] [CrossRef]
- Fyfe, J.; Gillett, N.; Zwiers, F. Overestimated global warming over the past 20 years. Nat. Clim. Chang. 2013, 3, 767–769. [Google Scholar] [CrossRef]
- Meehl, G.; Teng, H.; Arblaster, J. Climate model simulations of the observed early-2000s hiatus of global warming. Nat. Clim. Chang. 2014, 4, 898–902. [Google Scholar] [CrossRef] [Green Version]
- Hegerl, G.; Ballinger, A.; Booth, B.; Borchert, L.; Brunner, L.; Donat, M.; Doblas-Reyes, F.; Harris, G.; Lowe, J.; Mahmood, R.; et al. Toward Consistent Observational Constraints in Climate Predictions and Projections. Front. Clim. 2021, 3, 678109. [Google Scholar] [CrossRef]
- Mahmood, R.; Donat, M.; Ortega, P.; Doblas-Reyes, F.; Ruprich-Robert, Y. Constraining Decadal Variability Yields Skillful Projections of Near-Term Climate Change. Geophys. Res. Lett. 2021, 48, e2021GL094915. [Google Scholar] [CrossRef]
- Ebert, B.; Wilson, L.; Weigel, A.; Mittermaier, M.; Nurmi, P.; Gill, P.; Gober, M.; Joslyn, S.; Brown, B.; Fowler, T.; et al. Progress and challenges in forecast verification. Meteorol. Appl. 2013, 20, 130–139. [Google Scholar] [CrossRef]
- Bojovic, D.; Nicodemou, A.; Clair, A.S.; Christel, I.; Doblas-Reyes, F. Exploring the landscape of seasonal forecast provision by Global Producing Centres. Clim. Chang. 2002, 172, 8. [Google Scholar] [CrossRef]
- Ebert, P.; Milne, P. Methodological and conceptual challenges in rare and severe event forecast verification. Nat. Hazards Earth Syst. Sci. 2022, 22, 539–557. [Google Scholar] [CrossRef]
- Meehl, G.; Teng, H.; Smith, D.; Yeager, S.; Merryfield, W.; Doblas-reyes, F.; Glanville, A. The effects of bias, drift, and trends in calculating anomalies for evaluating skill of seasonal-to-decadal initialized climate predictions. Clim. Dynam. 2022, 7–8, 1–22. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).