Abstract
This paper investigates the incentive of credit rating agencies (CRAs) to bias ratings using a semiparametric, ordered-response model. The proposed model explicitly takes conflicts of interest into account and allows the ratings to depend flexibly on risk attributes through a semiparametric index structure. Asymptotic normality for the estimator is derived after using several bias correction techniques. Using Moody’s rating data from 2001 to 2016, I found that firms related to Moody’s shareholders were more likely to receive better ratings. Such favorable treatments were more pronounced in investment grade bonds compared with high yield bonds, with the 2007–2009 financial crisis being an exception. Parametric models, such as the ordered-probit, failed to identify this heterogeneity of the rating bias across different bond categories.
1. Introduction
While the Credit Rating Agencies’ (CRA) profits exploded with the growth of structured finance, the collapse of highly rated securities in the 2007–2009 financial crisis led to suspicions that the ratings were perhaps “too optimistic” during the boom years. One prevailing explanation for rating inflation is the perceived conflicts of interest. A long-standing conflict stems from the “issuer-paid” model, whereby CRAs are paid by the issuers seeking ratings and, hence, are incentivized to issue inflated ratings.1
In the past two decades, rating agencies have been increasingly owned by large financial institutions, which induces a conflict of interest that is less obvious: CRAs may inflate ratings to benefit issuers that are related to their shareholders. While much of the extant literature has focused on issuer-paid models, this paper examines the empirical relationship between rating inflation and this often-neglected source of conflicts of interest—what I call shared-ownership—within a novel econometric framework.
Credit ratings are determined by a plethora of issuer- and issue-level characteristics. The proposed model has a multiple-index structure, which allows ratings to depend on different classes of characteristics in a non-separable fashion. Three indices are employed to represent firm characteristics, bond characteristics, and the Moody-firm-ownership-index (MFOI), which is a shared-ownership index that I introduce later in this paper. As the model is estimated semiparametrically, it is not necessary to know how CRAs utilize these characteristics to assign ratings a priori to ensure consistent estimation.
While there are numerous studies on single-index models in the econometric literature,2 only a handful of studies are available on the estimation of multiple-index regression models. Identification results of multiple-index models were first established by Ichimura and Lee (1991) and Horowitz (1998), where the authors used semiparametric least squares (SLS) to estimate the index parameters. Donkers and Schafgans (2008) proposed a derivate-based estimation method to avoid the need to pre-specify the number of indices. A recent study, Ahn et al. (2017), proposed to estimate the index coefficients (up to scale) based on an eigenvalue approach.
Studies in the statistical literature, such as Xia et al. (2002) and Xia (2008), also employ different variants of multiple-index models to flexibly reduce the data dimension. All the aforementioned studies, with the exception of Ichimura and Lee (1991), required estimating nonparametric conditional mean functions and/or derivatives in the original space of regressors. Consequently, such methods may not behave well when the sample size is small relative to the number of regressors. This paper, in contrast, extends the maximum likelihood approach of Klein and Sherman (2002) to estimate the index parameters directly in a low dimension space spanned by the three indices. To the best of my knowledge, this is also the first study in estimating a multipe-index model where the dependent variable is ordinal.
Ordered response models are more complicated than ordinary regression setting in that there is no conditional mean function to analyze: the outcome variable, y, is merely a “label” for the ordered, nonquantitaive outcomes. In order to interpret the model, one typically refers to the probabilities themselves. This paper employs a multivariate kernel density estimator for the semiparametric rating probability function. Bias-reducing kernels are often used in the literature to ensure the estimators have an appropriately low order of bias, which is required to establish their asymptotic results conveniently. However, when the object of interest is a probability, these bias reducing kernels can deliver an estimated probability outside of [0, 1] and render the estimation results difficult to interpret. To circumvent this challenge, I obtain alternative bias reduction via a “recursive differencing” strategy proposed by Shen and Klein (2019) and then establish normality for the proposed estimator. 3
Using the Mergent’s Fixed Income Securities Database (FISD) for the years 2001 to 2016, I estimate Moody’s rating model year-by-year and characterize the average partial effects (APE) of MFOI, the aforementioned shared-ownership index. In a seminal paper, Kedia et al. (2017) found that the average rating for a Moody-related firm was 0.213 notch better than a comparable non-Moody-related firm for the period of 2001–2010.
As the employed model permits the partial effect of MFOI to flexibly depend on other characteristics in an interactive fashion, the contribution of this application to the pertaining empirical literature is to explore the heterogeneity of rating bias. The APE of MFOI is more pronounced in investment grade bonds than in high yield bonds; however, this pattern reversed during the 2007–2009 financial crisis, implying that high yield bonds were more likely to receive favorable ratings due to a closer liaison with Moody’s. A placebo test based on “false owners” revealed that the salient partial effects of MFOI were indicative of Moody’s bias toward firms related to its own shareholders.
The rest of this paper is organized as follows: In Section 2, I introduce the proposed measure of shared-ownership and the firm/bond characteristics that are employed in the model. Section 3 describes the model and the estimation strategy. Section 4 reports the results from simulation designs and the empirical data. Section 5 concludes this study. In Appendix A, I state the asymptotic properties for the proposed estimator and the assumptions required to establish them. The formal proofs and intermediate lemmas are contained in the Online Supplemental Material.
2. Data and Variable Construction
I formulate a model to investigate Moody’s ratings on corporate bonds at issuance (e.g., initial ratings) from 2001, when Moody’s went public, to 2016. From Mergent’s Fixed Income Securities Database (FISD), I obtain initial ratings on corporate bonds issued by public firms covered by either the Center for Research in Security Prices (CRSP) or Compustat. There is a distinction between the issuer rating and issue rating for corporate bonds. The former addresses the issuer’s overall credit creditworthiness and usually applies to senior unsecured debt, whereas the latter refers to specific debt obligations and considers the ranking in the capital structure such as secured or subordinated.
This paper builds a model for issue ratings; therefore, both firm and bond characteristics are considered as explanatory variables.4 Descriptions and summary statistics of these characteristics are provided in Table 1. Other than the standard firm-level characteristics, three bond characteristics are included: whether the bond is a senior security, the security level (collateralized by an asset or not), and the issue amount. All three characteristics are relevant to the loss on bond holders should a default event occur. After combining data from multiple sources, the final sample was composed of 10,557 bonds issued by 1370 firms.

Table 1.
Summary Statistics: A number of firm and bond characteristics were selected to predict credit ratings based on Baghai et al. (2014) and Kedia et al. (2017): (1) the value of the firm’s total assets (log(asset)), (2) long- and short-term debt divided by total assets (Book_lev). (3) Convertible debt divided by total assets (ConvDe_assets), (4) rental paymetns divided by total assets (Rent_Assets), (5) cash and marketable securities divided by total assets (Cash_assets), (6) long- and short-term debt divided by EBITDA (Debt_EBITDA), (7) EBITDA to interest payments (EBITA_int), (8) profitability, measured as EBITDA divided by sales (Profit), (9) tangibility, measured as net property, plant, and equipment divided by total assets (PPE_assets), (10) capital expenditures divided by total assets (CAPX_assets), (11) the volatility of profitability (Vol_profit), (12) the log of the issuing amount (log(issuing amount)), (13) a dummy variable indicating whether the bond is senior (seniority), and (14) a dummy variable indicating whether the bond is secured (security).
Measuring Conflicts of Interest
One lesson that investors and policy makers learned in the 2007–2009 financial crisis is that credit ratings are contaminated with conflicts of interest. CRAs with large market shares, such as Moody’s and Standard & Poor’s, are increasingly owned by large institutional investors, making their role as an unbiased financial market “gatekeeper” ever more suspicious.5 As noted by Kedia et al. (2017), large shareholders of credit rating agencies have economic incentives to influence the rating process. Specifically, they find Moody’s ratings on bonds issued by important investee firms of its two stable large shareholders6 are more favorable relative to ratings from S&P and Fitch.
To construct a measure for the “connectedness” between a bond issuer and Moody’s through common shareholders, I first obtained the list of Moody’s shareholders from Thomson Reuters (13F) in each quarter from 2001Q1–2016Q4. From Moody’s perspective, the economic interest of some shareholders were clearly more important than others. I approximate each shareholder j’s “influence” on Moody’s by the percentage of Moody’s stock that it holds, . Next, I obtained the portfolio weight of bond issuer i in shareholder j’s investment portfolio, termed . The shareholder’s manager type code (MGRNO) and the firm’s Committee on Uniform Securities Identification Procedures (CUSIP) number were used to match the shareholding data with the 1370 bond issuers.
Based on the information collected above, I construct the following variable, termed the Moody-Firm-Ownership-Index (MFOI), to summarily characterize a bond issuer i’s liaison with Moody’s shareholders,
Figure 1 provides an illustration on how this formula works. Assume that Moody’s has only two shareholders: Berkshire Hathaway, which owns 15% of Moody’s stocks, and Goldman Sachs, which owns 3% of Moody’s stocks. There are three bond issuers indexed by , and two of which are invested by the two aforementioned shareholders of Moody’s. Specifically, the value of issuer i’s equity accounts for 20% of Berkshire Hathaway’s portfolio and each of issuer i’s and j’s accounts for 10% of Goldman Sach’s portfolio. For these three issuers, and . As can be seen from Figure 2, bond issuers had increasingly strong connections with Moody’s prior to the financial crisis, as measured by the average of MFOI.
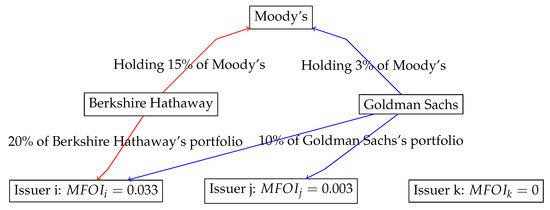
Figure 1.
An illustration.
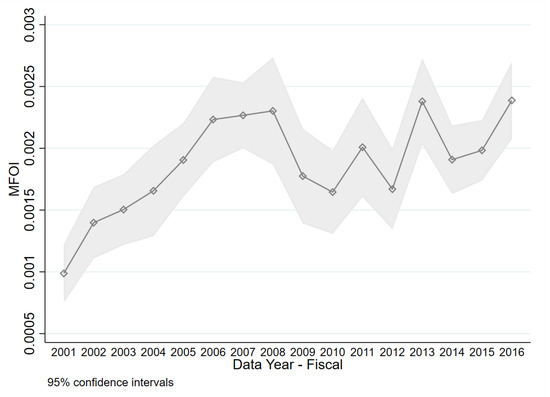
Figure 2.
Time series variation in conflicts of interest from 2001–2016.
Then what empirical relation is expected between the MFOI and credit ratings? By construction, a bond issuer i has a larger MFOI in two instances. First, when some of Moody’s shareholders increases their stakes in firm i due to favorable private information, increases for those shareholders and leads to a larger MFOI. One would anticipate the ratings to go up to reflect such favorable information. Secondly, the MFOI also tends to be large when the common shareholder has a strong influence over Moody’s (e.g., is large). Moody’s might have a greater incentive to assign favorable ratings. In both cases, a larger MFOI intuitively leads to a higher credit ratings. Below I present an econometric model to quantify the impact of MFOI on ratings.
3. Empirical Model
3.1. Model and Motivation for the Estimator
Credit ratings are discrete, ordered indicators of the credit worthiness of corporate bonds. Under Moody’s rating scale, the observed bond rating takes a value from 1 to 7,7 and is related to a bond’s latent default risk as follows
with the being parameters such that . Thus, the range of default risk is partitioned into seven mutually exclusive and exhaustive intervals, and the numerical rating indicates the interval into which a particular bond’s credit quality falls. The higher the default risk is, the lower the credit rating is. Consider the following model for ,
where .8 For each bond i, assume is a vector of firm characteristics, is a vector of the bond characteristics, and is the aforementioned measure of conflicts of interest. The model allows for both continuous as well as discrete characteristics. is a scalar error term summarizing private information, which the rating agency takes into account but is not observed to the econometrician. Instead of making distributional assumption about S, as with an ordered-probit model (OPM), I make an index assumption that will be provided below.
With , a key object of estimation interest is , which is the probability that a bond will be rated in category k conditional on the vector of explanatory variables. In order to estimate the above probability with a moderately sized sample, I define two indices,
and make the following assumption,
The employed approach is semiparametric because firm and bond characteristics enter the rating function as two parametric indices ( and , respectively) whereas the main variable of interest, , enters the rating function nonparametrically by itself.
In the empirical literature of bond rating, another prevailing approach to estimate the rating probability is the ordered-probit model (OPM), which assumes
Given the normality of S, the parametric counterpart of (6) is a known function of that does not vary across categories.9 Compared to OPM, the link function in the proposed semiparametric model (SIM) is left unknown and estimated nonparametrically. Therefore, researchers do not need to take a stand on the fashion that ratings depend on firm characteristics, bond characteristics, and conflicts of interest. Moreover, is category-specific and permits the rating agency to employ different rating criteria for each rating category.
3.2. Estimation Strategy
In the SIM described by Equations (4)–(6), the slope coefficients in the firm and bond indices, and , can only be identified up to location and scale.10 Consequently, I normalize the coefficient of a firm characteristics and a bond characteristics to one and define the normalized indices as:
where and . Note that the identifiable parameter captures the relative impact of other firm and bond characteristics to and , respectively. Below I develop an normal estimator for .
Specifically, I employ an estimator based on an extension of the approach in Klein and Sherman (2002) that maximizes the following estimated log-likelihood function:
where , is a semiparametric estimator of the rating probability defined in (6), and is a trimming function, which is introduced to stabilize the probabilistic estimator. Based on simulation evidence, we select the trimming threshold to be the 99th percentile.
The rating probability describes the probability that bond i is rated as category k conditional on the three indices. Intuitively, this probability can be estimated by a weighted average of across a group of bonds j that have similar characteristics to bond i. That is, if most similar bonds are rated as category k, the probability of bond i receiving a rating of k should be high. In practice, econometricians use kernels, which is a function that is symmetric and integrated to one, to take the average around a small neighborhood around bond i. Formally, this probability is estimated as
where is a binary variable indicating whether the similar bond j is rated as category k or not. The kernel function is
In this paper I use a second-order Gaussian kernel: . is a bandwidth parameter that goes to zero as sample size approaches infinity. Intuitively controls the number of similar bonds that are included in the kernel-weighted average in (10). A smaller bandwidth will lead to a smaller bias (only the j’s that are very similar to i are included) but a larger variance (fewer observations are included).
An important problem in practice is to select the bandwidth parameter h. I follow Silverman (1982) and set the bandwidth , where is the standard deviation of the j’th index. To ensure asymptotic normality of the proposed estimator, r must be selected in a manner such that (i) the estimated Hessian of the log-likehihood function defined in (9) converges uniformly to the expected Hessian at the true parameter values and (ii) the gradient is centered at zero (e.g., no asymptotic bias) and also converges to the true gradient.
As shown in Appendix B, the uniform convergence of the Hessian matrix will generate a upper bound (), whereas the bias reduction mechanism will generate a lower bound (). Based on the simulation evidence presented below, I chose , which is also closest to the MSE-optimal bandwidth in the case of a three-index model with a Gaussian kernel.
Unlike parametric estimators, the kernel-type estimator defined in (10) has a bias; the variance of the estimator also goes to zero at a slower (than parametric) rate. To establish asymptotic results, it is necessary to control the bias in the underlying density estimators therein. Compared to the single-index ordered model considered by Klein and Sherman (2002), the estimator developed here has a even slower convergence rate because the underlying density depends on a three-dimensional index vector (e.g., the curse of dimensionality).
I obtain bias reduction first by employing a “recursive differencing” strategy as proposed by Shen and Klein (2019). As a second source of bias reduction, I exploit a “residual” property of expected semiparametric probability functions. These bias controls are discussed in Appendix A in detail, with the required definitions and technical assumptions stated. The consistency and asymptotic normality of the proposed estimator are formally stated in Appendix B, with the proofs provided in the Online Supplemental Material.
4. Results
4.1. Simulation Evidence
Before applying the methodology to the bond rating data, Monte Carlo experiments were employed to investigate the finite sample performance of the proposed estimator. As noted above, the main advantage of the proposed multi-index semiparametric model is the ability to flexibly capture the interactive effects among covariates. As such, I consider the following data-generating process where the latent variable model has the form
is the latent response variable of theoretical interest; are explanatory variables; and are unknown parameters; and U is an error term independent of 11 The observed data consists of where
In each simulation, . The threshold points and are the 33th and 66th percentiles of the distribution. Of estimation interest is the slope parameter .
The object of the simulations is two fold. First, I compared the proposed multiple-index semiparametric estimator (SIM-M) with two other estimators in terms of precision. The two other estimators were the (1) ordered probit model (OPM) and (2) semiparametric single index model (SIM-1) considered by Klein and Sherman (2002). Second, I evaluated the performance of SIM-M under different bandwidth h and trimming parameters (defined in Definition A5 in Appendix A).
Specifically, I compared the bias, variance, and RMSE in six simulation designs, with the results presented in Table 2. These six simulations were generated by the permutation of three different trimming thresholds (90th percentile, 95th percentile, and 99th percentile) and two bandwidth parameters: a “small” bandwidth with and a “large” bandwidth with . The sample size was 2000 with a replication of 1000.

Table 2.
Simulation Evidence.
Across different designs, I found that the proposed SIM-M model generated the smallest RMSE. Apparently, both the single-index model (SIM-1) and ordered probit model (OPM) suffered from misspecification bias. Therefore, it is not surprising to find that these two models underperformed in terms of the RMSE. As for the choice of bandwidth and trimming parameters, I found that a large bandwidth and a high trimming threshold, 99th percentile, performed the best. As discussed in the previous section, ensures that the proposed SIM-M estimator has a asymptotic normal distribution. Within the range of permissible values, would minimize the MSE of the estimated conditional probability.
4.2. Empirical Illustration: Estimating Moody’s Rating Bias from 2001–2016
In this application, I estimate the heterogeneous impact of MFOI, the aforementioned shared-ownership index, on credit ratings in the described semiparametric model. Previous estimates reported in the literature were typically constrained to a single number by the functional form of the underlying regression model. For example, Kedia et al. (2017) found that the ratings assigned by Moody’s were, on average, 0.213 notches better than the ratings by S&P’s for firms related to Moody’s two major shareholders.
This number can be understood as the “average treatment effect” of a 0–1 variable capturing whether a bond issuer has a relationship with Moody’s shareholders. However, if the benefit of developing a rapport with Moody’s shareholders is actually heterogeneous, such an estimate is not informative on the effect that varies across relevant sub-populations and may not even be consistent for the overall population mean (Abrevaya et al. 2015). Using a flexible econometric approach, the application explores the heterogeneity of the shared-ownership effect across sub-populations defined by rating categories and/or possible values of issuer characteristics.
Specifically, I estimated the following model using Moody’s rating data from 2001–2016,
The included regressors are described in Section 2. For comparative purposes, a benchmark ordered-probit model (OPM) was estimated using the same data. Since the parameters in the proposed semiparametric model (SIM) are subject to scale normalization, I normalized the OPM-coefficient of and in the same way to ease the comparison.
Point estimates of the parameters from OPM and SIM are reported in Figure 3. The blue line in each subfigure depicts the semiparametric estimates, with the 95 percent confidence interval shown in grey-dotted lines.12 The yellow lines depict the comparable ordered-probit estimates. For characteristics, such as the Book-Leverage-Ratio (Book_lev) and profitability (profit), the SIM and OPM estimates had similar trends over time. However, the estimates are still statistically different from year to year. The coefficients of Seniority and Volatility of Profit were wildly different for most years in the sampling period. The huge estimation discrepancy between the point estimates suggests that OPM may subject to misspecification errors.
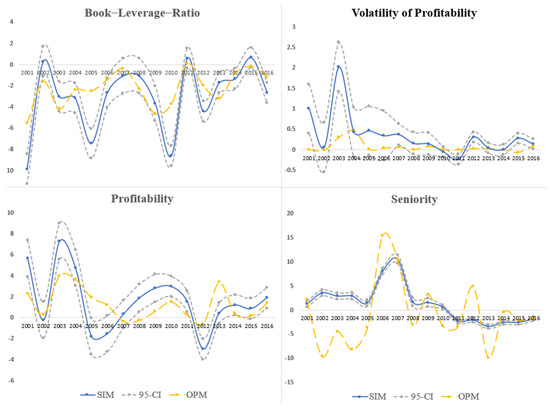
Figure 3.
Comparison of the Coefficient Estimates from SIM and OPM.
Since MFOI enters the semiparametric model nonparametrically by itself, we need to estimate its average partial effect (APE) to be able to quantify the impact of shared-ownership to ratings.13
In Figure 4, I report the APE of a one standard deviation change in the MFOI for the investment grade and high yield bonds, respectively. In non-crisis periods, the APE for investment grade bonds was uniformly larger than for high yield bonds, implying that investment grade bonds benefited more from an issuer’s shared-ownership with Moody’s than high yield bonds.
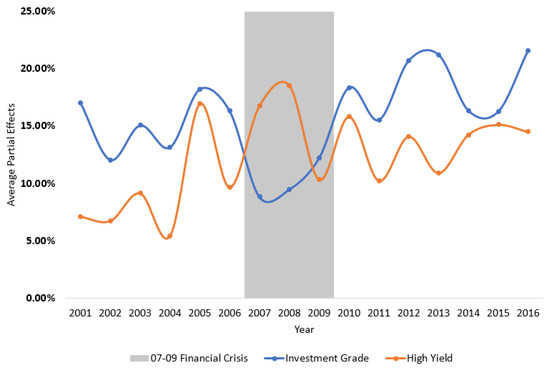
Figure 4.
Average partial effects of the MFOI.
This finding is relatively original in the literature. One possible explanation is related to the “reputation capital” view (Becker and Milbourn 2011; Bolton et al. 2012; White 2002). That is, low quality bonds are more likely to default implying a higher probability of triggering a reputation loss.14 To protect its reputation, Moody’s might be more conservative and apply a more stringent rating standard to low quality bonds.
It is intriguing that this pattern reversed during the 2007–2009 crisis. In 2008, as the MFOI ascends by one standard deviation, high-yield bonds were twice as likely to receive a better rating compared with investment grade bonds (18.5% vs. 9.4%). As can be seen from Table 3, from 2004 to 2008, the proportion of investment grade bonds increased from 57% to 90%. It is in the same period that Moody’s favorable treatment toward high yield bonds nearly quadrupled (from Figure 4, the APE on high-yield bonds increased from 5.4% to 18.5%). As one might intuitively expect, the ratings on some high-yield bonds were perhaps inflated as a result of the growing connection between bond issuers and Moody’s through common shareholders.

Table 3.
Distribution of Moody’s Ratings.
The differences in partial effects across rating categories are often “muted” in a parametric setting. In OPM, rating probabilities for all categories are governed by the same Gaussian cumulative distribution function; such a distribution function, moreover, is roughly linear in the center of its support, making it more challenging to identify the heterogeneous effect across rating categories. As can be seen from Figure 5, the ratio of APE between investment grade and high yield bonds from OPM, as depicted by the yellow-dashed line, remains near unity, implying that the two groups of bonds benefit almost equally from a strengthening shared-ownership relation.
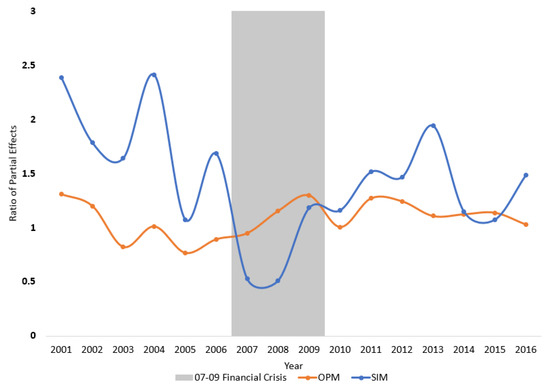
Figure 5.
Ratio of the APE between investment grade and high yield bonds.
4.3. A Placebo Test for Rating Bias
While a reasonably large set of characteristics were controlled for in the model, and there can be omitted variables that are correlated with the portfolio selection criteria of Moody’s shareholders. After all, institutional shareholders, irrespective of their relationship with Moody’s, tend to invest on firms with higher credit worthiness. As such, the partial effects of the MFOI may only reflect the impact of unobserved characteristics and not necessarily any “rating bias” from Moody’s. To make the analysis more meaningful, I performed a placebo test to check if the bias still existed for bonds related to a portfolio of “false owners” (institutional investors that do not own Moody’s).
Moody’s ten leading institutional owners are reported in Table 4, most of which are investment/wealth management companies, such as Vanguard and Fidelity. A placebo group was constructed using comparable asset managers that do not own Moody’s stocks. Starting with the fifteen largest asset management companies by AUM, I chose two mangers that do not own Moody’s—Merrill Lynch and BNY Mellon. A dummy variable Placebo was created that takes the value of one for firms who are owned by either firm and zero otherwise. The rating bias, as measured by the rating difference between the two groups, should be zero as the two “false owners” are used. As can be seen from Figure 6, for every year in the sample, except 2011 and 2015, the rating bias remained small and was not statistically different from zero.

Table 4.
Moody’s major institutional owners from 2001–2016.
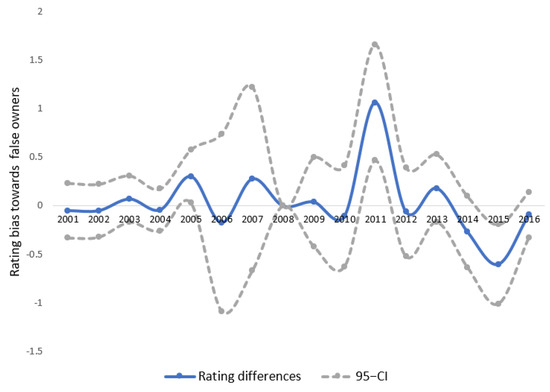
Figure 6.
Placebo test using Merrill Lynch and BNY Mellon as “False Owners”. Note: The rating difference in 2008 is not identified because all 446 bonds are issued by firms related with Merrill Lynch or BNY Mellon.
4.4. Bias in Issuer Ratings
This paper used bond ratings while the literature also studies issuer ratings. To check whether our empirical results held for issuer ratings, I re-estimated the model for bonds that were “senior-unsecured”—these bonds receive issuer ratings. Note that the bond index in the original model would be redundant in this case because all bonds within the firm receive the same issuer rating. As such, I estimated a double-index model with the firm characteristics and MFOI. The APEs of the MFOI for each year are reported in a similar fashion in Figure 7.
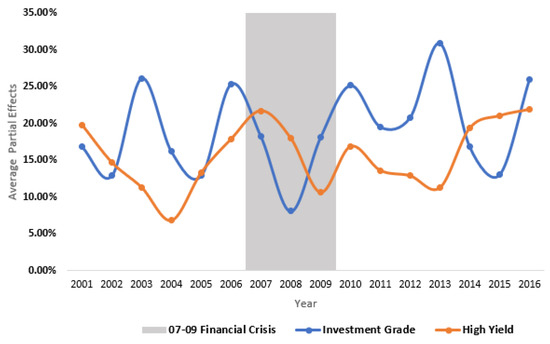
Figure 7.
The average partial effects of MFOI (on issuer ratings).
The economic magnitude of the APEs are not identical to those from the three-index model; however, this should not be too surprising because not all firms in the original sample issued senior unsecured bonds. In fact, the sample size decreases substantially from 10,557 to 7485 after focusing only on senior unsecured bonds. Nevertheless, the general patterns of APE are in accord with the three-index model reported in Figure 4. That is, our previous conclusions about the rating bias on bond ratings are likely to extend to issue ratings as well.
5. Conclusions
During the 2007–2009 financial crisis, credit rating agencies (CRAs) were criticized for assigning inflated ratings to mortgage-backed securities and other structured products. A similar phenomenon was documented on other asset classes, such as corporate bonds (Kedia et al. 2017; Strobl and Xia 2012) and CDOs (Griffin and Tang 2012). The relaxed rating standard was largely attributable to conflicts of interest arising out of the CRA’s business model. In this paper, I propose a semiparametric model to investigate to what extent Moody’s ratings are affected by the economic interests of its shareholders, which is pertinent for the regulation of credit rating agencies.
Compared with extant bond rating models, the proposed model has two key features: (i) I explicitly consider the impact of conflicts of interest on ratings through common shareholders, (ii) the model imposes few distributional and functional form restrictions on the underlying rating process. Specifically, explanatory variables enter the model in the form of multiple indices that can interact with each other freely. Asymptotic results of the index parameters estimator are established after several bias corrections. While the focus of this paper is on credit ratings, the estimation and inference framework with multiple-indices can be applied to other contexts.
By estimating the heterogeneous (partial) effects of MFOI, which is a self-constructed index for the degree of shared-ownership connection between Moody’s and bond issuers, I found that high-yield bonds were unlikely to be treated with favoritism. One plausible explanation for this phenomenon is that overrating a subprime bond would incur a greater expected reputation loss than overrating a safe bond.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/econometrics9020023/s1.
Funding
This research received no external funding.
Data Availability Statement
The data can be obtained from the author upon request.
Acknowledgments
Comments from the editor and three anonymous reviewers are sincerely appreciated. This paper is based on the first chapter of my Ph.D. dissertation titled “Semiparametric Estimation of Financial Risk: Corporate Default, Credit Ratings, and Implied Volatility”. I thank my advisor, Roger Klein, for his advice. I am also grateful to Bruce Mizrach, John Landon-Lane, Simi Kedia, Diana Knyazeva (FMA discussant), Hilary Sigman, Zhutong Gu, Shuyang Yang, Xiye Yang, Xu Tong (discussant), Geoff Clarke, Tom Fomby, and conference participants in the Financial Mangament Asscociations, Midwest Econometrics Group and Econometric society meetings for their helpful discussions. All errors remain mine.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CRA | Credit Rating Agency |
| MFOI | Moody-Firm-Ownership-Index, defined in Equation (1) |
| OPM | Ordered-Probit Model |
| SIM-M | Semiparametric multiple-index model with kernel (this paper) |
| SIM-1 | Semiparametric single-index model (Klein and Sherman 2002) |
Appendix A. Definitions and Assumptions
To formally describe the asymptotic results in Appendix B, I require the following definitions and technical assumptions. As discussed in Section 3, a “recursive differencing” estimator was employed to obtain bias controls. This estimator is formally defined in Definition A4, with the underlying index and density estimators defined in Definitions A1–A3.
Definition A1
(Firm and Bond Index).Let denote a continuous firm characteristics and denote the vector of firm characteristics other than such that for. and are defined similarly for the vector of bond characteristics. I define the firm and bond index as
Under Assumptions A1–A3 below, I define the normalized indices as:
where and are referred to as the index coefficients.
Definition A2
(Kernels).Let denotes the value of the normalized index for observation j, and denote a fixed point of interest. Define a multivariate kernel function
where and is a bandwidth parameter that goes to zero as the sample size approaches infinity.
Definition A3
(Density Estimator).Let denotes the joint density of the three-dimensional index at a fixed point , a (leave-one-out) kernel-weighted density estimator is defined as
Definition A4
(Estimated Probability).Referring to Definitions A2 and A3, an initial estimator for the probability that a bond with characteristics will be rated in category k, denoted , is defined as
Based on this initial estimator at v, a recursive-differencing estimator for , in the spirit of Shen and Klein (2019), is defined as
where is a bias-correction adjustment.
Definition A5
(Trimming Functions).Let denote the d-th column of a -dimensional continuous vector . Define and , where are, respectively, the lower and upper sample quantiles for . When , I refer to as X-trimming; With as the estimated index, when , I refer to as index trimming.
Definition A6
(First- and Second-Stage Estimator).Based on Definitions A1–A5, I define:
where is defined in Definition A1. The second stage estimator differs from the first stage in that the trimming function is based on the estimated index from the first stage: That is, I define the trimming function based on .
The intuition of the recursive differencing estimator is as follows: from the standard results, the bias of the initial Nadaraya–Watson estimator in (A5) goes to zero at the rate of as . Such a bias arises because the differences between and cannot be “washed away” by kernel averaging over j. However, by removing an estimate of this bias (e.g., ) from , the kernel-weighted average of turns out to be a better estimate of . Specifically, Shen and Klein (2019) proved that the bias of this “recursive differencing” estimator goes to zero at the rate of , whereas the variance stays at the same order at .
The proofs for asymptotic properties of the recursive differencing estimator also exploit a residual-like property of the derivative (with respect to the parameters ) of the expected semiparametric probability function: Under the index assumption, we have . This residual-like property, which is proven in Lemma 2.9, has been employed by Klein and Spady (1993) and Klein and Shen (2010) as bias control. To take advantage of this property, a two-stage estimation procedure described in Definition A6 is needed: I first estimate the model under X-trimming defined in Definition A5. The resulting estimates, , are employed to obtain the estimated indices. A second-stage estimator, , is then obtained from re-estimating the model with trimming based on estimated indices.
The trimming function defined in Definition A5 provides protection against small density denominators and hence “stabilizes” the probability estimator. In addition, the order of the bias increases near the boundary of the support for the variables on which we trim. Trimming resolves that as well. The trimming function restricts estimation in all stages to employ only the middle 99th percentile ( = 0.005, = 0.995 for all d) of the data. Such trimming thresholds are selected based on simulation evidence.15
To obtain convergence properties for the proposed estimator in Definition A4 and asymptotic normality for the second-stage estimator of the index parameters defined in Definition A6, I make the following assumptions.
Assumption A1
(Data).The vector (,) is over i. The categorical outcome has a discrete and finite support, taking values from 1 to k. The columns of are linearly independent with a probability of one. As stated in Definition A1 above, I require that and each contain at least one continuous regressor, termed and , respectively.
Assumption A2
(The Error Term).The error term is conditionally mean-independent of : and independent across i.
Assumption A3
(Continuous Firm and Bond Characteristics).Referring to the firm and bond index defined in Definition A1, I require the index coefficient of and to be nonzero: .
Assumption A4
(Index Assumption).Referring to the normalized index defined in Definition A1, let , the following index assumption is assumed to hold for all i and k:
Assumption A5
(Parameter Space).The vector of the true parameters values for the model lies in the interior of a compact parameter space, Θ.
Assumption A6
(Conditional Densities).Let denote the density of the index defined in Assumption A4 conditioning on and . Denote as the partial or cross partial derivatives up to order d. I assume and to be uniformly bounded for on the interior of its support.
Assumption A7
(Bandwidth Parameter).Referring to the kernel estimator defined in Definition A2, the bandwidth parameter as . Specifically, with , I choose according to Silverman (1982)16 where is the standard deviation of the three indices () and r is a parameter that affects the rate that h goes to zero. In this paper, .
Assumptions A1–A5 define the index model that I propose to estimate. An index formulation of low dimension is important for obtaining reasonable results in finite samples. In Assumption A3, I assume that the firm and bond indices satisfy the identification conditions in Ichimura and Lee (1991). Specifically, each index must contain at least one continuous variable that belongs to the model in the statistical sense. In addition, I require that the densities for continuous variables and the indices must be sufficiently smooth as implied by Assumption A6. The smoothness conditions are standard in the literature and have been discussed in Klein and Spady (1993).
Appendix B. Asymptotic Theorems
In this section, I provide and discuss the asymptotic properties for the two estimators defined in Definition A6. The online Supplementary Materials contains formal proofs for all required intermediate lemmas and the main theorems given below. In what follows, I first establish consistency for the estimators in both stages using standard uniform convergence arguments. Then, I turn to the sketch of proof for asymptotic normality of .
For , recall that the estimator maximizes the estimated log-likelihood function defined in Definition A6 for both stages. From Lemma 2.3 in the Online Supplemental Material, sup, where is obtained from by replacing all estimated functions with their probability limits. From standard argument, converges uniformly to its expectation E[]. It can be shown that E[] is uniquely maximized at , and therefore the estimators in both stages are consistent.
Theorem A1
(Consistency).Under Assumptions A1–A7 and with ,
Proof.
To derive the asymptotic distribution of the second stage estimator , recall that is obtained by maximizing the log-likelihood function defined in Definition A6 with the index-trimming. Let and denote the Gradient and Hessian matrices, which are the first and second derivatives of the log-likelihood function in (A8):
To simplify the presentation, I suppress the trimming function and denote the double summation as . From a Taylor expansion of the estimated Gradient at ,
Since the estimated gradient must be zero at , the above expression simplifies to
By Lemma 2.5 in the Online Supplemental Material, the estimated Hessian will uniformly converge to when the bandwidth parameter . The estimated gradient has an asymptotic expansion as follows:
In the Online Supplemental Material, I formally show that each term in the asymptotic expansion, except , is . The aforementioned residual-like property plays a critical role in showing . Combining (A13) and (A14), has the following asymptotic linear representation
where is the probability limit of the Hessian matrix evaluated at . After applying the Lindberg–Levy CLT, the second stage estimator defined in Definition A6 is -normal,
Theorem A1
(Normality).Assumptions A1–A7 and with the bandwidth parameter ,
where with , , and .
Proof.
See Online Supplemental Material. □
Notes
| 1. | For theoretical studies on the issuer-paid model and rating shopping, see Bolton et al. (2012); Sangiorgi et al. (2009); Skreta and Veldkamp (2009) and some empirical evidence (He et al. 2015; Jiang et al. 2012; Mathis et al. 2009). |
| 2. | Extensive literature addresses semiparametric models and the estimation of semiparametric single index models, including Härdle and Stoker (1989); Horowitz and Härdle (1996); Ichimura (1993); Klein and Spady (1993); Manski (1985); Powell et al. (1989). See Stewart (2005), Lewbel (2000), and Klein and Sherman (2002) for applications of a single-index model in the context of an ordered-response model. |
| 3. | Alternatively, one may also use the sieves method to estimate the rating probability. Such methods are more convenient when some prior information and constraints, such as monotonicity, additivity, and nonnegativity, needs to be incorporated in the conditional probabilities (Chen 2007). For instance, Coppejans (2007) estimates an ordered model with a quadratic-spline under the restriction that the distribution functions across all categories are the same. Such a constraint, however, is not appropriate in the current application because Moody’s rating standard can vary with categories. |
| 4. | Macro variables are not included because the model will be estimated separately for each year. |
| 5. | Moody’s was founded as a private company in 1900, acquired by Dun&Bradstreet (D&B) in 1962, and remained one of its divisions until 4 October 2000, when it was spun off and listed on the NYSE. The S&P has been a fully owned division of McGraw-Hill, a publicly traded company, since 1966. Going public makes CRAs more vulnerable to conflicts of interest. For example, Kedia et al. (2017) found that Moody’s assigned favorable ratings toward issuers that Moody’s shareholders have invested in. |
| 6. | From 2001 to 2010, Moody’s had two shareholders, Berkshire Hathaway and Davis Selected Advisors, which collectively own about 23.5% of Moody’s. |
| 7. | The numerical rating matches the seven ordinal rating categories: , and (from the highest credit quality to the lowest). |
| 8. | The vector is assumed to be exogenous throughout. Intuitively, and as one might have expected, some information contained in S, e.g., the manager’s ability, may also drive institutional investors’ investment decisions, implying that is endogenous. The problem of endogeneity can be handled, for example, using the control function approach proposed by Blundell and Powell (2004) provided with a valid exclusion restriction. |
| 9. | Specifically, the rating probability in an ordered-probit model is
In the case when in (7) and the variance of the homoskedastic error term is , identification is up to location and scale: one can, at most, identify , (the “pseudo cutoff points”), and (the “pseudo intercept”). See Amemiya (1981) for a discussion. |
| 10. | Since the functional form of in (6) is not specified, conditioning on the original index and a linear transformation of them deliver the same amount information on ratings. Therefore, without some normalization, the limiting log-likelihood function cannot be uniquely maximized at the true parameters, which is necessary for identification. |
| 11. | More specifically, u is generated from a distribution, standardized to have a mean of zero and unit variance. , and is a standardized . |
| 12. | Confidence Intervals were constructed based on the asymptotic results derived in Appendix B. |
| 13. | The partial effects for MFOI in the ordered-response model are,
The Average Partial Effect, or APE, is computed by evaluating the partial effect for each bond i and averaging the computed effects,
The above calculation can be performed for any category. That is, even for a C-rated bond, one can compute the change in the probability of this bond being rated into AAA. To make the presentation concise and practically relevant, I only report the APE for the category that is one-notch better than the current rating grade. That is, I interpret the APE as the probabilistic change of obtaining a better rating grade if the issuer’s share-ownership relationship with Moody’s strengthens by . |
| 14. | This implies that the CRA will be “punished” once a highly rated investment results in default. See Bolton et al. (2012) for a discussion. |
| 15. | The suggested trimming rule is indeed ad-hoc because the selected threshold may be bad for other DGP. The asymptotic theorems developed later abstracts away from the trimming issue. It is possible to develop a data-dependent optimal trimming rule similar to Ma and Wang (2019), which is left for future work. |
| 16. | To be specific, let , Silverman (1982) shows that the MSE-optimal . In the case with three indices, the constant is roughly 0.97. |
References
- Abrevaya, Jason, Yu-Chin Hsu, and Robert Lieli. 2015. Estimating conditional average treatment effects. Journal of Business & Economic Statistics 33: 485–505. [Google Scholar]
- Ahn, Hyungtaik, Hidehiko Ichimura, James L. Powell, and Paul A. Ruud. 2017. Simple estimators for invertible index models. Journal of Business & Economic Statistics 36: 1–10. [Google Scholar]
- Amemiya, Takeshi. 1981. Qualitative response models: A survey. Journal of Economic Literature 19: 1483–536. [Google Scholar]
- Baghai, Ramin P., Henri Servaes, and Ane Tamayo. 2014. Have rating agencies become more conservative? Implications for capital structure and debt pricing. The Journal of Finance 69: 1961–2005. [Google Scholar] [CrossRef]
- Becker, Bo, and Todd Milbourn. 2011. How did increased competition affect credit ratings? Journal of Financial Economics 101: 493–514. [Google Scholar] [CrossRef]
- Blundell, Richard W., and James L. Powell. 2004. Endogeneity in semiparametric binary response models. The Review of Economic Studies 71: 655–79. [Google Scholar] [CrossRef]
- Bolton, Patrick, Xavier Freixas, and Joel Shapiro. 2012. The credit ratings game. The Journal of Finance 67: 85–111. [Google Scholar] [CrossRef]
- Chen, Xiaohong. 2007. Large sample sieve estimation of semi-nonparametric models. In Handbook of Econometrics. Amsterdam: Elsevier BV, vol. 6, pp. 5549–632. [Google Scholar]
- Coppejans, Mark. 2007. On efficient estimation of the ordered response model. Journal of Econometrics 137: 577–614. [Google Scholar] [CrossRef]
- Donkers, Bas, and Marcia Schafgans. 2008. Specification and estimation of semiparametric multiple-index models. Econometric Theory 24: 1584–606. [Google Scholar] [CrossRef]
- Griffin, John M., and Dragon Yongjun Tang. 2012. Did subjectivity play a role in cdo credit ratings? The Journal of Finance 67: 1293–328. [Google Scholar] [CrossRef]
- Härdle, Wolfgang, and Thomas M. Stoker. 1989. Investigating smooth multiple regression by the method of average derivatives. Journal of the American Statistical Association 84: 986–95. [Google Scholar] [CrossRef]
- He, Jie, Jun Qian, and Philip E. Strahan. 2015. Does the market understand rating shopping? predicting mbs losses with initial yields. The Review of Financial Studies 29: 457–85. [Google Scholar] [CrossRef]
- Horowitz, Joel L. 1998. Semiparametric Methods in Econometrics: Lecture Notes in Statistics. New York: Springer Science & Business Media, vol. 131. [Google Scholar]
- Horowitz, Joel L., and Wolfgang Härdle. 1996. Direct semiparametric estimation of single-index models with discrete covariates. Journal of the American Statistical Association 91: 1632–40. [Google Scholar] [CrossRef]
- Ichimura, Hidehiko. 1993. Semiparametric least squares (sls) and weighted sls estimation of single-index models. Journal of Econometrics 58: 71–120. [Google Scholar] [CrossRef]
- Ichimura, Hidehiko, and Lung-Fei Lee. 1991. Semiparametric least squares estimation of multiple index models: Single equation estimation. In Nonparametric and Semiparametric Methods in Econometrics and Statistics. Paper presented at Fifth International Symposium in Economic Theory and Econometrics, Cambridge, UK, July 26; pp. 3–49. [Google Scholar]
- Jiang, John Xuefeng, Mary Harris Stanford, and Yuan Xie. 2012. Does it matter who pays for bond ratings? Historical evidence. Journal of Financial Economics 105: 607–21. [Google Scholar] [CrossRef]
- Kedia, Simi, Shivaram Rajgopal, and Xing Zhou. 2016. Large shareholders and credit ratings. Journal of Financial Economics 124: 632–53. [Google Scholar] [CrossRef]
- Klein, Roger, and Chan Shen. 2010. Bias corrections in testing and estimating semiparametric, single index models. Econometric Theory 26: 1683–718. [Google Scholar] [CrossRef]
- Klein, Roger W., and Robert P. Sherman. 2002. Shift restrictions and semiparametric estimation in ordered response models. Econometrica 70: 663–91. [Google Scholar] [CrossRef]
- Klein, Roger W., and Richard H. Spady. 1993. An efficient semiparametric estimator for binary response models. Econometrica: Journal of the Econometric Society 61: 387–421. [Google Scholar] [CrossRef]
- Lewbel, Arthur. 2000. Semiparametric qualitative response model estimation with unknown heteroscedasticity or instrumental variables. Journal of Econometrics 97: 145–77. [Google Scholar] [CrossRef]
- Ma, Xinwei, and Jingshen Wang. 2019. Robust inference using inverse probability weighting. Journal of the American Statistical Association 115: 1–10. [Google Scholar] [CrossRef]
- Manski, Charles F. 1985. Semiparametric analysis of discrete response: Asymptotic properties of the maximum score estimator. Journal of Econometrics 27: 313–33. [Google Scholar] [CrossRef]
- Mathis, Jerome, James McAndrews, and Jean-Charles Rochet. 2009. Rating the raters: Are reputation concerns powerful enough to discipline rating agencies? Journal of Monetary Economics 56: 657–74. [Google Scholar] [CrossRef]
- Powell, James L., James H. Stock, and Thomas M. Stoker. 1989. Semiparametric estimation of index coefficients. Econometrica: Journal of the Econometric Society 57: 1403–430. [Google Scholar] [CrossRef]
- Sangiorgi, Francesco, Jonathan Sokobin, and Chester Spatt. 2009. Credit-Rating Shopping, Selection and the Equilibrium Structure of Ratings. Technical Report, Working Paper. Pittsburgh: Stockholm School of Economics, Carnegie Mellon University. [Google Scholar]
- Shen, Chan, and Roger Klein. 2019. Recursive Differencing for Estimating Semiparametric Models. Available online: https://economics.rutgers.edu/downloads-hidden-menu/faculty-cv-s/1824-shen-and-klein-2019/file (accessed on 1 December 2019).
- Silverman, Bernhard W. 1982. Algorithm as 176: Kernel density estimation using the fast fourier transform. Journal of the Royal Statistical Society Series C (Applied Statistics) 31: 93–99. [Google Scholar] [CrossRef]
- Skreta, Vasiliki, and Laura Veldkamp. 2009. Ratings shopping and asset complexity: A theory of ratings inflation. Journal of Monetary Economics 56: 678–95. [Google Scholar] [CrossRef]
- Stewart, Mark B. 2005. A comparison of semiparametric estimators for the ordered response model. Computational Statistics & Data Analysis 49: 555–73. [Google Scholar]
- Strobl, Günter, and Han Xia. 2012. The Issuer-Pays Rating Model and Ratings Inflation: Evidence from Corporate Credit Ratings. Unpublished Working Paper. Available online: http://efa2011.efa-online.org/fisher.osu.edu/blogs/efa2011/files/APE_8_2.pdf (accessed on 1 December 2019).
- White, Lawrence J. 2002. The credit rating industry: An industrial organization analysis. In Ratings, Rating Agencies and the Global Financial System. Berlin: Springer, pp. 41–63. [Google Scholar]
- Xia, Yingcun. 2008. A multiple-index model and dimension reduction. Journal of the American Statistical Association 103: 1631–40. [Google Scholar] [CrossRef]
- Xia, Yingcun, Howell Tong, W. K. Li, and Li-Xing Zhu. 2002. An adaptive estimation of dimension reduction space. Journal of the Royal Statistical Society Series B Statistical Methodology 64: 363–410. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).