An Adaptive Beamforming Time with Round-Robin MAC Algorithm for Reducing Energy Consumption in MANET
Abstract
1. Introduction
2. Related Works
- Reducing collisions and retransmissions: This is one of the most common objective of MAC protocols for limiting the probability of interfering nodes. In this context, the work [26] proposes a novel deafness-aware (DA-MAC), with the goal to mitigate the deafness problem through a discrete-time Markov chain model. The model uses a double-channel schema in order to handle the directional RTS (DRTS); more specifically, the single channel provided by the directional MAC is split into two different logical channels used for filtering the data traffic and the control packets, respectively; the designed DA-MAC algorithm provides for several features that allows one to recognize and mitigate efficiently the collisions occurred because of deafness. The results highlight a reduction of the deafness duration and a good improvement of the aggregate throughput compared with some of the most significant existing works.
- Reducing overhearing: Wireless mobile nodes deplete battery life also because they overhear transmissions of their neighbors. One possible solution to mitigate this problem is to use dedicated and separated channel distinguishing control and data traffic so that nodes do not overhear undesired information. For example, the authors in [27] propose a schedule-based broadcast mechanism including data transmission timers for each node. In [28], two schemes are proposed in order to mitigate the deafness caused by persistent hearing of data and for handling the short retry limit (SRL) in directional environments.
- Minimize control overhead: Limiting the protocol overhead represents a critical challenge, especially when small packets are used [29,30,31]. Because of the important channel acquisition overhead, the high amount of small packets to be transmitted translates into a significant waste of energy. However, if mobile nodes perform multiple transmission slot requests with a single reservation message, the control overhead can be limited [32]. In [22], the authors propose two MAC protocols in which nodes use directional sectorized antennas. The scheduler and the protocols are designed with the aim to minimize the co-site interference issue that could arise in some directional contexts also by limiting the overall overhead in the network.
- Reducing beamforming time: In [3], the authors propose a tone DMAC mechanism that enable the transmission of special packets (out-of band tones) by nodes in omnidirectional mode; these tones can be processed by neighbors reducing considerably the large backoff time introduced by deafness. In [24], a round-robin MAC (RR-MAC) approach is presented with the goal to minimize the impact of deafness in directional MAC contexts. The round-robin mechanism was implemented by an algorithm that manages the assignment of the beam toward a certain sector also handling the incoming frames that could not temporally be transmitted in the channel by using waiting queues.
3. Omnidirectional and Directional Antennas Issues vs. Round-Robin MAC
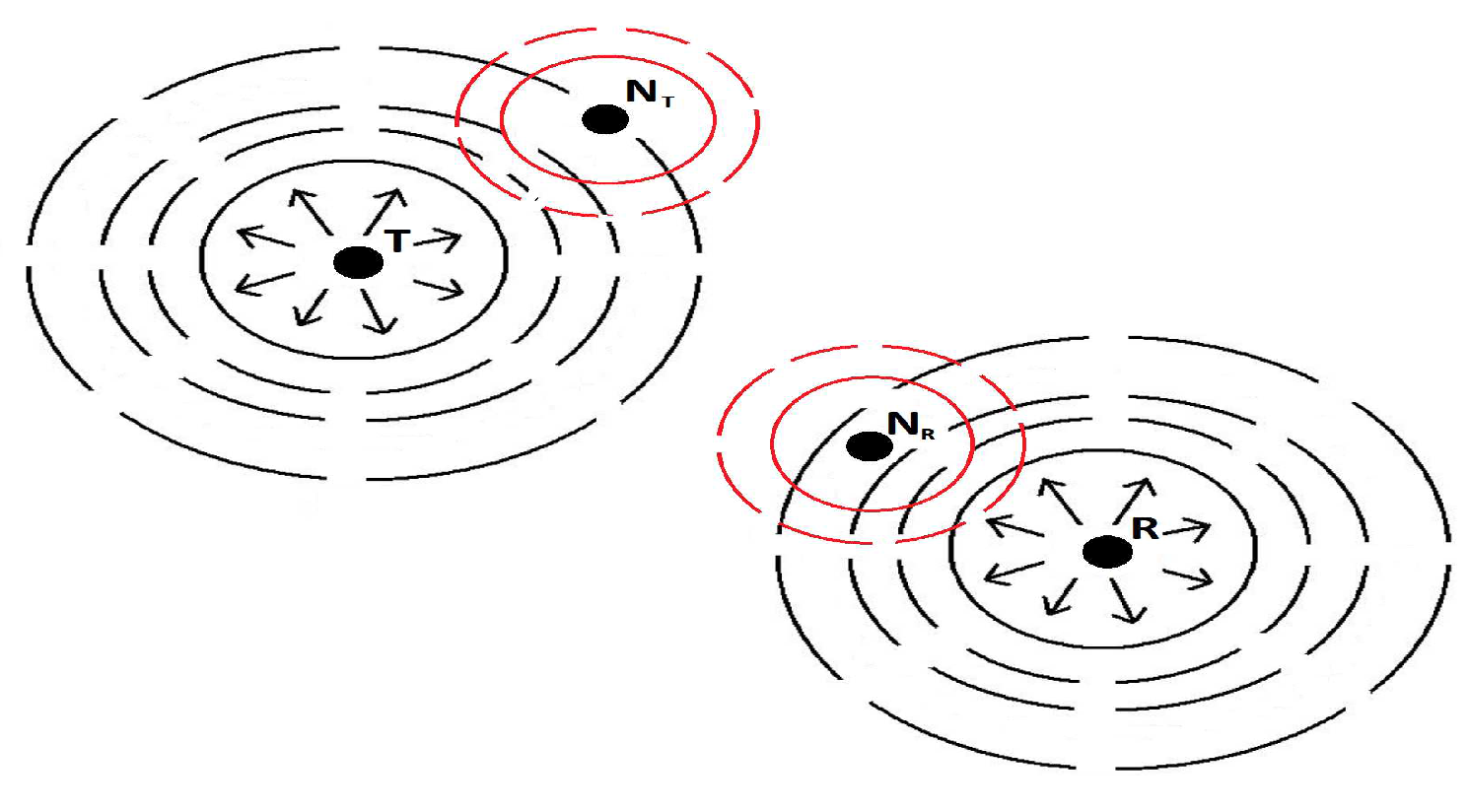
3.1. Directional Antennas in MANET Common Issues
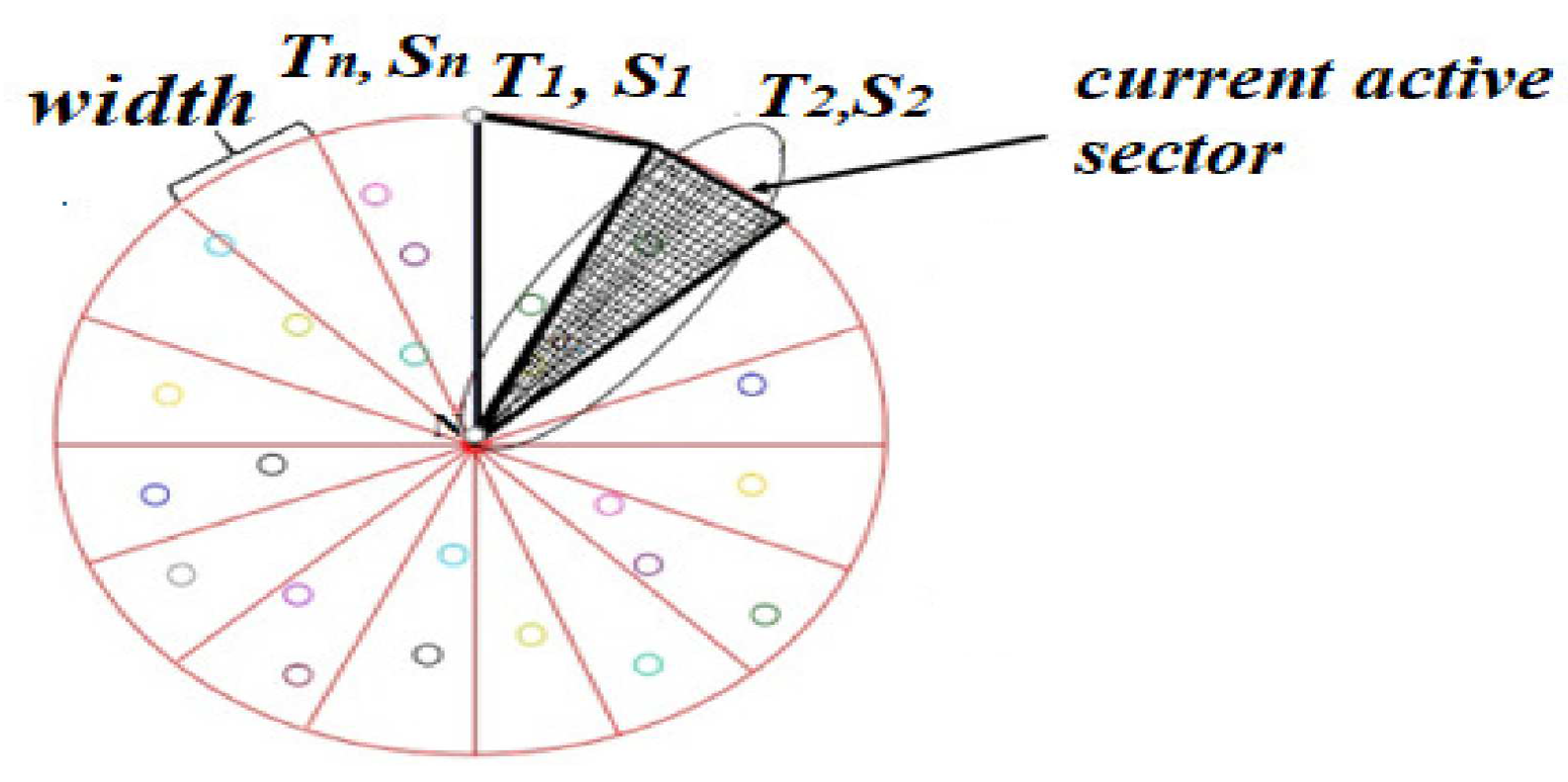
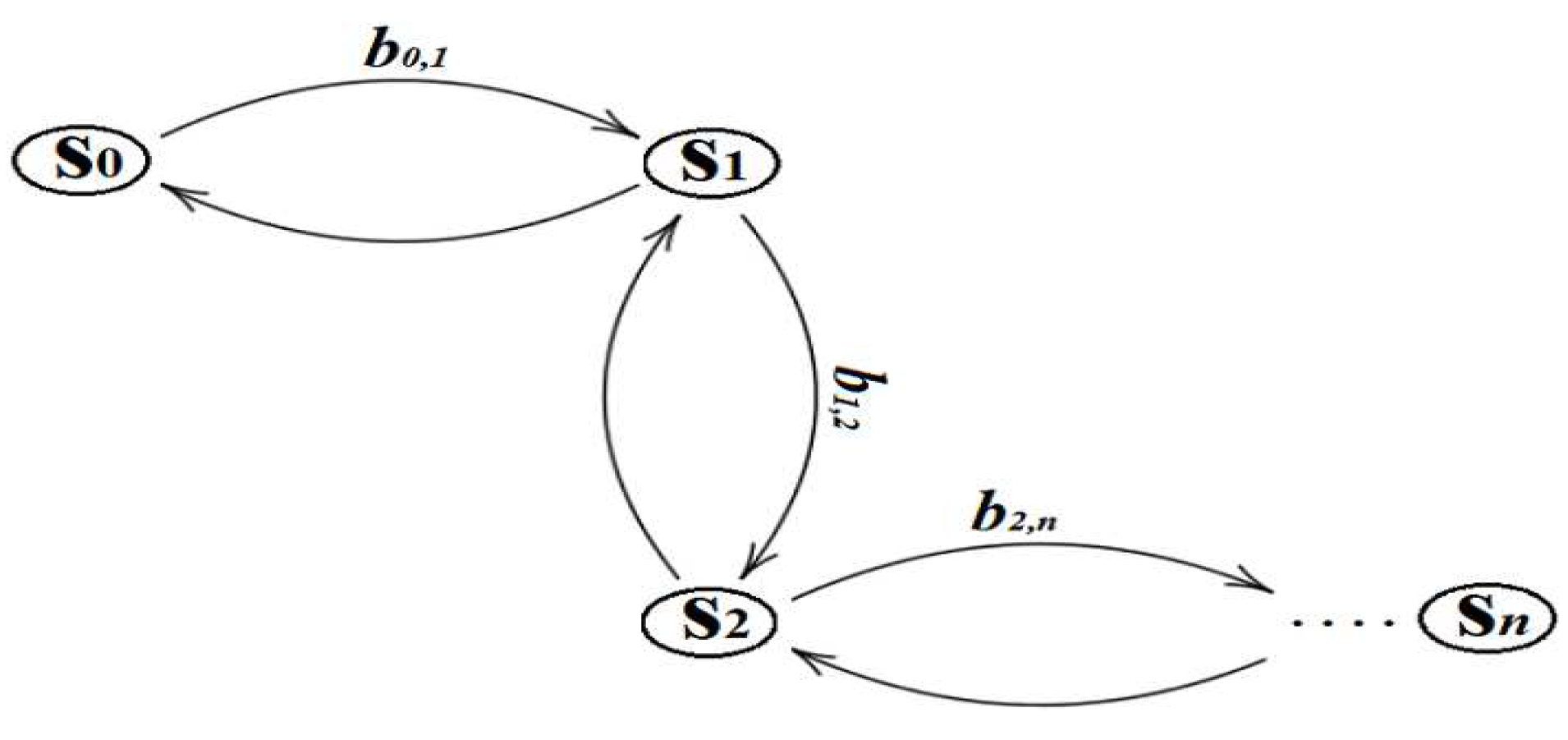
3.2. Round-Robin MAC Scheduling Issues
4. The Proposed Model
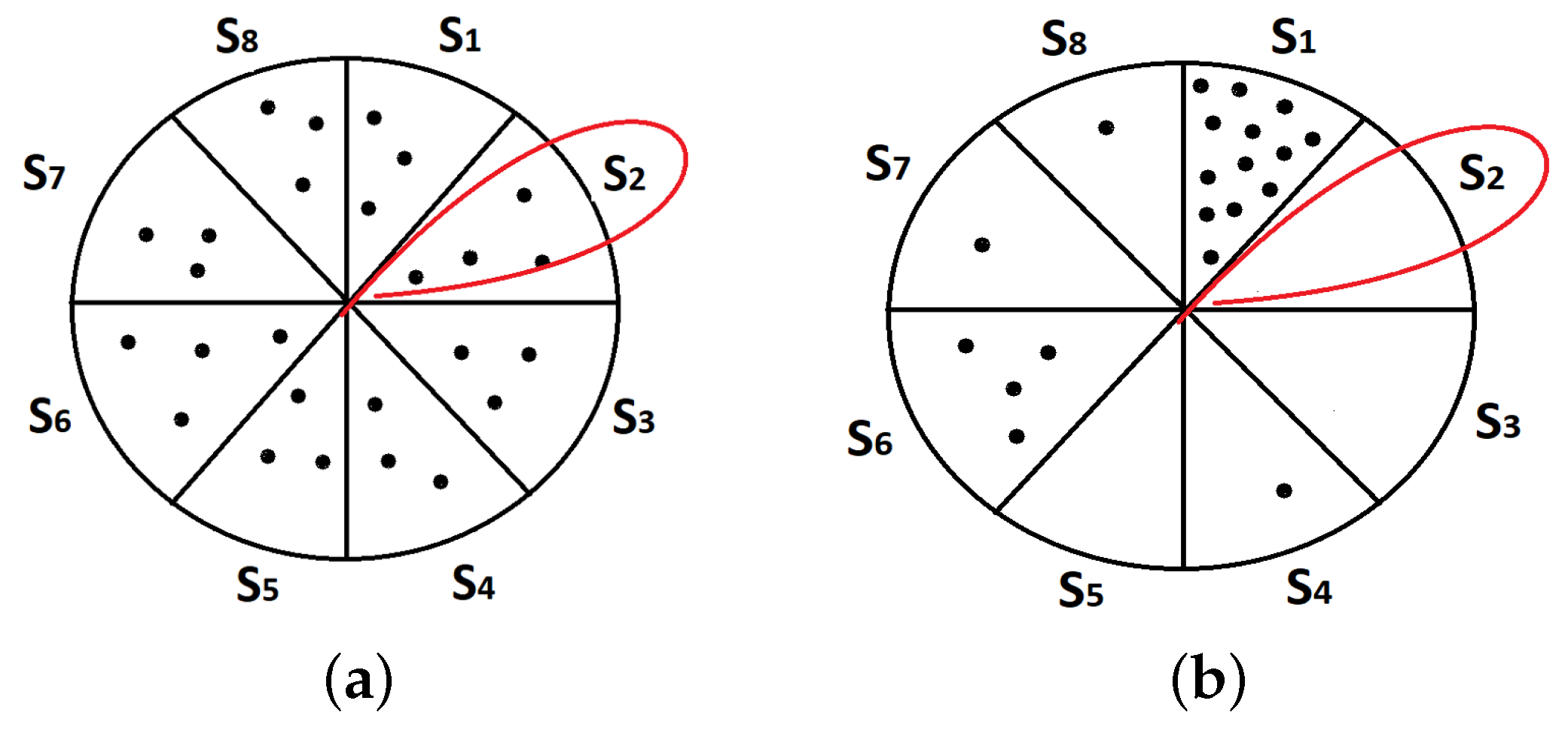
4.1. Comparison with RR-MAC and Motivations
- state: the set of the directions associated with a sector (in other terms, a state is a sector);
- transition: the switching process from a sector to another sector.
- = prob. that a node x attempts for a transmission in a randomly chosen sector.
- = prob. that there is at least a transmission in a certain sector.
- = prob. that at least one of the neighbors of x attempts for a transmission.
- = prob. that x is beamformed from at least one of its neighbors.
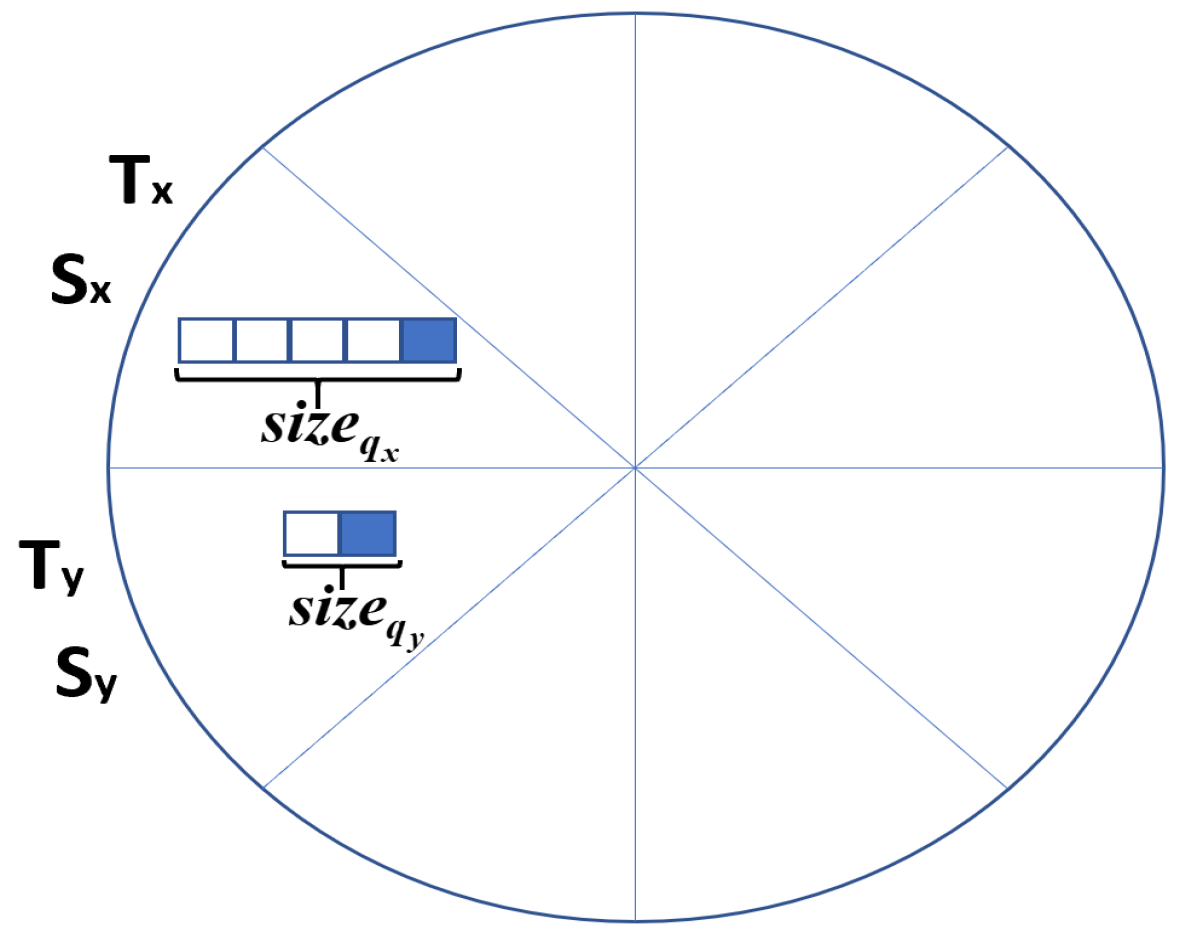
4.2. ABT-RRMAC Formulation
4.3. ABT-RRMAC Implementation
| Algorithm 1 ABT-RRMAC pseudo-code |
|
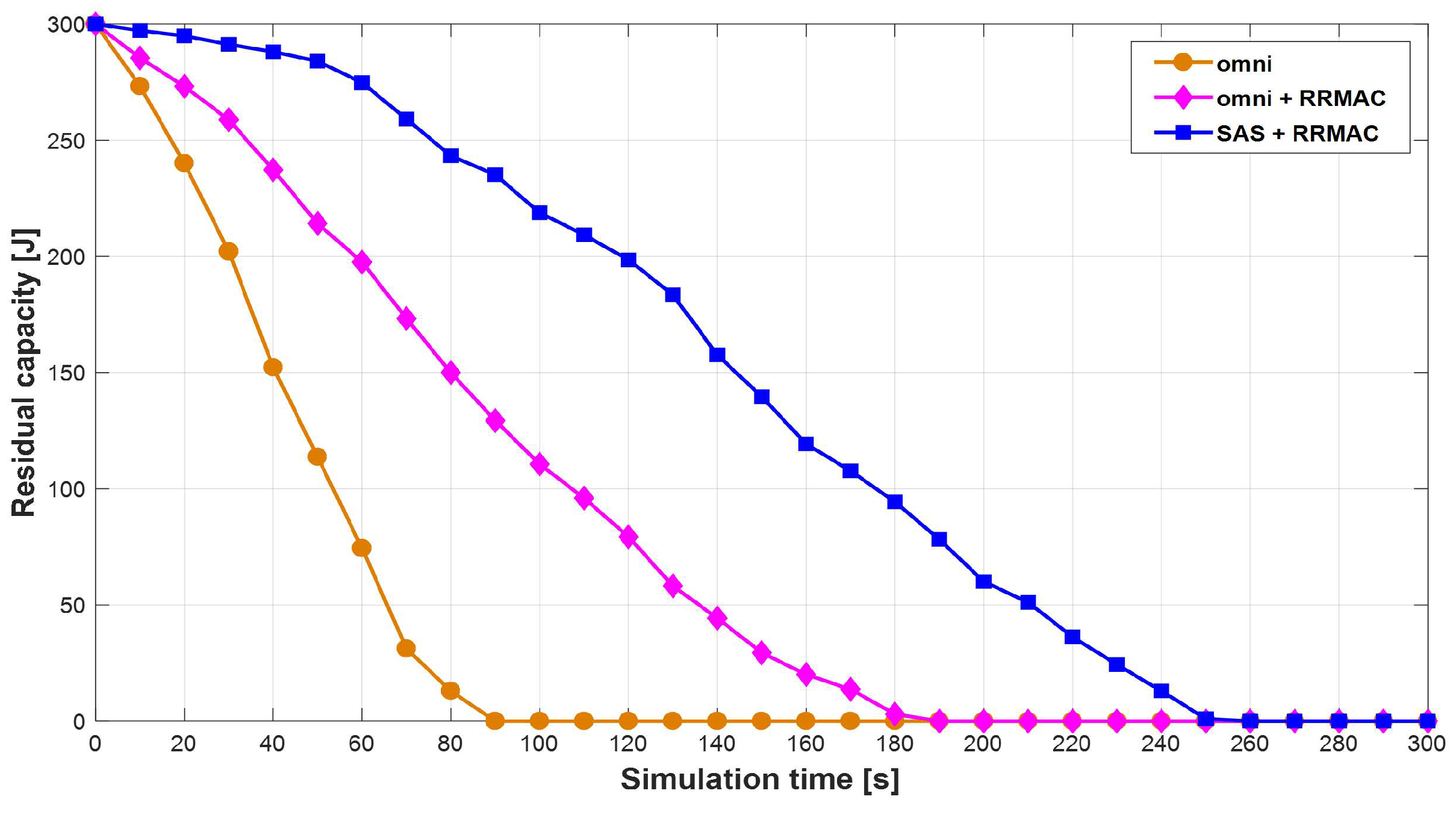
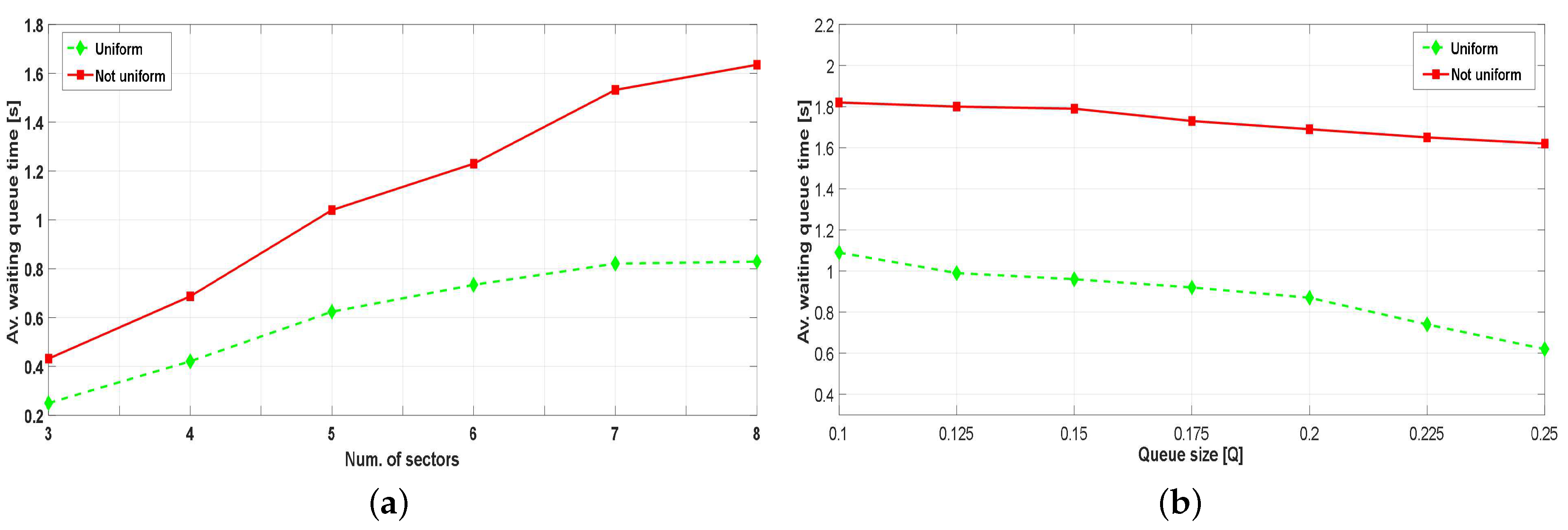
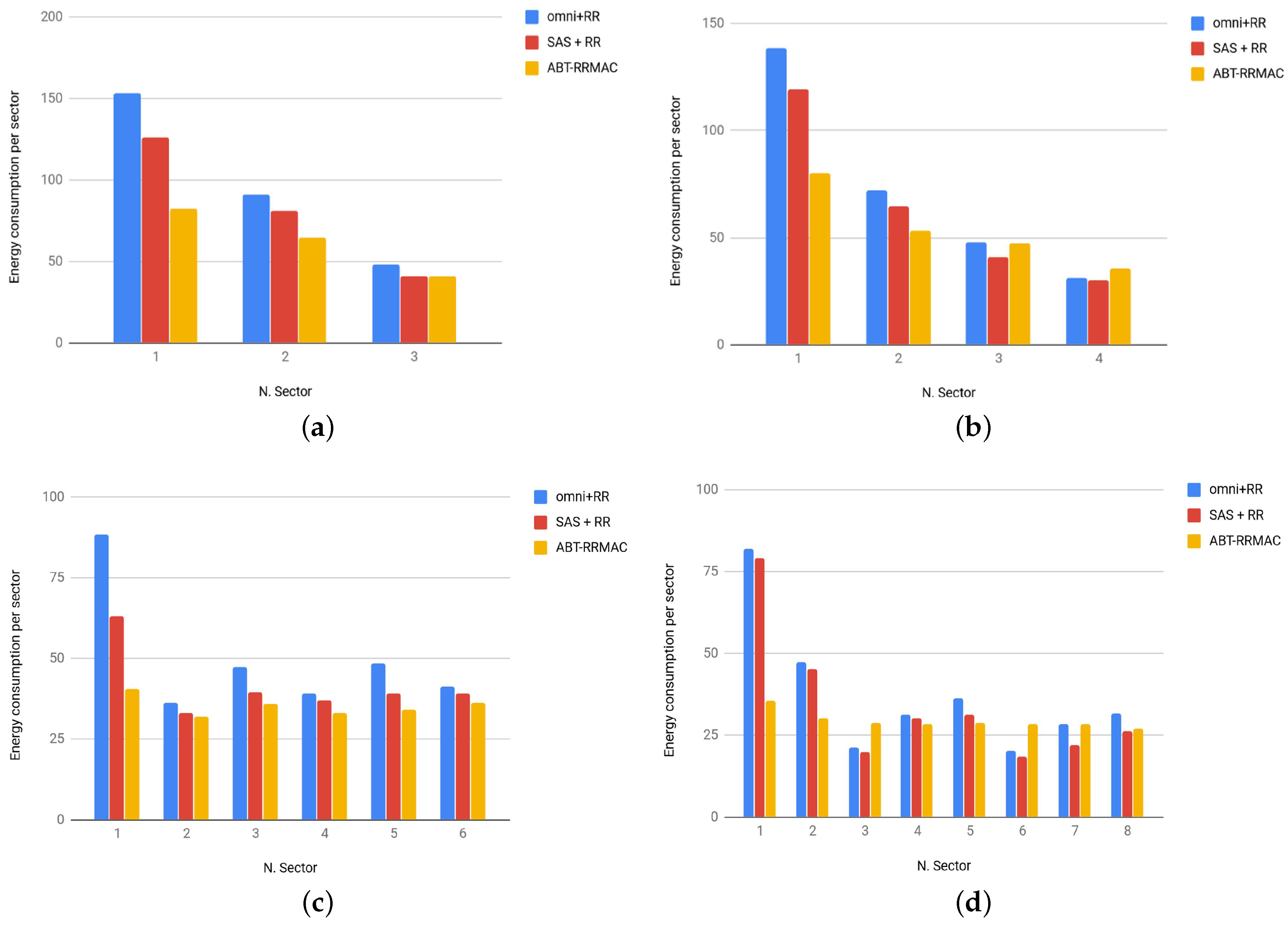
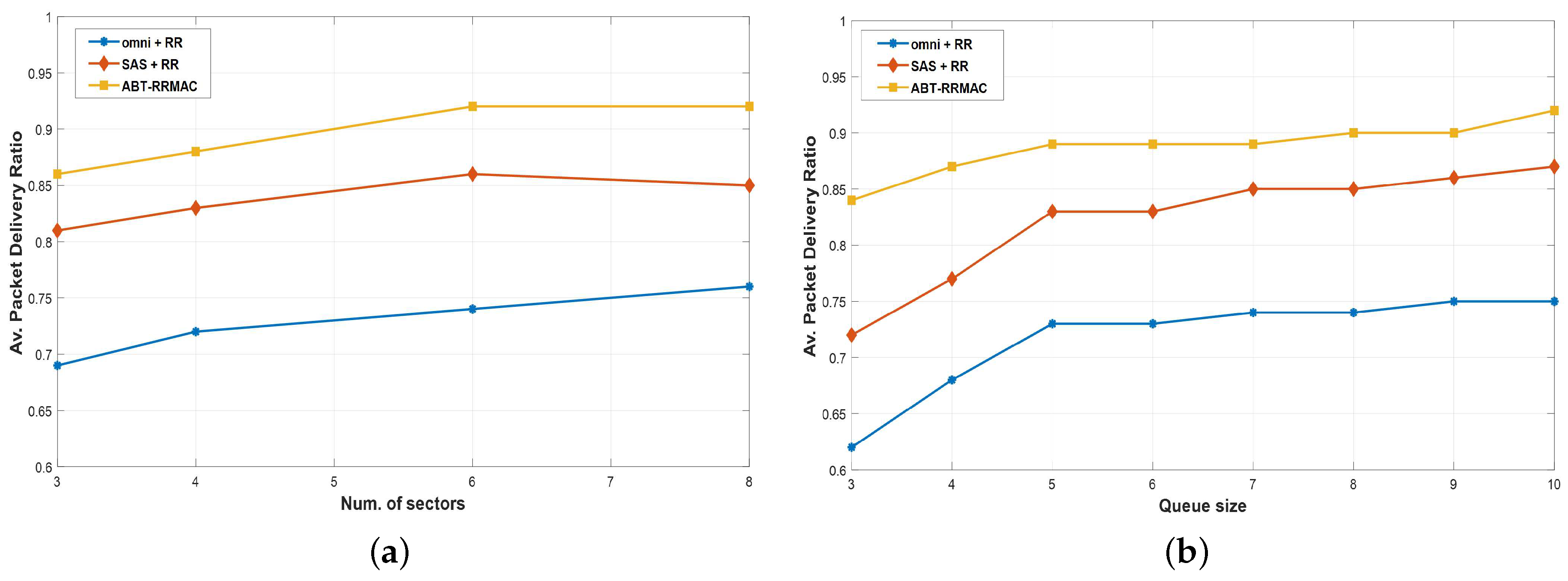
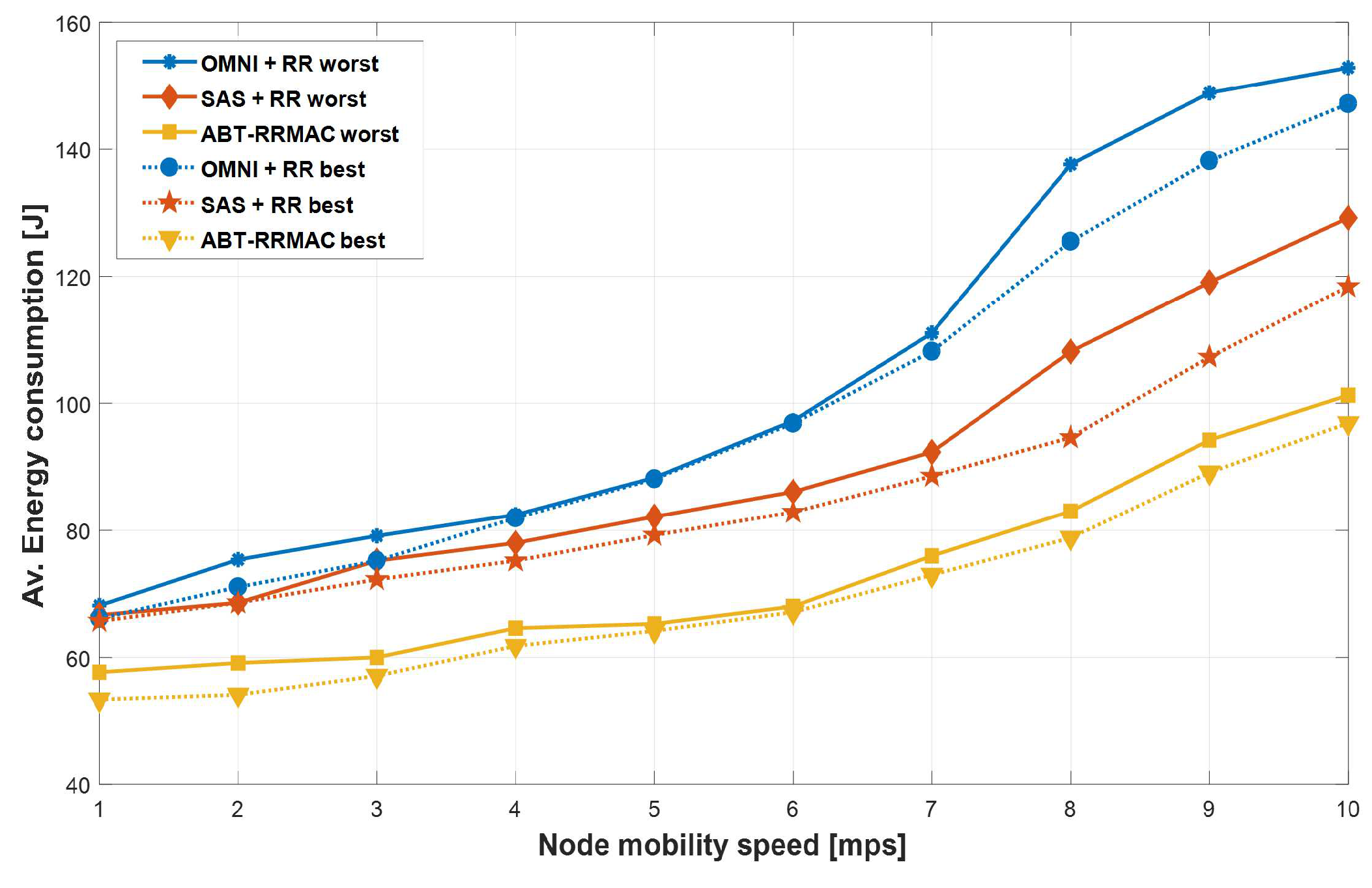
5. Performance Evaluation
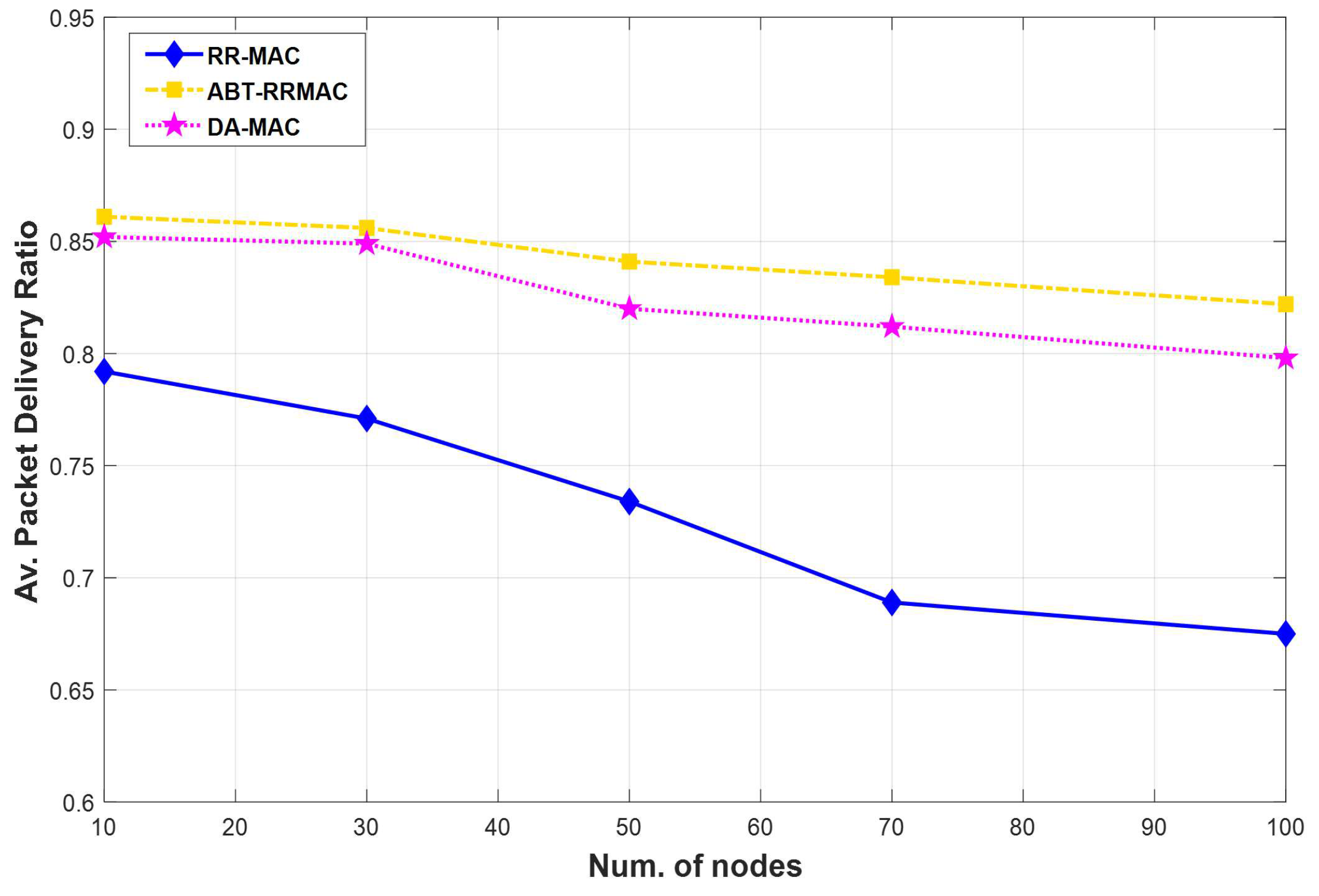
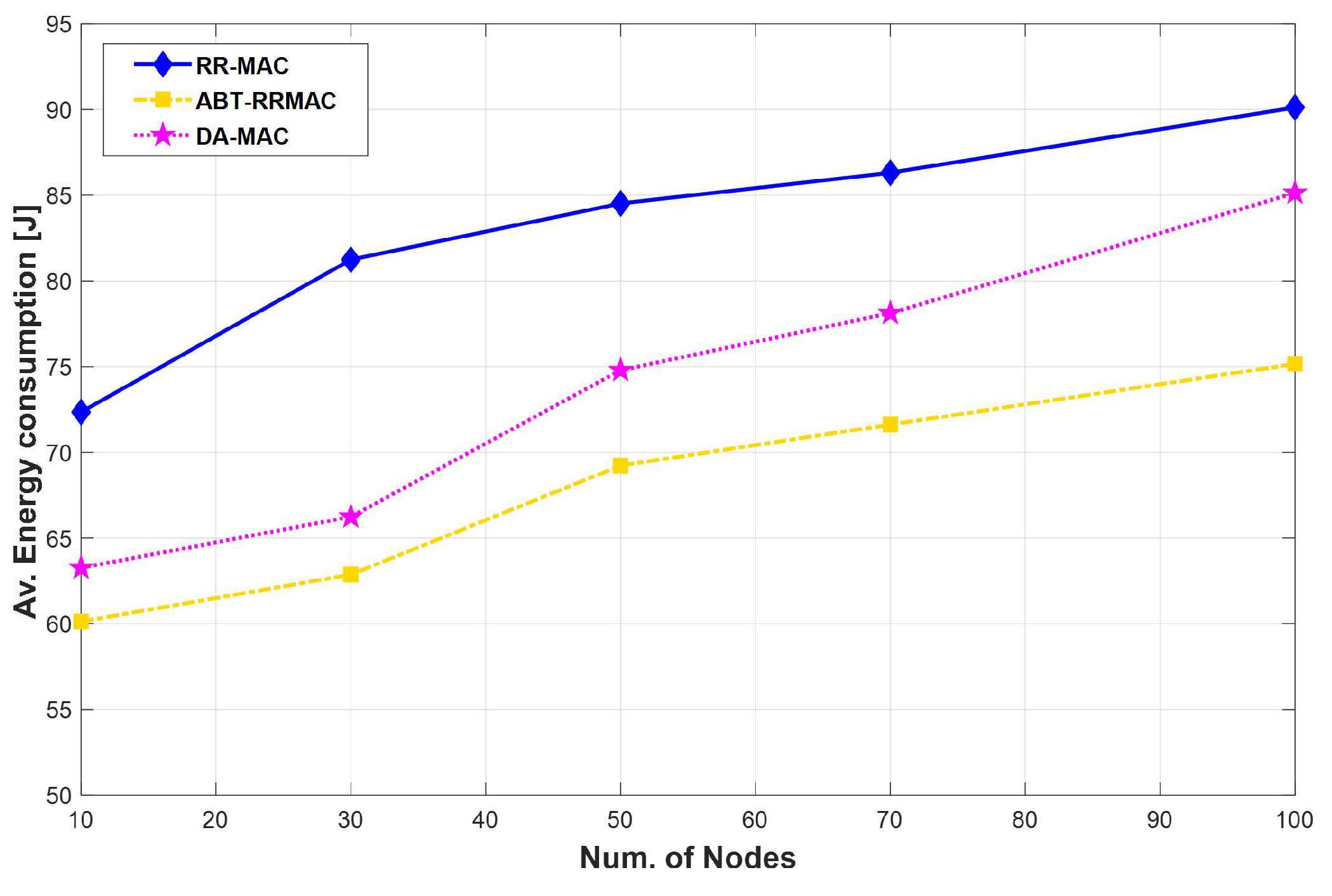
6. ABT-RRMAC Comparison with DA-MAC
6.1. DA-MAC Implementation and Motivations
- Although the DA-MAC does not deal with a sectorized approach as well as our proposal, the work is extremely related with the deafness problem but does not consider the energy consumption of nodes.
- Unlike the most of the cited related works that use the traditional directional antennas, DA-MAC establishes that the mobile nodes are equipped with a switched beam SAS technology. This feature is getting very close to our implementation model, which employs an SAS adaptive array.
6.2. Performance Evaluation
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SASs | smart antenna systems |
| MAC | medium access control |
| OMNI | omnidirectional |
| DMAC | directional medium access control |
| RR-MAC | round-robin MAC |
| ABT-RRMAC | adaptive beamforming round-robin medium access control |
| DA-MAC | deafness-aware medium access control |
| MANET | mobile ad hoc network |
| VANET | vehicular ad hoc network |
| SDMA | spatial division multiple access |
| DRTS | directional request to send |
| DCTS | directional clear to send |
| DNAV | directional network allocator vector |
| CPU | central Processing Unit |
| SRL | short Retry Limit |
| PDR | packet delivery ratio |
| AODV | ad hoc on demand distance vector |
References
- Dai, H.; Kam-Wing, N.G.; Min-You, W. An overview of MAC protocols with directional antennas in wireless ad hoc networks. In Proceedings of the International Conference Wireless and Mobile Communications (ICWMC), Bucharest, Romania, 29–31 July 2006. [Google Scholar]
- Huang, Z.; Chien-Chung, S. A comparison study of omnidirectional and directional MAC protocols for ad hoc networks. In Proceedings of the Global Telecommunications Conference (GLOBECOM), Taipei, Taiwan, 17–21 November 2002. [Google Scholar]
- Choudhury, R.R.; Vaidya, N.H. Deafness: A MAC problem in ad hoc networks when using directional antennas. In Proceedings of the IEEE International Conference on Network Protocols (ICNP), Berlin, Germany, 8 October 2004; pp. 283–292. [Google Scholar]
- Cassano, E.; Florio, F.; De Rango, F.; Marano, S. A performance comparison between ROC-RSSI and trilateration localization techniques for WPAN sensor networks in a real outdoor testbed. In Proceedings of the Wireless Telecommunications Symposium (WTS), Prague, Czech Republic, 22–24 April 2009; pp. 1–8. [Google Scholar]
- Arrawatia, M.; Baghini, M.S.; Kumar, G. Broadband bent triangular omnidirectional antenna for RF energy harvesting. IEEE Antennas Wirel. Propag. Lett. 2016, 15, 36–39. [Google Scholar] [CrossRef]
- Li, B.; Xue, Q. Polarization-reconfigurable omnidirectional antenna combining dipole and loop radiators. IEEE Antennas Wirel. Propag. Lett. 2016, 12, 1102–1105. [Google Scholar] [CrossRef]
- Gustafsson, M.; Sohl, C.; Kristensson, G. Physical limitations on antennas of arbitrary shape. Proc. R. Soc. Lond. A 2007, 463, 2589–2607. [Google Scholar] [CrossRef]
- De Rango, F.; Gerla, M.; Marano, S. A scalable routing scheme with group motion support in large and dense wireless ad hoc networks. Comput. Electr. Eng. 2006, 32, 224–240. [Google Scholar] [CrossRef]
- Dai, H.; Ng, K.; Li, M.; Wu, M. An overview of using directional antennas in wireless networks. Int. J. Commun. Syst. 2013, 26, 413–448. [Google Scholar] [CrossRef]
- Suhag, S.; Gupta, A.; Duhan, M. Improvement of QoS Parameters by using Directional Antennas in MANET. Int. J. 2016, 5, 1026–1031. [Google Scholar]
- Kumari, N.; Kumar, R.; Bajaj, R. Energy Efficient Communication Using Reconfigurable Directional Antenna in MANET. Procedia Comput. Sci. 2018, 125, 194–200. [Google Scholar] [CrossRef]
- Kumari, N.; Kumar, R.; Bajaj, R. Mobile ad hoc networks and energy efficiency using directional antennas: A Review. In Proceedings of the International Conference on Intelligent Computing and Control Systems (ICICCS), Madurai, India, 15–16 June 2017; pp. 1213–1219. [Google Scholar]
- Jiang, D.; Xu, Z.; Li, W.; Chen, Z. Network coding-based energy-efficient multicast routing algorithm for multi-hop wireless networks. J. Syst. Softw. 2015, 104, 152–165. [Google Scholar] [CrossRef]
- Patra, S.; Pandey, A.; Nandni, N.; Kumar, S.; Jha, V.; Kumar, M. Power pattern synthesis of smart antenna array using different adaptive algorithms. Int. J. Adv. Res. 2015, 3, 1459–1466. [Google Scholar]
- He, C.; Liang, X.; Zhou, B.; Geng, J.; Jin, R. Space-division multiple access based on time-modulated array. IEEE Antennas Wirel. Propag. Lett. 2015, 14, 610–613. [Google Scholar] [CrossRef]
- Niu, J.; Zhang, R.; Cai, L.; Yuan, J. A Fully-Distributed MAC Protocol for Mobile Ad Hoc Networks. In Proceedings of the International Conference on Communications (ICC), London, UK, 8–12 June 2015. [Google Scholar]
- Wang, G.; Xiao, P.; Li, W. A novel MAC protocol for wireless network using multi-beam directional antennas. In Proceedings of the International Conference on Computing, Networking and Communications (ICCNC), Santa Clara, CA, USA, 26–29 January 2017. [Google Scholar]
- Wang, J.; Ren, X.; Chen, F.J.; Chen, Y.; Xu, G. On MAC optimization for large-scale wireless sensor network. Wirel. Netw. 2016, 22, 1877–1889. [Google Scholar] [CrossRef]
- Zhou, B.; Lee, Y.Z.; Gerla, M.; De Rango, F. Geo-LANMAR: A scalable routing protocol for ad hoc networks with group motion. Wirel. Commun. Mob. Comput. 2006, 6, 982–1002. [Google Scholar] [CrossRef]
- Jones, C.; Sivalingam, K.; Agrawal, P.; Chen, J. Survey of energy efficient network protocols for wireless networks. Wirel. Netw. 2001, 7, 343–358. [Google Scholar] [CrossRef]
- Chou, J.; Petrovic, D.; Ramchandran, K. A distributed and adaptive signal processing approach to reduce energy consumption in sensor networks. In Proceedings of the Twenty-second Annual Joint Conference of the IEEE Computer and Communications Societies, San Francisco, CA, USA, 30 March–3 April 2003. [Google Scholar]
- Swaminathan, A.; Noneaker, D.L.; Russell, H.B. The design of a channel-access protocol for a wireless ad hoc network with sectored directional antennas. Ad Hoc Netw. 2012, 10, 284–298. [Google Scholar] [CrossRef]
- Inzillo, V.; De Rango, F.; Quintana, A.A. A sectorized directional MAC proposal for mitigating deafness and energy consumption in mobile ad hoc networks. In Proceedings of the 15th Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–2. [Google Scholar]
- Inzillo, V.; De Rango, F.; Santamaria, A.F.; Quintana, A.A. A round-robin MAC approach for limiting deafness in mobile ad hoc network beamforming environments. In Proceedings of the Wireless Days Conference (WD), Dubai, UAE, 3–5 April 2018; pp. 98–100. [Google Scholar]
- Wei, Y.; Heidemann, J.; Estrin, D. An energy-efficient MAC protocol for wireless sensor networks. In Proceedings of the Twenty-First Annual Joint Conference of the IEEE Computer and Communications Societies, New York, NY, USA, 23–27 June 2002. [Google Scholar]
- Na, W.; Park, L.; Cho, S. Deafness-aware MAC protocol for directional antennas in wireless ad hoc networks. Ad Hoc Netw. 2015, 24, 121–134. [Google Scholar] [CrossRef]
- Sivalingam, K.; Chen, J.; Agrawal, P.; Strivastava, M. Design and analysis of low-power access protocols for wireless and mobile ATM networks. Wirel. Netw. 2001, 6, 73–87. [Google Scholar] [CrossRef]
- Gossain, H.; Cordeiro, C.; Cavalcanti, D.; Agrawal, D. The deafness problems and solutions in wireless ad hoc networks using directional antennas. In Proceedings of the Global Telecommunications Conference Workshops (GLOBECOM), Dallas, TX, USA, 29 November–3 December 2004; pp. 108–113. [Google Scholar]
- Huang, P.; Xiao, X.; Soltani, S. The evolution of MAC protocols in wireless sensor networks: A survey. IEEE Commun. Surv. Tutor. 2013, 15, 101–120. [Google Scholar] [CrossRef]
- Huang, Z.; Chen, Y.; Li, C. PSR: A lightweight proactive source routing protocol for mobile ad hoc networks. IEEE Trans. Veh. Technol. 2014, 63, 859–868. [Google Scholar]
- Haider, M.; Knightly, M. Mobility resilience and overhead constrained adaptation in directional 60 GHz WLANs: Protocol design and system implementation. In Proceedings of the 17th International Symposium on Mobile Ad Hoc Networking and Computing (ISCC), Padeborn, Germany, 5–8 July 2016. [Google Scholar]
- Chen, J.; Sivalingam, K.; Agrawal, P.; Acharya, R. Scheduling multimedia services in a low-power MAC for wireless and mobile ATM networks. IEEE Trans. Multimed. 1999, 1, 187–201. [Google Scholar] [CrossRef]
- De la Chapelle, M.; Monk, A. Soft Handoff Method and Apparatus for Mobile Vehicles Using Directional Antennas. U.S. Patent 7555299, 5 April 2016. [Google Scholar]
- Lu, X.; Lio, P.; Hui, P.; Jin, H. A Location Prediction Algorithm for Mobile Communications Using Directional Antennas. Int. J. Distrib. Sens. Netw. 2013, 4, 1–10. [Google Scholar] [CrossRef]
- Inzillo, V.; De Rango, F.; Quintana, A.A.; Zampogna, L. Mobility Beamforming Prediction and a Round Robin Scheduling in a Directional MAC for MANET. In Proceedings of the Wireless and Mobile Networking Conference (WMNC), Prague, Czech Republic, 3–5 September 2018. [Google Scholar]
- Everett, E.; Sahai, A.; Sabharwal, A. Passive self-interference suppression for full-duplex infrastructure nodes. IEEE Trans. Wirel. Commun. 2014, 13, 680–694. [Google Scholar] [CrossRef]
- Korakis, T.; Jakllari, G.; Tassiulas, L. A protocol for full exploitation of directional antennas in ad hoc wireless networks. IEEE Trans. Mob. Comput. 2008, 1, 145–155. [Google Scholar] [CrossRef]
- Li, Y.; Safwat, A. On wireless ad hoc networks with directional antennas: Efficient collision and deafness avoidance mechanisms. EURASIP J. Wirel. Commun. Netw. 2008, 7, 867–882. [Google Scholar] [CrossRef]
- Divecha, B.; Abraham, A.; Grosan, C.; Sanyal, S. Impact of node mobility on MANET routing protocols models. J. Digit. Inf. Manag. (JDIM) 2007, 5, 19–23. [Google Scholar]
- Lenders, V.; Wagner, J.; May, M. Analyzing the impact of mobility in ad hoc networks. In Proceedings of the 2nd International Workshop On Multi-Hop Ad Hoc Networks: From Theory to Reality, Florence, Italy, 26 May 2006. [Google Scholar]
- Omnet++ Simulator, Vers. 5.2. 2018. Available online: www.omnetpp.org (accessed on 13 February 2018).
- Inzillo, V.; De Rango, F.; Quintana, A.A. A Low Energy Consumption Smart Antenna Adaptive Array System For Mobile Ad Hoc Networks. Int. J. Comput. 2017, 16, 124–132. [Google Scholar]
- Abdullah, A.A.; Cai, L.; Gebali, F. DSDMAC: Dual sensing directional MAC protocol for ad hoc networks with directional antennas. IEEE Trans. Veh. Technol. 2012, 61, 1266–1275. [Google Scholar] [CrossRef]
- Jha, J.; Chowdhury, S.; Ramya, G. Survey on various scheduling algorithms. Imp. J. Interdiscip. Res. 2017, 3, 1749–1752. [Google Scholar]
- Fataniya, B.; Patel, M. Survey on different method to improve performance of the round robin scheduling algorithm. Int. J. Res. Sci. Eng. Technol. 2018, 6, 69–77. [Google Scholar]
- Inzillo, V.; De Rango, F.; Santamaria, A.F.; Quintana, A.A. A new switched beam smart antenna model for supporting asymmetrical communications extending Inet Omnet++ framework. In Proceedings of the Performance Evaluation of Computer and Telecommunication Systems International Symposium (SPECTS), Seattle, WA, USA, 9–12 July 2017; pp. 1–7. [Google Scholar]

| Parameter | Value |
|---|---|
| SAS Array Elements Spacing | 0.5 |
| Steering Angle | 45 |
| Transmission Rate | 54 Mbps |
| Message Length | 512 Byte |
| Mobility Model | Random Waypoint |
| Node Mobility speed | from 1 to 10 mps |
| Routing Protocol | AODV |
| Network Load | 50% |
| Simulation Area Size | 500 m × 500 m |
| Simulation Time | 300 s |
| Number of Sectors | 3, 4, 6, 8 |
| Initial Battery Capacity | 300 J |
| Number of Sectors | omni + RR | SAS + RR | ABT-RRMAC |
|---|---|---|---|
| 3 | 52.96 | 42.79 | 20.55 |
| 4 | 47.02 | 39.6 | 19.03 |
| 6 | 19.04 | 20.69 | 3.03 |
| 8 | 18.71 | 18.15 | 2.62 |
| Symbol | Explanation |
|---|---|
| Q | term referred to the queue size |
| N | number of nodes |
| number of sectors | |
| queue weight | |
| queue weight vector | |
| i-th sector | |
| i-th sector time | |
| sector time | |
| i-th sector angle | |
| i-th sector queue size | |
| mean beamforming time | |
| wavelength | |
| s | seconds |
| m | meters |
| meters per seconds | |
| J | joules |
| decibel-milliwatts |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inzillo, V.; De Rango, F.; Quintana, A.A.; Santamaria, A.F. An Adaptive Beamforming Time with Round-Robin MAC Algorithm for Reducing Energy Consumption in MANET. J. Sens. Actuator Netw. 2018, 7, 50. https://doi.org/10.3390/jsan7040050
Inzillo V, De Rango F, Quintana AA, Santamaria AF. An Adaptive Beamforming Time with Round-Robin MAC Algorithm for Reducing Energy Consumption in MANET. Journal of Sensor and Actuator Networks. 2018; 7(4):50. https://doi.org/10.3390/jsan7040050
Chicago/Turabian StyleInzillo, Vincenzo, Floriano De Rango, Alfonso A. Quintana, and Amilcare F. Santamaria. 2018. "An Adaptive Beamforming Time with Round-Robin MAC Algorithm for Reducing Energy Consumption in MANET" Journal of Sensor and Actuator Networks 7, no. 4: 50. https://doi.org/10.3390/jsan7040050
APA StyleInzillo, V., De Rango, F., Quintana, A. A., & Santamaria, A. F. (2018). An Adaptive Beamforming Time with Round-Robin MAC Algorithm for Reducing Energy Consumption in MANET. Journal of Sensor and Actuator Networks, 7(4), 50. https://doi.org/10.3390/jsan7040050






