Abstract
Technological advantages in energy harvesting have been successfully applied in wireless sensor network environments, prolonging network’s lifetime, and, therefore, classical networking approaches like information dissemination need to be readdressed. More specifically, Probabilistic Flooding information dissemination is revisited in this work and it is observed that certain limitations arise due to the idiosyncrasies of nodes’ operation in energy harvesting network environments, resulting in reduced network coverage. In order to address this challenge, a modified version of Probabilistic Flooding is proposed, called Robust Probabilistic Flooding, which is capable of dealing with nodes of about to be exhausted batteries that resume their operation after ambient energy collection. In order to capture the behavior of the nodes’ operational states, a Markov chain model is also introduced and—based on certain observations and assumptions presented here—is subsequently simplified. Simulation results based on the proposed Markov chain model and a solar radiation dataset demonstrate the inefficiencies of Probabilistic Flooding and show that its enhanced version (i.e., Robust Probabilistic Flooding) is capable of fully covering the network on the expense of increased termination time in energy harvesting environments. Another advantage is that no extra overhead is introduced regarding the number of disseminated messages, thus not introducing any extra transmissions and therefore the consumed energy does not increase.
1. Introduction
Advantages in wireless communications and embedded hardware design, have enabled the extensive development of wireless sensor networks [1]. Wireless sensor nodes are of small size, low cost and are (usually) battery operating devices able to sense and transmit environmental information. Therefore, such devices are extensively used in various environments like underwater, vehicular and agricultural where conventional wired approaches are hard or inconceivable to be implemented. However, the resources required for the operation of the wireless nodes (e.g., energy supply) may be absent, resulting in network degradation [2].
The last decade’s technological advantages have resulted in the development of high performance, low-powered embedded devices being able to execute complex tasks. Furthermore, small-scale energy harvesting devices (e.g., solar panels, wind turbines, special antennas) may be attached to the power source and prolong their lifetime [3], allowing for the deployment of wireless sensor networks in a wide variety of environments regardless of the power infrastructure.
Prolonging the network’s lifetime using energy harvesting is essential in the sense of reducing sustainability costs. However, employing energy harvesting technologies in wireless environments results in increased system complexity. When the nodes rely only on the energy stored in batteries, they can efficiently adapt the power consumption according to the remaining energy. However, when solar panels or wind turbines can replenish the stored energy, the adaption of power consumption is a far more complicated task due to the probabilistic nature of the energy harvesting process. Even if the solar radiation is sufficient to recharge nodes’ batteries at certain periods of a day, some nodes may be unable to harvest solar energy (e.g., placed in a shady location) and run out of energy. However, these nodes may replenish their batteries at a later time and become operational. Thus, conventional protocols and mechanisms being widely used in wireless sensor networks need to be revisited under the perspective of energy harvesting.
Information dissemination plays a crucial role in modern network environments, being an underlying mechanism for various vital processes. This work aims to shed further light on information dissemination and particularly to adapt this mechanism in energy harvesting environments.
The stochastic nature of the energy collection process influences the operational state of the network’s nodes. Thus, nodes may be operational or non-operational according to their battery level. Therefore, when the energy collecting from the ambient environment is sufficient to recharge the batteries, nodes are expected to be in an operational state; otherwise, the nodes may run out of energy and become non-operational. Consequently, when the nodes belonging to the bottleneck links of the network are not operational, any conventional information dissemination mechanism is unable to proceed and reach all the operational nodes. Considering that the energy collection process may recharge these nodes at a later time, this motivates the revisiting the information dissemination mechanism and in particular Probabilistic Flooding (PF) [4].
In this work, we present a variant of the Probabilistic Flooding mechanism. i.e., Robust Probabilistic Flooding (RPF), capable of dealing with the nodes’ operational states and a Markov chain that captures the behavior of the energy harvesting environments. The proposed Markov chain is further analyzed and simplified in order to derive analytical expressions regarding the probability of a node to be in an operational or non-operational state and a charging or discharging state. An earlier version of this work has been presented in [5]. The main enhancement presented here is that the previous model is considered along with a solar radiation dataset obtained from the NASA Langley Research Center (LaRC) POWER Project [6] and also new simulations have been performed in a more realistic environment in order to compare the proposed information dissemination mechanism against PF. Still, it is shown that the proposed mechanism outperforms PF regarding coverage at the expense of increased termination time.
Past related work regarding probabilistic information dissemination and energy harvesting is presented in Section 2. Section 3 presents the proposed Markov chain model which is analyzed and simplified in Section 5. The proposed RPF mechanism is presented in Section 4 and evaluated later in Section 6. Finally, the conclusions are drawn in Section 7.
2. Past Related Work
The energy collection from the ambient environment has been extensively studied in the literature and is proposed as a suitable method for prolonging the systems’ lifetime. For example, in a system that is impossible to replace [7,8] or recharge [9] its batteries using conventional approaches (e.g., placed in a hostile environment), the energy collection from the ambient environment may be the only method to prolong their lifetime. A significant advantage of the ambient energy resources is that they can be free and, many times, even inexhaustible, leading to a significant reduction of maintenance costs. However, the stochastic behavior of ambient energy harvesting results in the collection of different amounts of energy over time. In order to alleviate this problem, energy prediction methods have been proposed in the literature. Authors in [10] present algorithms for determining energy consumption in systems with predictable and stochastic energy inputs and those in [11] propose a novel energy prediction model for multi-source energy harvesting wireless sensor networks, for providing accurate estimations about energy availability. Markov processes have also been proposed in order to model energy harvesting from ambient energy resources. In [12], a model is provided considering micro-solar power sources, whereas, in [13], a Markov-model-based method is proposed that sufficiently captures the energy level of body sensors [14] and predicts the probability of energy depletion. In order to prolong the network’s lifetime, authors in [15] present an adaptive duty cycling algorithm with nodes to autonomously adjust their operation cycle according to the energy availability in the environment. In [16], an adaptive duty cycling technique for wireless sensor network nodes is presented, whereas, in [17], a method regarding an oscillating energy harvesting system is presented. Authors in [18] present an introduction to Harvesting Aware Power Management, including topologies of Energy Harvesting Systems, the Energy Neutrality Principle and Power Management Techniques. The energy harvesting techniques have also been proposed in the area of Wireless NanoSensor Networks [19], which requires the use of nanoscale energy harvesting systems. In [20], an energy and spectrum-aware Media Access Control (MAC) protocol in the Terahertz Band is presented, using a scheduling algorithm which allows a large number of nanosensors to transmit their packets without inducing collisions. In the area of wireless energy transfer, authors in [21] propose the concept of energy cooperation where the network nodes exchange their remaining energy wirelessly improving the overall system performance, despite the loss incurred in energy transfer. In [22], a self-powered wireless system with one transmitter and one receiver is considered, in which the transmitter has no fixed power supplies and extracts energy only via wireless energy harvesting from ambient radio signals. The transmitter spends a fraction of time collecting energy and the remaining fraction of time is used for data transmission. The experimental results characterize how the maximal achievable throughput varies with energy harvesting rate. In [23], a general model is presented with non-ideal energy storage efficiency and transmit circuit power and a proposed protocol is considered, in which a fraction of time is devoted to energy harvesting and the remaining fraction is used for data transmission. The system outage performance is optimized by finding the optimal ratio between the time spent on energy harvesting and data transmission. Authors in [24] propose an adaptive energy harvesting management framework, which exploits an application’s tolerance to quality degradation based on energy harvesting conditions, whereas, in [25], a novel task allocation scheme for solar-powered sensor nodes that operates in two phases of task scheduling and task mapping is proposed. The main objective is to maximize the network’s lifetime while meeting the application’s requirement regarding time delay.
Routing plays a crucial role in wireless sensor network environments, since finding the optimal route among the nodes saves valuable network resources and prolongs the network’s lifetime. In the presence of energy harvesting, several routing algorithms have been proposed. In [26], two different routing protocols are proposed that combine geographic routing along with energy-aware routing techniques taking into account the realistic lossy wireless channel condition and the renewal capability of environmental energy supply when making routing decisions. Authors in [27] analyze and compare existing routing algorithms and propose a modified version of the Randomized Minimum Path Recovery Time algorithm [28] that outperforms the evaluated algorithms in scenarios where little energy is harvested from the environment. In [29], data collection for traffic monitoring/surveillance purposes for busy highways is considered. The nondeterministic polynomial time (NP) hardness of the problem is proved and a centralized and a distributed algorithm are proposed which demonstrating their efficiency. Data collection is also studied in [30] for energy harvesting sensor networks and it is shown that, during the process of forwarding, each additional link increases the overall probability of losing the sent message. Two data collection protocols are proposed and it is shown to achieve high delivery ratios. In [31], a cross-layer optimized multipath routing algorithm is proposed where a forwarding node chooses the next-hop node based on 2-hop neighbor information rather than 1-hop. A sleep scheduling scheme is also proposed that aims to maximize the network’s lifetime. In [32], an energy-aware opportunistic routing protocol for large-scale energy harvesting wireless sensor networks is proposed, where each node chooses the next-hop neighbor considering the available energy, the distance from the sink node and the amount of data to be transmitted, whereas, in [33], novel solutions are introduced for bounding sink-to-node communication delay in energy-harvesting sensor networks. These solutions are evaluated in a testbed and it is shown that energy consumption is improved compared with the proposed protocol in [34].
Probabilistic flooding has been proposed as a suitable alternative to blind flooding [35] in order to disseminate information in a network and reduce unnecessary transmissions, saving valuable network resources. In [36], probabilistic flooding performance is compared against an adaptive flooding approach that changes the (otherwise fixed) forwarding probability. In [37], suitable values for the threshold probability considering various topologies are derived and, in [38], asymptotic expressions for the case of random graphs are also derived. In [4], probabilistic flooding is studied using algebraic graph theory elements and an algorithm is introduced to estimate the threshold probability. Probabilistic flooding in generalized random graphs is studied in [39], while the case of peer-to-peer is studied in [40,41]. Gossip-based techniques are also used in wireless sensor network environments (e.g., [42]). Authors in [43] propose an opportunistic flooding algorithm, where each node chooses some of its neighbors to broadcast the information message and, in [44], they study gossip and epidemic algorithms for information broadcasting in geometric random graphs. In the area of mobile ad hoc networks in [45], a probabilistic broadcast for flooding is proposed, whereas, in [46], a balanced probabilistic flooding algorithm for wireless sensor networks is also proposed. A link correlation based probabilistic flooding algorithm in proposed in [47] and a variation of probabilistic flooding for reliable dissemination is proposed in [48]. Authors in [49] combine various flooding schemes, e.g., adaptive probability, in order to ensure reduced overhead while they compare their method against traditional and probabilistic flooding. An adaptive probabilistic mechanism based on the wave propagation is proposed in [50], while an energy efficient routing algorithm using probabilistic flooding is proposed in [51]. Probabilistic flooding has also been proposed for the area of nanonetworks by [52,53], and underwater environments by [54], whereas vehicular networks have also been the focus by [55,56]. An adaptive version for multi-path routing purposes is proposed by [57]. Authors in [58] propose an advanced probabilistic flooding mechanism considering both the popularity of resources and the distance from the initiator node. A method for evaluation of network-wide broadcast protocols is proposed in [59], whereas, in [60], the use of probabilistic flooding in their broadcast protocol for wireless body area networks is proposed. The work presented here is an extended version of a previous work in [5] that has been significantly enhanced to provide for further evaluation using traces from a realistic environment (i.e., solar radiation dataset obtained from the NASA Langley Research Center POWER Project funded through the NASA Earth Science/Applied Science Program [6]) and realistic network node specifications (i.e., based on the datasheet of MICA2-MPR400CB [61]).
3. The Energy Harvesting Network System
Let a network topology with n nodes and ℓ links be represented by a Graph G where and are the set of nodes and the set of links, respectively. Consequently, and . In addition, let denote node’s u neighbors. It is common practice in wireless sensor network environments that an operational node periodically transmits beacon frames to inform the neighbor nodes about its presence. A node is operational if the amount of the remaining energy in its battery is above a particular threshold. When the remaining energy falls below this threshold, the node becomes non-operational and thus is not participating in the network. Moreover, in energy harvesting environments, when the amount of energy collected is larger than the consumed energy, the node is charging; otherwise, it is discharging. Consequently, a node may be in four different states presented in Table 1 depending on its operational state (i.e., ON, OFF) and the amount of the collected energy from the ambient environment (i.e., C, D).

Table 1.
Node states.
Thus, ON-C corresponds to the state of a node which is operational and its battery is charging (i.e., State 1), ON-D corresponds to the state of a node that is operational and its battery is discharging (i.e., State 2), OFF-C corresponds to the state of a node that is non-operational and its battery is charging (i.e., State 3) and OFF-D corresponds to the state of a node that is non-operational and its battery is discharging (i.e., State 4).
Figure 1 depicts the four states and the corresponding transition probabilities as a Markov chain [62]. This chain is further studied and simplified in Section 5 and along with the realistic dataset obtained from the NASA Langley Research Center (LaRC) POWER Project [6] is used to compare the proposed information dissemination mechanism against PF in Section 6.
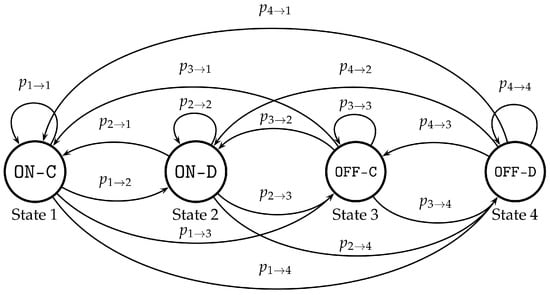
Figure 1.
Node state Markov chain.
4. Probabilistic Information Dissemination
Let s denote the node that plans to disseminate an information message to the network nodes (i.e., initiator node) using PF. Nodes that receive the particular message for the first time decides whether to forward this to their neighbors according to a fixed forwarding probability q. Any redundant messages received by the nodes are discarded. For the sake of simplicity, it is assumed that the dissemination process takes place in discrete time steps.
Let the coverage (i.e., the fraction of covered nodes by PF) at time step t be denoted by . Obviously, since only node s has the particular message at the beginning. In addition, let denote the termination time of the PF. The main objective here is to archive global outreach (i.e., cover all the nodes of the network) when the dissemination process finishes i.e., .
Due to its probabilistic nature, global outreach under PF is guaranteed with high probability and not deterministically. A large amount of studies (e.g., [4,36,37,63]) focuses on the particular value of q allowing for global outreach and at the same time the amount of messages kept minimized i.e., threshold probability, . The benefits obtained by this policy vary according to the value of the forwarding probability. If the value of q is smaller than , then coverage is small (i.e., ). If q is larger than , although the coverage is sightly increased compared to the case of , the amount of messages may be significantly increased.
This work aims to shed further light on the efficiency of PF in the presence of energy harvesting. Figure 2 depicts a network where a bottleneck exists between nodes u and v. Let the nodes be operating under the previously mentioned energy harvesting environment and assume that node s plans to disseminate an information message to the network under PF. At time step , node s forwards the particular message to its neighbors according to a forwarding probability sufficient to provide full coverage (i.e., ) under the assumption that all nodes are operating. However, when the energy is exhausted in either of nodes u or v, the nodes within the dotted area do not receive the particular message, even though the energy harvesting mechanism may replenish their batteries later.
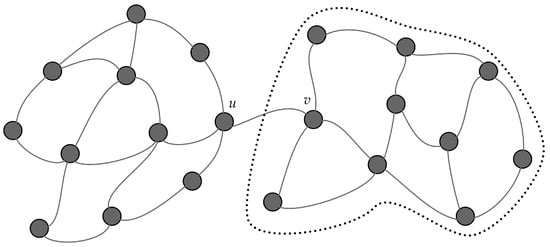
Figure 2.
Network topology with a bottleneck link . Nodes within the dotted line will not receive the information message if either u or v are not operating.
Based on this observation, it follows that, in order to adapt PF into energy harvesting environments, the nodes’ operational states should be taken into account. Consequently, under the proposed mechanism, each node that receives the information message for the first time selects a subset of its neighbors according to the forwarding probability regardless of their operational state. Subsequently, the node forwards the information message to the operating nodes and waits for the non-operating ones to become available and receive the particular message. If a node that plans to forward an information message to its neighbors runs out of energy, it suspends its operation and resumes as soon as the energy harvesting process replenishes its battery. The proposed mechanism called Robust Probabilistic Flooding (RPF) is presented in Algorithm 1.
Let denote the set of neighbors of node u, the subset of that remains to be covered under the proposed mechanism and the subset of that is operational at a particular time. It follows that and . It is assumed that every node periodically transmits beacons frames to inform the neighbor nodes about its presence.
At the initialization stage, every node (variable u) apart from the initiator (variable s) sets its status (variable isCovered) as uncovered (Line 9). The initiator node, randomly (according to the forwarding probability q) selects a fraction of its neighbors (i.e., function randomSelect) and constructs the set (). Subsequently, (Lines 6–8) forward the information message to each of the operating nodes in this set (i.e., ) and remove the particular node from .
After the initialization stage, every node that receives the information message for the first time updates its status as covered (Line 12), constructs the set (Line 13) and sends the particular message to each of the operating nodes in this set (Lines 14–16). The corresponding node periodically checks whether the non-operating neighbors in the set have been revived and sends the information message to them.
The proposed algorithm can be applied to energy harvesting environments since it takes into account the nodes’ operational states. It is shown in the simulations section that the coverage under RPF outperforms PF coverage at the expense of increased termination time. It is observed from Algorithm 1 that the number of messages is the same as in the case of the PF under non-energy harvesting environments. Another observation is that, when all the nodes of the network are operational, the proposed algorithm reduces to PF. Under RPF, every node has to maintain the set of nodes that need to be covered after they become operational again (i.e., ), thus an extra memory overhead is introduced. However, this overhead is not expected to be prohibitive for the node’s operation since it is bounded by the number of neighbors.
| Algorithm 1 Robust Probabilistic Flooding RPF(s,q) |
|
|
|
|
5. Markov Chain Analysis
In this section, the proposed four-state Markov chain is simplified and analyzed. It is observed from Figure 1 that certain transition probabilities can be merged and omitted. As it is mentioned in Section 3, a node is considered operational if its battery level is above a particular threshold. Thus, an operational node whose battery is being charged (i.e., ON-C) is not expected to transit directly to a non-operational state (i.e., OFF-C, OFF-D). Therefore, the transition probabilities and can be omitted. Similarly, the transition probabilities and can also be omitted, since a node being in a non-operational state and whose battery is discharging (i.e., OFF-D) first needs to collect a certain amount of energy in order to become operational again. Furthermore, a node that is operational and its battery is discharging (i.e., ON-D) is not expected to become non-operational and charge its battery (i.e., OFF-C) directly, thus and can be omitted. It should be mentioned that certain states have been ignored (e.g., energy harvester’s charging mechanism failure) in order to keep this model simple and derive tractable analytical expressions regarding the state probabilities.
Let and denote the probabilities that a node’s battery is charging and discharging, respectively, and it is expected to stay in the particular state. Let also denote the probability moving from the state ON-D to the state ON-C. Consequently, , and . In order to simplify further, the Markov chain and given that corresponds to the probability of moving from a discharging state to a charging mode of operation, analogously, it is assumed that the movement from the charging state OFF-C to the charging state OFF-D is equal to . Eventually, and given that the sum of the transition probabilities for a particular state equals to one, it follows that
Considering Equations (1)–(5) and the previous assumptions, the proposed four state Markov chain presented in Figure 1 can be simplified to the one presented in Figure 3.
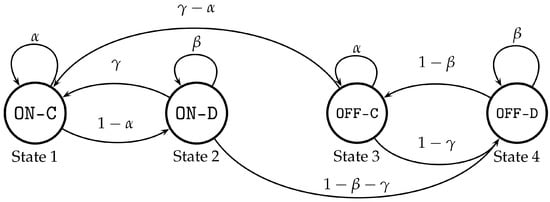
Figure 3.
The simplified Markov chain.
It is also assumed that the transition probabilities are larger than zero and smaller than one (i.e., for ); otherwise, the proposed Markov chain is reduced to a trivial one. Therefore, and or, and , respectively. Since , it follows that .
Let , , , denote the probability of a node be in state ON-C, ON-D, OFF-C, OFF-D, respectively. Equations (6)–(9) present the analytical expressions of these probabilities as a function of , and . The derivation steps are depicted in the Appendix:
Figure 4 depicts the probability of a node to be in state ON-C (i.e., ) as a function of , for and various values of . As it is expected, when equals to , it is . In addition, when equals to , it follows that ; consequently, increases monotonically.
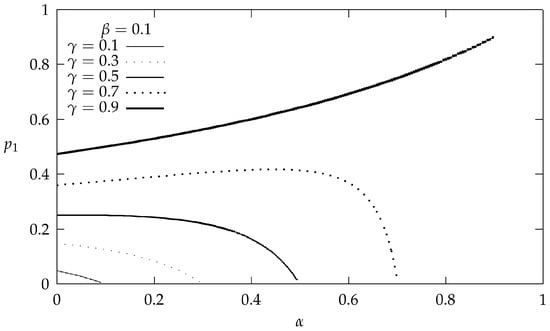
Figure 4.
as a function of , for and various values of .
The main objective of the proposed simplified Markov chain is to capture the basic behavior of the nodes’ operational states and it is used in the sequel for the evaluation of RPF.
6. Performance Evaluation
A simulation program in C++ has been developed to evaluate RPF against PF in geometric random graph (GRG) [64] topologies. At each timestep, the simulator checks whether a node has any packet to send to its neighbors and takes over the transmission. When the energy harvesting environment is activated, the simulator checks whether the receiver node is operating before transmitting the packet to it. If the receiver node is not operating, the sender node is informed and the packet is queued for transmission at next timestep. The number of nodes is for all simulation scenarios and they are independent identically distributed in plane. A link between any pair exists if their euclidean distance is equal or smaller than the connectivity radius .
6.1. Simulation Scenarios Evaluation
The main objective of this section is to compare the coverage efficiency of PF against RPF in energy harvesting environments. The simulations performed consider various GRG groups with connectivity radius , and . For each group, ten different topologies are created and the depicted results are the average values obtained by the simulations on these topologies. For each case, the forwarding probability is set to a value such that full coverage is ensured with high probability under non-energy harvesting environments (i.e., ). Network nodes are operating under the simplified proposed Markov model (i.e., Figure 3) when the energy harvesting environment is activated.
Columns 2 and 3 of Table 2 present the average number of links (ℓ) and the average number of neighbors (#Neighbors) for the three different GRG groups with connectivity radius , and , respectively. Columns 4 and 5 present the average value of the termination time () and the average number of sent messages under PF () using a forwarding probability of (i.e., Column 6) and considering non-energy harvesting environments.

Table 2.
Average values for ℓ, #Neighbors, , and for Probabilistic Flooding.
Figure 5 depicts PF coverage at termination time (i.e., )) as a function of under energy harvesting environment, for , , and various values of . Moreover, Figure 6 depicts PF coverage at termination time (i.e., ) as a function of under energy harvesting environment, for , , and various values of .
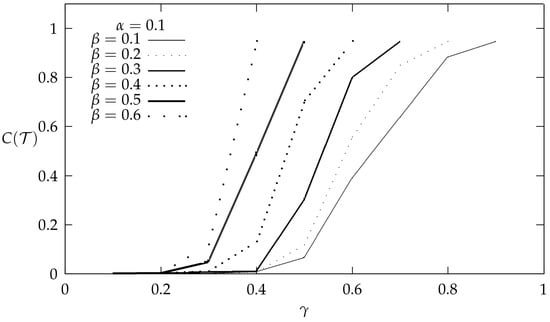
Figure 5.
Coverage at termination time under PF for and various values of as a function of for .
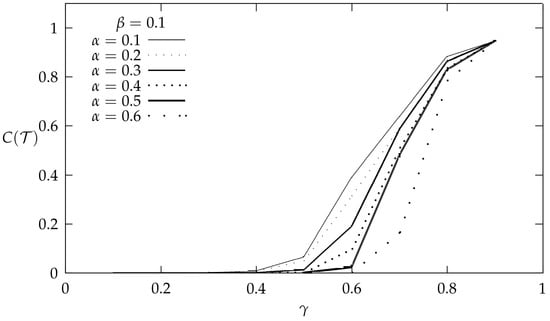
Figure 6.
Coverage at termination time () under PF as a function of for , and various values of .
It is observed in both figures that full coverage under PF is obtained only for a small range of values for , and , while, for the rest, the coverage is reduced. It is shown that the proposed Markov chain highlights the incapability of PF for full coverage under an energy harvesting environment.
The fact that PF fails to obtain full coverage is clearly shown in Figure 7 which depicts PF coverage at termination time as a function of the connectivity radius for various sets of and . Note that in all cases the forwarding probability is set to a value such that full coverage is ensured with high probability under non-energy harvesting environments.
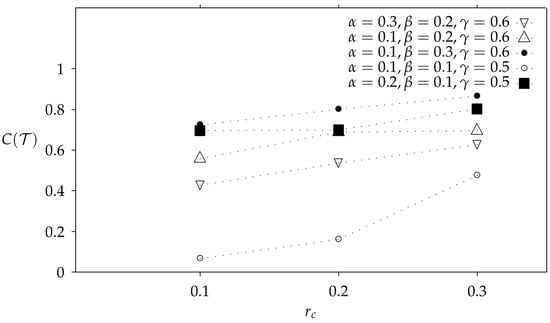
Figure 7.
Coverage at termination time under Probabilistic Flooding for three different sets of , and for , and .
Figure 8 depicts coverage as a function of time for , , under both PF and the proposed RPF and for all considered topology groups (i.e., , ). It is observed that the proposed mechanism obtains full coverage in all cases, while the coverage under PF is significantly reduced.
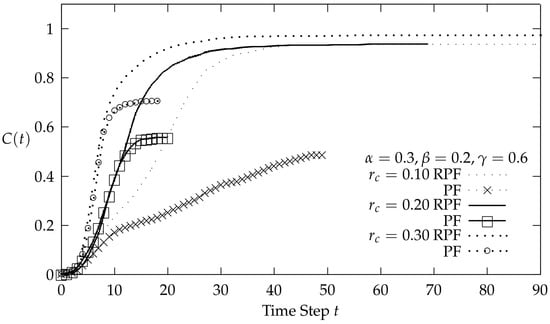
Figure 8.
Coverage () under Probabilistic Flooding and Robust Probabilistic Flooding for , and as a function of time (t).
It is also observed that both mechanisms expound the same increment rate regarding coverage for the first time steps. However, for the larger values of time, PF coverage is significantly reduced and only RPF succeeds at obtaining full coverage.
Figure 9 depicts termination time () under RPF as a function of the connectivity radius () for three different sets of and for a case of a non-energy harvesting environment. It is observed that termination time under energy harvesting environments is increased compared to the non-energy harvesting one. Note that in non-energy harvesting environments the proposed mechanism reduces to PF since there are no extra delays due to the nodes’ non-operational states.
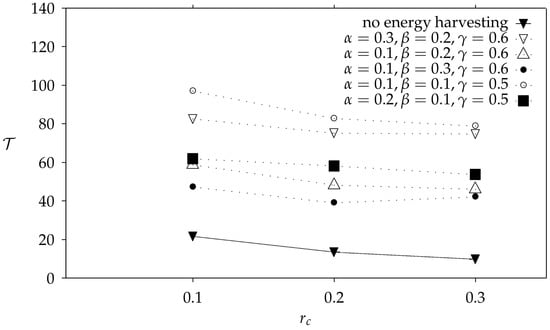
Figure 9.
Termination time under RPF for three different sets of , and for , and . Line “no energy harvesting” corresponds to the case that no energy harvesting is activated in the network.
Finally, it is shown that the RPF mechanism outperforms PF regarding coverage under the proposed four chain Markov model, without additional message costs, since it takes into account the nodes’ operational states. However, under the proposed mechanism, every node has to maintain the set of nodes that need to be covered. This introduces an extra memory overhead that is not expected to be discouraging for applying RPF in wireless sensor network environments since it is bounded by the number of neighbors.
6.2. Realistic Environment Evaluation
In order to evaluate the proposed RPF in a realistic environment, a solar radiation dataset for the city of Corfu in Greece between July 1983 and July 2017 was obtained from the NASA Langley Research Center (LaRC) POWER Project funded through the NASA Earth Science/Applied Science Program [6]. Furthermore, network nodes specifications are based on the datasheet of MICA2 (MPR400CB) [61]. Similar parameters regarding the simulation scenarios as for the previous cases are considered (e.g., random geometric graph topologies). The network nodes’ and the solar panel’s parameters are drawn in Table 3 and Table 4, respectively. Each node recharges its battery with a probability of and generates data packets that are forwarded towards the sink node, with a probability of . Along with these packets, sink node generates a data packet which is disseminated to the network using PF or RPF. Nodes’ batteries discharge during the night and when the remaining energy falls below 10%, they stop operating. When the sun rises, nodes’ batteries become charged by the insolation on the solar panel and when the remaining energy climbs above 20% nodes become operational again. At the time that the sink node starts to disseminate the information message in the network, a fraction of nodes may be in a non-operational state, resulting in a reduced coverage under PF.

Table 3.
Node parameters.

Table 4.
Solar panel parameters.
Figure 10 and Figure 11 depict simulation results regarding coverage at termination time under PF and RPF, respectively, as a function of initially operating nodes for three geometric random graph topologies with connectivity radius , and and three different forwarding probabilities. It is observed that PF coverage keeps low when the number of initially operating nodes is small, even for large values of the forwarding probability. For example, in Figure 10a and for the highest value of the forwarding probability, coverage is high (>0.8) for over 650 initially operating nodes. However, in Figure 11, it is observed that RPF coverage, for the same topologies and forwarding probabilities, remains high even for the smallest number of initially operating nodes.

Figure 10.
Simulation results regarding coverage at termination time under Probabilistic Flooding as a function of the number of nodes operating when Probabilistic Flooding started for three different geometric random graph topologies i.e., (a), (b) and (c).

Figure 11.
Simulation results regarding coverage at termination time under Robust Probabilistic Flooding as a function of the number of nodes operating when Robust Probabilistic Flooding started for three different geometric random graph topologies i.e., (a), (b) and (c).
Under the proposed RPF, the node that plans to forward the information message waits for its neighbors to become operational. This behavior results in an increased termination time of the proposed Algorithm 1. The latter is observed in Figure 12 and Figure 13, which depict simulation results regarding termination time under PF and RPF, respectively, as a function of initially operating nodes for three geometric random graph topologies with connectivity radius , and and three different forwarding probabilities. It is observed that the termination time of the RPF is significantly larger than this of the PF in all cases. For example, for the case of the geometric random graph with connectivity radius (i.e., Figure 12b and Figure 13b) with 500 initially operating nodes and for , the termination time under PF is 25, while, under RPF, it is 62. When all the nodes of the network are operational, there are no additional delays under RPF and thus the proposed Algorithm 1 reduces to PF. The latter is observed for all cases where the number of initial operating nodes equals 1000.

Figure 12.
Simulation results regarding termination time under Probabilistic Flooding as a function of the number of nodes operating when Probabilistic Flooding started for three different geometric random graph topologies i.e., (a), (b) and (c).

Figure 13.
Simulation results regarding termination time under Robust Probabilistic Flooding as a function of the number of nodes operating when Robust Probabilistic Flooding started for three different geometric random graph topologies i.e., (a), (b) and (c).
Figure 14 depicts simulation results regarding coverage as a function of time under PF and RPF, for three geometric random graph topologies with connectivity radius , and and for 200, 600 and 900 initially operating nodes. It is observed in all cases that, although RPF has a larger termination time, it offers higher coverage than PF at every timestep t. In the case of 200 initially operating nodes, PF fails to reach most of the network nodes. For the case of 600 initially operating nodes, PF coverage is still lower than that of RPF, while, for the case of 900 initially operating nodes, PF offers almost the same coverage as the proposed RPF.
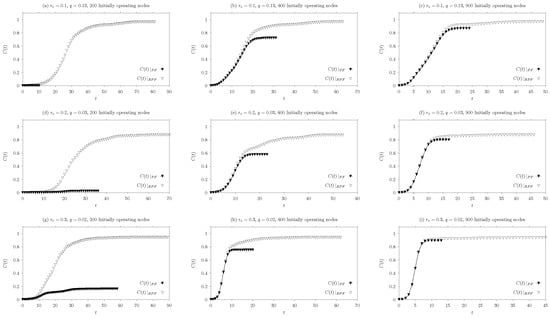
Figure 14.
Simulation results regarding coverage as a function of time under PF and RPF, for , and for initially operating nodes.
Figure 15 depicts simulation results regarding message efficiency (i.e., the fraction of coverage over the total sent messages) under PF and RPF as a function of the number of initially operating nodes for three different random geometric graph topologies. The dashed line depicts the minimum number of initially operating nodes needed to achieve coverage over 0.85 under PF. It is observed that both PF and RPF achieve almost the same message efficiency when coverage is larger than 0.85. In all cases, the message efficiency under RPF is nearly the same regardless of the number of initially operating nodes.

Figure 15.
Simulation results regarding message efficiency under PF and RPF as a function of the number of initially operating nodes for three different geometric random graph topologies i.e., and .
Figure 16 depicts simulation results regarding total energy consumption in mAh as a function of the connectivity radius when full coverage is achieved. It is observed that RPF consumes slightly more energy for the case or , while, for the cases of and both PF and RPF consume almost the same energy. This is an expected result since full coverage under PF is achieved for a large number of initially operating nodes and in this case both mechanisms operate similarly (i.e., RPF is reduced to PF).
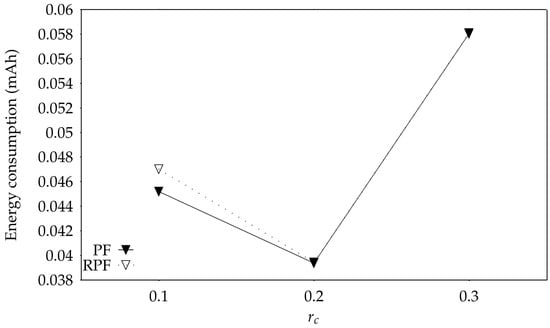
Figure 16.
Simulation results regarding energy consumption under PF and RPF as a function of the connectivity radius.
7. Conclusions
Probabilistic Flooding is revisited in this work in order to adapt to the new energy harvesting technological advantages. In such an environment, a certain amount of messages cannot be delivered and, therefore, conventional information dissemination mechanisms such as PF, fail to cover the network. In order to cope with this problem, a new probabilistic information mechanism is proposed called RPF, capable of dealing with nodes’ operational states.
A Markov chain model capable of capturing the nodes’ behavior in energy harvesting environments is also proposed. This model along with a solar radiation dataset obtained from the NASA Langley Research Center (LaRC) POWER Project is used for the simulation purposes. It is shown that the proposed RPF mechanism outperforms PF regarding coverage at the expense of increased termination time. However, RPF introduces an extra memory overhead that is not expected to be significant since it is bounded by the number of neighbors.
Author Contributions
The work presented here was carried out in collaboration among all authors. Conceptualization, G.K.; Formal analysis G.K.; Software, G.K. and G.T.; Supervision, K.O., Validation, G.K.; Writing—Original Draft Preparation, K.O.; Writing—Review & Editing, K.O.
Funding
This research received no external funding.
Acknowledgments
This work was supported in part by project “A Pilot Wireless Sensor Networks System for Synchronized Monitoring of Climate and Soil Parameters in Olive Groves,” (MIS 5007309) which is partially funded by European and National Greek Funds (ESPA) under the Regional Operational Programme “Ionian Islands 2014-2020.”
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The objective here is to derive the analytical expressions regarding , , and . It holds that . Based on the transition probabilities of the Markov chain presented in Figure 3, the following system of equations needs to be solved [62]:
Taking into account the second, third and fourth equations,
Next, , and are expressed as a function of ,
Note that the fifth equation (i.e.,) is always satisfied. Based on the first one (i.e., ), and, substituting accordingly, , or, , or, , or . Finally, . By substituting this expression for , the analytical expressions for , and are also derived.
References
- Akyildiz, I.; Su, W.; Sankarasubramaniam, Y.; Cayirci, E. Wireless sensor networks: A survey. Comput. Netw. 2002, 38, 393–422. [Google Scholar] [CrossRef]
- Anastasi, G.; Conti, M.; Di Francesco, M.; Passarella, A. Energy conservation in wireless sensor networks: A survey. Ad Hoc Netw. 2009, 7, 537–568. [Google Scholar] [CrossRef]
- Sudevalayam, S.; Kulkarni, P. Energy Harvesting Sensor Nodes: Survey and Implications. IEEE Commun. Surv. Tutor. 2011, 13, 443–461. [Google Scholar] [CrossRef]
- Koufoudakis, G.; Oikonomou, K.; Giannakis, K.; Aïssa, S. Probabilistic flooding coverage analysis for efficient information dissemination in wireless networks. Comput. Netw. 2018, 140, 51–61. [Google Scholar] [CrossRef]
- Kavvadia, E.; Koufoudakis, G.; Oikonomou, K. Robust probabilistic information dissemination in energy harvesting wireless sensor networks. In Proceedings of the 2014 13th Annual Mediterranean Ad Hoc Networking Workshop (MED-HOC-NET), Piran, Slovenia, 2–4 June 2014; pp. 63–70. [Google Scholar]
- Stackhouse, P.W.; Whitlock, C. Surface meteorology and Solar Energy (SSE) release 6.0, NASA SSE 6.0. In Earth Science Enterprise Program, National Aeronautic and Space Administration (NASA), Langley; NASA Langley Research Center: Hampton, VA, USA, 2008. Available online: http://eosweb.larc.nasa.gov/sse (accessed on 5 February 2018).
- Mao, S.; Cheung, M.H.; Wong, V.W. An optimal energy allocation algorithm for energy harvesting wireless sensor networks. In Proceedings of the 2012 IEEE International Conference on Communications (ICC), Ottawa, ON, Canada, 10–15 June 2012; pp. 265–270. [Google Scholar]
- Mohammed, H.M.G.E.D.; El, M.A.E.A.S.; Guindi, R. Novel radio frequency energy harvesting model. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference Melaka, Malaysia, Melaka, Malaysia, 6–7 June 2012; pp. 209–213. [Google Scholar]
- Elanzeery, H.; Guindi, R. Frequency survey simulation for developing novel radio frequency energy harvesting model. In Proceedings of the 2012 UKSim 14th International Conference on Computer Modelling and Simulation, Cambridge, UK, 28–30 March 2012; pp. 476–479. [Google Scholar]
- Gorlatova, M.; Wallwater, A.; Zussman, G. Networking low-power energy harvesting devices: Measurements and algorithms. IEEE Trans. Mob. Comput. 2013, 12, 1853–1865. [Google Scholar] [CrossRef]
- Cammarano, A.; Petrioli, C.; Spenza, D. Pro-Energy: A novel energy prediction model for solar and wind energy-harvesting wireless sensor networks. In Proceedings of the 2012 IEEE 9th International Conference on Mobile Ad-Hoc and Sensor Systems (MASS 2012), Las Vegas, NV, USA, 8–11 October 2012; pp. 75–83. [Google Scholar]
- Miozzo, M.; Zordan, D.; Dini, P.; Rossi, M. SolarStat: Modeling photovoltaic sources through stochastic Markov processes. In Proceedings of the 2014 IEEE International Energy Conference (ENERGYCON), Cavtat, Croatia, 13–16 May 2014; pp. 688–695. [Google Scholar]
- Ventura, J.; Chowdhury, K. Markov modeling of energy harvesting body sensor networks. In Proceedings of the 2011 IEEE 22nd International Symposium on Personal, Indoor and Mobile Radio Communications, Toronto, ON, Canada, 11–14 September 2011; pp. 2168–2172. [Google Scholar]
- Yang, G.Z.; Yang, G. Body Sensor Networks; Springer: Berlin, Germany, 2006; Volume 1. [Google Scholar]
- Hsu, J.; Zahedi, S.; Kansal, A.; Srivastava, M.; Raghunathan, V. Adaptive duty cycling for energy harvesting systems. In Proceedings of the 2006 International Symposium on Low Power Electronics and Design, Tegernsee, Bavaria, Germany, 4–6 October 2006; pp. 180–185. [Google Scholar]
- Vigorito, C.M.; Ganesan, D.; Barto, A.G. Adaptive control of duty cycling in energy-harvesting wireless sensor networks. In Proceedings of the 2007 4th Annual IEEE Communications Society Conference on Sensor, Mesh and Ad Hoc Communications and Networks, San Diego, CA, USA, 18–21 June 2007; pp. 21–30. [Google Scholar]
- Elmes, J.; Gaydarzhiev, V.; Mensah, A.; Rustom, K.; Shen, J.; Batarseh, I. Maximum energy harvesting control for oscillating energy harvesting systems. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 2792–2798. [Google Scholar]
- Pimentel, D.; Musílek, P. Power management with energy harvesting devices. In Proceedings of the 2010 23rd Canadian Conference on Electrical and Computer Engineering (CCECE), Calgary, AB, Canada, 2–5 May 2010; pp. 1–4. [Google Scholar]
- Akyildiz, I.F.; Brunetti, F.; Blázquez, C. Nanonetworks: A new communication paradigm. Comput. Netw. 2008, 52, 2260–2279. [Google Scholar] [CrossRef]
- Wang, P.; Jornet, J.M.; Malik, M.A.; Akkari, N.; Akyildiz, I.F. Energy and spectrum-aware MAC protocol for perpetual wireless nanosensor networks in the Terahertz Band. Ad Hoc Netw. 2013, 11, 2541–2555. [Google Scholar] [CrossRef]
- Gurakan, B.; Ozel, O.; Yang, J.; Ulukus, S. Energy cooperation in energy harvesting communications. IEEE Trans. Commun. 2013, 61, 4884–4898. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, E.; Li, J.; Yin, L.; Li, S. Throughput optimization for self-powered wireless communications with variable energy harvesting rate. In Proceedings of the 2013 IEEE Wireless Communications and Networking Conference (WCNC), Shanghai, China, 7–10 April 2013; pp. 830–835. [Google Scholar]
- Luo, S.; Zhang, R.; Lim, T.J. Optimal save-then-transmit protocol for energy harvesting wireless transmitters. IEEE Trans. Wirel. Commun. 2013, 12, 1196–1207. [Google Scholar] [CrossRef]
- Dang, N.; Bozorgzadeh, E.; Venkatasubramanian, N. QuARES: Quality-aware data collection in energy harvesting sensor networks. In Proceedings of the 2011 International Green Computing Conference and Workshops, Orlando, FL, USA, 25–28 July 2011; pp. 1–9. [Google Scholar]
- Edalat, N. Resource management and task allocation in energy harvesting sensor networks. In Proceedings of the 2012 IEEE International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), San Francisco, CA, USA, 25–28 June 2012; pp. 1–2. [Google Scholar]
- Zeng, K.; Ren, K.; Lou, W.; Moran, P.J. Energy-aware geographic routing in lossy wireless sensor networks with environmental energy supply. In Proceedings of the 3rd International Conference on Quality of Service in Heterogeneous Wired/Wireless Networks, Waterloo, ON, Canada, 7–9 August 2006; p. 8. [Google Scholar]
- Hasenfratz, D.; Meier, A.; Moser, C.; Chen, J.J.; Thiele, L. Analysis, comparison, and optimization of routing protocols for energy harvesting wireless sensor networks. In Proceedings of the 2010 IEEE International Conference on Sensor Networks, Ubiquitous, and Trustworthy Computing, Newport Beach, CA, USA, 7–9 June 2010; pp. 19–26. [Google Scholar]
- Lattanzi, E.; Regini, E.; Acquaviva, A.; Bogliolo, A. Energetic sustainability of routing algorithms for energy-harvesting wireless sensor networks. Comput. Commun. 2007, 30, 2976–2986. [Google Scholar] [CrossRef]
- Ren, X.; Liang, W.; Xu, W. Use of a mobile sink for maximizing data collection in energy harvesting sensor networks. In Proceedings of the 2013 42nd International Conference on Parallel Processing, Lyon, France, 1–4 October 2013; pp. 439–448. [Google Scholar]
- Yoshida, M.; Kitani, T.; Bandai, M.; Watanabe, T.; Chou, P.; Seah, W.K.G. Probabilistic data collection protocols for energy harvesting sensor networks. In Proceedings of the 2011 IEEE 36th Conference on Local Computer Networks, Bonn, Germany, 4–7 October 2011; pp. 366–373. [Google Scholar]
- Han, G.; Dong, Y.; Guo, H.; Shu, L.; Wu, D. Cross-layer optimized routing in wireless sensor networks with duty cycle and energy harvesting. Wirel. Commun. Mob. Comput. 2015, 15, 1957–1981. [Google Scholar] [CrossRef]
- Shafieirad, H.; Adve, R.S.; ShahbazPanahi, S. Max-SNR opportunistic routing for large-scale energy harvesting sensor networks. IEEE Trans. Green Commun. Netw. 2018, 2, 506–516. [Google Scholar] [CrossRef]
- Gu, Y.; He, T. Bounding communication delay in energy harvesting sensor networks. In Proceedings of the 2010 IEEE 30th International Conference on Distributed Computing Systems, Genova, Italy, 21–25 June 2010; pp. 837–847. [Google Scholar]
- Cao, Q.; Abdelzaher, T.F.; He, T.; Stankovic, J.A. Towards optimal sleep scheduling in sensor networks for rare-event detection. In Proceedings of the Fourth International Symposium on Information Processing in Sensor Networks (IPSN 2005), Boise, ID, USA, 15 April 2005; pp. 20–27. [Google Scholar]
- Segall, A. Distributed network protocols. IEEE Trans. Inf. Theory 1983, 29, 23–35. [Google Scholar] [CrossRef]
- Stauffer, A.O.; Barbosa, V.C. Probabilistic heuristics for disseminating information in networks. IEEE/ACM Trans. Netw. 2007, 15, 425–435. [Google Scholar] [CrossRef]
- Crisóstomo, S.; Schilcher, U.; Bettstetter, C.; Barros, J. Probabilistic flooding in stochastic networks: Analysis of global information outreach. Comput. Netw. 2012, 56, 142–156. [Google Scholar] [CrossRef]
- Oikonomou, K.; Kogias, D.; Stavrakakis, I. Probabilistic flooding for efficient information dissemination in random graph topologies. Comput. Netw. 2010, 54, 1615–1629. [Google Scholar] [CrossRef]
- Gaeta, R.; Sereno, M. Generalized probabilistic flooding in unstructured peer-to-peer networks. IEEE Trans. Parallel Distrib. Syst. 2011, 22, 2055–2062. [Google Scholar] [CrossRef]
- Banaei-Kashani, F.; Shahabi, C. Criticality-based analysis and design of unstructured peer-to-peer networks as “Complex systems”. In Proceedings of the 3rd IEEE/ACM International Symposium on Cluster Computing and the Grid, Tokyo, Japan, 12–15 May 2003; pp. 351–358. [Google Scholar]
- Tsoumakos, D.; Roussopoulos, N. Adaptive probabilistic search for peer-to-peer networks. In Proceedings of the Third International Conference on Peer-to-Peer Computing (P2P2003), Linkoping, Sweden, 1–3 September 2003; pp. 102–109. [Google Scholar]
- Zanaj, E.; Baldi, M.; Chiaraluce, F. Efficiency of the gossip algorithm for wireless sensor networks. In Proceedings of the 2007 15th International Conference on Software, Telecommunications and Computer Networks, Split-Dubrovnik, Croatia, 27–29 September 2007; pp. 1–5. [Google Scholar]
- Chang, D.; Cho, K.; Choi, N.; Kwon, T.T.; Choi, Y. A probabilistic and opportunistic flooding algorithm in wireless sensor networks. Comput. Commun. 2012, 35, 500–506. [Google Scholar] [CrossRef]
- Hu, R. Efficient probabilistic information broadcast algorithm over random geometric topologies. In Proceedings of the 2015 IEEE Global Communications Conference (GLOBECOM), San Diego, CA, USA, 6–10 December 2015; pp. 1–6. [Google Scholar]
- Sasson, Y.; Cavin, D.; Schiper, A. Probabilistic broadcast for flooding in wireless mobile ad hoc networks. In Proceedings of the 2003 IEEE Wireless Communications and Networking, New Orleans, LA, USA, 16–20 March 2003; Volume 2, pp. 1124–1130. [Google Scholar]
- Li, Q.; Rong, H.; Sun, W.; Wang, J.; Li, J. A correlation-based energy balanced probabilistic flooding algorithm in wireless sensor network. In Proceedings of the 2016 IEEE 83rd Vehicular Technology Conference (VTC Spring), Nanjing, China, 15–18 May 2016; pp. 1–5. [Google Scholar]
- Jianping, W.; Huihui, R.; Wei, S.; Qiyue, L. A correlation-based coverage-aware and energy-balanced probabilistic flooding algorithm. Int. J. Sens. Netw. 2017, 25, 207–217. [Google Scholar] [CrossRef]
- Drabkin, V.; Friedman, R.; Kliot, G.; Segal, M. On reliable dissemination in wireless ad hoc networks. IEEE Trans. Dependable Secure Comput. 2011, 8, 866–882. [Google Scholar] [CrossRef]
- Reina, D.; Toral, S.; Jonhson, P.; Barrero, F. Hybrid flooding scheme for mobile ad hoc networks. IEEE Commun. Lett. 2013, 17, 592–595. [Google Scholar] [CrossRef]
- Palmieri, F. A wave propagation-based adaptive probabilistic broadcast containment strategy for reactive MANET routing protocols. Pervasive Mob. Comput. 2017, 40, 628–638. [Google Scholar] [CrossRef]
- Agarwal, M.; Govil, M.; Sinha, M.; Jhankal, A. Energy conservation by improving flooding mechanism in MANET. J. Sci. Ind. Res. 2017, 76, 408–414. [Google Scholar]
- Saeed, T.; Lestas, M.; Pitsillides, A. Adaptive probabilistic flooding for nanonetworks employing molecular communication. In Proceedings of the 2016 23rd International Conference on Telecommunications (ICT), Thessaloniki, Greece, 16–18 May 2016; pp. 1–5. [Google Scholar]
- Saeed, T.; Lestas, M.; Pitsillides, A. Nature inspired node density estimation for molecular networks. Nano Commun. Netw. 2017, 12, 43–52. [Google Scholar] [CrossRef]
- Koseoglu, M.; Bereketli, A.; Yazgi, I.; Yeni, B. Probabilistic broadcast for dense AUV networks. In Proceedings of the OCEANS 2016 MTS/IEEE Monterey, Monterey, CA, USA, 19–23 September 2016; pp. 1–5. [Google Scholar]
- Xeros, A.; Lestas, M.; Andreou, M.; Pitsillides, A. Adaptive probabilistic flooding for information hovering in VANETs. In Proceedings of the Vehicular Networking Conference (VNC), Jersey City, NJ, USA, 13–15 December 2010; pp. 239–246. [Google Scholar]
- Mylonas, Y.; Lestas, M.; Pitsillides, A.; Ioannou, P.; Papadopoulou, V. Speed adaptive probabilistic flooding for vehicular ad hoc networks. IEEE Trans. Veh. Technol. 2015, 64, 1973–1990. [Google Scholar] [CrossRef]
- Betoule, C.; Bonald, T.; Clavier, R.; Rossi, D.; Rossini, G.; Thouenon, G. Adaptive probabilistic flooding for multipath routing. In Proceedings of the 2012 5th International Conference on New Technologies, Mobility and Security (NTMS), Istanbul, Turkey, 7–10 May 2012; pp. 1–6. [Google Scholar]
- Margariti, S.V.; Dimakopoulos, V.V. On probabilistic flooding search over unstructured peer-to-peer networks. Peer-to-Peer Netw. Appl. 2015, 8, 447–458. [Google Scholar] [CrossRef]
- Lichtblau, B.; Dittrich, A. Probabilistic breadth-first search-A method for evaluation of network-wide broadcast protocols. In Proceedings of the 2014 6th International Conference on New Technologies, Mobility and Security (NTMS), Dubai, United Arab Emirates, 30 March–2 April 2014; pp. 1–6. [Google Scholar]
- Badreddine, W.; Potop-Butucaru, M. Peak transmission rate resilient crosslayer broadcast for body area networks. arXiv, 2017; arXiv:1702.05031. [Google Scholar]
- Earth Observing Laboratory. MICA2—Wireless Measurement System, 2017. Available online: http://www.eol.ucar.edu (accessed on 27 November 2017).
- Papoulis, A. Probability, Random Variables, and Stochastic Processes; Mcgraw-Hill College: New York, NY, USA, 1999; ISBN 0070484775. [Google Scholar]
- Oikonomou, K.; Koufoudakis, G.; Aïssa, S. Probabilistic flooding coverage analysis in large scale wireless networks. In Proceedings of the 2012 19th International Conference on Telecommunications (ICT), Jounieh, Lebanon, 23–25 April 2012; pp. 1–6. [Google Scholar]
- Penrose, M. Random Geometric Graphs; Oxford University Press: Oxford, UK, 2003; ISBN 9780198506263. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).