1. Introduction
In recent years, the ongoing industrial revolution has witnessed significant advancements that enable the extensive and precise monitoring of various processes at a remarkably affordable cost. This progress is largely attributed to the emergence of the Internet of Things (IoT), which has evolved through the integration of diverse technologies, such as ubiquitous computing, commodity sensors, powerful embedded systems, and machine learning. One noteworthy application of IoT is its implementation in systems monitoring for diagnostic purposes. With the ability to connect and collect data from virtually everything and everywhere, IoT facilitates the comprehensive monitoring of complex systems, enabling the detection of anomalies and potential issues. By harnessing the power of IoT, industries can gain invaluable insights into the health and performance of their machinery and processes, thereby enhancing efficiency and predictive maintenance practices. This convergence of technologies paves the way for transformative changes in various sectors, unlocking new opportunities and optimizing operations across the industrial landscape [
1,
2,
3,
4,
5,
6,
7]. This paper introduces a novel predictive maintenance methodology, which relies on the continuous availability of new data. IoT is crucial in enabling this approach, creating a network that connects smart devices within an information system and facilitates data exchange with central storage. The network communication among IoT devices exhibits unique characteristics and variations compared to conventional devices [
8], particularly in cloud-fog environments [
9]. Addressing real-time implementation poses challenges due to potential delays. While monitoring may tolerate latency, IoT’s involvement in control raises significant issues. To overcome this, recent proposals have focused on imposing latency constraints on control commands [
10]. The state of the art reveals a lack of a generic maintenance cost model applicable in all industrial contexts, with proposed models often being case-specific or challenging to implement practically. Moreover, predictive maintenance model (PdM) cost optimization papers tend to overlook the concept of risk and seldom consider human decision-making uncertainty. Industrial maintenance in the past was viewed as a reactive background activity, performed only after system failure. However, with the emergence of preventive and predictive maintenance, the field has evolved significantly, offering various strategies with distinct benefits and challenges [
11]. Corrective maintenance maximizes equipment utilization but can be costly due to potential cascading damages. Preventive maintenance reduces repair costs and unplanned downtime, yet may lead to unnecessary repairs or catastrophic failures. In contrast, predictive maintenance, preferred in critical sectors like power plants and transportation systems, focuses on reliability and timely interventions [
12].
In order to facilitate maintenance decision-making, this research leverages raw sensor data to enhance the computation of deterioration indices for basic machinery systems. The intricacy of these systems and the dearth of previous data can provide challenges for traditional predictive maintenance techniques. In order to address these issues, we provide a clustering technique to identify possible equipment malfunctions, allowing policymakers to create predictive maintenance plans based on dependability. The approach is tested on mechanically stressed bus equipment (two doors especially), where failures might endanger public safety and necessitate costly shutdowns. Critical feature variable identification, classification strategies, validation metrics, and clustering-based future state prediction are all included in our proposed framework. This strategy offers an innovative and adaptable methodology that supports the creation of predictive maintenance plans even if historical data is limited.
The paper is structured as follows.
Section 2 analyses works in the literature,
Section 3 provides a detailed description of the methodology, known as the predictive maintenance model for a simple machinery system (PMM-SMS), presented as a series of well-defined steps. In
Section 4, the case study and results are presented, and the corresponding results are discussed. The conclusions are drawn in subsequent
Section 5.
2. Related Work
Predictive maintenance and industrial monitoring have been greatly influenced by the emergence of IoT technology. IoT integration with inexpensive sensors, machine learning, sophisticated embedded systems, and ubiquitous computing has made extensive monitoring and diagnosis in intricate industrial systems easier. The use of IoT to improve industrial processes has been thoroughly studied in the past, with a particular emphasis on predictive maintenance, anomaly detection, and diagnostic systems. Ref. [
13] focuses on a few key areas of IoT-based control research and applications in wind energy conversion systems with induction machines and electric motor systems.
Condition monitoring and fault diagnosis in modern manufacturing automation are vital for improving quality, productivity, and machinery protection [
14,
15]. A recent special issue on diagnosis and prognosis for complex industrial systems featured fifteen papers, categorized into model-based and data-driven approaches [
16]. Model-based methods rely on established system models and compare expected simulated performance indicators with observed data. In contrast, data-driven approaches, often based on clustering or machine learning, detect fault-related signals without prior fault information. In a previous work addressing complex industrial systems [
17], a
k-means-based fault-detection method isolates sensor faults without using specific fault information. Notably, vehicle maintenance constitutes around 40% of the total cost of subway maintenance, as indicated by statistics [
18]. The work [
19] highlights the need of precise remaining useful lifespan prediction for batteries and the continuous progress being made in this area. Even though there has been a lot of progress, more study is still needed to solve current problems and raise the precision and resilience of prediction techniques. Incorporating cutting-edge technologies and developing uniform assessment frameworks are essential if battery lifespan prediction is to remain helpful in the future. Recent studies on fault diagnosis have shown a shift from Bayesian network approaches [
20] to deep learning techniques. Support vector machine classifiers have been designed and tested for fault identification [
21], and highly accurate machine fault diagnosis approaches have been verified on mechanical datasets [
22]. In [
23], the aspect of synchronization in wireless sensor networks in diverse industrial applications is analyzed using low-cost sensor network topologies. A thorough analysis of the many methods used to find outliers in IoT systems can be found in [
24]. This survey is a useful tool for researchers and practitioners because it classifies these approaches, assesses their effectiveness, and discusses how they might be applied to various IoT domains. It outlines the major obstacles and potential paths for future study in this developing topic and emphasizes the significance of strong outlier detection in preserving the integrity and dependability of IoT systems. However, training deep models requires substantial computing power, which may not be readily available for low-cost machinery. To address this, a novel deep learning method using transfer learning has been proposed to accelerate training and achieve accurate fault diagnosis [
25]. Data acquisition remains a common challenge, as sensor failure can lead to insufficient data for analysis [
26]. Moreover, collecting enough failure data in practical industrial production hinders the application of intelligent diagnosis methods [
27]. The classification of faults varies based on application and data availability [
28]. In the context of additive manufacturing, intelligent learning algorithms combining hidden Markov models and support vector techniques have been used for modeling manufacturing operations [
14]. Controllable aspects of additive manufacturing processes have been analyzed, and a control framework integrating feedback loops has been proposed to enhance reliability and repeatability [
29].
Utilizing a variety of approaches, lifetime prediction is a crucial component of reliability and maintenance engineering that projects how long systems and individual components will last. Improvements in this field are being driven by developments in machine learning, data analytics, and sensor technologies, which have a substantial positive impact on a variety of businesses. In [
30], the main goal is to create a novel method for predicting battery lifespan, which is a crucial problem for energy storage devices. Accurate battery life prediction can greatly improve performance and dependability in applications such as consumer electronics, electric vehicles, and renewable energy systems. Related to battery charge lifetime, the work [
31] explores functions as vital resources for comprehending the state of battery lifespan prediction today and in the future. It highlights the value of multidisciplinary approaches by fusing conventional physics-based models with developments in machine learning, sensor technologies, and big data analytics. It seeks to ease the transition from theoretical research to real-world applications by addressing the difficulties and identifying best practices, which will ultimately lead to more dependable and effective battery systems.
Additionally, it applies to various transportation systems, addressing costly failures and improving overall decision-making in maintenance strategies. Experimental results on bus door data demonstrate the effectiveness of the proposed method. This approach stands out by offering greater transparency in the decision process compared to black-box models like neural networks, catering to the needs of decision-makers in simpler machinery systems. The presented steps aim to satisfy the demand for more knowledge on classification processes, feature variables’ importance, prediction reliability, and maintenance policy suggestions.
3. Materials and Methods
We propose a PMM-SMS based on several steps to create a predictive maintenance model as shown in
Figure 1. The initial two steps pertain to data collection, while the third step involves identifying critical parameters, conducting a preliminary analysis to consider fault-variable relationships. Subsequently, an accuracy analysis determines the optimal number of fault clusters. The fifth step involves validating the predictive maintenance approach using a subset of available data (training set). The final two steps focus on formulating an intervention policy for predictive maintenance.
3.1. Preliminary Analysis
The preliminary analysis involves studying the phenomena to be analyzed, considering potential variables that may influence fault states, such as temperature, pressure, and other physical indicators. Two methods are typically used for this analysis [
32]: consulting an expert (e.g., a mechanical engineer with experience in the system) to design a model and explore variable connections, or employing a statistical approach with a sufficiently large and uniform database. However, in this study, both criteria are unavailable, as is common in embedded systems for electrical components, where the process is challenging to model and data may be limited or non-uniform. As a result, a classification method has been adopted, forming the basis for subsequent steps in the analysis. Hereinafter, we refer to:
, as the input pattern of different variables, , characterizing the process;
, as the output pattern of different variables, , related to the system maintenance.
3.2. Obtain Data
In this step, all the necessary variables are acquired, collected, and stored in a database. To address potential bias among different plants and sensors, a normalization of the input and output variables is applied.
An advantage of using an embedded system based on IoT is the continuous real-time updating of the dataset. This feature enables classification methods to adapt and capture time-varying behaviors of the monitored system.
Condition monitoring involves measuring equipment parameters (e.g., vibration, temperature, lubricant analysis) to predict potential equipment failure. Two known methods for condition monitoring are trend monitoring and condition checking. Trend monitoring involves regularly measuring and interpreting data to detect deteriorations exceeding critical values. Condition checking entails performing periodic measurements with accurate indicators while the component operates to establish its current condition.
In this paper, we focus on a scenario where data do not directly support both trend monitoring and condition checking. Specifically, the data obtained from IoT sensors lack information about dangerous or normal parameter values/references. To address this challenge, we propose a general framework to effectively handle such situations.
3.3. Identify the Influence of the Variables
The Pearson correlation index serves as a statistical indicator, quantifying the direction and strength of the linear association between random variables. In this study, the Pearson correlation coefficient is utilized to identify critical parameters, aiming to reveal predictive relationships with practical implications.
Specifically, the Pearson correlation index measures the relationship between two sets of data, calculated as the ratio between the covariance
and the product of the standard deviations of the two variables
and
, as shown in Equation (
1):
This index lies between −1 and +1, reflecting only the linear correlation between the variables and not considering other types of correlation. Its numerical value is classified using criteria similar to those used in [
33]:
Strong correlation if
Moderate correlation if
Weak correlation if
3.4. Define the Number of States and Clustering
The
k-means algorithm is a widely used statistical method for classification problems, finding application in various contexts. It aims to partition the original dataset into
K distinct non-overlapping subgroups through an iterative process. The algorithm seeks to minimize the distance between each data point and the class centroids, employing the Euclidean distance (
2) to compute the classes [
34]:
Starting with randomly chosen centroids
, each data point is assigned to the class with the nearest centroid based on the Euclidean distance. At each step, the centroids are recalculated, and the process continues by reassigning each point to the closest cluster as described in (
3). The algorithm terminates when no more records are moved to a cluster, and the squared error is minimized:
To assess the prediction error, two estimators are computed based on the specific number of states used in the k-means: Bayesian information criterion (BIC) and Akaike information criterion (AIC).
While various metrics, such as the Wasserstein distance [
35], can be used to solve this type of problem, the Euclidean distance was found to be more effective in this particular case study.
3.4.1. Bayesian Information Criterion (BIC)
The BIC is an information criterion derived from the Akaike information criterion proposed by [
36]. Unlike the AIC, the BIC penalty (
4) depends on the sample size and not only on the number of parameters.
where
is the log-likelihood function,
K is the number of clusters and
n is the size of the dataset. According to the Gaussian assumption, the maximum likelihood estimate for the variance (
5) of the
i-th cluster is:
where
is the centroid of the
j-th cluster,
is the sample size of the
i-th cluster, and
is the
j-th point. Considering
M clusters, the log-likelihood (
6) is defined as:
where
which can be rewritten as shown in (
8) [
37]:
where
is the probability of the
i-th point, and
is the centroid of the cluster corresponding to the partitioning.
3.4.2. Akaike Information Criterion (AIC)
The AIC is a mathematical method used to evaluate the goodness level of a model to fit the data generated by the model (
9). It is used to compare different possible models and determine which one is the best fit for the data.
where
is defined according to (
6). The AIC is not related to the absolute quality of a model. It describes the quality relative to other models. If the model fits poorly, it will not give any warning of that. Clustering is performed into two steps:
Clustering with centroids defined on the output variables, that is defined on the optimal K clusters as identified by BIC and AIC;
Sub-clustering with centroids , defined on the input variables, that is for each cluster defined at the previous step a further clustering is defined as identified by a new BIC and AIC analysis performed on the input variables of the pattern present in each cluster.
3.5. Validation of the Model
This stage is crucial for confirming that the suggested strategy is reliable. Decision-makers may choose to increase the number of variables and modify the subsequent predictive maintenance policy in light of this validation. The dataset in a real-world case study may contain noisy vectors, which makes determining the ideal number of clusters more difficult. When data vectors are far removed from the cluster centroids, the
K-means method frequently has difficulty assigning clusters, making it unlikely that the data vectors belong to any of the presumptive clusters [
38]. We propose a possibility measure (
10)
to solve this problem.
denotes a 100% chance that a pattern, represented by a series of variables, is a member of a certain cluster, signifying the degree of confidence that the point actually belongs to a specific cluster. The variation inside the cluster, the distance to the centroid, and other metrics that show how well the point fits in the cluster are used to calculate this score. Since
is specified inside
, it is believed that the range of
is also within this interval. The distance between the two clusters under consideration is greater than the distance between the pattern
and its two closest centroids, so
is likewise bounded by
.
The terms
and
in (
11) and (
12), respectively, represent the reliability and degree of belonging to the closest cluster. They are defined as:
The coordinate vector of the centroid closest to the pattern
in this case is represented by
, while the coordinate vector of the second-closest centroid to the same pattern is indicated by
. As explained in the preceding paragraph, the variable
is computed for every input pattern, accounting for all centroids inside each sub-cluster. The decision-maker has two options based on the range of
values obtained: either adopt the technique (as mentioned in
Section 3.6) or validate the method’s performance on a different set of data (as detailed in
Section 3.3).
When
, precision and recall are employed for performance evaluation [
39]. Within each cluster denoted by the centroid
, precision (
13) is defined as the ratio of genuine positives to the total number of predicted positives:
Recall (
14) is the ratio of true positives to all actual positives in each cluster identified by centroid
:
The
score [
40] (
15), the harmonic mean of precision and recall, is used as a comprehensive performance indicator:
Moreover, we present mean average precision (mAP) and average precision (AP) as other performance indicators that are not reliant on . The area under the curve is denoted by in this context, and mAP is determined as the mean of for all classes . The training set is used to evaluate these performance indicators.
3.6. Prediction of Future States
In this phase, the predictive model aims to forecast the fault state and provide information about the system’s status and necessary maintenance for the testing set or new unclassified patterns. Referring to the testing set and a new available pattern, the method established in the preceding steps is employed to compute the output pattern classification based on the input pattern, along with its corresponding measure of the possibility that the pattern belongs to that classification.
When it comes to degradation models for components, they often involve defining intermediate states between perfect functioning and total failure. Two approaches for modeling degradation processes exist: discrete and continuous space degradation models. In this paper, we have chosen the discrete space degradation approach, which is addressed through classification, and maintenance decisions are made by computing certain scores. It is essential to select the degradation model that best fits the observed degradation data, known as the goodness-of-fit criterion. This criterion assesses the model’s ability to match the observed data.
3.7. Predictive Maintenance Policy
In this phase, specific policies related to the application of the method are defined. For instance, as demonstrated in the case study section, a policy could be established to apply maintenance to the input patterns classified as faults with a value higher than a certain threshold, such as the maximum value of the score. Additionally, a quality assurance method can be implemented to ensure the effectiveness of the proposed approach. For example, in the results section, the method is compared with a pattern recognition neural network (PRNN) and the support vector machine (SVM). If the policy proves to be unsatisfactory, adjustments can be made to the threshold (i.e., proceed to step F) or a decision can be made to enhance the dataset (i.e., go back to step D).
4. Results
This application pertains to a door system in a bus, and our aim is to develop a straightforward predictive maintenance system concerning the sensors, especially when limited data are accessible. In the subsequent subsection, we exemplify the previously described steps using this case study. In
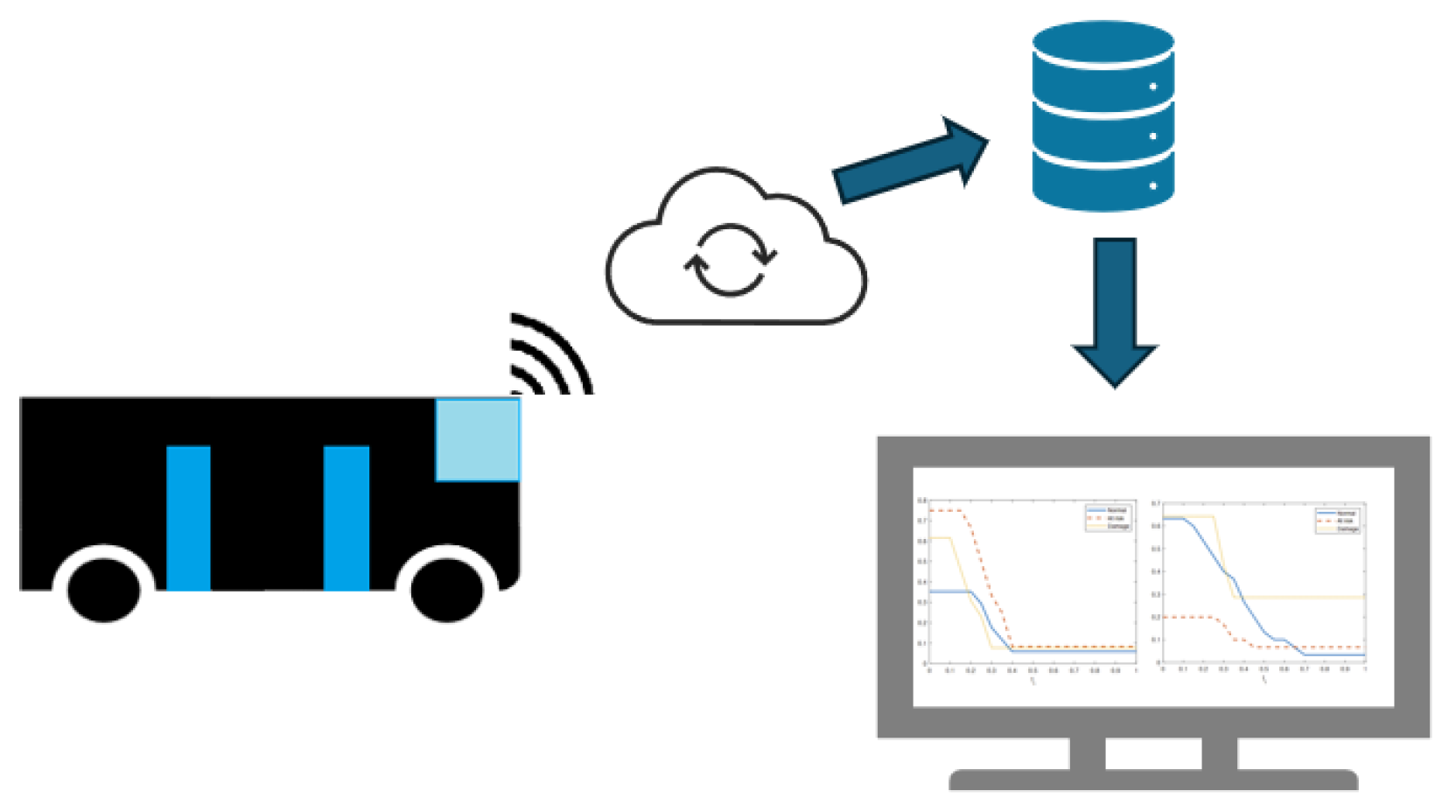
Figure 2, a schema related to the system architecture is reported. The data are sent by IoT interface to a cloud server for the storage and elaboration of the data.
4.1. Preliminary Analysis
IoT sensors provide data about the status of the device using a client–server architecture that forms the basis of the system architecture. The doors, which serve as the vehicle’s entry and leave ports, are essential to guarantee the security of the bus transportation service. To maintain a high level of service, they must open and close quickly and function flawlessly thousands of times. The doors are available in two varieties, electropneumatic and electric, and are usually completely glazed. Operators have switched back to pneumatic doors because of their higher dependability, even though electric doors were originally the favored option. Buses are usually equipped with two to four doors, depending on the type of vehicle, and they can have various opening modes. The doors open inside the vehicle and are equipped with safety devices to protect passengers. The bus cannot start until the doors are fully closed. For data analysis, a CAN-bus (controller area network) is employed, allowing real-time retrieval of specific information, including control signals, from the bus’s CAN. The CAN data bus is widely used to connect multiple devices through the same cable system and has been standardized using ISO 11898 [
41]. This system’s presence on the bus being studied enables the monitoring of various aspects, such as the state related to “open or close the bus access”. Key functions controlled through the CAN-bus include opening or closing the bus access and locking or unlocking the doors. Ensuring the safety of the doors is crucial to prevent accidents. However, the proper functioning of the doors is not always stable, and occasional failures may occur. The sensors send the data collected for monitoring and analysis to a server PC in real-time.
4.2. Obtain Data
In this case study, the input data for the pneumatic door system, defined in the previous subsection, consist of three sets: pressure, temperature, and humidity. Pressure represents the force exerted per unit area on the door, while temperature reflects the degree of thermal agitation of particles in the system. Higher temperatures may be associated with machinery stress, as discussed in
Section 4.3. Humidity, on the other hand, indicates the concentration of water vapor in the air and depends on the system’s door temperature and pressure.
As an additional output indicator, the number of shocks during a specific time period is available and serves as a measure of the door system’s reliability. More shocks may lead to increased damage to the door system, considering shocks as mechanical oscillating movements or vibrations around a stable equilibrium position. The frequent opening and closing of bus doors can contribute to their potential failure.
The data collected by the sensor network at various instants (
) are represented by the vector variable
, which includes the physical variables. On the other hand, the fault variables monitored by specific sensors at the same instants are represented by the vector variable
. These variables have been collected for both doors over a two-month period, with one sample taken daily. In
Table 1, a part of the sample data normalized for the analysis is reported. In the bottom row, the range used for the data normalization is reported.
4.3. Identify the Influence of the Variables
A preliminary analysis was conducted to identify the relationships by computing the Pearson correlation index
r. The correlation analysis between the four variables for both doors is presented in
Table 2 and
Table 3.
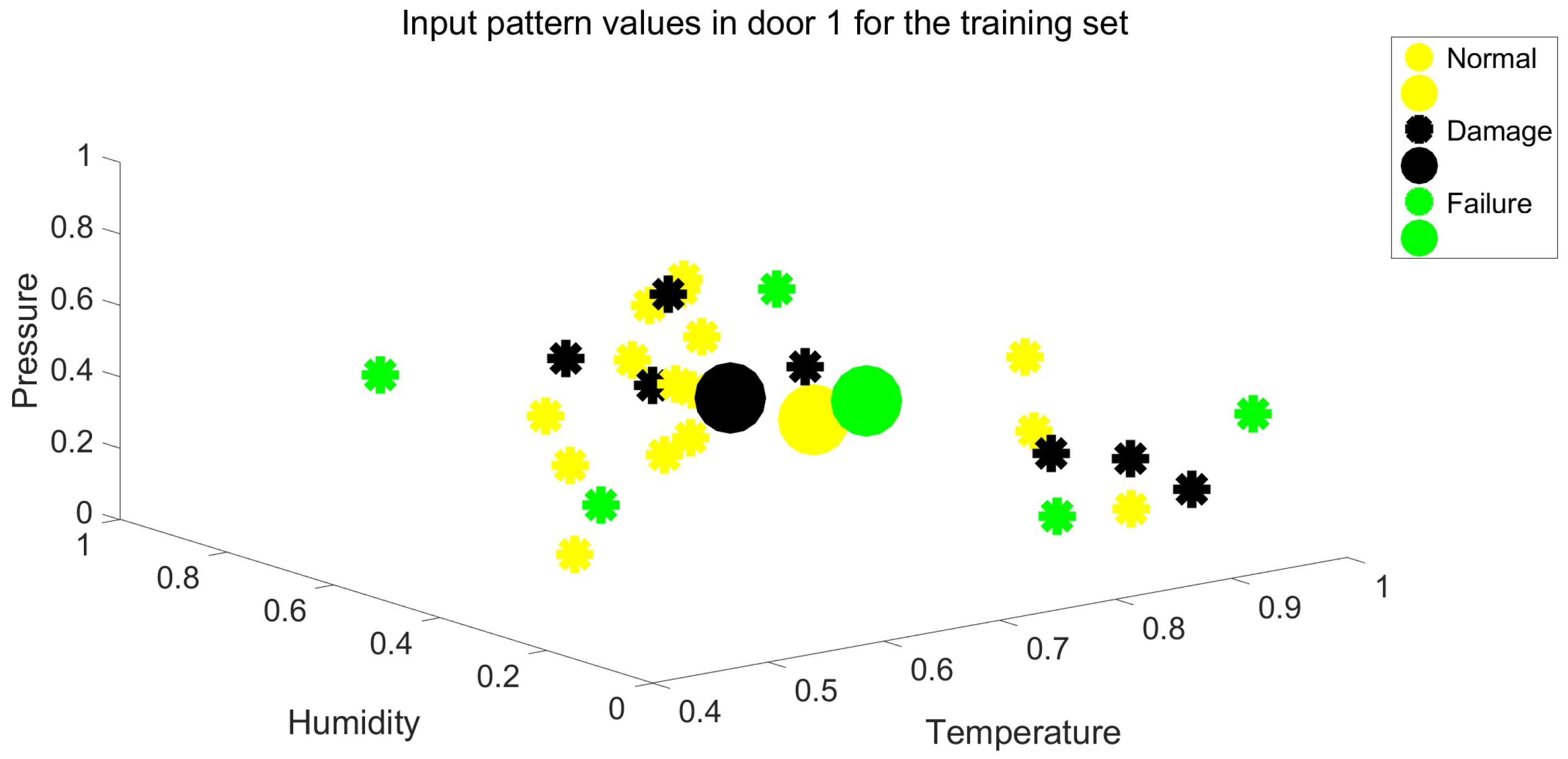
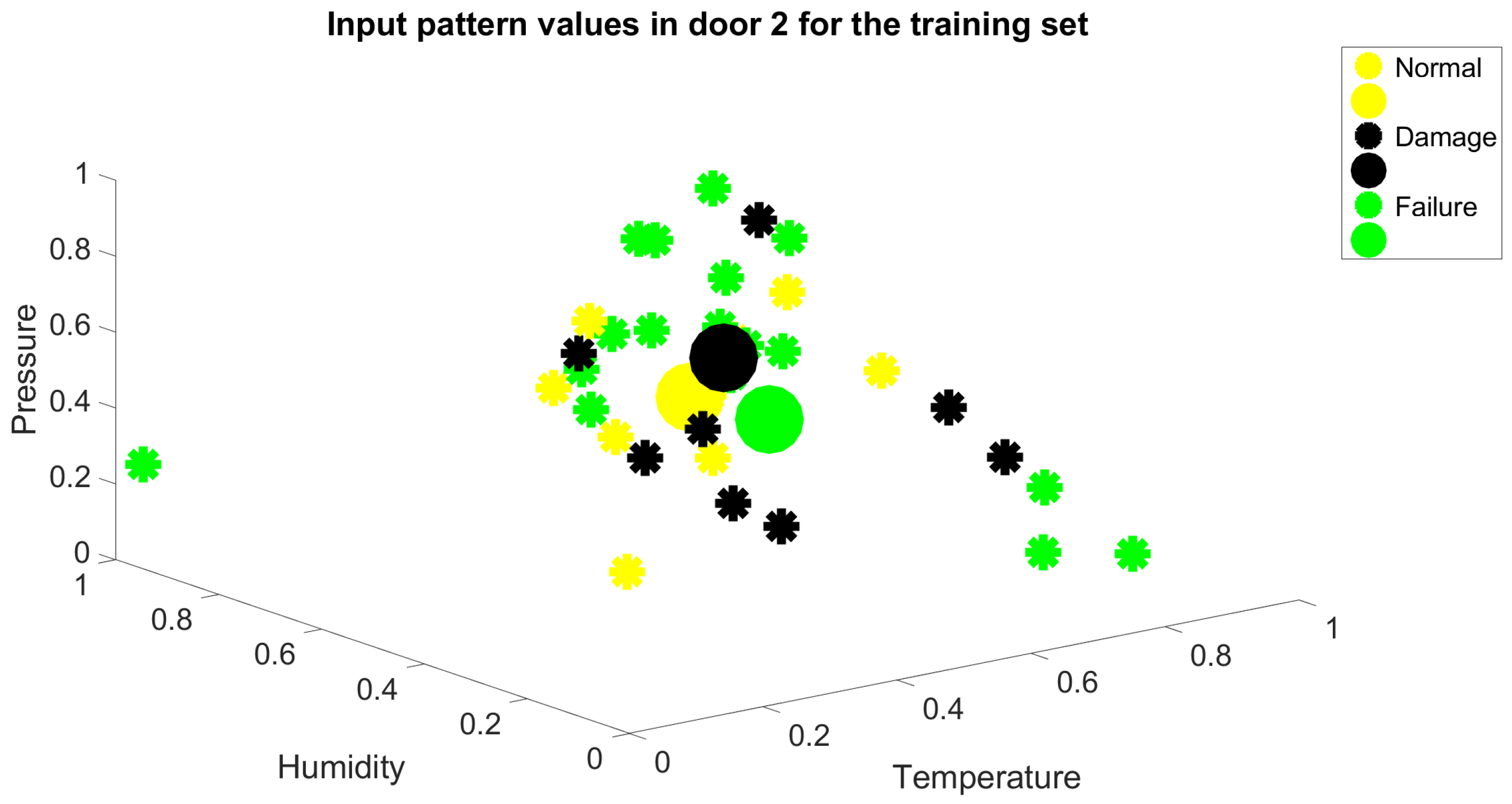
As observed, there is a low linear correlation between the input variables and the output variable. This phase is crucial to assess the value of the information set, comprising input and output variables, in contributing to predictive maintenance. During this phase, the information set may be refined to focus on more significant variables, providing an initial idea of the potential effectiveness of the results. In the case of
Table 2, it is evident that the information content is relatively poor. Spatial representations of the feature input variables for door system 1 and 2, shown in
Figure 3 and
Figure 4. The figures illustrate how the points are distributed across the three classes. The individual points inside each class are represented by the smaller circles, while the bigger ones are the centroids of the classes. The three centroids are clearly positioned very close to one another, and the overall clouds of cluster features are not well separated. These graphical findings further indicate that the input data’s quality is inadequate for a reliable classification from an information content perspective.
Due to the low correlation between input and output variables and the relatively limited dataset, achieving the goal of predictive maintenance becomes particularly challenging. Additionally, the statistics reported in
Table 2 and
Table 3 do not perfectly overlap, suggesting that, at this stage, the two door systems are considered as two distinct entities. However, this fact does not rule out the possibility that with a more extensive dataset, the two statistics may converge, allowing for a joint predictive maintenance approach for both systems. Such a decision can be made at step F.
Indeed, the analysis is conducted separately for the two doors, resulting in the creation of two distinct predictive models, one for each door. The dataset is divided into two parts for both doors: 75% for training (consisting of 42 patterns for door system 1 and 51 patterns for door system 2) and 25% for testing (comprising 12 patterns for door system 1 and 17 patterns for door system 2). The training set is utilized to construct the predictive model, while the test set is instrumental in evaluating the model effectiveness and efficiency.
4.4. Define the Number of States and Clustering
In this step, we determine the number of classes, which corresponds to the number of door states. To achieve this, we utilize two indexes, as described in
Section 3.4: the Bayesian information criterion (BIC) and the Akaike information criterion (AIC).
Table 4 shows the centroids of these classes, computed based on the output variables (shocks).
In both door systems, the optimal number of states resulting from the computation of the BIC and AIC indexes is 3. Specifically, Cluster 1 is associated with the “normal” state and contains 12 patterns for door 1 and 30 patterns for door 2. Cluster 2 is associated with the “at risk” state and contains 17 patterns for door 1 and 7 patterns for door 2. Cluster 3 is associated with the “damage” state and contains 13 patterns for door 1 and 14 patterns for door 2.
For each cluster, further clustering into sub-classes based on the input pattern has been defined, always considering the BIC and AIC.
Table 5 shows the resulting number of sub-classes obtained for each cluster.
Following the definition of sub-classes, the centroids of the different sub-classes, computed on the input variables, have been determined. The centroid information is presented in
Table 6 and
Table 7.
4.5. Validation of the Model
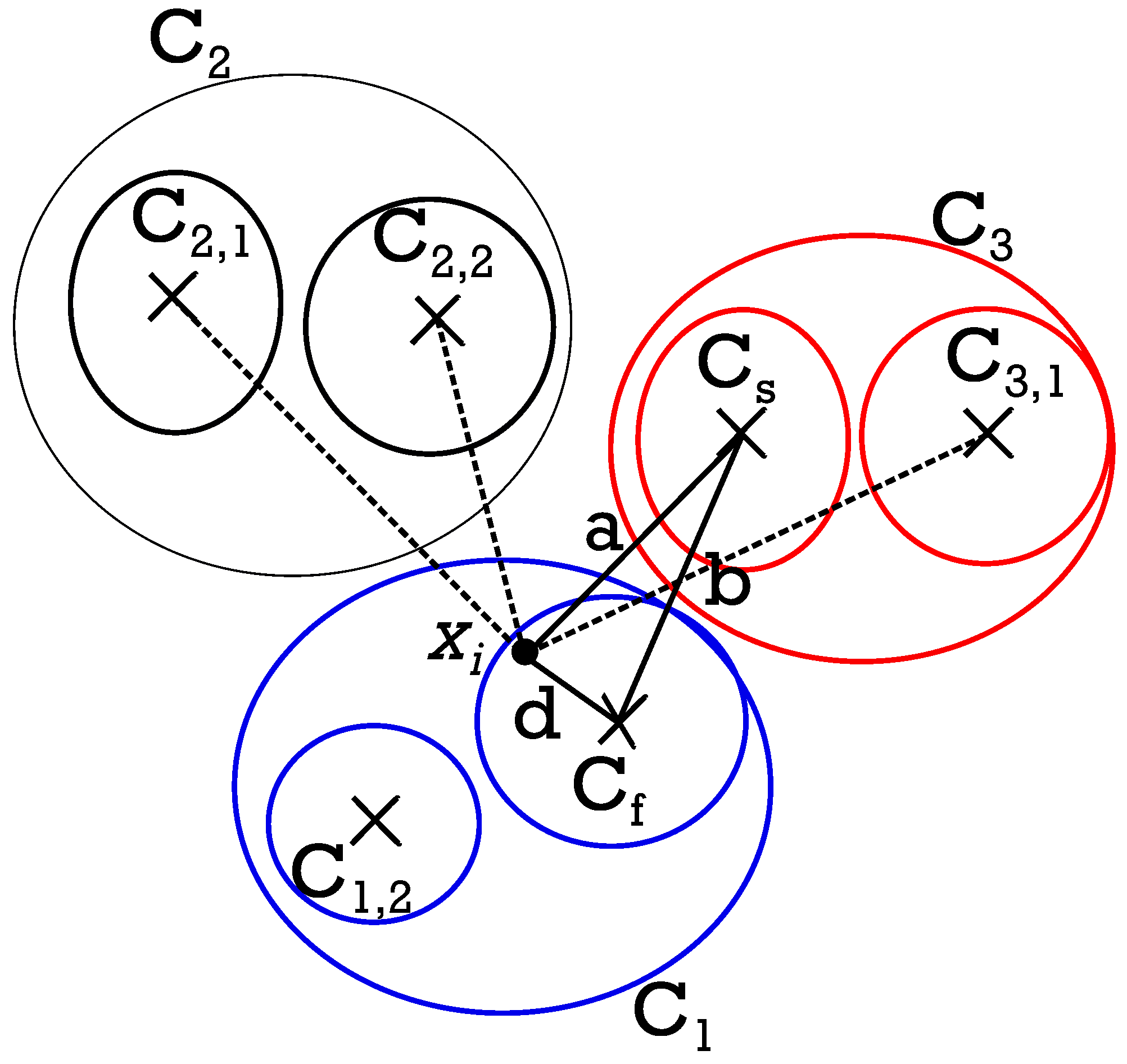
An example of terms utilized is shown in
Figure 5, which is based on the
computation for door 2, according to Equations (
10)–(
12).
In the figure, the dotted lines represent the distance between the pattern and all the centroids of the clusters, with and being the first and the second nearest classes to the pattern, respectively.
Figure 6,
Figure 7,
Figure 8,
Figure 9,
Figure 10 and
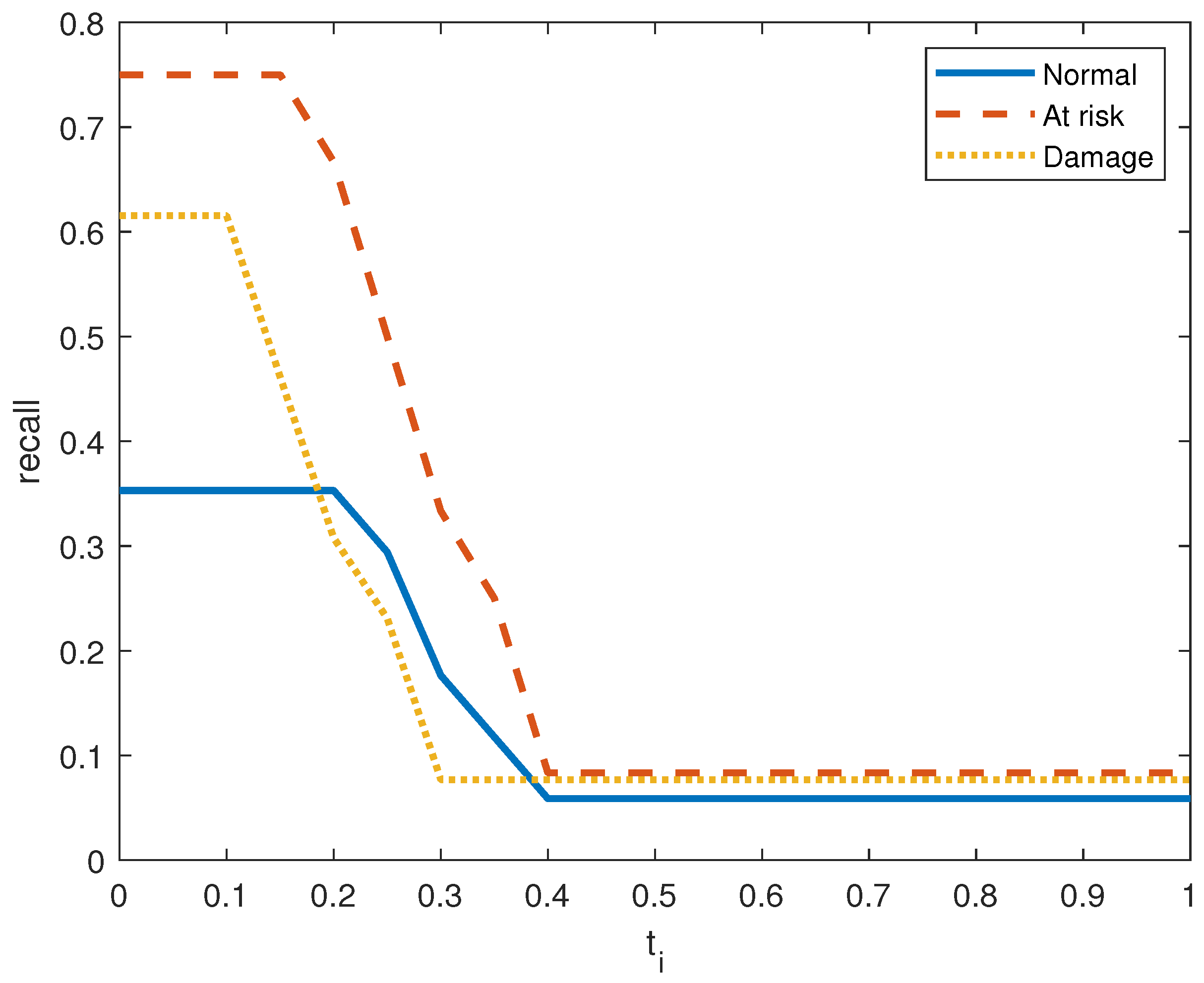
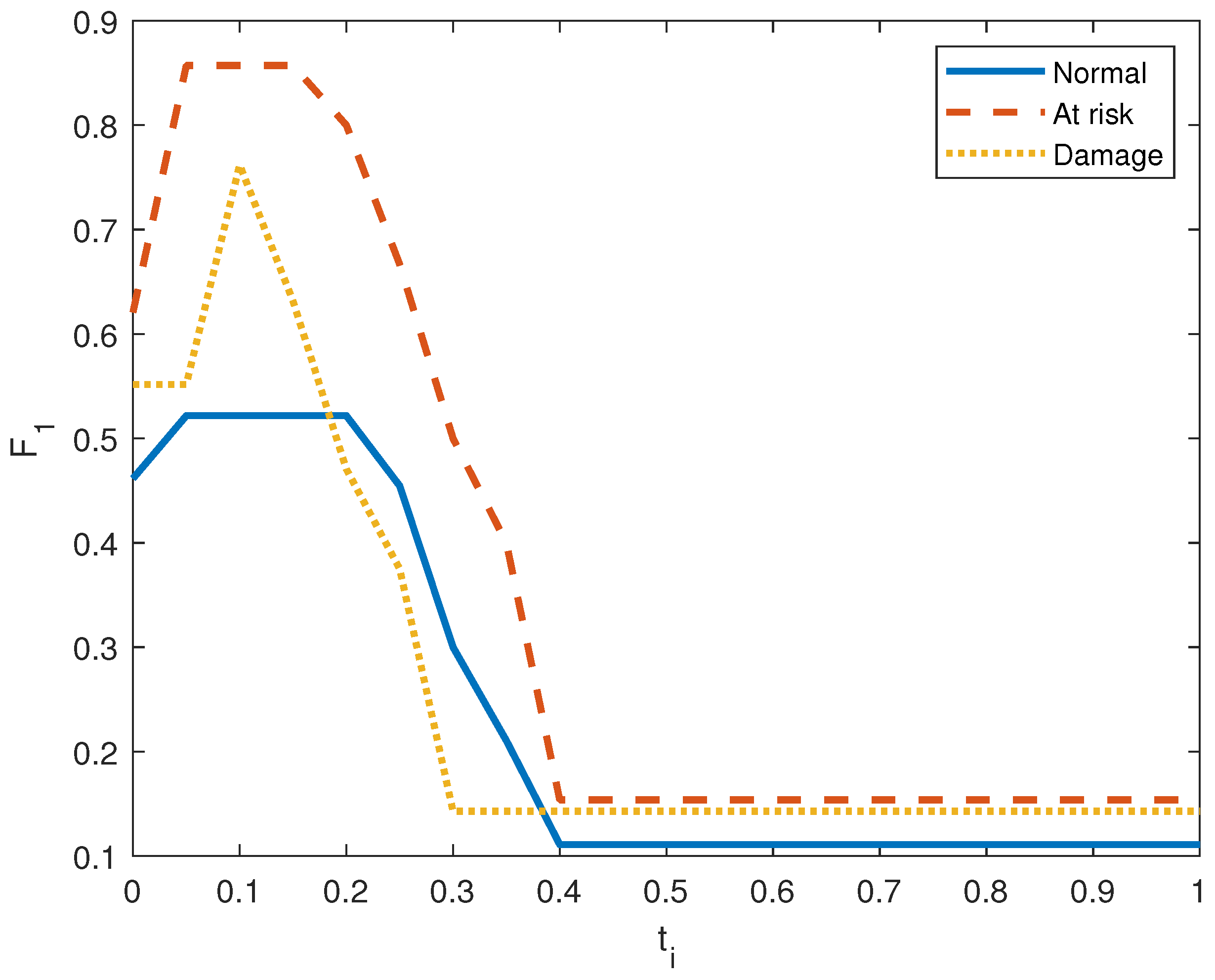
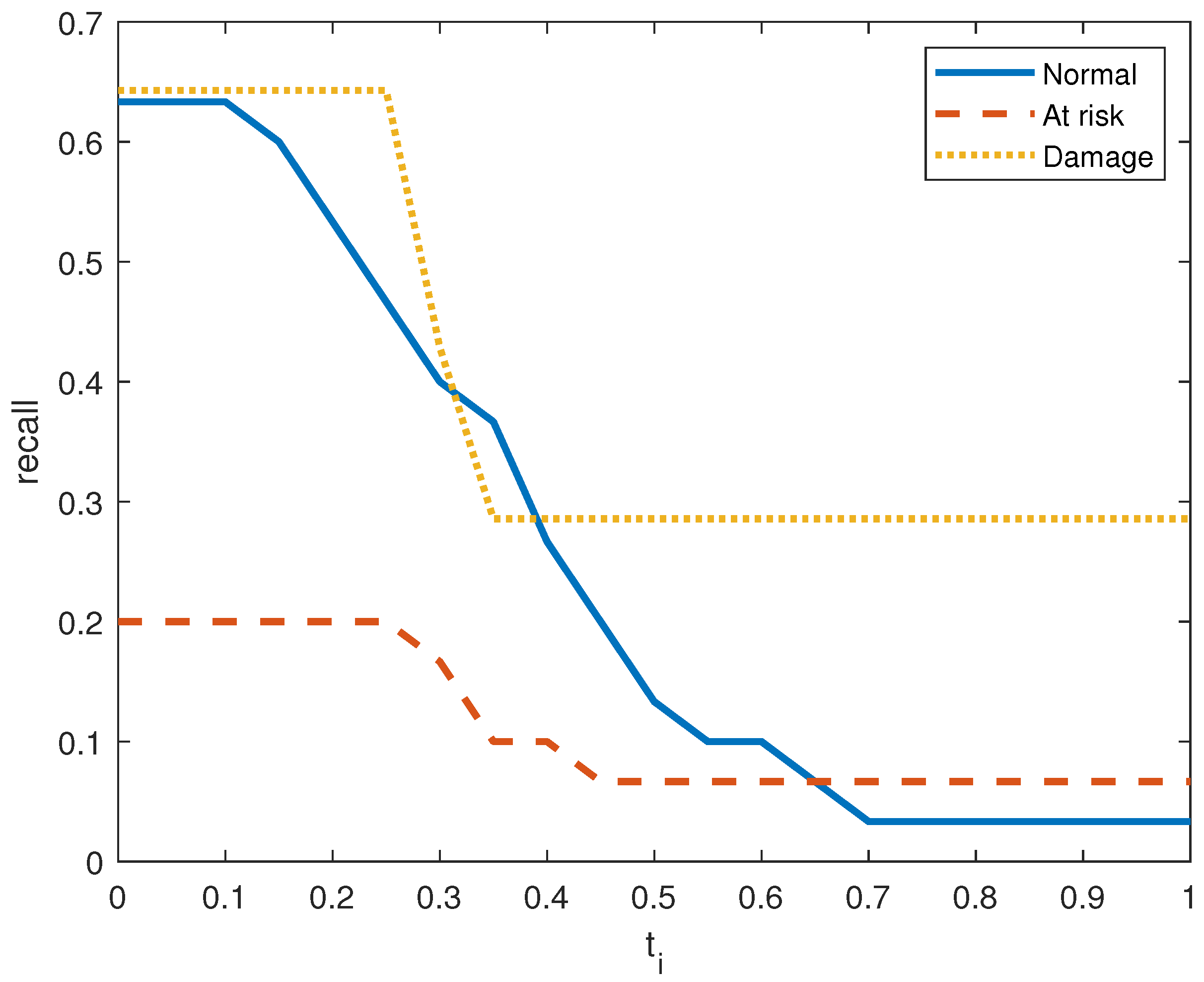
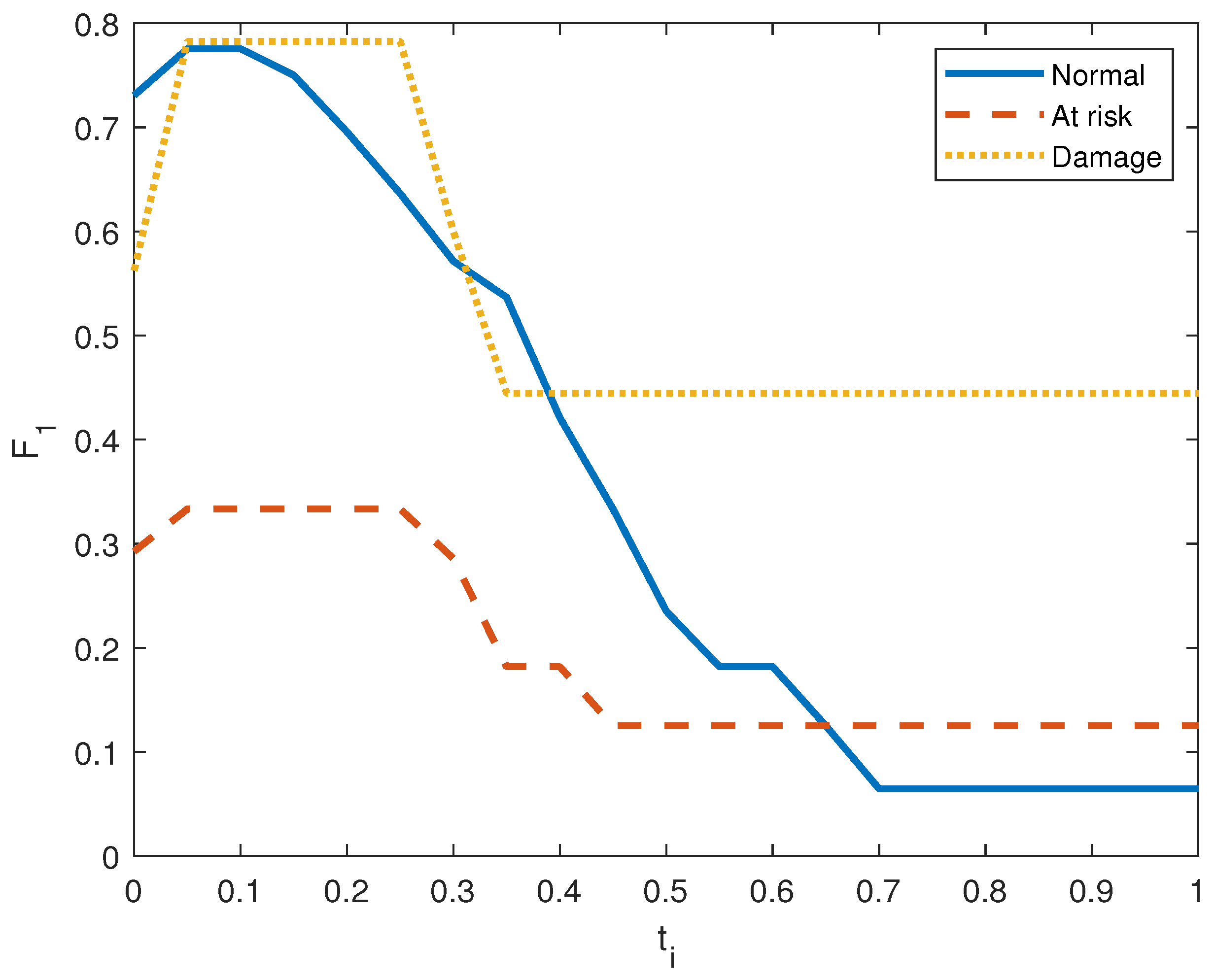
Figure 11 show the precision, recall, and
score on the three output classes for the two doors. The maximum
scores for each output class are reported in
Table 8. A high
score guarantees that the model reliably detects positive occurrences while reducing wrong predictions. It also suggests that the model works well in terms of recall and precision.
In door system 1, the average precision (AP) values for the three classes are 0.150, 0.193, and 0.169. For door system 2, they are 0.264, 0.114, and 0.398. By assigning greater weight to accurately identified instances that occur earlier in the sorted list, AP explains the prediction order. Better performance is indicated by a higher AP value, which runs from 0 to 1. For the door systems, the values are close to zero, which identifies a bad prediction.
Lastly, in door system 1, the mean average precision (mAP) values for the three classes are 0.007, 0.009, and 0.008. For door system 2, they are 0.013, 0.005, and 0.019. It is especially helpful in situations when there are several categories at play as it illustrates the model’s capacity to consistently rank pertinent things in several classes. For the door systems, the values are close to zero, which identifies a bad prediction.
As seen in
Figure 7 and
Figure 10, the model in both systems guarantees that a low percentage of false positives results in the majority of its positive predictions being right with high precision. From the small values of
, we obtain a high value for the precision. is The recall index is displayed in
Figure 6 and
Figure 9, which demonstrate that the model likewise attains high recall while successfully reducing false negatives and guaranteeing that the majority of positive occurrences are accurately detected. Recall is frequently taken into account in conjunction with accuracy to balance the trade-off between catching as many positives as feasible and reducing false positives.
4.6. Prediction of Future States
In this step, we evaluate the predictive model on the testing set and also on future unclassified samples.
Considering the maximum
score computed on the training set and the corresponding
values as defined in
Section 3.5,
Table 9 and
Table 10 (column PMM-SMS) present the precision, recall, and
score for the testing set of the two doors.
For door system 1, out of 12 patterns, 4 have been correctly classified as “normal”, 1 as “at risk”, and 1 as “damage”. Similarly, for door system 2, out of 17 patterns, 8 have been correctly classified as “normal”, 2 as “at risk”, and 1 as “damage”.
4.7. Predictive Maintenance Policy
The results presented in the previous section are highly satisfactory, with a precision of 100% achieved for both door systems. However, the recall and consequently the indicators are relatively lower. In simpler terms, the method demonstrates high accuracy, but it classifies a relatively small number of states.
At this stage, the decision maker has the option to adjust the threshold for
to potentially increase the number of classified states. They can also investigate whether the damage classification occurs more frequently in close proximity in time, leading to a reconsideration of the decision in
Section 4.6. Additionally, if the precision on future unclassified patterns deteriorates, the decision maker may opt to return to
Section 4.2 to add new sensors or gather more recent and comprehensive data. Alternatively, they could redefine the training and testing sets, potentially grouping different port systems together.
Despite the limited data, a comparison between the PMM-SMS, PRNN, and SVM techniques was carried out to provide quality assurance and show the efficacy of the suggested method. After a review of the literature, these comparison methodologies were chosen because of their applicability to maintenance prediction issues. For the SVM and PRNN methods, two training sessions were performed using the training sets of both door systems. Each input pattern consists of the normalized temperature, pressure, and humidity, which are the same features used in the PMM-SMS. The output pattern comprises the normalized number of shocks, classified into three classes based on their closest distance to the centroids defined in
Table 4. The results in
Table 9 and
Table 10 indicate that the approaches proposed exhibit the same performance for door system 1, while the PMM-SMS outperforms the machine learning methods for door system 2.
5. Discussion
In this work, we have presented and demonstrated a comprehensive process for defining predictive maintenance for simple machineries monitored by IoT. While some individual aspects of the proposed approach may not be entirely novel in the scientific community, the integrated viewpoint provided by the entire procedure offers valuable clarity and guidance. The unique challenges posed by the lack of models for these systems, the scarcity of historical data, and the varying behavior of the same simple machinery system under different implementations make traditional model-based or machine-learning predictive maintenance approaches impractical.
One of the significant challenges in deep learning problems is achieving accurate diagnosis results when dealing with massive volumes of data. Our approach addresses this issue by incorporating the reliability of the resulting classification, enabling the adoption of different maintenance plans according to various economic budgets. An important future development for this method lies in refining the step related to the predictive maintenance policy. Specifically, we aim to consider the “damage” and “at risk” classifications over time to provide further evidence for consecutive non-normal classifications. Furthermore, to enhance the method’s performance, we plan to incorporate the time stamp of sensor data in the clustering approach. This way, patterns that are closer in time will also be grouped closer in the related cluster.
The general framework proposed in this paper exhibits adaptability and can be effectively applied to complex systems with unique behaviors, potentially requiring a large number of models. To scale up the approach, we are planning to develop a web-based configuration panel to support the modeling phase. Additionally, we are working on modifying the procedure to run with several parallel threads, while directly accessing data available on a shared Internet folder, where IoT sensors regularly update their monitored information. Moreover, the classification algorithms employed for state identification can scale up to thousands of parameters and can serve as a real-time analytics tool.
The comparison between the PMM-SMS, PRNN, and SVM techniques as part of the quality assurance procedure. Normalized values of pressure, temperature, and humidity included each input pattern, in accordance with the characteristics employed in the PMM-SMS methodology. The outcomes demonstrate that for door system 1, all methods function similarly, while for door system 2, PMM-SMS outperforms machine learning techniques.
Overall, the proposed approach offers a promising pathway for predictive maintenance in simple machineries monitored by IoT, and its versatility makes it applicable to more complex systems as well. With further advancements and improvements, this methodology has the potential to contribute significantly to the realm of predictive maintenance, enabling optimized maintenance plans and cost-effective decision-making for industrial applications.
6. Conclusions
This paper contributes to a focus on the field of predictive maintenance for machinery systems. The key contributions of the paper can be summarized in different topics. The paper acknowledges the challenges posed by the complexity, diverse typologies, and limited operational lifespans of simple machinery systems monitored by IoT. It recognizes that traditional predictive maintenance approaches struggle due to the lack of extensive historical data, a common issue in such systems.
This study proposes a clustering-based process to identify potential machinery faults, even when faced with limited datasets. Clustering techniques are employed to group similar instances of sensor data, allowing for the identification of patterns that may indicate potential faults. The proposed approach provides a solution to the data scarcity problem, making it possible to perform predictive maintenance even in situations where historical data is limited. A distinctive feature of the proposed approach is its focus on empowering decision-makers. The clustering-based process not only identifies potential faults but also provides a basis for decision-makers to define predictive maintenance policies. This empowers organizations to tailor their maintenance strategies based on the reliability of the fault classifications, enhancing the adaptability and effectiveness of maintenance practices. The data validation is tested through a case study involving real sensor data from the doors of a transportation vehicle—specifically a bus. This practical application demonstrates the effectiveness and practical applicability of the clustering-based process in preemptively preventing faults and improving maintenance practices in a real-world scenario. It is highlighted the power of IoT sensor data, recognizing its potential in enhancing predictive maintenance strategies. By utilizing real-time data from sensors, the proposed approach stays relevant and responsive to the dynamic nature of machinery systems, offering a promising avenue for cost-effective predictive maintenance strategies. This work opens new possibilities for improving predictive maintenance methodologies in the domain of simple machinery systems monitored by IoT. The clustering-based approach offers a novel perspective on fault detection and prevention, as a starting point for more robust and adaptable maintenance strategies in the industry.
In summary, this paper contributes a novel clustering-based approach that overcomes data limitations, empowers decision-makers, and demonstrates practical applicability through a case study. The results should help to improve predictive maintenance plans in simple machinery systems monitored by IoT, with potential implications for improved reliability, cost-effectiveness, and overall system performance.
Author Contributions
Conceptualization, E.Z., M.S. and R.S.; methodology, E.Z., M.S. and R.S.; software, E.Z., M.S. and R.S.; validation, E.Z., M.S. and R.S.; formal analysis, E.Z., M.S. and R.S.; investigation, E.Z., M.S. and R.S.; resources, E.Z., M.S. and R.S.; data curation, E.Z., M.S. and R.S.; writing—original draft preparation, E.Z., M.S. and R.S.; writing—review and editing, E.Z., M.S. and R.S.; visualization, E.Z., M.S. and R.S.; supervision, E.Z., M.S. and R.S.; project administration, E.Z., M.S. and R.S.; funding acquisition, E.Z., M.S. and R.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Bajic, B.; Rikalovic, A.; Suzic, N.; Piuri, V. Industry 4.0 implementation challenges and opportunities: A managerial perspective. IEEE Syst. J. 2020, 15, 546–559. [Google Scholar] [CrossRef]
- Rikalovic, A.; Suzic, N.; Bajic, B.; Piuri, V. Industry 4.0 Implementation Challenges and Opportunities: A Technological Perspective. IEEE Syst. J. 2021, 16, 2797–2810. [Google Scholar] [CrossRef]
- Huan, H.; Liu, L.; Yao, Y.; Chen, X.; Zhan, J.; Liu, Q.; Lu, T.; Peng, C. Real-Time Predictive Temperature Measurement in Oil Pipeline: Modeling and Implementation on Embedded Wireless Sensing Devices. IEEE Trans. Ind. Electron. 2020, 68, 12689–12697. [Google Scholar] [CrossRef]
- Bersani, C.; Ruggiero, C.; Sacile, R.; Soussi, A.; Zero, E. Internet of Things Approaches for Monitoring and Control of Smart Greenhouses in Industry 4.0. Energies 2022, 15, 3834. [Google Scholar] [CrossRef]
- Göppert, J.; Walz, A.; Sikora, A. A Survey on Life-Cycle-Oriented Certificate Management in Industrial Networking Environments. J. Sens. Actuator Netw. 2024, 13, 26. [Google Scholar] [CrossRef]
- Borkowski, A.S. Low-Cost Internet of Things Solution for Building Information Modeling Level 3B—Monitoring, Analysis and Management. J. Sens. Actuator Netw. 2024, 13, 19. [Google Scholar] [CrossRef]
- Grabowska, S.; Gajdzik, B.; Saniuk, S. The role and impact of industry 4.0 on business models. In Sustainable Logistics and Production in Industry 4.0: New Opportunities and Challenges; Springer: Cham, Switzerland, 2020; pp. 31–49. [Google Scholar]
- Al-Qerem, A.; Alauthman, M.; Almomani, A.; Gupta, B.B. IoT transaction processing through cooperative concurrency control on fog–cloud computing environment. Soft Comput. 2020, 24, 5695–5711. [Google Scholar] [CrossRef]
- Cvitić, I.; Peraković, D.; Periša, M.; Gupta, B. Ensemble machine learning approach for classification of IoT devices in smart home. Int. J. Mach. Learn. Cybern. 2021, 12, 3179–3202. [Google Scholar] [CrossRef]
- Moustafa, R.; AlYahfoufi, M.; Abbas, N. Energy Efficient UAV-based Relay System for IoT Networks in Hazardous Industrial Areas. In Proceedings of the 2022 4th IEEE Middle East and North Africa COMMunications Conference (MENACOMM), Amman, Jordan, 6–8 December 2022; pp. 223–228. [Google Scholar]
- Ran, Y.; Zhou, X.; Lin, P.; Wen, Y.; Deng, R. A survey of predictive maintenance: Systems, purposes and approaches. arXiv 2019, arXiv:1912.07383. [Google Scholar]
- Selcuk, S. Predictive maintenance, its implementation and latest trends. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2017, 231, 1670–1679. [Google Scholar] [CrossRef]
- Ioannides, M.G.; Stamelos, A.P.; Papazis, S.A.; Stamataki, E.E.; Stamatakis, M.E. Internet of Things-Based Control of Induction Machines: Specifics of Electric Drives and Wind Energy Conversion Systems. Energies 2024, 17, 645. [Google Scholar] [CrossRef]
- Ge, M.; Xu, Y.; Du, R. An Intelligent Online Monitoring and Diagnostic System for Manufacturing Automation. IEEE Trans. Autom. Sci. Eng. 2008, 5, 127–139. [Google Scholar] [CrossRef]
- Gajdzik, B. Autonomous and professional maintenance in metallurgical enterprise as activities within total productive maintenance. Metalurgija 2014, 53, 269–272. [Google Scholar]
- Yin, S.; Ding, S.X.; Zhou, D. Diagnosis and prognosis for complicated industrial systems—Part I. IEEE Trans. Ind. Electron. 2016, 63, 2501–2505. [Google Scholar] [CrossRef]
- Zhou, Z.; Wen, C.; Yang, C. Fault isolation based on k-nearest neighbor rule for industrial processes. IEEE Trans. Ind. Electron. 2016, 63, 2578–2586. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Miao, J.; Li, C.; Yao, X. Preventive Maintenance Strategy for Train Doors Based on the Competitive Weibull Theory. Chin. J. Mech. Eng. 2020, 1–15. [Google Scholar] [CrossRef]
- Wang, S.; Jin, S.; Deng, D.; Fernandez, C. A critical review of online battery remaining useful lifetime prediction methods. Front. Mech. Eng. 2021, 7, 719718. [Google Scholar] [CrossRef]
- Cai, B.; Huang, L.; Xie, M. Bayesian networks in fault diagnosis. IEEE Trans. Ind. Inform. 2017, 13, 2227–2240. [Google Scholar] [CrossRef]
- Sun, W.; Zhao, R.; Yan, R.; Shao, S.; Chen, X. Convolutional discriminative feature learning for induction motor fault diagnosis. IEEE Trans. Ind. Inform. 2017, 13, 1350–1359. [Google Scholar] [CrossRef]
- Shao, S.; McAleer, S.; Yan, R.; Baldi, P. Highly accurate machine fault diagnosis using deep transfer learning. IEEE Trans. Ind. Inform. 2018, 15, 2446–2455. [Google Scholar] [CrossRef]
- Kilius, Š.; Gailius, D.; Knyva, M.; Balčiūnas, G.; Meškuotienė, A.; Dobilienė, J.; Joneliūnas, S.; Kuzas, P. Time Delay Characterization in Wireless Sensor Networks for Distributed Measurement Applications. J. Sens. Actuator Netw. 2024, 13, 31. [Google Scholar] [CrossRef]
- Samara, M.A.; Bennis, I.; Abouaissa, A.; Lorenz, P. A survey of outlier detection techniques in IoT: Review and classification. J. Sens. Actuator Netw. 2022, 11, 4. [Google Scholar] [CrossRef]
- Chen, Z.; Gryllias, K.; Li, W. Intelligent fault diagnosis for rotary machinery using transferable convolutional neural network. IEEE Trans. Ind. Inform. 2019, 16, 339–349. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Gearbox fault diagnosis using a deep learning model with limited data sample. IEEE Trans. Ind. Inform. 2020, 16, 6263–6271. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, R.; Li, X.; Chen, D.; Hu, Q. Task-sequencing meta learning for intelligent few-shot fault diagnosis with limited data. IEEE Trans. Ind. Inform. 2021, 18, 3894–3904. [Google Scholar] [CrossRef]
- Lu, S.; Gao, Z.; Xu, Q.; Jiang, C.; Zhang, A.; Wang, X. Class-imbalance privacy-preserving federated learning for decentralized fault diagnosis with biometric authentication. IEEE Trans. Ind. Inform. 2022, 18, 9101–9111. [Google Scholar] [CrossRef]
- Fang, Q.; Xiong, G.; Zhou, M.; Tamir, T.S.; Yan, C.B.; Wu, H.; Shen, Z.; Wang, F.Y. Process Monitoring, Diagnosis and Control of Additive Manufacturing. IEEE Trans. Autom. Sci. Eng. 2022, 21, 1041–1067. [Google Scholar] [CrossRef]
- Che, Y.; Stroe, D.I.; Hu, X.; Teodorescu, R. Semi-supervised self-learning-based lifetime prediction for batteries. IEEE Trans. Ind. Inform. 2022, 19, 6471–6481. [Google Scholar] [CrossRef]
- Qu, X.; Shi, D.; Zhao, J.; Tran, M.K.; Wang, Z.; Fowler, M.; Lian, Y.; Burke, A.F. Insights and reviews on battery lifetime prediction from research to practice. J. Energy Chem. 2024, 94, 716–739. [Google Scholar] [CrossRef]
- Roemer, M.J.; Byington, C.S.; Kacprzynski, G.J.; Vachtsevanos, G. An overview of selected prognostic technologies with application to engine health management. In Proceedings of the Turbo Expo: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 42371, pp. 707–715. [Google Scholar]
- Cohen, L.H. Life Events and Psychological Functioning: Theoretical and Methodological Issues; SAGE Publications, Incorporated: New York, NY, USA, 1988; Volume 90. [Google Scholar]
- Malviya, A.; Singh, V. The role and issues of clustering technique in designing maintainable object oriented system. Int. J. Comput. Sci. Eng. 2011, 3, 784–788. [Google Scholar]
- Ferracuti, F.; Freddi, A.; Monteriù, A.; Romeo, L. Fault Diagnosis of Rotating Machinery Based on Wasserstein Distance and Feature Selection. IEEE Trans. Autom. Sci. Eng. 2022, 19, 1997–2007. [Google Scholar] [CrossRef]
- Clement, E.P. Using normalized bayesian information criterion (BIC) to improve box-jenkins model building. Am. J. Math. Stat. 2014, 4, 214–221. [Google Scholar]
- Zhao, Q.; Hautamaki, V.; Fränti, P. Knee point detection in BIC for detecting the number of clusters. In Proceedings of the International Conference on Advanced Concepts for Intelligent Vision Systems; Springer: Berlin/Heidelberg, Germany, 2008; pp. 664–673. [Google Scholar]
- Hua, C.; Chen, Q.; Wu, H.; Wada, T. RK-means clustering: K-means with reliability. IEICE Trans. Inf. Syst. 2008, 91, 96–104. [Google Scholar] [CrossRef][Green Version]
- Davis, J.; Goadrich, M. The relationship between Precision-Recall and ROC curves. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, Pennsylvania, 25–29 June 2006; pp. 233–240. [Google Scholar]
- Chicco, D.; Jurman, G. The advantages of the Matthews correlation coefficient (MCC) over F1 score and accuracy in binary classification evaluation. BMC Genom. 2020, 21, 6. [Google Scholar] [CrossRef] [PubMed]
- ISO 11898-1:2024; Road Vehicles—Controller Area Network (CAN)—Part 1: Data Link Layer and Physical Coding Sublayer. ISO: Geneva, Switzerland, 2024.
Figure 1.
Schema of the proposed maintenance predictive steps.
Figure 1.
Schema of the proposed maintenance predictive steps.
Figure 2.
System architecture. Using IoT sensors, the data are collected and stored for the data analysis.
Figure 2.
System architecture. Using IoT sensors, the data are collected and stored for the data analysis.
Figure 3.
Spatial representation of the set of input feature for door system 1.
Figure 3.
Spatial representation of the set of input feature for door system 1.
Figure 4.
Spatial representation of the set of input feature for door system 2.
Figure 4.
Spatial representation of the set of input feature for door system 2.
Figure 5.
Distances , , shown for a generic pattern in door system 2.
Figure 5.
Distances , , shown for a generic pattern in door system 2.
Figure 6.
Recall performance metric in door system 1 for the three clusters.
Figure 6.
Recall performance metric in door system 1 for the three clusters.
Figure 7.
Precision performance metric in door system 1 for the three clusters.
Figure 7.
Precision performance metric in door system 1 for the three clusters.
Figure 8.
score in door system 1.
Figure 8.
score in door system 1.
Figure 9.
Recall performance metric in door system 2 for the three clusters.
Figure 9.
Recall performance metric in door system 2 for the three clusters.
Figure 10.
Precision performance metric in door system 2 for the three clusters.
Figure 10.
Precision performance metric in door system 2 for the three clusters.
Figure 11.
score in door system 2.
Figure 11.
score in door system 2.
Table 1.
Sample data collected.
Table 1.
Sample data collected.
| Temperature | Pressure | Humidity | N. Shock |
|---|
| 0.76 | 0.27 | 0.33 | 0.23 |
| 0.66 | 0.24 | 0.51 | 0.46 |
| 0.37 | 0.34 | 0.51 | 0.50 |
| [9–23] [°C] | [36–73] [Pa] | [–] [%] | [1–299] [·] |
Table 2.
Correlation between the variables of the door system 1.
Table 2.
Correlation between the variables of the door system 1.
| r | Temperature | Pressure | Humidity | Shock |
|---|
| Temperature | 1.000 | −0.4754 | -0.3462 | −0.0213 |
| Pressure | −0.4754 | 1.000 | 0.2034 | 0.3511 |
| Humidity | −0.3462 | 0.2034 | 1.000 | −0.0737 |
| Shock | −0.0213 | 0.3511 | −0.0737 | 1.000 |
Table 3.
Correlation between the variables of the door system 2.
Table 3.
Correlation between the variables of the door system 2.
| r | Temperature | Pressure | Humidity | Shock |
|---|
| Temperature | 1.000 | −0.1506 | −0.0592 | −0.2266 |
| Pressure | −0.1506 | 1.000 | 0.2024 | 0.0694 |
| Humidity | −0.0592 | 0.2024 | 1.000 | −0.2213 |
| Shock | −0.2266 | 0.0694 | −0.2213 | 1.000 |
Table 4.
Definition of the centroids of classes.
Table 4.
Definition of the centroids of classes.
| Centroid | Door 1 | Door 2 |
|---|
| 0.1000 | 0.1116 |
| 0.5044 | 0.4631 |
| 0.7942 | 0.8430 |
Table 5.
Definition of the number of sub-classes for each state in the two door systems.
Table 5.
Definition of the number of sub-classes for each state in the two door systems.
| Number of Sub-Classes | 1-Normal | 2-At Risk | 3-Damage |
|---|
| Door 1 | 2 | 1 | 2 |
| Door 2 | 2 | 2 | 2 |
Table 6.
Definition of the centroids of sub-classes in door system 1.
Table 6.
Definition of the centroids of sub-classes in door system 1.
| Centroid | Shock |
|---|
| 0.0821 |
| 0.1250 |
| 0.5044 |
| 0.7896 |
| 0.8500 |
Table 7.
Definition of the centroids of sub-classes in door system 2.
Table 7.
Definition of the centroids of sub-classes in door system 2.
| Centroid | Shock |
|---|
| 0.1157 |
| 0.0983 |
| 0.4421 |
| 0.4911 |
| 0.8678 |
| 0.8292 |
Table 8.
max score in the two doors.
Table 8.
max score in the two doors.
| Max Scores | Normal | At risk | Damage |
|---|
| Door 1 | 0.52 | 0.69 | 0.76 |
| Door 2 | 0.78 | 0.33 | 0.78 |
Table 9.
Performance index in the door system 1.
Table 9.
Performance index in the door system 1.
| State | Index | PMM-SMS | PRNN | SVM |
|---|
| | | 1.00 | 1.00 | 1.00 |
| Normal | | 0.57 | 0.57 | 0.57 |
| | | 0.73 | 0.73 | 0.73 |
| | | 1.00 | 1.00 | 1.00 |
| At risk | | 0.50 | 0.50 | 0.50 |
| | | 0.67 | 0.67 | 0.25 |
| | | 1.00 | 1.00 | n.d. |
| Damage | | 0.33 | 0.33 | 0 |
| | | 0.50 | 0.50 | n.d. |
Table 10.
Performance index in the door system 2.
Table 10.
Performance index in the door system 2.
| State | Index | PMM-SMS | PRNN | SVM |
|---|
| | | 1.00 | 1.00 | 1.00 |
| Normal | | 0.67 | 0.50 | 0.08 |
| | | 0.80 | 0.67 | 0.15 |
| | | 1.00 | 1.00 | 1.00 |
| At risk | | 1.00 | 0.50 | 0.50 |
| | | 1.00 | 0.67 | 0.67 |
| | | 1.00 | n.d. | 1.00 |
| Damage | | 0.33 | 0.00 | 0.33 |
| | | 0.50 | n.d. | 0.50 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).