Abstract
The integration of vehicle-to-grid (V2G) technology into smart energy management systems represents a significant advancement in the field of energy suppliers for Industry 4.0. V2G systems enable a bidirectional flow of energy between electric vehicles and the power grid and can provide ancillary services to the grid, such as peak shaving, load balancing, and emergency power supply during power outages, grid faults, or periods of high demand. In this context, reliable prediction of the availability of V2G as an energy source in the grid is fundamental in order to optimize both grid stability and economic returns. This requires both an accurate modeling framework that includes the integration and pre-processing of readily accessible data and a prediction phase over different time horizons for the provision of different time-scale ancillary services. In this research, we propose and compare two data-driven predictive modeling approaches to demonstrate their suitability for dealing with quasi-periodic time series, including those dealing with mobility data, meteorological and calendrical information, and renewable energy generation. These approaches utilize publicly available vehicle tracking data within the floating car data paradigm, information about meteorological conditions, and fuzzy weekend and holiday information to predict the available aggregate capacity with high precision over different time horizons. Two data-driven predictive modeling approaches are then applied to the selected data, and the performance is compared. The first approach is Hankel dynamic mode decomposition with control (HDMDc), a linear state-space representation technique, and the second is long short-term memory (LSTM), a deep learning method based on recurrent nonlinear neural networks. In particular, HDMDc performs well on predictions up to a time horizon of 4 h, demonstrating its effectiveness in capturing global dynamics over an entire year of data, including weekends, holidays, and different meteorological conditions. This capability, along with its state-space representation, enables the extraction of relationships among exogenous inputs and target variables. Consequently, HDMDc is applicable to V2G integration in complex environments such as smart grids, which include various energy suppliers, renewable energy sources, buildings, and mobility data.
1. Introduction
With global electric vehicle (EV) penetration projected to reach 60% by 2030 [1,2], the integration of EVs into the vehicle-to-grid (V2G) system and smart grids (SGs) is increasingly crucial. V2G technology, which enables bidirectional energy exchange between EVs and the grid, thereby transforming EVs into mobile energy storage units, is an integral part of the latest methodological and technological frameworks for SGs. These frameworks, including cyber-physical systems, automation, and real-time data exchange, are being developed under the umbrella of Industry 4.0, integrating renewable energy, buildings, and EVs into a comprehensive energy system that is responsive to dynamic industrial demands [3,4]. In smart energy management, which coordinates multiple energy carriers, V2G technology can support addressing uncertainties associated with renewable energy and load [5]—primary challenges for multi-energy microgrid operations—as well as managing energy price uncertainties [6].
As distributed energy storage units, EVs have, in fact, the potential to provide auxiliary services to the power grid [7,8,9]. However, a single vehicle cannot significantly benefit the grid, so EVs are typically grouped into fleets or aggregators. An aggregator acts as a consolidating entity, integrating multiple EVs to create a meaningful impact on the electrical grid by serving as the interface between the grid operator and the fleet. Considering current market regulations that impose a minimum capacity threshold and the limited maximum capacity of single V2G chargers, participation in the V2G market and dispatching must be facilitated by an aggregator. The role of an aggregator can be assumed by various business entities, including EV fleet operators, electric utility companies, or independent organizations such as automobile manufacturers or distributed generation managers. For an electric utility company managing a network of V2G hubs, predicting the energy provided to the grid presents unique challenges. Unlike an EV fleet operator, the utility company does not have a predefined schedule for EV plug-ins, complicating the prediction process.
Uncoordinated EV charging can increase load during peak hours and create local issues in distribution networks [10,11]. In contrast, effective management of the increasing number of EVs connected to the grid as ancillary service providers can yield significant benefits, including frequency and voltage regulation, enhanced transient stability, peak shaving, load balancing, and emergency power supply during outages, grid faults, or high-demand periods. These benefits can be achieved through well-planned and coordinated EV integration [12,13,14,15].
Given the increasing number of EVs that can support the power grid through aggregators, managing these resources has become increasingly complex. Coordinating EVs for grid support, particularly as they connect and disconnect, presents significant challenges and is often impractical. To ensure the reliability and economic viability of V2G systems for providers, accurate long- and short-term forecasting of aggregate available capacity (AAC), i.e., the amount of energy a fleet of EVs can provide when connected to the grid via aggregator hubs, is essential. This research addresses the need for accurate AAC forecasting to navigate the uncertainties of different energy markets. Long-term forecasting, focused on day-ahead predictions, supports the daily energy market. In contrast, short-term forecasting is critical for aggregators, who act as balancing service providers. These forecasts help meet bidding frequency requirements in the regulation market and facilitate operations in the intraday energy market, particularly for predefined intervals such as half-hourly settlement periods [16,17].
Insights into AAC prediction come primarily from understanding the availability of EVs to deliver energy via a V2G aggregator when needed. This availability can be influenced by various factors: drivers’ behavior, location of charging infrastructure [18], and vehicle characteristics. In the current technological framework, by integrating IoT sensors and communication devices into the V2G infrastructure, both in geographically dispersed EVs within the floating car data (FCD) paradigm [19] and in the V2G aggregators, real-time vehicle tracking data on status and localization as well as grid conditions can be collected, analyzed, and acted upon accordingly. This would enable seamless coordination between EVs and the power grid and optimize energy storage and distribution based on real-time requirements and conditions [20]. Meteorological data and calendar information (such as weekends and holidays) are considered exogenous features in this study. These are variables that are not involved in the internal dynamics of the V2G system but that can influence the accuracy of AAC predictions. Meteorological factors, such as weather conditions and temperature fluctuations, play a crucial role in determining the usage behavior of EVs. For instance, unfavorable weather conditions can impact driving behavior [21] and thus affect the availability of EVs for grid services. Similarly, weekends and national holidays lead to different usage patterns of EVs, as travel habits and energy consumption behavior often deviate from typical weekday routines [22,23].
From a methodological perspective, this study proposes using a state-space representation modeling approach, specifically dynamic mode decomposition with control (DMDc) [24], as an alternative to widely used machine learning (ML) methods for sequence time series forecasting, such as long short-term memory (LSTM) [25,26,27,28]. DMDc is an advanced version of dynamic mode decomposition (DMD) that incorporates both system measurements and exogenous or control inputs to identify input–output relationships and capture underlying dynamics. We specifically apply an extension known as Hankel DMDc (HDMDc) [29,30], which uses time-delayed state variables and exogenous inputs to broaden the state space. This approach, grounded in Koopman theory, has been successfully applied to quasi-periodically controlled systems, such as traffic corridors [31]. Specifically, we apply HDMDc and LSTM to aggregated FCD vehicle tracking data, incorporating exogenous factors such as meteorological data and fuzzy calendar-based information (weekends and holidays) to provide a holistic approach and comprehensive interpretation of the results. In this paper, we present several novel contributions to the field of V2G applications:
- We integrate and standardize different data sources, combining readily accessible FCD data on mobility patterns with weather conditions and calendar information. This seamless integration enhances the accuracy and reliability of V2G applications, ensuring that our methods can be readily adopted and replicated and thereby facilitating broader application and validation within the V2G and energy grid research community.
- We leverage fuzzy logic to derive a continuous and integrated holiday rate metric, a novel approach introduced as a proof of concept in [23]. This method synthesizes inputs from calendars, weekends, and national holidays, providing a continuous and accurate representation of holiday periods and allowing the model to learn driver habits from a one-year dataset.
- We propose using HDMDc as a state-space representation method, contrasting with the well-established LSTM networks and other black-box models commonly used in time series forecasting, particularly in the V2G field. This offers a novel perspective with potential improvements in model performance, interpretability, and transferability.
These innovations collectively advance the V2G domain by enhancing model accuracy, accessibility, and practical applicability.
The article is divided into the following sections. In Section 2, the state of the art in time series forecasting within the V2G domain is presented with a focus on AAC prediction and identifying the scientific gap this work aims to address. Section 3 details the theoretical background of the prediction models used: HDMDc and LSTM. The global system for predictive model identification is outlined in Section 4, which includes data collection, pre-processing, and aggregation to create appropriate time series for model identification. This section also covers the model prediction analysis for both HDMDc and LSTM. In Section 5, the model learning process is described, followed by the presentation and discussion of results. This section particularly focuses on comparing the performance of the models in predicting AAC over different time horizons using key performance indicators, in prediction versus target time series, and in regression plots. Finally, conclusions are drawn in Section 6.
2. Related Works
This section introduces a comprehensive literature review of existing models for predicting electrical quantities in the V2G domain. In particular, Table 1 summarizes previous research, classifying the works in terms of model and model class, prediction horizon, target variable, data source, and exogenous inputs—factors external to the internal system model but affecting the prediction.
Various models have been used in the literature to predict different V2G-related target variables: AAC [23,27,28,32,33,34], energy demand [35], schedulable energy capacity (SEC) [36,37] including charging and discharging load, load forecast for energy price determination [38], occupancy and energy charging load at V2G hubs [39], frequency containment reserve (FCR) participation [40], energy supply (ES) and peak demand (PD) [41], as well as drivers’ habits and preferences when connecting to V2G hubs [42].
These diverse applications all relate to the integration of V2G into smart grids, enabling operators to optimize the scheduling of EV participation in ancillary services and to meet demand in various markets. Such models are used for price determination in the day-ahead market, intraday power trading, and scheduling power sources at different times of the day to compensate for fluctuations in renewable energy and high-demand intervals. Accordingly, different time scales and prediction horizons are involved in modeling: the short-term scale of hours with a minimum settlement time of half an hour [23,32,33,35,36,37,38] and the one-day-ahead forecast scale [27,28,36,37,39]. The one-day-ahead forecast is determined offline for 24 h in advance and serves the day-ahead energy market. However, such long-term predictions are subject to significant uncertainty [37]. To mitigate this uncertainty, rolling predictions on the order of hours are introduced to meet the needs of short-term ancillary services.
These models are applied to various historical data sources: GPS localization and battery management system data from EVs fleets with a limited number of vehicles [27,28,33,34,36,40,42]; charging and discharging session information based on V2G infrastructures, here referred to as hubs [32,35,39]; simulated EV data [38,40]; and real-world extensive FCD mobility data and vehicle information [23,37,41]. Most models are trained using historical data of the same target variable, while some also incorporate features that are uncorrelated with the V2G system. These additional features, referred to as exogenous inputs, include calendar information [23,32,35,38,39], some including weekends [23,32,35] and holidays [23], meteorological [23,38] and energy market events [27,28,34], or price [42].
Another distinction between the models used to predict V2G variables lies in their classification. Previous research predominantly employs data-driven models, whereas deterministic models are seldom used for comparative predictions, as noted in [32], due to the energy supplier’s aversion to risk in predictions. Deterministic models are also utilized for static analyses rather than for making predictions, particularly in the analysis of mobility data to support V2G systems [41,42]. Dynamic nonlinear black-box models have been used extensively compared to linear regression models. These models account for nonlinear dynamics and are more effective in capturing the behavior of V2G systems compared to dynamic linear regression models. These black-box models include a number of techniques such as neural networks (NN) [23,32,34,36], long short-term memory networks (LSTM) [23,28] potentiated by K-means clustering and federated learning in [35] or by convolutional neural networks in (CNN)[27], random forest (RF) [39], gradient-boosted decision tree (GBDT) [37], and extreme gradient boosting (XGBoost) [40]. The few applications of dynamic linear autoregressive models are presented in [32,39].
In this highly complex context of predictive modeling, our work introduces innovations in multiple aspects of the methodological framework, as shown in the summary Table 1. The method is applied to short-term predictions covering intervals from one to four hours, aiming to enhance performance for periods exceeding one hour. Unlike most approaches, it utilizes generic FCD that can be easily obtained from insurance companies rather than relying on mobile phone GPS data. Additionally, for the first time, we have included exogenous factors such as weather data and fuzzified weekend and holiday rates, which have never been used for predictions exceeding half an hour. These features were initially analyzed by the authors in [23] for half-hour predictions as a proof of concept, demonstrating their effectiveness in improving predictive model performance. Notably, weather information has never been used in predictive models applied to real-world case studies, having only been utilized with simulated EV data [38].

Table 1.
State of the art in predictive models for V2G-related variables.
Table 1.
State of the art in predictive models for V2G-related variables.
| Model | Prediction | Data | Exogenous Inputs | Model Class | Target |
|---|---|---|---|---|---|
| Persistence model, Generalized linear model, NN [32] | Half-hour-ahead | Hub | Calendar, Weekends | Deterministic, Data-driven Dynamic Linear, Dynamic Nonlinear Black-Box | AAC |
| NN, LSTM [23] | Half-hour-ahead | Generic FCD Data | Meteo, Fuzzy Weekend and Holiday rate | Dynamic Nonlinear Black-Box | AAC |
| MAML-CNN-LSTM-Attention Algorithm [33] | Hour-ahead | EVs limited fleet (Rental Car Fleet) | - | Dynamic Nonlinear Black-Box | AAC |
| K-Means clustering, LSTM using federated learning [35] | Hour-ahead | Hub | Calendar, Weekends | Dynamic Nonlinear Black-Box | Energy demand |
| Multilayer perceptron (MLP) [38] | Hour-ahead | Simulated EVs and Consumer preferences | Calendar, Meteo | Dynamic Nonlinear Black-Box | Load forecast for electricity price determination |
| LSTM [36] | Offline (day-ahead) Rolling (hour-ahead) | EVs fleet | - | Dynamic Nonlinear Black-Box | SEC |
| GBDT [37] | Offline (Day-ahead) Rolling (hour-ahead) | Generic FCD Data | - | Dynamic Nonlinear Black-Box | SEC |
| CNN-LSTM [27,28] | Day-ahead | EVs Limited fleet | None/Market event | Dynamic Nonlinear Black-Box | AAC |
| LSTM, NAR [34] | Day-ahead | EVs Limited fleet | Market event simulation | Dynamic Nonlinear Black-Box | AAC |
| RF, SARIMA [39] | Day-ahead | Hub | Calendar | Dynamic Nonlinear Black-Box, Data-Driven Dynamic Linear | Occupancy and charging load for single EV |
| XGBoost [40] | Yearly | EVs limited fleet/Simulated Data | - | Dynamic Nonlinear Black-Box | FCR participation |
| Analytical: Vehicle contribution sum [41] | - | Generic FCD Data (Mobile Phone GPS) | - | Static Deterministic | Daily Aggregated V2G ES and PD |
| Analytical [42] | - | EVs limited fleet (Shared Mobility on Demand) | Energy price | Static Deterministic | Driver preference for V2G or mobility |
| HDMDc—This study | Rolling 1 to 4 hour-ahead | Generic FCD Data | Meteo, Fuzzy Weekend and Holiday rate | Data-Driven Dynamic Linear State Space | AAC |
The features in bold represent those shared with the HDMDc methods presented in this paper.
The main methodological innovation of our approach lies in the introduction of a data-driven dynamic linear state-space model: HDMDc. This approach significantly differs from black-box models, as it allows for the identification of a global model for the system that functions under varying operating conditions [43]. It also facilitates the extrapolation of complex relationships between the target variable and exogenous factors, thereby enabling energy providers to understand the model’s predictions. Furthermore, a state-space model is amenable to model order reduction techniques, which can extract the most significant dynamics and provide insights into the predictions made.
3. Methods: Theoretical Background
Two different approaches for prediction models were used: the HDMDc and the LSTM. Both are well suited for predicting time series and offer high accuracy and flexibility in modeling trends, seasonal patterns, and long-range temporal dependencies in the data. The HDMDc is a data-driven linear identification algorithm based on the dynamic system state space representation; it is able to capture various high-energy dynamics associated with different time scales. The LSTM is a nonlinear black-box algorithm based on the theory of recurrent neural networks (RNN) and is suitable for dynamic system identification thanks to long short-term memory. The theoretical foundations of both algorithms are explained in more detail in the following subsections.
3.1. HDMDc
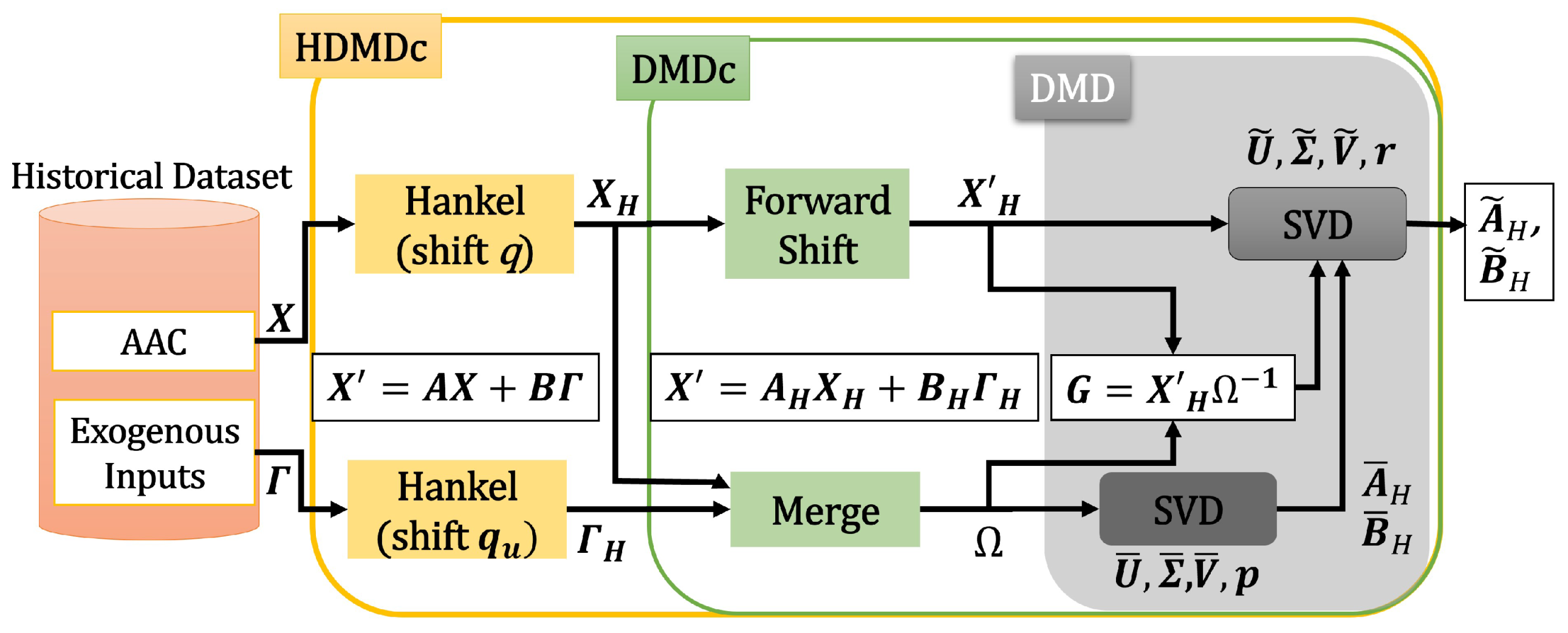
The algorithm produces a discrete state-space model; hence, the notation for discrete instances, , of the continuous time variable, , is used, where ), and is the sampling time of the model. Delay coordinates (i.e., ,, etc.) are also included in the state-space model to account for state delay in the system. This procedure allows for the creation of the augmented state space relevant to model nonlinear phenomena. Therefore, we define a state delay vector as
where q is the number of delay coordinates (including the current time-step) of the state, with , and is the number of state variables.
The input delay vector is defined as
where is the number of delay coordinates (including the current time-step) of the inputs, with , and is the number of the exogenous input variables.
The discrete state-space function is defined as
where is the state matrix, is the state delay system matrix, is the input matrix, and is the delay input matrix. The system output is assumed to be equal to the state, i.e., the output matrix is assumed to be the identity matrix. When dealing with system identification in which only an input/output time series is available, this assumption implies that should be chosen as the size of the process output vector. The training time series consist of discrete measurements of the outputs (i.e., ) and corresponding inputs (i.e., ).
The training data, exploring the augmented state space, thanks to the delay shifts, are organized in the following matrices:
where w represents the time snapshots and is the number of columns in the matrices, is the matrix X shifted forward by one time-step, is the matrix with delay states, and is the matrix of inputs. Moreover, to incorporate the dynamic effect of control inputs, an extended matrix of the exogenous inputs with time shifts (i.e., ) is created and included in the model. Equation (3) can now be combined with the matrices in Equations (4)–(9) to produce
Note that the primary objective of HDMDc is to determine the best-fit model matrices, A, , B, and given the data in , X, , , and [24].
Considering the definition of the Hankel matrix H for a generic single measurement time series and applying a d time shift:
we can introduce the synoptic notation:
with and being the Hankel matrices for the time series and , respectively. The and are the transformation matrices for the augmented state and inputs, with and .
Considering the matrix as the composition of the delayed inputs and outputs, and G as the global transformation matrix described in Equation (13):
we obtain
a truncated singular value decomposition (SVD) of the matrix results in the following approximation:
where the notation ˜ represents rank-p truncation of the corresponding matrix, , , and . Then, the approximation of G can be computed as
For reconstructing the approximate state matrices and , the matrix can be split in two separate components— related to the state and to the exogenous inputs:
where and .
The complete G matrix can therefore be split into
Due to the high dimensionality of the matrices, in order to obtain further optimization in the computation of the reconstructed system, a truncated SVD of the matrix results in the following approximation:
where the notation ^ represents rank-r truncation, , , and , and typically we consider . Considering the projection of the operators and on the low-dimensional space, we obtain
with and
A graphic view of the HDMDc algorithm is shown in Figure 1.
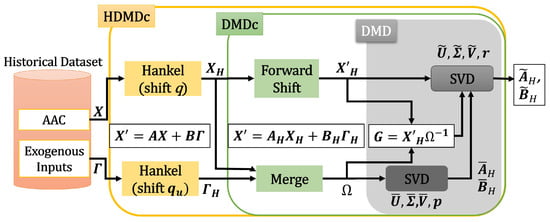
Figure 1.
HDMDc block diagram.
3.2. LSTM
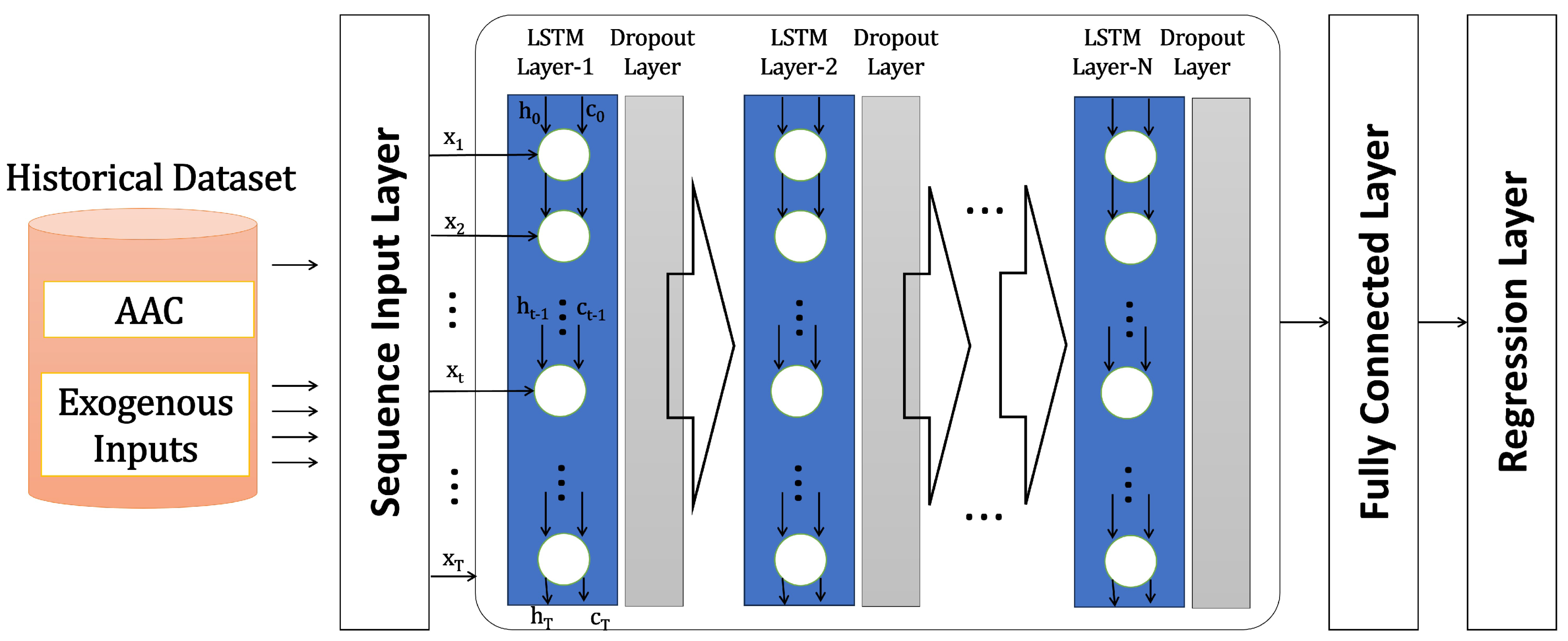
An LSTM network is a type of RNN that processes input data by iterating over time steps and updating the RNN state. The RNN state retains information from all preceding time steps. LSTM combines short-term memory with long-term memory through gate control, eliminating the standard RNN’s disappearing gradient problem and exploding gradient problem [44]. The utilization of a sequence-to-sequence LSTM neural network allows one to predict future values in a time series or sequence based on preceding time steps as input [26]. A simple LSTM architecture was applied: a sequence input layer, with its size depending on the number of input data features; LSTM hidden layers with ReLU activation and dropout implementation to avoid overfitting; a fully connected layer with the size of one, for prediction; and finally, a regression layer. The hyperparameters to be optimized are the LSTM depth (), the number of hidden units (), and the dropout probability ().
A graphic view of the LSTM architecture is shown in Figure 2.
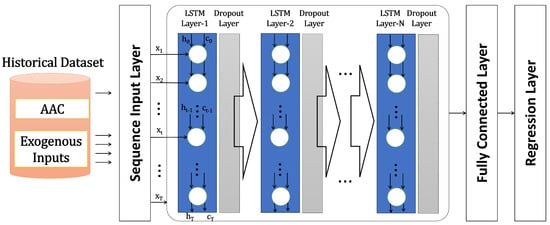
Figure 2.
Sequence-to-sequence LSTM block diagram.
4. System Model
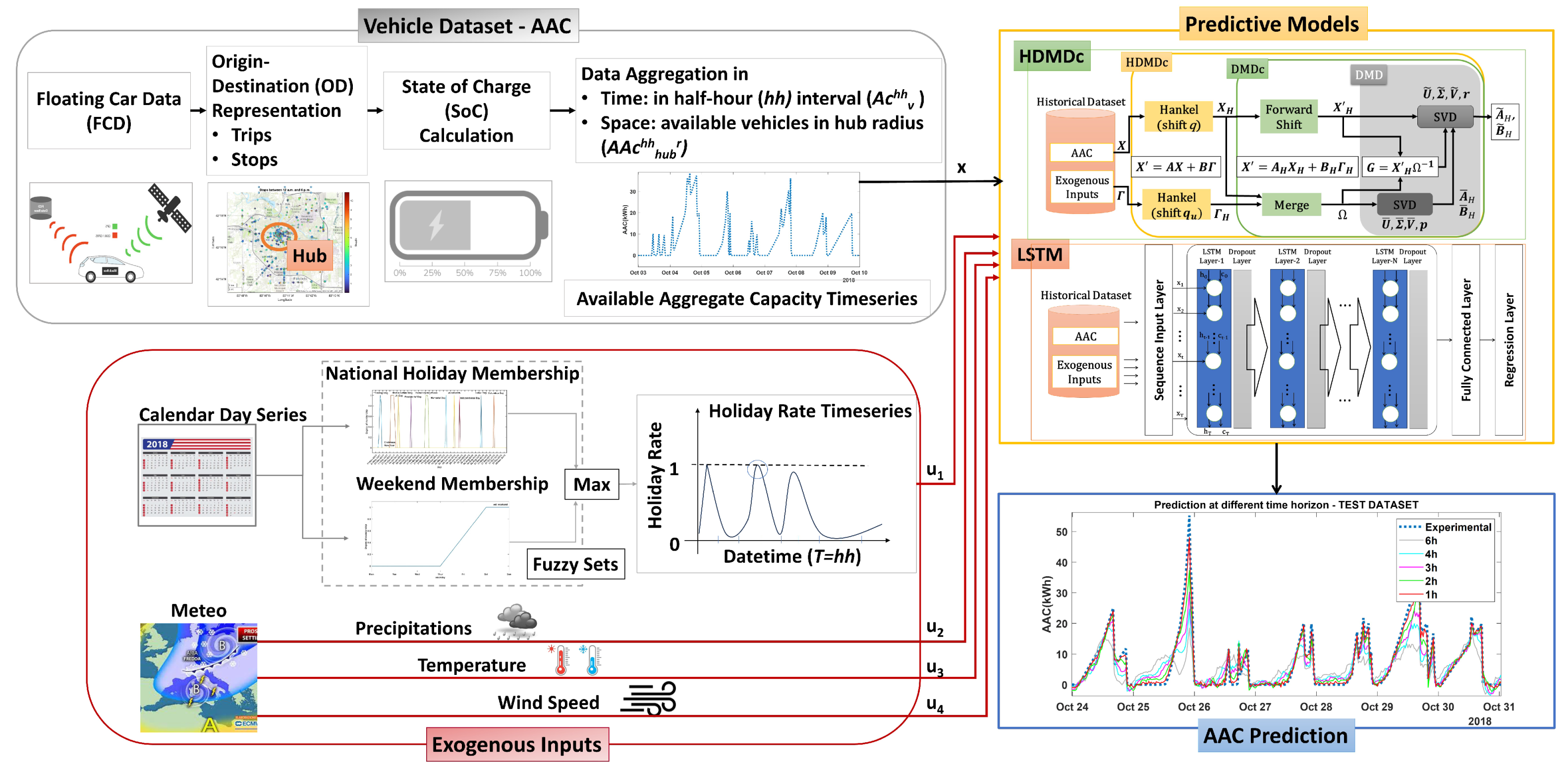
The proposed prediction model framework consists of several parts, as shown in Figure 3. The two blocks on the left refer to the data collection and pre-processing for the vehicle dataset and the extraction of the exogenous inputs. The first block comprises the acquisition of the FCD data and its description in terms of origin–destination (OD) with the aim of extracting the trips and stops and thus determining the state of charge () for each individual vehicle. A spatio-temporal aggregation is then performed to obtain the AAC time series, which is used as the target variable for the prediction models. In particular, the spatial aggregation was performed in a geographical area within a radius r from the selected hub, while the temporal aggregation was performed in half-hour () intervals to match the time scale of the intraday energy market as in most literature examples [23,27,28,32]. The second block is dedicated to extracting exogenous inputs, aiming to obtain continuous time series with sampling time. This includes fuzzy data for national holidays and weekends as well as meteorological data on precipitation, temperature, and wind speed. The core block consists of predictive models based on HDMDc and LSTM, enabling rolling predictions with different time horizons. A summary of the main variables involved is provided in Table 2.
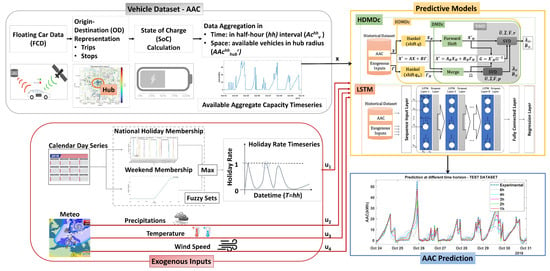
Figure 3.
AAC prediction model framework.

Table 2.
Predictive model framework variables.
4.1. Data Collection and Pre-Processing
The data collection and pre-processing stages were fundamental components of this research. Emphasis was placed on working with data obtained in real-world conditions: vehicle tracking FCD data in the domains of traffic analysis, logistics, and mobility; weather data available both as historical archives and forecasts; and well-known data such as calendar information and holidays. These data have undergone pre-processing to create a standardized format suitable for applying the algorithms under evaluation.
4.1.1. Vehicle Dataset
The vehicle energy dataset (VED) [45] is an open-access dataset of fuel- and energy-related information collected from 383 individual vehicles in Ann Arbor, MI, USA. It includes GPS records of vehicle routes and time-series data on fuel consumption, energy consumption, speed, and auxiliary energy use. The dataset covers a wide range of vehicles: 264 internal combustion engines (ICEs), 92 hybrid electric vehicles (HEVs), and 27 plug-in hybrid electric vehicles/electric vehicles (PHEV/EVs), operating in real-world conditions for one year from November 2017 to November 2018. Specifically, the following dynamic features can be selected: date, vehicle identifier, trip identifier, duration, latitude, and longitude. In addition, the HV battery is provided for the PHEVs and EVs. In order to create a benchmark dataset and considering the future projection for the EVs market, an assumption was made: the ICEs and HEVs were assumed to be EVs contributing to the V2G logic. For simplicity, they were assumed to be EVs of the same make and model (Nissan Leaf with a 40 kWh battery capacity). SoC for ICEs and HEVs was calculated as an indirect measure of distance traveled and charging stop intervals.
A first pre-processing step consisted of extracting an OD representation of the FCD data. In particular, stops with a duration of more than 30 min and trips from an origin to a destination were extracted from the VED data series. An initial visualization of the pre-processed data was made by plotting the stops on the global geographical area to identify points suitable as V2G hubs.
Figure 4 shows the density of stops during different daily intervals (0–6 a.m., 6 a.m.–12 a.m., 12 a.m.–6 p.m., and 6 p.m.–12 p.m.) and integrated over the entire data time interval. The color scale represents the duration of the stops in hours, assuming a minimum stop duration of 30 min. A candidate point of interest was selected and here referred to as , thanks to the high vehicle stop density and the location in the city center and university area, as shown in Figure 5.
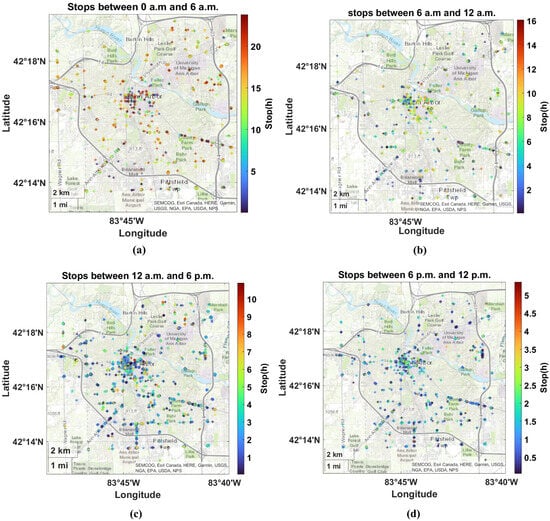
Figure 4.
Stop maps in different time intervals of the day integrated over the entire data time interval. The color bar shows the duration of the stops. The stop events started in the following time windows: (a) from 0 a.m. to 6 a.m., (b) from 6 a.m. to 12 a.m., (c) from 12 a.m. to 6 p.m., and (d) from 6 p.m. to 12 p.m.
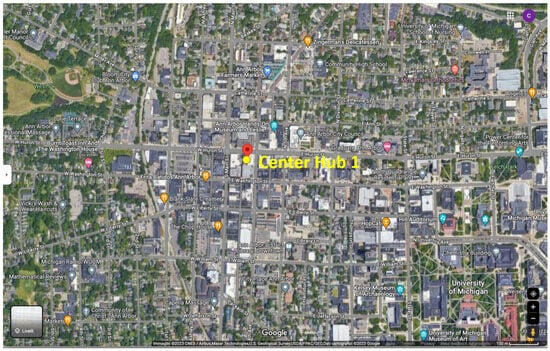
Figure 5.
Selection of the aggregation hub in the Ann Arbor Area: satellite view of area in the city center and university zone.
A second pre-processing phase consisted of calculating the for the non-electric vehicles according to [27,28]. This calculation was based on the following simplified assumptions: the vehicles’ discharge during the trips according to the distance traveled; when the vehicles stop, they feed energy into the grid if they are available for V2G, or they recharge at a rate that depends on the connection time if they are not available for V2G. The parameters used are as follows:
- Maximum battery charge at the start of the simulation:
- The minimum state of charge that must be maintained is set as a fixed value to cover the remaining part of the travel chain:
- The vehicles are considered available to supply energy to the grid when they are close to the hub and
- The energy consumption per kilometer traveled by a vehicle: km/kWh
- Rapid charging hour rating of a vehicle, typically using DC power, in the period from 7 a.m. to 7 p.m.: 50 kW
- Slow-charging hour rating of a vehicle in the time interval from 7 p.m. to 7 a.m.: 6 kW
- Efficiency of the charging process taking losses into account:
- Power rating of the export to the grid: 50 kW
In the third pre-processing step, the values were used to create a dataset aggregated in the space and time domain and to obtain time series to be used for predictive model identification. The aggregation in space refers to the assumption that the vehicles parked within a specific radius r from a selected V2G hub would connect to it. A vehicle parked within r from the hub in an interval, and respecting the requirement, is considered available () to feed energy into the V2G system in that interval. In particular, the real or simulated is used to determine the available capacity of a single vehicle (). This is defined as the capacity of each vehicle to provide energy to the grid in an period.
where the is the battery capacity. Equation (22) is considered for the available vehicles. The target feature to be predicted , i.e., the AAC in an interval and within r distance from the hub. It is defined in Equation (23):
As a result of such procedures, time series with an sampling rate can be determined with respect to the V2G hub and be fed into the dynamic prediction model.
4.1.2. Meteorological Dataset
The meteorological data can be extracted from the MeteoStat database using the Python API [46] based on the GPS coordinates of the geographical area under study. The information on precipitation in mm, temperature in °C, and wind speed in km/h can be extracted on an hourly basis for the period under investigation. The pre-processing of the meteorological information involved the imputing of the missing data, which were replaced with the average of the signal in the same week, and the resampling to the sampling interval.
4.1.3. National Holidays Dataset
State office closings for state holidays are considered additional information to be integrated into the input dataset. They are regulated by the Michigan Department of Civil Service Regulation 5a.08. Public Act 124 of 1865 is the Michigan law governing official state holidays [47,48]. Non-business days, as in Table 3, were considered in conjunction with weekend information to obtain a comprehensive holiday rate to be incorporated into the model.

Table 3.
Office of Retirement Services (ORS) non-business days.
A fuzzy model is applied in order to obtain a unified holiday rate resulting from the fuzzification of national holidays and weekend information for each day of the year [23].
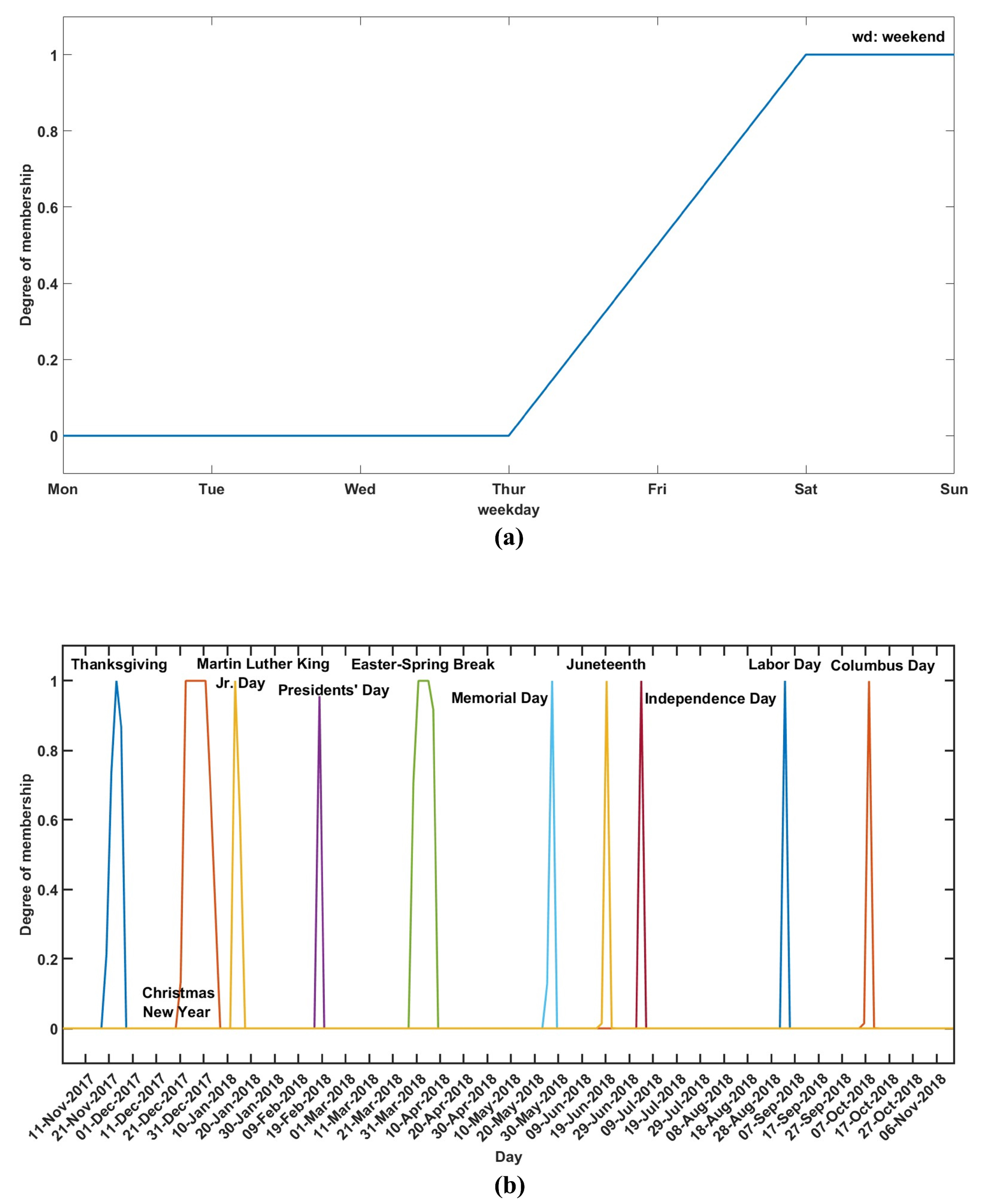
The information about holidays and weekends is represented by a discontinuous time series, which is not suitable for the identification of dynamic models. The goal of fuzzifying such inputs is to obtain a continuous time series, with time interval, that contains both weekend and holiday information. Fuzzy membership functions were developed to account for the effects that weekends and holidays might have on drivers’ habits on the days before and after these periods. The weekend and holiday membership functions, shown graphically in Figure 6a,b, respectively, were applied to the time series of calendar dates. When the weekend membership function is applied to a calendar day, it outputs a degree of truth, ranging from 0 to 1, indicating the likelihood of the day being a weekend. Similarly, applying the holiday membership function to a calendar day results in a continuous value between 0 and 1, representing the degree of truth for the day being a holiday. To create a single continuous dynamic feature that integrates both weekend and holiday information, the maximum value of these membership functions was taken.
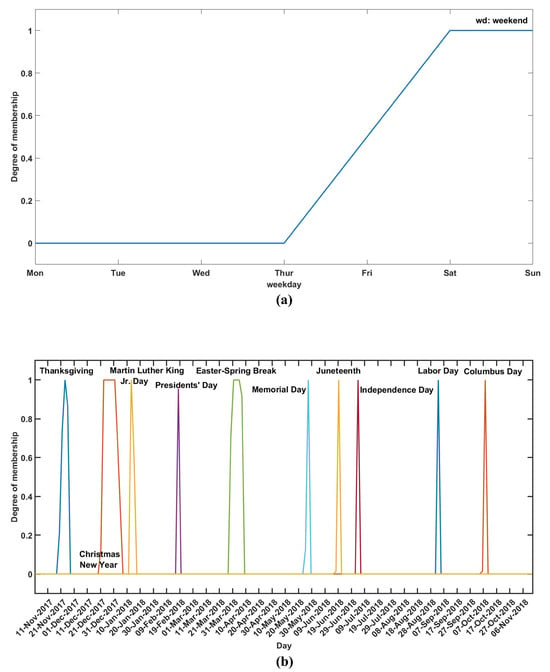
Figure 6.
Membership function for the fuzzification of the holiday rate: (a) weekend membership; (b) national holiday membership functions.
4.2. Model Prediction Analysis
Considering the prediction steps , the multi-step-ahead prediction is performed by iterating the one-step-ahead prediction times in a closed loop. This involves using the previously predicted value as an autoregressive term and feeding the inputs from the previous step into the model at each iteration, as shown in Equation (24), since the meteorological forecast and calendrical information are considered available within this time interval. During each iteration, any negative predicted values are replaced with zero and then fed into the model for the subsequent iteration.
where f is a general representation of the relationship between the rolling prediction at time -step-ahead and the previously predicted samples and the previous samples of the exogenous inputs.
4.2.1. HDMDc
The one-step-ahead predicted discrete time-series based on the Hankel transformation of the original time series (i.e., and ) and based on the identified matrices in Equations (20) and (21), and these are represented as in Equation (25):
with . The original time series is then extracted from considering only the rows with index where .
4.2.2. LSTM
The one-step-ahead time-series based on the LSTM transformation is based on a optimized structure of the network and can be represented in Equation (26) as
with being the simplified nonlinear representation of the input–output relationship in LSTM.
5. Results and Discussion
In this section, we first describe the models’ learning procedures, detailing the identification and prediction processes, and outlining the test cases. These test cases are subsequently elaborated upon in the results subsections for both HDMDc and LSTM.
5.1. Learning Procedure
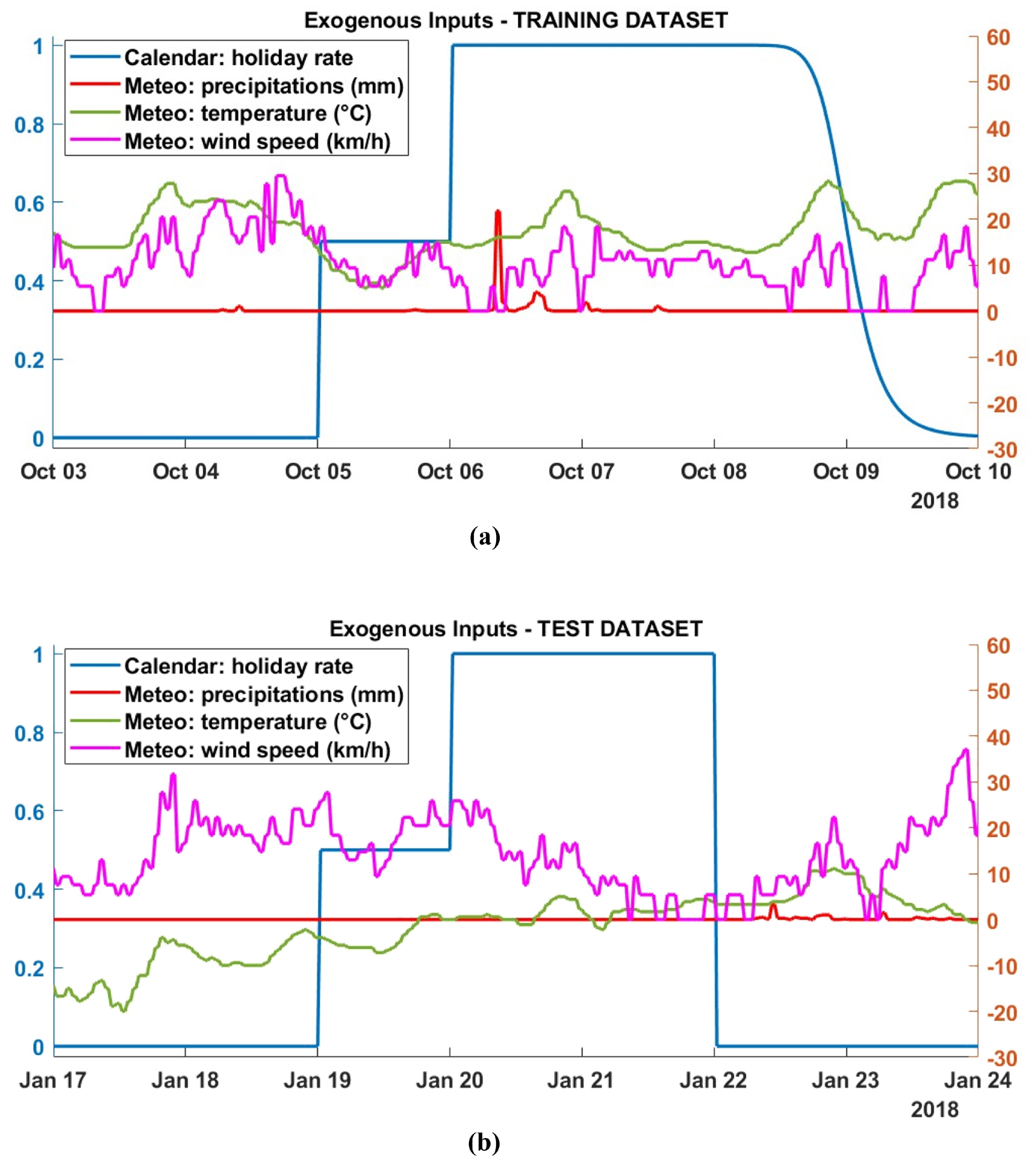
The data were divided into training (), validation (), and test data (). Specifically, in order to avoid seasonal bias and unbalanced datasets, the first two weeks per month were selected as training, then the following two weeks were divided, one for validation and one as test data. Such a choice ensures that all seasons, weekends, and national holidays are included in both the training and test phases, providing a thorough representation of diverse meteorological conditions and capturing these temporal variations across all datasets. As described in Section 4, the exogenous inputs are the fuzzified holiday rate and the meteorological information (precipitation, temperature, and wind speed). Figure 7 shows such inputs for two selected weeks: (a) from Wednesday, 3 October to Tuesday, 10 October 2018 from the training dataset and (b) from 17 to 24 January 2018 from the test dataset. The time series refers to the selected with a radius , as in Section 4.1.1 in Figure 5. It is provided as target and autoregressive term in the model identification process. In particular, the training and validation sessions were performed for one-step-ahead prediction, i.e., at each time step in the input sequences, the models learn to predict the value of the subsequent time step.
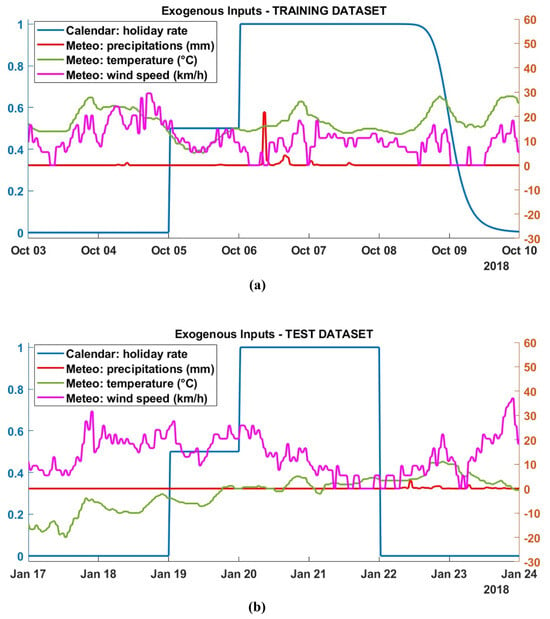
Figure 7.
Exogenous inputs: left y-axis—holiday rate (blue); right y-axis—precipitation in mm (red), temperature in °C (green), and wind speed in km/h (magenta). (a) Selection of a training set week (Wednesday 3 to Tuesday 10 October 2018). (b) Selection of a test set week (Wednesday 17 to Tuesday 24 January 2018).
Parameters choice, training, and test cases are here discussed for the two different predictive methods, HDMDc and LSTM, in Section 5.2 and Section 5.3, respectively. Both models’ performances in the training and test dataset are shown for different prediction steps (1 h (), 2 h (), 3 h (), 4 h ()) and compared in terms of KPIs, i.e., mean square error (), root mean square error () and correlation coefficient (R), predicted time series and, specifically for the HDMDc, also regression plots.
5.2. HDMDc
As a first step, the state and input variables have been extended by adding a series of delay coordinates to the state and inputs as described in Section 3. These delays, q and , as in the Equations (1) and (2), were both chosen to be equal to each other [43], with a value of 48 corresponding to 24 h. This choice was made based on considerations of the daily periodicity of the data for both the state and the inputs. The system order therefore increased from 1, given by the single state variable , to , as in Equation (12). The number of exogenous inputs increased from to . As a second step, once the model structure was determined, the HDMDc model was identified using the training dataset, and the state-space model matrices were obtained as in the Equations (20) and (21). Rolling -step-ahead prediction of the AAC signal was therefore performed by iterating Equation (25) for both the training and test datasets. The chosen set of prediction steps was , corresponding to 1, 2, 3, and 4 h.
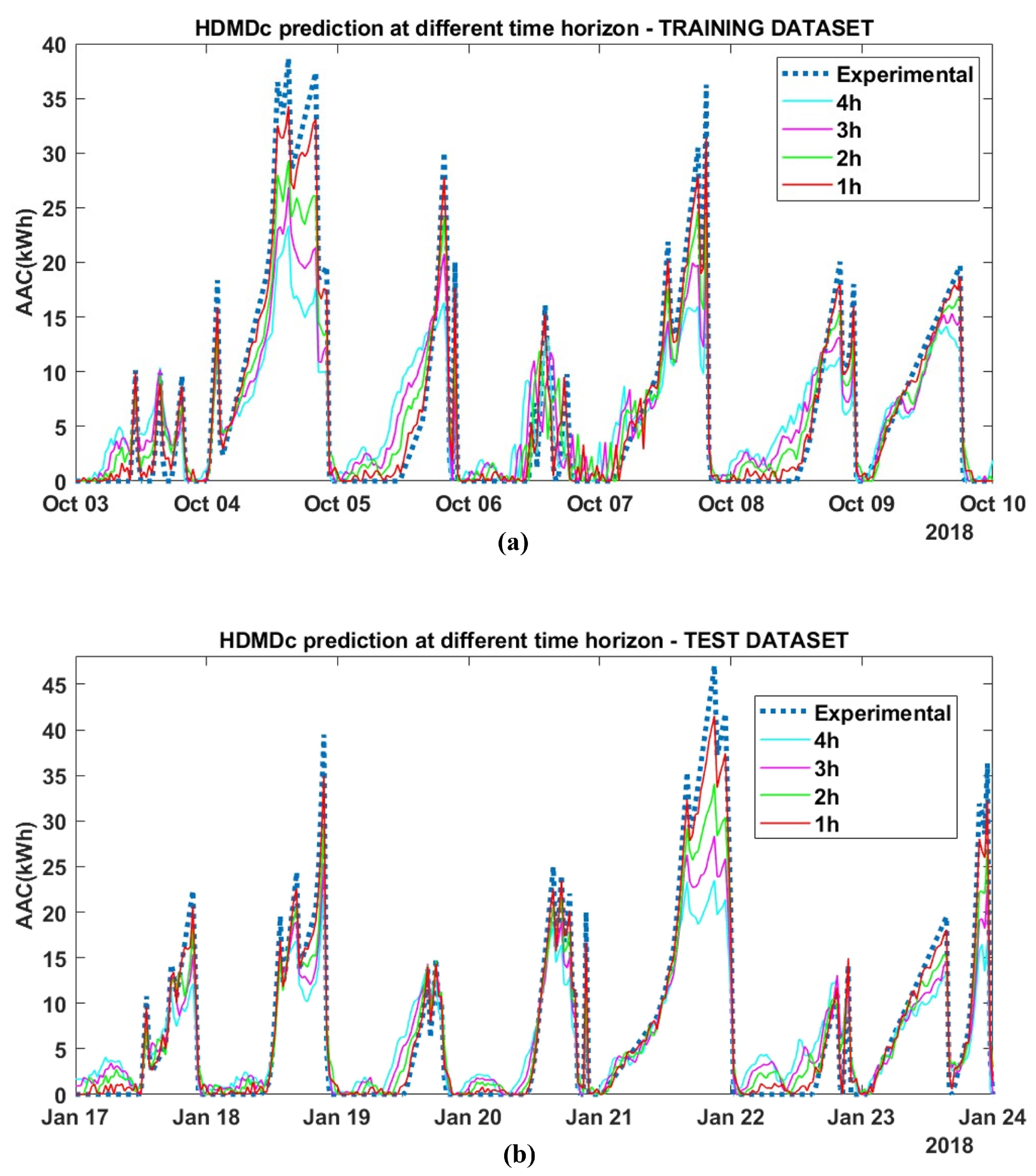
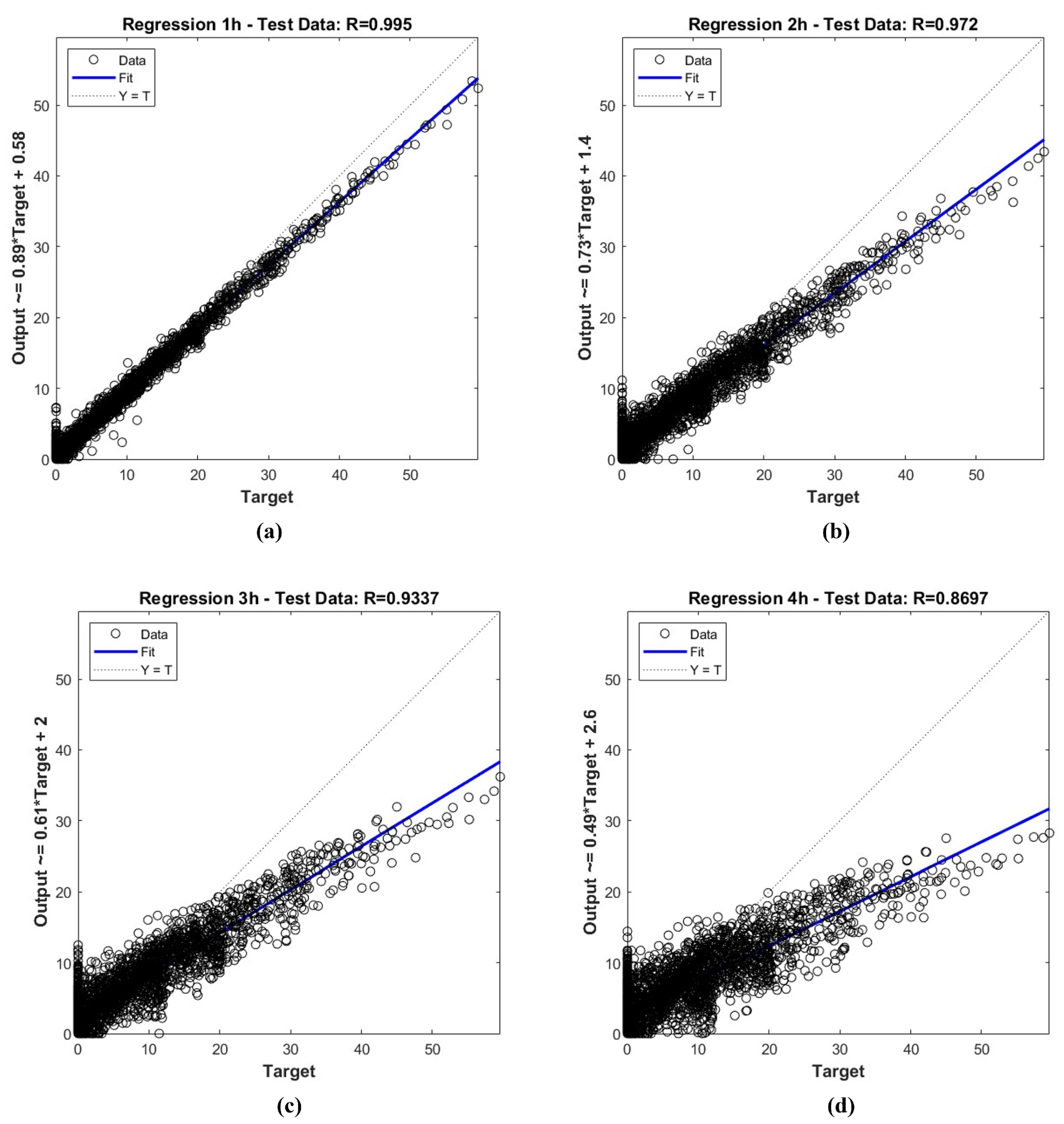
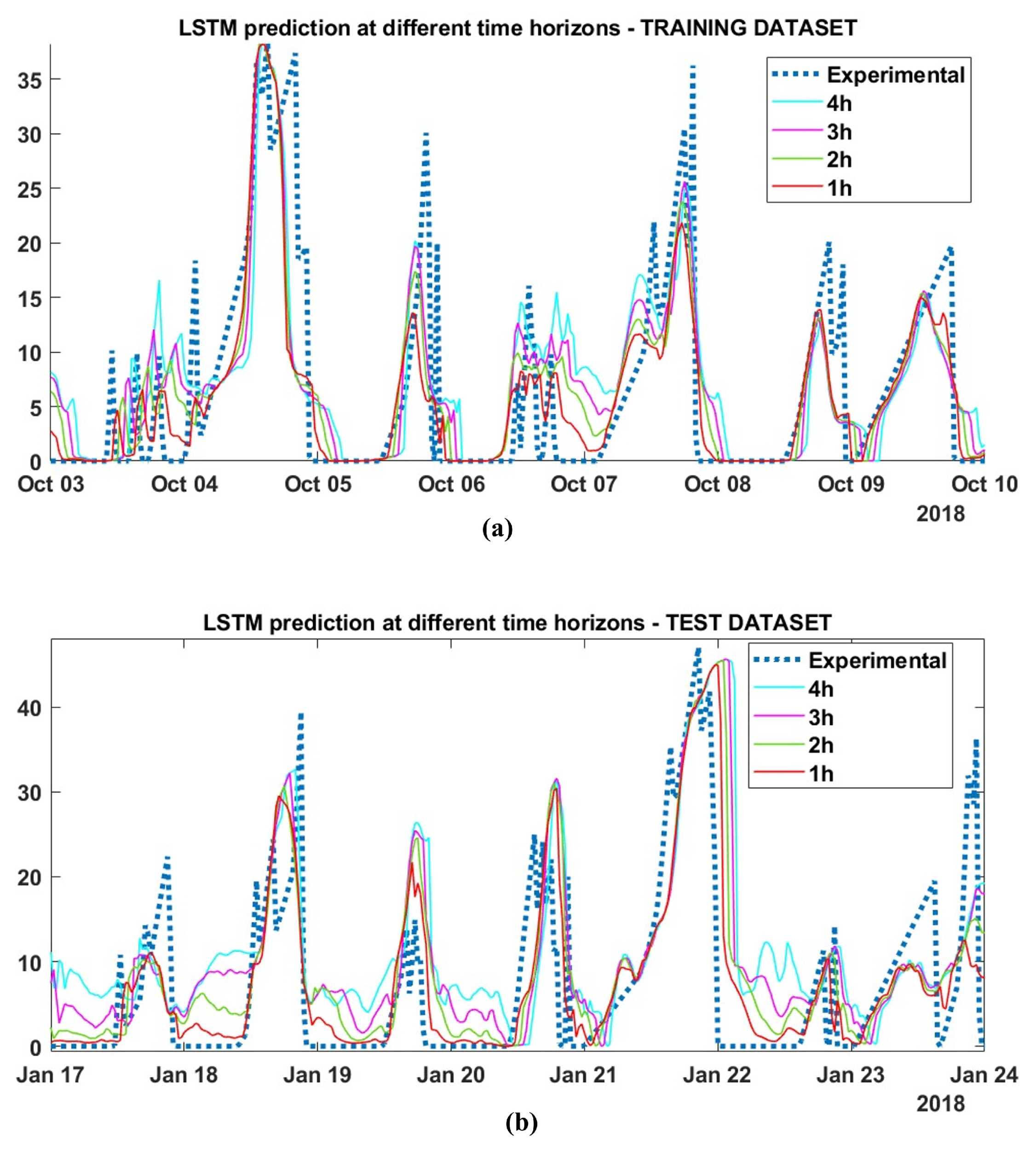
The key performance indicators are listed in Table 4 for both the training and test datasets. HDMDc performs well on both datasets for predictions up to 4 h. For long prediction horizons, the HDMDc shows some limitations: It underestimates the target AAC but maintains a good correlation (>) to the target. This observation, which can be derived from the macroscopic key performance indicators, is confirmed by the comparison between the predicted AAC time series and the experimental target value, as shown in Figure 8 for two selected weekly examples: (a) the training dataset and (b) the test datasets. The rising/falling slopes and peak shapes are also maintained for long prediction horizons, albeit on a lower scale. The same content, extended to the entire test dataset, is visible in the regression plots in Figure 9c,d, where the scatter is closely related to the regression line, even if underestimated. This could not be a critical issue from the energy provider’s perspective, since the primary interest is predicting the minimum AAC to sell to the energy market to avoid penalties.

Table 4.
HDMDc performances in the Training and Test Dataset.
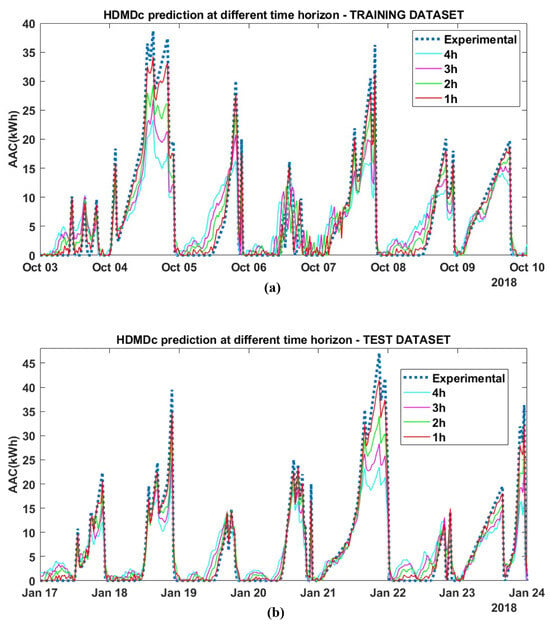
Figure 8.
HDMDc time series prediction with different time horizons: 1 h, 2 h, 3 h, and 4 h. (a) Selection of a training set week (Wednesday 3 to Tuesday 10 October 2018). (b) Selection of a test set week (Wednesday 17 to Tuesday 24 January 2018).
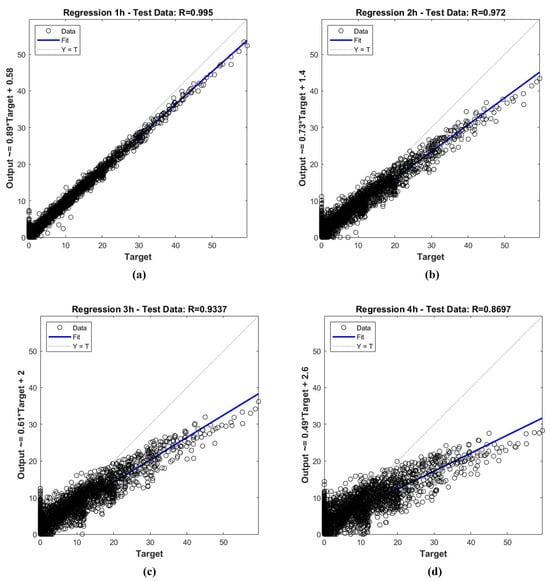
Figure 9.
HDMDc regression plots for prediction with different time horizons of the test dataset: (a) 1 h, (b) 2 h, (c) 3 h, and (d) 4 h.
These detailed observations provide valuable insights: the training dataset is well-designed, covering multiple system behaviors and indicating that the exogenous input features are relevant for predicting AAC [23]. The HDMDc effectively captures the global dynamics of the system without overfitting, consistent with Koopman theory. This theory allows for identifying a global model that operates properly across multiple system operating points, highlighting the advantage of the data-driven linear state-space model over nonlinear black-box models, as described in Section 2. These characteristics make the integration of exogenous input data sources and HDMDc a reliable candidate for automated prediction processes, supporting decision-making for energy providers and managing multiple energy sources in smart grids.
5.3. LSTM
In a first step, model optimization to determine the hyperparameters was performed utilizing a Bayesian algorithm using the training and validation datasets. The optimization was based on the minimization of the correlation coefficient (R) as a metric. The hyperparameter ranges were set to
- the LSTM depth between 1 and 3
- the number of hidden units between 50 and 350
- the dropout probability between and
- initial learn rate between and
The hyperparameters optimized in terms of R for the validation datasets were found to be 1 LSTM layers, 176 hidden units per layer, a dropout layer, and a initial learn rate.
In a second step, after the model structure was determined and identified by the optimization procedure, the LSTM model was used to reconstruct the AAC signal for the -step-ahead prediction by closed loop iteration for both the training and test datasets. As mentioned above, the negative values of the prediction were replaced by zero and used as an autoregressive sample for the subsequent prediction step.
Finally, the performance of LSMR prediction over the different selected time horizons was evaluated and compared. The key performance indicators are listed in Table 5 for the training and test datasets.The LSTM model performs acceptably on the training datasets for predictions up to 2 h and maintains a correlation of . However, its performance deteriorates rapidly for longer prediction horizons. In the test dataset, the model fails to achieve satisfactory performance and shows a poor correlation coefficient () for a prediction horizon of 1 hour, with a rapid decline for longer horizons. This observation derived from the macroscopic KPI is confirmed by the comparison between the predicted AAC time series and the experimental target values. Figure 10 show the predicted timeseries for two selected weekly examples: (a) the training dataset and (b) the test dataset. Among the nonlinear black-box models, the LSTM shows capability in managing integrated data sources and provides good performance for short-term predictions, as the authors have shown in a previous work [23], but as a limitation, it loses accuracy for longer predictions.

Table 5.
LSTM (1 layers, 176 hidden units, dropout layer, initial learn rate) performances on the training and test dataset.
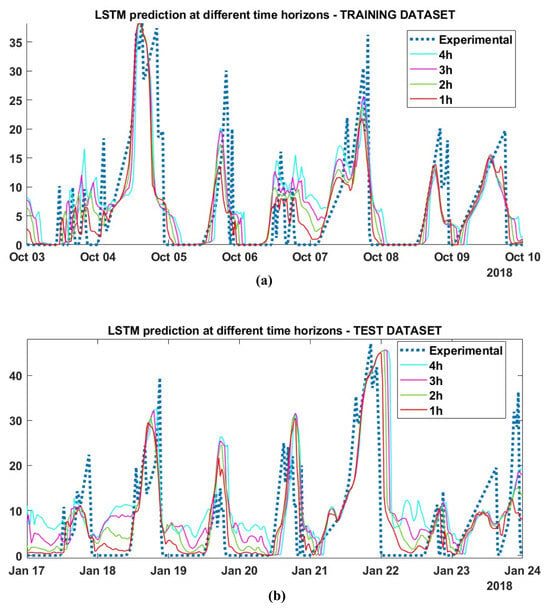
Figure 10.
LSTM time series prediction with different time horizons: 1 h, 2 h, 3 h, and 4 h. (a) Selection of a training set week (Wednesday 3 to Tuesday 10 October 2018). (b) Selection of a test set week (Wednesday 17 to Tuesday 24 January 2018).
6. Conclusions
This paper highlights the critical importance of forecasting energy availability for effective V2G implementation and underscores the role of interpretable yet computationally feasible methods like HDMDc in addressing this challenge. By employing such methodologies, stakeholders can better manage energy resources, optimize grid operations, and accelerate the transition towards a sustainable energy future.
The proposed methodological framework includes an initial pre-processing step aimed at obtaining timeseries that can be fed into the model identification process. In particular, the innovative contribution to the current body of literature resides in the integration of FCD tracking data, meteorological, and calendar variables through a fuzzy input set that includes national holidays and weekends. By pre-processing and integrating such contextual components, our methodology provides a more comprehensive insight into the intricate relationships within the V2G system.
The core of this work lies in the implementation and comparison of two different data-driven dynamic approaches for AAC rolling prediction over finite time horizons: the linear state space model based on HDMDc and the nonlinear black-box approach based on LSTM.
First, the design of the dataset, accounting for weekends, holidays, and various meteorological conditions and spanning one year, effectively captures multiple behaviors of the system due to intra- and inter-period variability. The good performance of HDMDc, along with previous studies [23], underscores the relevance of exogenous inputs in the AAC prediction process.
Regarding the two approaches, HDMDc demonstrates satisfactory performance and reliability over long prediction horizons, although it may exhibit some underestimation in long-term predictions. Nevertheless, it maintains a good and acceptable correlation within the application domain, which is crucial for energy providers who prioritize accurate prediction of minimum values. In contrast, LSTM’s effectiveness is limited to short-term predictions. This difference can be attributed to the inherent capabilities of the methods: although LSTM networks are effective for stochastic time series prediction due to the long-short-term memory effect, HDMDc, as a data-driven spatio-temporal method, decomposes a system into modes with varying temporal behaviors. This allows HDMDc to capture the global dynamics without overfitting, thereby extending its effectiveness over longer time horizons prediction. In addition, the state-space representation is prone to model order reduction and is able to reveal complex relationships between external features and electrical target variables moving towards model interpretation.
In conclusion, combining preliminary data processing, HDMDc, and LSTM predictive models within a robust methodological framework offers a comprehensive solution for predicting energy availability for V2G integration in complex environments.
HDMDc, in particular, has demonstrated its effectiveness as a data-driven state-space representation, providing several advantages and potential future research directions. This model could be trained on selected V2G hubs and then applied to different V2G hubs within the same category, based on the type of area activity (e.g., residential, commercial, industrial, or recreational), suggesting the transferability of the prediction framework.
Future research could also focus on developing a comprehensive decision support framework for smart energy systems that integrate multiple energy sources such as renewables, buildings, electric vehicles, and mobility, while accounting for uncertainties in electricity prices and energy market events.
Author Contributions
Conceptualization, L.P., F.S. and M.G.X.; methodology, L.P., F.S. and M.G.X.; software, F.S.; validation, L.P., F.S. and M.G.X.; formal analysis, L.P., F.S. and M.G.X.; investigation, L.P., F.S. and M.G.X.; resources, L.P. and M.G.X.; data curation, L.P., F.S. and M.G.X.; writing—original draft preparation, F.S.; writing—review and editing, L.P., F.S., M.G.X. and G.N.; visualization, F.S.; supervision, L.P., F.S. and M.G.X.; project administration, L.P., M.G.X. and G.N.; funding acquisition, L.P., M.G.X. and G.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was funded by the MASE—Consiglio Nazionale delle Ricerche within the project RICERCA DI SISTEMA 22-24-21.2 Progetto Integrato Tecnologie di accumulo elettrochimico e termico. CUP Master: B53C22008540001, UNIME-DI-RdS22-24:J43C23000670001 Linea 13.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| V2G | Vehicle-to-Grid |
| SG | Smart Grids |
| AAC | Available Aggregate Capacity |
| IoT | Internet of Things |
| FCD | Floating Car Data |
| OD | Origin-Destination |
| ICE | Internal Combustion Engine |
| HEV | Hybrid Electric Vehicle |
| PHEV | Plug-in Hybrid Electric Vehicle |
| EV | Electric vehicle |
| SoC | State of Charge |
| hh | Half Hour |
| HDMDc | Hankel Dynamic Mode Decomposition with Control |
| LSTM | Long Short-Term Memory |
References
- International Energy Agency. By 2030 EVs Represent More Than 60% of Vehicles Sold Globally, and Require an Adequate Surge in Chargers Installed in Buildings. In Proceedings of the IEA, Paris, 2022. Available online: https://www.iea.org/reports/by-2030-evs-represent-more-than-60-of-vehicles-sold-globally-and-require-an-adequate-surge-in-chargers-installed-in-buildings (accessed on 20 June 2024).
- International Energy Agency. Net Zero by 2050. A Roadmap for the Global Energy Sector. In Proceedings of the IEA, Paris, 2021. Available online: https://www.iea.org/reports/net-zero-by-2050 (accessed on 20 June 2024).
- Kamble, S.G.; Vadirajacharya, K.; Patil, U.V. Decision Making in Power Distribution System Reconfiguration by Blended Biased and Unbiased Weightage Method. J. Sens. Actuator Netw. 2019, 8, 20. [Google Scholar] [CrossRef]
- Ding, B.; Li, Z.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Jin, X.; Sun, H. A CCP-based distributed cooperative operation strategy for multi-agent energy systems integrated with wind, solar, and buildings. Appl. Energy 2024, 365, 123275. [Google Scholar] [CrossRef]
- Zhang, R.; Chen, Y.; Li, Z.; Jiang, T.; Li, X. Two-stage robust operation of electricity-gas-heat integrated multi-energy microgrids considering heterogeneous uncertainties. Appl. Energy 2024, 371, 123690. [Google Scholar] [CrossRef]
- Zhang, H.; Li, Z.; Xue, Y.; Chang, X.; Su, J.; Wang, P.; Guo, Q.; Sun, H. A Stochastic Bi-level Optimal Allocation Approach of Intelligent Buildings Considering Energy Storage Sharing Services. IEEE Trans. Consum. Electron. 2024, 1. [Google Scholar] [CrossRef]
- Naja, R.; Soni, A.; Carletti, C. Electric Vehicles Energy Management for Vehicle-to-Grid 6G-Based Smart Grid Networks. J. Sens. Actuator Netw. 2023, 12, 79. [Google Scholar] [CrossRef]
- Mojumder, M.R.H.; Ahmed Antara, F.; Hasanuzzaman, M.; Alamri, B.; Alsharef, M. Electric Vehicle-to-Grid (V2G) Technologies: Impact on the Power Grid and Battery. Sustainability 2022, 14, 13856. [Google Scholar] [CrossRef]
- Bortotti, M.F.; Rigolin, P.; Udaeta, M.E.M.; Grimoni, J.A.B. Comprehensive Energy Analysis of Vehicle-to-Grid (V2G) Integration with the Power Grid: A Systemic Approach Incorporating Integrated Resource Planning Methodology. Appl. Sci. 2023, 13, 11119. [Google Scholar] [CrossRef]
- Lillebo, M.; Zaferanlouei, S.; Zecchino, A.; Farahmand, H. Impact of large-scale EV integration and fast chargers in a Norwegian LV grid. J. Eng. 2019, 2019, 5104–5108. [Google Scholar] [CrossRef]
- Deb, S.; Tammi, K.; Kalita, K.; Mahanta, P. Impact of Electric Vehicle Charging Station Load on Distribution Network. Energies 2018, 11, 178. [Google Scholar] [CrossRef]
- Grasel, B.; Baptista, J.; Tragner, M. The Impact of V2G Charging Stations (Active Power Electronics) to the Higher Frequency Grid Impedance. Sustain. Energy Grids Netw. 2024, 38, 101306. [Google Scholar] [CrossRef]
- Fachrizal, R.; Qian, K.; Lindberg, O.; Shepero, M.; Adam, R.; Widén, J.; Munkhammar, J. Urban-scale energy matching optimization with smart EV charging and V2G in a net-zero energy city powered by wind and solar energy. eTransportation 2024, 20, 100314. [Google Scholar] [CrossRef]
- Karmaker, A.K.; Prakash, K.; Siddique, M.N.I.; Hossain, M.A.; Pota, H. Electric vehicle hosting capacity analysis: Challenges and solutions. Renew. Sustain. Energy Rev. 2024, 189, 113916. [Google Scholar] [CrossRef]
- Paine, G. Understanding the True Value of V2G. An Analysis of the Customers and Value Streams for V2G in the UK, Cenex, 2019. Available online: https://www.cenex.co.uk/app/uploads/2019/10/True-Value-of-V2G-Report.pdf (accessed on 20 June 2024).
- Afentoulis, K.D.; Bampos, Z.N.; Vagropoulos, S.I.; Keranidis, S.D.; Biskas, P.N. Smart charging business model framework for electric vehicle aggregators. Appl. Energy 2022, 328, 120179. [Google Scholar] [CrossRef]
- Barbero, M.; Corchero, C.; Canals Casals, L.; Igualada, L.; Heredia, F.J. Critical evaluation of European balancing markets to enable the participation of Demand Aggregators. Appl. Energy 2020, 264, 114707. [Google Scholar] [CrossRef]
- Dixon, J.; Bukhsh, W.; Bell, K.; Brand, C. Vehicle to grid: Driver plug-in patterns, their impact on the cost and carbon of charging, and implications for system flexibility. eTransportation 2022, 13, 100180. [Google Scholar] [CrossRef]
- Comi, A.; Rossolov, A.; Polimeni, A.; Nuzzolo, A. Private Car O-D Flow Estimation Based on Automated Vehicle Monitoring Data: Theoretical Issues and Empirical Evidence. Information 2021, 12, 493. [Google Scholar] [CrossRef]
- Li, M.; Wang, Y.; Peng, P.; Chen, Z. Toward Efficient Smart Management: A Review of Modeling and Optimization Approaches in Electric Vehicle-Transportation Network-Grid Integration. Green Energy Intell. Transp. 2024, 100181. [Google Scholar] [CrossRef]
- Bakhshi, V.; Aghabayk, K.; Parishad, N.; Shiwakoti, N. Evaluating Rainy Weather Effects on Driving Behaviour Dimensions of Driving Behaviour Questionnaire. J. Adv. Transp. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Gim, T.H.T. SEM application to the household travel survey on weekends versus weekdays: The case of Seoul, South Korea. Eur. Transp. Res. Rev. 2018, 10, 11. [Google Scholar] [CrossRef]
- Napoli, G.; Patanè, L.; Sapuppo, F.; Xibilia, M.G. A Comprehensive Data Analysis for Aggregate Capacity Forecasting in Vehicle-to-Grid Applications. In Proceedings of the 8th International Conference on Control, Automation and Diagnosis (ICCAD’24), Paris, France, 15–17 May 2024. [Google Scholar]
- Proctor, J.L.; Brunton, S.L.; Kutz, J.N. Dynamic Mode Decomposition with Control. SIAM J. Appl. Dyn. Syst. 2016, 15, 142–161. [Google Scholar] [CrossRef]
- Swathi Prathaa, P.; Rambabu, S.; Ramachandran, A.; Krishna, U.V.; Menon, V.K.; Lakshmikumar, S. Deep Learning and Dynamic Mode Decomposition for Inflation and Interest Rate Forecasting. In Proceedings of the 2022 13th International Conference on Computing Communication and Networking Technologies (ICCCNT), Kharagpur, India, 3–5 October 2022; pp. 1–7. [Google Scholar] [CrossRef]
- Curreri, F.; Patanè, L.; Xibilia, M.G. RNN- and LSTM-Based Soft Sensors Transferability for an Industrial Process. Sensors 2021, 21, 823. [Google Scholar] [CrossRef]
- Shipman, R.; Roberts, R.; Waldron, J.; Rimmer, C.; Rodrigues, L.; Gillott, M. Online Machine Learning of Available Capacity for Vehicle-to-Grid Services during the Coronavirus Pandemic. Energies 2021, 14, 7176. [Google Scholar] [CrossRef]
- Shipman, R.; Roberts, R.; Waldron, J.; Naylor, S.; Pinchin, J.; Rodrigues, L.; Gillott, M. We got the power: Predicting available capacity for vehicle-to-grid services using a deep recurrent neural network. Energy 2021, 221, 119813. [Google Scholar] [CrossRef]
- Mustavee, S.; Agarwal, S.; Enyioha, C.; Das, S. A linear dynamical perspective on epidemiology: Interplay between early COVID-19 outbreak and human mobility. Nonlinear Dyn. 2022, 109, 1233–1252. [Google Scholar] [CrossRef] [PubMed]
- Shabab, K.R.; Mustavee, S.; Agarwal, S.; Zaki, M.H.; Das, S. Exploring DMD-type Algorithms for Modeling Signalised Intersections. arXiv 2021, arXiv:2107.06369v1. [Google Scholar]
- Das, S.; Mustavee, S.; Agarwal, S.; Hasan, S. Koopman-Theoretic Modeling of Quasiperiodically Driven Systems: Example of Signalized Traffic Corridor. IEEE Trans. Syst. Man Cybern. Syst. 2023, 53, 4466–4476. [Google Scholar] [CrossRef]
- Graham, J.; Teng, F. Vehicle-to-Grid Plug-in Forecasting for Participation in Ancillary Services Markets. In Proceedings of the 2023 IEEE Belgrade PowerTech, Belgrade, Serbia, 25–29 June 2023. [Google Scholar] [CrossRef]
- Xu, M.; Ren, H.; Chen, P.; Xin, G. On the V2G capacity of shared electric vehicles and its forecasting through MAML-CNN-LSTM-Attention algorithm. IET Gener. Transm. Distrib. 2024, 18, 1158–1171. [Google Scholar] [CrossRef]
- Nogay, H.S. Estimating the aggregated available capacity for vehicle to grid services using deep learning and Nonlinear Autoregressive Neural Network. Sustain. Energy Grids Netw. 2022, 29, 100590. [Google Scholar] [CrossRef]
- Perry, D.; Wang, N.; Ho, S.S. Energy Demand Prediction with Optimized Clustering-Based Federated Learning. In Proceedings of the 2021 IEEE Global Communications Conference (GLOBECOM), Madrid, Spain, 7–11 December 2021; pp. 1–6. [Google Scholar] [CrossRef]
- Li, S.; Gu, C.; Li, J.; Wang, H.; Yang, Q. Boosting Grid Efficiency and Resiliency by Releasing V2G Potentiality through a Novel Rolling Prediction-Decision Framework and Deep-LSTM Algorithm. IEEE Syst. J. 2021, 15, 2562–2570. [Google Scholar] [CrossRef]
- Mao, M.; Zhang, S.; Chang, L.; Hatziargyriou, N.D. Schedulable capacity forecasting for electric vehicles based on big data analysis. J. Mod. Power Syst. Clean Energy 2019, 7, 1651–1662. [Google Scholar] [CrossRef]
- Gautam, A.; Verma, A.K.; Srivastava, M. A Novel Algorithm for Scheduling of Electric Vehicle Using Adaptive Load Forecasting with Vehicle-to-Grid Integration. In Proceedings of the 2019 8th International Conference on Power Systems (ICPS), Jaipur, India, 20–22 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Amara-Ouali, Y.; Goude, Y.; Hamrouche, B.; Bishara, M. A Benchmark of Electric Vehicle Load and Occupancy Models for Day-Ahead Forecasting on Open Charging Session Data. In Proceedings of the Thirteenth ACM International Conference on Future Energy Systems, New York, NY, USA, 11–16 May 2022; pp. 193–207. [Google Scholar] [CrossRef]
- Jahromi, S.N.; Abdollahi, A.; Heydarian-Forushani, E.; Shafiee, M. A Comprehensive Framework for Predicting Electric Vehicle’s Participation in Ancillary Service Markets; IET Smart Grid: London, UK, 2024. [Google Scholar]
- Schläpfer, M.; Chew, H.J.; Yean, S.; Lee, B.S. Using Mobility Patterns for the Planning of Vehicle-to-Grid Infrastructures that Support Photovoltaics in Cities. arXiv 2021, arXiv:2112.15006. [Google Scholar]
- Zeng, T.; Moura, S.; Zhou, Z. Joint Mobility and Vehicle-to-Grid Coordination in Rebalancing Shared Mobility-on-Demand Systems. IFAC PapersOnLine 2023, 56, 6642–6647. [Google Scholar] [CrossRef]
- Patanè, L.; Sapuppo, F.; Xibilia, M.G. Soft Sensors for Industrial Processes Using Multi-Step-Ahead Hankel Dynamic Mode Decomposition with Control. Electronics 2024, 13, 3047. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Oh, G.; Leblanc, D.J.; Peng, H. Vehicle Energy Dataset (VED), a Large-Scale Dataset for Vehicle Energy Consumption Research. IEEE Trans. Intel. Trans. Sys. 2022, 23, 3302–3312. [Google Scholar] [CrossRef]
- Meteo Stat Phyton API. Available online: https://dev.meteostat.net/python/ (accessed on 1 October 2023).
- Ann Arbour School Breaks. Available online: https://annarborwithkids.com/articles/winter-spring-break-schedules-2022/ (accessed on 1 October 2023).
- Michigan ORS Non-Business Days. Available online: https://www.michigan.gov/psru/ors-non-business-days (accessed on 1 October 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).