SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus
Abstract
1. Introduction
2. Results
2.1. Haplotype Block Construction
2.2. Estimates of Genetic Parameters Based on Pedigree
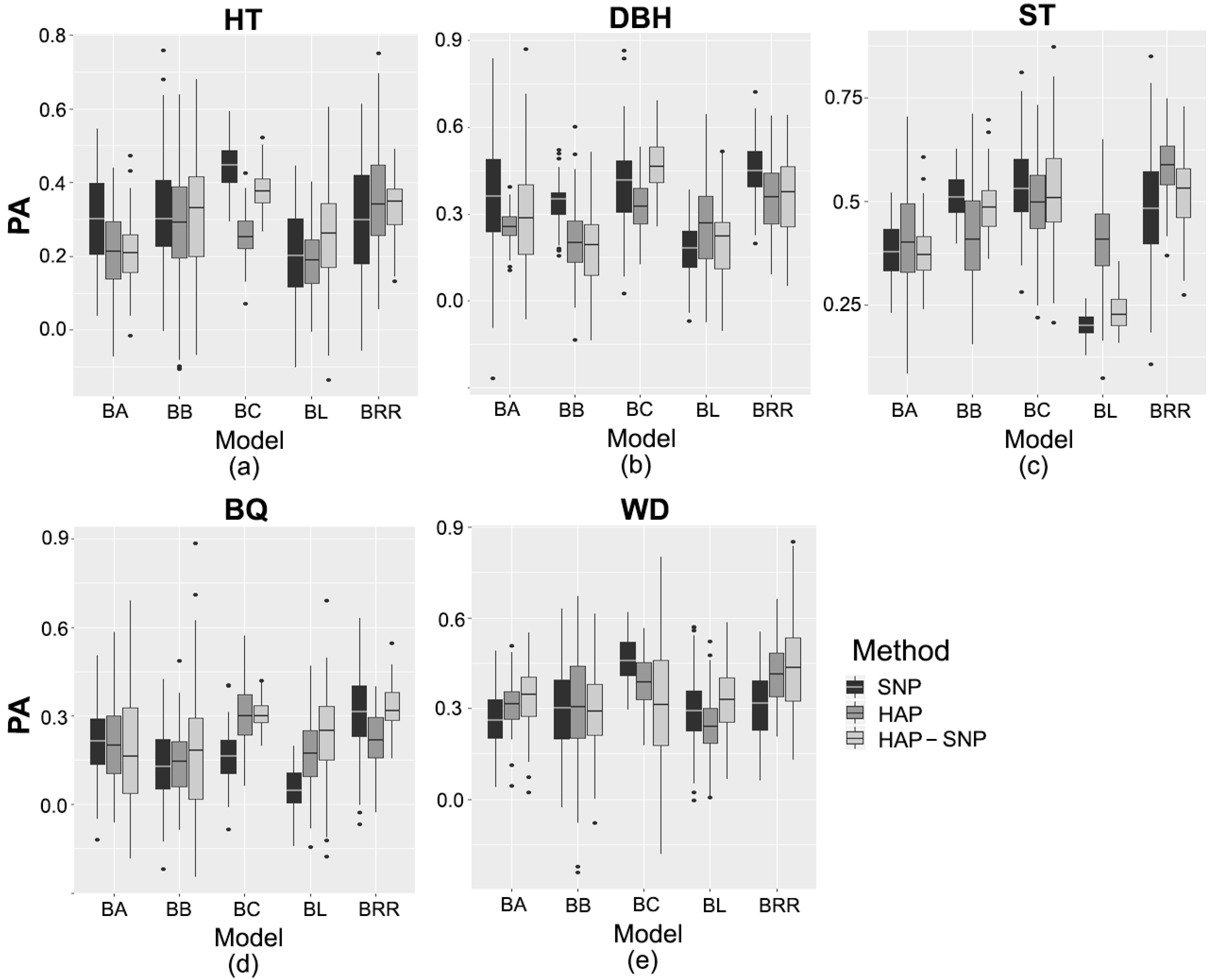
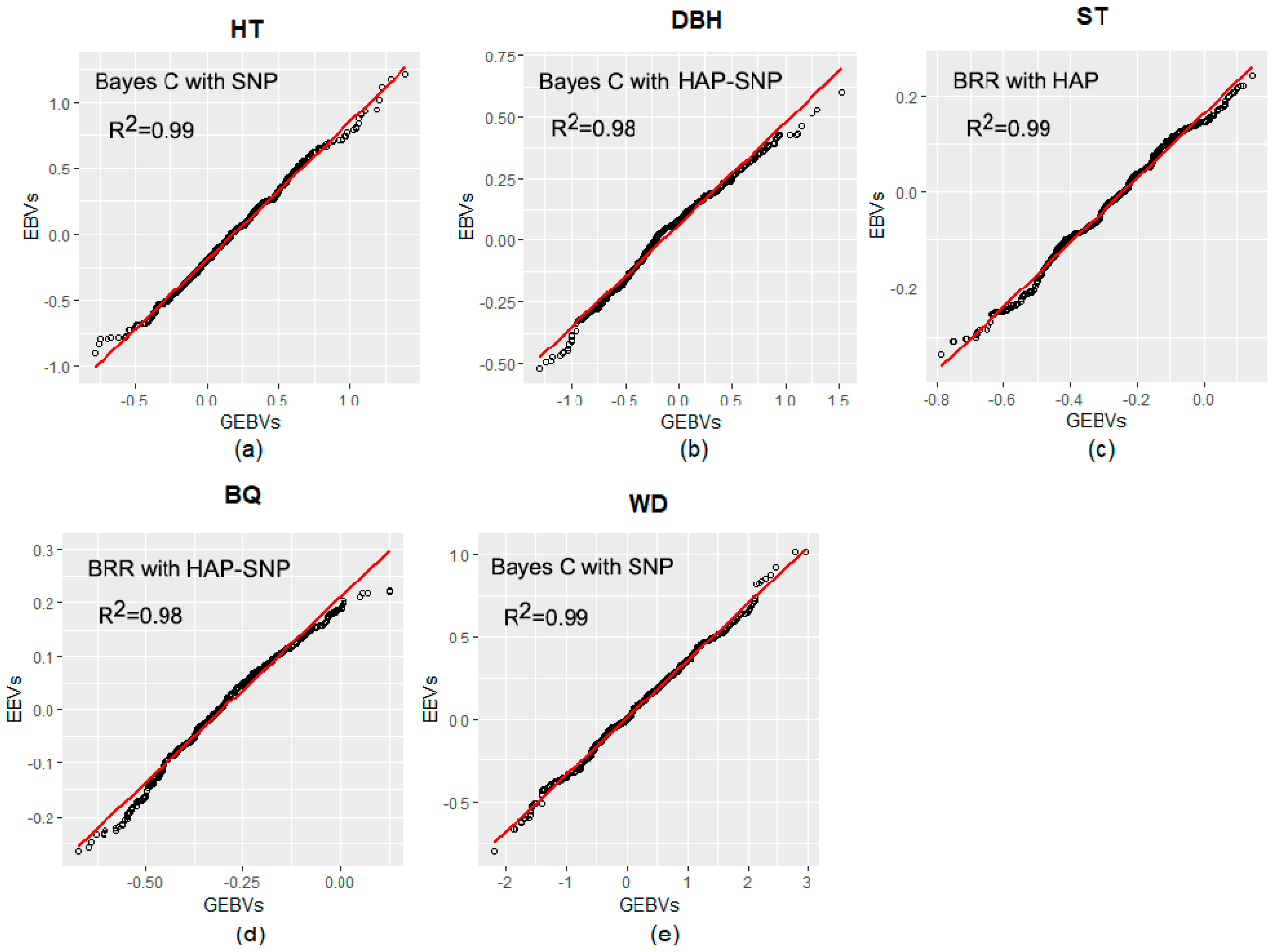
2.3. Prediction Based on Genomic Data
3. Discussion
3.1. Haplotype Blocks Construction
3.2. Performance of Pedigree and Genomic Prediction Models
4. Materials and Methods
4.1. Trial Conditions and Phenotyping
4.2. Genotyping, Linkage Disequilibrium and Haplotype Blocks
4.3. Prediction Models Based on Pedigree and Genomic Data
4.4. Heritability and Genetic Gain
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Meuwissen, T.H.; Hayes, B.J.; Goddard, M.E. Prediction of total genetic value using genome-wide dense marker maps. Genetics 2001, 157, 1819–1829. [Google Scholar]
- Gianola, D. Genomic-assisted prediction of genetic value with semiparametric procedures. Genetics 2006, 173, 1761–1776. [Google Scholar] [CrossRef]
- VanRaden, P.M. Efficient methods to compute genomic predictions. J. Dairy Sci. 2008, 91, 4414–4423. [Google Scholar] [CrossRef]
- Pérez, P.; de los Campos, G.; Crossa, J.; Gianola, D. Genomic-enabled prediction based on molecular markers and pedigree using the Bayesian linear regression package in R. Plant Genome 2010, 3, 106–116. [Google Scholar] [CrossRef]
- Habier, D.; Fernando, R.L.; Kizilkaya, K.; Garrick, D.J. Extension of the Bayesian alphabet for genomic selection. BMC Bioinform. 2011, 12, 186. [Google Scholar] [CrossRef]
- Resende, M.D.; Resende, M.F.; Sansaloni, C.P.; Petroli, C.D.; Missiaggia, A.A.; Aguiar, A.M.; Abad, J.M.; Takahashi, E.K.; Rosado, A.M.; Faria, D.A.; et al. Genomic selection for growth and wood quality in Eucalyptus: Capturing the missing heritability and accelerating breeding for complex traits in forest trees. New Phytol. 2012, 194, 116–128. [Google Scholar] [CrossRef]
- Gianola, D. Priors in whole-genome regression: The Bayesian alphabet returns. Genetics 2013, 194, 573–596. [Google Scholar] [CrossRef]
- Azevedo, C.F.; Silva, F.F.; de Resende, M.D.V.; Lopes, M.S.; Duijvesteijn, N.; Guimarães, S.E.F.; Lopes, P.S.; Kelly, M.J.; Viana, J.M.S.; Knol, E.F. Supervised independent component analysis as an alternative method for genomic selection in pigs. J. Anim. Breed. Genet. 2014, 131, 452–461. [Google Scholar] [CrossRef]
- Azevedo, C.F.; de Resende, M.D.V.; e Silva, F.F.; Viana, J.M.S.; Valente, M.S.F.; Resende, M.F.R.; Muñoz, P. Ridge, Lasso and Bayesian additive-dominance genomic models. BMC Genet. 2015, 16, 105. [Google Scholar] [CrossRef]
- Song, Q.; Hyten, D.L.; Jia, G.; Quigley, C.V.; Fickus, E.W.; Nelson, R.L.; Cregan, P.B. Development and evaluation of SoySNP50K, a high-density genotyping array for soybean. PLoS ONE 2013, 8, e54985. [Google Scholar] [CrossRef]
- Chen, H.; Xie, W.; He, H.; Yu, H.; Chen, W.; Li, J.; Yu, R.; Yao, Y.; Zhang, W.; He, Y.; et al. A high-density SNP genotyping array for rice biology and molecular breeding. Mol. Plant 2014, 7, 541–553. [Google Scholar] [CrossRef]
- Avni, R.; Nave, M.; Eilam, T.; Sela, H.; Alekperov, C.; Peleg, Z.; Dvorak, J.; Korol, A.; Distelfeld, A. Ultra-dense genetic map of durum wheat× wild emmer wheat developed using the 90K iSelect SNP genotyping assay. Mol. Breed. 2014, 34, 1549–1562. [Google Scholar] [CrossRef]
- Bayer, M.M.; Rapazote-Flores, P.; Ganal, M.; Hedley, P.E.; Macaulay, M.; Plieske, J.; Ramsay, L.; Russell, J.; Shaw, P.D.; Thomas, W.; et al. Development and evaluation of a barley 50k iSelect SNP array. Front. Plant Sci. 2017, 8, 1792. [Google Scholar] [CrossRef]
- Verde, I.; Bassil, N.; Scalabrin, S.; Gilmore, B.; Lawley, C.T.; Gasic, K.; Micheletti, D.; Rosyara, U.R.; Cattonaro, F.; Vendramin, E.; et al. Development and evaluation of a 9K SNP array for peach by internationally coordinated SNP detection and validation in breeding germplasm. PLoS ONE 2012, 7, e35668. [Google Scholar] [CrossRef]
- Bianco, L.; Cestaro, A.; Sargent, D.J.; Banchi, E.; Derdak, S.; Di Guardo, M.; Salvi, S.; Jansen, J.; Viola, R.; Gut, I.; et al. Development and validation of a 20K single nucleotide polymorphism (SNP) whole genome genotyping array for apple (Malus× domestica Borkh). PLoS ONE 2014, 9, e110377. [Google Scholar] [CrossRef]
- Unterseer, S.; Bauer, E.; Haberer, G.; Seidel, M.; Knaak, C.; Ouzunova, M.; Meitinger, T.; Strom, T.M.; Fries, R.; Pausch, H.; et al. A powerful tool for genome analysis in maize: Development and evaluation of the high density 600 k SNP genotyping array. BMC Genomes 2014, 15, 823. [Google Scholar]
- Silva-Junior, O.B.; Faria, D.A.; Grattapaglia, D. Flexible multi-species genome-wide 60K SNP chip developed from pooled resequencing of 240 Eucalyptus tree genomes across 12 species. New Phytol. 2015, 206, 1527–1540. [Google Scholar] [CrossRef]
- Mora, F.; Quitral, Y.A.; Matus, I.; Russell, J.; Waugh, R.; Del Pozo, A. SNP-based QTL mapping of 15 complex traits in barley under rain-fed and well-watered conditions by a mixed modeling approach. Front. Plant Sci. 2016, 7, 909. [Google Scholar] [CrossRef]
- Contreras-Soto, R.I.; Mora, F.; de Oliveira, M.A.R.; Higashi, W.; Scapim, C.A.; Schuster, I. A genome-wide association study for agronomic traits in soybean using SNP markers and SNP-based haplotype analysis. PLoS ONE 2017, 12, e0171105. [Google Scholar] [CrossRef]
- Rasheed, A.; Hao, Y.; Xia, X.; Khan, A.; Xu, Y.; Varshney, R.K.; He, Z. Crop breeding chips and genotyping platforms: Progress, challenges, and perspectives. Mol. Plant 2017, 10, 1047–1064. [Google Scholar] [CrossRef]
- Battenfield, S.D.; Sheridan, J.L.; Silva, L.D.; Miclaus, K.J.; Dreisigacker, S.; Wolfinger, R.D.; Peña, R.J.; Singh, R.P.; Jackson, E.W.; Fritz, A.K.; et al. Breeding-assisted genomics: Applying meta-GWAS for milling and baking quality in CIMMYT wheat breeding program. PLoS ONE 2018, 13, e0204757. [Google Scholar] [CrossRef]
- Li, C.X.; Xu, W.G.; Guo, R.; Zhang, J.Z.; Qi, X.L.; Hu, L.; Zhao, M.Z. Molecular marker assisted breeding and genome composition analysis of Zhengmai 7698, an elite winter wheat cultivar. Sci. Rep. 2018, 8, 322. [Google Scholar] [CrossRef]
- Maldonado, C.; Mora, F.; Scapim, C.A.; Coan, M. Genome-wide haplotype-based association analysis of key traits of plant lodging and architecture of maize identifies major determinants for leaf angle: hapLA4. PLoS ONE 2019, 14, e0212925. [Google Scholar] [CrossRef]
- Nordborg, M.; Tavaré, S. Linkage disequilibrium: What history has to tell us. Trends Genet. 2002, 18, 83–90. [Google Scholar] [CrossRef]
- Machiela, M.J.; Chanock, S.J. LDlink: A web-based application for exploring population-specific haplotype structure and linking correlated alleles of possible functional variants. Bioinformatics 2015, 31, 3555–3557. [Google Scholar] [CrossRef]
- Andersen, J.; Lübberstedt, T. Functional markers in plants. Trends Plant Sci. 2003, 8, 554–560. [Google Scholar] [CrossRef]
- Cuyabano, B.C.; Su, G.; Lund, M.S. Genomic prediction of genetic merit using LD based haplotypes in the Nordic Holstein population. BMC Genom. 2014, 15, 1171. [Google Scholar] [CrossRef]
- Calus, M.P.; Meuwissen, T.H.; Windig, J.J.; Knol, E.F.; Schrooten, C.; Vereijken, A.L.; Veerkamp, R.F. Effects of the number of markers per haplotype and clustering of haplotypes on the accuracy of QTL mapping and prediction of genomic breeding values. Genet. Sel. Evol. 2009, 41, 11. [Google Scholar] [CrossRef]
- Matias, F.I.; Galli, G.; Correia Granato, I.S.; Fritsche-Neto, R. Genomic prediction of autogamous and allogamous plants by SNPs and haplotypes. Crop Sci. 2017, 57, 2951–2958. [Google Scholar] [CrossRef]
- Sun, C.; Wang, B.; Yan, L.; Hu, K.; Liu, S.; Zhou, Y.; Guan, C.; Zhang, Z.; Li, J.; Zhang, J.; et al. Genome-wide association study provides insight into the genetic control of plant height in rapeseed (Brassica napus L.). Front. Plant Sci. 2016, 7, 1102. [Google Scholar] [CrossRef]
- Nimmakayala, P.; Abburi, V.L.; Saminathan, T.; Alaparthi, S.B.; Almeida, A.; Davenport, B.; Nadimi, M.; Davidson, J.; Tonapi, K.; Yadav, L.; et al. Genome-wide diversity and association mapping for capsaicinoids and fruit weight in Capsicum Annuum, L. Sci. Rep. 2016, 6, 38081. [Google Scholar] [CrossRef]
- Vinholes, P.; Rosado, R.; Roberts, P.; Borém, A.; Schuster, I. Single nucleotide polymorphism-based haplotypes associated with charcoal rot resistance in Brazilian soybean germplasm. Agron. J. 2018, 111, 182–192. [Google Scholar] [CrossRef]
- Nyine, M.; Wang, S.; Kiani, K.; Jordan, K.; Liu, S.; Byrne, P.; Haley, S.; Baenziger, S.; Chao, S.; Bowden, R.; et al. Genotype imputation in winter wheat using first generation haplotype map SNPs improves genome-wide association mapping and genomic prediction of traits. G3 Genes Genomes Genet. 2019, 9, 125–133. [Google Scholar] [CrossRef]
- Calus, M.P.L.; De Roos, A.P.W.; Veerkamp, R.F. Accuracy of genomic selection using different methods to define haplotypes. Genetics 2008, 178, 553–561. [Google Scholar] [CrossRef]
- De Roos, A.P.W.; Schrooten, C.; Druet, T. Genomic breeding value estimation using genetic markers, inferred ancestral haplotypes, and the genomic relationship matrix. J. Dairy Sci. 2011, 94, 4708–4714. [Google Scholar] [CrossRef]
- Boichard, D.; Guillaume, F.; Baur, A.; Croiseau, P.; Rossignol, M.N.; Boscher, M.Y.; Druet, T.; Genestout, L.U.C.I.E.; Colleau, J.J.; Journaux, L.; et al. Genomic selection in French dairy cattle. Anim. Prod. Sci. 2012, 52, 115–120. [Google Scholar] [CrossRef]
- Edriss, V.; Fernando, R.L.; Su, G.; Lund, M.S.; Guldbrandtsen, B. The effect of using genealogy-based haplotypes for genomic prediction. Genet. Sel. Evol. 2013, 45, 5. [Google Scholar] [CrossRef]
- Jónás, D.; Ducrocq, V.; Croiseau, P. The combined use of linkage disequilibrium–based haploblocks and allele frequency–based haplotype selection methods enhances genomic evaluation accuracy in dairy cattle. J. Dairy Sci. 2017, 100, 2905–2908. [Google Scholar] [CrossRef]
- Curtis, D.; North, B.V.; Sham, P.C. Use of an artificial neural network to detect association between a disease and multiple marker genotypes. Ann. Hum. Genet. 2001, 65, 95–107. [Google Scholar] [CrossRef]
- Yu, J.; Pressoir, G.; Briggs, W.H.; Bi, I.V.; Yamasaki, M.; Doebley, J.F.; McMullen, M.D.; Gaut, B.S.; Nielsen, D.M.; Holland, J.B.; et al. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Nat. Genet. 2006, 38, 203. [Google Scholar] [CrossRef]
- Jarquín, D.; Kocak, K.; Posadas, L.; Hyma, K.; Jedlicka, J.; Graef, G.; Lorenz, A. Genotyping by sequencing for genomic prediction in a soybean breeding population. BMC Genomes 2014, 15, 740. [Google Scholar] [CrossRef]
- Habyarimana, E. Genomic prediction for yield improvement and safeguarding of genetic diversity in CIMMYT spring wheat (Triticum aestivum L.). Aust. J. Crop. Sci. 2016, 10, 127. [Google Scholar]
- Ballesta, P.; Serra, N.; Guerra, F. Genomic prediction of growth and stem quality traits in Eucalyptus globulus Labill. at its southernmost distribution limit in Chile. Forests 2018, 9, 779. [Google Scholar] [CrossRef]
- Thavamanikumar, S.; McManus, L.J.; Ades, P.K.; Bossinger, G.; Stackpole, D.J.; Kerr, R.; Hadjigol, S.; Freeman, J.S.; Vaillancourt, R.E.; Zhu, P.; et al. Association mapping for wood quality and growth traits in Eucalyptus globulus ssp. globulus Labill identifies nine stable marker-trait associations for seven traits. Tree Genet. Genomes 2014, 10, 1661–1678. [Google Scholar]
- Durán, R.; Isik, F.; Zapata-Valenzuela, J.; Balocchi, C.; Valenzuela, S. Genomic predictions of breeding values in a cloned Eucalyptus globulus population in Chile. Tree Genet. Genomes 2017, 13, 74. [Google Scholar] [CrossRef]
- Thavamanikumar, S.; McManus, L.J.; Tibbits, J.F.; Bossinger, G. The significance of single nucleotide polymorphisms (SNPs) in Eucalyptus globulus breeding programs. Aust. For. 2011, 74, 23–29. [Google Scholar] [CrossRef]
- Cappa, E.P.; El-Kassaby, Y.A.; Garcia, M.N.; Acuña, C.; Borralho, N.M.; Grattapaglia, D.; Poltri, S.N.M. Impacts of population structure and analytical models in genome-wide association studies of complex traits in forest trees: A case study in Eucalyptus globulus. PLoS ONE 2013, 8, e81267. [Google Scholar] [CrossRef]
- Gabriel, S.B.; Schaffner, S.F.; Nguyen, H.; Moore, J.M.; Roy, J.; Blumenstiel, B.; Higgins, J.; DeFelice, M.; Lochner, A.; Faggart, M.; et al. The structure of haplotype blocks in the human genome. Science 2002, 296, 2225–2229. [Google Scholar] [CrossRef]
- Gupta, P.K.; Pawan, S.; Kulwal, P.L. Linkage disequilibrium and association studies in higher plants: Present status and future prospects. Plant Mol. Biol. 2005, 57, 461–485. [Google Scholar] [CrossRef]
- Fiil, A.; Lenk, I.; Petersen, K.; Jensen, C.S.; Nielsen, K.K.; Schejbel, B.; Andersen, J.R.; Lübberstedt, T. Nucleotide diversity and linkage disequilibrium of nine genes with putative effects on flowering time in perennial ryegrass (Lolium perenne L.). Plant Sci. 2011, 180, 228–237. [Google Scholar] [CrossRef]
- Pérez-Rodríguez, P.; Gianola, D.; González-Camacho, J.M.; Crossa, J.; Manès, Y.; Dreisigacker, S. Comparison between linear and non-parametric regression models for genome-enabled prediction in wheat. G3 Genes Genomes Genet. 2012, 2, 1595–1605. [Google Scholar] [CrossRef]
- Costa e Silva, J.C.; Hardner, C.; Potts, B.M. Genetic variation and parental performance under inbreeding for growth in Eucalyptus globulus. Ann. For. Sci. 2010, 67, 606. [Google Scholar] [CrossRef]
- Callister, A.N.; England, N.; Collins, S. Genetic analysis of Eucalyptus globulus diameter, straightness, branch size, and forking in Western Australia. Can. J. For. Res. 2011, 41, 1333–1343. [Google Scholar] [CrossRef]
- Mora, F.; Serra, N. Bayesian estimation of genetic parameters for growth, stem straightness, and survival in Eucalyptus globulus on an Andean Foothill site. Tree Genet Genomes 2014, 10, 711–719. [Google Scholar] [CrossRef]
- Resende, R.T.; Resende, M.D.V.; Silva, F.F.; Azevedo, C.F.; Takahashi, E.K.; Silva-Junior, O.B.; Grattapaglia, D. Assessing the expected response to genomic selection of individuals and families in Eucalyptus breeding with an additive-dominant model. Heredity 2017, 119, 245. [Google Scholar] [CrossRef]
- Tan, B.; Grattapaglia, D.; Martins, G.S.; Ferreira, K.Z.; Sundberg, B.; Ingvarsson, P.K. Evaluating the accuracy of genomic prediction of growth and wood traits in two Eucalyptus species and their F1 hybrids. BMC Plant Biol. 2017, 17, 110. [Google Scholar] [CrossRef]
- Pérez, P.; De Los Campos, G. Genome-wide regression and prediction with the BGLR statistical package. Genetics 2014, 198, 483–495. [Google Scholar] [CrossRef]
- Van den Berg, I.; Fritz, S.; Boichard, D. QTL fine mapping with Bayes C (π): A simulation study. Genet. Sel. Evol. 2013, 45, 19. [Google Scholar] [CrossRef]
- Suontama, M.; Klápště, J.; Telfer, E.; Graham, N.; Stovold, T.; Low, C.; McKinley, R.; Dungey, H. Efficiency of genomic prediction across two Eucalyptus nitens seed orchards with different selection histories. Heredity 2018, 122, 370–379. [Google Scholar] [CrossRef]
- Müller, B.S.; Neves, L.G.; de Almeida Filho, J.E.; Resende, M.F.; Muñoz, P.R.; dos Santos, P.E.; Paludzyszyn Filho, E.; Kirst, M.; Grattapaglia, D. Genomic prediction in contrast to a genome-wide association study in explaining heritable variation of complex growth traits in breeding populations of Eucalyptus. BMC Genomes 2017, 18, 524. [Google Scholar] [CrossRef]
- Lopez, G.A.; Potts, B.M.; Dutkowski, G.W. Genetic variation and inter-trait correlations in Eucalyptus globulus base population trials in Argentina. For. Genet. 2002, 9, 217–231. [Google Scholar]
- Blackburn, D.P.; Hamilton, M.G.; Harwood, C.E.; Baker, T.G.; Potts, B.M. Assessing genetic variation to improve stem straightness in Eucalyptus globulus. Ann. For. Sci. 2013, 70, 461–470. [Google Scholar] [CrossRef]
- Bartholomé, J.; Bink, M.C.; van Heerwaarden, J.; Chancerel, E.; Boury, C.; Lesur, I.; Isik, F.; Bouffier, L.; Plomion, C. Linkage and association mapping for two major traits used in the maritime pine breeding program: Height growth and stem straightness. PLoS ONE 2016, 11, e0165323. [Google Scholar]
- Yang, H.; Liu, T.; Xu, B. QTL detection for growth and form traits in three full-sib pedigrees of Pinus elliottii var. elliottii × P. caribaea var. hondurensis hybrids. Tree Genet. Genomes 2015, 11, 130. [Google Scholar] [CrossRef]
- Arriagada, O.; Mora, F.; Amaral Junior, A.T. Thirteen years under arid conditions: Exploring marker-trait associations in Eucalyptus cladocalyx for complex traits related to flowering, stem form and growth. Breed Sci. 2018, 68, 367–374. [Google Scholar] [CrossRef]
- Song, J.; Brendel, O.; Bodénès, C.; Plomion, C.; Kremer, A.; Colin, F. X-ray computed tomography to decipher the genetic architecture of tree branching traits: Oak as a case study. Tree Genet. Genomes 2017, 13, 5. [Google Scholar] [CrossRef]
- Monclus, R.; Leplé, J.C.; Bastien, C.; Bert, P.F.; Villar, M.; Marron, N.; Brignolas, F.; Jorge, V. Integrating genome annotation and QTL position to identify candidate genes for productivity, architecture and water-use efficiency in Populus spp. BMC Plant Biol. 2012, 12, 173. [Google Scholar] [CrossRef]
- Wolfe, M.D.; Del Carpio, D.P.; Alabi, O.; Ezenwaka, L.C.; Ikeogu, U.N.; Kayondo, I.S.; Lozano, R.; Okeke, U.G.; Ozimati, A.A.; Williams, E.; et al. Prospects for genomic selection in cassava breeding. Plant Genome 2017, 10, 1–9. [Google Scholar] [CrossRef]
- Valenzuela, C.E.; Ballesta, P.; Maldonado, C.; Baettig, R.; Arriagada, O.; Sousa Mafra, G.; Mora, F. Bayesian mapping reveals large-effect pleiotropic QTLs for wood density and slenderness index in 17-year-old trees of Eucalyptus cladocalyx. Forests 2019, 10, 241. [Google Scholar] [CrossRef]
- Beaulieu, J.; Doerksen, T.; Clément, S.; MacKay, J.; Bousquet, J. Accuracy of genomic selection models in a large population of open-pollinated families in white spruce. Heredity 2014, 113, 343. [Google Scholar] [CrossRef]
- Makowsky, R.; Pajewski, N.M.; Klimentidis, Y.C.; Vazquez, A.I.; Duarte, C.W.; Allison, D.B.; de Los Campos, G. Beyond missing heritability: Prediction of complex traits. PLoS Genet. 2011, 7, e1002051. [Google Scholar] [CrossRef]
- Lenz, P.R.; Beaulieu, J.; Mansfield, S.D.; Clément, S.; Desponts, M.; Bousquet, J. Factors affecting the accuracy of genomic selection for growth and wood quality traits in an advanced-breeding population of black spruce (Picea mariana). BMC Genome 2017, 18, 335. [Google Scholar] [CrossRef]
- Barrett, J.C.; Fry, B.; Maller, J.D.M.J.; Daly, M.J. Haploview: Analysis and visualization of LD and haplotype maps. Bioinformatics 2005, 21, 263–265. [Google Scholar] [CrossRef]
- Myburg, A.A.; Grattapaglia, D.; Tuskan, G.A.; Hellsten, U.; Hayes, R.D.; Grimwood, J.; Jenkins, J.; Lindquist, E.; Tice, H.; Bauer, D.; et al. The genome of Eucalyptus grandis. Nature 2014, 510, 356. [Google Scholar] [CrossRef]
- Breseghello, F.; Sorrells, M.E. Association mapping of kernel size and milling quality in wheat (Triticum aestivum L.) cultivars. Genetics 2006, 172, 1165–1177. [Google Scholar] [CrossRef]
- Hadfield, J.D. MCMC methods for multi-response generalized linear mixed models: The MCMCglmm R package. J. Stat. Softw. 2010, 33, 1–22. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing, 3.6.1; R Foundation for Statistical Computing: Vienna, Austria, 2019. [Google Scholar]
- Tibshirani, R. Regression shrinkage and selection via the lasso. J. R. Stat. Soc. 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Legarra, A.; Robert-Granié, C.; Croiseau, P.; Guillaume, F.; Fritz, S. Improved LASSO for genomic selection. Genet. Res. 2011, 93, 77–87. [Google Scholar] [CrossRef]
- Mora, F.; Ballesta, P.; Serra, N. Bayesian analysis of growth, stem straightness and branching quality in full-sib families of Eucalyptus globulus. Bragantia 2019, 78, 1–9. [Google Scholar] [CrossRef]
- Torres, L.G.; Rodrigues, M.C.; Lima, N.L.; Trindade, T.F.H.; e Silva, F.F.; Azevedo, C.F.; DeLima, R.O. Multi-trait multi-environment Bayesian model reveals G × E interaction for nitrogen use efficiency components in tropical maize. PLoS ONE 2018, 13, e0199492. [Google Scholar] [CrossRef]
- Volpato, L.; Alves, R.S.; Teodoro, P.E.; de Resende, M.D.V.; Nascimento, M.; Nascimento, A.C.C.; Ludke, W.H.; da Silva, F.L.; Borém, A. Multi-trait multi-environment models in the genetic selection of segregating soybean progeny. PLoS ONE 2019, 14, e0215315. [Google Scholar] [CrossRef]
- Mora, F.; Zúñiga, P.E.; Figueroa, C.R. Genetic variation and trait correlations for fruit weight, firmness and color parameters in wild accessions of Fragaria chiloensis. Agronomy 2019, 9, 506. [Google Scholar] [CrossRef]
- Baltunis, B.S.; Huber, D.A.; White, T.L.; Goldfarb, B.; Stelzer, H.E. Genetic gain from selection for rooting ability and early growth in vegetatively propagated clones of loblolly pine. Tree Genet. Genomes 2007, 3, 227–238. [Google Scholar] [CrossRef]
- Burdon, R.D. Short note: Coefficients of variation in variables with bounded scales. Silvae Genet. 2008, 57, 179–180. [Google Scholar] [CrossRef]
| Ch | SNPs | HAP-Blocks | HAPs | Max (kb) | Min (bp) | Max (SNPs) | Min (SNPs) |
|---|---|---|---|---|---|---|---|
| 1 | 924 | 75 | 219 | 381 | 61 | 6 | 2 |
| 2 | 1766 | 121 | 370 | 357 | 36 | 6 | 2 |
| 3 | 1587 | 99 | 299 | 123 | 30 | 11 | 2 |
| 4 | 893 | 71 | 207 | 31 | 31 | 5 | 2 |
| 5 | 1500 | 83 | 238 | 279 | 49 | 8 | 2 |
| 6 | 1474 | 144 | 407 | 343 | 63 | 6 | 2 |
| 7 | 1220 | 87 | 248 | 356 | 121 | 5 | 2 |
| 8 | 1811 | 152 | 418 | 482 | 70 | 6 | 2 |
| 9 | 946 | 89 | 249 | 94 | 34 | 5 | 2 |
| 10 | 1065 | 103 | 295 | 318 | 49 | 10 | 2 |
| 11 | 1236 | 113 | 329 | 250 | 75 | 12 | 2 |
| Total | 14,422 | 1137 | 3279 | - | - | - | - |
| Mean | 1311 | 103 | 298 | 274 | 54 | 7 | 2 |
| Trait/Model | Pedigree | SNP | HAP | HAP-SNP | ||||
|---|---|---|---|---|---|---|---|---|
| [CR] | GG [CR] | GG | GG | GG | ||||
| Tree height | ||||||||
| PBP | 0.15 [0.01–0.28] | 7.7 [5.4–10.3] | - | - | - | - | - | - |
| BA | - | - | 0.11 | 5.6 | 0.06 | 4.2 * | 0.10 | 5.2 * |
| BB | - | - | 0.27 | 6.0 | 0.11 | 3.6 * | 0.29 * | 6.3 |
| BC | - | - | 0.36 * | 7.9 | 0.28 | 6.6 | 0.36 * | 7.8 |
| BL | - | - | 0.07 | 4.2 * | 0.04 | 3.1 * | 0.06 | 3.6 * |
| BRR | - | - | 0.19 | 8.7 | 0.14 | 7.6 | 0.20 | 8.6 |
| Diameter at breast height | ||||||||
| PBP | 0.04 [<0.01–0.10] | 2.9 [1.4–4.5] | - | - | - | - | - | - |
| BA | - | - | 0.08 | 5.0 * | 0.04 | 3.8 | 0.07 | 4.2 |
| BB | - | - | 0.19 * | 4.9 * | 0.09 | 3.4 | 0.14 * | 3.3 |
| BC | - | - | 0.31 * | 7.2 * | 0.26 * | 6.6 * | 0.32 * | 7.2 * |
| BL | - | - | 0.05 | 3.6 | 0.05 | 4.1 | 0.05 | 3.4 |
| BRR | - | - | 0.16 * | 8.3 * | 0.12 * | 7.8 * | 0.16 * | 8.2 * |
| Stem straightness | ||||||||
| PBP | 0.06 [<0.01–0.14] | 4.4 [1.9–7.1] | - | - | - | - | - | - |
| BA | - | - | 0.10 | 4.4 | 0.09 | 4.7 | 0.09 | 4.1 |
| BB | - | - | 0.26 * | 5.7 | 0.18 * | 4.7 | 0.28 * | 5.5 |
| BC | - | - | 0.34 * | 7.1 | 0.30 * | 7.5 * | 0.34 * | 7.2 * |
| BL | - | - | 0.05 | 2.7 | 0.04 | 2.8 | 0.07 | 3.2 |
| BRR | - | - | 0.18 * | 7.6 * | 0.15 * | 7.9 * | 0.20 * | 8.0 * |
| Branch quality | ||||||||
| PBP | 0.05 [<0.01–0.11] | 3.9 [1.4–6.0] | - | - | - | - | - | - |
| BA | - | - | 0.04 | 2.2 | 0.04 | 2.7 | 0.05 | 2.3 |
| BB | - | - | 0.12 * | 2.4 | 0.10 | 2.7 | 0.08 | 1.8 |
| BC | - | - | 0.29 * | 5.0 | 0.25 * | 5.4 | 0.29 * | 4.9 |
| BL | - | - | 0.03 | 2.0 | 0.03 | 2.3 | 0.04 | 2.0 |
| BRR | - | - | 0.15 * | 6.2 * | 0.12 * | 6.4 * | 0.15 * | 6.1 * |
| Wood density | ||||||||
| PBP | 0.46 [0.22–0.69] | 9.7 [7.5–12] | - | - | - | - | - | - |
| BA | - | - | 0.07 * | 2.0 * | 0.05 * | 2.0 * | 0.08 * | 2.1 * |
| BB | - | - | 0.17 * | 2.2 * | 0.12 * | 1.9 * | 0.16 * | 2.1 * |
| BC | - | - | 0.34 | 3.2 * | 0.26 | 3.0 * | 0.33 | 3.1 * |
| BL | - | - | 0.06 * | 1.7 * | 0.04 * | 1.7 * | 0.06 * | 1.8 * |
| BRR | - | - | 0.16 * | 3.6 * | 0.12 * | 3.4 * | 0.17 * | 3.5 * |
| Trait/Markers | Genomic Model | ||||
|---|---|---|---|---|---|
| BA | BB | BC | BL | BRR | |
| Tree height | |||||
| SNP | 0.31 bA | 0.32 bA | 0.44 aA | 0.21 cB | 0.30 bA |
| HAP | 0.21 cdB | 0.28 bA | 0.25 bcC | 0.19 dB | 0.35 aA |
| HAP-SNP | 0.21 dB | 0.31 bA | 0.38 aB | 0.26 cA | 0.33 bA |
| Diameter at breast height | |||||
| SNP | 0.35 bA | 0.34 bA | 0.39 bB | 0.17 cB | 0.45 aA |
| HAP | 0.26 bcB | 0.21 cB | 0.33 aC | 0.26 bA | 0.36 aB |
| HAP-SNP | 0.28 cAB | 0.19 dB | 0.46 aA | 0.20 dB | 0.37 bB |
| Stem straightness | |||||
| SNP | 0.38 cA | 0.52 abA | 0.54 aA | 0.20 dC | 0.48 bB |
| HAP | 0.40 cA | 0.42 cB | 0.50 bA | 0.40 cA | 0.58 aA |
| HAP-SNP | 0.38 bA | 0.49 aA | 0.52 aA | 0.23 cB | 0.52 aB |
| Branch quality | |||||
| SNP | 0.22 bA | 0.13 cA | 0.16 cB | 0.06 dC | 0.31 aA |
| HAP | 0.20 bA | 0.14 cA | 0.28 aA | 0.17 bcB | 0.22 bB |
| HAP-SNP | 0.19 bA | 0.18 bA | 0.31 aA | 0.24 bA | 0.33 aA |
| Wood density | |||||
| SNP | 0.26 bB | 0.30 bA | 0.46 aA | 0.29 bA | 0.32 bB |
| HAP | 0.32 bA | 0.31 bA | 0.39 aB | 0.24 cB | 0.41 aA |
| HAP-SNP | 0.34 bA | 0.29 bA | 0.32 bC | 0.33 bA | 0.44 aA |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ballesta, P.; Maldonado, C.; Pérez-Rodríguez, P.; Mora, F. SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus. Plants 2019, 8, 331. https://doi.org/10.3390/plants8090331
Ballesta P, Maldonado C, Pérez-Rodríguez P, Mora F. SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus. Plants. 2019; 8(9):331. https://doi.org/10.3390/plants8090331
Chicago/Turabian StyleBallesta, Paulina, Carlos Maldonado, Paulino Pérez-Rodríguez, and Freddy Mora. 2019. "SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus" Plants 8, no. 9: 331. https://doi.org/10.3390/plants8090331
APA StyleBallesta, P., Maldonado, C., Pérez-Rodríguez, P., & Mora, F. (2019). SNP and Haplotype-Based Genomic Selection of Quantitative Traits in Eucalyptus globulus. Plants, 8(9), 331. https://doi.org/10.3390/plants8090331





