Modeling Growth Dynamics of Lemna minor: Process Optimization Considering the Influence of Plant Density and Light Intensity
Abstract
1. Introduction
2. Methods
2.1. Plant Material
2.2. Re-Circulating Controlled Agriculture Environment System
2.3. Variants and Repetitions
2.4. Data Collection
2.5. Nutrient Solution
2.6. Determination of the Crude Protein Content
2.7. Growth Model Development, Fitting and Comparison
2.8. Methods of the Model Validation
2.9. Methods of the Model Utilization for Process Optimization
3. Results and Discussion
3.1. Growth Data
3.2. Growth Model
3.3. Model Fitting
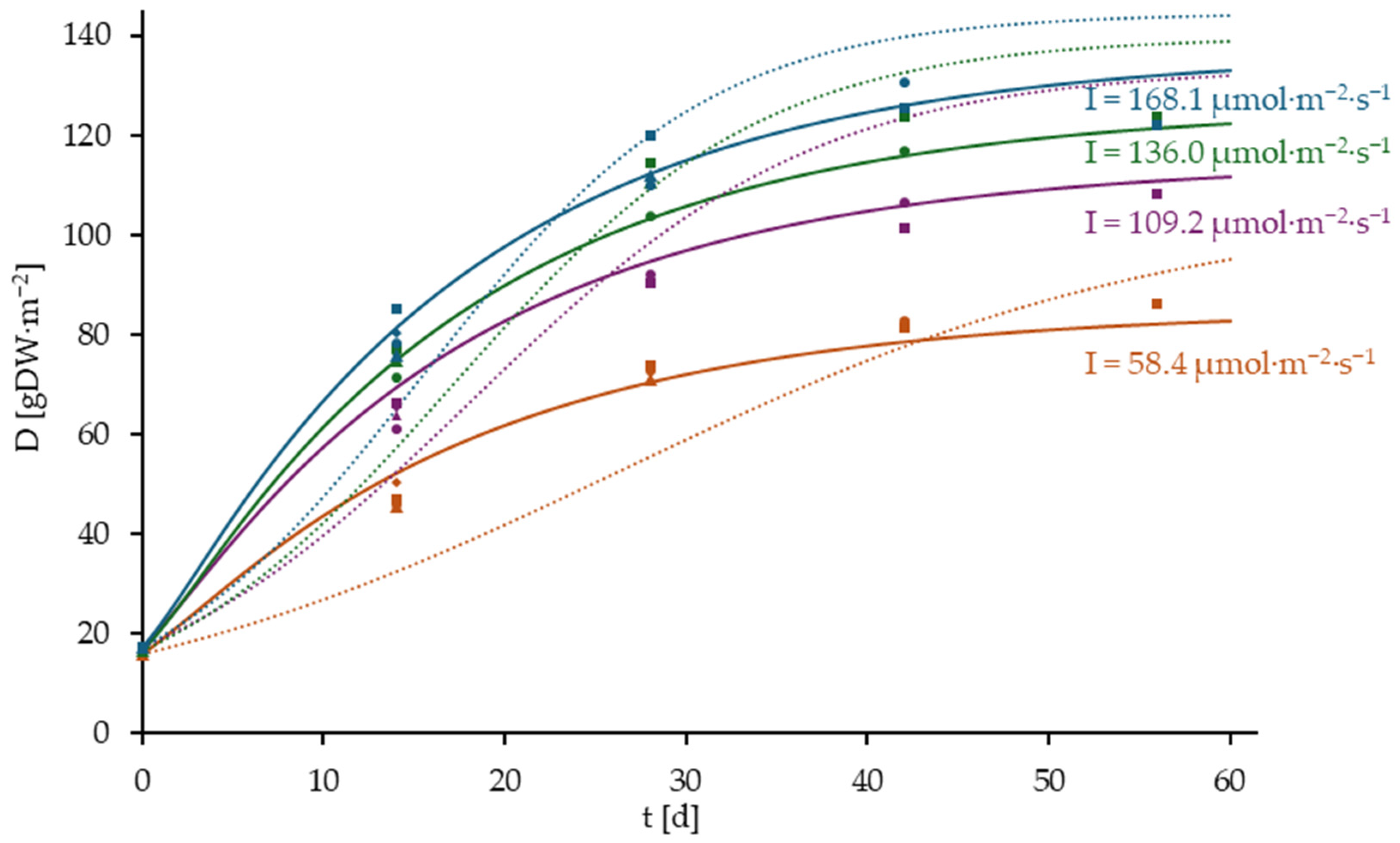
3.4. Results of the Model Validation
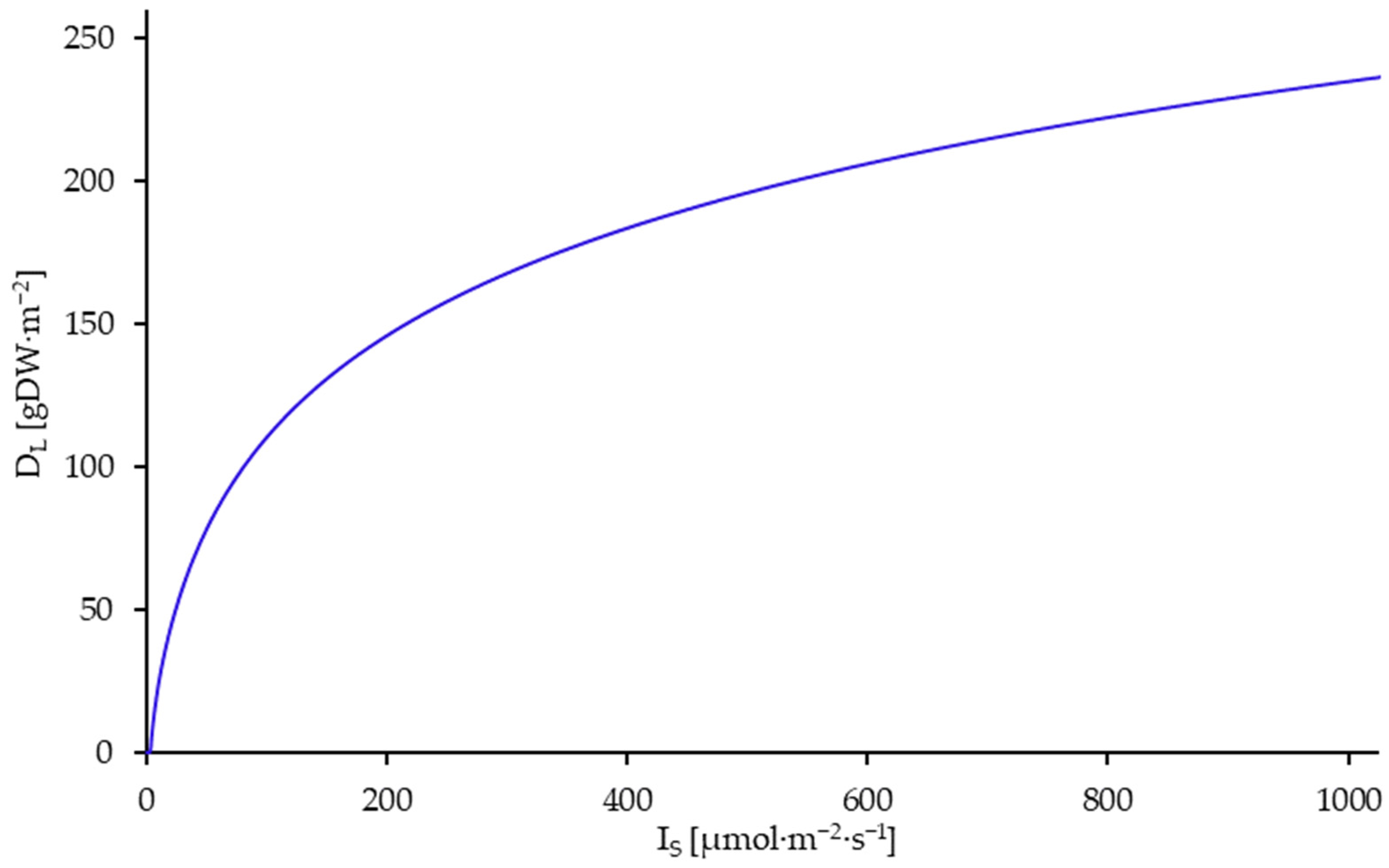
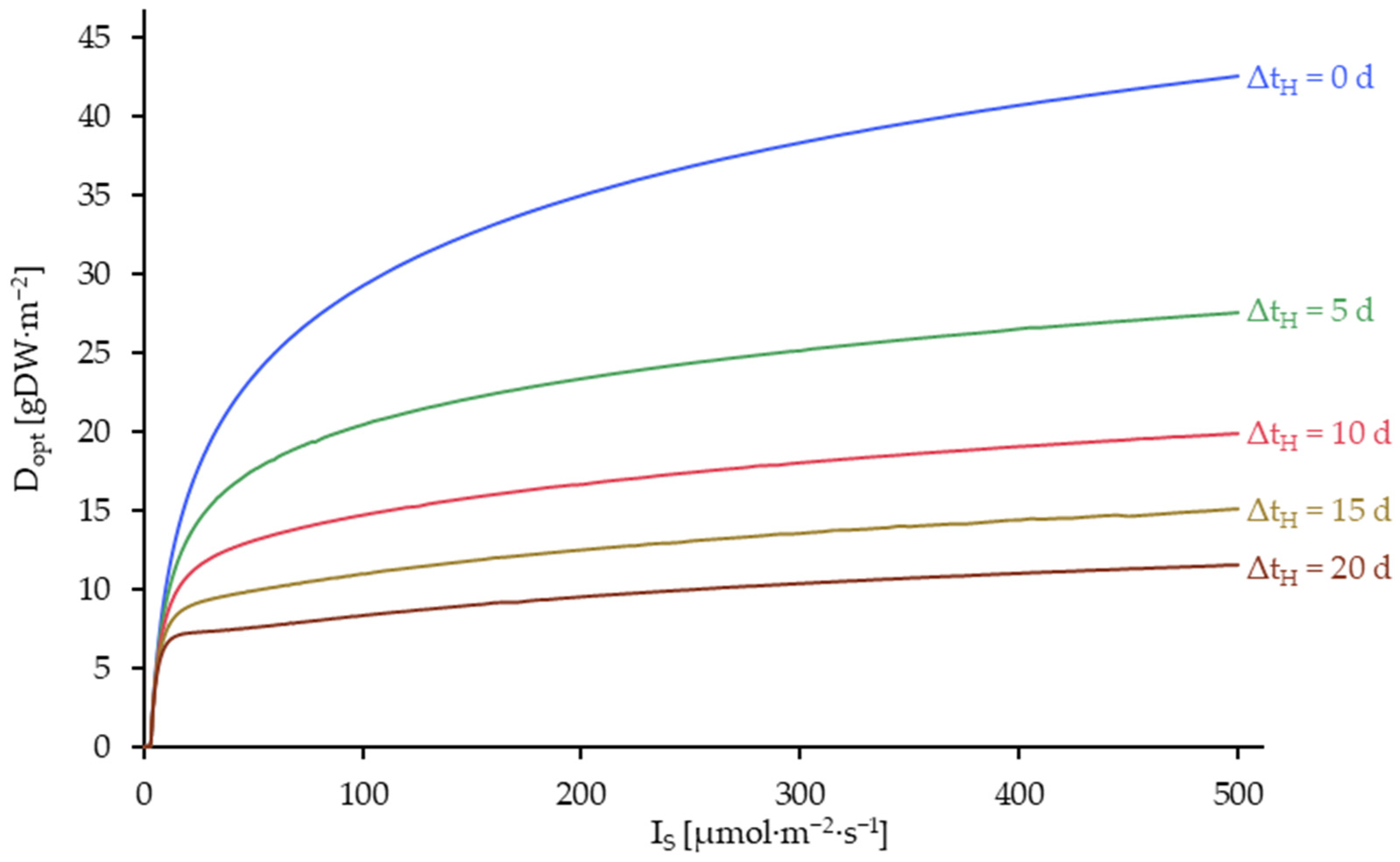
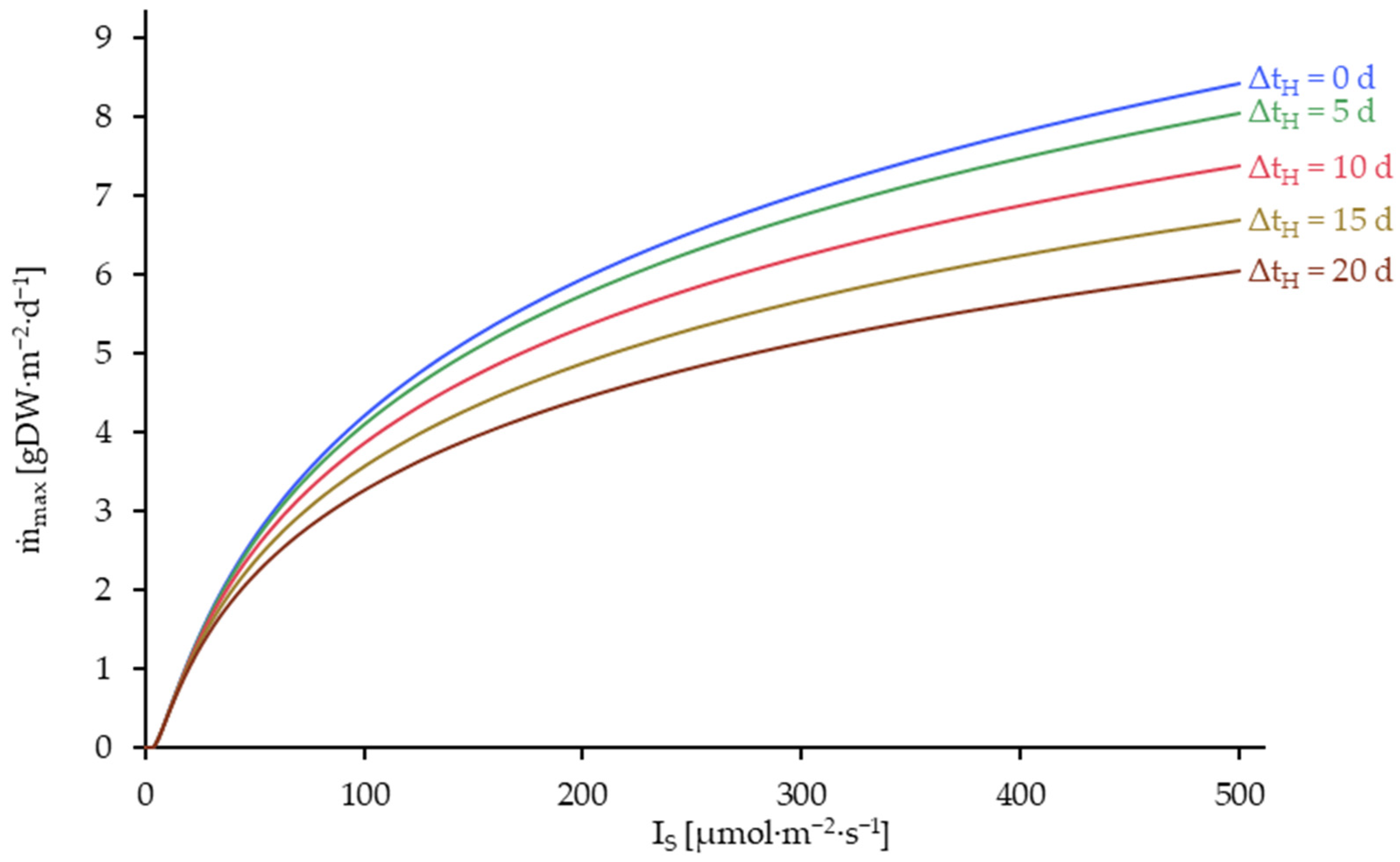
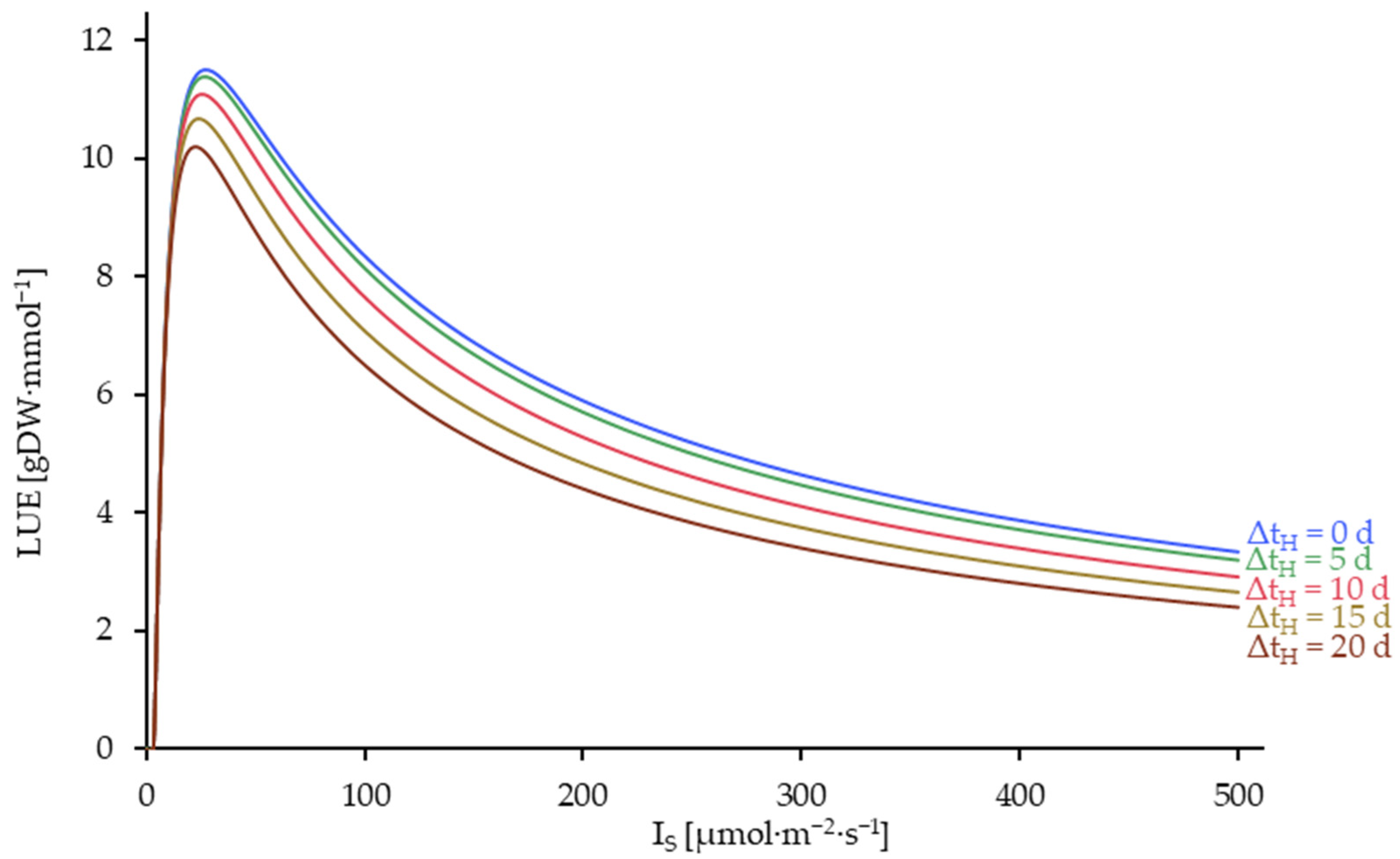
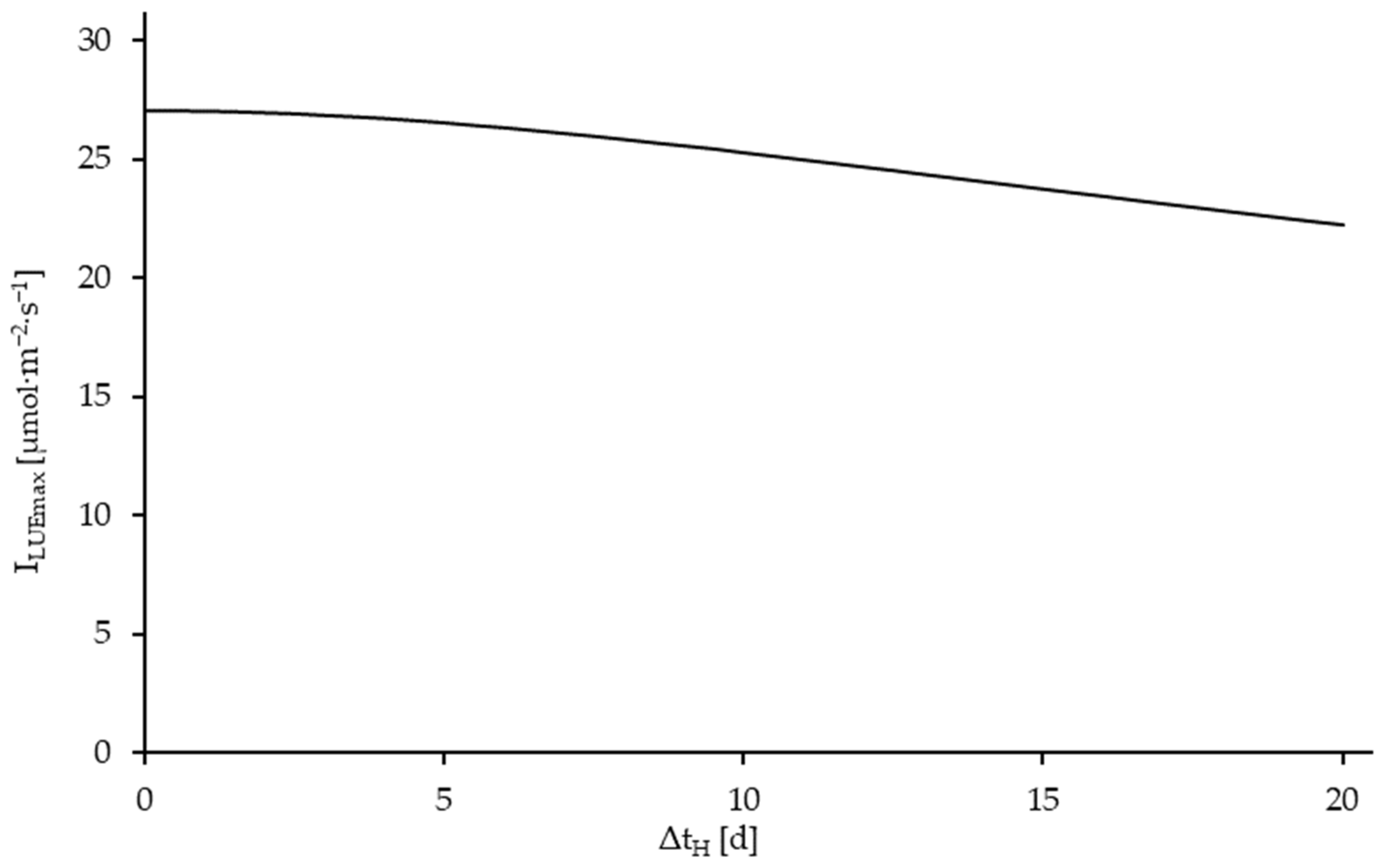
3.5. Results of the Model Utilization for Process Optimization
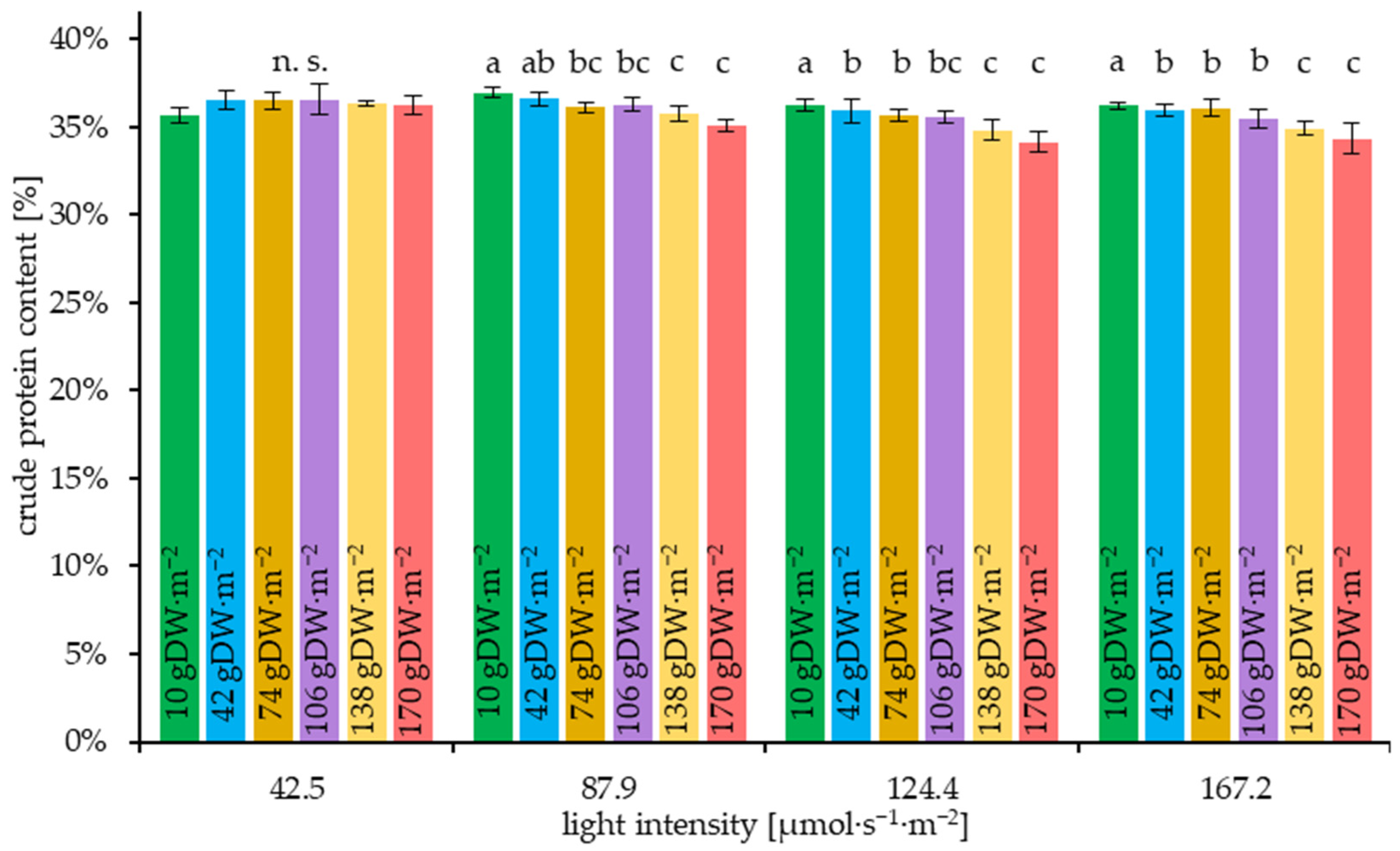
3.6. Results of the Crude Protein Content
3.7. Limitations
4. Conclusions
Outlook
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects 2024: Summary of Results, 1st ed.; United Nations, Department of Economic and Social Affairs: New York, NY, USA, 2024; ISBN 978-9-211-06513-8.
- Tilman, D.; Balzer, C.; Hill, J.; Befort, B.L. Global food demand and the sustainable intensification of agriculture. Proc. Natl. Acad. Sci. USA 2011, 108, 20260–20264. [Google Scholar] [CrossRef] [PubMed]
- Henchion, M.; Hayes, M.; Mullen, A.M.; Fenelon, M.; Tiwari, B. Future protein supply and demand: Strategies and factors influencing a sustainable equilibrium. Foods 2017, 6, 53. [Google Scholar] [CrossRef]
- Berger, A.; Messner, D.; Richerzhagen, C. Neue Paradigmen der Entwicklungspolitik: Urbanisierung im Zeitalter des Klimawandels. In Globalisierungsgestaltung und Internationale Übereinkommen; Frey, A., Jäger, T., Messner, D., Fischedick, M., Hartmann-Wendels, T., Eds.; Springer: Wiesbaden, Germany, 2014; pp. 59–98. ISBN 978-3-658-03660-7. [Google Scholar]
- Sree, K.S.; Sudakaran, S.; Appenroth, K.-J. How fast can angiosperms grow? Species and clonal diversity of growth rates in the genus Wolffia (Lemnaceae). Acta Physiol. Plant. 2015, 37, 204. [Google Scholar] [CrossRef]
- Appenroth, K.-J.; Augsten, H. Wasserlinsen und ihre Nutzung. BiuZ 1996, 26, 187–195. [Google Scholar] [CrossRef]
- Sharma, J.G.; Kumar, A.; Saini, D.; Targay, N.L.; Khangembam, B.K.; Chakrabarti, R. In vitro digestibility study of some plant protein sources as aquafeed for carps Labeo rohita and Cyprinus carpio using pH-Stat method. Indian J. Exp. Biol. 2016, 54, 606–611. [Google Scholar]
- Iatrou, E.I.; Kora, E.; Stasinakis, A.S. Investigation of biomass production, crude protein and starch content in laboratory wastewater treatment systems planted with Lemna minor and Lemna gibba. Environ. Technol. 2019, 40, 2649–2656. [Google Scholar] [CrossRef] [PubMed]
- Appenroth, K.-J.; Sree, K.S.; Böhm, V.; Hammann, S.; Vetter, W.; Leiterer, M.; Jahreis, G. Nutritional value of duckweeds (Lemnaceae) as human food. Food Chem. 2017, 217, 266–273. [Google Scholar] [CrossRef]
- Mes, J.J.; Esser, D.; Somhorst, D.; Oosterink, E.; van der Haar, S.; Ummels, M.; Siebelink, E.; van der Meer, I.M. Daily Intake of Lemna minor or Spinach as Vegetable Does Not Show Significant Difference on Health Parameters and Taste Preference. Plant Foods Hum. Nutr. 2022, 77, 121–127. [Google Scholar] [CrossRef] [PubMed]
- EFSA (European Food Safety Authority). Technical Report on the notification of fresh plants of Wolffia arrhiza and Wolffia globosa as a traditional food from a third country pursuant to Article 14 of Regulation (EU) 2015/2283. EFSA Support. 2021, 18, 6658E. [Google Scholar] [CrossRef]
- Martin, M.; Molin, E. Environmental Assessment of an Urban Vertical Hydroponic Farming System in Sweden. Sustainability 2019, 11, 4124. [Google Scholar] [CrossRef]
- Petersen, F.; Demann, J.; von Salzen, J.; Olfs, H.-W.; Westendarp, H.; Wolf, P.; Appenroth, K.-J.; Ulbrich, A. Re-circulating Indoor Vertical Farm: Technicalities of an automated duckweed biomass production system and protein feed product quality evaluation. J. Clean. Prod. 2022, 380, 134894. [Google Scholar] [CrossRef]
- Calicioglu, O.; Sengul, M.Y.; Valappil Femeena, P.; Brennan, R.A. Duckweed growth model for large-scale applications: Optimizing harvesting regime and intrinsic growth rate via machine learning to maximize biomass yields. J. Clean. Prod. 2021, 324, 129120. [Google Scholar] [CrossRef]
- Coughlan, N.E.; Walsh, É.; Bolger, P.; Burnell, G.; O’Leary, N.; O’Mahoney, M.; Paolacci, S.; Wall, D.; Jansen, M.A. Duckweed bioreactors: Challenges and opportunities for large-scale indoor cultivation of Lemnaceae. J. Clean. Prod. 2022, 336, 130285. [Google Scholar] [CrossRef]
- Petersen, F.; Demann, J.; Restemeyer, D.; Olfs, H.-W.; Westendarp, H.; Appenroth, K.-J.; Ulbrich, A. Influence of Light Intensity and Spectrum on Duckweed Growth and Proteins in a Small-Scale, Re-Circulating Indoor Vertical Farm. Plants 2022, 11, 1010. [Google Scholar] [CrossRef] [PubMed]
- Paolacci, S.; Harrison, S.; Jansen, M.A.K. The invasive duckweed Lemna minuta Kunth displays a different light utilisation strategy than native Lemna minor Linnaeus. Aquat. Bot. 2018, 146, 8–14. [Google Scholar] [CrossRef]
- Stewart, J.J.; Adams, W.W.; Escobar, C.M.; López-Pozo, M.; Demmig-Adams, B. Growth and Essential Carotenoid Micronutrients in Lemna gibba as a Function of Growth Light Intensity. Front. Plant Sci. 2020, 11, 480. [Google Scholar] [CrossRef]
- Driever, S.M.; van Nes, E.H.; Roijackers, R.M.M. Growth limitation of Lemna minor due to high plant density. Aquat. Bot. 2005, 81, 245–251. [Google Scholar] [CrossRef]
- Monette, F.; Lasfar, S.; Millette, L.; Azzouz, A. Comprehensive modeling of mat density effect on duckweed (Lemna minor) growth under controlled eutrophication. Water Res. 2006, 40, 2901–2910. [Google Scholar] [CrossRef]
- Lasfar, S.; Monette, F.; Millette, L.; Azzouz, A. Intrinsic growth rate: A new approach to evaluate the effects of temperature, photoperiod and phosphorus-nitrogen concentrations on duckweed growth under controlled eutrophication. Water Res. 2007, 41, 2333–2340. [Google Scholar] [CrossRef]
- Schmitt, W.; Bruns, E.; Dollinger, M.; Sowig, P. Mechanistic TK/TD-model simulating the effect of growth inhibitors on Lemna populations. Ecol. Model. 2013, 255, 1–10. [Google Scholar] [CrossRef]
- van Dyck, I.; Vanhoudt, N.; i Batlle, J.V.; Horemans, N.; Nauts, R.; van Gompel, A.; Claesen, J.; Vangronsveld, J. Effects of environmental parameters on Lemna minor growth: An integrated experimental and moddeling approach. J. Environ. Manag. 2021, 30, 113705. [Google Scholar] [CrossRef] [PubMed]
- Femeena, P.V.; Roman, B.; Brennan, R.A. Maximizing duckweed biomass production for food security at low light intensities: Experimental results and an enhanced predictive model. Environ. Chall. 2023, 11, 100709. [Google Scholar] [CrossRef]
- Rutgers Duckweed Stock Cooperative at the Rutgers University, NJ, USA: Database of Duckweed Clones. Available online: http://www.ruduckweed.org/database.html (accessed on 14 February 2025).
- Petersen, F.; Demann, J.; Restemeyer, D.; Ulbrich, A.; Olfs, H.-W.; Westendarp, H.; Appenroth, K.-J. Influence of the Nitrate-N to Ammonium-N Ratio on Relative Growth Rate and Crude Protein Content in the Duckweeds Lemna minor and Wolffiella hyalina. Plants 2021, 10, 1741. [Google Scholar] [CrossRef]
- VDLUFA. Methode A 6.1.1.1: Bestimmung von Nitrat-Stickstoff durch UV-Absorption. In Methodenbuch Band I: Die Untersuchung von Böden; VDLUFA: Darmstadt, Germany, 2012. [Google Scholar]
- VDLUFA. Methode A 6.1.4.1: Bestimmung von mineralischem Stickstoff (Nitrat und Ammonium) in Bodenprofilen (Nmin-Labormethode). In Methodenbuch Band I: Die Untersuchung von Böden; VDLUFA: Darmstadt, Germany, 2012. [Google Scholar]
- DIN EN ISO 11885; Water Quality—Determination of Selected Elements by Inductively Coupled Plasma Optical Emission Spectrometry (ICP-OES). 2007th ed. Beuth Verlag GmbH: Berlin, Germany, 2009.
- R Core Team R: A Language and Environment for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 15 January 2025).
- RStudio Team RStudio: Integrated Development Environment for R. Available online: https://posit.co/ (accessed on 15 January 2025).
- Pebesma, E.J. Multivariable geostatistics in S: The gstat package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Gräler, B.; Pebesma, E.; Heuvelink, G. Spatio-Temporal Interpolation using gstat. R J. 2016, 8, 204–218. [Google Scholar] [CrossRef]
- Edzer, J.; Pebesma, J.; Bivand, R.S. Classes and methods for spatial data in R. R J. 2005, 2, 9–13. [Google Scholar]
- Bivand, R.; Pebesma, E.J.; Gómez-Rubio, V. Applied Spatial Data Analysis with R, 2nd ed.; Springer Science+Business Media: New York, NY, USA, 2013; ISBN 978-1-461-47618-4. [Google Scholar]
- Wickham, H. ggplot2: Elegant Graphics for Data Analysis, 2nd ed.; Springer Science+Business Media: New York, NY, USA, 2016; ISBN 978-3-319-24277-4. [Google Scholar]
- Pedersen, T.L. ggforce: Accelerating ‘ggplot2’: R Package Version 0.4.2. Available online: https://CRAN.R-project.org/package=ggforce (accessed on 15 January 2025).
- Garnier, S.; Ross, N.; Rudis, R.; Camargo, A.P.; Sciaini, M.; Scherer, C. Viridis—Colorblind-Friendly Color Maps for R: Viridis Package Version 0.6.5. Available online: https://sjmgarnier.github.io/viridis/ (accessed on 15 January 2025).
- Andrews, F.M. Die Wirkung der Zentrifugalkraft auf Pflanzen. Jahrbücher Wisenschaftlichen Bot. 1915, 53, 221–253. [Google Scholar]
- DIN EN ISO 20079; Water Quality—Determination of the Toxic Effect of Water Constituents and Waste on Duckweed (Lemna minor): Duckweed Growth Inhibition Test, 2006–2012. Beuth Verlag GmbH: Berlin, Germany, 2006.
- DIN EN ISO 16634-1; Food Products—Determination of the Total Nitrogen Content by Combustion According to the Dumas Principle and Calculation of the Crude Protein Content: Part 1: Oilseeds and Animal Feeding Stuffs, 1:2008. Beuth Verlag GmbH: Berlin, Germany, 2008.
- VDLUFA. Methode 4.1.2: Bestimmung von Rohprotein mittels Dumas-Verbrennungsmethode. In VDLUFA-Methodenbuch Band III: Die chemische Untersuchung von Futtermitteln, 3rd ed.; VDLUFA: Darmstadt, Germany, 2012. [Google Scholar]
- Thiex, N.J.; Manson, H.; Anderson, S.; Persson, J.-Å. Determination of Crude Protein in Animal Feed, Forage, Grain, and Oilseeds by Using Block Digestion with a Copper Catalyst and Steam Distillation into Boric Acid: Collaborative Study. J. AOAC Int. 2002, 85, 309–317. [Google Scholar] [CrossRef] [PubMed]
- Casal, J.A.; Vermaat, J.E.; Wiegman, F. A test of two methods for plant protein determination using duckweed. Aquat. Bot. 2000, 67, 61–67. [Google Scholar] [CrossRef]
- Begtsson, H. Progressr: An Inclusive, Unifying API for Progress Updates: R Package Version 0.15.1. Available online: https://CRAN.R-project.org/package=progressr (accessed on 15 January 2025).
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving Differential Equations in R: Package deSolve. J. Stat. Soft. 2010, 33, 1–25. [Google Scholar] [CrossRef]
- Weston, S. doParallel: Foreach Parallel Adaptor for the Parallel’ Package: R Package Version 1.0.17. Available online: https://CRAN.R-project.org/package=doParallel (accessed on 15 January 2025).
- Weston, S. Foreach: Provides Foreach Looping Construct: R Package Version 1.5.2. Available online: https://CRAN.R-project.org/package=foreach (accessed on 15 January 2025).
- Ishizawa, H.; Onoda, Y.; Kitajima, K.; Kuroda, M.; Inoue, D.; Ike, M. Coordination of leaf economics traits within the family of the world’s fastest growing plants (Lemnaceae). J. Ecol. 2021, 109, 2950–2962. [Google Scholar] [CrossRef]
- Ishizawa, H.; Onoda, Y.; Kitajima, K.; Kuroda, M.; Inoue, D.; Ike, M. Coordination of leaf economics traits within the family of the world’s fastest growing plants (Lemnaceae): Dataset. Dryad Repos. 2021. [Google Scholar] [CrossRef]
- Baptiste, A. gridExtra: Miscellaneous Functions for “Grid” Graphics: R Package Version 2.3. Available online: https://CRAN.R-project.org/package=gridExtra (accessed on 15 January 2025).
- Romano, L.E.; Iovane, M.; Izzo, L.G.; Aronne, G. A Machine-Learning Method to Assess Growth Patterns in Plants of the Family Lemnaceae. Plants 2022, 11, 1910. [Google Scholar] [CrossRef]
- Jupsin, H.; Richard, H.; Vasel, J.L. Contribution of floating macrophytes (Lemna sp.) to pond modelization. Water Sci. Technol. 2005, 51, 283–289. [Google Scholar] [CrossRef] [PubMed]
- Filbin, G.J.; Hough, R.A. Photosynthesis, photorespiration, and productivity in Lemna minor L. Limnol. Oceanogr. 1985, 30, 322–334. [Google Scholar] [CrossRef]
- van Espen, P. 24.4: X-ray Fluorescence Spectrometry. In Analytical Chemistry: A Modern Approach to Analytical Science, 2nd ed.; Mermet, J.-M., Otto, M., Valcárcel, M., Kellner, R.A., Widmer, H.M., Eds.; Wiley-VCH: Weinheim, Germany, 2004; pp. 668–695. ISBN 978-3-527-30590-2. [Google Scholar]
- Pasos-Panqueva, J.; Baker, A.; Camargo-Valero, M.A. Unravelling the impact of light, temperature and nutrient dynamics on duckweed growth: A meta-analysis study. J. Environ. Manag. 2024, 366, 121721. [Google Scholar] [CrossRef]
- Ögren, E.; Öquist, G.; Hallgren, J.-E. Photoinhibition of photosynthesis in Lemna gibba as induced by the interaction between light and temperature. I. Photosynthesis in vivo. Physiol. Plant. 1984, 62, 181–186. [Google Scholar] [CrossRef]
- Martindale, W.; Bowes, G. The effects of irradiance and CO2 on the activity and activation of ribulose-1, 5-bisphosphate carboxylase/oxygenase in the aquatic plant Spirodela polyrhiza. J. Exp. Bot. 1996, 47, 781–784. [Google Scholar] [CrossRef]
- Walsh, É.; Kuehnhold, H.; O’Brien, S.; Coughlan, N.E.; Jansen, M.A.K. Light intensity alters the phytoremediation potential of Lemna minor. Environ. Sci. Pollut. Res. 2021, 28, 16394–16407. [Google Scholar] [CrossRef]


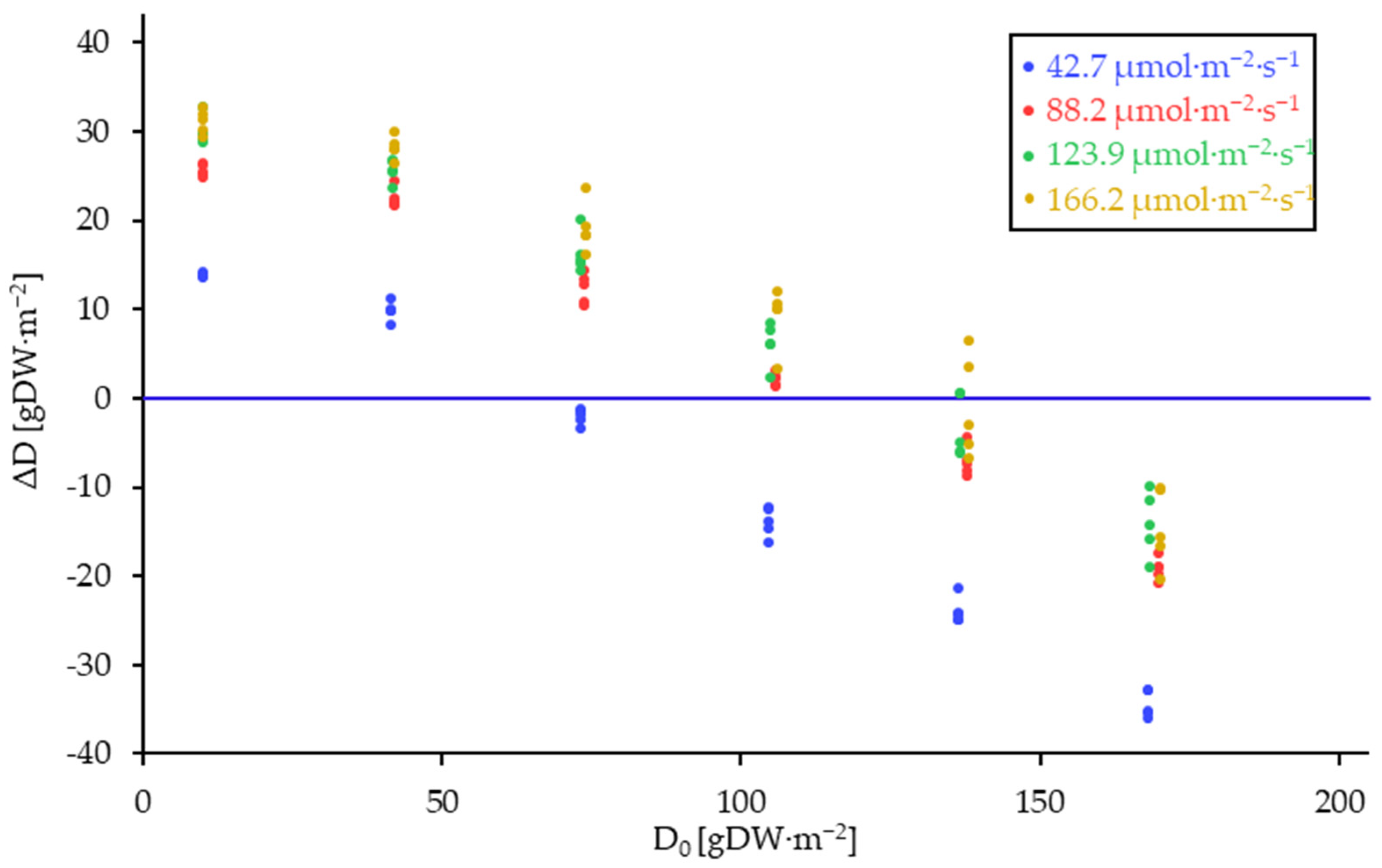
 ) consisting of D0 and D7. Blue dashed lines represent DL.
) consisting of D0 and D7. Blue dashed lines represent DL.
 ) consisting of D0 and D7. Blue dashed lines represent DL.
) consisting of D0 and D7. Blue dashed lines represent DL.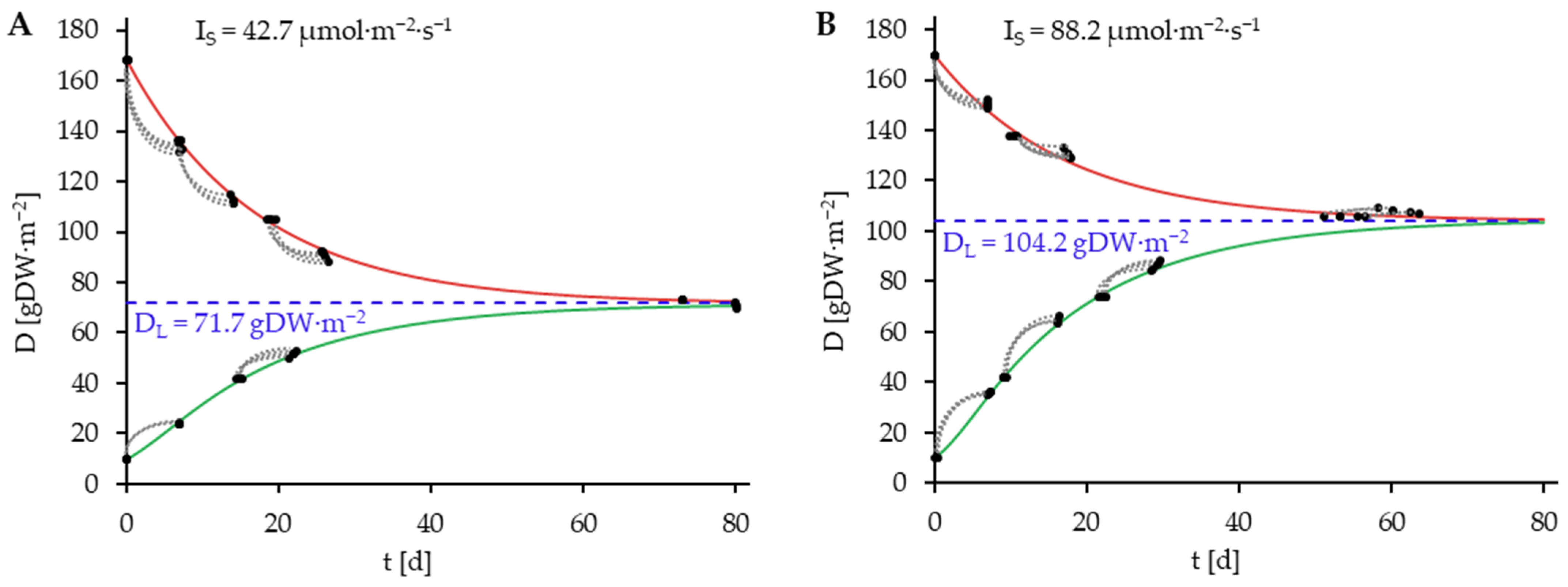
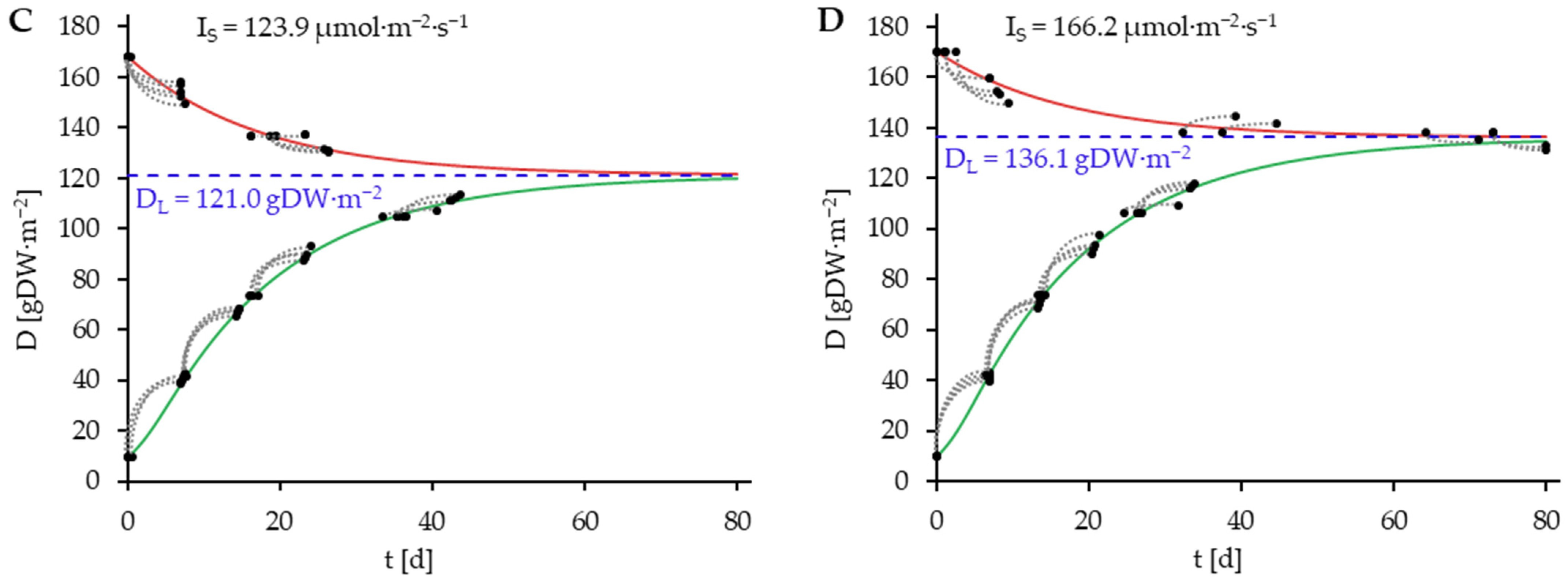
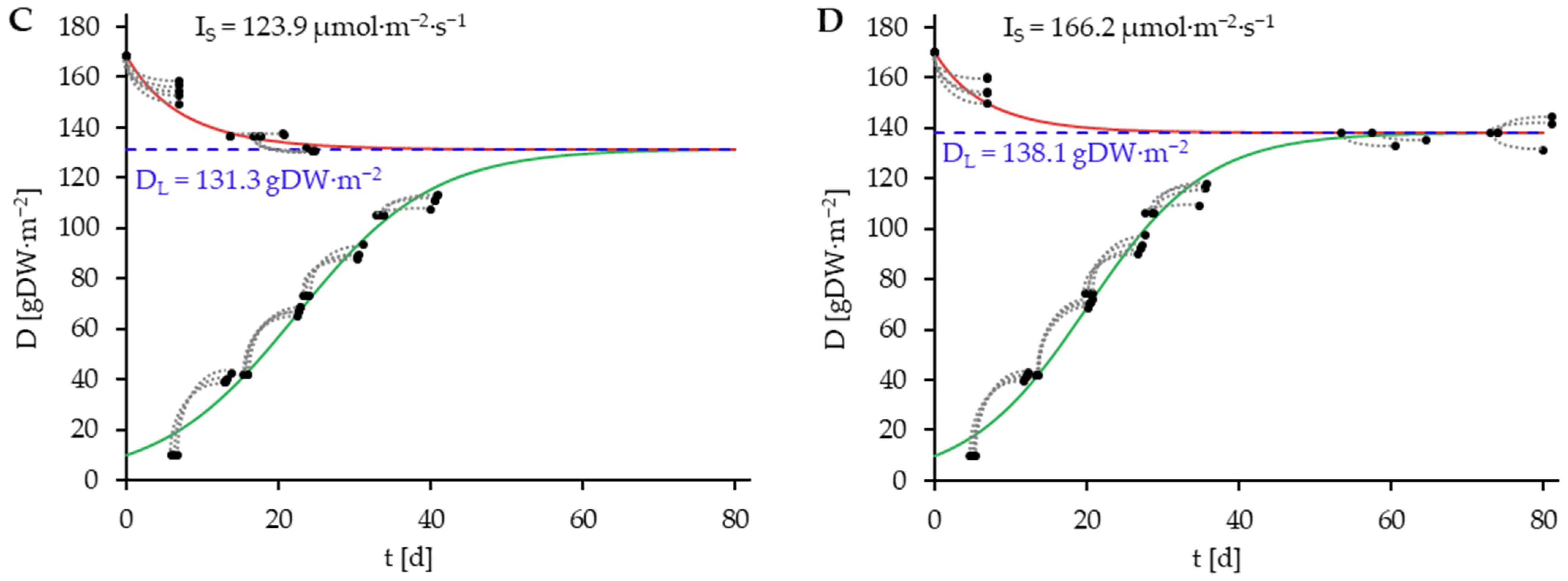
 ) consisting of D0 and D7. Blue dashed Lines represent DL.
) consisting of D0 and D7. Blue dashed Lines represent DL.
 ) consisting of D0 and D7. Blue dashed Lines represent DL.
) consisting of D0 and D7. Blue dashed Lines represent DL.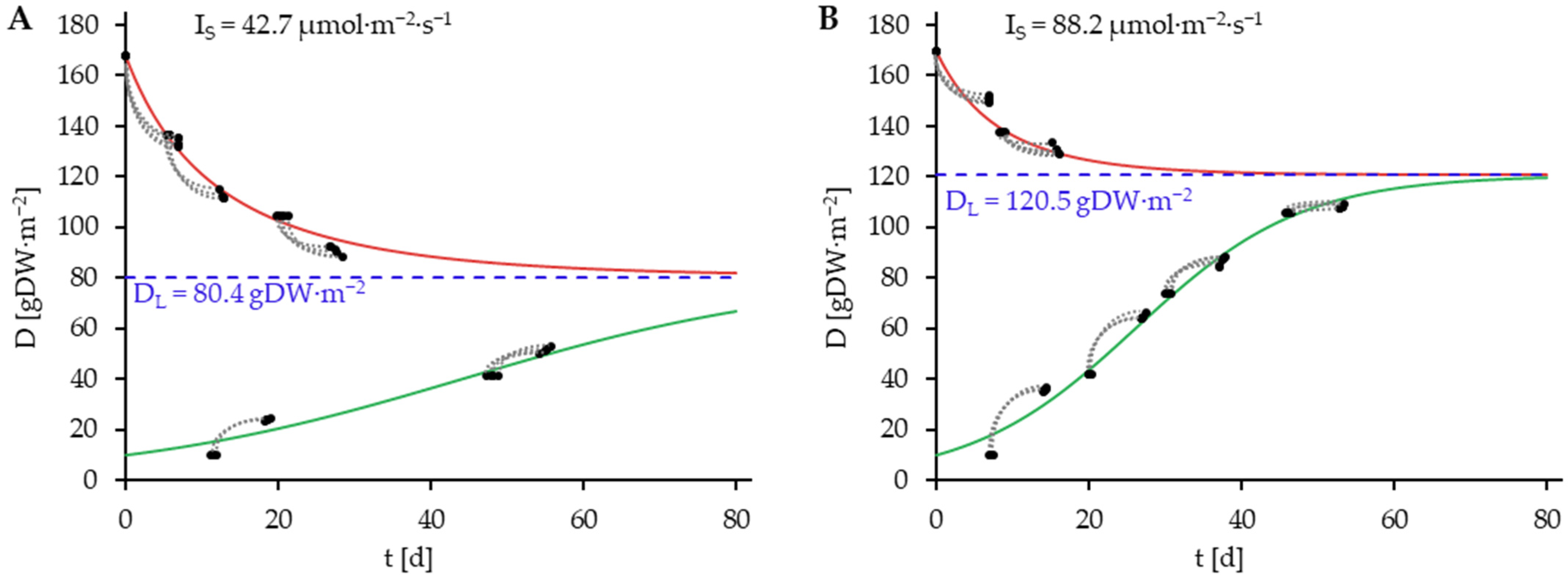
| Realized Values | |||
|---|---|---|---|
| Parameter | Target Values | Mean | Standard Deviation |
| Water temperature | 23 °C | 22.9 °C | 0.3 °C |
| pH | 7.0 | 7.06 | 0.16 |
| EC | 700 µS·cm−1 | 683.4 µS·cm−1 | 14.9 µS·cm−1 |
| Flow rate | 400–600 L∙h−1 | 400–600 L∙h−1 | - |
| Photoperiod | 14 h/24 h = 0.5833 | 14 h/24 h = 0.5833 | 0 |
| Culture trial duration | 7 d | 7 d | 0 |
| Realized Concentration [mg∙L−1] | ||||
|---|---|---|---|---|
| Nutrient | Target Concentration [mg∙L−1] | Mean | Standard Deviation | Method |
| NO3−-N | 12.2 | 11.0 | 0.7 | [27] |
| NH4+-N | 3.5 | 5.5 | 0.8 | [28] |
| PO43−-P | 3.1 | 2.6 | 0.3 | [29] |
| K+ | 38.4 | 33.2 | 0.8 | |
| SO42−-S | 39.3 | 49.3 | 3.6 | |
| Mg2+ | 9.9 | 9.7 | 0.3 | |
| Ca2+ | 53.5 | 62.0 | 2.2 | |
| Na+ | 17.4 | 19.93 | 0.98 | |
| Mn2+ | 0.072 | 0.413 | 0.148 | |
| Zn2+ | - | 0.164 | 0.023 | |
| Fe3+ | 0.154 | 0.079 | 0.054 | |
| BO33−-B | 0.025 | 0.019 | 0.005 | |
| Cu2+ | - | 0.016 | 0.004 | |
| Plant Density [gDW·m−2] | Light Intensity [µmol·s−1·m−2] n = 5 |
|---|---|
| 10 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 | |
| 42 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 | |
| 74 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 | |
| 106 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 | |
| 138 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 | |
| 170 | 42.7 |
| 88.2 | |
| 123.9 | |
| 166.2 |
| Variable/Parameter | Declaration | Unit |
|---|---|---|
| I | Light intensity as photon flux density in the photosynthetically active spectral range | µmol·m−2·s−1 |
| IS | Light intensity as photon flux density in the photosynthetically active spectral range at surface of plant layer | µmol·m−2·s−1 |
| D | Plant density as dry weight per area | gDW·m−2 |
| DL | Limit density. Population-ecological capacity limit of the duckweed culture | |
| t | time | d |
| rphot,i | Intrinsic photosynthesis rate; theoretical photosynthesis rate at maximum light saturation and without interspecific competition | d−1 |
| fphot | Limitation of the photosynthesis rate | - |
| Average Limitation of the photosynthesis rate of the entire duckweed culture | - | |
| rresp | Respiration rate | d−1 |
| E | Photoperiod | h·h−1 |
| k | Half-saturation constant of the light intensity | µmol·m−2·s−1 |
| Depth in plant cover | mm | |
| h | Average thickness of plant cover | mm |
| ε | attenuation constant of the light intensity when penetrating duckweed biomass, in terms of h | mm−1 |
| attenuation constant of the light intensity when penetrating duckweed biomass, in terms of D | gDW−1·m2 | |
| c | Proportionality constant of h and D | mm·gDW−1·m2 |
| Parameter | Initial Parameter Estimates | Value | Unit | p-Value | Std.-Error |
|---|---|---|---|---|---|
| rphot,i | 0.5 | 0.6965 | d−1 | 0.000 | 0.00879 |
| rresp | 0.05 | 0.0583 | d−1 | 0.000 | 0.00152 |
| 0.1 | 0.1209 | m2·gDW−1 | 0.000 | 0.00034 | |
| k | 20 | 17.2640 | µmol·m−2·s−1 | 0.000 | 0.54400 |
| E | - | 14·24−1 = 0.5833 | h·h−1 | - | - |
| R2 | - | 0.9950 | - | - | - |
| Parameter | Initial Parameter Estimates | Value | Unit | p-Value | Std.-Error |
|---|---|---|---|---|---|
| rphot,i | 0.2 | 0.4602 | d−1 | 0.000 | 0.00286 |
| rresp | 0.02 | 0.0788 | d−1 | 0.000 | 0.0030 |
| hD | 70 | 223.7906 | m2·gDW−1 | 0.000 | 3.7984 |
| KI | 30 | 50.4300 | µmol·m−2·s−1 | 0.000 | 3.1935 |
| E | - | 14·24−1 = 0.5833 | h·h−1 | - | - |
| R2 | - | 0.9498 | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
von Salzen, J.; Petersen, F.; Ulbrich, A.; Streif, S. Modeling Growth Dynamics of Lemna minor: Process Optimization Considering the Influence of Plant Density and Light Intensity. Plants 2025, 14, 1722. https://doi.org/10.3390/plants14111722
von Salzen J, Petersen F, Ulbrich A, Streif S. Modeling Growth Dynamics of Lemna minor: Process Optimization Considering the Influence of Plant Density and Light Intensity. Plants. 2025; 14(11):1722. https://doi.org/10.3390/plants14111722
Chicago/Turabian Stylevon Salzen, Jannis, Finn Petersen, Andreas Ulbrich, and Stefan Streif. 2025. "Modeling Growth Dynamics of Lemna minor: Process Optimization Considering the Influence of Plant Density and Light Intensity" Plants 14, no. 11: 1722. https://doi.org/10.3390/plants14111722
APA Stylevon Salzen, J., Petersen, F., Ulbrich, A., & Streif, S. (2025). Modeling Growth Dynamics of Lemna minor: Process Optimization Considering the Influence of Plant Density and Light Intensity. Plants, 14(11), 1722. https://doi.org/10.3390/plants14111722








