Regional Terrain Complexity Assessment Based on Principal Component Analysis and Geographic Information System: A Case of Jiangxi Province, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Introduction of Jiangxi Province and Data Sources
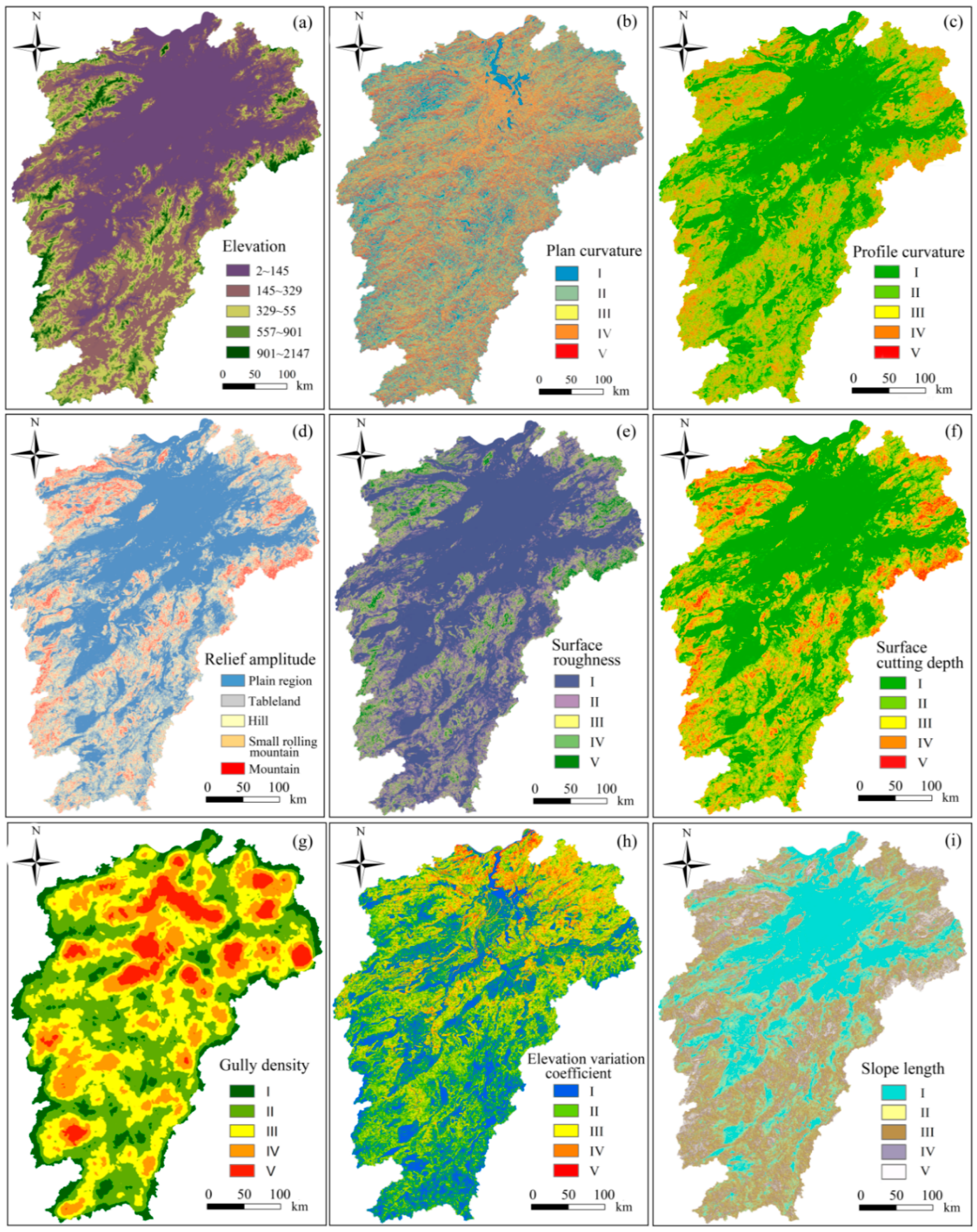
2.2. Description of Terrain Factors
2.3. Modeling Procedures of TCA
2.4. Description of the Methods
2.4.1. Principal Component Analysis
2.4.2. Variation Coefficient Method
2.4.3. K-Means Clustering Model
3. Results
3.1. TCA Using Principal Component Analysis
3.1.1. Terrain Factor Analysis
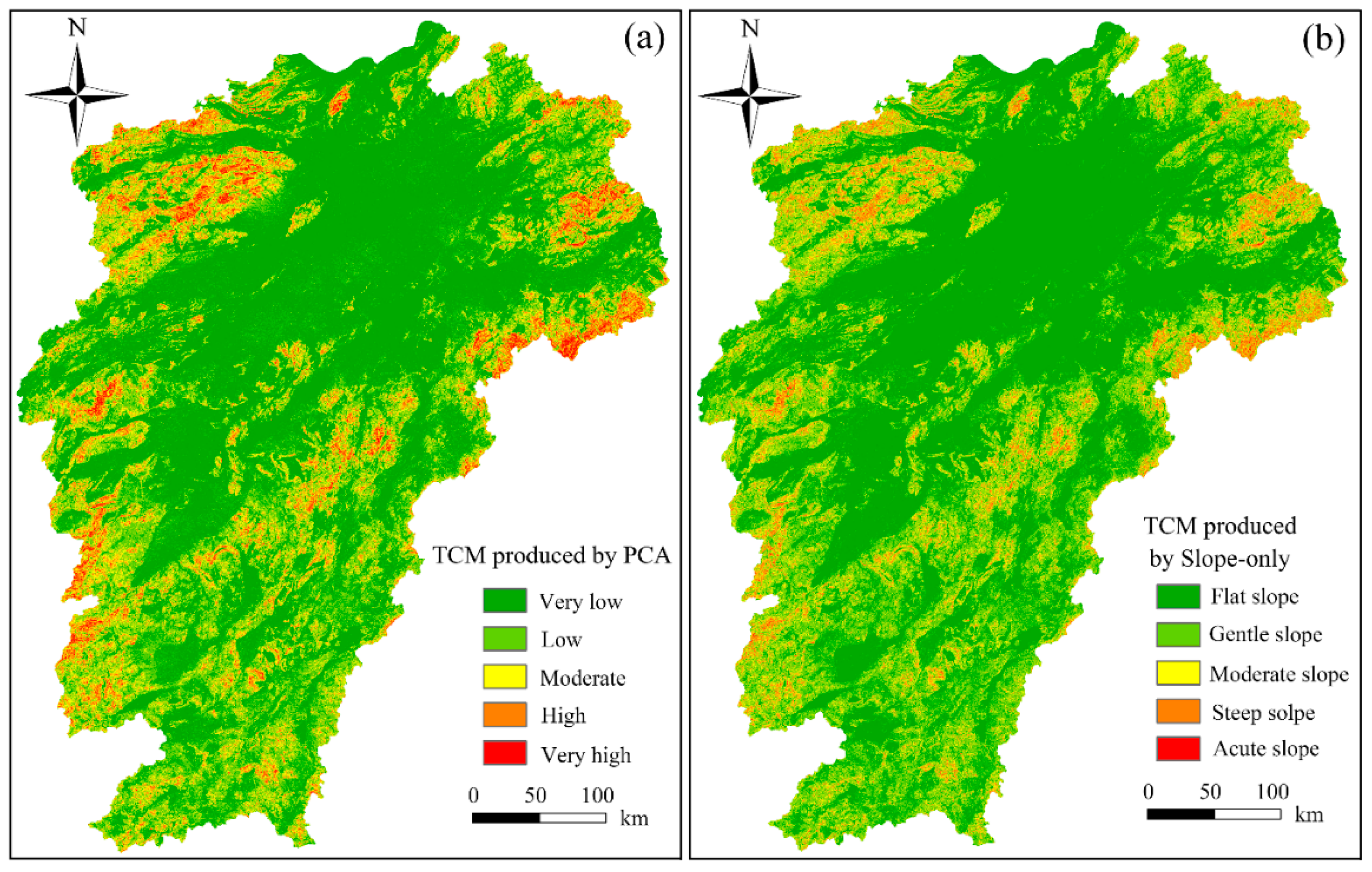
3.1.2. Terrain Complexity Assessment
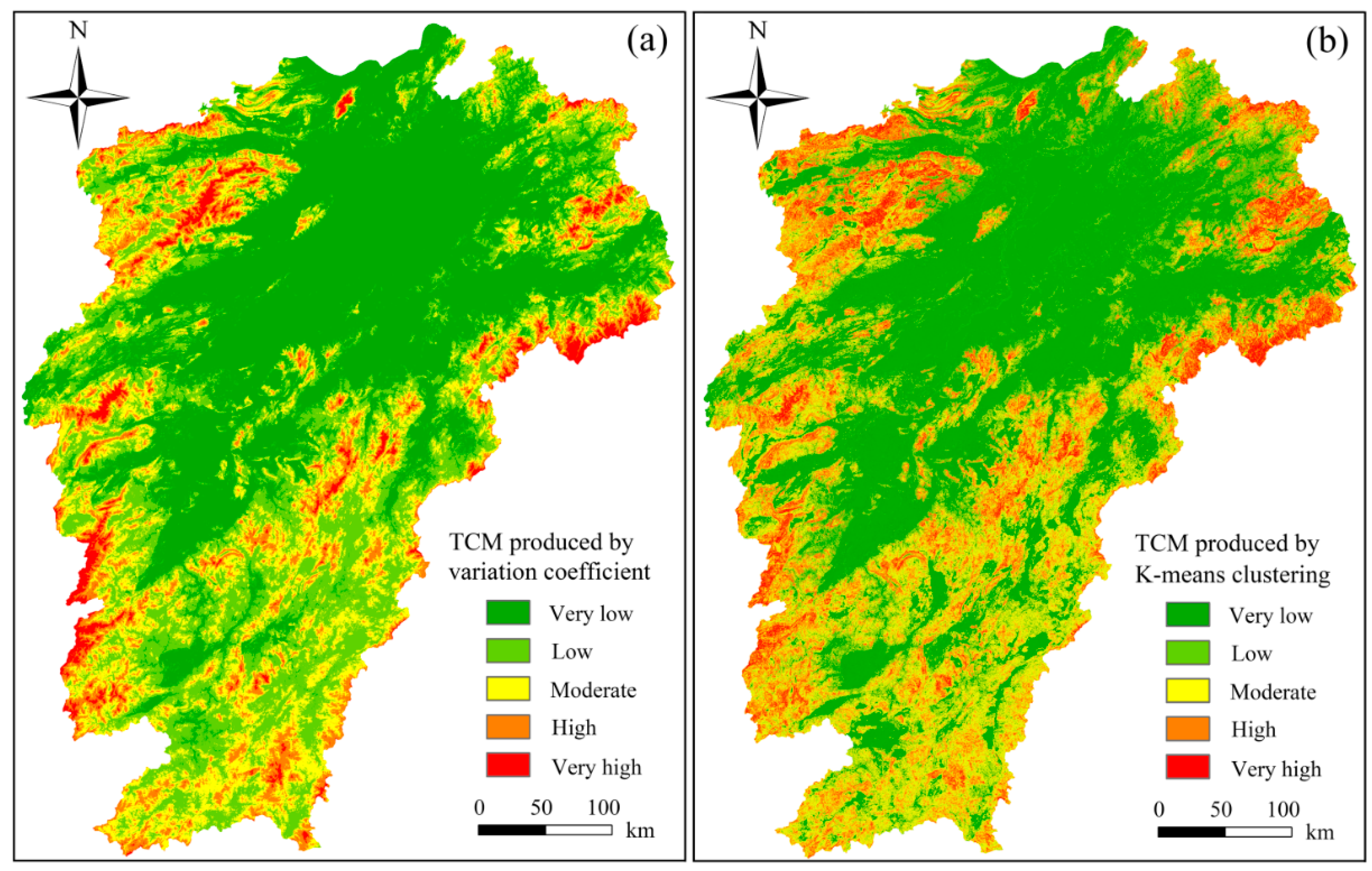
3.2. TCA Using Variation Coefficient Method
3.3. TCA Using K-Means Clustering Model
4. Discussion
4.1. Accuracy Assessment of the Four Models
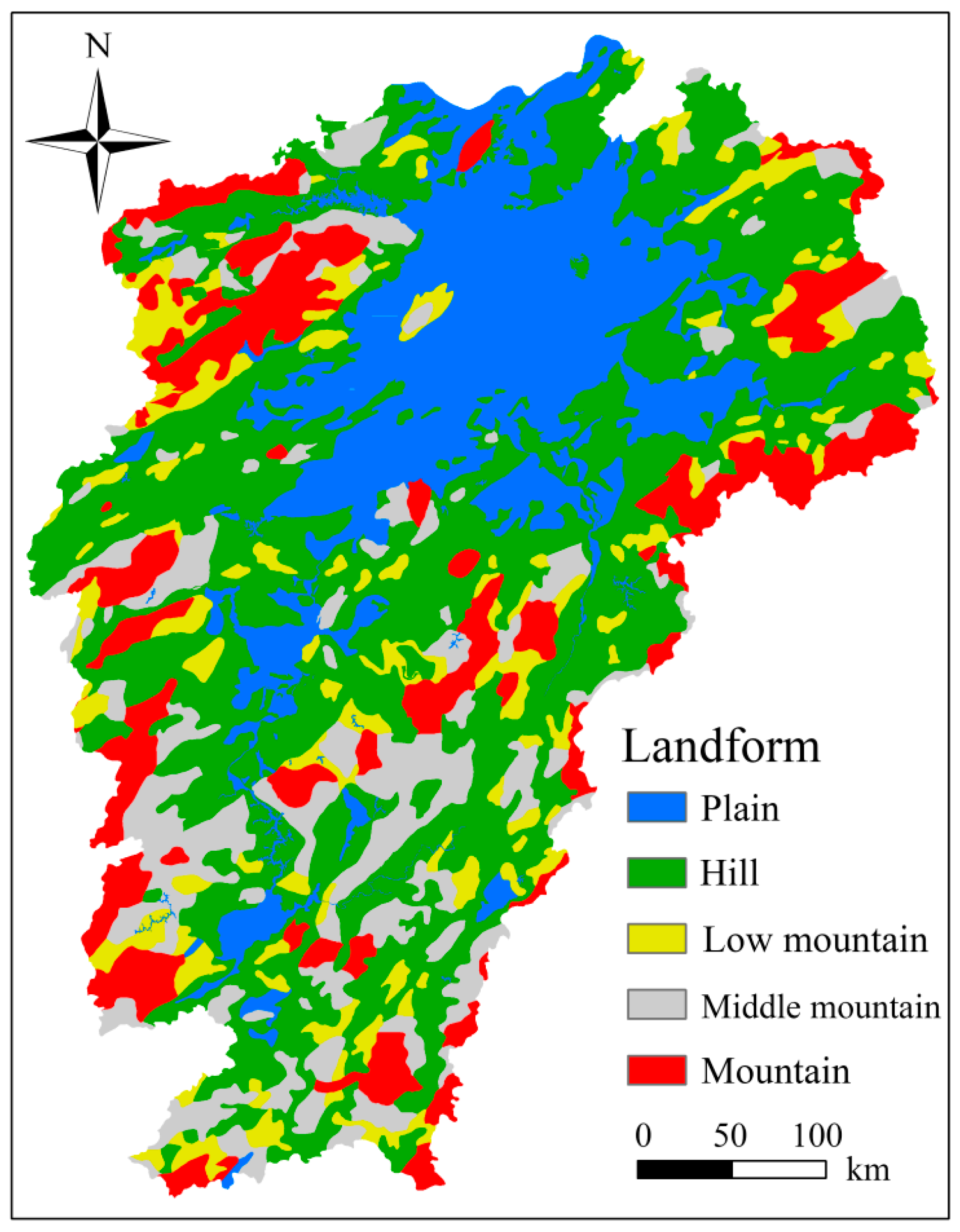
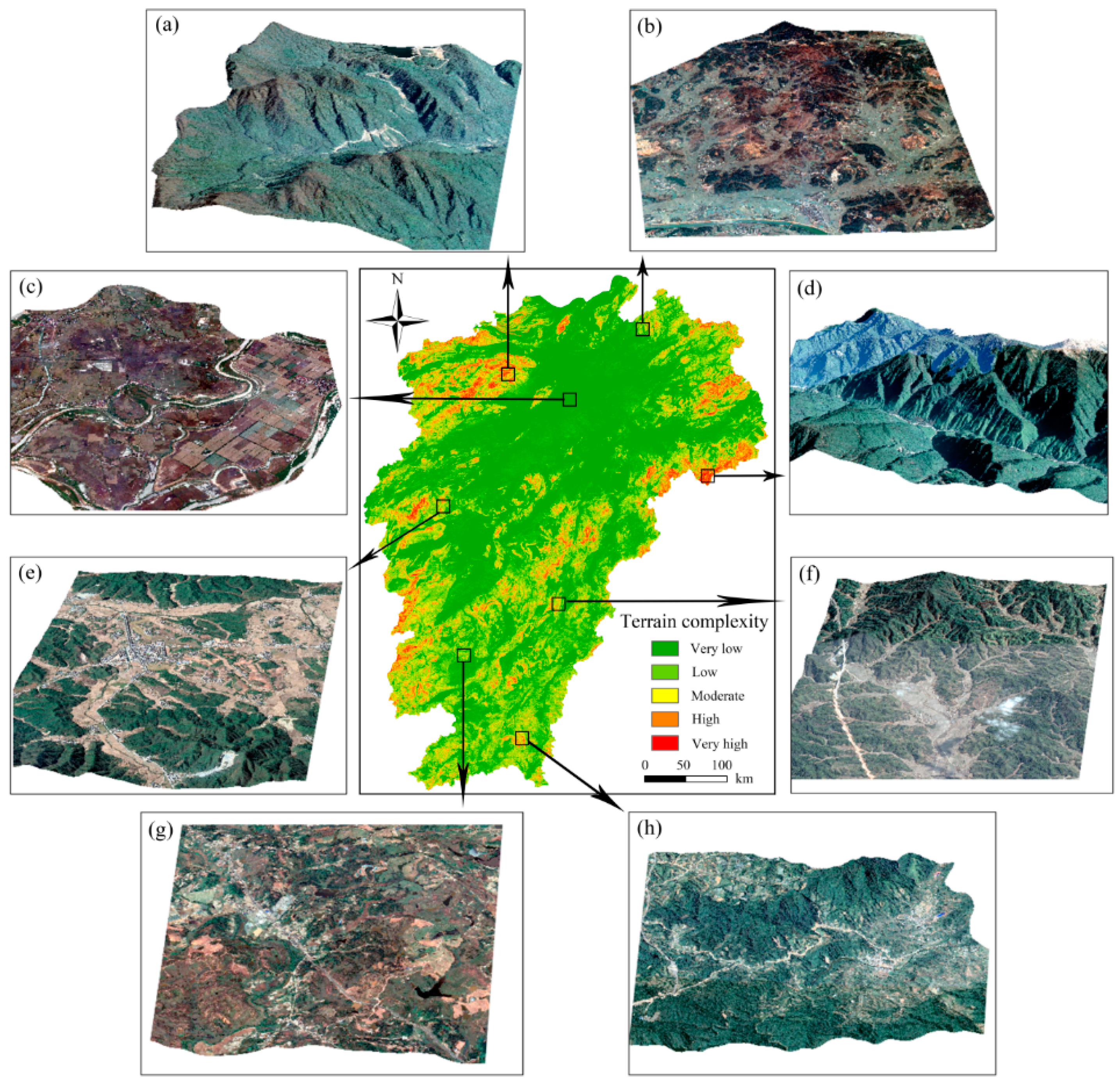
4.2. TCA Compared with Three-Dimensional Aerial Images
4.3. Limitations and Research Prospects
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Huang, C.; Yang, J.; Jiang, P. Assessing impacts of urban form on landscape structure of urban green spaces in china using landsat images based on google earth engine. Remote Sens. 2018, 10, 1569. [Google Scholar] [CrossRef]
- Levin, E.; Shults, R.; Habibi, R.; An, Z.; Roland, W. Geospatial virtual reality for cyberlearning in the field of topographic surveying: Moving towards a cost-effective mobile solution. ISPRS Int. J. Geo-Inf. 2020, 9, 433. [Google Scholar] [CrossRef]
- Li, S.; Zhang, S.; Li, T.; Gao, Y.; Chen, Q.; Zhang, X. Modeling the optimal baseline for a spaceborne bistatic sar system to generate dems. ISPRS Int. J. Geo-Inf. 2020, 9, 108. [Google Scholar] [CrossRef]
- Jaljolie, R.; Van Oosterom, P.; Dalyot, S. Spatial data structure and functionalities for 3d land management system implementation: Israel case study. ISPRS Int. J. Geo-Inf. 2018, 7, 10. [Google Scholar] [CrossRef]
- Ha, T.; Choi, J.Y.; Yoo, J.; Chun, I.; Shim, J. Transformation of small-scale meteorological tsunami due to terrain complexity on the western coast of korea. J. Coast. Res. 2014, 70, 284–289. [Google Scholar] [CrossRef]
- Farmakis-Serebryakova, M.; Hurni, L. Comparison of relief shading techniques applied to landforms. ISPRS Int. J. Geo-Inf. 2020, 9, 253. [Google Scholar] [CrossRef]
- Yang, X.; Tang, G.; Meng, X.; Xiong, L. Saddle position-based method for extraction of depressions in fengcong areas by using digital elevation models. ISPRS Int. J. Geo-Inf. 2018, 7, 136. [Google Scholar] [CrossRef]
- Aguilar, F.J.; Agüera, F.; Aguilar, M.A.; Carvajal, F. Effects of terrain morphology, sampling density, and interpolation methods on grid dem accuracy. Photogramm. Eng. Remote Sens. 2005, 71, 805–816. [Google Scholar] [CrossRef]
- Liu, Y.B.; Smedt, F.D.; Hoffmann, L.; Pfister, L. Assessing land use impacts on flood processes in complex terrain by using gis and modeling approach. Environ. Model. Assess. 2005, 9, 227–235. [Google Scholar] [CrossRef]
- Huang, F.; Chen, L.; Yin, K.; Huang, J.; Gui, L. Object-oriented change detection and damage assessment using high-resolution remote sensing images, tangjiao landslide, three gorges reservoir, china. Environ. Earth Sci. 2018, 77, 183. [Google Scholar] [CrossRef]
- Prasannakumar, V.; Vijith, H.; Geetha, N. Terrain evaluation through the assessment of geomorphometric parameters using DEM and GIS: Case study of two major sub-watersheds in Attapady, South India. Arab. J. Geosci. 2013, 6, 1141–1151. [Google Scholar] [CrossRef]
- Tianwen, L.I.; Liu, X.; Tang, G. Influence of terrain complexity on slope and aspect. J. Mt. Res. 2004, 22, 272–277. [Google Scholar]
- Huaxing, L.U.; Liu, X.; Tang, G. Terrain complexity assessment based on multivariate analysis. J. Mt. Sci. 2012, 30, 616–621. [Google Scholar]
- Long, Y.; Zhou, T.; Tang, G.; Liu, X. Research on terrain complexity of several typical regions of loess landform based on fractal method. J. Mt. Sci. 2007, 25, 385–392. [Google Scholar]
- Ashenfelter, K.T.; Eberhard, K.M. Effects of verb complexity on speech errors. Mem. Cogn. 2007, 35, 1527–1541. [Google Scholar] [CrossRef]
- Chambers, T.C.; Drinnan, A.N.; Mcloughlin, S. Some morphological features of wollemi pine (wollemia nobilis: Araucariaceae) and their comparison to cretaceous plant fossils. Int. J. Plant. Sci. 1998, 159, 160–171. [Google Scholar] [CrossRef]
- Rawat, J.S.; Joshi, R.C. Remote-sensing and gis-based landslide-susceptibility zonation using the landslide index method in igo river basin, eastern himalaya, india. Int. J. Remote Sens. 2012, 33, 3751–3767. [Google Scholar] [CrossRef]
- Thompson, J.A.; Bell, J.C.; Butler, C.A. Digital elevation model resolution: Effects on terrain attribute calculation and quantitative soil-landscape modeling. Geoderma 2015, 100, 67–89. [Google Scholar] [CrossRef]
- Bartlett, M.S.; Movellan, J.R.; Sejnowski, T.J. Face recognition by independent component analysis. IEEE Trans. Neural Netw. 2002, 13, 1450–1464. [Google Scholar] [CrossRef]
- Gasmi, A.; Gomez, C.; Zouari, H.; Masse, A.; Ducrot, D. Pca and svm as geo-computational methods for geological mapping in the southern of tunisia, using aster remote sensing data set. Arab. J. Geosci. 2016, 9, 753. [Google Scholar] [CrossRef]
- Lan, L.; Li, C.F.; Lei, Y.M.; Yin, J.Y.; Zhao, J.J. Feature extraction for hyperspectral remote sensing image using weighted pca-ica. Arab. J. Geosci. 2017, 10, 307. [Google Scholar]
- Zhao, X.; Wang, W.; Chu, X.; Li, C.; Kimuli, D. Early detection of aspergillus parasiticus infection in maize kernels using near-infrared hyperspectral imaging and multivariate data analysis. Appl. Sci. 2017, 7, 90. [Google Scholar] [CrossRef]
- Marchetti, M.; Offroy, M.; Abdat, F.; Branchu, P.; Bourson, P.; Jobard, C.; Durmont, J.-F.; Casteran, G. Chemometrics-assisted monitoring in raman spectroscopy for the biodegradation process of an aqueous polyfluoroalkyl ether from a fire-fighting foam in an environmental matrix. Environments 2020, 7, 4. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Z.; Yin, X. A novel probabilistic power flow algorithm based on principal component analysis and high-dimensional model representation techniques. Energies 2020, 13, 3520. [Google Scholar] [CrossRef]
- Geng, D.; Zhang, H.; Wu, H. Short-term wind speed prediction based on principal component analysis and lstm. Appl. Sci. 2020, 10, 4416. [Google Scholar] [CrossRef]
- Schwartz, C.; Ramos, L.P.; Duarte, L.T.; Pinho, M.d.S.; Pettersson, M.I.; Vu, V.T.; Machado, R. Change detection in uwb sar images based on robust principal component analysis. Remote Sens. 2020, 12, 1916. [Google Scholar] [CrossRef]
- Gao, J.; Chai, S.; Zhang, B.; Xia, Y. Research on network intrusion detection based on incremental extreme learning machine and adaptive principal component analysis. Energies 2019, 12, 1223. [Google Scholar] [CrossRef]
- Samsonov, T.E. Automated conflation of digital elevation model with reference hydrographic lines. ISPRS Int. J. Geo-Inf. 2020, 9, 334. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Jiang, S.-H.; Zhou, C.; Huang, J.; Guo, Z. Landslide susceptibility prediction based on a semi-supervised multiple-layer perceptron model. Landslides 2020. [Google Scholar] [CrossRef]
- Pham, B.T.; Bui, D.T.; Prakash, I.; Dholakia, M.B. Hybrid integration of multilayer perceptron neural networks and machine learning ensembles for landslide susceptibility assessment at himalayan area (india) using gis. Catena 2017, 149, 52–63. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Huang, J.; Lei, G.; Peng, W. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 2017, 223, 11–22. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, L.; Fan, L.; Huang, J.; Huang, F.; Chen, J.; Zhang, Z.; Wang, Y. Landslide susceptibility prediction modeling based on remote sensing and a novel deep learning algorithm of a cascade-parallel recurrent neural network. Sensors 2020, 20, 1576. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Huang, F.; Yan, L.; Cao, Z.; Chen, J.; Ye, Z. Landslide susceptibility prediction using particle-swarm-optimized multilayer perceptron: Comparisons with multilayer-perceptron-only, bp neural network, and information value models. Appl. Sci. 2019, 9, 3664. [Google Scholar] [CrossRef]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide susceptibility prediction based on remote sensing images and gis: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. CATENA 2020, 191, 104580. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Du, Z.; Yao, C.; Huang, J.; Jiang, Q.; Chang, Z.; Li, S. Landslide susceptibility prediction considering regional soil erosion based on machine-learning models. ISPRS Int. J. Geo-Inf. 2020, 9, 377. [Google Scholar] [CrossRef]
- Hong, H.; Ilia, I.; Tsangaratos, P.; Chen, W.; Xu, C. A hybrid fuzzy weight of evidence method in landslide susceptibility analysis on the wuyuan area, china. Geomorphology 2017, 290, 1–16. [Google Scholar] [CrossRef]
- Huang, F.; Yao, C.; Liu, W.; Li, Y.; Liu, X. Landslide susceptibility assessment in the nantian area of china: A comparison of frequency ratio model and support vector machine. Geomat. Nat. Hazards Risk 2018, 9, 919–938. [Google Scholar] [CrossRef]
- Han, X.Y.; Qian, J.; Wang, L.; Liu, F.; Mao, Z.Q. Progress in studying multi-scale process of soil erosion(water erosion) and soil conservation in the loess plateau. J. Glaciol. Geocryol. 2012, 34, 1487–1498. [Google Scholar]
- Liu, W.; Wan, S.; Huang, F.; Luo, X.; Fu, M. Experimental study of subsurface erosion in granitic under the conditions of different soil column angles and flow discharges. Bull. Eng. Geol. Environ. 2019, 78, 5877–5888. [Google Scholar] [CrossRef]
- Li, Y.; Huang, J.; Jiang, S.-H.; Huang, F.; Chang, Z. A web-based gps system for displacement monitoring and failure mechanism analysis of reservoir landslide. Sci. Rep. 2017, 7, 17171. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Zhang, G.; Zhou, C.; Zhang, J. Landslide groundwater level time series prediction based on phase space reconstruction and wavelet analysis-support vector machine optimized by pso algorithm. Earth Sci. J. China Univ. Geosci. 2015, 40, 1254–1265. [Google Scholar]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Lin, G.F.; Chang, M.J.; Huang, Y.C.; Ho, J.Y. Assessment of susceptibility to rainfall-induced landslides using improved self-organizing linear output map, support vector machine, and logistic regression. Eng. Geol. 2017, 224, 62–74. [Google Scholar] [CrossRef]
- Szymura, T.H.; Szymura, M.; Pietrzak, M. Influence of land relief and soil properties on stand structure of overgrown oak forests of coppice origin with sorbus torminalis. Dendrobiology 2014, 71, 49–58. [Google Scholar] [CrossRef]
- Liu, L. The ups and downs of North America: Evaluating the role of mantle dynamic topography since the mesozoic. Rev. Geophys. 2015, 53, 1022–1049. [Google Scholar] [CrossRef]
- Zhang, F.; Chen, L.I.; Meng, B.; Zhao, H.; Liu, Z. Investigation of surface deformation characteristic and removal mechanism for k9 glass based on varied cutting-depth nano-scratch. J. Mech. Eng. 2016, 52, 65–71. [Google Scholar] [CrossRef]
- Parhad, P.; Likhite, A.; Bhatt, J.; Peshwe, D. The effect of cutting speed and depth of cut on surface roughness during machining of austempered ductile iron. Trans. Indian Inst. Met. 2015, 68, 99–108. [Google Scholar] [CrossRef]
- Robinson, I.K. Crystal truncation rods and surface roughness. Phys. Rev. B Condens. Matter 1986, 33, 3830. [Google Scholar] [CrossRef]
- Zhao, J.; Vanmaercke, M.; Chen, L.; Govers, G. Vegetation cover and topography rather than human disturbance control gully density and sediment production on the chinese loess plateau. Geomorphology 2016, 274, 92–105. [Google Scholar] [CrossRef]
- Guo, Z.; Yin, K.; Gui, L.; Liu, Q.; Huang, F.; Wang, T. Regional rainfall warning system for landslides with creep deformation in three gorges using a statistical black box model. Sci. Rep. 2019, 9, 8962. [Google Scholar] [CrossRef]
- Kaneta, M.; Miyai, N.; Yamamoto, M.; Oka, M.; Utsumi, M.; Shiba, M.; Arita, M. 3d.08: Arterial stiffness and autonomic nervous function on orthostatic blood pressure-elevation in hypertensive patients. J. Hypertens. 2015, 33 (Suppl. 1), e42. [Google Scholar] [CrossRef]
- Tubaro, M.; Sciahbasi, A.; Ricci, R.; Ciavolella, M.; Di, C.D.; Bisconti, C.; Ferraiuolo, G.; Del, P.M.; Mennuni, M.; Monti, F. Early invasive versus early conservative strategy in non-st-elevation acute coronary syndrome: An outcome research study. Eur. Heart J. Acute Cardiovasc. Care 2017, 76, 511–527. [Google Scholar] [CrossRef] [PubMed]
- Liu, B.Y.; Nearing, M.A.; Shi, P.J.; Jia, Z.W. Slope length effects on soil loss for steep slopes. Soil Sci. Soc. Am. J. 2000, 64, 1759–1763. [Google Scholar] [CrossRef]
- Huang, F.; Chen, J.; Yao, C.; Chang, Z.; Jiang, Q.; Li, S.; Guo, Z. Susle: A slope and seasonal rainfall-based rusle model for regional quantitative prediction of soil erosion. Bull. Eng. Geol. Environ. 2020. [Google Scholar] [CrossRef]
- Malhi, A.; Gao, R.X. Pca-based feature selection scheme for machine defect classification. IEEE Trans. Instrum. Meas. 2004, 53, 1517–1525. [Google Scholar] [CrossRef]
- Eldridge, S.M.; Ashby, D.; Kerry, S. Sample size for cluster randomized trials: Effect of coefficient of variation of cluster size and analysis method. Int. J. Epidemiol. 2006, 35, 1292. [Google Scholar] [CrossRef] [PubMed]
- Weiss, E.; Milich, L. Errors in a standard method for generating interannual ndvi coefficient of variation (cov) images. Int. J. Remote Sens. 1997, 18, 3743–3748. [Google Scholar] [CrossRef]
- Çoşkun, G. A new slip safety risk scale of natural stones with statistical k-means clustering analysis. Arab. J. Geosci. 2018, 11, 799. [Google Scholar] [CrossRef]
- Moghimi, A.; Khazai, S.; Mohammadzadeh, A. An improved fast level set method initialized with a combination of k-means clustering and otsu thresholding for unsupervised change detection from sar images. Arab. J. Geosci. 2017, 10, 293. [Google Scholar] [CrossRef]
- Tipping, M.E.; Bishop, C.M. Mixtures of probabilistic principal component analyzers. Neural Comput. 2014, 11, 443–482. [Google Scholar] [CrossRef]
- Zhao, Y.N.; Niu, R.Q.; Li, J.; Peng, L.; Wang, Y. Prediction of landslide displacement based on kernel principal component analysis and neural network-markov chain. In Advanced Materials Research; Trans Tech Publ.: Freienbach, Switzerland, 2013; pp. 1512–1520. [Google Scholar]


| Principal Component | Eigenvalue | Explanatory Contribution Rate (%) | Cumulative Contribution Rate (%) |
|---|---|---|---|
| 1 | 5.518 | 55.179 | 55.179 |
| 2 | 1.184 | 11.843 | 67.022 |
| 3 | 1.007 | 10.072 | 77.094 |
| 4 | 0.900 | 9.000 | 86.094 |
| 5 | 0.569 | 5.687 | 91.781 |
| 6 | 0.373 | 3.735 | 95.515 |
| 7 | 0.260 | 2.605 | 98.120 |
| 8 | 0.145 | 1.449 | 99.569 |
| 9 | 0.024 | 0.235 | 99.804 |
| 10 | 0.020 | 0.196 | 100 |
| Terrain Factors | |||||
|---|---|---|---|---|---|
| elevation (E) | 0.780 | −0.477 | 0.019 | 0.180 | 0.036 |
| slope (S) | 0.961 | 0.036 | −0.085 | 0.066 | −0.091 |
| plan curvature (Plc) | −0.238 | −0.107 | 0.927 | 0.198 | −0.140 |
| profile curvature (Prc) | 0.724 | 0.044 | 0.251 | −0.019 | 0.534 |
| relief amplitude (Rel) | 0.956 | 0.059 | 0.068 | 0.062 | −0.130 |
| surface roughness (Rou) | 0.944 | 0.021 | 0.063 | 0.090 | −0.147 |
| surface cutting depth (Scd) | 0.859 | 0.014 | −0.131 | 0.159 | −0.317 |
| gully density (Gd) | −0.272 | 0.477 | −0.127 | 0.812 | 0.134 |
| elevation variation coefficient (Evc) | 0.316 | 0.840 | 0.187 | −0.335 | −0.103 |
| slope length (L) | 0.829 | 0.067 | 0.001 | −0.118 | 0.294 |
| Terrain Factor | E | S | Plc | Prc | Rel | Rou | Scd | Gd | Ecv | L |
|---|---|---|---|---|---|---|---|---|---|---|
| Variable coefficient | 0.923 | 0.967 | 0.680 | 0.981 | 0.920 | 0.964 | 0.030 | 0.577 | 0.701 | 0.232 |
| Weight value | 0.132 | 0.139 | 0.097 | 0.141 | 0.132 | 0.138 | 0.004 | 0.083 | 0.101 | 0.033 |
| Terrain Factor | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| elevation (E) | 2.122 | −0.489 | −0.654 | 0.444 | 1.171 |
| slope (S) | 2.855 | 0.138 | −0.801 | 0.190 | 1.462 |
| plan curvature (Plc) | −0.706 | −0.054 | 0.174 | 0.016 | −0.391 |
| profile curvature (Prc) | 1.215 | 0.281 | −0.681 | 0.305 | 1.095 |
| relief amplitude (Rel) | 2.752 | 0.240 | −0.794 | 0.168 | 1.424 |
| surface roughness (Rou) | 2.765 | 0.146 | −0.769 | 0.162 | 1.429 |
| surface cutting depth (Scd) | 3.940 | −0.109 | −0.548 | −0.116 | 1.212 |
| gully density (Gd) | 0.407 | 1.745 | −0.410 | −0.251 | 0.284 |
| elevation variation coefficient (Evc) | −0.372 | 0.322 | 0.259 | −0.366 | −0.301 |
| slope length (L) | 1.165 | 0.578 | −0.979 | 0.749 | 0.959 |
| PCA | Slope-Only | Variation Coefficient | K-Means Clustering | |||||
|---|---|---|---|---|---|---|---|---|
| TCA Level | Area/km2 | Percentage/% | Area/km2 | Percentage/% | Area/km2 | Percentage/% | Area/km2 | Percentage/% |
| very low | 61,156 | 36.64 | 83,442 | 50.00 | 66,395 | 39.78 | 74,493 | 44.63 |
| low | 67,954 | 40.72 | 56,538 | 33.88 | 48,384 | 28.99 | 19,004 | 11.39 |
| moderate | 25,274 | 15.14 | 22,409 | 13.43 | 32,383 | 19.40 | 45,098 | 27.02 |
| high | 10,078 | 6.04 | 4271 | 2.56 | 15,495 | 9.28 | 23,247 | 13.93 |
| Very high | 2438 | 1.46 | 240 | 0.14 | 4243 | 2.54 | 5058 | 3.03 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Yang, J.; Zhang, B.; Li, Y.; Huang, J.; Chen, N. Regional Terrain Complexity Assessment Based on Principal Component Analysis and Geographic Information System: A Case of Jiangxi Province, China. ISPRS Int. J. Geo-Inf. 2020, 9, 539. https://doi.org/10.3390/ijgi9090539
Huang F, Yang J, Zhang B, Li Y, Huang J, Chen N. Regional Terrain Complexity Assessment Based on Principal Component Analysis and Geographic Information System: A Case of Jiangxi Province, China. ISPRS International Journal of Geo-Information. 2020; 9(9):539. https://doi.org/10.3390/ijgi9090539
Chicago/Turabian StyleHuang, Faming, Jianbo Yang, Biao Zhang, Yijing Li, Jinsong Huang, and Na Chen. 2020. "Regional Terrain Complexity Assessment Based on Principal Component Analysis and Geographic Information System: A Case of Jiangxi Province, China" ISPRS International Journal of Geo-Information 9, no. 9: 539. https://doi.org/10.3390/ijgi9090539
APA StyleHuang, F., Yang, J., Zhang, B., Li, Y., Huang, J., & Chen, N. (2020). Regional Terrain Complexity Assessment Based on Principal Component Analysis and Geographic Information System: A Case of Jiangxi Province, China. ISPRS International Journal of Geo-Information, 9(9), 539. https://doi.org/10.3390/ijgi9090539






