Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis
Abstract
1. Introduction
2. Material and Methods
2.1. Algorithm Description
2.1.1. Topographic Surface
2.1.2. Terrain Parameters: Neighbor Elevations and Geometries
2.1.3. Terrain Derivatives
2.1.4. Terrain Attributes
2.2. Package Description
2.3. Statistical Evaluation
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moore, I.D.; Grayson, R.B.; Ladson, A.R. Digital terrain modelling: A review of hydrological, geomorphological, and biological applications. Hydrol. Process. 1991, 5, 3–30. [Google Scholar] [CrossRef]
- Amatulli, G.; Domisch, S.; Tuanmu, M.-N.; Parmentier, B.; Ranipeta, A.; Malczyk, J.; Jetz, W. A suite of global, cross-scale topographic variables for environmental and biodiversity modeling. Sci. Data 2018, 5, 180040. [Google Scholar] [CrossRef]
- Pike, R.J. Geomorphometry-diversity in quantitative surface analysis. Prog. Phys. Geogr. Earth Env. 2000, 24, 1–20. [Google Scholar] [CrossRef]
- Bogaart, P.W.; Troch, P.A. Curvature distribution within hillslopes and catchments and its effect on the hydrological response. Hydrol. Earth Syst. Sci. 2006, 10, 925–936. [Google Scholar] [CrossRef]
- Alexander, C.; Deák, B.; Heilmeier, H. Micro-topography driven vegetation patterns in open mosaic landscapes. Ecol. Indic. 2016, 60, 906–920. [Google Scholar] [CrossRef]
- Oliveira, S.; Pereira, J.M.C.; San-Miguel-Ayanz, J.; Lourenço, L. Exploring the spatial patterns of fire density in Southern Europe using Geographically Weighted Regression. Appl. Geogr. 2014, 51, 143–157. [Google Scholar] [CrossRef]
- McGuire, K.J.; McDonnell, J.J.; Weiler, M.; Kendall, C.; McGlynn, B.L.; Welker, J.M.; Seibert, J. The role of topography on catchment-scale water residence time. Water Resour. Res. 2005, 41. [Google Scholar] [CrossRef]
- Florinsky, I.V. Digital Terrain Analysis in Soil Science and Geology; Academic Press: Cambridge, MA, USA, 2016; ISBN 9780128046326. [Google Scholar]
- USGS EROS. USGS EROS Archive-Digital Elevation-Shuttle Radar Topography Mission (SRTM) Void Filled. Available online: https://doi.org/10.5066/F7F76B1X (accessed on 4 April 2020).
- JAXA EORC. ALOS Global Digital Surface Model “ALOS World 3D-30m (AW3D30)”. Available online: https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm (accessed on 4 April 2020).
- Liu, X.; Hu, G.; Chen, Y.; Li, X.; Xu, X.; Li, S.; Pei, F.; Wang, S. High-resolution multi-temporal mapping of global urban land using Landsat images based on the Google Earth Engine Platform. Remote Sens. Env. 2018, 209, 227–239. [Google Scholar] [CrossRef]
- Olaya, V.; Conrad, O. Geomorphometry in SAGA. In Developments in Soil Science; Elsevier: Amsterdam, The Netherlands, 2009; Volume 33, pp. 293–308. [Google Scholar]
- Miliaresis, G. The Landcover Impact on the Aspect/Slope Accuracy Dependence of the SRTM-1 Elevation Data for the Humboldt Range. Sensors 2008, 8, 3134–3149. [Google Scholar] [CrossRef]
- Bindzárová Gergeľová, M.; Kuzevičová, Ž.; Labant, S.; Gašinec, J.; Kuzevič, Š.; Unucka, J.; Liptai, P. Evaluation of Selected Sub-Elements of Spatial Data Quality on 3D Flood Event Modeling: Case Study of Prešov City, Slovakia. Appl. Sci. 2020, 10, 820. [Google Scholar] [CrossRef]
- Xia, J.; Yang, C.; Li, Q. Building a spatiotemporal index for Earth Observation Big Data. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 245–252. [Google Scholar] [CrossRef]
- Danielson, J.J.; Gesch, D.B. Global Multi-Resolution Terrain Elevation Data 2010 (GMTED2010); U.S. Geo-logical Survey Open-File Report 2011–1073; United States Geological Survey (USGS): Sioux Falls, SD, USA, 2011. [Google Scholar]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Env. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Abernathey, R.; Paul, K.; Hamman, J.; Rocklin, M.; Lepore, C.; Tippett, M.; Henderson, N.; Seager, R.; May, R.; Del Vento, D. Pangeo NSF Earthcube Proposal. Available online: https://figshare.com/articles/Pangeo_NSF_Earthcube_Proposal/5361094 (accessed on 10 March 2020).
- mundialis GmbH & Co. KG. Actinia: Geoprocessing in the Cloud. Available online: https://actinia.mundialis.de/ (accessed on 10 March 2020).
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Donchyts, G.; Baart, F.; Winsemius, H.; Gorelick, N.; Kwadijk, J.; van de Giesen, N. Earth’s surface water change over the past 30 years. Nat. Clim. Chang. 2016, 6, 810–813. [Google Scholar] [CrossRef]
- Crowley, M.A.; Cardille, J.A.; White, J.C.; Wulder, M.A. Multi-sensor, multi-scale, Bayesian data synthesis for mapping within-year wildfire progression. Remote Sens. Lett. 2019, 10, 302–311. [Google Scholar] [CrossRef]
- Demattê, J.A.M.; Safanelli, J.L.; Poppiel, R.R.; Rizzo, R.; Silvero, N.E.Q.; Mendes, W.S.; Bonfatti, B.R.; Dotto, A.C.; Salazar, D.F.U.; Mello, F.A.O.; et al. Bare Earth’s Surface Spectra as a Proxy for Soil Resource Monitoring. Sci. Rep. 2020, 10, 4461. [Google Scholar] [CrossRef]
- USGS EROS. GTOPO30-Global 1-km Digital Raster Data Derived from a Variety of Sources. Available online: https://doi.org/10.5066/F7DF6PQS (accessed on 10 March 2020).
- Florinsky, I.V. Spheroidal equal angular DEMs: The specificity of morphometric treatment. Trans. GIS 2017, 21, 1115–1129. [Google Scholar] [CrossRef]
- Brainerd, J.; Pang, A. Interactive map projections and distortion. Comput. Geosci. 2001, 27, 299–314. [Google Scholar] [CrossRef]
- Koenderink, J.J.; van Doorn, A.J. Surface shape and curvature scales. Image Vis. Comput. 1992, 10, 557–564. [Google Scholar] [CrossRef]
- Gauss, C.F. General Investigations of Curved Surfaces of 1827 and 1825; Princeton University Library: Princeton, NY, USA, 1902. [Google Scholar]
- Florinsky, I.V. An illustrated introduction to general geomorphometry. Prog. Phys. Geogr. Earth Env. 2017, 41, 723–752. [Google Scholar] [CrossRef]
- Tamiminia, H.; Salehi, B.; Mahdianpari, M.; Quackenbush, L.; Adeli, S.; Brisco, B. Google Earth Engine for geo-big data applications: A meta-analysis and systematic review. ISPRS J. Photogramm. Remote Sens. 2020, 164, 152–170. [Google Scholar] [CrossRef]
- Florinsky, I.V.; Pankratov, A.N. A universal spectral analytical method for digital terrain modeling. Int. J. Geogr. Inf. Sci. 2016, 30, 2506–2528. [Google Scholar] [CrossRef]

| Attribute | Unit | Description |
|---|---|---|
| Elevation | meter | Height of terrain above sea level |
| Slope | degree | Slope gradient |
| Aspect | degree | Compass direction |
| Hillshade | dimensionless | Brightness of the illuminated terrain |
| Northernness | dimensionless | Degree of orientation to North |
| Easternness | dimensionless | Degree of orientation to East |
| Horizontal curvature | meter | Curvature tangent to the contour line |
| Vertical curvature | meter | Curvature tangent to the slope line |
| Mean curvature | meter | Half-sum of the two orthogonal curvatures |
| Minimal curvature | meter | Lowest value of curvature |
| Maximal curvature | meter | Highest value of curvature |
| Gaussian curvature | meter | Product of maximal and minimal curvatures |
| Shape Index | dimensionless | Continuous form of the Gaussian classification |
| Attribute | Region | Reference | Pearson’s r | rMAE 1 |
|---|---|---|---|---|
| Aspect | Near global SRTM DEM 30 m | GEE | 0.89 * | 13% |
| Slope | Near global SRTM DEM 30 m | GEE | 0.98 * | 2% |
| Aspect | Mount Ararat SRTM DEM 30 m | SAGA GIS | 0.96 * | 4% |
| Slope | Mount Ararat SRTM DEM 30 m | SAGA GIS | 0.98 * | 3% |
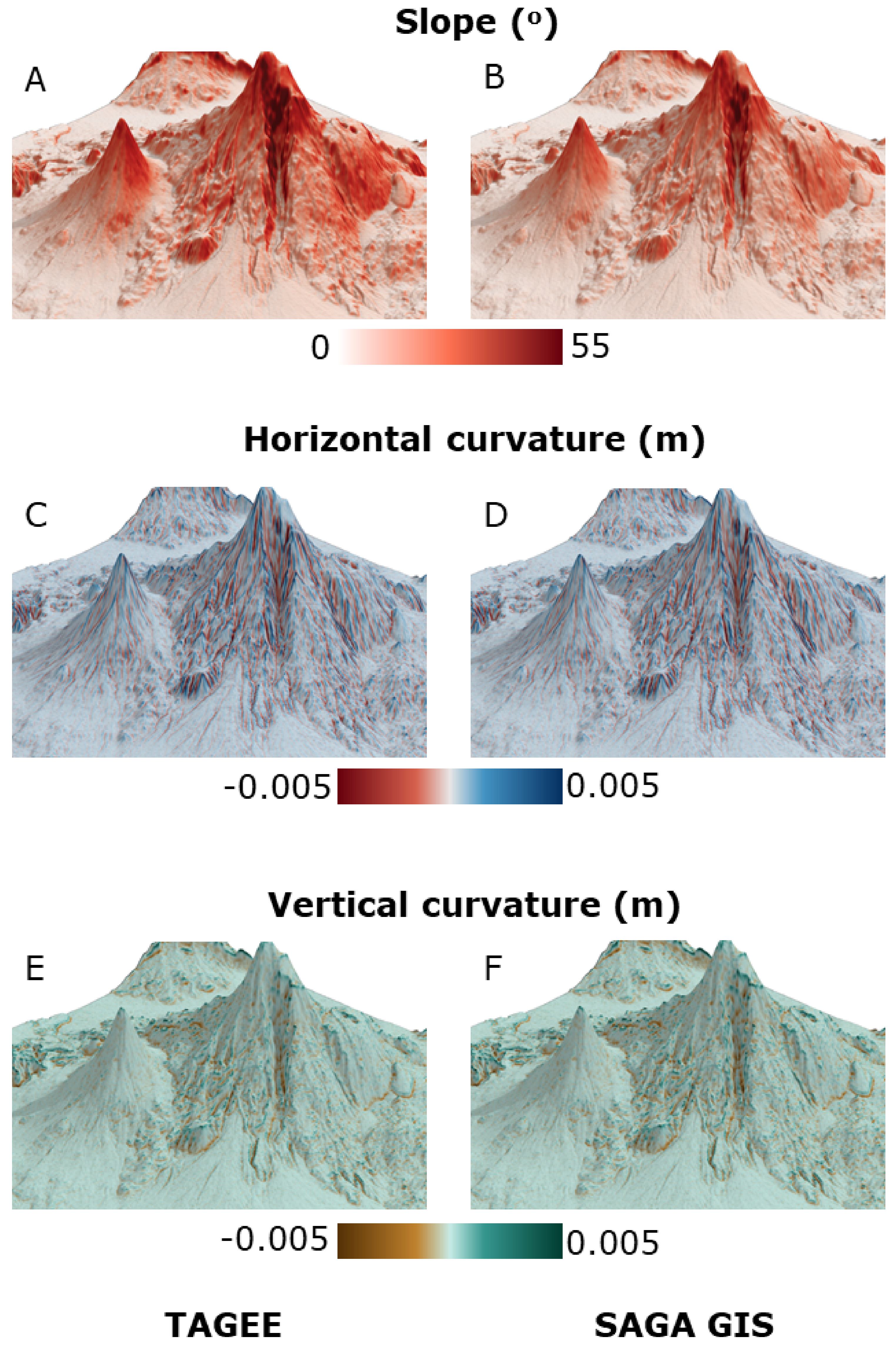
| Horizontal curvature | Mount Ararat SRTM DEM 30 m | SAGA GIS | 0.98 * | 4% |
| Vertical curvature | Mount Ararat SRTM DEM 30 m | SAGA GIS | 0.98 * | 4% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Safanelli, J.L.; Poppiel, R.R.; Ruiz, L.F.C.; Bonfatti, B.R.; Mello, F.A.d.O.; Rizzo, R.; Demattê, J.A.M. Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis. ISPRS Int. J. Geo-Inf. 2020, 9, 400. https://doi.org/10.3390/ijgi9060400
Safanelli JL, Poppiel RR, Ruiz LFC, Bonfatti BR, Mello FAdO, Rizzo R, Demattê JAM. Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis. ISPRS International Journal of Geo-Information. 2020; 9(6):400. https://doi.org/10.3390/ijgi9060400
Chicago/Turabian StyleSafanelli, José Lucas, Raul Roberto Poppiel, Luis Fernando Chimelo Ruiz, Benito Roberto Bonfatti, Fellipe Alcantara de Oliveira Mello, Rodnei Rizzo, and José A. M. Demattê. 2020. "Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis" ISPRS International Journal of Geo-Information 9, no. 6: 400. https://doi.org/10.3390/ijgi9060400
APA StyleSafanelli, J. L., Poppiel, R. R., Ruiz, L. F. C., Bonfatti, B. R., Mello, F. A. d. O., Rizzo, R., & Demattê, J. A. M. (2020). Terrain Analysis in Google Earth Engine: A Method Adapted for High-Performance Global-Scale Analysis. ISPRS International Journal of Geo-Information, 9(6), 400. https://doi.org/10.3390/ijgi9060400






