Landslide Susceptibility Prediction Considering Regional Soil Erosion Based on Machine-Learning Models
Abstract
1. Introduction
2. Materials
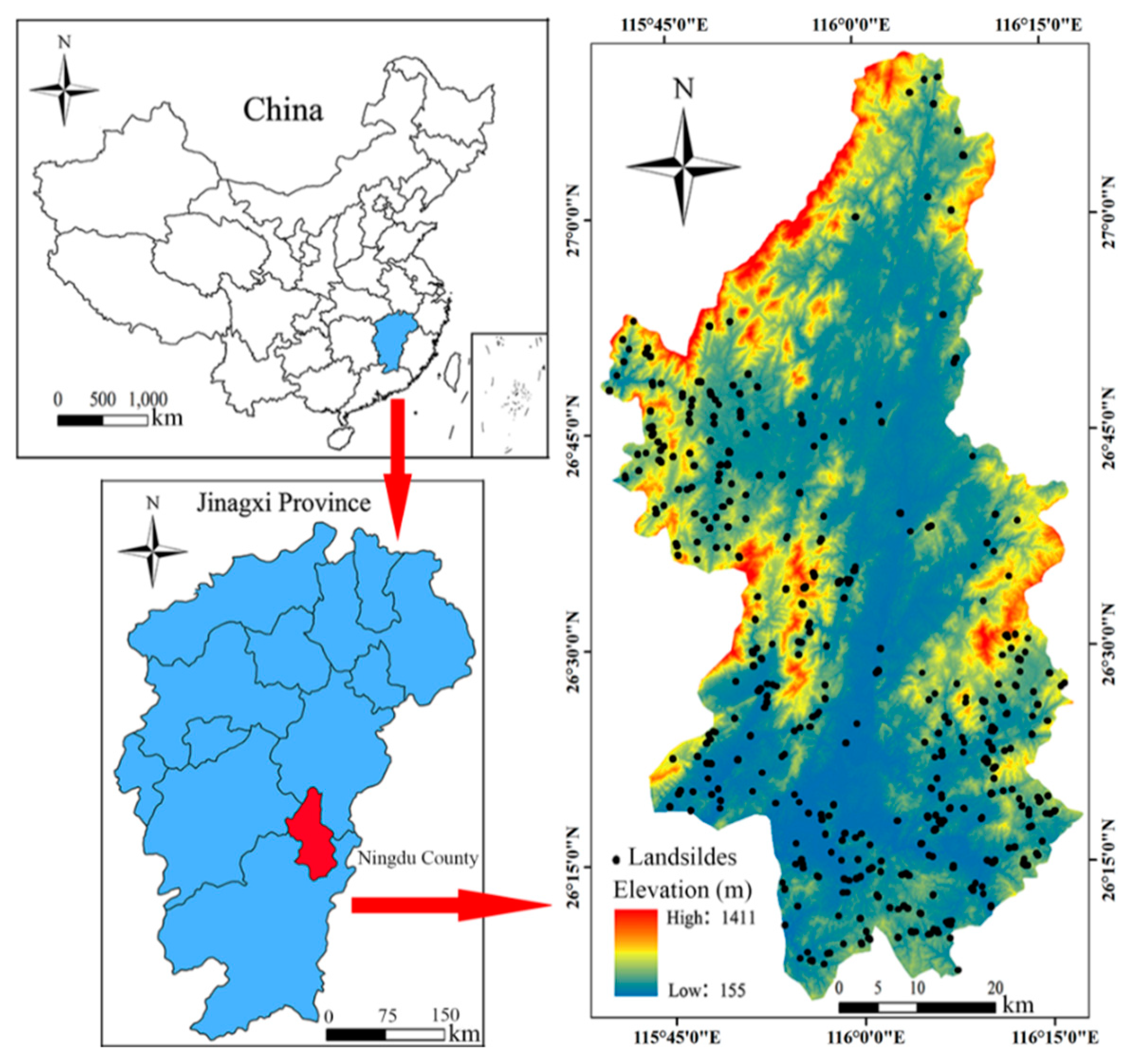
2.1. Introduction to Ningdu County and Landslide Inventory
2.2. Conventional Landslide Predisposing Factors
2.3. Spatial Database Analysis
3. Methods
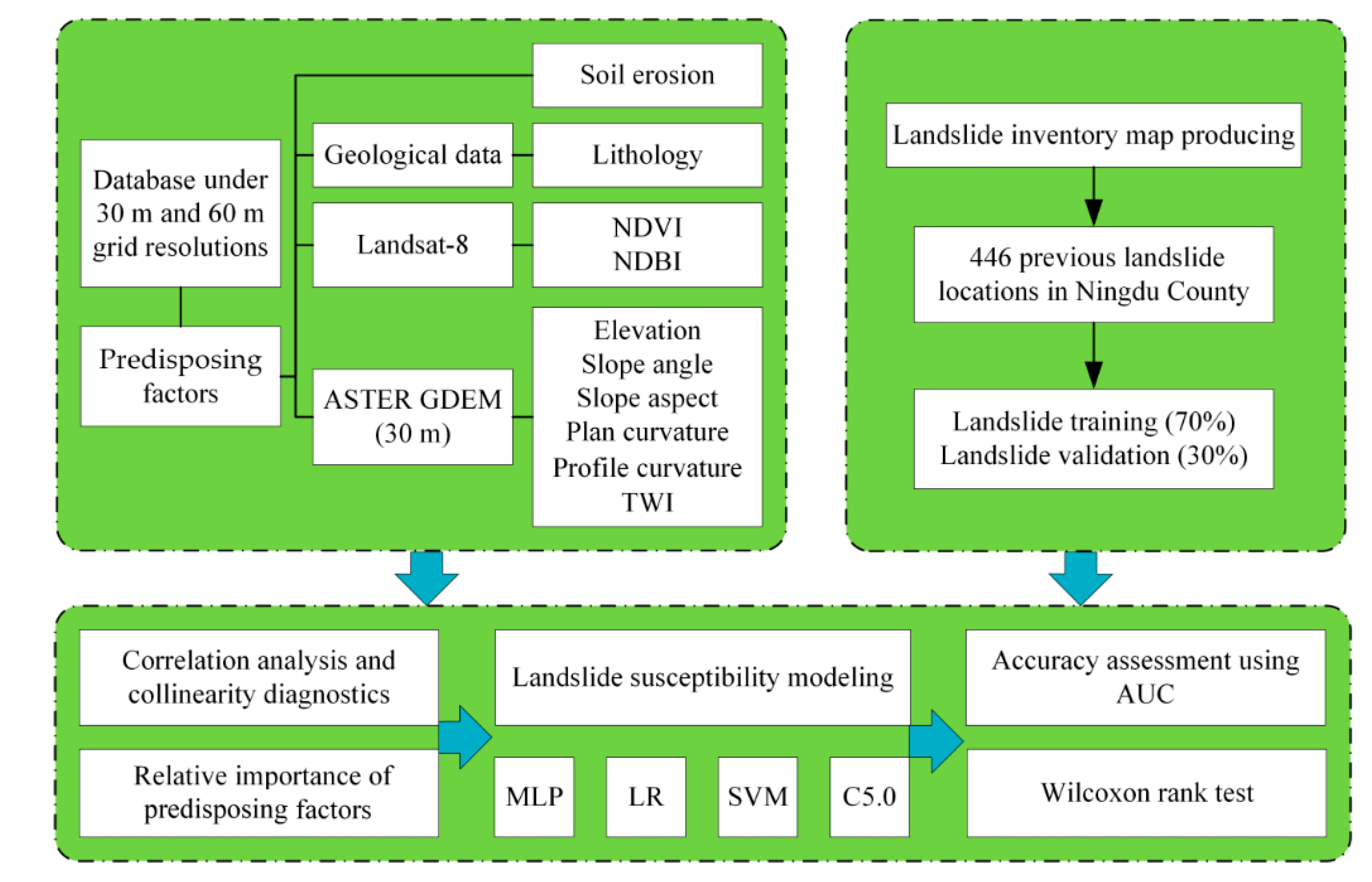
3.1. Modelling Processes Analysis
3.2. Frequency Ratio Analysis
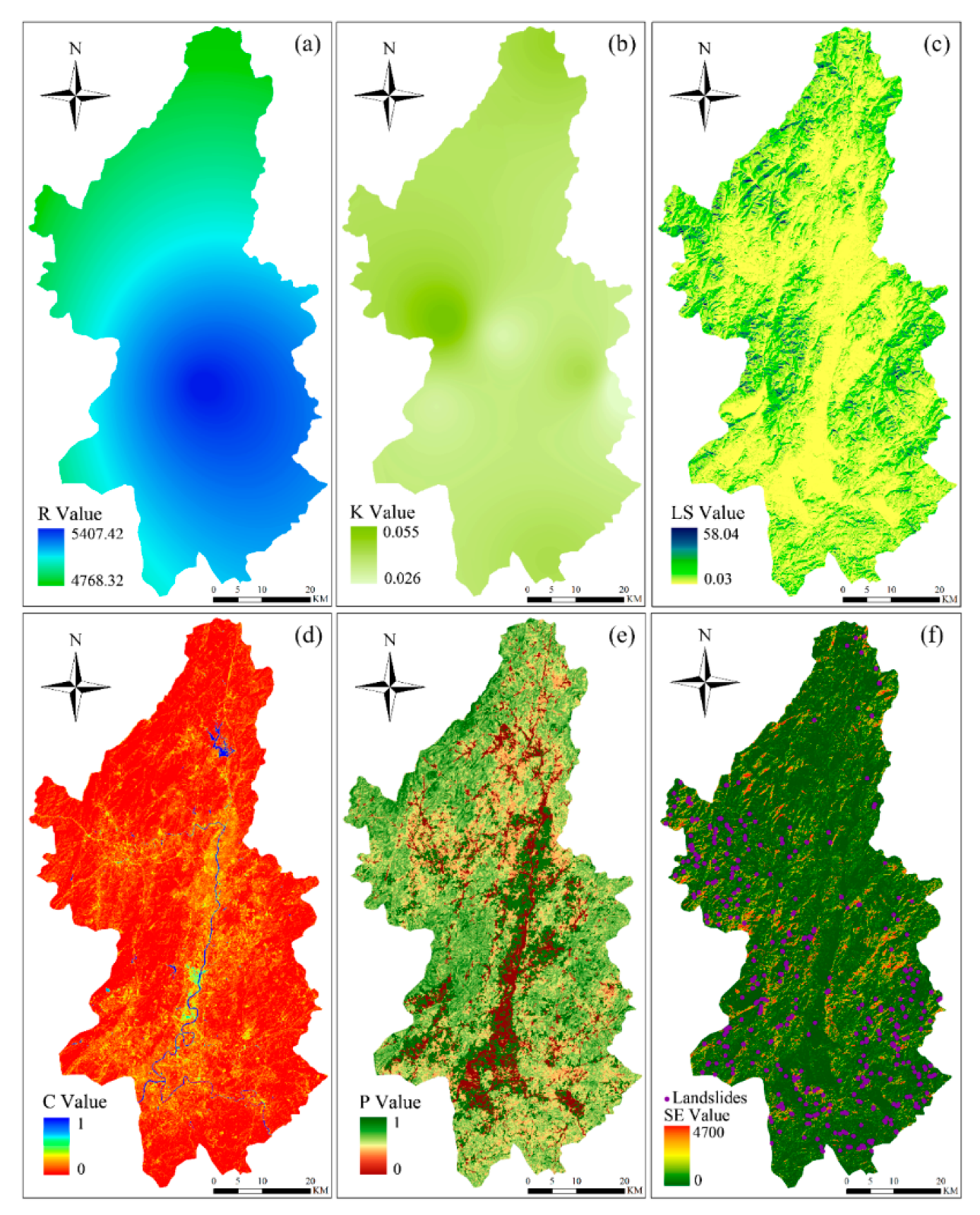
3.3. Modelling of Soil Erosion (SE) Intensity
3.4. Results of Soil Erosion Intensity Calculation
3.5. Landslide Susceptibility Prediction Model
3.5.1. Multilayer Perceptron (MLP)
3.5.2. Logistic Regression (LR) Model
3.5.3. Support Vector Machine (SVM)
3.5.4. C5.0 Decision Tree (C5.0 DT)
3.5.5. Statistically Significant Differences of Landslide Susceptibility Prediction (LSP) Models
4. Results
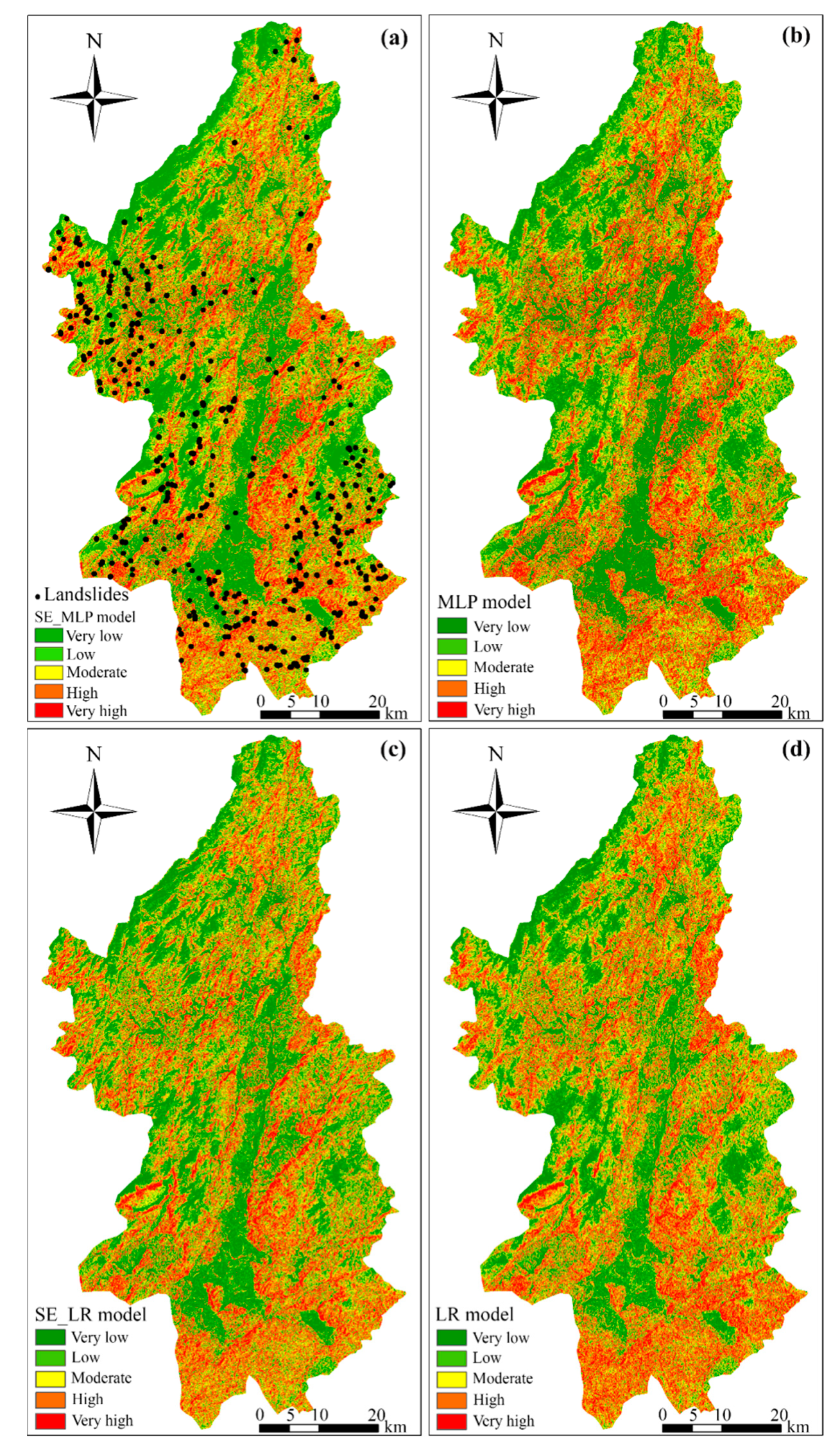
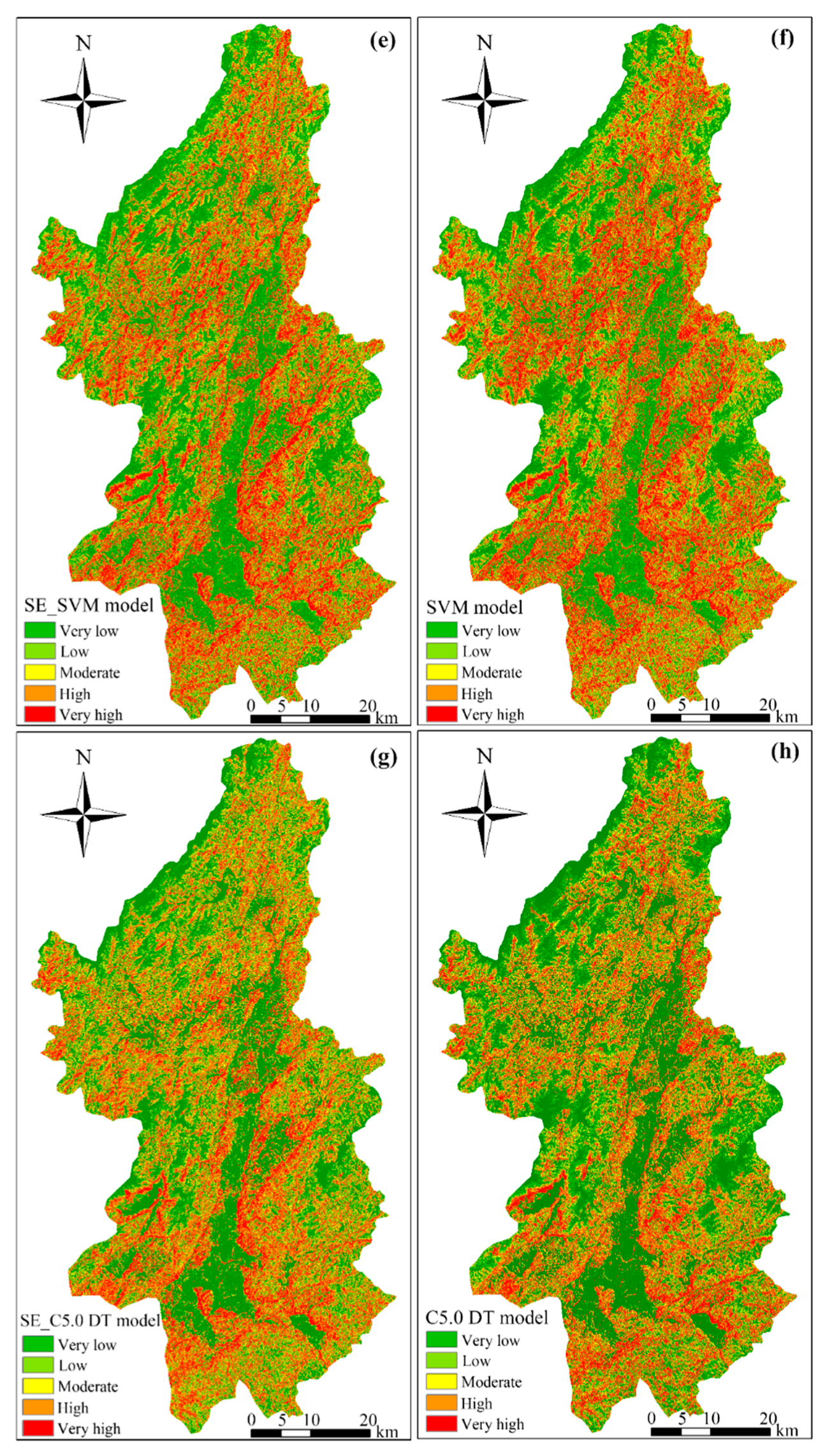
4.1. LSP Results under 30 m Resolution
4.1.1. Landslide Susceptibility Maps (LSMs) of MLP Model
4.1.2. LSMs of LR model
4.1.3. LSMs of SVM and C5.0 DT Models
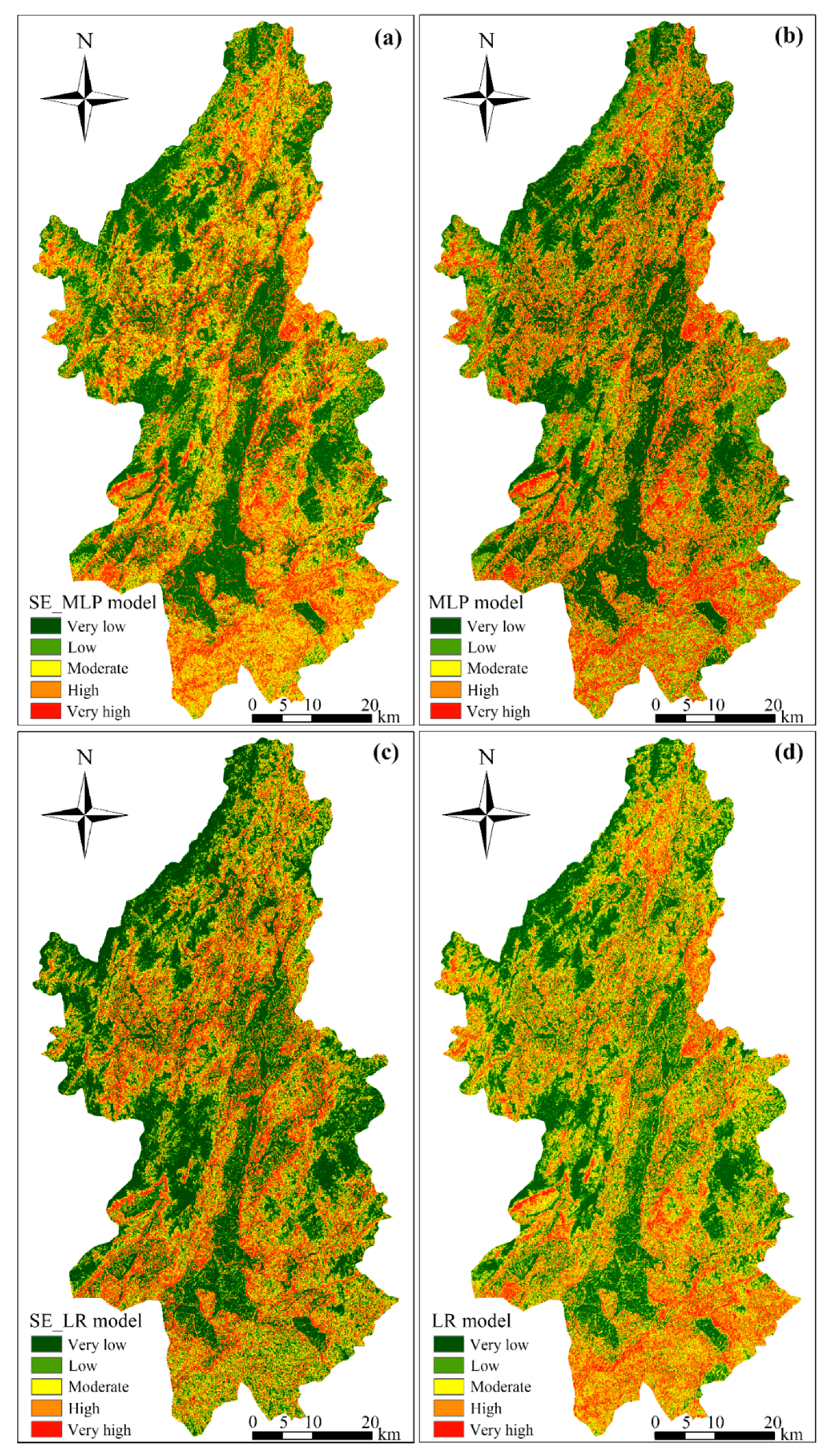
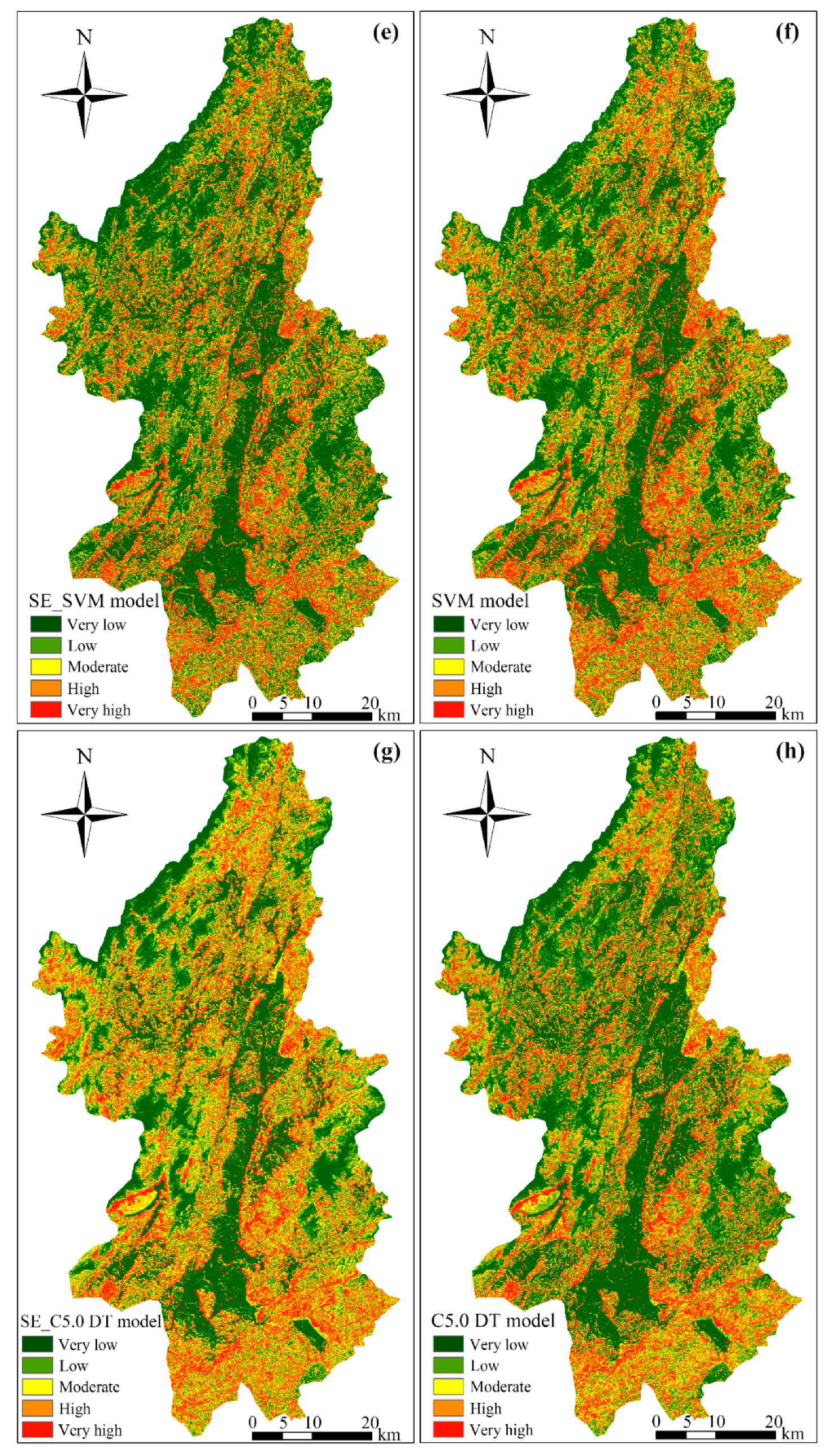
4.2. LSP Results under 60 m Resolution
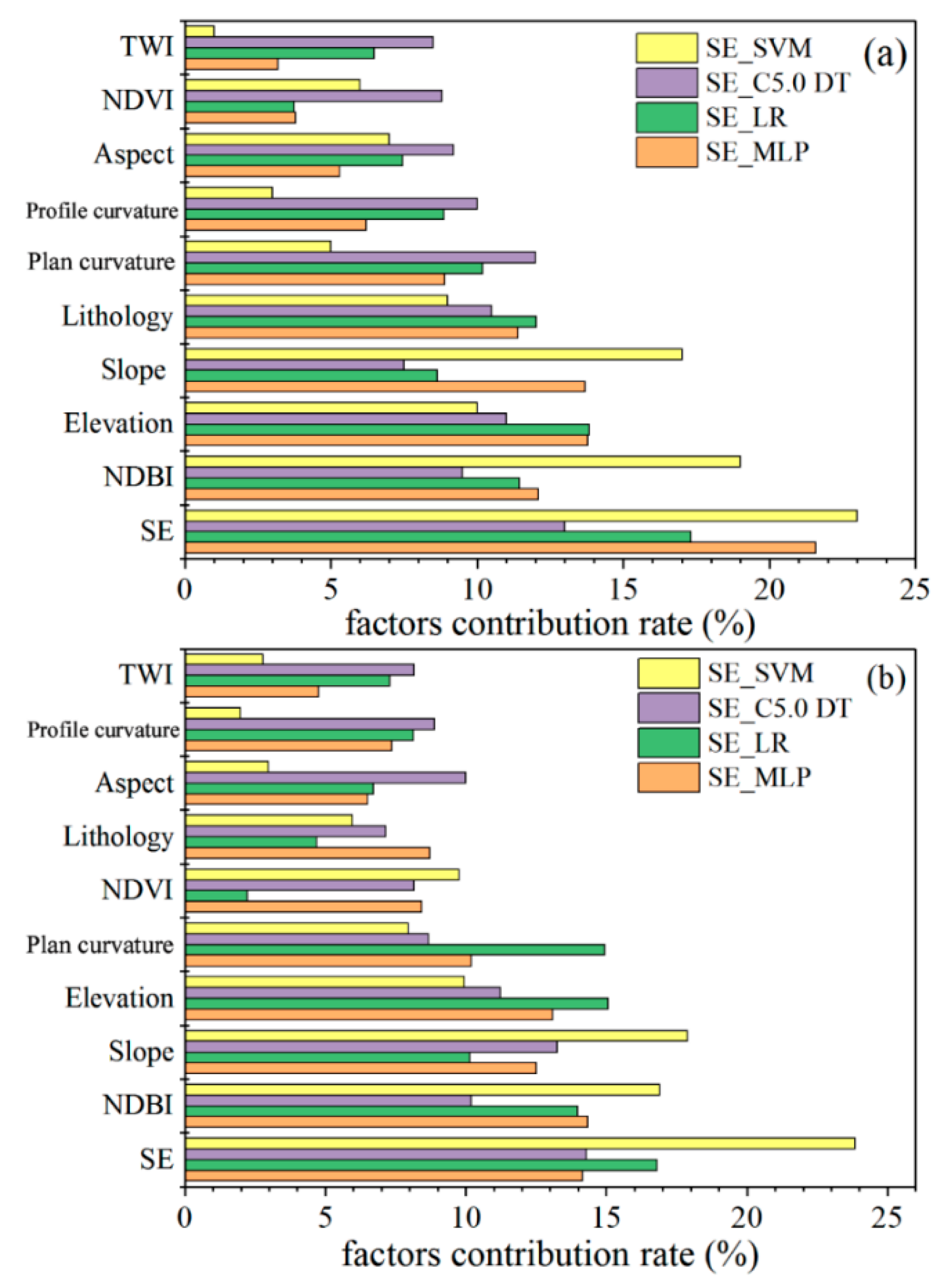
4.2.1. LSP Related Spatial Dataset Analysis
4.2.2. LSMs Using SE-Based Model and Single Model
5. Discussion
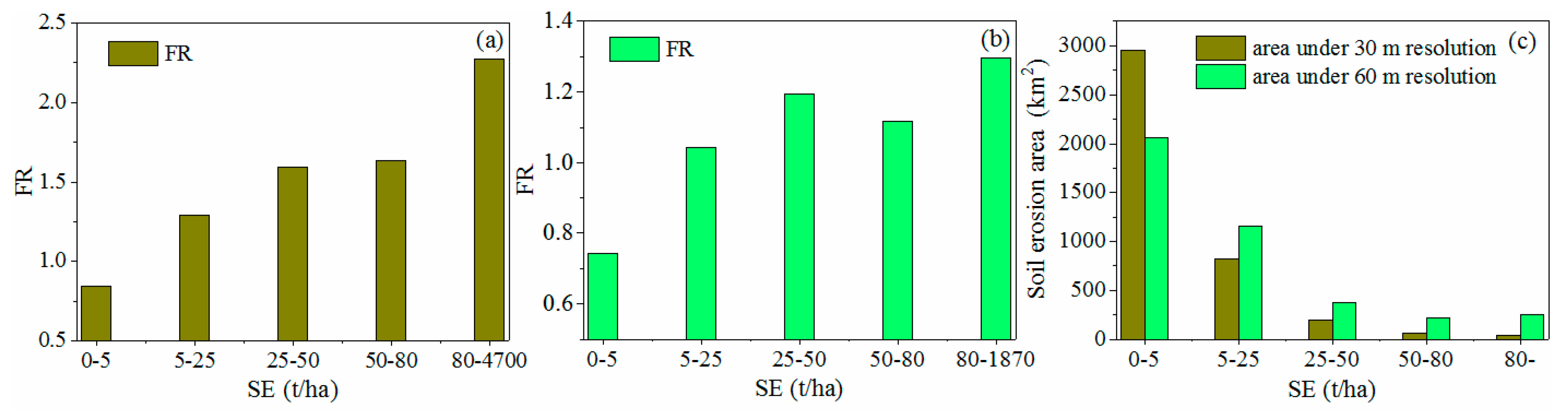
5.1. Frequency Ratio Analysis of SE Factor under Different Resolutions
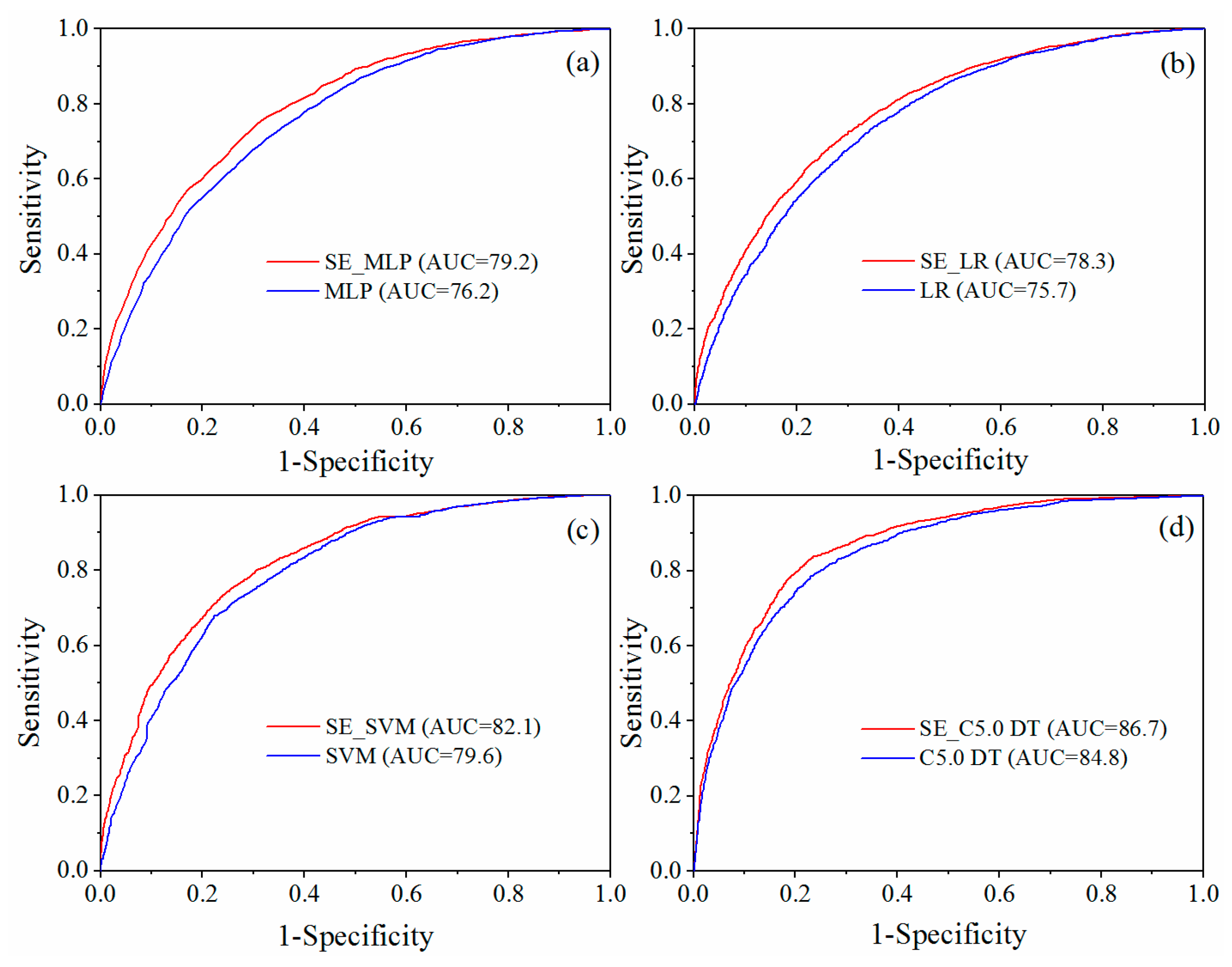
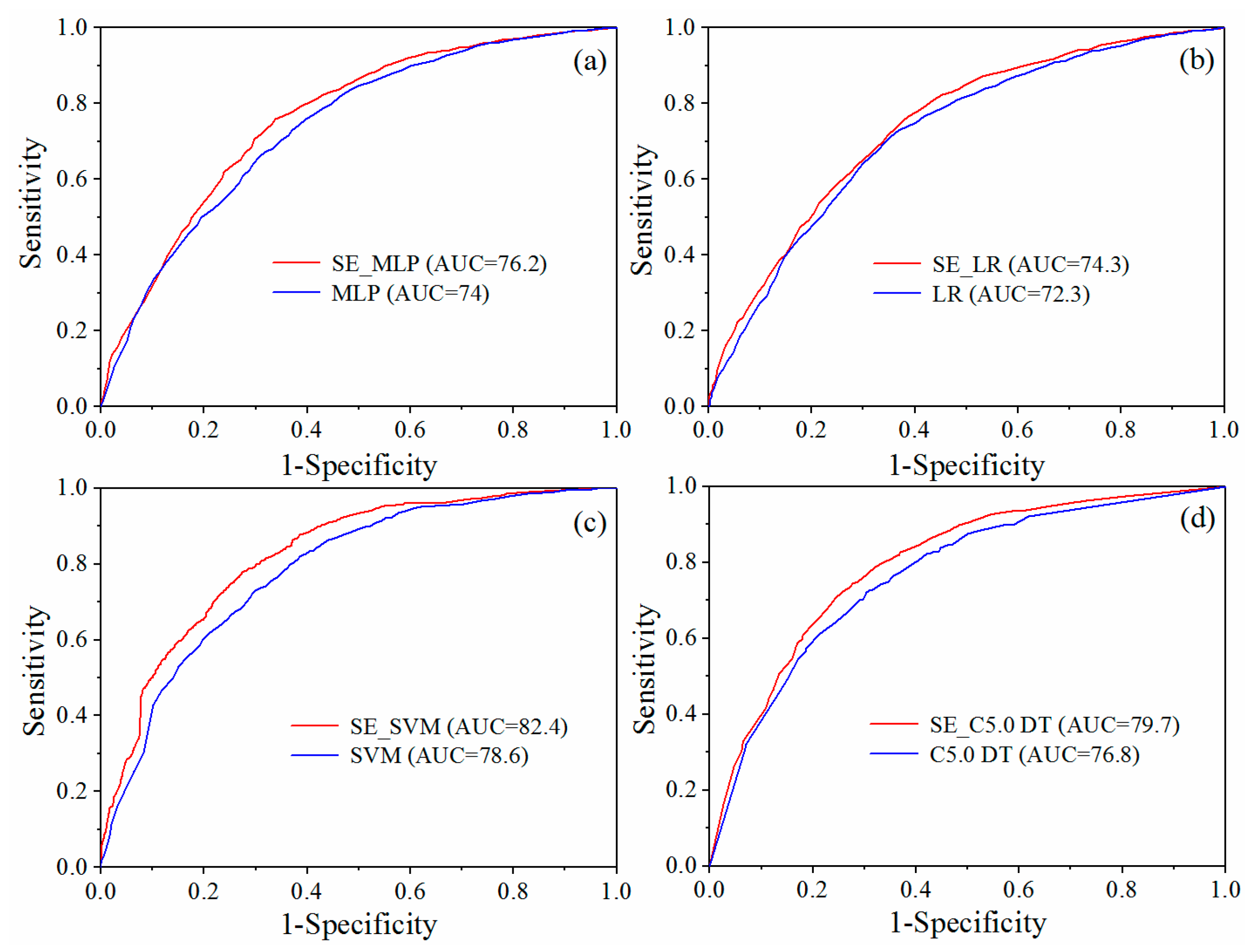
5.2. Accuracy Comparisons of SE-Based Models and Single Models under Different Resolutions
5.3. Statistical Differences between SE-Based Models and Single Models
6. Conclusions
- (1)
- The FR analysis suggests that the FR value of SE gradually increases with the rise of soil erosion class, and the landslides are more inclined to the higher class soil erosion area. Furthermore, it can be concluded that the contribution of SE factor in all models is the largest under both 30 m and 60 m grid resolutions. That is to say, the SE factor plays the most important role in LSP modelling compared to the other traditional predisposing factors.
- (2)
- The comparison results show that the prediction accuracies of the four types of SE-based models are all higher than those of the single model under both 30 m and 60 m resolutions. In addition, the LSP accuracy under 30 m resolution is generally higher than that under 60 m resolution. Hence, it can be concluded that it is appropriate for LSP under 30 m resolution in Ningdu County, and the SE-based models are more appropriate for the LSP under both resolutions.
- (3)
- In general, under the conditions of 30 m and 60 m resolutions and the influences of SE factor, the C5.0 DT and SVM models show higher LSP performance than the MLP and LR models.
- (4)
- As a whole, the predicted distribution regularities of landslide susceptibility in Ningdu County can provide a theoretical basis for reducing local landslide risk and improving the control ability of geological disasters.
Author Contributions
Funding
Conflicts of Interest
References
- Huang, F.; Wang, Y.; Dong, Z.; Wu, L.; Guo, Z.; Zhang, T. Regional landslide susceptibility mapping based on grey relational degree model. Earth Sci. 2019, 44, 664–676. [Google Scholar]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Pradhan, B.; Segoni, S.; Alamri, A.M. Rainfall induced landslide studies in indian himalayan region: A critical review. Appl. Sci. 2020, 10, 2466. [Google Scholar]
- Li, Y.; Huang, J.; Jiang, S.-H.; Huang, F.; Chang, Z. A web-based gps system for displacement monitoring and failure mechanism analysis of reservoir landslide. Sci. Rep. 2017, 7, 17171. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Uncertainty of the soil–water characteristic curve and its effects on slope seepage and stability analysis under conditions of rainfall using the markov chain monte carlo method. Water 2017, 9, 758. [Google Scholar] [CrossRef]
- Chen, W.; Peng, J.; Hong, H.; Shahabi, H.; Pradhan, B.; Liu, J.; Zhu, A.X.; Pei, X.; Duan, Z. Landslide susceptibility modelling using gis-based machine learning techniques for chongren county, jiangxi province, china. Sci. Total Environ. 2018, 626, 1121–1135. [Google Scholar] [CrossRef]
- Dikshit, A.; Sarkar, R.; Pradhan, B.; Jena, R.; Drukpa, D.; Alamri, A.M. Temporal probability assessment and its use in landslide susceptibility mapping for eastern bhutan. Water 2020, 12, 267. [Google Scholar] [CrossRef]
- Cao, J.; Zhang, Z.; Wang, C.; Liu, J.; Zhang, L. Susceptibility assessment of landslides triggered by earthquakes in the western sichuan plateau. Catena 2019, 175, 63–76. [Google Scholar] [CrossRef]
- Razavizadeh, S.; Solaimani, K.; Massironi, M.; Kavian, A. Mapping landslide susceptibility with frequency ratio, statistical index, and weights of evidence models: A case study in northern iran. Environ. Earth Sci. 2017, 76, 499. [Google Scholar] [CrossRef]
- Ahmed, B.; Rahman, M.; Islam, R.; Sammonds, P.; Zhou, C.; Uddin, K.; Al-Hussaini, T.M. Developing a dynamic web-gis based landslide early warning system for the chittagong metropolitan area, bangladesh. Isprs Int. J. Geo-Inf. 2018, 7, 485. [Google Scholar] [CrossRef]
- Meena, S.R.; Ghorbanzadeh, O.; Blaschke, T. A comparative study of statistics-based landslide susceptibility models: A case study of the region affected by the gorkha earthquake in nepal. Isprs Int. J. Geo-Inf. 2019, 8, 94. [Google Scholar] [CrossRef]
- Ge, Y.; Chen, H.; Zhao, B.; Tang, H.; Zhong, P. A comparison of five methods in landslide susceptibility assessment: A case study from the 330-kv transmission line in gansu region, china. Environ. Earth Sci. 2018, 77, 662. [Google Scholar] [CrossRef]
- Carlà, T.; Raspini, F.; Intrieri, E.; Casagli, N. A simple method to help determine landslide susceptibility from spaceborne insar data: The montescaglioso case study. Environ. Earth Sci. 2016, 75, 1492. [Google Scholar] [CrossRef]
- Wu, X.; Niu, R.; Ren, F.; Peng, L. Landslide susceptibility mapping using rough sets and back-propagation neural networks in the three gorges, china. Environ. Earth Sci. 2013, 70, 1307–1318. [Google Scholar] [CrossRef]
- Huang, F.; Zhang, J.; Zhou, C.; Wang, Y.; Huang, J.; Zhu, L. A deep learning algorithm using a fully connected sparse autoencoder neural network for landslide susceptibility prediction. Landslides 2020, 17, 217–229. [Google Scholar] [CrossRef]
- Huang, F.; Yao, C.; Liu, W.; Li, Y.; Liu, X. Landslide susceptibility assessment in the nantian area of china: A comparison of frequency ratio model and support vector machine. Geomat. Nat. Hazards Risk 2018, 9, 919–938. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Huang, J.; Gui, L.; Wang, P. Landslide susceptibility mapping based on self-organizing-map network and extreme learning machine. Eng. Geol. 2017, 223, 11–22. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Lombardo, L. Comparative assessment using boosted regression trees, binary logistic regression, frequency ratio and numerical risk factor for gully erosion susceptibility modelling. Catena 2019, 183, 104223. [Google Scholar] [CrossRef]
- Guo, Z.; Yin, K.; Gui, L.; Liu, Q.; Huang, F.; Wang, T. Regional rainfall warning system for landslides with creep deformation in three gorges using a statistical black box model. Sci. Rep. 2019, 9, 8962. [Google Scholar] [CrossRef]
- Erener, A.; Mutlu, A.; Sebnem Düzgün, H. A comparative study for landslide susceptibility mapping using gis-based multi-criteria decision analysis (mcda), logistic regression (lr) and association rule mining (arm). Eng. Geol. 2016, 203, 45–55. [Google Scholar] [CrossRef]
- Duan, X.; Bing, L.; Gu, Z.; Li, R.; Feng, D. Quantifying soil erosion effects on soil productivity in the dry-hot valley, southwestern china. Environ. Earth Sci. 2016, 75, 1164. [Google Scholar] [CrossRef]
- Deng, H.; Wu, L.Z.; Huang, R.Q.; Guo, X.G.; He, Q. Formation of the siwanli ancient landslide in the dadu river, china. Landslides 2016, 14, 385–394. [Google Scholar] [CrossRef]
- Correa, S.W.; Mello, C.R.; Chou, S.C.; Curi, N.; Norton, L.D. Soil erosion risk associated with climate change at mantaro river basin, peruvian andes. Catena 2016, 147, 110–124. [Google Scholar] [CrossRef]
- Pradhan, B.; Chaudhari, A.; Adinarayana, J.; Buchroithner, M.F. Soil erosion assessment and its correlation with landslide events using remote sensing data and gis: A case study at penang island, malaysia. Environ. Monit. Assess. 2012, 184, 715–727. [Google Scholar] [CrossRef]
- Rozos, D.; Skilodimou, H.D.; Loupasakis, C.; Bathrellos, G.D. Application of the revised universal soil loss equation model on landslide prevention. An example from n. Euboea (evia) island, greece. Environ. Earth Sci. 2013, 70, 3255–3266. [Google Scholar] [CrossRef]
- Chen, Z.; Liang, S.; Ke, Y.; Yang, Z.; Zhao, H. Landslide susceptibility assessment using evidential belief function, certainty factor and frequency ratio model at baxie river basin, nw china. Geocarto Int. 2017, 34, 348–367. [Google Scholar] [CrossRef]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the inje area, korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Tsangaratos, P.; Ilia, I. Comparison of a logistic regression and naïve bayes classifier in landslide susceptibility assessments: The influence of models complexity and training dataset size. Catena 2016, 145, 164–179. [Google Scholar] [CrossRef]
- Zhang, K.; Wu, X.; Niu, R.; Yang, K.; Zhao, L. The assessment of landslide susceptibility mapping using random forest and decision tree methods in the three gorges reservoir area, china. Environ. Earth Sci. 2017, 76, 405. [Google Scholar] [CrossRef]
- Chang, Z.; Du, Z.; Zhang, F.; Huang, F.; Chen, J.; Li, W.; Guo, Z. Landslide susceptibility prediction based on remote sensing images and gis: Comparisons of supervised and unsupervised machine learning models. Remote Sens. 2020, 12, 502. [Google Scholar] [CrossRef]
- Song, Y.; Niu, R.; Xu, S.; Ye, R.; Peng, L.; Guo, T.; Li, S.; Chen, T. Landslide susceptibility mapping based on weighted gradient boosting decision tree in wanzhou section of the three gorges reservoir area (china). Isprs Int. J. Geo-Inf. 2019, 8, 4. [Google Scholar] [CrossRef]
- Ramesh, V.; Anbazhagan, S. Landslide susceptibility mapping along kolli hills ghat road section (india) using frequency ratio, relative effect and fuzzy logic models. Environ. Earth Sci. 2015, 73, 8009–8021. [Google Scholar] [CrossRef]
- Zhu, L.; Huang, L.; Fan, L.; Huang, J.; Huang, F.; Chen, J.; Zhang, Z.; Wang, Y. Landslide susceptibility prediction modeling based on remote sensing and a novel deep learning algorithm of a cascade-parallel recurrent neural network. Sensors 2020, 20, 1576. [Google Scholar] [CrossRef]
- Huang, F.; Wu, P.; Ziggah, Y. Gps monitoring landslide deformation signal processing using time-series model. Int. J. Signal Process. Image Process. Pattern Recognit. 2016, 9, 321–332. [Google Scholar] [CrossRef]
- Youssef, A.M.; Pourghasemi, H.R.; Pourtaghi, Z.S.; Alkatheeri, M.M. Landslide susceptibility mapping using random forest, boosted regression tree, classification and regression tree, and general linear models and comparison of their performance at wadi tayyah basin, asir region, saudi arabia. Landslides 2016, 13, 839–856. [Google Scholar] [CrossRef]
- Chen, W.; Wang, J.; Xie, X.; Hong, H.; Trung, N.V.; Bui, D.T.; Wang, G.; Li, X. Spatial prediction of landslide susceptibility using integrated frequency ratio with entropy and support vector machines by different kernel functions. Environ. Earth Sci. 2016, 75, 1344. [Google Scholar] [CrossRef]
- Huang, F.; Yin, K.; Zhang, G.; Zhou, C.; Zhang, J. Landslide groundwater level time series prediction based on phase space reconstruction and wavelet analysis-support vector machine optimized by pso algorithm. Earth Sci. -J. China Univ. Geosci. 2015, 40, 1254–1265. [Google Scholar]
- Huang, F.; Huang, J.; Jiang, S.; Zhou, C. Landslide displacement prediction based on multivariate chaotic model and extreme learning machine. Eng. Geol. 2017, 218, 173–186. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, Q.; Tang, M.; Nie, W.; Ma, S.; Xu, Z. Comparison of two optimized machine learning models for predicting displacement of rainfall-induced landslide: A case study in sichuan province, china. Eng. Geol. 2017, 218, 213–222. [Google Scholar] [CrossRef]
- Li, D.; Huang, F.; Yan, L.; Cao, Z.; Chen, J.; Ye, Z. Landslide susceptibility prediction using particle-swarm-optimized multilayer perceptron: Comparisons with multilayer-perceptron-only, bp neural network, and information value models. Appl. Sci. 2019, 9, 3664. [Google Scholar] [CrossRef]
- Zhu, G.; Li, Y. Types and changes of chinese climate zones from 1961 to 2013 based on koppen climate classification. Arid Land Geogr. 2015, 38, 1121–1132. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Korte, D.M.; Shakoor, A. Landslide susceptibility and soil loss estimates for drift creek watershed, lincoln county, oregon. Environ. Eng. Geosci. 2019, 26, 167–184. [Google Scholar] [CrossRef]
- Cavazzi, S.; Corstanje, R.; Mayr, T.; Hannam, J.; Fealy, R. Are fine resolution digital elevation models always the best choice in digital soil mapping? Geoderma 2013, 195-196, 111–121. [Google Scholar] [CrossRef]
- Cama, M.; Conoscenti, C.; Lombardo, L.; Rotigliano, E. Exploring relationships between grid cell size and accuracy for debris-flow susceptibility models: A test in the giampilieri catchment (sicily, italy). Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Huang, F.; Cao, Z.; Guo, J.; Jiang, S.-H.; Li, S.; Guo, Z. Comparisons of heuristic, general statistical and machine learning models for landslide susceptibility prediction and mapping. CATENA 2020, 191, 104580. [Google Scholar] [CrossRef]
- Sameen, M.I.; Sarkar, R.; Pradhan, B.; Drukpa, D.; Alamri, A.M.; Park, H.-J. Landslide spatial modelling using unsupervised factor optimisation and regularised greedy forests. Comput. Geosci. 2020, 134. [Google Scholar] [CrossRef]
- Chen, W.; Pourghasemi, H.R.; Panahi, M.; Kornejady, A.; Wang, J.; Xie, X.; Cao, S. Spatial prediction of landslide susceptibility using an adaptive neuro-fuzzy inference system combined with frequency ratio, generalized additive model, and support vector machine techniques. Geomorphology 2017, 297, 69–85. [Google Scholar] [CrossRef]
- Huang, F.; Chen, L.; Yin, K.; Huang, J.; Gui, L. Object-oriented change detection and damage assessment using high-resolution remote sensing images, tangjiao landslide, three gorges reservoir, china. Environ. Earth Sci. 2018, 77, 183. [Google Scholar] [CrossRef]
- Huang, F.; Huang, J.; Jiang, S.-H.; Zhou, C. Prediction of groundwater levels using evidence of chaos and support vector machine. J. Hydroinform. 2017, 19, 586–606. [Google Scholar] [CrossRef]
- Liu, W.; Luo, X.; Huang, F.; Fu, M. Prediction of soil water retention curve using bayesian updating from limited measurement data. Appl. Math. Model. 2019, 76, 380–395. [Google Scholar] [CrossRef]
- Kritikos, T.; Davies, T. Assessment of rainfall-generated shallow landslide/debris-flow susceptibility and runout using a gis-based approach: Application to western southern alps of new zealand. Landslides 2015, 12, 1051–1075. [Google Scholar] [CrossRef]
- Su, C.; Wang, L.; Wang, X.; Huang, Z.; Zhang, X. Mapping of rainfall-induced landslide susceptibility in wencheng, china, using support vector machine. Nat. Hazards 2015, 76, 1759–1779. [Google Scholar] [CrossRef]
- Huang, F.; Luo, X.; Liu, W. Stability analysis of hydrodynamic pressure landslides with different permeability coefficients affected by reservoir water level fluctuations and rainstorms. Water 2017, 9, 450. [Google Scholar] [CrossRef]
- Bui, D.T.; Tuan, T.A.; Klempe, H.; Pradhan, B.; Revhaug, I. Spatial prediction models for shallow landslide hazards: A comparative assessment of the efficacy of support vector machines, artificial neural networks, kernel logistic regression, and logistic model tree. Landslides 2016, 13, 361–378. [Google Scholar]
- Ahmed, B.; Dewan, A. Application of bivariate and multivariate statistical techniques in landslide susceptibility modeling in chittagong city corporation, bangladesh. Remote Sens. 2017, 9, 304. [Google Scholar] [CrossRef]
- Karan, S.K.; Ghosh, S.; Samadder, S.R. Identification of spatially distributed hotspots for soil loss and erosion potential in mining areas of upper damodar basin - india. Catena 2019, 182, 9. [Google Scholar] [CrossRef]
- Kinnell, P.I.A. Determining soil erodibilities for the usle-mm rainfall erosion model. Catena 2018, 163, 424–426. [Google Scholar] [CrossRef]
- Mhaske, S.N.; Pathak, K.; Basak, A. A comprehensive design of rainfall simulator for the assessment of soil erosion in the laboratory. Catena 2019, 172, 408–420. [Google Scholar] [CrossRef]
- Ganasri, B.P.; Ramesh, H. Assessment of soil erosion by rusle model using remote sensing and gis—A case study of nethravathi basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- Zhang, H.D.; Zhang, R.H.; Qi, F.; Liu, X.; Niu, Y.; Fan, Z.F.; Zhang, Q.H.; Li, J.Z.; Yuan, L.; Song, Y.Y.; et al. The csle model based soil erosion prediction: Comparisons of sampling density and extrapolation method at the county level. Catena 2018, 165, 465–472. [Google Scholar] [CrossRef]
- Vanacker, V.; Ameijeiras-Marino, Y.; Schoonejans, J.; Cornelis, J.T.; Minella, J.P.G.; Lamouline, F.; Vermeire, M.L.; Campforts, B.; Robinet, J.; Van de Broek, M.; et al. Land use impacts on soil erosion and rejuvenation in southern brazil. Catena 2019, 178, 256–266. [Google Scholar] [CrossRef]
- Xue, J.; Lyu, D.; Wang, D.; Wang, Y.; Yin, D.; Zhao, Z.; Mu, Z. Assessment of soil erosion dynamics using the gis-based rusle model: A case study of wangjiagou watershed from the three gorges reservoir region, southwestern china. Water 2018, 10, 1817. [Google Scholar] [CrossRef]
- Pesquer, L.; Cortés, A.; Pons, X. Parallel ordinary kriging interpolation incorporating automatic variogram fitting. Comput. Geosci. 2011, 37, 464–473. [Google Scholar] [CrossRef]
- Yuan, L.; Yang, G.; Zhang, Q.; Li, H. Soil erosion assessment of the poyang lake basin, china: Using usle, gis and remote sensing. J. Remote Sens. GIS 2016, 5, 2. [Google Scholar]
- Zhong, R.-l.; Xiao, X.; Zhang, P.-c.; Cen, Y. Research on spatial variability statement methods of soil anti-erodibility in jiangxi province. J. Yangtze River Sci. Res. Inst. 2010, 27, 13–18. [Google Scholar]
- Liu, B.; Nearing, M.; Risse, L. Slope gradient effects on soil loss for steep slopes. Trans. ASAE 1994, 37, 1835–1840. [Google Scholar] [CrossRef]
- Lu, J.; Chen, X.; Li, H.; Liu, H.; Xiao, J.; Yin, J. Soil erosion changes based on gis/rs and usle in poyang lake basin. Trans. Chin. Soc. Agric. Eng. 2011, 27, 337–344. [Google Scholar]
- Shi, D.; Shi, X.; Li, D. Study on dynamic monitoring of soil erosion using remote sensing technique. Acta Pedol. Sin. 1996, 33, 48–58. [Google Scholar]
- Li, H.; Yang, L.; Lei, j. Soil erosion analysis in red soil hilly region by using hj-ccd: A case study in ganzhou. Remote sensing information. Remote Sens. Inf. 2016, 31, 122–129. [Google Scholar]
- Pourghasemi, H.R.; Teimoori Yansari, Z.; Panagos, P.; Pradhan, B. Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11. [Google Scholar] [CrossRef]
- Hong, H.; Pourghasemi, H.R.; Pourtaghi, Z.S. Landslide susceptibility assessment in lianhua county (china): A comparison between a random forest data mining technique and bivariate and multivariate statistical models. Geomorphology 2016, 259, 105–118. [Google Scholar] [CrossRef]
- Sevgen, E.; Kocaman, S.; Nefeslioglu, H.A.; Gokceoglu, C. A novel performance assessment approach using photogrammetric techniques for landslide susceptibility mapping with logistic regression, ann and random forest. Sensors 2019, 19, 3940. [Google Scholar] [CrossRef] [PubMed]
- Tien Bui, D.; Shahabi, H.; Shirzadi, A.; Chapi, K.; Alizadeh, M.; Chen, W.; Mohammadi, A.; Ahmad, B.B.; Panahi, M.; Hong, H.; et al. Landslide detection and susceptibility mapping by airsar data using support vector machine and index of entropy models in cameron highlands, malaysia. Remote Sens. 2018, 10, 1527. [Google Scholar] [CrossRef]
- Xu, C.; Dai, F.; Xu, X.; Lee, Y.H. Gis-based support vector machine modeling of earthquake-triggered landslide susceptibility in the jianjiang river watershed, china. Geomorphology 2012, 145, 70–80. [Google Scholar] [CrossRef]
- Saito, H.; Nakayama, D.; Matsuyama, H. Comparison of landslide susceptibility based on a decision-tree model and actual landslide occurrence: The akaishi mountains, japan. Geomorphology 2009, 109, 108–121. [Google Scholar] [CrossRef]
- Tseng, C.J.; Lu, C.J.; Chang, C.C.; Chen, G.D.; Cheewakriangkrai, C. Integration of data mining classification techniques and ensemble learning to identify risk factors and diagnose ovarian cancer recurrence. Artif. Intell. Med. 2017, 78, 47–54. [Google Scholar] [CrossRef]
- Golkarian, A.; Naghibi, S.A.; Kalantar, B.; Pradhan, B. Groundwater potential mapping using c5.0, random forest, and multivariate adaptive regression spline models in gis. Environ. Monit. Assess. 2018, 190, 149. [Google Scholar] [CrossRef]
- Wu, X.; Ren, F.; Niu, R. Landslide susceptibility assessment using object mapping units, decision tree, and support vector machine models in the three gorges of china. Environ. Earth Sci. 2013, 71, 4725–4738. [Google Scholar] [CrossRef]
- Chen, W.; Xie, X.; Wang, J.; Pradhan, B.; Hong, H.; Bui, D.T.; Duan, Z.; Ma, J. A comparative study of logistic model tree, random forest, and classification and regression tree models for spatial prediction of landslide susceptibility. Catena 2017, 151, 147–160. [Google Scholar] [CrossRef]
- Cantarino, I.; Carrion, M.A.; Goerlich, F.; Martinez Ibañez, V. A roc analysis-based classification method for landslide susceptibility maps. Landslides 2018, 16, 265–282. [Google Scholar] [CrossRef]
- Hong, H.; Panahi, M.; Shirzadi, A.; Ma, T.; Liu, J.; Zhu, A.X.; Chen, W.; Kougias, I.; Kazakis, N. Flood susceptibility assessment in hengfeng area coupling adaptive neuro-fuzzy inference system with genetic algorithm and differential evolution. Sci. Total Environ. 2018, 621, 1124–1141. [Google Scholar] [CrossRef] [PubMed]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
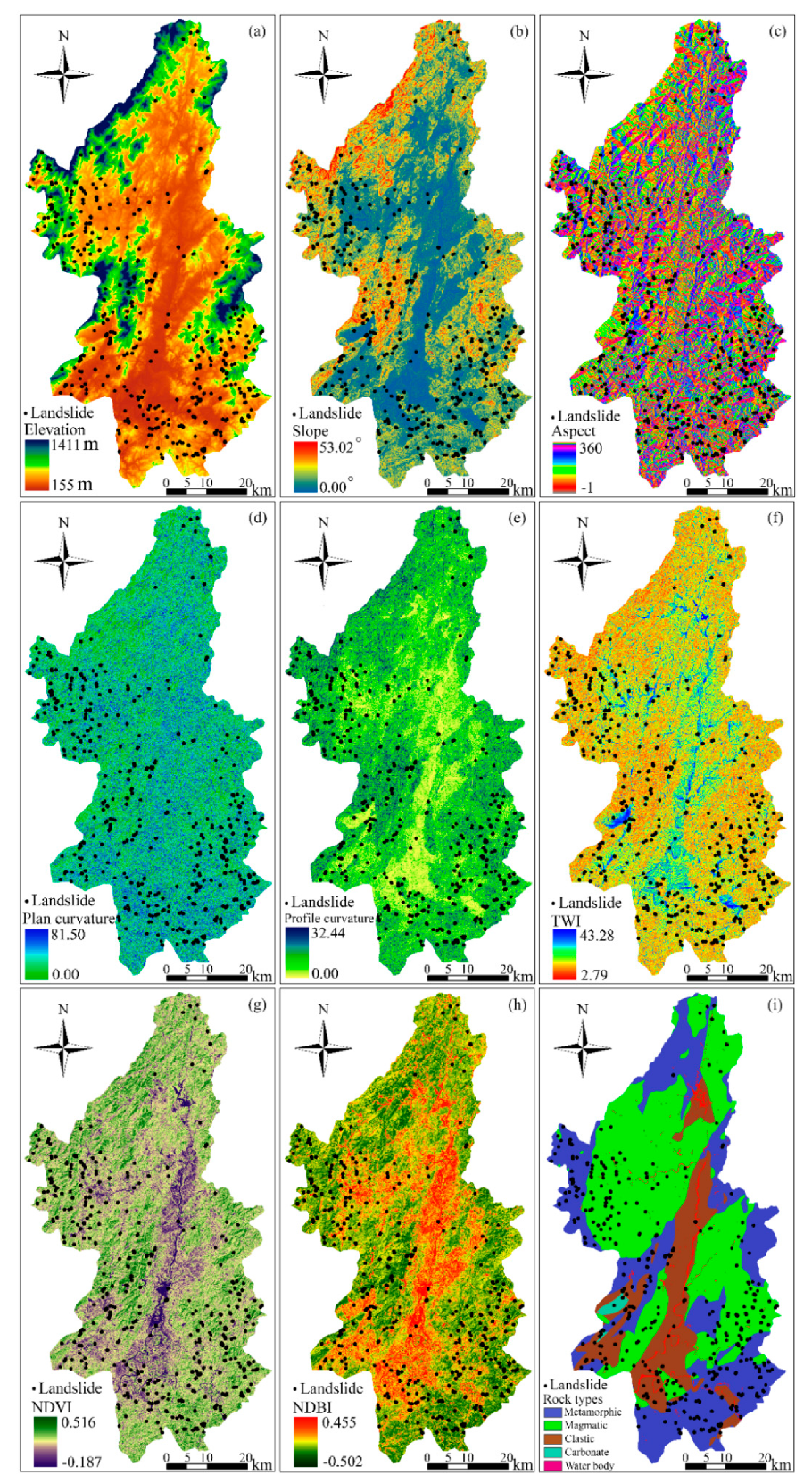
| Predisposing Factors | Classification |
|---|---|
| Elevation (m) | [155,244); [244,322); [322,411); [411,509); [509,618); [618,751); [751,938); [938,1411) |
| Slope (°) | [0.00,3.53); [3.53,7.27); [7.27,11.23); [11.23,15.18); [15.18,19.33); [19.33,24.12); [24.12,30.35); [30.35,53.02) |
| Aspect | Flat; North; Northeast; East; Southeast; South; Southwest; West; Northwest |
| Plan curvature | [0.00,9.91); [9.91,18.22); [18.22,27.48); [27.48,37.39); [37.39,47.94); [47.94,58.81); [58.81,70.64); [70.64,81.50) |
| Profile curvature | [0.00,1.53); [1.53,3.05); [3.05,4.71); [4.71,6.48); [6.48,8.52); [8.52,11.06); [11.06,14.75); [14.75,32.44) |
| TWI | [2.79,5.65); [5.65,7.24); [7.24,9.15); [9.15,11.69); [11.69,15.34); [15.34,24.39); [24.39,43.28) |
| NDVI | [−0.187,0.025); [0.025,0.131); [0.131,0.196); [0.196,0.243); [0.243,0.282); [0.282,0.321); [0.321,0.362); [0.362,0.516) |
| NDBI | [−0.502,−0.379); [−0.379,−0.337); [−0.337,−0.292); [−0.292,−0.244); [−0.244,−0.191); [−0.191,−0.135); [−0.135,−0.067); [−0.067,0.455) |
| Lithology | metamorphic rock; magmatic rock; clastic rock; carbonate rock; water body |
| SE (t/ha) | [0,5); [5,25); [25,50); [50,80); [80,4700.75) |
| Variables | β | Standard Error | SIG | Collinear Statistics | |
|---|---|---|---|---|---|
| Variance Inflation Factor | Tolerance | ||||
| Elevation | 1.589 | 0.115 | 0.000 | 1.102 | 0.907 |
| Slope | 0.993 | 0.060 | 0.000 | 1.172 | 0.853 |
| Aspect | 0.857 | 0.144 | 0.000 | 1.042 | 0.960 |
| Plan curvature | 1.020 | 0.167 | 0.000 | 1.083 | 0.924 |
| Profile curvature | 1.170 | 0.086 | 0.000 | 1.117 | 0.895 |
| Lithology | 1.383 | 0.105 | 0.000 | 1.077 | 0.928 |
| NDBI | 1.313 | 0.106 | 0.000 | 1.575 | 0.635 |
| NDVI | 0.429 | 0.155 | 0.006 | 1.592 | 0.628 |
| TWI | 0.744 | 0.136 | 0.000 | 1.100 | 0.909 |
| SE | 1.989 | 0.112 | 0.000 | 1.018 | 0.982 |
| constant | -11.969 | 0.398 | 0.000 | - | - |
| Variables | β | Standard Error | SIG | Collinear Statistics | |
|---|---|---|---|---|---|
| Variance Inflation Factor | Tolerance | ||||
| Elevation | 1.382 | 0.166 | 0.000 | 1.191 | 0.839 |
| Slope | 0.93 | 0.083 | 0.000 | 1.136 | 0.880 |
| Aspect | 0.617 | 0.215 | 0.003 | 1.033 | 0.968 |
| Plan curvature | 1.372 | 0.156 | 0.000 | 1.084 | 0.922 |
| Profile curvature | 0.748 | 0.212 | 0.000 | 1.132 | 0.883 |
| Lithology | 0.431 | 0.151 | 0.000 | 1.089 | 0.918 |
| NDBI | 1.283 | 0.14 | 0.000 | 1.796 | 0.557 |
| NDVI | 0.205 | 0.208 | 0.000 | 1.910 | 0.524 |
| TWI | 0.669 | 0.136 | 0.001 | 1.045 | 0.957 |
| SE | 1.543 | 0.207 | 0.000 | 1.004 | 0.998 |
| constant | -9.127 | 0.511 | 0.000 | - | - |
| Gird Resolution | Models | AUC with SE (%) | AUC with No SE (%) | Improvement (%) |
|---|---|---|---|---|
| 30 m | MLP | 79.2 | 76.2 | 3.94 |
| LR | 78.3 | 75.7 | 3.43 | |
| SVM | 82.1 | 79.6 | 3.14 | |
| C5.0 DT | 86.7 | 84.8 | 2.24 | |
| 60 m | MLP | 76.2 | 74.0 | 2.97 |
| LR | 74.3 | 72.3 | 2.77 | |
| SVM | 82.4 | 78.6 | 4.83 | |
| C5.0 DT | 79.7 | 76.8 | 3.78 |
| Resolution | Parameter | MLP | LR | SVM | C5.0 DT |
|---|---|---|---|---|---|
| 30 m | Z | −3.323 | −2.879 | −5.871 | −2.358 |
| P | 0.001 | 0.004 | 0.000 | 0.018 | |
| 60 m | Z | −6.703 | −2.223 | −3.176 | −6.953 |
| P | 0.000 | 0.026 | 0.001 | 0.000 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, F.; Chen, J.; Du, Z.; Yao, C.; Huang, J.; Jiang, Q.; Chang, Z.; Li, S. Landslide Susceptibility Prediction Considering Regional Soil Erosion Based on Machine-Learning Models. ISPRS Int. J. Geo-Inf. 2020, 9, 377. https://doi.org/10.3390/ijgi9060377
Huang F, Chen J, Du Z, Yao C, Huang J, Jiang Q, Chang Z, Li S. Landslide Susceptibility Prediction Considering Regional Soil Erosion Based on Machine-Learning Models. ISPRS International Journal of Geo-Information. 2020; 9(6):377. https://doi.org/10.3390/ijgi9060377
Chicago/Turabian StyleHuang, Faming, Jiawu Chen, Zhen Du, Chi Yao, Jinsong Huang, Qinghui Jiang, Zhilu Chang, and Shu Li. 2020. "Landslide Susceptibility Prediction Considering Regional Soil Erosion Based on Machine-Learning Models" ISPRS International Journal of Geo-Information 9, no. 6: 377. https://doi.org/10.3390/ijgi9060377
APA StyleHuang, F., Chen, J., Du, Z., Yao, C., Huang, J., Jiang, Q., Chang, Z., & Li, S. (2020). Landslide Susceptibility Prediction Considering Regional Soil Erosion Based on Machine-Learning Models. ISPRS International Journal of Geo-Information, 9(6), 377. https://doi.org/10.3390/ijgi9060377






