Modelling Offset Regions around Static and Mobile Locations on a Discrete Global Grid System: An IoT Case Study
Abstract
1. Introduction
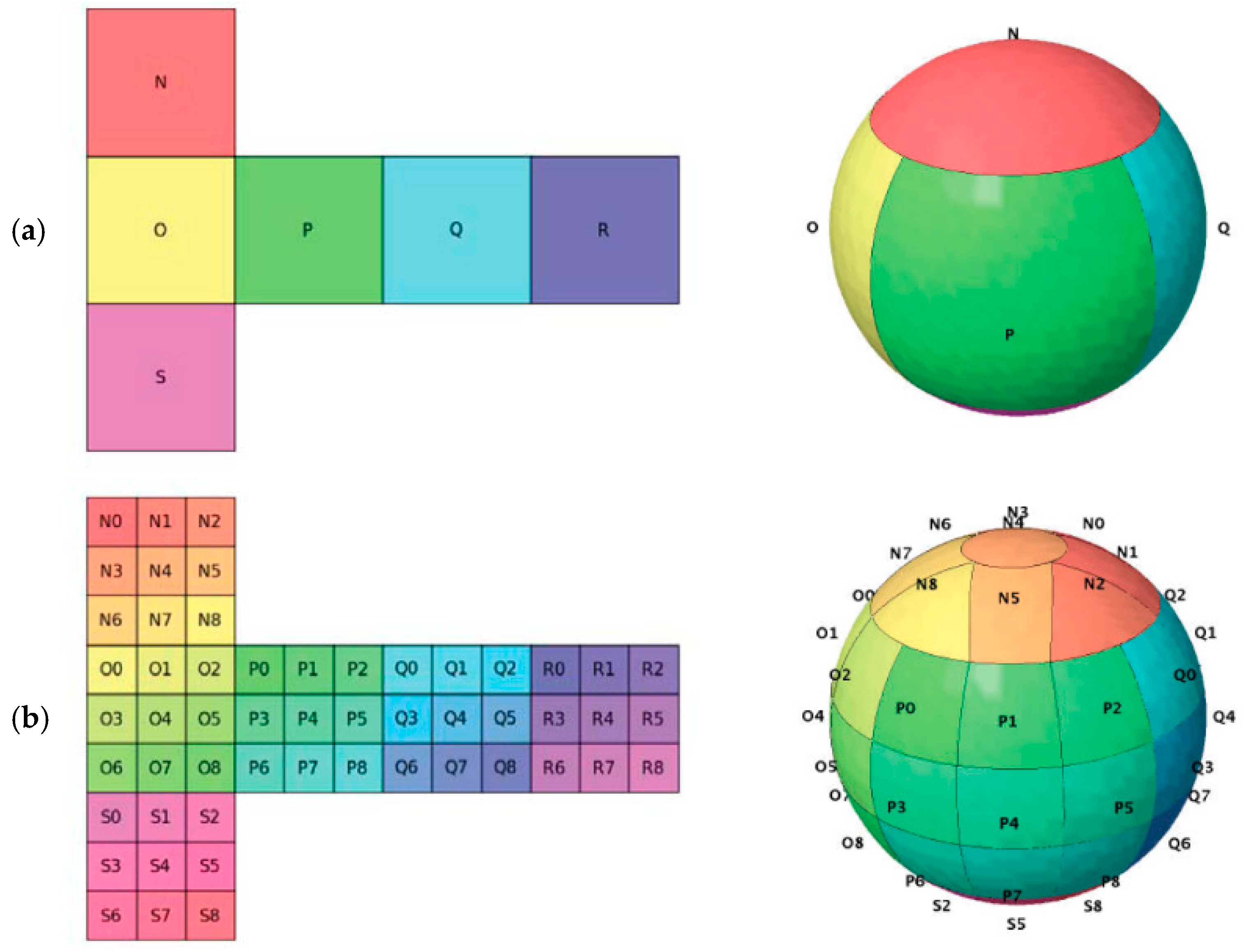
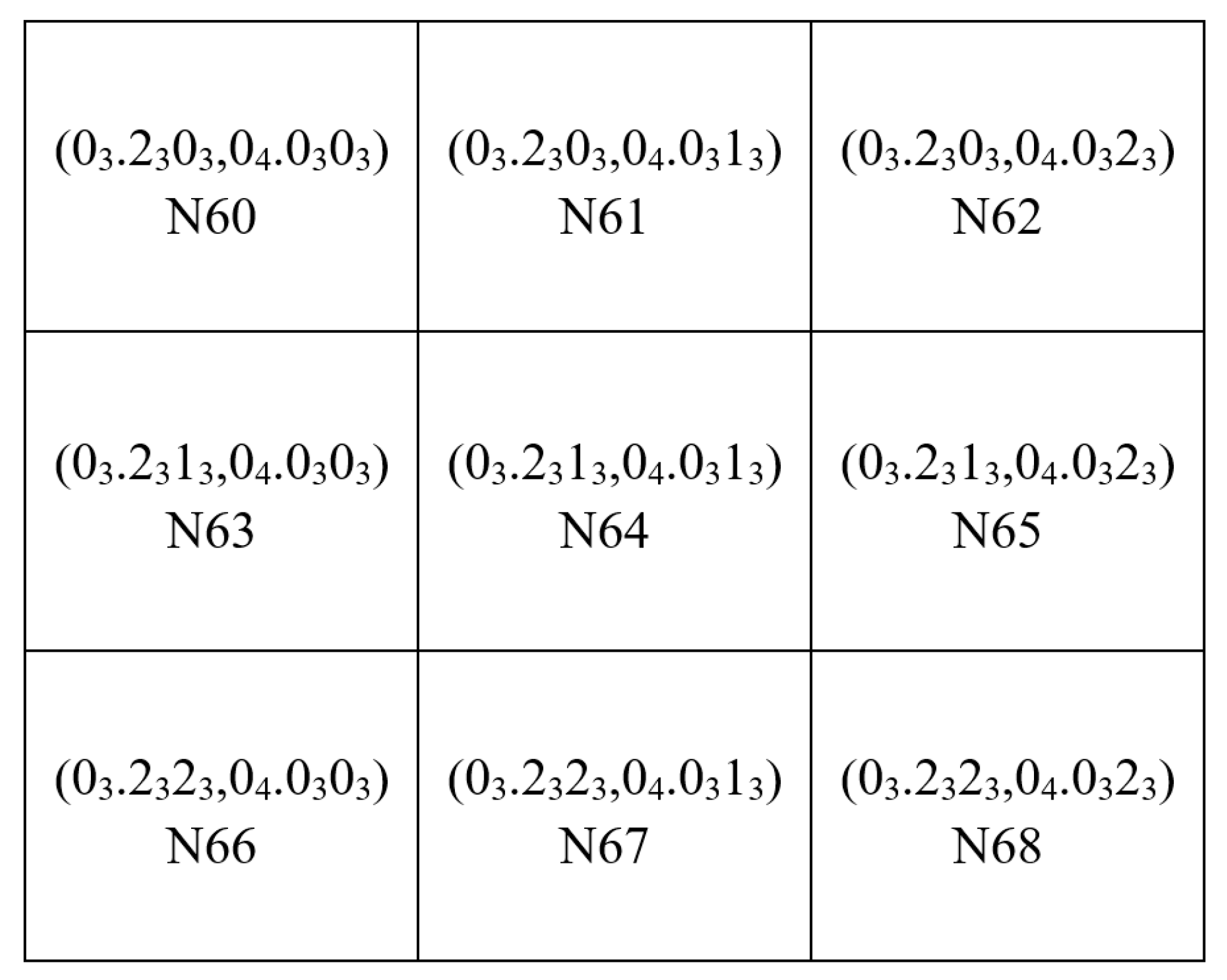
2. The rHEALPix DGGS
3. Static Offset Regions
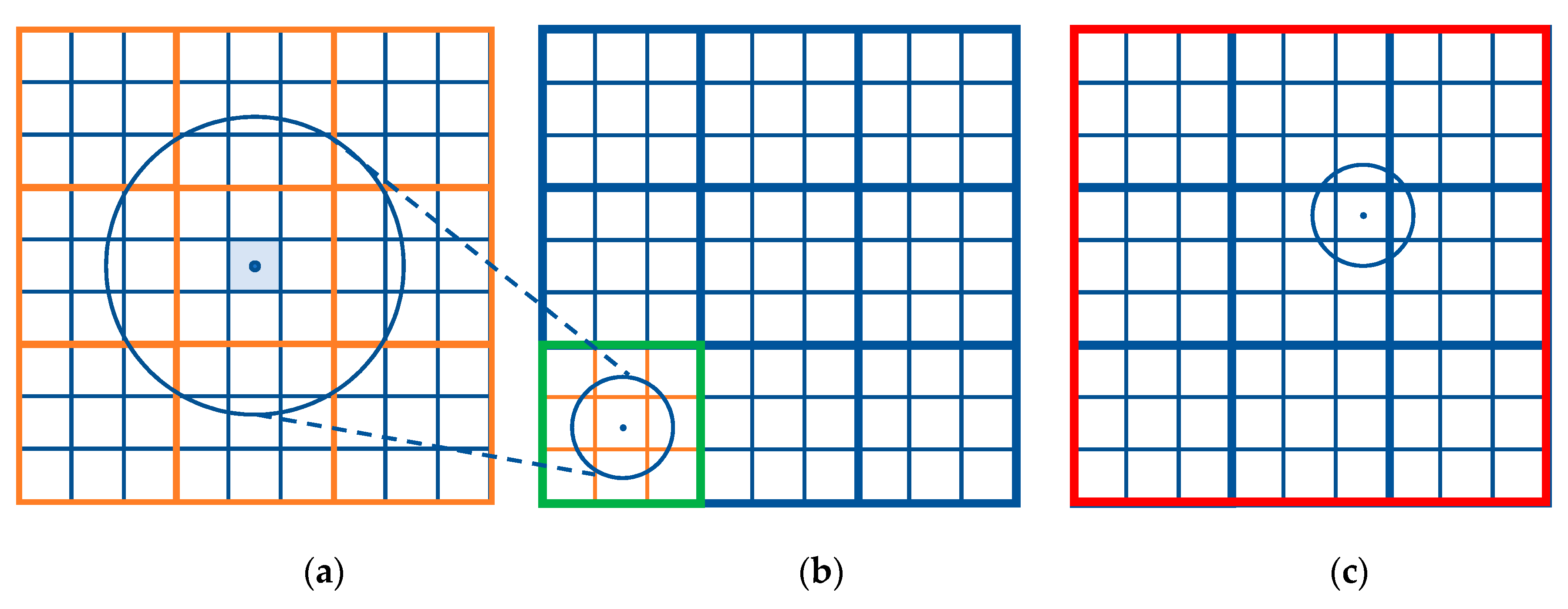
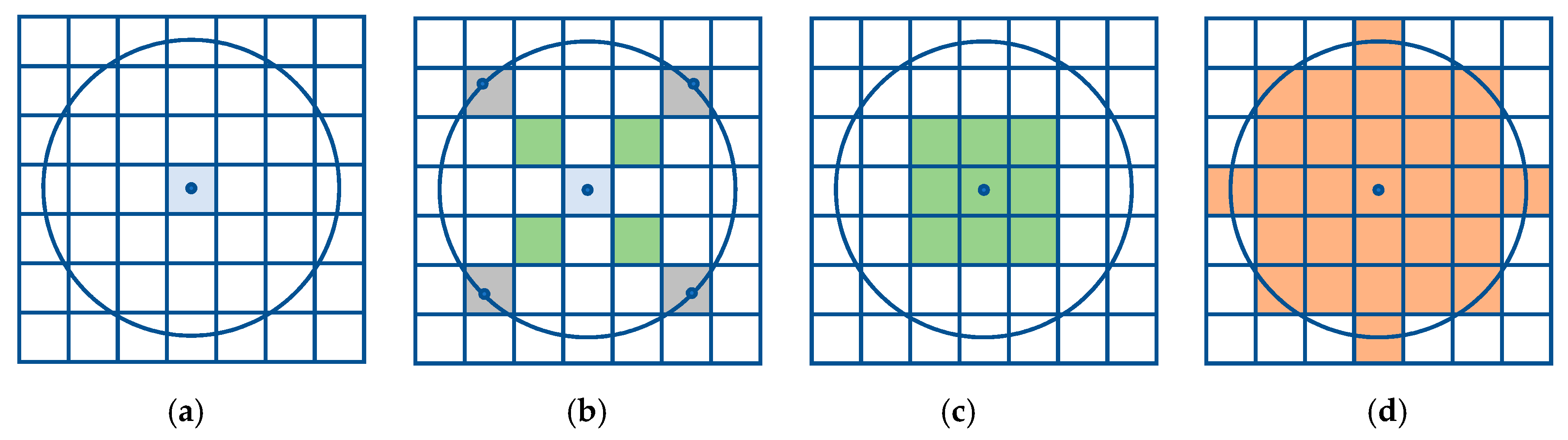
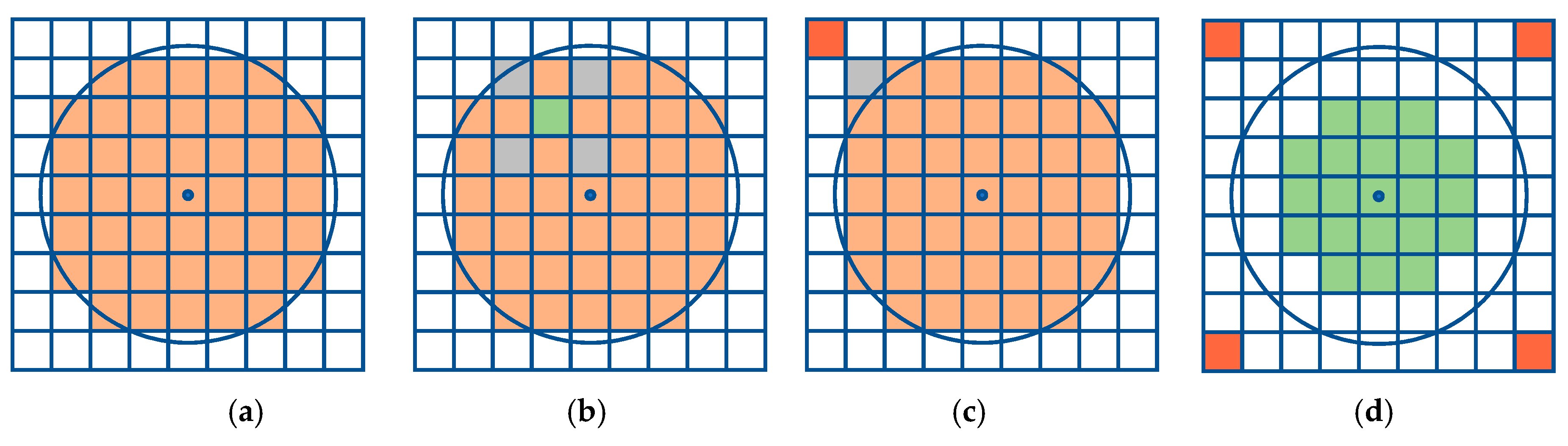
3.1. Single Resolution
| Algorithm 1. Pseudocode to perform the single resolution method |
| Input: point , offset radius , resolution |
Result: set of cells that represent the offset region
|
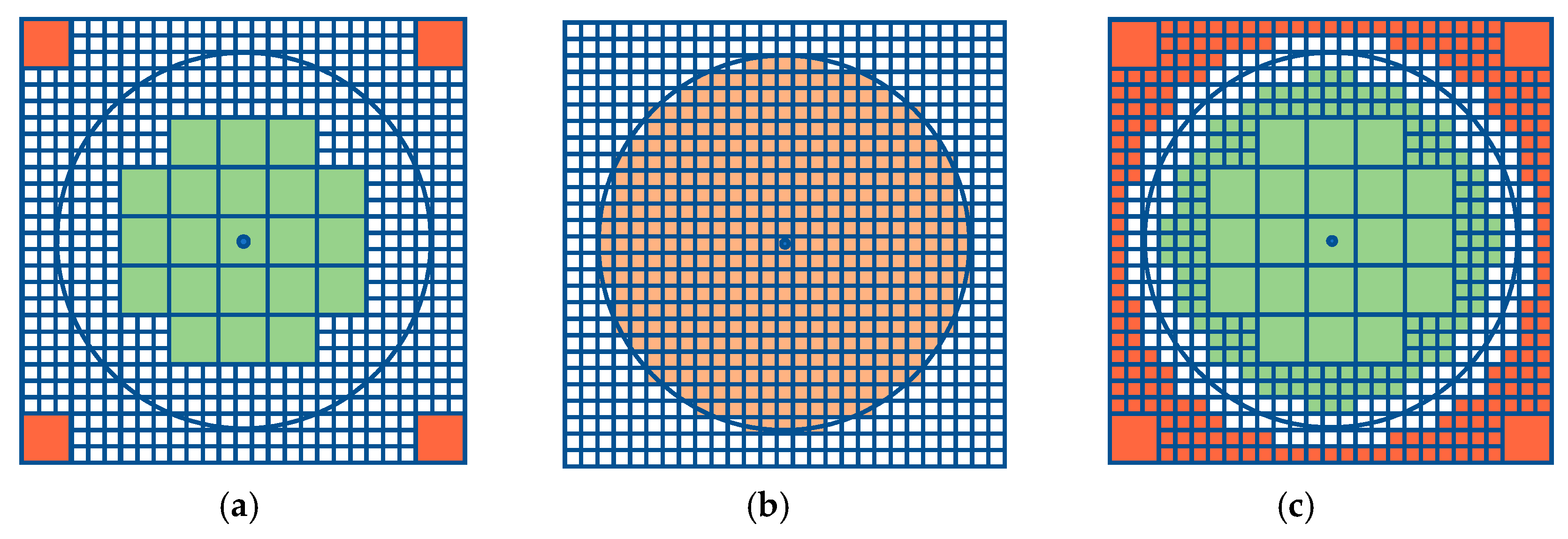
3.2. Multiresolution
| Algorithm 2. Pseudocode to perform the multiresolution method |
| Input: point , offset radius , coarse resolution , fine resolution , initial set of cells that represent the search space, initial set of cells that represent the offset region |
Result: set of cells that represent the offset region
|
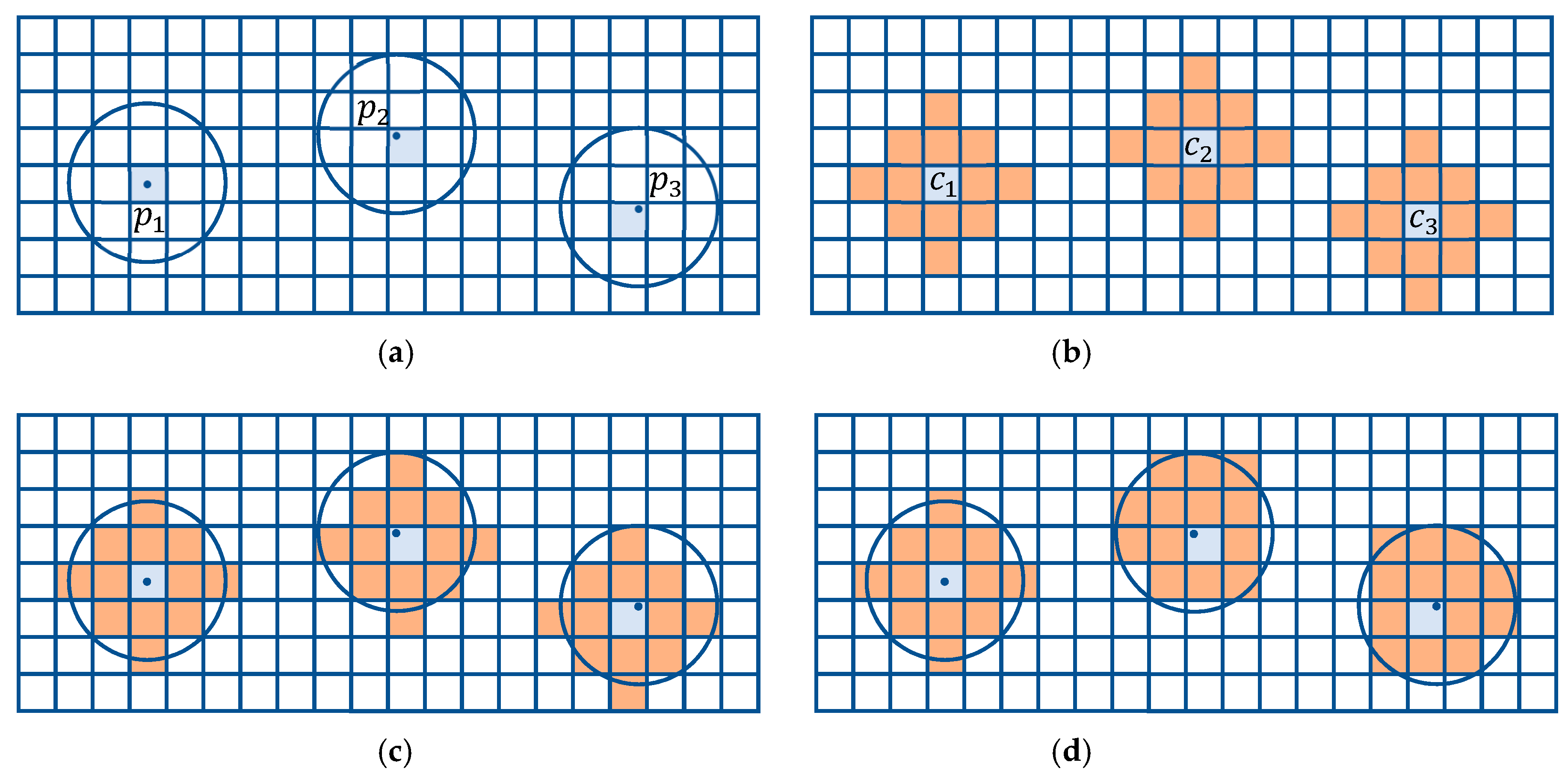
4. Mobile Offset Regions
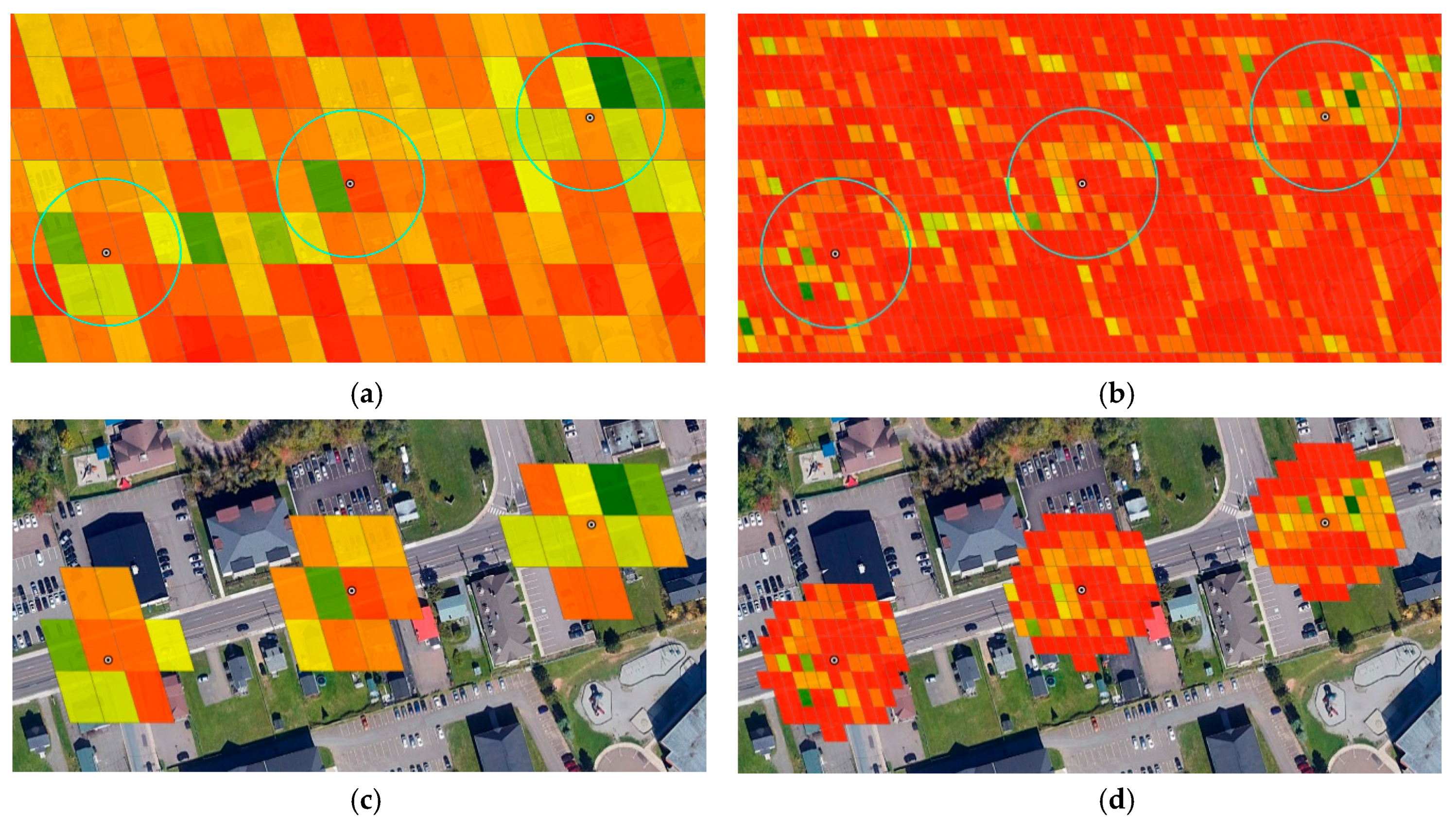
5. Results
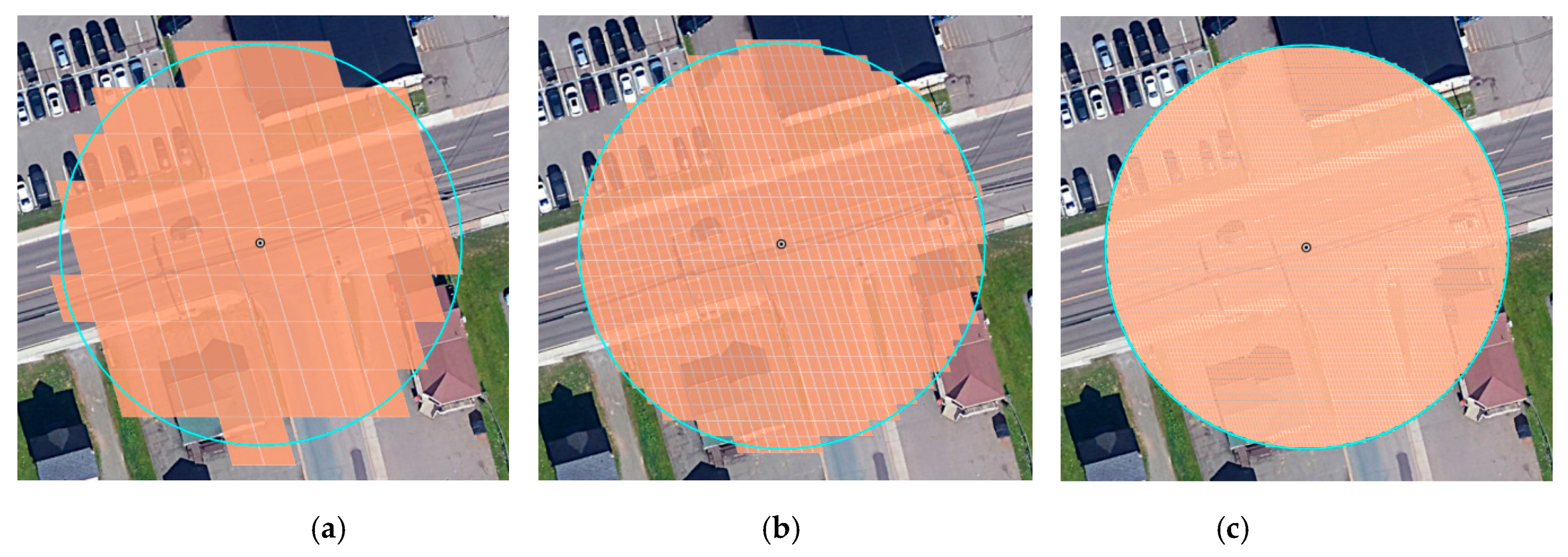
5.1. Static Offset Regions
5.2. Mobile Offset Regions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Van der Zee, E.; Scholten, H. Spatial dimensions of big data: Application of geographical concepts and spatial technology to the internet of things. In Big Data and Internet of Things: A Roadmap for Smart Environments; Bessis, N., Dobre, C., Eds.; Springer: Cham, Switzerland, 2014; pp. 137–168. [Google Scholar] [CrossRef]
- Cao, H.; Wachowicz, M. The design of an IoT-GIS platform for performing automated analytical tasks. Comput. Environ. Urban Syst. 2019, 74, 23–40. [Google Scholar] [CrossRef]
- Kamilaris, A.; Ostermann, F. Geospatial analysis and the internet of things. ISPRS Int. J. Geo Inf. 2018, 7, 269. [Google Scholar] [CrossRef]
- Sun, G.; Chang, V.; Ramachandran, M.; Sun, Z.; Li, G.; Yu, H.; Liao, D. Efficient location privacy algorithm for Internet of Things (IoT) services and applications. J. Netw. Comput. Appl. 2017, 89, 3–13. [Google Scholar] [CrossRef]
- Eldrandaly, K.A.; Abdel-Basset, M.; Shawky, L.A. Internet of spatial things: A new reference model with insight analysis. IEEE Access 2019, 7, 19653–19669. [Google Scholar] [CrossRef]
- Granell, C.; Kamilaris, A.; Kotsev, A.; Ostermann, F.O.; Trilles, S. Internet of things. In Manual of Digital Earth; Guo, H., Goodchild, M., Annoni, A., Eds.; Springer: Singapore, 2020; pp. 387–423. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Alderson, T.; Samavati, F. A survey of digital earth. Comput. Graph. 2015, 53, 95–117. [Google Scholar] [CrossRef]
- Alderson, T.; Purss, M.; Du, X.; Mahdavi-Amiri, A.; Samavati, F. Digital earth platforms. In Manual of Digital Earth; Guo, H., Goodchild, M., Annoni, A., Eds.; Springer: Singapore, 2020; pp. 25–54. [Google Scholar] [CrossRef]
- Sahr, K.; White, D. Discrete global grid systems. In Proceedings of the 30th Symposium on the Interface, Computing Science and Statistics, Minneapolis, MN, USA, 13–16 May 1998; pp. 269–278. [Google Scholar]
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic discrete global grid systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Topic 21: Discrete Global Grid Systems Abstract Specification. Available online: http://docs.opengeospatial.org/as/15-104r5/15-104r5.html (accessed on 2 August 2018).
- Amiri, A.; Samavati, F.; Peterson, P. Categorization and conversions for indexing methods of discrete global grid systems. ISPRS Int. J. Geo Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Li, Z. Geospatial Big Data Handling with High Performance Computing: Current Approaches and Future Directions. 2019. Available online: https://arxiv.org/abs/1907.12182 (accessed on 21 March 2020).
- Purss, M.B.J.; Peterson, P.R.; Strobl, P.; Dow, C.; Sabeur, Z.A.; Gibb, R.G.; Ben, J. Datacubes: A discrete global grid systems perspective. Cartogr. Int. J. Geogr. Inf. Geovis. 2019, 54, 63–71. [Google Scholar] [CrossRef]
- Sirdeshmukh, N.; Verbree, E.; Oosterom, P.V.; Psomadaki, S.; Kodde, M. Utilizing a discrete global grid system for handling point clouds with varying locations, times, and levels of detail. Cartogr. Int. J. Geogr. Inf. Geovis. 2019, 54, 4–15. [Google Scholar] [CrossRef]
- Yao, X.; Li, G.; Xia, J.; Ben, J.; Cao, Q.; Zhao, L.; Ma, Y.; Zhang, L.; Zhu, D. Enabling the big earth observation data via cloud computing and DGGS: Opportunities and challenges. Remote Sens. 2019, 12, 62. [Google Scholar] [CrossRef]
- Birk, F. Design and Implementation of a Scalable Crowdsensing Platform for Geospatial Data. Master’s Thesis, Ulm University, Ulm, Germany, 2018. [Google Scholar]
- H3: Uber’s Hexagonal Hierarchical Spatial Index. Available online: https://eng.uber.com/h3/ (accessed on 27 September 2019).
- Sahr, K. On the optimal representation of vector location using fixed-width multi-precision quantizers. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. ISPRS Arch. 2013, 40, 1–8. [Google Scholar] [CrossRef]
- Purss, M.B.J.; Liang, S.; Gibb, R.; Samavati, F.; Peterson, P.; Ben, J.; Dow, C.; Saeedi, S. Applying discrete global grid systems to sensor networks and the Internet of Things. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5581–5583. [Google Scholar] [CrossRef]
- Alderson, T.; Mahdavi-Amiri, A.; Samavati, F. Offsetting spherical curves in vector and raster form. Vis. Comput. 2018, 34, 973–984. [Google Scholar] [CrossRef]
- Gibb, R.; Raichev, A.; Speth, M. The rHEALPix Discrete Global Grid System. 2016. Available online: https://datastore.landcareresearch.co.nz/dataset/rhealpix-discrete-global-grid-system (accessed on 17 July 2018). [CrossRef]
- Gibb, R.G. The rHEALPix Discrete Global Grid System. In IOP Conference Series: Earth and Environmental Science, Proceedings of the 9th Symposium of the International Society for Digital Earth (ISDE), Halifax, NS, Canada, 5–9 October 2015; IOP Publishing: Bristol, UK, 2016. [Google Scholar] [CrossRef]
- Sahr, K. Central place indexing: Hierarchical linear indexing systems for mixed-aperture hexagonal discrete global grid systems. Cartogr. Int. J. Geogr. Inf. Geovis. 2019, 54, 16–29. [Google Scholar] [CrossRef]

| Cell Resolution | Cells in Offset | Single Resolution Method | Multiresolution Method | Time Reduction (%) | ||
|---|---|---|---|---|---|---|
| Cells in Search Space | Time (s) | Cells in Search Space | Time (s) | |||
| 13 | 83 | 132 | 0.05 | - | - | - |
| 14 | 762 | 976 | 0.38 | 675 | 0.25 | 34 |
| 15 | 6837 | 8574 | 3.3 | 2268 | 1.1 | 67 |
| 16 | 61,633 | 74,886 | 29 | 7020 | 4.2 | 86 |
| Cell Resolution | Cells in Offset | Cell Error | Offsets Incorrect (%) | |
|---|---|---|---|---|
| Mean | Std. Dev. | |||
| 12 | 11 | 3 | 1 | 100 |
| 13 | 85 | 8 | 3 | 99.7 |
| Cell Resolution | Resolution | Resolution | ||||||
|---|---|---|---|---|---|---|---|---|
| Cell Error | Offsets Incorrect (%) | Cells in Offset at res. | Cell Error | Offsets Incorrect (%) | Cells in Offset at res. | |||
| Mean | Std. Dev. | Mean | Std. Dev. | |||||
| 12 | 0.7 | 0.8 | 49.7 | 85 | 0.2 | 0.5 | 17.4 | 759 |
| 13 | 3 | 2 | 94.4 | 759 | 0.6 | 0.9 | 39.1 | 6855 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bowater, D.; Wachowicz, M. Modelling Offset Regions around Static and Mobile Locations on a Discrete Global Grid System: An IoT Case Study. ISPRS Int. J. Geo-Inf. 2020, 9, 335. https://doi.org/10.3390/ijgi9050335
Bowater D, Wachowicz M. Modelling Offset Regions around Static and Mobile Locations on a Discrete Global Grid System: An IoT Case Study. ISPRS International Journal of Geo-Information. 2020; 9(5):335. https://doi.org/10.3390/ijgi9050335
Chicago/Turabian StyleBowater, David, and Monica Wachowicz. 2020. "Modelling Offset Regions around Static and Mobile Locations on a Discrete Global Grid System: An IoT Case Study" ISPRS International Journal of Geo-Information 9, no. 5: 335. https://doi.org/10.3390/ijgi9050335
APA StyleBowater, D., & Wachowicz, M. (2020). Modelling Offset Regions around Static and Mobile Locations on a Discrete Global Grid System: An IoT Case Study. ISPRS International Journal of Geo-Information, 9(5), 335. https://doi.org/10.3390/ijgi9050335






