A Simple Semantic-Based Data Storage Layout for Querying Point Clouds
Abstract
1. Introduction
2. Three Basic Approaches for Storing Point Clouds
2.1. The File-Based Approach
2.2. The RDBMS Approach
2.3. The Big Data Approach
- Key-value stores where values (which may also be completely unstructured, that is, Blobs) are stored under a unique key. The values in key-values pairs may be of different types and may be added at runtime without the risk of generating a conflict [40]. In Reference [41], the authors note that key-value stores have evolved so that it is possible to test for the existence of a value without knowing the key (value-based lookup).
- Column-oriented stores, also known as wide-column stores, partition the data vertically so that distinct values of a given column get stored consecutively in the same file [42]. Columns may be further grouped into families so that each family gets stored contiguously on disk. In this respect, a wide-column store can be seen as an extension of key-value stores; each column-family is a collection of (nested) key-value pairs [41].
- Graph databases which excel in managing data with many relationships [40]. An example would be social networks data. With the use of convolutional neural networks in point clouds [43], graphs are a promising tool, especially in the process of classifying the semantics of the point cloud. Since graph databases can be considered as a class to themselves, we do not examine their use with points clouds in this work.
2.4. On Indexing Multidimensional Data: The B+Tree Index
We assume that the index itself is so voluminous that only rather small parts of it can be kept in main store at one time.
2.5. Semantic3D: A Simple Semantic Point Cloud Scheme
3. Materials and Methods
3.1. The Sample Point Clouds
3.2. Using SDBL via Python
3.3. Using SDBL via PostgreSQL
3.4. The Queries That Were Used
3.5. Querying the Data in SDBL Using Python
3.6. Querying the Same SDBL Data in PostgreSQL
- Fragmented table: the dataset is fragmented into rows so that all points in a table belong to the same . The index is a basic B-tree composite non-clustered index. A total of nine fragmented tables are generated for the MEDIUM and the LARGE datasets, and only two fragmented tables ( and ) for the SMALL dataset. The attributes in each fragment table are .
- Fragmented PostGIS table (SMALL and MEDIUM datasets only): basically as above, but now the attributes are and S (for the SMALL dataset) and and I (for the MEDIUM dataset). These four attributes are incorporated into the PostGIS type ‘Point’. For the SMALL dataset, the index is made up of three separate functional indexes, which are for attributes X, Y and S (referring to ). For the MEDIUM dataset, only two functional indexes are needed, for attributes X and Y. This PostGIS option is tested only for the SMALL and MEDIUM datasets, and only two fragmented tables (those that are actually queried) are generated for each dataset.
- Unfragmented benchmark table: the dataset, now comprised of attributes is contained in a single flat PostgreSQL table (without PostGIS) and without the use of fragmentation. This table acts as a benchmark for the other PostgreSQL tests and since it contains points from different semantic IDs, an additional B-tree index on attribute was created in addition to the basic B-tree composite (non-clustered) index.
- Patch-table: this approach is only used with the SMALL dataset. The patches are created out of points that have the same building ID and the table is indexed via a GIST index on the PCPOINT type. The single patch-table contains the four attributes .
3.7. Data Preparation for Using SDBL via Python
3.8. Data Preparation for Using SDBL via PostgreSQL
3.9. The Software and Hardware That Was Used
4. Results
4.1. The Results for the Small Dataset
4.1.1. A More Complex Query Using the Extended Small Dataset
1 Pts_Block_grouped = Pts_BlockXY.loc[Pts_BlockXY.groupby(‘s’).z.idxmax()]
- Python-with-groupby: uses a single file under folder ‘ID_5’ that is read into a dataframe. The dataframe is then pre-processed so that building IDs marked for exclusion in the query are dropped and only points within the given range are included. Finally, the pandas groupby function is applied to the resulting dataframe to yield the final set of maximum Z-coordinate points (Pts_Block_grouped in Listing 1) for each building ID.
- Python-without-groupby: reads each file from a separate sub-folder (under parent folder ‘ID_5’) that is within the given range (and which does not belong to a building ID marked for exclusion) into a temporary dataframe df. From df, the maximum Z-coordinate is then computed and appended to a list to yield the final result.
- Fragmented table: uses a PostgreSQL table that contains all the points (rows) related to buildings, with a table structure that is identical to the one used for the downsampled SMALL dataset. The fragmented table contains 906,926 rows, the number of points related to buildings in the extended dataset.
1 EXPLAIN ANALYZE 2 SELECT MAX(Z) FROM P2xyz_s_5 3 WHERE X > = 378020 AND Y > = 6664206 4 GROUP BY S HAVING S NOT IN (‘416793804’,‘416794274’)
4.2. The Results for the Medium Dataset
4.3. The Results for the Large Dataset
1 EXPLAIN ANALYZE 2 SELECT * FROM P2xyz_L_0 WHERE X = 42.552 AND Y = 94.641 AND Z = 2.531 3 UNION 4 SELECT * FROM P2xyz_L_1 WHERE X = 42.552 AND Y = 94.641 AND Z = 2.531 5 …… 6 UNION 7 SELECT * FROM P2xyz_L_8 WHERE X = 42.552 AND Y = 94.641 AND Z = 2.531
1 EXPLAIN ANALYZE SELECT * FROM P2xyz_L WHERE X = 42.552 2 AND Y = 94.641 AND Z = 2.531
5. Discussion and Conclusions
5.1. Advantages of the Presented SDBL Approach
5.2. Limitations of the Presented SDBL Approach
5.3. How the Presented SDBL Approach Relates to Previous Work
5.4. Future Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BIM | Building Information Modeling |
| PCDMS | Point Cloud Data Management System |
| SDBL | Semantic Data Based Layout |
| RDBMS | Relational Database Management System |
Appendix A
1 def get_sem_xyz_points(cur_dir,semanticID): 2 SDIR_PREFIX = “ID_” 3 semantic_dir1 = os.path.join(cur_dir, SDIR_PREFIX + semanticID) 4 semantic_dir = os.path.join(semantic_dir1, “xyz.fff”) 5 return feather.read_dataframe(semantic_dir)
1 def qry_pts_inxy_range(ptsblock,min_x,min_y): 2 AND_ = ’ & ’;OFF_X = 500;OFF_Y = 500 3 restrict = ’’ 4 if min_x is not None: 5 restrict = restrict + ’ x > = ’ + repr(min_x) 6 restrict = restrict + AND_ + ’ x < = ’ + repr(min_x + OFF_X) 7 if min_y is not None: 8 if restrict ! = ’’: 9 restrict = restrict + ’ & ’ 10 else: 11 pass 12 restrict = restrict + ’ y > = ’ + repr(min_y) 13 restrict = restrict + AND_ + ’ y < = ’ + repr(min_y + OFF_Y) 14 else: 15 pass 16 return ptsblock.query(restrict)
1 CREATE INDEX Semantics ON S_Lidar USING GIST(geometry(pa));
1 EXPLAIN ANALYZE SELECT * FROM P2xyz_s_5 WHERE s = ‘416793804’;
1 INSERT INTO Points_s_5(pt) 2 SELECT PC_MAKEPOINT(1,ARRAY[X,Y,X,5]) FROM p2xyz_s_5 AS VALUES;
1 EXPLAIN ANALYZE SELECT PC_ASTEXT(PT) FROM Points_s_2;
1 EXPLAIN ANALYZE SELECT pt 2 FROM S_lidar, Pc_Explode(pa) AS pt WHERE PC_Get(pt, ‘S’) = ‘5’
References
- Vo, A.V.; Laefer, D.F.; Bertolotto, M. Airborne laser scanning data storage and indexing: State-of-the-art review. Int. J. Remote Sens. 2016, 37, 6187–6204. [Google Scholar] [CrossRef]
- Haala, N.; Petera, M.; Jens Kremerb, G.H. Mobile LiDAR mapping for 3D point cloud collection in urban: A performance test. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1119–1124. [Google Scholar] [CrossRef]
- Kukko, A.; Kaartinen, H.; Hyyppä, J.; Chen, Y. Multiplatform Mobile Laser Scanning: Usability and Performance. Sensors 2012, 12, 11712–11733. [Google Scholar] [CrossRef]
- Remondino, F.; Spera, M.G.; Nocerino, E.; Menna, F.; Nex, F. State of the art in high density image matching. Photogramm. Rec. 2014, 29, 144–166. [Google Scholar] [CrossRef]
- Khoshelhamand, K.; Elberink, S.O. Accuracy and Resolution of Kinect Depth Data for Indoor Mapping Applications. Sensors 2012, 12, 1437–1454. [Google Scholar] [CrossRef] [PubMed]
- Weinmann, M.; Schmidt, A.; Mallet, C.; Hinz, S.; Rottensteiner, F.; Jutzi, B. Contextual Classification of Point Cloud Data by Exploiting Individual 3D Neighborhoods. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 271–278. [Google Scholar] [CrossRef]
- Koppula, H.S.; Anand, A.; Joachims, T.; Saxena, A. Semantic Labeling of 3D Point Clouds for Indoor Scenes. In Advances in Neural Information Processing Systems, Proceedings of the 25th Annual Conference on Neural Information Processing Systems (NIPS 2011), Granada, Spain, 12–14 December 2011; Shawe-Taylor, J., Zemel, R.S., Bartlett, P.L., Pereira, F.C.N., Weinberger, K.Q., Eds.; Curran Associates: Red Hook, NY, USA, 2011; pp. 244–252. [Google Scholar]
- Virtanen, J.P.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Turppa, T.; Hyyppä, H.; Hyyppä, J. Nationwide Point Cloud—The Future Topographic Core Data. ISPRS Int. J. Geo-Inf. 2017, 6, 243. [Google Scholar] [CrossRef]
- Ekman, P. Scene Reconstruction from 3D Point Clouds. Master’s Thesis, Aalto University School of Science, Espoo, Finland, 2017. [Google Scholar]
- Chu, E.; Beckmann, J.; Naughton, J. The Case for a Wide-table Approach to Manage Sparse Relational Data Sets. In Proceedings of the 2007 ACM SIGMOD International Conference on Management of Data (SIGMOD ’07), Beijing, China, 12–14 June 2007; ACM: New York, NY, USA, 2007; pp. 821–832. [Google Scholar] [CrossRef]
- Alvanaki, F.; Goncalves, R.; Ivanova, M.; Kersten, M.; Kyzirakos, K. GIS Navigation Boosted by Column Stores. Proc. VLDB Endow. 2015, 8, 1956–1959. [Google Scholar] [CrossRef]
- Ramamurthy, R.; DeWitt, D.J.; Su, Q. A Case for Fractured Mirrors. VLDB J. 2003, 12, 89–101. [Google Scholar] [CrossRef]
- Asano, T.; Ranjan, D.; Roos, T.; Welzl, E.; Widmayer, P. Space-filling Curves and Their Use in the Design of Geometric Data Structures. Theor. Comput. Sci. 1997, 181, 3–15. [Google Scholar] [CrossRef]
- Kim, J.; Seo, S.; Jung, D.; Kim, J.S.; Huh, J. Parameter-Aware I/O Management for Solid State Disks (SSDs). IEEE Trans. Comput. 2012, 61, 636–649. [Google Scholar] [CrossRef]
- van Oosterom, P.; Martinez-Rubi, O.; Ivanova, M.; Horhammer, M.; Geringer, D.; Ravada, S.; Tijssen, T.; Kodde, M.; Gonçalves, R. Massive Point Cloud Data Management. Comput. Graph. 2015, 49, 92–125. [Google Scholar] [CrossRef]
- Psomadaki, S. Using a Space Filling Curve for the Management of Dynamic Point Cloud Data in a Relational DBMS. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2016. [Google Scholar]
- Vo, A.V.; Konda, N.; Chauhan, N.; Aljumaily, H.; Laefer, D.F. Lessons learned with laser scanning point cloud management in Hadoop HBase. In Advanced Computing Strategies for Engineering, Proceedings of the 25th EG-ICE International Workshop 2018, Lausanne, Switzerland, 10–13 June 2018; Smith, I.F.C., Domer, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; Part II; pp. 1–16. [Google Scholar]
- Sippu, S.; Soisalon-Soininen, E. Transaction Processing: Management of the Logical Database and Its Underlying Physical Structure; Springer: Berlin, Germany, 2015. [Google Scholar]
- Richter, R.; Döllner, J. Concepts and techniques for integration, analysis and visualization of massive 3D point clouds. Comput. Environ. Urban Syst. 2014, 45, 114–124. [Google Scholar] [CrossRef]
- Isenburg, M. LASzip: Lossless Compression of Lidar Data. Photogramm. Eng. Remote Sens. 2013, 79, 209–217. [Google Scholar] [CrossRef]
- van Oosterom, P.; Martinez-Rubi, O.; Tijssen, T.; Gonçalves, R. Realistic Benchmarks for Point Cloud Data Management Systems. In Advances in 3D Geoinformation. Lecture Notes in Geoinformation and Cartography; Abdul-Rahman, A., Ed.; Springer: Cham, Swizerland, 2017; pp. 1–30. [Google Scholar] [CrossRef]
- Martinez-Rubi, O.; van Oosterom, P.; Gonçalves, R.; Tijssen, T.; Ivanova, M.; Kersten, M.L.; Alvanaki, F. Benchmarking and Improving Point Cloud Data Management in MonetDB. SIGSPATIAL Spec. 2014, 6, 11–18. [Google Scholar] [CrossRef]
- Boehm, J. File-centric Organization of large LiDAR Point Clouds in a Big Data context. In Proceedings of the IQmulus 1st Workshop on Processing Large Geospatial Data, Cardiff, UK, 8 July 2014; pp. 69–76. [Google Scholar]
- Guan, X.; Van Oosterom, P.; Cheng, B. A Parallel N-Dimensional Space-Filling Curve Library and Its Application in Massive Point Cloud Management. ISPRS Int. J. Geo-Inf. 2018, 7, 327. [Google Scholar] [CrossRef]
- Poux, F.; Hallot, P.; Neuville, R.; Billen, R. Smart point cloud: Definition and remaining challenges. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, IV-2/W1, 119–127. [Google Scholar] [CrossRef]
- Chamberlin, D.D.; Boyce, R.F. SEQUEL: A Structured English Query Language. In Proceedings of the 1974 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control (SIGFIDET ’74), Ann Arbor, MI, USA, May 1974; ACM: New York, NY, USA, 1974; pp. 249–264. [Google Scholar] [CrossRef]
- Codd, E.F. A Relational Model of Data for Large Shared Data Banks. Commun. ACM 1970, 13, 377–387. [Google Scholar] [CrossRef]
- Bayer, R.; McCreight, E. Organization and Maintenance of Large Ordered Indices. In Proceedings of the 1970 ACM SIGFIDET (Now SIGMOD) Workshop on Data Description, Access and Control, SIGFIDET ’70, Rice University, Houston, TX, USA, July 1970; ACM: New York, NY, USA, 1970; pp. 107–141. [Google Scholar] [CrossRef]
- Schön, B.; Bertolotto, M.; Laefer, D.F.; Morrish, S. Storage, manipulation, and visualization of LiDAR data. In Proceedings of the 3rd ISPRS International Workshop 3D-ARCH 2009, Trento, Italy, 25–28 February 2009. [Google Scholar]
- PostgreSQL 11.2 Documentation. Documentation, The PostgreSQL Global Development Group, USA. 2019. Available online: https://www.postgresql.org/files/documentation/pdf/11/postgresql-11-A4.pdf (accessed on 15 October 2019).
- Blasby, D. Building a Spatial Database in PostgreSQL. Report, Refractions Research. 2001. Available online: http://postgis.refractions.net/ (accessed on 15 October 2019).
- Ramsey, P. LIDAR in PostgreSQL with PointCloud. Available online: http://s3.cleverelephant.ca/foss4gna2013-pointcloud.pdf (accessed on 15 October 2019).
- Zicari, R.V. Big Data: Challenges and Opportunities. In Big Data Computing; Akerkar, R., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2014; pp. 103–128. [Google Scholar]
- Sicular, S. Gartner’s Big Data Definition Consists of Three Parts, Not to Be Confused with Three ’V’s. Available online: http://businessintelligence.com/bi-insights/gartners-big-data-definition-consists-of-three-parts-not-to-be-confused-with-three-vs/ (accessed on 3 September 2019).
- Zicari, R.V.; Rosselli, M.; Ivanov, T.; Korfiatis, N.; Tolle, K.; Niemann, R.; Reichenbach, C. Setting Up a Big Data Project: Challenges, Opportunities, Technologies and Optimization. In Big Data Optimization: Recent Developments and Challenges, Studies in Big Data 18; Emrouznejad, A., Ed.; Springer: Cham, Switzerland, 2016; pp. 17–45. [Google Scholar] [CrossRef]
- Evans, M.R.; Oliver, D.; Zhou, X.; Shekhar, S. Spatial Big Data: Case Studies on Volume, Velocity and Variety. In Big Data: Techniques and Technologies in GeoInformatics; Karimi, H.A., Ed.; Taylor and Francis: Boca Raton, FL, USA, 2010; pp. 149–173. [Google Scholar]
- Wadkar, S.; Siddalingaiah, M. Pro Apache Hadoop; Apress: New York, NY, USA, 2014. [Google Scholar]
- Cattell, R. Scalable SQL and NoSQL Data Stores. SIGMOD Rec. 2011, 39, 12–27. [Google Scholar] [CrossRef]
- Gessert, F.; Wingerath, W.; Friedrich, S.; Ritter, N. NoSQL Database Systems: A Survey and Decision Guidance. Comput. Sci. 2017, 32, 353–365. [Google Scholar] [CrossRef]
- Hecht, R.; Jablonski, S. NoSQL Evaluation: A Use Case Oriented Survey. In Proceedings of the 2011 International Conference on Cloud and Service Computing (CSC ’11), Hong Kong, China, 12–14 December 2011; IEEE Computer Society: Washington, DC, USA, 2011; pp. 336–341. [Google Scholar] [CrossRef]
- Davoudian, A.; Chen, L.; Liu, M. A Survey on NoSQL Stores. ACM Comput. Surv. 2018, 51, 40:1–40:43. [Google Scholar] [CrossRef]
- Héman, S. Updating Compressed Column-Stores. Ph.D. Thesis, Vrije Universiteit Amsterdam, Amsterdam, The Netherlands, 2015. [Google Scholar]
- Wang, Y.; Sun, Y.; Liu, Z.; Sarma, S.E.; Bronstein, M.M.; Solomon, J.M. Dynamic Graph CNN for Learning on Point Clouds. ACM Trans. Graph. 2019, 38, 146:1–146:12. [Google Scholar] [CrossRef]
- Xiang, L.; Shao, X.; Wang, D. Providing R-Tree Support for MongoDB. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2016, XLI-B4, 545–549. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: Simplified Data Processing on Large Clusters. Commun. ACM 2008, 51, 107–113. [Google Scholar] [CrossRef]
- Dean, J.; Ghemawat, S. MapReduce: A Flexible Data Processing Tool. Commun. ACM 2010, 53, 72–77. [Google Scholar] [CrossRef]
- Santos, M.Y.; Costa, C.; Galvão, J.A.; Andrade, C.; Martinho, B.A.; Lima, F.V.; Costa, E. Evaluating SQL-on-Hadoop for Big Data Warehousing on Not-So-Good Hardware. In Proceedings of the 21st International Database Engineering & Applications Symposium, IDEAS 2017, Bristol, UK, 12–14 July 2017; ACM: New York, NY, USA, 2017; pp. 242–252. [Google Scholar] [CrossRef]
- Floratou, A.; Minhas, U.F.; Özcan, F. SQL-on-Hadoop: Full Circle Back to Shared-nothing Database Architectures. Proc. VLDB Endow. 2014, 7, 1295–1306. [Google Scholar] [CrossRef]
- Armbrust, M.; Xin, R.S.; Lian, C.; Huai, Y.; Liu, D.; Bradley, J.K.; Meng, X.; Kaftan, T.; Franklin, M.J.; Ghodsi, A.; et al. Spark SQL: Relational Data Processing in Spark. In Proceedings of the 2015 ACM SIGMOD International Conference on Management of Data, SIGMOD ’15, Melbourne, VIC, Australia, 31 May–4 June 2015; ACM: New York, NY, USA, 2015; pp. 1383–1394. [Google Scholar] [CrossRef]
- Pajic, V.; Govedarica, M.; Amovic, M. Model of Point Cloud Data Management System in Big Data Paradigm. ISPRS Int. J. Geo-Inf. 2018, 7, 265. [Google Scholar] [CrossRef]
- Comer, D. The Ubiquitous B-Tree. ACM Comput. Surv. 1979, 11, 121–137. [Google Scholar] [CrossRef]
- Wedekind, H. On the selection of access paths in a data base system. In Proceedings of the IFIP Working Conference Data Base Management, Cargese, Corsica, France, 1–5 April 1974; Klimbie, J., Koffeman, K., Eds.; North-Holland: Amsterdam, The Netherlands, 1974; pp. 385–397. [Google Scholar]
- Johnson, T.; Shasha, D. B-trees with Inserts and Deletes: Why Free-at-empty is Better Than Merge-at-half. J. Comput. Syst. Sci. 1993, 47, 45–76. [Google Scholar] [CrossRef][Green Version]
- Garcia-Molina, H.; Ullman, J.D.; Widom, J. Database System Implementation; Prentice-Hall: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Ooi, B.C.; Tan, K.L.; Tan, K.L. B-trees: Bearing Fruits of All Kinds. Aust. Comput. Sci. Commun. 2002, 24, 13–20. [Google Scholar]
- Cura, R.; Perret, J.; Paparoditis, N. A scalable and multi-purpose point cloud server (PCS) for easier and faster point cloud data management and processing. ISPRS J. Photogramm. Remote Sens. 2017, 127, 39–56. [Google Scholar] [CrossRef]
- Terry, J. Indexing Multidimensional Point Data. Ph.D. Thesis, Institute for Integrated and Intelligent Systems, Griffith University, South Brisbane, Australia, 2008. [Google Scholar]
- Bayer, R.; Markl, V. The UB-Tree: Performance of Multidimensional Range Queries; Technical Report, Institut für Informatik; TU München: Munich, Germany, 1999. [Google Scholar]
- Lawder, J. The Application of Space-filling Curves to the Storage and Retrieval of Multi-Dimensional Data. Ph.D. Thesis, University of London (Birkbeck College), London, UK, 2000. [Google Scholar]
- Mokbel, M.F.; Aref, W.G. Irregularity in Multi-dimensional Space-filling Curves with Applications in Multimedia Databases. In Proceedings of the Tenth International Conference on Information and Knowledge Management (CIKM ’01), Atlanta GA, USA, 5–10 October 2001; ACM: New York, NY, USA, 2001; pp. 512–519. [Google Scholar] [CrossRef]
- Ghane, A. The Effect of Reordering Multi-Dimensional Array Data on CPU Cache Utilization. Master’s Thesis, Simon Fraser University, Burnaby, BC, Canada, 2013. [Google Scholar]
- Dandois, J.P.; Baker, M.; Olano, M.; Parker, G.G.; Ellis, E.C. What is the Point? Evaluating the Structure, Color, and Semantic Traits of Computer Vision Point Clouds of Vegetation. Remote Sens. 2017, 9, 355. [Google Scholar] [CrossRef]
- Hackel, T.; Savinov, N.; Ladicky, L.; Wegner, J.D.; Pollefeys, K.S.M. Semantic3D.net: A new Large-scale Point Cloud Classification Benchmark. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, II-3/W4, 91–98. [Google Scholar] [CrossRef]
- Weinmann, M.; Weinmann, M.; Schmidt, A.; Mallet, C.; Bredif, M. A Classification-Segmentation Framework for the Detection of Individual Trees in Dense MMS Point Cloud Data Acquired in Urban Areas. Remote Sens. 2017, 9, 277. [Google Scholar] [CrossRef]
- Pusala, M.K.; Salehi, M.A.; Katukuri, J.R.; Xie, Y.; Raghavan, V. Massive Data Analysis: Tasks, Tools, Applications, and Challenges. In Advances in 3D Geoinformation. Lecture Notes in Geoinformation and Cartography; Springer: New Delhi, India, 2016; pp. 11–40. [Google Scholar]
- National Land Survey of Finland. Maps and Spatial Data. Available online: https://www.maanmittauslaitos.fi/en/maps-and-spatial-data/expert-users/product-descriptions/laser-scanning-data (accessed on 3 December 2019).
- National Land Survey of Finland. Topographic Database. Available online: https://www.maanmittauslaitos.fi/en/maps-and-spatial-data/expert-users/product-descriptions/topographic-database (accessed on 3 December 2019).
- Poux, F.; Neuville, R.; Nys, G.A.; Billen, R. 3D Point Cloud Semantic Modelling: Integrated Framework for Indoor Spaces and Furniture. Remote Sens. 2018, 10, 1412. [Google Scholar] [CrossRef]
- Al-Kateb, M.; Sinclair, P.; Au, G.; Ballinger, C. Hybrid Row-column Partitioning in Teradata. Proc. VLDB Endow. 2016, 9, 1353–1364. [Google Scholar] [CrossRef]
- McKinney, W. Pandas: Powerful Python Data Analysis Toolkit. Available online: https://pandas.pydata.org/pandas-docs/stable/pandas.pdf (accessed on 12 December 2019).
- Ramm, J. feather Documentation Release 0.1.0. Available online: https://buildmedia.readthedocs.org/media/pdf/plume/stable/plume.pdf (accessed on 12 December 2019).
- Bayer, M. SQLAlchemy Documentation: Release 1.0.12. Available online: https://buildmedia.readthedocs.org/media/pdf/sqlalchemy/rel_1_0/sqlalchemy.pdf (accessed on 12 December 2019).
- Sinthong, P.; Carey, M.J. AFrame: Extending DataFrames for Large-Scale Modern Data Analysis (Extended Version). arXiv 2019, arXiv:1908.06719. [Google Scholar]
- Wang, J.; Shan, J. Space-Filling Curve Based Point Clouds Index. In Proceedings of the 8th International Conference on GeoComputation, GeoComputation CD-ROM, Ann Arbor, MI, USA, 31 July–3 August 2005; pp. 1–16. [Google Scholar]
- Xu, S.; Oude Elberink, S.; Vosselman, G. Entities and Features for Classficication of Airborne Laser Scanning Data in Urban Area. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, I-4, 257–262. [Google Scholar] [CrossRef]
- Vosselman, G. Point cloud segmentation for urban scene classification. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-7/W2, 257–262. [Google Scholar] [CrossRef]
- rapidlasso GmbH. LaStools. Available online: https://rapidlasso.com/lastools/ (accessed on 31 December 2019).
- Thomas, H.; Goulette, F.; Deschaud, J.E.; Marcotegui, B.; LeGall, Y. Semantic Classification of 3D Point Clouds with Multiscale Spherical Neighborhoods. In Proceedings of the 2018 International Conference on 3D Imaging, Modeling, Processing, Visualization and Transmission (3DIMPVT), Verona, Italy, 5–8 September 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 390–398. [Google Scholar] [CrossRef]
- Poux, F.; Billen, R. Voxel-Based 3D Point Cloud Semantic Segmentation: Unsupervised Geometric and Relationship Featuring vs Deep Learning Methods. ISPRS Int. J. Geo-Inf. 2019, 8, 243. [Google Scholar] [CrossRef]
- Bayer, R. Software Pioneers; Chapter B-trees and Databases, Past and Future; Springer: New York, NY, USA, 2002; pp. 232–244. [Google Scholar]
- El-Mahgary, S.; Soisalon-Soininen, E.; Orponen, P.; Rönnholm, P.; Hyyppä, H. OVI-3: An Incremental, NoSQL Visual Query System with Directory-Based Indexing. Working Paper.
- Özdemir, E.; Remondino, F. Classification of aerial point clouds with deep learning. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-2/W13, 103–110. [Google Scholar] [CrossRef]
- Cura, R.; Perret, J.; Paparoditis, N. Point Cloud Server (PCS): Point Clouds in-base management and processing. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W5, 531–539. [Google Scholar] [CrossRef]
- Poux, F. The Smart Point Cloud: Structuring 3D Intelligent Point Data. Ph.D. Thesis, University of Liège, Liège, Belgium, 2019. [Google Scholar]
Sample Availability: The full datasets, together with the Python scripts, are available from https://doi.org/10.5281/zenodo.3540413. |
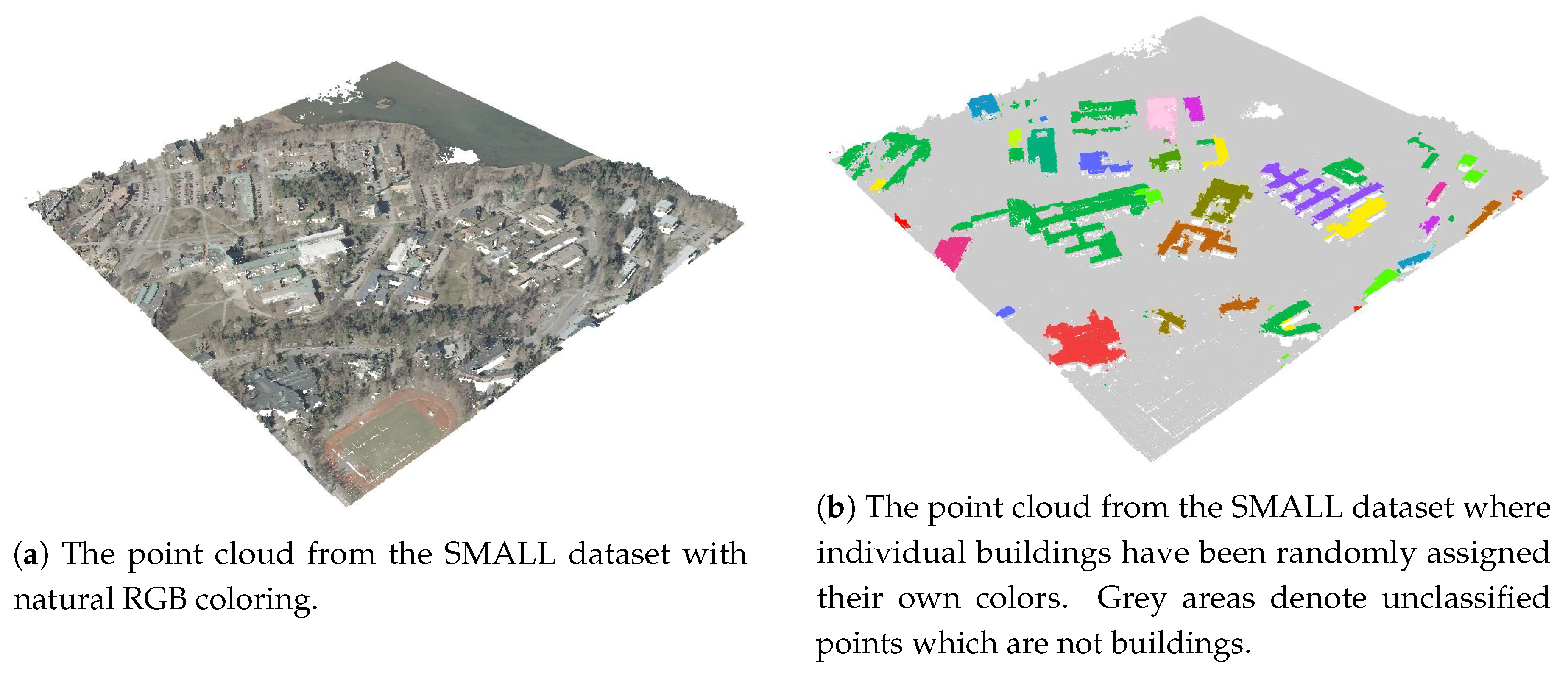


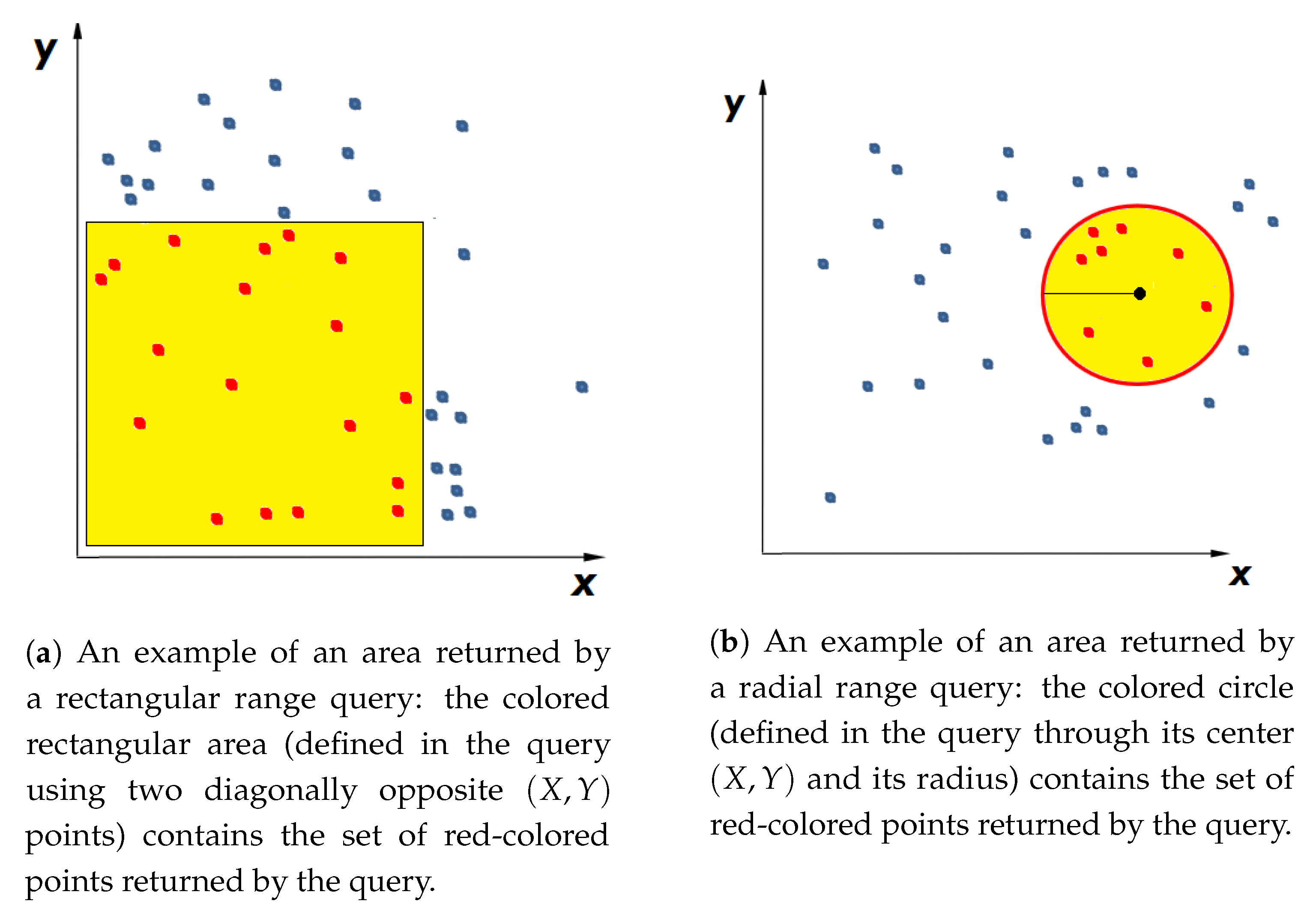
| SMALL Dataset | MEDIUM Dataset | LARGE Dataset |
|---|---|---|
| 368,408 points representing the Otaniemi area in Espoo Finland. Source: National Land Survey of Finland, cropped sub-sample based on the ETR-TM35FIN coordinate system | 29,697,591 points from Bildstein station, source: Semantic3D [63], file: bildstein_station1_xyz_intensity_rgb.7z. | 496,702,861 points from a station, source: Semantic3D [63], file: sg27_station2_intensity_rgb.7z. |
| Query ID | Description |
|---|---|
| Point Query | Load all points where (buildings). |
| Point Query | Load all points that refer to a particular building ID (ID = 416793804). |
| Point Query | Load all points that refer to a particular building ID (ID = 41679427). |
| Rectangular Query | Load all points that refer to buildings and that are within a given rectangle. |
| Radial Query | Load all points that refer to buildings and that are within a given radius. |
| Query ID | Description |
|---|---|
| Point Query | Load all points where (buildings). |
| Range | Load all points that refer to buildings and where the x-coordinate |
| Point Query | Load all points where (natural terrain). |
| Rectangular Query | Load all points that refer to buildings and that are within a given rectangle. |
| Radial Query | Load all points that refer to buildings and that are within a given radius. |
| Small Dataset (ms) | Preparation Time | Point Query | Point Query | Point Query | Rectangular Query | Radial Query |
|---|---|---|---|---|---|---|
| Generate Semantic Files/Load Data | Points with Class ID = 5 (Buildings) | Points in Building with ID = 416793804 | Points in Building with ID = 416794274 | Points from Query within a Given Rectangle | Points from Query within a Given Radius | |
| Python | 3885 | 12.34 | 14.23 | 15.79 | 12.27 | 42.27 |
| Fragmented table | 4080 | 8.99 (3.46) | 1.92 (0.32) | 2.4 (0.42) | 7.76 (5.35) | 4.47 (1.99) |
| Fragmented PostGIS table | 14,555 | 110.403 (107.952) | 11.99 (4.17) | 13.66 ( 5.66) | 17.5 (16.03) | 26.62 (16.81) |
| Unfragmented benchmark table (No PostGIS) | 6919 | 53.88 (40.75) | 1.77 (0.31) | 2.16 (0.46) | 205.14 (203.91) | 52.94 (12.9) |
| Patch table | 13,128 | 83.85 (79.00) | 86.71 (81.47) | 86.26 (72.24) | 226.1 (207.81) | 273.05 (177.93) |
| No of points returned | - | 41,865 | 1386 | 1951 | 19,722 | 2556 |
| Medium Dataset (ms) | Preparation Time | Point Query | Range Query | Point Query | Rectangular Query | Radial Query |
|---|---|---|---|---|---|---|
| Generate Semantic Files/Load Data | Points with Class ID = 5 (Buildings) | Points with Class ID = 5 and X > 20 | Points with Class ID = 2 (Natural Terrain) | Points from Query within a Given Rectangle | Points from Query within a Given Radius | |
| Python | 43,806 | 46.53 | 62.48 | 93.39 | 109.344 | 108.67 |
| Fragmented table | 347,500 | 155.3 (153.61) | 174.42 (154.93) | 595.43 (444.49) | 102.33 (59.60) | 84.04 (42.77) |
| Fragmented PostGIS table | 48,791 | 3311.96 (2330.27) | 2123.12 (1999.72) | 6307.97 (6106.05) | 2758.13 (2618.52) | 2207.35 (2123.22) |
| Unfragmented benchmark table (No PostGIS) | 274,937 | 225.72 (154.99) | 518.52 (188.78) | 1009.53 (722.183) | 327.3 (180.11) | 381 (200.1) |
| No of points returned | - | 1,242,205 | 385,664 | 3,508,530 | 261,911 | 68,160 |
| Large Dataset (s) | Preparation Time | Point Query | Range Query | Point Query | Rectangular Query | Radial Query |
|---|---|---|---|---|---|---|
| Generate Semantic Files/Load Data | Points with Class ID = 5 (Buildings) | Points with Class ID = 5 and X > 20 | Points with Class ID = 2 (Natural Terrain) | Points from Query within a Given Rectangle | Points from Query within a Given Radius | |
| Python | 426 | 1.37 | 3.44 | 3.06 | 3.64 | 5.65 |
| Fragmented table | 5882 | 27.87 (10.92) | 10.56 (10.41) | 61.43 (21.45) | 1.83 (1.39) | 1.15 (0.89) |
| Unfragmented benchmark table (No PostGIS) | 9368 | 73.01 (22.49) | 122.07 (22.5) | 103.32 (72.18) | 20.25 (2.43) | 14.24 (1.23) |
| No of points returned | - | 89,036,106 | 33,361,461 | 184,550,983 | 945,357 | 246,762 |
| Point Query for Large Dataset (Returns a Single Point) (ms) | Python with Pandas (ms) | Fragmented Table (ms) | Unfragmented Table (ms) |
|---|---|---|---|
| Locating a specific point () that has (hardscape). | 7880 (47,710) | 29.5 (1.5) | 45.5 (0.22) |
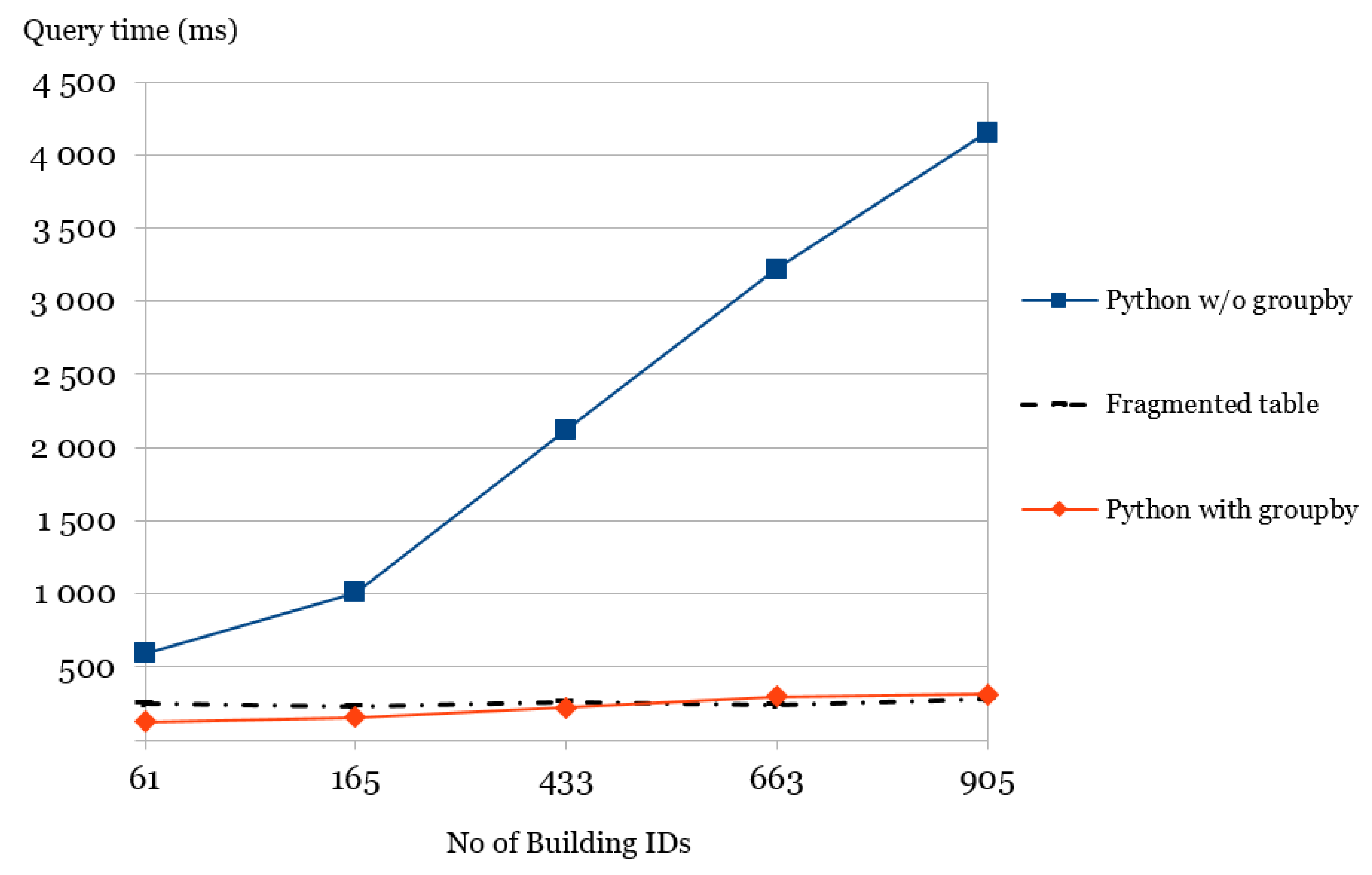
| Complex Queries (Five Different Ranges) Uses the Extended Small Dataset to locate the Max. Z-Coordinate in Each Building ID Other Than ID = ‘41679380’ and ID = ‘416794274’ in a Given Region , Defined Below. | No of Building IDs Touched | Python with Groupby (ms) | Fragmented Table (ms) | Python w/o Groupby (ms) |
|---|---|---|---|---|
| 379,020 and 6,674,206 | 61 | 125 | 250 | 590 |
| 379,520 and 6,667,206 | 165 | 156 | 230 | 1010 |
| 378,520 and 6,667,206 | 433 | 219 | 260 | 2120 |
| 378,200 and 6,667,006 | 663 | 297 | 240 | 3220 |
| 378,020 and 6,664,206 | 905 | 310 | 280 | 4150 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Mahgary, S.; Virtanen, J.-P.; Hyyppä, H. A Simple Semantic-Based Data Storage Layout for Querying Point Clouds. ISPRS Int. J. Geo-Inf. 2020, 9, 72. https://doi.org/10.3390/ijgi9020072
El-Mahgary S, Virtanen J-P, Hyyppä H. A Simple Semantic-Based Data Storage Layout for Querying Point Clouds. ISPRS International Journal of Geo-Information. 2020; 9(2):72. https://doi.org/10.3390/ijgi9020072
Chicago/Turabian StyleEl-Mahgary, Sami, Juho-Pekka Virtanen, and Hannu Hyyppä. 2020. "A Simple Semantic-Based Data Storage Layout for Querying Point Clouds" ISPRS International Journal of Geo-Information 9, no. 2: 72. https://doi.org/10.3390/ijgi9020072
APA StyleEl-Mahgary, S., Virtanen, J.-P., & Hyyppä, H. (2020). A Simple Semantic-Based Data Storage Layout for Querying Point Clouds. ISPRS International Journal of Geo-Information, 9(2), 72. https://doi.org/10.3390/ijgi9020072





