The tourist site of interest classification that was obtained from the Naïve Bayes machine learning mining model conforms to tourists’ interests and needs. Under the condition, we design an optimal tourist site mining algorithm based on the membership degree searching propagating tree to mine tourist sites with optimal geographic distribution. The mined optimal tourist sites are designed as nodes of tour routes to develop a smart tour route planning algorithm combined with factors, such as tourism GIS services, traffic information services, and tourist site information services, which influence tourists’ travel experiences. The algorithm can output optimal tour routes, which conform to actual conditions, meet tourists’ interests and motive benefits, and decrease travel expenditures. Meanwhile, sub-optimal tour routes are also provided for tourists.
3.1. Optimal Tourist Site Mining Algorithm based on Membership Degree Searching Propagating Tree
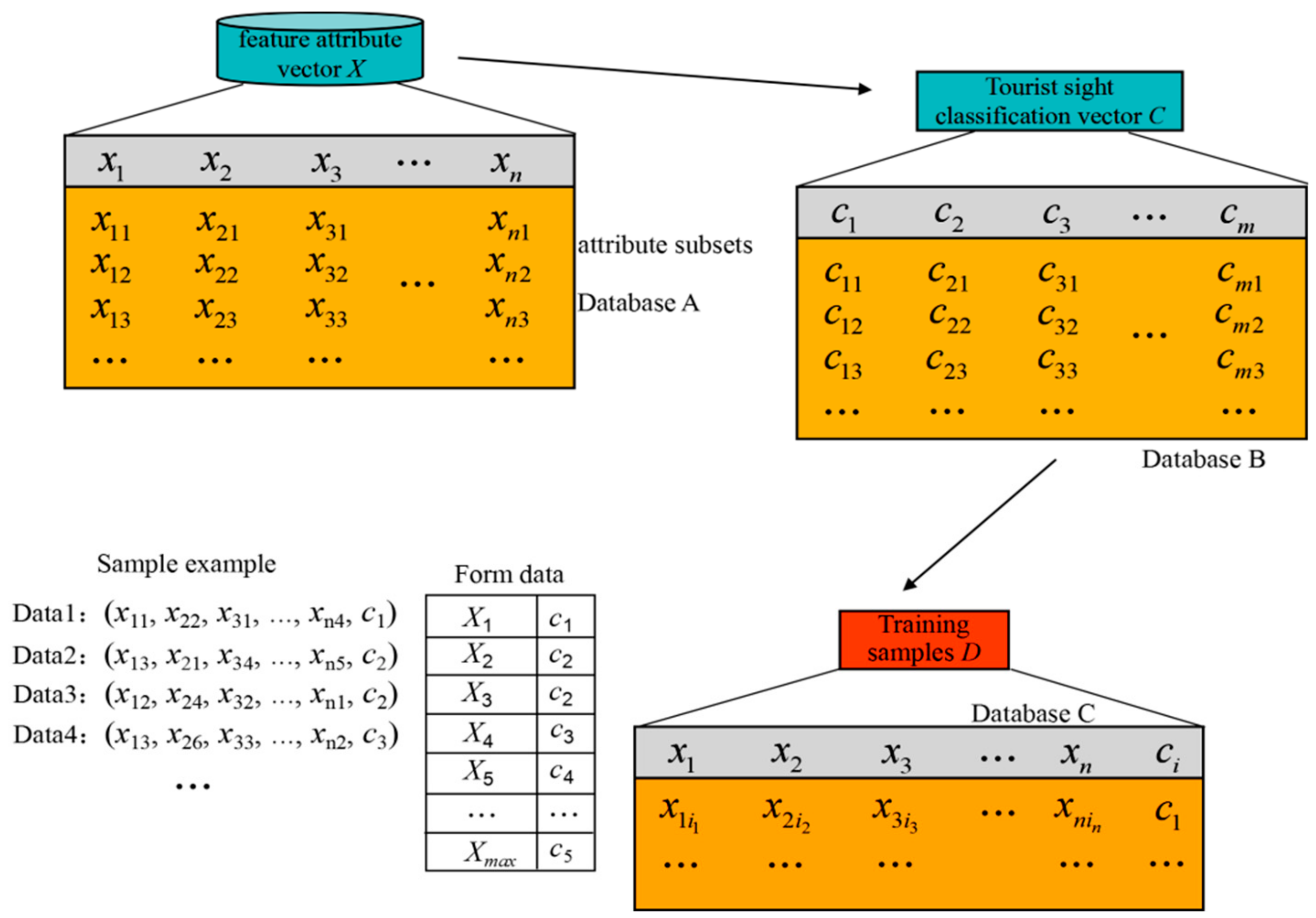
The tourist site of interest classification distribution matrix formed by the Naïve Bayes machine learning mining process is the critical model for smart machine to learn tourists’ needs and interests. In the matrix , arbitrary row represents one feasible sort of tourist site classification and quantity. Each row’s classification and quantity can meet the needs of tourists, but they differ in specific tourist sites, which will output different tour routes. According to the definition, as to one row of matrix , the feasible sort of classification and quantity is , but not all the sorts are the optimal ones. The tourists start from temporary accommodation in the city, visit all selected tourist sites, and finally return to temporary accommodation, and the whole process forms an integrated tour route. The selected tourist sites should meet the needs and interests while costing the minimum expenditure. Thus, within the neighbourhood range of a temporary accommodation center, the nearer to the center, the more beneficial of the tourist site will be. Thus, in , there are different sorts of tourist classifications and quantities and only one sort is optimal in geographic distribution. The membership degree relationship is used to set up the neighbourhood searching arc for the seed tourist site and to iterate the tourist sites to generate the propagating tree. The process of searching for subordinate seed tourist sites is in the range of one tourist site cluster or cross-cluster, that is, the tourist sites may belong to the same cluster or different clusters. The final output result of the process is a propagating tree with optimal geographic distributed tourist sites, and notes on the tree are the mined optimal tourist sites.
Definition 7. Tourist site clustering center. The temporary accommodation which is confirmed and checked in before the trip is set as the starting point and terminal point of the whole tour activity. The temporary accommodation is the first critical point of the planned tour route, which is called the tourist site clustering center. The centeris determined by the temporary accommodation’s location, here defined as the longitude and latitude.
The center will change with the tourist’s decision on the temporary accommodation and will directly influence the propagating tree’s formation, shape and distribution, and influence the mined optimal tourist sites.
Definition 8. Seed tourist siteand seed tourist site vector. Starting from tourist site clustering center, searched and confirmed optimal tourist sites within neighbourhood via objective function and membership degree are called seed tourist site. Under the condition of one sort of tourist site classification and quantity, the searched seed tourist sites for each tourist site classificationis, and, is the total quantity of seed tourist sites, according to the tourist site of interest classification distribution matrix and its arbitrary row vector . We store seed tourist sites in the sequence of the propagating tree’s nodes in the vector element from left to right in order, and this vector is called the seed tourist site vector .
Under the condition of the confirmed tourist site clustering center , matrix can generate seed tourist site vectors , and , according to the definition. Each stores the searched optimal tourist sites of row .
Definition 9. Subordinate seed tourist siteand non-subordinate seed tourist site. As to one seed tourist site, the searched and confirmed tourist site which is closest to starting centeror seed tourist siteand it will be listed to store in propagating tree nodes via subordinate function and membership degree relationship model is called subordinate seed tourist site. In the same searching process, other tourist sites that are not listed to store in propagating tree nodes are called non-subordinate seed tourist site.
Definition 10. Seed tourist site searching arc. We set initial seed tourist siteas the circle center, and take the neighbourhood radius confirmed by the objective function as the arc. The arc is used to search the subordinate seed tourist site. The combined structure of the radius and arc is called the seed tourist site searching arc. The seed tourist site searching arc is the direction and path to search the seed tourist site. In one searching process, a smart machine scans all of the tourist sites, and seed tourist site will be bound to pass the seed tourist site searching arc with a minimum objective function value.
Definition 11. Optimal tourist site propagating tree. The structure tree searched and confirmed by seed tourist sites and subordinate seed tourist site generation model is called the optimal tourist site propagating tree. The nodes of the optimal tourist site propagating tree are tourist sites, which are optimally geographic distributed, conform to tourists’ interests and feature attributes, and cost the least expenditure.
According to the definition, under the condition of the confirmed tourist site clustering center , matrix can generate optimal tourist site propagating trees , and . The optimal tourist site mining algorithm that is based on the membership degree searching propagating tree is designed and developed, according to definition and the thought of optimal tourist site propagating tree modeling.
Step 1. Confirm the propagating tree universe of discourse
According to the definition of the tourist site classification vector , as to one certain tourism city, the specific tourist site of No. tourist site classification is . The tourist site quantity of is , .
We set the city tourist site set as , which is called the universe of discourse. is the feature vector of samples to be observed, and it relates to one point of universe of discourse feature space, that is, the tourist site in city geographic space. is the feature attribute value of No. dimensions of feature vectors. As to the tourist site itself, feature attribute values contain the tourist site’s longitude , tourist site’s latitude , and tourist site’s attraction index .
Step 2. Divide the propagating tree universe of discourse into clusters
Starting from the tourist site clustering center
, we divide the propagating tree universe of discourse into
clusters
, and each division cluster
relates to one tourist site classification, which forms a tourist site cluster
. Thus, the clusters of propagating tree universe of discourse are
,
, …,
, and they meet the formula (7) conditions.
In the process of searching seed tourist sites starting from the tourist site clustering center , the searched subordinate seed tourist site and initial seed tourist site may be in the same classification cluster or in the different classification clusters, and the searching process should meet the constraint conditions. Here, the seed tourist sites in the same classification cluster are noted as , while in the different classification cluster, they are noted as .
Step 3. Set up the objective function and subordinate function
The space searching relationship of the tourist site clustering center , seed tourist site , and subordinate seed tourist site is determined by the clustering principle of , , and . The principle is the second order Minkowski distance. According to the definition of tourist site feature attributes, the Minkowski distance between the tourist site clustering center and the first mined seed tourist site , and the Minkowski distance between the seed tourist site and subordinate seed tourist site are determined by their feature attributes. Other than the tourist site’s longitude , latitude , and tourist site attraction index , there exist factors that influence the process to search the subordinate seed tourist site.
Definition 12. Membership degree direct influence factor. In the process of single searching, the factors that directly influence whether one certain tourist site is the subordinate seed tourist siteof initial seed tourist siteor not are called the membership degree direct influence factors,.
Definition 13. Membership degree indirect influence factor. In the process of single searching, the factors that indirectly influence whether one certain tourist site is the subordinate seed tourist siteof initial seed tourist siteor not are called the membership degree indirect influence factors,.
The membership degree direct influence factors
include the ferry distance between the tourist site clustering center
and tourist site (km), the ferry distance between the two tourist sites (km), the quantity of subways and bus lines between the ferry interval, the taxi fee of the ferry interval and the road traffic jam index, according to the actual travel process and city tourism service. The membership degree indirect influence factors
include the quantity of traffic light between the tourist site clustering center
and the tourist site, the quantity of traffic light between two tourist sites, the average walking distance from a tourist site to the nearest subway or bus station (km), the average waiting time for a taxi (h), and the average quantity of traffic jammed roads. According to definition, factor s
and
are represented in text format. The symbol “
” stands for factors
, and the symbol “
” stands for factors
. The text format is defined as <Factor, Relationship, Algorithm, Attribute>, and each factor is represented, as follows.
| < Direct factor 1: <, ferry distance, temporary accommodation → tourist site (km, ), |
| , >; |
| Indirect factor 1: <, quantity of traffic light, temporary accommodation → tourist site |
| (), , >> |
| < Direct factor 2: <, ferry distance, tourist site → tourist site (km, ), , >; |
| Indirect factor 2: <, quantity of traffic light, tourist site → tourist site (), |
| , >> |
| < Direct factor 3: <, quantity of subway and bus line (), , > |
| Indirect factor 3: <, ferry distance, tourist site → nearest subway or bus station (km, |
| ), , >> |
| < Direct factor 4: <, taxi fee of ferry distance, (), , > |
| Indirect factor 4: <, average waiting time of taxi, (h, ), , >> |
| < Direct factor 5: <, road traffic jam index, (), , > |
| Indirect factor 5: <, average quantity of traffic jam, (), , >>. |
According to the definition, the city tourist site set
can be stored as a
dimension matrix. The matrix’s columns relates to specific tourist sites, while the rows relates to the feature attribute. The feature attributes include the membership degree direct influence factors
, membership degree indirect influence factors
, tourist site longitude
, tourist site latitude
, the tourist site attraction index
, and
. According to Definitions 12 and 13, factors
and
of the tourist site clustering center
and first searched seed tourist site, seed tourist site, and subordinate seed tourist site are determined by the tourist site clustering center
and relative tourist sites, in which, if one point changes, the values of factors
and
will change simultaneously, thus the values of factors
and
are fluctuating. The objective function of the tourist site clustering center
and first searched seed tourist site, seed tourist site, and subordinate seed tourist site are determined by feature attributes, as shown in formula (8).
Definition 14. Objective function descending order vector. In the process of single searching subordinate seed tourist site, we store the searched objective function values in a vector in the sequence of elements from left to right in descending order, and this vector is called the objective function descending order vector.
Definition 15. Objective function fluctuating curve. In the process of single searching a subordinate seed tourist site , the fluctuating curve, which reflects objective function values tendency, is called the objective function fluctuating curve.
The objective function fluctuating curve changes with the tourist site clustering center and the selected tourist site classification and quantity . When or changes greatly, the objective function fluctuating curve tendency will also change greatly. In the process of searching the subordinate seed tourist site starting from the clustering center or seed tourist site , in one time of searching, one group of objective function values will be generated. The objective function fluctuating curve visually reflects the affinities relationship between the seed tourist site and other tourist sites in one single searching process.
Definition 16. Seed tourist site full rank for classification. As to one certain nonzero tourist site classificationof tourist site classification and quantityin matrix, during the searching process, when the quantity of the searched seed tourist site for this classification reaches, the seed tourist site for the classificationis full rank under the condition of, and it is noted as. When the seed tourist site for the classification is full rank, the propagating tree will not accept further searched seed tourist sites of the same classification.
One single searching process only confirms and mines one tourist site as the subordinate tourist site and, meanwhile, the other tourist sites are non-subordinate tourist sites. The subordinate function
, which is noted by the membership degree that represents the subordinate relationship between tourist site
and initial seed tourist site
or the tourist site clustering center
in one single searching process. The subordinate function is formula (9).
Definition 17. Membership degree distribution matrix. When the tourist siteis the subordinate seed tourist site for the clustering centeror initial seed tourist site, the membership degree value of tourist siteis 1, or the value is 0. One single searching process can confirm one tourist site’s membership degree value as 1, and other tourist sites’ values as 0. The matrix that represents the subordinate relationship of all tourist sites via subordinate function values is called the membership degree distribution matrix.
As shown in formula (10), it represents the distribution of seed tourist sites. The matrix row is one sort of tourist site classification and quantity. The matrix column is the membership degree of the No.
tourist site for the sort of tourist site classification and quantity. The quantity of column is
, and vacant elements are noted as 0. When the clustering center
or
changes, the membership degree distribution matrix will also change.
Step 4. Set up the optimal tourist site mining algorithm
Objective function descending order vector stores objective function values. If the tourist site classification relating to the first element of objective function value is not full rank and not listed in the previous seed tourist sites, and then the tourist site relating to the objective function value is mined as subordinate seed tourist site of the tourist site clustering center or initial seed tourist site , if in the same cluster, note it as , if in the different cluster, we note it as . Tourist sites relating to the objective function values on other elements are non-subordinate seed tourist sites . Starting from the clustering center , the process of searching the seed tourist site vector and obtaining the objective function descending order vector , as well as the membership degree distribution matrix is as follows.
Sub-step 1. Confirm matrix . The tourist selects one sort of tourist site classification and quantity vector .
Sub-step 2. We set up dimension seed tourist site vector , dimension objective function descending order vector and dimension membership degree distribution matrix, and set all elements as 0.
Sub-step 3. We set up the Open list and Closed list. The open list is used to store all non-seed tourist sites to be searched. The Closed list is used to store all searched seed tourist sites. The storage format of the Open list and Closed list is the same as the tourist site classification vector , and the elements for the two lists are set in the sequence of the tourist site classification and order. The Open list and Closed list contain elements, respectively, according to the definition. We store all elements of the city tourist site set in the Open list.
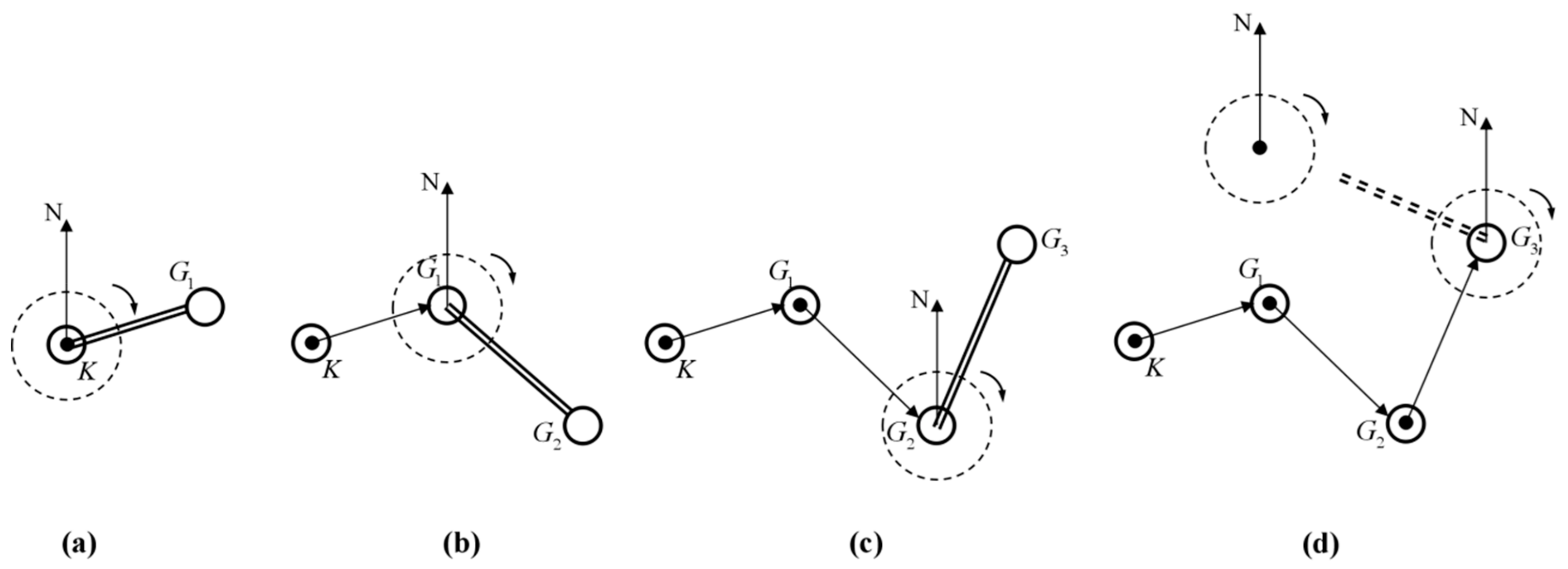
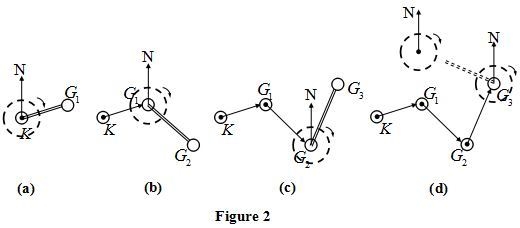
Sub-step 4. Search and confirm the No.1 seed tourist site . Here is the definition of seed tourist site searching angle.
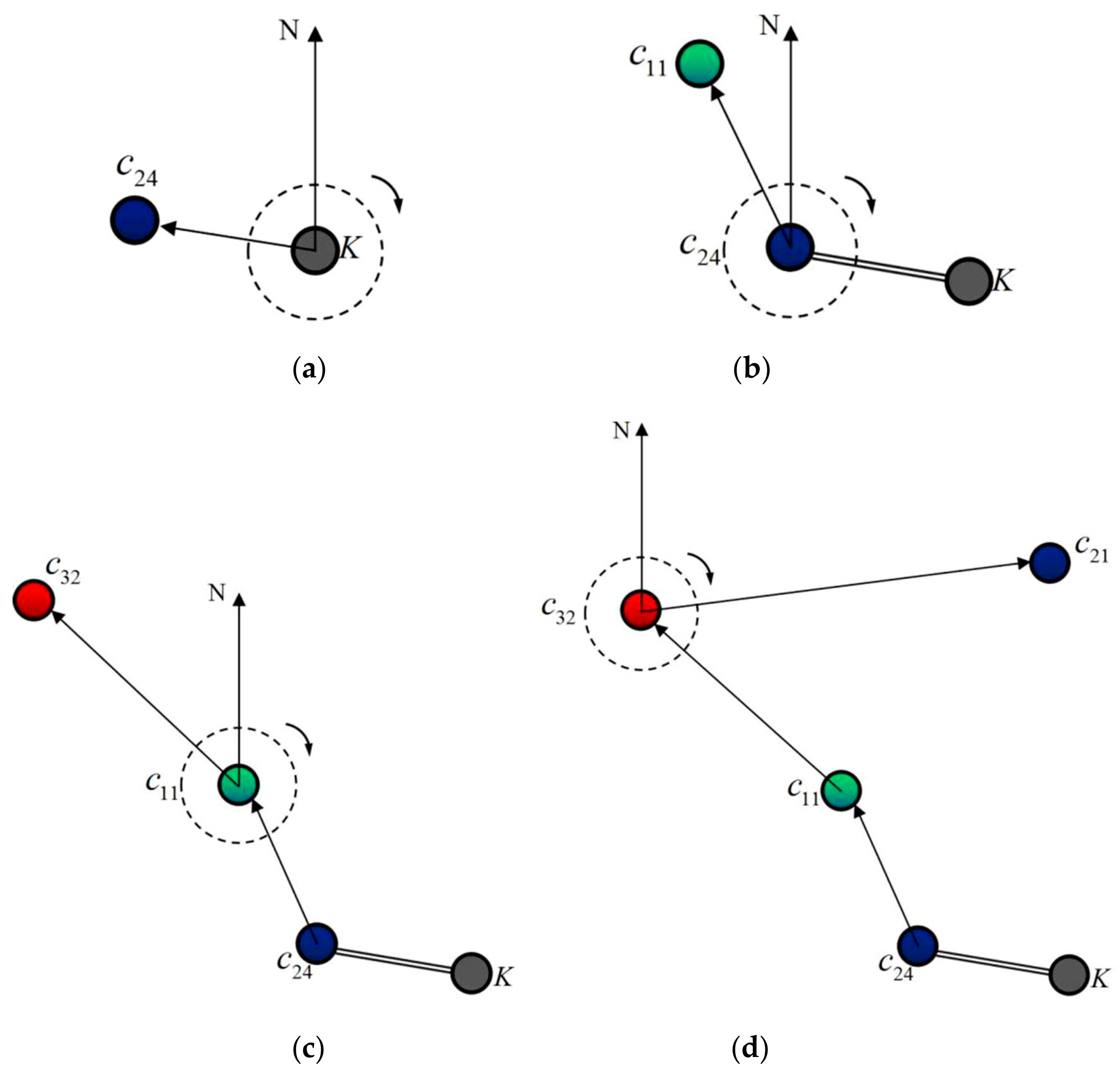
Definition 18. Seed tourist site searching angle. Starting from one certain central point, we draw a raydirecting to the geographic north and another rayconnecting with the central point and another point. The included angle from the north rayto rayin a clockwise direction is called the searching angle. If the central point is the clustering centeror initial seed tourist site, the other point is one tourist siteto be searched, and the included angle from the ray of the clustering centeror initial seed tourist siteto the ray of the tourist siteis called the seed tourist site searching angle, noted asor.
The process of searching the No.1 seed tourist site is as follows.
(I) The clustering center is set as the central point to confirm the searching angle , , …, for tourist sites;
(II) search and calculate the objective function value in the direction of the searching angle and objective function value in the direction of the searching angle ;
① if , store into the first element of vector , and store into the second element of vector ;
② if , store into the first element of vector , and store into the second element of vector ;
(III) search and calculate the objective function value on the direction of the searching angle :
① if , keep the first and second element unchanged, and store into the third element of vector ;
② if , keep the first element unchanged, and descend to the third element of vector ;
③ if , descend and to the second and third elements of vector , and ascend to the first element of vector ; and,
④ as to , the comparison method of and other two values is the same as step (III) sub-steps ①–③.
(IV) Return to step (I)–(III) and continue searching and comparing the objective function values of other searching angles, store the function values into vector , and finally find the objective function descending order vector and objective function fluctuating curve searched by the central point of the clustering center .
(V) Extract the first element value of vector , and its searching angle’s related tourist site is . Enter the following judgment steps:
① Search the Closed list. If appears in the Closed list, jump to the second element of vector ;
② If appears in the Closed list, continue to jump to the third element of vector ;
③ Start searching from tourist site , according to the method of step (V) sub-steps ① and ②, if tourist site appears in the Closed list, continue searching; if one certain tourist site does not appear in the Closed list, then jump to step ④, ;
④ Judge and confirm the tourist site classification for tourist site :
(i) If the tourist site classification is not full rank , and then confirm tourist site , as the No.1 seed tourist site and store it into the first element of the seed tourist site vector . Confirm the seed tourist site’s membership degree to the clustering center is 1. The other tourist sites’ membership degrees are all 0. Store into the Closed list and delete from the Open list; and,
(ii) If the tourist site classification is full rank , return to step (V) sub-steps ①–③ and search the next tourist site which does not appear in the Closed list. Enter the judgment of step (V) sub-step ④. Repeat the process until the seed tourist seed is searched and confirmed, and then store it into the first element of vector .
Sub-step 5. Search and confirm the No.2 seed tourist site and subsequent seed tourist sites.
(I) According to Sub-step 4, set the initial seed tourist site as the central point. Search the No.2 seed tourist site in the whole geographic range and store it into vector. Confirm the membership degree of the seed tourist site to initial seed tourist site as 1, other tourist sites’ membership degrees as set as 0. Store into the Close list, and delete it from the Open list;
① If the tourist site classification for the seed tourist site is not full rank , that is, and are in the same cluster, note as ; and,
② If the tourist site classification for the seed tourist site is full rank , that is, and are in two different clusters, note as .
(II) Set the initial seed tourist site as the central point. Search the No.3 seed tourist site in the whole geographic range and store it into vector. Confirm the membership degree of the seed tourist site to initial seed tourist site as 1, and set the other tourist sites’ membership degrees as set as 0. Store into the Close list, and delete it from the Open list. The method to note the cluster is the same as Sub-step 5 step (I); and,
(III) According to Sub-step 5 step (I) and (II), search and store subsequent seed tourist sites until each tourist site of interest classification
gets to full rank
,
, and also the seed tourist site vector
is full rank. The method to note cluster is the same as Sub-step 5 step (I). In the process of searching the seed tourist site, the objective function descending order vector and objective function curve relating to each seed tourist site are also obtained.
Figure 2 shows the process of searching and mining subordinate seed tourist sites with previously searched seed tourist sites as the central points.
Step 5. Generate the optimal tourist site propagating tree
Starting from the clustering center , generate the optimal tourist site propagating tree in the sequence of the seed tourist site vector element. This tree is the tendency of optimal tourist sites that meet tourists’ needs and interests and have the optimal geographic distribution. It is also the visualized process for a smart machine to output the optimal tourist sites according to the selected tourist classification and quantity.
Step 6. Generate the membership degree distribution matrix .
Based on the searched seed tourist site vector , the membership degree distribution matrix is generated. This matrix can intuitively reflect the quantity of the seed tourist sites as well as their distribution of each tourist site classification.
3.2. Tour Route Planning Algorithm Modeling based on Optimal Closed-loop Structure
The smart machine automatically plans optimal tour routes that meet tourists’ best motive benefits, according to the tourists’ interests learned from the Naïve Bayes machine learning module and optimal tourist sites searched by the membership degree searching propagating tree. All of the designed and developed algorithms are based on one-day trips. Within one day, the smart machine confirms no more than five optimal tourist sites for tourists and ensures that all of the mined tourist sites not only meet tourists’ needs and interests, cost the least expenditure with the optimal geographic distribution, but also consider tourists’ physical conditions, which helps tourists to have sufficient time to visit all the recommended tourist sites. Starting from temporary accommodation , the whole trip of ferrying from one tourist site to another and visiting each tourist site and then returning to is an integrated closed-loop process, in which the quantity of visited optimal tourist sites is set as , being noted as , . Under the condition of confirmed , there will be sorts of tour routes, but not all of the tour routes can meet the tourists’ best motive benefits, there should be optimal ones and sub-optimal ones. The optimal ones will be the first important recommendation to tourists, while the sub-optimal ones will also be recommended to tourists. The attraction and motive benefits of one tour route for tourists depends on the influence of all the factors on the tour route, including factors and in the actual trip, which are extracted to set up the objective function .
Definition 19. Generation tree of the closed-loop structure. Starting from the temporary accommodation, the whole trip of ferrying from one tourist site to another and visiting each tourist site and then returning tois an integrated closed-loop structure, and this structure is called a generation tree closed-loop structure.
According to the quantity of tourist sites , the quantity of closed-loop structures can be confirmed, , . One closed-loop structure relates to one tour route generation tree.
Definition 20. Generation tree sub-unit. In the whole trip process of one closed-loop structure, tourists will passindependent ferry intervals, and each ferry interval is called generation tree sub-unit.
According to the closed-loop structure, the ferry interval between and tourist, between two tourist sites, and between tourist site and are noted as , , and . A generation tree sub-unit is the basic unit structure to output a sub-unit motive function value and generation tree motive function value. Here, it is defined that generation tree sub-units are independent from each other; tourists’ motive benefit obtained in one sub-unit has no relationship with another sub-unit.
Definition 21. Sub-unit motive function. In each sub-unit, the function is designed with the same initial motive iteration valueto iterate with the membership degree direct influence factorsand indirect influenceand output motive iteration value of independent interval. This function is called the sub-unit motive function, as shown in formula (11).
The sub-unit motive function
reflects the motive benefits of the ferry interval. The higher the function value is, the bigger the influence of factors on motive benefits will be, and the more satisfaction tourists will have. In the ferry interval of a sub-unit, the motive function
is a monotone increasing function whose values will increase with tourists ferry distance increases. It finally outputs a maximum value of the interval, which is the sub-unit motive function
value. Different sub-units have different function values, thus the whole trip’s sub-unit motive function
values fluctuate with distance. Sub-unit motive function
value has the feature of non-direction, that is, in the same sub-unit, function
value remains unchanged back and forth.
Definition 22. Sub-unit motive weight. The reciprocal of the sub-unit motive functionvalue is defined as the sub-unit motive weight. The sub-unit motive weightis the edge weight for two connecting point in the closed-loop. It is used as an edge weight parameter to search the optimal closed-loop structure.
According to the definition, the sub-unit motive weight
meets formula (12). The sub-unit motive weight
also has the non-direction feature. Thus, the graph that is composed by the clustering center
and seed tourist sites
is connected and non-direction graph.
Definition 23. Generation tree weight function. The function which is iterated by thesub-unit motive weightand reflects the motive benefits of one generation tree closed-loop’s tour route is called the generation tree weight function, as shown in formula (13). One generation tree weight functionrelates to one tour route, and the lower the function value is, the more motive benefits the tourists will get from the tour route.
According to definition, in one closed-loop structure, the generation tree weight function
is a monotone increasing function whose value increases with tourists’ ferrying distance increases, and finally outputs a maximum value.
function
values are the elements for generation tree weight function minimum heap.
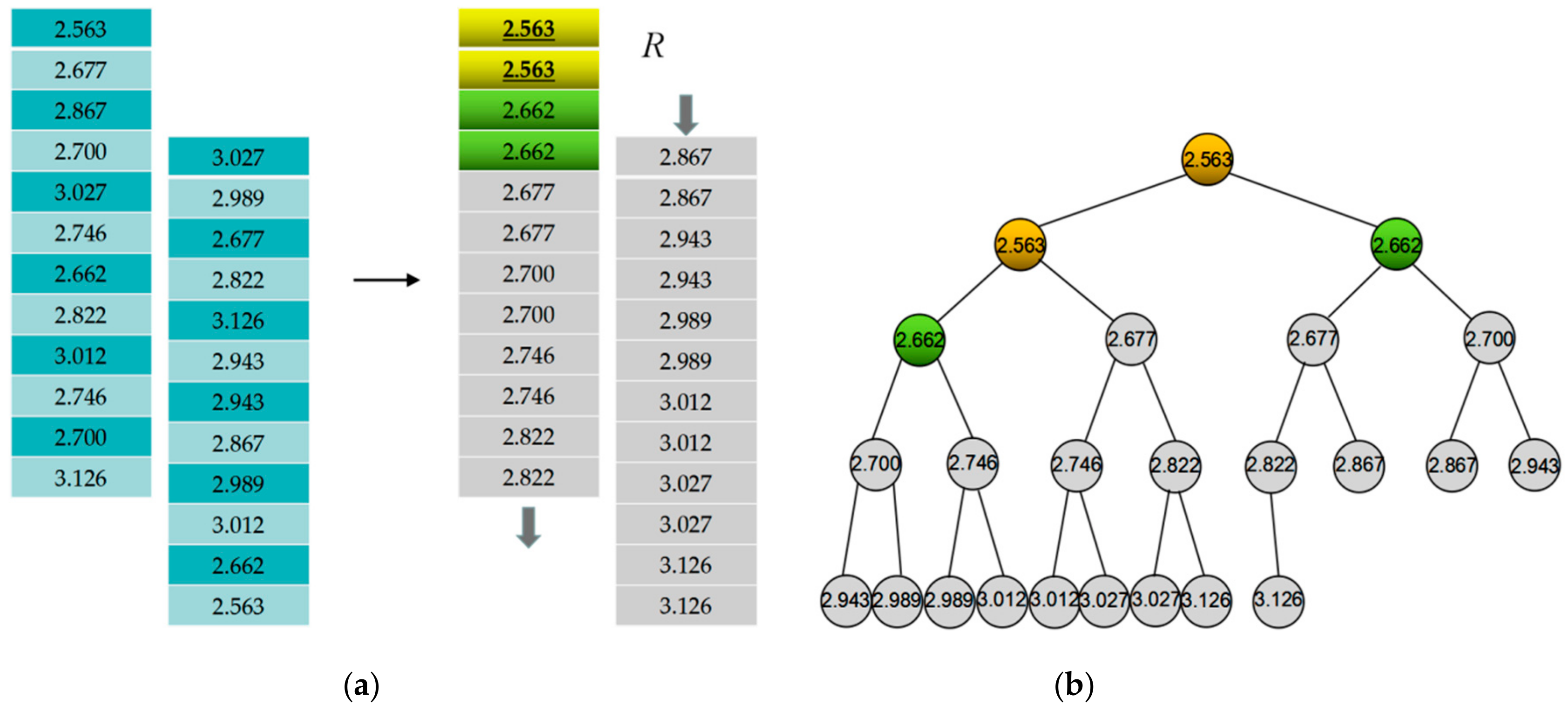
Definition 24. Generation tree weight function minimum heap. The minimum heap, which is formed by generation tree weight function values stored as array elements, is called the generation tree weight function minimum heap.
According to the seed tourist site quantity and generation tree quantity , the minimum heap meets the following conditions:
(1) it contains elements;
(2) set , its element serial numbers , , …, meet: , ,;
(3) the level of parent node is No.0. The height of the tree is , and the other nodes are either on the No. level or on the No. level;
(4) when , there are nodes on the No. level;
(5) the branch nodes of the No. level all gather on the left of the tree;
(6) element value of each node is smaller than its child nodes; and,
(7) of all the node elements in the same level, left element is smaller than the right one.
According to the the definition, tour route planning algorithm modeling that is based on optimal closed-loop structure is set up. The basic thought is, motive weights between clustering center and each seed tourist site , seed tourist site , and seed tourist site are confirmed by sub-unit motive function. By searching the generation tree weight function values, a minimum heap sorting algorithm is used to confirm the minimum heap with weight function values in ascending order, and finally confirm the optimal tour routes and sub-optimal tour routes. The specific steps for the algorithm are as follows.
Step 1. Confirm the algorithm parameters:
(I) Confirm and . Extract the basic geographic information data of a certain tourism city and confirm the membership degrees direct influence factors and indirect influence factors between the clustering center and each seed tourist site, seed tourist site , and seed tourist site ;
(II) Confirm , and . Extract the basic geographic information data and confirm the longitude and latitude coordinates of the clustering center and each seed tourist site . Mine the tourism data information and obtain tourist site attraction indexes. Set the attraction index of the clustering center as , as it is the starting point of the tour route.
Step 2. Iterate and calculate the sub-unit motive function values. From formula (11), the motive function values between the clustering center and each seed tourist site , seed tourist site , and seed tourist site .
Sub-step 1 Confirm the motive function values between the clustering center and each seed tourist site . The clustering center is the starting point and terminal point of the tour route;
Sub-step 2. Confirm motive function values between arbitrary two seed tourist sites.
Step 3. Confirm the sub-unit motive weight. According to the sub-unit motive function values, confirm the sub-unit motive weights between the clustering center and each seed tourist site , seed tourist site , and seed tourist site . The motive weight value is the edge weight of the connected and non-direction graph composed of the clustering center and each seed tourist site .
Step 4. Search generation tree weight function minimum heap . Through an edge correcting method to search the generation tree weight function values relating to generation tree closed-loop’s tour routes. Search and obtain the generation tree weight function minimum heap sorted by the generation tree weight function values in array via a sorting algorithm.
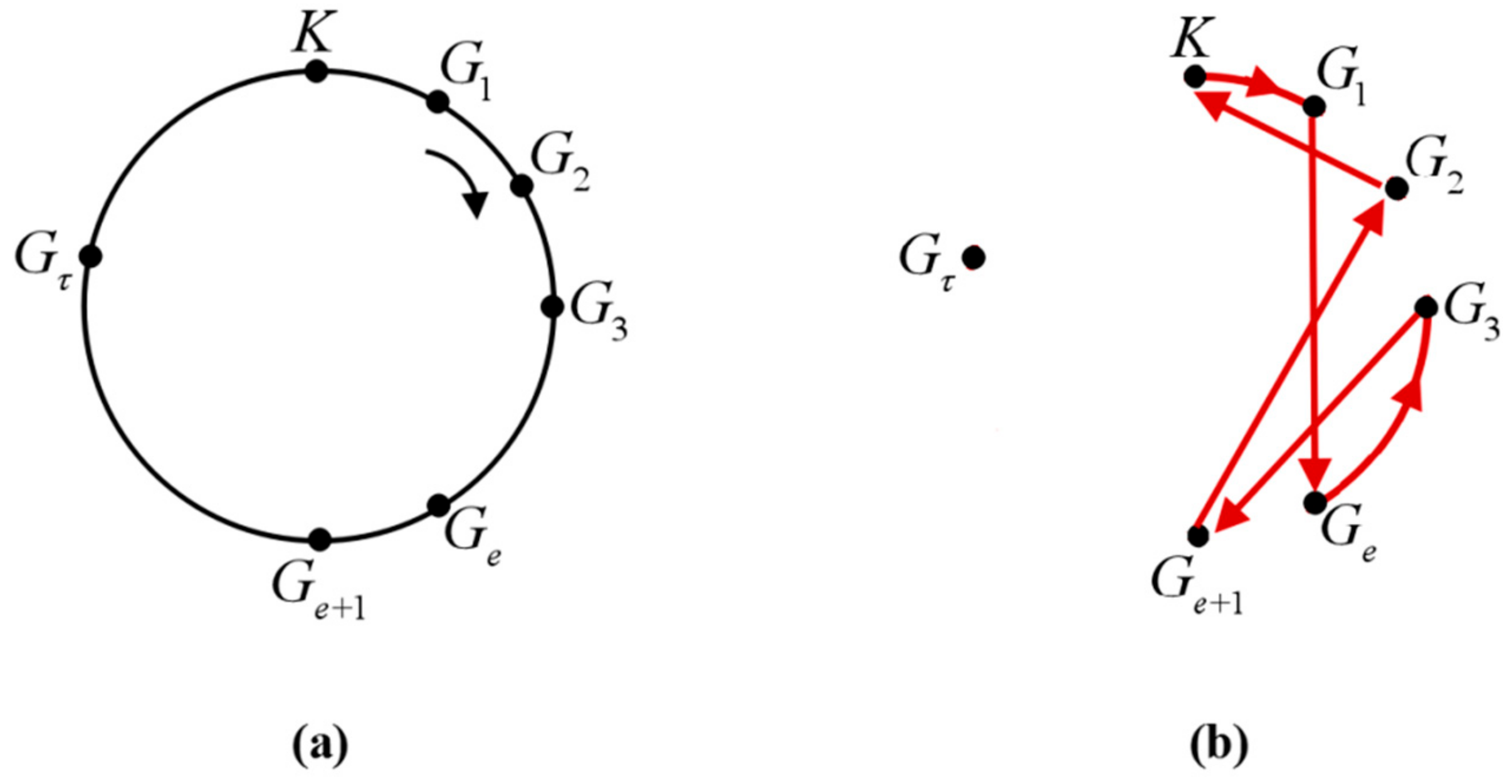
Sub-step 1. Set up a generation tree basic structure loop. Define a virtual closed-loop circle and evenly place points of the clustering center
and all seed tourist sites
on the circle. The connecting arc or line between two points can be clipped or connected in accordance with algorithm conditions, as shown in
Figure 3. For the convenience of setting up the algorithm, note the clustering center
as
, seed tourist site
as
, and son on, and the seed tourist site
as
.
Sub-step 2. Search the initial generation tree closed-loop structure , and set:
, , and .
(I) in structure , search the sub-unit motive weights of adjacent and ;
(II) iterate the generation tree weight function value of the closed-loop structure ; and,
(III) store the weight function value into the parent node of minimum heap .
Sub-step 3. Search the next generation tree closed-loop structure . Find and meet the following conditions:
(1) ;
(2) .
Clip and rebuild the closed-loop structure :
(I) delete sub-unit in ;
(II) delete sub-unit in ;
(III) add sub-unit ; and,
(IV) add sub-unit .
The structure of the rebuilt generation tree closed-loop is:
. Search the weight function value of generation tree closed-loop structure .
(V) In structure , search the sub-unit motive weights of adjacent and ;
(VI) iterate the generation tree weight function value of the closed-loop structure ; and,
(VII) compare the generation tree weight function value and , and update the generation tree weight function minimum heap :
① If :
(i) keep the weight function value storing in the parent node of minimum heap unchanged; and,
(ii) store the weight function value into the child node of parent node in minimum heap .
② If :
(i) delete the parent node value ; and,
(ii) store the weight function value into the parent node in minimum heap ; and,
(iii) store the weight function value into the child node of parent node in minimum heap .
Sub-step 4. Return to Sub-step 3 and use the same method to search the next generation tree closed-loop structure .
(I) in structure , search sub-unit motive weights of adjacent and ;
(II) iterate the generation tree weight function value of the closed-loop structure ; and,
(III) compare the generation tree weight function values , and , and then update the generation tree weight function minimum heap :
① If :
(i) if , keep the weight function values and storing unchanged, store the weight function value into the child node of parent node in minimum heap ;
(ii) if , keep the weight function value storing unchanged, delete the child node value and store the weight function value into the child node of parent node , store the weight function value into the child node of parent node in minimum heap ; and,
(iii) if , delete the child node and values, store the weight function value into the parent node . Store the weight function value and into the child node and of parent node respectively in minimum heap .
② If :
(i) if , keep the weight function values and storing unchanged, store the weight function value into the child node of parent node in minimum heap ;
(ii) if , keep the weight function value storing unchanged, delete the child node value, and store the weight function value into the child node of parent node , store the weight function value into the child node of parent node in minimum heap ; and,
(iii) if , delete the child node and values, store the weight function value into the parent node, and store the weight function values and into the child node and of parent node , respectively in minimum heap .
Sub-step 5. Return to Sub-step 3, and use the same method to search all generation tree closed-loop structures − and find the rebuilt generation tree weight function minimum heap . As step 4 ends, enter Step 5.
Step 5. Output tour route sorting heap relating to generation tree weight function minimum heap . The weight function value relates to the generation tree closed-loop structure , which relates to the tour route. According to the algorithm rule, the weight function value that is stored in the parent node of minimum heap relates to the optimal tour route. As its output generation tree motive weight function value is the minimum one, the iteration value of all sub-unit motive function values is the maximum one. In the aspect of the comprehensive output result, the optimal tour route performs best on tourist site classification, tourist quantity, confirmed specific tourist sites, tourist sites distribution, tour sequence, GIS service, traffic information service, and tourist site star level, etc. The two child nodes of the parent node relate to sub-optimal tour routes. A smart machine will output the visualized results for tourists according to the input conditions.