Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China
Abstract
1. Introduction
2. Materials and Methods
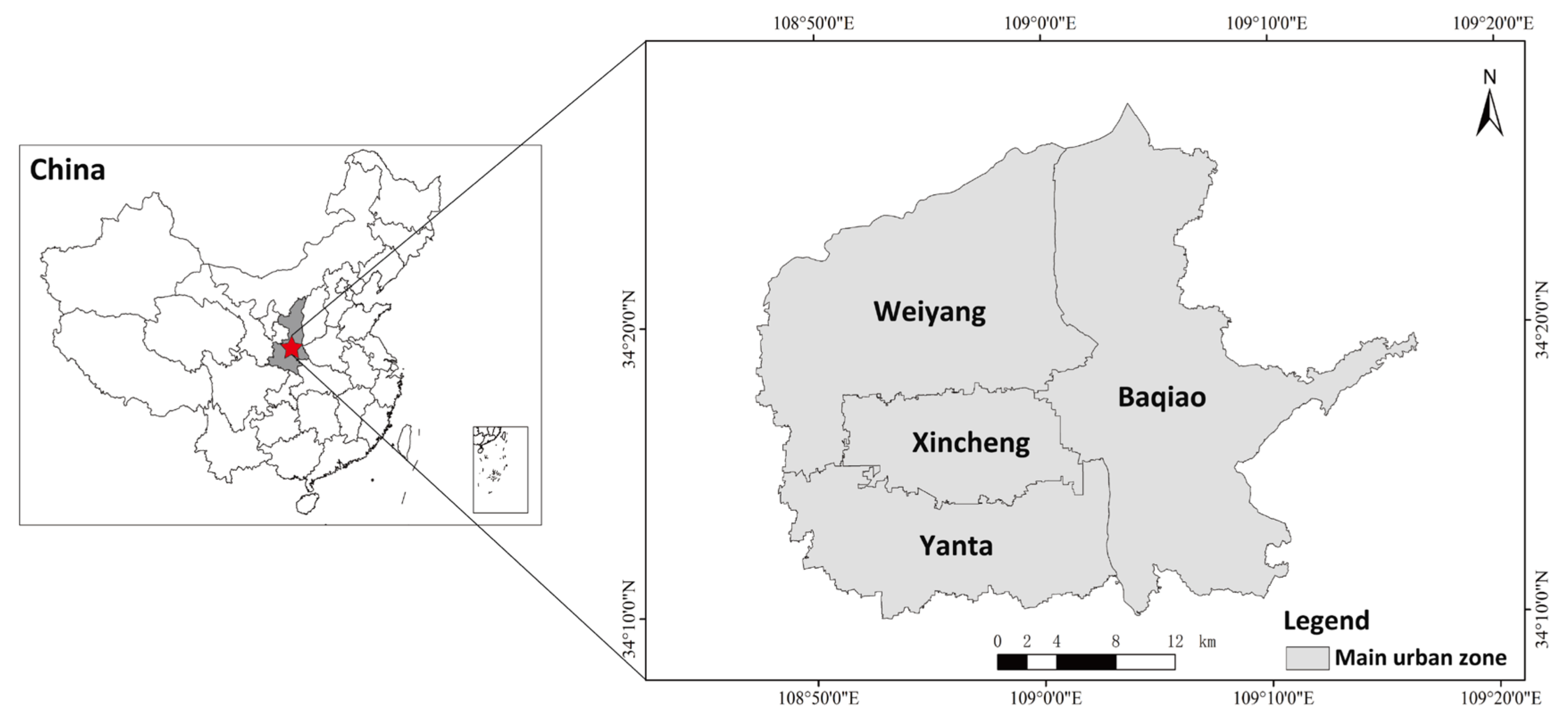
2.1. Study Area
2.2. Data Source and Preprocessing
2.3. Calculation of Aboveground Biomass for Urban Forests
2.4. Spatial Analysis with the Geographical Detector
2.4.1. Individual Impacts of GFs on the Spatial Distribution of Aboveground Biomass
2.4.2. Interaction Impacts of Geographical Factors on the Spatial Distribution of Aboveground Biomass
2.4.3. Comparing the Impacts of Different Categories for Each GF
2.5. Comparing the Impacts for Different GFs
3. Results
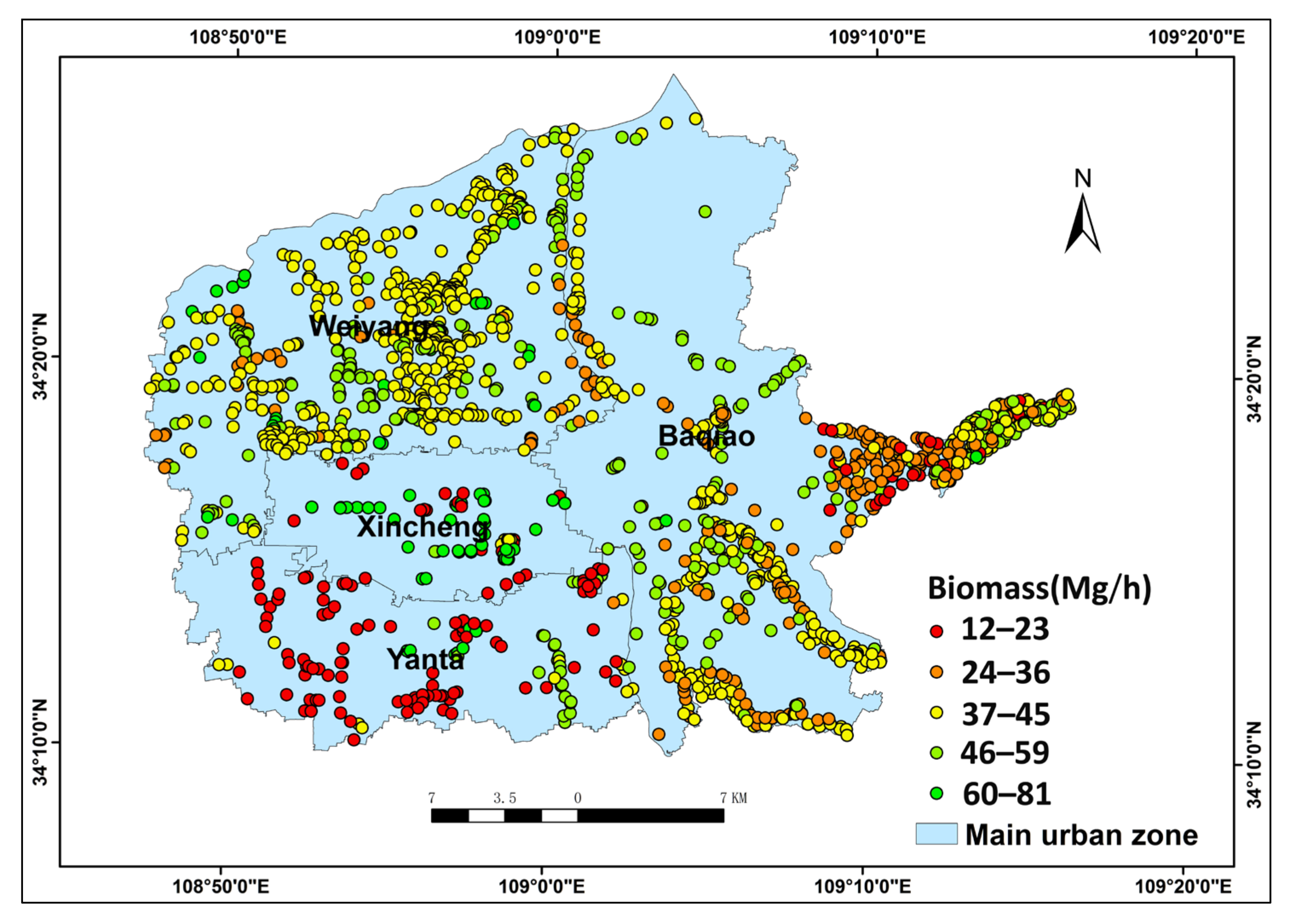
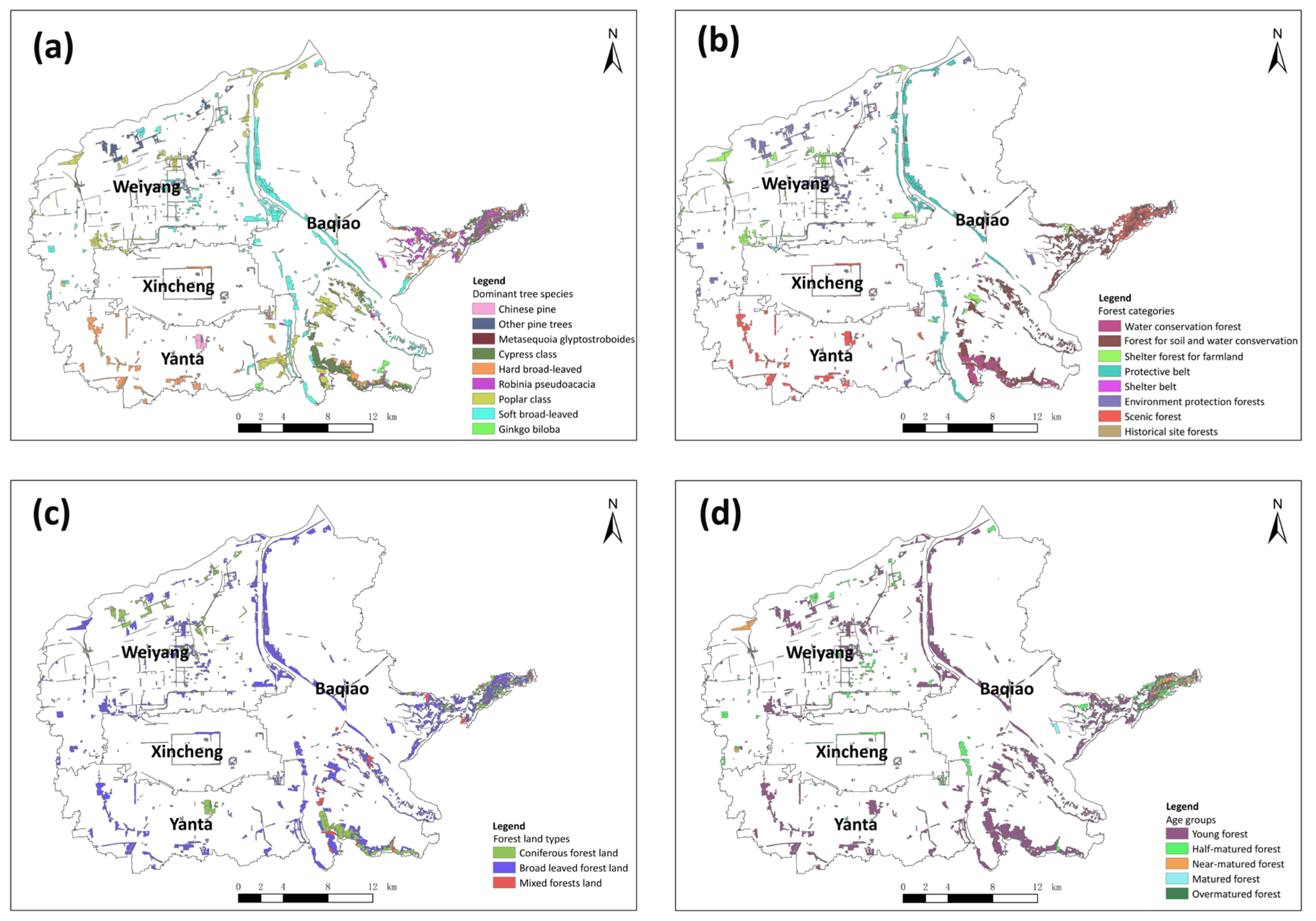
3.1. The Distributions of Urban Forest Biomass and Its Influencing Factors
3.2. Detecting the Contribution of the Four Influencing Factors
3.3. Detecting the Contribution of Interactions between the Four Influencing Factors
3.4. Comparing the Difference of the Contribution among Subtypes
4. Discussion
4.1. The Significance of Studying the Spatial Heterogeneity of Urban Forest Biomass
4.2. Challenges and Future Directions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Chinese Pine | Other Pine Trees | Metasequoia Glyptostroboides | Parker Class | Hard Broad-Leaved | Robinia Pseudoacacia | Poplar Class | Soft Broad-Leaved | Ginkgo Biloba | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Chinese pine | - | Y | - | Y | N | Y | Y | Y | Y | 18.4 |
| Other pine trees | Y | - | - | Y | Y | Y | Y | Y | N | 49.9 |
| Metasequoia glyptostroboides | - | - | - | - | - | - | - | - | - | 58.6 |
| Parker class | Y | Y | - | - | Y | Y | Y | Y | Y | 44.0 |
| Hard broad-leaved | N | Y | - | Y | - | Y | Y | Y | Y | 19.6 |
| Robinia pseudoacacia | Y | Y | - | Y | Y | - | Y | Y | Y | 32.9 |
| Poplar class | Y | Y | - | Y | Y | Y | - | Y | N | 47.3 |
| Soft broad-leaved | Y | Y | - | Y | Y | Y | Y | - | Y | 38.6 |
| Ginkgo biloba | Y | N | - | Y | Y | Y | N | Y | - | 56.3 |
| 18.4 | 49.9 | 58.6 | 44.0 | 19.6 | 32.9 | 47.3 | 38.6 | 56.3 |
| Water Conservation Forest | Forest for Soil and Water Conservation | Shelter Forest for Farmland | Protective Belt | Shelter Belt | Environmental Protection Forests | Scenic Forest | Historical Sites Forests | ||
|---|---|---|---|---|---|---|---|---|---|
| Water conservation forest | - | N | N | N | N | N | N | N | 38.6 |
| Forest for soil and water conservation | N | - | Y | Y | N | Y | N | Y | 36.3 |
| Shelter forest for farmland | N | Y | - | N | N | N | Y | N | 43.9 |
| Protective belt | N | Y | N | - | N | N | Y | N | 41.5 |
| Shelter belt | N | N | N | N | - | N | N | N | 41.5 |
| Environmental protection forests | N | Y | N | N | N | - | Y | N | 43.3 |
| Scenic forest | N | N | Y | Y | N | Y | - | Y | 35.7 |
| Historical sites Forests | N | Y | N | N | N | N | Y | - | 64.4 |
| 38.6 | 36.3 | 43.9 | 41.5 | 41.5 | 43.3 | 35.7 | 64.4 |
| Young Forest | Half-Mature Forest | Near-Mature Forest | Mature Forest | Overmature Forest | ||
|---|---|---|---|---|---|---|
| Young forest | - | Y | Y | Y | - | 37.5 |
| Half-mature forest | Y | - | Y | Y | - | 43.1 |
| Near-mature forest | Y | Y | - | Y | - | 54.2 |
| Mature forest | Y | Y | Y | - | - | 78.6 |
| Overmature forest | - | - | - | - | - | 55.7 |
| 37.5 | 43.1 | 54.2 | 78.6 | 55.7 |
References
- United Nations. World Urbanization Prospects: The 2018 Revision; United Nations Publications: New York, NY, USA, 2019. [Google Scholar]
- Collier, P.; Venables, A.J. Urbanization in developing economies: The assessment. Oxf. Rev. Econ. Policy 2017, 33, 355–372. [Google Scholar] [CrossRef]
- World Urbanization Prospects. Available online: https://esa.un.org/unpd/wup/publications/fles/wup2014-highlights.Pdf (accessed on 11 November 2014).
- China Statistical Yearbook. Available online: http://www.stats.gov.cn/tjsj/ndsj/2018/indexch.htm (accessed on 29 November 2018).
- Zhang, Z.B. Report on the Healthy Development of China’s New Urbanization (2016); Social Science Literature Press: Beijing, China, 2017. [Google Scholar]
- Orum, A.M.; Iossifova, D. East Asian Urbanization. In The Wiley Blackwell Encyclopedia of Urban and Regional Studies; Orum, A.M., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar] [CrossRef]
- Bolund, P.; Hunhammar, S. Ecosystem services in urban areas. Ecol. Econ. 1999, 29, 293–301. [Google Scholar] [CrossRef]
- Nowak, D.J.; Greenfield, E.J.; Hoehn, R.E.; Lapoint, E. Carbon storage and sequestration by trees in urban and community areas of the United States. Environ. Pollut. 2013, 178, 229–236. [Google Scholar] [CrossRef] [PubMed]
- Timilsina, N.; Staudhammer, C.L.; Escobedo, F.J.; Lawrence, A. Tree biomass, wood waste yield, and carbon storage changes in an urban forest. Landsc. Urban Plan. 2014, 127, 18–27. [Google Scholar] [CrossRef]
- Abdi, R.; Endreny, T.; Nowak, D. A model to integrate urban river thermal cooling in river restoration. J. Environ. Manag. 2020, 258, 110023. [Google Scholar] [CrossRef] [PubMed]
- Elmqvist, T.; Fragkias, M.; Goodness, J.; Güneralp, B.; Marcotullio, P.J.; McDonald, R.I.; Parnell, S.; Schewenius, M.; Sendstad, M.; Seto, K.C.; et al. Urbanization, Biodiversity and Ecosystem Services: Challenges and Opportunities: A Global Assessment; Springer: Dordrecht, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Nowak, D.J.; Daniel, E.C. Carbon storage and sequestration by urban trees in the USA. Environ. Pollut. 2002, 116, 381–389. [Google Scholar] [CrossRef]
- Nowak, D.J. Atmospheric carbon dioxide reduction by Chicago’s urban forest. In Chicago’s Urban Forest Ecosystem: Results of the Chicago Urban Forest Climate Project; Forest Service US: Washington, DC, USA, 1994; pp. 83–94. Available online: https://www.fs.usda.gov/treesearch/pubs/4285 (accessed on 11 December 2020).
- Li, L.; Zhou, X.; Chen, L.; Chen, L.; Zhang, Y.; Liu, Y. Estimating urban vegetation biomass from Sentinel-2A image data. Forests 2020, 11, 125. [Google Scholar] [CrossRef]
- Hu, S.; Chen, L.; Li, L.; Zhang, T.; Yuan, L.; Cheng, L.; Wang, J.; Wen, M. Simulation of Land Use Change and Ecosystem Service Value Dynamics under Ecological Constraints in Anhui Province, China. Int. J. Environ. Res. Public Health 2020, 17, 4228. [Google Scholar] [CrossRef]
- McPherson, E.G. Atmospheric carbon dioxide reduction by Sacramento’s urban forest. J. Arboric. 1998, 24, 215–223. [Google Scholar]
- Aguaron, E.; McPherson, E.G. Comparison of methods for estimating carbon dioxide storage by Sacramento’s urban forest. In Carbon Sequestration in Urban Ecosystems; Springer: Dordrecht, The Netherlands, 2012; pp. 43–71. [Google Scholar] [CrossRef]
- Rowntree, R.A.; Nowak, D.J. Quantifying the role of urban forests in removing atmospheric carbon dioxide. J. Arboric. 1991, 17, 269–275. [Google Scholar]
- Dutilleul, P.R.L. Spatio-Temporal Heterogeneity: Concepts and Analyses; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wang, J.F.; Zhang, T.L.; Fu, B.J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.F.; Xu, C.D. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Li, M.; Im, J.; Quackenbush, L.J.; Liu, T. Forest biomass and carbon stock quantification using airborne LiDAR data: A case study over Huntington Wildlife Forest in the Adirondack Park. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3143–3156. [Google Scholar] [CrossRef]
- Gleason, C.J.; Im, J. Forest biomass estimation from airborne LiDAR data using machine learning approaches. Remote Sens. Environ. 2012, 125, 80–91. [Google Scholar] [CrossRef]
- Rauf, A. Distribution, above-ground biomass and carbon stock of the vegetation in Taman Beringin Urban Forest, Medan City, North Sumatra, Indonesia. Malays. For. 2017, 80, 73–84. [Google Scholar]
- Pesola, L.; Cheng, X.; Sanesi, G.; Colangelo, G.; Elia, M.; Lafortezza, R. Linking above-ground biomass and biodiversity to stand development in urban forest areas: A case study in Northern Italy. Landsc. Urban Plan. 2017, 157, 90–97. [Google Scholar] [CrossRef]
- Shen, G.; Wang, Z.; Liu, C.; Han, Y. Mapping aboveground biomass and carbon in Shanghai’s urban forest using Landsat ETM+ and inventory data. Urban For. Urban Greening 2020, 51, 126655. [Google Scholar] [CrossRef]
- Baker, T.R.; Phillips, O.L.; Malhi, Y.; Almeida, S.; Arroyo, L.; di Fiore, A.; Erwin, T.; Killeen, T.J.; Laurance, S.G.; Laurance, W.F.; et al. Variation in wood density determines spatial patterns in Amazonian forest biomass. Glob. Chang. Biol. 2004, 10, 545–562. [Google Scholar] [CrossRef]
- López-Serrano, P.M.; Corral-Rivas, J.J.; Díaz-Varela, R.A.; Álvarez-González, J.G.; López-Sánchez, C.A. Evaluation of radiometric and atmospheric correction algorithms for aboveground forest biomass estimation using Landsat 5 TM data. Remote Sens. 2016, 8, 369. [Google Scholar] [CrossRef]
- Luo, S.; Wang, C.; Xi, X.; Nie, S.; Fan, X.; Chen, H.; Ma, D.; Liu, J.; Zou, J.; Lin, Y.; et al. Estimating forest aboveground biomass using small-footprint full-waveform airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2019, 83, 101922. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Hartig, F.; Latifi, H.; Berger, C.; Hernández, J.; Corvalán, P.; Koch, B. Importance of sample size, data type and prediction method for remote sensing-based estimations of aboveground forest biomass. Remote Sens. Environ. 2014, 154, 102–114. [Google Scholar] [CrossRef]
- Foody, G.M.; Cutler, M.E.; McMorrow, J.; Pelz, D.; Tangki, H.; Boyd, D.S.; Douglas, I.A.N. Mapping the biomass of Bornean tropical rain forest from remotely sensed data. Glob. Ecol. Biogeogr. 2001, 10, 379–387. [Google Scholar] [CrossRef]
- Kimes, D.S.; Nelson, R.F.; Manry, M.T.; Fung, A.K. Attributes of neural networks for extracting continuous vegetation variables from optical and radar measurements. Int. J. Remote Sens. 1998, 19, 2639–2663. [Google Scholar] [CrossRef]
- Xi’an 2015 National Economic and Social Development Statistical Bulletin. Available online: www.xatj.gov.cn (accessed on 12 December 2016).
- Fang, J.; Liu, G.; Xu, S. Biomass and net production of forest vegetation in China. Acta Ecol. Sin. 1996, 16, 497–508. (In Chinese) [Google Scholar]
- Fang, J.Y.; Wang, G.G.; Liu, G.H.; Xu, S.L. Forest biomass of China: An estimate based on the biomass—Volume relationship. Ecol. Appl. 1998, 8, 1084–1091. [Google Scholar]
- Fang, J.; Chen, A.; Peng, C.; Zhao, S.; Ci, L. Changes in forest biomass carbon storage in China between 1949 and 1998. Science 2001, 292, 2320–2322. [Google Scholar] [CrossRef]
- Luo, W.; Jasiewicz, J.; Stepinski, T.; Wang, J.; Xu, C.; Cang, X. Spatial association between dissection density and environmental factors over the entire conterminous United States. Geophys. Res. Lett. 2016, 43, 692–700. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, J.; Wu, J.; Driskell, L.; Wang, W.; Zhang, T.; Xue, G.; Zheng, X. Spatial analysis of neural tube defects in a rural coal mining area. Int. J. Environ. Health Res. 2010, 20, 439–450. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, J.; Li, X.; Ren, D.; Zhu, J. Geographical detector-based risk assessment of the under-five mortality in the 2008 Wenchuan earthquake, China. PLoS ONE 2011, 6, e21427. [Google Scholar] [CrossRef]
- Zou, B.; Wilson, J.G.; Zhan, F.B.; Zeng, Y.; Wu, K. Spatial-temporal variations in regional ambient sulfur dioxide concentration and source-contribution analysis: A dispersion modeling approach. Atmos. Environ. 2011, 45, 4977–4985. [Google Scholar] [CrossRef]
- Wang, J.F.; Hu, Y. Environmental health risk detection with GeogDetector. Environ. Model. Softw. 2012, 33, 114–115. [Google Scholar] [CrossRef]
- Zhu, Z.; Wang, J.; Hu, M.; Jia, L. Geographical detection of groundwater pollution vulnerability and hazard in karst areas of Guangxi Province, China. Environ. Pollut. 2019, 245, 627–633. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Liao, L.; Liu, X. Spatial Analysis Tutorial; Science Press: Beijing, China, 2010. [Google Scholar]
- Yao, Z.; Liu, J.; Zhao, X.; Long, D.; Wang, L. Spatial dynamics of aboveground carbon stock in urban green space: A case study of Xi’an, China. J. Arid. Land 2015, 7, 350–360. [Google Scholar] [CrossRef]
- Kim, Y.S.; Lee, J.K.; Chung, G.C. Tolerance and susceptibility of Ginkgo to air pollution. In Ginkgo Biloba A Global Treasure; Springer: Tokyo, Japan, 1997; pp. 233–242. [Google Scholar] [CrossRef]
- Matyssek, R.; Giinthardt-Goerg, M.S.; Schmutz, P.; Saurer, M.; Landolt, W.; Bücher, J.B. Response mechanisms of birch and poplar to air pollutants. J. Sustain. For. 1997, 6, 3–22. [Google Scholar] [CrossRef]
- Barwise, Y.; Prashant, K. Designing vegetation barriers for urban air pollution abatement: A practical review for appropriate plant species selection. npj Clim. Atmos. Sci. 2020, 3, 1–19. [Google Scholar] [CrossRef]
- Miao, J.L. Analysis of climatic characteristics and meteorological conditions of acid rain in Xi’an. Shaanxi Meteorol. 2013, 36–39. (In Chinese) [Google Scholar] [CrossRef]
- Xi’an Environmental Status Bulletin. 2017. Available online: http://xaepb.xa.gov.cn/xxgk/hjzkgb/hjzkgb/5d8b5a9cf99d65052290af21.html (accessed on 18 December 2018).
- Cheng, Y.; Zhang, C.; Zhao, X.; von Gadow, K. Biomass-dominant species shape the productivity-diversity relationship in two temperate forests. Ann. For. Sci. 2018, 75, 1–9. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, G.; Wang, Q. Effects of climate and forest age on the ecosystem carbon exchange of afforestation. J. For. Res. 2020, 31, 365–374. [Google Scholar] [CrossRef]
- Li, S.; Su, J.; Lang, X.; Liu, W.; Ou, G. Positive relationship between species richness and aboveground biomass across forest strata in a primary Pinus kesiya forest. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ. 2009, 113, 182–196. [Google Scholar] [CrossRef]
- Singh, K.K.; Gagné, S.A.; Meentemeyer, R.K. Urban Forests and Human Well-Being. Compr. Remote Sens. 2018, 287–305. [Google Scholar] [CrossRef]
- Christine, B.; Katrin, R. The role of urban green space for human well-being. Ecol. Econ. 2015, 120, 139–152. [Google Scholar]
- Kang, M.N.; Shawn, L. Aboveground biomass estimation of tropical street trees. J. Urban Ecol. 2018, 4, 1–6. [Google Scholar]
- Wang, Z.; Shen, G.; Zhu, Y.; Liu, C. Spatiotemporai dynamics of urban forest biomass in Shanghai, China. In Proceedings of the 2015 Fourth International Conference on Agro-geoinformatics, Istanbul, Turkey, 20–24 July 2015. [Google Scholar]
- Zhang, H.; Song, T.; Wang, K.; Yang, H.; Yue, Y.; Zeng, Z.; Peng, W.; Zeng, F. Influences of stand characteristics and environmental factors on forest biomass and root–shoot allocation in southwest China. Ecol. Eng. 2016, 91, 7–15. [Google Scholar] [CrossRef]
- Edna, R.; Matthias, C.; Jens, H.; Anja, R.; Andreas, H. Spatial heterogeneity of biomass and forest structure of the Amazon rain forest: Linking remote sensing, forest modelling and field inventory. Glob. Ecol. Biogeogr. 2017, 26, 1–11. [Google Scholar]
- Röser, D.; Asikainen, A.; Raulund-Rasmussen, K.; Stupak, I. Sustainable Use of Forest Biomass for Energy; Managing Forest Ecosystems: New York, NY, USA, 2008. [Google Scholar] [CrossRef]
- Zhang, X.; Ni-meister, W. Remote Sensing of Forest Biomass. Biophys. Appl. Satell. Remote Sens. 2013, 63–98. [Google Scholar] [CrossRef]
| Serial Number | Tree Species | a | b | R2 | Tree Type |
|---|---|---|---|---|---|
| 1 | Chinese pine | 0.7554 | 5.0928 | 0.980 | Coniferous tree |
| 2 | Other pine trees | 0.5168 | 33.2378 | 0.970 | Coniferous tree |
| 3 | Metasequoia glyptostroboides | 0.4158 | 41.3318 | 0.980 | Coniferous tree |
| 4 | Cypress class | 0.6129 | 26.1451 | 0.980 | Coniferous tree |
| 5 | Hard broad-leaved | 0.9644 | 0.8485 | 0.980 | Deciduous tree |
| 6 | Robinia pseudoacacia | 0.7564 | 8.3103 | 0.986 | Deciduous tree |
| 7 | Poplar class | 0.4754 | 30.6034 | 0.930 | Deciduous tree |
| 8 | Soft broad-leaved | 0.4754 | 30.6034 | 0.930 | Deciduous tree |
| 9 | Ginkgo biloba | 0.4158 | 41.3318 | 0.980 | Deciduous tree |
| GFs | Categories | Number of Categories |
|---|---|---|
| Dominant tree species | Chinese pine, Other pine trees, Metasequoia glyptostroboides, Parker class, Hard broad-leaved, Robinia pseudoacacia, Poplar class, Soft broad-leaved, and Ginkgo biloba | 9 |
| Forest categories | Water conservation forests, Forest for soil and water conservation, Shelter forest for farmland, Protective belt, Shelter belts, Environmental protection forests, Scenic forests, and Historical site forests | 8 |
| Forestland types | Coniferous forestland, Broad leaved forestland, Mixed forestland | 3 |
| Age groups | Young forest, Half-matured forest, Near-matured forest, Matured forest, Overmatured forest | 5 |
| Dominant Tree Species | Age Group | Forest Category | Land Type |
|---|---|---|---|
| 0.595 | 0.202 | 0.087 | 0.076 |
| Dominant Tree Species | Forest Category | Forestland Type | Age Group | |
|---|---|---|---|---|
| Dominant tree species | - | Y | Y | Y |
| Forest category | Y | - | N | Y |
| Forestland type | Y | N | - | Y |
| Age group | Y | Y | Y | - |
| Comparison Type | Interaction |
|---|---|
| Weaken, nonlinear | |
| Weaken, single factor nonlinear | |
| Enhance, bilinear | |
| Independent | |
| Enhance, nonlinear |
| Factor Interaction (A) | Factor Combination (B+C) | Comparative Result | Ratio (Interaction/Combination) | Explanation |
|---|---|---|---|---|
| dominant tree species ∩ forest category = 0.784 | dominant tree species (0.595) + forest category (0.087) | A > B+C | 1.15 | Non-Linear Enhancement |
| dominant tree species ∩ land types = 0.604 | dominant tree species (0.595), land types (0.076) | A > max (B, C) | 1.02 | Bilinear, Enhancement |
| dominant tree species ∩ age groups = 0.847 | dominant tree species (0.595) + age groups (0.202) | A > B+C | 1.06 | Non-Linear Enhancement |
| forest category ∩ land types = 0.269 | forest category (0.087) + land types (0.076) | A > B+C | 1.65 | Non-Linear Enhancement |
| forest category ∩ age groups = 0.445 | forest category (0.087) + age groups (0.202) | A > B+C | 1.54 | Non-Linear Enhancement |
| land types ∩ age groups = 0.348 | forest category (0.076) + age groups (0.202) | A > B+C | 1.25 | Non-Linear Enhancement |
| Coniferous Forestland | Broadleaved Forestland | Mixed Forestland | Average Plot Biomass (Mg/h) | |
|---|---|---|---|---|
| Coniferous forestland | - | Y | Y | 46.5 |
| Broad leaved forestland | Y | - | N | 38.0 |
| Mixed forestland | Y | N | - | 38.2 |
| Average plot biomass | 46.5 | 38.0 | 38.2 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Liu, J.; Hao, H.; Yang, Y. Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China. ISPRS Int. J. Geo-Inf. 2020, 9, 744. https://doi.org/10.3390/ijgi9120744
Zhao X, Liu J, Hao H, Yang Y. Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China. ISPRS International Journal of Geo-Information. 2020; 9(12):744. https://doi.org/10.3390/ijgi9120744
Chicago/Turabian StyleZhao, Xuan, Jianjun Liu, Hongke Hao, and Yanzheng Yang. 2020. "Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China" ISPRS International Journal of Geo-Information 9, no. 12: 744. https://doi.org/10.3390/ijgi9120744
APA StyleZhao, X., Liu, J., Hao, H., & Yang, Y. (2020). Quantifying the Spatial Heterogeneity and Driving Factors of Aboveground Forest Biomass in the Urban Area of Xi’an, China. ISPRS International Journal of Geo-Information, 9(12), 744. https://doi.org/10.3390/ijgi9120744





