Next Article in Journal
Assessing Emergency Shelter Demand Using POI Data and Evacuation Simulation
Next Article in Special Issue
Where Urban Youth Work and Live: A Data-Driven Approach to Identify Urban Functional Areas at a Fine Scale
Previous Article in Journal
A GRID-Based Spatial Interpolation Method as a Tool Supporting Real Estate Market Analyses
Previous Article in Special Issue
Mapping Creative Industries: A Case Study on Supporting Geographical Information Systems in the Olomouc Region, Czech Republic
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 9
Issue 1
10.3390/ijgi9010040
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore

by
Kai Cao
1,2,*,
Muyang Liu
1,
Shu Wang
1,
Mengqi Liu
1,
Wenting Zhang
3,
Qiang Meng
4 and
Bo Huang
5
1
Department of Geography, National University of Singapore, Singapore 119077, Singapore
2
School of Information Systems, Singapore Management University, Singapore 188065, Singapore
3
College of Resources and Environment, Huazhong Agricultural University, Wuhan 430070, China
4
Department of Civil and Environmental Engineering, National University of Singapore, Singapore 119077, Singapore
5
Department of Geography and Resource Management, The Chinese University of Hong Kong, Hong Kong, China
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2020, 9(1), 40; https://doi.org/10.3390/ijgi9010040
Submission received: 8 December 2019 / Revised: 28 December 2019 / Accepted: 30 December 2019 / Published: 14 January 2020
(This article belongs to the Special Issue Geospatial Methods in Social and Behavioral Sciences)
Browse Figures
Versions Notes

Abstract

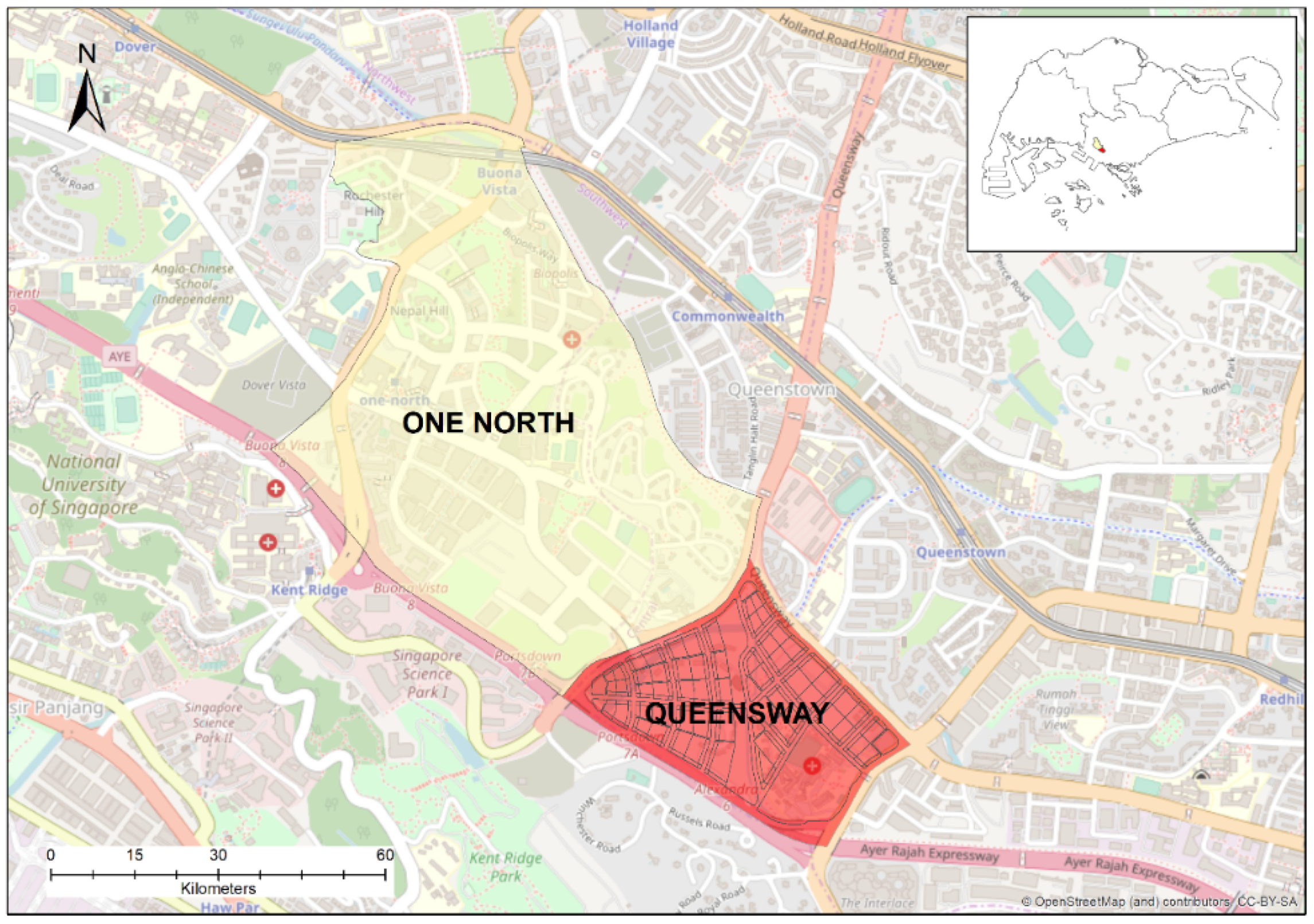
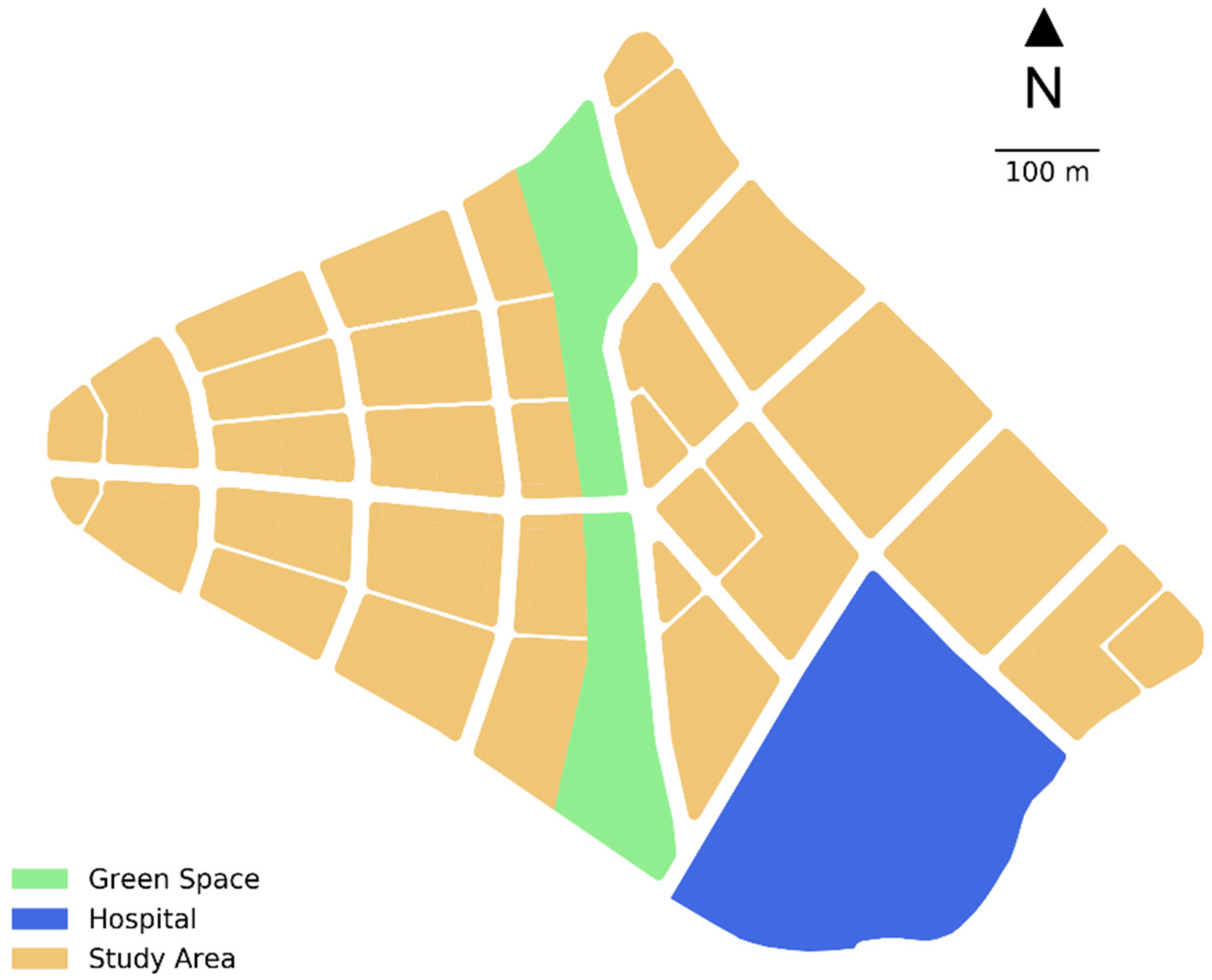
In this research, the concept of livability has been quantitatively and comprehensively reviewed and interpreted to contribute to spatial multi-objective land use optimization modelling. In addition, a multi-objective land use optimization model was constructed using goal programming and a weighted-sum approach, followed by a boundary-based genetic algorithm adapted to help address the spatial multi-objective land use optimization problem. Furthermore, the model is successfully and effectively applied to the case study in the Central Region of Queenstown Planning Area of Singapore towards livability. In the case study, the experiments based on equal weights and experiments based on different weights combination have been successfully conducted, which can demonstrate the effectiveness of the spatial multi-objective land use optimization model developed in this research as well as the robustness and reliability of computer-generated solutions. In addition, the comparison between the computer-generated solutions and the two real planned scenarios has also clearly demonstrated that our generated solutions are much better in terms of fitness values. Lastly, the limitation and future direction of this research have been discussed.
Keywords: spatial multi-objective land use optimization; boundary-based genetic algorithm; livability; accessibility; smart planning; Singapore spatial multi-objective land use optimization; boundary-based genetic algorithm; livability; accessibility; smart planning; Singapore

Share and Cite

MDPI and ACS Style

Cao, K.; Liu, M.; Wang, S.; Liu, M.; Zhang, W.; Meng, Q.; Huang, B. Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore. ISPRS Int. J. Geo-Inf. 2020, 9, 40. https://doi.org/10.3390/ijgi9010040

AMA Style

Cao K, Liu M, Wang S, Liu M, Zhang W, Meng Q, Huang B. Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore. ISPRS International Journal of Geo-Information. 2020; 9(1):40. https://doi.org/10.3390/ijgi9010040

Chicago/Turabian Style

Cao, Kai, Muyang Liu, Shu Wang, Mengqi Liu, Wenting Zhang, Qiang Meng, and Bo Huang. 2020. "Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore" ISPRS International Journal of Geo-Information 9, no. 1: 40. https://doi.org/10.3390/ijgi9010040

APA Style

Cao, K., Liu, M., Wang, S., Liu, M., Zhang, W., Meng, Q., & Huang, B. (2020). Spatial Multi-Objective Land Use Optimization toward Livability Based on Boundary-Based Genetic Algorithm: A Case Study in Singapore. ISPRS International Journal of Geo-Information, 9(1), 40. https://doi.org/10.3390/ijgi9010040

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop