Map Matching for Urban High-Sampling-Frequency GPS Trajectories
Abstract
1. Introduction
2. Related Works
2.1. Local Matching Methods
2.2. Global Matching Methods
3. Intersection Trajectory Segment Matching
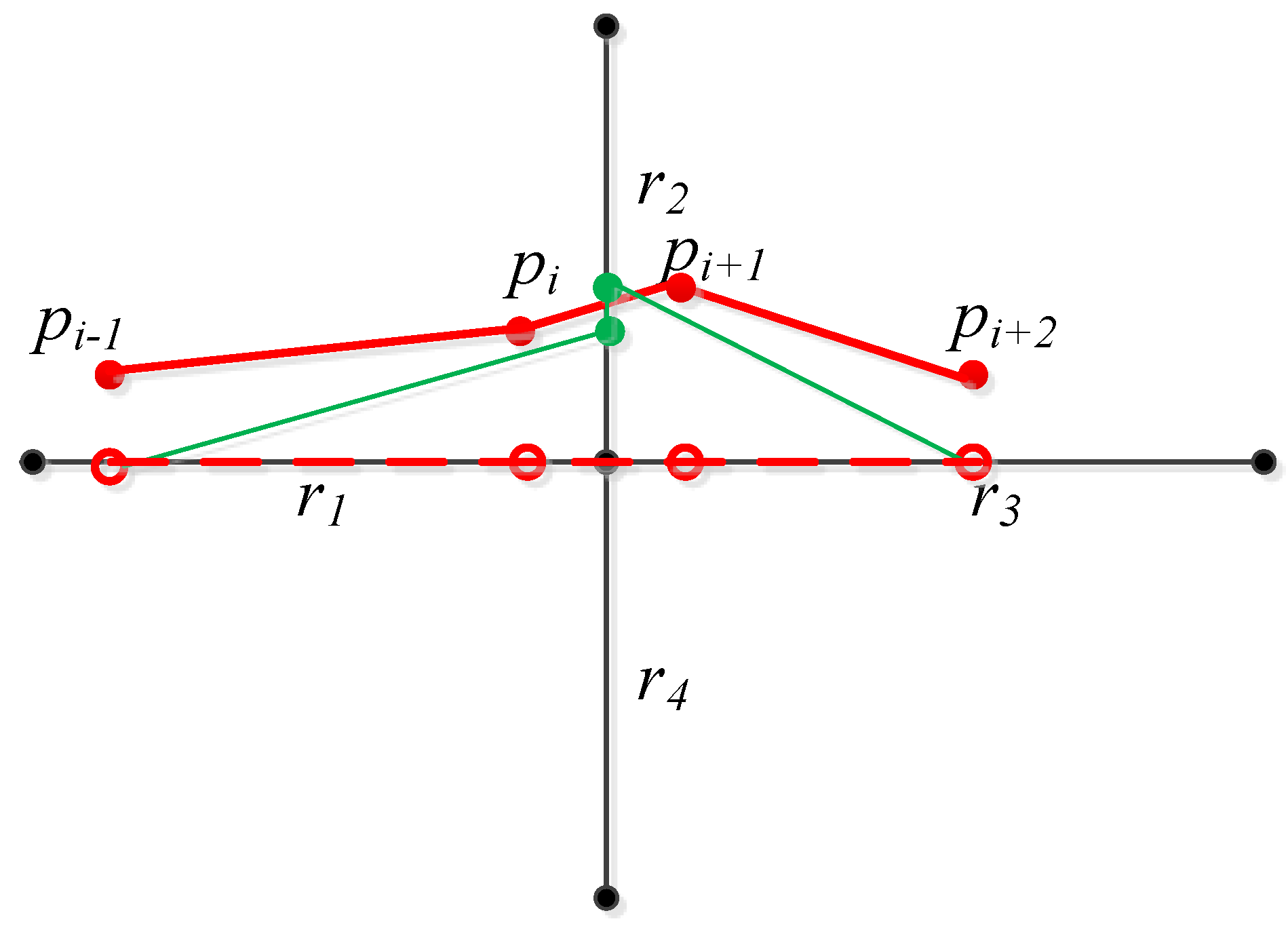
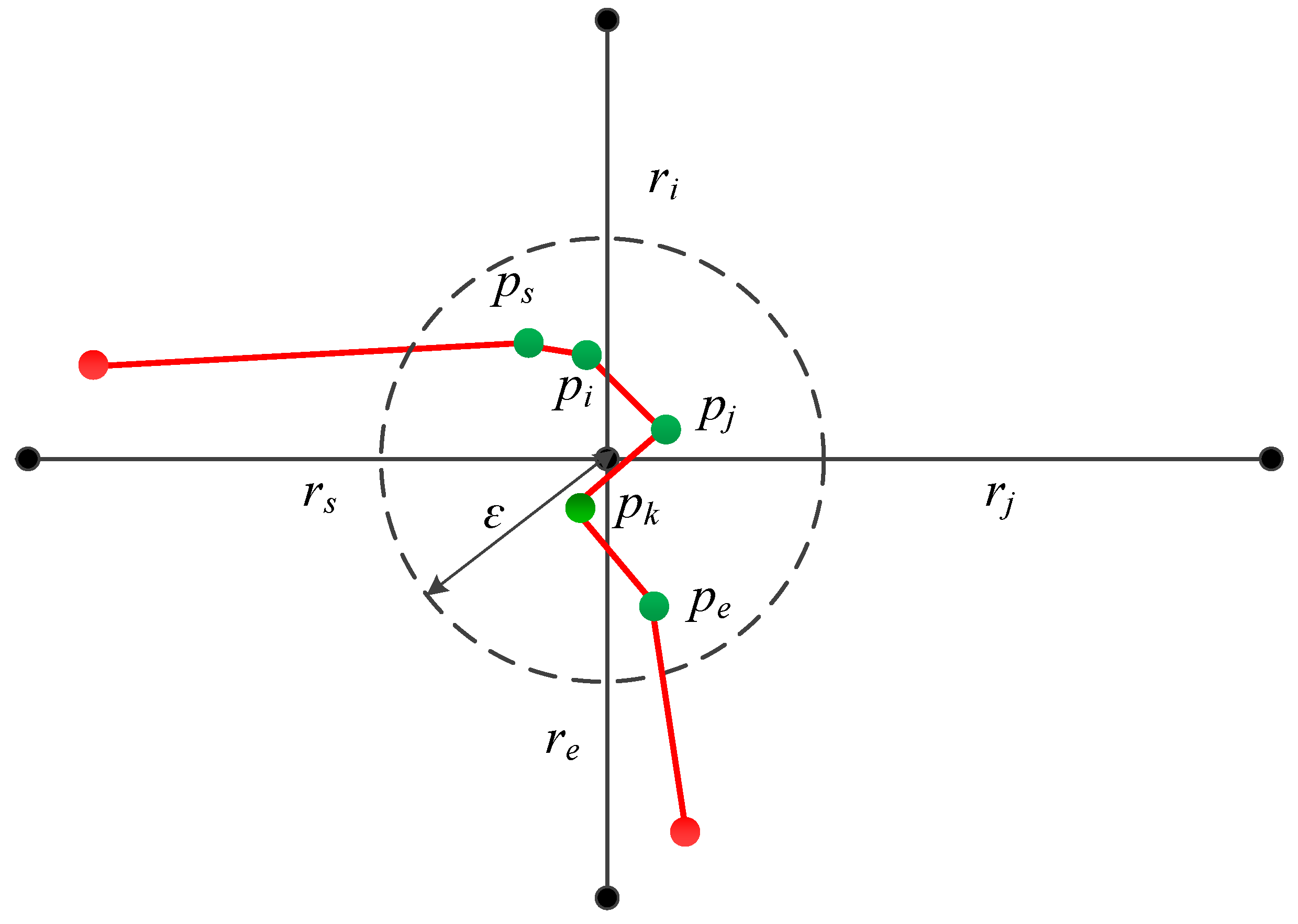
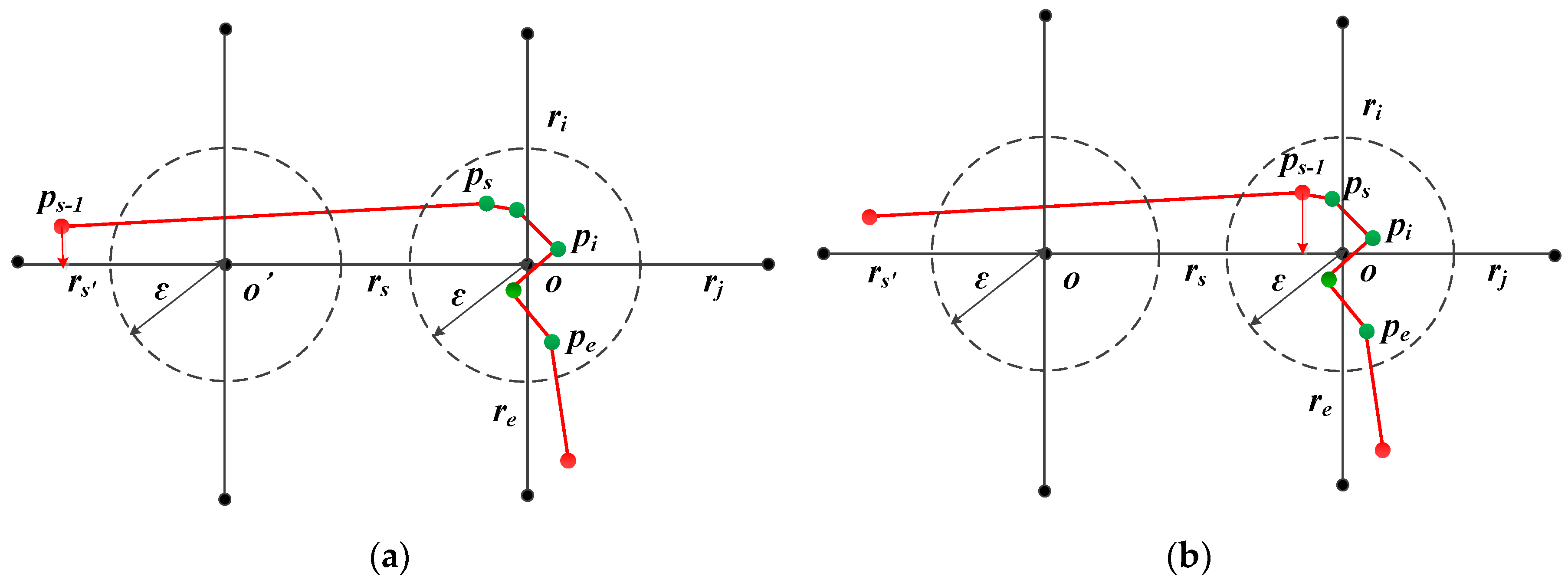
3.1. Classification of Intersection Trajectory Point
- Type 1 (Inside point). The intersection trajectory point is located within the angle between the inbound road section and the outbound road section, such as point pk in Figure 2.
- Type 2 (Inbound-road-related point). The intersection trajectory point is located within the angle between the inbound road section and any other road section, except the outbound section, such as points ps and pi in Figure 2.
- Type 3 (Outbound-road-related point). The intersection trajectory point is located within the angle between the outbound road section and any other road section, except the inbound section, such as point pe in Figure 2.
- Type 4 (Outside point). The intersection trajectory point is located within the angle between the other two road sections, except the inbound and outbound sections, such as point pj in Figure 2.
3.2. Matching Rules
- Rule I: An inside point is matched using the shortest distance method.
- Rule II: An inbound-road-related point is matched to the inbound road section.
- Rule III: An outbound-road-related point is matched to the outbound road section.
- Rule IV: An outside point is matched to the intersection.
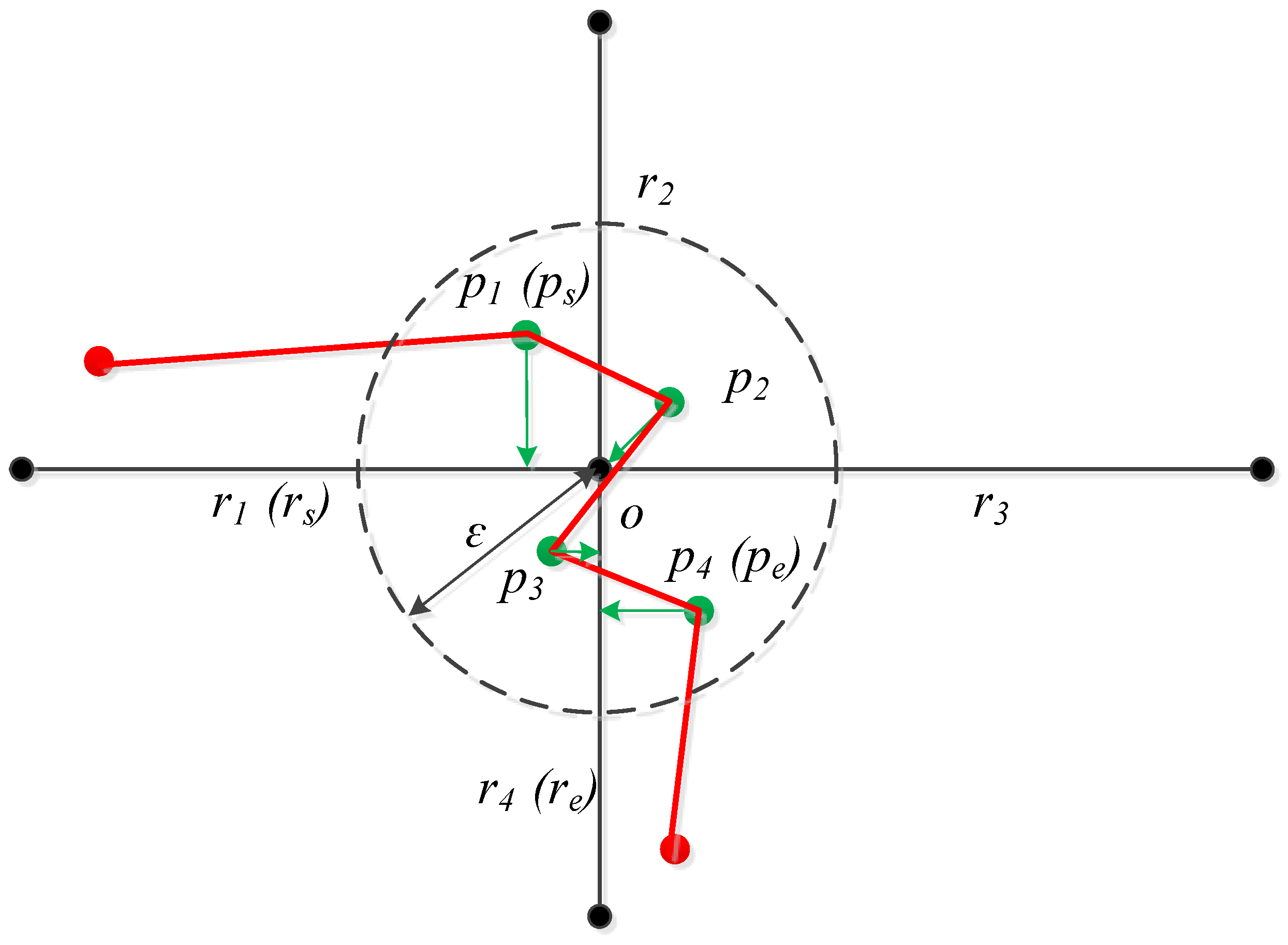
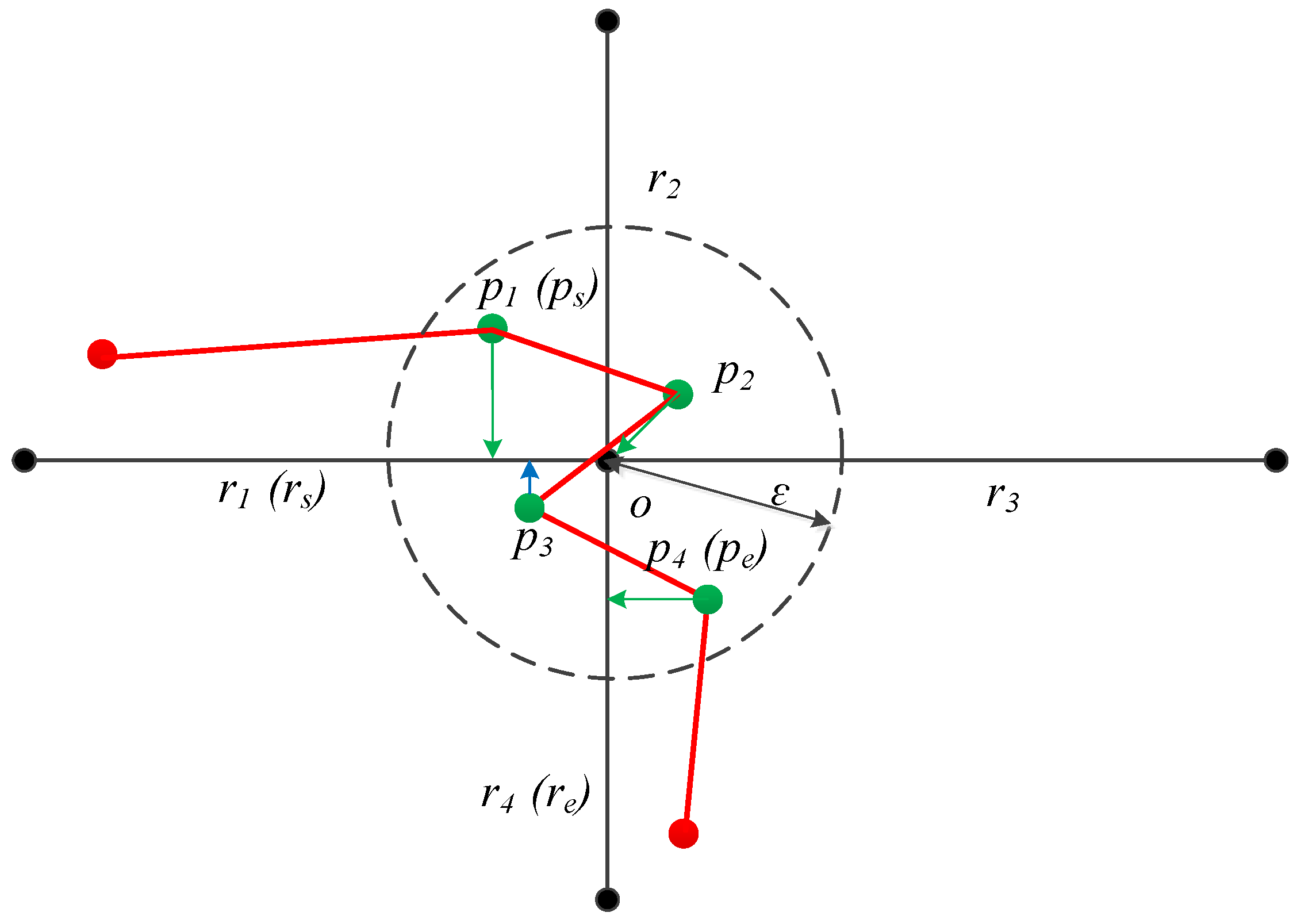
3.3. Abnormity Adjustment
- Rule V: The road segments matched by intersection trajectory points strictly follow the “inbound road section–intersection–outbound road section” sequence.
- IF ri = re AND ri+1 = o, THEN ri = o.
- IF ri = re AND ri+1 = rs, THEN ri = o, ri+1 = o.
- IF ri = o AND ri+1 = rs, THEN ri+1 = o.
- No adjustment is made in any other situation.
3.4. Intersection Trajectory Segment Matching Algorithm
| Algorithm 1 The intersection trajectory segment matching algorithm (InterectTrajMatch) |
| Input: Intersection trajectory points P = {pi|i = 1, …, n}, inbound road section rs, outbound road section re, intersection point o, intersection-related Road Sections R = {ri|i = 1, …, m} |
| Output: The matched road section sequence RM = {rmi|i = 1, …, n} |
| 1: Initialize dlist as an empty list; //dlist is a list of candidate distances 2: Initialize rmlist as an empty list; //rmlist is a list of candidate matched road sections |
| 3: for i = 1 to n do //Traversing P |
| 4: for j = 1 to m do //Traversing R |
| 5: d = Distance(pi, rj); |
| 6: dlist.add(d); |
| 7: end for |
| 8: R.sort(dlist); //sort by distance value on dlist |
| 9: GetShortestTwoSections(R, ref r1, ref r2); //get two road sections with the shortest distance |
| 10: rm = MatchbyRule1234(r1, r2, re, rs, o); //find matched road section by rule I, II, III, IV |
| 11: rmlist.add(rm); |
| 12: end for |
| 13:RM = AdjustbyRule5(rmlist); //adjust match road section by rule V. |
| 14: return ; |
3.5. Matching of Inbound Road Section and Outbound Road Section
3.6. Error Radius ε
4. Segmented Trajectory Matching Method
| Algorithm 2 Segmented trajectory matching algorithm |
| Input: Trajectory points P = {pi|i = 1, …, n}, intersection points O = {oi|i = 1, …, m}, road sections R = {ri|i = 1, …, k}, error radius ε |
| Output: The matched road section sequence RM |
| 1: Initialize plist as an empty list; //plist is a list of candidate intersection trajectory point 2: Initialize rrlist as an empty list; //rrlist is a list of candidate intersection-related road section 3: Initialize rmlist as an empty list; //rmlist is a list of candidate matched road section. |
| 4:rf = MatchFirstPoint(p1, R); //match first point by shortest distance method from all roads. |
| 5:RM.add(rf); |
| 6:rs = rf; //rs means inbound road section |
| 7: for i = 2 to n do //Traversing from |
| 8: oc = FindCurrentIntersectionPoint(rf, O); //oc is the intersection close to point pi |
| 9: if (Distance(pi, oc) ≤ ε) |
| 10: plist.add(pi); |
| 11: else |
| 12: rrlist = FindRelatedRoadSections (oc, R); //rrlist is oc-related road section sets |
| 13: if (plist.count > 0) |
| 14: re = MatchbyLookAhead(pi−1, rrlist); //match outbound point by Look Ahead method [8], re is the outbound road section |
| 15: rmlist = InterectTrajMatch(plist, rs, re, oc, rrlist); //Agorithm 1 |
| 16: RM.add(rmlist); |
| 17: plist.clear(); |
| 18: else |
| 19: re = MatchbyLookAhead(pi, rrlist); |
| 20: RM.add(re); |
| 21: end if |
| 22: rs = re; //current matched road section is next inbound section |
| 23: end if |
| 24: end for |
| 25: return RM |
5. Experiment and Results
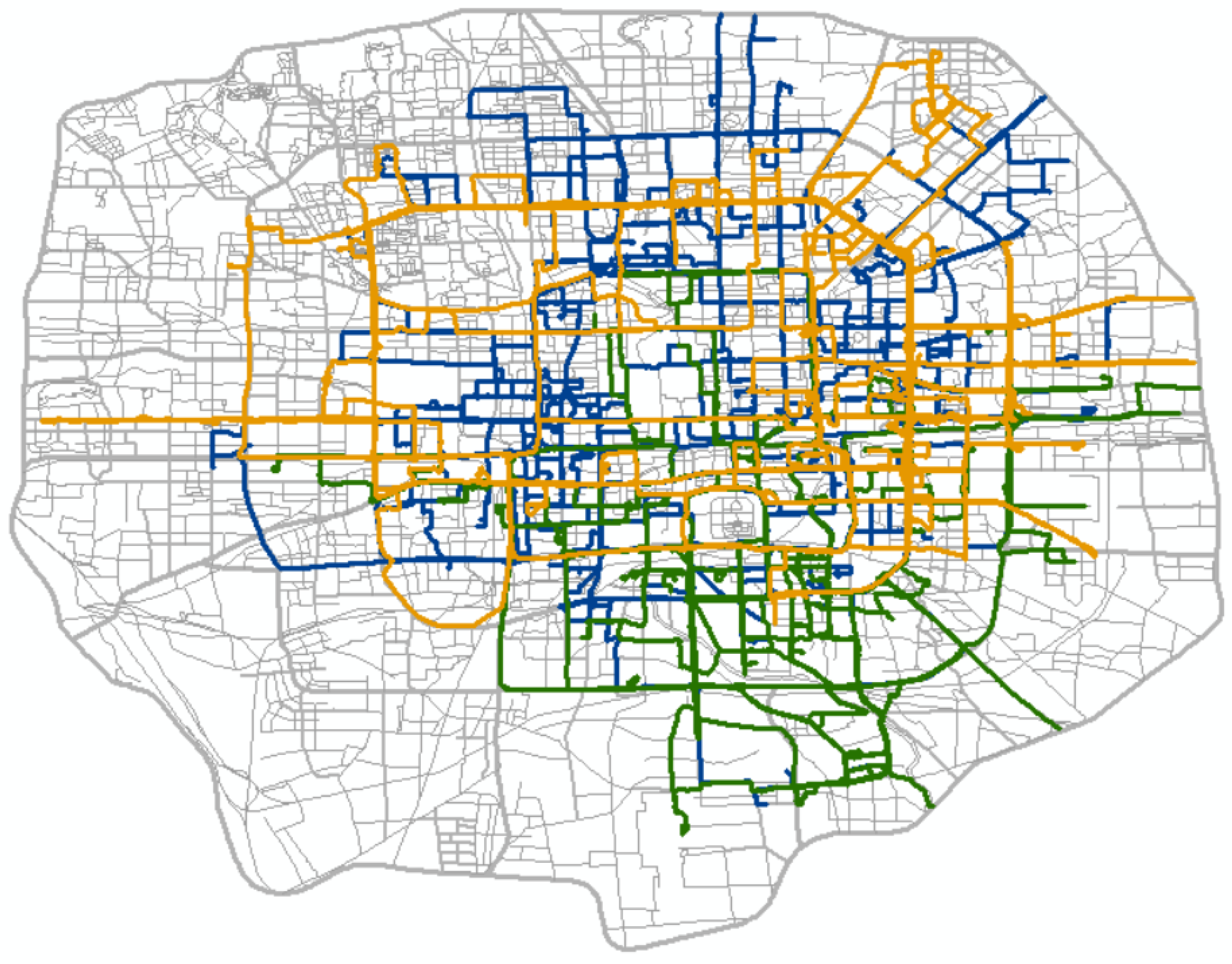
5.1. Experimental Data and Scheme
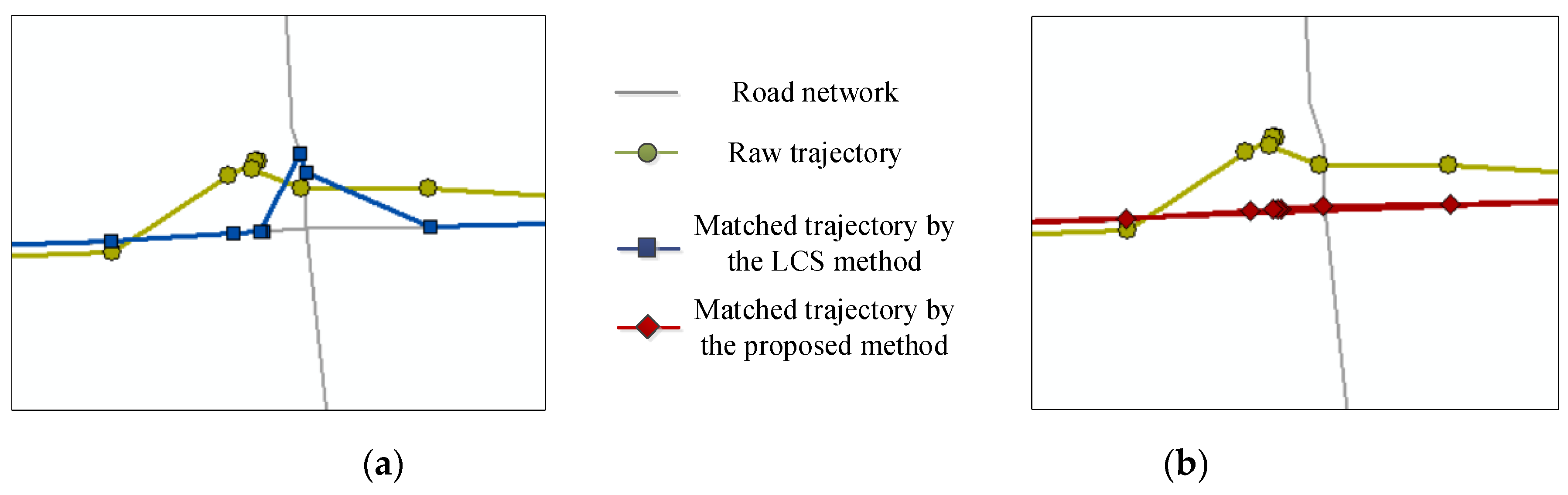
5.2. Comparison of Intersection Matching Methods
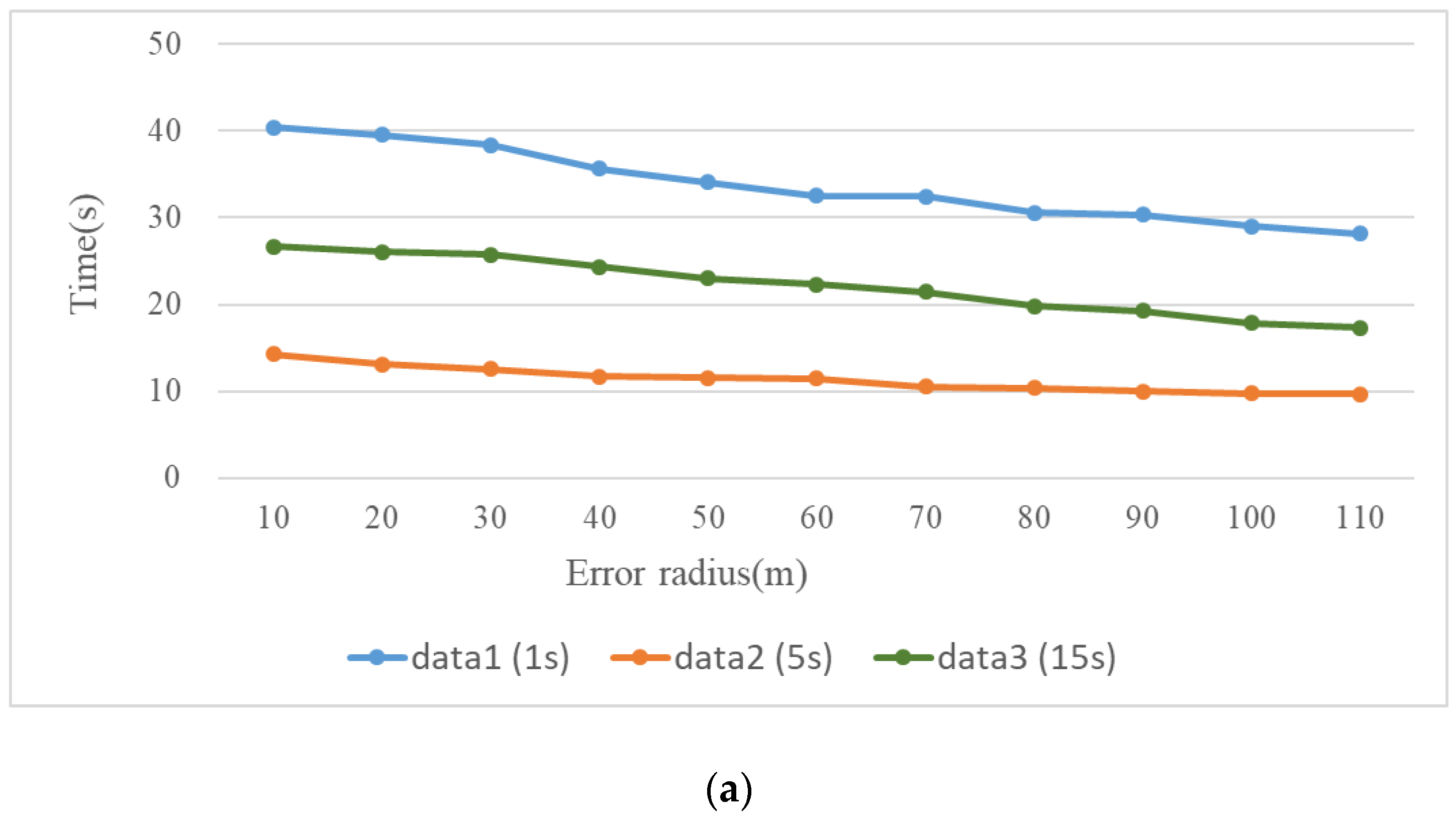
5.3. Efficiency Analysis
5.4. Accuracy Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Quddus, M.A.; Ochieng, W.Y.; Noland, R.B. Current map-matching algorithms for transport applications: State-of-the art and future research directions. Transp. Res. Part C Emerg. Technol. 2007, 15, 312–328. [Google Scholar] [CrossRef]
- Lou, Y.; Zhang, C.; Zheng, Y.; Xie, X.; Wang, W.; Huang, Y. Map-matching for low-sampling-rate GPS trajectories. In Proceedings of the 17th ACM Sigspatial International Symposium on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009. [Google Scholar]
- Bataineh, S.; Bahillo, A.; Díez, L.; Onieva, E.; Bataineh, I. Conditional random field-based offline map matching for indoor environments. Sensors 2016, 16, 1302. [Google Scholar] [CrossRef] [PubMed]
- Hashemi, M.; Karimi, H.A. A critical review of real-time map-matching algorithms: Current issues and future directions. Comput. Environ. Urban Syst. 2014, 48, 153–165. [Google Scholar] [CrossRef]
- Wang, H.; Li, J.; Hou, Z.; Fang, R.; Mei, W.; Huang, J. Research on parallelized real-time map matching algorithm for massive GPS data. Clust. Comput. 2017, 20, 1123–1134. [Google Scholar] [CrossRef]
- Zhu, L.; Holden, J.R.; Gonder, J.D. Trajectory Segmentation Map-Matching Approach for Large-Scale, High-Resolution GPS Data. Transp. Res. Rec. 2017, 2645, 67–75. [Google Scholar] [CrossRef]
- Qi, H.; Di, X.; Li, J. Map-matching algorithm based on the junction decision domain and the hidden Markov model. PLoS ONE 2019, 14, e0216476. [Google Scholar] [CrossRef] [PubMed]
- Brakatsoulas, S.; Pfoser, D.; Salas, R.; Wenk, C. On map-matching vehicle tracking data. In Proceedings of the 31st International Conference on Very Large Data Bases, Trondheim, Norway, 30 August–2 September 2005; pp. 853–864. [Google Scholar]
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, X.; Sun, G.Z. An Interactive-Voting Based Map Matching Algorithm. In Proceedings of the Eleventh International Conference on Mobile Data Management, Kanas City, MO, USA, 23–26 May 2010. [Google Scholar]
- Greenfeld, J.S. Matching GPS Observations to Locations on a Digital Map. In Proceedings of the 81st Annual Meeting of the Transportation Research Board, Washington, DC, USA, 13–17 January 2002; pp. 164–173. [Google Scholar]
- White, C.E.; Bernstein, D.; Kornhauser, A.L. Some map matching algorithms for personal navigation assistants. Transp. Res. Part C Emerg. Technol. 2000, 8, 91–108. [Google Scholar] [CrossRef]
- Hsueh, Y.L.; Chen, H.C. Map matching for low-sampling-rate GPS trajectories by exploring real-time moving directions. Inf. Sci. 2018, 433, 55–69. [Google Scholar] [CrossRef]
- Quddus, M.A.; Ochieng, W.Y.; Zhao, L.; Noland, R.B. A general map matching algorithm for transport telematics applications. GPS Solut. 2003, 7, 157–167. [Google Scholar] [CrossRef]
- Hashemi, M.; Karimi, H.A. A weight-based map-matching algorithm for vehicle navigation in complex urban networks. J. Intell. Transp. Syst. 2016, 20, 573–590. [Google Scholar] [CrossRef]
- Sharath, M.N.; Velaga, N.R.; Quddus, M.A. A dynamic two-dimensional (D2D) weight-based map-matching algorithm. Transp. Res. Part C Emerg. Technol. 2019, 98, 409–432. [Google Scholar] [CrossRef]
- Hu, G.; Shao, J.; Liu, F.; Wang, Y.; Shen, H.T. If-matching: Towards accurate map-matching with information fusion. IEEE Trans. Knowl. Data Eng. 2016, 29, 114–127. [Google Scholar] [CrossRef]
- Zhao, X.; Cheng, X.; Zhou, J.; Xu, Z.; Dey, N.; Ashour, A.S.; Satapathy, S.C. Advanced topological map matching algorithm based on D–S theory. Arabian J. Sci. Eng. 2018, 43, 3863–3874. [Google Scholar] [CrossRef]
- Alt, H.; Efrat, A.; Rote, G.; Wenk, C. Matching planar maps. J. Algorithms 2003, 49, 262–283. [Google Scholar] [CrossRef]
- Yin, H.; Wolfson, O. A Weight-based Map Matching Method in Moving Objects Databases. In Proceedings of the 16th International Conference on Scientific and Statistical Database Management, Santorini Island, Greece, 21–23 June 2004; pp. 437–438. [Google Scholar]
- Wei, H.; Wang, Y.; Forman, G.; Zhu, Y. Map Matching by Fréchet Distance and Global Weight Optimization; Technical Paper; Department of Computer Science and Engineering, 2013; p. 19. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.716.7193&rep=rep1&type=pdf (accessed on 10 December 2019).
- Millard-Ball, A.; Hampshire, R.C.; Weinberger, R.R. Map-matching poor-quality GPS data in urban environments: The pgMapMatch package. Transp. Plan. Technol. 2019, 42, 539–553. [Google Scholar] [CrossRef]
- Knapen, L.; Bellemans, T.; Janssens, D.; Wets, G. Likelihood-based offline map matching of GPS recordings using global trace information. Transp. Res. Part C Emerg. Technol. 2018, 93, 13–35. [Google Scholar] [CrossRef]
- Rappos, E.; Robert, S.; Cudré-Mauroux, P. A force-directed approach for offline GPS trajectory map matching. In Proceedings of the 26th ACM Sigspatial International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 6–9 November 2018; pp. 319–328. [Google Scholar]
- Newson, P.; Krumm, J. Hidden Markov map matching through noise and sparseness. In Proceedings of the ACM Sigspatial International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 4–6 November 2009. [Google Scholar]
- Koller, H.; Widhalm, P.; Dragaschnig, M.; Graser, A. Fast hidden Markov model map-matching for sparse and noisy trajectories. In Proceedings of the 2015 IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas, Spain, 15–18 September 2015; pp. 2557–2561. [Google Scholar]
- Yang, C.; Gidofalvi, G. Fast map matching, an algorithm integrating hidden Markov model with precomputation. Int. J. Geogr. Inf. Sci. 2018, 32, 547–570. [Google Scholar] [CrossRef]
- Szwed, P.; Pekala, K. An Incremental Map-Matching Algorithm Based on Hidden Markov Model. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, ICAISC 2014, Zakopane, Poland, 1–5 June 2014; pp. 579–590. [Google Scholar]
- Mohamed, R.; Aly, H.; Youssef, M. Accurate real-time map matching for challenging environments. IEEE Trans. Intell. Transp. Syst. 2016, 18, 847–857. [Google Scholar] [CrossRef]
- Jagadeesh, G.R.; Srikanthan, T. Online map-matching of noisy and sparse location data with hidden Markov and route choice models. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2423–2434. [Google Scholar] [CrossRef]
- Algizawy, E.; Ogawa, T.; El-Mahdy, A. Real-time large-scale map matching using mobile phone data. ACM Trans. Knowl. Discov. Data 2017, 11, 52. [Google Scholar] [CrossRef]
- Yuan, J.; Zheng, Y.; Xie, X.; Sun, G. Driving with knowledge from the physical world. In Proceedings of the 17th ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 316–324. [Google Scholar]
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, W.; Xie, X.; Sun, G.; Huang, Y. T-drive: Driving directions based on taxi trajectories. In Proceedings of the 18th Sigspatial International Conference on Advances in Geographic Information Systems, San Jose, CA, USA, 2–5 November 2010; pp. 99–108. [Google Scholar]
- Ministry of Housing and Urban-Rural Development of the People’s Republic of China. Code for Design of Urban Road Engineering (CJJ37-2012); China Building Industry Press: Beijing, China, 2012.
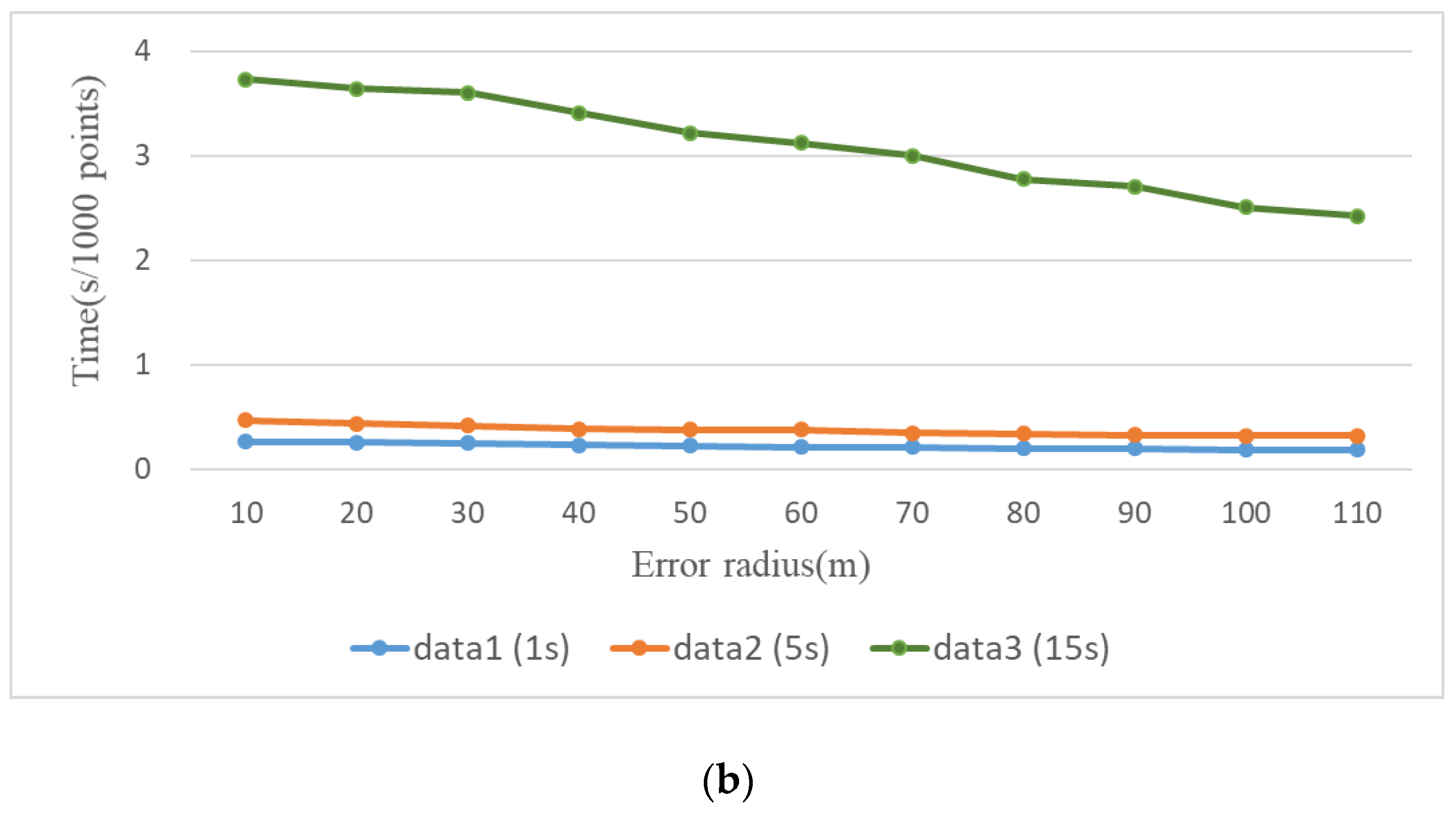
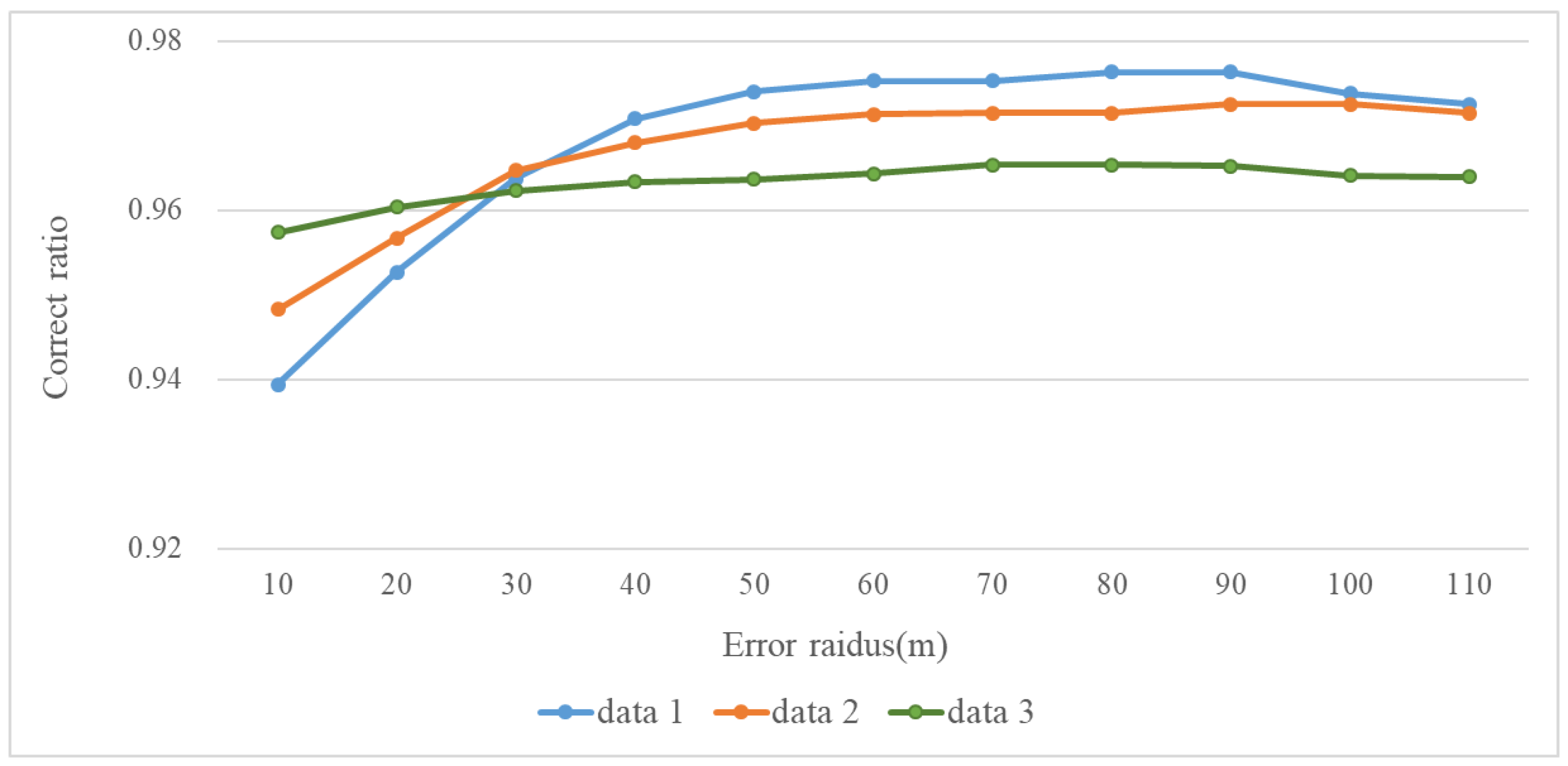
| Number | Sampling Interval (s) | Number of Trajectory Points |
|---|---|---|
| 1 | 1 | 151,542 |
| 2 | 5 | 30,156 |
| 3 | 15 | 7141 |
| Methods | Running Total Time (s) | ||
|---|---|---|---|
| Data 1 | Data 2 | Data 3 | |
| this method, 60 m | 32.5 | 11.5 | 22.3 |
| LCS, 95% | 348.5 | 99.5 | 67.8 |
| decision domain HMM, 60 m | 454.6 | 120.6 | 96.4 |
| Methods | All Trajectory Points Matching Accuracy | Intersection Trajectory Points Matching Accuracy | ||||
|---|---|---|---|---|---|---|
| Data 1 | Data 2 | Data 3 | Data 1 | Data 2 | Data 3 | |
| this method, 60 m | 0.978 | 0.971 | 0.964 | 0.995 | 0.987 | 0.980 |
| LCS, 95% | 0.952 | 0.958 | 0.963 | 0.857 | 0.869 | 0.894 |
| decision domain HMM, 60 m | 0.972 | 0.969 | 0.965 | 0.992 | 0.985 | 0.977 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Zhang, L.; Ge, J.; Long, Y.; Che, W. Map Matching for Urban High-Sampling-Frequency GPS Trajectories. ISPRS Int. J. Geo-Inf. 2020, 9, 31. https://doi.org/10.3390/ijgi9010031
Liu M, Zhang L, Ge J, Long Y, Che W. Map Matching for Urban High-Sampling-Frequency GPS Trajectories. ISPRS International Journal of Geo-Information. 2020; 9(1):31. https://doi.org/10.3390/ijgi9010031
Chicago/Turabian StyleLiu, Minshi, Ling Zhang, Junlian Ge, Yi Long, and Weitao Che. 2020. "Map Matching for Urban High-Sampling-Frequency GPS Trajectories" ISPRS International Journal of Geo-Information 9, no. 1: 31. https://doi.org/10.3390/ijgi9010031
APA StyleLiu, M., Zhang, L., Ge, J., Long, Y., & Che, W. (2020). Map Matching for Urban High-Sampling-Frequency GPS Trajectories. ISPRS International Journal of Geo-Information, 9(1), 31. https://doi.org/10.3390/ijgi9010031





