Abstract
Soil health plays a major role in the ability of any nation to meet the Sustainable Development Goals. Understanding the spatial variability of soil health indicators (SHIs) may help decision makers develop effective policy strategies and make appropriate management decisions. SHIs are often spatially correlated, and if this is the case, a geostatistical model is required to capture the spatial interactions and uncertainty. Geostatistical simulation provides equally probable realizations that can account for uncertainty in the variables. This study used the following SHIs extracted from the Africa Soil Information Service “Legacy Database” for Nigeria: bulk density, organic matter, and total nitrogen. Maximum and minimum autocorrelation factors (MAF) and independent component analysis (ICA) are two techniques that can be used to transform correlated SHIs into uncorrelated factors/components that can be simulated independently. To confirm spatial orthogonality, the relative deviation from orthogonality, τ(h), and spatial diagonalization efficiency, k(h), approach 0 and 1 for both techniques. To validate the performance of each technique, 100 equally probable realizations were simulated by using MAF and ICA. Direct and cross-variograms showed adequate reproduction, using E-type, where E was defined as the “conditional expectation” of realizations (i.e., average estimate of realizations). It should be noted that only direct variograms of MAF and ICA were independently simulated. The average of 100 back-transformed simulated realizations and randomly selected realizations compared well with the original variables, in terms of spatial distribution, correlation, and pattern. Overall, both techniques were able to reproduce important geostatistical features of the original variables, making them important in joint simulations of spatially correlated variables in soil management.
1. Introduction
Soil health indicators (SHIs) play an important role in sustainable agriculture. Information about soil health will be relevant to any country aiming to achieve the Sustainable Development Goals, (SDGs) especially “Zero Hunger” and “Zero Poverty”. Information on soil properties can be used in water and nutrient management, to support biomass production [1], and contribute to the functioning of the ecosystem [2]. In other words, the delivery of ecosystem goods and services through sustainable agriculture practices and management depends on soil resources [3]. Furthermore, soil is directly linked to the atmosphere, and if agricultural practices are not controlled, the release of trace gases, such as methane (CH4), carbon dioxide (CO2), and dinitrous oxide (N2O), may be amplified [3].
The United States Department of Agriculture has characterized SHIs into three types: chemical, physical and biological. Examples of physical, chemical and biological SHIs, respectively, are bulk density (BD), organic carbon (OC), and total nitrogen (TN). Due to human factors such as land management (tillage) and the usage of fertilizer and manure, these SHIs may be correlated. In other words, locations with high TN may also have high OC (positive correlation), and areas with high soil compaction may have low OC and TN (negative correlation).
Generally, soil variables are heterogeneous [4] and vary in space and time [5]. As such, it is in the best interest of decision-makers, scientists and other stakeholders to understand the spatial pattern of soil characteristics. When developing policies, soil maps are often created and used; however, little attention has been given to the accuracy of these maps [6]. As reported by Heuvelink and Brown [7], uncertainty can stem from sources such as measurement error, model ambiguity and vagueness. In addition, the Food and Agriculture Organization of the United Nations (FAO) [8] has identified four sources of uncertainty in soil mapping: soil measurement, covariates, models and spatial data. Using data with high uncertainty for important decision making is ill-advised [9]. Previous research has characterized the uncertainty of soil mapping by using various techniques at the local, regional and national scales [10,11,12,13]. Therefore, the objective of the current study is not to review these techniques, as the mathematical and technical aspects of each technique can be found in the cited literature; rather, the objective of this paper is to apply two robust linear decorrelation transformation methods to spatally correlated SHIs for geostatistcal simualtion.
To analyze the spatial structure or variability of soil properties, previous studies have used a variogram [14,15]. A variogram or semi-variogram quantifies the spatial continuity or autocorrelation of the dataset. This involves calculating half the difference squared among two locations. When this is plotted (known as an “experimental variogram”), a covariance function (e.g., exponential, spherical, nugget, circular, etc.) may be fitted to the data to estimate three important parameters: sill (the variance where the variogram reaches a “plateau”); range (the maximum distance where there is no correlation in the datasets); and nugget (small variability in the data due to measurement error). A cross-variogram is required when two variables are correlated.
Joint simulation of spatially correlated SHIs may be applicable in environmental science or agricultural planning and management, as it can help assess the spatial variability and cross-correlation of the variables. When performing geostatistical simulations, the correlated variables must be transformed into a format that renders them uncorrelated [16]. From a field and laboratory measurement standpoint, chemical and biological soil properties may be expensive and laborious to sample and analyze and can lead to high levels of uncertainty (due to under-sampling) [17]. This is especially true when compared with physical properties such as BD, which are generally less expensive to measure and lead to less uncertainty. The spatial relationships among variables may help reduce the variance of the estimation error, especially when using interpolation methods such as co-kriging [18,19]. According to Goovaerts [20], fitting an appropriate linear model of co-regionalization (LMC) would allow the estimation of the variables. However, this would involve the processing of large nodes, which can render computation difficult, cumbersome and expensive, especially when there are more than three variables [21,22]. One plausible solution is to transform the variables into uncorrelated factors that can be simulated independently [16,23,24,25].
The linear transformation methods used to generate spatially uncorrelated factors include principal component analysis (PCA), minimum and maximum autocorrelation factors (MAF), minimum spatial cross-correlation, uniformly weighted exhaustive diagonalization, and independent component analysis (ICA). Reviewing these methods is beyond the scope of the current study; however, a description of several of these important applications can be found in [21,22,24,25,26,27,28,29,30]. Two of the aforementioned techniques—MAF and ICA—were used in the current study. These methods were selected due to their flexibility in handling geospatial datasets, robust computation, and prior success in using them to examine spatial structures in environmental datasets [21,22,31,32].
The primary objective of the present study is to compare the ability of the two methods to simulate three spatially correlated SHIs (i.e., BD, OC, and TN), using an international scale dataset extracted from the Africa Soil Information Service (AfSIS). The primary objective of AfSIS is to provide digital soil maps for Sub-Saharan Africa [33]. Recently, Boluwade [34] used interpolated SHIs from AfSIS for Nigeria as a basis for the partition of Nigeria’s smallest administrative units into regions that could be used for planning and sustainable agriculture. However, these maps were developed by using ordinary kriging (OK), which has a smoothening effect. This study aims to update that work. As per Boluwade [34], Nigeria was selected as the study area.
The remainder of this paper is arranged as follows. Section 2 describes the SHI dataset used, as well as the joint simulation methods, including MAF, ICA, and SGS. In Section 3, the results of using each technique are discussed in relation to various validation methods. Section 4 summarizes the findings and draws conclusions.
2. Materials and Methods
2.1. Description of the Dataset and Study Area
Nigeria was selected for this study for several reasons. As of 2017, Nigeria had the largest population in Africa, with more than 190 million people [35]. With an estimated annual population growth of 2.5%, the country’s population is projected to exceed 400 million in 2050 [36,37]. Smallholder-based agriculture is primarily used in Nigeria, with approximately 50% of the population employing this method [35]. According to the FAO [38], more than half of the population lives below the poverty line. With the 2030 SDGs still far out of reach, the country faces an enormous challenge, and information on soil health management will be paramount to their success in achieving the goals. The SHIs used in this study (OC, TN, and BD) were extracted from the AfSIS website (https://www.isric.org/projects/africa-soil-profiles-database-afsp). The AfSIS database is compiled by the International Soil Reference and Information Centre (ISRIC). ISRIC aims to serve the global community and raise awareness regarding the importance of soil management [39]. AfSIS compiles data from two databases: the AfSIS Sentinel Site Database and the African Soil Profile Database (also known as the “Legacy Database”) [39]. Legacy Database version 1.2 was used in the current study. According to Leenaars et al. [39], the database has more than 18,532 soil profiles, of which 17,160 are geo-referenced records covering 40 countries in Sub-Saharan Africa. The dataset covers almost all of Nigeria in terms of spatial distribution (Figure 1).
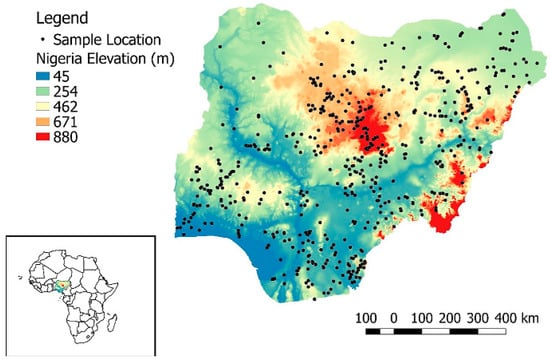
Figure 1.
Map of Nigeria, showing the location of sample sites.
In previous work on SHIs in Nigeria, Boluwade [34] extracted SHIs from AfSIS with substantial levels of missing data. Using the gridded Normalized Difference Vegetation Index (NDVI) and topography as auxiliary variables, the random forest-based imputation technique (missForest) was used to impute missing values. In the same study, the author reported an acceptable normalized root mean square error (NRMSE) of 1.27%. The correlation between the three SHIs was preserved after imputation (Boluwade, 2019). Figure 2 shows the correlation matrix of the three SHIs. OC and TN are positively correlated , whereas BD is negatively correlated with both TN and OC . To confirm the spatial correlation and dependency, the direct and cross-variograms of the three variables can be estimated by using the function fit.lmc in the gstat package in R statistical software [40]. Figure 3 shows that OC and TN have a positive spatial correlation, whereas BD has a negative spatial correlation with OC and TN. This reflects areas in Nigeria with high BD and a possible deficit of nutrients and organic matter. In practical applications, soils that are compacted (high BD) may have limited micro-organic activity, which is essential to nutrient availability and organic activities. This established relationship depicted in Figure 3 is used as a benchmark to validate the two techniques used in the current study. In other words, the back-transformed simulated factors (minimum and maximum autocorrelation factors; MAF) and components (independent component analysis; ICA) in data space need to retain this relationship to be considered valid [22]. Table 1, which is a reproduction of the work by Boluwade [34], shows the descriptive statistics of the SHIs. In Nigeria, BD, OC and TN have an average value of 1.31 g/cm3, 10.52 g/kg, and 0.92 g/kg, respectively. Moreover, BD ranges from 0.73 to 1.84 g/cm3, and OC ranges from 0.20 to 91 g/kg. TN ranges from 0.01 to 8.90 g/kg. Table 1 also shows that OC and TN have high coefficients of variation (CV) of 89.4% and 95.65%, respectively. These high values may be a result of land management practices such as fertilizer and manure applied at farms scattered across the country. Correspondingly, BD has the lowest CV at 9%. This suggests that of the three SHIs, land management practices such as tillage have the lowest impact on BD. Furthermore, Nigeria has three main ecological zones: the northern Sudan Savannah, the Guinea Savannah and rainforest zone with sandy, sandy-loam, and clay-loam dominant soil types, respectively [34].
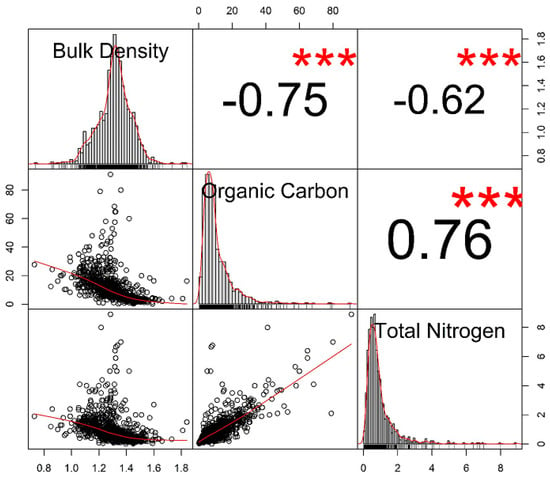
Figure 2.
Scatter matrix plots of soil health indicators showing the scatterplot matrix, with histograms, kernel density overlays, correlation, and significance levels (*** p < 0.001).
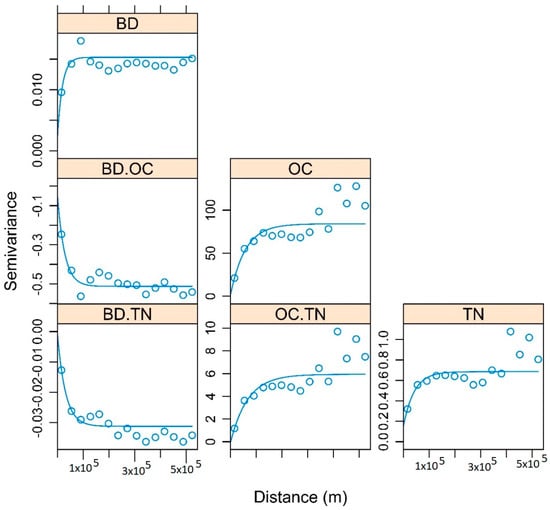
Figure 3.
Direct and cross-experimental variograms of the original soil health indicators (SHIs): BD = bulk density (g/cm3); TN = total nitrogen (g/kg); and OC = organic carbon (g/kg) (semivariance is expressed as units of each SHI).

Table 1.
Descriptive statistics of the examined soil health indicators in Nigeria *.
2.2. ICA
ICA is a linear decomposition of correlated variables into independent components (hereafter IC) that are uncorrelated. According to Hyvärinen et al. [41], the original correlated variables are assumed to be linear mixtures or combinations of some unknown latent variables. The original dataset must be centered, which can be achieved by subtracting the mean of each column of the data matrix, from each variable [41]. This is done to simplify the ICA algorithm [41]. Pre-whitening is then required to project the data into their principal components, , with K representing the pre-whitening matrix. Finally, according to Boluwade and Madramootoo [22], the “mean vector of Z(s) to be zero and also its variance covariance is the identity matrix, which has a variance of 1 and is uncorrelated”. For a random and whitened vector, Z(s) can be expressed as a mixture of the independent components of the following:
where is the source matrix, which also includes the required IC, and A is a mixture matrix. According to Tercan and Sohrabian [32], both A and are unknown and are only estimated by using the knowledge of Z(s). The IC are obtained through the unmixing matrix:
Therefore, W is the demixing matrix and also represents the rows of the inverse matrix, A−1; thus, the linear combination is calculated as follows:
and would be equal to the ICs [41].
The derived components can now be used in the sequential Gaussian simulation (SGS). More technical details and the implementation of ICA for spatially correlated variables have been described by Sohrabian and Ozcelik [31], Tercan and Sohrabian [32], and Boluwade and Madramootoo [22]. The step-by-step procedure for using ICA for spatially correlated SHIs is shown in Figure 4. The ica package in R statistical software [42], which was developed based on the FastICA algorithm [43], was used to perform ICA in the current study.
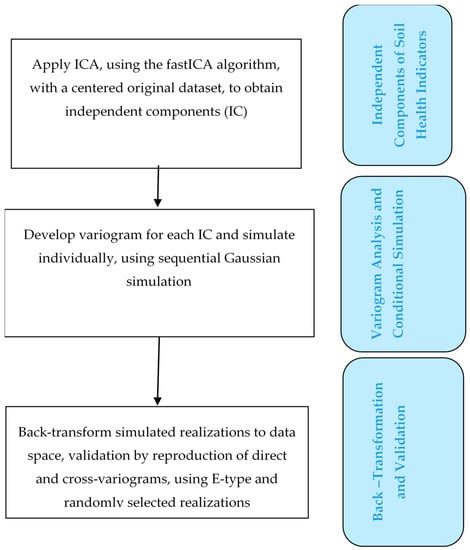
Figure 4.
Workflow of independent component analysis (ICA) and sequential Gaussian simulation.
2.3. MAF
The concept of MAF was first introduced by Switzer and Green [44] and implemented in geostatistics by Desbarats and Dimitrakpoulos [21]. The MAF method can be used to transform correlated variables into uncorrelated factors, which can then be simulated separately. The MAF mathematical formulation has been well-documented in Desbarats and Dimitrakpoulos [21], Rondon [45], Boucher et al. [46], and Bandarian et al. [47]. Generally, MAFs can be obtained by doing PCA twice [48,49,50]. In other words, in the PCA first transformation, the spectral decomposition of the covariance matrix of the original variables is performed to obtain the principal components (PC), while in the second PCA step, the transformation would maximize or minimize the variance increments of the PCs obtained in the first step. In other words, MAF involves deriving its factors from a normal score transformed random variable, , with s denoting geographical coordinates, by first doing a PCA at lag, h = 0, and it also involves computing the covariance matrix [48,49,50]:
Equation (4) is then spectrally decomposed to obtain the matrix of eigenvalues, D1 and the Q1, orthonormal of the eigenvectors:
The standardized (i.e., in this case, normal–scored transformed) PCA components, PCA1, PCA2, …, PCAp are therefore obtained as follows:
The second step involves doing another PCA at any lag distance greater than zero that can be chosen arbitrarily, using the cross-variance matrix of the PCA factors obtained from the 1st step. In other words, an experimental omni-directional symmetric cross-variance matrix is necessary, using the PCA matrix [21,49]. Therefore, the spectral decomposition of the cross-variance matrix will yield D2 (2nd matrix of eigenvalues) and Q2 (2nd matrix of the orthonormal of the eigenvectors) through:
Therefore, the MAF, M, can be computed as follows:
The MAF coefficients or loadings, also called the “A matrix”, can be obtained as follows:
In other words, MAF factors can be finally defined as follows:
Figure 5 shows the steps required to implement MAF. To back-transform simulated realization MAF, each realization is multiplied by A−1, where A−1 is the transformation inverse matrix. A function was written in R statistical software and used to compute MAF following the example in Haugen et al. [50].
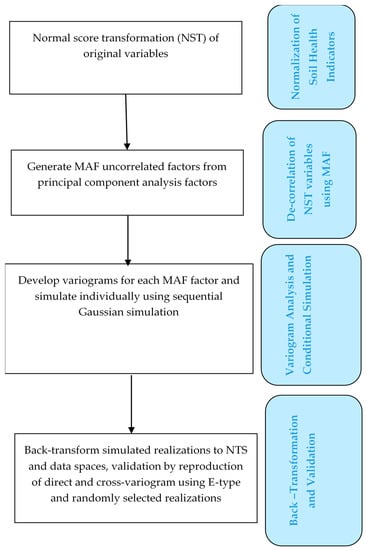
Figure 5.
Workflow of minimum and maximum factors (MAF) and simulations.
2.4. SGS
The SGS method has been used extensively in the mining industry to characterize uncertainty in heterogeneous ore bodies [21,29]. SGS provides equally probable outcomes (realizations) compared to the mean value of the object (i.e., using the traditional interpolation method). SGS can be used to characterize both local and spatial variability. This makes it a better representation of the true variability of each SHI and provides a platform to evaluate the local and spatial uncertainty of each SHI. According to Goovaerts [51], stochastic simulation is a key tool in modeling uncertainty. The steps involved in SGS are shown in Figure 6.
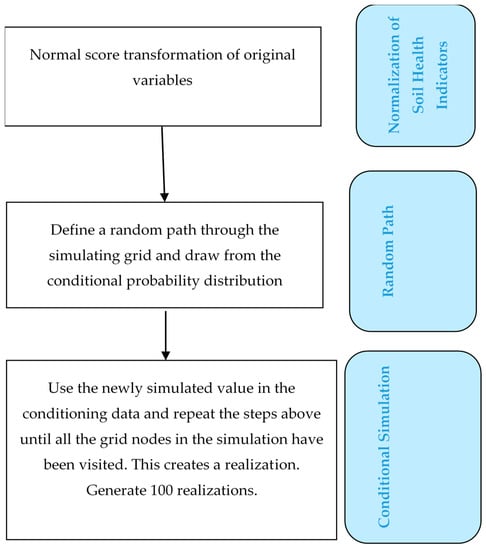
Figure 6.
Workflow of conditional sequential Gaussian simulations.
2.5. Verification and Validation of MAF and ICA Algorithms in the Joint Simulation of Soil Health Indicators
Verification measures are needed to confirm that MAF and ICA correctly decorrelate and reproduce the original SHIs. Back-transformed realizations should have the same geostatistical properties, structures, direct-variograms, and cross-variograms as the original variables.
The following measures were tested:
- (a)
- The test for spatial orthogonality assesses how well the methods (i.e., MAF and ICA) orthogonalize the variogram matrices at various lag distances [29,52]:
- According to Muller [52] and Tercan [29], τ(h) is the relative deviation from orthogonality that compares the “sum of off-diagonal elements with the sum of the absolute values of the diagonal elements of the factor or component experimental variogram matrix for each lag ”;
- The relative deviation from orthogonality can therefore be defined as:where γMAF (h: k, j) is the cross-variogram of the MAF or ICA, and γMAF (h: k, k) is the direct variogram of the MAF or IC. M is the variogram matrices length. For perfect spatial orthogonally, τ(h) = 0.
- The spatial diagonalization efficiency is a measure that compares the sum of squares of off-diagonal elements in ΓMAF (h) with those of the attribute of the semi-variogram matrix ΓY (h):where γY (h: zk, zj) represents the cross-variograms of the original variables. For perfect orthogonality, k(h) = 1.
- (b)
- Reproduction of direct and cross-variograms, using the average of realizations and randomly selected realizations:For both algorithms to be valid, the direct and cross-variograms of the original variables should be reproduced by the back-transformed simulated realizations. A total of 100 realizations would be averaged (in data space). This is defined as E-type, where E is the “conditional expectation” of realizations (i.e., average estimate of realizations) [51,53], and their direct and cross-variograms would be compared with those of the original variables for both MAF and ICA. In addition, randomly selected back-transformed simulated realizations would be compared. The goal is to ensure these realizations reproduce the spatial structure and characteristics of the original variable;
- (c)
- Reproduction of the original distribution, cross-correlation, and spatial pattern:Cross-correlation between E-type of the back-transformed realizations and original variables would be compared. The reproduction of the histogram of the original variables would also be explored. In addition to the quantitative comparison above, visual inspections in the form of the reproduction of the spatial pattern of the original variable and back-transformed simulated realizations would be considered. This is to ensure consistency and to validate spatial dependency within the variables and also to guarantee the spatial relationship among the variables.
3. Results and Discussion
3.1. MAF and ICA Results
Using the “ica” package in R statistics for ICA decomposition, the W, estimated unmixing matrix, was obtained as follows:
The pre-whitening matrix, K, was obtained as follows:
Figure 7 shows the cross-correlations between the three obtained ICs. Examining the figure, it is evident that the variables were uncorrelated. As shown in Figure 7, the ICs are assumed to be non-Gaussian (but one of the ICs can be Gaussian) and mutually independent [22]. However, it was still necessary to test the spatial orthogonality of the components before simulation. This is to ensure that correlation is removed at all distances. Each component (i.e., IC1, IC2, and IC3) was simulated separately, using the SGS technique to generate 100 realizations and then back-transformed from NST to ICA space. The mixing matrix, , was used to multiply the back-transformed simulated realizations with the addition of the mean values removed during centering, bringing the simulated values into the data space.
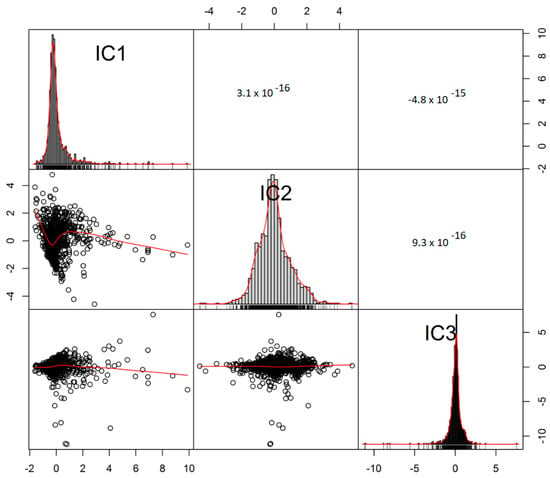
Figure 7.
Correlation matrix plot showing a lack of correlation between the independent components.
For the MAF technique, the spectral decomposition of the experimental omni-directional symmetric cross-variance matrix (h = 30 m) for the PCA factors was obtained with eigenvectors as follows:
The shift lag h = 30 m, was chosen arbitrarily since the original AfSIS datasets came from different sources, which makes the determination of sampling spacing (for h) difficult. The PCA matrix was multiplied with Q2 to obtain the MAF factors. As shown in Figure 8, the plot reveals a lack of correlation amongst the factors. The MAF factors were simulated separately. To back-transform the MAF to NST space, matrix A−1, shown below, was used to multiply the simulated realizations:
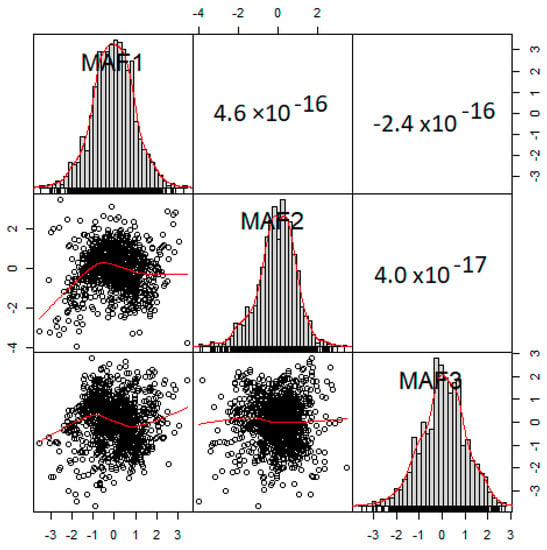
Figure 8.
Correlation matrix plot showing a lack of correlation between the minimum and maximum autocorrelation factors.
To illustrate the performance of both MAF and ICA, using the AfSIS datasets, the following verification results were considered:
- (a)
- Performance evaluation if MAF factors and ICA components are orthogonal for all lag distances, using the measure of spatial orthogonality;
- (b)
- Reproduction of both direct and cross-variograms of original SHIs, using an average of 100 back-transformed simulated realizations for both MAF and ICA;
- (c)
- Reproduction of direct and cross-variograms of original SHIs, using randomly selected back-transformed simulated realizations for both MAF and ICA; and
- (d)
- Exploration of the distribution (histogram), cross-correlation, and spatial pattern of original SHIs and back-transformed simulated realizations.
3.2. Performance Evaluation of MAF and ICA Decorrelation, Using the Spatial Orthogonality Measures
The results in Figure 9 show the measures of orthogonality for MAF and ICA. It is clear that the overall decorrelation performances of both techniques were comparable. Furthermore, between lag distances of 500 to 1500 m, it shows that ICA has better decorrelation results than MAF from both a τ(h) and k(h) standpoint. From Figure 9, the average τ(h) for all distances is 0.1 and 0.15 for ICA and MAF, respectively. Although the ideal value should be zero, the average τ(h) could be approximate to zero. In addition, the average k(h) for all distances is 0.98 for both ICA and MAF. In addition, the ideal value should be 1. This can also be approximate to 1. Based on these satisfactory metrics, it can be concluded that decorrelation was achieved by using both techniques. Therefore, both MAF and ICA can be considered independent. In other words, cross-correlations have been removed. According to Tercan [29], both MAF factors and ICA can be considered approximately spatially orthogonal.
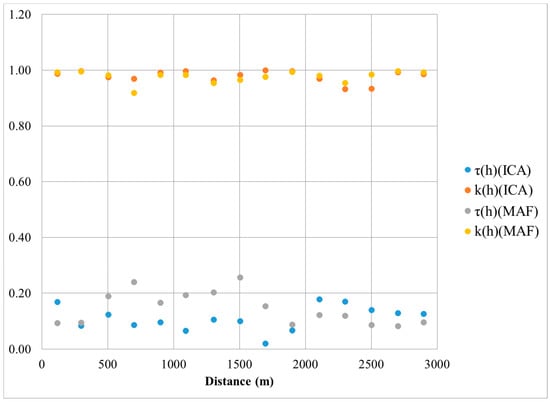
Figure 9.
Approximate spatial orthogonality for the MAF factors and ICA components. According to Tercan [29], it is ideal if τ(h) = 0 and k(h) = 1.
3.3. Reproduction of Original Direct Variograms
Figure 10 shows the plots of the direct-variograms of each SHI, using MAF (first row) and ICA (second row) for the original datasets and the conditional realizations. The red dots and solid blue line indicate experimental variogram and corresponding fitted exponential covariance function respectively. It is clear that both techniques adequately reproduced the direct-variograms of the original variables. The same exponential covariance function was fitted (blue solid line) to both the original experimental variogram (red dots) and the back-transformed simulated realizations (black solid lines).
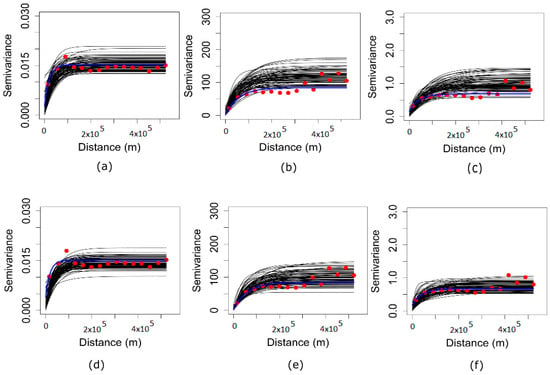
Figure 10.
Direct variograms of 100 realizations (black solid lines) for soil health indicators (SHIs), using MAF (first row) and ICA (second row) together with that of (a,d) original bulk density (g/cm3) (red dots); original organic matter (g/kg) (b,e) (red dots); original total nitrogen (g/kg) (c,f) (red dots). Solid blue line denotes the fitted exponential covariance function of original data. Semivariance is expressed in units of each SHI.
3.4. Reproduction of Direct and Cross-Variograms, Using E-Type of Simulations
To test whether both methods accurately reproduced the cross-variograms of the original variables, the average of the back-transformed realizations (E-type) was examined. The goal was to assess the level of similarity between the co-regionalization model and that of the original variables. Figure 11a shows the direct and cross-variogram of the E-type for MAF. It is clear that the direct and cross-variograms were adequately reproduced. All other spatial features of the original SHIs were correctly reproduced, despite the fact that the cross-variograms were not used in modeling. Figure 11b shows the direct and cross-variograms of the E-type, using ICA. It is evident that all spatial features of the original SHIs were captured and reproduced. Figure 11a,b agrees well with Figure 3: both show a positive correlation between Etype.OC and Etype.TN and a negative correlation between Etype.TN, Etype.OC, and Etype.BD.
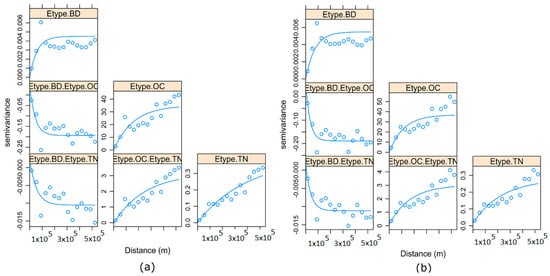
Figure 11.
Direct and cross-experimental variograms for average realizations (E-type) for (a) MAF and (b) ICA (Etype.BD = Average of 100 realizations for bulk density (g/cm3); Etype.OC = average of 100 realizations for organic carbon (g/kg); Etype.TN = average of 100 realizations for total nitrogen (g/kg). Semivariance is expressed in units of each variable.
3.5. Reproductions of Original Variograms and Cross-Variograms, Using Randomly Selected Realizations
The direct and cross-variograms of randomly selected back-transformed simulated realizations #36 (a and b) and #86 (c and d) are shown in Figure 12 with MAF and ICA in the first column and second column, respectively. As evident in both plots, both direct and cross-variograms were accurately reproduced by using the same exponential covariance function as the original dataset. In each realization, the spatial features of the original variables excluded from the modeling process were accurately reproduced. Note that only the direct variogram of the MAF factors and IC were modeled.
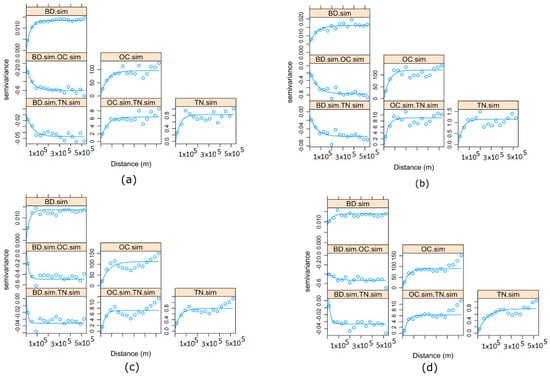
Figure 12.
Direct and cross-experimental variograms for randomly selected realizations #36 (a and b) and #86 (c and d) (a) MAF (first column) (b) ICA (second column) (BD.sim = bulk density (g/cm3); OC.sim = organic carbon (g/kg); TN.sim = total nitrogen (g/kg)). Semi-variance is expressed in units of each variable.
3.6. Reproduction of Distributions, Cross-Correlation, and Spatial Patterns of Original Variables by E-Type
The final test consists of analyzing the reproduction of the distribution, correlation and spatial pattern of the original variable. Figure 13a shows the cross-correlation and histogram of original variables and the E-type of the back-transformed realizations of MAF. Figure 13b also shows the cross-correlation and histogram of the original variables and the E-type of the back-transformed realizations of ICA. The cross-correlations between the E-type of the back-transformed realizations were correctly reproduced by using both MAF and ICA. There were improvements in the positive correlations between the variables. The positive correlation between E-type of OC and TN improved from 0.76 to 0.81 and 0.90 for MAF and ICA, respectively. Furthermore, the distributions of the back-transformed realizations were correctly reproduced for both MAF and ICA techniques.
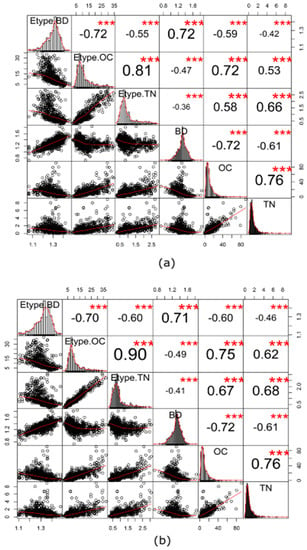
Figure 13.
Cross-correlation and histogram of the E-type of back-transformed realization and original variables for (a) MAF and (b) ICA (EType.BD = average of 100 realizations for bulk density (g/cm3); Etype.OC = average of 100 realizations for organic carbon (g/kg); Etype.TN = average of 100 realizations for total nitrogen (g/kg)). Semivariance is expressed in units of each variable, significance levels (*** p < 0.001).
Figure 14 shows the spatial pattern of the E-type of MAF (second column) and E-type of ICA (third column). For BD (first row), it is clear that there are similarities across the maps, with low values in the southern part of the country and high values in the north. This suggests that the algorithms accurately predicted and reproduced the original BD. The second row shows the original OC and E-types of MAF and ICA. There are spatial similarities between these maps as well. These similarities can be confirmed by examining the third row, which shows the maps of the original TN and E-types of MAF and ICA. The smoothening effect shown in the original maps (first column) is a characteristic of the OK method (estimation), whereas the other columns were generated from the realization of an SGS technique.
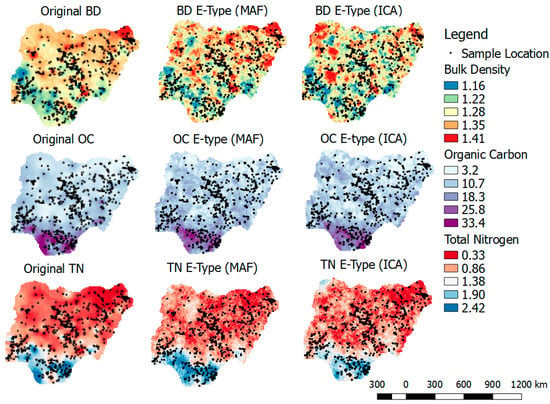
Figure 14.
Original soil health indicators and simulations of the back-transformed simulated average realizations (E-type), using MAF (second column) and ICA (third column) (BD E-type = average of 100 realizations for bulk density (g/cm3); OC E-type = average of 100 realizations for organic carbon (g/kg); TN E-type = average of 100 realizations for total nitrogen (g/kg)).
Furthermore, randomly selected realizations #36 and #86 were used to generate surfaces and compared with the original variable. In Figure 15, the first row shows the comparison of original BD and randomly selected realizations #36 and #86, respectively, using the MAF technique. As shown in the figure, there is more variability in the realization plots compared to the original variable. When compared with the E-type plots (Figure 14), Figure 15 shows greater variability. This indicates that the E-types (average of realizations) will tend to approach the mean of the original variables compared with the individual realization. This high variability effect is also observed in other variables (second and third rows) in Figure 15. Figure 16 shows a similar level of variability, using realizations #36 and #86 for the ICA technique. Comparing Figure 15 and Figure 16, it is evident that there are no marked differences, implying that using either of the two methods would produce very similar maps.
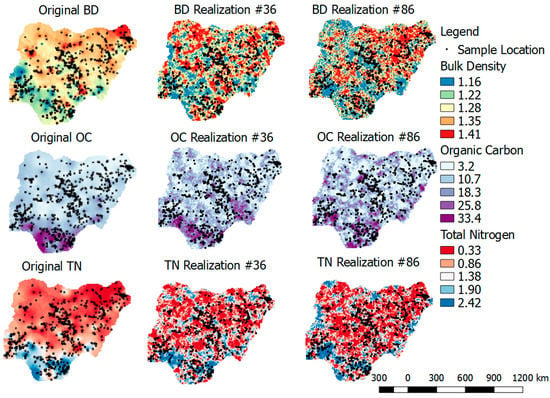
Figure 15.
Original soil health indicators and simulations of the back-transformed simulated randomly selected realizations #36 (second column) and #86 (third column), using MAF (BD = bulk density (g/cm3); OC = organic carbon (g/kg); and TN = total nitrogen (g/kg)).
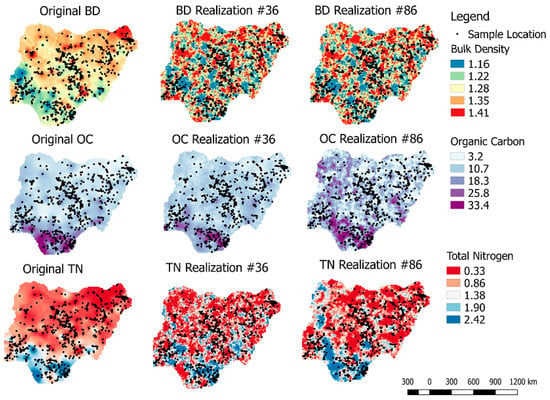
Figure 16.
Original soil health indicators and simulations of the back-transformed simulated randomly selected realizations #36 (second column) and #86 (third column), using independent component analysis (BD = bulk density (g/cm3); OC = organic carbon (g/kg); and TN = total nitrogen (g/kg)).
3.7. Importance of Uncertainty in Simulating Spatially Correlated Variables and Implications for Best Management Practices (BMP) in Sustainable Management
The results of this study are applicable in several domains. In the field of earth/environmental science, measuring and estimating the spatial variability of variables is frequently of interest. In most cases, these datasets are sparse and data can stem from several sources. Although the AfSIS dataset has been quality controlled, the current sample size for Nigeria remains disproportionate to the geographical area, posing a challenge. Indeed, there is inherent uncertainty in the spatial model prediction and bias in unsampled locations, especially when traditional methods of interpolation such as OK are applied. On the other hand, geostatistical simulation algorithms are efficient methods that can help characterize this uncertainty by generating realizations. These realizations have equal probable representations of reality. Decision making based on several probable outcomes of a phenomenon is superior to that based on a single outcome (i.e., estimation). In fact, it has been found that the impacts of soil-property uncertainty can either amplify or buffer the effects of climate change on crop yield [54]. From the perspective of best management practices (BMP) for land management, fertilizer, or organic manure management, generated realizations provide decision makers, scientists, and stakeholder greater assurance than single estimated outcomes using OK. Accurately predicted SHIs can also be useful in regulatory activities, operational practices for soil remediation and pollution control, and the preservation of terrestrial ecosystems [55].
As is the case in many developing countries, further work needs to be done in spatial data collection in Africa. AfSIS datasets comprise continental-based data, implying that local variability may still not be accounted for, meaning that current AfSIS data sample sizes for each country may not be sufficient for full spatial representation. Therefore, on a national scale, such as in Nigeria, there is a need to strengthen initiatives, programs, and policies related to soil sampling and data sharing and to raise awareness of the importance of assessing soil health. Future work should examine the accuracy of the two techniques used in this paper (MAF and ICA) by using larger sample sizes.
4. Conclusions and Recommendation
This paper presented two techniques (MAF and ICA) that have wide applications in geology or the quantification uncertainties of open mines, but few applications related to agriculture. As is the case in geological analysis, agricultural soil properties are correlated in both space and time. This is particularly true if both natural and anthropogenic factors influence the dynamics of the variables. The traditional method is to interpolate or estimate them; however, this approach has inherent limitations. Interpolation methods such as OK suffer from smoothening effects, in that they underestimate large values, while overestimating small values. In this study, both techniques provide MAF factors and IC, which can be simulated separately. Both methods were applied to the SHIs OC, BD, and TN, using Nigeria as a case study. SHIs were transformed into separate factors and components that were simulated independently, obtaining 100 realizations. The following conclusions can be drawn from this study:
- (a)
- Comparative analysis between the two methods revealed no marked differences in their performance. However, NST is necessary before MAF transformation. In the case of ICA, it was unnecessary to perform NST before transformation. In other words, NST was only used for IC while generating equally probable realizations via SGS. Therefore, IC can be used directly in other applications that do not require SGS simulation;
- (b)
- Both techniques satisfy the two criteria for spatial orthogonality suggested by Tercan (1999). These are absolute deviation from diagonality () and relative deviation from diagonality (), with ideal values of approximately 0 and 1, respectively. In other words, the MAF and ICA should be spatially orthogonal with a correlation at zero for all distances before they are used in SGS;
- (c)
- If MAF and ICA are simulated independently, both methods only require one direct variogram for each factor/component. This is in contrast to the three direct and three cross-variograms that would be needed if a traditional approach such as the model of co-regionalization was used. In other words, both MAF and ICA correctly reproduced the direct and cross-variograms of the original variables despite the variograms of MAF factors and ICA being simulated independently;
- (d)
- The back-transformed simulated variogram realizations were comparable with the original variables of each variable. Moreover, the E-type, which is the average of 100 realizations, compared well with the original variables. The cross-correlation, histograms, and spatial pattern of the back-transformed realizations, using the E-types, were correctly reproduced.
Overall, these two methods successfully de-correlated the spatially correlated variables, and only the direct variograms of the ICA and MAF factors were necessary for the simulation. Both methods reproduced the spatial structure and characteristics of the original variables, despite the fact that the cross-variograms were not used in the simulation. Decision-making based on several equally probable realizations will continue to play a key role in reducing uncertainty in soil mapping, leading to BMPs in the face of other challenges, such as climate change.
Funding
This research received no external funding.
Acknowledgments
The constructive suggestions of the editors and three anonymous reviewers are highly appreciated.
Conflicts of Interest
The author declare no conflicts of interest.
References
- Greiner, L.; Nussbaum, M.; Papritz, A.; Zimmermann, S.; Gubler, A.; Grêt-Regamey, A.; Keller, A. Uncertainty indication in soil function maps—Transparent and easy-to-use information to support sustainable use of soil resources. Soil 2018, 4, 123–139. [Google Scholar] [CrossRef]
- Bouma, J. Soil science contributions towards Sustainable Development Goals and their implementation: Linking soil functions with ecosystem services. J. Plant Nutr. Soil Sci. 2014, 177, 111–120. [Google Scholar] [CrossRef]
- Blum, W.E.H. Role of soils for satisfying global demands as defined by the U.N. Sustainable Development Goals (SDGs). In Rattan. Horn, Rainer; Takashi, K., Ed.; Schweizerbart’sche Verlagsbuchhandlung: Stuttgart, Germany, 2018. [Google Scholar]
- Boluwade, A.; Madramootoo, C.A. Modeling the Impacts of spatial heterogeneity in the castor watershed on runoff, sediment and phosphorus loss using swat: I. impacts of spatial variability of soil properties. Water Air Soil Pollut. 2013, 224, 1692. [Google Scholar] [CrossRef] [PubMed]
- Reyes, J.; Wendroth, O.; Matocha, C.; Zhu, J. Delineating site-specific Management zones and evaluating soil water temporal dynamics in a farmer’s field in Kentucky. Vadose Zone J. 2019, 18, 180143. [Google Scholar] [CrossRef]
- Schulp, C.J.E.; Burkhard, B.; Maes, J.; Van Vliet, J.; Verburg, P.H. Uncertainties in Ecosystem Service Maps: A Comparison on the European Scale. PLoS ONE 2014, 9, e109643. [Google Scholar] [CrossRef]
- Heuvelink, G.; Brown, J. Uncertain Environmental Variables in GIS. In Encyclopedia of GIS; Springer: Boston, MA, USA, 2008. [Google Scholar] [CrossRef]
- FAO. Measuring and Modelling Soil Carbon Stocks and Stock Changes in Livestock Production Systems: Guidelines for Assessment (Version 1); Livestock Environmental Assessment and Performance (LEAP) Partnership; FAO: Rome, Italy, 2019; 170p.
- Zhang, J.X.; Goodchild, M.F. Uncertainty in Geographical Information; Taylor and Francis: New York, NY, USA, 2002. [Google Scholar]
- Burrough, P.A. Multiscale sources of spatial variation in soil, the application of fractal concepts to nested levels of soil variation. J. Soil Sci. 1993, 34, 577–597. [Google Scholar] [CrossRef]
- Heuvelink, G.B.M.; Webster, R. Modelling soil variation: Past, present, and future. Geoderma 2001, 100, 269–301. [Google Scholar] [CrossRef]
- Odgers, N.P.; Mcbratney, A.B.; Minasny, B. Digital soil property mapping and uncertainty estimation using soil class probability rasters. Geoderma 2015, 238, 190–198. [Google Scholar] [CrossRef]
- Poggio, L.; Gimona, A.; Brewer, M.J. Regional scale mapping of soil properties and their uncertainty with a large number of satellite-derived covariates. Geoderma 2013, 209–210, 1–14. [Google Scholar] [CrossRef]
- Goovaerts, P. Spatial orthogonality of the principal components computed from coregionalized variables. Math. Geol. 1993, 25, 281–302. [Google Scholar] [CrossRef]
- Bivand, R.S.; Pebesma, E.J.; Gomez-Rubio, V. Applied Spatial Data Analysis with R; Springer: New York, NY, USA, 2008; pp. 251–268. [Google Scholar]
- Barnett, R.M. Sphereing and Min/Max Autocorrelation Factors. In Geostatistics Lessons; Deutsch, J.L., Ed.; 2017; Available online: http://www.geostatisticslessons.com/pdfs/sphereingmaf.pdf (accessed on 22 October 2019).
- Baharom, A.S.T.; Shibusawa, S.; Kodaira, M.; Kandac, R. Multiple-depth mapping of soil properties using a visible and near infrared real-time soil sensor for a paddy field. Eng. Agric. Environ. Food. 2015, 8, 13–17. [Google Scholar] [CrossRef]
- Yalçin, E. Cokriging and its effect on the estimation precision. J. S. Afr. Inst. Min. Metall. 2005, 105, 223–228. [Google Scholar]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Desbarats, A.J.; Dimitrakopoulos, R. Geostatistical simulation of regionalized pore-size distributions using min/max autocorrelation factors. Math. Geol. 2000, 32, 919–941. [Google Scholar] [CrossRef]
- Boluwade, A.; Madramootoo, C.A. Geostatistical independent simulation of spatially correlated soil variables. Comput. Geosci. 2015, 85, 3–15. [Google Scholar] [CrossRef]
- Dimitrakopoulos, R.; Makie, S. Joint simulation of mine spoil uncertainty for rehabilitation decision making. In geoENV VI—Geostatistics for Environmental Applications; Soares, A., Pereira, M.J., Dimitrakopoulos, R., Eds.; Springer: Dordrecht, The Netherlands, 2008; Volume 15, pp. 345–355. [Google Scholar]
- Sohrabian, B.; Tercan, A.E. Introducing minimum spatial cross-correlation kriging as a new estimation method of heavy metal contents in soils. Geoderma 2014, 226–227, 317–331. [Google Scholar] [CrossRef]
- Sohrabian, B.; Tercan, E. Multivariate geostatistical simulation by minimising spatial cross-correlation. C. R. Geosci. 2014, 346, 64–74. [Google Scholar] [CrossRef]
- Vargas-Guzman, J.A.; Dimitrakopoulos, R. Computation properties of min/max autocorrelation factors. Comput. Geosci. 2002, 29, 715–723. [Google Scholar] [CrossRef]
- Mueller, U.A.; Ferreira, J. The U-WEDGE transformation method for multivariate geostatistical simulation. Math. Geosci. 2012, 44, 427–448. [Google Scholar] [CrossRef]
- Tichavsky, P.; Yeredor, A. Fast Approximate Joint Digonalization Incorporating Weight Matrices. IEEE Trans. Signal Process. 2009, 57, 878–891. [Google Scholar] [CrossRef]
- Tercan, A.E. Importance of orthogonalization algorithm in modeling conditional distributions orthogonal transformed indicator methods. Math. Geol. 1999, 31, 155–173. [Google Scholar]
- Xie, T.; Myers, D.E.; Long, A.E. Fitting matrix-valued variogram models by simultaneous diagonalization, Part II: Application. Math. Geol. 1995, 27, 877–888. [Google Scholar] [CrossRef]
- Sohrabian, B.; Ozcelik, Y. Determination of exploitable blocks in an andesite quarry using independent component kriging. Int. J. Rock Mech. Min. Sci. 2012, 55, 71–79. [Google Scholar] [CrossRef]
- Tercan, A.; Sohrabian, B. Multivariate geostatistical simulation of coal quality data by independent components. Int. J. Coal Geol. 2013, 112, 53–66. [Google Scholar] [CrossRef]
- Africa Soil Information Service (AfSIS). Data. Available online: http://africasoils.net/services/data/ (accessed on 22 October 2019).
- Boluwade, A. Regionalization and Partitioning of Soil Health Indicators for Nigeria Using Spatially Contiguous Clustering for Economic and Social-Cultural Developments. ISPRS Int. J. Geo-Inf. 2019, 8, 458. [Google Scholar] [CrossRef]
- World Bank. Nigeria’s Booming Population Requires More and Better Jobs. Available online: https://www.worldbank.org/en/news/press-release/2016/03/15/nigerias-booming-population-requires-more-and-better-jobs (accessed on 22 October 2019).
- Rockström, J.; Falkenmark, M. Agriculture: Increase water harvesting in Africa. Nature 2015, 519, 283–285. [Google Scholar] [CrossRef]
- Voice of America, 2019. Nigeria’s Population Projected to Double by 2050. Available online: https://www.voanews.com/a/nigeria-population/4872735.html (accessed on 22 October 2019).
- FAO. Small Family Farms Country Factsheet. 2018. Available online: http://www.fao.org/3/I9930EN/i9930en.pdf (accessed on 22 October 2019).
- Leenaars, J.G.B.; van Oostrum, A.J.M.; Gonzalez, M.R. Africa Soil Profiles Database, Version 1.2. A Compilation of Georeferenced and Standardised Legacy Soil Profile Data for Sub-Saharan Africa (with Dataset); ISRIC Report 2014/01; Africa Soil Information Service (AfSIS) project and ISRIC—World Soil Information: Wageningen, The Netherlands, 2014; 162p. [Google Scholar]
- Pebesma, E. Multivariable geostatistics in S: The GSTAT package. Comput. Geosci. 2004, 30, 683–691. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Karhunen, J.; Oja, E. Independent Component Analysis; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Helwig, N.E. ica: Independent Component Analysis. R Package Version 1.0-2. 2018. Available online: https://CRAN.R-project.org/package=ica (accessed on 22 October 2019).
- Hyvärinen, A.; Oja, E. Independent component analysis: Algorithms and applications. Neural Netw. 2000, 13, 411–430. [Google Scholar] [CrossRef]
- Switzer, P.; Andrew, G. Min/Max Autocorrelation Factors for Multivariate Spatial Imagery: Technical Report 6; Department of Statistics, Stanford University: Stanford, CA, USA, 1984. [Google Scholar]
- Rondon, O. Teaching aid: Minimum/maximum autocorrelation factors for joint simulation of attributes. Math. Geosci. 2012, 44, 469–504. [Google Scholar] [CrossRef]
- Boucher, A.; Dimitrakopoulos, R.; Vargas-Guzmán, J.A. Joint simulations, optimal drillhole spacing and the role of the stockpile. In Quantitative Geology and Geostatistics, Geostatisitcs Banff 2004; Leuangthong, O., Deutsch, C.V., Eds.; Springer: Dordrecht, The Netherlands, 2005; Volume 14, pp. 35–44. [Google Scholar]
- Bandarian, E.M.; Bloom, L.M.; Mueller, U.A. Direct minimum/maximum autocorrelation factors for multivariate simulation. Comput. Geosci. 2008, 34, 190–200. [Google Scholar] [CrossRef]
- Woillez, M.; Rivoirard, J.; Pierre, P. Using min/max autocorrelation factors of survey-based indicators to follow the evolution of fish stocks in time. Aquat. Living Resour. 2009, 22, 193–200. [Google Scholar] [CrossRef]
- Elogne, S.; Leuangthong, O. Implementation of the Min/Max Autocorrelation Factors and Application to a Real Data Example. 2008. Available online: http://www.ccgalberta.com/ccgresources/report10/2008-406_maf.pdf. (accessed on 26 October 2019).
- Haugen, M.A.; Rajaratnam, B.; Switzer, P. Extracting Common Time Trends from Concurrent Time Series: Maximum Autocorrelation Factors with Application to Tree Ring Time Series Data. arxiv 2015, arXiv:1502.01073v3. [Google Scholar]
- Goovaerts, P. Geostatistical Modelling of Uncertainty in Soil Science. Geoderma 2001, 103, 3–26. [Google Scholar] [CrossRef]
- Mueller, U. Spatial decorrelation methods: Beyond MAF and PCA. In Proceedings of the Ninth International Geostatistics Congress, Oslo, Norway, 11–15 June 2012. [Google Scholar]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Folberth, C.; Skalský, R.; Moltchanova, E.; Balkovič, J.; Azevedo, L.B.; Michael Obersteiner, M.; van der Velde, M. Uncertainty in soil data can outweigh climate impact signals in global crop yield simulations. Nat. Commun. 2016, 7, 11872. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (USEPA). Best Management Practices (BMPs) for Soils Treatment Technologies. Suggested Operational Guidelines to Prevent CrossMedia Transfer of Contaminants During Cleanup Activities. Available online: https://www.epa.gov/sites/production/files/2016-01/documents/bmpfin.pdf (accessed on 26 October 2019).
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).