1. Introduction
In a relatively short span of time, the field of Geographic Information Systems (GIS) went from data wanton to data galore. The proliferation of Earth Observation programmes, coupled with the rising trend towards Open Data, has made a wealth of high quality, high resolution, globally covering data available to researchers and spatial data analysts. The sheer volume of data has become a challenge in itself. Today, data users must carefully consider storage and, more importantly, computation costs.
In the particular case of global rasters, analysts of big spatial data are often confronted with datasets provided in awkward map projections, that greatly increase demands on storage and computation.
Table 1 compares the areas of the co-domain and land masses of various projections computed with
GRASS [
1]. These areas equate to the number of cells in a global raster with a cell side of 1 km. The Marinus of Tyre and Mercator projections, even though arguably the most popular projections in Earth Sciences today, impose massive overheads in storage space and computation time with the number of extra raster cells they require to discretise the surface of the globe. In order to minimise the size of the datasets and render them spatially representative of the surface of the Earth, big spatial data researchers often undertake as first task a re-projection with an equal-area projection.
The re-projection to an equal-area projection reduces the number of cells in the raster, which in theory leads to a loss of information (or spatial resolution). However, the raw datasets from which global data products are developed are primarily collected in the geodesic domain and therefore not subject to distortion. For example, the Moderate Resolution Imaging Spectrometer (MODIS) space-borne sensor managed by NASA collects images of the Earth in its bands 1 and 2 with cells of approximately 250 m in side ( ha). Some of the products developed from this sensor are published in the Marinus of Tyre projection with a cell side of 8 arc-seconds, meaning that at a latitude of their area is down to ha. At that latitude half of the cells in such raster are either interpolated or replicated from the raw data.
If the need to store and compute datasets in an equal-area projection is obvious to big spatial data analysts, exactly how to do it may not be simple. In first place, the number of equal area projections supported by FOSS4G is rather limited, more so when solely considering those applicable globally. Since the late XX century, modern methods have been introduced, resulting in equal-area projections that address distance and angular distortions simultaneously [
2]. However, these modern equal-projections do not find full support among the core FOSS4G libraries:
geographiclib [
3],
PROJ [
4] and
GDAL [
5]. Moreover, distortions that may result from the algorithmic implementations in these programmes are not simple to assess. Therefore, the choice of map projection in a big spatial data context supported by FOSS4G may not be straightforward.
There are few studies in the literature reporting software based comparisons of map projections, especially when considering the global scale. The study conducted by Seong et al. [
6] is possibly the closest to address this question. However, these authors were primarily concerned with the loss and replication of cell values in categorical rasters when re-projected. These authors assessed four popular equal-area projections, that are common to this study: Sinusoidal, Mollweide, Eckert IV and Hammer. For their purposes, Seong et al. concluded that the Sinusoidal is the most performant. Two important caveats in this study should be taken into account: (i) the Gauss-Krüger projection was used as reference, not the geodetical domain, and (ii) the comparison was conducted within 52 small areas of 3 by 3 km spread randomly around the globe. This study can not be considered exhaustive and it is possible results would have been different had it been conducted globally. A final aspect: Seong et al. exclusively employed commercial software in their work.
Capek [
7] evaluated an assortment of one hundred global projections using a benchmark composed by ratios of areal, angular and distance distortions, restricted to pre-set maxima. For each projection assessed, only the areas within which distortions remained below the pre-set maxima were used in the assessment. Setting this maxima implied that for each projection the area contributing to the comparison was different. Capek did not assess the performance of interrupted projections, like the Homolosine or the Eumorphic and also left out projections based on polyhedra, such as the Dymaxion or the equal-area projections developed by Snyder. Within equal-area projections Capek rated the Hufnagel X, developed in 1989, as the most performant. Such projection remains rare and is not supported by FOSS4G. Capek conducted his study using both computer and cartometric processing (depending on the projection). In some cases relevant differences are observed between the two computations.
Mulcahy and Clarke [
8] reported a series of ten different methods used to portray distortions in map projections. Most of the methods inventoried are merely visual and may not be used in analytic comparisons. A distinct exception is Tissot’s indicatrix which allows for analytic assessment and is visually expressive too. A few other methods beyond Tissot’s indicatrix also allow both but their nature is similar, based on geometric structures. These authors further note that Tissot’s indicatrix is most often used in discrete form and not as the infinitesimal ellipse originally proposed by Tissot.
This study addresses the question of selecting an appropriate equal-area projection supported by FOSS4G to optimise the storage and processing of big spatial data. The goal was to exhaustively measure angular and distance distortions across the globe for a series of candidate projections. These distortions were assessed within a regular positioning framework, so that each area of the globe could have the same importance in the assessment. Considering that some global data only concern land, as is the case with soils or demographics, distortions over land masses were also assessed independently.
This article reports the process and results of this study. Materials and methods are laid out in
Section 2, with results presented in
Section 3.
Section 4 reflects on these results and
Section 5 closes with conclusions and future research directions.
2. Materials and Methods
2.1. Selected Projections
In previous work FOSS4G support was assessed for a series of equal-area projections [
9]. In that earlier study support was defined as full implementation by FOSS4G sanctioned by the OSGeo Foundation, in particular the
PROJ and
GDAL libraries, plus the correct display of raster layers in cartography programmes (e.g.,
QGis [
10],
gvSIG [
11]). In general, the newer the projection the less likely it is to be supported. The pseudo-cylindrical projections developed around the turn of the XX century, like the series proposed by Eckert [
12], are supported but many other relevant projections developed later, like the Eumorphic [
13] or the polyhedral proposed by Snyder [
2], are not implemented by any of the OSGeo sanctioned programmes.
Besides the somewhat popular Eckert IV, the only other relevant projection from the XX century supported by FOSS4G is the Homolosine, proposed by Goode [
14]. Another relevant projection found to be fully usable is the one proposed by Hammer [
15], which was developed in an attempt to address the extreme distortions at the edges of elliptical equal-area projections. Beyond these were also considered the centenary Sinusoidal projection (in use since at least the XVI century [
16]) and the original elliptical projection developed by Mollweide at the beginning of the XIX century [
16] and still popular today. The set of projections assessed in this study was thus defined as: Sinusoidal, Mollweide, Hammer, Eckert IV and Homolosine.
Table 2 presents the corresponding
PROJ strings. Other equal-area projections are supported by FOSS4G but do not present enough unique characteristics to set them markedly apart from the quintet analysed. The list of projections supported by
PROJ can be accessed at
https://proj.org/operations/projections/index.html (note that many of these are not supported by
GDAL and/or
GeoTools). Possibly avoiding mathematical complexity (and computation burden), software developers have favoured projections in the vein of those proposed around the turn of the XX century, with a single interruption and approachable formulations.
2.2. Discrete Indicatrices
The indicatrix proposed by Tissot [
17] is a popular and effective method of depicting the distortions induced by a map projection. It features extensively in reference educational and technical textbooks [
8,
18]. The indicatrix is itself a simple object: an infinitesimal shape defined on the surface of the sphere or the ellipsoid. Usually, a series of indicatrices are positioned at regular intervals of latitude and longitude and are then projected onto the plane with different projections for visual comparison. Once projected, the shape, area and perimeter of the indicatrix changes. In conformal projections, Tissot’s indicatrices appear as circles, in pseudo-cylindrical equal-area projections they tend to acquire an elliptic shape.
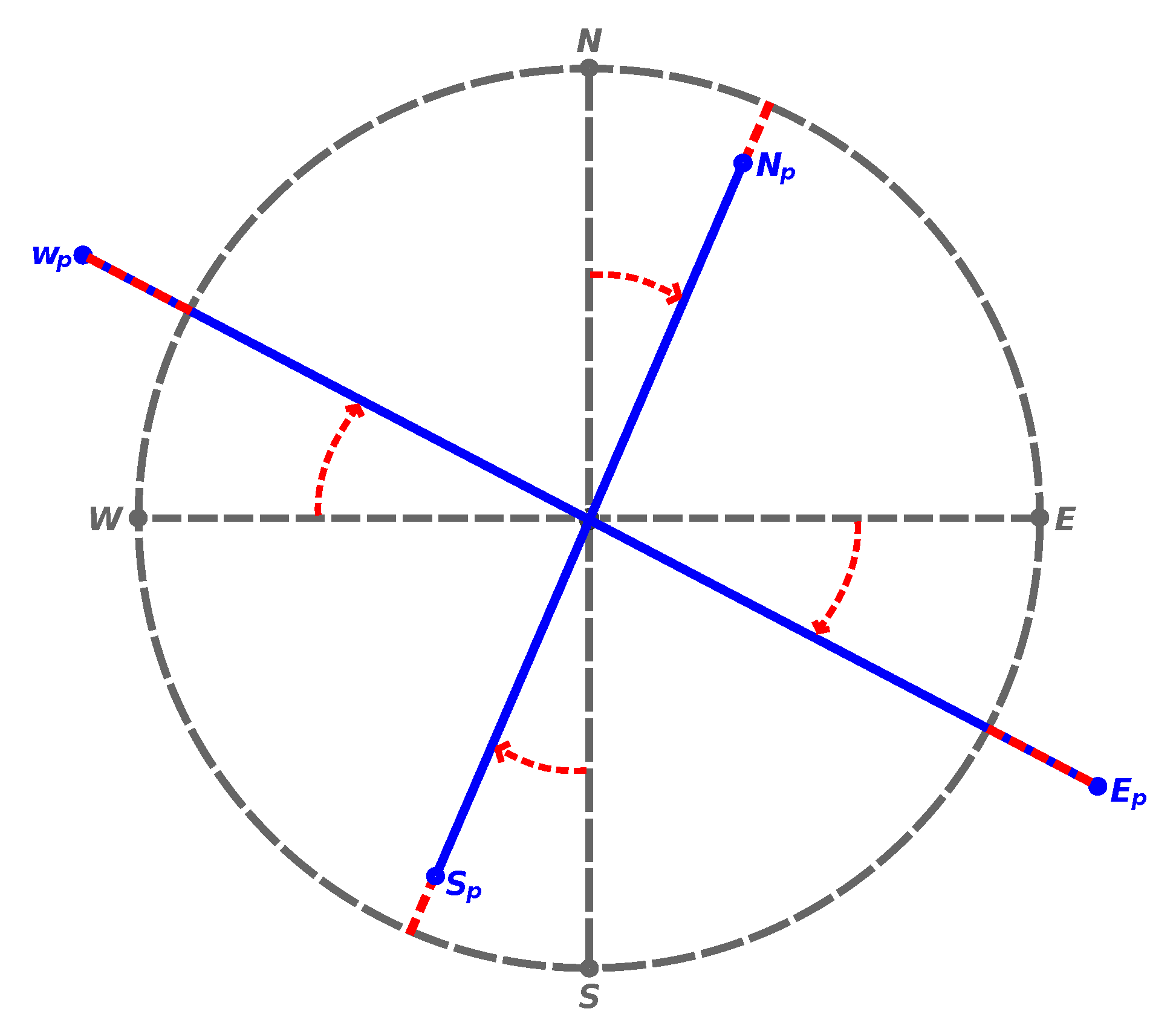
In this study discrete constructions inspired on Tissot’s indicatrix are used to compute distortion. Each discrete indicatrix is defined in the Geodetic domain as a shape of 1 km radius around a central point. From the central point of the indicatrix a set of four stems is developed, aligned with the four cardinal directions. Each of the four stems is 1 km long, being in fact a geodesic line (or loxodrome). This construction provides a discrete measure of distortion (i.e., non-analytic), than can thus be computed directly with common FOSS4G.
The geodesics composing the discrete indicatrices used in this study were computed with the geographiclib library, a cornerstone of FOSS4G, underlying many important packages (like PROJ). To compute a geodesic, geographiclib takes as inputs: (i) the coordinates of a starting point, (ii) an azimuth and (iii) a distance. The coordinates of the end point of the geodesic are the output. This computation is also referred to as the direct geodesic. For each indicatrix four geodesics are thus computed, all with the same starting point (the centre) and distance (1000 m) but with four different azimuths: , , and .
2.3. Discrete Global Grid
The positioning of the indicatrices used in this study is a crucial aspect to provide a balanced comparison of the five projections under analysis. It deals with two essential requirements: (i) guaranteeing that the comparison is not restricted to a single region of the globe and (ii) ensuring that every region of the globe (and of the projection co-domain) has a similar weight in the comparison. A comparison carried on a restricted region of the globe ignores the necessary spatial variation of deformations within the projection co-domain. In global cartograms, distortion indicatrices are often presented at regular intervals of latitude and longitude. This practice lends more weight to the indicatrices closer to the poles. In order to avoid such biases, distortions must be assessed across the entire geographic domain, or alternatively, following a regular discrete tessellation of the ellipsoid.
The indicatrices used in this study were positioned on the globe according to an hexagonal discrete global grid developed from the Snyder’s icosahedral equal-projection. This kind of grid is commonly known as Icosahedral Snyder Equal-Area Grid (ISEAG) [
19]. A discrete distortion indicatrix was positioned at the centre of each cell in this grid.
The software package
dggridR [
20] for the R programming language was used to create the ISEAG. This package wraps the ISEAG creation functions originally developed by Sahr in the C language. The grid was created with an aperture number of 3 and a resolution of 7, resulting in a cell area of 23 322 km
. This translated into a total of 21,872 indicatrices positioned at an average distance of 165 km from their immediate neighbours.
2.4. Computation of Distortions
The discrete indicatrices described above were thus projected onto the plane with each of the five projections selected. Angular and distance distortions where computed as follows. The length of each indicatrix stem was computed and subtracted from the original 1000 m. The angles between the stems aligned with the North and South directions where obtained with Equation (
1), whereas for the East and West directions Equation (
2) was used. In these equations
are the cartographic coordinates of the stem end point and
are the coordinates of the indicatrix centre.
For each indicatrix four different angular distortions and four different distance distortions were obtained.
Figure 1 summarises these computations visually.
3. Results
The distortion computation methods described above were implemented by a computer programme coded mostly in the Python language (R was used to interact with the
dggridR library). The Python implementation of the
geographiclib library greatly simplifies its use. The resulting programme is available at Codeberg (
https://codeberg.org/ldesousa/projections-compare) under an open source licence.
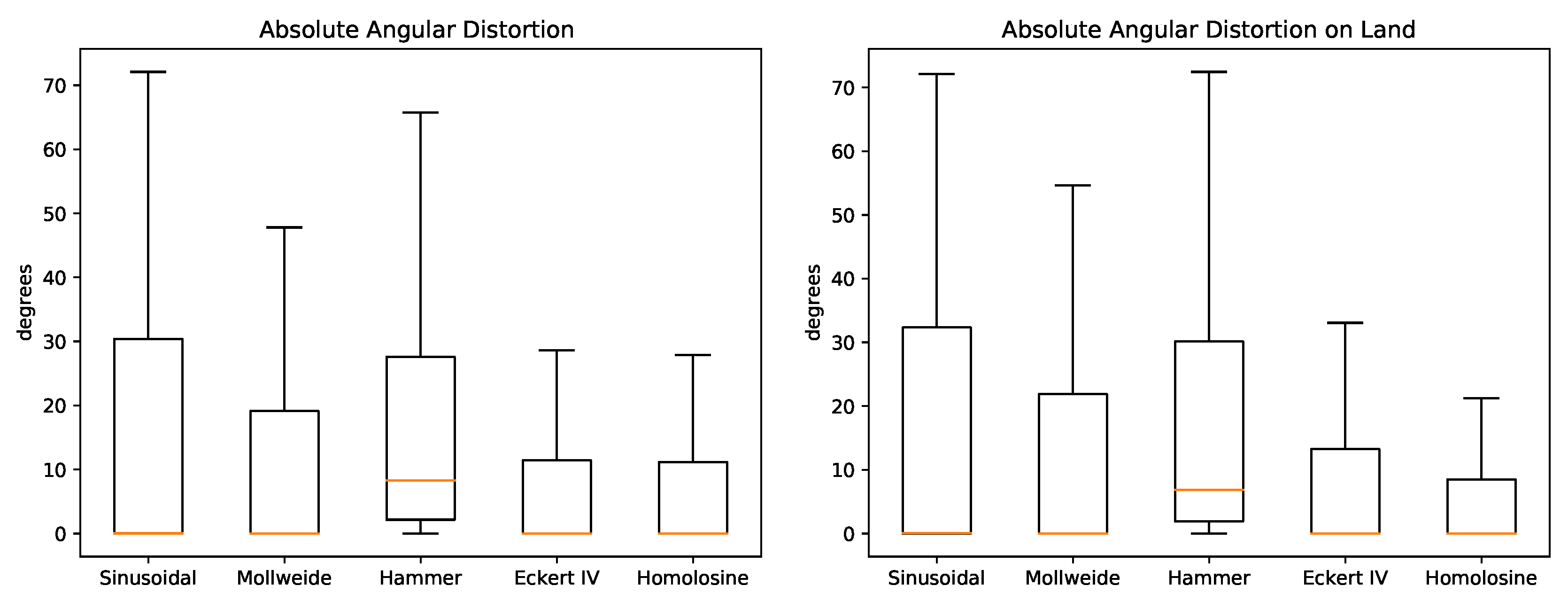
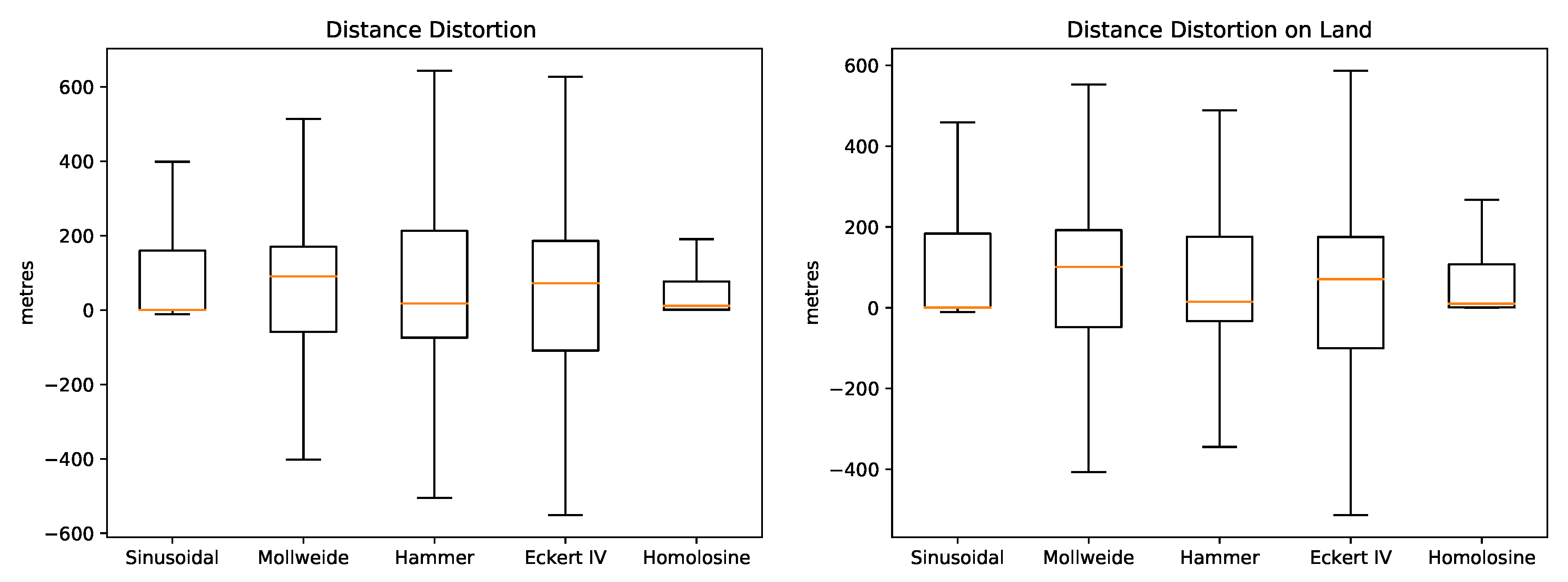
Figure 2 show boxplots of the absolute angular distortions for the five projections. Essential statistics for these distortion distributions are found in
Table 3. The wide difference between the familiar RMSE and MAE metrics is due to a relevant number of outliers with high distortions (essentially the edges of the projection co-domain). Apart from the Hammer projection, all projections yield a mean angular distortion close to zero but between them the distribution is varied. The Homolosine and Eckert IV show the narrowest distributions, which reflects on the lowest mean absolute distortions. Concerning land masses alone, the distributions are somewhat similar to the global but in this case the Homolosine stands out more clearly with the lowest mean and tightest distribution.
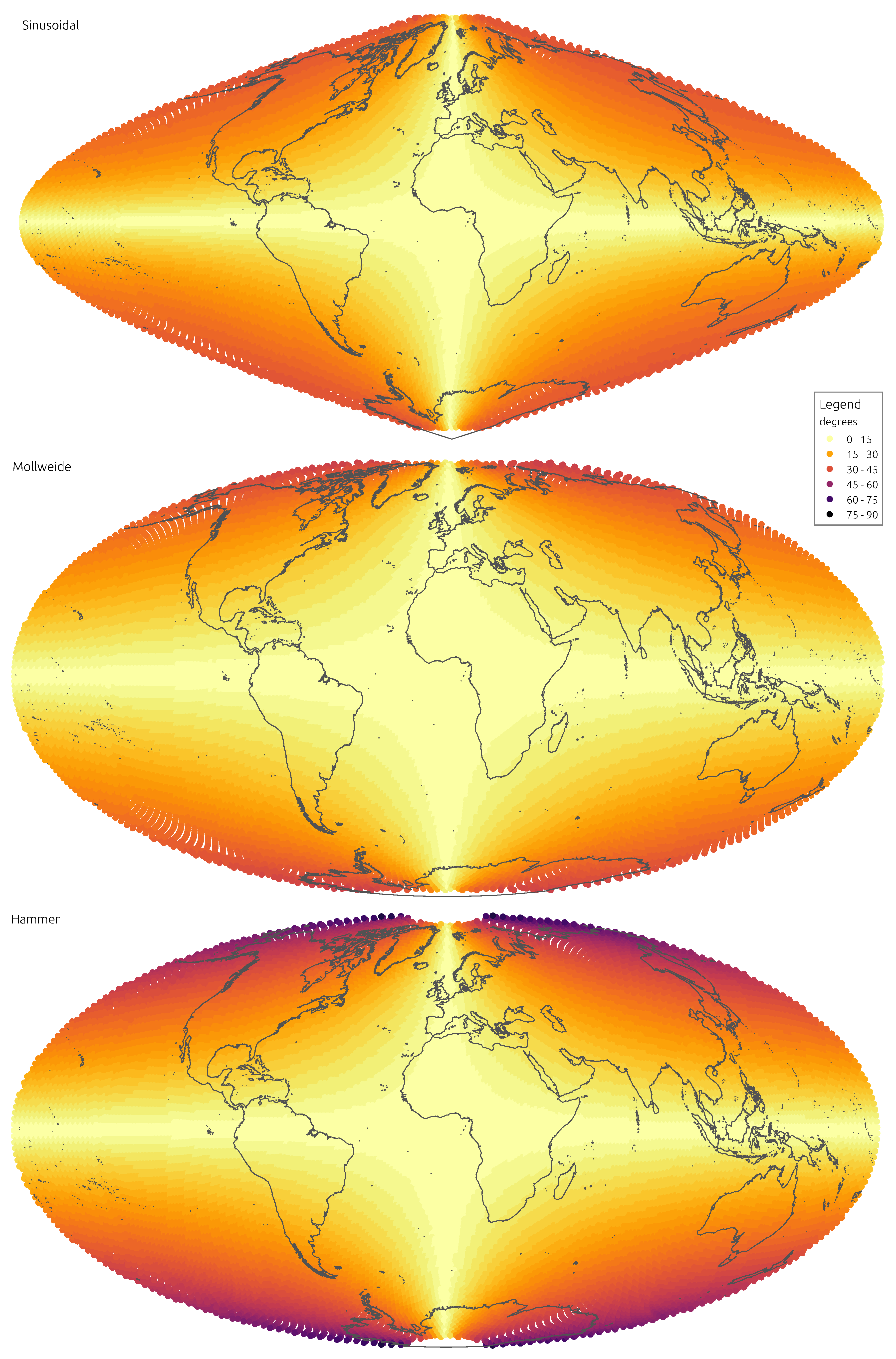
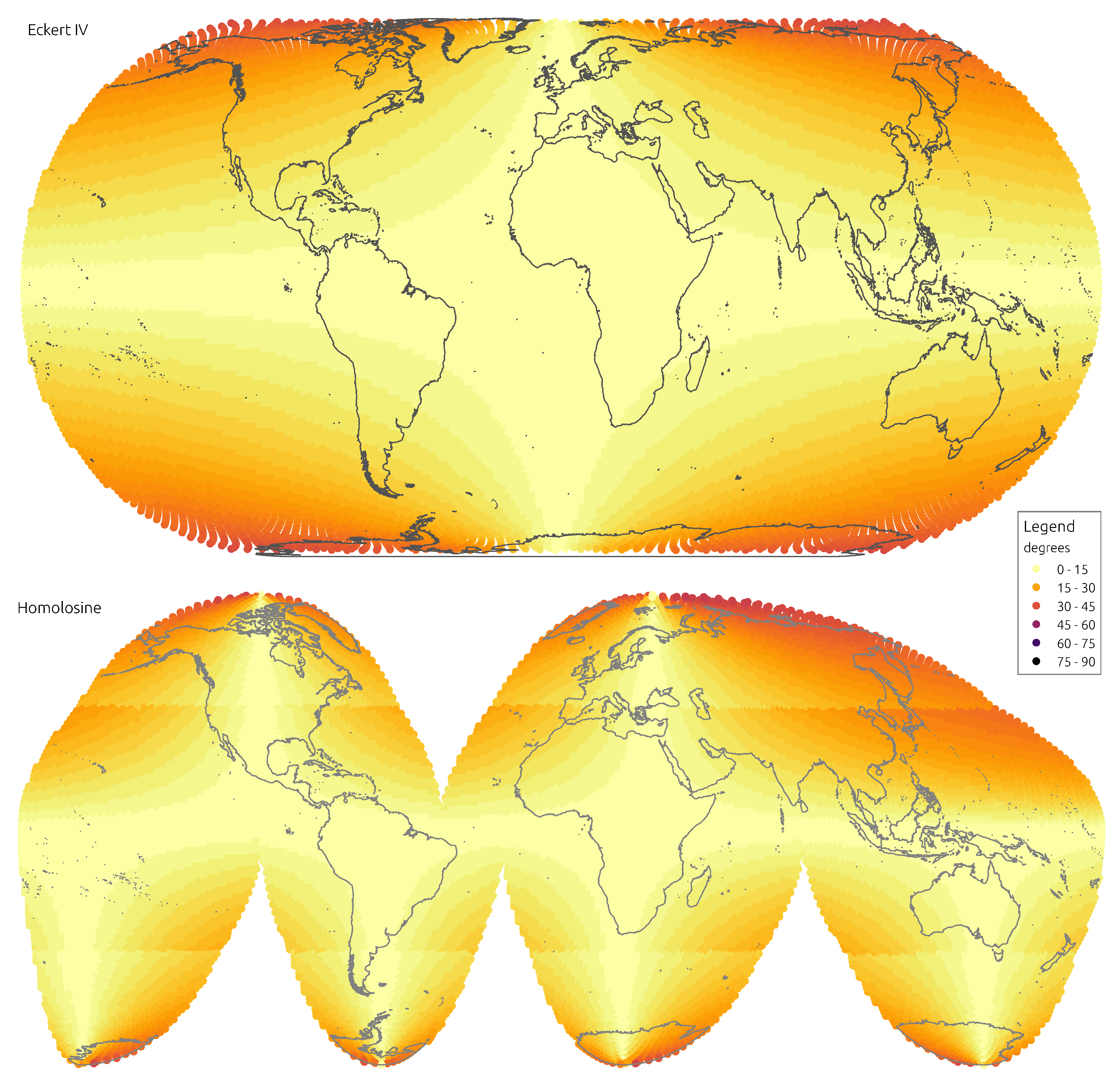
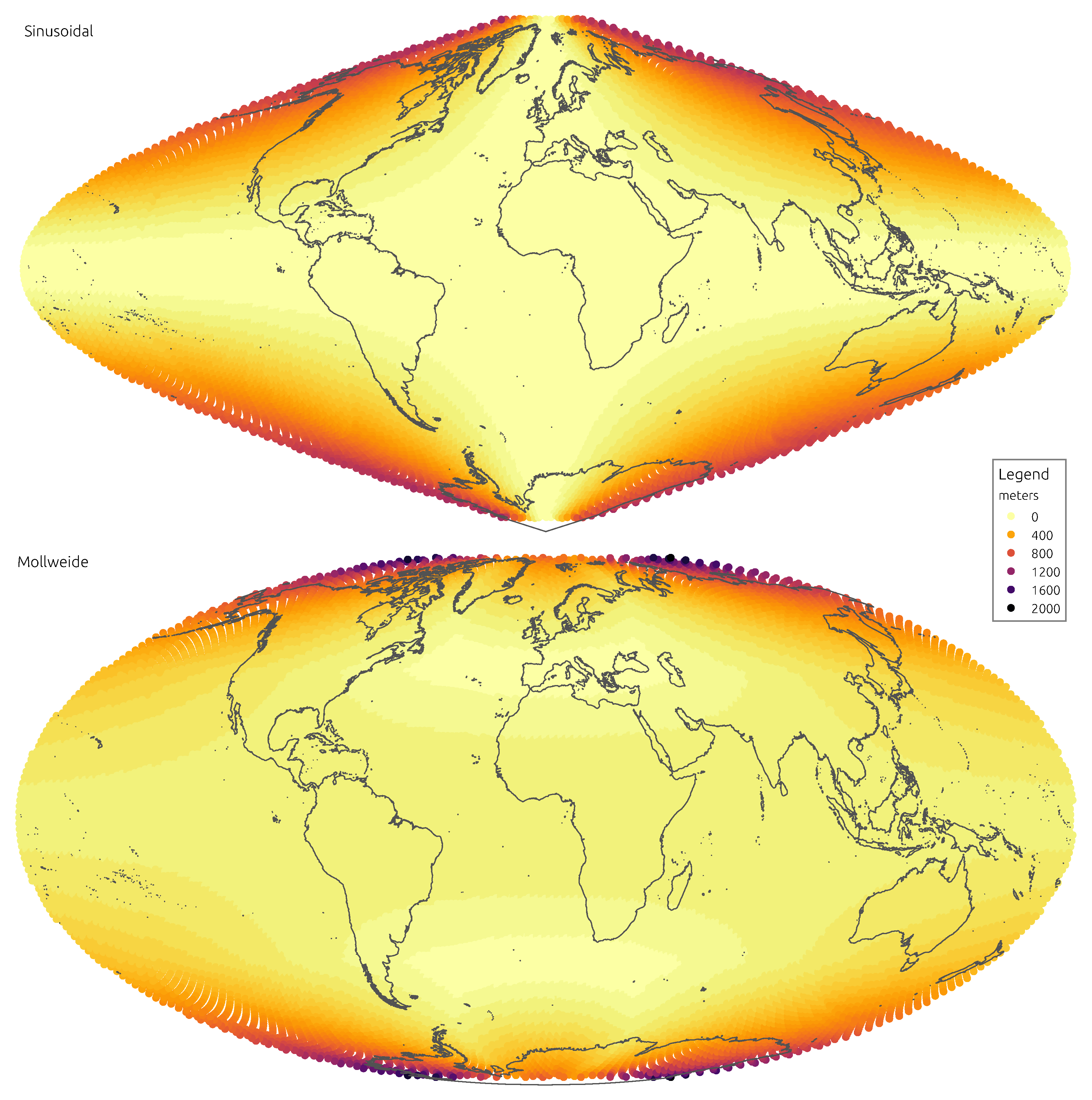
Figure 3 and
Figure 4 convey the spatial distribution of angular distortion, showing mean absolute distortion at the location of each discrete indicatrix.
Figure 5 and
Table 4 summarise distance distortions distributions. The rank is somewhat different for distances, with the Sinusoidal alone yielding a median close to zero. However, the narrowest distribution is the one obtained with the Homolosine, which also results in the lowest mean distortion. The distributions of distance distortions restricted to land masses are almost the same. But in this case the Homolosine yields distinctively the lowest mean and upper quantiles.
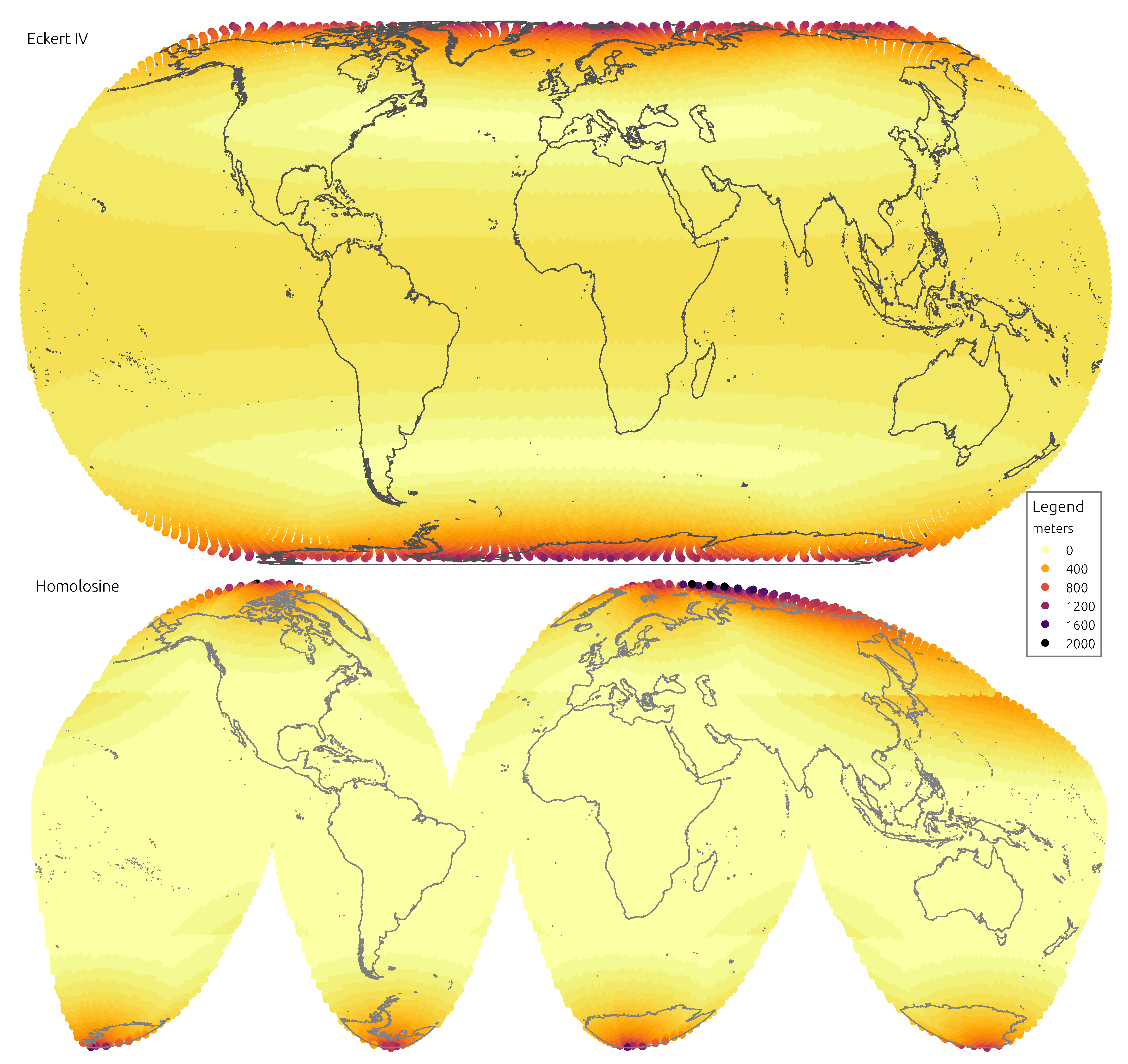
Figure 6 and
Figure 7 display the spatial distribution of mean absolute distance distortions.
4. Discussion
4.1. Projection Performance
The Sinusoidal projection performs rather well in preserving distances, unsurprisingly, since it is equidistant along parallels. As to angles, it is clearly the worst, with the second highest mean distortion and the highest quantiles. When considering land masses alone, the Sinusoidal retains the poor performance on angles and loses some of the advantage on distances. A marked characteristic of this projection is the uneven spatial distribution of distortions, as they gradually impose with distance from the central point. Land masses like Alaska, Japan or New Zealand are deeply affected, whereas much of Africa and Europe are almost untouched. If the Sinusoidal had an important role in the Cartography of times passed, it comes out as a largely outdated projection in the age of micro-processors.
Even though one of the oldest projections in analysis, the Mollweide performs relatively well. It clearly improves over the Sinusoidal on angles, appearing in the middle of the rank but without imposing too much of a penalty on distances. Distance distortions are ameliorated in land, where the Mollweide appears in the middle of the rank. This is also reflected in the spatial distribution of distortions, which are more relegated to higher latitudes. The Mollweide projection is a classical example of a compromise equal-area formulation, that retains its relevance today. It is still a projection to consider when conveying global data in which both angular and distance accuracy are relevant.
The Hammer projection is unique among those analysed, with distinctive distortions distributions, however, the results it yields are some of the worst. It clearly ranks last in angular distortion but it fails to balance that with a higher performance on distances. The comparison with the ancient Sinusoidal is particularly penalising, the Hammer projection always presents worse distortions. Spatial patterns of distortion are similar to those of the Sinusoidal, with marked differences across continents and oceans. Already when it was first proposed this projection was not among the most performant, it is therefore difficult to justify its use today.
The Eckert IV projection is the most complex to analyse. At face value it appears as a compromise projection, trading angular accuracy for distance distortion, the exact opposite of the Sinusoidal. This is patent in mean distortions, the Eckert IV is close to the Homolosine on angles but is the worst on distances. However, when the analysis is restricted to land masses, distance distortions are less evident and close to those of the Hammer and Mollweide projections. The trade off proposed by the Eckert IV projection is better illustrated by the spatial distribution of distortions. The distortions remain constant across oceans and land, with a sharp increase north of and south of . The Eckert IV is perhaps the best replacement for the Homolosine when interruptions may not be so convenient, for instance to work with oceanic or geological data.
The Homolosine shows the best results when considering both the mean or the quantiles of distortions. It is similar to the Sinusoidal for distances and better than EckertIV for angles. When restricting the analysis to land, the advantage of the Homolosine is even more evident, with lower distortions for all measures. The spatial distribution of distortions is also the most even across the five continents, with the largest distortions well consigned to higher latitudes. The main weakness is its focus on land masses, achieved with four more interruptions than the traditional single interruption at E. When working with data covering oceans, for instance, the Homolosine may not be the most appropriate. Especially when computations relying on cell neighbourhood are involved, the additional interruptions imposed by the Homolosine may not be tolerable at all. However, in most cases it is difficult not to select it as the most relevant and performing projection to work with global data on FOSS4G.
Finally, it is important to consider that the projection used at computation time in a big spatial data context may not necessarily match the projection(s) used to present or serve the end result. For instance, a global raster computed on the Homolosine projection may be served through a WCS supporting various projections, even non-equal formulations. Such strategy may be applied when interruptions are deemed applicable to computation but not desirable when presenting results (e.g., to overlay with datasets from other sources).
4.2. Difficulties with FOSS4G
Whereas it was possible to complete this study with FOSS4G, the use of the Homolosine projection is not entirely straightforward. For instance,
GDAL supports the projection but the correct application of its inverse requires explicit parametrisation (
https://github.com/OSGeo/gdal/issues/959). Since programmes using
GDAL are not aware of this parametrisation, they generally apply the projection incorrectly in re-projections between different coordinate systems. Therefore any re-projections to and from a coordinate system including the Homolosine projection must always be carried out directly with
GDAL.
Cartography FOSS4G programmes (commonly known as “desktop”) present a further obstacle, since they ignore that the co-domain of a map projection is finite in most cases. Therefore, programmes like
QGis or
gvSIG portray vector objects spanning over areas that do not have correspondence on the surface of the ellipsoid. To address this problem, a discrete co-domain in vector form was developed that can be used to clean cartograms in such programmes [
21].
A particular issue was identified concerning the Sinusoidal projection: the areas of polygons computed in this projection are somewhat different from those obtained with the other projections.
Table 5 shows the differences between the Homolosine and the other four projections for the areas of five large countries (computed with
QGis). The Sinusoidal is markedly off, even if the difference is little more than 0.3% of the total area of the geometry. The exact cause has not been identified so far, but this is another reason to avoid using the Sinusoidal projection.
A further problem that affects not only the Homolosine but equal-area projections in general, is the absence of a coordinate system code issued by the European Petroleum Survey Group (EPSG). Programmes like
MapServer [
22], for instance, do not admit any coordinate system that is not indexed by the EPSG. Even if this issue can be partially addressed by introducing “fake” ESPG codes into the
PROJ database, this dependence by OSGeo sanctioned software on the Petroleum industry is something to reflect upon.
Certain hurdles have not yet been overcome, since some programmes simply do not support the Homolosine projection. This is the case with
GeoTools [
23], for instance. And as it relies on
GeoTools, the popular cloud computing platform Google Earth Engine [
24] does not allow the retrieval or computation of datasets in the Homolosine projection.
These remaining issues with FOSS4G are important—but not impairing—and can certainly be resolved; a reminder that FOSS4G requires continuous investment and nurturing.
5. Conclusions and Future Work
This study clearly indicates the Homolosine as the most performant of the equal-area projections analysed. Its interruptions minimise both angular and distance distortions in a way that finds no parallel. To support data primarily related to land masses, the Homolosine is on a league of its own. The International Soil Reference and Information Centre (ISRIC) has recently adopted the Homolosine projection in consequence of these results. In doing so, ISRIC was able to reduce in more than 40% the average computation time required by its global soil mapping framework. In tandem, the size of its global raster maps, produced with a cell side of 250 m, was reduced in more than 1 billion cells. This reduction allowed access to statistics methods that heretofore had not been in reach. The Homolosine projection is also opening the opportunity for ISRIC to further increase the spatial resolution of its reference products.
In general, the results obtained divide the projections considered in two groups: those that maintain relevance today and those that only retain historical interest. Together with the Homolosine, the Mollweide and the Eckert IV projections are worth considering to support global data, all depending on the compromise to strike between accuracy and interruptions. As for the Sinusoidal and Hammer projections, they yield too large and uneven distortions to justify their use in modern times.
The results from this study make clear the advantages of interruptions in equal-area projections: they allow to tackle angular and distance distortions simultaneously. It would therefore be useful to expand support in FOSS4G to other interrupted projections such as the Eumorphic or Snyder’s formulations based on the icosahedron and the dodecahedron. Nevertheless, interruptions are not a panacea, they may appear awkward representing a surface that is in fact continuous and, more importantly, may not be suitable to all kinds of analyses or computations. But regarding data portrayal, researchers and data analysts need not to present results on the same projection used to store and analyse data. Simple re-projections (without datum shift) are competently supported by FOSS4G.
Various of the projections assessed attempt to minimise distortion on land masses and all yield high distortions in the polar regions. In some cases, like the Homolosine and the Eckert IV, this is intentional. In this study the intersection of the equator with the Greenwhich meridian was used as the central point of projection. It is therefore worth asking whether this point is optimal. A further study could focus on this question, particularly relevant for the single interruption projections.
Finally, it is useful to consider cartography beyond planet Earth. Projections like the Homolosine or the Eumorphic include ad hoc interruptions aligned with the oceans and continents of Earth. As increasingly more data is collected in other planets of the solar system, it is relevant to revisit this kind of projections and develop interruptions that may apply more universally.