Abstract
The cultural heritage of a region, be it a highly visited one or not, is a formidable asset for the promotion of its tourism. In many places around the world, an important part of this cultural heritage has been catalogued by initiatives backed by governments and organisations. However, as of today, most of this data has been mostly unknown, or of difficult access, to the general public. In this paper, we present research that aims to leverage this data to promote tourism. Our first field of application focuses on the French Pyrenees. In order to achieve our goal, we worked on two fronts: (i) the ability to export this data from their original databases and data models to well-known open data platforms; and (ii) the proposition of an open-source algorithm and framework capable of recommending a sequence of cultural heritage points of interests (POIs) to be visited by tourists. This itinerary recommendation approach is original in many aspects: it not only considers the user preferences and popularity of POIs, but it also integrates different contextual information about the user as well as the relevance of specific sequences of POIs (strong links between POIs). The ability to export the cultural heritage data as open data and to recommend sequences of POIs are being integrated in a first prototype.
1. Introduction
Cultural heritage, such as architecture, handcrafts, and traditions, has been increasingly catalogued in many regions around the world. However, as of now, this rich data has been accessed almost exclusively by experts (e.g., historians, geographers, anthropologists). In this paper, we propose an approach to leverage this data for the promotion of tourism in a specific region. We use the region of the French Pyrenees as a case study. However, our proposals are intended to be suitable for any other region of the world.
During the 18th and 19th centuries, dreams of nature and new experiences gave start to a thriving tourism industry in the region of the Pyrenees. Many tourists would come for leisure and enjoyment, but others would also seek healing and therapies. These mountains suddenly experienced a surge in general public interest and therefore attracted an ever-growing number of western visitors. In the wake of this growth, different hotels, resorts and other building were erected to host these people in the exotic nature of the Pyrenees, known for its hot springs, mild weather, interesting local culture, and in the 20th century for its snow and white-water rivers too. These important activities greatly enriched the tangible cultural heritage (architecture, furniture, etc.) in the Pyrenees and also the intangible part of it (traditions, social events, cuisine, etc.)
As of today, an important part of this inheritance has been catalogued and registered in several different databases across the south-west of France, but not all of it. We take part in a multidisciplinary European Project (FEDER TCVPyr) that aims to create a comprehensive catalogue of this cultural heritage related to tourism in the French Pyrenees. This catalogue is yet to be finished, but at the end a database containing all of the most important points of interest (POIs) georeferenced for tourists in the region should be available. Examples of POIs include natural hot springs, casinos, hotels, villas, winter sport stations, other natural wonders, and even cultural events and traditions related to specific locations. In fact, this data has an enormous potential to be used not only by tourists, but also by experts (e.g., historians and anthropologists), tourism providers, and the general public (tourists, local population, etc.)
In this context, we present two main contributions related to leveraging this cultural heritage data: (i) an open-source framework capable of exporting cultural heritage from our database to well-known open data providers such as Wikipedia and OpenStreetMap; and (ii) an open-source algorithm and framework capable of recommending a sequence of cultural heritage POIs to be visited by tourists according to their preferences, as well as the context and strong links between POIs.
Currently, the French government employs at least two different software (RenablLP2 and Gertrude), each one having different data models (format) to manage and store cultural heritage data. In addition, different (widely unknown) systems are also used to make this information available to the general public and experts. In our first main contribution, we aim to reduce this heterogeneity, especially for the general public, by unifying this data into a single model capable of being published in already established and widely accessed open data providers. We present an application that adopts this model and automatically publishes cultural heritage POIs into Wikipedia according to the principles of publication and reuse of machine-readable data proposed in [1].
The second main contribution of this paper is the contextualized recommendation of itineraries (i.e., sequences of POIs to be visited). This recommendation takes into account the user profile, his location, his device features, and also some other parameters such as how much time is available for the tourist to visit the POIs and what is his means of transportation. A recommendation could also be enriched with information extracted from open data. For example, if an exhibition is happening close to the user’s location, the user’s itinerary may be enriched with a link to a ticketing service.
In the literature, this process of itinerary recommendation (or generation) is usually separated into two steps. First, a score representing the pertinence of each POI is estimated. Then, an itinerary is built according to the score and other contextual elements (e.g., distance) [2,3].
We propose a hybrid approach for the recommendation of itineraries. We use a content-based approach to calculate the score of POIs according to the profile of the user (modelling his preferences) and his context. But we also refine and adjust the score of each POI using a collaborative-filtering approach that takes into account its popularity with other tourists and also its relevance when preceded by the previous POI in the itinerary.
Collaborative filtering is achieved through the incorporation of the pheromone deposition and evaporation system in our approach. This principle is inspired by the ant colony optimisation algorithm (ACO). The difference of our approach compared to the traditional ACO is that our objective is not to find an optimal path to go to a given destination, but to implement a co-influence communication [4] between tourists based-on pheromones (i.e., passage frequency between POIs). In fact, this is one of the original aspects of our proposition. ACO algorithms have been widely used in e-commerce recommendations [5,6,7], but they are not common in the recommendation of POIs.
In the end, our approach generates a list of POIs that are not only pertinent to the preferences of the user (tourist), but also spatially, temporally, and sequentially relevant. Moreover, adjusting the score according to its popularity and sequence relevancy fights overspecialisation [8] and increases the novelty and serendipity [9] of our recommendations.
In Section 2, we discuss related work in the areas of open data publication and recommender systems and itinerary generation. In Section 3, we detail the architecture of the platform we conceived to support both the publishing of our data as open data and the recommendation of POIs. Section 4 presents the unified data model we propose to gather cultural heritage information from heterogeneous sources. In this section, we also propose a framework to publish cultural heritage information as open data. Next, we detail our approach to generating and recommending itineraries. Finally, in Section 5 we conclude the paper and sketch future work.
2. Related Work
The first contribution of our work consists of an approach to publish cultural heritage data as open data. Much has been done in the area of open data publication. For example, recent work tries to overcome open data publication and reuse challenges [10]. Ref. [10] focuses on open data quality measurement. Ref. [11] details categories of open data producers (e.g., public administration) and re-users (e.g., citizens). Ref. [1] points out 24 challenges related to the publication of open government data (OGD). Some of these challenges are particularly interesting to our work, namely: (i) too many OGD initiatives, (ii) not enough [accessible] resources, (iii) no standard process or policy for OGD publication, (iv) there is not always a centralised OGD portal available, and (v) lack of suitable software tools for OGD publication. Ref. [12] describes a first experiment of cultural heritage data publication on Wikipedia where three hundred cultural heritage POIs were converted to Wikipedia articles. However, the export process to Wikipedia is entirely manual and the texts originally written by experts were rewritten for the purpose of presenting the scientific information to the general public. Focusing on open data and cultural heritage data, some recent work aims to link cultural heritage data with linked open data (LOD) [13,14]. These projects’ main purpose is cultural heritage corpora enrichment via LOD content and vice versa.
The second contribution of our work focuses on recommending touristic itineraries to the user. As part of itinerary generation, it is essential to model data such as users, context, and itineraries. In what follows, we consider that the user/tourist model and user/tourist profile are synonymous.
The user model defines the user profile. This profile generally includes the information that characterise her/him (e.g., gender, age category, socio-professional activities), her/his preferences (e.g., thematic and historical preferences) and/or age group (e.g., child, adult, elderly person). Some of this information is provided directly by the user (e.g., gender, age category, preferences), others can be deduced from her/his interactions (e.g., her/his “Likes”, her/his age group). Preferences can be derived from notes the user assigns to POIs or comments published. Depending on the POIs that the user has visited, it is also possible to deduce which group of users she/he belongs to. In [15], for example, the user profile is characterised by her/his name, office location, and social networks (e.g., friends on Facebook), and her/his preferences are deduced from POIs that he/she, or his/her friends, have visited and shared on social networks (e.g., Facebook). The approaches proposed in [16,17] consider only the preferences of the user. These preferences are derived from the visitor’s review comments. The works mentioned here make use of comments shared by members of social networks (Yelp (https://www.yelp.com/writeareview/), TripAdvisor (https://www.tripadvisor.com/), and Foursquare (https://foursquare.com/)). They use a learning-based system to determine whether or not a user has enjoyed a visit from her/his review comments. This allows the determination of the user’s preferences and fills out her/his profile.
An itinerary is formed by an ordered list of POIs. The itinerary indicates the POIs visit order, the estimated duration of the visit ffor each POI, and the route between couples of POIs. An itinerary generation system helps the user prepare her/his trip. The majority of itinerary generation systems are based on the resolution of the Orienteering Problem (OP), which is a scoring system described in the operational research literature that was implemented for the first time by Tsiligirides [18]. In our case, OP consists in collecting points that are assigned to POIs. The objective is to maximise the number of points collected while respecting constraints (e.g., the duration of the whole route). According to Ayala et al. [3], OP is a combination of the “travelling salesman’s problem” and of the ”knapsack problem”, both of which are operational research problems. Several propositions have been made to extend OP, for example: TOP, TDOP and TDTOPTW where T stands for Team (i.e., taking into account a team, each POI must be visited by, at most, one team member), TD stands for Time-Dependent (i.e., taking into account the travel time between POIs), and TW stands for Time-Window (i.e., taking into account opening and closing hours of POIs). The itinerary generation process is often composed of two phases: POI scoring and itinerary construction. Some approaches incorporate a third phase, which is the adaptation of the generated itinerary. In this case, the user can intervene to modify the itinerary (e.g., add or remove a POI, change the order of POIs to be visited), and the system must be able to adapt to this modification with respect to the user context (e.g., the visit duration) [2]. In most cases, itinerary generation consists of evaluating the relevance score of a set of POIs and then constructing an itinerary composed of POIs with the highest scores.
Differences between itinerary generation approaches are mainly at the POI scoring stage. POI recommendation approaches can be categorised into three categories according to how the scoring is performed: content-based approaches, collaborative filtering approaches, and hybrid approaches.
Content-based approaches use POIs and/or user information to match POI characteristics to the user’s preferences and context. Several techniques can be used to define this correspondence: activation-propagation techniques [19], agent-based systems [20], probabilistic approaches [20], biology-inspired approaches (e.g., based on neural networks [21]), etc. One advantage of content-based approach is that it does not suffer from cold start problems when a new POI is added. That is, it is capable of recommending a new item even if no one has interacted with it so far. [22] considers that recommendation systems have different types of cold start problems: problems with new users (who do not have a history and/or profile), problems related to new POIs (which have not yet received any evaluation), and finally, problems related to specific users (who have different preferences from others).
Collaborative filtering approaches use information about other users with similar characteristics (e.g., age, socio-professional activities, visit evaluation feedback) to recommend POIs to a given user. Several techniques are used by these approaches, such as clustering techniques, allowing, for example, the grouping of users according to their profile [23] or according to their friendship links on social networks, or even ant colony algorithms dedicated to the calculation of traces of pheromones left by users [24]. In the latter case, the recommendation considers only the popularity of a POI. The advantage of collaborative filtering approaches is that they allow the recommendation of POIs without requiring specific information about them. However, cold start is a real challenge in this category since it is necessary to have information about other users and new items tend not to be recommended.
Hybrid approaches combine the content-based and collaborative filtering approaches. Different forms of combination have been considered [25]: (i) separate implementation of content-based and collaborative filtering approaches and then the combination of recommendation results, (ii) integration of some content-based treatments into a collaborative filtering approach, (iii) integrating some collaborative filtering-based treatments into a content-based approach, (iv) proposing a general approach that integrates both content-based and collaborative filtering approaches. In the first category, we can mention the approaches of [15,16,26], which are differentiated by the techniques employed for content processing and collaborative filtering. Refs. [15,16] use a linear function, while [26] uses a prediction function to combine the recommendation results. The approach we propose is in the fourth category of hybrid approaches (i.e., category (iv)). As part of itinerary generation, the POI recommendation strategy we propose is conducted iteratively. At each iteration, we recalculate the potential of a candidate POI, i.e., its global relevance score, taking into account the POIs already integrated into the itinerary being constructed.
POI recommendation systems and itinerary generation may or may not be context-sensitive. Those that are context-sensitive are called CARS, or context-aware recommender systems. According to Schmidt et al. [27], contexts can be classified into three categories: the context of the user (e.g., location, time, budget, social affinity, social status), computer context or resource context (e.g., network connection, communication cost, available bandwidth, type of processor), and physical context (e.g., traffic conditions, temperature, weather, brightness).
Two surveys in the area of recommender systems applied to the field of tourism [28,29] have been recently published and should receive special attention. These surveys present classifications of recommender systems in terms of (i) interface, (ii) data source types, (iii) formalisation and algorithms, (iv) methods of evaluation of the systems. According to these surveys, there are two categories of recommender systems in term of interface: web application and mobile application. The use of a mobile application is interesting compared to web applications because they allow a system to be accessed from any place with an internet connection. Moreover, a mobile application has access to the user’s current location and is therefore able to suggest POIs around him [28]. Regarding the data source types, a few types are identified: geo-tagged photographs or social medias, location-based social networks or GPS trajectory traces [29]. According to the formalisation and algorithms, as indicated above, there are three main categories of recommender systems: content-based systems, collaborative systems, and hybrid ones. Half of the works presented in [28] implement hybrid systems. Several recommendation systems integrate artificial intelligence techniques such as multi-agent systems [30,31,32], optimisation techniques (ant colony optimisation [33], genetic algorithms [34], iterated local search [2,35], greedy randomised adaptive search methods [36]), automatic clustering (k-nearest neighbours approach [37,38], k-means algorithms [39,40], fuzzy c-means [41]), management of uncertainty (Bayesian networks, fuzzy logic [42,43], rule-based approaches [44], and knowledge representation (ontologies [45,46,47]). For the evaluation of these systems, four methods are proposed in [29]: (1) real-life evaluations (based on precision, recall, and the harmonic mean of both precision and recall), (2) heuristic-based evaluations (based on total POI recommended, POI popularity or tourist interest), (3) crowd-based evaluations (using qualitative measures that focus on user experiences), and (4) online controlled experiments (design-based variants and algorithm-based variants).
There is, to our knowledge, little research dedicated to itinerary generation/recommendation in the domain of cultural heritage data. The authors of [48] explain that existing works generally apply the approaches presented above to cultural POI recommendation in the context of multimedia systems. They propose an approach based on the analysis of multimedia objects, notably images taken from the Web, to recommend visit itineraries. In another example, [49] use a social graph (i.e., affinities between users) in their system of recommending works of art exhibited in museums.
To highlight Pyrenean cultural heritage POIs while avoiding cold start problems and getting as close as possible to user preferences, we plan to set up a hybrid approach that integrates both the content-based approach and the collaborative filtering approach. This approach allows the compiling of a list of pertinent POIs while suggesting with parsimony one or more original POIs to complement those that closely correspond to the user’s preferences. In order to do so, we integrate an ant colony algorithm in our solution. This algorithm is quite common in the recommendation of e-commerce products but is far from popular in POIs itinerary recommendation. Unlike Wang et al. [50], who use an ant colony optimisation algorithm to calculate a crowd-aware trip (i.e., adaptation of POI visiting order according to crowdedness knowledge), we propose to make use of ant pheromones to compute the social dimension of a POI accuracy score.
In the following section, we present the two main contributions of this paper: (i) an open-source framework to export cultural heritage to well-known open data providers; and (ii) an open-source algorithm and framework to recommend a sequence (itinerary) of cultural heritage POIs to be visited by tourists.
3. Handling Heterogeneous Cultural Heritage Data
Figure 1 presents the general architecture of our proposed solution. This architecture is split in two parts according to their roles: (a) data integration; and (b) data leveraging.
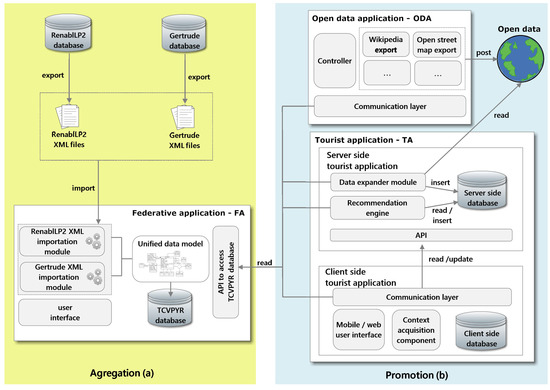
Figure 1.
Overview of the architecture of our proposed solution.
As briefly discussed in the introduction, the cultural heritage data that we use in this work comes from different and heterogeneous sources. The data integration part is responsible for integrating this data into a single database in a homogeneous data model. More specifically, this integration is achieved through the integration system. The goal of this operation is simply to facilitate the use and manipulation of our data. The integration system is discussed in more details in the next section.
The data leveraging part actually contains two applications. The first one, the Open Data Application, is responsible for publishing information from our database into the databases of other open data providers. The second one, the Tourist Application, recommends relevant itineraries to be followed by tourists in a specific region of the Pyrenees. Both applications are described in Section 4.
3.1. A Unified Model for Cultural Heritage Data
In order to collect cultural heritage data, a researcher (e.g., historian or anthropologist) typically visits a POI in the Pyrenees, gathers some information, and then saves it digitally using one of two software: RenablLP2 or Gertrude. (Both of these software have been traditionally used to manage cultural heritage data in France. Different regions adopt one or the other.) Both software are capable of exporting data from their database into XML files. However, the data coming from each of them is very different in terms of structure, existing fields, and field names.
In order to facilitate the use and manipulation of this data, we propose and adopt a unified and homogeneous model (Figure 2). This model describes all subjects (i.e., POIs that are studied by researchers): buildings, objects, etc. Each subject is georeferenced, has a global description, historic description, and a list of persons that are relevant to it (e.g., the architect or sculptor who created it). A subject might also be linked to another subject: a building might be a composition of other smaller buildings or a piece of furniture might be inside a building. This model focuses on describing the information useful for our applications only. The integration system populates our database using this model.
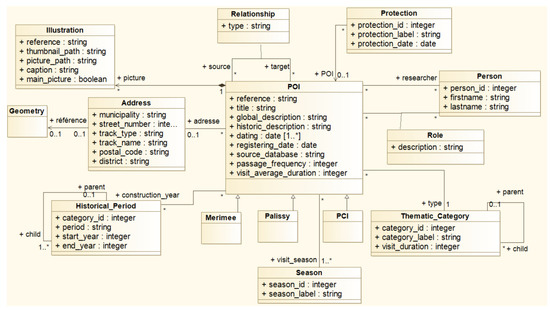
Figure 2.
Unified cultural heritage point of interest (POI) data model.
This data model respects the current standards adopted by the cultural heritage research community in France (e.g., Mérimée (http://www.culture.gouv.fr/Espace-documentation/Bases-de-donnees/Palissy-consultable-depuis-le-moteur-Collections) [51], Palissy (http://www.culture.gouv.fr/Espace-documentation/Bases-de-donnees/Merimee-consultable-depuis-le-moteur-Collections)) and is also able to be easily exported to other models [48].
3.2. Importing Heterogeneous Data
In order to import heterogeneous data to our database, the integration system starts by reading XML data originating from RenablLP2 or Gertrude. Figure 3 presents an example of an XML file (from RenablLP2) containing a POI. These files are treated and imported by the importer components (Figure 4) in order to transform them from their original model into our model. These data are then stored in an Elasticsearch (https://www.elastic.co) database and become accessible through a consultation API (used by our applications). The integration system has been already developed (The results can be seen here: http://tcvpyr.iutbayonne.univ-pau.fr/) and is fully functional.
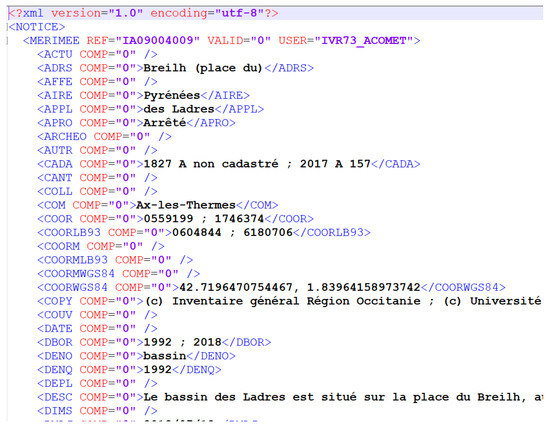
Figure 3.
XML export file sample.
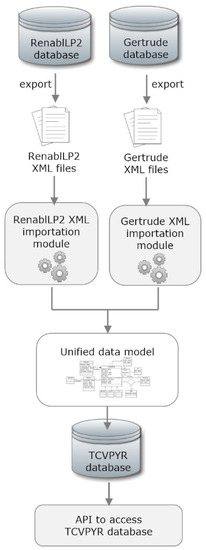
Figure 4.
Data merge process.
4. Leveraging Cultural Heritage Data
We propose two approaches to leverage cultural heritage POIs, both making use of open data concepts. One consists in publishing this data into the database of well-known open data platforms such as Wikipedia. The other one consists in an open-source application capable of recommending personalised touristic itineraries. Not only is this application open-source, but the services developed to support this application (such as the one allowing recommendation) will be also be publicly accessible and available to anyone interested.
In the next section, we present a proposal to publish our database as open data.
4.1. Cultural Heritage Open Data Publication
We propose a fully automated open data publication process according to the work of Kucera et al. [1] and Abella et al. [11] on open data publication and reuse challenges. For us, data producers are the experts from the public administrations of the Pyrenees (i.e., Aquitaine and Occitanie regions), data re-users are professionals such as tourism offices, and end-users include tourists and academics.
Our proposition is implemented within a software that supports an automated publication (challenge (v), Section 2) of cultural heritage POIs. It should be noted that this is a strength of our process as most of the current Wikipedia publication processes are manual. We automatically create concepts in Wikidata linked to each cultural heritage POI and corresponding images are published in Wikimedia Commons. Then, the Wikipedia article can be put online.
Figure 1 and Figure 5 present the architecture of our open data application responsible for publishing our cultural heritage data as open data. In order to do so, this application uses a communication layer capable of performing HTTP requests that are handled by an API that communicates directly with the database. Once it has the required data, one or more export components are used to communicate with the database of an open data provider.
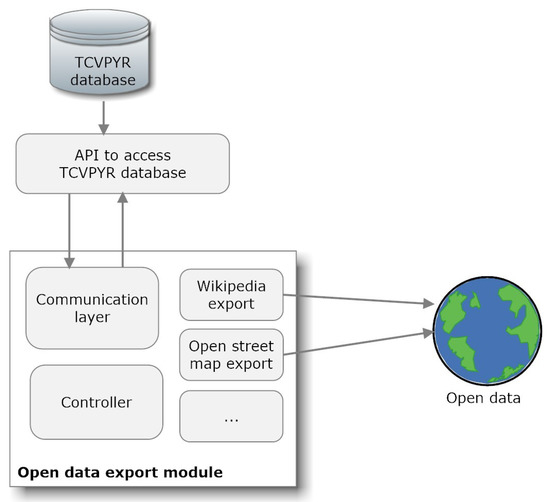
Figure 5.
Cultural heritage data dissemination through open data platforms.
Figure 6 shows an example of a French Wikipedia article published by our application. This article is based on the “Bassin des Ladres”, (https://fr.wikipedia.org/wiki/Bassin_des_Ladres) an ancient pool in the town of Ax-les-Thermes registered in our database. The component responsible for publishing on Wikipedia has been developed in Java and uses an API called JWiki (https://github.com/fastily/jwiki) to interact with Wikipedia. As of now, only one component, able to export our data to Wikipedia, has been developed as a prototype. More export components may be implemented similarly. We plan to implement a new one to publish our data in OpenStreetMap in the near future.
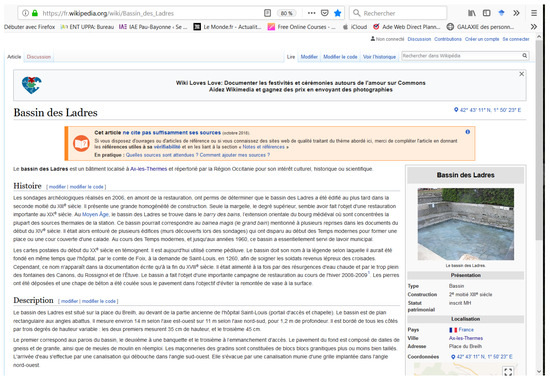
Figure 6.
An example of a cultural heritage object (POI) exported to Wikipedia.
Wikipedia was chosen as our first target open data platform in order to take into account challenges number (i), (ii), (iii), and (iv) mentioned in Section 2. In order to deal with the heterogeneity of ways in which open data is normally published, the French Ministry of Culture is launching a big project named the POP platform. (www.pop.culture.gouv.fr/) The aim of this platform is to give general public access to the cultural heritage collected by all its services. However, we believe that as of now, Wikipedia still is a de facto standard for publishing open data in a generally accepted and popular platform and centralised portal. We are yet to overcome other challenges pointed out by Kucera et al. [1] such as legal challenges and also political and social ones.
4.2. The Tourist Application and Its Recommendation Mechanism
In this paper, we focus on the use of our cultural heritage data to recommend itineraries to tourists. In our approach, an itinerary is built progressively, re-evaluating the pertinence of each POI after a new one is added. This characteristic is extremely important to make sure the relevancy of the sequence is taken into account. For example, suppose three POIs A, B, and C have relevancy scores of 1, , and , respectively. Now suppose a tourist is able to visit only two of the three POIs. One could argue that visiting A and then B would be the best itinerary, since it has the highest sum score. However, if A represents a beach and B represents a fancy restaurant, it is very unlikely that A followed by B is a good itinerary to be followed. This scenario is even more clear if we suppose that C is a place where many people go after visiting B (e.g., an ice-cream shop). Thus, it is extremely important not to analyse each POI’s pertinence individually only, but also in the particular sequence in which it appears.
One particularity of our approach lies in the use of a thesaurus used in cultural heritage classification. This thesaurus allows us to analyse POIs not only as seen by experts but also as seen by lay tourists. In particular, we are able to determine the semantic links between POIs, between users, and between a POI and a user. Thus, we are able, for example, to calculate the distance between a POI and the profile (preferences) of a user by measuring their similarity according to this thesaurus and our knowledge base.
Another particularity of our approach lies in the incorporation of an ant colony algorithm in our recommendation mechanism. Thus, similarly to what happens in commercial systems that suggest articles based on the principle “a client who has seen this article has also liked this other one”, we determine what items are pertinent in a specific sequence. Previous interactions of users with the systems are said to leave behind a pheromone trail indicating the paths (sequences) to follow. Thus, our recommendations are not limited to items similar to other items previously liked by the user. This characteristic tends to reduce overspecialisation [8] and to foster novelty and serendipity [9] of recommendations.
Figure 7 illustrates the architecture of the Tourist Application that incorporates our recommendation mechanism and follows a client/server model. On the side of the server, two components can be seen: a data expander and a recommendation engine. The former is responsible for consulting data from our main database, enriching it with data from open data (e.g., Datatourisme, WikiData) and storing it in a second database. We opted to maintain two separate databases in our project because our original and primary database contains only authoritative data produced by experts. The second database contains a mix of this data with crowdsourced data. Besides enriched cultural heritage data, this database also stores the history of interactions between all users and POIs, such as POIs visited and sequences followed. The Recommendation Engine uses all this data to generate and suggest an itinerary when requested by the user. Once the suggested itinerary is accepted by the user, it is stored in a small client-side database that ensures it can be followed even when no internet connection is available.
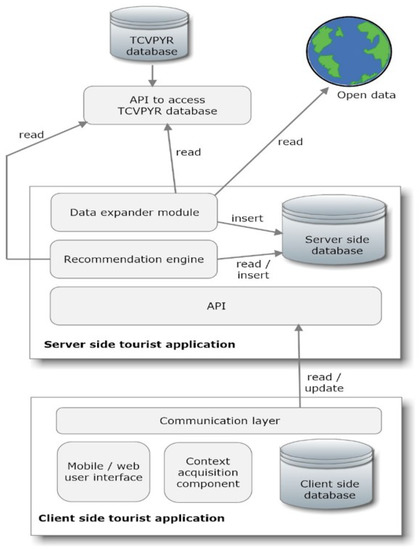
Figure 7.
The Tourist Application.
In the next section, we discuss how we model elements such as the user, his context, and an itinerary in order to implement our recommendation mechanism.
4.3. Models
4.3.1. User Model
The user model describes the elements characterising a user of our Tourist Application. In our model, a user is composed of a gender, age category (e.g., kid, adult, or elderly), and his preferences. A user can have different thematic preferences (e.g., park, museum) and historical preferences (e.g., 15th century).
Figure 8 illustrate a UML class diagram of our user model.
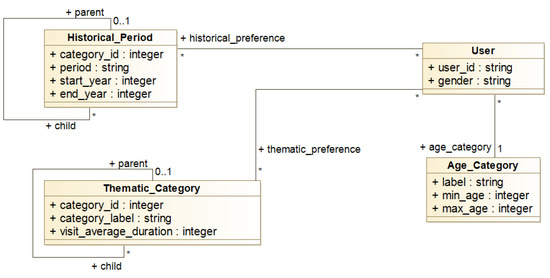
Figure 8.
User model.
4.3.2. Context Model
In our approach, the context is composed of three parts: user, physical, and resource contexts (see Figure 9).
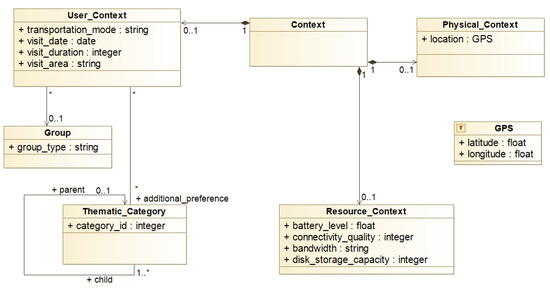
Figure 9.
Context model.
The user context completes the profile with information specific to a given visit/trip. For example, it models what means of transportation will be used, the date, duration, and location (touristic destination or current location if already there). The user can also inform other characteristics relevant to his trip such as whether he is alone or part of a group. If he is part of a group, he may also inform whether he is accompanied by children, elderly people, etc.). The idea is that any proposed itinerary should take into consideration this kind of information. For example, someone with kids might benefit from a visit to a park to let them play.
The physical context is the geographical coordinate of a POI or the location of a user during his visit. This information changes in real time according to his actual location using a GPS. The resource context groups information related to the user’s mobile device (e.g., battery level) and its environment (connection quality and bandwidth). Once again, this information will be used to adapt the itinerary in real time if needed.
4.3.3. Itinerary Model
In our work, an itinerary is a sequence of stages (containing a POI to be visited). It is also defined in terms of its generation date and means of transportation to be adopted. Each stage is numbered according to its order in the sequence of stages of an itinerary. The information concerning the estimated duration to visit each POI and the total duration of the whole itinerary is also available. Figure 10 presents our itinerary model.
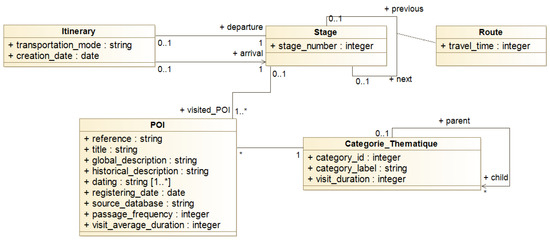
Figure 10.
Itinerary model.
4.4. A Recommendation Algorithm for Itineraries
In this section, we present the main contribution of our work: an algorithm to recommend tourist itineraries leveraging our cultural heritage database. This algorithm is a TDOP (see Section 2) in which the travelling time between POIs is taken into account.
Algorithm 1 describes the main structure of our approach. Some particularities are described later.
| Algorithm 1: Itinerary recommendation—pseudocode |
 |
The algorithm starts by filtering out POIs that are not geographically relevant to the user (line 1). Then, an estimated score for each POI is calculated a first time (the scoring function is described in detail later in Formula (1) of Section 4.4.1). Once finished, the origin (first POI to visit) is defined and inserted into the itinerary. Next, if there are any POIs in the region left and there is enough time to visit one, the two last steps are repeated. The scoring will be performed once again, this time also taking into consideration the last POI visited and the relevance of the sequence, and the highest scoring POI will be added as a next step into the itinerary. At the end, an itinerary containing an ordered list of POIs to be visited is generated and recommended to the user.
4.4.1. The Scoring Function
One of the most important parts of any recommender algorithm is its scoring function. In fact, almost any recommender algorithm in its basic form could be seen as having two parts: (i) estimating the score of each item; and (ii) recommending the items with the highest score. Thus, the main differences between most algorithms lie mainly in how these scores are estimated.
In our work, we propose that the score correspond to the weighted sum of three values (as seen in Formula (1)), representing the pertinence of a POI when taking into consideration user preferences (), POI position in a sequence and visit time (), and the preferences of other users ().
where , is the POI to be evaluated, and t is a specific time.
The scoring function needs a set of seven different input data in order to estimate the pertinence score of each POI. Figure 11 depicts a complete list of its inputs, namely:
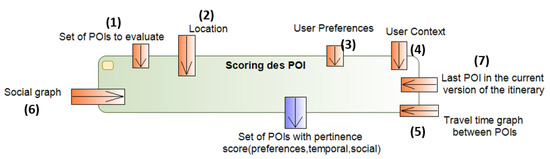
Figure 11.
Input and output of the scoring function.
- Set of POIs to evaluate (input no. 1)The scoring functions should, of course, receive a list of POIs to be evaluated. Each POI is represented according to the model described in Section 3.2.
- Location (input no. 2)The location is a geographical coordinate corresponding to the position of the last POI added to the itinerary being constructed. It is defined as part of the physical context (Section 4.3.2).
- User preferences (input no. 3)The preferences of the user are composed of thematic and historical preferences. They are described in Section 4.3.1.
- User context (input no. 4)The user context defines the mode of transportation (e.g., driving, cycling), a date, the estimated visit duration, and the group (alone, with kids, with adults, etc.). These elements are described in Section 4.3.2.
- Travel time graph: (input no. 5)The graph contains information about the time required to travel between POIs. It is defined as , where V is a set of POIs and E is a set of paths (edges) linking two POIs. In our model, we consider that each pair of POIs is linked (i.e., this is a complete graph). The values composing these edges are calculated only once, except if a new edge is inserted in the graph. Since we consider three transportation modes in this paper (on foot, cycling, and driving), each edge contains three values.Figure 12 illustrates the travel time graph between POIs. Each edge contains a triplet of values (, , ) where represents on foot travel time between and , represents cycling travel time between and , and represents driving travel time between and .
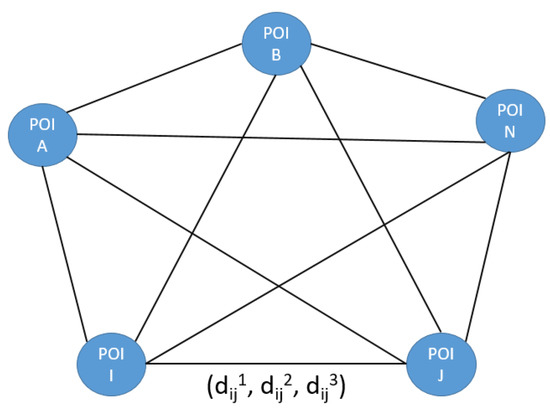 Figure 12. Travel time graph.
Figure 12. Travel time graph. - Social graph: (input no. 6)The graph models the relevance of POIs according to the whole set of users and the relevance of a particular sequence of POIs (pheromone trails). This graph is defined as , where V is the set of POIs and E is the set of edges linking two POIs.Figure 13 illustrates the information about the pheromone trails. Each vertex (POI) has a list of values defining its score for each user. That is, this list is composed of a tuple (score of for user u) and (identity of user u who visited ).
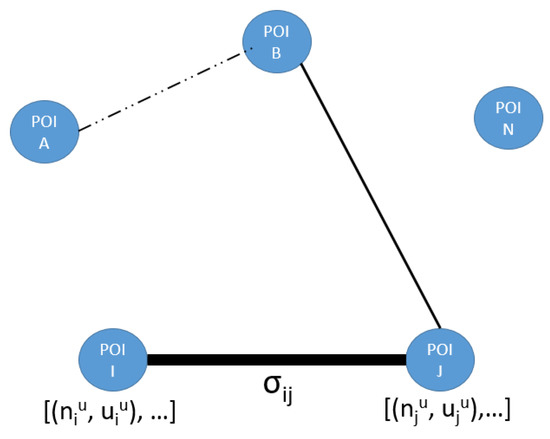 Figure 13. Social graph.Each edge has a value representing the intensity of the link between two POIs. This intensity is defined in terms of past interactions with the set of users of the system and the two POIs. We adopt the hypothesis that if two POIs are frequently visited successively, there is a strong link between them (according to the users’ preferences). This modelling choice inserts characteristics of collaborative filtering algorithms in our approach. Moreover, we also increase the score of a POI for a user if other users like it. This hypothesis is implemented through the incorporation of an ant colony algorithm in our solution. We consider that each user is an ant and that every time an ant passes from one POI to another, a specific quantity of pheromone is left in the path. Whenever the amount of pheromone reaches a certain amount, it means a strong link between two POIs exist. Figure 13 presents the pheromone in terms of edges. The bolder these edges are, the stronger is the pheromone trail left between the two edges.Here, one of the main advantages of using ant colony algorithms is that they take into account not only the links (i.e., passages) existing between vertices but also their absence during a long period. Thus, if a particular path (sequence) is not followed after some time, the pheromone left there will “evaporate”.
Figure 13. Social graph.Each edge has a value representing the intensity of the link between two POIs. This intensity is defined in terms of past interactions with the set of users of the system and the two POIs. We adopt the hypothesis that if two POIs are frequently visited successively, there is a strong link between them (according to the users’ preferences). This modelling choice inserts characteristics of collaborative filtering algorithms in our approach. Moreover, we also increase the score of a POI for a user if other users like it. This hypothesis is implemented through the incorporation of an ant colony algorithm in our solution. We consider that each user is an ant and that every time an ant passes from one POI to another, a specific quantity of pheromone is left in the path. Whenever the amount of pheromone reaches a certain amount, it means a strong link between two POIs exist. Figure 13 presents the pheromone in terms of edges. The bolder these edges are, the stronger is the pheromone trail left between the two edges.Here, one of the main advantages of using ant colony algorithms is that they take into account not only the links (i.e., passages) existing between vertices but also their absence during a long period. Thus, if a particular path (sequence) is not followed after some time, the pheromone left there will “evaporate”. - Last POI in the current itinerary (input no. 7)The last POI in current version of the itinerary (under construction) is also used to evaluate the score of candidate POIs. In fact, the pheromone (sequence pertinence) can only be assessed when two POIs are being analysed (the last one in the sequence and the new one to be added).
Once all this input data is provided, the scoring function calculates and outputs the set of POIs, each POI being associated with its respective score according to the formula (1)) previously presented. In the following, we describe how each part of the function is calculated, namely the pertinence of a POI according to the user preferences (), its position in a sequence and visit time (), and the preferences of other users ().
- User preference pertinence ()We adopt the hypothesis that if the user is interested in a thematic category or historical period, then he is also interested in other semantically similar categories. For example, if the user likes visiting churches, he might enjoy visiting a monastery too. These are two semantically close concepts. In this sense, the function that calculates the pertinence of a POI according to the user’s preference actually measures the semantic similarity between categories that the user is interested in and categories of the POI.and model the semantic similarity between a POI and the thematic and historical categories liked by a user. This similarity function adopted was initially proposed by Wu and Palmer [52]. It takes into consideration the distance between concepts according to a thesaurus and the depth of their first common concept (Least Common Subsummer).
- Temporal pertinence ()The temporal pertinence is defined according to the travel time () between the last POI added to the itinerary and the candidate POI . It also takes into consideration the remaining available time for the trip.Formula (3) formally defines the temporal pertinence of a POI.where i is the transportation mode of the user, is the commuting time between and , and is the remaining time at instant t.In this model, the shorter the time to reach the candidate POI, the greater its score (closer to 1).
- Social PertinenceSocial pertinence is defined by the number of users at instant t who recently went from the last POI added to the itinerary to the candidate POI. This pertinence also takes into account the popularity of the candidate POI at instant t of the evaluation. To define the social pertinence of a POI, we use the graph.Formula (4) defines the social pertinence of a POI formally.with ,where is the last POI added to the itinerary, is the popularity of at instant t, and is represented by the frequency with which tourists travelled from to at instant t.The popularity of a POI is defined in terms of the frequency at which users travelled from the last POI to the POI being analysed and by the score given by other users evaluating the POI. The popularity takes into account the neighbourhood context: indeed, it is normalised by the score and the visit frequency of neighbouring POIs. Note that a set of neighbour POIs is determined by a POI and a geographic neighbourhood radius, which is defined as parameter.Thus, the popularity of a POI is defined by Formula (5):withwhere V is a list of POIs, neighbours of , ranked by their overall assessment ratings. Thus, is a function that computes the position of within the list V according to the average of ratings associated with . In the same way, is a list of POIs, neighbours of , ranked in terms of the frequency with which they have been visited from their neighbouring POIs. The function is a function that computes the position of within the list .Thus, the closer the rank of a POI is to the first position, the higher is its popularity score.The intensity of a link between two POIs and is defined as follows:where t is the instant of the intensity calculation.and are explained in detail below.According to the “ant colony” approach incorporated in our algorithm, a user is represented by an ant. For this reason, when a user visits a POI and then a POI , he deposits pheromones on the path between and (see Section 4.4.1, Figure 13). For each passage on the path - , a quantity Q (predefined) of pheromones is accumulated on the corresponding edge in the graph. corresponds to the total amount (quantity) of pheromones that is accumulated between and at instant t. Finally, corresponds to the maximal value of in the graph (, where each is the quantity of the accumulated pheromones on the paths between POIs of a given city. is dynamic and evolves over time.Thus, when the amount of pheromones on the path – is high (close to ) due to many users taking this path, a visitor should be invited to take the path – when he visits the POI or vice versa.Note that is stored in the graph. This total amount of pheromones is updated every time a user takes this path. Thus, the reinforcement principle of pheromones between and is defined bywith .Moreover, the total amount of pheromone on a path (noted ) decreases progressively if nobody follows this path for a certain period of time.The evaporation principle of pheromones is defined by formula (8):with ,where is the evaporation rate.In our approach, in accordance with the approach presented in [53] and another one in [54], we choose a slow evaporation. As in [53], we fixed the value to , which allows us to keep traces of previous visits for a long time while avoiding “the saturation of the arcs with pheromones”.
4.5. Experiments
In order to evaluate our proposal, we developed a prototype that implements part of our model for the recommendation of itineraries. Particularly, it currently does not take into account the social pertinence. A few experiments were performed using the prototype according to two different hypotheses. The results are presented below followed by a brief analysis comparing the functionalities of our proposition to those of similar systems used in the tourism domain.
4.5.1. Experimentation of Our Itinerary Generation Approach
We conducted a first series of experiments according to different working hypotheses on a data set composed of a sample of 120 POIs located in the town of Bagnères de Luchon. Our objective was to experiment with (i) the itinerary generation algorithm and (ii) the weights and . Because our prototype does not currently take into account social pertinence, our scenario does not integrate social constraints such as the popularity of POIs or the intensity of the links between them (i.e., ). We have defined the following settings:
Starting point: “town hall square“
Temporal criteria: Travel time = “60 minutes”; Transportation mode = “on foot”
Preferences: = {“museum/casino”, “carving/painting”}; = {“contemporary period”}
We studied two hypotheses:
Hypothesis 1 (H1).
; ; ; ; .
Hypothesis 2 (H2).
; ; ; ; .
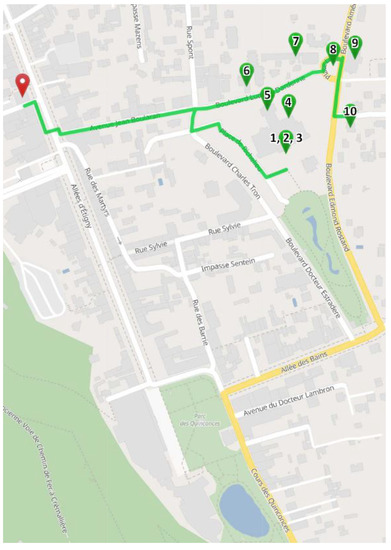
Figure 14.
H1 itinerary.
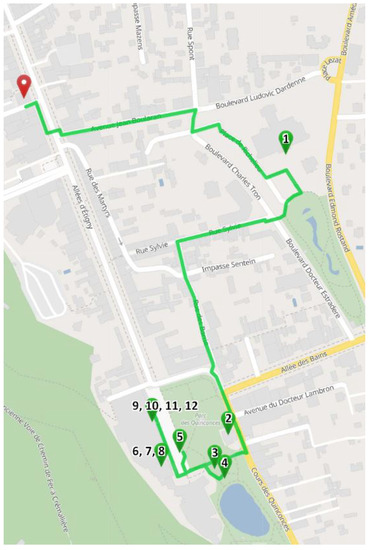
Figure 15.
H2 itinerary.
H1 (Figure 14) gives an itinerary and set of POIs that are mostly different from H2 (Figure 15). Table 1 describes the results obtained in terms of number of POIs and average value/score according to its pertinence (see Formulas (1)–(3)) in our experiments.

Table 1.
Experiment results.
For both hypotheses, it is possible to note that the system proposes itineraries composed of relevant POIs respecting the pertinence. The average relevance score P (i.e., formula (1) combines relevance results corresponding to preference and temporal criteria) of the POIs of the H1 route is 0.74 while that of the H2 route is 0.90. With regard to the preference criteria, the average score in H1 is 0.67, and 0.87 in H2. The choice of the coefficient in the H2 framework favours the preference relevance. Indeed, the proposed POIs result in a better average score in H2. With regard to the temporal criteria, the average score in H1 is 0.81, and 0.94 in H2. The choice of the coefficient in the H2 framework gives less significance to the travel time constraint—despite a longer circuit, the proposed POIs always respect the temporal constraints. Here, we see an unexpected effect with an increase in the number of POIs to visit due to some longer distances being offset by shorter POI visit times for many of them, as well as numerous short paths. The travel time of the itinerary added to the visit time of each POI always respects the time criteria.
H2 also gives better results in other experiments, but it still needs to be confirmed by extensive testing. The weighting coefficients and perfectly play their roles in tuning preferences. After some new experiments, we expect to be able to propose default initialisation values for these parameters.
4.5.2. Comparison to Similar Approaches
In addition to the experimentation, we compare our approach to similar ones that are presented in [55,56]. The comparison is based on (i) input and output data of the recommendation engine and (ii) implemented algorithms. Ref. [55] recommends POIs while [56] recommends touristic and leisure activities. In our approach, we recommend cultural heritage POIs. All three approaches have the same output, which is an ordered list of POIs/activities to visit during a given period. However, they do not have the same input. Ref. [55] takes as input a set of trajectories crossing a set of POIs, whereas our approach and the one presented in [56] take as input a set of candidate POIs/activities. All three approaches take into consideration visit duration, user preferences, distance between POIs/activities, and POI/activity popularity. In addition to the popularity of POIs (visitor ratings), we take into consideration the intensity of the links between two POIs (although not in our experiments), which corresponds to the number of visitors who have passed through these two POIs in one itinerary. Taking into account the intensity of the links is one of the main original aspects of our approach. This principle of serendipity makes it possible to propose POIs possibly far from the visitor’s preferences but potentially interesting. In regards to the implemented algorithms, in [55], itinerary generation is considered as a type of “generalised maximum coverage problem” [57]. Thus, the approach implements an algorithm that allows the system to find an itinerary covering a maximum number of POIs in a given city. Note that no relevance score for POIs is computed. In [56], Moreno et al. propose a sequential filtering approach where (i) a spreading algorithm manages each visitor’s preferences within nodes of his/her proper ontology; (ii) the relevance of activities is computed incrementally (first filter: price of the activity, second filter: activity duration, etc.); and (iii) heuristic rules define the activity sequencing. In our proposition, we opted for a combination of criteria: we select POIs whose characteristics are closest to visitors’ preferences on the basis of an ontology of heritage concepts. This semantic similarity score is combined with other results corresponding to POI popularity, visiting duration, and serendipity. We propose an itinerary generation algorithm that iteratively selects the next POI. Actually, when the POIs/activities are numerous, heuristic rules might be difficult to define, whereas the combination of parameters in our approach seems to be easier to tune.
5. Conclusions
In this paper, we presented our research that aimed at leveraging cultural heritage data to promote tourism in the French Pyrenees. In order to do so, we worked on two fronts: (i) the ability to export this data from their original databases and data models to well-known open data platforms, and (ii) the proposition of an open-source algorithm and framework to recommend a sequence of cultural heritage points of interests (POIs) to be visited by a tourist. The idea is to assist in the opening up of cultural heritage data (often catalogued but largely unknown or difficult to find) to the general public as well as to experts.
We first showed how we created a unified cultural heritage database from heterogeneous sources. In order to do so, we proposed a unified data model that follows the cultural heritage research community standards. This unified data model also enabled us to propose and develop an application to publish information from our database to well-known open data providers such as Wikipedia.
The second important part of our work, and one we gave more attention to, consisted in the recommendation of a sequence of cultural heritage POIs. We proposed a hybrid approach that benefits from content-based and collaborative filtering strengths. The content-based aspect takes into consideration the profile of a user (e.g., his location, means of transportation, availability time-window, preferences, etc.) to recommend POIs that are pertinent. Collaborative filtering is implemented using an ant colony algorithm that adjusts or refines the recommendation, taking into account the popularity of POIs according to other users and also the relevance of a POI in a specific sequence (i.e., how relevant a POI is after another given POI). To the extent of our knowledge, ant colony algorithms have been commonly used in some recommender systems, but not so much when it comes to recommending an itinerary composed of a sequence of POIs. This hybrid approach reduces some well-known types of cold start problems and increases the novelty and serendipity of recommendations. Although we used the Pyrenees region as a case study, this recommendation approach could be adopted in any other region, regardless of the concentration of POIs being low (e.g., somewhere with little cultural heritage) or very high (e.g., the Paris region). The scoring function of the recommendation process always makes it possible to propose a number of relevant POIs whose visit duration will respect the tourist’s time constraints.
The Integration Application and a first prototype to visualise POIs in our base have been published and are currently available. (Source code available at: https://git.univ-pau.fr/liuppa/TCVPYR/importateur).
In future work, we plan to test this first version of our recommendation application on a varied and larger panel of users. This experiment will make it possible to define initial values for the coefficients of the different relevance measurement formulas. We will also compare the results of our system with those of route generation based solely on geographical and temporal criteria. In addition, we are working on a new version of the recommendation prototype that incorporates both the physical and resource user context elements, which has not yet been the subject of experimentation. This version is intended to dynamically adapt an itinerary according to the context. This new prototype should be also able to enrich our recommendations with open data resources (e.g., Datatourisme) in order to offer users cultural events close to their location and preferences. Finally, we also plan to generalise our approach by feeding the recommender system with heritage POIs (e.g., Pyrenean POIs exported by us or by others) directly published on Wikipedia (i.e., without going through our local databases).
Author Contributions
Conceptualization: Landy Rajaonarivo and André Fonteles; Discussion for the improvement of the proposed approaches: Christian Sallaberry, Marie-Noëlle Bessagnet, Annig Le Parc Lacayrelle, Philippe Roose, Patrick Etcheverry and Christophe Marquesuzaà; Implementation of the proposed ideas: Landy Rajaonarivo, André Fonteles, Cécile Cayèré and Quentin Coudert; Implementation and study of experiments: Marie-Noëlle Bessagnet and Cécile Cayèré; Writing-original draft: Christian Sallaberry and Landy Rajaonarivo; Writing—Review and Editing: André Fonteles, Christian Sallaberry, Landy Rajaonarivo, Marie-Noëlle Bessagnet, Annig Le Parc Lacayrelle, Philippe Roose, Patrick Etcheverry and Christophe Marquesuzaà.
Funding
This research was funded by the European Regional Development Fund (ERDF), grant number DATRM - SRMT 16009458 / MP0014253. Project TCV-PYR http://tcvpyr.iutbayonne.univ-pau.fr/ (2017–2020) is held in collaboration with the Occitanie-Méditerranée and Nouvelle-Aquitaine regions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kucera, J.; Chlapek, D.; Klímek, J.; Necaskỳ, M. Methodologies and Best Practices for Open Data Publication. In DATESO, MATFYZPRESS, Czech Republic. Available online: https://pdfs.semanticscholar.org/de74/2866db8eafa9e2022fad269bf32e328ea8aa.pdf (accessed on 2 April 2019).
- Garcia, A.; Arbelaitz, O.; Linaza, M.T.; Vansteenwegen, P.; Souffriau, W. Personalized tourist route generation. In International Conference on Web Engineering; Springer: Berlin/Heidelberg, Germany, 2010; pp. 486–497. [Google Scholar]
- Ayala, V.A.A.; Gülsen, K.C.; Alzogbi, A.; Färber, M.; Muñiz, M.; Lausen, G. A Delay-Robust Touristic Plan Recommendation Using Real-World Public Transportation Information. In Proceedings of the 2nd Workshop on Recommenders in Tourism Co-Located with 11th ACM Conference on Recommender Systems (RecSys 2017), Como, Italy, 27 August 2017; pp. 9–17. [Google Scholar]
- Dorigo, M.; Bonabeau, E.; Theraulaz, G. Ant algorithms and stigmergy. Future Gen. Comput. Syst. 2000, 16, 851–871. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, F. A novel e-commerce customer continuous purchase recommendation model research based on colony clustering. Int. J. Wirel. Mob. Comput. 2016, 11, 309–317. [Google Scholar] [CrossRef]
- Zhang, X.; Pang, X. Analysis on the Mobile Electronic Commerce Recommendation Model based on the Ant Colony Algorithm. In Proceedings of the 2015 International Conference on Industrial Technology and Management Science, Tianjin, China, 27–28 March 2015. [Google Scholar]
- Minjing, P.; Xinglin, L.; Ximing, L.; Mingliang, Z.; Xianyong, Z.; Xiangming, D.; Mingfen, W. Recognizing intentions of E-commerce consumers based on ant colony optimization simulation. J. Intell. Fuzzy Syst. 2017, 33, 2687–2697. [Google Scholar] [CrossRef]
- Abbassi, Z.; Amer-Yahia, S.; Lakshmanan, L.V.; Vassilvitskii, S.; Yu, C. Getting recommender systems to think outside the box. In Proceedings of the Third ACM Conference on Recommender Systems, New York, NY, USA, 23–25 October 2009; pp. 285–288. [Google Scholar]
- Herlocker, J.L.; Konstan, J.A.; Terveen, L.G.; Riedl, J.T. Evaluating collaborative filtering recommender systems. ACM Trans. Inf. Syst. (TOIS) 2004, 22, 5–53. [Google Scholar] [CrossRef]
- Vetrò, A.; Canova, L.; Torchiano, M.; Minotas, C.O.; Iemma, R.; Morando, F. Open data quality measurement framework: Definition and application to Open Government Data. Gov. Inf. Q. 2016, 33, 325–337. [Google Scholar] [CrossRef]
- Abella, A.; Ortiz-de Urbina-Criado, M.; De Pablos-Heredero, C. The process of open data publication and reuse. J. Assoc. Inf. Sci. Technol. 2019, 70, 296–300. [Google Scholar] [CrossRef]
- Castéret, J.J.; Larché, M. Le projet << PCILAB >> pour la valorisation numérique de l’inventaire français du PCI. Les Cahiers du CFPCI 2018, 5, 102–112. [Google Scholar]
- Daquino, M.; Mambelli, F.; Peroni, S.; Tomasi, F.; Vitali, F. Enhancing semantic expressivity in the cultural heritage domain: exposing the Zeri Photo Archive as Linked Open Data. J. Comput. Cult. Herit. (JOCCH) 2017, 10, 21. [Google Scholar] [CrossRef]
- Candela, G.; Escobar, P.; Carrasco, R.C.; Marco-Such, M. A linked open data framework to enhance the discoverability and impact of culture heritage. J. Inf. Sci. 2018. [Google Scholar] [CrossRef]
- Kesorn, K.; Juraphanthong, W.; Salaiwarakul, A. Personalized attraction recommendation system for tourists through check-in data. IEEE Access 2017, 5, 26703–26721. [Google Scholar] [CrossRef]
- Aliannejadi, M.; Mele, I.; Crestani, F. User model enrichment for venue recommendation. In Asia Information Retrieval Symposium; Springer: Cham, Switzerland, 2016; pp. 212–223. [Google Scholar]
- Logesh, R.; Subramaniyaswamy, V.; Vijayakumar, V.; Li, X. Efficient User Profiling Based Intelligent Travel Recommender System for Individual and Group of Users. Mobile Netw. Appl. 2018, 1–16. [Google Scholar] [CrossRef]
- Tsiligirides, T. Heuristic methods applied to orienteering. J. Oper. Res. Soc. 1984, 35, 797–809. [Google Scholar] [CrossRef]
- Bahramian, Z.; Ali Abbaspour, R.; Claramunt, C. A context-aware tourism recommender system based on spreading activation method. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, XLII-4/W4, 333–339. [Google Scholar] [CrossRef]
- Costa, H.; Furtado, B.; Pires, D.; Macedo, L.; Cardoso, A. Context and intention-awareness in pois recommender systems. In Proceedings of the 6th ACM Conferences on Recommender Systems, 4th Workshop on Context-Aware Recommender Systems, RecSys, Dublin, Ireland, 9–13 September 2012. [Google Scholar]
- Bahramian, Z.; Abbaspour, R.; Claramunt, C. A Cold Start Context-Aware Recommender System for Tour Planning Using Artificial Neural Network and Case Based Reasoning. Mob. Inf. Syst. 2017, 2017, 9364903. [Google Scholar] [CrossRef]
- Kłopotek, M.A. Approaches to “Cold-Start” in recommender systems. Stud. Inf. Syst. Inf. Technol. 2009, 1, 47–54. [Google Scholar]
- Wang, J.; Lin, K.; Li, J. A collaborative filtering recommendation algorithm based on user clustering and Slope One scheme. In Proceedings of the 2013 8th International Conference on Computer Science & Education, Colombo, Sri Lanka, 26–28 April 2013; pp. 1473–1476. [Google Scholar]
- Dennouni, N.; Peter, Y.; Lancieri, L.; Slama, Z. Towards an Incremental Recommendation of POIs for Mobile Tourists without Profiles. Int. J. Intell. Syst. Appl. 2018, 10, 42–52. [Google Scholar] [CrossRef]
- Bartolini, I.; Moscato, V.; Pensa, R.G.; Penta, A.; Picariello, A.; Sansone, C.; Sapino, M.L. Recommending multimedia visiting paths in cultural heritage applications. Multimed. Tools Appl. 2016, 75, 3813–3842. [Google Scholar] [CrossRef]
- De Pessemier, T.; Dhondt, J.; Vanhecke, K.; Martens, L. TravelWithFriends: A hybrid group recommender system for travel destinations. In Proceedings of the Workshop on Tourism Recommender Systems (TouRS15), in Conjunction with the 9th ACM Conference on Recommender Systems (RecSys 2015), Vienna, Austria, 16–20 September 2015; pp. 51–60. [Google Scholar]
- Schmidt, A.; Beigl, M.; Gellersen, H. There is more to context than location. Comput. Graph. 1999, 23, 893–901. [Google Scholar] [CrossRef]
- Borràs, J.; Moreno, A.; Valls, A. Intelligent tourism recommender systems: A survey. Expert Syst. Appl. 2014, 41, 7370–7389. [Google Scholar] [CrossRef]
- Lim, K.H.; Chan, J.; Karunasekera, S.; Leckie, C. Tour recommendation and trip planning using location-based social media: A survey. Knowl. Inf. Syst. 2018, 1–29. [Google Scholar] [CrossRef]
- Batet, M.; Moreno, A.; Sánchez, D.; Isern, D.; Valls, A. Turist@: Agent-based personalised recommendation of tourist activities. Expert Syst. Appl. 2012, 39, 7319–7329. [Google Scholar] [CrossRef]
- Ceccaroni, L.; Codina, V.; Palau, M.; Pous, M. PaTac: Urban, ubiquitous, personalized services for citizens and tourists. In Proceedings of the 2009 Third International Conference on Digital Society, Cancun, Mexico, 1–7 February 2009; pp. 7–12. [Google Scholar]
- Lorenzi, F.; Loh, S.; Abel, M. PersonalTour: A recommender system for travel packages. In Proceedings of the 2011 IEEE/WIC/ACM International Conferences on Web Intelligence and Intelligent Agent Technology, Lyon, France, 22–27 August 2011; Volume 2, pp. 333–336. [Google Scholar]
- Lee, C.S.; Chang, Y.C.; Wang, M.H. Ontological recommendation multi-agent for Tainan City travel. Expert Syst. Appl. 2009, 36, 6740–6753. [Google Scholar] [CrossRef]
- Kurata, Y.; Hara, T. CT-planner4: Toward a more user-friendly interactive day-tour planner. In Information and Communication Technologies in Tourism 2014; Springer: Cham, Switzerland, 2013; pp. 73–86. [Google Scholar]
- Garcia, A.; Vansteenwegen, P.; Arbelaitz, O.; Souffriau, W.; Linaza, M.T. Integrating public transportation in personalised electronic tourist guides. Comput. Oper. Res. 2013, 40, 758–774. [Google Scholar] [CrossRef]
- Souffriau, W.; Vansteenwegen, P.; Berghe, G.V.; Van Oudheusden, D. The planning of cycle trips in the province of East Flanders. Omega 2011, 39, 209–213. [Google Scholar] [CrossRef]
- Martinez, L.; Rodriguez, R.M.; Espinilla, M. Reja: A georeferenced hybrid recommender system for restaurants. In Proceedings of the 2009 IEEE/WIC/ACM International Joint Conference on Web Intelligence and Intelligent Agent Technology, Washington, DC, USA, 15–18 September 2009; pp. 187–190. [Google Scholar]
- Noguera, J.M.; Barranco, M.J.; Segura, R.J.; MartíNez, L. A mobile 3D-GIS hybrid recommender system for tourism. Inf. Sci. 2012, 215, 37–52. [Google Scholar] [CrossRef]
- Gavalas, D.; Kenteris, M. A web-based pervasive recommendation system for mobile tourist guides. Pers. Ubiquit. Comput. 2011, 15, 759–770. [Google Scholar] [CrossRef]
- Pinho, J.; da Silva, B.; Moreno, M.; de Almeida, A.; Martins, C.L. Applying recommender methodologies in tourism sector, highlights in practical applications of agents and multiagent systems. Adv. Intell. Soft Comput. 2011, 89, 101–108. [Google Scholar]
- Fenza, G.; Fischetti, E.; Furno, D.; Loia, V. A hybrid context aware system for tourist guidance based on collaborative filtering. In Proceedings of the 2011 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011), Taipei, Taiwan, 27–30 June 2011; pp. 131–138. [Google Scholar]
- Hsu, F.M.; Lin, Y.T.; Ho, T.K. Design and implementation of an intelligent recommendation system for tourist attractions: The integration of EBM model, Bayesian network and Google Maps. Expert Syst. Appl. 2012, 39, 3257–3264. [Google Scholar] [CrossRef]
- Huang, Y.; Bian, L. A Bayesian network and analytic hierarchy process based personalized recommendations for tourist attractions over the Internet. Expert Syst. Appl. 2009, 36, 933–943. [Google Scholar] [CrossRef]
- Lamsfus, C.; Alzua-Sorzabal, A.; Martín, D.; Salvador, Z.; Usandizaga, A. Human-centric Ontology-based Context Modelling in Tourism. In KEOD; Springer: Berlin/Heidelberg, Germany, 2009; pp. 424–434. [Google Scholar]
- Sánchez, D.; Moreno, A. Pattern-based automatic taxonomy learning from the Web. Ai Commun. 2008, 21, 27–48. [Google Scholar]
- Sánchez, D.; Moreno, A. Learning non-taxonomic relationships from web documents for domain ontology construction. Data Knowl. Eng. 2008, 64, 600–623. [Google Scholar] [CrossRef]
- Wang, W.; Zeng, G.; Tang, D. Bayesian intelligent semantic mashup for tourism. Concurr. Comput. Pract. Exp. 2011, 23, 850–862. [Google Scholar] [CrossRef]
- Ardissono, L.; Kuflik, T.; Petrelli, D. Personalization in cultural heritage: The road travelled and the one ahead. User Model. User-Adapted Interact. 2012, 22, 73–99. [Google Scholar] [CrossRef]
- Hong, M.; Jung, J.J.; Piccialli, F.; Chianese, A. Social recommendation service for cultural heritage. Pers. Ubiquitous Comput. 2017, 21, 191–201. [Google Scholar] [CrossRef]
- Wang, X.; Leckie, C.; Chan, J.; Lim, K.H.; Vaithianathan, T. Improving Personalized Trip Recommendation by Avoiding Crowds. In Proceedings of the 25th ACM International on Conference on Information and Knowledge Management, Indianapolis, IN, USA, 24–28 October 2016; ACM: New York, NY, USA, 2016; pp. 25–34. [Google Scholar]
- Hamon, F. Grands ensembles, demande de patrimonialisation et base Mérimée. Hist. Urbaine 2007, 125–132. [Google Scholar] [CrossRef]
- Wu, Z.; Palmer, M. Verbs semantics and lexical selection. In Proceedings of the ACL ’94 32nd Annual Meeting on Association for Computational Linguistics, Las Cruces, New Mexico, 27–30 June 1994; pp. 133–138. [Google Scholar]
- Anagnostopoulos, A.; Atassi, R.; Becchetti, L.; Fazzone, A.; Silvestri, F. Tour recommendation for groups. Data Min. Knowl. Discov. 2017, 31, 1157–1188. [Google Scholar] [CrossRef]
- Sriphaew, K.; Sombatsricharoen, K. Food tour recommendation using modified ant colony algorithm. In Proceedings of the 5th International Conference on Computing and Informatics, ICOCI 2015, Istanbul, Turkey, 11–13 August 2015. [Google Scholar]
- Brilhante, I.; Macedo, J.A.; Nardini, F.M.; Perego, R.; Renso, C. Tripbuilder: A tool for recommending sightseeing tours. In European Conference on Information Retrieval; Springer: Cham, Switzerland, 2014; pp. 771–774. [Google Scholar]
- Moreno, A.; Valls, A.; Isern, D.; Marin, L.; Borràs, J. Sigtur/e-destination: ontology-based personalized recommendation of tourism and leisure activities. Eng. Appl. Artif. Intell. 2013, 26, 633–651. [Google Scholar] [CrossRef]
- Cohen, R.; Katzir, L. The generalized maximum coverage problem. Inf. Process. Lett. 2008, 108, 15–22. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).