Regionalization Analysis and Mapping for the Source and Sink of Tourist Flows
Abstract
1. Introduction
2. Study Area and Data Description
3. Methodology
3.1. Travel Rates from Origin to Nanjing
3.2. Geographic Concentration Index of Scenic Spots
3.3. Moran’s I Index of Global Spatial Autocorrelation
3.4. Geographical Regionalization Modeling
4. Results
4.1. Spatial Autocorrelation Measurement of Regional Variables
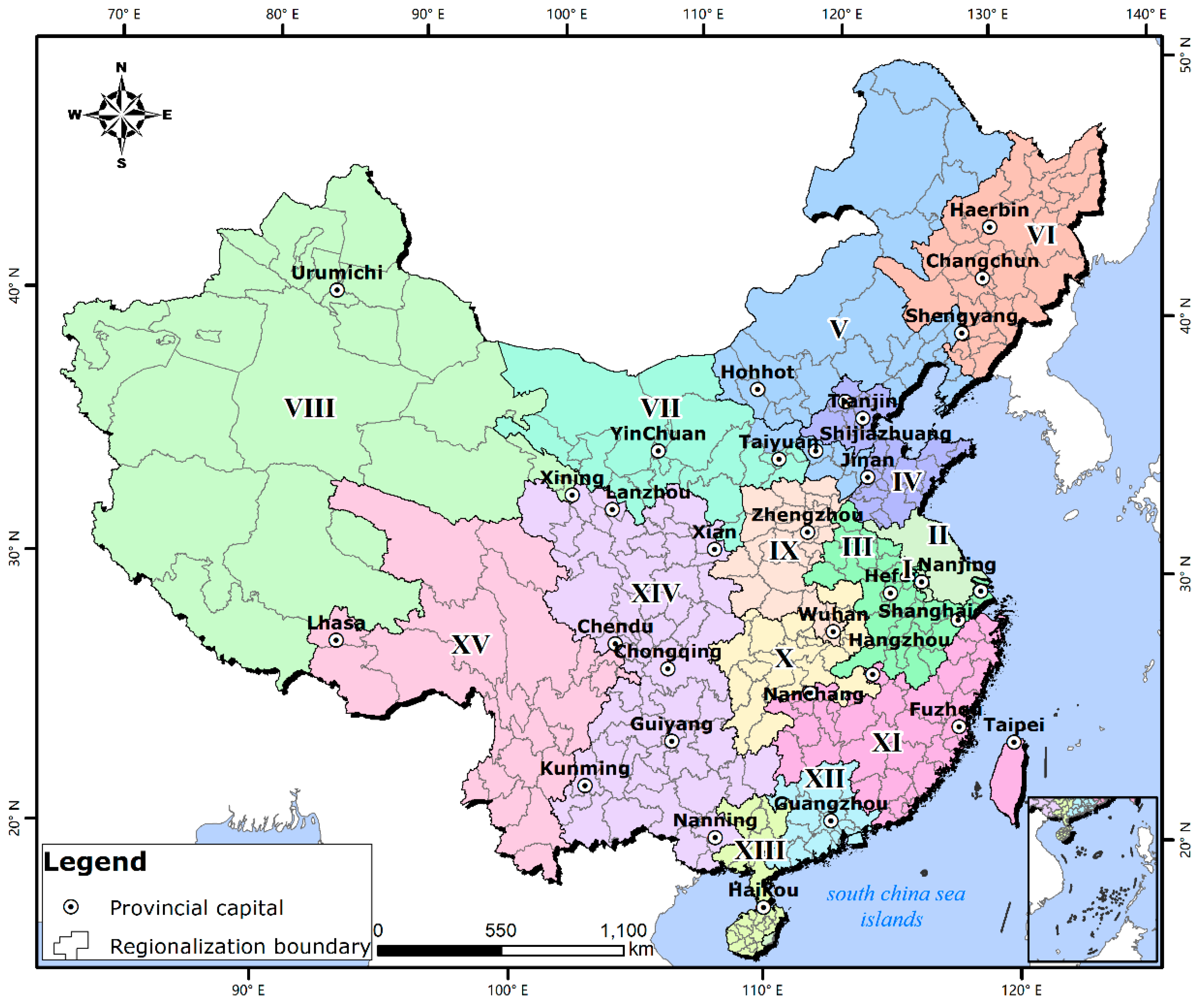
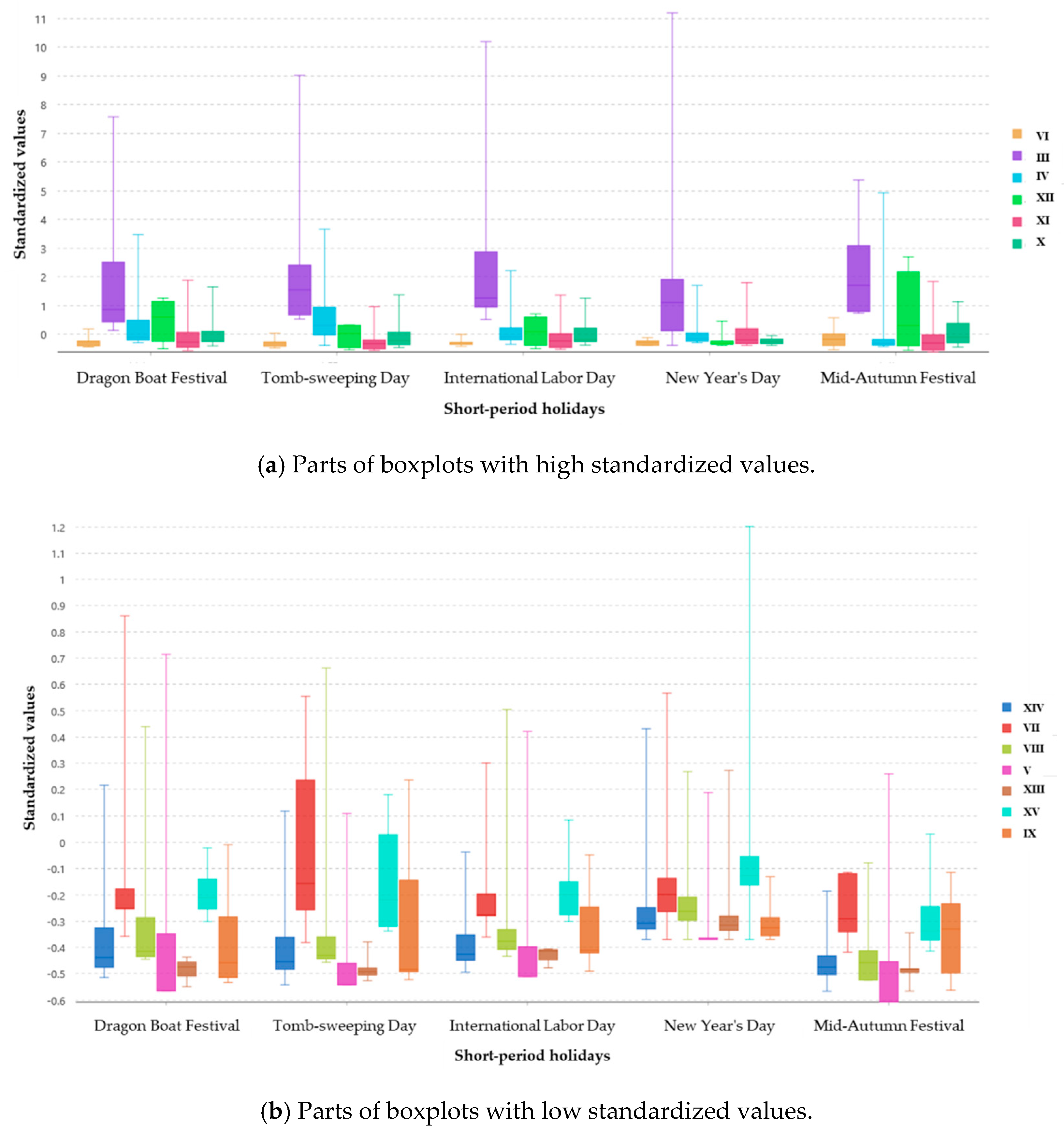
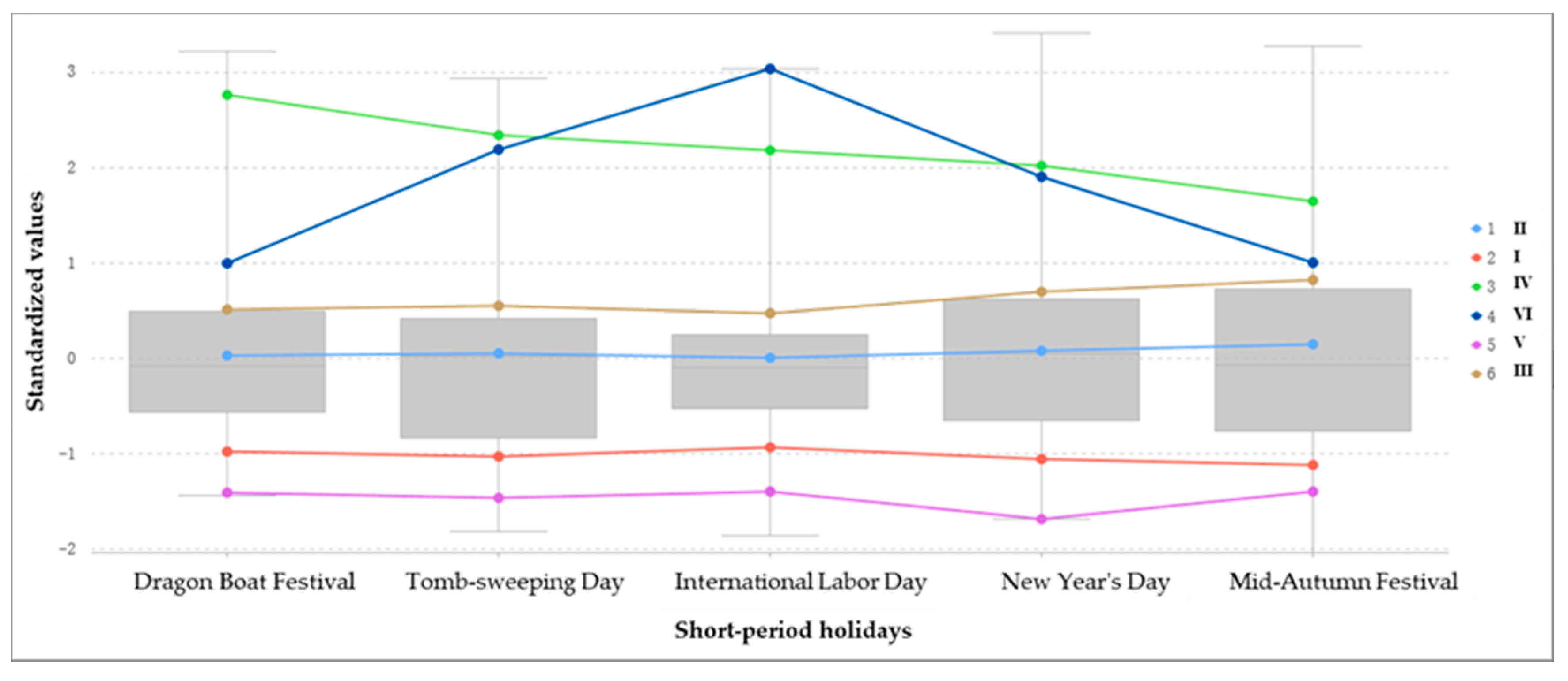
4.2. Regionalization of Tourist Flow Intensity
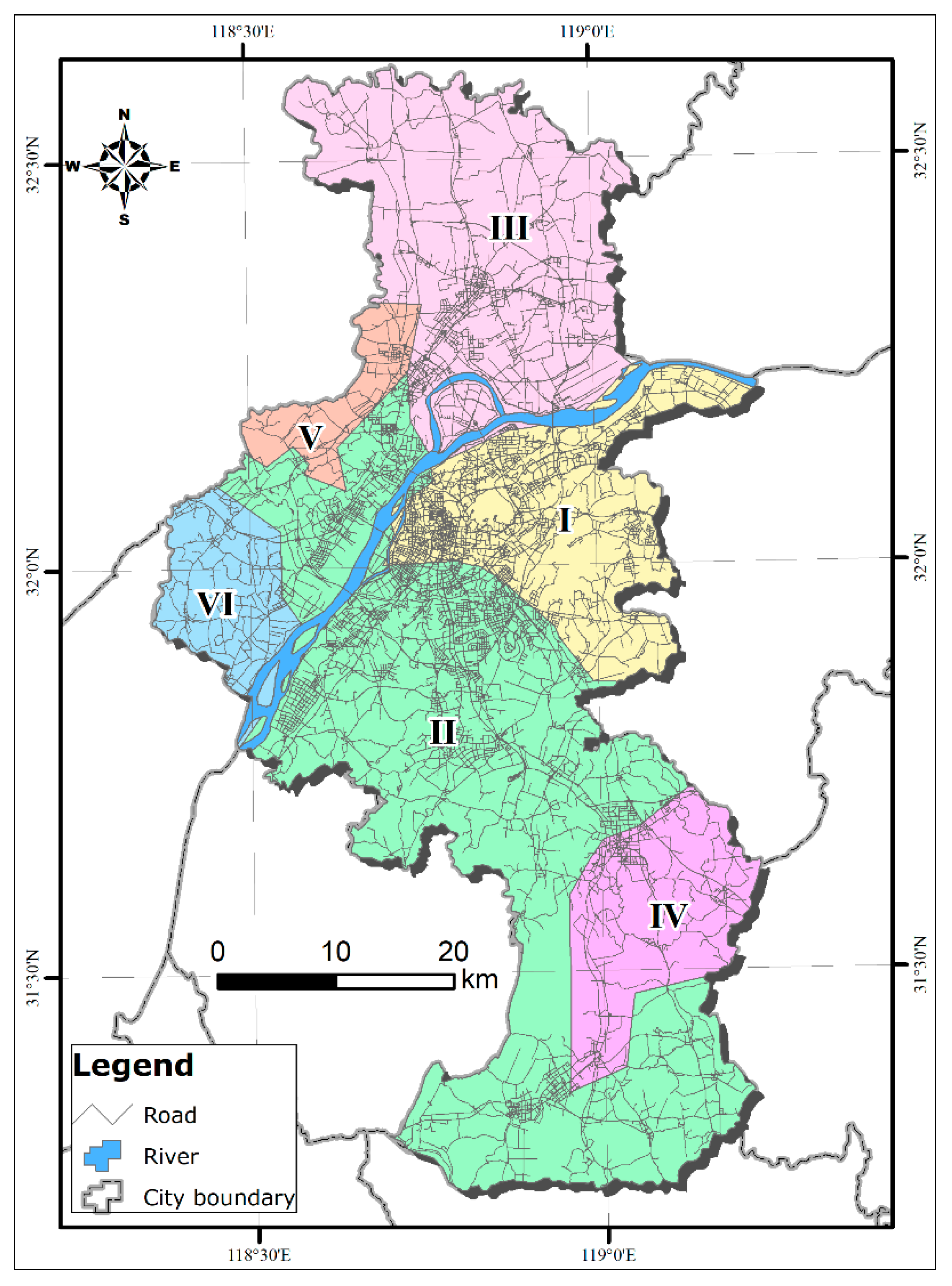
4.3. Regionalization of Tourist Flow Sink
5. Discussion
5.1. Reliability of Data and Recognition of Tourist Flow
5.2. Relationship between Regionalization and Geospatial Cognition
6. Conclusions and Future Directions
6.1. Conclusions
6.2. Future Directions
Author Contributions
Funding
Conflicts of Interest
References
- Bao, J.G.; Ma, L.J.C. Tourism geography in china, 1978–2008: Whence, what and whither? Prog. Hum. Geog. 2011, 35, 3–20. [Google Scholar]
- Pandy, W.R.; Rogerson, C.M. The timeshare industry of Africa: A study in tourism geography. Bull. Geogr. Socio-Econ. Ser. 2013, 21, 97–109. [Google Scholar] [CrossRef][Green Version]
- Youyin, Z.; Jing, G.; Yaofeng, M. Tourist flow research progress, evaluation and outlook. Tour. Trib./Lvyou Xuekan 2013, 28, 38–46. [Google Scholar]
- Degen, W. The influence of Beijing-Shanghai high-speed railway on tourist flow and time-space distribution. Tour. Trib./Lvyou Xuekan 2014, 29, 75–82. [Google Scholar]
- Feng, N.; Li, J. A couple analysis of the extraversion online tourism information, inbound tourist flow: A case of the American, Canadian inbound tourist flow. Tour. Trib. 2014, 29, 79–86. [Google Scholar]
- Xi, Y.; Wang, Z.F.; Department of Culture Industry Management, Hunan University of Commerce; Business College of Jishou University. Exploratory analysis of Hunan tourist flow agglomeration and diffusion based on traffic network. Areal Res. Dev. 2014, 3, 1–28. [Google Scholar]
- Fuchs, M.; Hopken, W.; Lexhagen, M. Big data analytics for knowledge generation in tourism destinations—A case from Sweden. J. Destin. Mark. Manag. 2014, 3, 198–209. [Google Scholar] [CrossRef]
- Irudeen, R.; Samaraweera, S. Big data solution for Sri Lankan development: A case study from travel and tourism. In Proceedings of the 2013 International Conference on Advances in ICT for Emerging Regions (ICTer), Colombo, Sri Lanka, 11–15 December 2013; pp. 207–216. [Google Scholar]
- Xiang, Z.; Fesenmaier, D.R. Big data analytics, tourism design and smart tourism. In Analytics in Smart Tourism Design; Springer: Cham, Switzerland, 2017; pp. 299–307. [Google Scholar]
- Li, J.J.; Xu, L.Z.; Tang, L.; Wang, S.Y.; Li, L. Big data in tourism research: A literature review. Tour. Manag. 2018, 68, 301–323. [Google Scholar] [CrossRef]
- March, R.; Woodside, A.G. Testing theory of planned versus realized tourism behavior. Ann. Tour. Res. 2005, 32, 905–924. [Google Scholar] [CrossRef]
- Miller, D.; Merrilees, B.; Coghlan, A. Sustainable urban tourism: Understanding and developing visitor pro-environmental behaviours. J. Sustain. Tour. 2015, 23, 26–46. [Google Scholar] [CrossRef]
- Woodside, A.G.; Hsu, S.Y.; Marshall, R. General theory of cultures’ consequences on international tourism behavior. J. Bus. Res. 2011, 64, 785–799. [Google Scholar] [CrossRef]
- Buhalis, D.; Law, R. Progress in information technology and tourism management: 20 years on and 10 years after the internet—The state of Etourism research. Tour. Manag. 2008, 29, 609–623. [Google Scholar] [CrossRef]
- Martin, B.G. Weather, climate and tourism—A geographical perspective. Ann. Tour. Res. 2005, 32, 571–591. [Google Scholar] [CrossRef]
- Khan, S.A.R.; Dong, Q.L.; Wei, S.B.; Zaman, K.; Zhang, Y. Travel and tourism competitiveness index: The impact of air transportation, railways transportation, travel and transport services on international inbound and outbound tourism. J. Air. Transp. Manag. 2017, 58, 125–134. [Google Scholar] [CrossRef]
- Louca, C. Income and expenditure in the tourism industry: Time series evidence from Cyprus. Tour. Econ. 2006, 12, 603–617. [Google Scholar] [CrossRef]
- Min, L. Research on income difference between urban and rural inhabitants during tourism development in zhangjiajie. J. Jishou Univ. Nat. Sci. Ed. 2011, 3, 103–106. [Google Scholar]
- Iwashita, C. Media representation of the UK as a destination for Japanese tourists: Popular culture and tourism. Tour. Stud. 2006, 6, 59–77. [Google Scholar] [CrossRef]
- Smith, S. A sense of place: Place, culture and tourism. Tour. Recreat. Res. 2015, 40, 220–233. [Google Scholar] [CrossRef]
- Astawa, I.P.; Triyuni, N.N.; Santosa, I.D.M.C. Sustainable tourism and harmonious culture: A case study of cultic model at village tourism. J. Phys. Conf. Ser. 2018, 953, 012057. [Google Scholar] [CrossRef]
- Hongsong, P.; Lin, L.; Xingfu, L. The network structure of cross-border tourism flow based on the social network method: A case of Lugu lake region. Sci. Geogr. Sin. 2014, 34, 1041–1050. [Google Scholar]
- Crampon, L.; Tan, K. A model of tourism flow into the pacific. Tour. Rev. 1973, 28, 98–104. [Google Scholar] [CrossRef]
- Hemson, G.; Maclennan, S.; Mills, G.; Johnson, P.; Macdonald, D. Community, lions, livestock and money: A spatial and social analysis of attitudes to wildlife and the conservation value of tourism in a human-carnivore conflict in botswana. Biol. Conserv. 2009, 142, 2718–2725. [Google Scholar] [CrossRef]
- Tsai, P.W.; Chen, Z.S.; Xue, X.S.; Chang, J.F. Studying the influence of tourism flow on foreign exchange rate by iabc and time-series models. In Advances in Intelligent Information Hiding and Multimedia Signal Processing, Pt I; Springer: Cham, Switzerland, 2018; Volume 81, pp. 225–232. [Google Scholar]
- Yang, X.Z.; Wang, Q. Exploratory space-time analysis of inbound tourism flows to china cities. Int. J. Tour. Res. 2014, 16, 303–312. [Google Scholar]
- Kelly, J.; Haider, W.; Williams, P.W. A behavioral assessment of tourism transportation options for reducing energy consumption and greenhouse gases. J. Travel Res. 2007, 45, 297–309. [Google Scholar] [CrossRef]
- Bieger, T.; Wittmer, A. Air transport and tourism—Perspectives and challenges for destinations, airlines and governments. J. Air Transp. Manag. 2006, 12, 40–46. [Google Scholar] [CrossRef]
- Papatheodorou, A.; Rosselló, J.; Xiao, H. Global economic crisis and tourism: Consequences and perspectives. J. Travel Res. 2010, 49, 39–45. [Google Scholar] [CrossRef]
- Klabbers, M.; Timmermans, H. Measuring tourism consumer behaviour using escape: A multimedia interview engine for stated choice and preference experiments. In Information and Communication Technologies in Tourism 1999; Springer: Vienna, Austria, 1999; pp. 179–190. [Google Scholar]
- Strang, E.; Peterson, Z.D. Unintentional misreporting on self-report measures of sexually aggressive behavior: An interview study. J. Sex Res. 2017, 54, 971–983. [Google Scholar] [CrossRef]
- Kawase, J.; Kurata, Y.; Yabe, N. When and where tourists are viewing exhibitions: Toward sophistication of GPS-assisted tourist activity surveys. In Proceedings of the Information and Communication Technologies in Tourism 2012, Helsingborg, Sweden, 25–27 January 2012; pp. 415–425. [Google Scholar]
- Zheng, W.; Huang, X.T.; Li, Y. Understanding the tourist mobility using GPS: Where is the next place? Tour. Manag. 2017, 59, 267–280. [Google Scholar] [CrossRef]
- Dijk, J.V.; Jong, T.D. Post-processing GPS-tracks in reconstructing travelled routes in a GIS-environment: Network subset selection and attribute adjustment. Ann. GIS 2017, 23, 203–217. [Google Scholar] [CrossRef]
- Li, H.; Gao, W. Study on region difference of tourism development in Guangdong province based on spatial statistical analysis. J. Xinyang Norm. Univ. Nat. Sci. Ed. 2016, 29, 71–74. [Google Scholar]
- Li, M.M.; Fang, L.; Huang, X.T.; Goh, C. A spatial-temporal analysis of hotels in urban tourism destination. Int. J. Hosp. Manag. 2015, 45, 34–43. [Google Scholar] [CrossRef]
- Kline, C.; Hao, H.; Alderman, D.; Kleckley, J.W.; Gray, S. A spatial analysis of tourism, entrepreneurship and the entrepreneurial ecosystem in North Carolina, USA. Tour. Plan. Dev. 2014, 11, 305–316. [Google Scholar] [CrossRef]
- Morley, C.; Rossello, J.; Santana-Gallego, M. Gravity models for tourism demand: Theory and use. Ann. Tour. Res. 2014, 48, 1–10. [Google Scholar] [CrossRef]
- Baggio, R.; Scott, N.; Cooper, C. Network science a review focused on tourism. Ann. Tour. Res. 2010, 37, 802–827. [Google Scholar] [CrossRef]
- Zhang, H.P.; Zhou, X.X.; Gu, X.; Zhou, L.; Ji, G.L.; Tang, G.A. Method for the analysis and visualization of similar flow hotspot patterns between different regional groups. ISPRS Int. J. Geo-Inf. 2018, 7, 328. [Google Scholar] [CrossRef]
- Wang, H.; Huang, H.; Ni, X.; Zeng, W. Revealing spatial-temporal characteristics and patterns of urban travel: A large-scale analysis and visualization study with taxi GPS data. ISPRS Int. J. Geo-Inf. 2019, 8, 257. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, H.-P.; Ji, G.; Tang, G.-A. A method to mine movement patterns between zones: A case study of subway commuters in Shanghai. IEEE Access 2019, 7, 67795–67806. [Google Scholar] [CrossRef]
- Agiomirgianakis, G.; Serenis, D.; Tsounis, N. Short-and long-run determinants of tourist flows: The case of South Korea. In Advances in Applied Economic Research; Springer: Cham, Switzerland, 2017; pp. 861–872. [Google Scholar]
- Han, Y.; Wang, S.; Ren, Y.; Wang, C.; Gao, P.; Chen, G. Predicting station-level short-term passenger flow in a citywide metro network using spatiotemporal graph convolutional neural networks. ISPRS Int. J. Geo-Inf. 2019, 8, 243. [Google Scholar] [CrossRef]
- Lu, Z.B.; Rao, W.M.; Wu, Y.J.; Guo, L.; Xia, J.X. A kalman filter approach to dynamic od flow estimation for urban road networks using multi-sensor data. J. Adv. Transport. 2015, 49, 210–227. [Google Scholar] [CrossRef]
- Li, X.; Huang, G.; Tang, J. Passenger flow forecasting based on od-matrix estimation model. J. China Railw. Soc. 2008, 30, 7–12. [Google Scholar]
- Alexander, L.; Jiang, S.; Murga, M.; Gonzalez, M.C. Origin-destination trips by purpose and time of day inferred from mobile phone data. Transport. Res. C Emerg. Technol. 2015, 58, 240–250. [Google Scholar] [CrossRef]
- Miah, S.J.; Vu, H.Q.; Gammack, J.; McGrath, M. A big data analytics method for tourist behaviour analysis. Inf. Manag. 2017, 54, 771–785. [Google Scholar] [CrossRef]
- Nie, Y.M.; Zhang, H.M. A relaxation approach for estimating origin-destination trip tables. Netw. Spat. Econ. 2010, 10, 147–172. [Google Scholar] [CrossRef]
- Lankford, P.M. Regionalization: Theory and alternative algorithms. Geogr Anal. 1969, 1, 196–212. [Google Scholar] [CrossRef]
- Getis, A.; Aldstadt, J. Constructing the spatial weights matrix using a local statistic. Geogr. Anal. 2004, 36, 90–104. [Google Scholar] [CrossRef]
- Marcon, E.; Puech, F. Measures of the geographic concentration of industries: Improving distance-based methods. J. Econ. Geogr. 2010, 10, 745–762. [Google Scholar] [CrossRef]
- Lewis, D.B. Elementary statistics for geographers, 3rd ed.; Guilford Press: New York, NY, USA, 2010; p. 464. [Google Scholar]
- Maurel, F.; Sedillot, B. A measure of the geographic concentration in French manufacturing industries. Reg. Sci. Urban Econ. 2004, 29, 575–604. [Google Scholar] [CrossRef]
- Wu, H.; Hayes, M.J.; Weiss, A.; Hu, Q. An evaluation of the standardized precipitation index, the china-z index and the statistical z-score. Int. J. Climatol. 2001, 21, 745–758. [Google Scholar] [CrossRef]
- Assuncao, R.M.; Neves, M.C.; Camara, G.; Da Costa Freitas, C. Efficient regionalization techniques for socio-economic geographical units using minimum spanning trees. Int. J. Geogr. Inf. Sci. 2006, 20, 797–811. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Performance evaluation of some clustering algorithms and validity indices. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 1650–1654. [Google Scholar] [CrossRef]
- Marty, P.F. An introduction to digital convergence: Libraries, archives, and museums in the information age. Libr. Quart. 2010, 80, 1–5. [Google Scholar] [CrossRef]
- Andris, C.; Xi, L.; Ferreira, J., Jr. Challenges for social flows. Comput. Environ. Urban Syst. 2018, 70, 197–207. [Google Scholar] [CrossRef]
- Andris, C. Integrating social network data into gisystems. Int. J. Geogr. Inf. Sci. 2016, 30, 2009–2031. [Google Scholar] [CrossRef]
- Midler, J.C. Non-Euclidean geographic spaces: Mapping functional distances. Geogr. Anal. 1982, 14, 189–203. [Google Scholar] [CrossRef]
- Wang, Y.X.; Wang, F.H.; Zhang, Y.; Liu, Y. Delineating urbanization “source-sink” regions in china: Evidence from mobile app data. Cities 2019, 86, 167–177. [Google Scholar] [CrossRef]
- Li, Q.; Xu, M.X.; Liu, G.B.; Zhao, Y.G.; Tuo, D.F. Cumulative effects of a 17-year chemical fertilization on the soil quality of cropping system in the loess hilly region, China. J. Plant Nutr. Soil Sci. 2013, 176, 249–259. [Google Scholar] [CrossRef]
- Lu, G.N.; Batty, M.; Strobl, J.; Lin, H.; Zhu, A.X.; Chen, M. Reflections and speculations on the progress in Geographic Information Systems (GIS): A geographic perspective. Int. J. Geogr. Inf. Sci. 2019, 33, 346–367. [Google Scholar] [CrossRef]
- Soll, D. Feeding gotham: The political economy and geography of food in New York city, 1790–1860. J. Interdiscipl. Hist. 2018, 48, 417–418. [Google Scholar] [CrossRef]
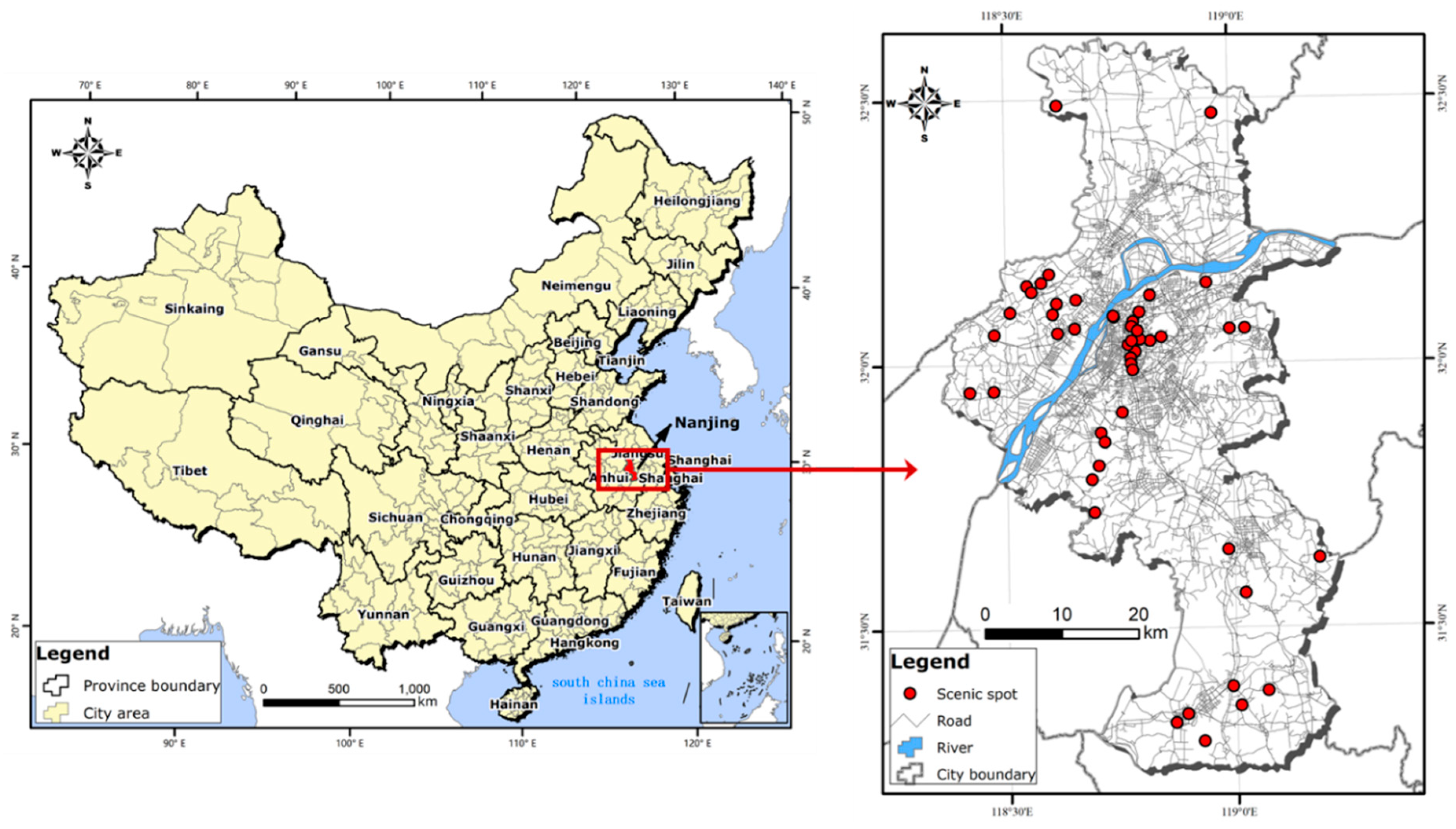
| Short-Period Holidays | Periods of Time | Total Number of Tourists |
|---|---|---|
| New Year’s Day | 2017/12/30–2018/01/01 | 224.40 million |
| Tomb-Sweeping Day | 2018/04/05–2018/04/07 | 426.68 million |
| International Labor Day | 2018/04/29–2018/05/01 | 493.04 million |
| Dragon Boat Festival | 2018/06/16–2018/06/18 | 268.06 million |
| Mid-Autumn Festival | 2018/09/22–2018/09/24 | 630.53 million |
| Attribute Name | Attribute Type | Attribute Description |
|---|---|---|
| Origin_city | string | Source city of tourist |
| Destination_city | string | Nanjing city |
| Visited_date | datetime | Date of visit |
| Scenic_spot | string | Visited scenic spots in Nanjing |
| Short-Period Holidays | Global Moran’s I Index | Z-Score |
|---|---|---|
| New Year’s Day | 0.327 *** | 19.56 |
| Tomb-Sweeping Day | 0.333 *** | 18.71 |
| International Labor Day | 0.371 *** | 21.37 |
| Dragon Boat Festival | 0.323 *** | 18.14 |
| Mid-Autumn Festival | 0.347 *** | 18.98 |
| Short-Period Holidays | Global Moran’s I Index | Z-Score |
|---|---|---|
| New Year’s Day | 0.202 *** | 3.23 |
| Tomb-Sweeping Day | 0.287 *** | 4.47 |
| International Labor Day | 0.214 *** | 3.43 |
| Dragon Boat Festival | 0.303 *** | 4.76 |
| Mid-Autumn Festival | 0.294 *** | 4.55 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, Q.; Zhang, H.; Chen, M.; Chen, C. Regionalization Analysis and Mapping for the Source and Sink of Tourist Flows. ISPRS Int. J. Geo-Inf. 2019, 8, 314. https://doi.org/10.3390/ijgi8070314
Gu Q, Zhang H, Chen M, Chen C. Regionalization Analysis and Mapping for the Source and Sink of Tourist Flows. ISPRS International Journal of Geo-Information. 2019; 8(7):314. https://doi.org/10.3390/ijgi8070314
Chicago/Turabian StyleGu, Qiushi, Haiping Zhang, Min Chen, and Chongcheng Chen. 2019. "Regionalization Analysis and Mapping for the Source and Sink of Tourist Flows" ISPRS International Journal of Geo-Information 8, no. 7: 314. https://doi.org/10.3390/ijgi8070314
APA StyleGu, Q., Zhang, H., Chen, M., & Chen, C. (2019). Regionalization Analysis and Mapping for the Source and Sink of Tourist Flows. ISPRS International Journal of Geo-Information, 8(7), 314. https://doi.org/10.3390/ijgi8070314






