An Urban Road-Traffic Commuting Dynamics Study Based on Hotspot Clustering and a New Proposed Urban Commuting Electrostatics Model
Abstract
1. Introduction
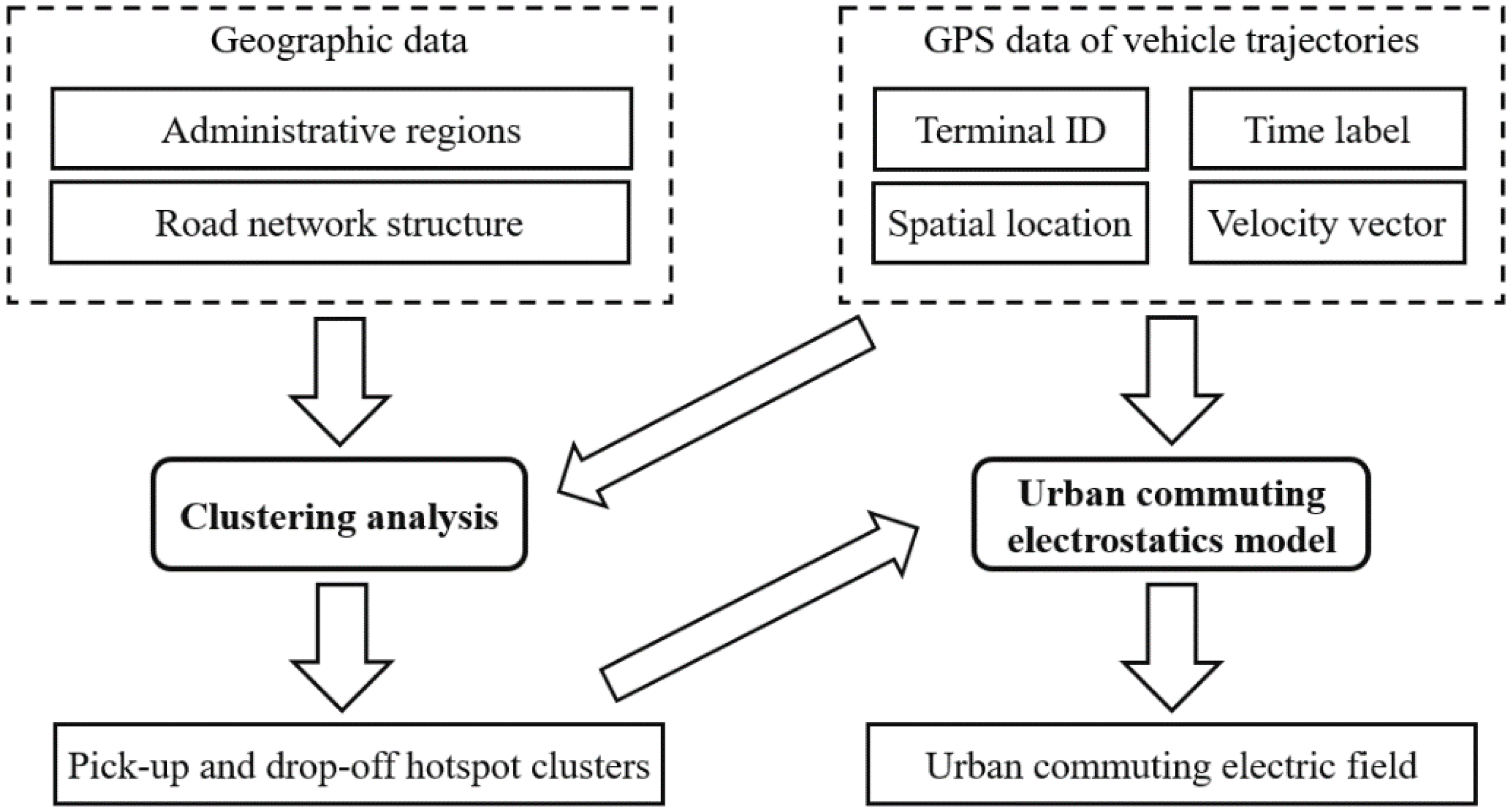
2. Methodology
2.1. Origin-Destination (O-D) Hotspot Clustering Model
2.2. Classical Theory of Electrostatics
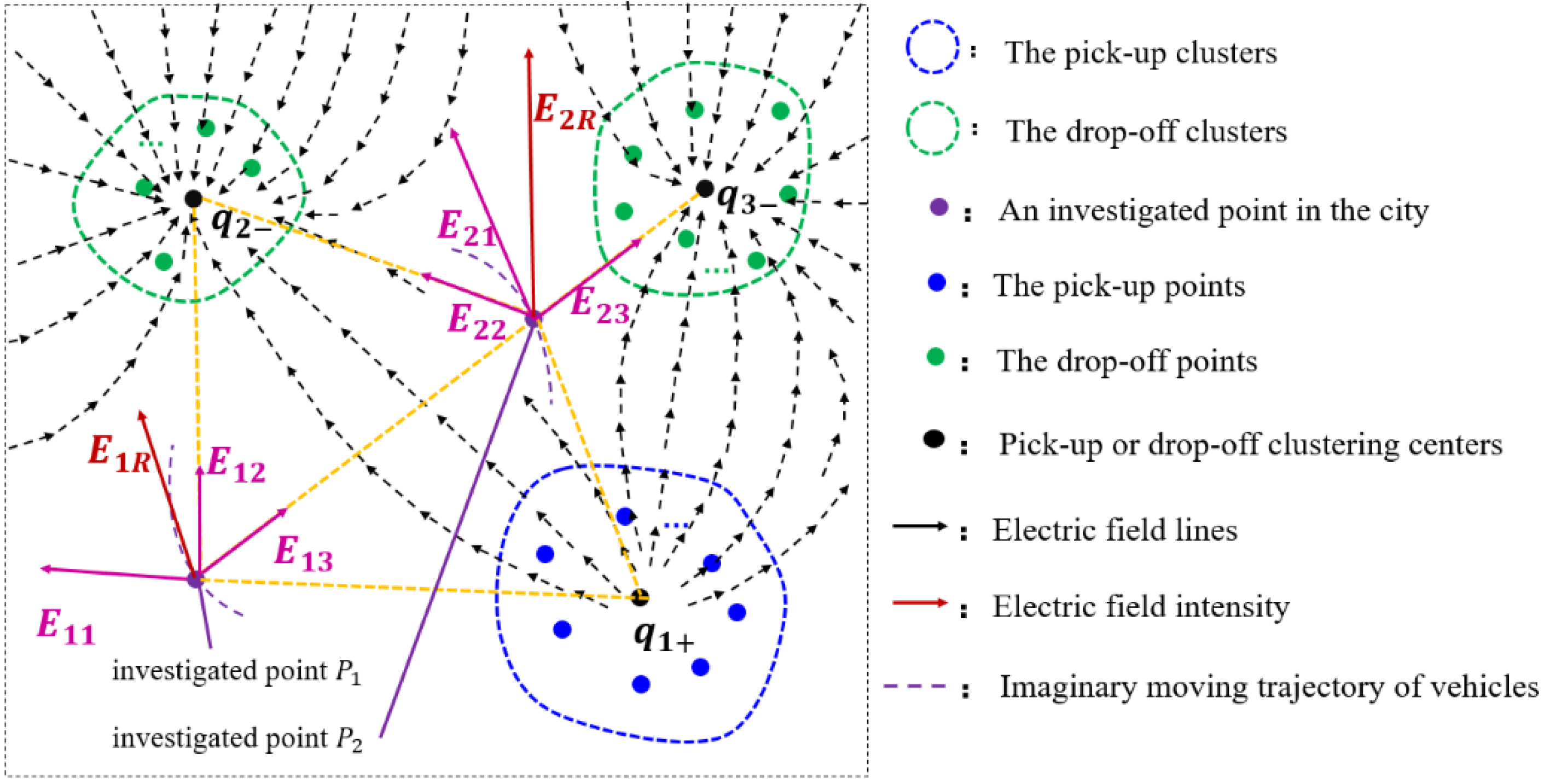
2.3. Urban Commuting Electrostatics Model
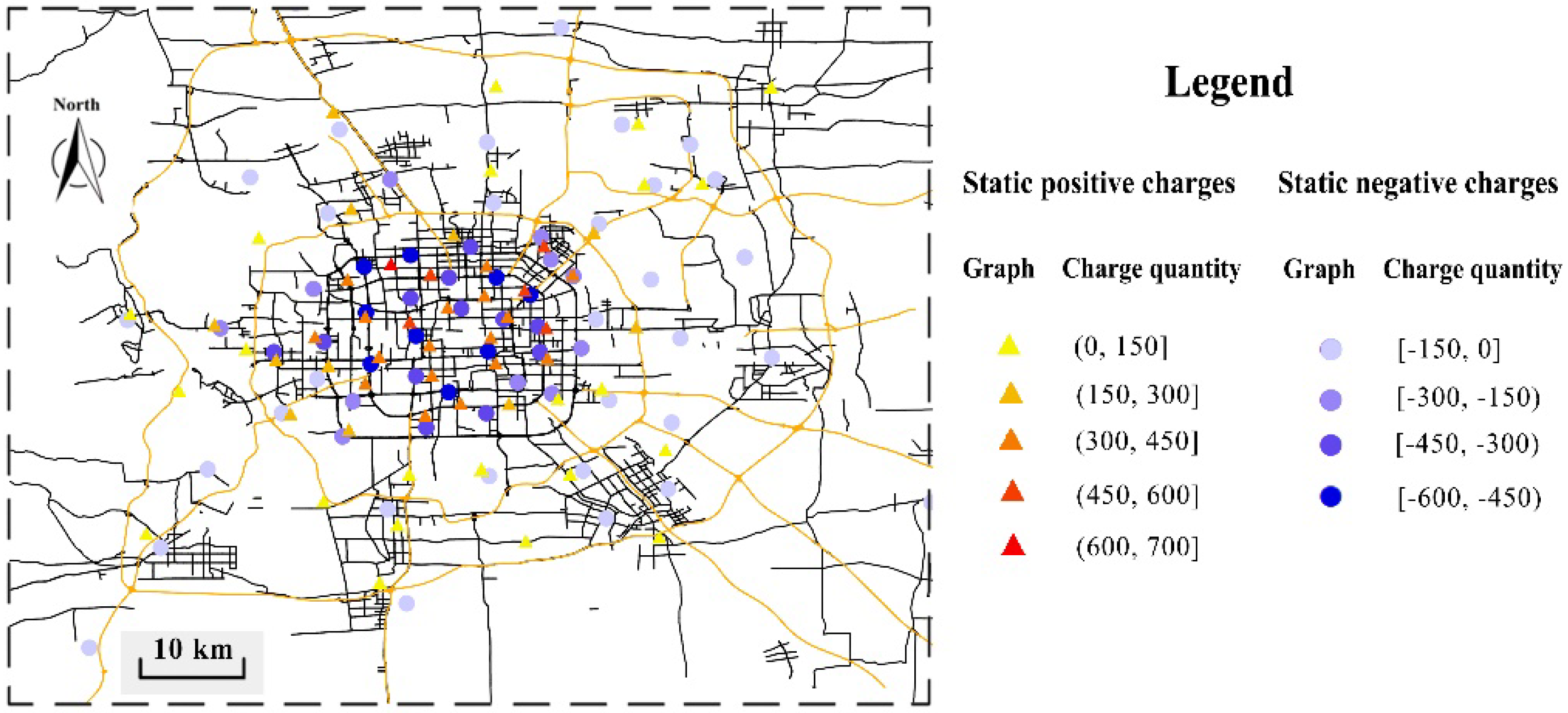
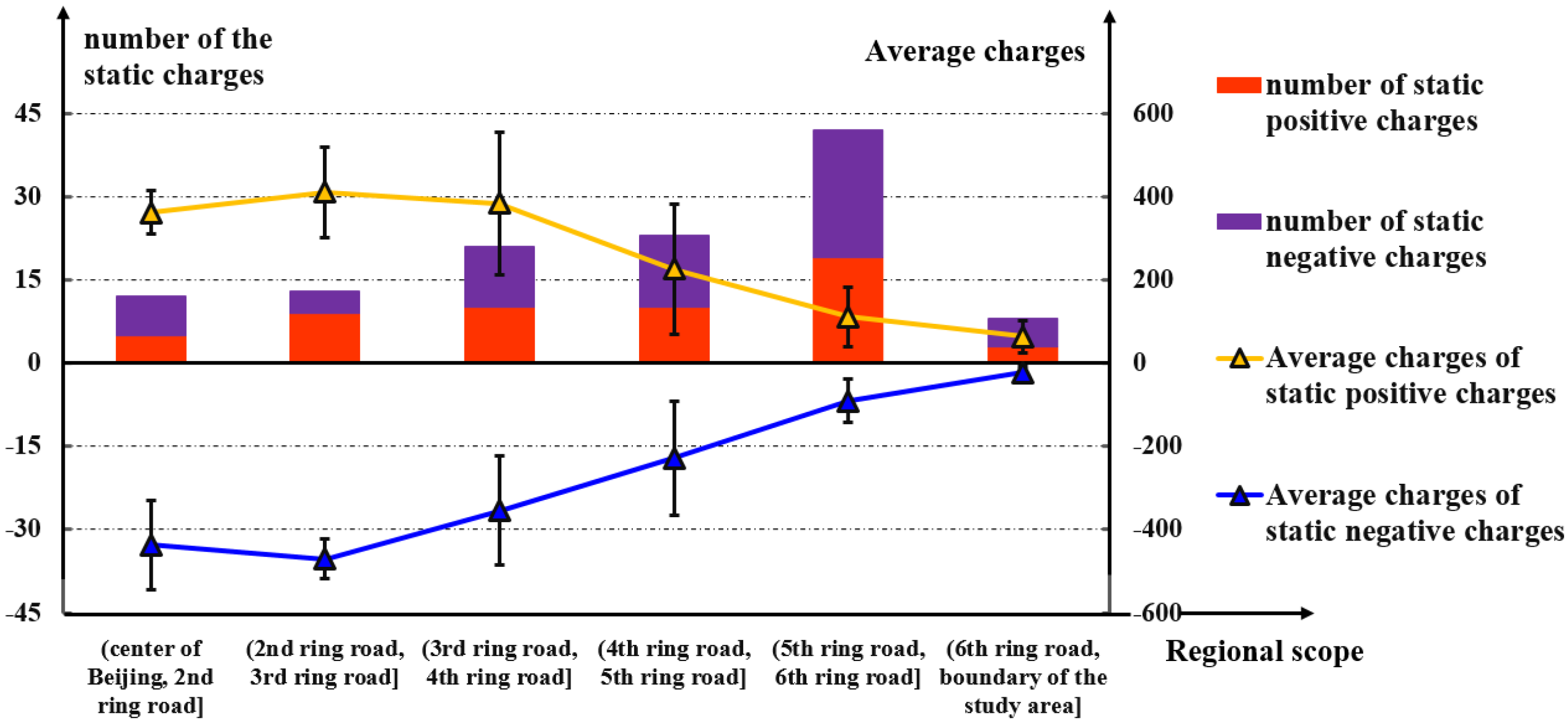
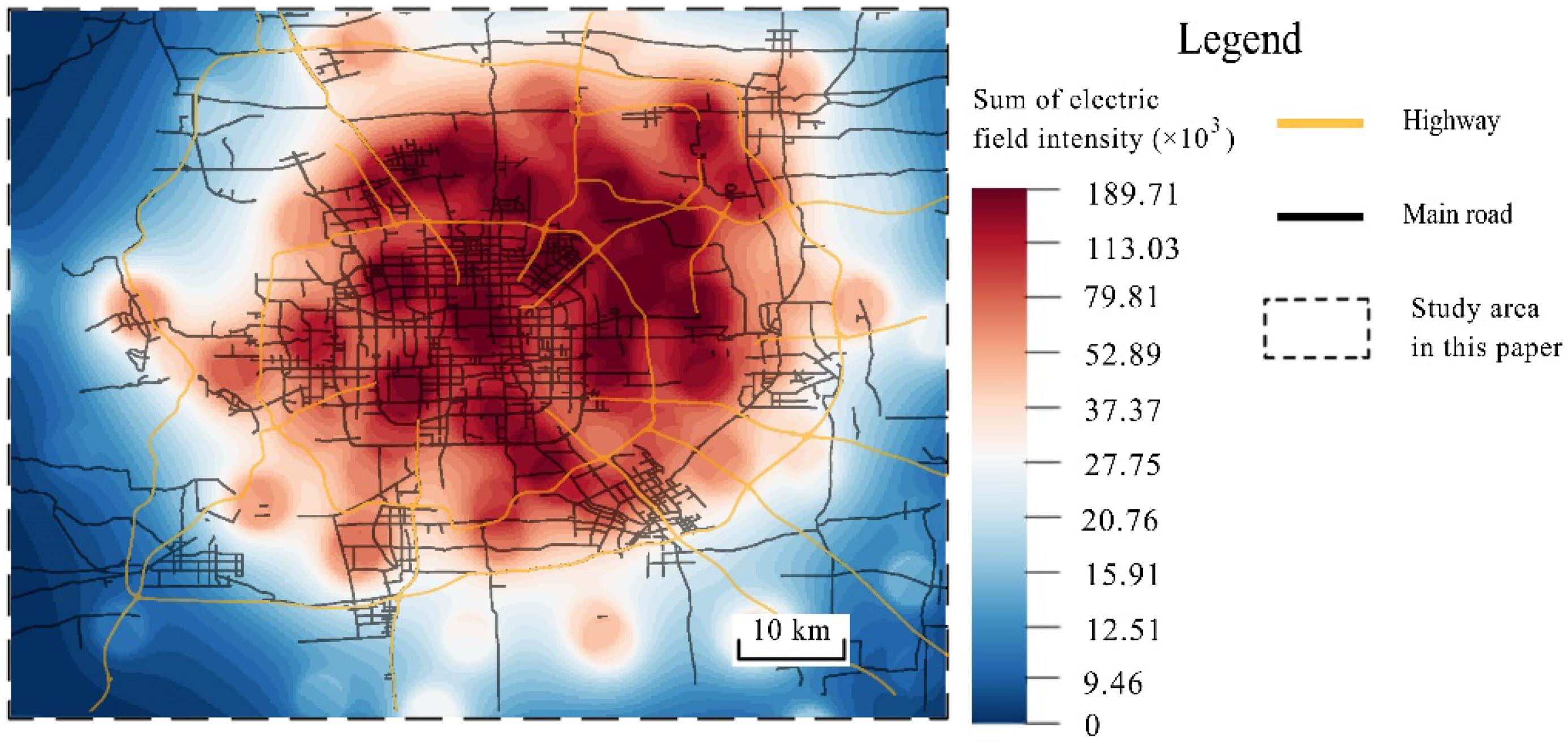
- The sum of the electric field intensities at a specific road point could reflect the importance of the road point to a certain extent. The road point has a greater probability of being a transportation hub or a transportation hotspot if the sum of the electric field intensities is bigger, since a bigger sum of the electric field intensities means that the road point is affected by more pick-up and drop-off hotspot clusters at a relatively close distance and bears more traffic-commuting pressure.
- The vector sum of the directions of the electric field at a road point can reflect the road-traffic commuting direction with the maximum probability at that point. The comprehensive performance of vehicles at a specific road point (denoted by ) tends to head in the same direction as the electric field at , since that specific direction represents the direction of the commuting function undertaken by in the entire urban road-traffic commuting system.
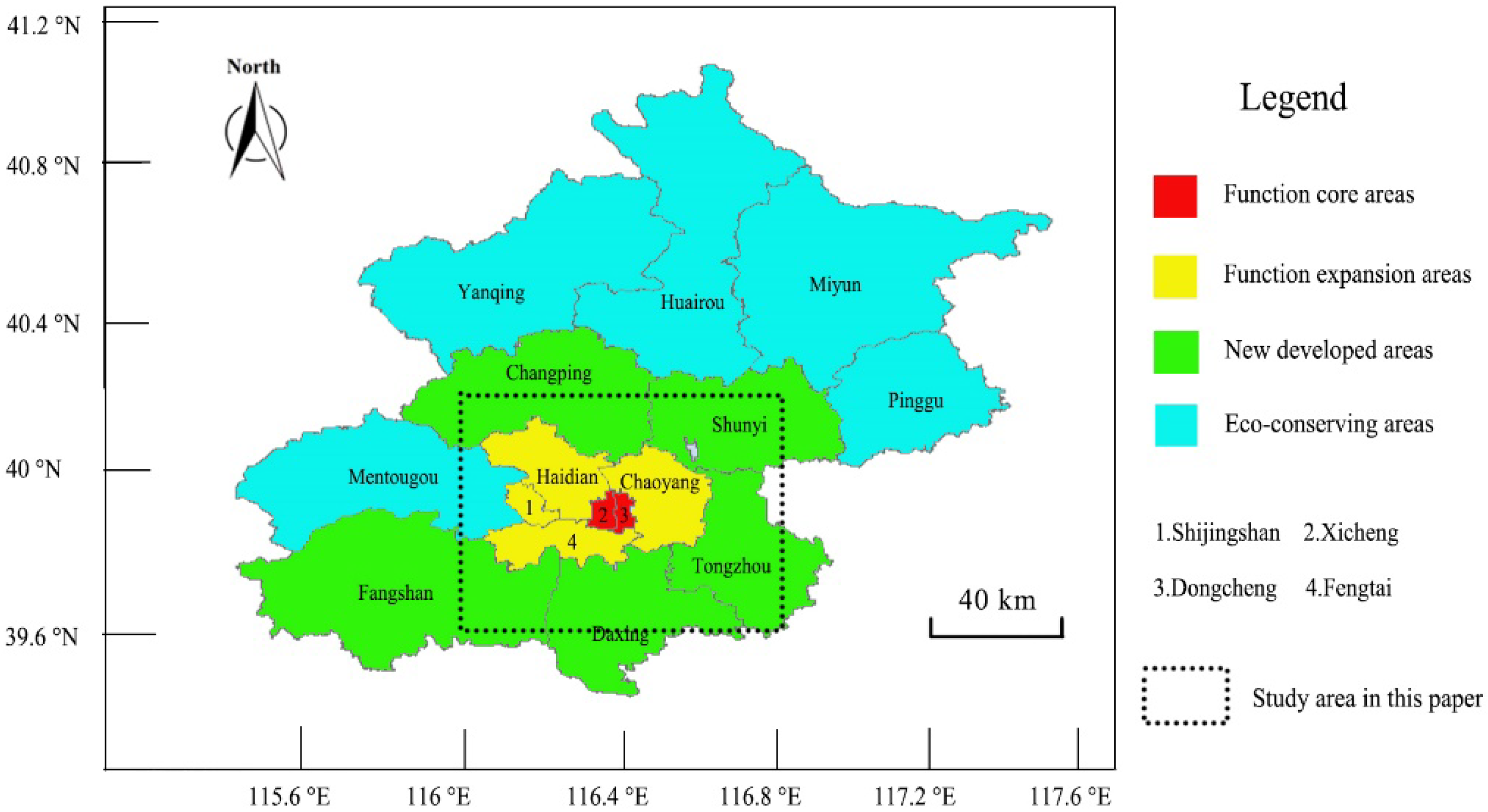
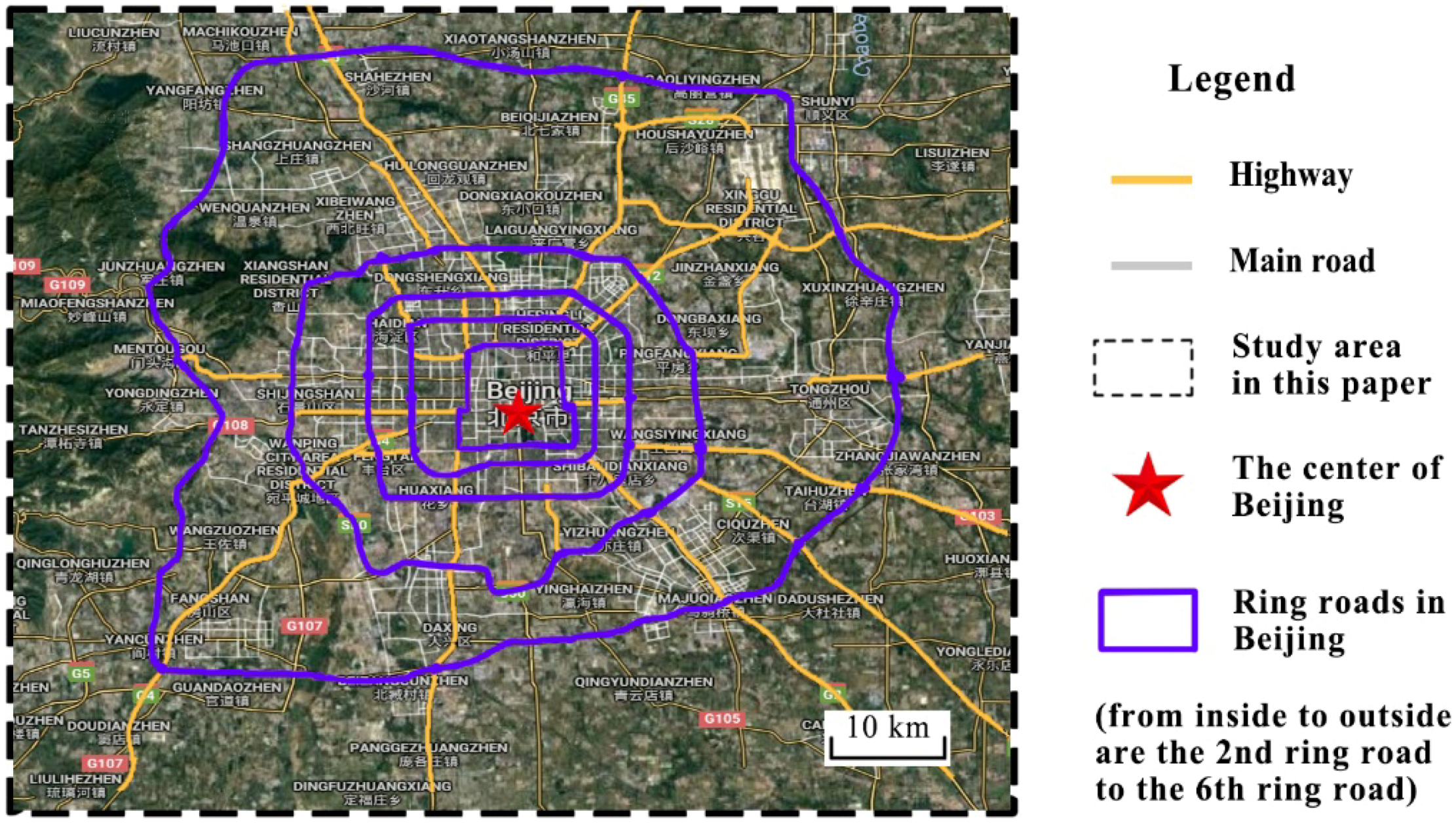
3. Study Area and Data Resources
3.1. Study Area
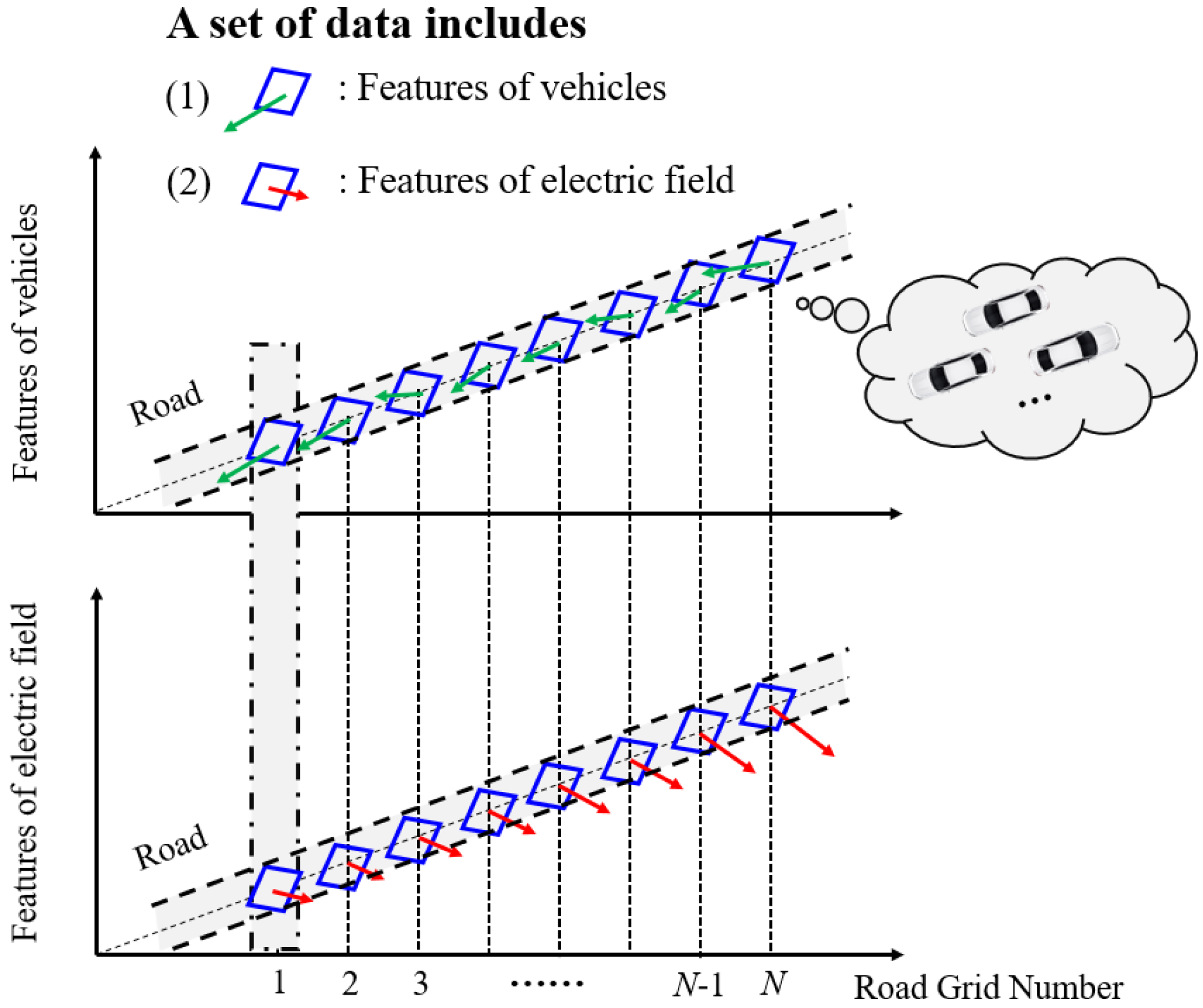
3.2. Data Resources
4. Results
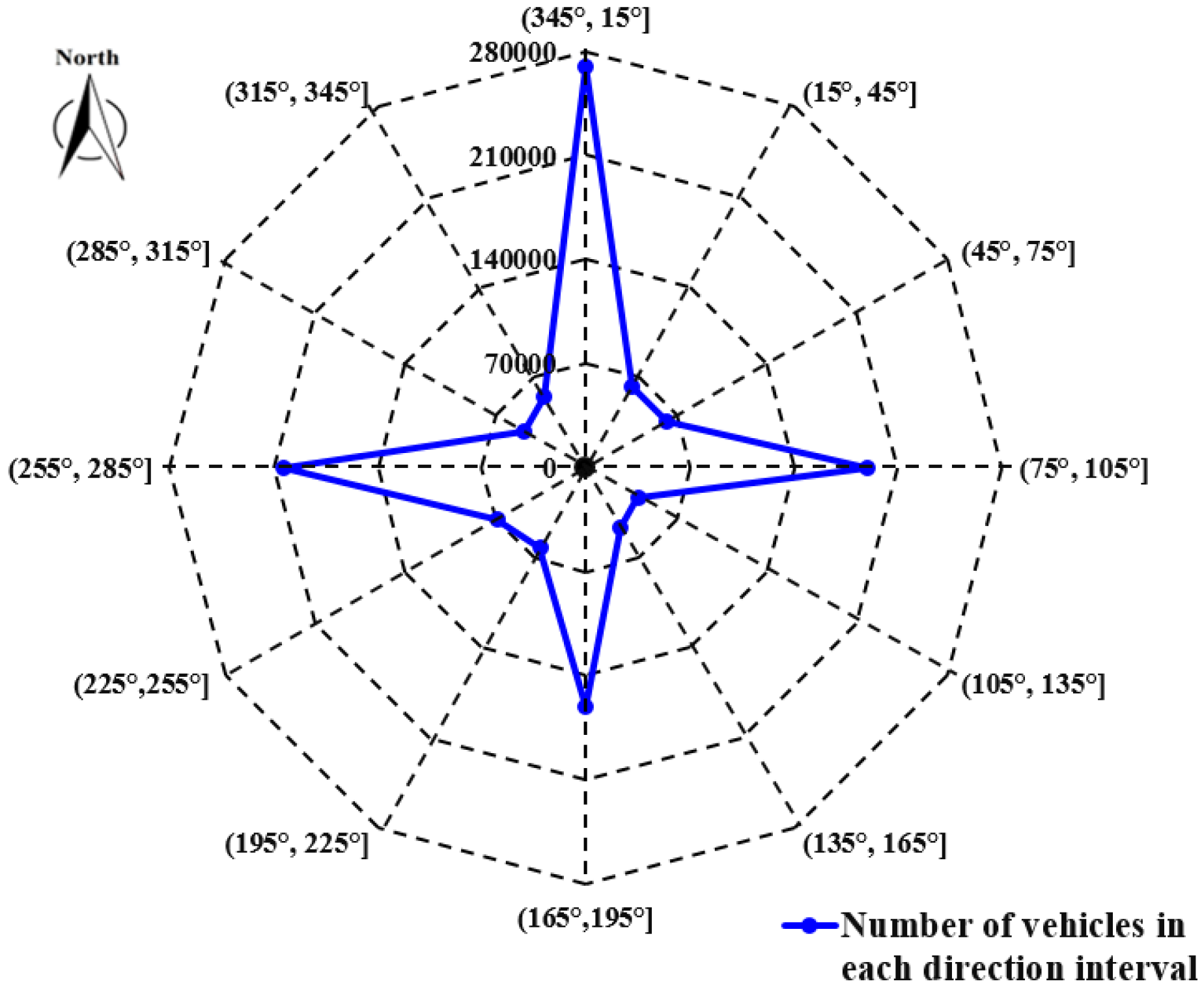
4.1. Features of the Urban Commuting Electric Field
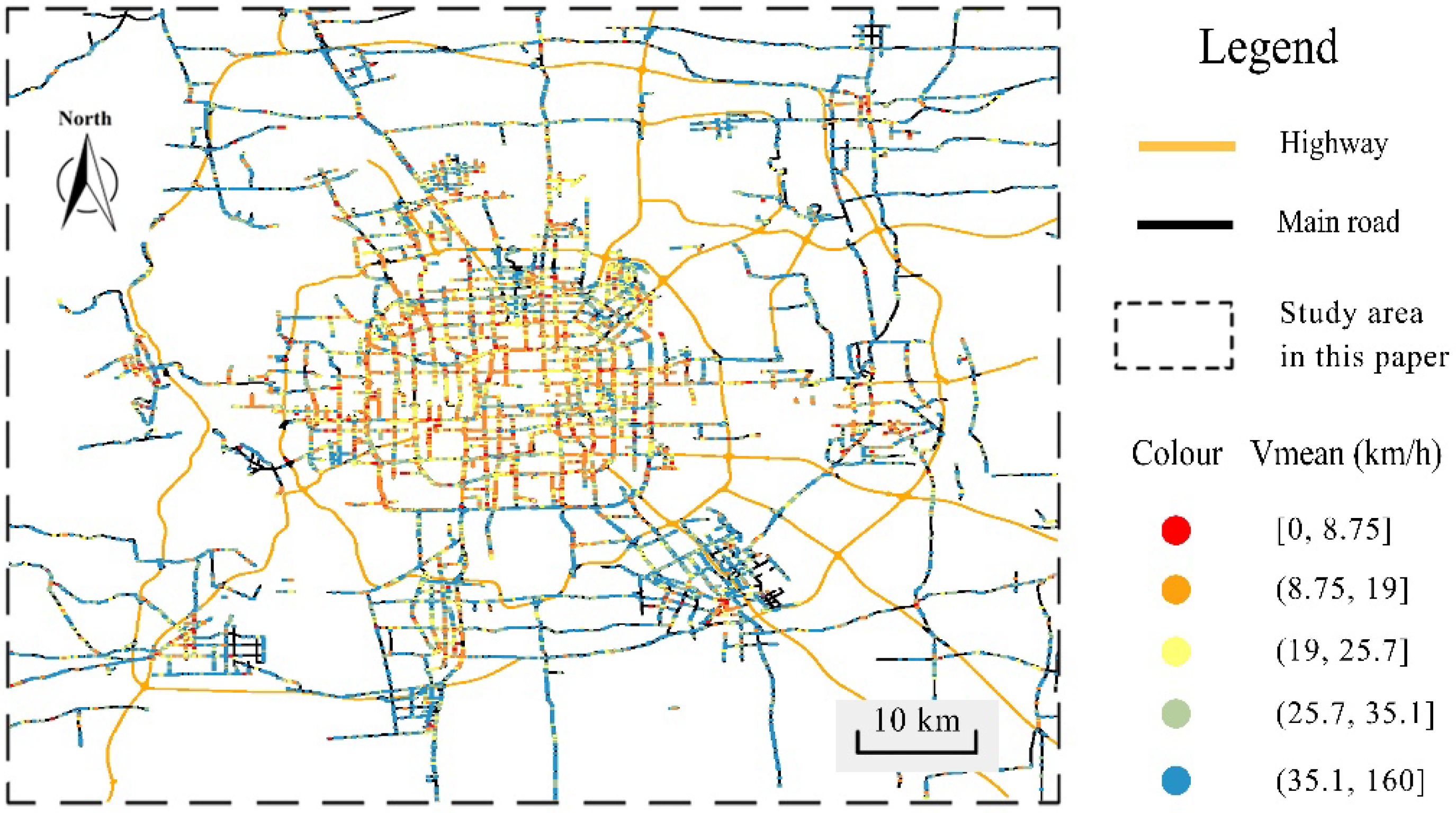
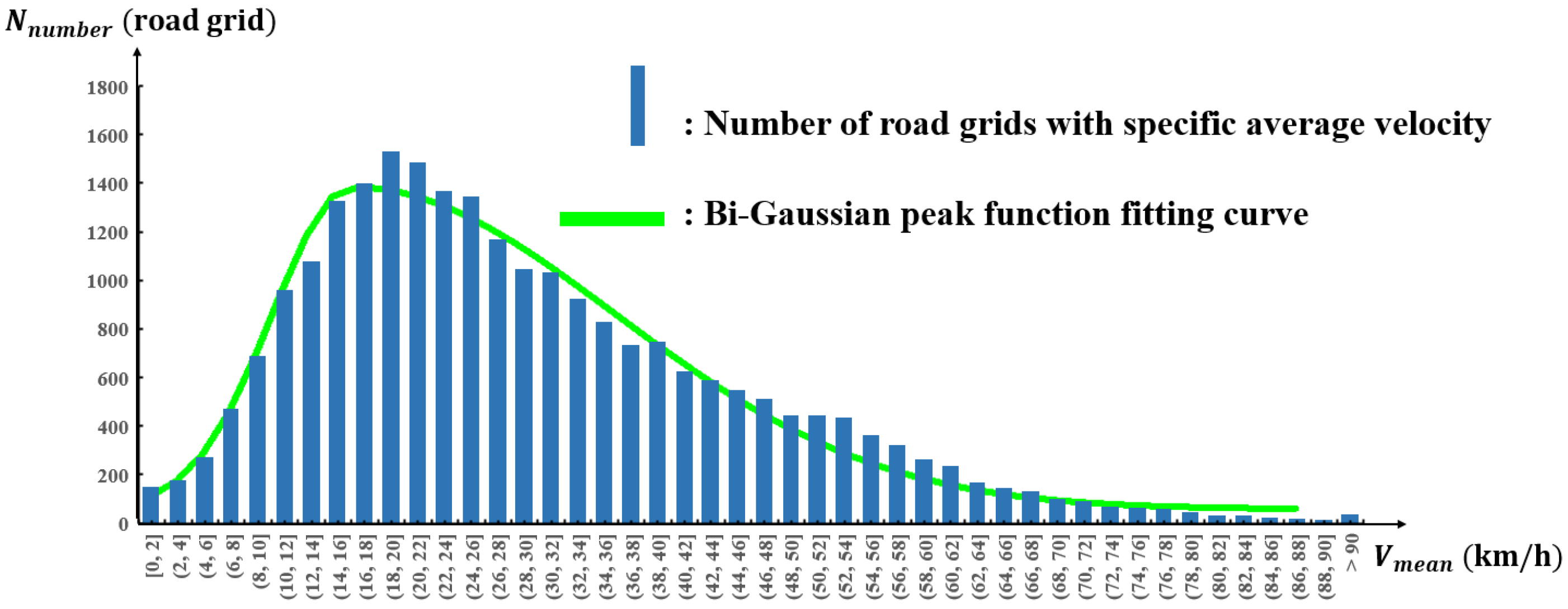
4.2. Features of Urban Road-Traffic Commuting
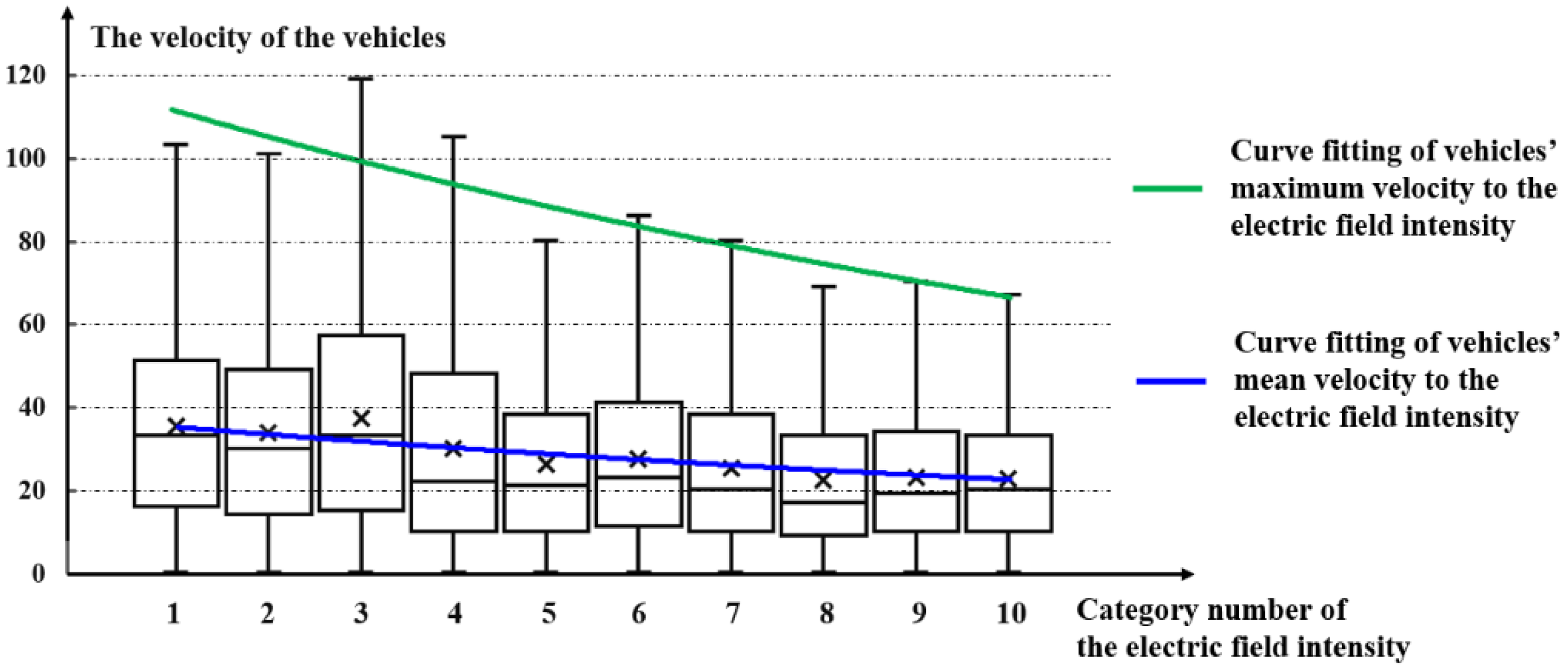
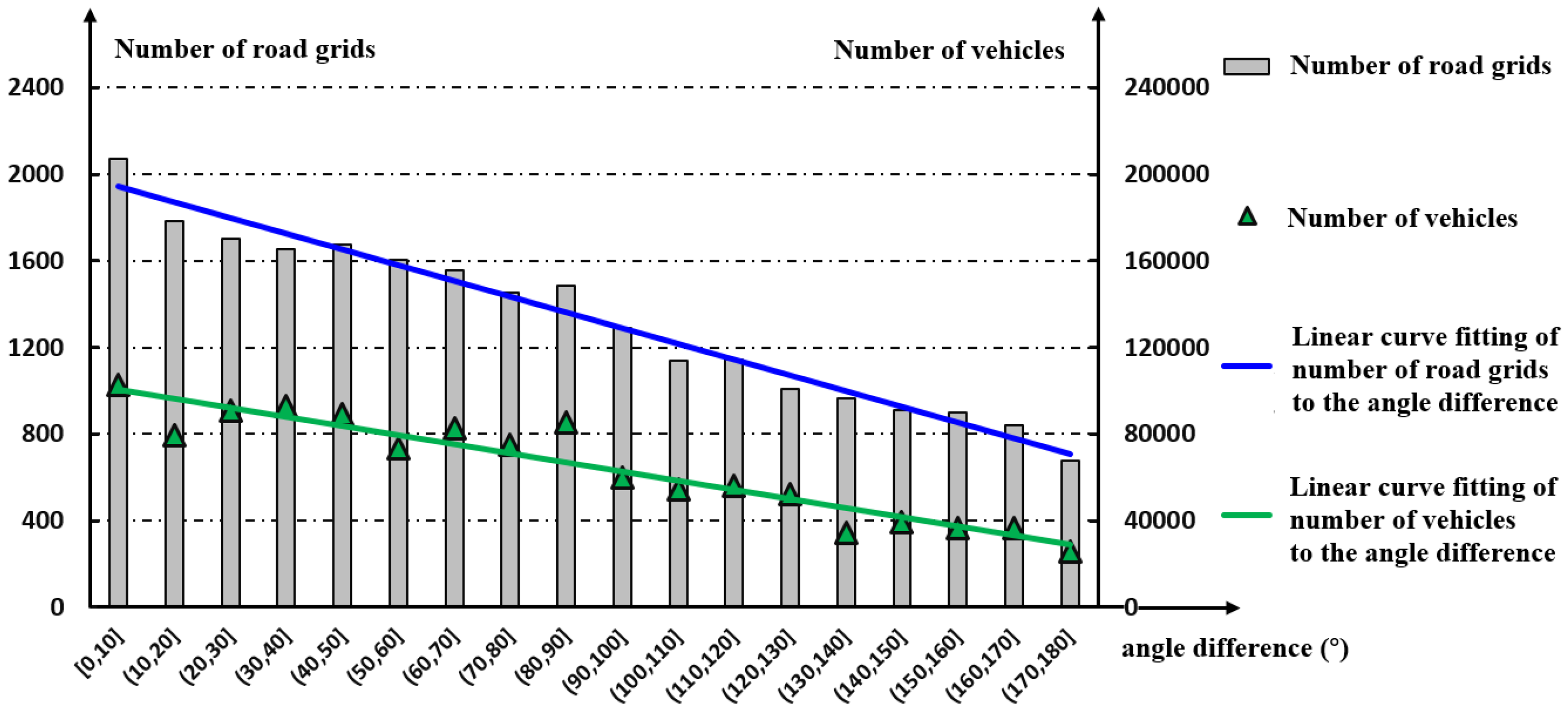
4.3. Correlation between the Urban Commuting Electric Field and Urban Road-Traffic Commuting
5. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tabuchi, T. Urban agglomeration and dispersion: A synthesis of alonso and krugman. J. Urban Econ. 1998, 44, 333–351. [Google Scholar] [CrossRef]
- David, M.; Nicholas, S.W.; Julia, F.; Brad, W. Use our infographics to explore the rise of the urban planet. Science. 2016. Available online: http://www.sciencemag.org/news/2016/05/use-our-infographics-explore-rise-urban-planet (accessed on 14 November 2018). [CrossRef]
- Agryzkov, T.; Oliver, J.L.; Tortosa, L.; Vicent, J.F. Analyzing the commercial activities of a street network by ranking their nodes: A case study in Murcia, Spain. Int. J. Geogr. Inf. Sci. 2014, 28, 479–495. [Google Scholar] [CrossRef]
- Yao, Z.Y.; Kim, C. The Changes of Urban Structure and Commuting: An Application to Metropolitan Statistical Areas in the United States. Int. Reg. Sci. Rev. 2019, 42, 3–30. [Google Scholar] [CrossRef]
- Duarte, C.M.; Fernández, M.T. The Influence of Urban Structure on Commuting: An Analysis for the Main Metropolitan Systems in Spain. In Proceedings of the Urban Transitions Conference, Shanghai, China, 5–9 September 2016. [Google Scholar] [CrossRef]
- Andersson, M.; Lavesson, N.; Niedomysl, T. Rural to urban long-distance commuting in Sweden: Trends, characteristics and pathways. J. Rural Stud. 2018, 59, 67–77. [Google Scholar] [CrossRef]
- Ma, X.L.; Zhang, J.Y.; Ding, C.; Wang, Y.P. A geographically and temporally weighted regression model to explore the spatiotemporal influence of built environment on transit ridership. Comput. Environ. Urban Syst. 2018, 70, 113–124. [Google Scholar] [CrossRef]
- Salas-Olmedo, M.H.; Nogués, S. Analysis of commuting needs using graph theory and census data: A comparison between two medium-sized cities in the UK. Appl. Geogr. 2012, 35, 132–141. [Google Scholar] [CrossRef]
- Hiribarren, G.; Herrera, J.C. Real time traffic states estimation on arterials based on trajectory data. Transp. Res. B 2014, 69, 19–30. [Google Scholar] [CrossRef]
- Cole-Hunter, T.; Donaire-Gonzalez, D.; Curto, A.; Ambros, A.; Valentin, A.; Garcia-Aymerich, J.; Martínez, D.; Braun, L.M.; Mendez, M.; Jerrett, M.; et al. Objective correlates and determinants of bicycle commuting propensity in an urban environment. Transp. Res. D 2015, 40, 132–143. [Google Scholar] [CrossRef]
- Nasri, A.; Zhang, L. Multi-level urban form and commuting mode share in rail station areas across the United States; a seemingly unrelated regression approach. Transp. Policy 2018, 5. [Google Scholar] [CrossRef]
- Ma, X.L.; Liu, C.C.; Wen, H.M.; Wang, Y.P.; Wu, Y.J. Understanding commuting patterns using transit smart card data. J. Transp. Geogr. 2017, 58, 135–145. [Google Scholar] [CrossRef]
- Chae, J.; Thom, D.; Jang, Y.; Kim, S.Y.; Ertl, T.; Ebert, D.S. Public behavior response analysis in disaster events utilizing visual analytics of microblog data Computers & Graphics. Comput. Graph. 2014, 38, 51–60. [Google Scholar] [CrossRef]
- Sun, C.S.; Pei, X.; Hao, J.H.; Wang, Y.W.; Zhang, Z. Role of road network features in the evaluation of incident impacts on urban traffic mobility. Transp. Res. B 2018, 117, 101–116. [Google Scholar] [CrossRef]
- Agryzkov, T.; Oliver, J.L.; Tortosa, L.; Vicent, J.F. An algorithm for ranking the nodes of an urban network based on the concept of PageRank vector. Appl. Math. Comput. 2012, 219, 2186–2193. [Google Scholar] [CrossRef]
- Agryzkov, T.; Marti, P.; Tortosa, L.; Vicent, J.F. Measuring urban activities using Foursquare data and network analysis: A case study of Murcia (Spain). Int. J. Geogr. Inf. Sci. 2017, 31, 100–121. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Li, W.W.; Zhang, F.; Liu, R.Y.; Du, Z.H. Identifying Urban Functional Zones Using Public Bicycle Rental Records and Point-of-Interest Data. ISPRS Int. J. Geo-Inf. 2018, 7, 459. [Google Scholar] [CrossRef]
- Wan, L.; Gao, S.; Wu, C.; Jin, Y.; Mao, M.R.; Yang, L. Big data and urban system model—Substitutes or complements? A case study of modelling commuting patterns in Beijing. Comput. Environ. Urban Syst. 2018, 68, 64–77. [Google Scholar] [CrossRef]
- Misra, A. Using vehicular data to understand urban mobility & events. In Proceedings of the 2017 IEEE 42nd Conference on Local Computer Networks: Workshops, Singapore, 14–17 October 2017. [Google Scholar] [CrossRef]
- Sun, J.P.; Wen, H.M.; Gao, Y.; Hu, Z.W. Metropolitan Congestion Performance Measures Based on Mass Floating Car Data. In Proceedings of the International Joint Conference on Computational Sciences and Optimization, Sanya, China, 24–26 April 2009. [Google Scholar] [CrossRef]
- Fu, X.; Sun, M.P.; Sun, H. Taxi Commute Recognition and Temporal-spatial Characteristics Analysis Based on GPS Data. China J. Highw. Transp. 2017, 30, 134–143. [Google Scholar] [CrossRef]
- Mao, F.; Ji, M.H.; Liu, T. Mining spatiotemporal patterns of urban dwellers from taxi trajectory data. Front. Earth Sci. 2016, 10, 205–221. [Google Scholar] [CrossRef]
- Casey, H.J. Applications to traffic engineering of the law of retail gravitation. Traff. Q. 1955, IX, 23–25. [Google Scholar]
- Krings, G.; Calabrese, F.; Ratti, C.; Blondel, V.D. Scaling behaviors in the communication network between cities. In Proceedings of the 12th IEEE International Conference on Computational Science and Engineering, CSE, Vancouver, BC, Canada, 29–31 August 2009. [Google Scholar] [CrossRef]
- Ortúzar, J.D.; Willumsen, L.G. Trips distribution modelling. In Modelling Transport, 4th ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2011; p. 182. [Google Scholar]
- Yang, Y.D.; Fan, Y.Y.; Wets, R.J.B. Stochastic travel demand estimation: Improving network identifiability using multi-day observation sets. Transp. Res. B 2018, 107, 192–211. [Google Scholar] [CrossRef]
- Gao, J.R.; Yu, B.; Pan, D.Z. Accurate lithography hotspot detection based on PCA-SVM classifier with hierarchical data clustering. In Proceedings of the SPIE-The International Society for Optical Engineering, Design-Process-Technology Co-Optimization for Manufacturability VIII, San Jose, CA, USA, 26–27 February 2014. [Google Scholar] [CrossRef]
- Wang, L.; Hu, K.Y.; Ku, T.; Wu, J.W. Urban mobility dynamics based on flexible discrete region partition. Int. J. Distrib. Sens. Netw. 2014, 2014, 782649. [Google Scholar] [CrossRef]
- Zhang, P.D.; Deng, M.; Shi, Y.; Zhao, L. Detecting hotspots of urban residents’ behaviours based on spatio-temporal clustering techniques. GeoJournal 2017, 82, 923–935. [Google Scholar] [CrossRef]
- Schoier, G.; Borruso, G. Spatial data mining for highlighting hotspots in personal navigation routes. Int. J. Data Warehous. 2012, 8, 45–61. [Google Scholar] [CrossRef][Green Version]
- Qin, K.; Zhou, Q.; Wu, T.; Xu, Y.Q. Hotspots detection from trajectory data based on spatiotemporal data field clustering. International Archives of the Photogrammetry. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2017, 42, 1319–1325. [Google Scholar] [CrossRef]
- Hussain, S.F.; Haris, M. A k-means based co-clustering (kCC) algorithm for sparse, high dimensional data. Expert Syst. Appl. 2019, 118, 20–34. [Google Scholar] [CrossRef]
- Li, M.C.; Han, S.; Shi, J. An enhanced ISODATA algorithm for recognizing multiple electric appliances from the aggregated power consumption dataset. Energy Build. 2017, 140, 305–316. [Google Scholar] [CrossRef]
- Liu, Q.J.; Zhao, Z.M.; Li, Y.X.; Li, Y.Y. Feature selection based on sensitivity analysis of fuzzy ISODATA. Neurocomputing 2012, 85, 29–37. [Google Scholar] [CrossRef]
- Ni, X.Y.; Huang, H.; Zhou, S.W.; Su, B.N.; Meng, Y.Y.; Huang, Z.L. Spatial data mining and O-D hotspots discovery in cities based on an O-D hotspots clustering model using vehicles’ GPS data—A case study in the morning rush hours in Beijing, China. In Proceedings of the 4th ACM SIGSPATIAL International Workshop on Safety and Resilience 2018, Seattle, WA, USA, 6–9 November 2018. [Google Scholar] [CrossRef]
- Clustering Algorithm-ISODATA Algorithm. Available online: https://www.cnblogs.com/huadongw/articles/4101306.html (accessed on 20 January 2019).
- Zhang, N.; Li, Y.G. A human behavior integrated hierarchical model of airborne disease transmission in a large city. Build. Environ. 2017, 127, 211–220. [Google Scholar] [CrossRef]
- Annual Data of the Province in China. Available online: http://data.stats.gov.cn/easyquery.htm?cn=E0103 (accessed on 1 August 2018).
- Ni, X.Y.; Huang, H.; Du, W.P. Relevance analysis and short-term prediction of PM2.5 concentrations in Beijing based on multi-source data. Atmos. Environ. 2017, 150, 146–161. [Google Scholar] [CrossRef]
- Li, Q.; Liao, F.X.; Timmermans, H.J.P.; Huang, H.; Zhou, J. Incorporating free-floating car-sharing into an activity-based dynamic user equilibrium model: A demand-side model. Transp. Res. B 2018, 107, 102–123. [Google Scholar] [CrossRef]
- Yuan, N.J.; Zheng, Y.; Xie, X.; Wang, Y.Z.; Zheng, K.; Xiong, H. Discovering urban functional zones using latent activity trajectories. IEEE Trans. Knowl. Data Eng. 2015, 27, 712–725. [Google Scholar] [CrossRef]
- Hörcher, D.; Graham, D.J.; Anderson, R.J. Crowding cost estimation with large scale smart card and vehicle location data. Transp. Res. B 2017, 95, 105–125. [Google Scholar] [CrossRef]
| Parameter | Meaning |
|---|---|
| Prospective number of clustering centers in the model | |
| Number of initial clustering centers | |
| Number of groups that could be merged into one merging step | |
| Number of iterations in the iteration operation | |
| Collection mark of the clusters, | |
| Number of samples in the cluster , | |
| Minimum number of samples in a clustering center; the clustering center will be deleted if the number of samples is less than | |
| Standard deviation of the distribution of the between-sample distance in a clustering center | |
| Minimum distance between two clustering centers; the clustering centers will be merged if the distance between them is less than |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ni, X.; Huang, H.; Meng, Y.; Zhou, S.; Su, B. An Urban Road-Traffic Commuting Dynamics Study Based on Hotspot Clustering and a New Proposed Urban Commuting Electrostatics Model. ISPRS Int. J. Geo-Inf. 2019, 8, 190. https://doi.org/10.3390/ijgi8040190
Ni X, Huang H, Meng Y, Zhou S, Su B. An Urban Road-Traffic Commuting Dynamics Study Based on Hotspot Clustering and a New Proposed Urban Commuting Electrostatics Model. ISPRS International Journal of Geo-Information. 2019; 8(4):190. https://doi.org/10.3390/ijgi8040190
Chicago/Turabian StyleNi, Xiaoyong, Hong Huang, Yangyang Meng, Shiwei Zhou, and Boni Su. 2019. "An Urban Road-Traffic Commuting Dynamics Study Based on Hotspot Clustering and a New Proposed Urban Commuting Electrostatics Model" ISPRS International Journal of Geo-Information 8, no. 4: 190. https://doi.org/10.3390/ijgi8040190
APA StyleNi, X., Huang, H., Meng, Y., Zhou, S., & Su, B. (2019). An Urban Road-Traffic Commuting Dynamics Study Based on Hotspot Clustering and a New Proposed Urban Commuting Electrostatics Model. ISPRS International Journal of Geo-Information, 8(4), 190. https://doi.org/10.3390/ijgi8040190





