HiXDraw: An Improved XDraw Algorithm Free of Chunk Distortion
Abstract
:1. Introduction
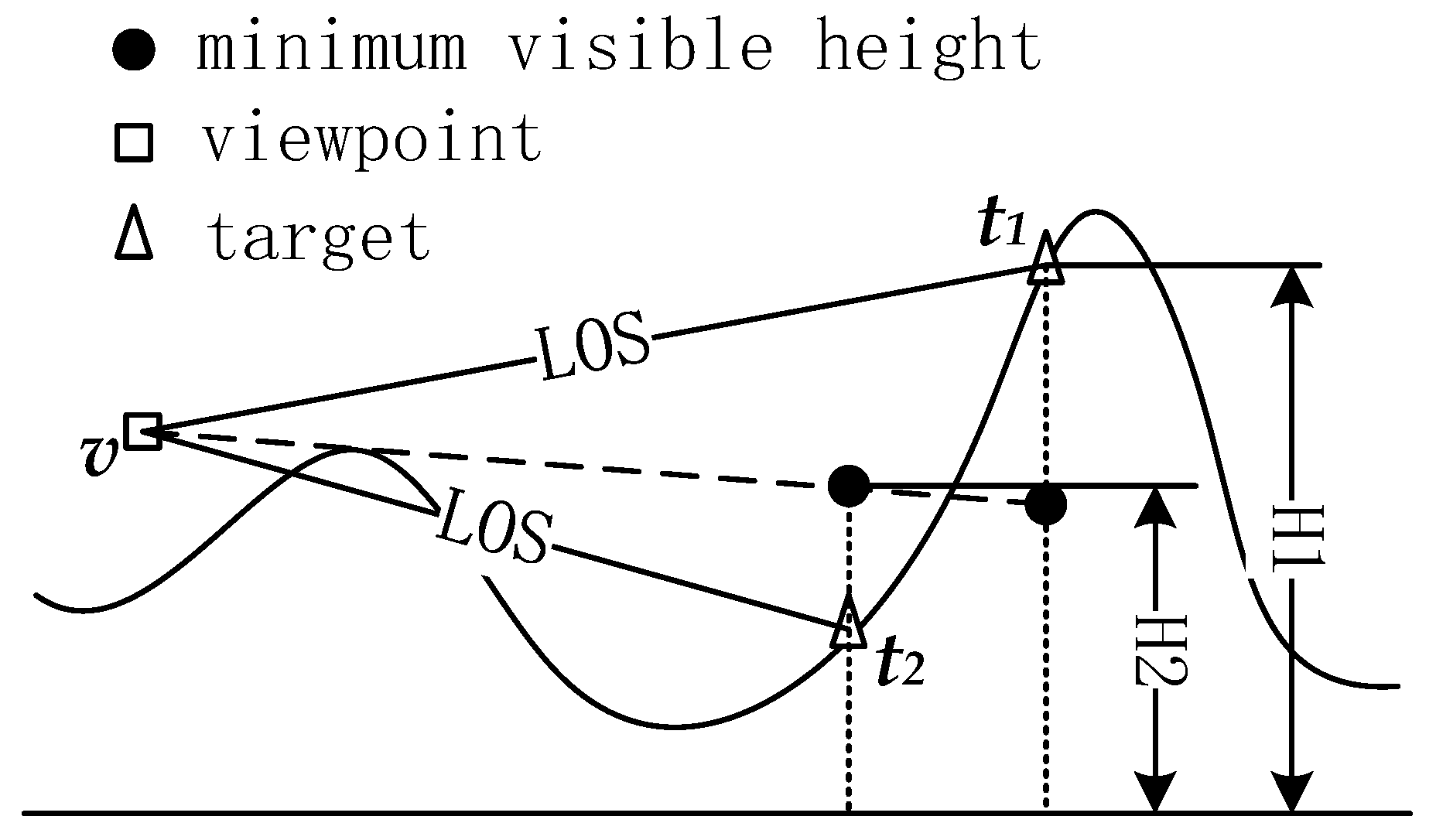
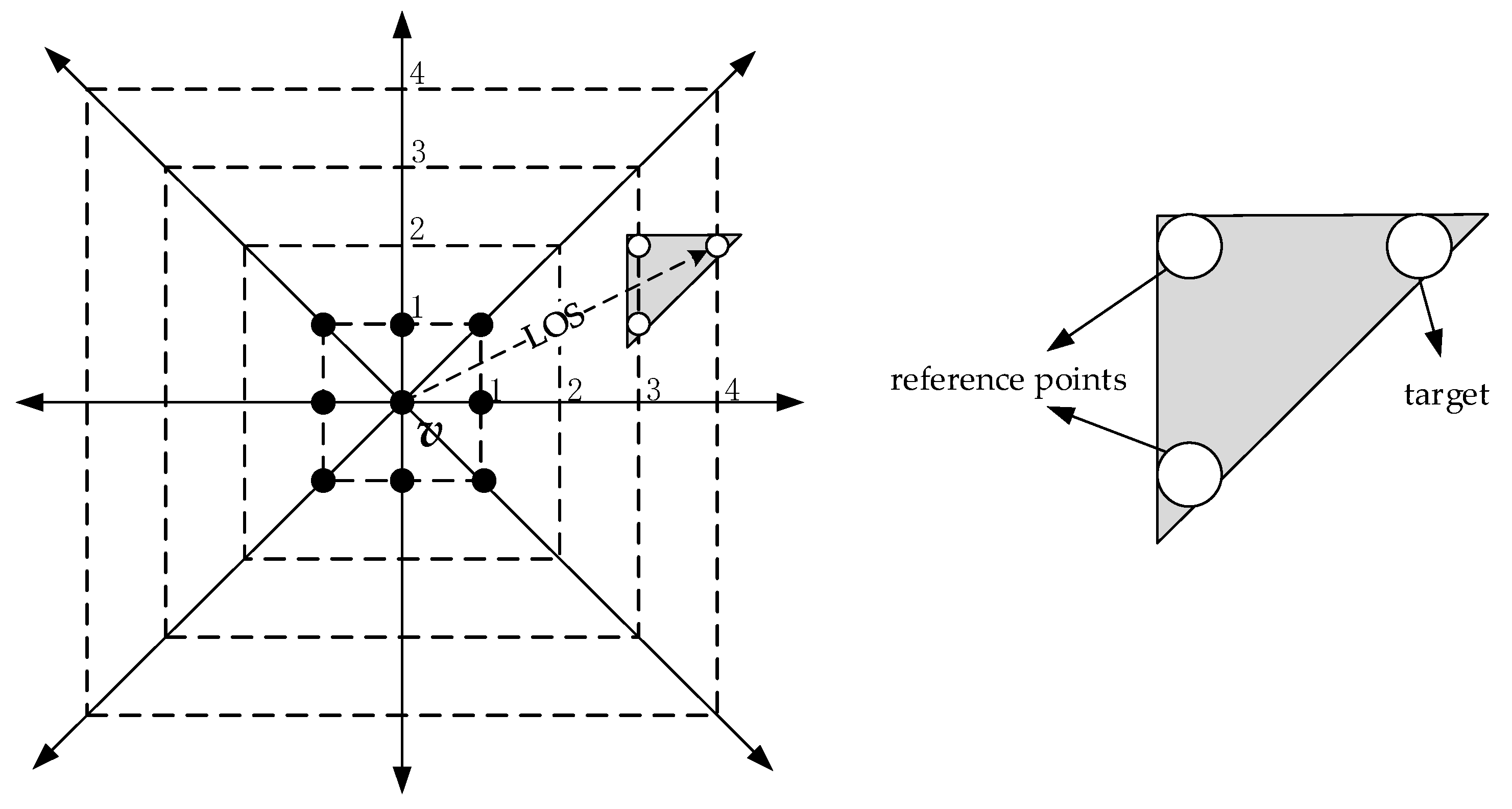
- Criteria for appropriateness: A point should not contribute to calculating the visibility and LOS height if this point is not 4-neighbor adjacent to the LOS.
- Criteria for adequacy: Every point that is 4-neighbor adjacent to the LOS should contribute to calculating the visibility and LOS height.
2. Related Works
2.1. Viewshed Algorithms
2.2. Improvements of XDraw
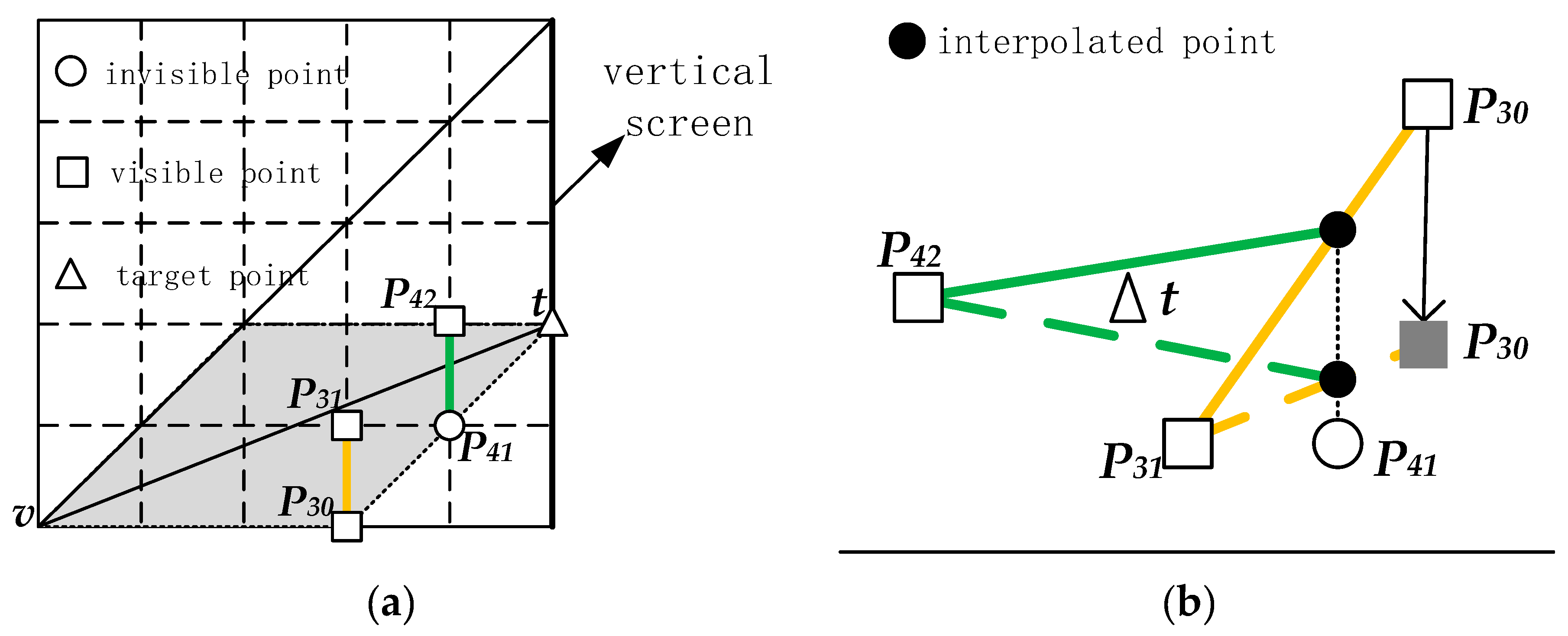
3. Improved XDraw Algorithm
| Algorithm: HiXDraw INPUT: (1) the elevation of the target and its two reference points (2) the visibility of two reference points (3) the auxiliary grid at two reference points OUTPUT: (1)the auxiliary grid of the target, (2)the visibility of the target
|
4. Experimental Results
4.1. Experimental Setup
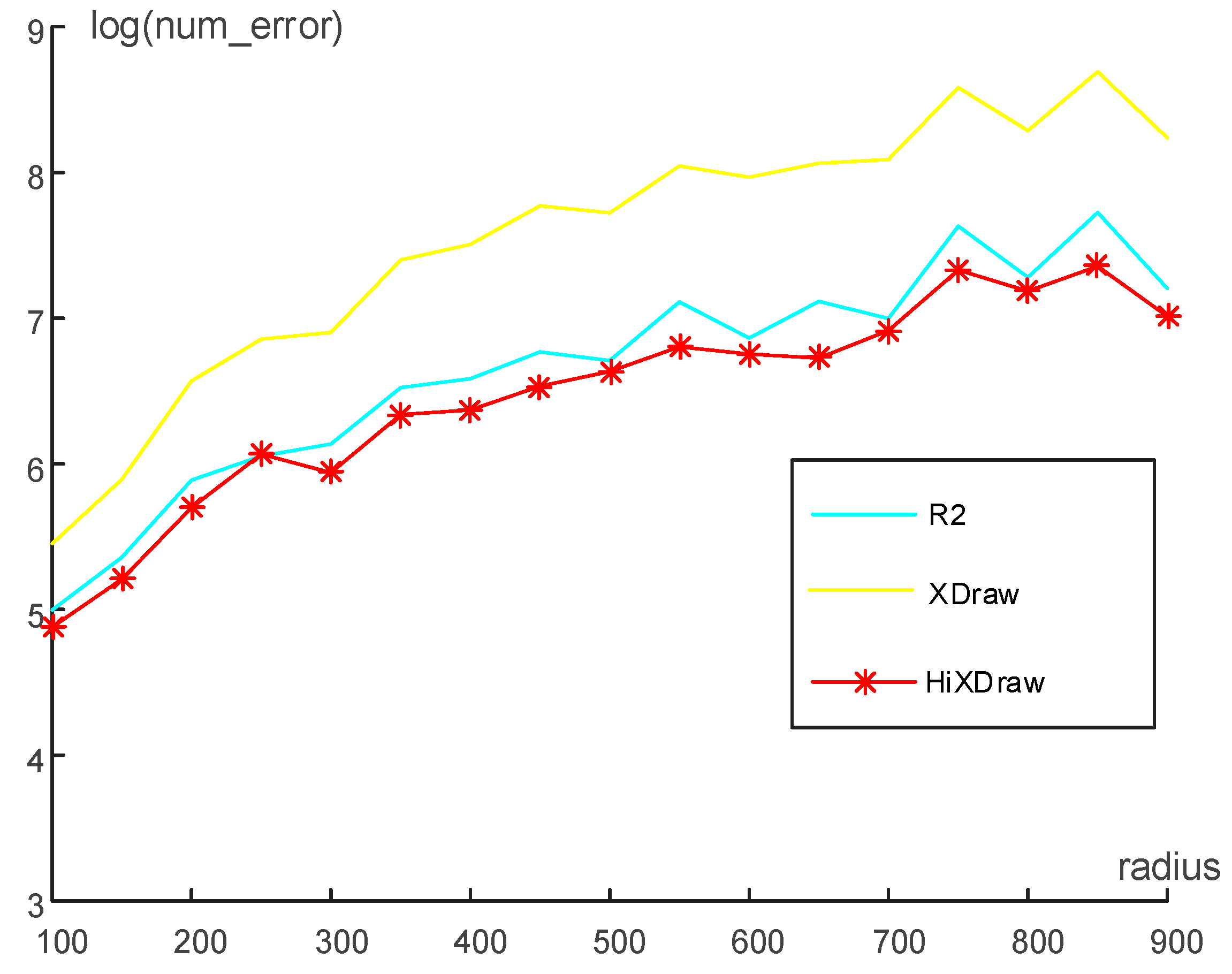
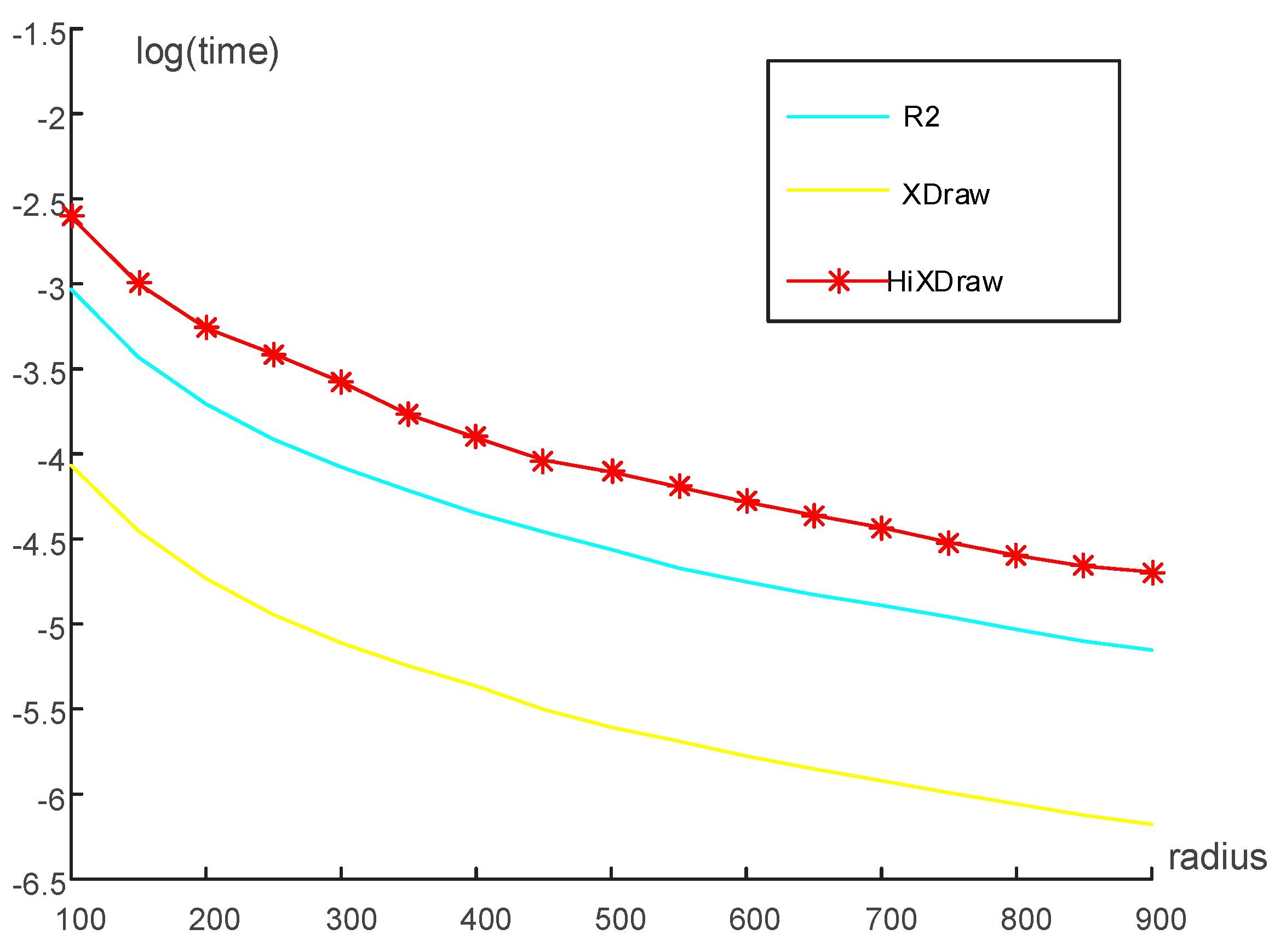
4.2. Experiment 1: Compare the Accuracy and Efficiency of HiXDraw, R2 and XDraw
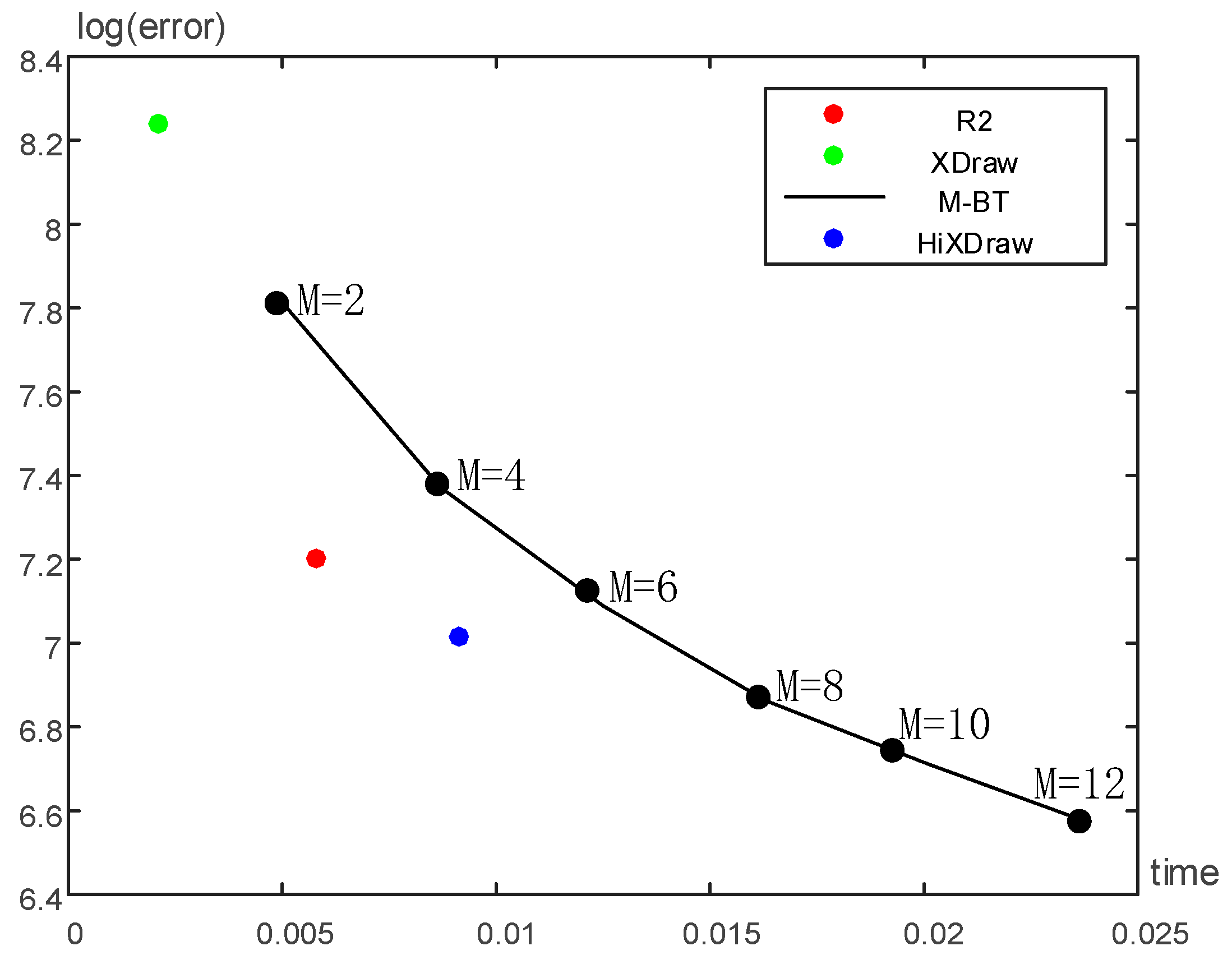
4.3. Experiment 2: Compare the Performance of HiXDraw and M-BT
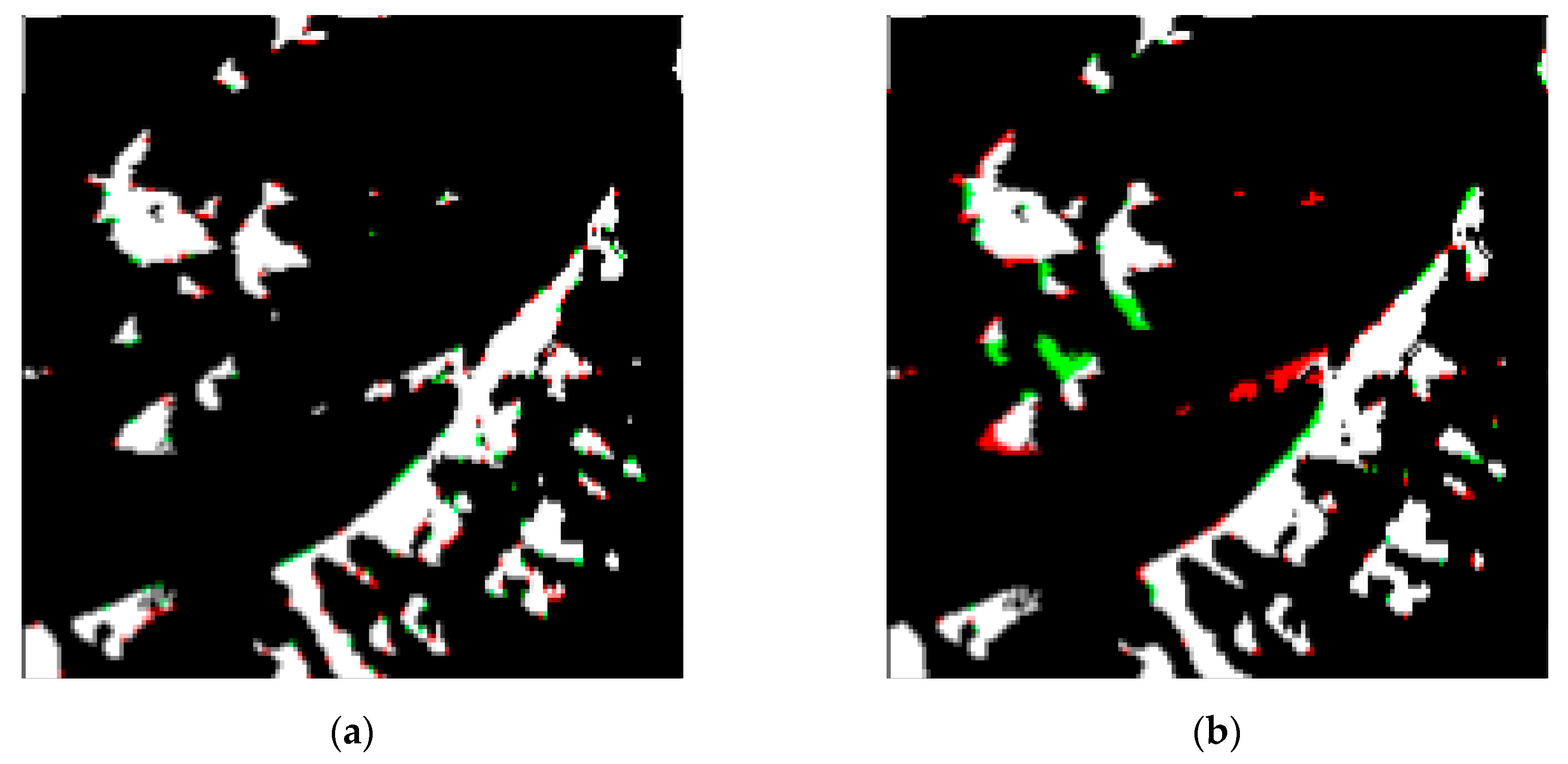
4.4. Experiment 3: Compare the Performance of HiXDraw and Zhi’s Method
4.5. Experiment 4: A Pillar Experiment
5. Conclusions
6. Future works
- (Better efficiency) Speed up HiXDraw with an I/O efficient operation and parallel computing. As we have mentioned in Section 2, many previous works had accelerated the original XDraw by implementing XDraw I/O-efficiently or by adapting XDraw to various parallel technologies. HiXDraw does not change the overall procedure of XDraw, making it possible to apply the speed up to the new method easily.
- (Better accuracy) Improve the selection of contributing points with a more reasonable criterion. The criteria for choosing contributing points is open for further discussion. Other criteria considering more factors other than azimuth can be proposed to achieve better performance. For example, suppose one of the contributing points has the smallest angle but another contributing point is closest to the viewpoint and is much more dominant, should we ignore the influence of the dominant point? How to consider the influence of all the candidate contributing points comprehensively? Whether other points, such as the invisible reference points, should be included in the consideration? Future works should examine other factors and design new criteria.
- (Better accuracy) Besides, involving other “relevant” terrain data into the computation of visibility may be another direction of improving accuracy. By constructing the reference plane using two reference points and the viewpoint, XDraw assumes that the reference plane is higher than all the grid points within this triangle. Unfortunately, this assumption is not always correct. [31] illustrated a counterexample. We may solve this problem by taking more terrain data along the LOS into consideration.
- (More applications) The contributing points used to construct the reference plane is no longer in the same row or column. The position of the contributing point is arbitrary. So there exists a possibility that we may apply HiXDraw to TIN terrain models in the future.
Author Contributions
Funding
Conflicts of Interest
References
- Franklin, W.R.; Ray, C.K.; Mehta, S. Geometric algorithms for siting of air defense missile batteries. Res. Proj. Battle Columb. Div. Deliv. Order 1994, 2756. [Google Scholar]
- Li, J.; Zheng, C.; Hu, X. An Effective Method for Complete Visual Coverage Path Planning. In Proceedings of the 2010 Third International Joint Conference on Computational Science and Optimization (CSO), Huangshan, China, 28–31 May 2010; Volume 1, pp. 497–500. [Google Scholar]
- Yaagoubi, R.; Yarmani, M.E.; Kamel, A.; Khemiri, W. HybVOR: A voronoi-based 3D GIS approach for camera surveillance network placement. ISPRS Int. J. Geo-Inf. 2015, 4, 754–782. [Google Scholar] [CrossRef]
- Kaučič, B.; Zalik, B. Comparison of viewshed algorithms on regular spaced points. In Proceedings of the 18th Spring Conference on Computer Graphics, Budmerice, Slovakia, 24–27 April 2002; ACM: New York, NY, USA, 2002; pp. 177–183. [Google Scholar]
- Teng, Y.A.; Davis, L.S. Visibility Analysis on Digital Terrain Models and Its Parallel Implementation; University of Maryland, Center for Automation Research, Computer Vision Laboratory: College Park, MD, USA, 1992. [Google Scholar]
- Toma, L. Viewsheds on terrains in external memory. Sigspatial Spec. 2012, 4, 13–17. [Google Scholar] [CrossRef]
- Van Kreveld, M.J. Variations on Sweep Algorithms: Efficient Computation of Extended Viewsheds and Class Intervals; Utrecht University, Information and Computing Sciences: Utrecht, The Netherlands, 1996. [Google Scholar]
- Or, D.C.; Shaked, A. Visibility and Dead-Zones in Digital Terrain Maps. In Computer Graphics Forum; Blackwell Science Ltd.: Edinburgh, UK, 1995; Volume 14, pp. 171–180. [Google Scholar]
- Fishman, J.; Haverkort, H.; Toma, L. Improved visibility computation on massive grid terrains. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WD, USA, 4–6 November 2009; ACM: New York, NY, USA, 2009; pp. 121–130. [Google Scholar]
- Haverkort, H.; Toma, L. A Comparison of I/O-Efficient Algorithms for Visibility Computation on Massive Grid Terrains. arXiv, 2018; arXiv:1810.01946. [Google Scholar]
- Haverkort, H.; Toma, L.; Zhuang, Y. Computing visibility on terrains in external memory. J. Exp. Algorithmics (Jea) 2009, 13, 5. [Google Scholar] [CrossRef]
- Ferreira, C.R.; Andrade, M.V.A.; Magalhaes, S.V.G.; Franklin, W.R. An efficient external memory algorithm for terrain viewshed computation. ACM Trans. Spat. Algorithms Syst. (TSAS) 2016, 2, 6. [Google Scholar] [CrossRef]
- Haverkort, H.; Toma, L.; Wei, B.P.F. On IO-efficient viewshed algorithms and their accuracy. In Proceedings of the 21st ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Orlando, FL, USA, 5–8 Npvember 2013; ACM: New York, NY, USA, 2013; pp. 24–33. [Google Scholar]
- Ferreira, C.R.; Magalhães, S.V.; Andrade, M.V.; Franklin, W.R.; Pompermayer, A.M. More efficient terrain viewshed computation on massive datasets using external memory. In Proceedings of the 20th International Conference on Advances in Geographic Information Systems, Redondo Beach, CA, USA, 6–9 November 2012; ACM: New York, NY, USA, 2012; pp. 494–497. [Google Scholar]
- Osterman, A.; Benedičič, L.; Ritoša, P. An IO-efficient parallel implementation of an R2 viewshed algorithm for large terrain maps on a CUDA GPU. Int. J. Geogr. Inf. Sci. 2014, 28, 2304–2327. [Google Scholar] [CrossRef]
- Axell, T.; Fridén, M. Comparison between GPU and Parallel CPU Optimizations in Viewshed Analysis. Master’s Thesis, Department of Computer Science and Engineering, Chalmers University of Technology, Gothenburg, Sweden, 2015. [Google Scholar]
- Zhao, Y.; Padmanabhan, A.; Wang, S. A parallel computing approach to viewshed analysis of large terrain data using graphics processing units. Int. J. Geogr. Inf. Sci. 2013, 27, 363–384. [Google Scholar] [CrossRef]
- Ferreira, C.; Andrade, M.V.; Magalhães, S.V.; Franklin, W.R.; Pena, G.C. A Parallel Sweep Line Algorithm for Visibility Computation; GeoInfo: São Paulo, Brazil, 2013; pp. 85–96. [Google Scholar]
- Ferreira, C.R.; Andrade, M.V.; Magalhães, S.V.; Franklin, W.R.; Pena, G.C. A parallel algorithm for viewshed computation on grid terrains. J. Inf. Data Manag. 2014, 5, 171. [Google Scholar]
- Dou, W.; Li, Y.; Wang, Y. A fine-granularity scheduling algorithm for parallel XDraw viewshed analysis. Earth Sci. Inform. 2018, 1–15. [Google Scholar] [CrossRef]
- Wang, J.; Robinson, G.J.; White, K. Generating viewsheds without using sightlines. Photogramm. Eng. Remote Sens. 2000, 66, 87–90. [Google Scholar]
- Izraelevitz, D. A fast algorithm for approximate viewshed computation. Photogramm. Eng. Remote Sens. 2003, 69, 767–774. [Google Scholar] [CrossRef]
- Zhi, Y.; Wu, L.; Sui, Z.; Cai, H. An improved algorithm for computing viewshed based on reference planes. In Proceedings of the IEEE 2011 19th International Conference on Geoinformatics, Shanghai, China, 24–26 June 2011; pp. 1–5. [Google Scholar]
- Wu, H.; Pan, M.; Yao, L.; Luo, B. A partition-based serial algorithm for generating viewshed on massive DEMs. Int. J. Geogr. Inf. Sci. 2007, 21, 955–964. [Google Scholar] [CrossRef]
- Xu, Z.Y.; Yao, Q. A novel algorithm for viewshed based on digital elevation model. In Proceedings of the Asia-Pacific Conference on Information Processing (APCIP 2009), Shenzhen, China, 18–19 July 2009; Volume 2, pp. 294–297. [Google Scholar]
- Carabaño, J.; Sarjakoski, T.; Westerholm, J. Efficient implementation of a fast viewshed algorithm on SIMD architectures. In Proceedings of the Proceedings of the 23rd Euromicro International Conference on Parallel, Disturbed, and Network-Based Processing, Turku, Finland, 4–6 March 2015. [Google Scholar]
- Cauchi-Saunders, A.J.; Lewis, I.J. GPU enabled XDraw viewshed analysis. J. Parallel Distrib. Comput. 2015, 84, 87–93. [Google Scholar] [CrossRef]
- Song, X.D.; Tang, G.A.; Liu, X.J.; Dou, W.F.; Li, F.Y. Parallel viewshed analysis on a PC cluster system using triple-based irregular partition scheme. Earth Sci. Inform. 2016, 9, 511–523. [Google Scholar] [CrossRef]
- Li, Y.N.; Dou, W.F.; Wang, Y.L. Design and Implementation of parallel XDraw algorithm based on triangle region division. In Proceedings of the 2017 16th International Symposium on Distributed Computing and Applications to Business, Engineering and Science (DCABES), AnYang, China, 13–16 October 2017; pp. 41–44. [Google Scholar]
- Dou, W.; Li, Y. A fault-tolerant computing method for Xdraw parallel algorithm. J. Supercomput. 2018, 74, 2776–2800. [Google Scholar] [CrossRef]
- Yu, J.; Wu, L.; Hu, Q.; Yan, Z.; Zhang, S. A synthetic visual plane algorithm for visibility computation in consideration of accuracy and efficiency. Comput. Geosci. 2017, 109, 315–322. [Google Scholar] [CrossRef]
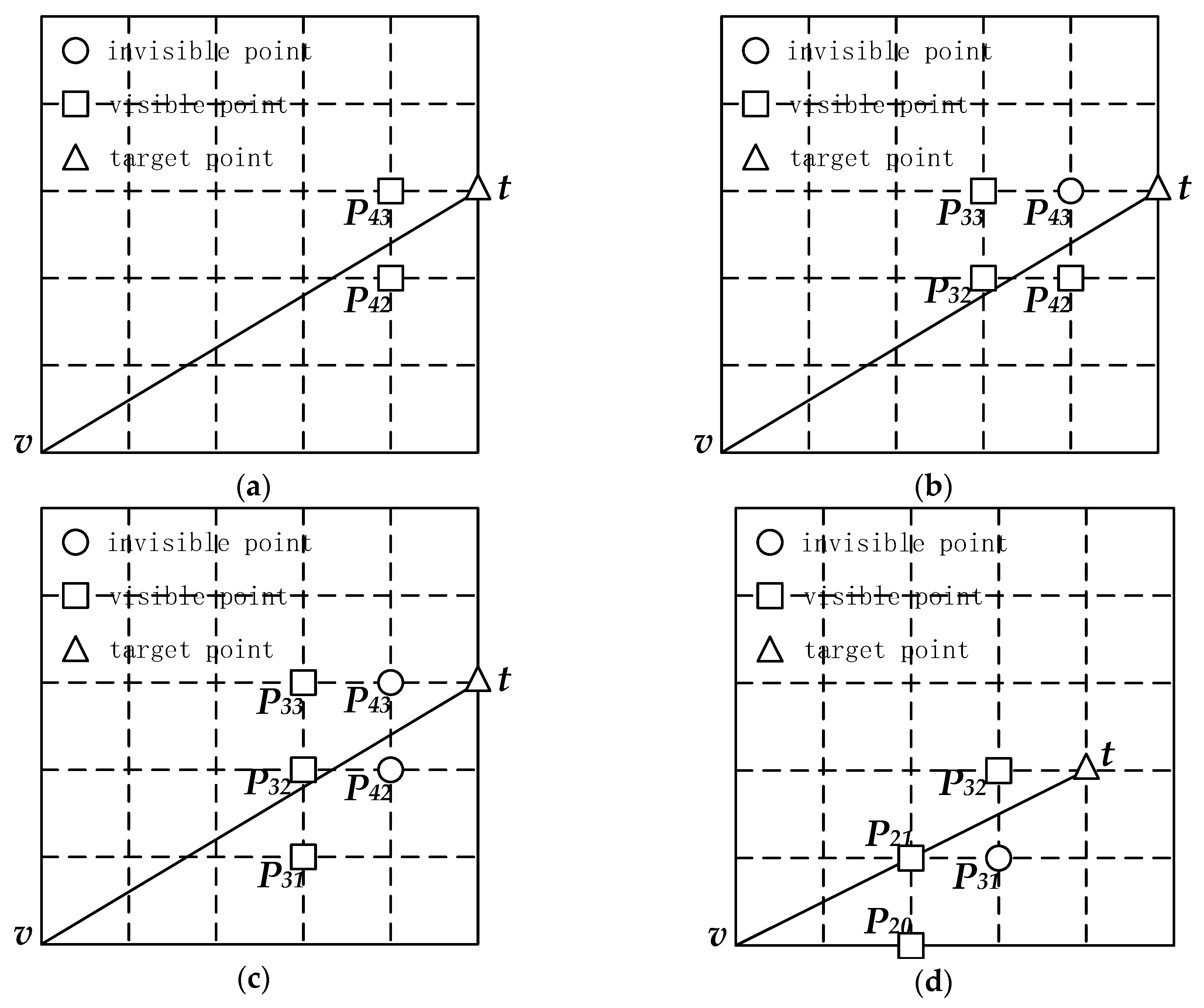




| Attribute | P1 | P2 |
|---|---|---|
| Case visible | NULL | NULL |
| Case invisible | {x, y, elev} | {x, y, elev} 1 |
| Algorithms | Radius | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
|---|---|---|---|---|---|---|---|---|---|---|
| XDraw | time 1 | 1.71 | 0.88 | 0.60 | 0.47 | 0.37 | 0.31 | 0.27 | 0.23 | 0.21 |
| error | 233.3 | 713.6 | 994.6 | 1823.7 | 2261.2 | 2891.3 | 3262.7 | 3977.8 | 3786.4 | |
| R2 | time | 4.82 | 2.46 | 1.70 | 1.29 | 1.04 | 0.86 | 0.75 | 065 | 0.58 |
| error | 147.9 | 360.8 | 462.0 | 724.0 | 820.5 | 957.9 | 1094.6 | 1452.9 | 1345.2 | |
| HiXDraw | time | 7.38 | 3.84 | 2.80 | 2.01 | 1.65 | 1.38 | 1.19 | 1.01 | 0.92 |
| error | 131.5 | 298.7 | 379.9 | 583.8 | 760.6 | 856.9 | 1007.5 | 1320.3 | 1110.4 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, G.; Li, J.; Wu, J.; Ma, M.; Wang, L.; Jing, N. HiXDraw: An Improved XDraw Algorithm Free of Chunk Distortion. ISPRS Int. J. Geo-Inf. 2019, 8, 153. https://doi.org/10.3390/ijgi8030153
Zhu G, Li J, Wu J, Ma M, Wang L, Jing N. HiXDraw: An Improved XDraw Algorithm Free of Chunk Distortion. ISPRS International Journal of Geo-Information. 2019; 8(3):153. https://doi.org/10.3390/ijgi8030153
Chicago/Turabian StyleZhu, Guangyang, Jun Li, Jiangjiang Wu, Mengyu Ma, Li Wang, and Ning Jing. 2019. "HiXDraw: An Improved XDraw Algorithm Free of Chunk Distortion" ISPRS International Journal of Geo-Information 8, no. 3: 153. https://doi.org/10.3390/ijgi8030153
APA StyleZhu, G., Li, J., Wu, J., Ma, M., Wang, L., & Jing, N. (2019). HiXDraw: An Improved XDraw Algorithm Free of Chunk Distortion. ISPRS International Journal of Geo-Information, 8(3), 153. https://doi.org/10.3390/ijgi8030153





