A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal
Abstract
1. Introduction
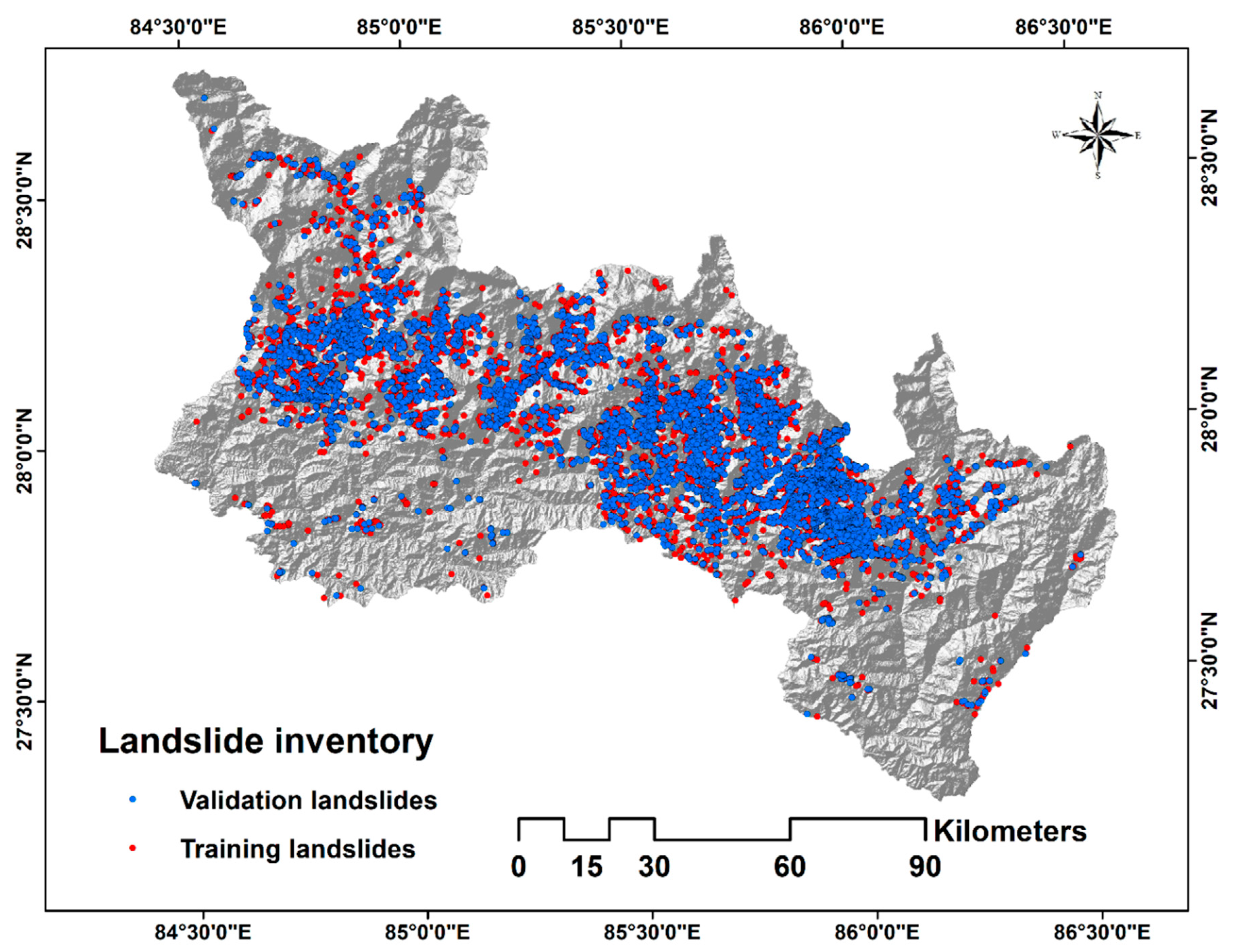
2. Study Area and Inventory Data Set
Landslide Inventory Data Set
3. Materials and Methods
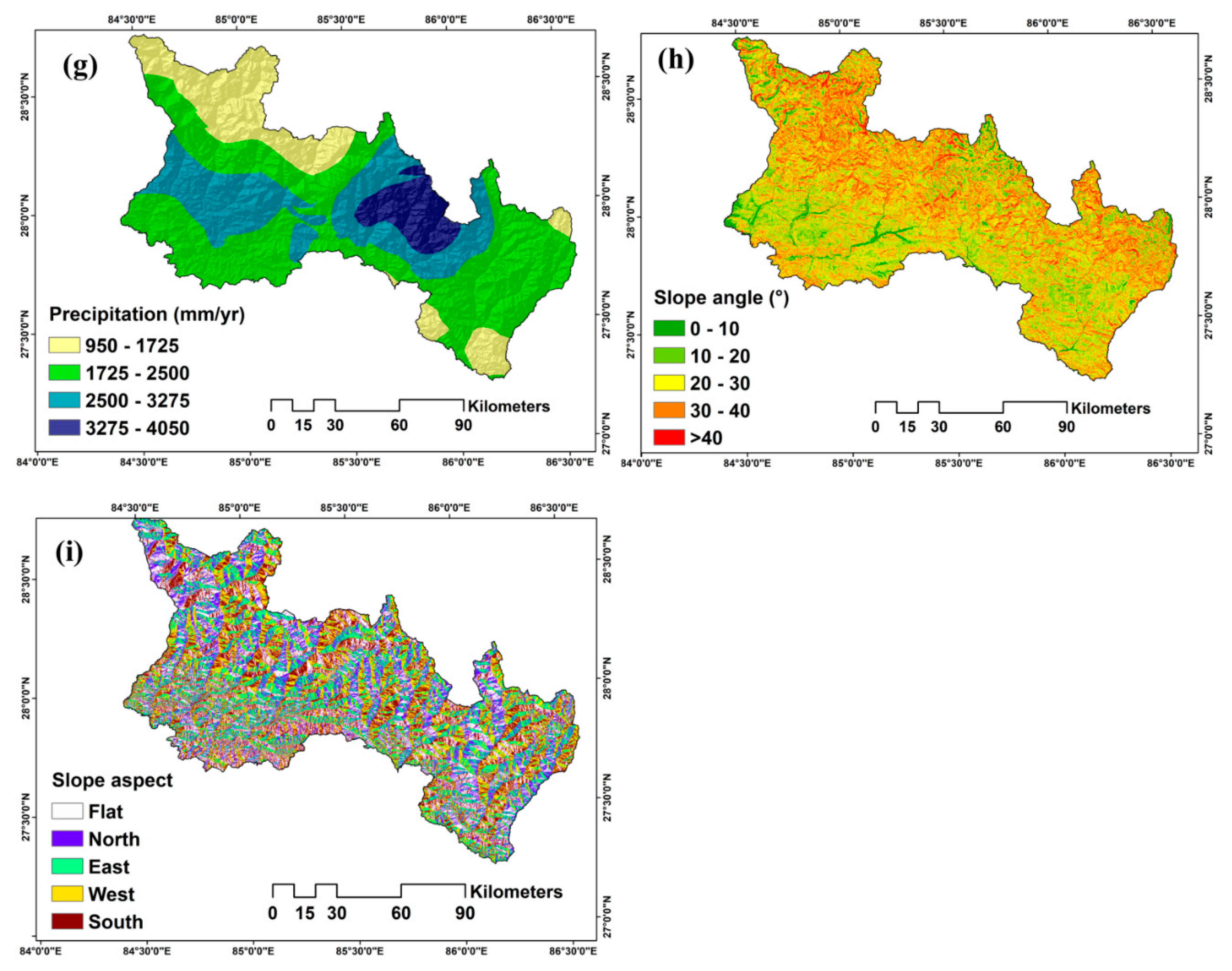
3.1. Landslide Conditioning Factors
3.2. Methods
3.2.1. Analytical Hierarchy Process (AHP)
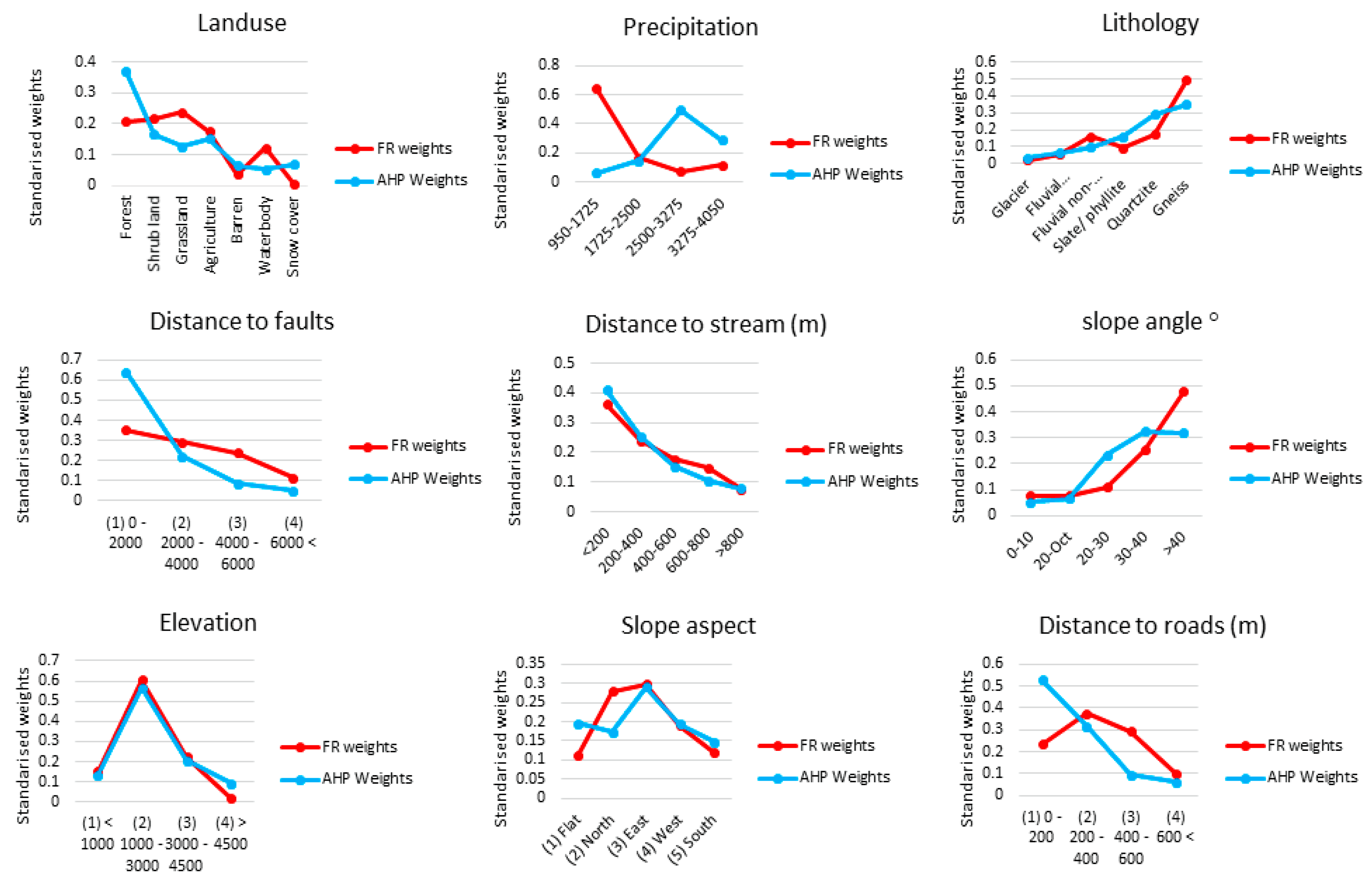
3.2.2. Frequency Ratio (FR)
3.2.3. Hybrid Spatial Multi-Criteria Evaluation (SMCE)
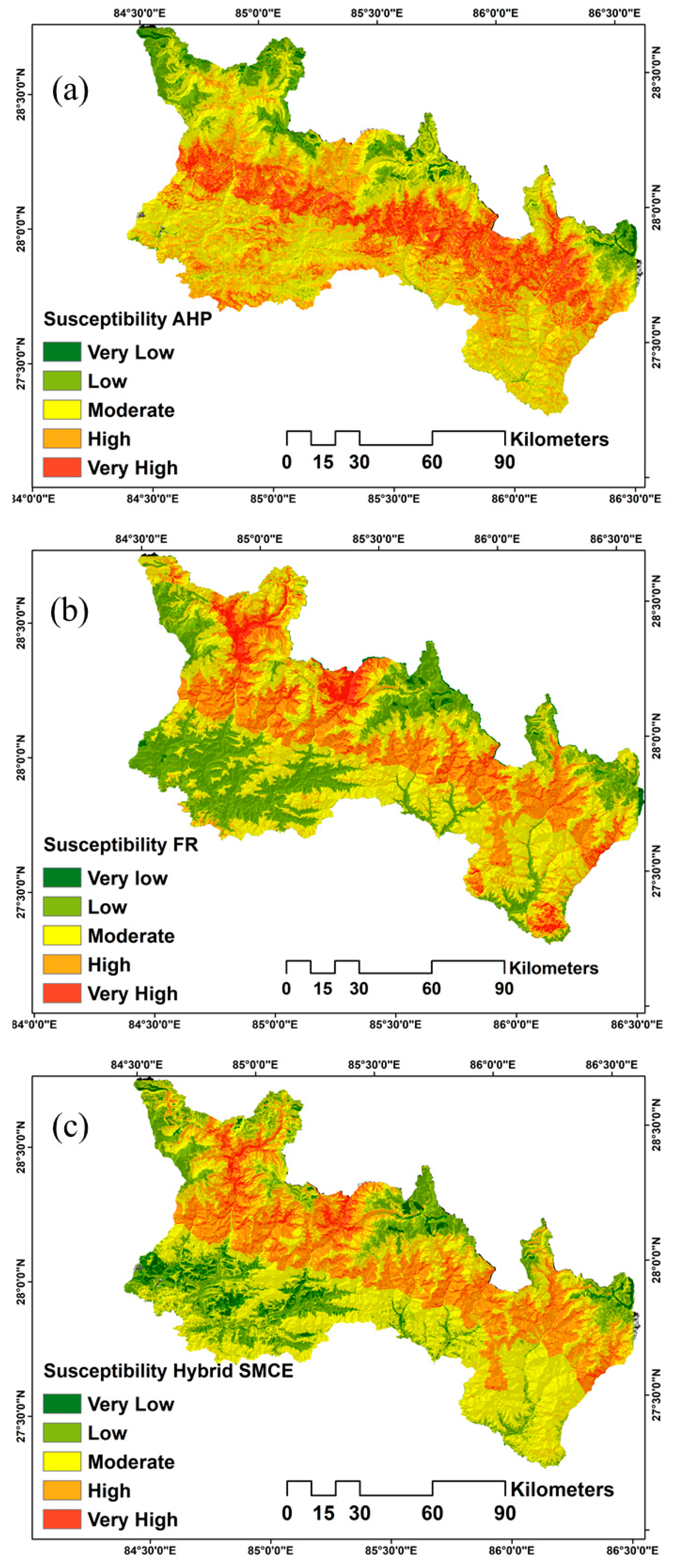
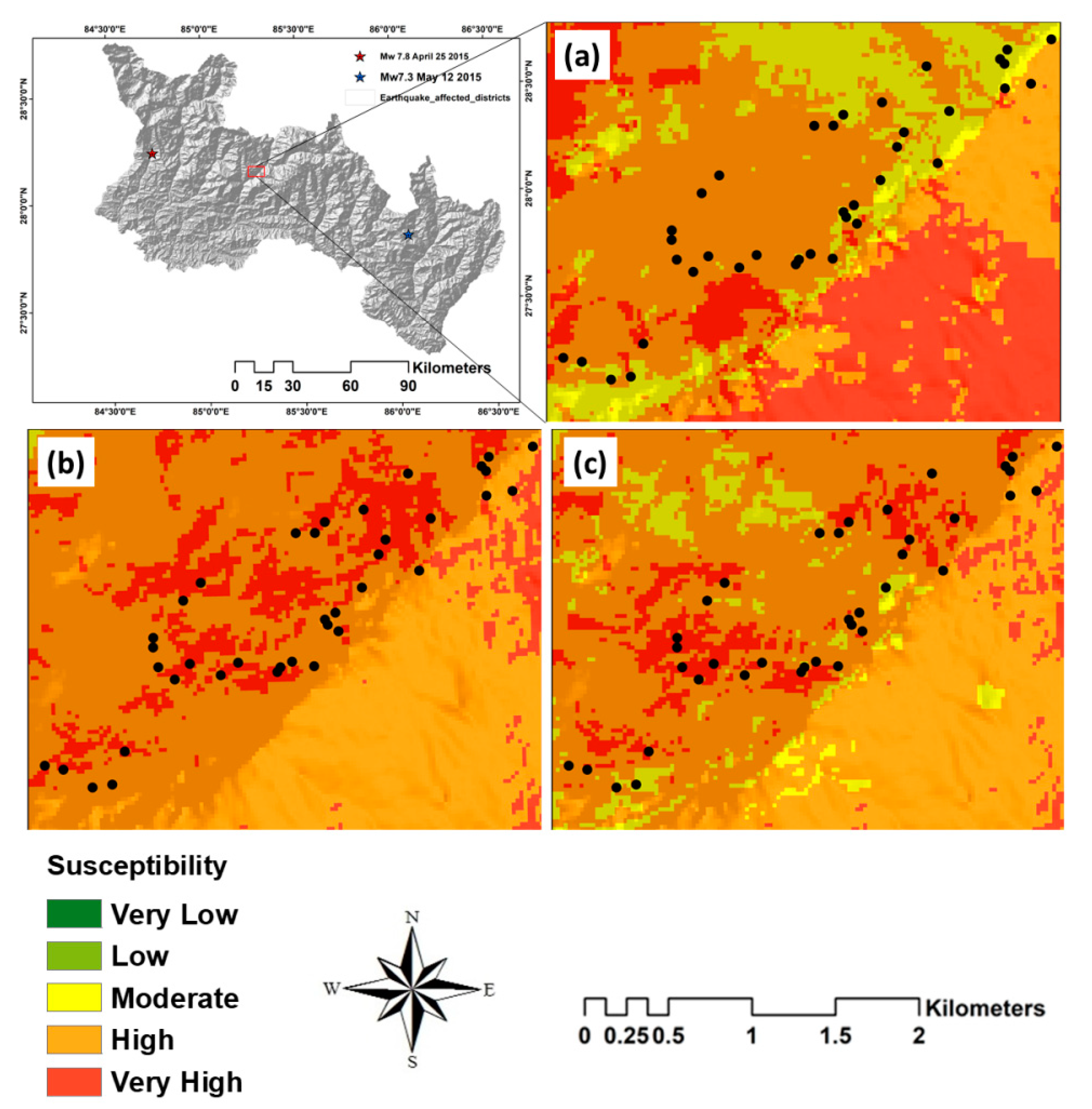
4. Results
5. Validation
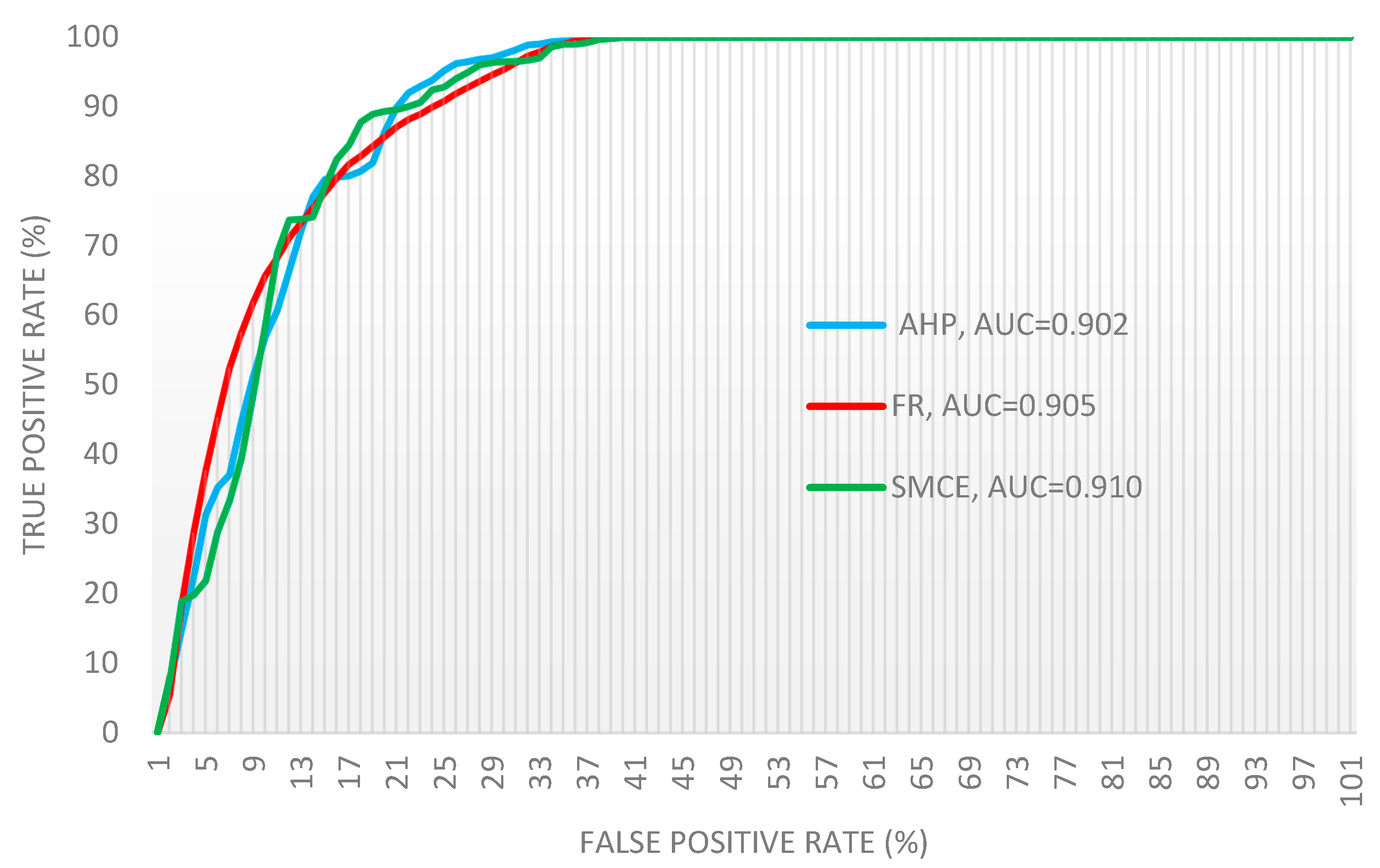
5.1. Receiver Operating Characteristics (ROC)
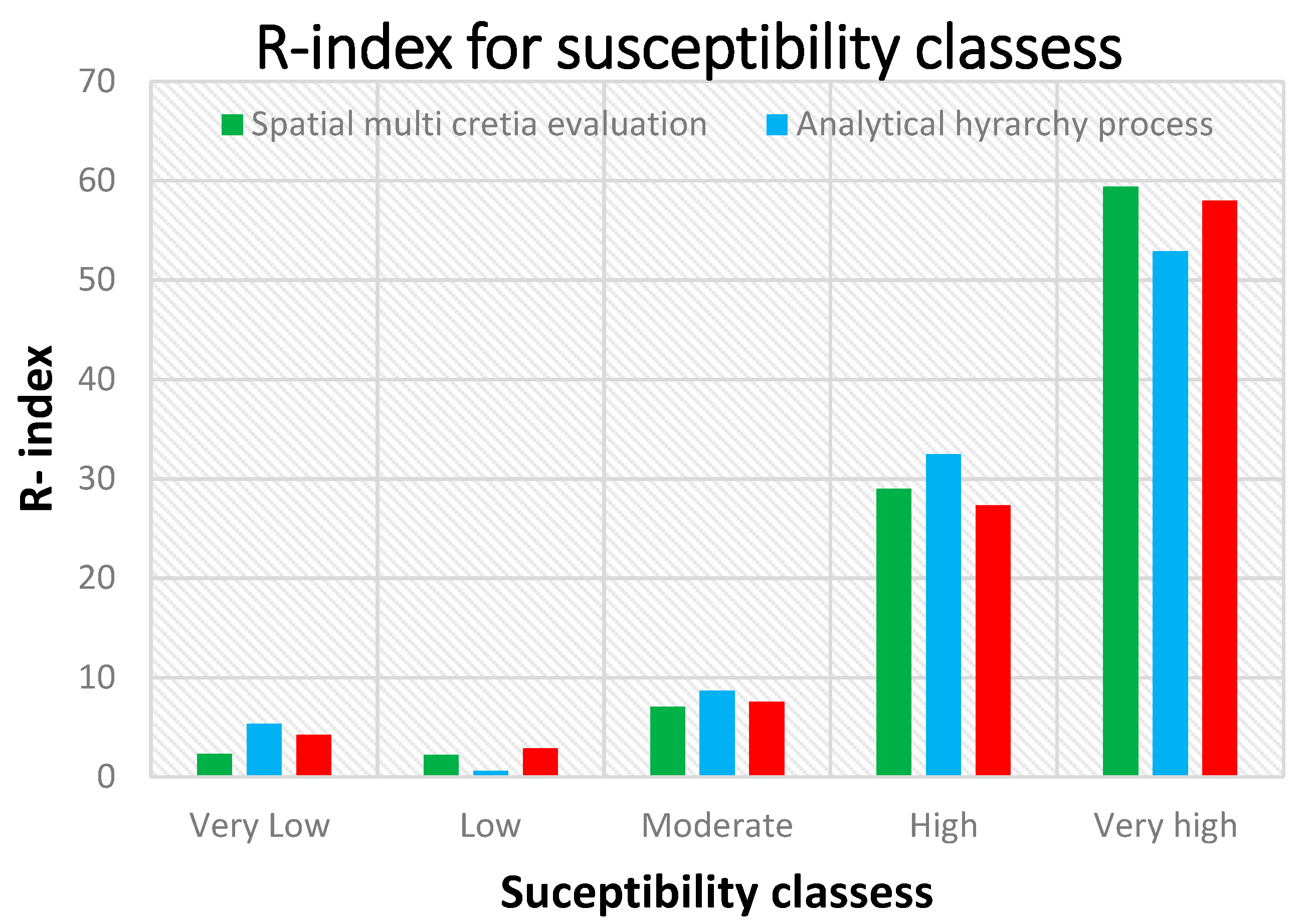
5.2. Relative Landslide Density (R-index)
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Manandhar, P.K. Disaster Review 2013; Department of Water Induced Disaster Prevention: Kathmandu, Nepal, 2015.
- Ni, J.; Barazangi, M. Seismotectonics of the himalayan collision zone: Geometry of the underthrusting indian plate beneath the himalaya. J. Geophys. Res. Solid Earth 1984, 89, 1147–1163. [Google Scholar] [CrossRef]
- Dahal, R.K. Engineering geological issues after Gorkha earthquake 2015 in Nepal—A preliminary understanding. In Proceedings of the 10th Asian Regional Conference of IAEG, Kyoto, Japan, 26–29 September 2015. [Google Scholar]
- Kargel, J.; Leonard, G.; Shugar, D.H.; Haritashya, U.; Bevington, A.; Fielding, E.; Fujita, K.; Geertsema, M.; Miles, E.; Steiner, J. Geomorphic and geologic controls of geohazards induced by Nepal’s 2015 Gorkha earthquake. Science 2016, 351, aac8353. [Google Scholar] [CrossRef] [PubMed]
- Martha, T.R.; Roy, P.; Mazumdar, R.; Govindharaj, K.B.; Kumar, K.V. Spatial characteristics of landslides triggered by the 2015 m w 7.8 (Gorkha) and m w 7.3 (Dolakha) earthquakes in Nepal. Landslides 2017, 14, 697–704. [Google Scholar] [CrossRef]
- Regmi, A.D.; Dhital, M.R.; Zhang, J.-Q.; Su, L.-J.; Chen, X.-Q. Landslide susceptibility assessment of the region affected by the 25 April 2015 Gorkha earthquake of Nepal. J. Mt. Sci. 2016, 13, 1941–1957. [Google Scholar] [CrossRef]
- Roback, K.; Clark, M.K.; West, A.J.; Zekkos, D.; Li, G.; Gallen, S.F.; Chamlagain, D.; Godt, J.W. The size, distribution, and mobility of landslides caused by the 2015 mw 7.8 Gorkha earthquake, Nepal. Geomorphology 2018, 301, 121–138. [Google Scholar] [CrossRef]
- Chigira, M. Inventory Mapping of Landslides Induced by the Gorkha Earthquake. Available online: https://www.jst.go.jp/inter/sicp/country/j-rapid/nepal/pdf/j-rapid_nepal_chigira.pdf (accessed on 5 February 2019).
- Gnyawali, K.R.; Maka, S.; Adhikari, B.R.; Chamlagain, D.; Duwal, S.; Dhungana, A.R. Spatial implications of earthquake induced landslides triggered by the April 25 Gorkha earthquake mw 7.8: Preliminary analysis and findings. In Proceedings of the International Conference on Earthquake Engineering and Post Disastor Reconstruction Planning, Bhaktapur, Nepal, 24–26 April 2016; pp. 50–58. [Google Scholar]
- Guzzetti, F.; Reichenbach, P.; Ardizzone, F.; Cardinali, M.; Galli, M. Estimating the quality of landslide susceptibility models. Geomorphology 2006, 81, 166–184. [Google Scholar] [CrossRef]
- Hervás, J.; Van Den Eeckhaut, M.; Legorreta, G.; Trigila, A. Landslide inventory and susceptibility and hazard zoning. Landslide Sci. Pract. 2013, 1, 1–2. [Google Scholar]
- Keefer, D.K. Landslides caused by earthquakes. Geol. Soc. Am. Bull. 1984, 95, 406–421. [Google Scholar] [CrossRef]
- Keefer, D.K. Investigating landslides caused by earthquakes—A historical review. Surv. Geophys. 2002, 23, 473–510. [Google Scholar] [CrossRef]
- Gorsevski, P.V.; Brown, M.K.; Panter, K.; Onasch, C.M.; Simic, A.; Snyder, J. Landslide detection and susceptibility mapping using lidar and an artificial neural network approach: A case study in the Cuyahoga Valley National Park, Ohio. Landslides 2016, 13, 467–484. [Google Scholar] [CrossRef]
- Saba, S.B.; Ali, M.; van der Meijde, M.; van der Werff, H. Co-seismic landslides automatic detection on regional scale with sub-pixel analysis of multi temporal high resolution optical images: Application to southwest of Port Au Prince, Haiti. J. Himal. Earth Sci. 2017, 50, 74–92. [Google Scholar]
- Huang, F.; Chen, L.; Yin, K.; Huang, J.; Gui, L. Object-oriented change detection and damage assessment using high-resolution remote sensing images, Tangjiao Landslide, Three Gorges Reservoir, China. Environ. Earth Sci. 2018, 77, 183. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Meena, S.R.; Tiede, D.; Aryal, J. Evaluation of different machine learning methods and deep-learning convolutional neural networks for landslide detection. Remote Sens. 2019, 11, 196. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Jankowski, P.; Blaschke, T. A gis based spatially-explicit sensitivity and uncertainty analysis approach for multi-criteria decision analysis. Comput. Geosci. 2014, 64, 81–95. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. Multi-criteria risk evaluation by integrating an analytical network process approach into GIS-based sensitivity and uncertainty analyses. Geomat. Nat. Hazards Risk 2018, 9, 127–151. [Google Scholar] [CrossRef]
- Hasekioğulları, G.D.; Ercanoglu, M. A new approach to use ahp in landslide susceptibility mapping: A case study at Yenice (Karabuk, Nw Turkey). Nat. Hazards 2012, 63, 1157–1179. [Google Scholar] [CrossRef]
- Kanwal, S.; Atif, S.; Shafiq, M. GIS based landslide susceptibility mapping of northern areas of Pakistan, a case study of Shigar and Shyok Basins. Geomat. Nat. Hazards Risk 2017, 8, 348–366. [Google Scholar] [CrossRef]
- Mondal, S.; Maiti, R. Integrating the analytical hierarchy process (AHP) and the frequency ratio (FR) model in landslide susceptibility mapping of Shiv-Khola Watershed, Darjeeling Himalaya. Int. J. Disaster Risk Sci. 2013, 4, 200–212. [Google Scholar] [CrossRef]
- Myronidis, D.; Papageorgiou, C.; Theophanous, S. Landslide susceptibility mapping based on landslide history and analytic hierarchy process (AHP). Nat. Hazards 2016, 81, 245–263. [Google Scholar] [CrossRef]
- Park, S.; Choi, C.; Kim, B.; Kim, J. Landslide susceptibility mapping using frequency ratio, analytic hierarchy process, logistic regression, and artificial neural network methods at the Inje Area, Korea. Environ. Earth Sci. 2013, 68, 1443–1464. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Pradhan, B.; Gokceoglu, C. Application of fuzzy logic and analytical hierarchy process (AHP) to landslide susceptibility mapping at Haraz Watershed, iran. Nat. Hazards 2012, 63, 965–996. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Multicriteria Decision Analysis in Geographic Information Science; Springer: New York, NY, USA, 2016. [Google Scholar]
- Ghorbanzadeh, O.; Blaschke, T.; Aryal, J.; Gholaminia, K. A new gis-based technique using an adaptive neuro-fuzzy inference system for land subsidence susceptibility mapping. J. Spat. Sci. 2018. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Rostamzadeh, H.; Blaschke, T.; Gholaminia, K.; Aryal, J. A new gis-based data mining technique using an adaptive neuro-fuzzy inference system (ANFIS) and k-fold cross-validation approach for land subsidence susceptibility mapping. Nat. Hazards 2018, 94, 497–517. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Kerle, N. Random forests and evidential belief function-based landslide susceptibility assessment in western Mazandaran province, Iran. Environ. Earth Sci. 2016, 75, 185. [Google Scholar] [CrossRef]
- Wu, Y.; Li, W.; Wang, Q.; Liu, Q.; Yang, D. Landslide Susceptibility Assessment Using Frequency Ratio, Statistical Index and Certainty Factor Models for the Gangu County, China. Arab. J. Geosci. 2016. [Google Scholar] [CrossRef]
- Ozdemir, A.; Altural, T. A comparative study of frequency ratio, weights of evidence and logistic regression methods for landslide susceptibility mapping: Sultan Mountains, SW Turkey. J. Asian Earth Sci. 2013, 64, 180–197. [Google Scholar] [CrossRef]
- Pradhan, B. Landslide susceptibility mapping of a catchment area using frequency ratio, fuzzy logic and multivariate logistic regression approaches. J. Indian Soc. Remote Sens. 2010, 38, 301–320. [Google Scholar] [CrossRef]
- Razandi, Y.; Pourghasemi, H.R.; Neisani, N.S.; Rahmati, O. Application of analytical hierarchy process, frequency ratio, and certainty factor models for groundwater potential mapping using gis. Earth Sci. Inform. 2015, 8, 867–883. [Google Scholar] [CrossRef]
- Umar, Z.; Pradhan, B.; Ahmad, A.; Jebur, M.N.; Tehrany, M.S. Earthquake induced landslide susceptibility mapping using an integrated ensemble frequency ratio and logistic regression models in west sumatera province, indonesia. CATENA 2014, 118, 124–135. [Google Scholar] [CrossRef]
- Wang, L.-J.; Guo, M.; Sawada, K.; Lin, J.; Zhang, J. A comparative study of landslide susceptibility maps using logistic regression, frequency ratio, decision tree, weights of evidence and artificial neural network. Geosci. J. 2016, 20, 117–136. [Google Scholar] [CrossRef]
- Wang, Q.; Li, W. A gis-based comparative evaluation of analytical hierarchy process and frequency ratio models for landslide susceptibility mapping. Phys. Geogr. 2017, 38, 318–337. [Google Scholar] [CrossRef]
- Lee, S.; Pradhan, B. Landslide hazard mapping at selangor, malaysia using frequency ratio and logistic regression models. Landslides 2007, 4, 33–41. [Google Scholar] [CrossRef]
- Chen, W.; Sun, Z.; Han, J. Landslide susceptibility modeling using integrated ensemble weights of evidence with logistic regression and random forest models. Appl. Sci. 2019, 9, 171. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. An uncertainty and sensitivity analysis approach for gis-based multicriteria landslide susceptibility mapping. Int. J. Geogr. Inf. Sci. 2014, 28, 610–638. [Google Scholar] [CrossRef] [PubMed]
- Omid Ghorbanzadeh, B.F.; Blaschke, T.; Khosravi, R. Spatially explicit sensitivity and uncertainty analysis for the landslide risk assessment of the gas pipeline networks. In Proceedings of the 21st AGILE Conference on Geo-Information Science, Lund, Sweden, 12–15 June 2018. [Google Scholar]
- Boerboom, L.; Flacke, J.; Sharifi, A.; Alan, O. Web-Based Spatial Multi-Criteria Evaluation (SMCE) Software, ITC Working Paper 1, for the ForestClim Project 25. Available online: https://www.researchgate.net/publication/267999302_Web-based_spatial_multi-criteria_evaluation_SMCE_software (accessed on 5 February 2019).
- Alcaraz Tarragüel, A.; Krol, B.; van Westen, C. Analysing the possible impact of landslides and avalanches on cultural heritage in Upper Svaneti, Georgia. J. Cult. Herit. 2012, 13, 453–461. [Google Scholar] [CrossRef]
- Pourghasemi, H.R. Landslide susceptibility mapping using a spatial multi criteria evaluation model at Haraz Watershed, Iran. In Terrigenous Mass Movements; Springer: Berlin/Heidelberg, Germany, 2012; pp. 1–398. [Google Scholar]
- Nsengiyumva, J.B.; Luo, G.; Nahayo, L.; Huang, X.; Cai, P. Landslide susceptibility assessment using spatial multi-criteria evaluation model in rwanda. Int. J. Environ. Res. Public Health 2018, 15, 243. [Google Scholar] [CrossRef] [PubMed]
- Hong, H.; Shahabi, H.; Shirzadi, A.; Chen, W.; Chapi, K.; Ahmad, B.B.; Roodposhti, M.S.; Hesar, A.Y.; Tian, Y.; Bui, D.T. Landslide susceptibility assessment at the Wuning Area, China: A comparison between multi-criteria decision making, bivariate statistical and machine learning methods. Nat. Hazards 2018, 1–40. [Google Scholar] [CrossRef]
- Bilham, R.; Larson, K.; Freymueller, J. Gps measurements of present-day convergence across the nepal himalaya. Nature 1997, 386, 61. [Google Scholar] [CrossRef]
- Meena, S.R. Web based landslide management system for nepal. In Proceedings of the 33rd Himalaya-Karakorum-Tibet Workshop (HKT), Lausanne, Switzerland, 10–12 September 2018; pp. 109–110. [Google Scholar]
- Roback, K.; Clark, M.; West, A.; Zekkos, D.; Li, G.; Gallen, S.; Godt, J. Map data of landslides triggered by the 25 April 2015 mw 7.8 Gorkha, Nepal earthquake. US Geol. Surv. Data Release 2017. [Google Scholar] [CrossRef]
- Termeh, S.V.R.; Kornejady, A.; Pourghasemi, H.R.; Keesstra, S. Flood susceptibility mapping using novel ensembles of adaptive neuro fuzzy inference system and metaheuristic algorithms. Sci. Total Environ. 2018, 615, 438–451. [Google Scholar] [CrossRef]
- Pourghasemi, H.R. Gis-based forest fire susceptibility mapping in Iran: A comparison between evidential belief function and binary logistic regression models. Scand. J. For. Res. 2016, 31, 80–98. [Google Scholar] [CrossRef]
- Guzzetti, F.; Mondini, A.C.; Cardinali, M.; Fiorucci, F.; Santangelo, M.; Chang, K.-T. Landslide inventory maps: New tools for an old problem. Earth-Sci. Rev. 2012, 112, 42–66. [Google Scholar] [CrossRef]
- Basheer, I.A.; Hajmeer, M. Artificial neural networks: Fundamentals, computing, design, and application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, O.B. Landslide susceptibility mapping at hoa binh province (vietnam) using an adaptive neuro-fuzzy inference system and GIS. Comput. Geosci. 2012, 45, 199–211. [Google Scholar]
- Feizizadeh, B.; Roodposhti, M.S.; Jankowski, P.; Blaschke, T. A gis-based extended fuzzy multi-criteria evaluation for landslide susceptibility mapping. Comput. Geosci. 2014, 73, 208–221. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, M. Mass Movement Hazard Analysis and Presentation of Suitable Regional Model Using GIS (Case Study: A Part of Haraz Watershed). Master’s Thesis, Tarbiat Modarres University International Campus, Tehran, Iran, 2008; p. 80. [Google Scholar]
- Raja, N.B.; Įiįek, I.; Türkoğlu, N.; Aydin, O.; Kawasaki, A. Correction to: Landslide susceptibility mapping of the sera river basin using logistic regression model. Nat. Hazards 2018, 91, 1423. [Google Scholar] [CrossRef]
- Gökceoglu, C.; Aksoy, H. Landslide susceptibility mapping of the slopes in the residual soils of the Mengen Region (turkey) by deterministic stability analyses and image processing techniques. Eng. Geol. 1996, 44, 147–161. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Kim, Y.-T. Relative effect method of landslide susceptibility zonation in weathered granite soil: A case study in Deokjeok-ri Creek, South Korea. Nat. Hazards 2014, 72, 1189–1217. [Google Scholar] [CrossRef]
- Saaty, T.L. Analytic heirarchy process. Wiley Statsref Stat. Ref. Online 1980. [Google Scholar]
- Cabrera-Barona, P.; Ghorbanzadeh, O. Comparing classic and interval analytical hierarchy process methodologies for measuring area-level deprivation to analyze health inequalities. Int. J. Environ. Res. Public Health 2018, 15, 140. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H.; Ugawa, N. Landslide susceptibility mapping using gis-based weighted linear combination, the case in Tsugawa Area of Agano River, Niigata Prefecture, Japan. Landslides 2004, 1, 73–81. [Google Scholar] [CrossRef]
- Saaty, T.L.; Vargas, L.G. Inconsistency and rank preservation. J. Math. Psychol. 1984, 28, 205–214. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Moslem, S.; Blaschke, T.; Duleba, S. Sustainable urban transport planning considering different stakeholder groups by an interval-ahp decision support model. Sustainability 2018, 11, 9. [Google Scholar] [CrossRef]
- Sahnoun, H.; Serbaji, M.M.; Karray, B.; Medhioub, K. GIS and multi-criteria analysis to select potential sites of agro-industrial complex. Environ. Earth Sci. 2012, 66, 2477–2489. [Google Scholar] [CrossRef]
- Pirnazar, M.; Karimi, A.Z.; Feizizadeh, B.; Ostad-Ali-Askari, K.; Eslamian, S.; Hasheminasab, H.; Ghorbanzadeh, O.; Hamedani, M.H. Assessing flood hazard using gis based multi-criteria decision making approach; study area: East-Azerbaijan Province (Kaleybar Chay Basin). J. Flood Eng. 2017, 8, 203–223. [Google Scholar]
- Saaty, T.L. A scaling method for priorities in hierarchical structures. J. Math. Psychol. 1977, 15, 234–281. [Google Scholar] [CrossRef]
- Malczewski, J.; Rinner, C. Introduction to GIS-mcda. In Multicriteria Decision Analysis in Geographic Information Science; Springer: New York, NY, USA, 2015; pp. 23–54. [Google Scholar]
- Saaty, T.L. The Analytic Hierarchy Process: Planning, Priority Setting, Resource Allocation; McGraw-Hill International Book Co: New York, NY, USA, 1980; p. 287. [Google Scholar]
- Pal, S.; Talukdar, S. Application of frequency ratio and logistic regression models for assessing physical wetland vulnerability in punarbhaba river basin of indo-bangladesh. Hum. Ecol. Risk Assess. Int. J. 2018, 24, 1291–1311. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M. Landslide susceptibility mapping using gis-based statistical models and remote sensing data in tropical environment. Sci. Rep. 2015, 5, 9899. [Google Scholar] [CrossRef] [PubMed]
- Akgün, A.; Bulut, F. GIS-based landslide susceptibility for Arsin-Yomra (Trabzon, North Turkey) region. Environ. Geol. 2007, 51, 1377–1387. [Google Scholar] [CrossRef]
- Shahabi, H.; Hashim, M.; Ahmad, B.B. Remote sensing and gis-based landslide susceptibility mapping using frequency ratio, logistic regression, and fuzzy logic methods at the Central Zab Basin, Iran. Environ. Earth Sci. 2015, 73, 8647–8668. [Google Scholar] [CrossRef]
- Günther, A.; Van Den Eeckhaut, M.; Malet, J.-P.; Reichenbach, P.; Hervás, J. Climate-physiographically differentiated pan-european landslide susceptibility assessment using spatial multi-criteria evaluation and transnational landslide information. Geomorphology 2014, 224, 69–85. [Google Scholar] [CrossRef]
- Malczewski, J. GIS and Multicriteria Decision Analysis; John Wiley & Sons: New York, NY, USA, 1999. [Google Scholar]
- Rahman, R.; Saha, S. Remote sensing, spatial multi criteria evaluation (SMCE) and analytical hierarchy process (AHP) in optimal cropping pattern planning for a flood prone area. J. Spat. Sci. 2008, 53, 161–177. [Google Scholar] [CrossRef]
- Abdollahi, S.; Pourghasemi, H.R.; Ghanbarian, G.A.; Safaeian, R. Prioritization of effective factors in the occurrence of land subsidence and its susceptibility mapping using an SVM model and their different kernel functions. Bull. Eng. Geol. Environ. 2018, 1–18. [Google Scholar] [CrossRef]
- Linden, A. Measuring diagnostic and predictive accuracy in disease management: An introduction to receiver operating characteristic (ROC) analysis. J. Eval. Clin. Pract. 2006, 12, 132–139. [Google Scholar] [CrossRef] [PubMed]
- Ghorbanzadeh, O.; Feizizadeh, B.; Blaschke, T. An interval matrix method used to optimize the decision matrix in AHP technique for land subsidence susceptibility mapping. Environ. Earth Sci. 2018, 77, 584. [Google Scholar] [CrossRef]
- Pourghasemi, H.; Gayen, A.; Park, S.; Lee, C.-W.; Lee, S. Assessment of landslide-prone areas and their zonation using logistic regression, logitboost, and naïvebayes machine-learning algorithms. Sustainability 2018, 10, 3697. [Google Scholar] [CrossRef]
- Baird, C.; Healy, T.; Johnson, K.; Bogie, A.; Dankert, E.W.; Scharenbroch, C. A Comparison of Risk Assessment Instruments in Juvenile Justice; National Council on Crime and Delinquency: Madison, WI, USA, 2013. [Google Scholar]
- Baeza, C.; Corominas, J. Assessment of shallow landslide susceptibility by means of multivariate statistical techniques. Earth Surf. Process. Landf. 2001, 26, 1251–1263. [Google Scholar] [CrossRef]
- Junior, F.R.L.; Osiro, L.; Carpinetti, L.C.R. A comparison between fuzzy ahp and fuzzy topsis methods to supplier selection. Appl. Soft Comput. 2014, 21, 194–209. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Ghorbanzadeh, O. GIS-based interval pairwise comparison matrices as a novel approach for optimizing an analytical hierarchy process and multiple criteria weighting. GI_Forum 2017 2017, 1, 27–35. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T. GIS-multicriteria decision analysis for landslide susceptibility mapping: Comparing three methods for the urmia lake basin, iran. Nat. Hazards 2013, 65, 2105–2128. [Google Scholar] [CrossRef]
- Shahabi, H.; Khezri, S.; Ahmad, B.B.; Hashim, M. Landslide susceptibility mapping at Central Zab Basin, Iran: A comparison BETWEEN analytical hierarchy process, frequency ratio and logistic regression models. Catena 2014, 115, 55–70. [Google Scholar] [CrossRef]

| Importance | Definition | Explanation |
|---|---|---|
| 1 | Equal importance | Contribution to objective is equal |
| 3 | Moderate importance | The attribute is slightly favored over another |
| 5 | Strong importance | The attribute is strongly favored over another |
| 7 | Very strong importance | The attribute is very strongly favored over another |
| 9 | Extreme importance | Evidence favoring one attribute is of the highest possible order of affirmation |
| 2, 4, 6, 8 | Intermediate values | When compromise is needed |
| Groups | Topography | Geological | Hydrological | Manmade | Weights |
|---|---|---|---|---|---|
| Topography | 1 | - | - | - | 0.30 |
| Geological | 1 | 1 | - | - | 0.30 |
| Hydrological | 0.83 | 0.83 | 1 | - | 0.25 |
| Manmade | 0.5 | 0.5 | 0.6 | 1 | 0.15 |
| Groups | Hybrid SMCE Group Weights | Factors | Hybrid SMCE Factor Weights |
|---|---|---|---|
| Topography | 30 | DEM | 0.3 |
| Slope | 0.36 | ||
| Aspect | 0.34 | ||
| Geological | 30 | Faults | 0.4 |
| Lithology | 0.6 | ||
| Hydrological | 25 | Drainage | 0.5 |
| Precipitation | 0.5 | ||
| Manmade | 15 | Land use | 0.8 |
| Distance to roads | 0.2 |
| Factors | Classes | Pairwise Comparison Matrices | Eigenvalues | CR | Number of Landslides | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Land use | Forest | 1 | 0.37 | 11,854 | |||||||
| Shrub land | 1/5 | 1 | 0.166 | 782 | |||||||
| Grassland | 1/3 | 1/3 | 1 | 0.126 | 4803 | ||||||
| Agriculture | 1/3 | 1/3 | 1 | 1 | 0.153 | 5555 | |||||
| Barren | 1/5 | 1/2 | 1/3 | 1/5 | 1 | 0.063 | 316 | ||||
| Waterbody | 1/5 | 1/2 | 1/3 | 1/3 | 1/2 | 1 | 0.053 | 31 | |||
| Snow cover | 1/5 | 1 | 1/2 | 1/3 | 1 | 1 | 1 | 0.068 | 97 | ||
| 0.092 | |||||||||||
| Precipitation (mm) | 950–1725 | 1 | 0.067 | 1349 | |||||||
| 1725–2500 | 2 | 1 | 0.147 | 5296 | |||||||
| 2500–3275 | 7 | 3 | 1 | 0.493 | 9456 | ||||||
| 3275–4050 | 5 | 2 | 1/2 | 1 | 0.291 | 7275 | |||||
| 0.006 | |||||||||||
| Lithology | Glacier | 1 | 0.034 | 8 | |||||||
| Fluvial calcareous | 2 | 1 | 0.062 | 79 | |||||||
| Fluvial non-calcareous | 3 | 2 | 1 | 0.098 | 260 | ||||||
| Slate/ phyllite | 5 | 3 | 2 | 1 | 0.161 | 1151 | |||||
| Quartzite | 8 | 4 | 3 | 2 | 1 | 0.293 | 2429 | ||||
| Gneiss | 9 | 5 | 4 | 3 | 1 | 1 | 0.35 | 19,512 | |||
| 0.009 | |||||||||||
| Distance to fault (m) | (1) 0–2000 | 1 | 0.641 | 4161 | |||||||
| (2) 2000–4000 | 1/2 | 1 | 0.221 | 3471 | |||||||
| (3) 4000–6000 | 1/3 | 1/3 | 1 | 0.086 | 2690 | ||||||
| (4) 6000 < | 1/2 | 1/2 | 1 | 1 | 0.050 | 13,117 | |||||
| 0.03 | |||||||||||
| Distance to drainage (m) | <200 | 1 | 0.41 | 8942 | |||||||
| 200–400 | 1/2 | 1 | 0.254 | 4708 | |||||||
| 400–600 | 1/3 | 1/2 | 1 | 0.152 | 3047 | ||||||
| 600–800 | 1/4 | 1/3 | 1/2 | 1 | 0.104 | 2038 | |||||
| >800 | 1/4 | 1/3 | 1/2 | 1/2 | 1 | 0.078 | 4703 | ||||
| 0.032 | |||||||||||
| Slope (%) | 0–10 | 1 | 0.053 | 733 | |||||||
| 10–20 | 3 | 1 | 0.067 | 2380 | |||||||
| 20–30 | 8 | 7 | 1 | 0.235 | 5600 | ||||||
| 30–40 | 9 | 8 | 3 | 1 | 0.325 | 8922 | |||||
| >40 | 9 | 8 | 3 | 3 | 1 | 0.320 | 5773 | ||||
| 0.054 | |||||||||||
| Elevation (m) | (1) <1000 | 1 | 0.133 | 1704 | |||||||
| (2) 1000–3000 | 5 | 1 | 0.566 | 18,520 | |||||||
| (3) 3000–4500 | 2 | 1/3 | 1 | 0.206 | 3001 | ||||||
| (4) > 4500 | 1 | 1/5 | 1/2 | 1 | 0.093 | 188 | |||||
| 0.024 | |||||||||||
| Aspect | (1) Flat | 1 | 0.195 | 1303 | |||||||
| (2) North | 1/2 | 1 | 0.172 | 4419 | |||||||
| (3) East | 2 | 1 | 1 | 0.291 | 9219 | ||||||
| (4) West | 1 | 1 | 1/2 | 2 | 1 | 0.193 | 5399 | ||||
| (5) South | 1 | 1 | 1/2 | 1/2 | 1 | 1 | 0.147 | 3068 | |||
| 0.058 | |||||||||||
| Distance to roads (m) | (1) 0–200 | 1 | 0.527 | 11,316 | |||||||
| (2) 200–400 | 1/3 | 1 | 0.315 | 5403 | |||||||
| (3) 400–600 | 1/5 | 1/5 | 1 | 0.095 | 2634 | ||||||
| (4) 600< | 1/6 | 1/6 | 1/2 | 1 | 0.061 | 4085 | |||||
| 0.069 | |||||||||||
| Classes | Pixels of Each Class | % of Pixels | Landslide Pixels | % of Pixels | FR | |
|---|---|---|---|---|---|---|
| Land use | Forest | 6,769,546 | 42.22 | 7,357,500 | 50.63 | 0.207 |
| Shrub land | 436,382 | 2.72 | 495,900 | 3.41 | 0.216 | |
| Grassland | 2,428,461 | 15.14 | 3,038,400 | 20.90 | 0.238 | |
| Agriculture | 3,691,183 | 23.02 | 3,378,600 | 23.25 | 0.174 | |
| Barren | 951,485 | 5.93 | 182,700 | 1.25 | 0.037 | |
| Waterbody | 34,993 | 0.21 | 22,500 | 0.15 | 0.122 | |
| Snow cover | 1,718,690 | 10.72 | 55,800 | 0.38 | 0.006 | |
| Precipitation (mm) | 950–1725 | 200,439 | 13.87 | 4,824,736 | 38.030 | 0.641 |
| 1725–2500 | 409,972 | 28.37 | 2,546,432 | 20.072 | 0.166 | |
| 2500–3275 | 576,685 | 39.91 | 1,629,936 | 12.848 | 0.075 | |
| 3275–4050 | 258,008 | 17.85 | 1,135,232 | 8.948 | 0.117 | |
| Lithology | Glacier | 94,829 | 0.51 | 4500 | 0.03 | 0.021 |
| Fluvial calcareous | 341,548 | 1.85 | 43,200 | 0.30 | 0.055 | |
| Fluvial non-calcareous | 427,676 | 2.31 | 157,500 | 1.08 | 0.160 | |
| Slate/phyllite | 3,334,366 | 18.04 | 717,300 | 4.94 | 0.093 | |
| Quartzite | 3,671,637 | 19.86 | 1,473,300 | 10.15 | 0.174 | |
| Gneiss | 10,615,038 | 57.42 | 12,123,000 | 83.50 | 0.496 | |
| Distance to fault (m) | (1) 0–2000 | 1,378,839 | 7.95 | 2,583,900 | 17.77 | 0.353 |
| (2) 2000–4000 | 1,361,041 | 7.85 | 2,114,100 | 14.54 | 0.293 | |
| (3) 4000–6000 | 1,329,324 | 7.67 | 1,678,500 | 11.55 | 0.238 | |
| (4) 6000< | 13,273,150 | 76.54 | 8,160,300 | 56.14 | 0.116 | |
| Distance to drainage (m) | <200 | 3,285,083 | 17.83 | 4,824,736 | 38.03 | 0.362 |
| 200–400 | 2,625,570 | 14.25 | 2,546,432 | 20.07 | 0.239 | |
| 400–600 | 2,280,177 | 12.38 | 1,629,936 | 12.85 | 0.176 | |
| 600–800 | 1,907,245 | 10.35 | 1,135,232 | 8.95 | 0.147 | |
| >800 | 8,323,424 | 45.18 | 2,550,352 | 20.10 | 0.076 | |
| Slope (%) | 0–10 | 1,158,724 | 6.76 | 425,055 | 3.05 | 0.076 |
| 10–20 | 3,806,967 | 22.21 | 1,432,083 | 10.27 | 0.078 | |
| 20–30 | 6,322,939 | 36.89 | 3,342,678 | 23.98 | 0.110 | |
| 30–40 | 4,377,817 | 25.54 | 5,345,525 | 38.35 | 0.254 | |
| >40 | 1,474,304 | 8.60 | 3,393,546 | 24.35 | 0.480 | |
| Elevation (m) | (1) <1000 | 2,976,275 | 17.33 | 1,030,307 | 7.39 | 0.152 |
| (2) 1000–3000 | 7,962,478 | 46.37 | 10,985,916 | 78.80 | 0.607 | |
| (3) 3000–4500 | 3,586,956 | 20.89 | 1,816,616 | 13.03 | 0.223 | |
| (4) >4500 | 2,646,440 | 15.41 | 109,497 | 0.79 | 0.018 | |
| Aspect | (1) Flat | 1,899,660 | 11.08 | 1,480,366 | 10.62 | 0.113 |
| (2) North | 3,304,522 | 19.28 | 3,542,704 | 25.42 | 0.279 | |
| (3) East | 4,238,423 | 24.73 | 4,625,604 | 33.18 | 0.298 | |
| (4) West | 4,004,391 | 23.36 | 2,661,554 | 19.09 | 0.190 | |
| (5) South | 3,693,755 | 21.55 | 1,628,661 | 11.68 | 0.119 | |
| Distance to roads (m) | (1) 0–200 | 9,064,140 | 49.098 | 6,143,424 | 48.39 | 0.234 |
| (2) 200–400 | 3,973,078 | 21.521 | 4,304,160 | 33.91 | 0.374 | |
| (3) 400–600 | 1,237,434 | 6.703 | 1,048,992 | 8.26 | 0.293 | |
| (4) 600< | 4,186,516 | 22.677 | 1,197,952 | 9.44 | 0.099 |
| Models | Susceptibility Class | Number of Pixels | Area (m²) | Area Percentage (ni) | Number of Landslides | Landslide Percentage (Ni) | R- Index |
|---|---|---|---|---|---|---|---|
| Hybrid SMCE | Very Low | 53,100 | 481,282,200 | 3.35 | 130 | 0.55 | 3 |
| Low | 656,100 | 2,926,548,000 | 20.35 | 755 | 3.22 | 2 | |
| Moderate | 4,664,700 | 6,508,665,000 | 45.26 | 5320 | 22.70 | 7 | |
| High | 11,235,600 | 3,814,145,000 | 26.52 | 12,780 | 54.52 | 29 | |
| Very high | 3,942,000 | 648,798,300 | 4.51 | 4454 | 19.00 | 59 | |
| AHP | Very Low | 6300 | 167,919,300 | 1.17 | 71 | 0.30 | 5 |
| Low | 64,800 | 1,554,764,000 | 10.81 | 74 | 0.32 | 1 | |
| Moderate | 3,978,900 | 6,563,949,000 | 45.65 | 4528 | 19.32 | 9 | |
| High | 9,473,400 | 4,198,336,000 | 29.20 | 10,816 | 46.15 | 32 | |
| Very high | 7,028,100 | 1,894,469,000 | 13.17 | 7948 | 33.91 | 53 | |
| FR | Very Low | 61,200 | 154,024,200 | 1.07 | 69 | 0.29 | 4 |
| Low | 998,100 | 3,768,698,000 | 26.11 | 1150 | 4.91 | 3 | |
| Moderate | 3,970,800 | 5,621,287,000 | 38.94 | 4504 | 19.22 | 8 | |
| High | 9,657,900 | 3,801,150,000 | 26.33 | 11,015 | 46.99 | 27 | |
| Very high | 5,905,800 | 1,090,157,000 | 7.55 | 6701 | 28.59 | 58 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meena, S.R.; Ghorbanzadeh, O.; Blaschke, T. A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal. ISPRS Int. J. Geo-Inf. 2019, 8, 94. https://doi.org/10.3390/ijgi8020094
Meena SR, Ghorbanzadeh O, Blaschke T. A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal. ISPRS International Journal of Geo-Information. 2019; 8(2):94. https://doi.org/10.3390/ijgi8020094
Chicago/Turabian StyleMeena, Sansar Raj, Omid Ghorbanzadeh, and Thomas Blaschke. 2019. "A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal" ISPRS International Journal of Geo-Information 8, no. 2: 94. https://doi.org/10.3390/ijgi8020094
APA StyleMeena, S. R., Ghorbanzadeh, O., & Blaschke, T. (2019). A Comparative Study of Statistics-Based Landslide Susceptibility Models: A Case Study of the Region Affected by the Gorkha Earthquake in Nepal. ISPRS International Journal of Geo-Information, 8(2), 94. https://doi.org/10.3390/ijgi8020094








