1. Introduction
People live in and act on space but deal and interact with place; Curry [
1] argues that place is a human invention to describe space. Within the domain of Geographical Information Science (henceforth GIScience), place is the result of combining space, as defined in mathematics and physics, with human experience [
2]. Two of the most fundamental queries that GIScience is tasked to address regarding spatial information are the localization and identification or categorization of places (e.g., “where is that” and “what is there”). The philosophical difficulties, however, of grasping the complicated nature of human experience, as well as the vague spatial projection of elusive entities, raises various challenges in the attempt to represent and process place within digital systems. An emerging question is whether elaborate and adequately quantifiable representations of place exist that can benefit from the capabilities of GIS and recent advancements, such as machine learning, to allow effective place search in the sense of localization and identification of places on space.
There have been several efforts to formalize the notion of place to, among others, enable a human-friendly way of searching space, a process that will henceforth be termed
place search. A prominent approach is to use gazetteers [
3], which treat place as typed place names associated spatial footprints, sometimes augmented with further semantics using ontologies. However, gazetteers predominantly focus on thematic and spatial information and are unable to capture how people interact with places. Other approaches rely on narratives to extract place-related information [
4] about place localization in the form of qualitative spatial relations associated with known locations; as with gazetteers, their focus is solely on locating places of interest. Purely data-driven approaches [
5] rely exclusively on statistical patterns, which may make search results less interpretable by humans. Hence, current place search approaches are not well-equipped to answer queries accurately and convincingly such as “locate shopping areas, even if they are not explicitly denoted as shopping malls”.
As a step towards addressing these limitations, in previous work [
6,
7] we proposed the model of functional space, representing place as a system that satisfies one or more purposes by offering particular functions; such functions are enabled or disabled by the spatial organization of the constituent elements of a place. Places, then, are formalized as design patterns (henceforth referred to simply as patterns), which define how the composition of a place supports a particular set of functions. These patterns are extracted from text analysis and enable function-based search of space, that is, locating places that support particular functions. However, the patterns require that support (or non-support) of a function depends on fully satisfying a set of rules, without offering any choice in between. Also, the extraction process highly depends on narratives which may reflect ideal or generic definitions of a place. Because of these characteristics, place search using such patterns may be less effective when dealing with inconsistent, incomplete or vague data, or when searching for places that do not strictly conform to narratives.
Considering the aforementioned limitations, this work is dedicated to address the question of whether the existing formalizations of place can be adjusted to provide an adequately quantifiable representation that allows: (a) an elaborate conceptualization of place that goes beyond geo-located place names, (b) integration within GIS and (c) (semi-)automated extraction process of patterns of place that deal with the vague way that people describe places. In this article, which is a revised and extended version of [
8], we increase the effectiveness, flexibility and applicability of function-based search of space by proposing two enhanced versions of the original patterns that lift both restrictions of exclusively relying on narratives and of only allowing a function to be “supported” or “not supported”. Specifically, the contributions of this article are the following:
Definition and formalization of empirical patterns of place that allow elements within to be necessarily or possibly included, using the relevant notions in modal logic in combination to empirical data
Enhanced pattern extraction process that uses empirical knowledge to revise and complement the knowledge derived from narratives
Definition and formalization of probabilistic patterns of place that assign probabilistic weights to the constituents of a function that is associated with a place
Automated calculation of weights in probabilistic patterns by relying on Statistical Relational Learning (SRL) [
9,
10], sometimes called Relational Machine Learning (RML) in the literature
Identification and delineation of places, along with a confidence rating denoting how close they are to the pattern used in the search
We evaluate the potential benefits of these contributions to place search by investigating how each of the three different patterns can enable a place search system to locate all places in London, UK that support functionality similar to a shopping mall. In particular, in this work we will attempt to locate and grade all the regions within the city of London that operate similar to a shopping mall. To avoid confusion and/or biased results, we adapt a generic and widely acceptable definition of shopping mall (based on Western world standards): “[...] a large retail complex containing a variety of stores and often restaurants and other business establishments housed in a series of connected or adjacent buildings or in a single large building” (
https://www.dictionary.com/browse/mall). The experiment shows that the newly proposed patterns allow for increased accuracy in the delineation of place search results as well as a clear indication of the level of function support.
The remainder of this article is organized as follows.
Section 2 offers a concise summary of research efforts related to modeling and searching for places.
Section 3 introduces empirical and probabilistic patterns of place and proposes methodologies for extracting them. Then,
Section 4 presents results of an experiment applying the proposed methodologies for the use case of identifying and locating the shopping areas in London, UK. These results, along with advantages, limitations and potential applications of the proposed approach are discussed in
Section 5, followed by concluding remarks and directions for future research in
Section 6.
2. Related Work
The most prevalent method of place search relies on digital gazetteers [
3], which are spatially referenced catalogs of place names. They provide a linkage between the human and physical world, by encoding relations between place names, space footprints, spatial categories, temporal information, and so on. Given these characteristics, searching places based on gazetteers amounts to actions such as keyword-based search on specific place names and types or extracting place names based on footprints. This severely limits their applicability in scenarios where more elaborate search conditions are required.
The use of ontologies [
11] overcomes these limitations by providing search based on semantics rather than keywords. The benefits of ontologies have been leveraged by several research efforts broadly within Geographic Information Retrieval (GIR). For instance, Jones et al. [
12] define an ontological model of place including information about the place type, name, centroid, as well as relations to other places. They then use this model to match a place name in a query with others that refer to equivalent or nearby locations, based on partonomic, Euclidean, and thematic distance. A more elaborate model is that of CIDOC CRM [
13], an upper level ontology that provides a detailed representation of knowledge about places in the form of qualitative spatial descriptions of semantics-driven entities such as events. A place entity is identified by a representative place name and provides the intermediate (human-friendly) node between events and their spatial projection. Such ontologies can facilitate sophisticated search focusing on the semantics captured by classes, hierarchies, and properties within the ontologies. However, in terms of spatial representation, ontologies predominantly rely on relative spatial information and any absolute information is either limited (e.g., point) or non-existent.
Integrating ontologies within GIR has resulted in several geographical search engines, such as SPIRIT [
14,
15], which relies on a place ontology modeling place names, footprints, and relations, similarly to the aforementioned approaches. The engine relies on a novel combination of textual and spatial indexing to reduce search time. The GeoShare project [
16] also produced an ontology-based search engine that evaluates candidate regions based on conceptual, spatial, and temporal relevance, relying on place names, relative spatial/partonomic distance and period names, respectively. Ontological gazetteers [
17] represent another example of enhancing place search by enriching the traditional structure of place names and spatial footprints with additional semantics in the form of knowledge graphs. These involve thematic information about places of interest such as types, activities, hierarchies, and so on. Spatial information is represented as geometric entities (points, lines or polygons) with fiat boundaries [
18]. While the aforementioned GIR systems significantly enhance the ability to search places based on thematic and spatial information, they are unable to capture (and, hence, search based on) other facets of place, such as information on how people interact with places. As argued by MacEachren [
19], most GIR research has been space-centric, focusing on recognizing and geolocating place names rather than interpreting why a place is a relevant result even without an associated place name.
The concept of semantic places [
4] is established following a meta-modeling approach based on relational semantics derived from text corpora. This allows searching for places based not only on properties but also relations between different places (including implicit ones) and other entities. This formalization is close to the human perception of space using objects and relations between them. However, this approach is highly dependent on natural language, which makes it context-dependent. Additionally, the focus is restricted to the problem of localizing place relative to a known location, without exploring the potential use of narratives to extract intrinsic characteristics of place that may enhance the search process.
On the other side of the spectrum, the work in [
5] follows a bottom-up, data-driven approach. Particularly, it places emphasis on the extraction of semantic signatures of places, in the form of co-occurrence patterns of points of interest, using LDA topic modeling and statistical analysis. These patterns are then used to discover similar regions that comply with the aforementioned signatures. The unsupervised and purely data-driven nature of this method implies certain limitations in terms of interpretability: as the presented information is not framed by any model, it is not easily comprehensible from a human perspective whether and why the discovered regions are acceptable results for a particular place search request.
In previous work [
6,
7], we proposed the function-based model of place, which is built on the assumption that place is space associated with particular functionality. According to this model, a place is regarded as a system of interconnected physical objects, whose spatial configuration, denoted as composition, enables particular functions and hence satisfies human purposes intertwined with the aforementioned functions. For instance, the human purpose of shopping is satisfied by a set of functions including shopping experience and walkability, which in turn are enabled by the existence of a variety of shops in a close distance, accessible via walkable routes. Under this model, places are formalized as patterns which are defined as sets of components, composition rules, and functional implications, as shown in
Table 1. Components refer to categories of physical entities that constitute a place and which enable, enhance, hinder, or block certain functions. Composition rules, shown in
Table 2 refer to the relations that frame the components of a place, in terms of both spatial and semantic configuration. Functional implications link each specific function to a first-order logic formula comprised of composition rules, with the semantics that a function is supported by a place if the associated formula is true.
Patterns are created through text analysis. Specifically, narratives, such as dictionaries, Wikipedia pages, design guidelines and similar sources, are analyzed to extract information about the functions and the composition of a place. The patterns enable function-based search of space [
6], that is, locating places that support particular functions. However, the rigid rules that describe these patterns can be more restrictive than necessary in some use cases. In particular, since the composition rules are expressed as logical formulas, they can either hold or not hold (and the associated function can either be permitted or forbidden). This hinders the effectiveness of place search, especially when dealing with inconsistent data or in cases of increased vagueness that require some elements of a pattern to be optional. Furthermore, pattern extraction highly depends on narratives, which often reflect the widely acceptable or the most general definition of a place, abstracting away the diversity that characterizes the real world.
In the remainder of this article, we propose two novel patterns of place that refine and extend the original ones to address these limitations, using modal logic and statistical relational learning. Information retrieval researchers have employed relational learning, Bayesian learning, and probabilistic logic methodologies previously; however, in the context of GIR, such efforts have purely focused on space. Examples include the seminal work of Califf and Mooney [
21] on learning pattern matching rules, the work of Walker et al. [
22] to integrate spatial knowledge into Bayesian learning and the use of Probabilistic Datalog to model GIR concepts [
23]. To the best of our knowledge, this work is the first to exploit statistical relational learning for the purpose of modeling and searching for places.
3. Methodology
In this section, we first analyze the extensions required to represent and formalize empirical composition patterns of place, including the process of extracting such patterns automatically based on spatial analysis and statistics. Then, we explain the rationale behind probabilistic composition patterns, followed by the adaptations required for their formalization and extraction.
3.1. Empirical Patterns of Place
The initial definition of design patterns of place, as introduced in [
7], relies on the extraction of knowledge from textual descriptions, such as dictionary or encyclopedia definitions of a place. In this sense, patterns essentially offer a commonly accepted blueprint for the place under consideration. In the remainder of this document, we will refer to these patterns as
theoretical patterns to differentiate them from the newly introduced ones.
Theoretical patterns require that all the composition rules for each function included within are supported by a particular area for it to be considered a place that conforms to the pattern. In relation to the elements in
Table 1, a function in
is supported only if all composition rules
in
included in the related formula
f in
hold. In reality, however, these composition rules are not all equally strongly associated with the particular function. Some of them may be considered essential, without which the place cannot function at all as expected, while others may simply improve the experience of a person and contribute an added value regarding that function.
Moreover, the threshold values within composition rules (values
T,
N,
R and
D in
Table 2) are derived exclusively from textual descriptions and general assumptions. Hence, they tend to suggest lower or higher limits that are broader than what is usually expected, e.g., suggesting much larger distances in proximity rules than necessary. To address both issues, we introduce an extended pattern variant called
empirical pattern, where empirical knowledge is used to differentiate composition rules within functional implications according to their necessity and adjust threshold values within.
The proposed extension is made possible by applying the principles of modal logic [
24]. This extension to standard formal logics, such as propositional and first-order logic, introduces operators that express modalities, i.e., expressions that qualify a logical statement. Several different modalities have been expressed, ranging from alethic and temporal, to deontic and epistemic ones. For our purposes, only two alethic modalities are required, specifically those expressing necessity and possibility.
As with theoretical patterns, empirical patterns conform to the fundamental assumption that place is space with ascribed functions and are formalized using the elements in
Table 1. The fundamental difference is that the logical formulas
within elements in
can also include the modal operators “necessarily” and “possibly”, denoted as □ and ⋄, respectively, to attribute a certainty level to the included composition rules. Considering the above, the semantics of a functional implication change slightly: a particular function is enabled, if, at minimum, the necessary composition rules within the functional implication formula hold.
3.2. Extracting Empirical Patterns
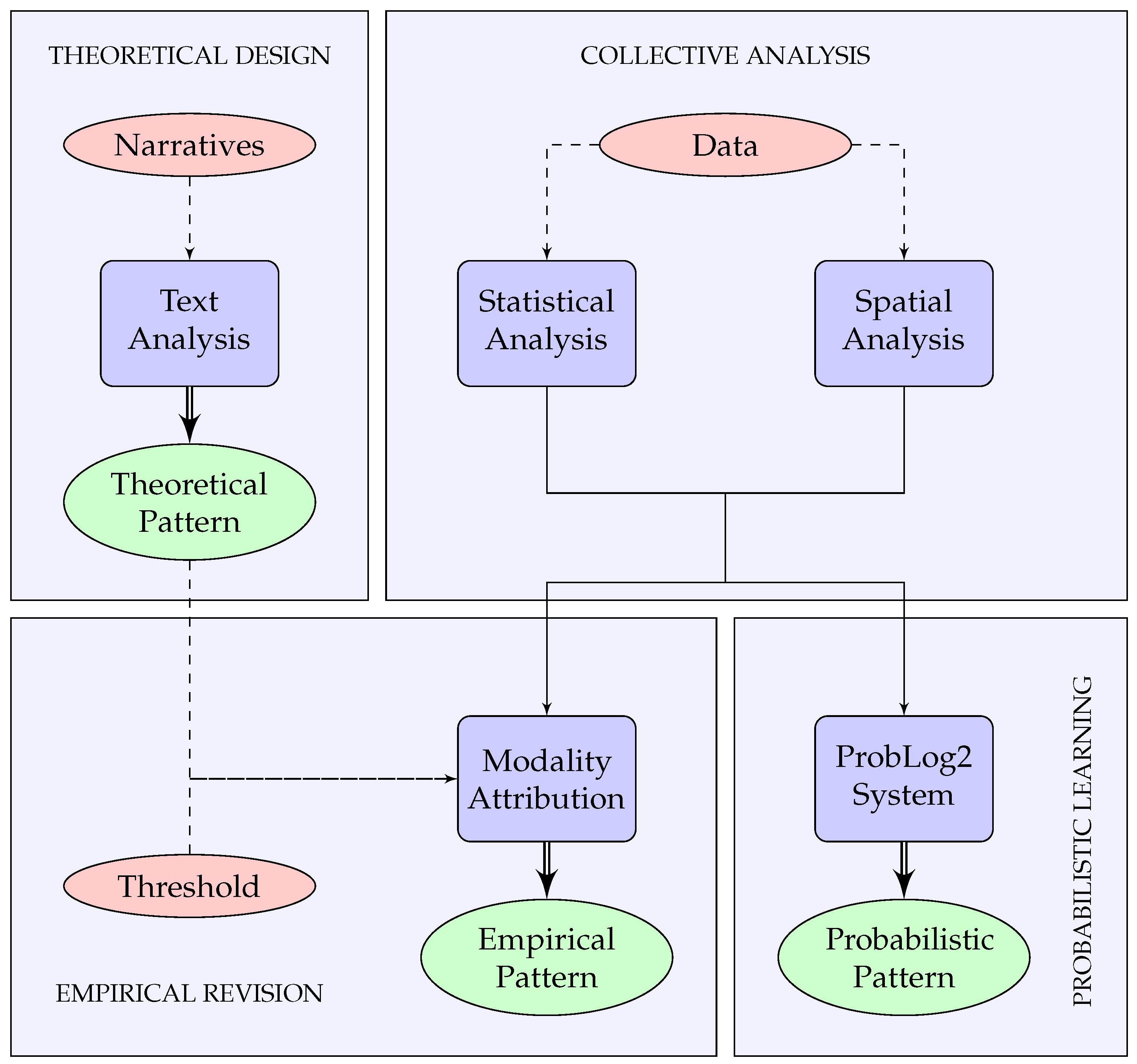
Theoretical patterns are extracted by solely relying on narratives to derive functions supported by a place. However, following the same process is not enough for empirical patterns. This is because narratives such as dictionary or encyclopedia definitions rarely contain the level of information required to decide whether a composition rule is a necessary or possible prerequisite for a function to be supported. To achieve automated creation of empirical patterns, we propose an extraction process that uses both theoretical and empirical knowledge. According to this process, an empirical pattern of place is no longer a strict reflection of the written word, but a combination of text-based and data-based information acquired through the phases of
theoretical design,
collective analysis and
empirical revision.
Figure 1 illustrates the extraction process, which is analyzed in the rest of this section.
The phase of theoretical design is, in essence, the process followed to derive a theoretical pattern and uses text analysis to derive knowledge about the components, composition rules, and functions of a place. This pattern is regarded as a collection of “echoes”, after Alexander’s 15 structural properties [
25] and describes the expected features that would enable the functions of the place under question.
The second phase, collective analysis, focuses on the analysis of regions that are considered as the ideal candidates of the place for which the theoretical pattern was created. More specifically, spatial and semantic data are acquired for a wide range of ideally defined instances of the place under question. Considering the latter as anchors, additional data is collected about adjacent components conforming to requirements listed in the theoretical pattern.
The next step aims to extract and describe the most significant composition rules that characterize the ideal places under question. This is achieved by classifying the aggregated data into context-specific categories by conducting statistical and spatial analysis. Statistical analysis includes extraction of the population count and the average frequency of occurrences per category. Spatial analysis, on the other hand, focuses on the mean distance between components and the centroids of the ideal candidates of place.
The final phase, empirical revision, essentially converts a theoretical pattern to an empirical pattern by deciding whether each of the composition rules within functional implications are necessary or possible. To achieve this, a context-specific significance threshold is required, and classification follows a simple convention: in cases where this threshold is exceeded, this suggests that the associated composition rule is necessary; in all other cases the particular rule is considered possible.
Additionally, we adjust numerical values within composition rules: (1) in case of minimum thresholds, e.g., minimum number of shops, we adjust the value to the minimum observed during analysis; (2) in case of maximum thresholds, e.g., maximum distance between shops, we adjust the value to the maximum observed during analysis. The output of the described process is an empirical pattern that includes the required and optional information that describe the composition of the place under question.
3.3. Probabilistic Patterns of Place
Empirical patterns allow for a more realistic view of function support in terms of the spatial composition that enables a function. The choice of modalities to achieve this is because they offer a concise and natural manner of assessing necessity. However, this assessment on the level of necessity of a composition rule is purely qualitative and is limited to the two levels of necessity and possibility. In some use cases, these characteristics may not be desired. For instance, it may be necessary to explain in quantifiable terms the level of support of a particular function, such as a functionality rating. Also, since a threshold is employed to decide whether a rule is necessary or possible, this may lead to cases where two rules are associated with different modalities, even though both are close to the threshold, due to one being slightly lower and the other slightly higher.
One way to provide a quantitative alternative to the flexibility offered by modalities is using probabilities. Probabilistic logic has been an active research field ever since the term was coined in Nilsson’s seminal work [
26] but has received renewed attention as the foundation for a wide array of machine learning techniques. The fundamental difference of probabilistic logics compared to standard logics is that probabilities, instead of true/false values, are attached to logical statements. Based on a probabilistic logic foundation, we propose an additional variant of theoretical patterns called
probabilistic patterns, where the level of support of composition rules within functional implications is quantified using probabilities.
As previously, probabilistic patterns are formalized using the elements in
Table 1. The main difference is that formulas
within elements in
are probabilistic logic formulas, with probabilistic weights attached to each composition rule statement contained within. Given this, a functional implication now states that a particular function is enabled with a probability that depends on the individual probabilities of the composition rules within. We assume that all probabilities for each composition rule are independent, which is the basic instance of the so-called distribution semantics of probabilistic logic, as explained in [
27].
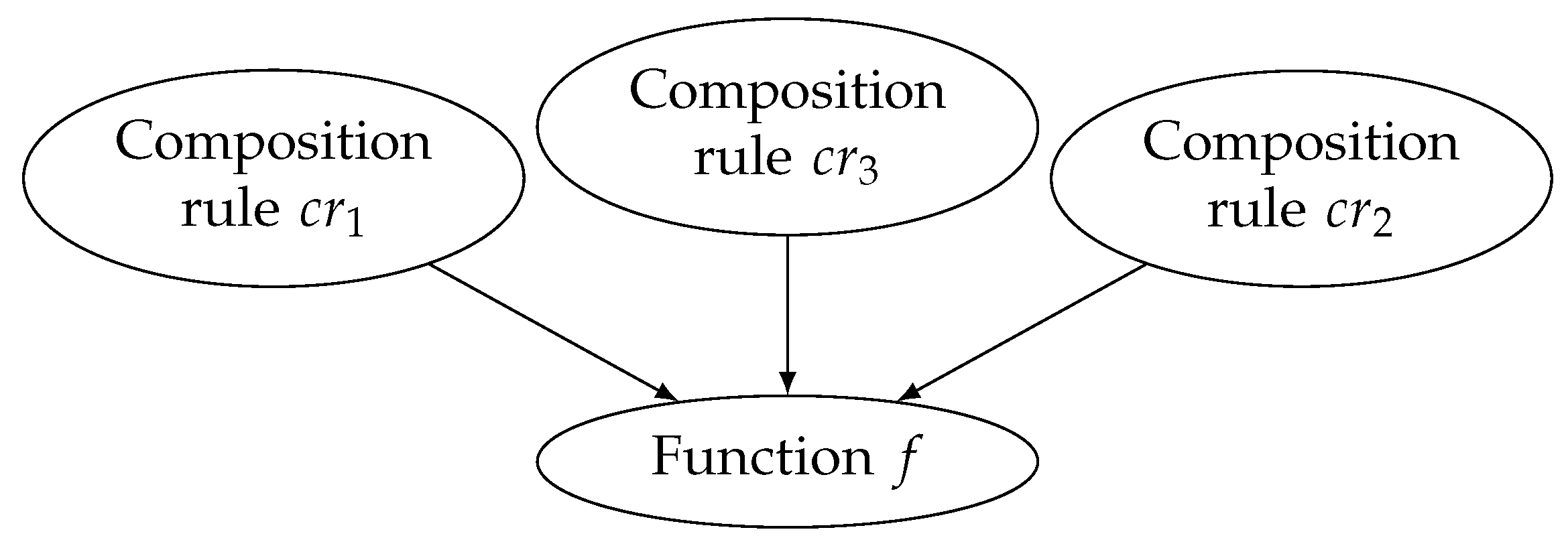
Each functional implication in a probabilistic pattern is related to an instance of a Bayesian network [
28]. For instance, a functional implication for a function
f that is related to three composition rules
is represented by the Bayesian network in
Figure 2. Each composition rule is associated with a prior probability, while edges represent conditional dependencies. Based on this network, we want to calculate the conditional probabilities of
, given that
f is supported.
3.4. Learning Probabilistic Patterns
As is the case with empirical patterns, extracting probabilistic patterns requires three phases. The first two phases of theoretical design and collective analysis are similar to the ones described in
Section 3.2. The third phase is dedicated to calculating probabilities for the composition rules in the theoretical pattern. We propose a statistical relational learning approach, specifically learning from interpretations of probabilistic inductive logic programs [
27]. An overview of the complete process is shown in
Figure 1.
Logic programming, in general, refers to querying and reasoning based on rule-based formal logic representations. Inductive logic programming is an extension that is capable of learning logic programs by extracting knowledge from positive and negative examples. Probabilistic inductive logic programming combines the flexibility of probabilities with the interpretability and intuitive nature of logic programming and the potential of machine learning based on induction.
Learning based on probabilistic logic programming is an appropriate solution for extracting probabilistic patterns for three main reasons. First, probabilistic patterns (as well as theoretical and empirical ones) are easily translatable to logic programs due to their first-order logic encoding and the rule-based structure of functional implications. Second, probabilities are the defining feature of both probabilistic patterns and probabilistic logic programming. Finally, the use of machine learning techniques that rely on models that are comprehensible from a human perspective, will enable an explainable place search process. In other words, it will be possible to answer whether and why particular areas are returned as answers to a given place search query.
Learning probabilistic patterns follows the process of learning from interpretations [
29]. Particularly, probabilities for each composition rule and associated functional implication are learned based on example areas from real-world data that belong to one of the four possible cases: (1) areas where the composition rule holds and the function is supported by that area; (2) areas where the composition rule does not hold and the function is not supported by that area; (3) areas where the composition rule is true but the function is not supported by that area; and (4) areas where the composition rule is not true and the function is not supported by that area. Cases 1 and 4 are called positive examples, since they conform to the initial theoretical pattern, with cases 2 and 3 representing negative examples.
To extract positive and negative examples, we rely on statistical and spatial analysis, as in the empirical revision process described in
Section 3.2. We also take into account the revised values for parameters within composition rules (e.g., lower bounds for occurrence, or higher bounds for proximity). We use these values, instead of the ones in the theoretical pattern, since they are considered less broad and more accurate. For each candidate area, we calculate truth values for all composition rules and functions. Depending on the availability of data, each candidate area can contribute a maximum number of examples equal to the number of functions in the pattern.
Having extracted positive and negative examples, we then feed them into ProbLog2 [
30], a probabilistic logic programming system capable of learning from interpretations. The system learns the probabilities for each dependency in the corresponding Bayesian network, as well as the prior probabilities for each composition rule. Using these probabilities, the system infers the conditional probabilities attached to composition rules, given that the associated functions are supported. This concludes the process of creating probabilistic patterns.
4. Experiment and Results
This section demonstrates the proposed methodology and evaluates the application of empirical and probabilistic patterns in place search using the example of shopping malls in London, UK. The objective of the described experiment is to create patterns which can enable a place search system to locate places that offer functions similar to a shopping mall, even if they are not explicitly defined as such. By convention, we refer to these places as shopping areas, for which the ideal representatives are the standard shopping malls.
4.1. Theoretical Pattern
To create a theoretical pattern for places functioning as shopping areas we perform textual analysis on the following sources: Wikipedia reference (
https://en.wikipedia.org/wiki/en/Shopping_mall), Oxford dictionary definition (
https://en.oxforddictionaries.com/definition/mall) and an Irish government report on retail design guidelines [
31]. This analysis is performed manually by the authors for the purposes of this demonstration. Automating the analysis is out of the scope of this manuscript and is planned to be explored in future work. Indicatively, since the dictionary definition of a shopping mall discusses “[...] variety of stores and often restaurants [...]”, we conclude that a mall includes stores and restaurants. In return, store and restaurant definitions state that the former is a place “[...] where merchandise is sold [...]”, while the latter’s owner “[...] prepares and serves food and drinks to customers [...]”. Consequently, a shopping mall is equipped with the functions of shopping experience and sustenance (which is part of leisure). Based on the analysis demonstrated here, we consider a simplified structure of shopping areas, consisting of shops, amenities, road junctions and transport stops (including both public transport stops and taxi stands). Through these components, shopping areas support five functions: (1) shopping experience, based on the existence of shops; (2) leisure, based on the existence of amenities; (3) walkability, requiring that shops and amenities are within a walkable distance; (4) accessibility to drivers, through road junctions within a minimum driving distance; and (5) accessibility to non-drivers, through transport stops within a walkable distance. The list of components and functions are summarized in
Table 3.
To keep the design pattern as generic as possible we consider several assumptions and common trends that would facilitate the least strict composition of the aforementioned functions, while maintaining their nature. In particular, based on Azmi et al. [
32] (p. 4), we assume that a walkable distance between two neighboring facilities cannot exceed 500 m, while the driving distance between a shopping area and the closest highway junction cannot be more than 5000 m; the latter ensures a tolerable driving time within a low-speed road network. Shopping experience implies several shopping opportunities for a potential customer, consequently a shopping area is required to be equipped with at least two shops to facilitate the minimum number of options. The function of leisure is more flexible, requesting the existence of at least one amenity within the shopping area, whereas the ratio of shops and amenities is adjusted to 2:1 to enforce the trade of goods, as opposed to facilities, as the primary function of a shopping area. Finally, walkability and accessibility conform to the walkable and driving distance assumptions stated earlier.
Every component used in our example complies with the definitions provided by the OpenStreetMap platform (
https://wiki.openstreetmap.org/wiki/Main_Page). A shop (
https://wiki.openstreetmap.org/wiki/Key:shop) is considered to be a merchandise business specialized on trading goods that cover basic and/or more advanced needs such as clothing, groceries, luxury products, and so on. Since amenities (
https://wiki.openstreetmap.org/wiki/Key:amenity) cover a great variety of facilities, we only include those that focus on the provision of community facilities: “entertainment, arts & culture” (e.g., movie theaters, coffee shops, bars), “sustenance” (e.g., restaurants, snack bars, food court), “healthcare” (i.e., hairdressers, massage and beauty services) and “financial” (i.e., cash points or banks). Transport stop components, on the other hand, are specialized by the category “transportation”, while road junctions correspond to the category “highway” in OpenStreetMap (
https://wiki.openstreetmap.org/wiki/Key:highway).
To represent the five functions, we use composition rules Occurrence, Correlation and Proximity in
Table 2. This results in the theoretical pattern depicted in
Table 4.
4.2. Empirical Pattern
To extract an empirical pattern for places functioning as shopping areas, we conduct empirical revision as discussed in
Section 3.2. We use data acquired from OpenStreetMap (
https://www.openstreetmap.org/), collecting a set of 65 polygons outlining shopping malls in London, UK. Using the centroids of these polygons, we aggregate: (1) point geometries of shops, amenities, and transport stops within a 500 m radius; and (2) road junction points within a 5000 m radius.
Table 5 illustrates indicative results of the spatial and statistical analysis applied on the acquired components for all the collected instances of shopping malls. For the calculation of mean values and coefficients of variation, we exclude extreme outliers (e.g., isolated instances of malls with more than 300 shops, while the rest do not exceed 100). The complete dataset and analysis results are available at
https://github.com/gmparg/IJGI-Patterns.
For the construction of the empirical pattern, we assume that a variable is significant and, hence, it implies a necessary composition rule, if the coefficient of variation for the corresponding mean value is less than 80%. Values more than this level result in less significant variables and, thus, refer to possible rules. For instance, for the indicative results in
Table 5, Count (Shop) and Proximity (Shop, Amenity) are considered necessary composition rules, while the rest are considered possible composition rules. Note that a different choice of threshold and metric may be made depending on how flexible the pattern needs to be.
Using the results of spatial and statistical analysis, we attribute necessity (□) or possibility (⋄) to all composition rules. We also adjust numerical values within composition rules, as described in
Section 3.2. As a result, we obtain the empirical pattern shown in
Table 6, where changes compared to the theoretical pattern are marked in bold.
4.3. Probabilistic Pattern
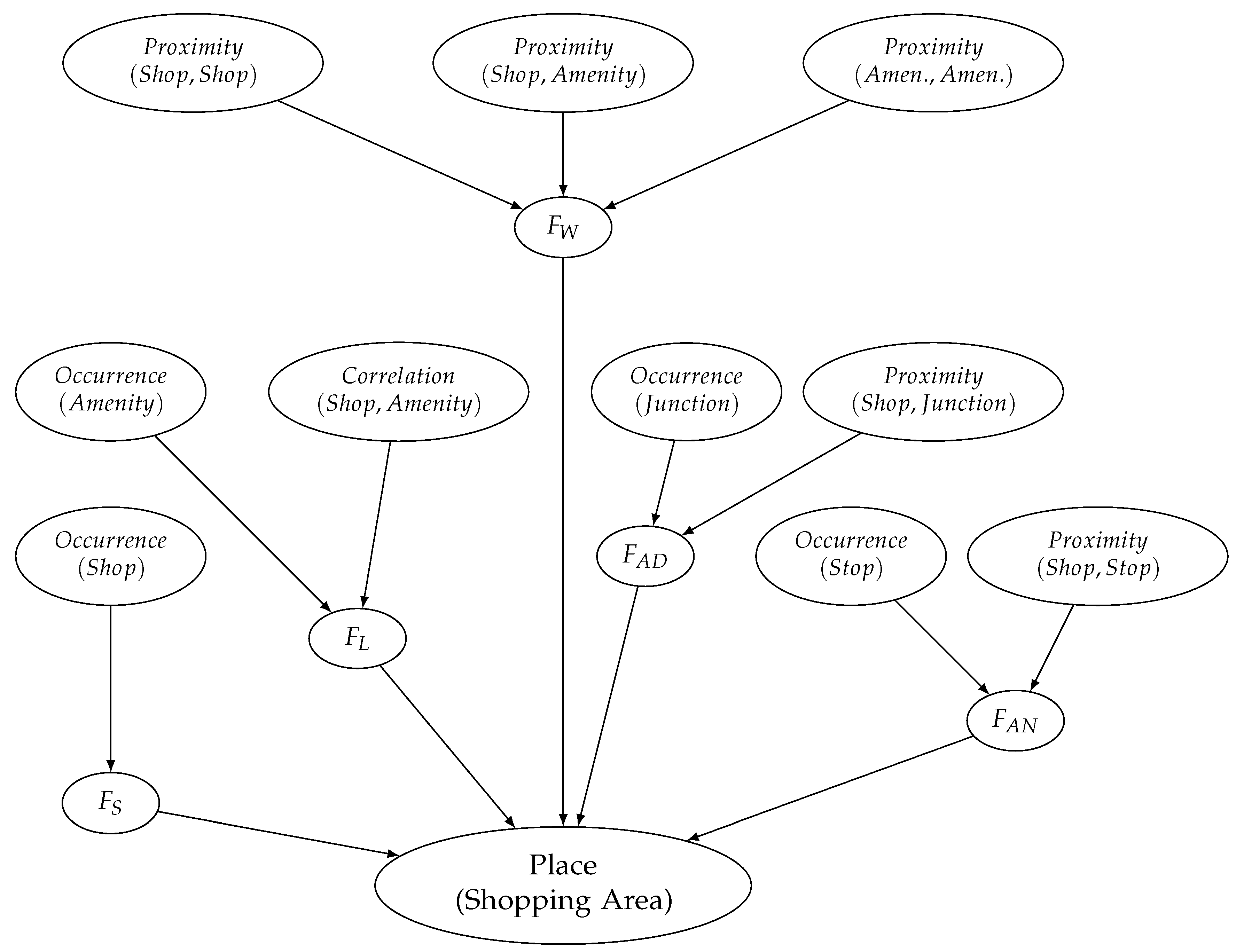
To create a probabilistic pattern for places functioning as shopping areas, we first convert the functional implications within a theoretical pattern into a probabilistic logic program. The encoding for the leisure function using ProbLog syntax is shown in Listing 1; the full ProbLog code can be found at
https://github.com/gmparg/IJGI-Patterns.
| Listing 1. ProbLog encoding for leisure function. |
f_l :- occ_amen, corr_s_a, p_occ_corr.
f_l :- \+occ_amen, corr_s_a, p_corr_s_a.
f_l :- occ_amen, \+corr_s_a, p_occ_amen.
f_l :- \+occ_amen, \+corr_s_a, p_neither. |
For instance, the first logic programming clause is read as follows:
f_l is true, if both
occ_amen and
corr_s_a are true, with a probability
p_occ_corr.
occ_amen is a simplified predicate for
, while
corr_s_a is a predicate representing
.
\+ is the negation as failure operator, meaning failure to prove that the predicate operand holds.
p_occ_corr is the probability that the leisure function is supported, given that both composition rules for occurrence and correlation hold.
p_corr_s_a,
p_occ_amen and
p_neither are defined accordingly. These four clauses are equivalent to a Bayesian network that links the leisure function with the associated composition rules. The full Bayesian network for all five functions is shown in
Figure 3.
We then use the results of spatial and statistical analysis to extract positive and negative examples. Given the nature of the dataset (actual shopping malls), we can extract the following example types: (1) shopping malls that support a particular function, while at the same time all relevant composition rules are satisfied; (2) shopping malls that support a particular function, but do so without satisfying all composition rules. Hence, for each shopping mall in the dataset we attribute truth values to all composition rules in
Figure 3, while all functions are considered to be true.
Having extracted positive and negative examples, we encode them as evidence for the ProbLog system. For example, an instance of a shopping area which supports the function of leisure without satisfying the composition rule on correlation between shops and amenities is encoded using the logic programming facts in Listing 2.
| Listing 2. Example ProbLog encoding for evidence. |
evidence(occ_amen, true).
evidence(corr_s_a, false).
evidence(f_l, true). |
We then task the ProbLog v2.1 system (the latest version capable of both inference and learning) to learn probabilities for all predicates (facts in logic programming) based on the positive and negative examples supplied as evidence. This results in a new probabilistic logic program containing these probabilities. For instance, the encoding for the leisure function after learning probabilities is shown in Listing 3.
| Listing 3. Example ProbLog encoding for evidence. |
f_l :- occ_amen, corr_s_a, p_occ_corr.
f_l :- \+occ_amen, corr_s_a, p_corr_s_a.
f_l :- occ_amen, \+corr_s_a, p_occ_amen.
f_l :- \+occ_amen, \+corr_s_a, p_neither.
0.538461538461538::occ_amen.
0.538461538461538::corr_s_a.
0.999999999999679::p_occ_corr.
0.688997112547912::p_corr_s_a.
0.952464846231911::p_occ_amen.
0.999999999948175::p_neither. |
Finally, using inference on the probabilistic logic program, we calculate the conditional probabilities for all composition rules, given that the associated functions are supported; e.g., for the program above we include the facts in Listing 4.
| Listing 4. Example ProbLog encoding for evidence. |
evidence(f_l, true).
query(occ_amen).
query(corr_s_a). |
The resulting probabilistic pattern which includes all calculated probabilities is shown in
Table 7.
4.4. Place Search Results
To evaluate the three patterns, we conduct three function-based search processes for shopping areas, each relying on one of the patterns. Pattern matching is realized by converting each pattern to a sequence of spatial queries and procedures, implemented using PostGIS (
https://postgis.net/) v2.4 and QGIS (
https://www.qgis.org/) v3.0.2. Particularly, every function included in the patterns is expressed as a query that reflects the implied composition rules. Afterwards, the generated queries are issued on the database.
To decide whether a candidate region is included in the results using theoretical patterns, we use the following formula: . This means that a candidate region is considered to be able to function as a shopping area if it provides, as minimum, the function of shopping experience (considered as an essential function), as well as one of the other four functions. Please note that more or less restrictive function combinations can be used, depending on the scenario at hand.
The results are illustrated in
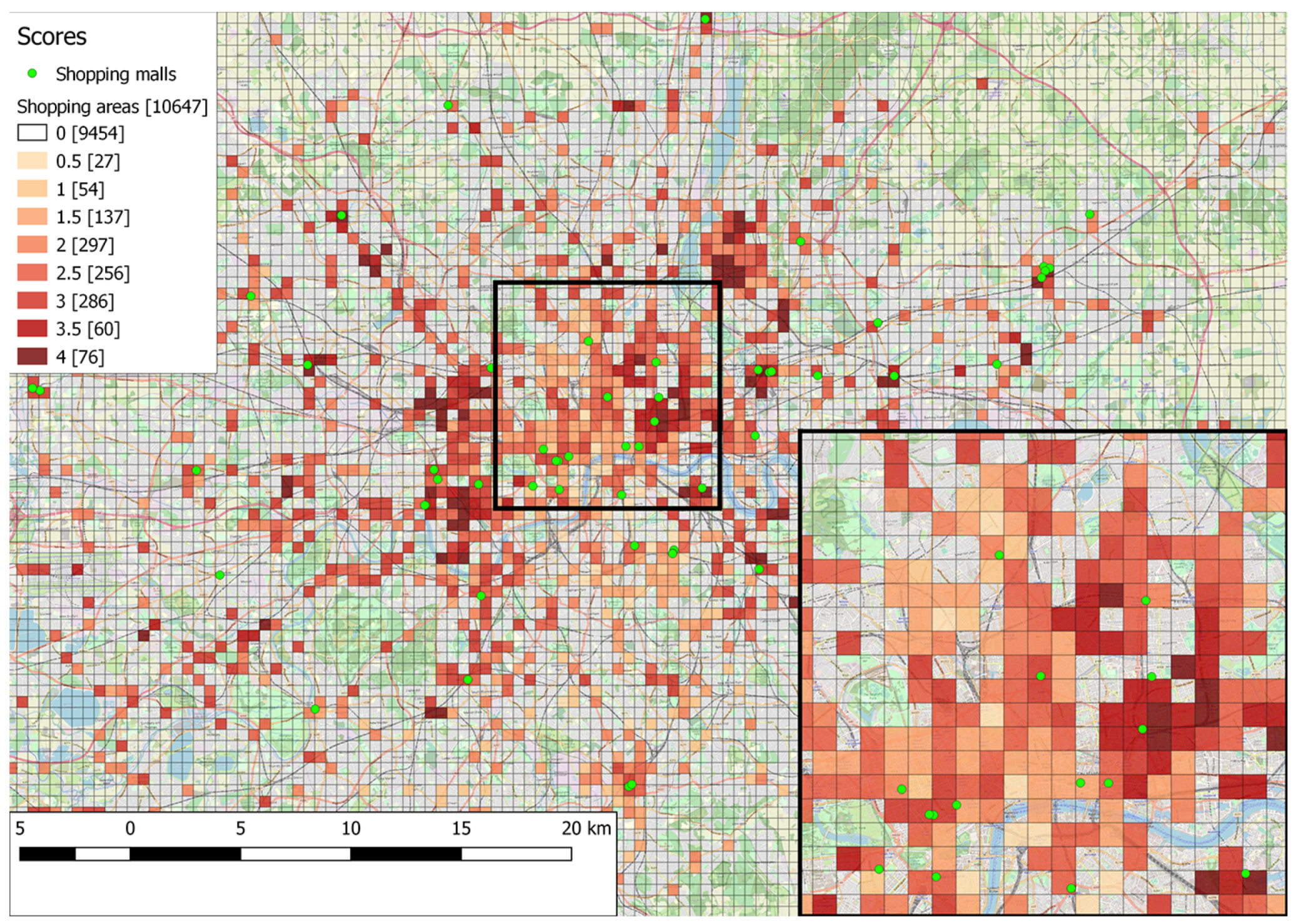
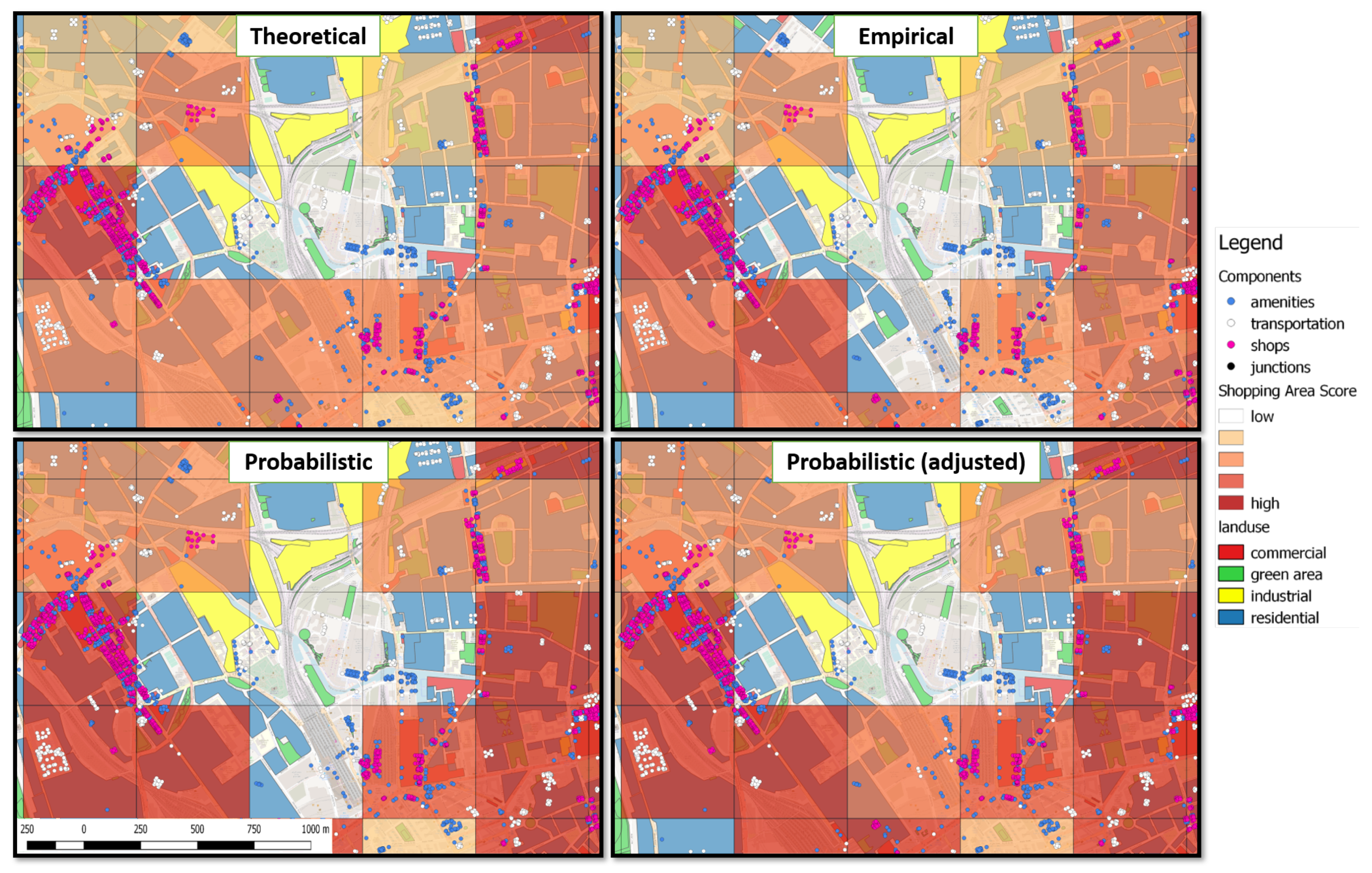
Figure 4, where the study area is split using a grid of 500 m × 500 m cells, with a total of 10,647 cells. The cell size is selected based on the assumption that a walkable distance should not exceed 500 m. A heat map representation is employed, based on the number of functions satisfied within a particular cell. The lighter color represents minimum support (shopping experience and only one of the others, with a score value of 1), while the darkest color represents highest support (shopping experience and all four other functions, meaning a score value of 4). Green circles are used to indicate the locations of actual shopping malls.
As with the theoretical pattern, a candidate region for the empirical case must again support the function of shopping experience and at least one of the others as minimum, to be included in the results. However, if two candidate regions support the same function, the score is proportional to the number of possible composition rules that are satisfied. For instance, if two regions support the shopping experience and leisure functions, but one only satisfies the minimum number of amenities (necessary rule), while the other also achieves the required ratio between shops and amenities (possible rule), the first is scored with 1.5 while the second with 2.
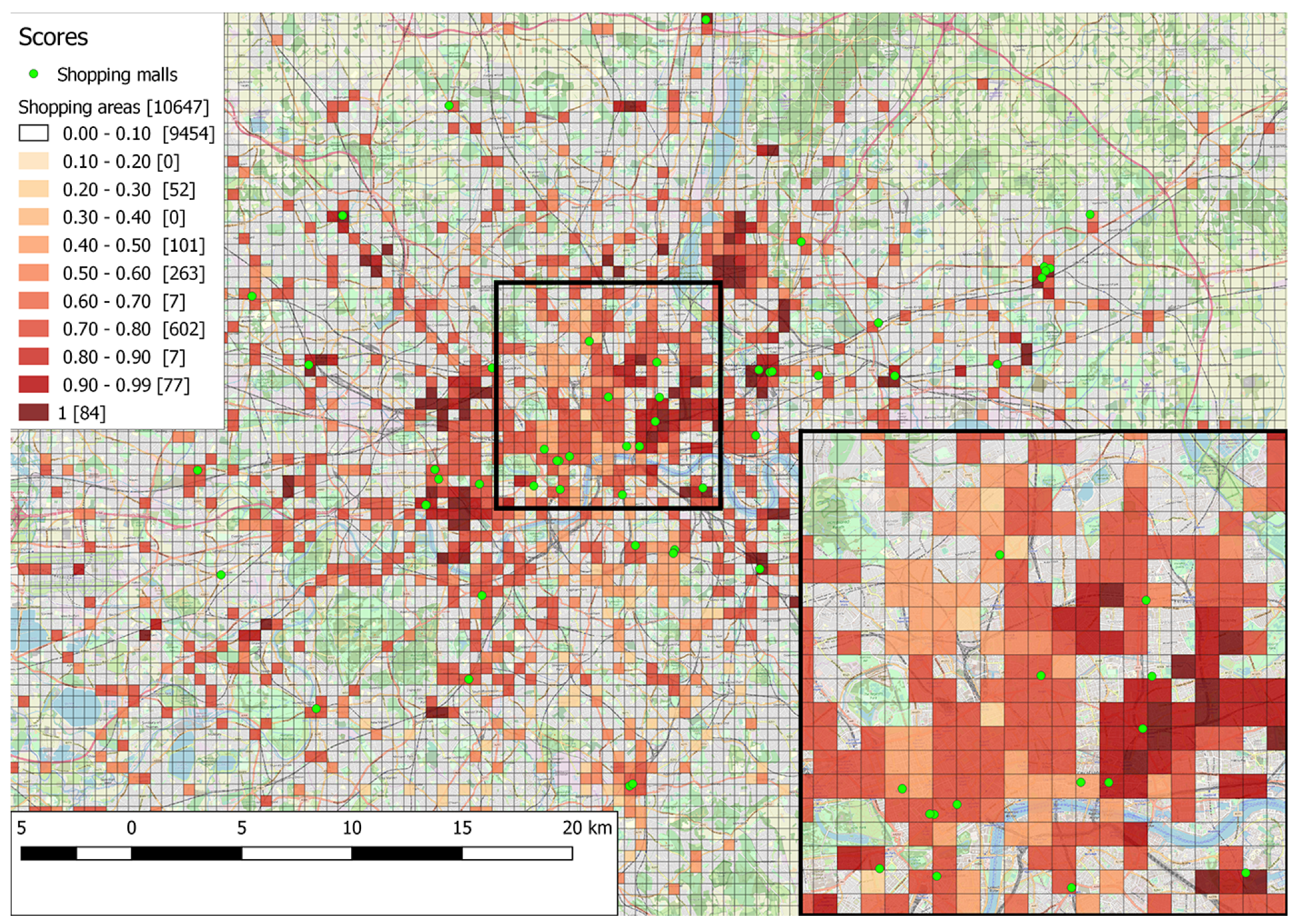
Figure 5 illustrates the results retrieved using the empirical pattern, where the heat map representation follows this scoring scheme.
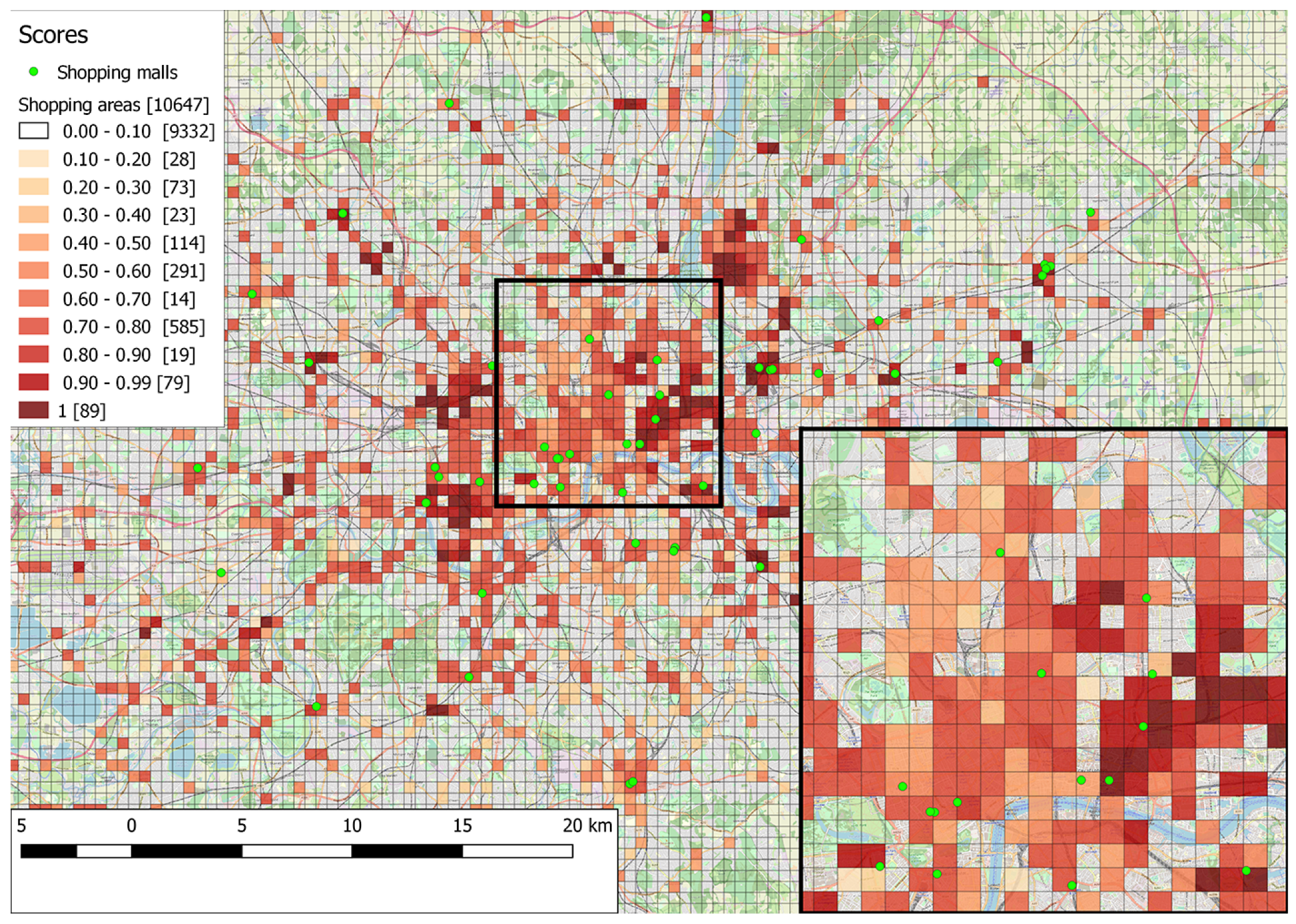
In the case of the probabilistic pattern, probability calculations with ProbLog allow for a more fine-grained score attribution. For each function, we have previously calculated different probabilities, depending on which associated composition rules are satisfied, e.g., probabilities of supporting leisure when neither, both, or only one of the occurrence and correlation rules hold. We use these probabilities as score values, instead of adding 1 to the score for each supported function. The resulting score formula is
, essentially expressing the actual numerical probability that a particular area satisfies the functionality of a shopping mall, as described in the pattern. With this formula, not supporting the essential function of shopping experience results in a score of 0, while in all other cases, the score is increased proportionally to the number of supported functions and the associated probabilities of supporting them. The results of using probabilistic patterns and the aforementioned scoring scheme are shown in
Figure 6.
The aforementioned scoring scheme assumes clear cut cases: for a function that is associated with two rules, specific scores are given when both, or either of them are satisfied. If a composition rule is not satisfied, the scheme does not take into account the distance from the minimum or maximum thresholds that led to the rule not being satisfied. For instance, the same score is attributed if two regions do not satisfy the rule of limiting distance between shops and road junctions to 4978m, even if one of them is really close to the threshold, while the other one is very far. To address this, we employ an alternative score formula, where the score for each function is adjusted proportionally to the distances from thresholds within those composition rules that are not satisfied. Results using this formula are presented in
Figure 7.
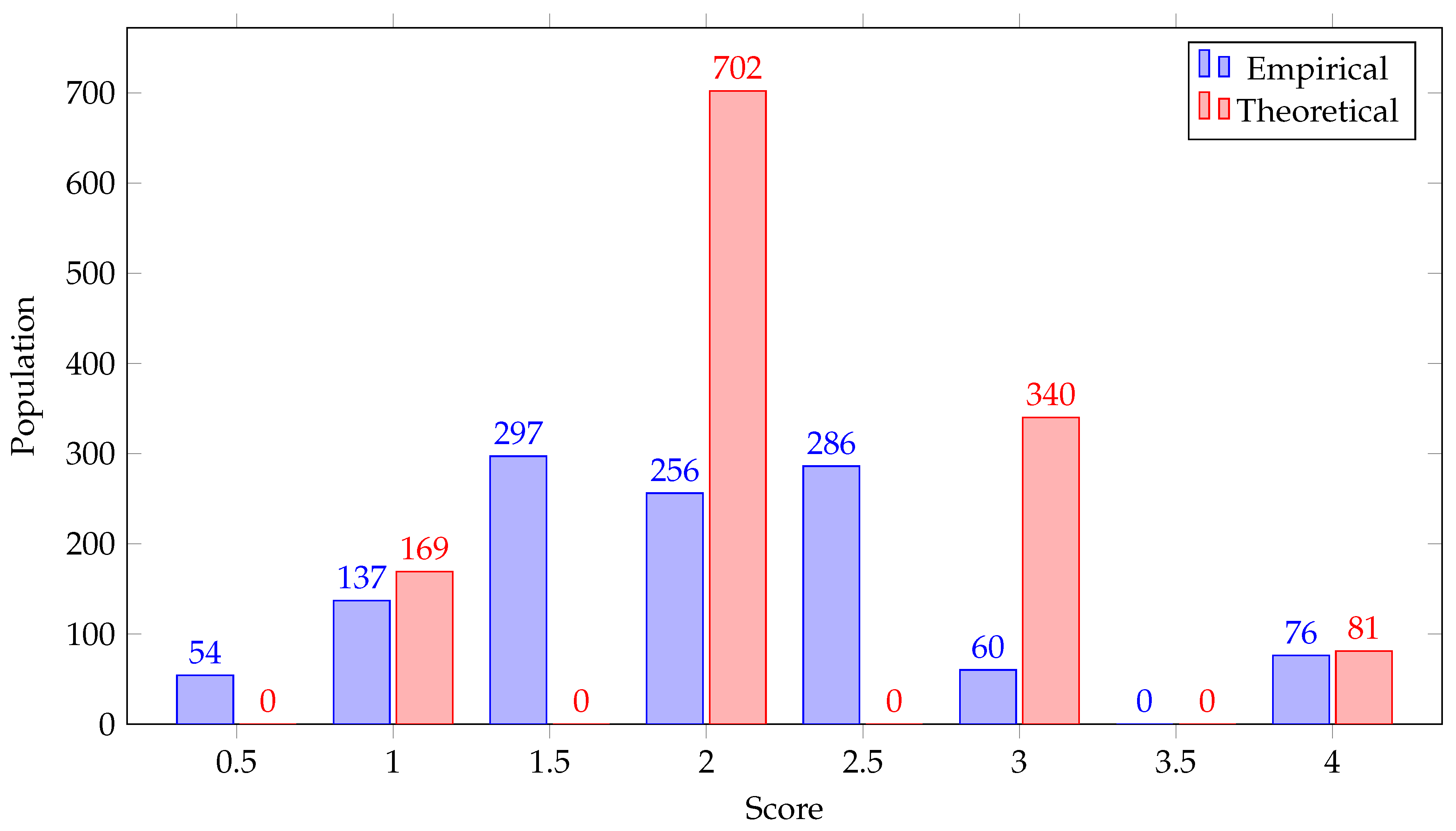
Table 8 summarizes the results presented in figures in numerical form.
5. Discussion
5.1. Results Analysis
As evidenced by the results in
Figure 4, searching for shopping areas using the theoretical pattern achieves perfect recall: all actual shopping malls extracted from the OpenStreetMap database using the filter “mall” (
https://wiki.openstreetmap.org/wiki/Tag:shop%3Dmall) (indicated with green circles) are within one of the identified areas. Additionally, several other areas are identified, which have a varying level of support of the five functions included in the pattern but are not explicitly identified as shopping malls in OpenStreetMap. This exemplifies the benefits of function-based search of places as opposed to simple keyword-based search: instead of only returning regions that are annotated with terms similar to keywords such as “shopping areas”, function-based search is also capable of including regions that support a minimum level of functionality associated with a shopping area, while also providing a rough indication of the level of function support. Furthermore, searching places using patterns assigns an estimated spatial extent to the candidate shopping areas; this extent does not have to be supplied beforehand, as is the case with gazetteer placename entries.
Results using the empirical pattern (
Figure 5) improve on the ones based on the theoretical one in three ways. First, an increased number of cells are excluded from being potential shopping areas (126 more, see
Table 8) and other cells are scored lower than previously; this is due to the stricter threshold values in composition rules that were calculated by the empirical revision process. Second, several cells get higher scores, due to composition rules having a possibility rather than a necessity modality. The way cells have shifted from one score category to another is better illustrated in
Figure 8. Finally, there is a more fine-grained representation of the level of support, since there are now 7 different score levels, as opposed to 4. These improvements allow for a more accurate coverage and a better understanding of how well each area satisfies the functions of a shopping mall, without however compromising recall: areas occupied by actual shopping malls are still included in the results.
In what concerns the probabilistic pattern (
Figure 6), an even more fine-grained representation is achieved, with score values occupying the complete probability range of 0-100%. The number of cells that are scored under 10% is more in agreement with the empirical rather than the theoretical pattern, since probabilistic patterns include the empirically revised thresholds. In general, cells are attributed higher probabilities than the corresponding empirical or theoretical scores. This is the benefit provided by probabilistic logic learning as opposed to first-order logic with modals: the learning process assigns a probabilistic value ranging from 0 to 100% to each composition rule as opposed to a standard Boolean value. Please note that every cell assigned with a non-zero score in the empirical pattern results is also included in probabilistic pattern results and vice-versa; the difference is only in the value of the assigned score.
As expected, results with the adjusted score formula for probabilistic patterns (
Figure 7) show that less cells are scored with less than 10%. This is because a non-zero probability is attributed when a particular composition rule has been violated but this was a result of only slightly exceeding thresholds. For the same reason, probability values are more well distributed, with more cells having probabilities in the 10–39% range. Flexibility is increased, since scoring does not depend on the duality of Boolean values: even if a composition rule is violated, it still contributes slightly to the overall probability, to a degree proportional to the distance from the threshold that caused the violation. The adjusted score formula for probabilistic patterns essentially reduces the effects of the Modifiable Area Unit Problem (MAUP) [
33].
Figure 9 is a comparative evaluation of an indicative subset of the cells identified by each pattern with regard to the stated land use of the area in OpenStreetMap. In all cases, industrial areas are correctly excluded from search results (ranked lowest), while all commercial areas are included, with a single exception on the mid-right part of the grid; this exception is due to OpenStreetMap flagging this area as commercial, without, however, including any shop or amenity data points within. In terms of residential areas, some of them are included in the results because of the cell size, which is large enough to contain pairs of residential and commercial areas that are adjacent. Others, however, are correctly included, since they indicate parts of residential areas which are spatially organized in a way that enables, in part, the functionality described in the patterns.
5.2. Advantages and Limitations
Based on the individual pattern characteristics and the results presented here, we can deduce the following use cases for each different pattern type. Theoretical patterns have the least amount of dependencies, since they can produce results without relying on the availability of suitable and relevant data or the skillset necessary for statistical and spatial analysis and statistical relational learning. Hence, they can produce function-based place search results when the aforementioned data and skills are unavailable. Empirical and probabilistic patterns, on the other hand, are suitable when there is a need for a more accurate and detailed view of the level of support of a functionality set of a place, taking into account empirical evidence. Probabilistic patterns and their results are especially interpretable compared to the rest, since they represent the likelihood of an area functioning as a specific place; for instance, areas that have a probability higher than 90% can easily be understood as operating equivalently to a shopping mall.
As is the case with any data-driven approach, the success of empirical revision and statistical relational learning heavily depends on data quantity and quality, which is not the case with theoretical patterns. Indicatively, learning probabilities is affected by the correctness of examples, i.e., whether they are correctly perceived as positive or negative based on the available data. Also, action must be taken to ensure that there is no bias within the dataset; for instance, in the shopping area example, we make sure to represent equally positive and negative examples for each particular function. Moreover, spatial and statistical analysis are computationally expensive, since they involve determining relations between spatial entities, which is not required by less elaborate approaches, such as gazetteers.
It should be noted that the described methodologies are affected by the inability to indicate ground truth. The only exception is the case of shopping areas resulting from our methodologies which contain actual shopping malls, in which case we can safely trust that these results are accurate. In terms of regions not considered as shopping areas by our methodologies, evaluation can only rely on aggregations such as land use. In particular,
Figure 9 depicts that none of the shopping areas identified by the proposed methodologies falls within industrial or green areas, which, by definition, would not be able to support shopping-related functions. However, due to the grid size and incomplete data, some identified shopping areas contain segments of areas of incompatible land use. Regarding evaluating whether our methodologies attribute correct or trustworthy scores to each cell, we are unable to rely on either of the aforementioned processes. Since place is a product of human thinking, judging whether one place is correctly rated higher than another can only be evaluated based on human opinion. Hence, a more accurate evaluation of the presented results could be possible through survey-based processes where people interested in a particular place functionality comment on whether higher-scored areas better serve their purposes. A further limitation in terms of the theoretical design process is that it depends on choosing widely accepted and extended descriptions of the place under question; composition rules must then be determined by experts. Other approaches such as searching using gazetteers only need a vocabulary of places.
In contrast to other purely data-driven approaches, such as [
5], the proposed combination of a formal model of place and statistical relational learning makes the search results based on probabilistic patterns highly interpretable. Based on the learned probabilities and the composition rules that make up the functions within a pattern, it is straightforward to explain why a particular area is included or excluded from search results for a particular place. This is not possible in cases where either the search process is not underpinned by a formal model of place or the employed machine learning technique is opaque, such as (deep) neural networks.
The dependency of pattern-based representations on narratives raises important obstacles; indicatively, natural language processing has many technical difficulties and the extracted information is often highly vague and context-dependent. This dependence on context raises a notable trade-off that affects the transferability of patterns to other geographical areas (e.g., cities in countries with different cultures): as a theoretical pattern becomes more specific, it depends more on source narratives and, in return, becomes less transferable. Consequently, it is less likely to identify places of the same category that may differ in culture or architecture. For instance,
Section 4 demonstrates the identification/localization of shopping areas based on the standards of the Western world; this specialization is achieved by relying on narratives that deal with descriptions of shopping areas in Western countries and would, naturally, be less accurate when applied to areas where Eastern world cultural standards are the norm. However, it is still generic enough to apply to any city in the Western world, though this requires further experiments to be confirmed.
Empirical and probabilistic patterns build upon theoretical ones; consequently, they inherit context dependency issues. However, they can address vagueness issues by relying on empirical evidence to determine the significance of each composition rule within each function, provided that the dataset used is representative enough. Even so, the theoretical pattern remains the nucleus of all pattern types, ensuring that data-driven decisions conform to a well-defined “mold” that serves the original purpose of place search, which is to emphasize a humanistic point of view, rather than adopt a pure data science perspective.
5.3. Potential Applications
The use of theoretical patterns can allow search engines to go beyond traditional search of semantically infused, geo-located place names. Geographic search engines that rely on such patterns can facilitate dynamic search of place using elements that are closer to human understanding of place, such as activities, functions, and real objects. Furthermore, the constructive nature of the patterns allows for the localization and identification of places from simple components, which is ideal when searching for places without specific names or categories.
Empirical patterns can improve the functionality of geographic search engines even more, allowing the discovery of places that share similar characteristics or belong in the same category but differ in a cultural sense without relying on predefined semantics but using empirical data. Finally, the introduction of statistical relational learning brings a new perspective in the traditionally theoretical work of digital place representation. It allows (semi-)automated ways of extracting patterns of places, as well as identifying places and hence attributing a region with place-related properties even in the case of the region under question is described by incomplete or vague information (e.g., a strip mall without a specific name or a flea market).
6. Conclusions
This study contributes to the formalization of place and its application in place search. In particular, we introduced two pattern-based formalizations of place that loosen restrictions in terms of how a particular place supports a function. Empirical patterns provide the capability to express that a composition rule is necessary or possible, while probabilistic patterns attach numerical weights to each composition rule. Furthermore, we proposed methodologies to extract such patterns beginning from theoretical, narrative-based patterns. Empirical patterns rely on empirical revision based on statistical and spatial analysis, while probabilistic patterns use the same analysis results to extract positive and negative examples based on which probabilities are learned using statistical relational learning.
The proposed patterns provide a more detailed representation of the functionality supported by a place that is closer to reality and can lead to more accurate results in function-based search of space; this is evidenced by the conducted experiment of locating shopping areas in London, UK. Particularly, depending on the availability of relevant data, empirical patterns employ more realistic thresholds and provide a more fine-grained scoring scheme for candidate areas, while probabilistic patterns combine these benefits with the well-understood notion of probability.
This work indicates that place can be treated as a functional region and be formalized as a system using both narratives and spatial data, which can then be used to power function-based place search engines. Research directions to explore function-based place search further include: (1) extending the formalization of composition rules to allow the introduction of new rules or the modification of existing ones; (2) investigating ways to improve extraction of knowledge from narratives, such as corpus analysis; (3) conducting survey-based experiments to better evaluate the effectiveness of the proposed methodologies; and (4) examining whether learning can be used at lower or higher levels, to learn values within composition rules, or overall probabilities for functions, respectively.