Re-Arranging Space, Time and Scales in GIS: Alternative Models for Multi-Scale Spatio-Temporal Modeling and Analyses
Abstract
1. Introduction
2. Triangular Model
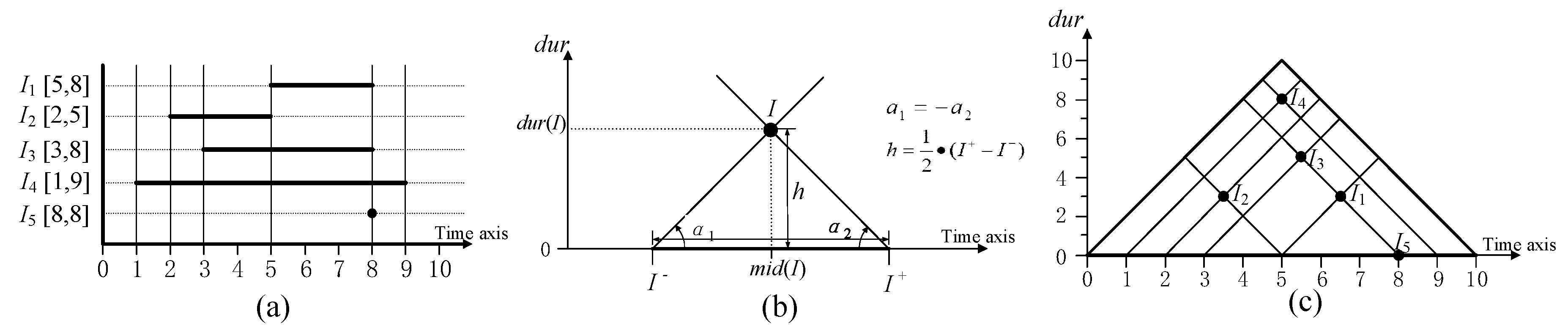
2.1. Concept
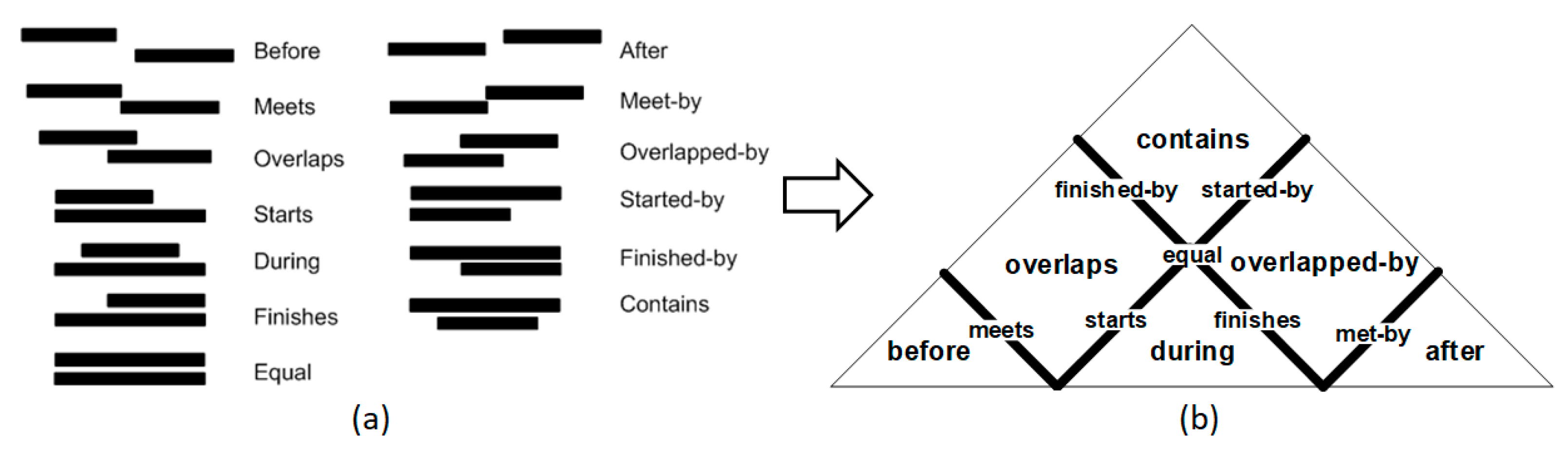
2.2. Analysis of Crisp Time Intervals
2.3. Imperfect Time Interval
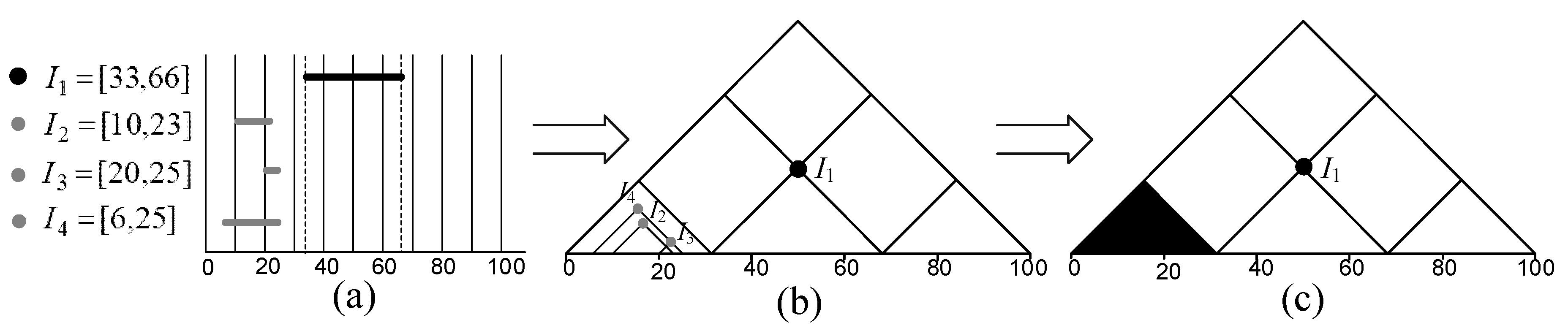
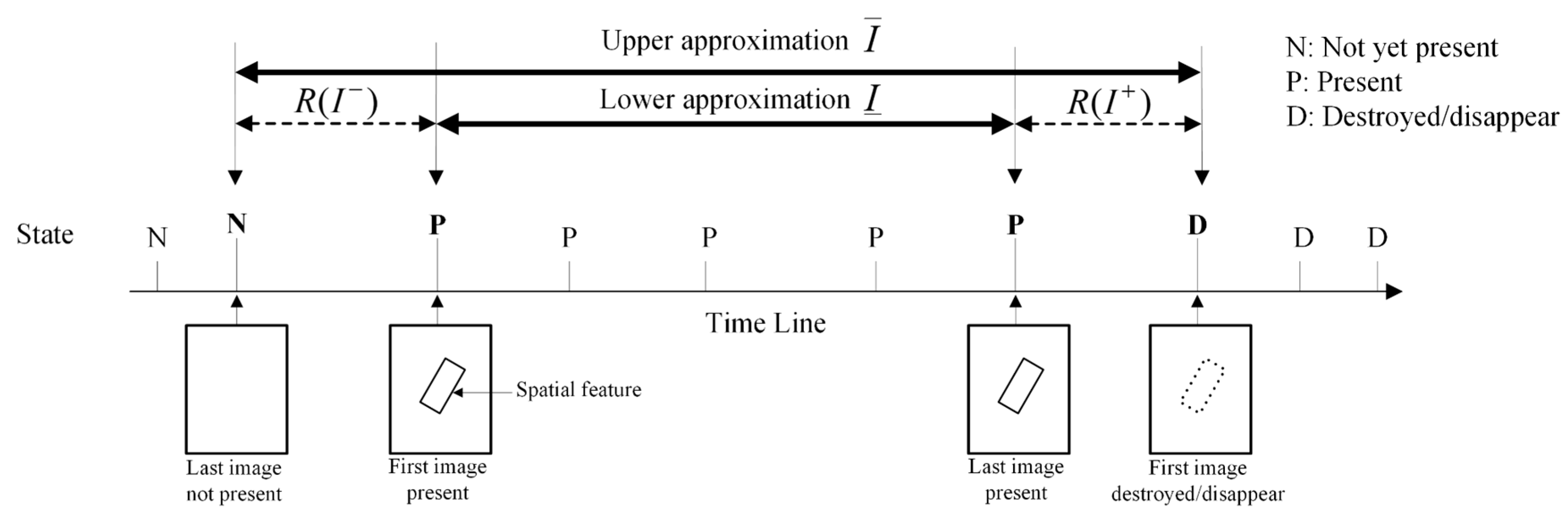
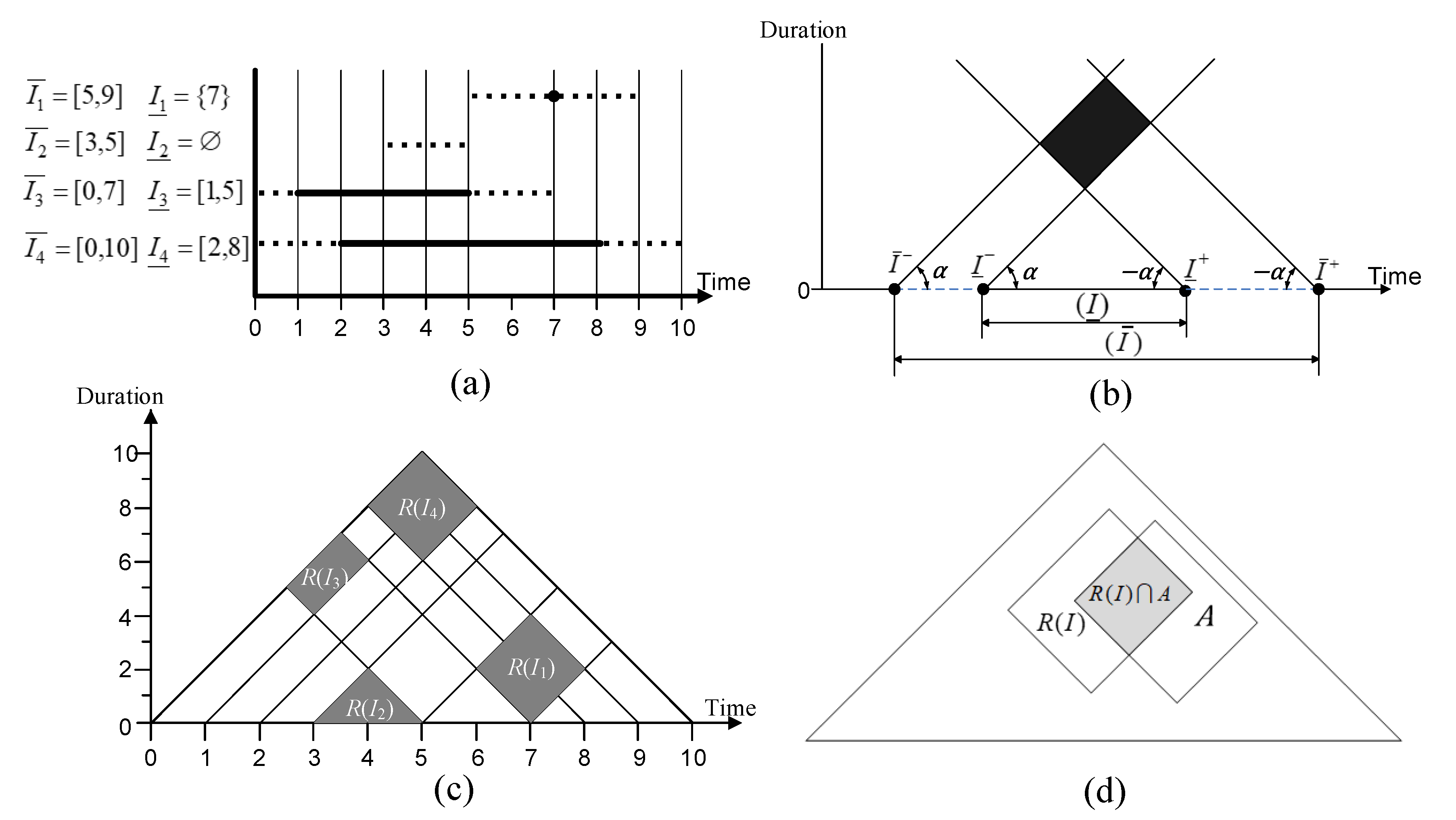
2.3.1. Rough Time Interval
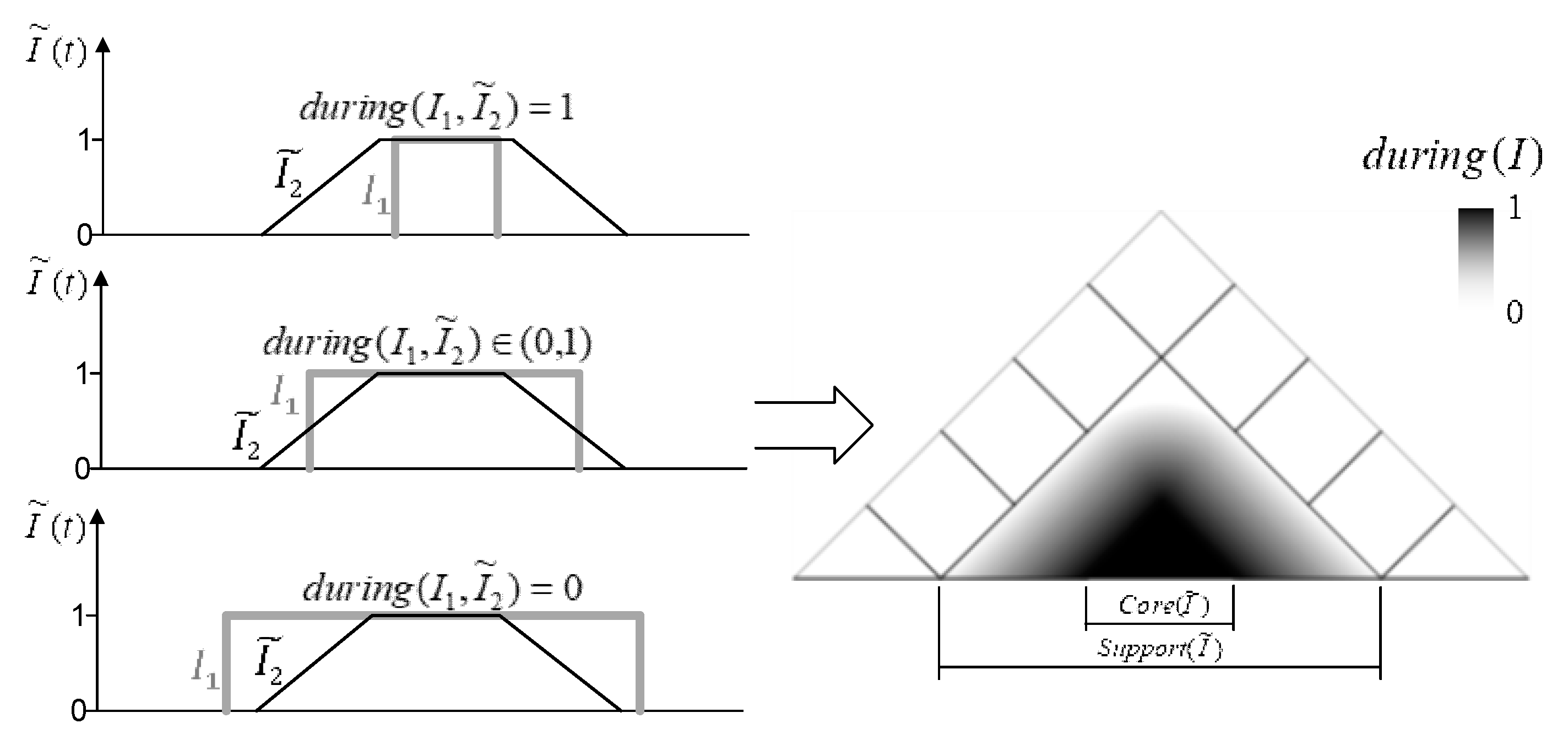
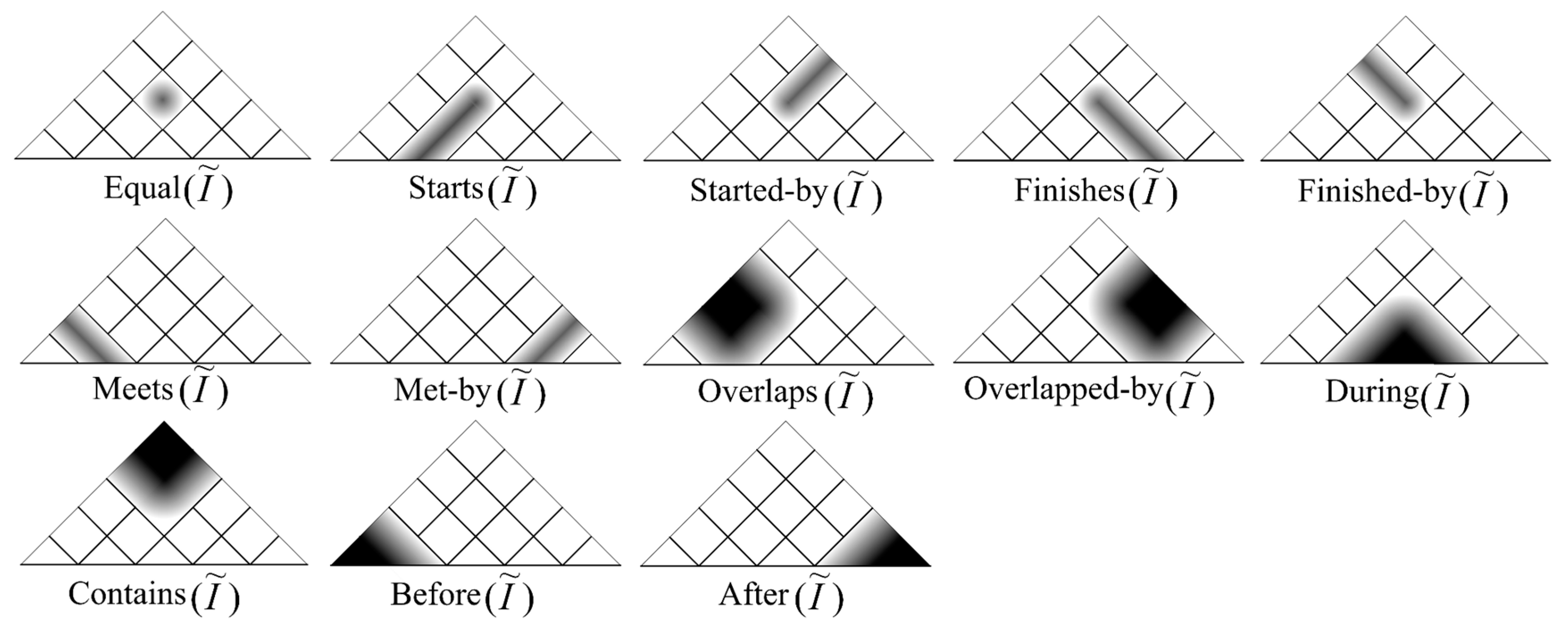
2.3.2. Fuzzy Time Interval
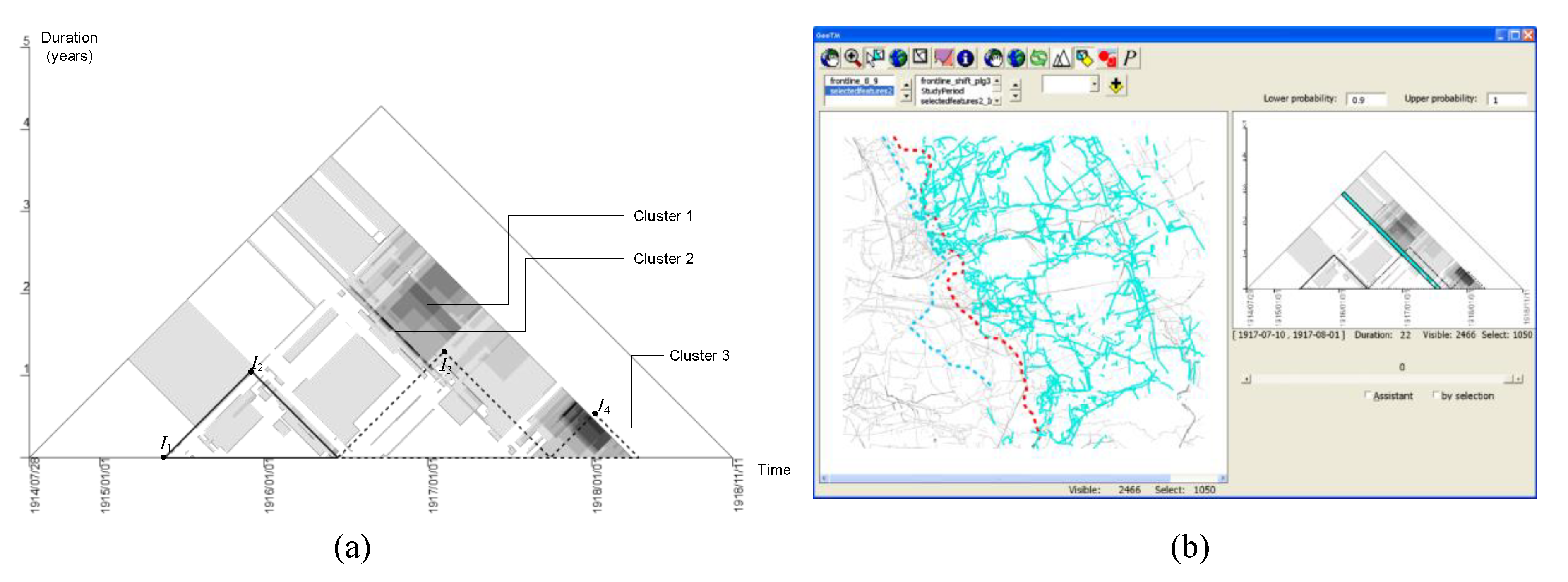
2.4. Time Series
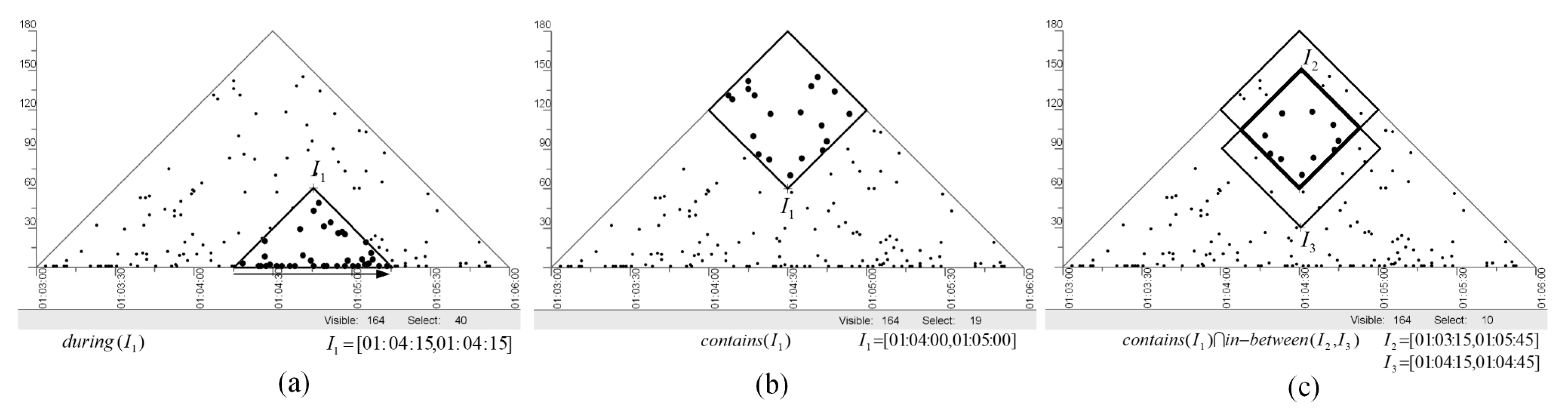
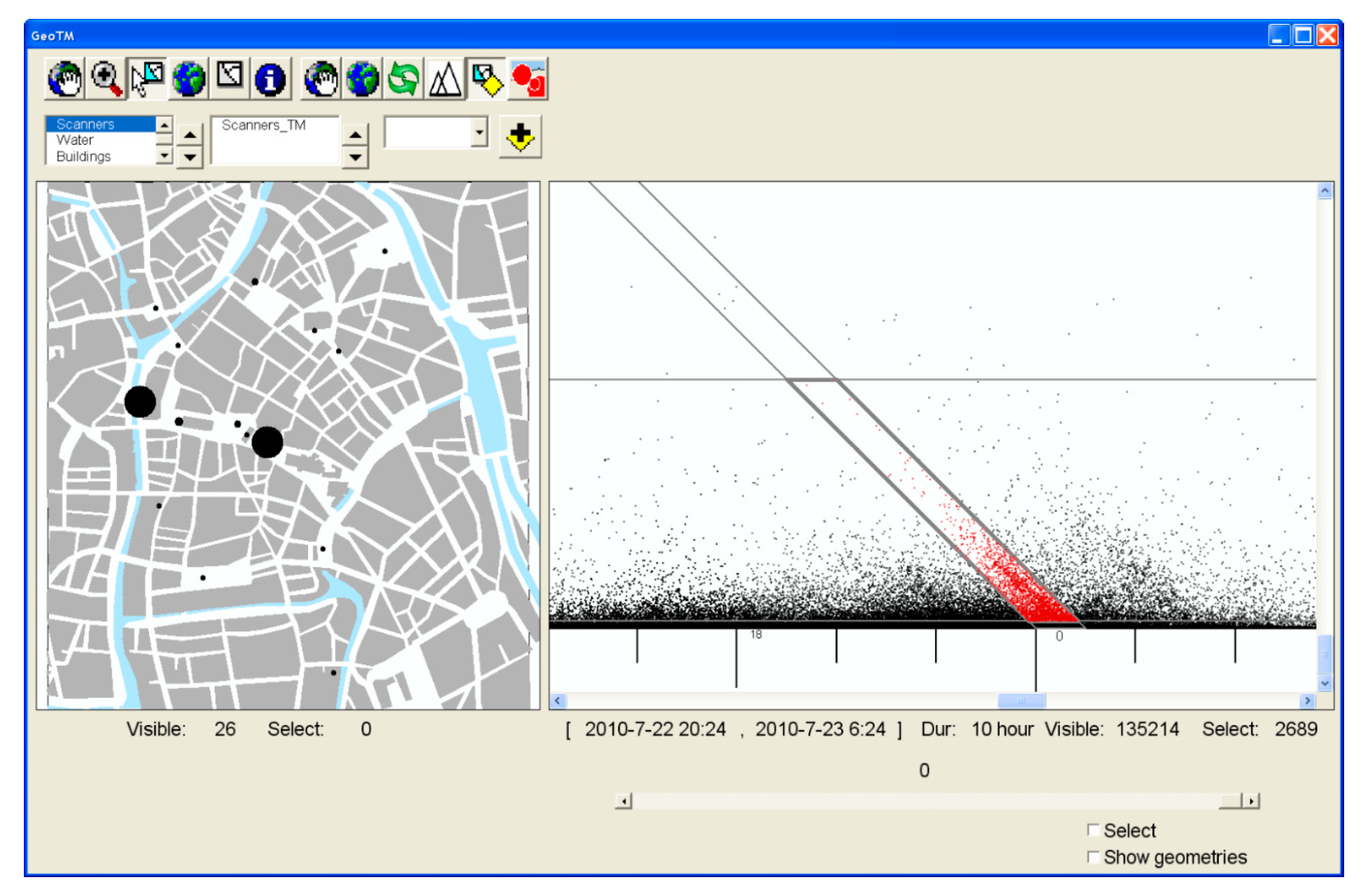
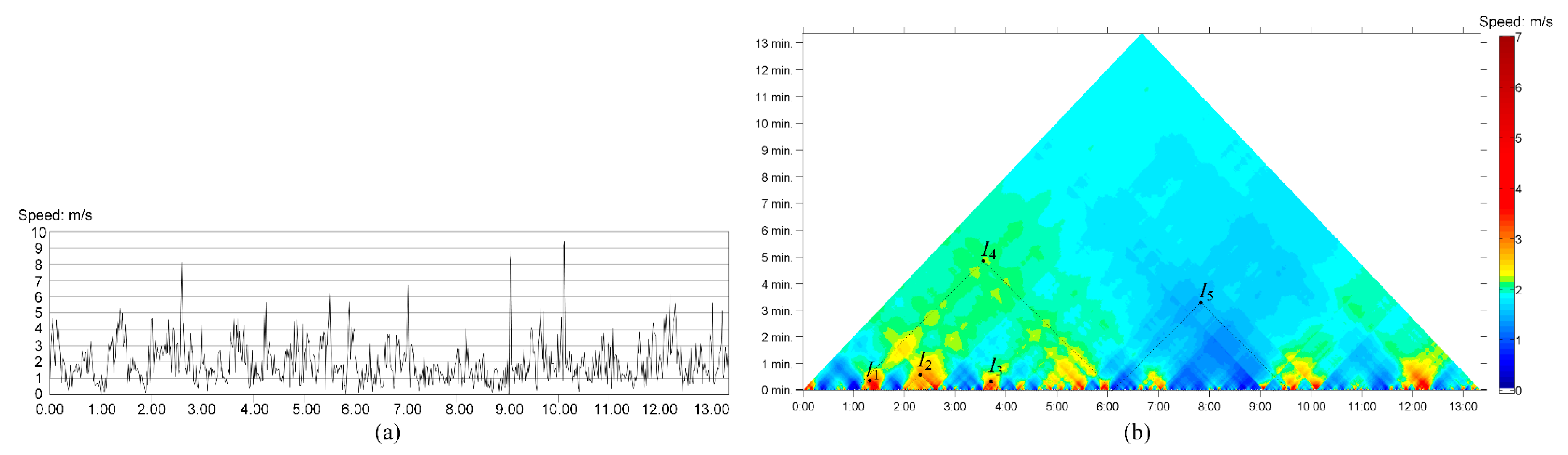
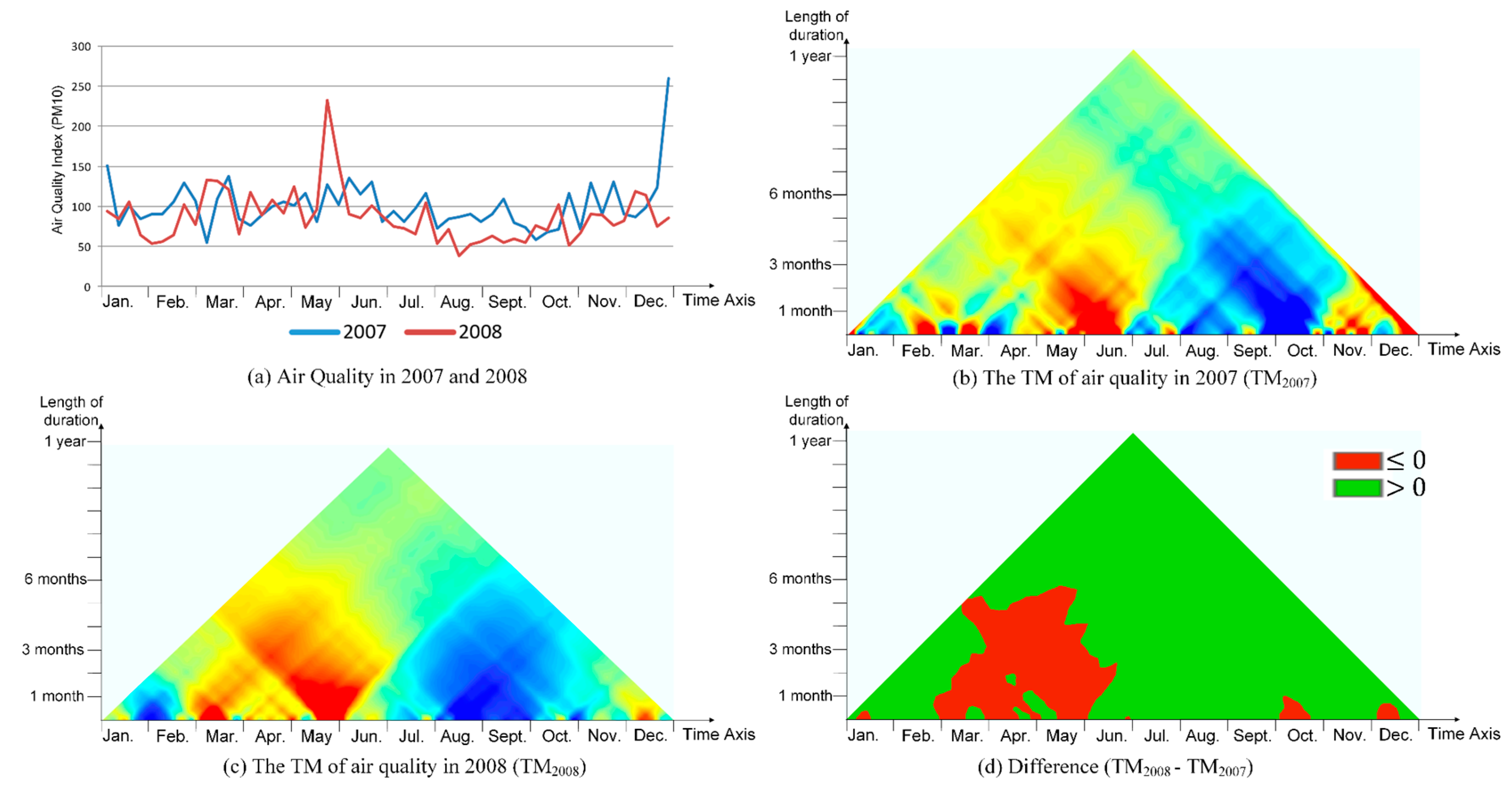
2.4.1. Visualization
2.4.2. Map Algebra for CTM
3. Pyramid Model
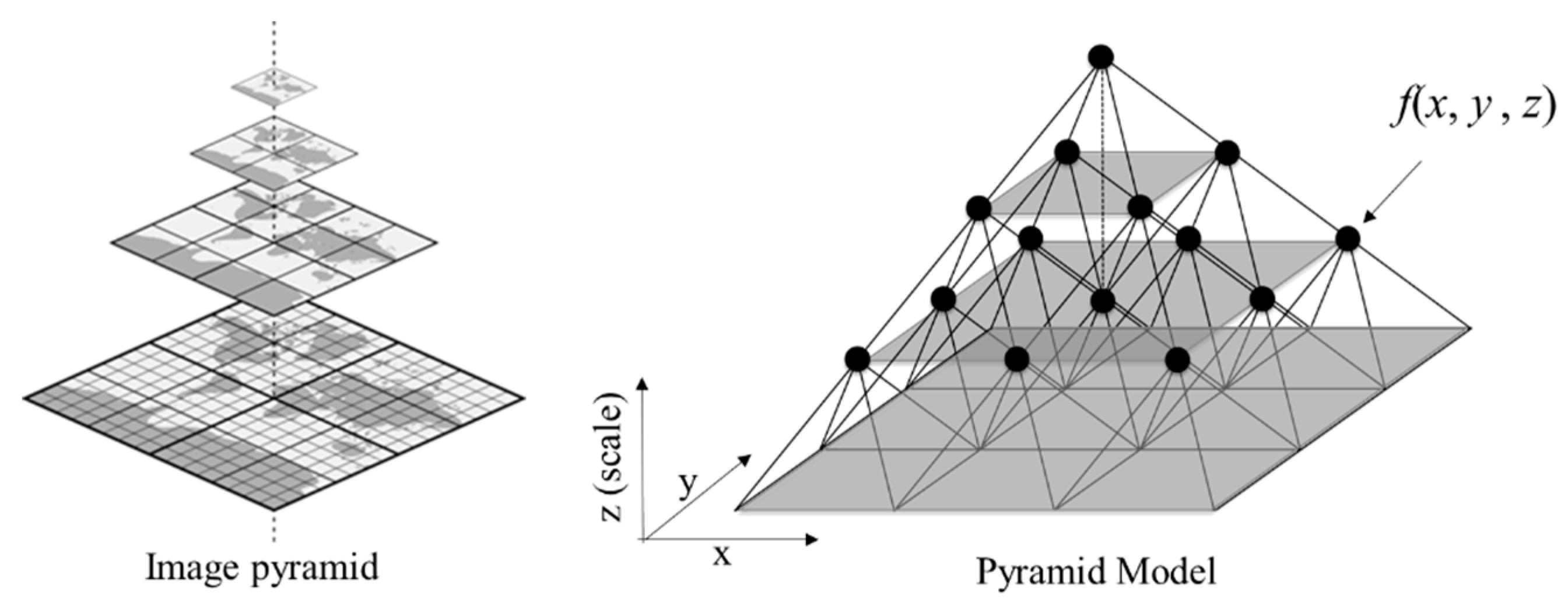
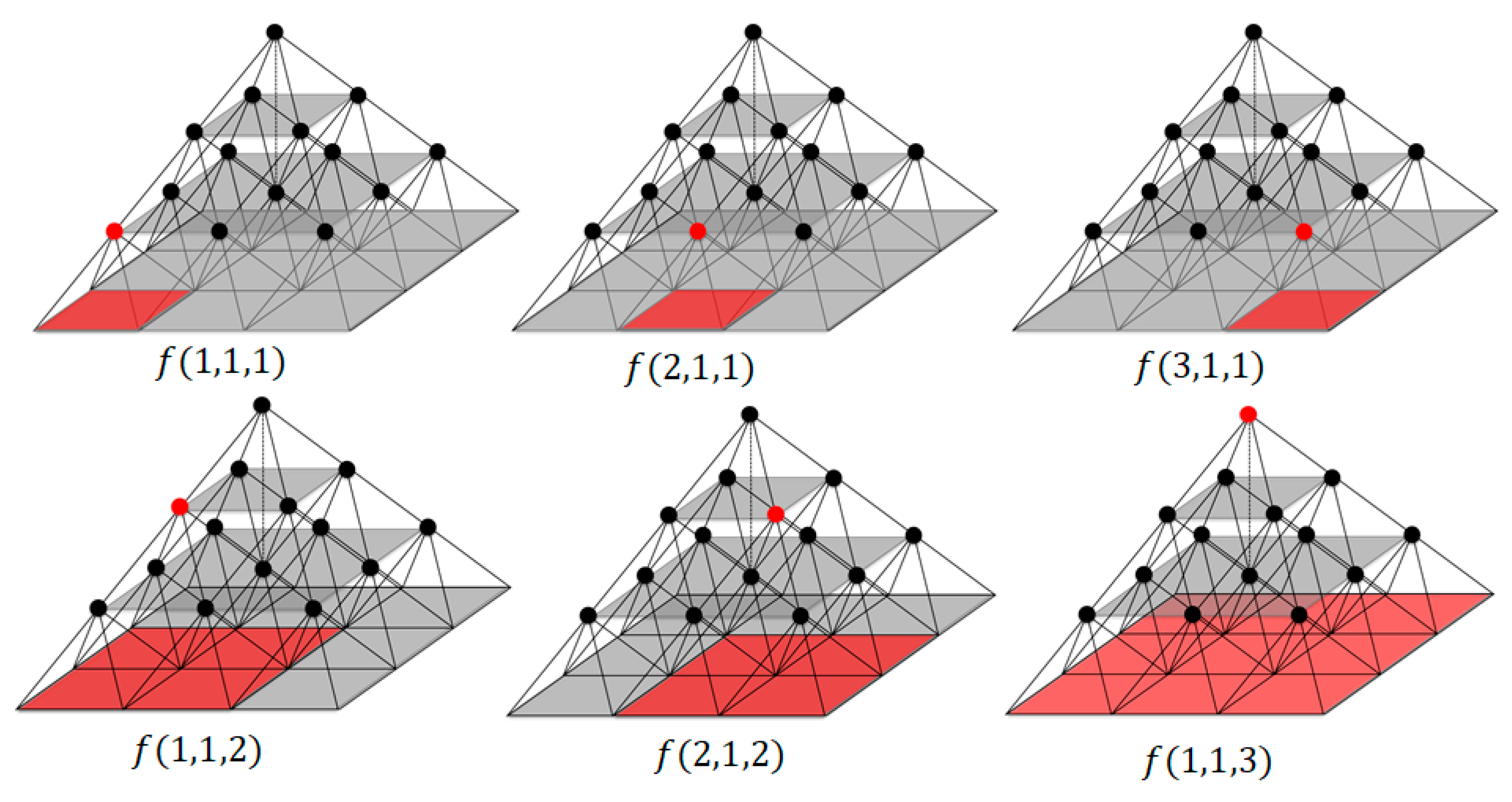
3.1. The Concept
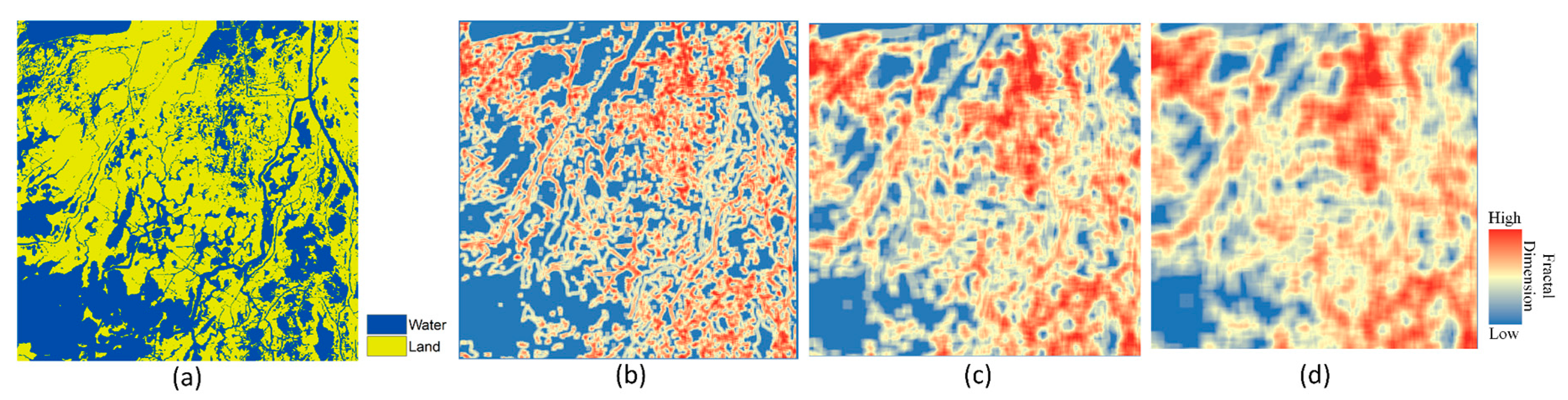
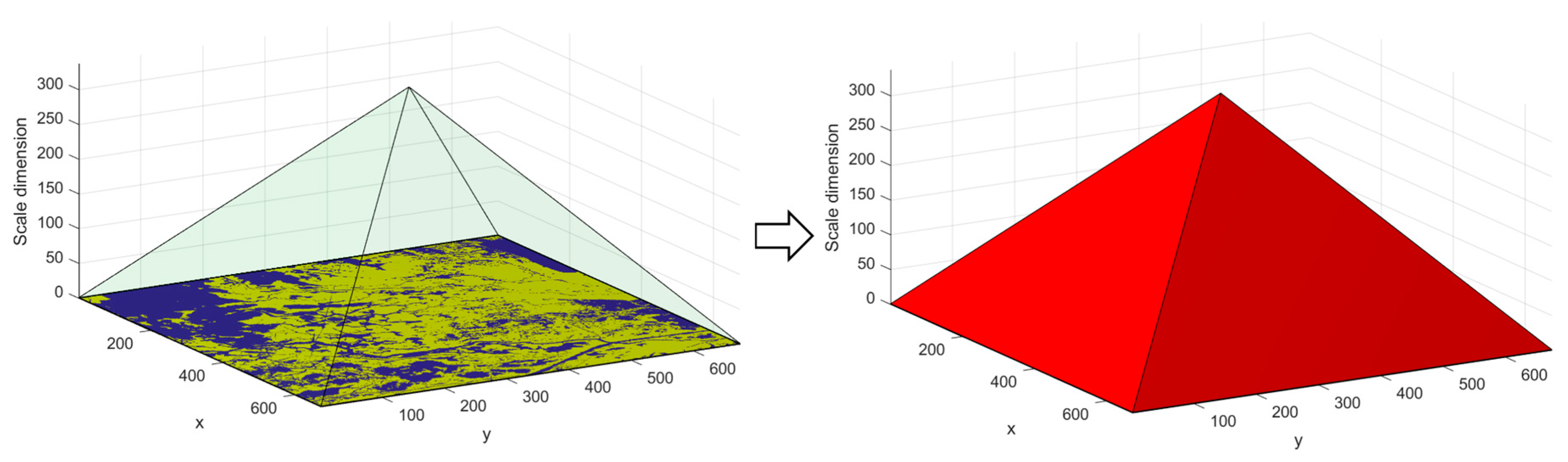
3.2. Multi-Scale Spatial Analysis
4. A Multi-Scale Analytical Framework
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Pelekis, N.; Theodoulidis, B.; Kopanakis, I.; Theodoridis, Y. Literature review of spatio-temporal database models. Knowl. Eng. Rev. 2004, 19, 235–274. [Google Scholar] [CrossRef]
- Pant, N.; Fouladgar, M.; Elmasri, R.; Jitkajornwanich, K. A Survey of Spatio-Temporal Database Research. In Intelligent Information and Database Systems; Nguyen, N.T., Hoang, D.H., Hong, T.-P., Pham, H., Trawiński, B., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 115–126. [Google Scholar]
- Overmars, K.P.; de Koning, G.H.J.; Veldkamp, A. Spatial autocorrelation in multi-scale land use models. Ecol. Model. 2003, 164, 257–270. [Google Scholar] [CrossRef]
- Veldkamp, A.; Verburg, P.H.; Kok, K.; de Koning, G.H.J.; Priess, J.; Bergsma, A.R. The Need for Scale Sensitive Approaches in Spatially Explicit Land Use Change Modeling. Environ. Model. Assess. 2001, 6, 111–121. [Google Scholar] [CrossRef]
- Burnett, C.; Blaschke, T. A multi-scale segmentation/object relationship modelling methodology for landscape analysis. Ecol. Model. 2003, 168, 233–249. [Google Scholar] [CrossRef]
- Townshend, I.; Awosoga, O.; Kulig, J.; Fan, H. Social cohesion and resilience across communities that have experienced a disaster. Nat. Hazards 2015, 76, 913–938. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Demsar, U.; Dransch, D.; Dykes, J.; Fabrikant, S.I.; Jern, M.; Kraak, M.-J.; Schumann, H.; Tominski, C. Space, time and visual analytics. Int. J. Geogr. Inf. Sci. 2010, 24, 1577–1600. [Google Scholar] [CrossRef]
- Kraak, M.-J. The space-time cube revisited from a geovisualization perspective. In Proceedings of the 21st International Cartographic Conference, Durban, South Africa, 10–16 August 2003; pp. 1988–1996. [Google Scholar]
- Gatalsky, P.; Andrienko, N.; Andrienko, G. Interactive analysis of event data using space-time cube. In Proceedings of the Eighth International Conference on Information Visualisation, IV 2004, London, UK, 16 July 2004; pp. 145–152. [Google Scholar] [CrossRef]
- Miller, H.J. Modelling accessibility using space-time prism concepts within geographical information systems. Int. J. Geogr. Inf. Syst. 1991, 5, 287–301. [Google Scholar] [CrossRef]
- Andrienko, N.; Andrienko, G.; Gatalsky, P. Exploratory spatio-temporal visualization: An analytical review. J. Vis. Lang. Comput. 2003, 14, 503–541. [Google Scholar] [CrossRef]
- Kulpa, Z. Diagrammatic Representation of Interval Space in Proving Theorems about Interval Relations. Reliab. Comput. 1997, 3, 209–217. [Google Scholar] [CrossRef]
- Van de Weghe, N.; Docter, R.; De Maeyer, P.; Bechtold, B.; Ryckbosch, K. The triangular model as an instrument for visualising and analysing residuality. J. Archaeol. Sci. 2007, 34, 649–655. [Google Scholar] [CrossRef]
- Qiang, Y.; Delafontaine, M.; Versichele, M.; De Maeyer, P.; Van de Weghe, N. Interactive Analysis of Time Intervals in a Two-Dimensional Space. Inf. Vis. 2012, 11, 255–272. [Google Scholar] [CrossRef]
- Qiang, Y.; Delafontaine, M.; Asmussen, K.; Stichelbaut, B.; De Tré, G.; De Maeyer, P.; Van De Weghe, N. Modelling imperfect time intervals in a two-dimensional space. Control Cybern. 2010, 39, 983–1010. [Google Scholar]
- Qiang, Y.; Matthias, D.; Neutens, T.; Stichelbaut, B.; Tré, G.D.; Maeyer, P.D.; de Weghe, N.V. Analysing Imperfect Temporal Information in GIS Using the Triangular Model. Cartogr. J. 2012, 49, 265–280. [Google Scholar] [CrossRef]
- Qiang, Y.; Chavoshi, S.H.; Logghe, S.; De Maeyer, P.; Van De Weghe, N. Multi-scale analysis of linear data in a two-dimensional space. Inf. Vis. 2014, 13, 248–265. [Google Scholar] [CrossRef]
- Qiang, Y.; Valcke, M.; De Maeyer, P.; Van de Weghe, N. Representing time intervals in a two-dimensional space: An empirical study. J. Vis. Lang. Comput. 2014, 25, 466–480. [Google Scholar] [CrossRef]
- Van de Weghe, N.; De Roo, B.; Qiang, Y.; Versichele, M.; Neutens, T.; De Maeyer, P. The continuous spatio-temporal model (CSTM) as an exhaustive framework for multi-scale spatio-temporal analysis. Int. J. Geogr. Inf. Sci. 2014, 28, 1047–1060. [Google Scholar] [CrossRef]
- Allen, J.F. Maintaining Knowledge About Temporal Intervals. Commun. ACM 1983, 26, 832–843. [Google Scholar] [CrossRef]
- Cohn, A.G.; Bennett, B.; Gooday, J.; Gotts, N.M. Qualitative Spatial Representation and Reasoning with the Region Connection Calculus. GeoInformatica 1997, 1, 275–316. [Google Scholar] [CrossRef]
- Delafontaine, M.; Versichele, M.; Neutens, T.; Van de Weghe, N. Analysing spatiotemporal sequences in Bluetooth tracking data. Appl. Geogr. 2012, 34, 659–668. [Google Scholar] [CrossRef]
- Pawlak, Z. Rough Sets. Int. J. Comput. Inf. Sci. 1982, 11, 341–356. [Google Scholar] [CrossRef]
- Billiet, C.; Van de Weghe, N.; Deploige, J.; De Tré, G. Visualizing and Reasoning with Imperfect Time Intervals in 2-D. IEEE Trans. Fuzzy Syst. 2017, 25, 1698–1713. [Google Scholar] [CrossRef]
- Zhang, P.; Beernaerts, J.; Zhang, L.; Van de Weghe, N. Visual exploration of match performance based on football movement data using the Continuous Triangular Model. Appl. Geogr. 2016, 76, 1–13. [Google Scholar] [CrossRef]
- Lindeberg, T. Scale-Space Theory in Computer Vision; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- Jolion, J.-M.; Rosenfeld, A. A Pyramid Framework for Early Vision; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1994. [Google Scholar]
- De Cola, L.; Montagne, N. The pyramid system for multiscale raster analysis. Comput. Geosci. 1993, 19, 1393–1404. [Google Scholar] [CrossRef]
- Yang, C.; Wong, D.W.; Yang, R.; Kafatos, M.; Li, Q. Performance-improving techniques in web-based GIS. Int. J. Geogr. Inf. Sci. 2005, 19, 319–342. [Google Scholar] [CrossRef]
- Xia, Y.; Yang, X. Remote Sensing Image Data Storage and Search Method Based on Pyramid Model in Cloud. In Rough Sets and Knowledge Technology; Li, T., Nguyen, H.S., Wang, G., Grzymala-Busse, J.W., Janicki, R., Hassanien, A.-E., Yu, H., Eds.; Springer: Berlin/Heidelberg, Germnay, 2012; pp. 267–275. [Google Scholar]
- Lam, N.S.-N.; Cheng, W.; Zou, L.; Cai, H. Effects of landscape fragmentation on land loss. Remote Sens. Environ. 2018, 209, 253–262. [Google Scholar] [CrossRef]
- Shaffer, M. Minimum viable populations: Coping with uncertainty. Viable Popul. Conserv. 1987, 69, 86. [Google Scholar]
- Couvillion, B.R.; Steyer, G.D.; Wang, H.; Beck, H.J.; Rybczyk, J.M. Forecasting the Effects of Coastal Protection and Restoration Projects on Wetland Morphology in Coastal Louisiana under Multiple Environmental Uncertainty Scenarios. J. Coast. Res. 2013, 33, 29–50. [Google Scholar] [CrossRef]
- Scaife, W.B.; Turner, R.E.; Costanza, R. Recent land loss and canal impacts in coastal Louisiana. Environ. Manag. 1983, 7, 433–442. [Google Scholar] [CrossRef]
- Turner, R.E. Wetland Loss in the Northern Gulf of Mexico: Multiple Working Hypotheses. Estuaries 1997, 20, 1–13. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qiang, Y.; Van de Weghe, N. Re-Arranging Space, Time and Scales in GIS: Alternative Models for Multi-Scale Spatio-Temporal Modeling and Analyses. ISPRS Int. J. Geo-Inf. 2019, 8, 72. https://doi.org/10.3390/ijgi8020072
Qiang Y, Van de Weghe N. Re-Arranging Space, Time and Scales in GIS: Alternative Models for Multi-Scale Spatio-Temporal Modeling and Analyses. ISPRS International Journal of Geo-Information. 2019; 8(2):72. https://doi.org/10.3390/ijgi8020072
Chicago/Turabian StyleQiang, Yi, and Nico Van de Weghe. 2019. "Re-Arranging Space, Time and Scales in GIS: Alternative Models for Multi-Scale Spatio-Temporal Modeling and Analyses" ISPRS International Journal of Geo-Information 8, no. 2: 72. https://doi.org/10.3390/ijgi8020072
APA StyleQiang, Y., & Van de Weghe, N. (2019). Re-Arranging Space, Time and Scales in GIS: Alternative Models for Multi-Scale Spatio-Temporal Modeling and Analyses. ISPRS International Journal of Geo-Information, 8(2), 72. https://doi.org/10.3390/ijgi8020072





