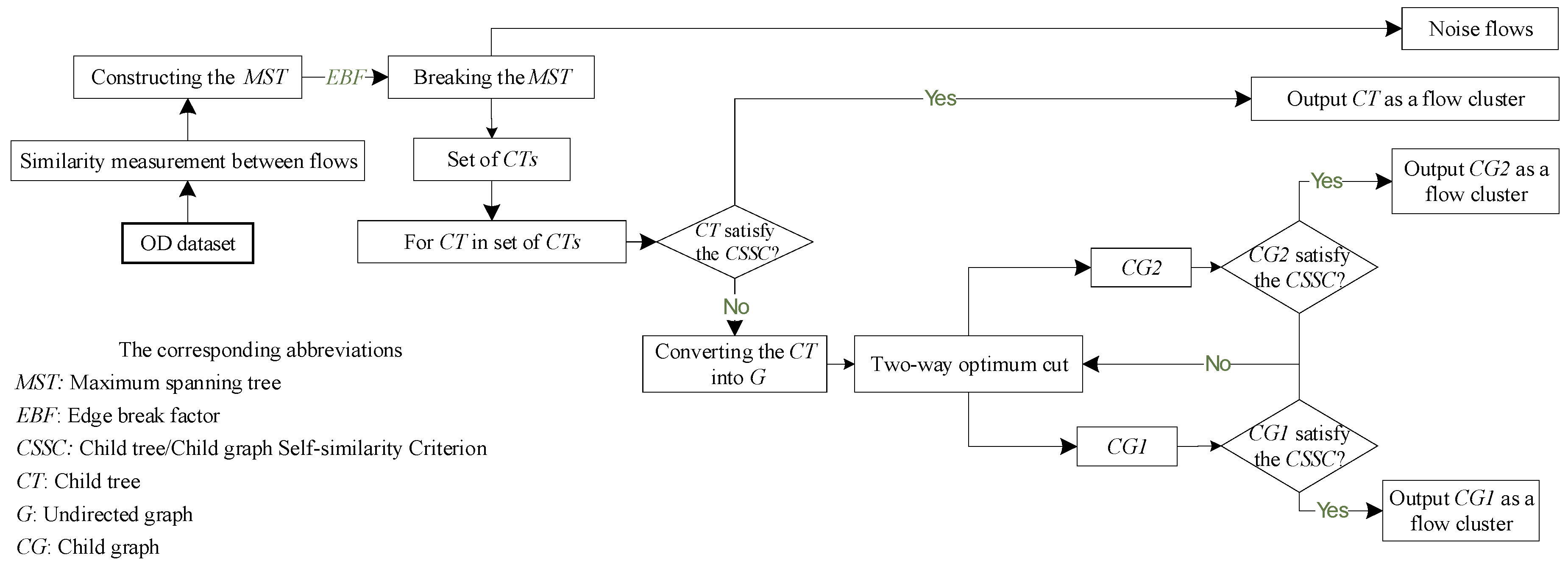
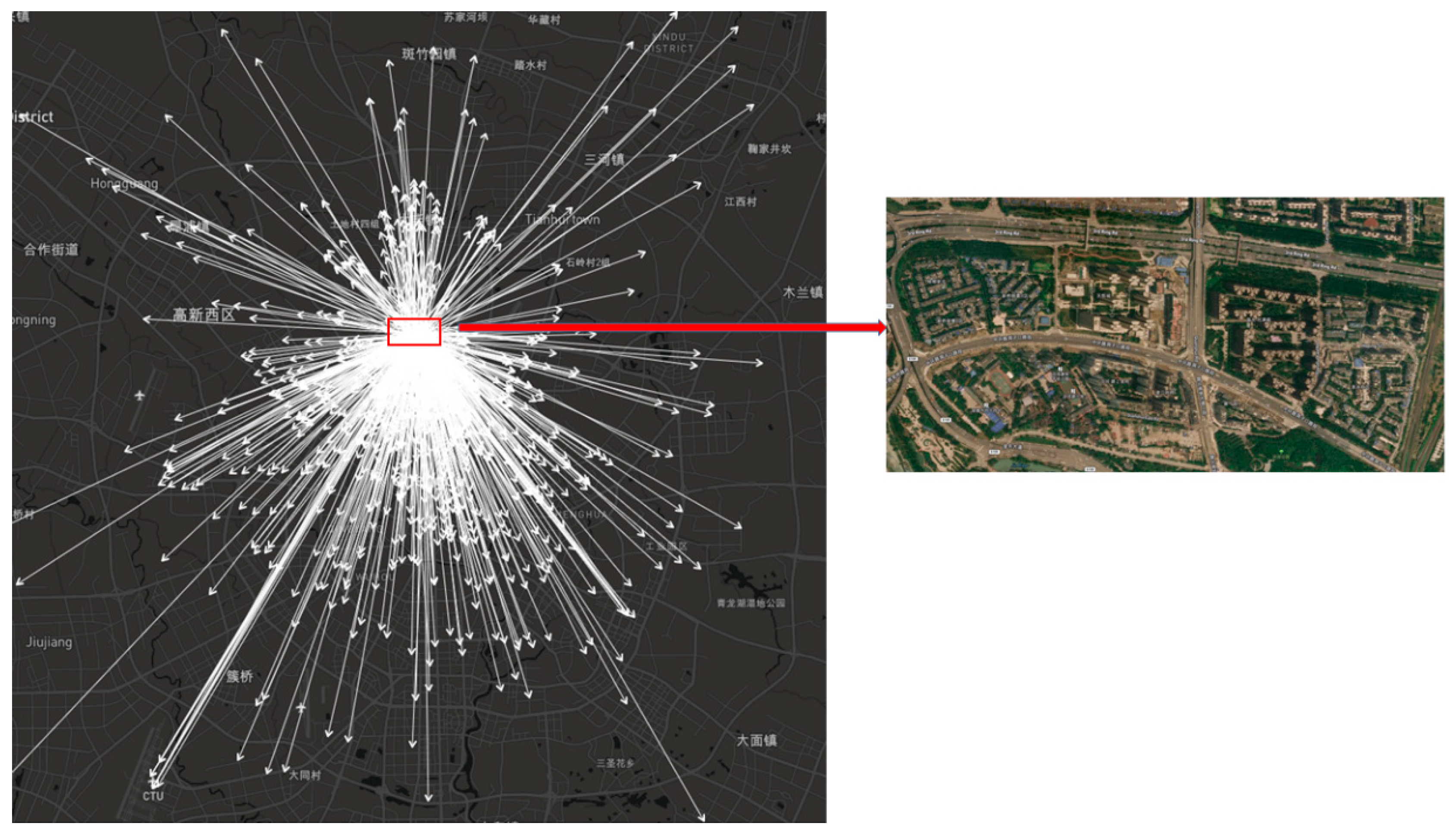
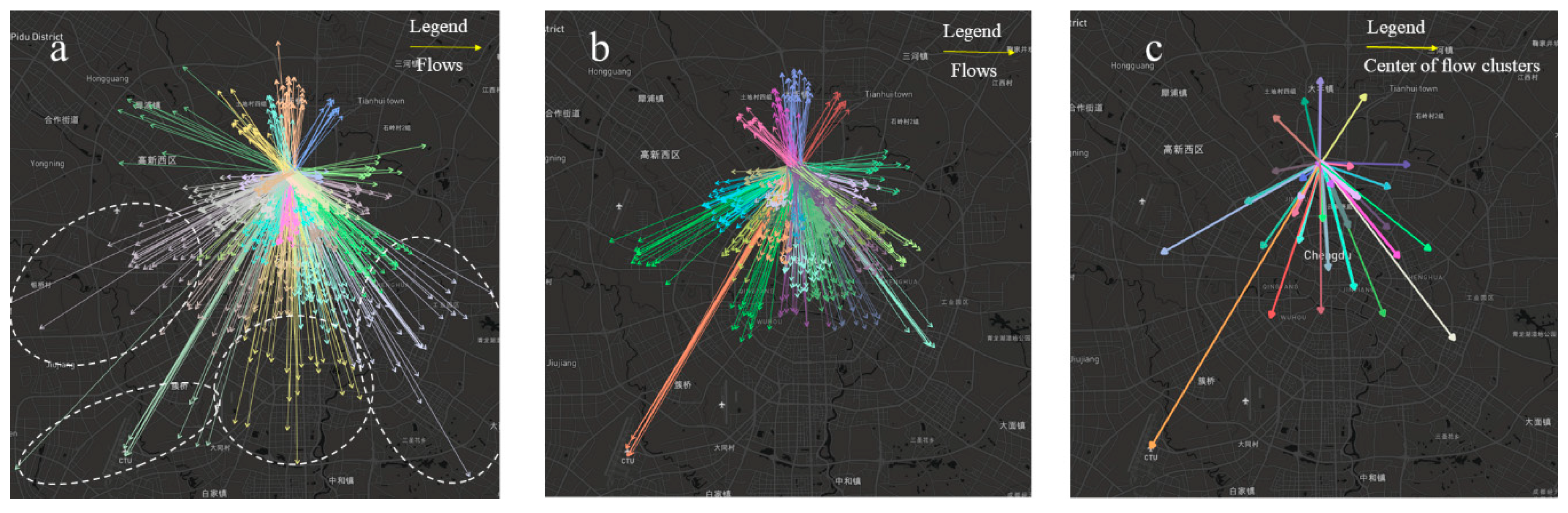
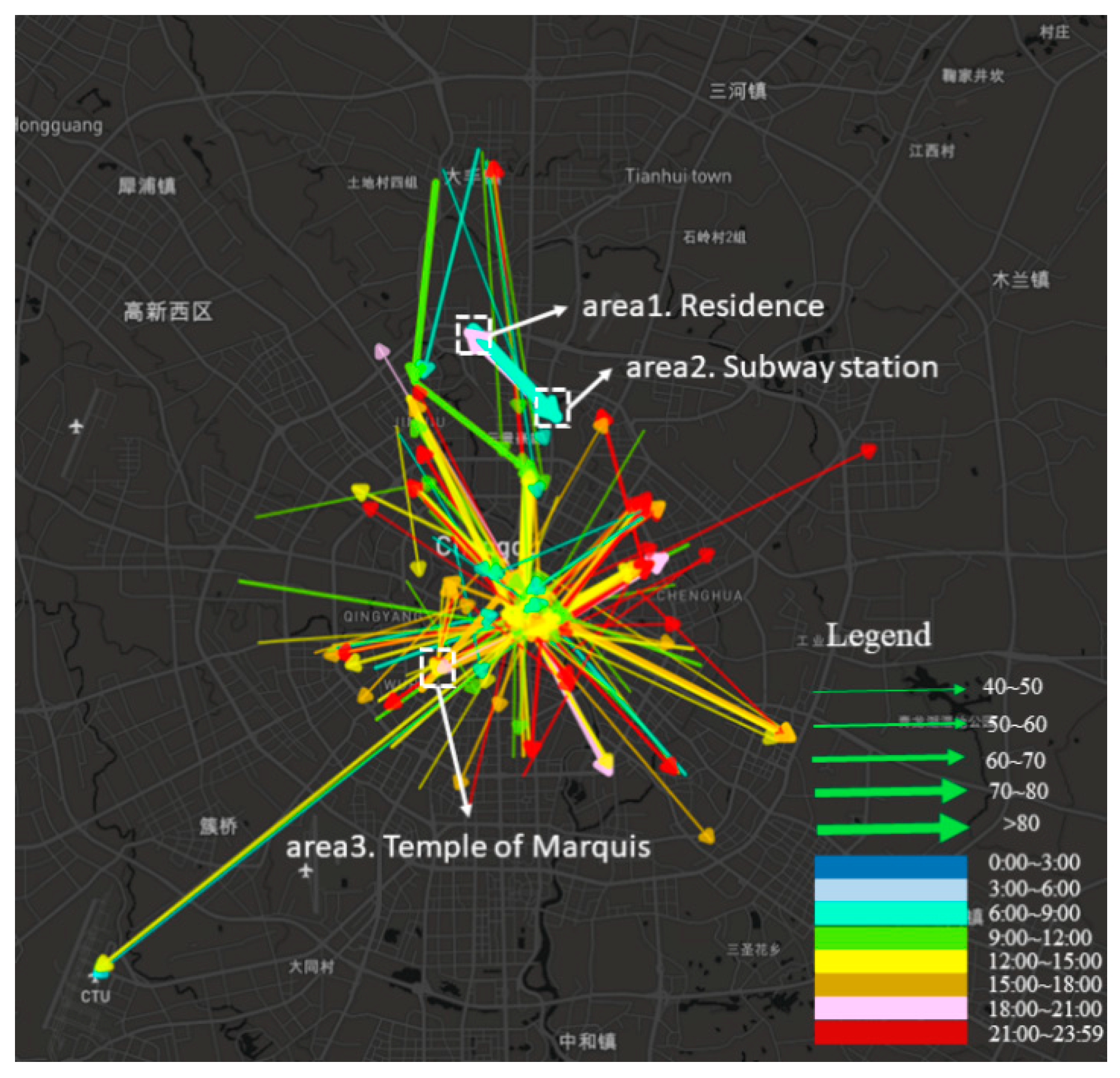
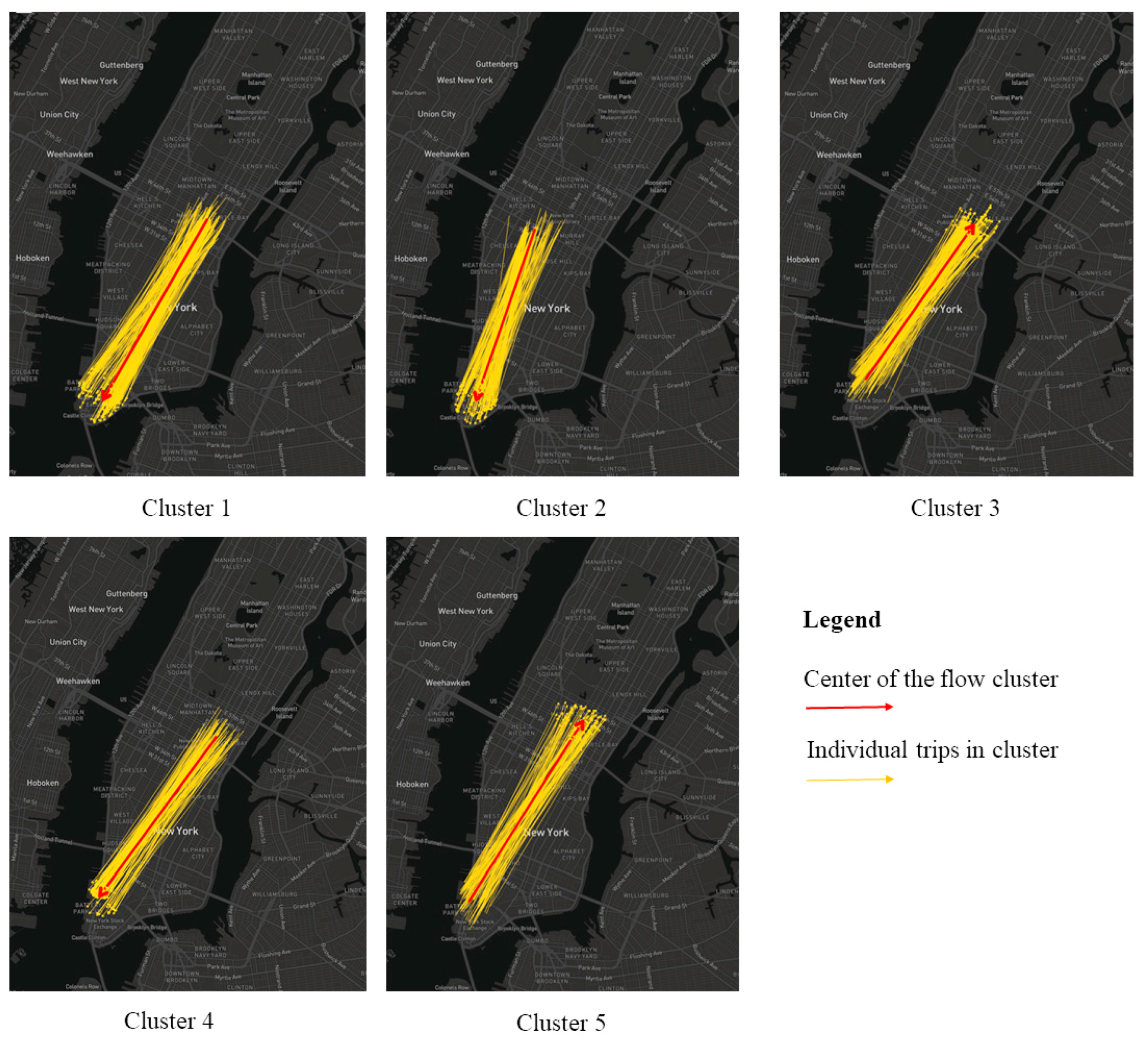
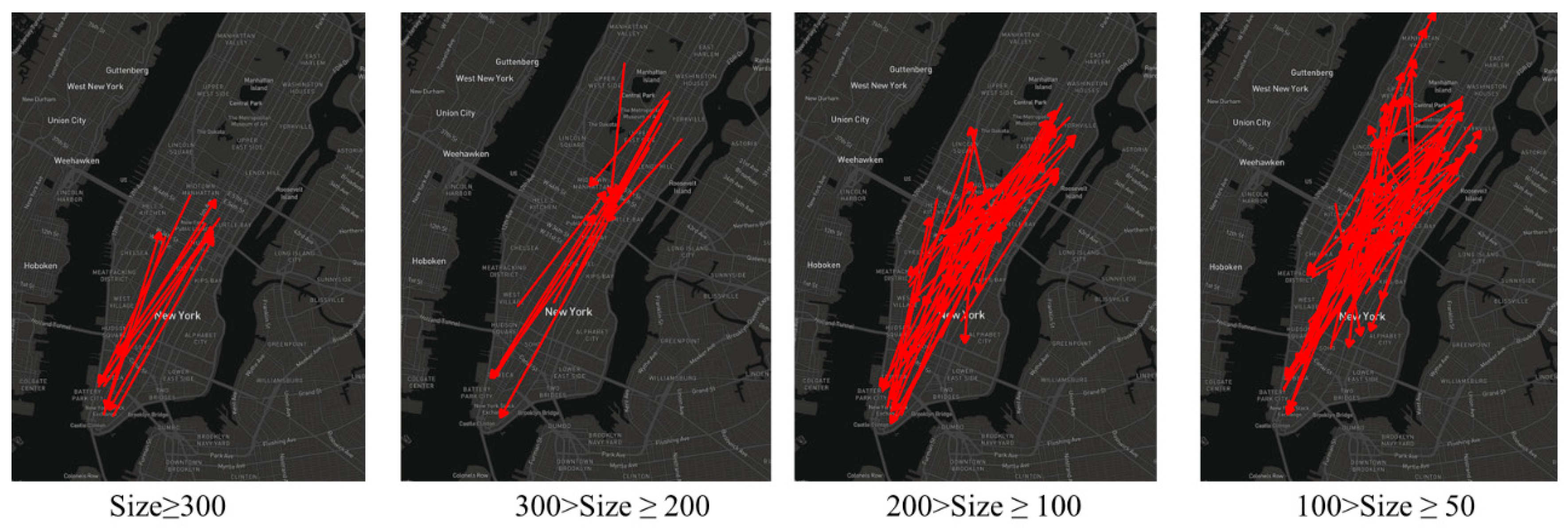
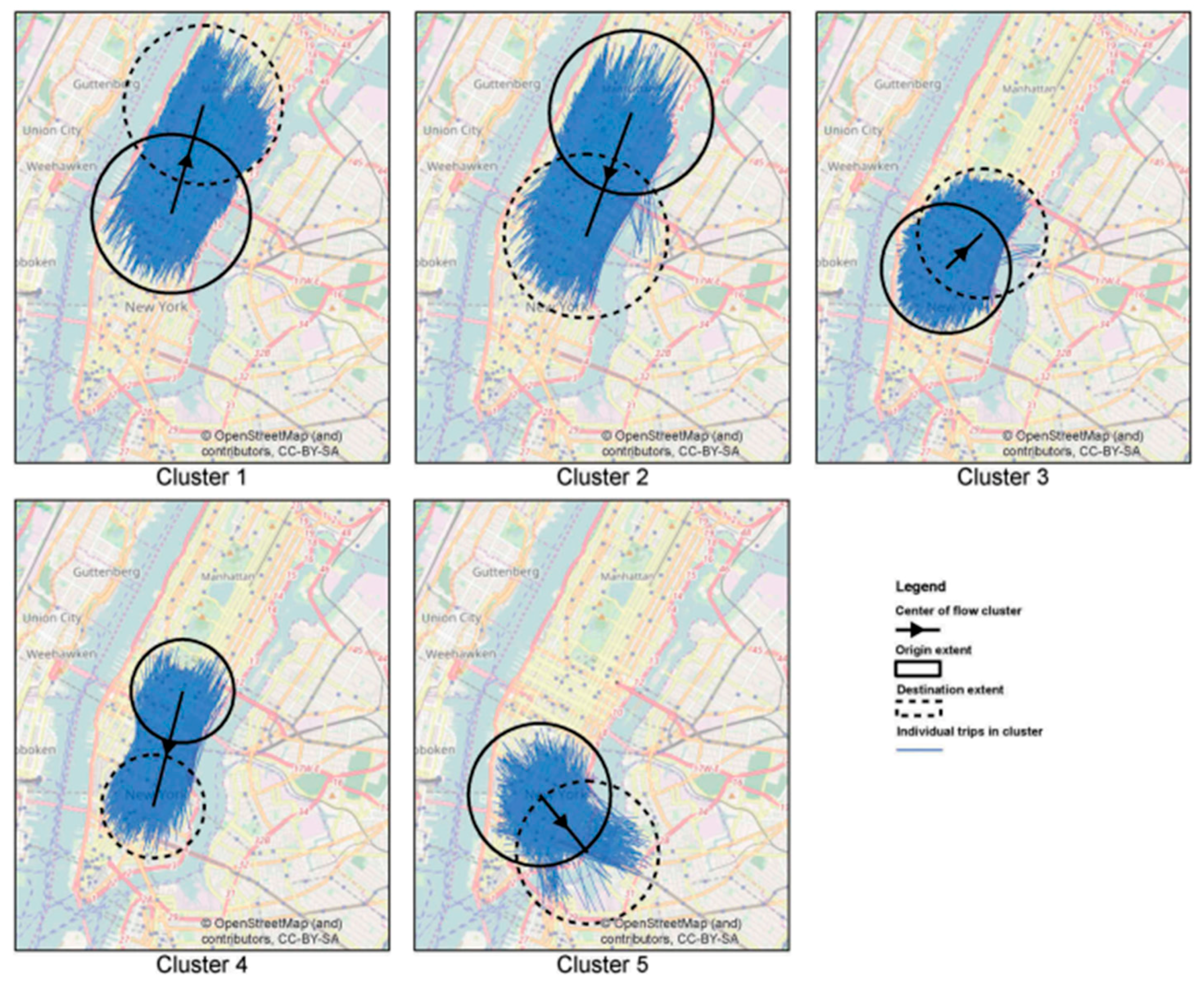
In this section, we propose a novel OD flow-clustering algorithm called “Tree-based and Optimum Cut-based Origin-Destination Flow Clustering” (TOCOFC) to obtain OD flow clusters from an enormous amount of raw OD flow data. TOCOFC can identify the spatial and spatiotemporal joint clustering of OD flow data, and different clustering results can be obtained by tuning the clustering parameters. TOCOFC has four steps. First, an OD flow similarity measurement method that quantifies the spatial similarity relationship between OD flows into a quantitative value is used. Furthermore, we extend this method to measure the spatiotemporal similarity between OD flows. Second, a maximum spanning tree
MST(
V,
E) is constructed, and we define the similarity value between pairs of OD flows as the weight of the corresponding
E. Then, we break the
MST to filter the noise flows and acquire a set of child trees. Third, we develop the
CSSC (Child tree/Child graph Self-Similarity Criterion) to estimate whether the OD flows (
Vs) in the child tree or child graph can be organized as an OD flow cluster for output. Last, we reshape the child tree that does not satisfy
CSSC into an undirected graph
G(
V,
E). Then, a recursive, graph-based optimum-cut method is used to partition
G into child graphs, and the recursion process stops when the child graph satisfies the
CSSC. We repeat the partition process until all the child trees that were partitioned into child graphs satisfy the
CSSC. The whole clustering process is displayed in
Figure 1.
3.1. Similarity Measurement Method of the OD Flow
To ensure that there is a similarity relationship between two OD flows, it is required that these two flows are not only geographically adjacent but also remain similar in direction.
Definition 1. Spatial similarity between OD flows: The quantitative value of the similarity relationship between two flows in terms of spatial position. The spatial similarity sim(fi, fj) between two OD flows fi and fj is defined as The variables
ratioO,
ratioD, and
func(ratio) are defined as
where
dist(
Oi,Oj) and
dist(
Di,Dj) represent the Euclidean distance between two origin points of a flow and two destination points of a flow, respectively.
disLimit is a parameter related to the length of
fi, which we explain clearly in Remark 1, and a is a parameter used for preventing a local effect caused by the numerical value of one of the ratios (
ratioO,
ratioD) being extremely small, which we explain clearly in Remark 2.
The range of the similarity value of two OD flows, which are calculated by Equations (1)–(4), is 0 to 0.75. Zero is the minimum value of two similar OD flows, and the more similar the two flows are, the greater the similarity value is.
Remark 1. In Figure 2, there are three cases used for showing the spatial similarity relationship between OD flows and proving it has to do with the length of the OD flows. In
Figure 2a,
Oi and
Oj are the origin points of OD flows
fi and
fj, respectively,
Di and
Dj are the destination points of OD flows
fi and
fj, respectively, and the parameter
disLimit is the radius of the circle whose center is
Oi or
Dj. If both
dist(Oi,Oj) and
dist(Oi,Oj) are less than
disLimit, then we can say
fi and
fj are similar. However, the value of
disLimit is hard to determine; if we set
disLimit to a fixed value, it will cause two errors:
Intuitively, the extent of similarity of the flows in
Figure 2a is higher than that of the flows in
Figure 2b, but under the circumstances of a fixed
disLimit, the ratio
dist(Oi,Oj)/disLimit and the ratio
dist(Di,Dj)/disLimit in
Figure 2a,b are similar. That is, the quantitative error is caused by a fixed
disLimit.
In
Figure 2c,
fi and
fj are obviously not similar, but they are concluded to be similar flows if they are judged by a fixed
disLimit.
Thus,
disLimit cannot be a fixed value. He. et al. [
12] proposed that the length of an OD flow must be greater than
2disLimit/sin45° (≈
2.83disLimit) to guarantee an angle between two OD flows of less than 45. Therefore, in this paper, we set
disLimit to vary with the length of the flow, that is
where
k is a parameter greater than 2.83. Usually, we set
k to 2.83.
Remark 2. Two ratios, ratioO (dist(Oi,Oj)/disLimit) and ratioD (dist(Di,Dj)/disLimit), are used to calculate the similarity value of two flows to determine whether they are similar or the extent of their similarity. When both ratios are less than or equal to 1, we can say these two flows are similar, and the smaller the value of the ratios, the higher the similarity. It is worth noting that when one of the ratios is small, the similarity value calculated by the above equations is greater than 0 even when the other ratio is larger than 1, which is the local effect we mentioned above. Therefore, a piecewise function Equation (4) is proposed to prevent this local effect. In the cases where the ratio is greater than 1, the parameter a of the power function, func(ratio) in Equation (4), will alleviate this negative local effect when a is larger than 1. The larger the value of parameter a, the better the mitigation effect. One plus the ratio also achieves such a mitigation effect.
Remark 3. Clearly, the similarity value calculated by Equations (1)–(4) has a feature: asymmetry. In other words, sim(fi, fj) and sim(fj, fi) are not equivalent when the length of fi is not equal to the length of fj. Although the difference between sim(fi, fj) and sim(fj, fi) is not large because there is not much difference in the length of two similar flows, we adopt the larger one as the uniform similarity value for the sake of convenience for subsequent research. With the above description, the uniform spatial similarity between two OD flows can be calculated as Definition 2. Spatiotemporal similarity between OD flows: The quantitative value of the similarity relationship between two flows taking into account the spatial and temporal information. The spatiotemporal similarity (sim_ST(fi, fj)) between two OD flows fi and fj, which is extended from Equation (1), is defined aswhere ratioT is defined as timeSpan(fi, fj) represents the time difference between OD flow fi and fj, and there are two ways to calculate the time difference:
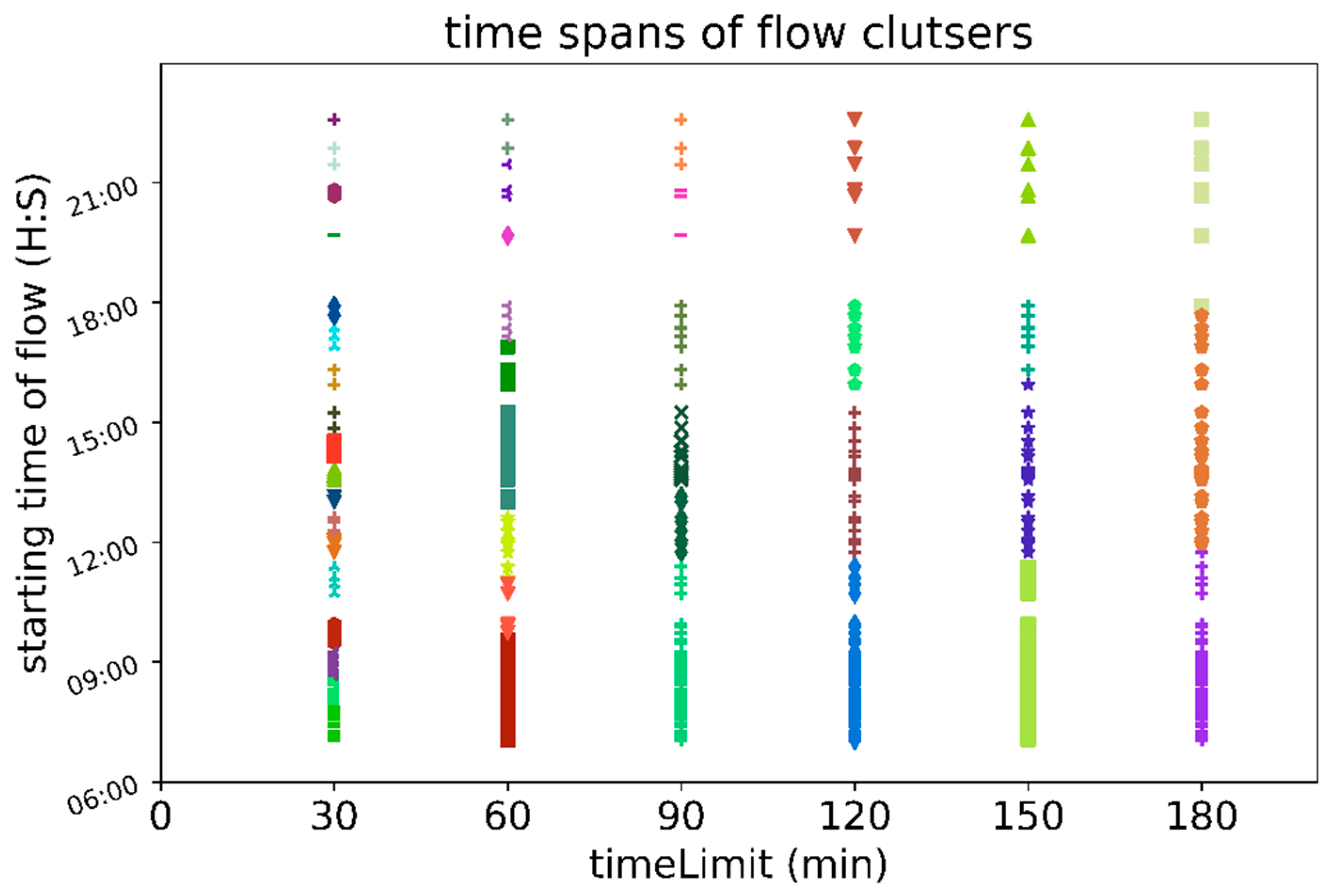
If timeSpan(fi, fj) is larger than timeLimit, then we can say that fi and fj have no temporal similarity. Thus, timeLimit is a parameter similar to disLimit because both are used for calculating the ratios; however, disLimit is a parameter that depends on the length of the OD flow, and timeLimit is set artificially, without any relation to the OD flow itself. We can set timeLimit to any value, such as 5 min, 10 min, 15 min, 30 min, 45 min, and 1 h, depending on what kind of clustering results we want.
Remark 4. The uniform spatiotemporal similarity of two OD flows is defined as follows: 3.2. Construct the Maximum Spanning Tree and Its Child Tree
Definition 3. Maximum spanning tree. The maximum spanning tree is a concept opposite to that of the minimum spanning tree. In an undirected connected graph, if there is a connected subgraph containing all the nodes and part of the edges of the original graph and there is no loop (or simple circuits) in the subgraph, then we call this kind of subgraph a spanning tree of the original graph. A maximum spanning tree has the maximum weight among all the spanning trees.
The variable V is a collection of OD flows, MST represents the maximum spanning tree for V, and E represents the set of edges in the MST. For each edge(u,v) ∈ E, we set the edge(u,v) weight with simu,v or sim_STu,v.
The MST is constructed from an arbitrary root vertex (an OD flow) and grows until the MST spans all the vertices in V. At each step in the process of growing the MST, we add the heaviest edge that connects V to an isolated vertex (one has not been added to the MST before) to the MST.
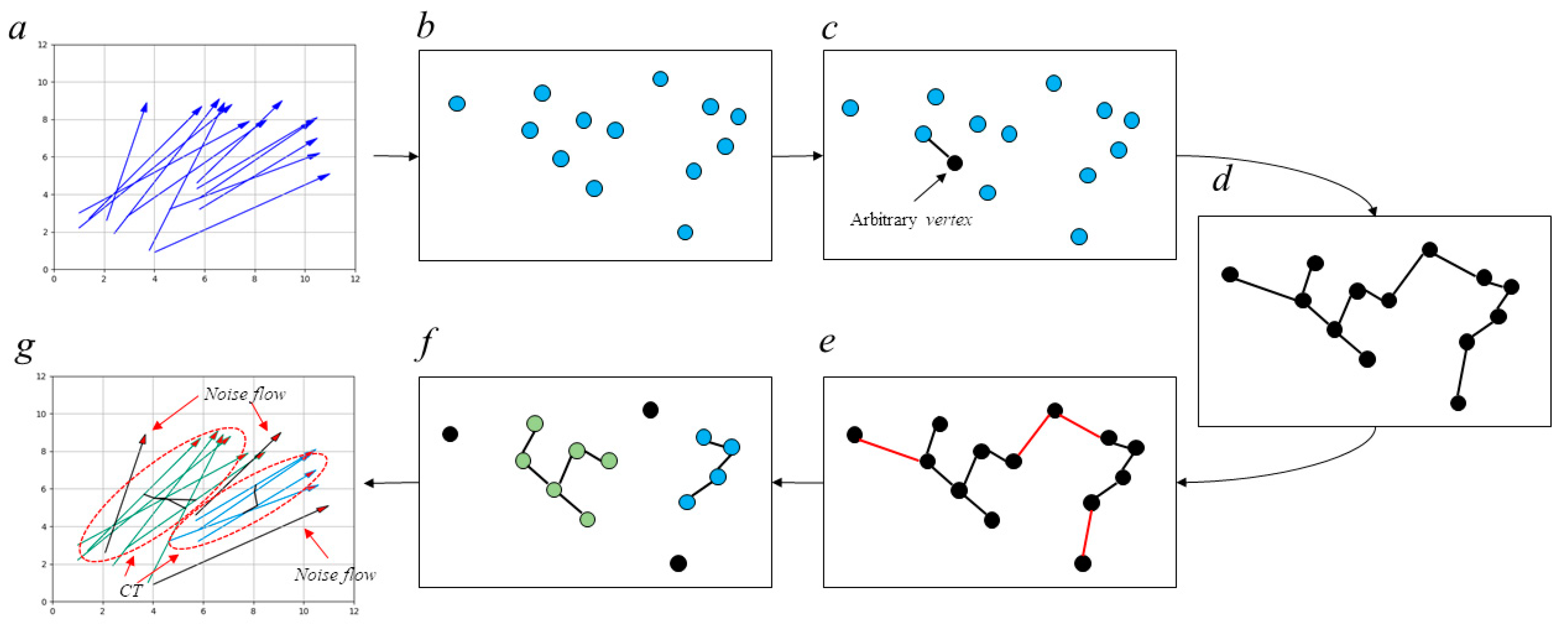
After the MST has been constructed, a factor named “Edge Breakup Factor (EBF)” is utilized to split the MST into many child trees. The value of the EBF is usually set to 0 because 0 is the lowest similarity value of two similar flows. CT denotes the child tree.
By searching for
edges whose weight value is less than that of the
EBF in the
MST and removing them, we can obtain several relatively small
CTs. A simple and intuitive example is shown in
Figure 3, with the purpose of illustrating the procedure of constructing an
MST and splitting it into child trees.
Remark 5. If there exists a CT that has only one vertex and no edge, we call it a noise flow.
Remark 6. There is no similarity relationship between the CTs. According to the characteristics of the MST, the edge with the greatest weight between the CTs is the one that has been broken up due to its weight being lower than the value of the EBF (which is actually 0), so there is no vertex (OD flow) in one of the CTs related to the other CTs.
The benefits of constructing the MST and splitting it into CTs are as follows:
Extracting noise flows and excluding them from the next clustering steps to prevent a loss of clustering accuracy.
Splitting the high-scale MST into several smaller CTs that do not have similar relationships to each other can increase the clustering efficiency of the subsequent steps without any accuracy loss.
There is no similarity relationship between the CTs, so we can cluster all the CTs separately parallel to each other.
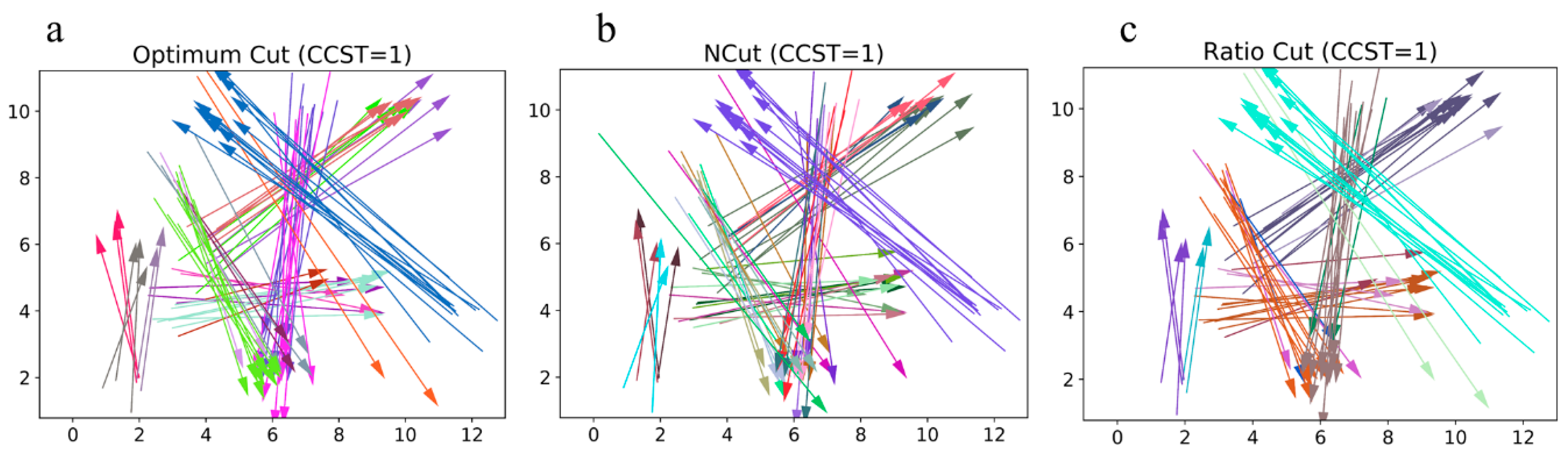
3.4. Cut-Based Graph Clustering Method
The procedure of cut-based graph clustering is employed if there are some CTs that cannot meet the requirements of the CSSC. In this part, we first convert the CT that needs to be cut into an undirected connected graph. Then, a cut-based graph clustering algorithm using a global cut criterion is used to partition this graph into several child graphs that meet the requirements of the CSSC.
Graph theory cutting algorithm [
15,
22,
23,
24,
25] is now a very mature clustering algorithm, which has very significant effects in clustering complex data.
The cut-based graph clustering algorithm using a global cut criterion, also named spectral clustering, has become more popular in recent years because it is simple to implement and usually has a better clustering result than that of the tradition clustering algorithm. There have been many global cut criteria, such as the minimum cut [
22], normalized cut [
23] and ratio cut [
26]. Although these cut criteria can indeed prevent skewed cuts efficiently, they usually perform poorly when the number of
vertices in the graph is large. Considering the number of clusters required for the clustering method, based on the criteria mentioned above and the reality that
CTs vary greatly, it is impossible to give an exact number of clusters to guarantee that all the clustering results satisfy the
CSSC. To overcome the limitations above, a recursive two-way optimum-cut graph clustering method proposed by Li [
15] is utilized to partition the graph into child graphs. We will introduce the details of this method applied in the OD flow clustering below.
Given a CT that needs to be cut, we convert it into a weighted undirected graph G (V, E) where the vertex set V is the same as the V in the CT and the edge set E is the set of unordered pairs of V. The weight of each edge is first calculated by the similarity measurement method of the OD flow, then we set the weight of the edge(u,v) with a weight less than 0 to 0. N = |V| denotes the number of vertices and W is a symmetrical matrix with W(i, j) = w(Vi, Vj), where w(Vi, Vj) represents the weight between vertex Vi and Vj.
During the clustering process, we tried to find the best cut to partition G into two disjointed child Graphs, CG1 and CG2, where CG1 ≠ Ø, CG2 ≠ Ø, CG1 ∩ CG2 = Ø, and CG1 ∪ CG2 = G.
Definition 6. Intraweight. The intraweight (IW) of the CG is defined as Definition 7. Cut-weight. The cut-weight (CW) of the G is defined as The best cut tries to minimize the value of the
CW(
G) and maximize the value of the
IW(
CG1) and
IW(
CG2) simultaneously. To achieve this, we propose the following optimum-cut criterion:
which is similar to the optimum-cut criterion proposed by Li [
15].
Li [
15] has discussed the feasibility of optimizing the optimum-cut criterion and gave an effective sample-based method to obtain the division results. On the theoretical basis of Li [
15], the steps of the optimum cut-based graph partition are as follows:
Step 1: Given a G
(V, E) converted from a
CT, let
d(
u) = d(
u) =
be the total weight from
vertex u to all the other vertices. With the definition of
N and
d,
D is an
N × N diagonal matrix with
d = (
d(V1),
d(V2), …,
d(VN)) on its diagonal. The normalized Laplacian matrix is denoted by
L, which is represented as follows:
Step 2: Let λ2 be the second smallest eigenvalue of L, α2 be the eigenvector corresponding to λ2 and .
Step 3: Draw n (usually 400) independent random sample points uniformly from [min(x2), max(x2)].
Step 4: Select each sample point as a split point to partition
x2 into two parts and calculate the value of
Step 5: Choose the sample point as the optimal split point whose value of
is the smallest value of all the sample points. Then, use the optimal split point to bisect G into CG1 and CG2.
Remark 7. The value of IW(CG) is 0 when the number of vertices in CG is 1, which violates the principle that the denominator must not be zero. Therefore, we replace IW(CG) with a small positive number when this situation happens.
However, this sample-based division method is not suitable for a very large amount of data because of its low computational efficiency. Thus, we chose
k-means as an alternative method to partition
x2 into two parts, which was also proven to be feasible by Li [
15].
Furthermore, a recursive strategy is adopted to repartition the CG that cannot meet the requirements of the CSSC. Based on the CSSC, we can decide which CT should be partitioned, which CG should be repartitioned, and when the process of recursive repartition should be stopped.
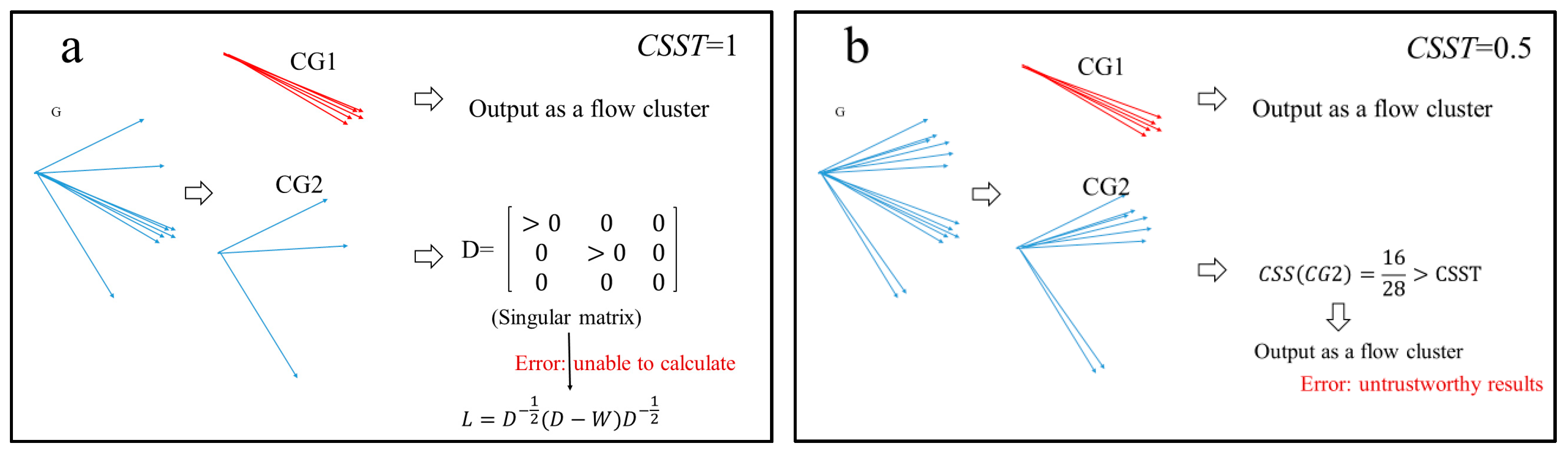
Remark 8. Two serious problems occur in the process of repartitioning the CGs:
Problem 1.If, in the CG that needs to be further cut, there exists one or more noise flows, the matrix D corresponding to CG will be a singular matrix, which is forbidden in the process of calculating the normalized Laplacian matrix.
Problem 2.When the CSST is less than 1, there exist some CGs that satisfy the CSSC, but it can be partitioned into two CGs without any similarity relationship.
Figure 4 intuitively illustrates these two problems with two simple examples. Clearly, Problem 1 disturbs the partitioning process, and Problem 2 makes the clustering results untrustworthy.
To cope with these two problems, we extract the
vertices of the
CGs that exist from one of the above problems and use them to construct an
MST, and then we split it into
CTs; this is similar to the step that we introduced in
Section 3.2, which is very helpful for dealing with these two problems.
After obtaining all the CGs that satisfy the CSSC, we organize all the vertices in each CG into a flow cluster.
3.5. Algorithm and Performance Analysis
From the description in the previous sections, it can be seen that our algorithm mainly consists of three steps:
- step 1.
Compute the similarity value between flows.
- step 2.
Construct the MST.
- step 3.
Cut the tree or graph.
Given n OD flows, step 1 has the time complexity of
O(
n2) for calculating the similarity value between flows, and the result of the calculation is stored as a matrix for the subsequent steps to prevent repeated calculations. In step 2, the
MST’s construction runs in time
O(
E+
VlgV) by using Fibonacci heaps [
26]. As
n OD flows can be seen as
n vs. and there are (
n−1)*
n/2 Es between the n
Vs, the complexity for constructing the
MST is equivalent to
O(
n2+
nlgn). Step 3 takes
O(
n) to compute the diagonal matrix
D in each iteration if there is no noise flow. Assuming that the
MST has been split into
k balanced
CTs, the time complexity of computing the normalized Laplacian matrix
L is
O(
n3/
k2). It is worth noting that the weight matrix
W is a sparse matrix. By using some tricks of sparse matrix operation, the time complexity of computing
L can be reduced to
O(
n2/
k2). Then, the
k-means algorithm takes
O(
n) to partition the eigenvector. Therefore, the overall time complexity spent in the first iteration of step 3 is
O(
n2/
k2+2
n). In the worst case, the first iteration is calculated in
O(
n2+2
n). In the next iteration, as an increasing number of flows are output as clusters,
k becomes increasingly large, and the time consumption is less than that of the first iteration. Assume that the clustering process ends after m iterations, and the whole computation procedure of step 3 is less than
O(
m*
n2+2
n*
m).
According to the above steps, the whole computation procedure of the TOCOFC algorithm costs approximately O((m+1)*n2+2n*m+n*lgn+n). Since m ≪ n, the time complexity of TOCOFC is approximately O(n2).
Next, we introduce the memory consumption of the TOCOFC algorithm. In step 1, the similarity value between the flows is calculated and stored as a matrix, which needs a large memory space. We realize that most of the values in this matrix are 0 because there is not a similar relationship between most flows, which means that the matrix storing the similarity information between the flows is a sparse matrix. Therefore, we use a triple table in our experiments to store useful information for practical applications, which reduces the space complexity of step 1 from O(n*n) to O(a*n) (a is the average number of similar flows). In the next steps, we use the same method to store the calculation results. The space complexity consumed by each iteration in the above iterative process is similar to or less than that of step 1. Since a ≪ n, the overall space complexity of TOCOFC is O(n).