A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery
Abstract
1. Introduction
2. Related Basic Theory
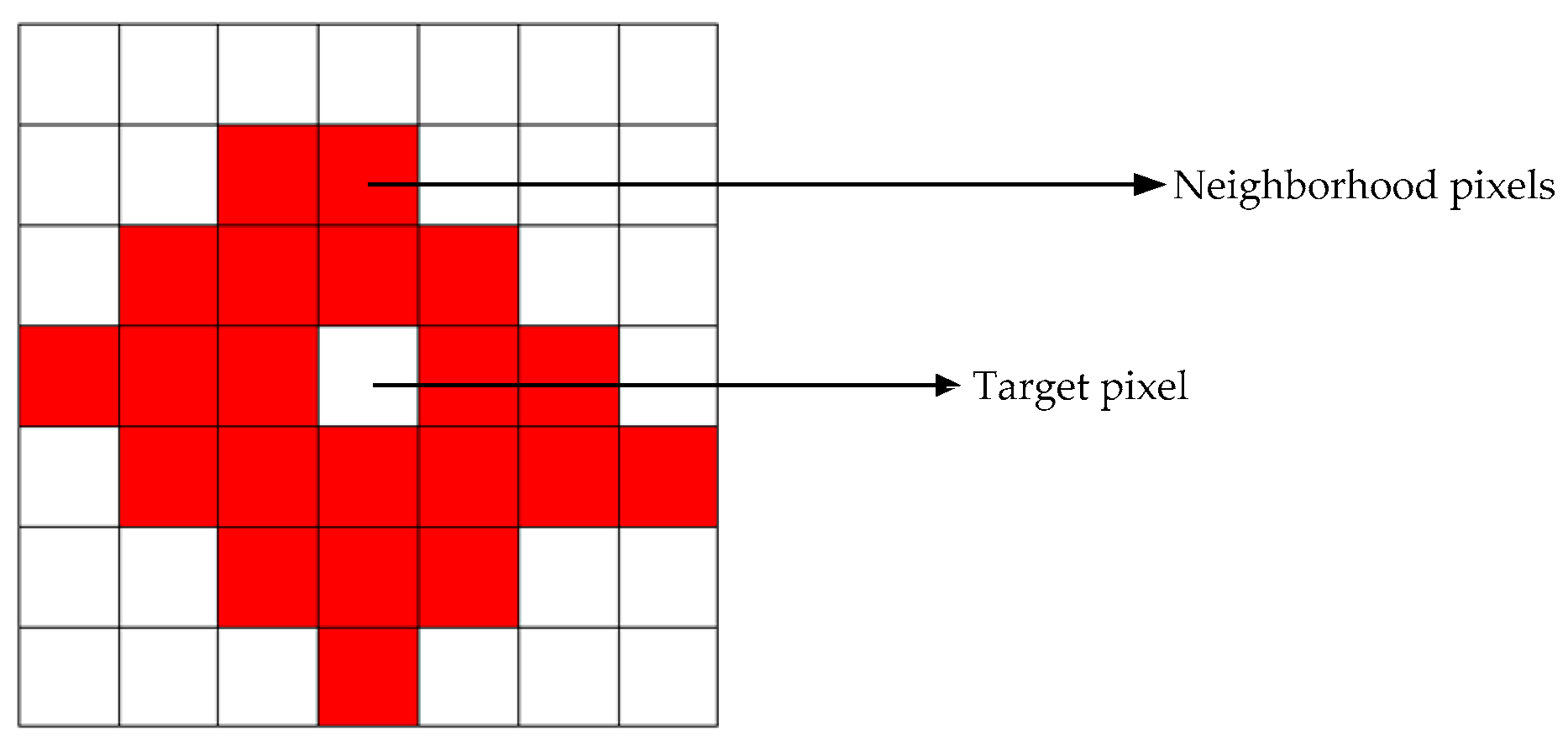
2.1. Spatial Dependence of Images
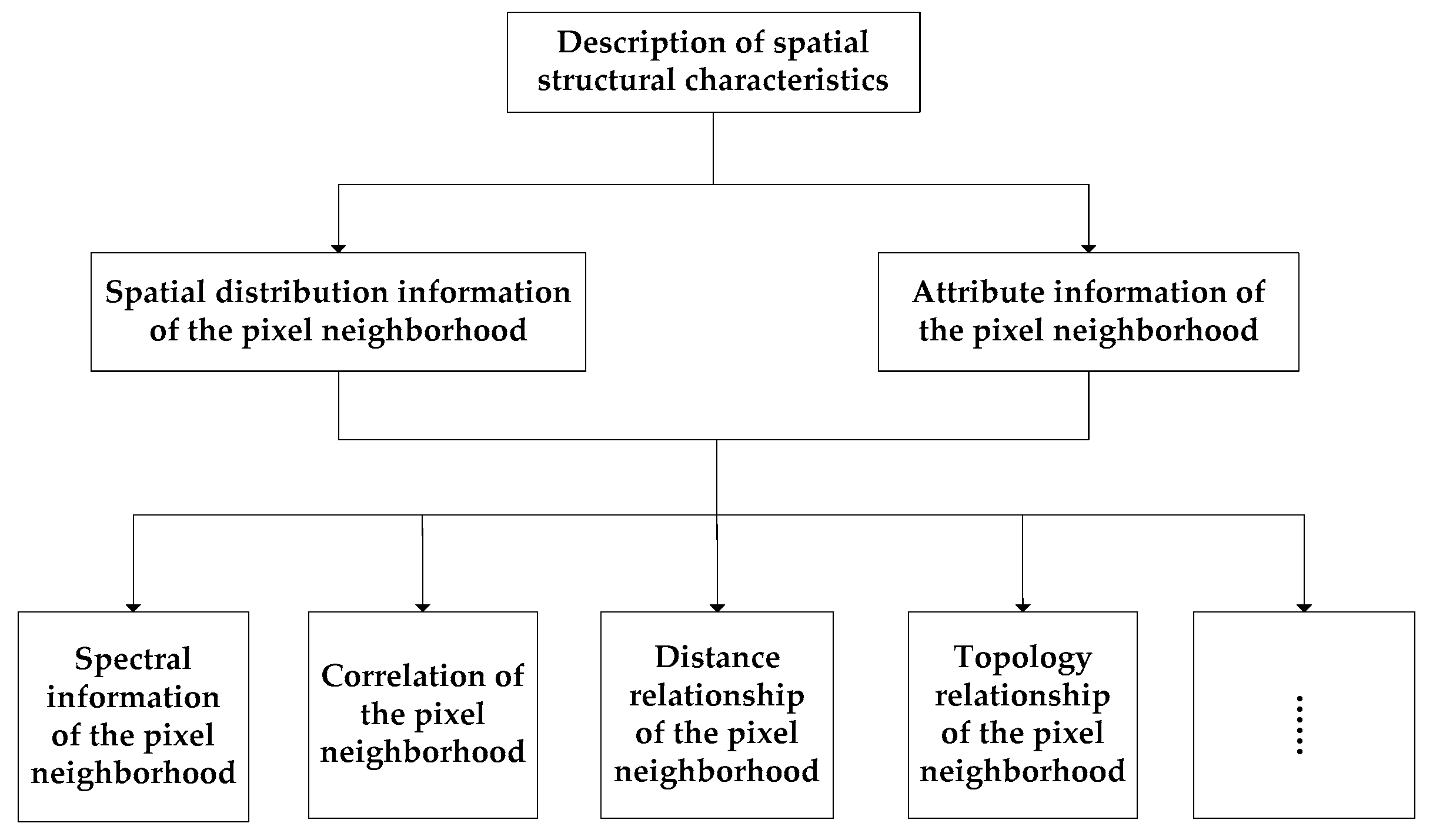
2.2. Spatial Structural Characteristics of Images
2.3. Image Entropy
3. A Multilevel Mapping Strategy-Based Information Measurement Scheme
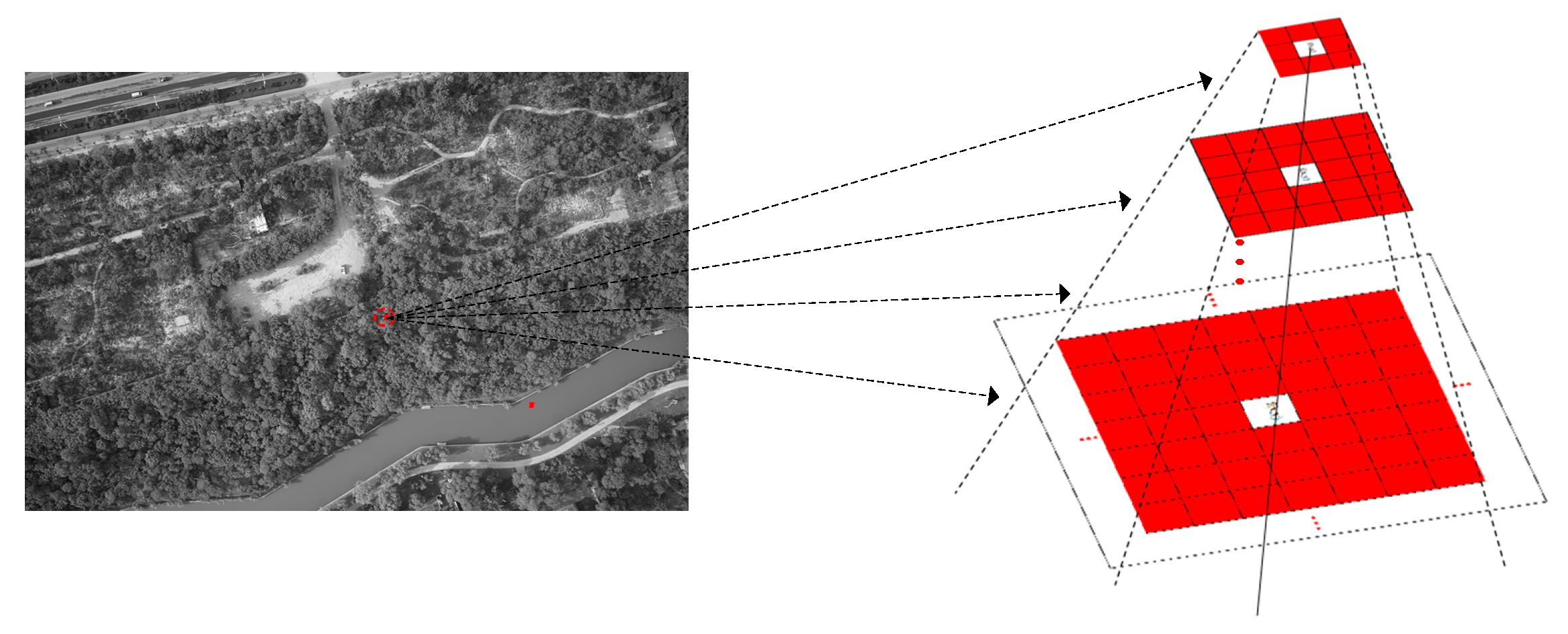
3.1. Multilevel Pixel Neighborhood Model
3.2. A Multilevel Geometrical Mapping Entropy (MGME) Model
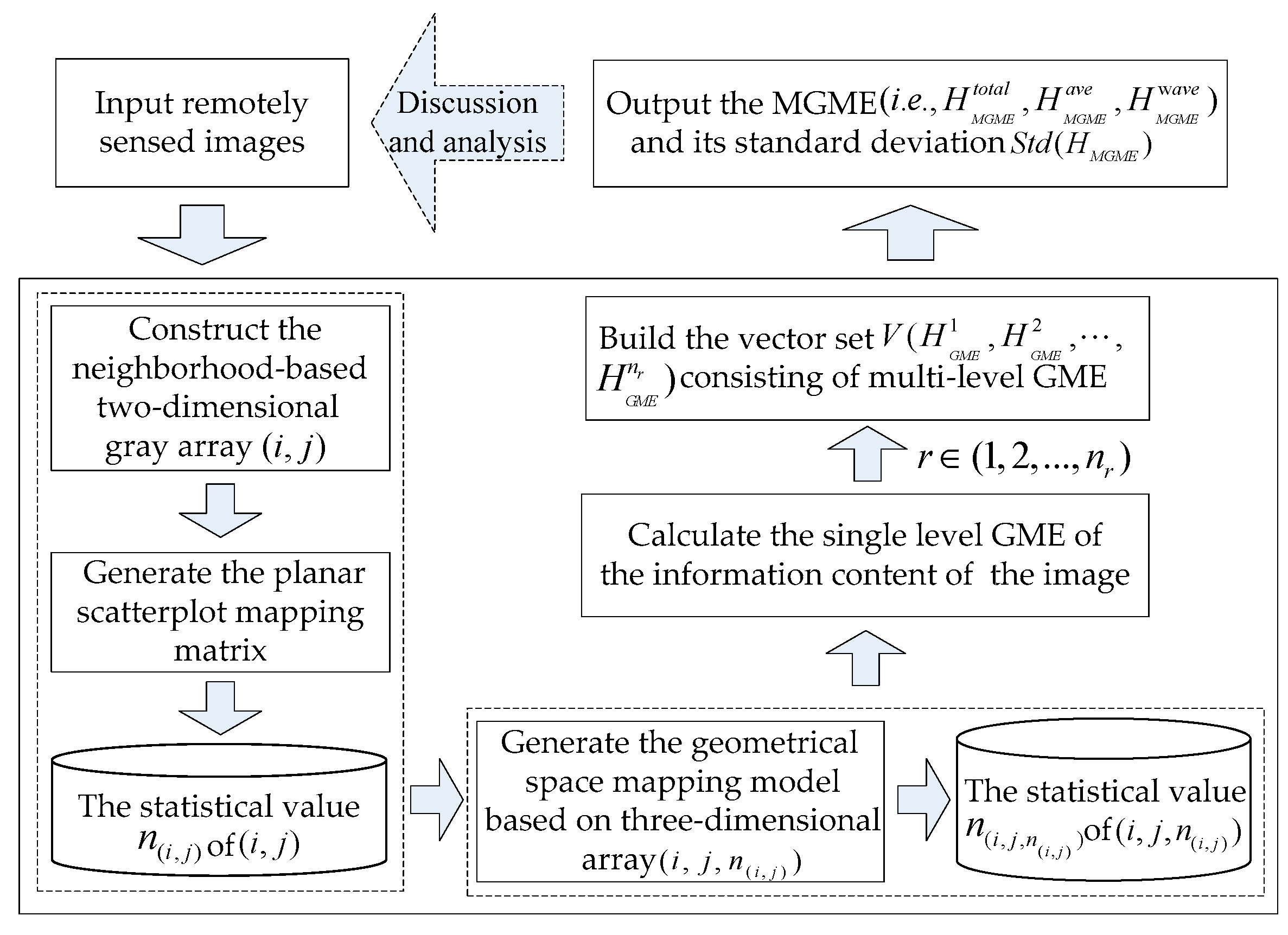
3.2.1. A Multilevel-Mapping-Strategy-Based Measurement Scheme
3.2.2. Description of the MGME Model
4. Experiments and Analysis
- A 0.5 m resolution image of a reservoir area located in the Zhengzhou region, obtained from the DigitalGlobe platform in 2018;
- An image of farmland obtained from the UC Merced Land Use Dataset with USGS National Map Urban Area Imagery in 2010 with 0.3 m resolution [60];
- A UAV image of a local area in the district of the lower and middle reaches of the Yellow River in 2015;
- Landsat TM image of a mountainous region provided by NASA.
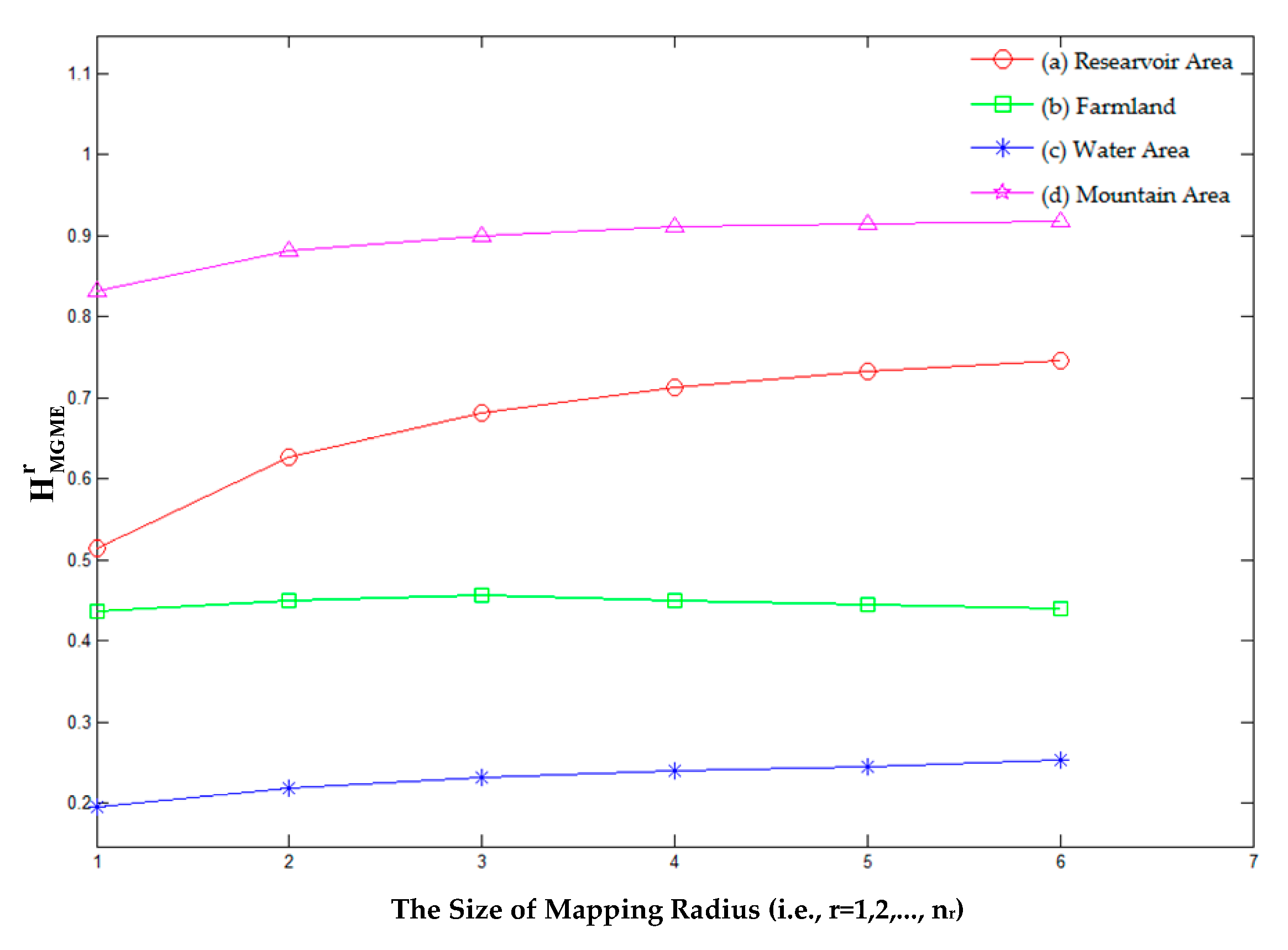
4.1. Experiment 1
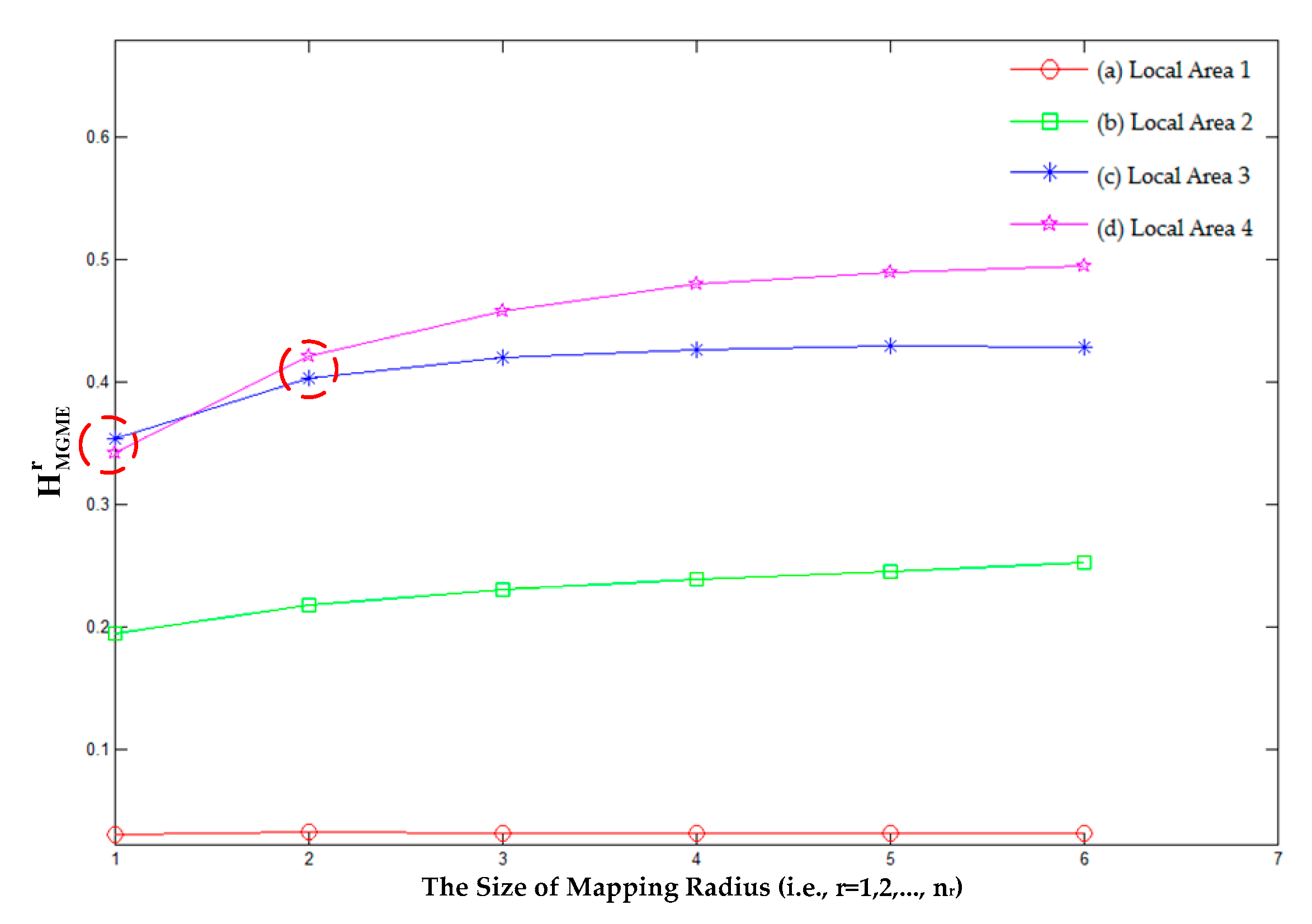
4.2. Experiment 2
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alonso, K.; Datcu, M. Accelerated probabilistic learning concept for mining heterogeneous earth observation images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3356–3371. [Google Scholar] [CrossRef]
- Ma, Y.; Wu, H.; Wang, L.; Huang, B.; Ranjan, R.; Zomaya, A.; Jie, W. Remote sensing big data computing: Challenges and opportunities. Future Generati. Comput. Syst. 2015, 51, 47–60. [Google Scholar] [CrossRef]
- Chen, J.; Dowman, I.; Li, S.; Li, Z.; Madden, M.; Mills, J.; Paparoditis, N.; Rottensteiner, F.; Sester, M.; Toth, C. Information from imagery: ISPRS scientific vision and research agenda. ISPRS J. Photogr. Remote Sens. 2016, 115, 3–21. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Chanussot, J.; Moon, W.M. Very high-resolution remote sensing: Challenges and opportunities [point of view]. Proc. IEEE 2012, 100, 1907–1910. [Google Scholar] [CrossRef]
- Kitchin, R. Big data and human geography: Opportunities, challenges and risks. Dialog. Hum. Geogr. 2013, 3, 262–267. [Google Scholar] [CrossRef]
- Li, Z.; Shen, H.; Li, H.; Xia, G.; Gamba, P.; Zhang, L. Multi-feature combined cloud and cloud shadow detection in GaoFen-1 wide field of view imagery. Remote Sens. Environ. 2017, 191, 342–358. [Google Scholar] [CrossRef]
- Johnson, B.; Xie, Z. Unsupervised image segmentation evaluation and refinement using a multiscale approach. ISPRS J. Photogr. Remote Sens. 2011, 66, 473–483. [Google Scholar] [CrossRef]
- Xie, L.; Li, G.; Xiao, M.; Peng, L. Novel classification method for remote sensing images based on information entropy discretization algorithm and vector space model. Comput. Geosci. 2016, 89, 252–259. [Google Scholar] [CrossRef]
- Ma, C.; Wei, X.; Fu, C.; Liu, J.; Wei, L. A Content-Based Remote Sensing Image Change Information Retrieval Model. ISPRS Int. J. Geo-Inform. 2017, 6, 310. [Google Scholar] [CrossRef]
- Erus, G.; Loménie, N. How to involve structural modeling for cartographic object recognition tasks in high-resolution satellite images? Pattern Recognit. Lett. 2010, 31, 1109–1119. [Google Scholar] [CrossRef]
- Huang, X.; Zhang, L.; Li, P. Classification and extraction of spatial features in urban areas using high-resolution multispectral imagery. IEEE Geosci. Remote Sens. Lett. 2007, 4, 260–264. [Google Scholar] [CrossRef]
- Qin, K.; Chen, Y.; Gan, S.; Feng, X.; Ren, W. Review on methods of spatial structural feature modeling of high resolution remote sensing images. J. Image Gr. 2013, 18, 1055–1064. [Google Scholar]
- Chen, Y.; Qin, K.; Gan, S.; Wu, T. Structural feature modeling of high-resolution remote sensing images using directional spatial correlation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1727–1731. [Google Scholar] [CrossRef]
- Quartulli, M.; Olaizola, I.G. A review of EO image information mining. ISPRS J. Photogr. Remote Sens. 2013, 75, 11–28. [Google Scholar] [CrossRef]
- Tang, X.; Zhang, X.; Liu, F.; Jiao, L. Unsupervised deep feature learning for remote sensing image retrieval. Remote Sens. 2018, 10, 1243. [Google Scholar] [CrossRef]
- Daschiel, H.; Datcu, M. Information mining in remote sensing image archives: System evaluation. IEEE Trans. Geosci. Remote Sens. 2005, 43, 188–199. [Google Scholar] [CrossRef]
- Datcu, M.; Seidel, K.; D′Elia, S.; Marchetti, P. Knowledge-driven information mining in remote-sensing image archives. ESA Bull. 2002, 110, 26–33. [Google Scholar]
- Zhou, W.; Newsam, S.; Li, C.; Shao, Z. PatternNet: A benchmark dataset for performance evaluation of remote sensing image retrieval. ISPRS J. Photogr. Remote Sens. 2018, 145, 197–209. [Google Scholar] [CrossRef]
- Datcu, M.; Daschiel, H.; Pelizzari, A.; Quartulli, M.; Galoppo, A.; Colapicchioni, A.; Pastori, M.; Seidel, K.; Marchetti, P.G.; d′Elia, S. Information mining in remote sensing image archives: System concepts. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2923–2936. [Google Scholar] [CrossRef]
- Tsai, D.-Y.; Lee, Y.; Matsuyama, E. Information entropy measure for evaluation of image quality. J. Digit. Imaging 2008, 21, 338–347. [Google Scholar] [CrossRef]
- Hu, L.; He, Z.; Liu, J.; Zheng, C. Method for measuring the information content of terrain from digital elevation models. Entropy 2015, 17, 7021–7051. [Google Scholar] [CrossRef]
- Malila, W.A. Comparison of the information contents of Landsat TM and MSS data. Photogr. Eng. Remote Sens. 1985, 51, 1449–1457. [Google Scholar]
- Sun, J.; Zhang, X.; Cui, J.; Zhou, L. Image retrieval based on color distribution entropy. Pattern Recognit. Lett. 2006, 27, 1122–1126. [Google Scholar] [CrossRef]
- Li, Z.; Liu, Q.; Gao, P. Entropy-based cartographic communication models: Evolution from special to general cartographic information theory. Acta. Geod. Cartogr. Sin. 2016, 45, 757–767. [Google Scholar]
- Chen, T.M.; Staelin, D.H.; Arps, R.B. Infornation content analysis of landsat image data for compression. IEEE Trans. Geosci. Remote Sens. 1987, GE-25, 499–501. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Y. Measurement of information and uncertainty of remote sensing and GIS data. Geomat. Inf. Sci. Wuhan Univ. 2006, 31, 569–572. [Google Scholar]
- Zhang, Y.; Zhang, J. Measure of information content of remotely sensed images accounting for spatial correlation. Acta Geod. Cartogr. Sin. 2015, 44, 1117–1124. [Google Scholar]
- Blacknell, D.; Oliver, C. Information content of coherent images. J. Phys. D Appl. Phys. 1993, 26, 1364. [Google Scholar] [CrossRef]
- Moore, R.K. Tradeoff between picture element dimensions and noncoherent averaging in side-looking airborne radar. IEEE Trans. Aerosp. Electron. Syst. 1979, AES-15, 697–708. [Google Scholar] [CrossRef]
- Narayanan, R.M.; Desetty, M.; Reichenbach, S. Effect of spatial resolution on information content characterization in remote sensing imagery based on classification accuracy. Int. J. Remote Sens. 2002, 23, 537–553. [Google Scholar] [CrossRef]
- Román-Roldán, R.; Quesada-Molina, J.; Martínez-Aroza, J. Multiresolution-information analysis for images. Signal Process. 1991, 24, 77–91. [Google Scholar] [CrossRef]
- Price, J.C. Comparison of the information content of data from the landsat-4 thematic mapper and the multispectral scanner. IEEE Trans. Geosci. Remote Sens. 1984, GE-22, 272–281. [Google Scholar] [CrossRef]
- Verde, N.; Mallinis, G.; Tsakiri-Strati, M.; Georgiadis, C.; Patias, P. Assessment of radiometric resolution impact on remote sensing data classification accuracy. Remote Sens. 2018, 10, 1267. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Li, Z. A hierarchy-based solution to calculate the configurational entropy of landscape gradients. Landsc. Ecol. 2017, 32, 1133–1146. [Google Scholar] [CrossRef]
- Cushman, S.A. Calculating the configurational entropy of a landscape mosaic. Landsc. Ecol. 2016, 31, 481–489. [Google Scholar] [CrossRef]
- Cushman, S. Calculation of configurational entropy in complex landscapes. Entropy 2018, 20, 298. [Google Scholar] [CrossRef]
- Gao, P.; Zhang, H.; Li, Z. An efficient analytical method for computing the Boltzmann entropy of a landscape gradient. Trans. GIS 2018, 22, 1046–1063. [Google Scholar] [CrossRef]
- Razlighi, Q.R.; Rahman, M.T.; Kehtarnavaz, N. Fast computation methods for estimation of image spatial entropy. J. Real-Time Image Process. 2011, 6, 137–142. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogr. Remote Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Henebry, G.M. Detecting change in grasslands using measures of spatial dependence with Landsat TM data. Remote Sens. Environ. 1993, 46, 223–234. [Google Scholar] [CrossRef]
- Wulder, M.; Boots, B. Local spatial autocorrelation characteristics of remotely sensed imagery assessed with the Getis statistic. Int. J. Remote Sens. 1998, 19, 2223–2231. [Google Scholar] [CrossRef]
- Itti, L.; Koch, C. Computational modelling of visual attention. Nat. Rev. Neurosci. 2001, 2, 194. [Google Scholar] [CrossRef] [PubMed]
- Pelizzari, A.; Descargues, V.; Datcu, M.P. Visual information mining in remote sensing image archives. In Image and Signal Processing for Remote Sensing VII; International Society for Optics and Photonics; SPIE: Philadelphia, PA, USA, 2002; pp. 241–251. [Google Scholar]
- Cheng, H.D.; Sun, Y. A hierarchical approach to color image segmentation using homogeneity. IEEE Trans. Image Process. 2000, 9, 2071–2082. [Google Scholar] [PubMed]
- Puissant, A.; Hirsch, J.; Weber, C. The utility of texture analysis to improve per—pixel classification for high to very high spatial resolution imagery. Int. J. Remote Sens. 2005, 26, 733–745. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Li, Z.; Huang, P. Quantitative measures for spatial information of maps. Int. J. Geogr. Inf. Sci. 2002, 16, 699–709. [Google Scholar] [CrossRef]
- Chen, P.; Shi, W. Measuring the spatial relationship information of multi-layered vector data. ISPRS Int. J. Geo-Inf. 2018, 7, 88. [Google Scholar] [CrossRef]
- Uchida, S.; Tsai, D.Y. Evaluation of radiographic images by entropy: Application to development process. Jpn. J. Appl. Phys. 1978, 17, 2029. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, P.; Xiao, Y. A Modeling and measurement approach for the uncertainty of features extracted from remote sensing images. Remote Sens. 2019, 11, 1841. [Google Scholar] [CrossRef]
- Datcu, M.; Seidel, K.; Walessa, M. Spatial information retrieval from remote-sensing images. I. Information theoretical perspective. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1431–1445. [Google Scholar] [CrossRef]
- Quweider, M. Spatial entropy-based cost function for gray and color Image segmentation with dynamic optimal partitioning. Int. J Comput. Sci. Netw. Secur. 2012, 12, 64. [Google Scholar]
- Akçay, H.G.; Aksoy, S. Automatic detection of geospatial objects using multiple hierarchical segmentations. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2097–2111. [Google Scholar] [CrossRef]
- Bruzzone, L.; Carlin, L. A multilevel context-based system for classification of very high spatial resolution images. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2587–2600. [Google Scholar] [CrossRef]
- Elmqvist, N.; Dragicevic, P.; Fekete, J.D. Rolling the dice: Multidimensional visual exploration using scatterplot matrix navigation. IEEE Trans. Vis. Comput. Gr. 2008, 14, 1539–1148. [Google Scholar] [CrossRef]
- Sedlmair, M.; Munzner, T.; Tory, M. Empirical guidance on scatterplot and dimension reduction technique choices. IEEE Trans. V. Comput. Gr. 2013, 19, 2634–2643. [Google Scholar] [CrossRef]
- Touchette, P.E.; MacDonald, R.F.; Langer, S.N. A scatter plot for identifying stimulus control of problem behavior. J. Appl. Behave. Anal. 1985, 18, 343–351. [Google Scholar] [CrossRef]
- Bovolo, F. A multilevel parcel-based approach to change detection in very high resolution multitemporal images. IEEE Geosci. Remote Sens. Lett. 2008, 6, 33–37. [Google Scholar] [CrossRef]
- Yang, Y.; Newsam, S. Geographic image retrieval using local invariant features. IEEE Trans. Geosci. Remote Sens. 2013, 51, 818–832. [Google Scholar] [CrossRef]
- Franklin, S.; Wulder, M.; Lavigne, M. Automated derivation of geographic window sizes for use in remote sensing digital image texture analysis. Comput. Geosci. 1996, 22, 665–673. [Google Scholar] [CrossRef]
- Li, D.; Wang, S.; Li, D. Spatial Data Mining Theories and Application; Springer: Beijing, China, 2015. [Google Scholar]

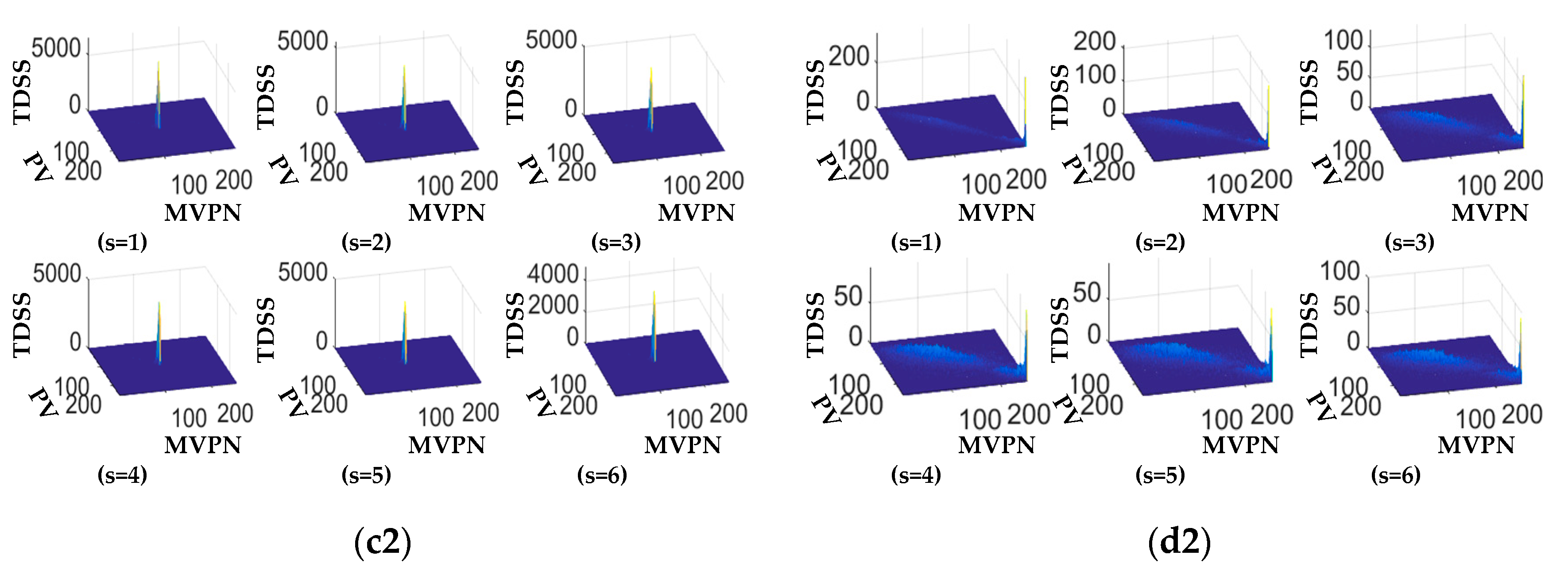

| Experimental Images | Traditional Method | Multilevel Geometrical Mapping Entropy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r = 1 | r = 2 | r = 3 | r = 4 | r = 5 | r = 6 | ||||||
| (a) Reservoir Area | 7.193 | 0.514 | 0.626 | 0.681 | 0.713 | 0.732 | 0.745 | 0.669 | 0.678 | 4.011 | 0.079 |
| (b) Farmland | 6.432 | 0.436 | 0.450 | 0.456 | 0.450 | 0.445 | 0.440 | 0.446 | 0.460 | 2.667 | 0.007 |
| (c) Water Area | 4.425 | 0.195 | 0.218 | 0.231 | 0.239 | 0.245 | 0.253 | 0.230 | 0.232 | 1.381 | 0.019 |
| (d) Mountain Area | 7.827 | 0.832 | 0.882 | 0.899 | 0.911 | 0.915 | 0.917 | 0.893 | 0.894 | 5.356 | 0.030 |
| Experimental Images | Traditional Method | Multilevel Geometrical Mapping Entropy | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| r = 1 | r = 2 | r = 3 | r = 4 | r = 5 | r = 6 | ||||||
| (a) Local Area 1 | 3.097 | 0.030 | 0.032 | 0.032 | 0.032 | 0.032 | 0.032 | 0.032 | 0.032 | 0.190 | 0.001 |
| (b) Local Area 2 | 4.425 | 0.195 | 0.218 | 0.231 | 0.239 | 0.245 | 0.253 | 0.230 | 0.232 | 1.381 | 0.019 |
| (c) Local Area 3 | 5.595 | 0.354 | 0.403 | 0.421 | 0.427 | 0.430 | 0.429 | 0.411 | 0.412 | 2.464 | 0.027 |
| (a) Local Area 1 | 5.550 | 0.342 | 0.442 | 0.458 | 0.480 | 0.490 | 0.496 | 0.448 | 0.454 | 2.688 | 0.053 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, S.; Zhou, X.; Zhang, J. A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery. ISPRS Int. J. Geo-Inf. 2019, 8, 464. https://doi.org/10.3390/ijgi8100464
Fang S, Zhou X, Zhang J. A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery. ISPRS International Journal of Geo-Information. 2019; 8(10):464. https://doi.org/10.3390/ijgi8100464
Chicago/Turabian StyleFang, Shimin, Xiaoguang Zhou, and Jing Zhang. 2019. "A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery" ISPRS International Journal of Geo-Information 8, no. 10: 464. https://doi.org/10.3390/ijgi8100464
APA StyleFang, S., Zhou, X., & Zhang, J. (2019). A Multilevel Mapping Strategy to Calculate the Information Content of Remotely Sensed Imagery. ISPRS International Journal of Geo-Information, 8(10), 464. https://doi.org/10.3390/ijgi8100464






