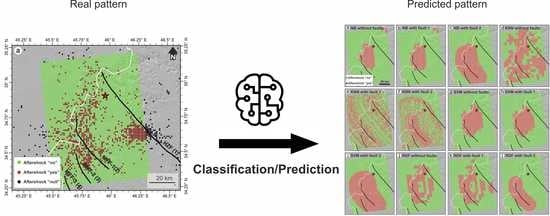
Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective
Abstract
1. Introduction
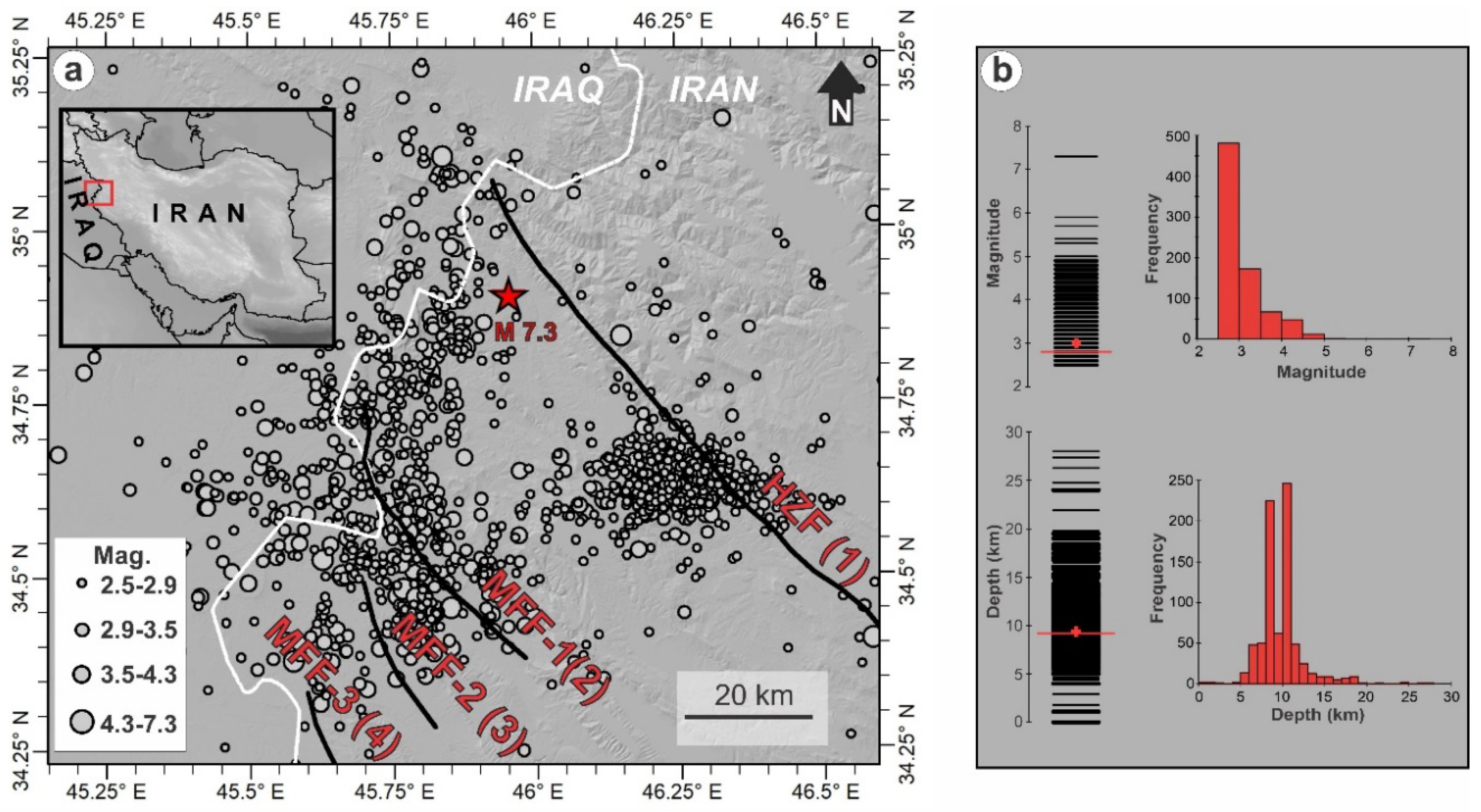
2. Pilot Area and Data
2.1. Aftershocks
2.2. Slip Distribution, Coulomb Stress Change, and Fault Maps
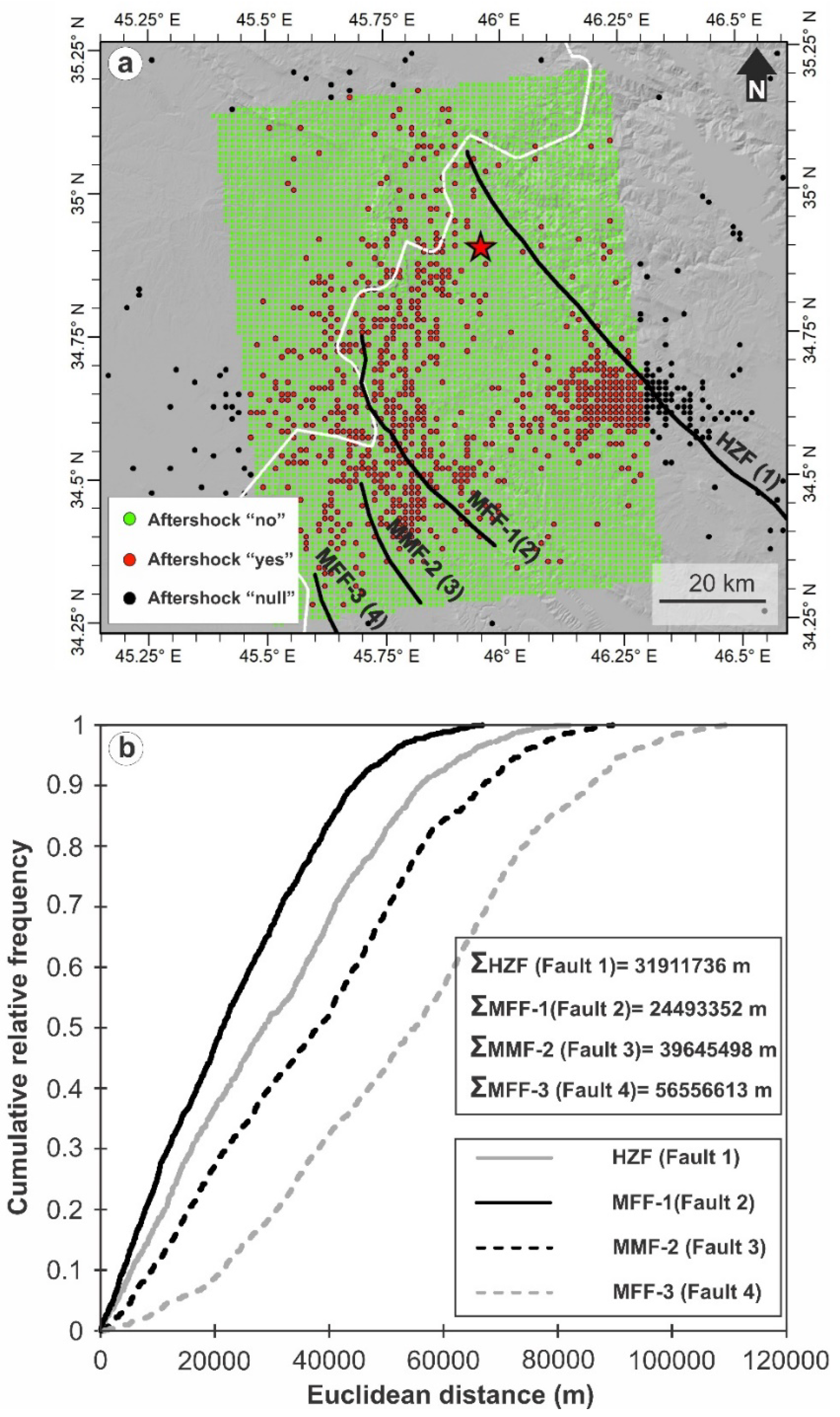
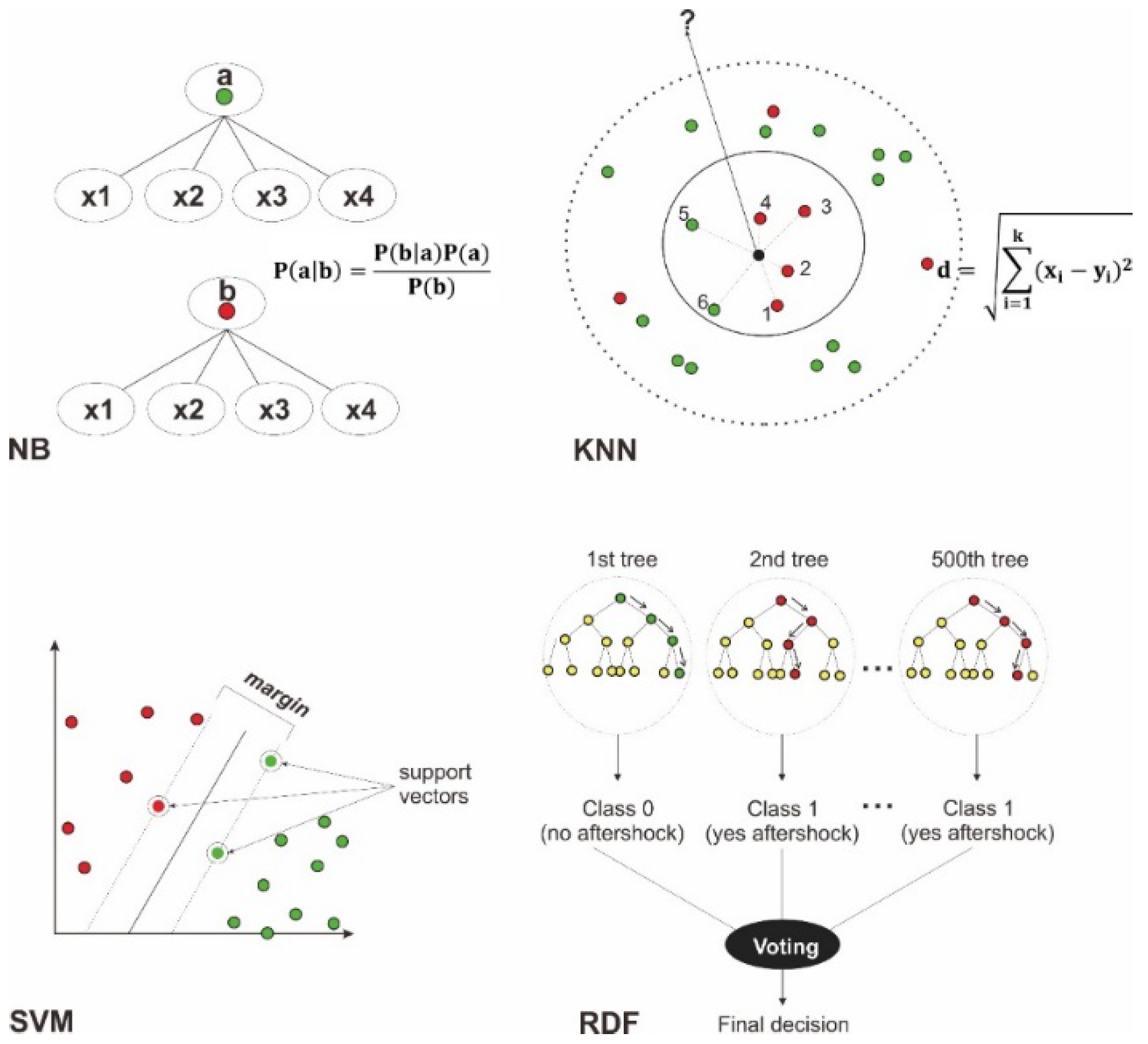
3. Binary Aftershock Map and Classification
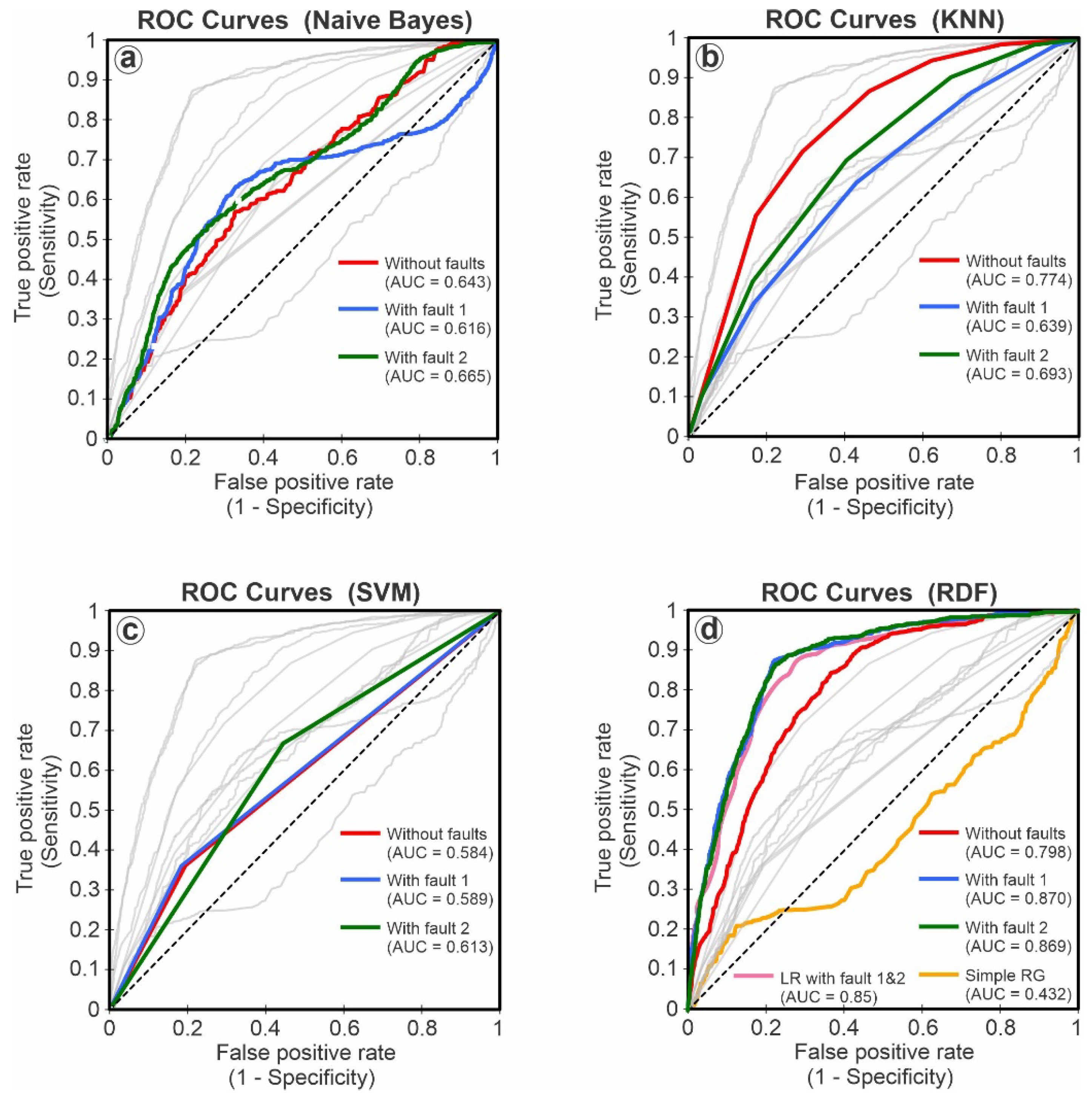
4. Results and Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jia, Y.; Ma, J. What can machine learning do for seismic data processing? An interpolation application. Geophysics 2017, 82, V163–V177. [Google Scholar] [CrossRef]
- Asim, K.M.; Idris, A.; Iqbal, T.; Martínez-Álvarez, F. Earthquake prediction model using support vector regressor and hybrid neural networks. PLoS ONE 2018, 13, e0199004. [Google Scholar] [CrossRef] [PubMed]
- Kong, Q.; Trugman, D.T.; Ross, Z.E.; Bianco, M.J.; Meade, B.J.; Gerstoft, P. Machine Learning in Seismology: Turning Data into Insights. Seismol. Res. Lett. 2018, 90, 3–14. [Google Scholar] [CrossRef]
- Kortström, J.; Uski, M.; Tiira, T. Automatic classification of seismic events within a regional seismograph network. Comput. Geosci. 2016, 87, 22–30. [Google Scholar] [CrossRef]
- Che, I.-Y.; Jun, M.-S.; Jeon, J.-S. A compound linear discriminant method for small-magnitude seismic events and its application to the North Korea seismic event of October 9, 2006. Earth Planets Space 2007, 59, e41–e44. [Google Scholar] [CrossRef][Green Version]
- Lyubushin, A.; Kaláb, Z.; Lednická, M.; Mohamed, H. Discrimination of earthquakes and explosions using multi-fractal singularity spectrums properties. J. Seismol. 2013, 17, 975–983. [Google Scholar] [CrossRef]
- Rouet-Leduc, B.; Hulbert, C.; Lubbers, N.; Barros, K.; Humphreys, C.J.; Johnson, P.A. Machine learning predicts laboratory earthquakes. Geophys. Res. Lett. 2017, 44, 9276–9282. [Google Scholar] [CrossRef]
- Panakkat, A.; Adeli, H. Recurrent neural network for approximate earthquake time and location prediction using multiple seismicity indicators. Comput. Aided Civ. Infrastruct. Eng. 2009, 24, 280–292. [Google Scholar] [CrossRef]
- Zamani, A.; Sorbi, M.R.; Safavi, A.A. Application of neural network and ANFIS model for earthquake occurrence in Iran. Earth Sci. Inform. 2013, 6, 71–85. [Google Scholar] [CrossRef]
- DeVries, P.M.R.; Viégas, F.; Wattenberg, M.; Meade, B.J. Deep learning of aftershock patterns following large earthquakes. Nature 2018, 560, 632–634. [Google Scholar] [CrossRef]
- Mignan, A.; Broccardo, M. One neuron versus deep learning in aftershock prediction. Nature 2019, 574, E1–E3. [Google Scholar] [CrossRef] [PubMed]
- Karimzadeh, S.; Matsuoka, M.; Miyajima, M.; Adriano, B.; Fallahi, A.; Karashi, J. Sequential SAR coherence method for the monitoring of buildings in Sarpole-Zahab, Iran. Remote Sens. 2018, 10, 1255. [Google Scholar] [CrossRef]
- Miyajima, M.; Fallahi, A.; Ikemoto, T.; Samaei, M.; Karimzadeh, S.; Setiawan, H.; Talebi, F.; Karashi, J. Site investigation of the Sarpole-Zahab earthquake, Mw 7.3 in SW Iran of November 12, 2017. JSCE J. Disaster FactSheets 2018, FS2018-E-0002. Available online: http://committees.jsce.or.jp/disaster/system/files/FS2018-E0002_0.pdf (accessed on 10 October 2019).
- Global Centroid Moment Tensor (GCMT). Global CMT Catalog Search. Available online: https://www.globalcmt.org/CMTsearch.html (accessed on 11 October 2018).
- United States Geological Survey. Mw 7.3—Iran/Iraq border. Available online: https://www.usgs.gov/news/magnitude-73-earthquake-iraniraq-border (accessed on 11 October 2018).
- Kuang, J.; Ge, L.; Metternicht, G.I.; Ng, A.H.-M.; Wang, H.; Zare, M.; Kamranzad, F. Coseismic deformation and source model of the 12 November 2017 MW 7.3 Kermanshah Earthquake (Iran–Iraq border) investigated through DInSAR measurements. Int. J. Remote Sens. 2018, 40, 532–554. [Google Scholar] [CrossRef]
- Vajedian, S.; Motagh, M.; Mousavi, Z.; Motaghi, K.; Fielding, E.; Akbari, B.; Wetzel, H.-U.; Darabi, A. Coseismic deformation field of the Mw 7.3 12 November 2017 Sarpol-e Zahab (Iran) earthquake: A decoupling horizon in the Northern Zagros Mountains inferred from InSAR observations. Remote Sens. 2018, 10, 1589. [Google Scholar] [CrossRef]
- Yang, Y.H.; Hu, J.C.; Yassaghi, A.; Tsai, M.C.; Zare, M.; Chen, Q.; Wang, Z.G.; Rajabi, A.M.; Kamranzad, F. Midcrustal thrusting and vertical deformation partitioning constraint by 2017 Mw 7.3 Sarpol Zahab earthquake in Zagros Mountain belt, Iran. Seismol. Res. Lett. 2018, 89, 2204–2213. [Google Scholar] [CrossRef]
- Okada, Y. Surface deformation due to shear and tensile faults in a half-space. Bull. Seismol. Soc. Am. 1985, 75, 1135–1154. [Google Scholar]
- Atzori, S.; Hunstad, I.; Chini, M.; Salvi, S.; Tolomei, C.; Bignami, C.; Stramondo, S.; Trasatti, E.; Antonioli, A.; Boschi, E. Finite fault inversion of DInSAR coseismic displacement of the 2009 L’Aquila earthquake (Central Italy). Geophys. Res. Lett. 2009, 36, L15305. [Google Scholar] [CrossRef]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Harris, R.A. Introduction to special section: Stress triggers, stress shadows, and implications for seismic hazard. J. Geophys. Res. Solid Earth 1998, 103, 24347–24358. [Google Scholar] [CrossRef]
- Nostro, C.; Belardinelli, M.E.; Cocco, M. Static stress changes in extensional regimes: An application to Southern Apennines (Italy). Bull. Seismol. Soc. Am. 1997, 87, 234–248. [Google Scholar]
- Parsons, T.; Stein, R.S.; Simpson, R.W.; Reasenberg, P.A. Stress sensitivity of fault seismicity: A comparison between limited-offset oblique and major strike-slip faults. J. Geophys. Res. Solid Earth 1999, 104, 20183–20202. [Google Scholar] [CrossRef]
- Stein, R.S.; Barka, A.A.; Dieterich, J.H. Progressive failure on the North Anatolian fault since 1939 by earthquake stress triggering. Geophys. J. Int. 1997, 128, 594–604. [Google Scholar] [CrossRef]
- Toda, S.; Stein, R.S.; Reasenberg, P.A.; Dieterich, J.H.; Yoshida, A. Stress transferred by the 1995 Mw = 6.9 Kobe, Japan, shock: Effect on aftershocks and future earthquake probabilities. J. Geophys. Res. Solid Earth 1998, 103, 24543–24565. [Google Scholar] [CrossRef]
- Hardebeck, J.L.; Nazareth, J.J.; Hauksson, E. The static stress change triggering model: Constraints from two Southern California aftershock sequences. J. Geophys. Res. 1998, 1032, 24427–24438. [Google Scholar] [CrossRef]
- Mallman, E.P.; Zoback, M.D. Assessing elastic coulomb stress transfer models using seismicity rates in southern California and Southwestern Japan. J. Geophys. Res. 2007, 112, B03304. [Google Scholar] [CrossRef]
- Hessami, K.; Jamali, F.; Tabassi, H. Major Active Faults of Iran; International Institute of Earthquake Engineering and Seismology: Tehran, Iran, 2003. [Google Scholar]
- Vapnik, V. Estimation of Dependences Based on Empirical Data; Springer: New York, NY, USA, 1979. [Google Scholar]
- Motevalli, A.; Pourghasemi, H.R.; Zabihi, M. Assessment of GIS-based machine learning algorithms for spatial modeling of landslide susceptibility: Case study in Iran. Ref. Modul. Earth Syst. Environ. Sci. 2018, 258–276. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Wieland, M.; Liu, W.; Yamazaki, F. Learning change from synthetic aperture radar images: Performance evaluation of a support vector machine to detect earthquake and Tsunami-induced changes. Remote Sens. 2016, 8, 792. [Google Scholar] [CrossRef]
- Platt, J. Sequential minimal optimization: A fast algorithm for training support vector machines. CiteSeerX 1998. Available online: https://www.semanticscholar.org/paper/Sequential-Minimal-Optimization%3A-A-Fast-Algorithm-Platt/53fcc056f79e04daf11eb798a7238e93699665aa (accessed on 10 October 2019).
- Breiman, L.; Friedman, J.; Olshen, R.; Stone, C. Classification and Regression Trees; Chapman and Hall, Wadsworth: New York, NY, USA, 1984. [Google Scholar]


| Logistic Regression (LR) | Naive Bayes (NB) | K-Nearest Neighbor (KNN) | Support Vector Machine (SVM) | Random Forest (RDF) | |
|---|---|---|---|---|---|
| Without Fault | - | OA 78% | OA 58% | OA 74% | OA 73% |
| With Fault 1 | OA 74% | OA 78% | OA 58% | OA 75% | OA 76% |
| With Fault 2 | OA 74% | OA 65% | OA 61% | OA 57% | OA 75% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karimzadeh, S.; Matsuoka, M.; Kuang, J.; Ge, L. Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective. ISPRS Int. J. Geo-Inf. 2019, 8, 462. https://doi.org/10.3390/ijgi8100462
Karimzadeh S, Matsuoka M, Kuang J, Ge L. Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective. ISPRS International Journal of Geo-Information. 2019; 8(10):462. https://doi.org/10.3390/ijgi8100462
Chicago/Turabian StyleKarimzadeh, Sadra, Masashi Matsuoka, Jianming Kuang, and Linlin Ge. 2019. "Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective" ISPRS International Journal of Geo-Information 8, no. 10: 462. https://doi.org/10.3390/ijgi8100462
APA StyleKarimzadeh, S., Matsuoka, M., Kuang, J., & Ge, L. (2019). Spatial Prediction of Aftershocks Triggered by a Major Earthquake: A Binary Machine Learning Perspective. ISPRS International Journal of Geo-Information, 8(10), 462. https://doi.org/10.3390/ijgi8100462