A Relief Dependent Evaluation of Digital Elevation Models on Different Scales for Northern Chile
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Global Digital Elevation Models (GDEMs)
3.1.1. Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) GDEM
3.1.2. Advanced Land Observing Satellite (ALOS) World 3D
3.1.3. Shuttle Radar Topography Mission (SRTM)
3.1.4. TanDEM-X World DEM ™
3.2. Local Digital Elevation Models
3.2.1. Pléiades
3.2.2. Satellite Pour l’Observation de la Terre (SPOT) 6/7
3.3. Ground Truth Elevation Data
3.3.1. Ice, Cloud, and Land Elevation satellite (ICESat)
3.3.2. ICESat-2
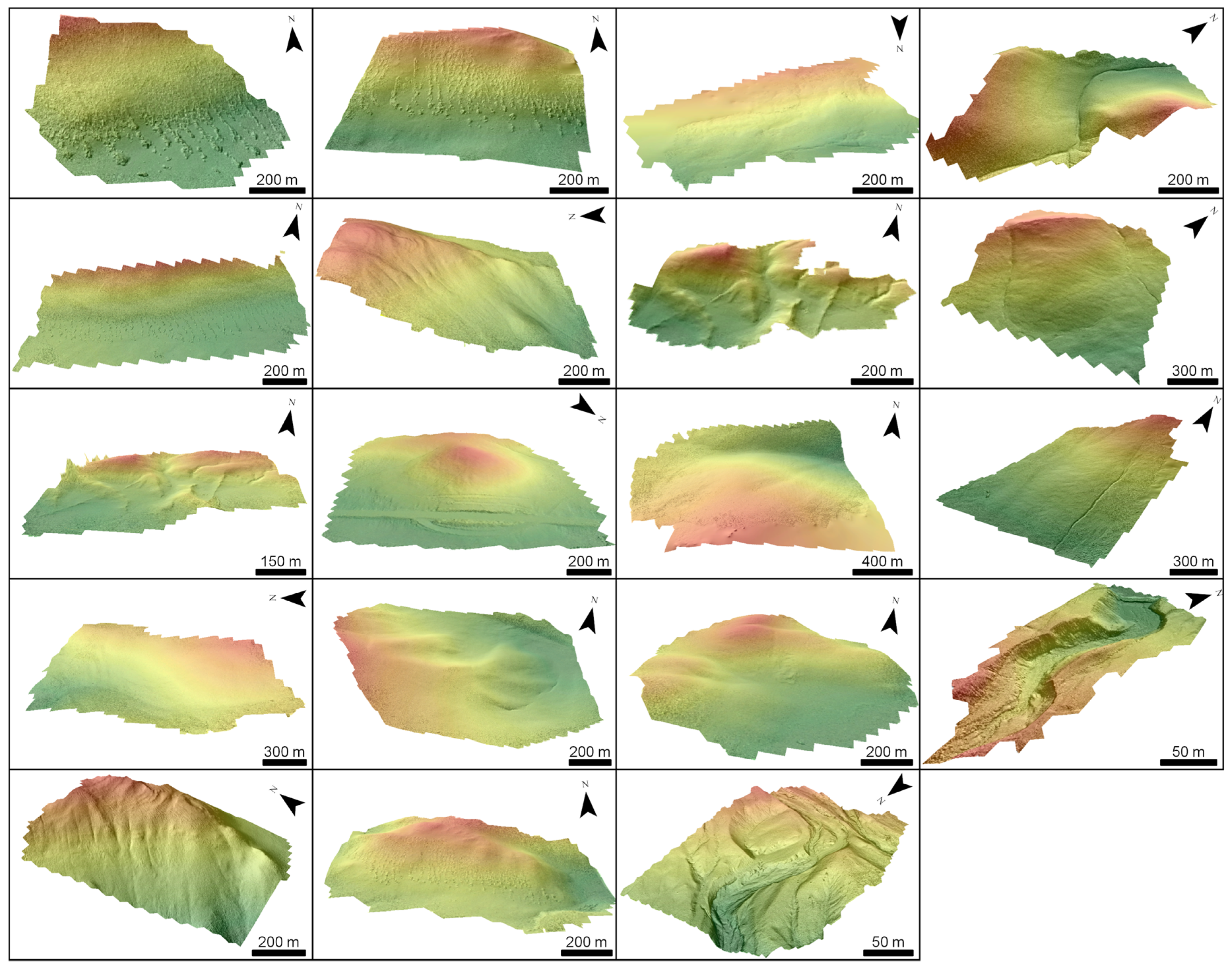
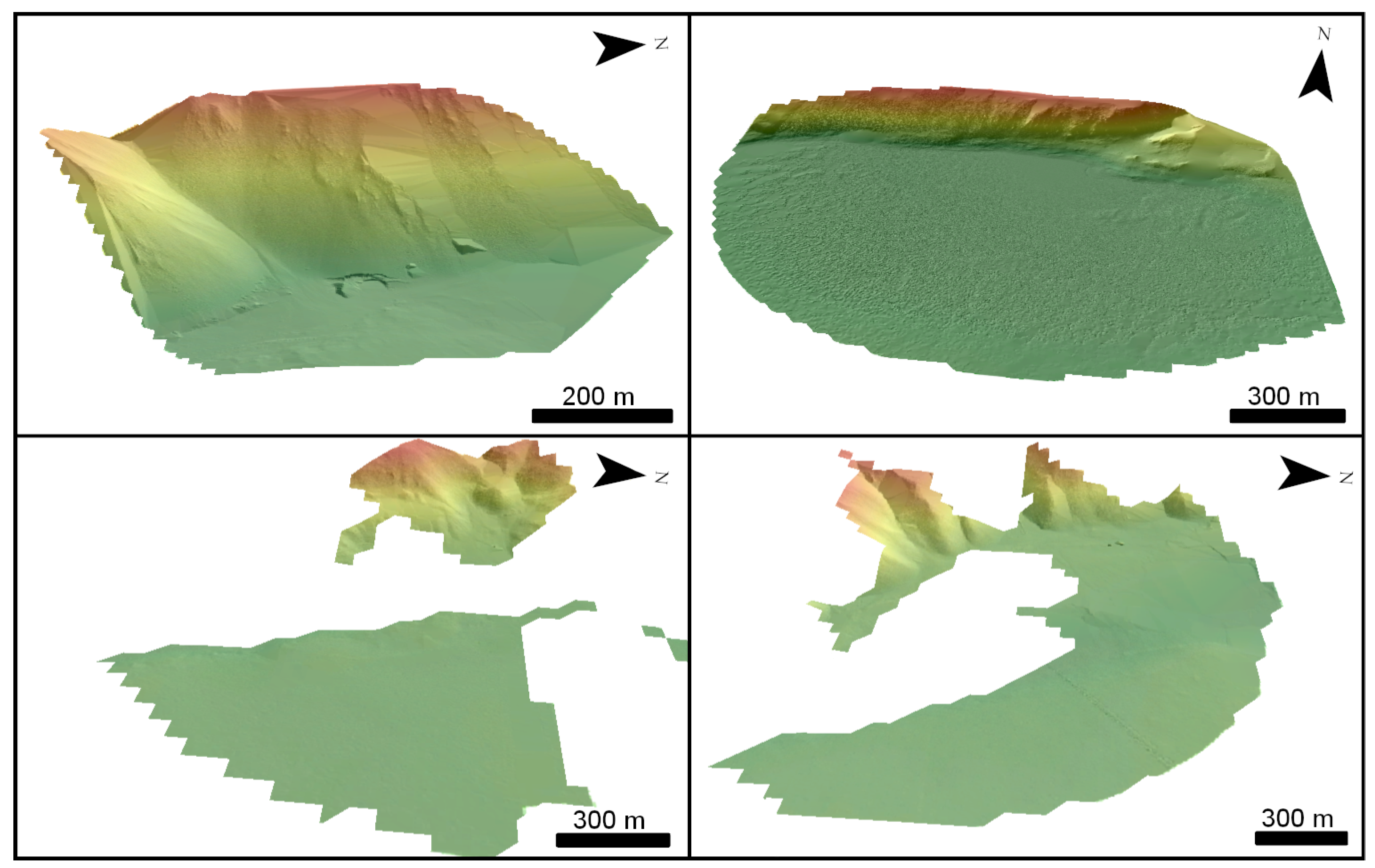
3.3.3. Very High-Resolution DEMs Derived by Unmanned Aerial Vehicle (UAV)
3.3.4. Terrestrial Laser Scanning
3.4. Accuracy Assessment
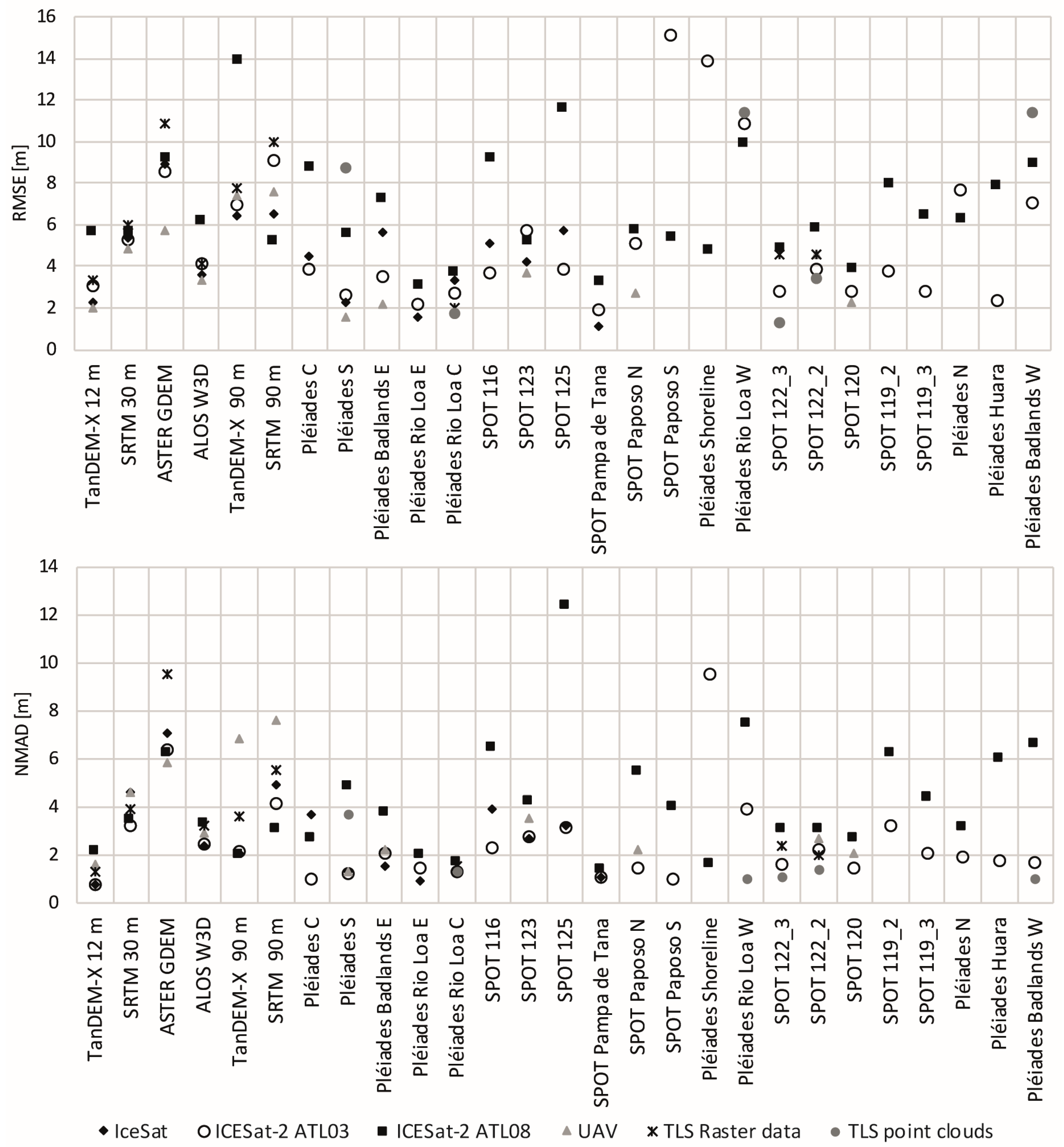
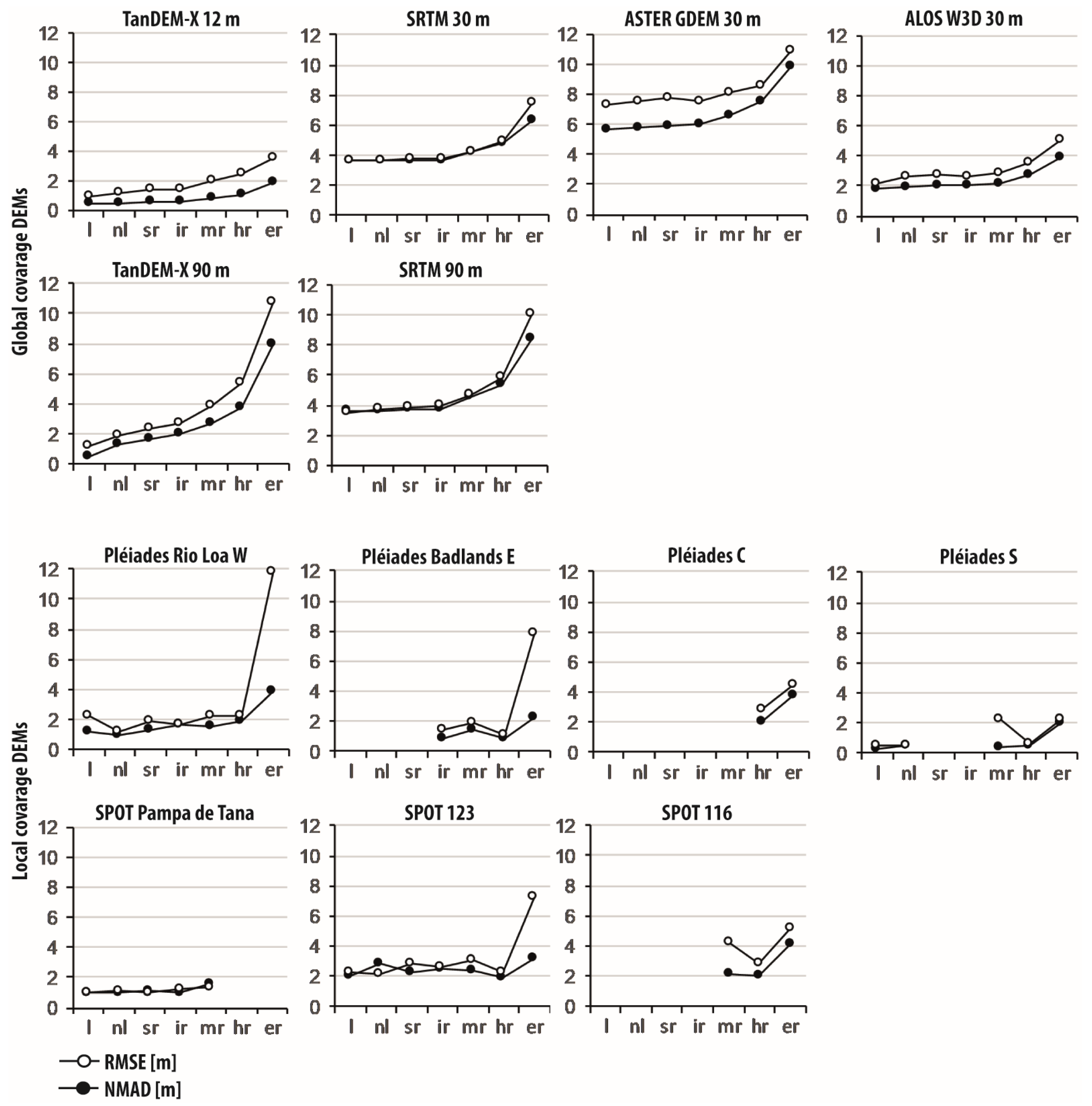
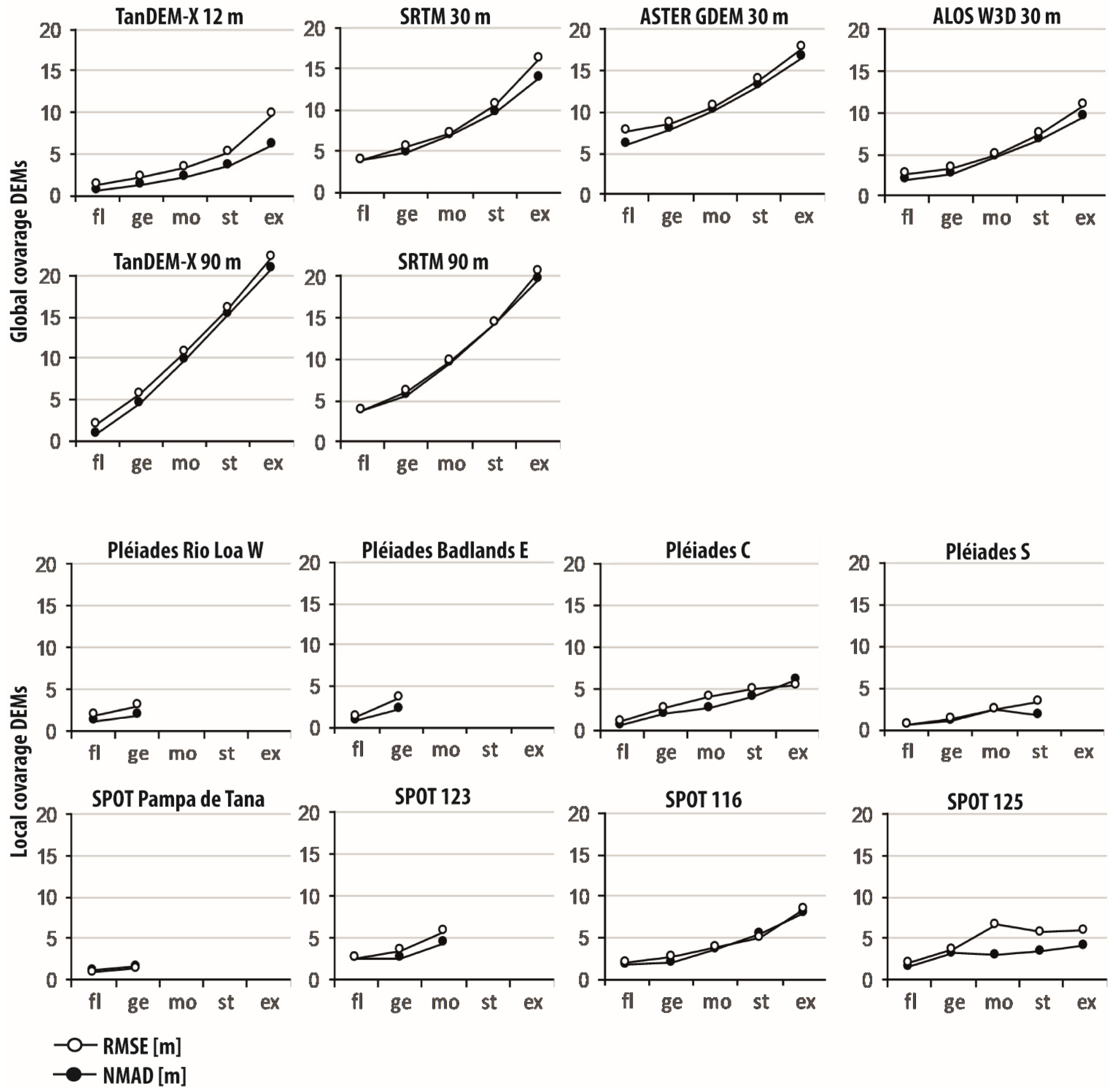
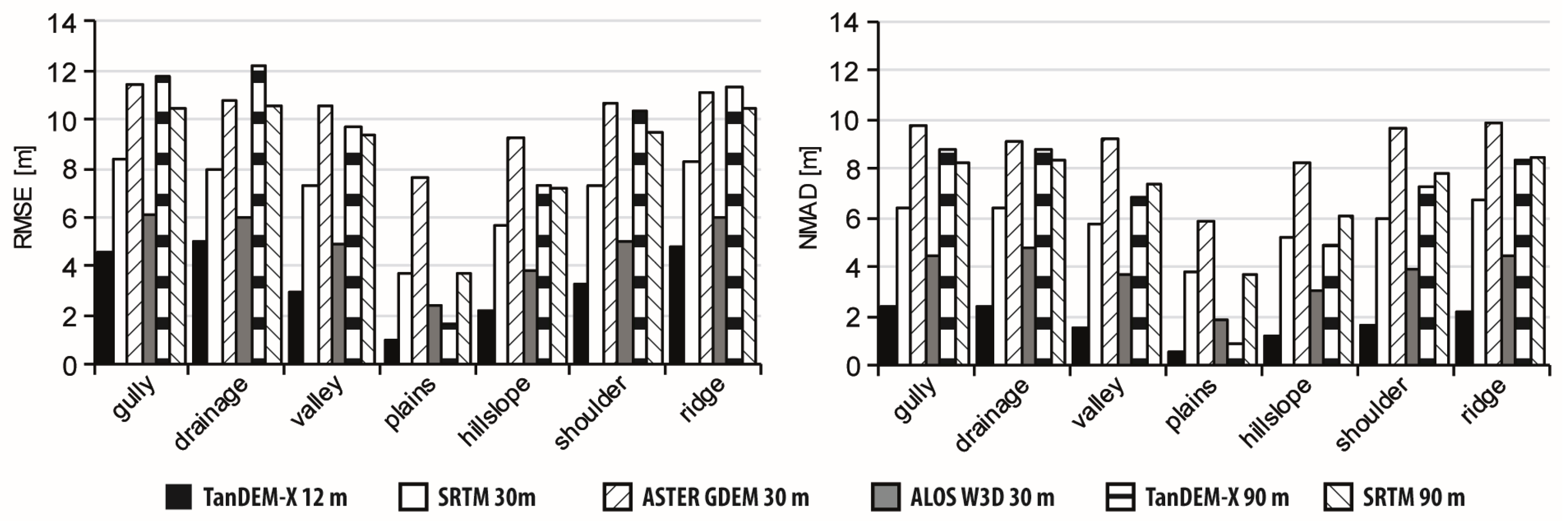
4. Results
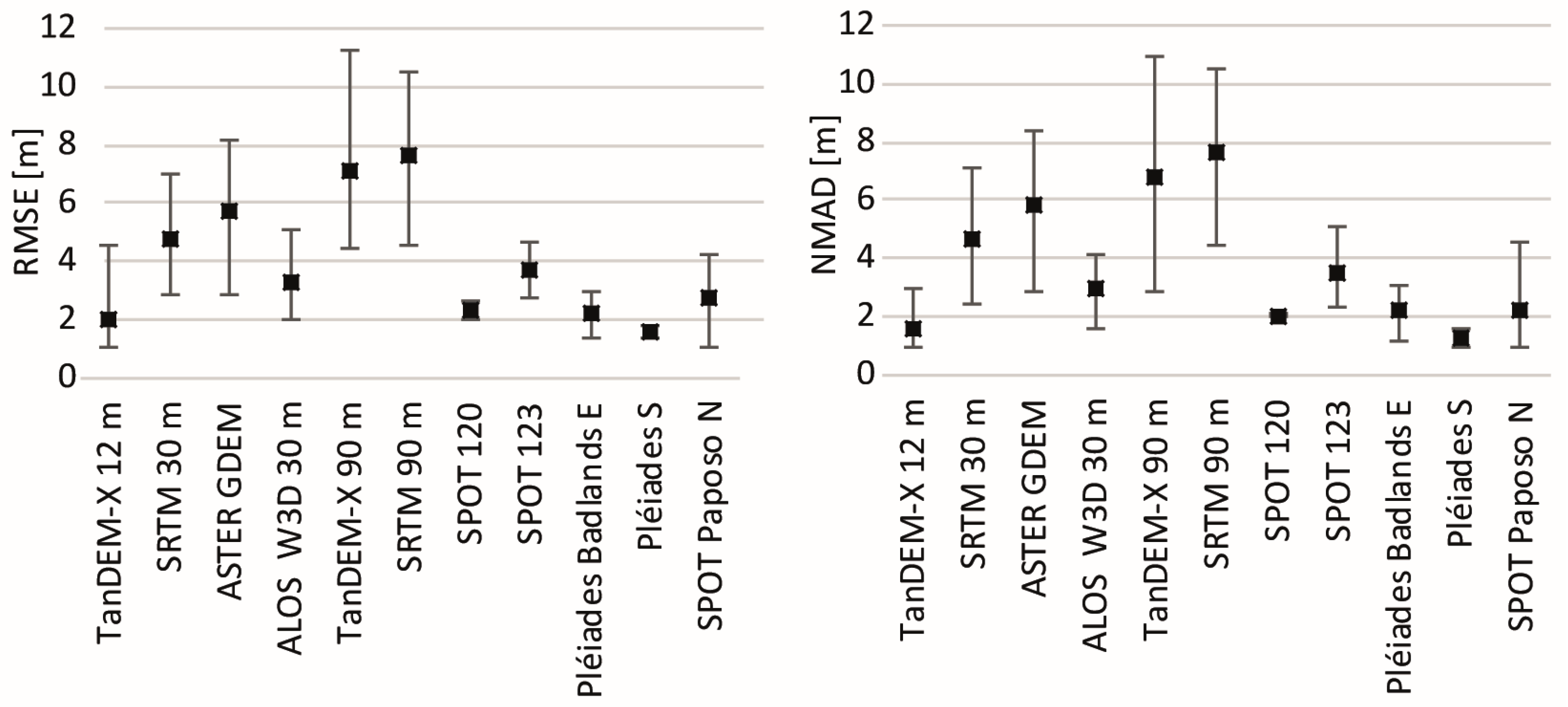
4.1. Overall Accuracies
4.2. Terrain-Dependent Accuracies
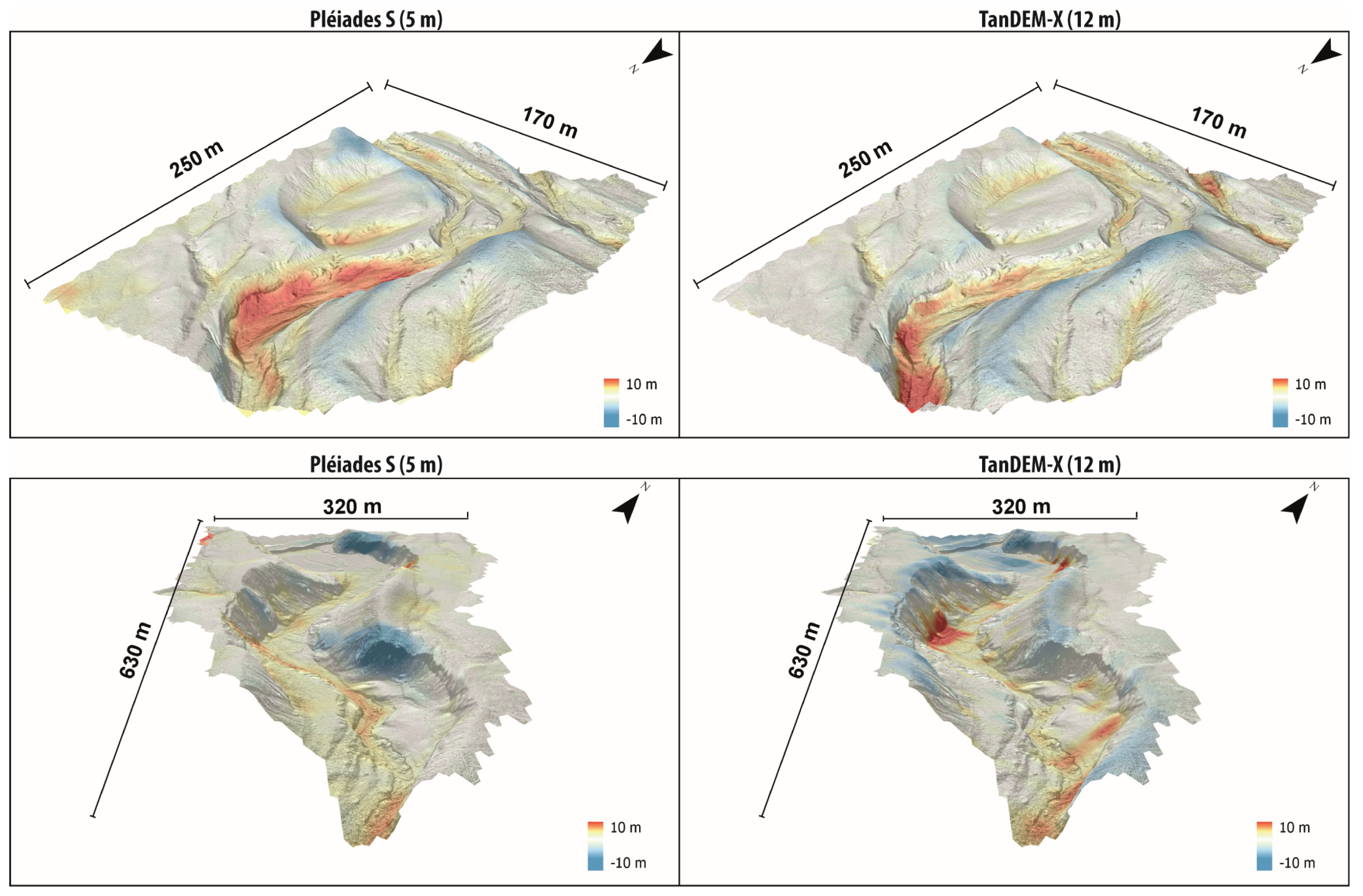
4.3. Local-Scale Evaluation
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| ICESat | ICESat-2 ATL03 | ICESat-2 ATL08 | UAV DEMs | TLS Raster Data | TLS Point Clouds | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DEM | GSD | RMSE [m] | NMAD [m] | No. Points | RMSE [m] | NMAD [m] | No. Points | RMSE [m] | NMAD [m] | No. Points | RMSE [m] | NMAD [m] | No. Rasters | RMSE [m] | NMAD [m] | No. Rasters | RMSE [m] | NMAD [m] | No. Points |
| TanDEM-X | 12m | 2.3 | 0.8 | 453434 | 3.1 | 0.8 | 392333 | 5.7 | 2.2 | 643926 | 2.0 | 1.6 | 19 | 3.3 | 1.3 | 4 | - | - | - |
| SRTM | 30m | 5.4 | 4.6 | 453434 | 5.3 | 3.2 | 392333 | 5.7 | 3.5 | 643926 | 4.8 | 4.6 | 19 | 6.0 | 3.9 | 4 | - | - | - |
| ASTER GDEM | 30m | 8.9 | 7.1 | 453434 | 8.6 | 6.4 | 392333 | 9.2 | 6.2 | 643926 | 5.7 | 5.8 | 19 | 10.9 | 9.5 | 4 | - | - | - |
| ALOS W3D | 30m | 3.6 | 2.4 | 447372 | 4.1 | 2.4 | 392043 | 6.2 | 3.3 | 636761 | 3.3 | 2.9 | 19 | 4.1 | 3.2 | 4 | - | - | - |
| TanDEM -X | 90m | 6.4 | 2.1 | 453434 | 7.0 | 2.1 | 392333 | 13.9 | 2.0 | 643926 | 7.4 | 6.8 | 19 | 7.8 | 3.6 | 4 | - | - | - |
| SRTM | 90m | 6.5 | 4.9 | 453434 | 9.1 | 4.1 | 392333 | 5.2 | 3.0 | 643926 | 7.6 | 7.6 | 19 | 10.0 | 5.5 | 4 | - | - | - |
| Pléiades C | 5m | 4.5 | 3.7 | 629 | 3.9 | 1.0 | 11796 | 8.8 | 2.7 | 67 | - | - | - | - | - | - | - | - | - |
| Pléiades S | 5m | 2.3 | 1.3 | 273 | 2.6 | 1.2 | 9852 | 5.6 | 4.8 | 154 | 1.6 | 1.3 | 2 | - | - | - | 8.7 | 3.6 | 1004405 |
| Pléiades Badlands E | 5m | 5.6 | 1.5 | 158 | 3.5 | 2.1 | 12131 | 7.3 | 3.8 | 244 | 2.2 | 2.2 | 4 | - | - | - | - | - | - |
| Pléiades Rio Loa E | 5m | 1.6 | 0.9 | 634 | 2.2 | 1.4 | 271078 | 3.1 | 2.0 | 1819 | - | - | - | - | - | - | - | - | - |
| Pléiades Rio Loa C | 5m | 3.3 | 1.4 | 475 | 2.7 | 1.3 | 124934 | 3.7 | 1.7 | 1057 | - | - | - | 2.0 | 1.5 | 1 | 1.7 | 1.2 | 242730 |
| SPOT 116 | 5m | 5.1 | 3.9 | 1293 | 3.7 | 2.3 | 55427 | 9.2 | 6.5 | 614 | - | - | - | - | - | - | - | - | - |
| SPOT 123 | 5m | 4.2 | 2.7 | 424 | 5.7 | 2.8 | 34806 | 5.2 | 4.2 | 648 | 3.7 | 3.5 | 4 | - | - | - | - | - | - |
| SPOT 125 | 5m | 5.7 | 3.2 | 958 | 3.9 | 3.2 | 75149 | 11.6 | 12.3 | 388 | - | - | - | - | - | - | - | - | - |
| SPOT Pampa de Tana | 5m | 1.1 | 1.1 | 445 | 1.9 | 1.1 | 67805 | 3.3 | 1.4 | 417 | - | - | - | - | - | - | - | - | - |
| SPOT Paposo N | 5m | - | - | - | 5.1 | 1.5 | 143298 | 5.8 | 5.4 | 951 | 2.7 | 2.2 | 4 | - | - | - | - | - | - |
| SPOT Paposo S | 5m | - | - | - | 15.1 | 1.0 | 2235 | 5.4 | 4.0 | 695 | - | - | - | - | - | - | - | - | - |
| Pléiades Shoreline | 5m | - | - | - | 13.9 | 9.6 | 177271 | 4.8 | 1.6 | 294 | - | - | - | - | - | - | - | - | - |
| Pléiades Rio Loa W | 5m | - | - | - | 10.9 | 3.9 | 4793 | 9.9 | 7.5 | 407 | - | - | - | - | - | - | 11.4 | 0.9 | 880609 |
| SPOT 122_3 | 5m | - | - | - | 2.8 | 1.6 | 26349 | 4.9 | 3.0 | 220 | - | - | - | 4.6 | 2.4 | 1 | 1.3 | 1.0 | 230017 |
| SPOT 122_2 | 5m | - | - | - | 3.9 | 2.2 | 68967 | 5.9 | 3.1 | 449 | 4.6 | 2.7 | 1 | 4.6 | 2.0 | 1 | 3.4 | 1.3 | 347589 |
| SPOT 120 | 5m | - | - | - | 2.8 | 1.4 | 66810 | 3.9 | 2.7 | 281 | 2.3 | 2.1 | 2 | - | - | - | - | - | - |
| SPOT 119_2 | 5m | - | - | - | 3.8 | 3.2 | 77527 | 8.0 | 6.2 | 599 | - | - | - | - | - | - | - | - | - |
| SPOT 119_3 | 5m | - | - | - | 2.8 | 2.0 | 52071 | 6.5 | 4.4 | 456 | - | - | - | - | - | - | - | - | - |
| Pléiades N | 5m | - | - | - | 7.7 | 1.9 | 2551 | 6.3 | 3.1 | 200 | - | - | - | - | - | - | - | - | - |
| Pléiades Huara | 5m | - | - | - | 2.4 | 1.7 | 73224 | 7.9 | 6.0 | 572 | - | - | - | - | - | - | - | - | - |
| Pléiades Badlands W | 5m | - | - | - | 7.1 | 1.7 | 839 | 9.0 | 6.6 | 63 | - | - | - | - | - | - | 11.4 | 0.9 | 880609 |
References
- Wilson, J.P. Digital terrain modeling. Geomorphology 2012, 137, 107–121. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45. [Google Scholar] [CrossRef]
- Tachikawa, T.; Kaku, M.; Iwasaki, A.; Gesch, D.B.; Oimoen, M.J.; Zhang, Z.; Danielson, J.J.; Krieger, T.; Curtis, B.; Haase, J.; et al. ASTER Global Digital Elevation Model Version 2-Summary of Validation Results, 2nd ed.; NASA: Washington, DC, USA, 2011.
- Takaku, J.; Tadono, T.; Tsutsui, K. Generation of high resolution global DSM from ALOS PRISM. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, XL-4, 243–248. [Google Scholar] [CrossRef]
- Tadono, T.; Ishida, H.; Oda, F.; Naito, S.; Minakawa, K.; Iwamoto, H. Precise global DEM generation by ALOS PRISM. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, II-4, 71–76. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. Tandem-x: A satellite formation for high-resolution SAR interferometry. IEEE Geosci. Remote 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Brautigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. 2017, 132, 119–139. [Google Scholar] [CrossRef]
- Sofia, G.; Hillier, J.K.; Conway, S.J. Frontiers in geomorphometry and earth surface dynamics: Possibilities, limitations and perspectives. Earth Surf. Dyn. 2016, 4, 721–725. [Google Scholar] [CrossRef]
- Dragut, L.; Blaschke, T. Automated classification of landform elements using object-based image analysis. Geomorphology 2006, 81, 330–344. [Google Scholar] [CrossRef]
- Mokarram, M.; Seif, A.; Sathyamoorthy, D. Landform classification via fuzzy classification of morphometric parameters computed from digital elevation models: Case study on Zagros Mountains. Arab. J. Geosci. 2015, 8, 4921–4937. [Google Scholar] [CrossRef]
- Kramm, T.; Hoffmeister, D.; Curdt, C.; Maleki, S.; Khormali, F.; Kehl, M. Accuracy assessment of landform classification approaches on different spatial scales for the Iranian Loess Plateau. ISPRS Int. Geo-Inf. 2017, 6, 366. [Google Scholar] [CrossRef]
- Huang, L.C.; Liu, L.; Jiang, L.M.; Zhang, T.J. Automatic mapping of thermokarst landforms from remote sensing images using deep learning: A case study in the Northeastern Tibetan Plateau. Remote Sens. 2018, 10, 2067. [Google Scholar] [CrossRef]
- Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Measuring hyperscale topographic anisotropy as a continuous landscape property. Geosciences 2018, 8, 278. [Google Scholar]
- Bishop, M.P.; James, L.A.; Shroder, J.F.; Walsh, S.J. Geospatial technologies and digital geomorphological mapping: Concepts, issues and research. Geomorphology 2012, 137, 5–26. [Google Scholar] [CrossRef]
- Tarolli, P.; Sofia, G. Human topographic signatures and derived geomorphic processes across landscapes. Geomorphology 2016, 255, 140–161. [Google Scholar] [CrossRef]
- Schwanghart, W.; Groom, G.; Kuhn, N.J.; Heckrath, G. Flow network derivation from a high resolution DEM in a low relief, agrarian landscape. Earth Surf. Process. Landf. 2013, 38, 1576–1586. [Google Scholar] [CrossRef]
- Drisya, J.; Kumar, D.S. Comparison of digitally delineated stream networks from different spaceborne digital elevation models: A case study based on two watersheds in South India. Arab. J. Geosci. 2016, 9, 710. [Google Scholar] [CrossRef]
- Rossman, N.R.; Zlotnik, V.A.; Rowe, C.M. An approach to hydrogeological modeling of a large system of groundwater-fed lakes and wetlands in the Nebraska Sand Hills, USA. Hydrogeol. J. 2018, 26, 881–897. [Google Scholar] [CrossRef]
- Kalambukattu, J.G.; Kumar, S.; Raj, R.A. Digital soil mapping in a Himalayan watershed using remote sensing and terrain parameters employing artificial neural network model. Environ. Earth Sci. 2018, 77, 203. [Google Scholar] [CrossRef]
- Marques, K.P.P.; Dematte, J.A.M.; Miller, B.A.; Lepsch, I.F. Geomorphometric segmentation of complex slope elements for detailed digital soil mapping in Southeast Brazil. Geoderma Reg. 2018, 14, e00175. [Google Scholar] [CrossRef]
- Guo, L.; Shi, T.Z.; Linderman, M.; Chen, Y.Y.; Zhang, H.T.; Fu, P. Exploring the influence of spatial resolution on the digital mapping of soil organic carbon by airborne hyperspectral VNIR imaging. Remote Sens. 2019, 11, 1032. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation height estimation from shuttle radar topography mission and national elevation datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Leempoel, K.; Parisod, C.; Geiser, C.; Daprà, L.; Vittoz, P.; Joost, S. Very high-resolution digital elevation models: Are multi-scale derived variables ecologically relevant? Methods Ecol. Evolut. 2015, 6, 1373–1383. [Google Scholar] [CrossRef]
- Moudry, V.; Lecours, V.; Gdulova, K.; Gabor, L.; Moudra, L.; Kropacek, J.; Wild, J. On the use of global DEMs in ecological modelling and the accuracy of new bare-earth DEMs. Ecol. Model 2018, 383, 3–9. [Google Scholar] [CrossRef]
- Blaszczyk, M.; Ignatiuk, D.; Grabiec, M.; Kolondra, L.; Laska, M.; Decaux, L.; Jania, J.; Berthier, E.; Luks, B.; Barzycka, B.; et al. Quality assessment and glaciological applications of digital elevation models derived from space-borne and aerial images over two tidewater glaciers of Southern Spitsbergen. Remote Sens. 2019, 11, 1121. [Google Scholar] [CrossRef]
- Gesch, D.B. Best practices for elevation-based assessments of sea-level rise and coastal flooding exposure. Front. Earth Sci. 2018, 6, 230. [Google Scholar] [CrossRef]
- Mmbando, G.A.; Kleyer, M. Mapping precipitation, temperature, and evapotranspiration in the Mkomazi River Basin, Tanzania. Climate 2018, 6, 63. [Google Scholar] [CrossRef]
- Goodchild, M.F. Scale in GIS: An overview. Geomorphology 2011, 130, 5–9. [Google Scholar] [CrossRef]
- Kienzle, S. The effect of DEM raster resolution on first order, second order and compound terrain derivatives. Trans. GIS 2004, 8, 83–111. [Google Scholar] [CrossRef]
- Zhang, W.H.; Montgomery, D.R. Digital elevation model grid size, landscape representation, and hydrologic simulations. Water Resour. Res. 1994, 30, 1019–1028. [Google Scholar] [CrossRef]
- Smith, M.P.; Zhu, A.X.; Burt, J.E.; Stiles, C. The effects of dem resolution and neighborhood size on digital soil survey. Geoderma 2006, 137, 58–69. [Google Scholar] [CrossRef]
- Sorensen, R.; Seibert, J. Effects of dem resolution on the calculation of topographical indices: TWI and its components. J. Hydrol. 2007, 347, 79–89. [Google Scholar] [CrossRef]
- Deng, Y.; Wilson, J.P.; Bauer, B.O. DEM resolution dependencies of terrain attributes across a landscape. Int. J. Geogr. Inf. Sci. 2007, 21, 187–213. [Google Scholar] [CrossRef]
- Kim, D.; Zheng, Y.B. Scale-dependent predictability of DEM-based landform attributes for soil spatial variability in a coastal dune system. Geoderma 2011, 164, 181–194. [Google Scholar] [CrossRef]
- Grohmann, C.H.; Smith, M.J.; Riccomini, C. Multiscale analysis of topographic surface roughness in the Midland Valley, Scotland. IEEE Geosci. Remote 2011, 49, 1200–1213. [Google Scholar] [CrossRef]
- Lindsay, J.B.; Cockburn, J.M.H.; Russell, H.A.J. An integral image approach to performing multi-scale topographic position analysis. Geomorphology 2015, 245, 51–61. [Google Scholar] [CrossRef]
- Newman, D.R.; Lindsay, J.B.; Cockburn, J.M.H. Evaluating metrics of local topographic position for multiscale geomorphometric analysis. Geomorphology 2018, 312, 40–50. [Google Scholar] [CrossRef]
- Grieve, S.W.D.; Mudd, S.M.; Milodowski, D.T.; Clubb, F.J.; Furbish, D.J. How does grid-resolution modulate the topographic expression of geomorphic processes? Earth Surf. Dyn. 2016, 4, 627–653. [Google Scholar] [CrossRef]
- Grieve, S.W.D.; Mudd, S.M.; Hurst, M.D.; Milodowski, D.T. A nondimensional framework for exploring the relief structure of landscapes. Earth Surf. Dyn. 2016, 4, 309–325. [Google Scholar] [CrossRef]
- Zhao, S.M.; Cheng, W.M.; Zhou, C.H.; Chen, X.; Zhang, S.F.; Zhou, Z.P.; Liu, H.J.; Chai, H.X. Accuracy assessment of the ASTER GDEM and SRTM3 DEM: An example in the Loess Plateau and North China Plain of China. Int. J. Remote Sens. 2011, 32, 8081–8093. [Google Scholar] [CrossRef]
- Suwandana, E.; Kawamura, K.; Sakuno, Y.; Kustiyanto, E.; Raharjo, B. Evaluation of ASTER GDEM2 in comparison with GDEM1, SRTM DEM and topographic-map-derived DEM using inundation area analysis and RTK-DGPS data. Remote Sens. 2012, 4, 2419–2431. [Google Scholar] [CrossRef]
- Mukherjee, S.; Joshi, P.K.; Mukherjee, S.; Ghosh, A.; Garg, R.D.; Mukhopadhyay, A. Evaluation of vertical accuracy of open source digital elevation model (DEM). Int. J. Appl. Earth Obs. 2013, 21, 205–217. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C. Comparison of free high resolution digital elevation data sets (ASTER GDEM2, SRTM v2.1/v4.1) and validation against accurate heights from the Australian National Gravity database. Aust. J. Earth Sci. 2014, 61, 213–226. [Google Scholar] [CrossRef]
- Satge, F.; Bonnet, M.P.; Timouk, F.; Calmant, S.; Pillco, R.; Molina, J.; Lavado-Casimiro, W.; Arsen, A.; Cretaux, J.F.; Garnier, J. Accuracy assessment of SRTM v4 and ASTER GDEM v2 over the altiplano watershed using ICESat/GLAS data. Int. J. Remote Sens. 2015, 36, 465–488. [Google Scholar] [CrossRef]
- Caglar, B.; Becek, K.; Mekik, C.; Ozendi, M. On the vertical accuracy of the ALOS World 3D-30m digital elevation model. Remote Sens. Lett. 2018, 9, 607–615. [Google Scholar] [CrossRef]
- Wessel, B.; Huber, M.; Wohlfart, C.; Marschalk, U.; Kosmann, D.; Roth, A. Accuracy assessment of the globalTanDEM-X digital elevation model with GPS data. ISPRS J. Photogramm. 2018, 139, 171–182. [Google Scholar] [CrossRef]
- Altunel, A.O. Evaluation of TanDEM-X 90 m digital elevation model. Int. J. Remote Sens. 2019, 40, 2841–2854. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Gann, D.; Ross, M.; Biswas, H.; Li, Y.P.; Rhome, J. Comparison of TanDEM-X DEM with LiDAR data for accuracy assessment in a coastal urban area. Remote Sens. 2019, 11, 876. [Google Scholar] [CrossRef]
- Hu, Z.H.; Peng, J.W.; Hou, Y.L.; Shan, J. Evaluation of recently released open global digital elevation models of Hubei, China. Remote Sens. 2017, 9, 262. [Google Scholar] [CrossRef]
- Alganci, U.; Besol, B.; Sertel, E. Accuracy assessment of different digital surface models. ISPRS Int. Geo-Inf. 2018, 7, 114. [Google Scholar] [CrossRef]
- Florinsky, I.; Skrypitsyna, T.; Luschikova, O. Comparative accuracy of the AW3D30 DSM, ASTER GDEM, and SRTM1 DEM: A case study on the Zaoksky testing ground, Central European Russia. Remote Sens. Lett. 2018, 9, 706–714. [Google Scholar] [CrossRef]
- Jain, A.O.; Thaker, T.; Chaurasia, A.; Patel, P.; Singh, A.K. Vertical accuracy evaluation of SRTM-gl1, GDEM-v2, AW3D30 and CartoDEM-v3.1 of 30-m resolution with dual frequency GNSS for Lower Tapi Basin India. Geocarto Int. 2018, 33, 1237–1256. [Google Scholar] [CrossRef]
- Li, H.; Zhao, J.Y. Evaluation of the newly released worldwide AW3D30 DEM over typical landforms of China using two global DEMs and ICESat/GLAS data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4430–4440. [Google Scholar] [CrossRef]
- Yahaya, S.I.; El Azzab, D. Vertical accuracy assessment of global digital elevation models and validation of gravity database heights in Niger. Int. J. Remote Sens. 2019, 40. [Google Scholar] [CrossRef]
- Pipaud, I.; Loibl, D.; Lehmkuhl, F. Evaluation of TanDEM-X elevation data for geomorphological mapping and interpretation in high mountain environments-A case study from SE Tibet, China. Geomorphology 2015, 246, 232–254. [Google Scholar] [CrossRef]
- Becek, K.; Koppe, W.; Kutoglu, S.H. Evaluation of vertical accuracy of the WorldDEM (tm) using the runway method. Remote Sens. 2016, 8, 934. [Google Scholar] [CrossRef]
- Podgorski, J.; Kinnard, C.; Petlicki, M.; Urrutia, R. Performance assessment of TanDEM-X DEM for mountain glacier elevation change detection. Remote Sens. 2019, 11, 187. [Google Scholar] [CrossRef]
- Zhang, K.Q.; Gann, D.; Ross, M.; Robertson, Q.; Sarmiento, J.; Santana, S.; Rhome, J.; Fritz, C. Accuracy assessment of ASTER, SRTM, ALOS, and TDX DEMs for Hispaniola and implications for mapping vulnerability to coastal flooding. Remote Sens. Environ. 2019, 225, 290–306. [Google Scholar] [CrossRef]
- Purinton, B.; Bookhagen, B. Validation of digital elevation models (DEMs) and comparison of geomorphic metrics on the Southern Central Andean Plateau. Earth Surf. Dyn. 2017, 5, 211–237. [Google Scholar] [CrossRef]
- Grohmann, C.H. Evaluation of TanDEM-X DEMs on selected Brazilian sites: Comparison with SRTM, ASTER GDEM and ALOS AW3D30. Remote Sens. Environ. 2018, 212, 121–133. [Google Scholar] [CrossRef]
- Liu, K.; Song, C.Q.; Ke, L.H.; Jiang, L.; Pan, Y.Y.; Ma, R.H. Global open-access DEM performances in earth’s most rugged region High Mountain Asia: A multi-level assessment. Geomorphology 2019, 338, 16–26. [Google Scholar] [CrossRef]
- Holmes, K.W.; Chadwick, O.A.; Kyriakidis, P.C. Error in a USGS 30-meter digital elevation model and its impact on terrain modeling. J. Hydrol. 2000, 233, 154–173. [Google Scholar] [CrossRef]
- Grohmann, C.H. Effects of spatial resolution on slope and aspect derivation for regional-scale analysis. Comput. Geosci. 2015, 77, 111–117. [Google Scholar] [CrossRef]
- Houston, J.; Hartley, A.J. The Central Andean west-slope rainshadow and its potential contribution to the origin of hyper-aridity in the Atacama Desert. Int. J. Climatol. 2003, 23, 1453–1464. [Google Scholar] [CrossRef]
- Hartley, A.J.; Chong, G.; Houston, J.; Mather, A.E. 150 million years of climatic stability: Evidence from the Atacama Desert, Northern Chile. J. Geol. Soc. 2005, 162, 421–424. [Google Scholar] [CrossRef]
- Dunai, T.J.; Lopez, G.A.G.; Juez-Larre, J. Oligocene-Miocene age of aridity in the Atacama Desert revealed by exposure dating of erosion-sensitive landforms. Geology 2005, 33, 321–324. [Google Scholar] [CrossRef]
- Walk, J.; Stauch, G.; Reyers, M.; Vásquez, P.; Sepúlveda, F.A.; Bartz, M.; Hoffmeister, D.; Brückner, H.; Lehmkuhl, F. Gradients in climate, geology, and topography affecting coastal alluvial fan morphodynamics in hyperarid regions–the Atacama perspective. Glob. Planet Chang. 2019. [Google Scholar] [CrossRef]
- May, S.M.; Hoffmeister, D.; Wolf, D.; Bubenzer, O. Zebra stripes in the Atacama Desert revisited–granular fingering as a mechanism for zebra stripe formation? Geomorphology 2019, 344, 46–59. [Google Scholar] [CrossRef]
- Abrams, M.; Bailey, B.; Tsu, H.; Hato, M. The ASTER Global DEM. Photogramm. Eng. Remote Sens. 2010, 76, 344–348. [Google Scholar]
- Hirano, A.; Welch, R.; Lang, H. Mapping from ASTER stereo image data: DEM validation and accuracy assessment. ISPRS J. Photogramm. Remote Sens. 2003, 57, 356–370. [Google Scholar] [CrossRef]
- Abrams, M.; Crippen, R. ASTER GDEM v3 (ASTER Global DEM); User Guide; California Institute of Technology: Pasadena, CA, USA, 2019. [Google Scholar]
- Tadono, T.; Shimada, M.; Murakami, H.; Takaku, J. Calibration of PRISM and AVNIR-2 onboard ALOS “daichi”. IEEE Geosci. Remote 2009, 47, 4042–4050. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T. Quality updates of ‘AW3D’ Global DSM generated from ALOS PRISM. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5666–5669. [Google Scholar]
- Rodríguez, E.; Morris, C.S.; Belz, J.E.; Chapin, E.C.; Martin, J.M.; Daffer, W.; Hensley, S. An Assessment of the SRTM Topographic Products; Jet Propulsion Laboratory (JPL): Pasadena, CA, USA, 2005. [Google Scholar]
- Reuter, H.I.; Nelson, A.; Jarvis, A. An evaluation of void-filling interpolation methods for SRTM data. Int. J. Geogr. Inf. Sci. 2007, 21, 983–1008. [Google Scholar] [CrossRef]
- Wessel, B. TanDEM-X Ground Segment–DEM Products Specification Document; EOC: Munich, Germany, 2016. [Google Scholar]
- Rizzoli, P.; Brautigam, B.; Kraus, T.; Martone, M.; Krieger, G. Relative height error analysis of TanDEM-X elevation data. ISPRS J. Photogramm. 2012, 73, 30–38. [Google Scholar] [CrossRef]
- Keys, L.; Baade, J. Uncertainty in catchment delineations as a result of digital elevation model choice. Hydrology 2019, 6, 13. [Google Scholar] [CrossRef]
- Astrium GEO-Information Services. Pléiades Imagery User Guide V 2.0; Astrium: Paris, France, 2012. [Google Scholar]
- De Lussy, F.; Kubik, P.; Greslou, D.; Pascal, V.; Gigord, P.; Cantou, J.P. Pleiades-HR image system products and quality. Pleiades-HR image system products and geometric accuracy. In Proceedings of the ISPRS Hannover Workshop, Hannover, Germany, 17–20 May 2005. [Google Scholar]
- Gleyzes, M.A.; Perret, L.; Kubik, P. Pleiades system architecture and main performances. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 39, 537–542. [Google Scholar] [CrossRef]
- Poli, D.; Remondino, F.; Angiuli, E.; Agugiaro, G. Evaluation of Pleiades-1a triplet on Trento testfield. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, XL-1/W1, 287–292. [Google Scholar] [CrossRef]
- Rieg, L.; Klug, C.; Nicholson, L.; Sailer, R. Pleiades tri-stereo data for glacier investigations-examples from the European Alps and the Khumbu Himal. Remote Sens. 2018, 10, 1563. [Google Scholar] [CrossRef]
- Astrium GEO-Information Services. SPOT 6 & SPOT 7 Imagery-User Guide; Astrium: Paris, France, 2013. [Google Scholar]
- Maune, D.F. Digital Elevation Model Technologies and Applications: The DEM Users Manual, 2nd ed.; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 2007; 655p. [Google Scholar]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett. 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn. 2002, 34, 405–445. [Google Scholar] [CrossRef]
- Duong, H.; Lindenbergh, R.; Pfeifer, N.; Vosselman, G. ICESat full-waveform altimetry compared to airborne laser scanning altimetry over The Netherlands. IEEE Trans. Geosci. Remote 2009, 47, 3365–3378. [Google Scholar] [CrossRef]
- Huang, X.D.; Xie, H.J.; Liang, T.G.; Yi, D.H. Estimating vertical error of SRTM and map-based DEMs using ICESat altimetry data in the Eastern Tibetan Plateau. Int. J. Remote Sens. 2011, 32, 5177–5196. [Google Scholar] [CrossRef]
- Zhao, S.M.; Cheng, W.M.; Zhou, C.H.; Liu, H.J.; Su, Q.M.; Zhang, S.F.; He, W.C.; Wang, L.; Wu, W.J. Using MLR to model the vertical error distribution of ASTER GDEM v2 data based on ICESat/GLA14 data in the Loess Plateau of China. Z. Geomorphol. 2017, 61, 9–26. [Google Scholar] [CrossRef]
- Baghdadi, N.; Lemarquand, N.; Abdallah, H.; Bailly, J.S. The relevance of GLAS/ICESat elevation data for the monitoring of river networks. Remote Sens. 2011, 3, 708–720. [Google Scholar] [CrossRef]
- Markus, T.; Neumann, T.; Martino, A.; Abdalati, W.; Brunt, K.; Csatho, B.; Farrell, S.; Fricker, H.; Gardner, A.; Harding, D.; et al. The ice, cloud, and land elevation satellite-2 (ICESat-2): Science requirements, concept, and implementation. Remote Sens. Environ. 2017, 190, 260–273. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ALT08 land and vegetation product for the ICESat-2 mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Neuenschwander, L.A.; Magruder, A.L. Canopy and terrain height retrievals with ICESat-2: A first look. Remote Sens. 2019, 11, 1721. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Höhle, J.; Höhle, M. Accuracy assessment of digital elevation models by means of robust statistical methods. ISPRS J. Photogramm. 2009, 64, 398–406. [Google Scholar] [CrossRef]
- Riley, S.J.; DeGloria, S.D.; Elliot, R. A terrain ruggedness index that quantifies topographic heterogeneity. Int. J. Sci. 1999, 5, 23–27. [Google Scholar]
- Weiss, A.D. Topographic position and landforms analysis. In ESRI Users Conference; ESRI: San Diego, CA, USA, 2001. [Google Scholar]
- Boulton, S.J.; Stokes, M. Which DEM is best for analyzing fluvial landscape development in mountainous terrains? Geomorphology 2018, 310, 168–187. [Google Scholar] [CrossRef]
- Huber, M.; Wessel, B.; Kosmann, D.; Felbier, A.; Schwieger, V.; Habermeyer, M.; Wendleder, A.; Roth, A. Ensuring globally the TanDEM-X height accuracy: Analysis of the reference data sets ICESat, SRTM andKGPS-tracks. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Cape Town, South Africa, 12–17 July 2009; pp. II-769–II-772. [Google Scholar]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Takaku, J.; Tadono, T.; Tsutsui, K.; Ichikawa, M. Validation of ‘AW3D’ Global DSM generated from ALOS PRISM. In Proceedings of the XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Graf, L.; Moreno-de-las-Heras, M.; Ruiz, M.; Calsamiglia, A.; Garcia-Comendador, J.; Fortesa, J.; Lopez-Tarazon, J.A.; Estrany, J. Accuracy assessment of digital terrain model dataset sources for hydrogeomorphological modelling in small Mediterranean catchments. Remote Sens. 2018, 10, 2014. [Google Scholar] [CrossRef]
- Mouratidis, A.; Ampatzidis, D. European digital elevation model validation against extensive global navigation satellite systems data and comparison with SRTM DEM and ASTER GDEM in Central Macedonia (Greece). ISPRS Int. Geo-Inf. 2019, 8, 108. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kramm, T.; Hoffmeister, D. A Relief Dependent Evaluation of Digital Elevation Models on Different Scales for Northern Chile. ISPRS Int. J. Geo-Inf. 2019, 8, 430. https://doi.org/10.3390/ijgi8100430
Kramm T, Hoffmeister D. A Relief Dependent Evaluation of Digital Elevation Models on Different Scales for Northern Chile. ISPRS International Journal of Geo-Information. 2019; 8(10):430. https://doi.org/10.3390/ijgi8100430
Chicago/Turabian StyleKramm, Tanja, and Dirk Hoffmeister. 2019. "A Relief Dependent Evaluation of Digital Elevation Models on Different Scales for Northern Chile" ISPRS International Journal of Geo-Information 8, no. 10: 430. https://doi.org/10.3390/ijgi8100430
APA StyleKramm, T., & Hoffmeister, D. (2019). A Relief Dependent Evaluation of Digital Elevation Models on Different Scales for Northern Chile. ISPRS International Journal of Geo-Information, 8(10), 430. https://doi.org/10.3390/ijgi8100430





