TLS Measurement during Static Load Testing of a Railway Bridge
Abstract
1. Introduction
2. Materials and Methods
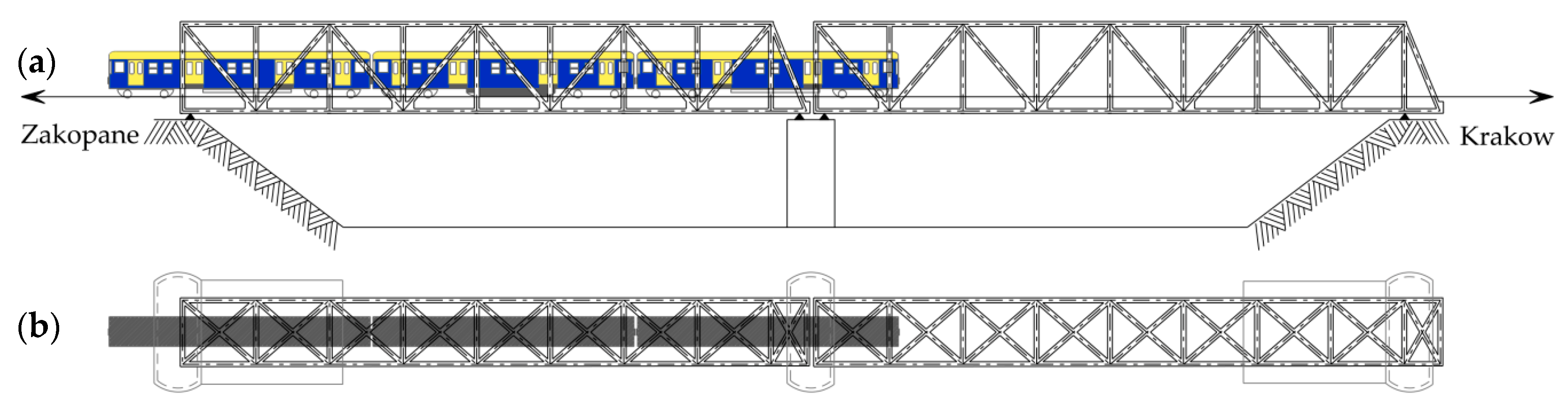
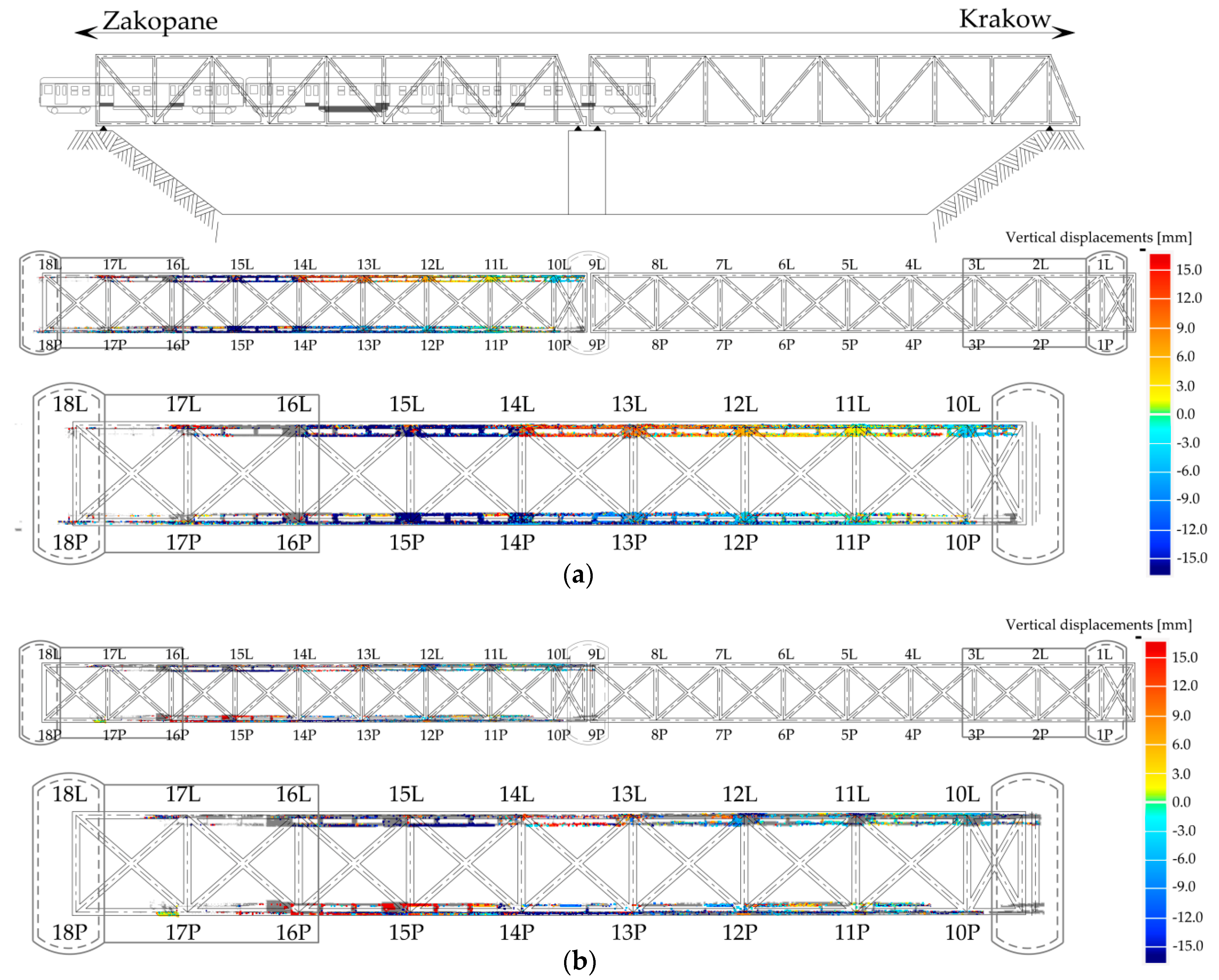
2.1. Tested Bridge
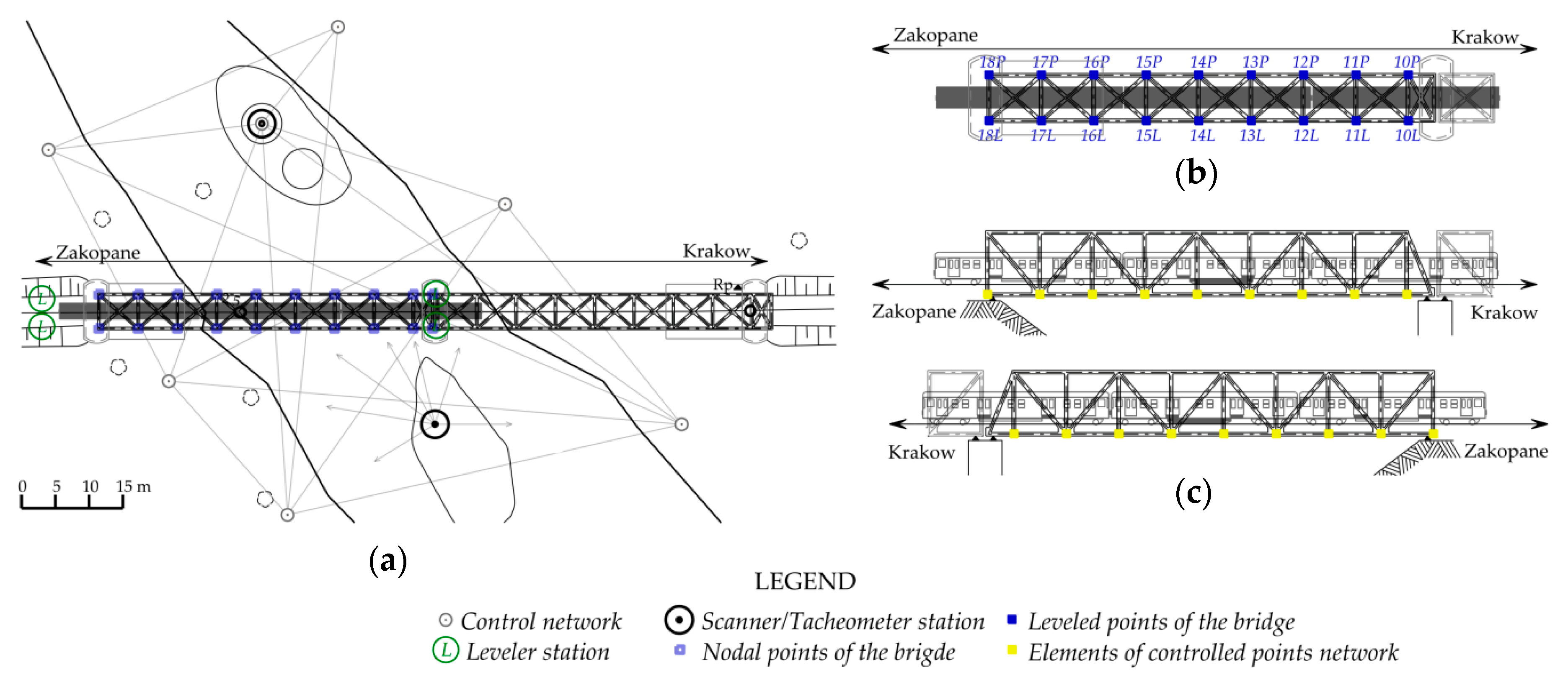
2.2. Bridge Static Load Testing
2.3. Survey and TLS Measurements
2.4. TLS Data Processing
3. Results and Discussion
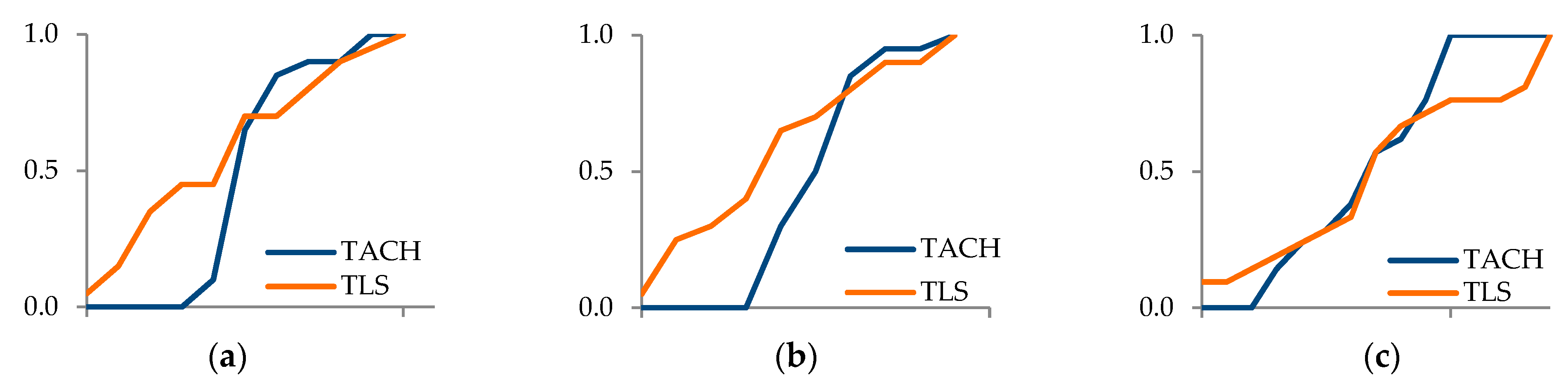
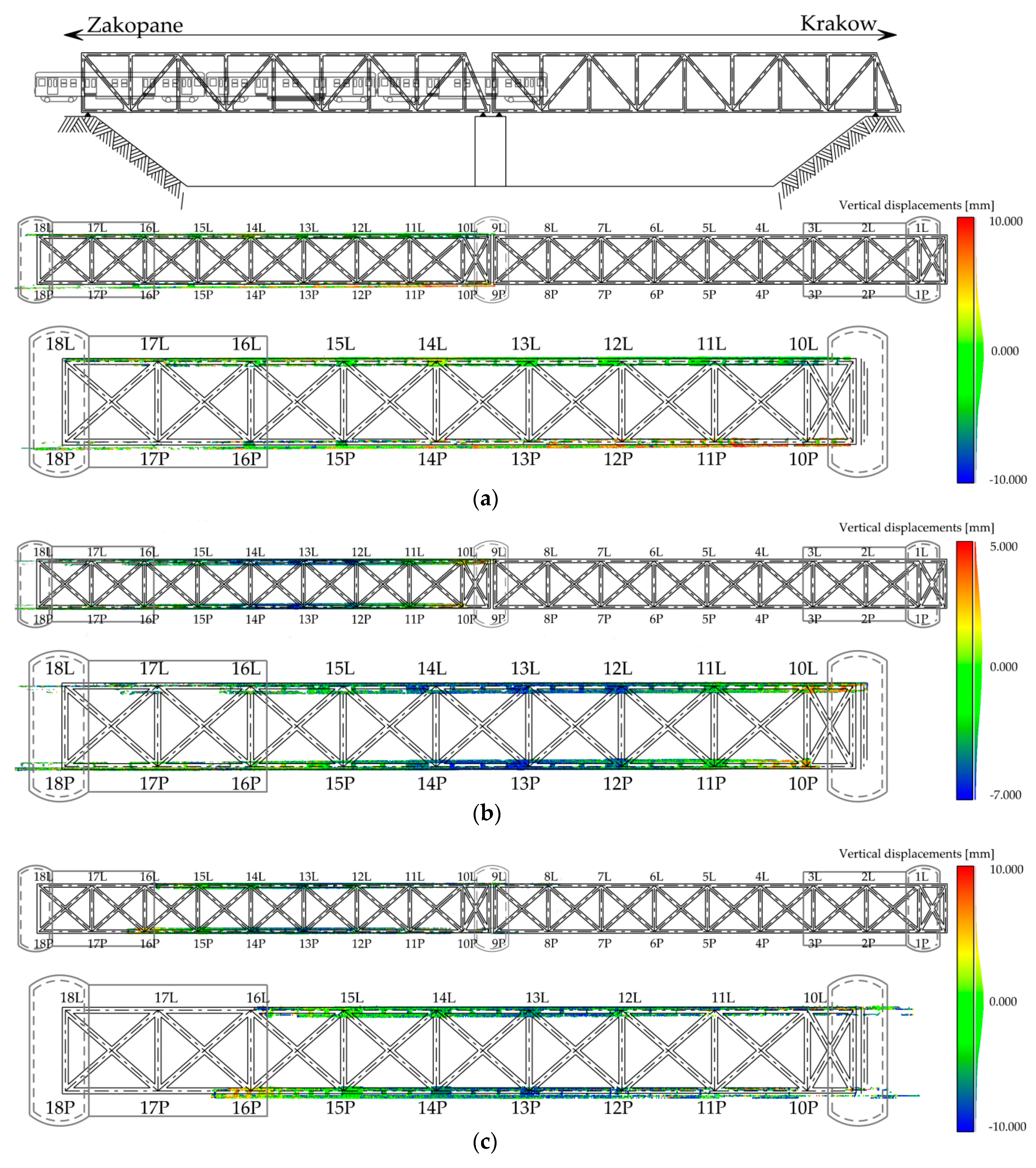
3.1. B&W Target Analysis (1)
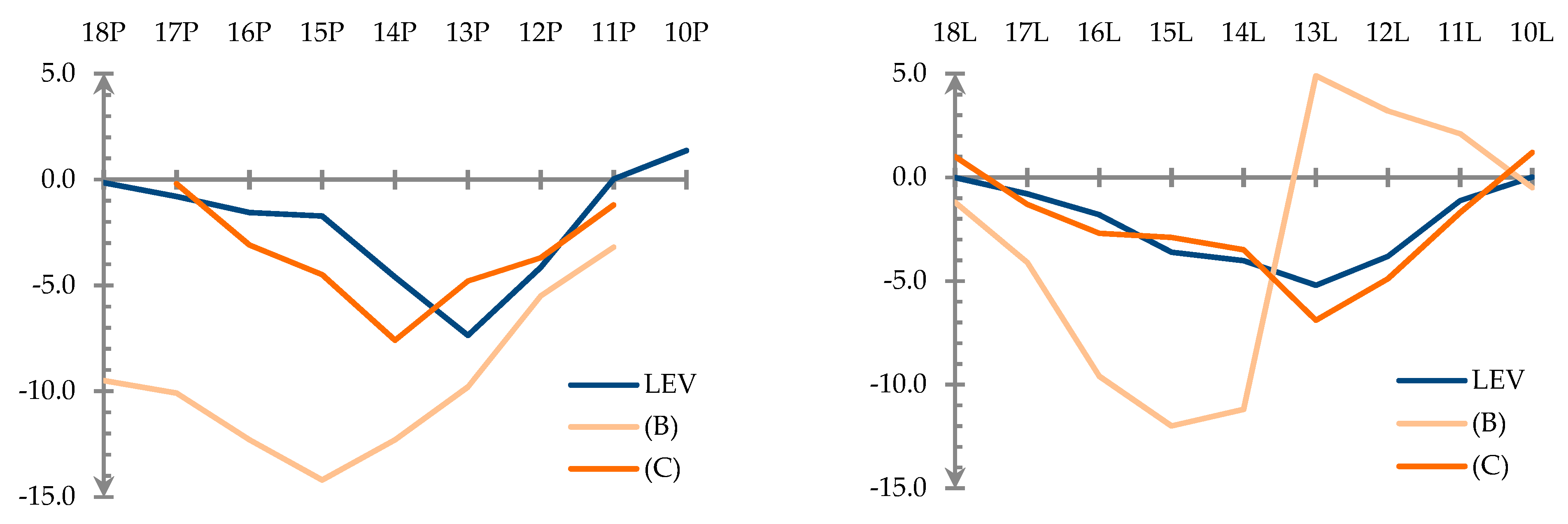
3.2. Point Cloud Analysis (2)
3.3. Mesh Surface Analysis (3)
4. Conclusions
- The registration of point clouds in stages with vertical adjustments of TLS data provided scan data, the accuracy of which is high enough to identify vertical displacement of structural elements with the same accuracy as in the case of reflectorless measurements.
- The accuracy of the determination of the centre of B&W targets based on a high-resolution point cloud is similar to the accuracy of reflectorless tacheometry (carried out in several repeats with two positions of the telescope).
- The determination of structural displacement based on differential models from raw point clouds after gross manual filtration is an unreliable method that fails to identify periodic dislocations of the same values and sign as traditional methods. The reason for the failed determinations is the application of cloud to cloud registration for differentiation. This type of registration matches point clouds using the least square method and minimises the Euclidean distance between them, thus removing periodic displacement.
- The large number of observations, which is typical of 3D data, in the differentiation of raw point clouds does not result in a reduction of the mean error of displacement values compared to traditional methods.
- Georeferencing of the external coordinate system of point clouds – determined with high relative reliability and using precise traditional methods – reduces the assumed resultant mean error of displacement by half during the differentiation of the point clouds.
- By improving the reliability of spatial data, filtration algorithms eliminate systematic errors almost completely.
- Generalisation and homogenisation of point clouds (after georeferencing only) with algorithms for generating surface models do not facilitate a reliable determination of displacement.
- Surface models are recommended only for high-resolution numerical data subjected to filtering algorithms.
- The use of surface models for investigating object stability is justified only for point clouds, the density of which is around 2 mm. In the case of less favourable resolutions, numerical data are lost when generating surface models and in the process of filtering and generating surface models.
- The maximum value of the displacement during the static load test (−7.4 mm) was lower than the maximum design deflection (−18.2 mm). A detailed inspection of the railway bridge, which was carried out with the participation of a railway diagnostician before and after the trial load, did not find any irregularities in the structure of the tested object.
Author Contributions
Funding
Conflicts of Interest
References
- Taylor, W.M. Iron, Engineering and Architectural History in Crisis: Following the Case of the River Dee Bridge Disaster, 1847. Archit. Hist. 2013, 1, 23. [Google Scholar]
- Klasztorny, M. Dynamika mostów belkowych obciążonych pociągami szybkobieżnymi (en. Dynamics of Beam Bridges Loaded with High-Speed Trains); Wydawnictwa Naukowo-Techniczne: Warszawa, Poland, 2005. [Google Scholar]
- Kużawa, M.J.; Cruz, P.J.S.; Bień, J. Analysis and fatigue evaluation of Pinhao bridge in Portugal. Mosty stalowe: Projektowanie, technologie budowy, badania, utrzymanie. In Proceedings of the Tytuł ten podsumowuje konferencję, Wroclaw, Poland, 27–28 November 2008. [Google Scholar]
- Gordon, S.; Lichti, D. Modeling Terrestrial Laser Scanner Data for Precise Structural Deformation Measurement. J. Surv. Eng. 2007, 133, 72–80. [Google Scholar] [CrossRef]
- Georgopoulos, G.D.; Telioni, E.C.; Tsontzou, A. The contribution of laser scanning technology in the estimation of ancient Greek monuments’ deformations. Surv. Rev. 2018, 48, 303–308. [Google Scholar] [CrossRef]
- Xu, X.; Bureick, J.; Yang, H.; Neumann, I. TLS-based composite structure deformation analysis validated with laser tracker. Comp. Struct. 2018, 202, 60–65. [Google Scholar] [CrossRef]
- Cho, S.; Park, S.; Cha, G.; Oh, T. Development of Image Processing for Crack Detection on Concrete Structures through Terrestrial Laser Scanning Associated with the Octree Structure. Appl. Sci. 2018, 8, 2373. [Google Scholar] [CrossRef]
- Wujanz, D.; Burger, M.; Tschirschwitz, F.; Nietzschmann, T.; Neitzel, F.; Kersten, T.P. Determination of Intensity-Based Stochastic Models for Terrestrial Laser Scanners Utilising 3D-Point Clouds. Sensors 2018, 18, 2187. [Google Scholar] [CrossRef] [PubMed]
- Mukupa, W.; Roberts, G.W.; Hancock, C.M.; Al-Manasir, K. A review of the use of terrestrial laser scanning application for change detection and deformation monitoring of structures. Surv. Rev. 2017, 49, 99–116. [Google Scholar] [CrossRef]
- Kędzierski, M.; Fryśkowska, A.; Wilińska, M. Naziemny skaning laserowy obiektów inżynieryjno—Drogowych (en. Terrestrial laser scanning of engineering and road objects). Biuletyn WAT 2007, 59, 285–308. [Google Scholar]
- Gosliga, R.; Lindenbergh, R.; Pfeifer, N. Deformation analysis of a bored tunnel by means of Terrestrial Laser Scanning. ISPRS 2006, 36, 5. [Google Scholar]
- Leica Geosystems. Leica Cyclone 7.2 Tutorial, Part: Registration. 2007. Available online: https://arf.berkeley.edu/files/webfiles/all/arf/equipment/field/3d_scanner/cyrax_leica_laser/Cyclone/Cyclone%205.8.pdf (accessed on 10 November 2018).
- Toś, C.; Wolski, B.; Zielina, L. Zastosowanie tachimetru skanującego w praktyce geodezyjnej (en. Application of the total station in surveying practice). Środowisko. Czasopismo techniczne 2010, 16, 1–17. [Google Scholar]
- Lichti, D.D.; Gordon, S.J.; Tipdecho, T. Error models and propagation in directly georeferenced terrestrial laser scanner networks. J. Surv. Eng. 2005, 131, 135–142. [Google Scholar] [CrossRef]
- Weinmann, M.; Jutzi, B. Geometric point quality assessment for the automated, markerless and robust registration of unordered TLS point clouds. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, II-3/W5, 89–96. [Google Scholar] [CrossRef]
- Van Genechten, B.; Schueremans, L. Laserscanning for heritage documentation. Wiadomości konserwatorskie 2009, 26, 727–737. [Google Scholar]
- Foley, J.D.; Van Dam, A.; Feiner, S.K.; Hughes, J.F.; Philips, R.L. Wprowadzenie do grafiki komputerowej (en. Introduction to Computer Graphics); Wydawnictwa Naukowo-Techniczne: Warszawa, Poland, 2001. [Google Scholar]
- Pyka, K.; Mikrut, S.; Moskal, A.; Pastucha, E.; Tokarczyk, R. Problemy automatycznego modelowania i teksturowania obiektów opisujących skrajnię linii kolejowych (en. Problems of automatic modeling and texturing of objects describing objects of railway lines). Archiwum Fotogrametrii, Kartografii i Teledetekcji 2013, 25, 177–188. [Google Scholar]
- Quintero, M.S.; Genechten, B.; Bruyne, M.; Poelman, R.; Hankar, M.; Barnes, S.; Caner, H.; Craven, P.; Budei, L.; Heine, E.; et al. 3D RiskMapping. Theory and Practice on Terrestrial Laser Scanning. Training Material Based on Practicial Applications; Universidad Politécnica de Valencia: València, Spain, 2008. [Google Scholar]
- Izdebski, W. Wykłady z systemów informacji o terenie (en. Lectures on land information systems); Politechnika Warszawska: Warszawa, Poland, 2015. [Google Scholar]
- Mitka, B.; Piech, I. Modele powierzchni terenu (en. Surface models). Infrastruktura i Ekologia terenów wiejskich 2012, 3, 167–180. [Google Scholar]
- Lichti, D.D.; Gordon, S.J.; Stewart, M.P.; Franke, J.; Tsakiri, M. Comparison of digital photogrammetry and laser scanning. Int. Soc. Photogram. Remote Sens. 2008, 39–44. Available online: https://www.researchgate.net/profile/Jochen_Franke3/publication/245716767_Comparison_of_Digital_Photogrammetry_and_Laser_Scanning/links/541ba09d0cf25ebee98d98f3/Comparison-of-Digital-Photogrammetry-and-Laser-Scanning.pdf (accessed on 5 November 2018).
- Zogg, H.M.; Ingensand, H. Terrestrial laser scanning for deformation monitoring—Load tests on the Felsenau Viaduct (ch). Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2008, 37, 555–562. [Google Scholar]
- Lovas, T.; Barsi, A.; Detrekoi, A.; Dunai, L.; Csak, Z.; Polgar, A.; Berenyi, A.; Kibedy, Z.; Szocs, K. Terrestrial laser scanning in deformation measurements of structures. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2008, 37, 527–532. [Google Scholar]
- Mill, T.; Ellmann, A.; Kisa, M.; Idnurm, J.; Idnurm, S.; Horemuz, M.; Aavik, A. Geodetic monitoring of bridge deformations occurring during static load testing. Baltic J. Road Bridge Eng. 2015, 10, 17–27. [Google Scholar] [CrossRef]
- Lõhmus, H.; Ellmann, A.; Märdla, S.; Idnurm, S. Terrestrial laser scanning for the monitoring of bridge load tests—Two case studies. Surv. Rev. 2018, 50, 270–284. [Google Scholar] [CrossRef]
- Łaziński, P.; Pradelok, S. Badanie odbiorcze wieloprzęsłowego wiaduktu kolejowego nasuwanego poprzecznie (en. Acceptance test of multi-span railway over-slip rail); Wrocławskie dni mostowe. Obiekty mostowe w infrastrukturze miejskiej: Wrocław, Poland, 2013. [Google Scholar]
- Chróścielewski, J.; Malinowski, M.; Miśkiewicz, M. Próbne obciążenia mostu przez Wisłę w Puławach (en. Load tests of the bridge over the Vistula River in Puławy); Wrocławskie dni mostowe. Mosty stalowe. Projektowanie, technologie budowy, badania, utrzymanie: Wrocław, Poland, 2008. [Google Scholar]
- The Polish Committee for Standardization (Polski Komitet Normalizacyjny—PKN). PN-S-10050:1989 Obiekty mostowe—Konstrukcje stalowe—Wymagania i badania. (en. Bridge structures—Steel constructions—Requirements and tests.); Polski Komitet Normalizacyjny—PKN: Warszawa, Poland, 1989. [Google Scholar]
- Mitka, B. Możliwości zastosowania naziemnych skanerów laserowych w procesie dokumentacji i modelowania obiektów zabytkowych (en. Possibilities of using terrestrial laser scanners in the process of documentation and modeling of historic buildings). Archiwum Fotogrametrii i Teledetekcji 2007, 17, 525–534. [Google Scholar]
- Boehler, W.; Marbs, A. Investigating Laser Scanner Accuracy. 2003. Available online: www.leica-geosystems.com (accessed on 4 November 2018).
- Gawronek, P. Methodology of Determining Stability of Bridges Using Terrestrial Laser Scanning. Ph.D. Thesis, Faculty of Environmental Engineering and Land Surveying, University of Agriculture in Krakow, Kraków, Poland, 2017. (In Polish). [Google Scholar]
- United States Department of Commerce. Report of a Special Test. NIST Test No. 681/280055-10. 2010. Available online: https://3dssupport.microsoftcrmportals.com/66d243af5d014342b9de97b5c8cac2e (accessed on 2 November 2018).
- Edelsbrunner, H.; Facello, M.A.; Fu, P.; Qian, J.; Nekhayev, D.V. Wrapping 3D Scanning Data. In Proceedings of the Photonics West ‘98 Electronic Imaging, San Jose, CA, USA, 6 March 1998. [Google Scholar]
- Plucińska, A.; Pluciński, E. Probabilistyka (en. Probability); Wydawnictwo Naukowo-Techniczne: Warszawa, Poland, 2000. [Google Scholar]
- Shen-En, C. Laser Scanning Technology for Bridge Monitoring. In Laser Scanner Technology; InTech: London, UK, 2012; ISBN 978-953-51-0280-9. [Google Scholar]
- Bitelli, G.; Dubbini, M.; Zanutta, A. Terrestrial laser scanning and digital photogrammetry techniques to monitor landslides bodies. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2004, 3, 246–251. [Google Scholar]
- Schäfer, T.; Weber, T.; Kyrinovic, P.; Zámecniková, M. Deformation measurement using terrestrial laser scanning at the hydropower station of Gabcikovo. In Proceedings of the INGEO 2004 and FIG Regional Central and Eastern European Conference on Engineering Surveying, Bratislava, Slovakia, 11–13 November 2004. [Google Scholar]
- Tsakiri, M.; Lichti, D.D.; Pfeifer, N. Terrestrial laser scanning for deformation monitoring. In Proceedings of the 3rd IAG/12th FIG Symposium, Baden, Austria, 22–24 May 2006. [Google Scholar]
- Ioannidis, C.; Valani, A.; Georgopoulos, A.; Tsiligiris, E. 3D Model Generation for Deformation Analysis Using Laser Scanning Data of a Cooling Tower. In Proceedings of the 12th FIG Symposium, Baden, Austria, 22–24 May 2006. [Google Scholar]
- Alba, M.; Fregonese, L.; Prandi, F.; Scaioni, M.; Valgoi, P. Structural monitoring of a large dam by terrestrial laser scanning. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2006, 36, 6. [Google Scholar]
- Oliveira, A.; Oliveira, J.F.; Pereira, J.M.; De Araújo, B.R.; Boavida, J. 3D modelling of laser scanned and photogrammetric data for digital documentation: The Mosteiro da Batalha case study. J. Real-Time Image Process. 2014, 9, 673–688. [Google Scholar] [CrossRef]
- Delaloye, D. Development of a New Methodology for Measuring Deformation in Tunnels and Shafts with Terrestrial Laser Scanning (LIDAR) Using Elliptical Fitting Algorithms. Master’s Thesis, Queen’s University, Kingston, ON, Canada, 2012. [Google Scholar]
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogram. Remote Sens. 2008, 63, 142–154. [Google Scholar] [CrossRef]
- Kim, M.K.; Kim, S.; Sohn, H.G.; Kim, N.; Park, J.S. A New Recursive Filtering Method of Terrestrial Laser Scanning Data to Preserve Ground Surface Information in Steep-Slope Areas. ISPRS Int. J. Geo-Inf. 2017, 6, 359. [Google Scholar] [CrossRef]
- Rosser, N.J.; Petley, D.N.; Lim, M.; Dunning, S.A.; Allison, R.J. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol. 2005, 38, 363–375. [Google Scholar] [CrossRef]
- Barbarella, M.; Di Benedetto, A.; Fiani, M.; Guida, D.; Lugli, A. Use of DEMs Derived from TLS and HRSI Data for Landslide Feature Recognition. ISPRS Int. J. Geo-Inf. 2018, 7, 160. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, J.; Lindenbergh, R.; Hofland, B.; Ferreira, V.G. Range Image Technique for Change Analysis of Rock Slopes Using Dense Point Cloud Data. Remote Sens. 2018, 10, 1792. [Google Scholar] [CrossRef]

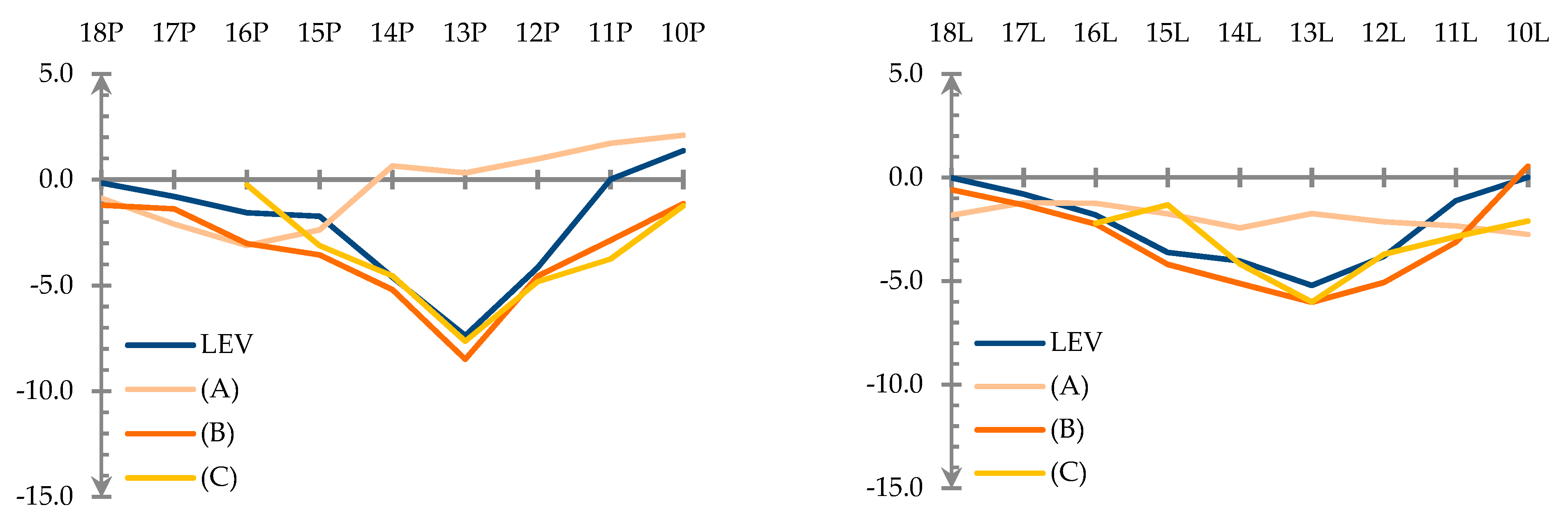
| Stage 1 | Tie Points | Georeference Data |  | |
| 1 | HDS targets |  | (X, Y) of points of the control network | |
| 2 | white sphere targets 2 |  | (X, Y) of sphere targets from the results of the 1st stage (H) of the centres of the sphere targets from precise levelling | |
| (1) | (2) | (3) | ||
|---|---|---|---|---|
| B&W Target Analysis | Point Cloud Analysis | Mesh Surface Analysis | ||
| Displacement determination method | Periodic comparison of changes in spatial positions of B&W targets of the controlled point network | Periodic differential models of point clouds of lower girder beams, vertical displacement analysis (dH) | Periodic differentiation of surface models of lower girder beams, vertical displacement analysis (dH) | |
| Reference | Tacheometry of the controlled point network | Precise levelling of structural protrusions of girders | Precise levelling of structural protrusions of girders | |
| Input datasets | (A) | Raw point clouds | ||
| (B) | Georeferenced point clouds | Georeferenced point clouds | Georeferenced point clouds | |
| (C) | Georeferenced and algorithm-filtered point clouds | Georeferenced and algorithm-filtered point clouds |
| MAE [m] | RMS [m] |  | |
| Before static loading | 0.001 | 0.001 | |
| During static loading | 0.001 | 0.001 |
| Displacement | Significance Level (α) | Cluster Size | Value of Statistic λ(D = sup| F1(TLS)—F2(TACH)|) | True Hypothesis |
|---|---|---|---|---|
| Along the OX axis | 0.01 | 1 mm | λ = 1.42 < λα1 = 1.63 | H0—good conformity of displacement in both samples |
| Along the OY axis | λ = 1.11 < λα1 = 1.63 | H0—good conformity of displacement in both samples | ||
| vertical | λ = 0.77 < λα1 = 1.63 | H0—good conformity of displacement in both samples | ||
| 1critical value of the statistic | ||||
| Datasets | |||
|---|---|---|---|
| (A) | (B) | (C) | |
| Raw point clouds | Georeferenced point clouds | Georeferenced and algorithm-filtered point clouds | |
| [mm] | ±2.4 | ±2.4 | ±2.4 |
| Parameters for assessing differences in displacement values, TLS vs. LEV [mm] | |||
| ±3.0 | ±1.0 | ±1.1 | |
| ±2.1 | ±0.8 | ±0.7 | |
| ±7.7 | ±2.0 | ±2.4 | |
| −1.1 | 0.8 | 0.3 | |
| Procedure, Input Datasets | Significance Level (α) | Rejection Interval | Value of Statistic | True Hypothesis |
|---|---|---|---|---|
| (2), (A) | 0.01 | [6.4078, ∞] | 28.1250 | Ha |
| (2), (B) | [6.4078, ∞] | 3.1250 | H0 | |
| (2), (C) | [4.1069, ∞] | 2.9410 | H0 | |
| 1a quantile of order 1-α from the Chi-Square distribution with k=n-1 degrees of freedom | ||||
| Datasets | ||
|---|---|---|
| (B) | (C) | |
| Georeferenced point clouds | Georeferenced and algorithm-filtered point clouds | |
| [mm] | ±2.4 | ±2.4 |
| Parameters for assessing differences in displacement values, TLS vs. LEV [mm] | ||
| ±6.9 | ±1.3 | |
| ±5.5 | ±0.8 | |
| ±12.5 | ±3.0 | |
| 3.3 | 0.3 | |
| Procedure, Input Datasets | Significance Level (α) | Rejection Interval | Value of Statistic | True Hypothesis |
|---|---|---|---|---|
| (3), (B) | 0.01 | [5.8122, ∞] | 140.5156 | Ha |
| (3), (C) | [5.2293, ∞] | 4.6944 | H0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gawronek, P.; Makuch, M. TLS Measurement during Static Load Testing of a Railway Bridge. ISPRS Int. J. Geo-Inf. 2019, 8, 44. https://doi.org/10.3390/ijgi8010044
Gawronek P, Makuch M. TLS Measurement during Static Load Testing of a Railway Bridge. ISPRS International Journal of Geo-Information. 2019; 8(1):44. https://doi.org/10.3390/ijgi8010044
Chicago/Turabian StyleGawronek, Pelagia, and Maria Makuch. 2019. "TLS Measurement during Static Load Testing of a Railway Bridge" ISPRS International Journal of Geo-Information 8, no. 1: 44. https://doi.org/10.3390/ijgi8010044
APA StyleGawronek, P., & Makuch, M. (2019). TLS Measurement during Static Load Testing of a Railway Bridge. ISPRS International Journal of Geo-Information, 8(1), 44. https://doi.org/10.3390/ijgi8010044






